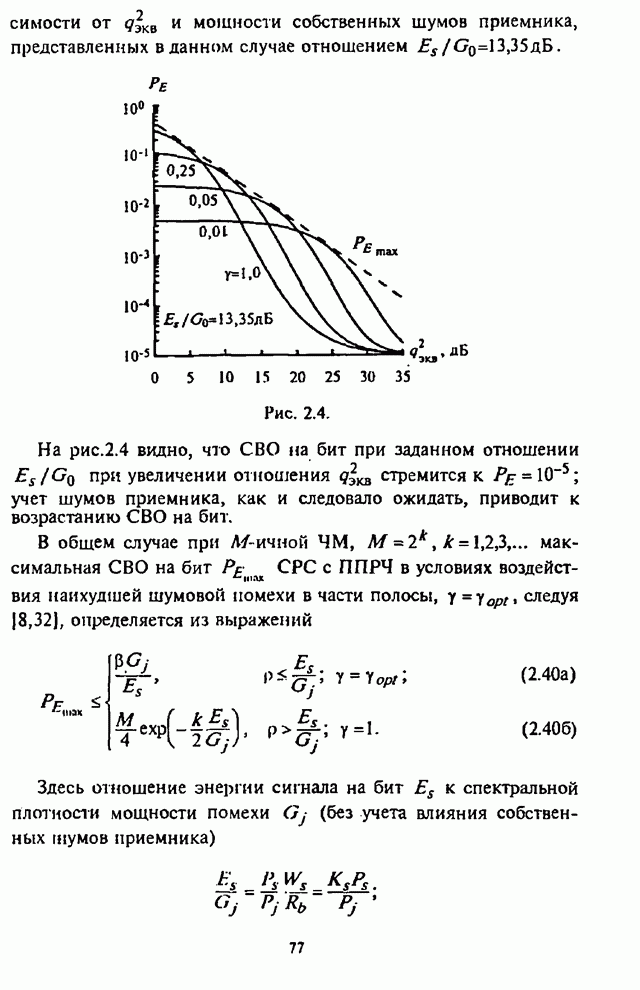
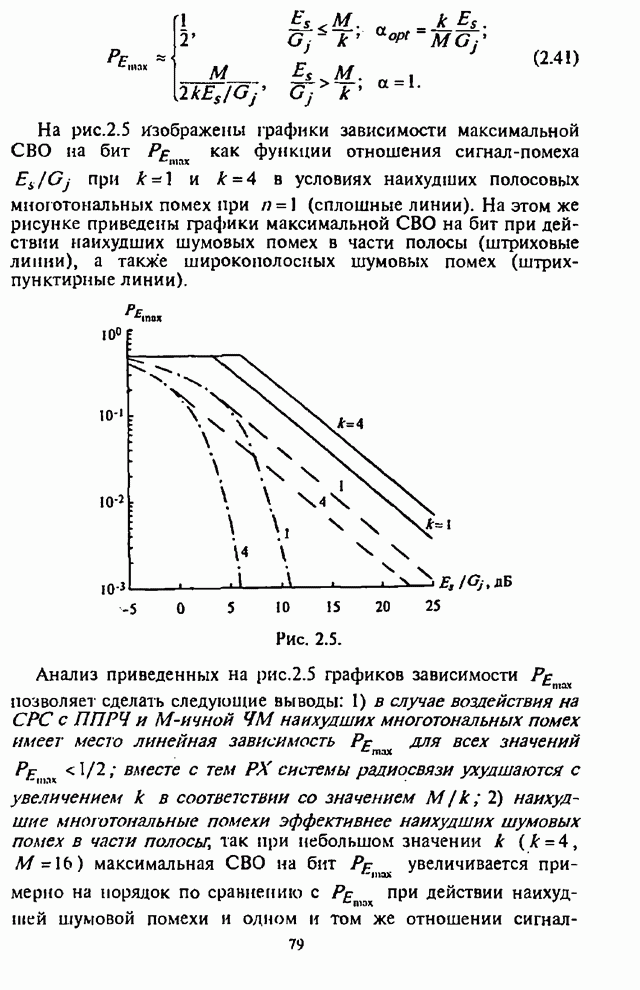
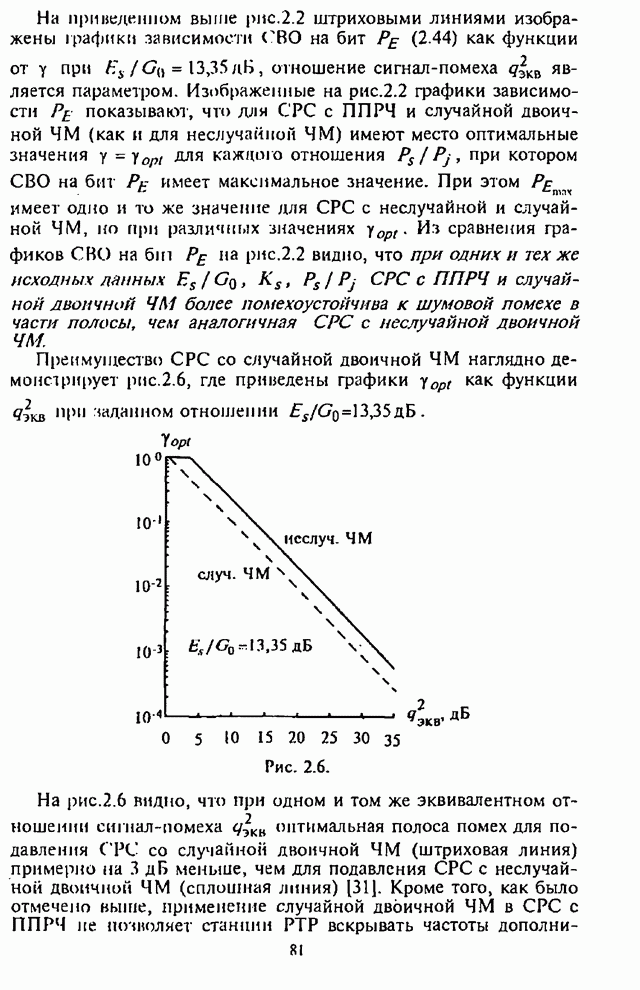
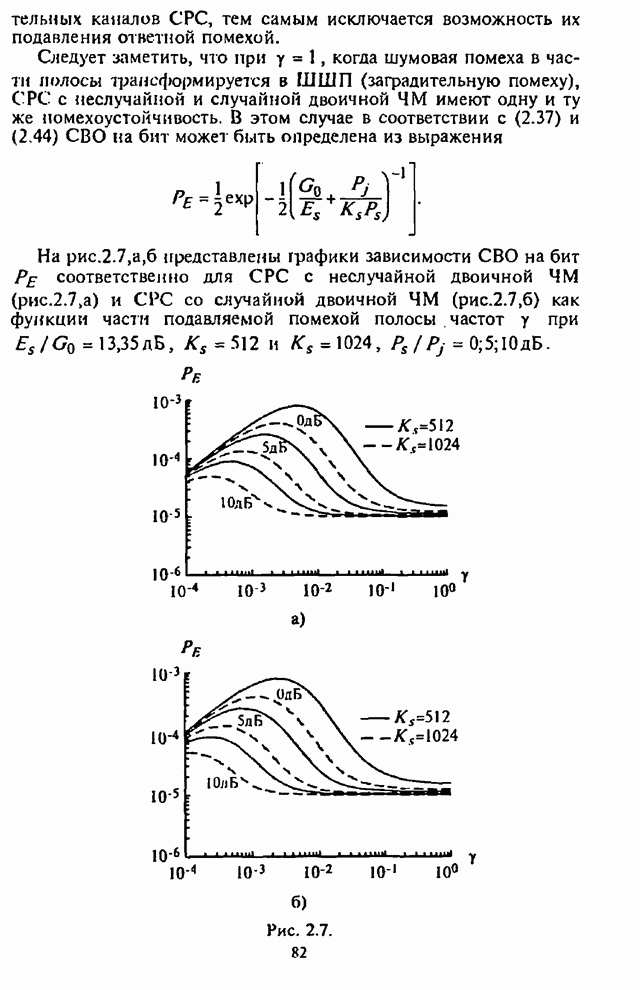
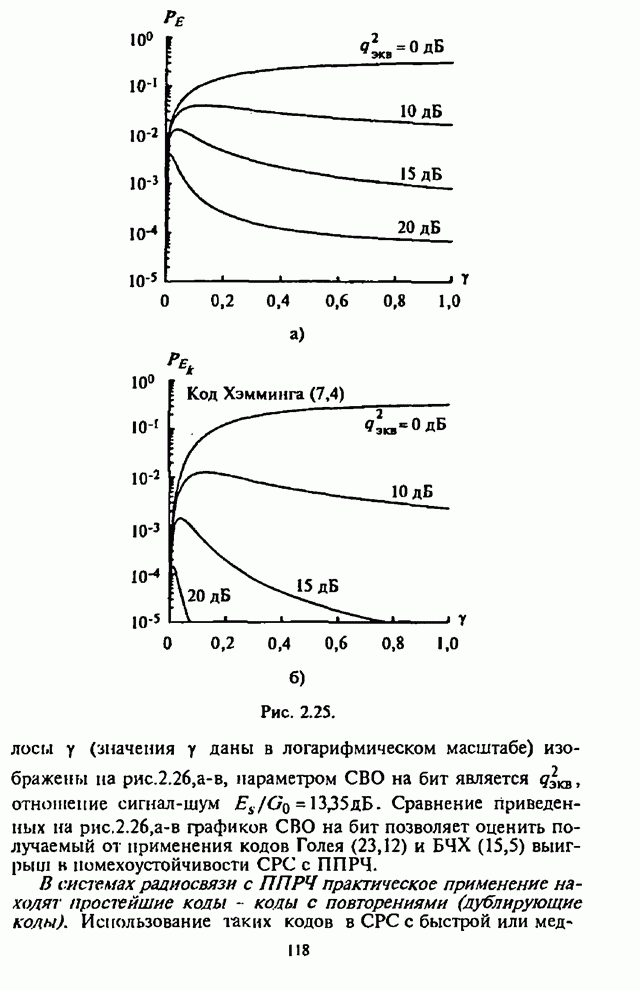
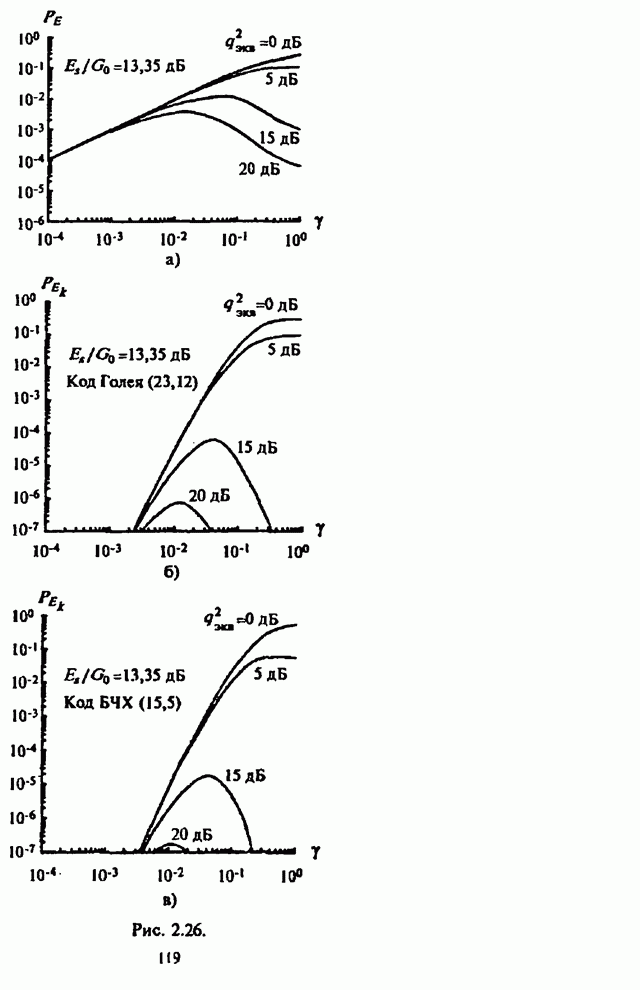
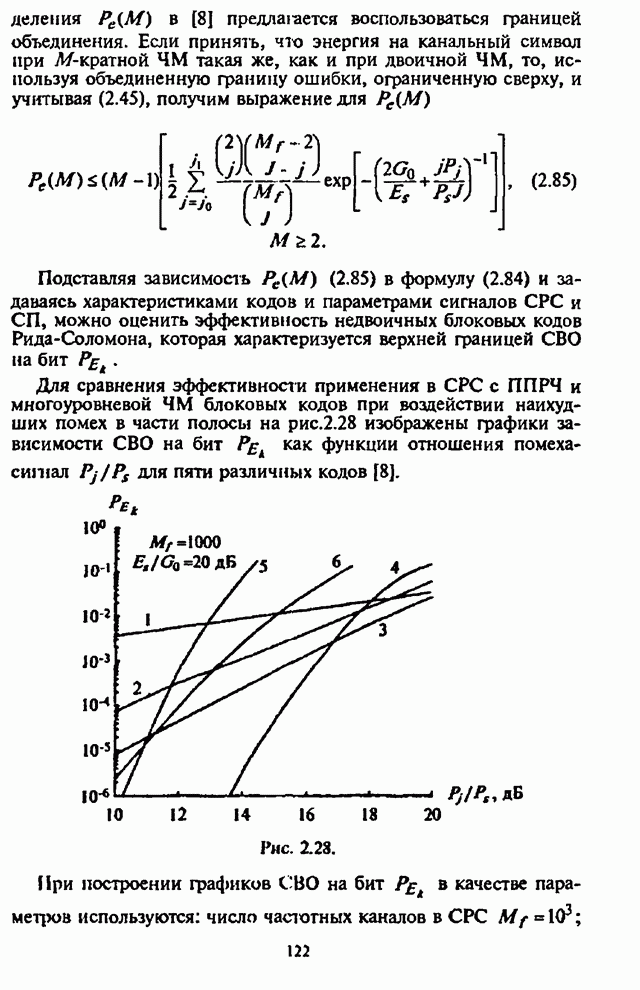
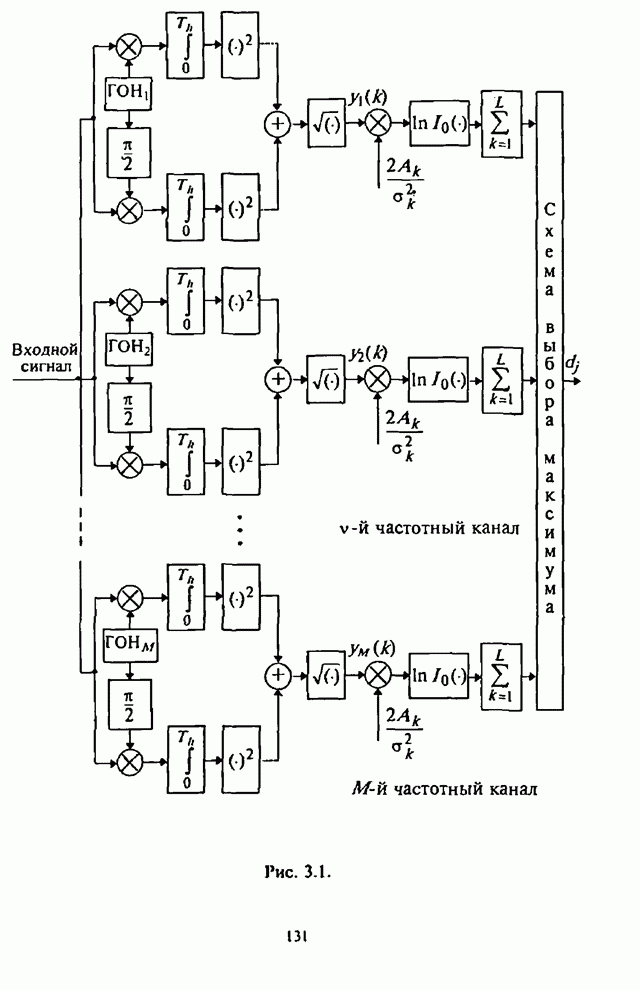
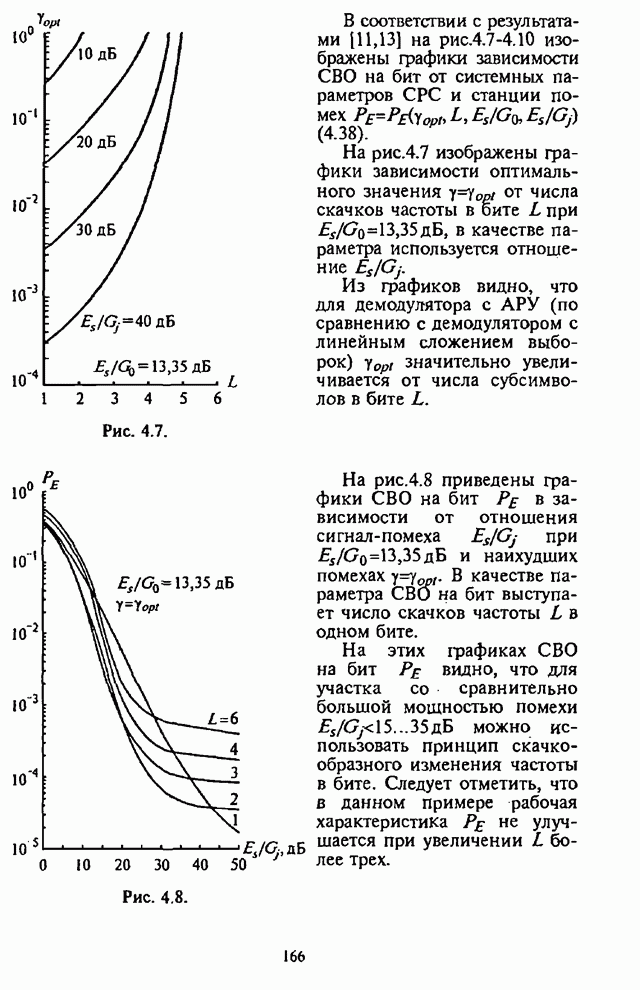
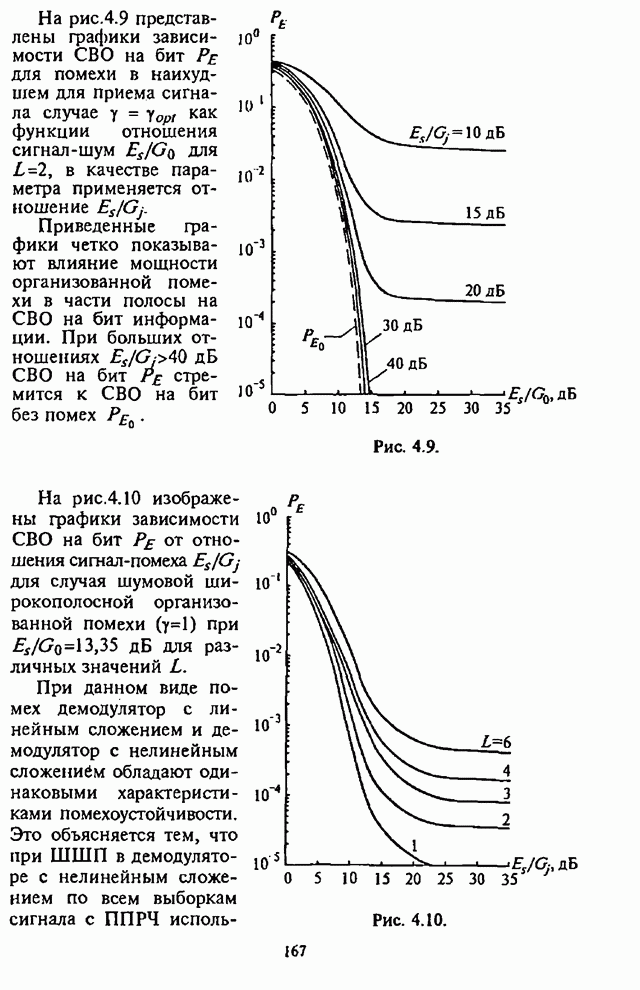
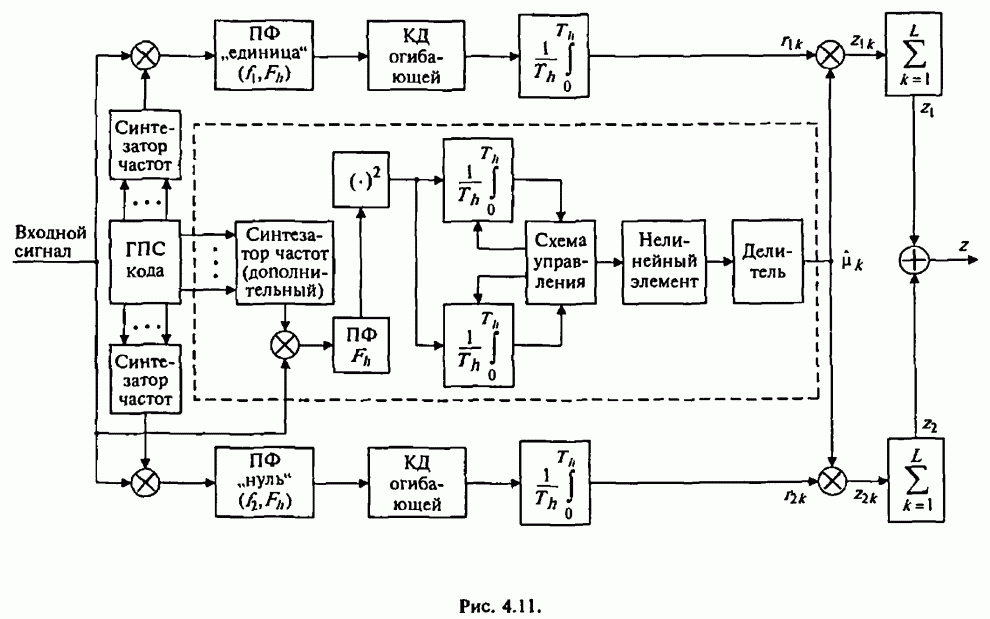
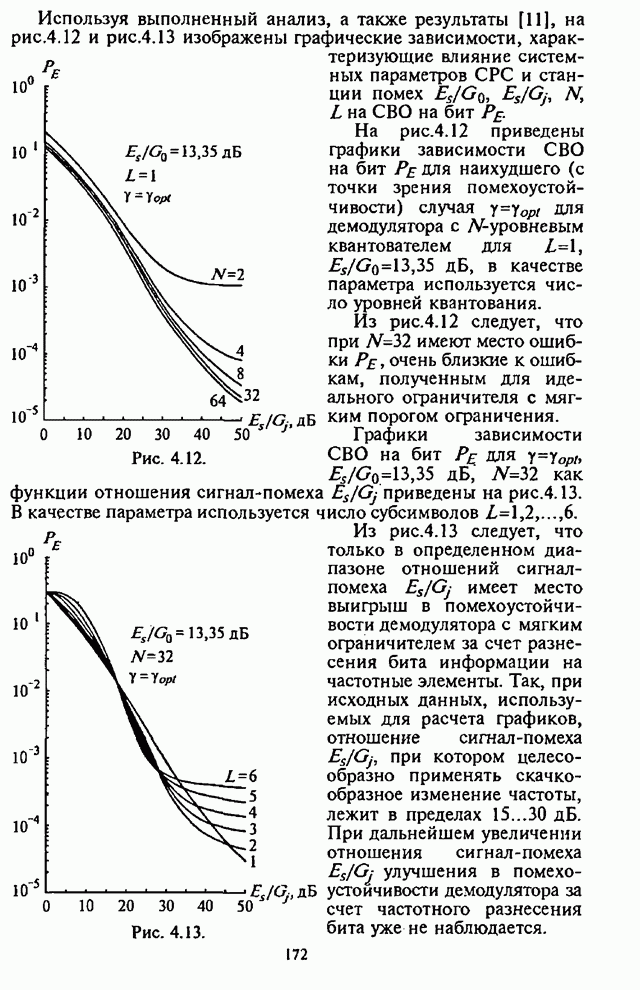
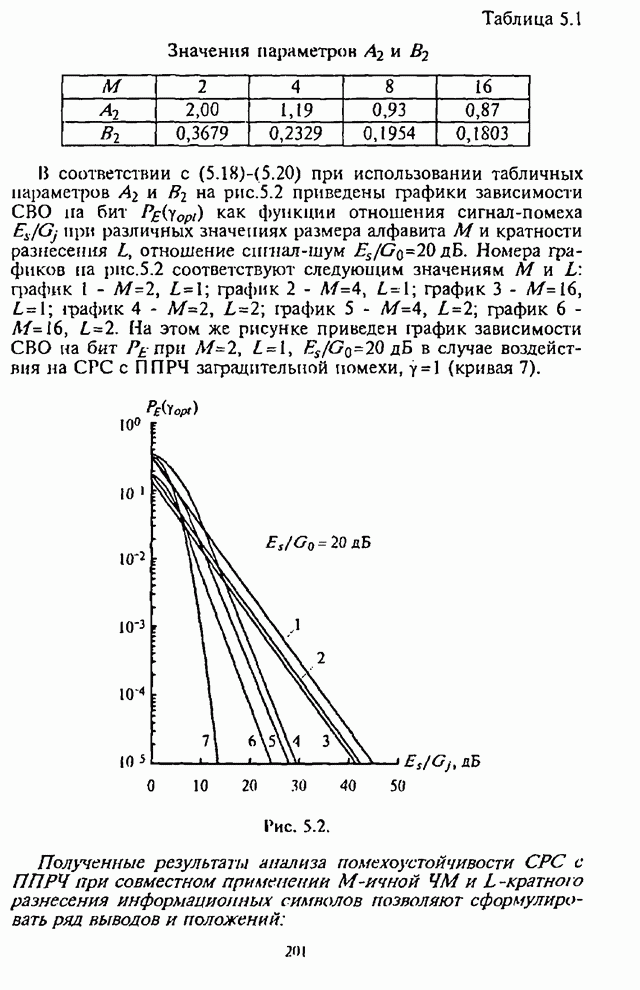
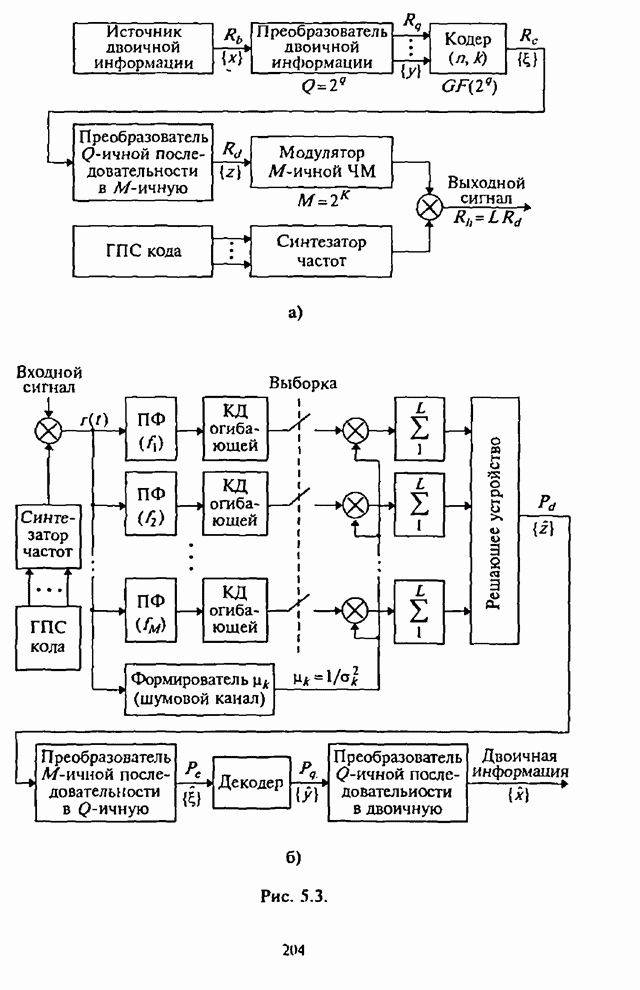
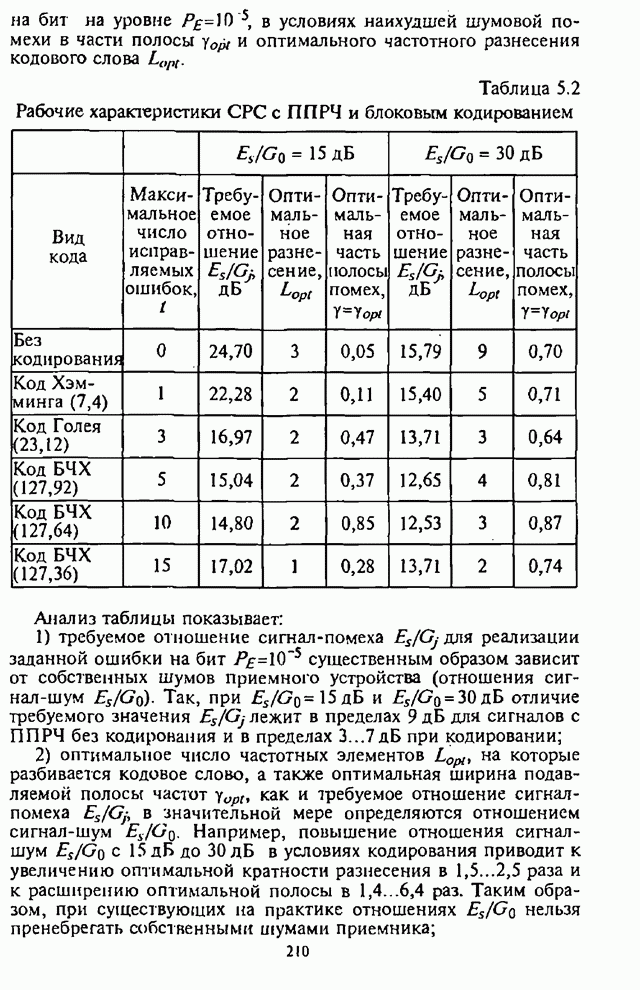
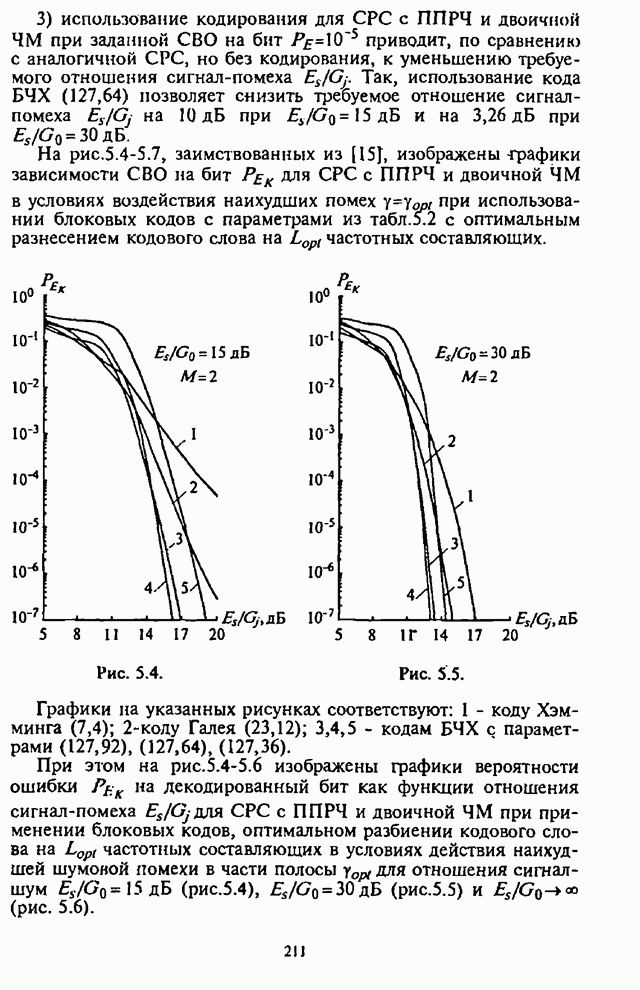
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
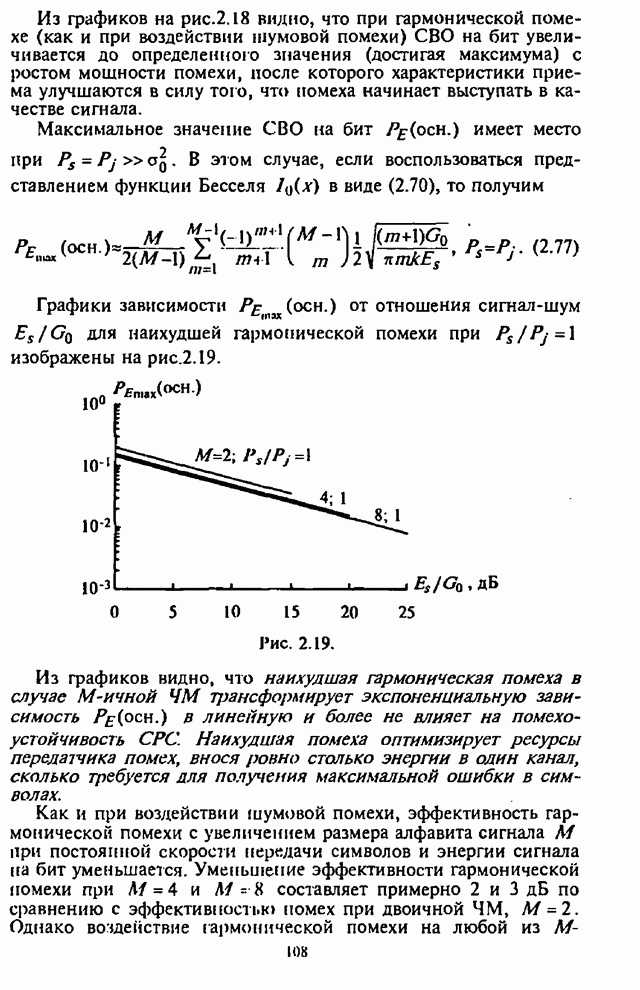
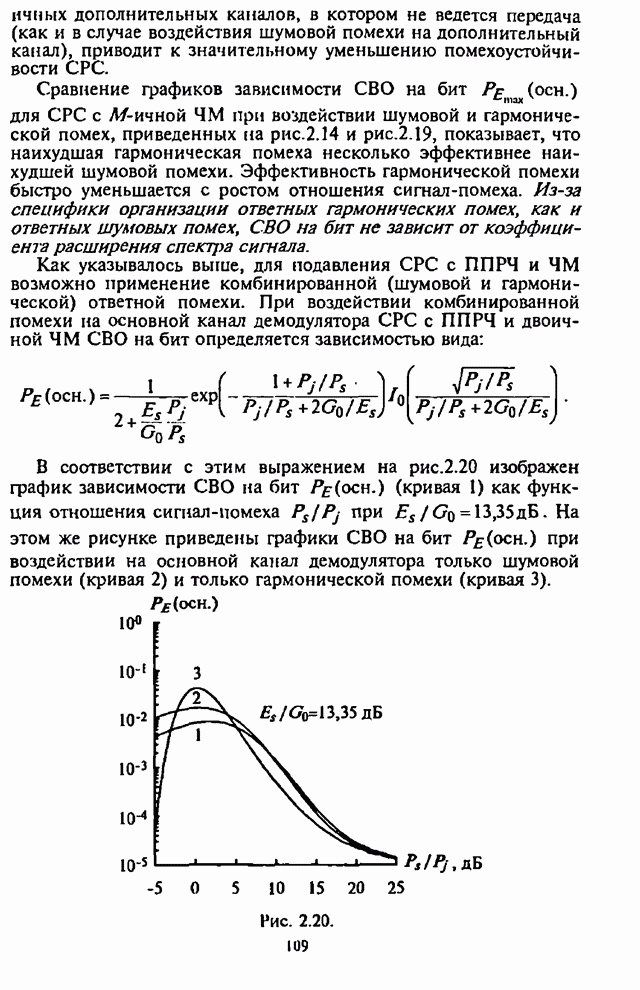
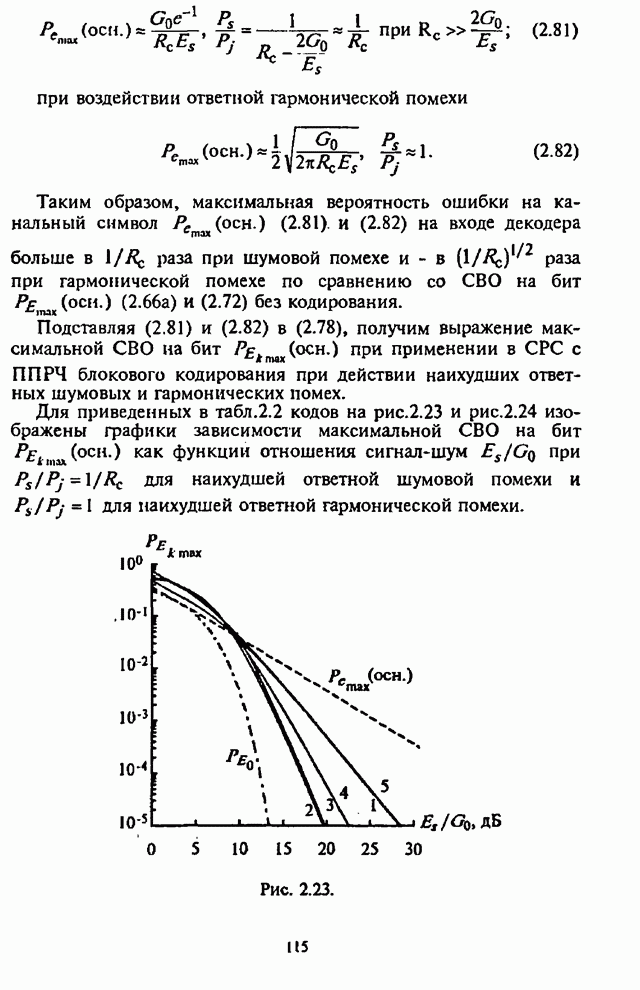
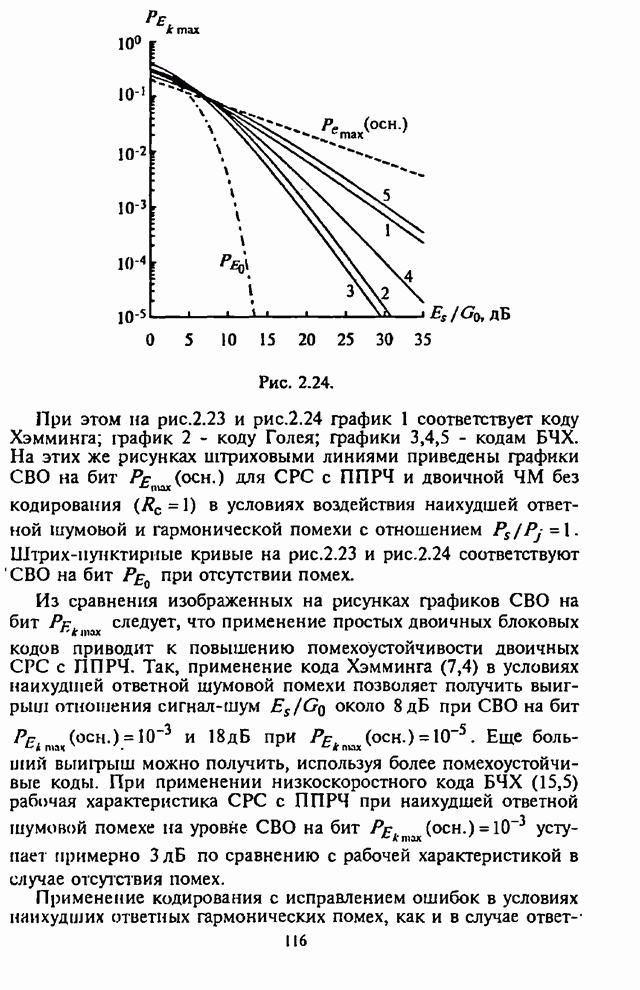
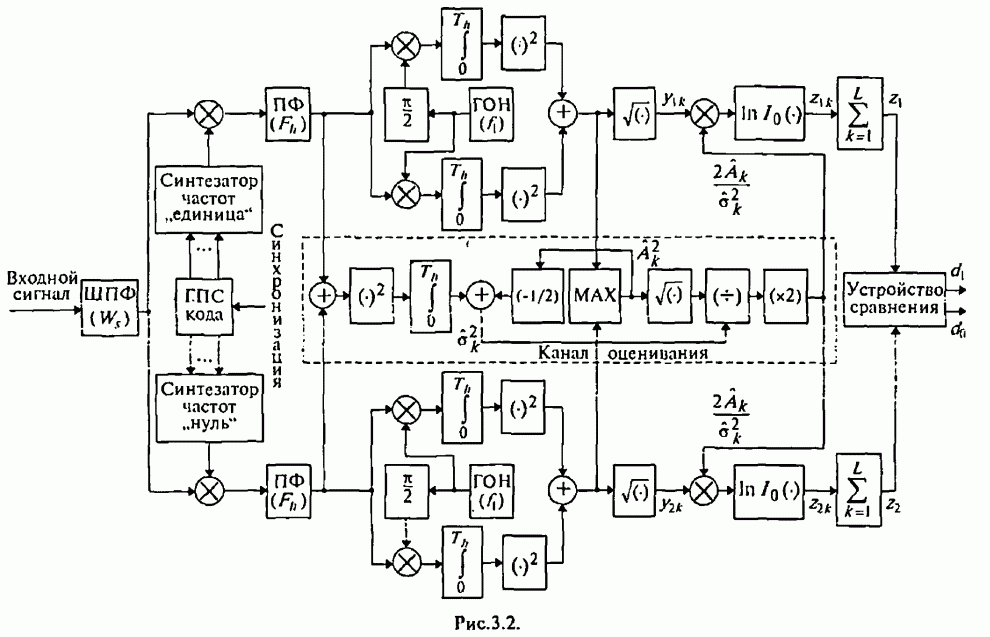
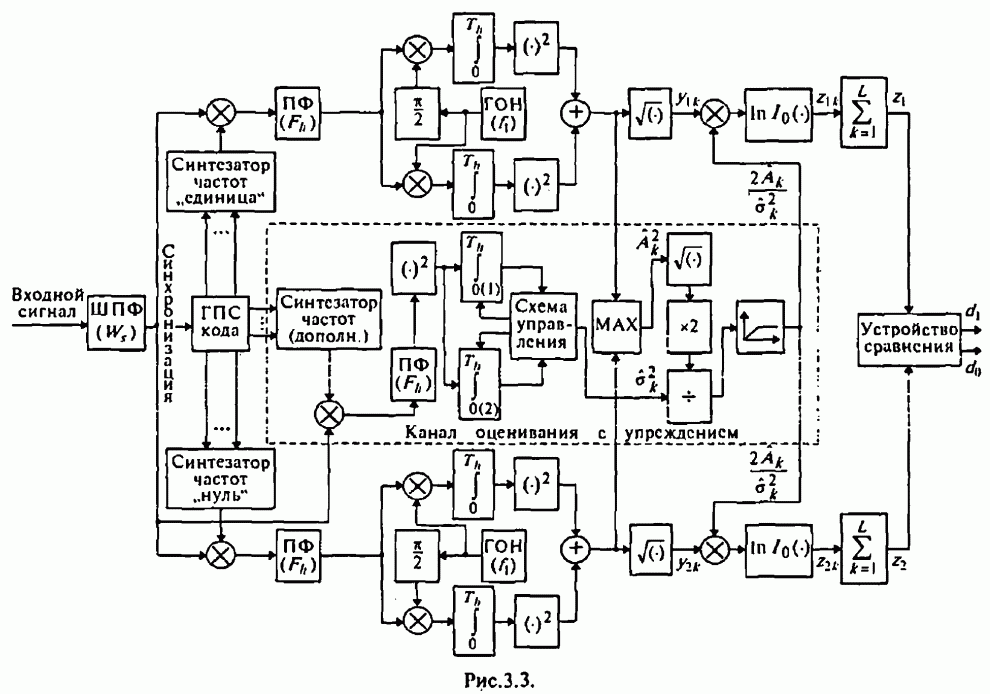
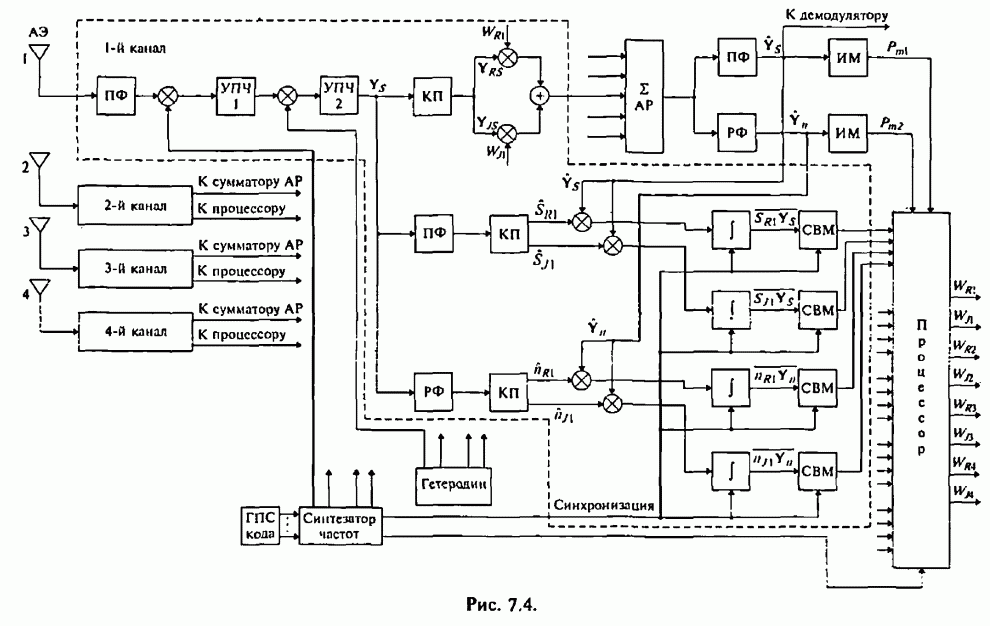
7.2. Максиминный алгоритм обработки сигналов и помех
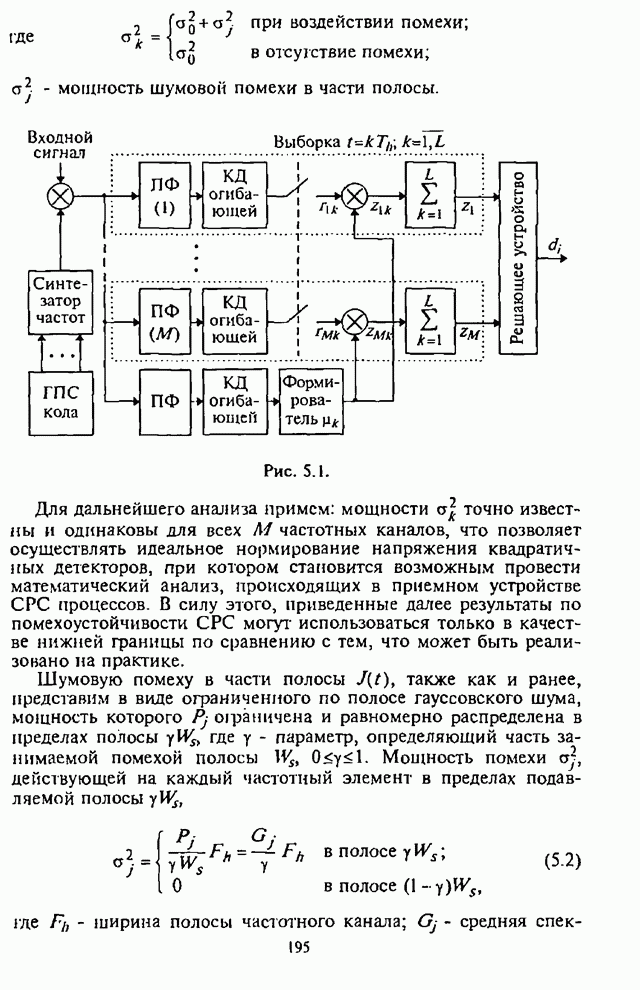
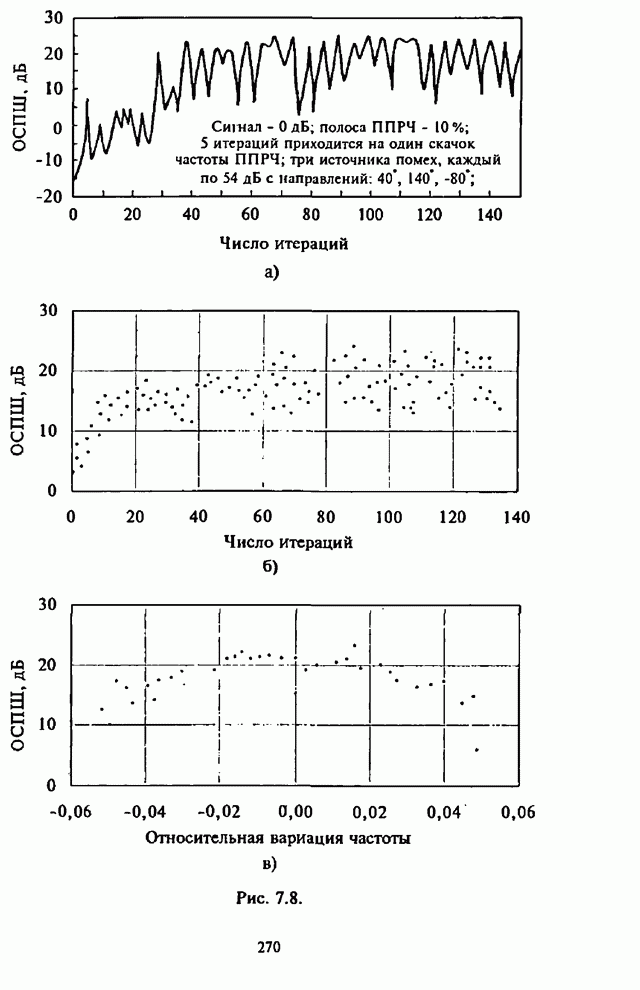
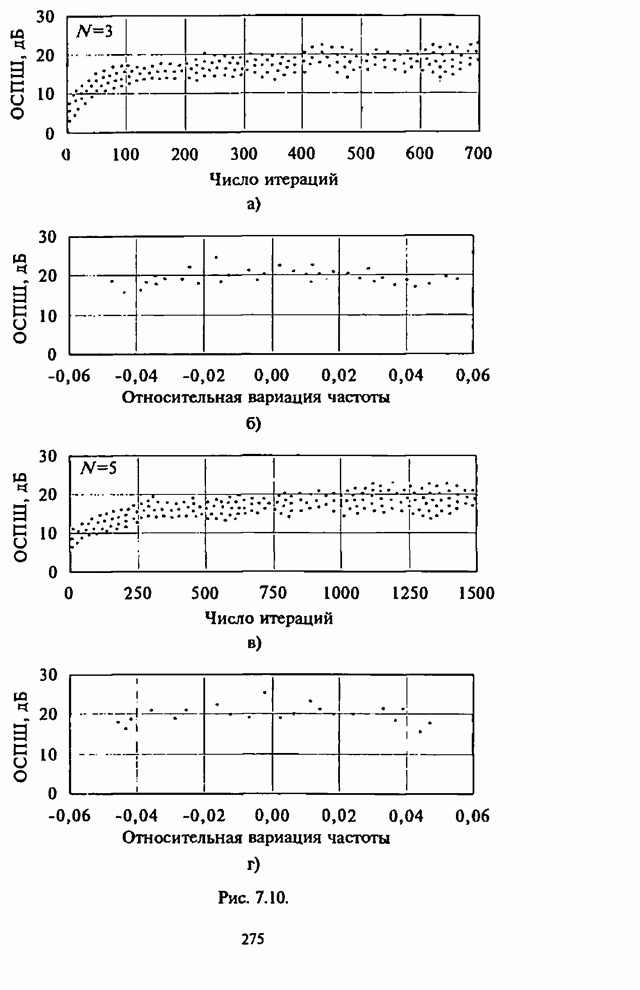
Уменьшение отрицательного влияния приведенных выше нежелательных последствий, возникающих при совместном использовании сигналов с ППРЧ и ААР, позволяет обеспечить разработанный в [77-80] максиминный алгоритм, который при скачках частоты достаточно быстро восстанавливает способность подавления помех.
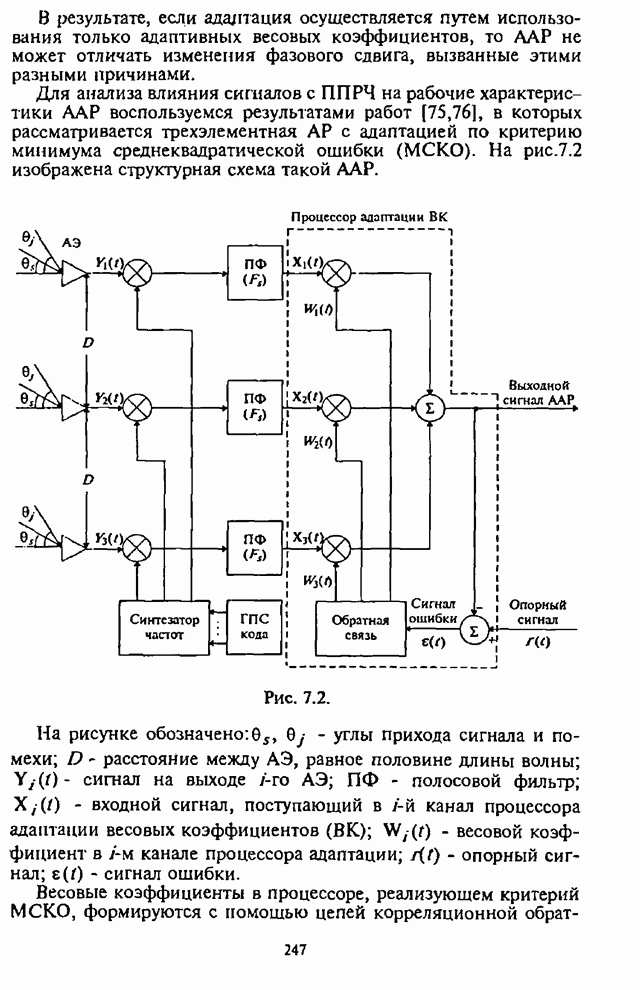
Алгоритм назван максиминным потому, что он максимизирует ОСПШ посредством итеративной регулировки ВК с помощью двух корреляторов, один из которых используется для максимизации мощности полезного сигнала, а другой - для минимизации мощности помехи. Ниже кратко рассматривается сущность максиминного алгоритма и его возможности.
При этом предполагается, что полезный сигнал и помеха являются стационарными стохастическими процессами.
Если
![]() - вектор ВК
адаптивной антенной решетки, a
- вектор ВК
адаптивной антенной решетки, a ![]() и
и ![]() - вектор полезного сигнала и вектор
помеха+шум на входах АЭ, то сигнальную
- вектор полезного сигнала и вектор
помеха+шум на входах АЭ, то сигнальную ![]() и помеховую
и помеховую ![]() составляющие на выходе ААР можно
представить в виде:
составляющие на выходе ААР можно
представить в виде:
![]() ; (7.34)
; (7.34)
![]() . (7.35)
. (7.35)
Мощность выходного полезного сигнала при детерминированном векторе ВК определяется из выражения
![]() , (7.36)
, (7.36)
где
![]() - символ
транспонирования и комплексного сопряжения;
- символ
транспонирования и комплексного сопряжения; ![]() - корреляционная матрица вектора
полезного сигнала
- корреляционная матрица вектора
полезного сигнала ![]() ,
,
![]() . (7.37)
. (7.37)
Выражение для мощности составляющей помеха+шум на выходе ААР имеет вид:
![]() , (7.38)
, (7.38)
где
![]() -
корреляционная матрица вектора помеха+шум
-
корреляционная матрица вектора помеха+шум ![]() ,
,
![]() . (7.39)
. (7.39)
Следовательно, выходное ОСПШ будет определяться равенством
 . (7.40)
. (7.40)
С целью максимизации ОСПШ на выходе ААР применяется градиентный алгоритм корректировки весовых коэффициентов, который для дискретно-временных систем имеет вид [74,77]:
![]() , (7.41)
, (7.41)
где
![]() - текущие
моменты дискретизации;
- текущие
моменты дискретизации; ![]() - константа, регулирующая скорость
сходимости алгоритма;
- константа, регулирующая скорость
сходимости алгоритма; ![]() - градиент.
- градиент.
Вектор
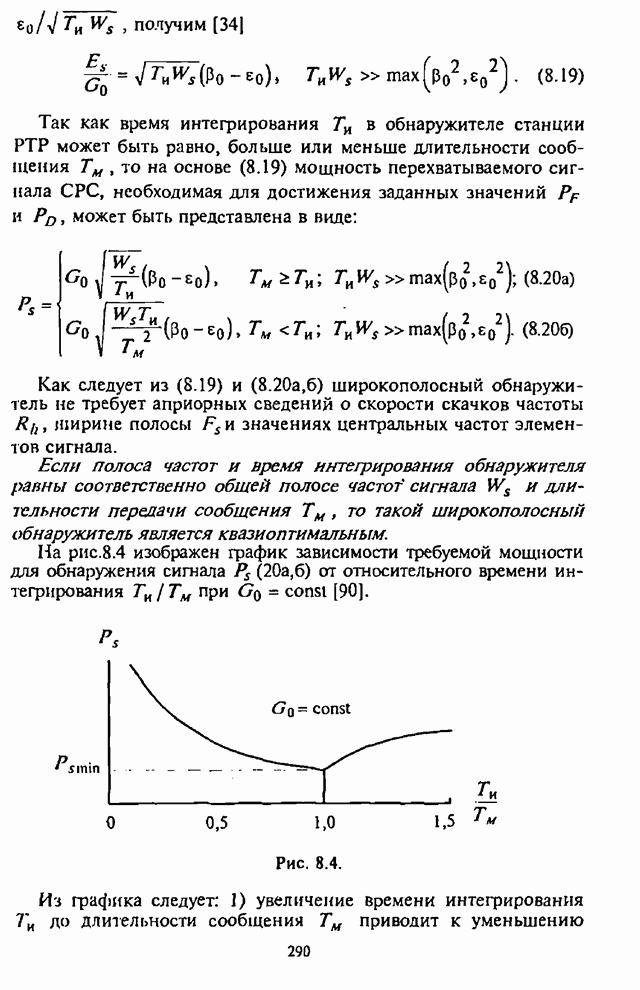
ВК в терминах действительной ![]() и мнимой
и мнимой ![]() составляющих имеет вид:
составляющих имеет вид:
![]() . (7.42)
. (7.42)
Градиент
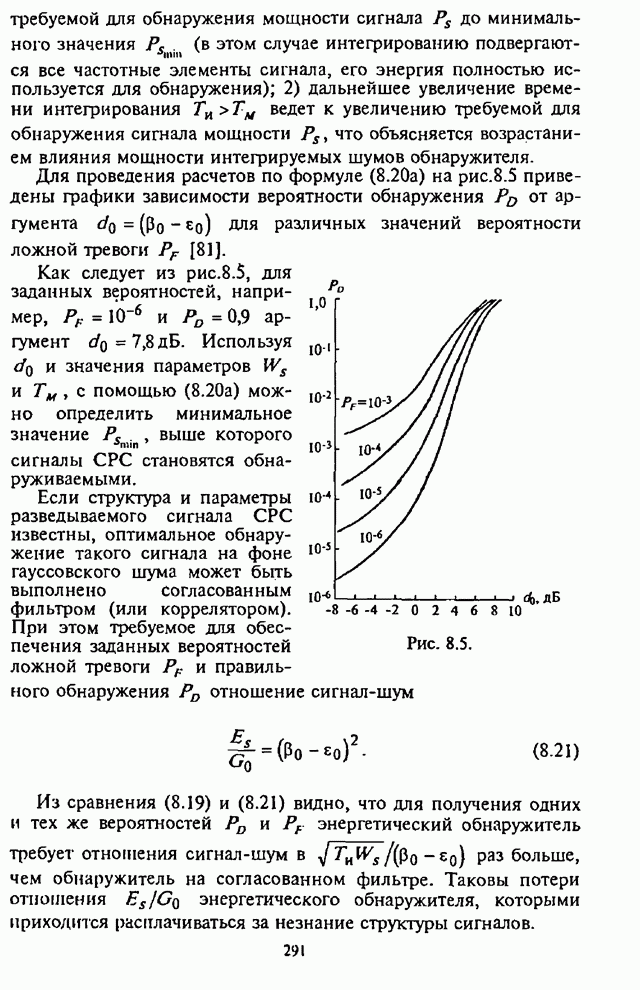
![]() в (7.41),
соответствующий данному вектору ВК
в (7.41),
соответствующий данному вектору ВК ![]() , так же может быть представлен в
комплексной форме
, так же может быть представлен в
комплексной форме
![]() . (7.43)
. (7.43)
Непосредственное
вычисление градиента ![]() с
учётом (7.36) и (7.38) приводит к следующему выражению
с
учётом (7.36) и (7.38) приводит к следующему выражению
 . (7.44)
. (7.44)
На
основе (7.44) уравнение для вектора ВК ![]() может быть представлено в виде:
может быть представлено в виде:
 . (7.45)
. (7.45)
Заметим,
что если полезный сигнал и помеха представляют собой узкополосные процессы, то ![]() является постоянной
величиной, а правая часть уравнения (7.45) линейна относительно
является постоянной
величиной, а правая часть уравнения (7.45) линейна относительно ![]() .
.
Входящие
в (7.45) составляющие ![]() и
и ![]() могут быть записаны в виде следующих
выражений:
могут быть записаны в виде следующих
выражений:
![]() ; (7.46)
; (7.46)
![]() ; (7.47)
; (7.47)
где
![]() и
и ![]() - действительные
составляющие сигнала
- действительные
составляющие сигнала ![]() и
помехи
и
помехи ![]() ,
представленных в комплексной форме
,
представленных в комплексной форме
![]() ; (7.48)
; (7.48)
![]() . (7.49)
. (7.49)
В
максиминном алгоритме математические ожидания ![]() и
и ![]() оцениваются на
оцениваются на ![]() -й итерации нулём усреднения по
времени на конечных интервалах, что обозначим как
-й итерации нулём усреднения по
времени на конечных интервалах, что обозначим как ![]() и
и ![]() .
.
Используя эти оценочные значения, выражение (7.45) можно записать в виде:
 , (7.50)
, (7.50)
где
![]() - оценки
мощности сигнала
- оценки
мощности сигнала ![]() и
мощности помехи
и
мощности помехи ![]() на
на
![]() -й итерации;
-й итерации; ![]() ;
; ![]() - оценка ОСПШ на
- оценка ОСПШ на ![]() -й итерации.
-й итерации.
Вектор
полезного сигнала ![]() и
вектор помеха+шум
и
вектор помеха+шум ![]() на
входе АЭ могут быть представлены через действительную и мнимую составляющие
на
входе АЭ могут быть представлены через действительную и мнимую составляющие
![]() ; (7.51)
; (7.51)
![]() . (7.52)
. (7.52)
С
учётом соотношений (7.50)-(7.52) можно записать действительную ![]() и мнимую
и мнимую ![]() составляющие вектора
ВК в виде:
составляющие вектора
ВК в виде:
 , (7.53)
, (7.53)
 . (7.54)
. (7.54)
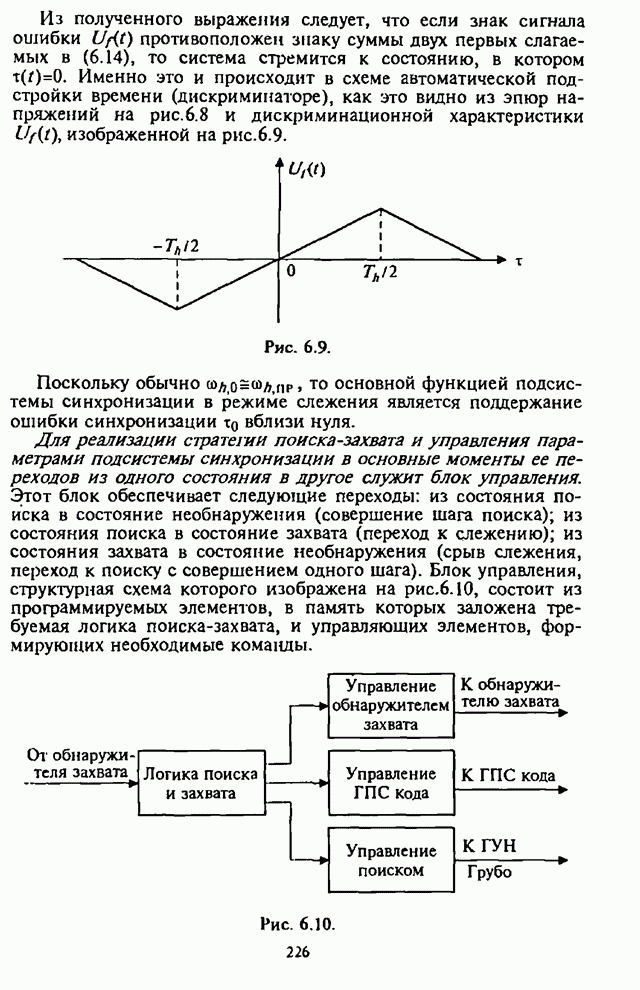
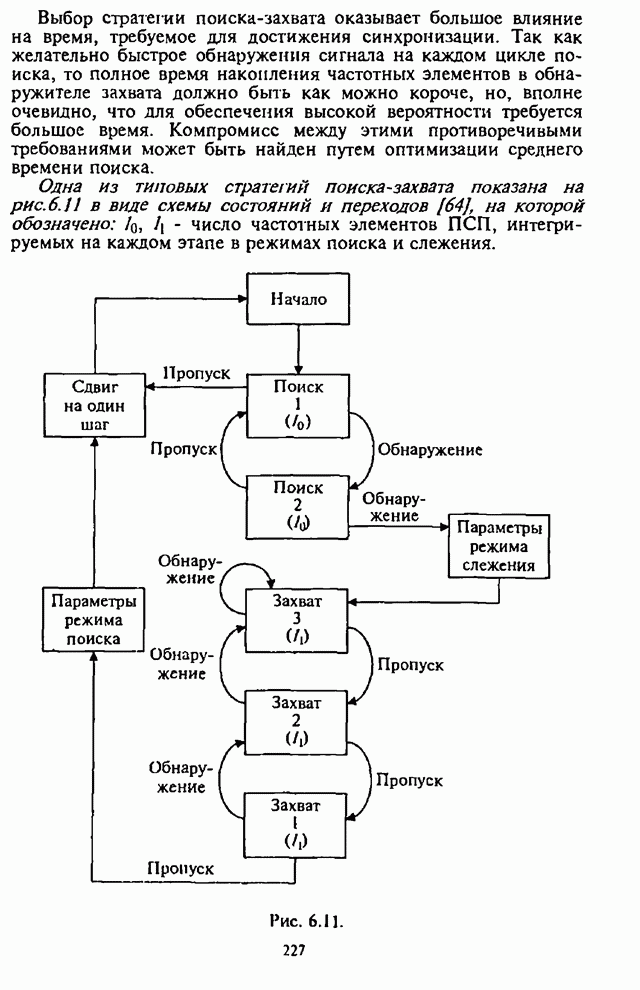
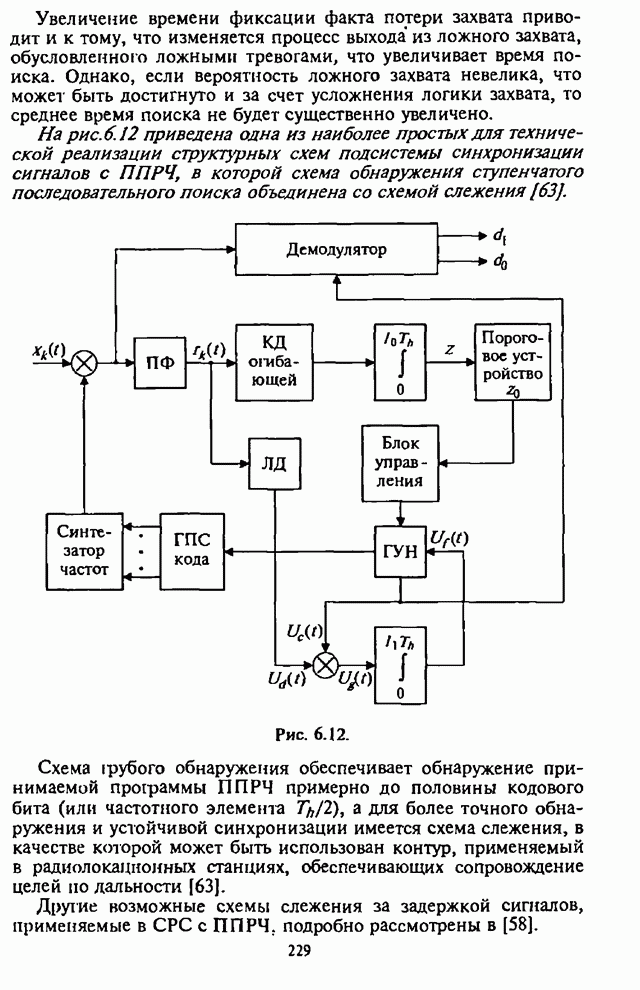
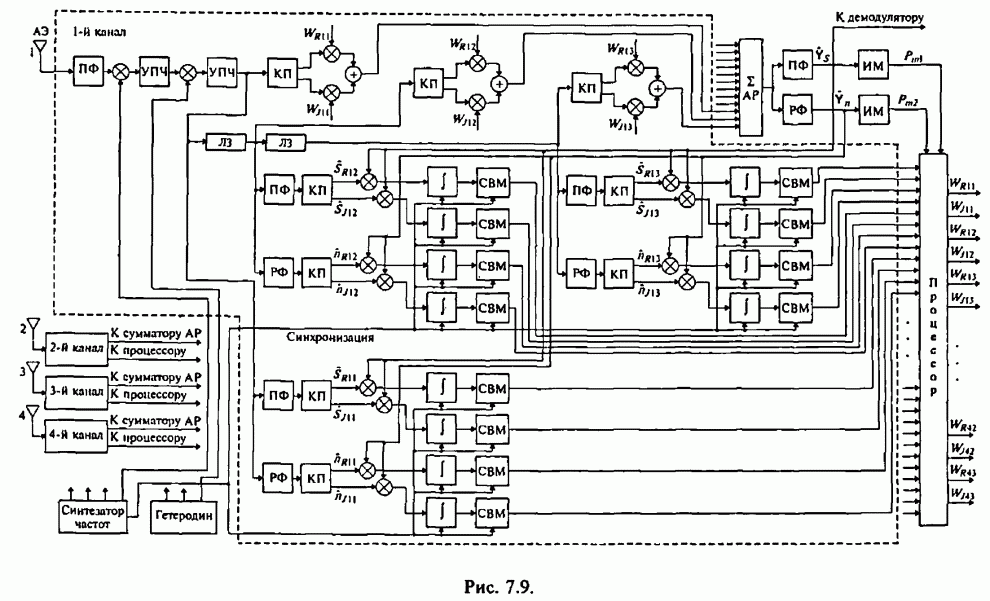
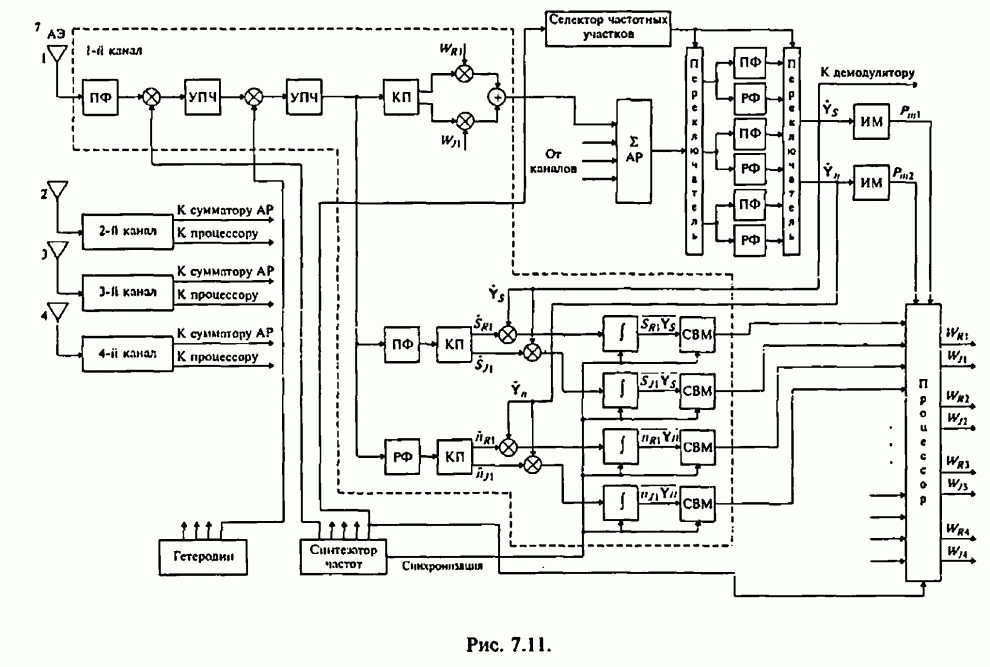
Полученные выше соотношения (7.53) и (7.54), описывающие действительную и мнимую части вектора ВК, лежат в основе реализации максиминного алгоритма.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие
- Введение
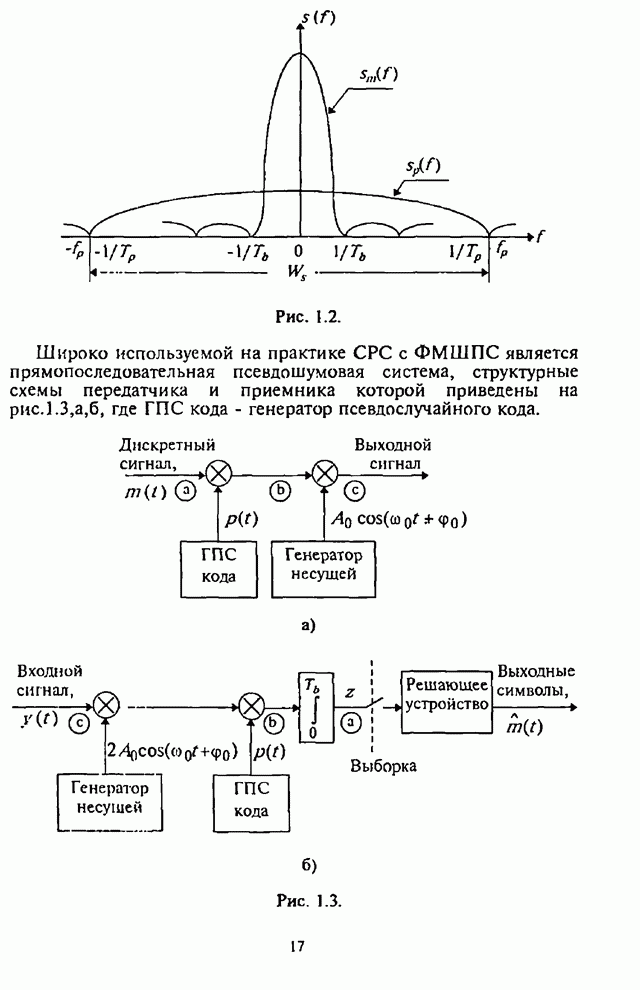
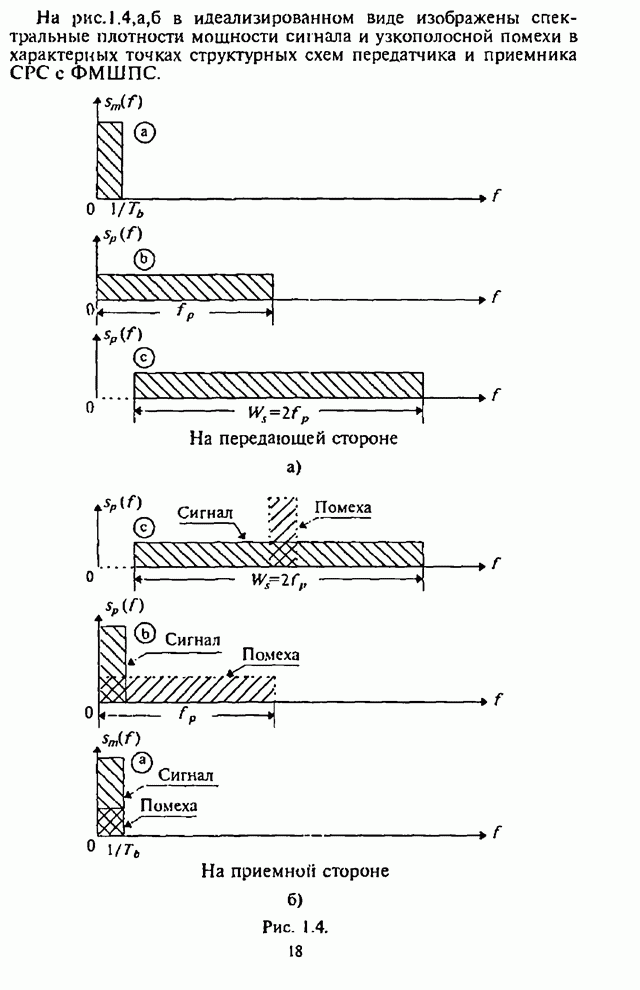
- Глава 1. Системы радиосвязи с расширением спектра сигналов методом псевдослучайной перестройки рабочей частоты: общие принципы
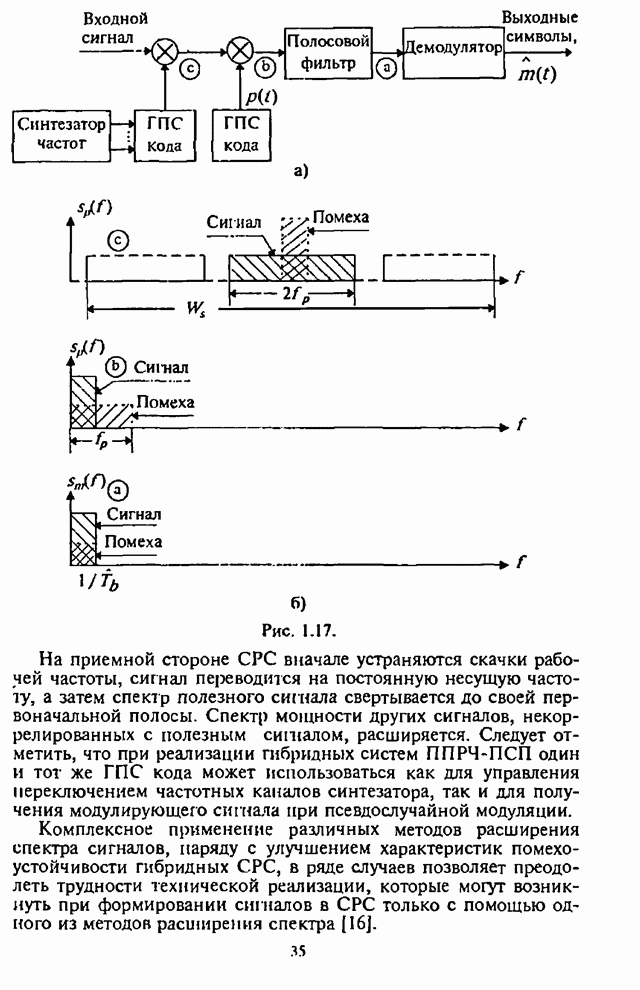
- 1.1. Краткая характеристика расширения спектра сигналов методом ППРЧ
- 1.1.1. Основные принципы и методы расширения спектра сигналов
- 1.1.2. Метод псевдослучайной перестройки рабочей частоты
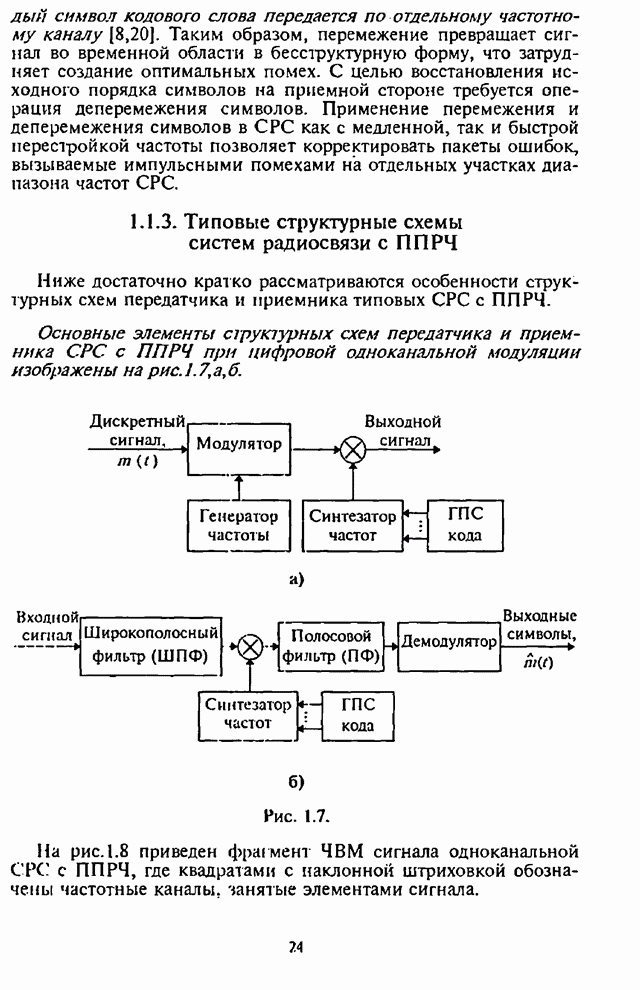
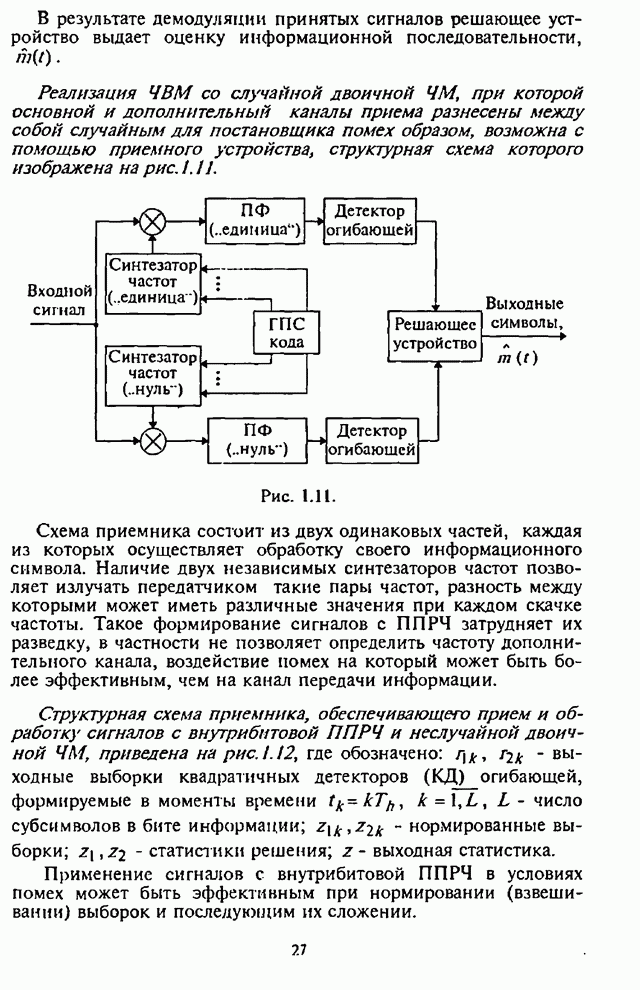
- 1.1.3. Типовые структурные схемы систем радиосвязи с ППРЧ
- 1.2. Коэффициент расширения спектра сигнала и запас помехоустойчивости системы радиосвязи с ППРЧ
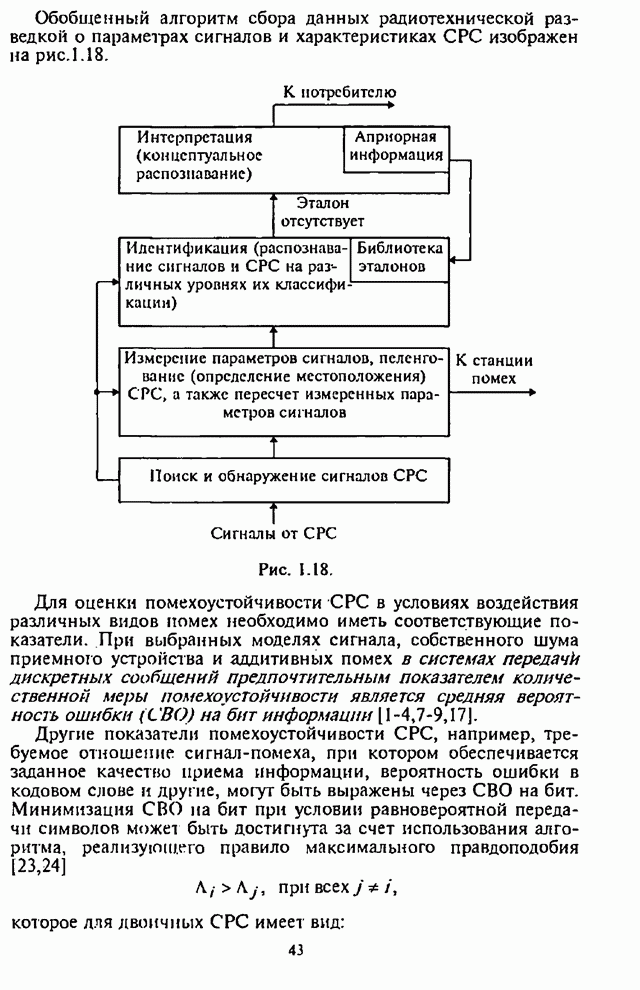
- 1.3. Общая характеристика помехозащищенности систем радиосвязи с ППРЧ
- 1.3.1. Помехоустойчивость систем радиосвязи с ППРЧ
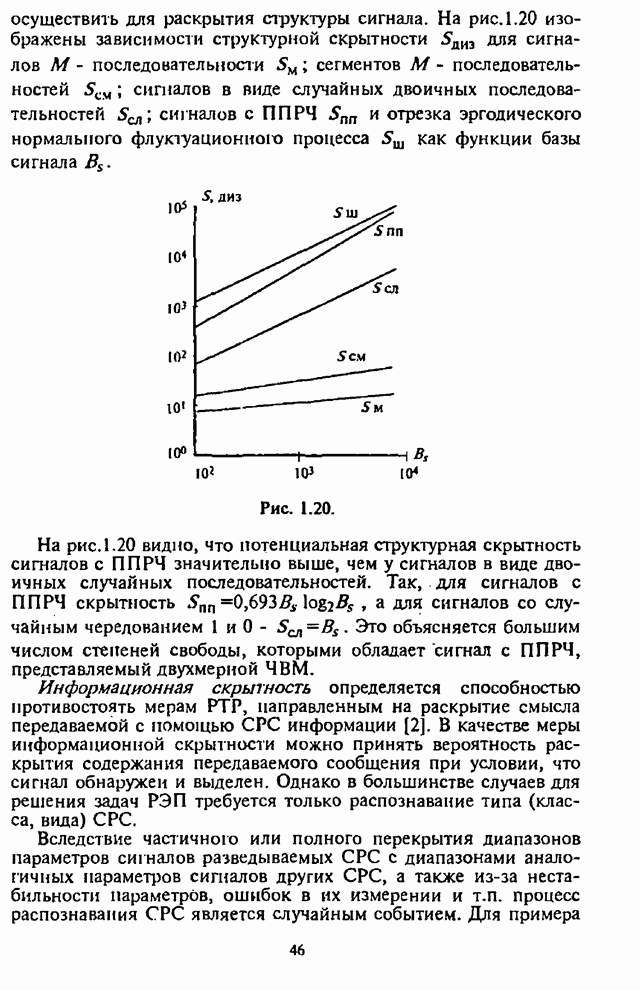
- 1.3.2. Скрытность сигналов систем радиосвязи с ППРЧ
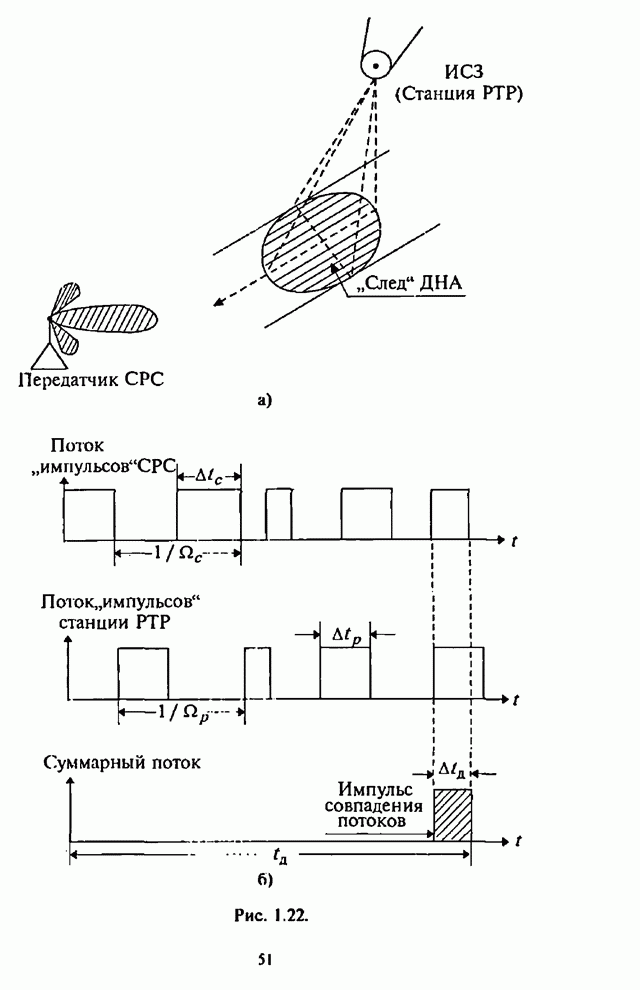
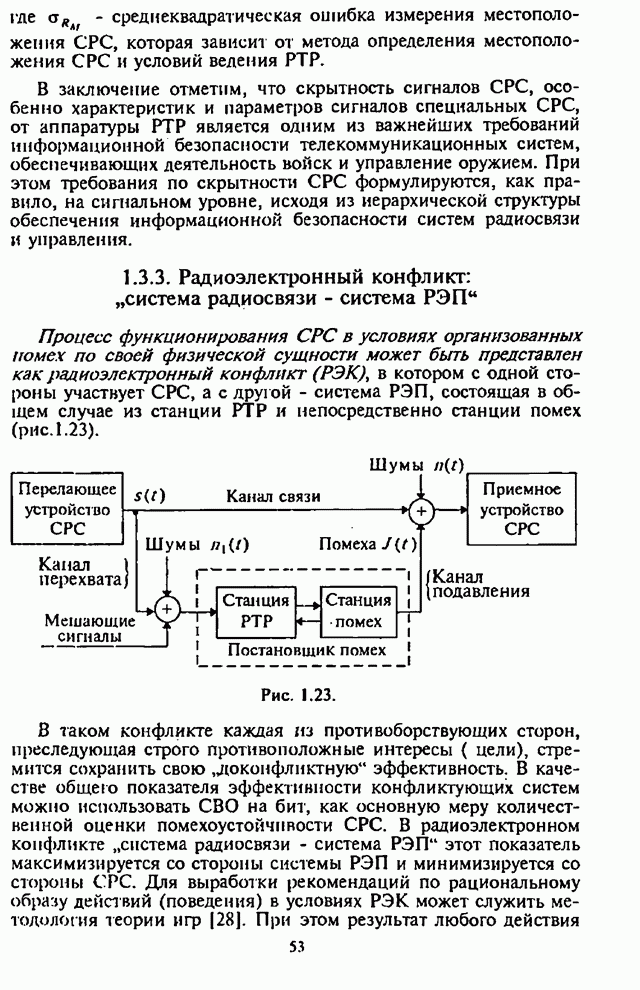
- 1.3.3. Радиоэлектронный конфликт: «система радиосвязи — система РЭП»
- 1.4. Модели и краткая характеристика основных видов помех
- Глава 2. Помехоустойчивость типовых систем радиосвязи с ППРЧ и частотной манипуляцией
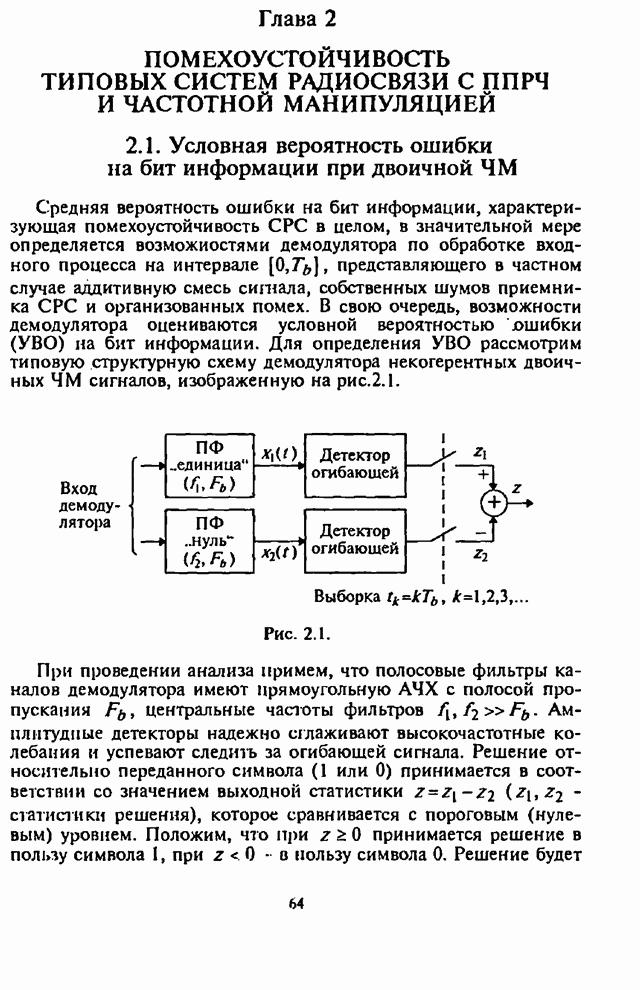
- 2.1. Условная вероятность ошибки на бит информации при двоичной ЧМ
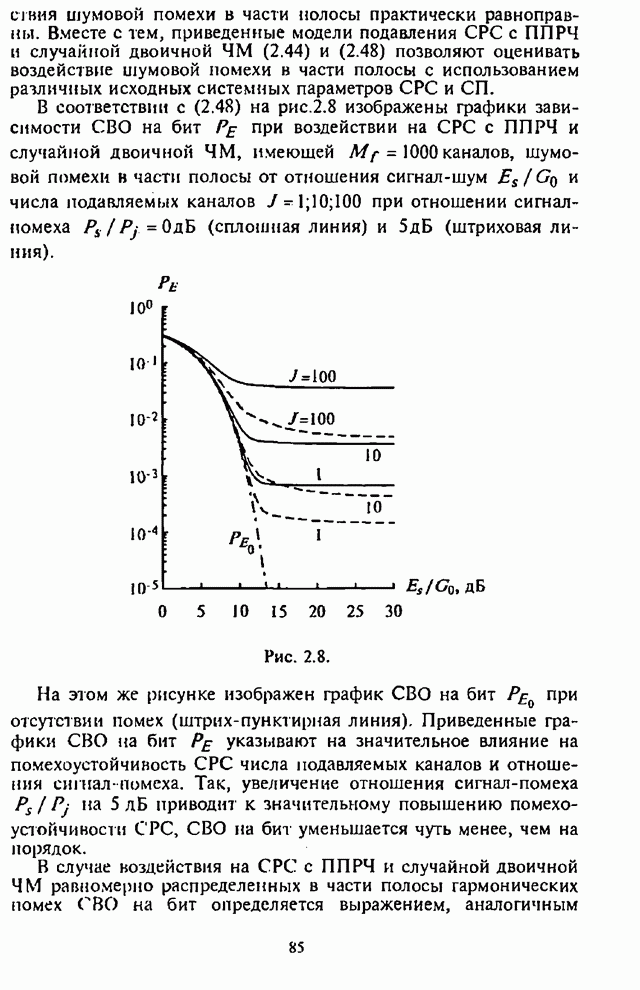
- 2.2. Оценка воздействия шумовой помехи в части полосы на системы радиосвязи с ППРЧ и неслучайной ЧМ
- 2.3. Оценка воздействия шумовой помехи в части полосы на системы радиосвязи с ППРЧ и случайной двоичной ЧМ
- 2.4. Оценка воздействия ответных помех на системы радиосвязи с ППРЧ и ЧМ
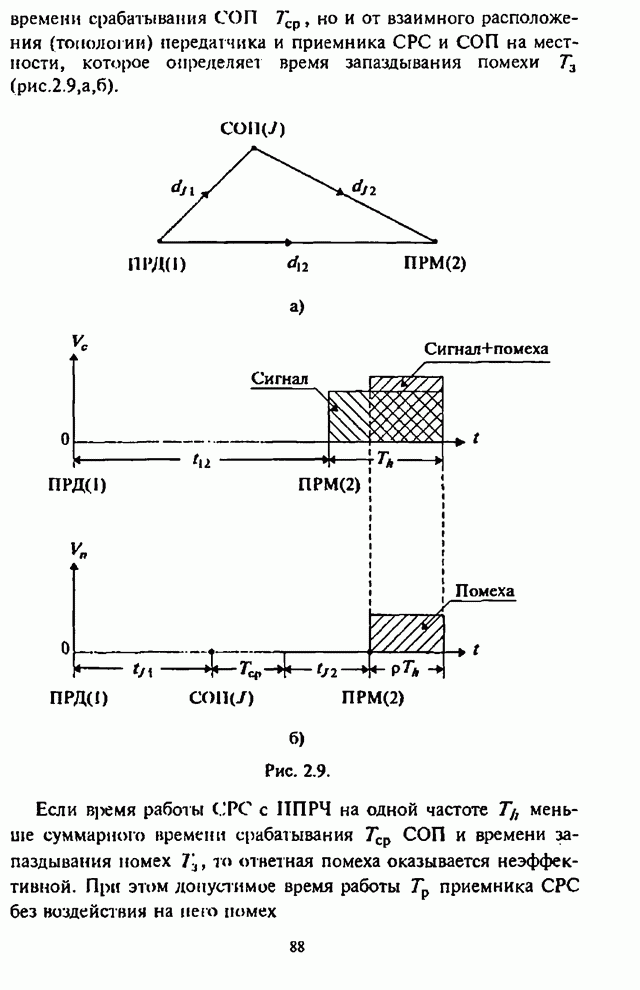
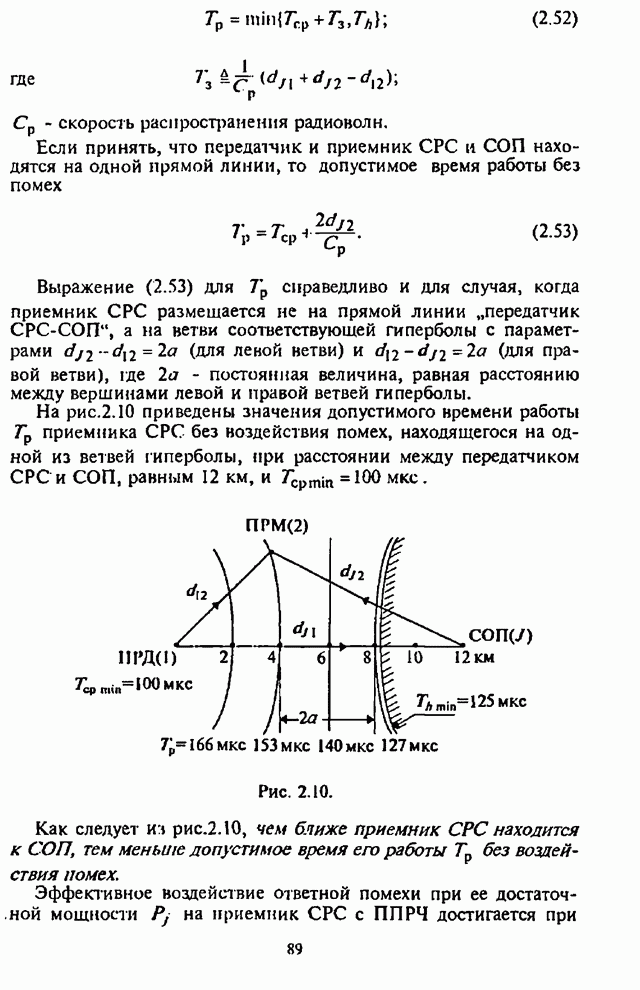
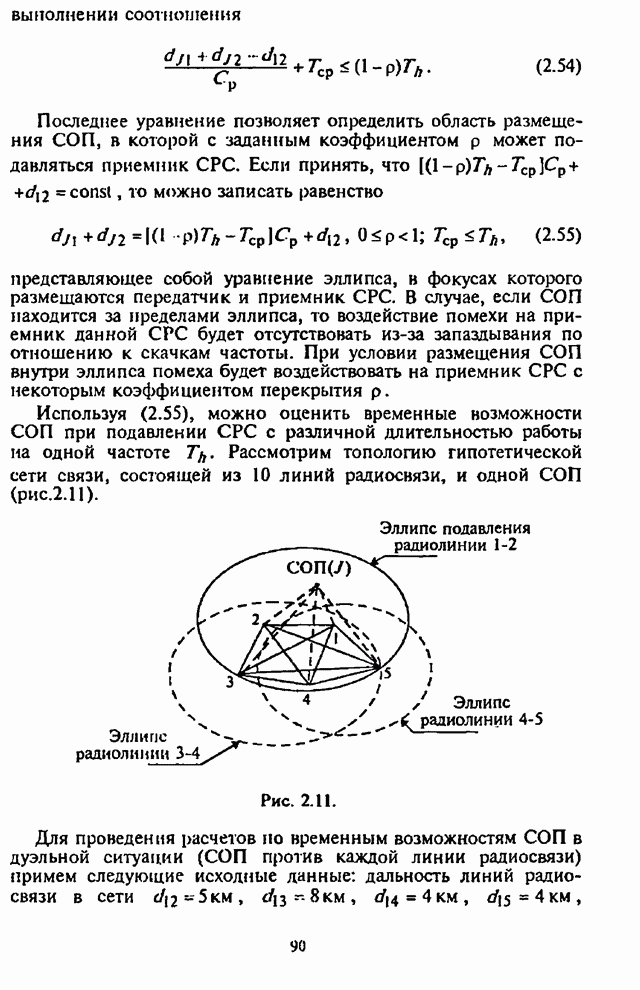
- 2.4.1. Оценка временных возможностей станции ответных помех
- 2.4.2. Оценка воздействия ответных шумовых помех на системы радиосвязи с ППРЧ и ЧМ
- 2.4.3. Оценка воздействия ответных гармонических помех на системы радиосвязи с ППРЧ и ЧМ
- 2.5. Помехоустойчивость систем радиосвязи с ППРЧ, двоичной ЧМ и блоковым кодированием
- Глава 3. Синтез и анализ эффективности адаптивных алгоритмов различения сигналов с ППРЧ, частотной модуляцией и разнесением символов по частоте
- 3.1. Синтез оптимального адаптивного алгоритма различения сигналов с внутрисимвольной ППРЧ и ЧМ
- 3.2. Квазиоптимальный адаптивный алгоритм различения сигналов с внутрисимвольной ППРЧ и двоичной ЧМ
- 3.3. Оценка помехоустойчивости синтезированного адаптивного алгоритма различения сигналов с внутрисимвольной ППРЧ и двоичной ЧМ
- 3.3.1. Случай «слабых» сигналов
- 3.3.2. Случай «сильных» сигналов
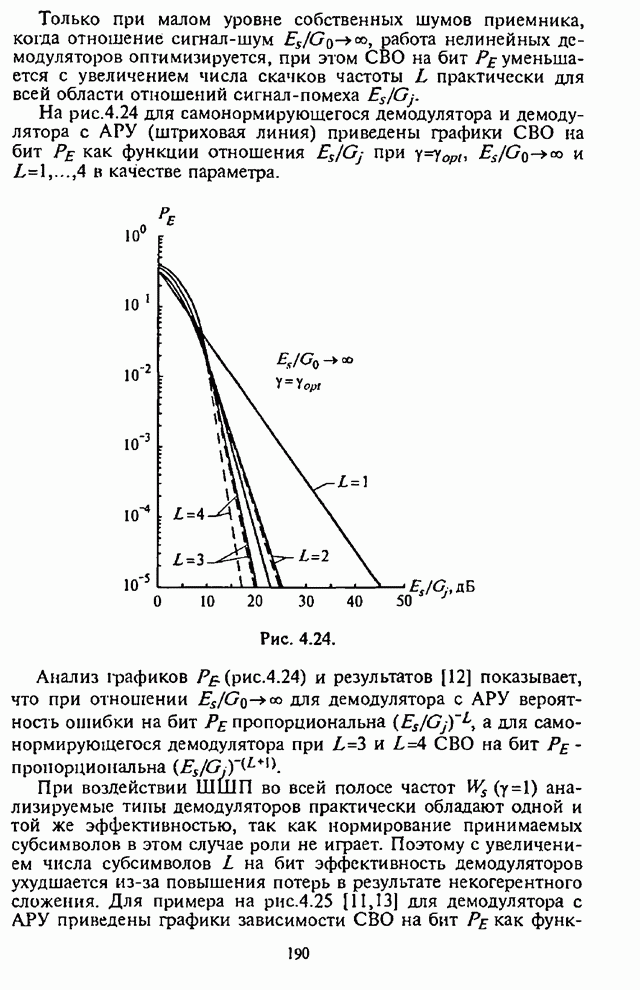
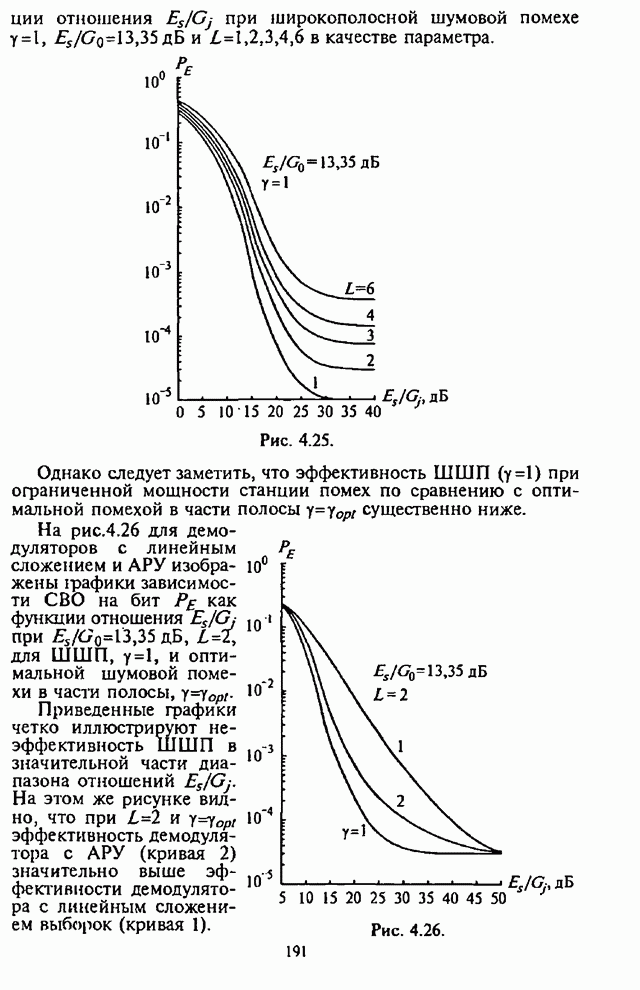
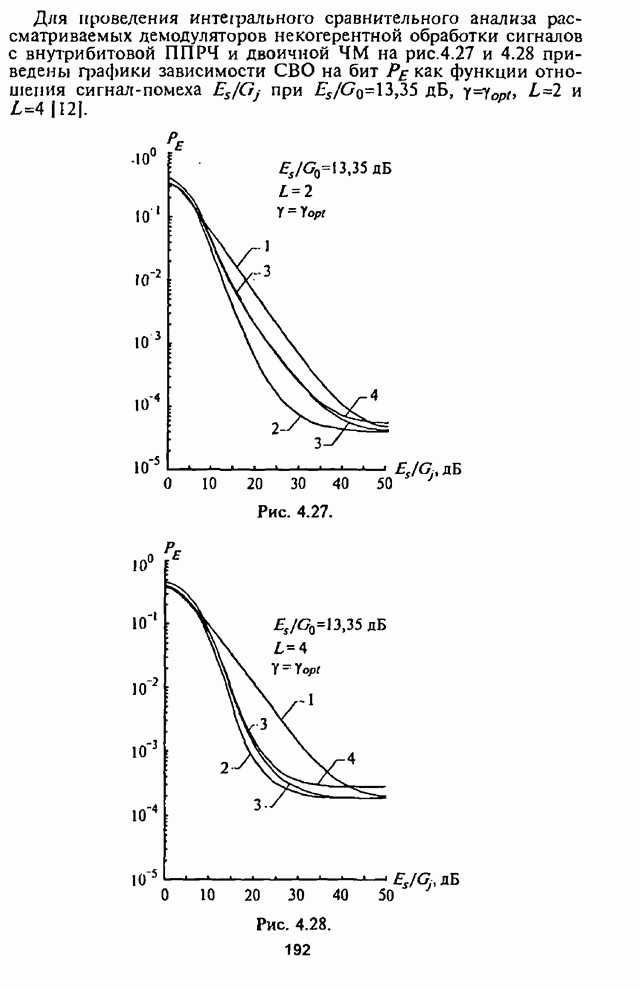
- Глава 4. Помехоустойчивость адаптивных алгоритмов демодуляции сигналов с внутрибитовой ППРЧ и двоичной частотной манипуляцией
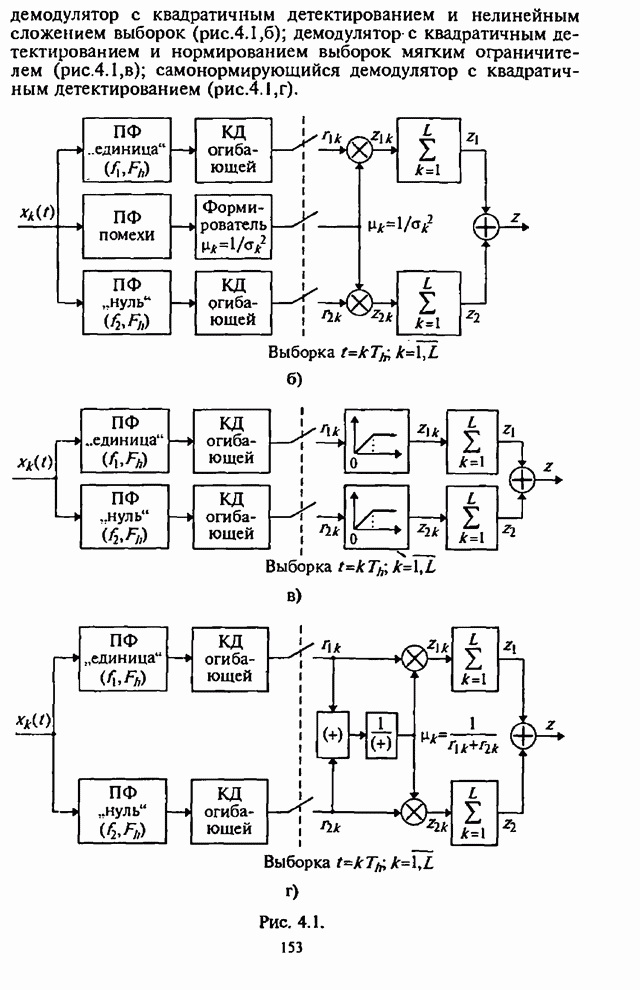
- 4.1. Структурные схемы демодуляторов
- 4.2. Помехоустойчивость демодулятора с линейным сложением выборок
- 4.3. Помехоустойчивость демодулятора с нелинейным сложением выборок
- 4.4. Помехоустойчивость демодулятора с мягким ограничителем
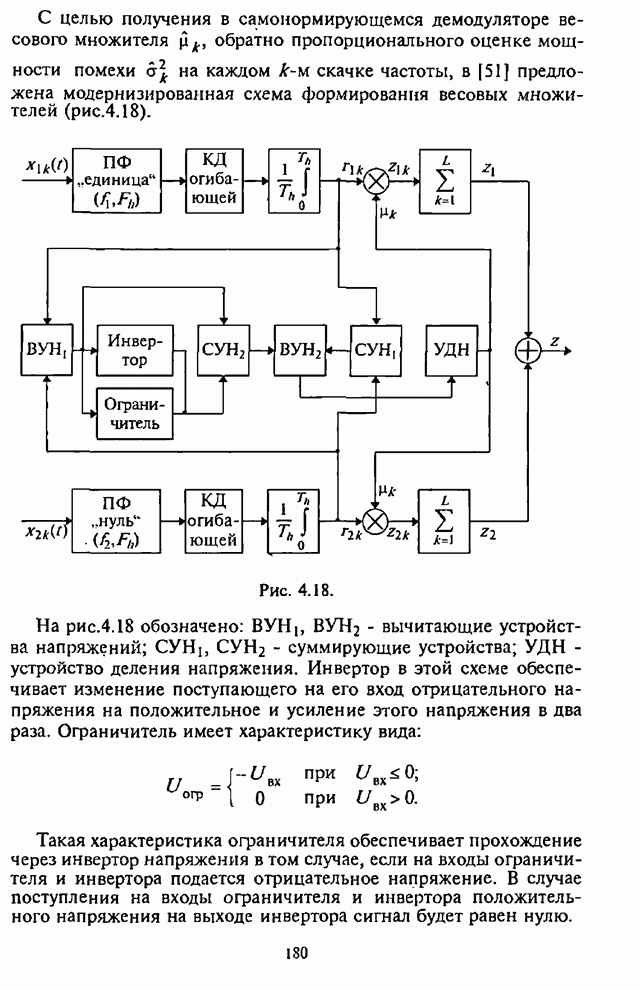
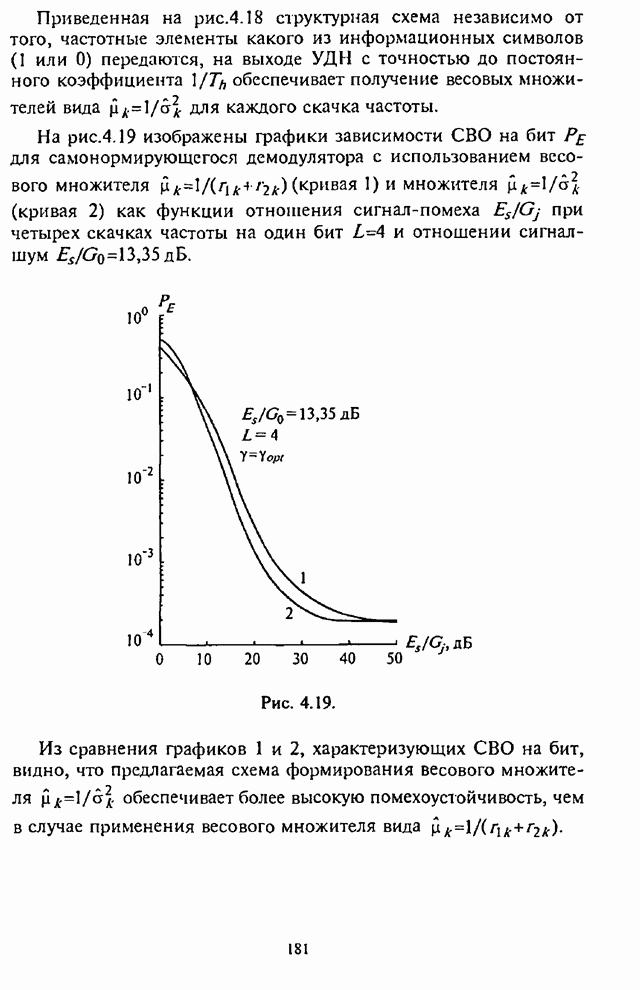
- 4.5. Помехоустойчивость самонормирующегося демодулятора
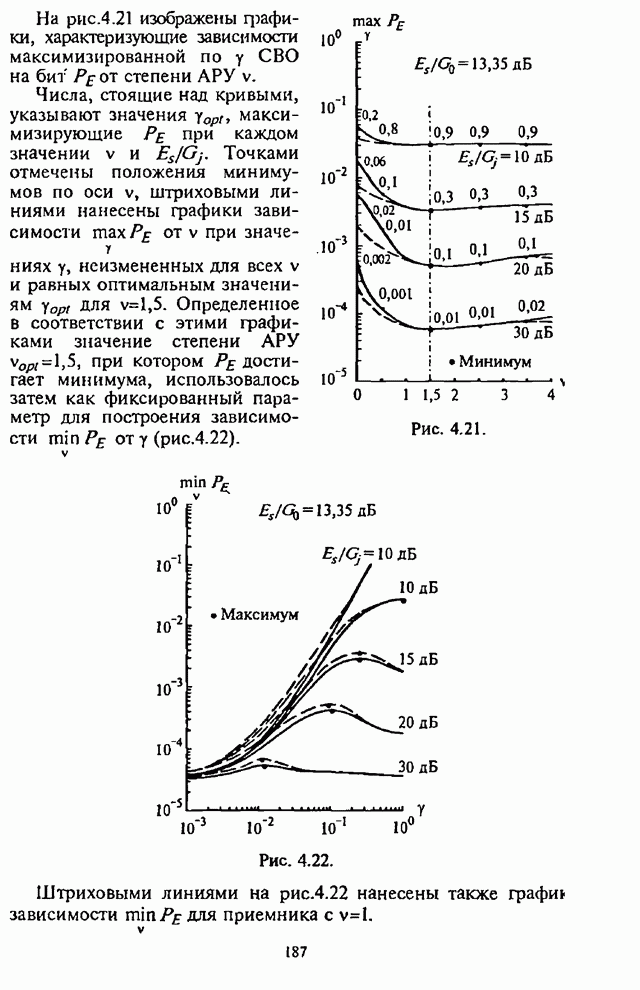
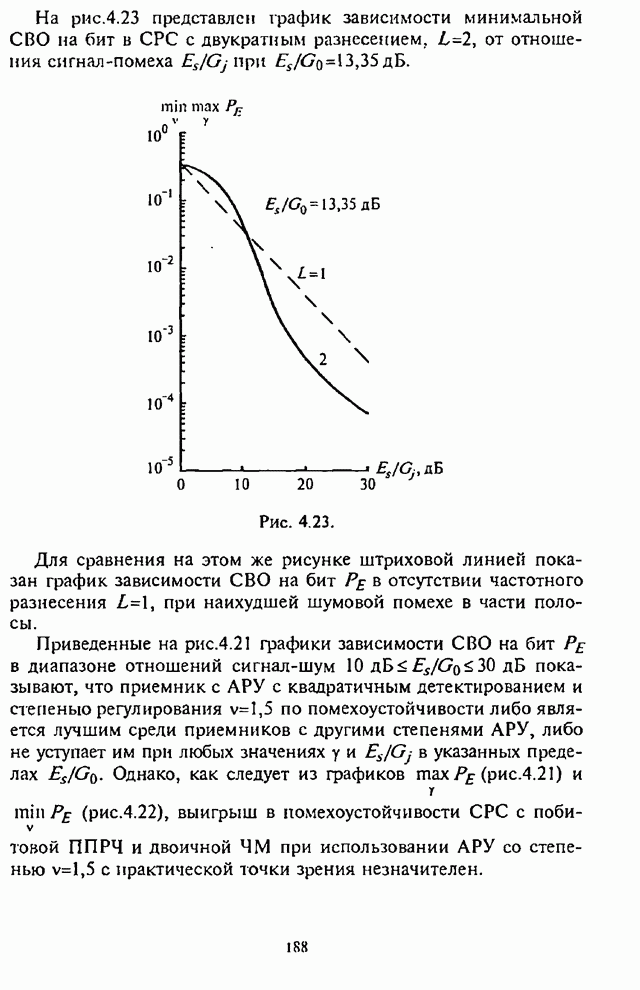
- 4.6. Влияние адаптивной регулировки усиления на помехоустойчивость СРС
- 4.7. Сравнительный анализ помехоустойчивости демодуляторов сигналов с внутрибитовой ППРЧ и двоичной ЧМ
- Глава 5. Помехоустойчивость систем радиосвязи с ППРЧ при совместном применении частотной модуляции, разнесения символов по частоте и блокового кодирования
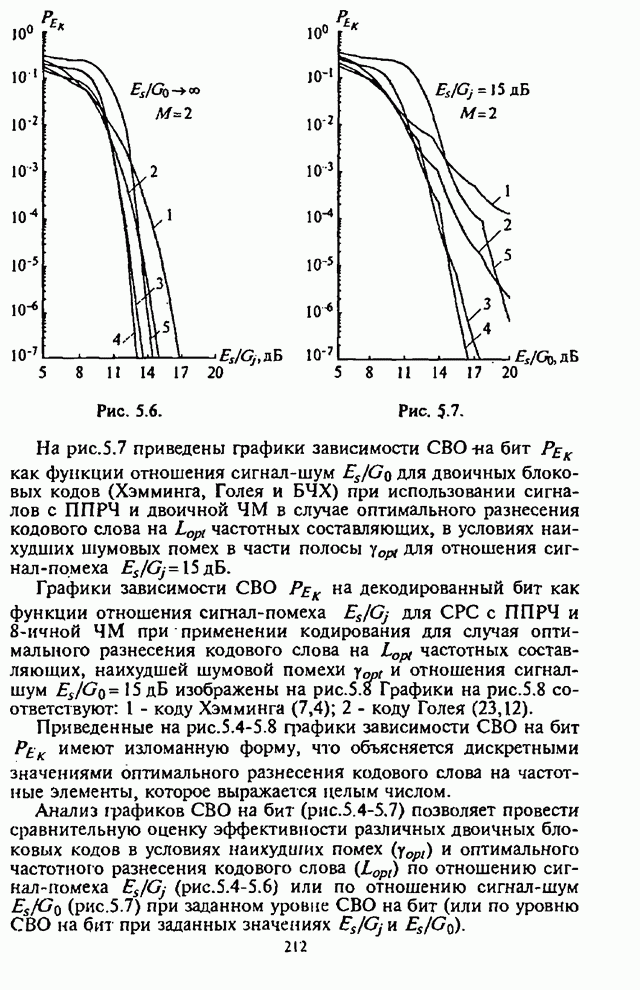
- 5.1. Помехоустойчивость систем радиосвязи с ППРЧ при M-ичной ЧМ и L-кратным разнесении символов по частоте
- 5.1.1. Условная вероятность ошибки на бит информации
- 5.1.2. Анализ средней вероятности ошибки на бит информации
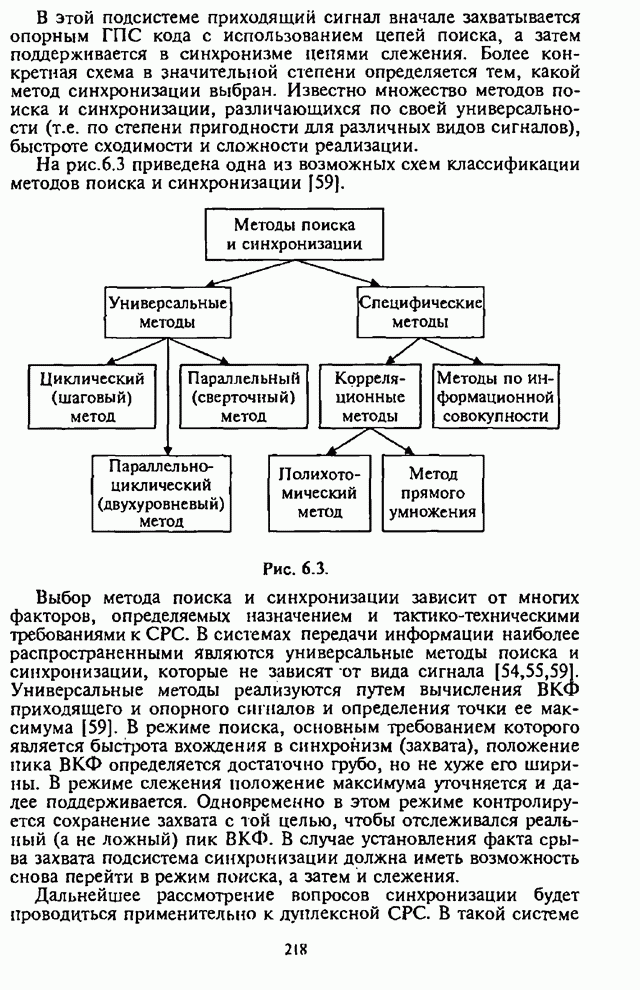
- 5.2. Помехоустойчивость систем радиосвязи с ППРЧ, M-ичной ЧМ, блоковым кодированием и L-кратным частотным разнесением кодовых слов
- 5.2.1. Структурная схема системы радиосвязи
- 5.2.2. Средняя вероятность ошибки на бит информации
- 5.2.3. Анализ средней вероятности ошибки на бит информации
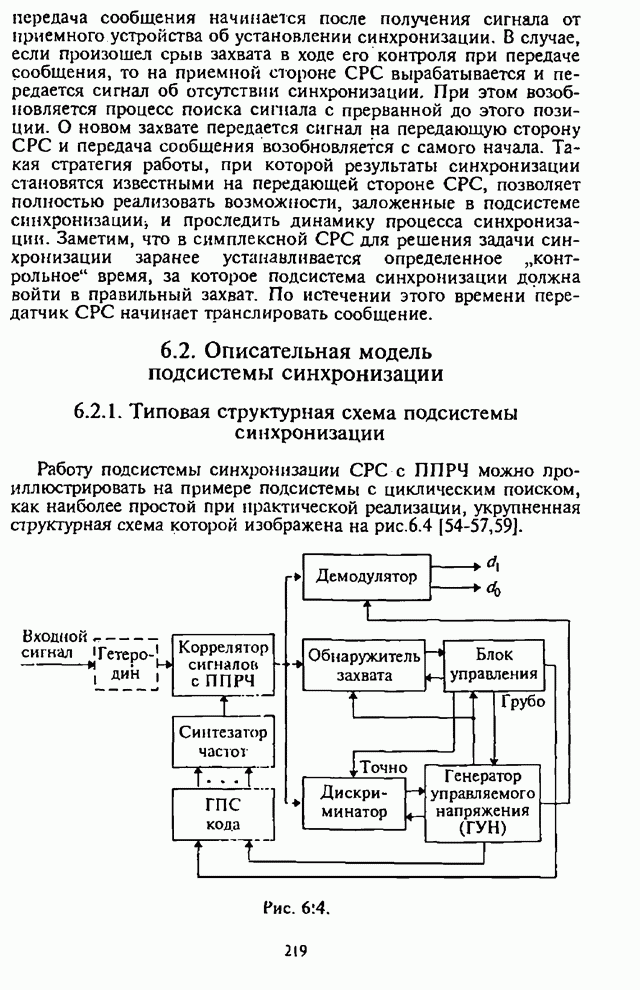
- Глава 6. Синхронизация в системах радиосвязи с псевдослучайной перестройкой рабочей частоты
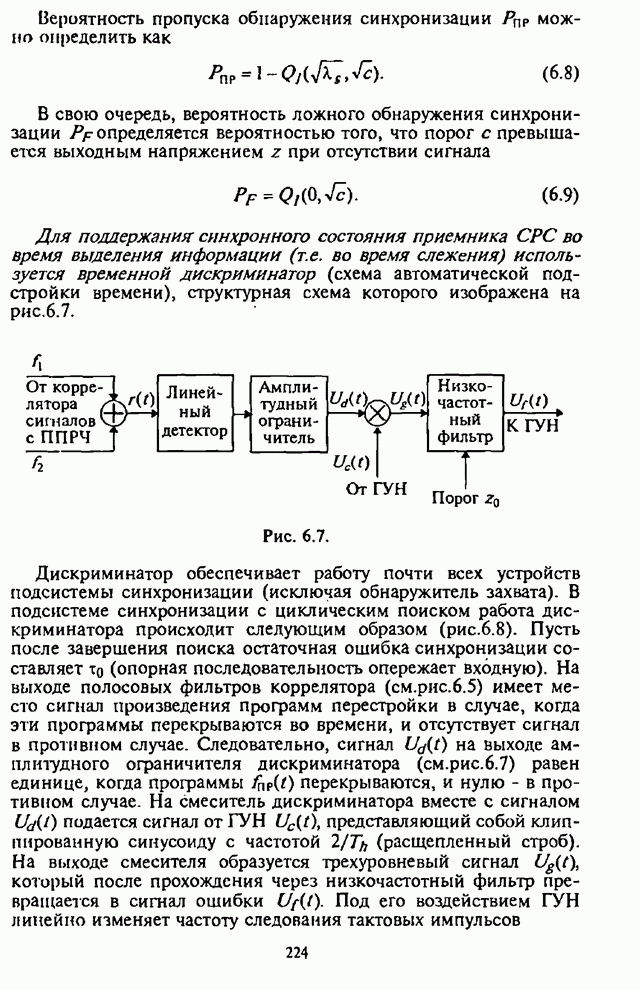
- 6.1. Назначение подсистемы синхронизации
- 6.2. Описательная модель подсистемы синхронизации
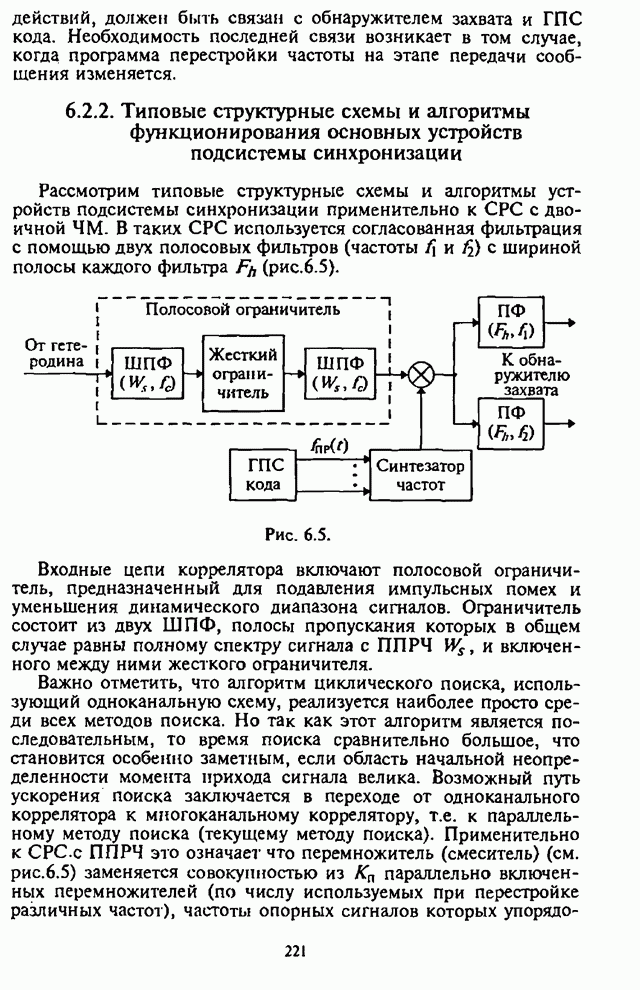
- 6.2.1. Типовая структурная схема подсистемы синхронизации
- 6.2.2. Типовые структурные схемы и алгоритмы функционирования основных устройств подсистемы синхронизации
- 6.3. Показатели и оценка эффективности циклических процедур поиска
- Приложение П.6.1. Верхняя граница среднего нормированного времени поиска
- Приложение П.6.2. Верхняя граница вероятности правильного обнаружения
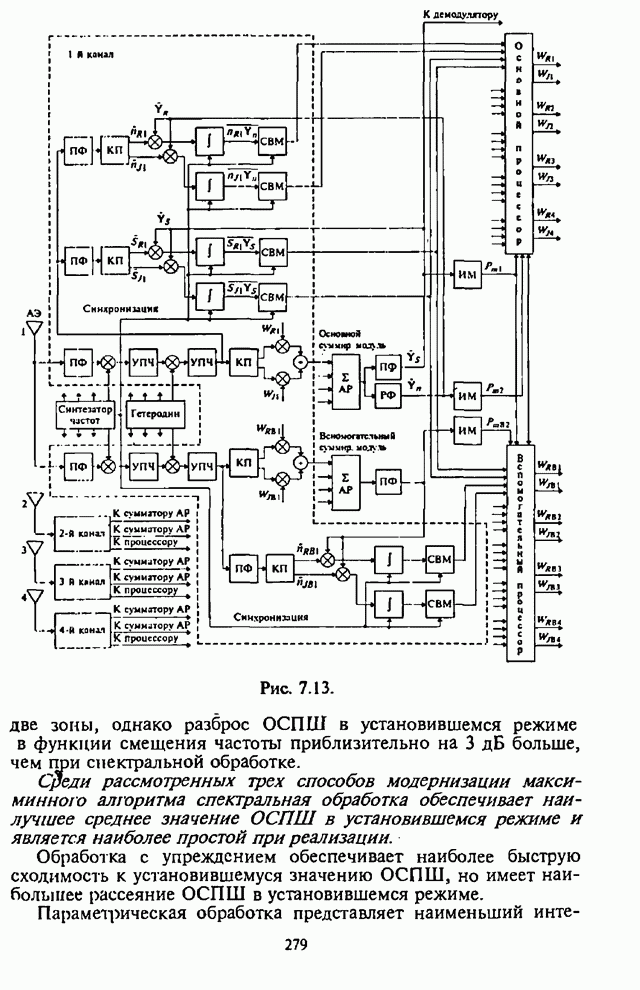
- Глава 7. Адаптивные антенные решетки в системах радиосвязи с псевдослучайной перестройкой рабочей частоты
- 7.1. Влияние сигналов с ППРЧ на характеристики адаптивной антенной решетки
- 7.2. Максиминный алгоритм обработки сигналов и помех
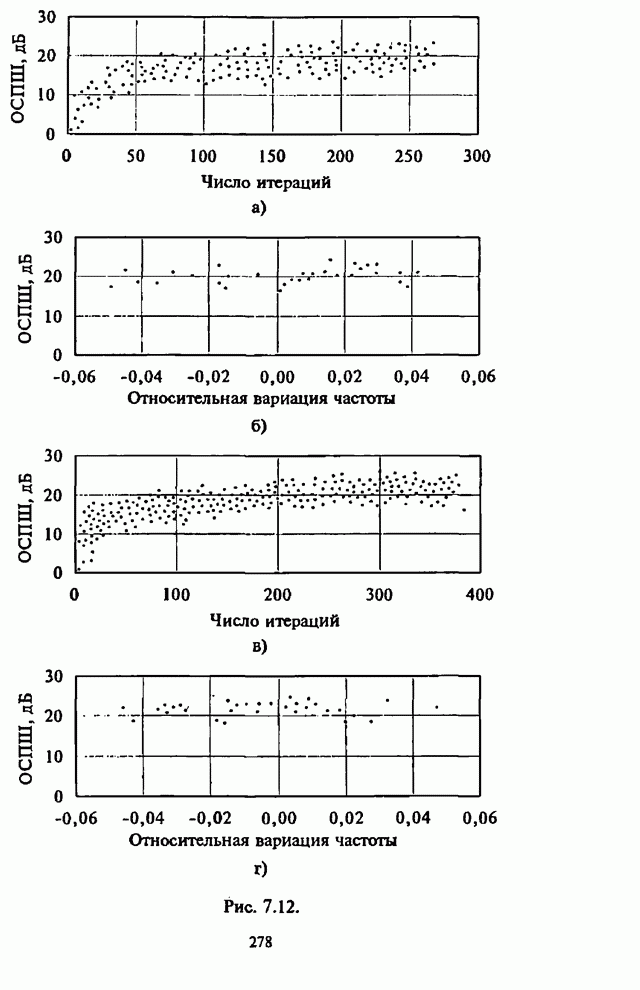
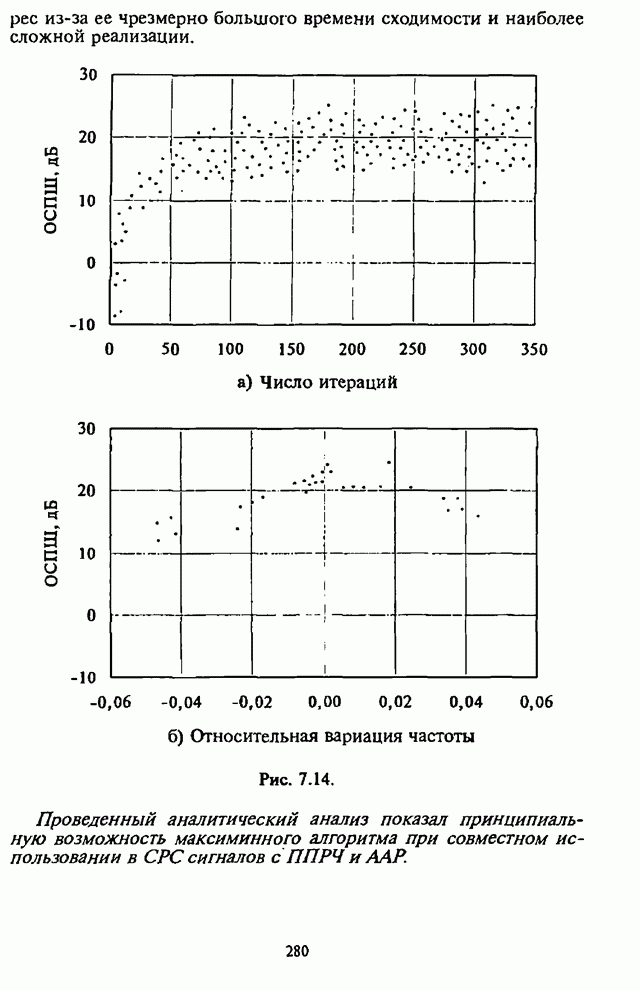
- 7.3. Реализация и возможности максиминного алгоритма
- 7.4. Модернизация максиминного алгоритма
- 7.4.1. Параметрическая обработка
- 7.4.2. Спектральная обработка
- 7.4.3. Обработка с упреждением
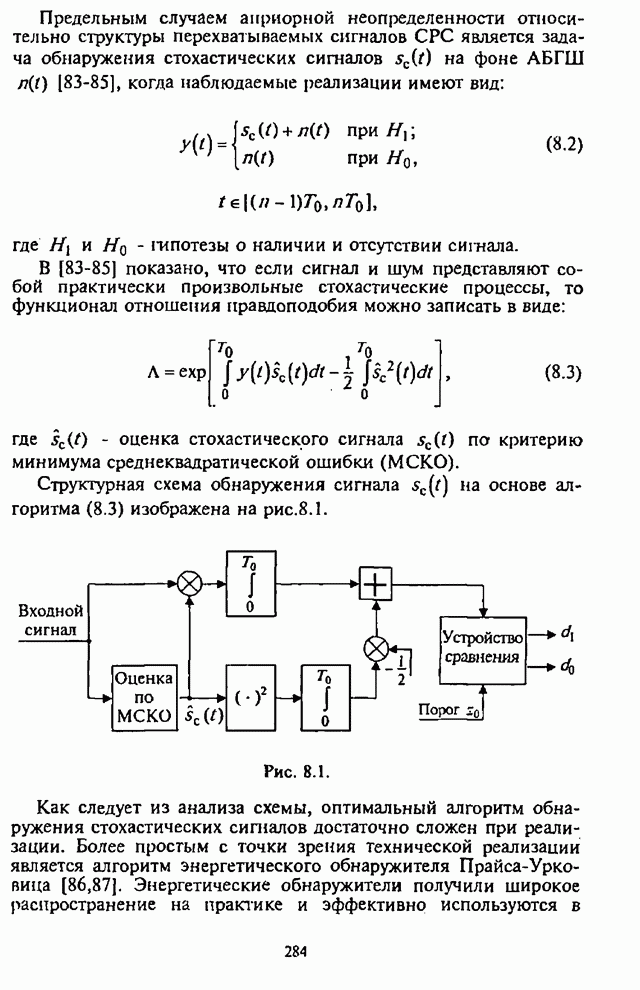
- Глава 8. Обнаружение сигналов с псевдослучайной перестройкой рабочей частоты
- 8.1. Обнаружение сигналов неизвестной структуры
- 8.2. Широкополосный энергетический обнаружитель
- 8.3. Многоканальные энергетические обнаружители
- 8.3.1. Квазиоптимальный многоканальный обнаружитель
- 8.3.2. Многоканальный обнаружитель типа сумматора с блоком фильтров
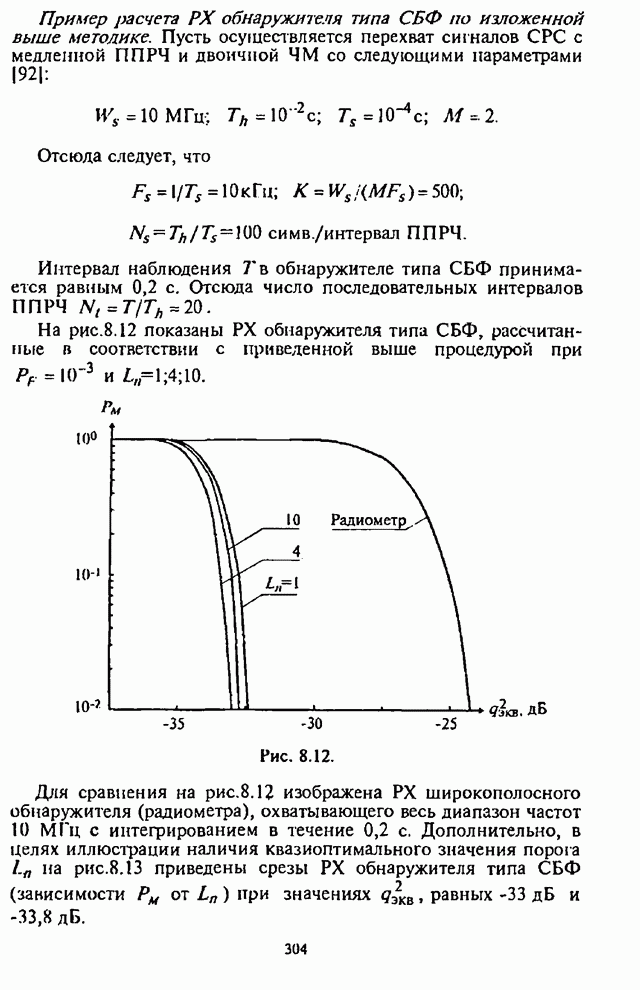
- 8.3.3. Модель обнаружителя типа сумматора с блоком фильтров при перехвате сигналов с медленной ППРЧ
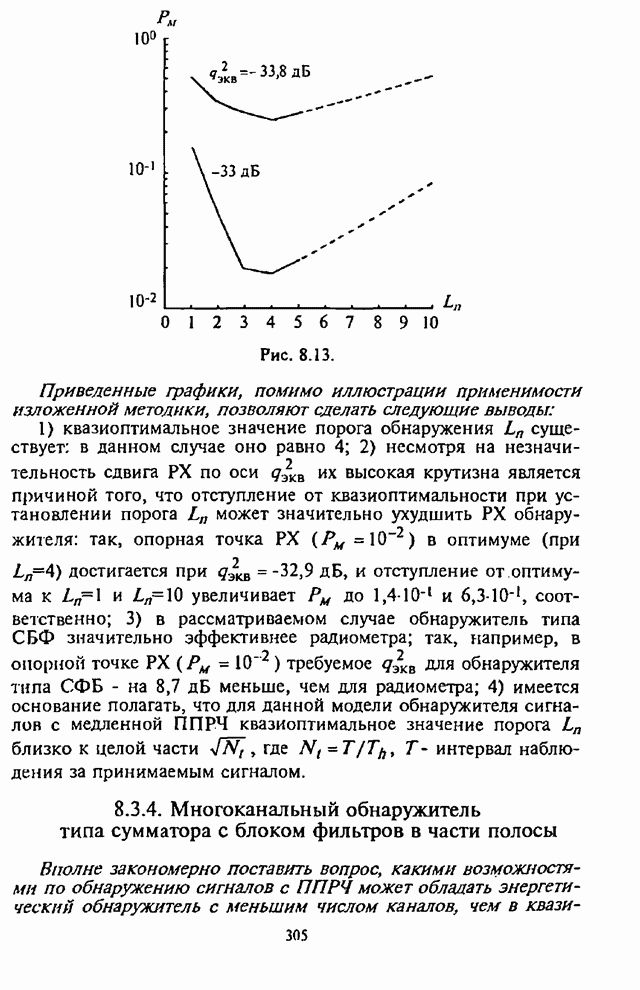
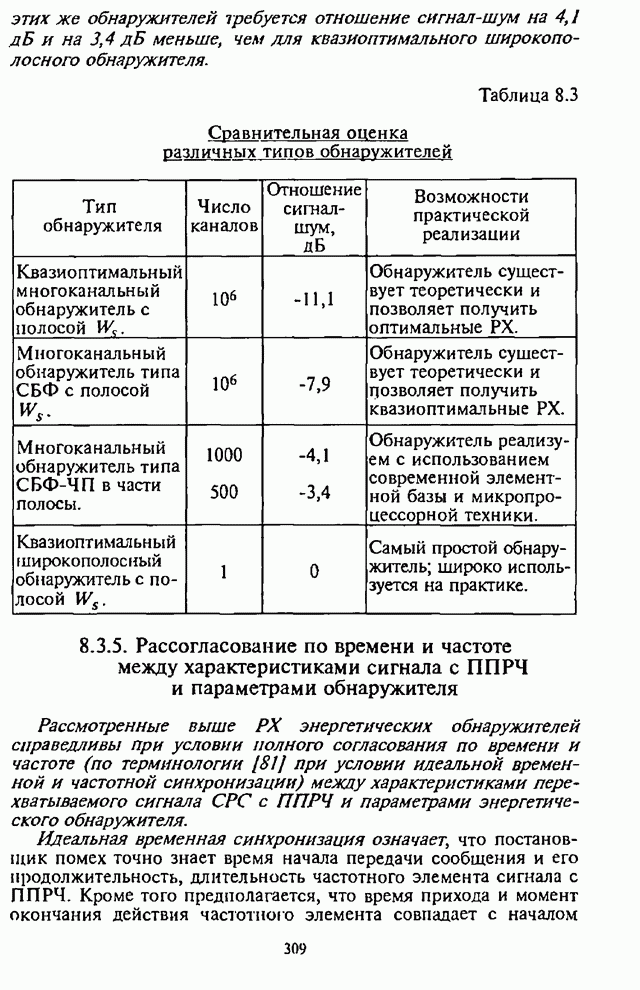
- 8.3.4. Многоканальный обнаружитель типа сумматора с блоком фильтров в части полосы
- 8.3.5. Рассогласование по времени и частоте между характеристиками сигнала с ППРЧ и параметрами обнаружителя
- 8.4. Многоканальный адаптивный энергетический обнаружитель в условиях воздействия мешающих сигналов
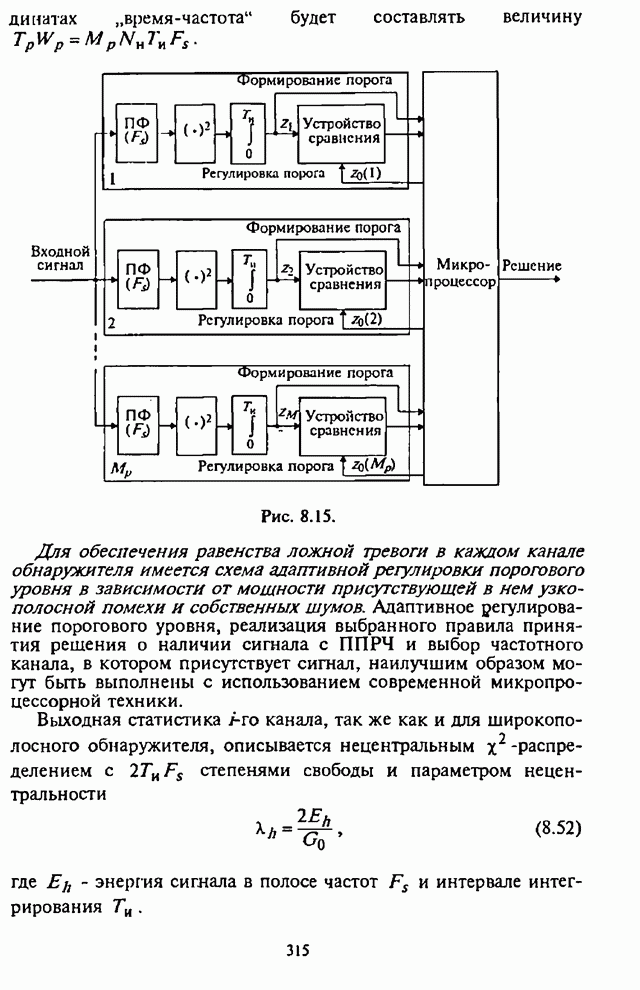
- 8.4.1. Структурная схема многоканального адаптивного энергетического обнаружителя с регулировкой порогового уровня
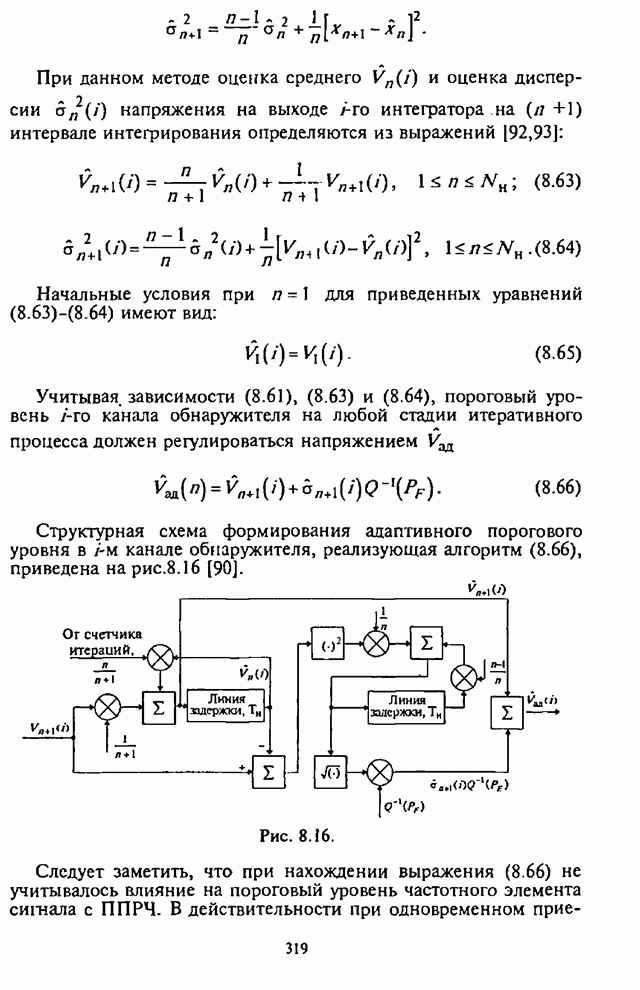
- 8.4.2. Вероятность ложной тревоги и адаптивная регулировка порогового уровня
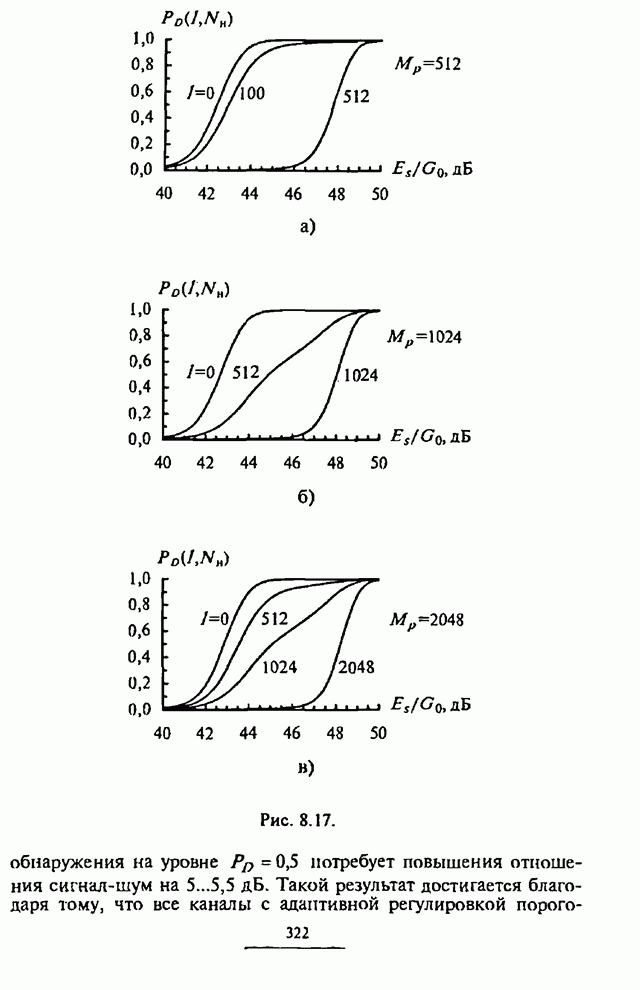
- 8.4.3. Вероятность обнаружения
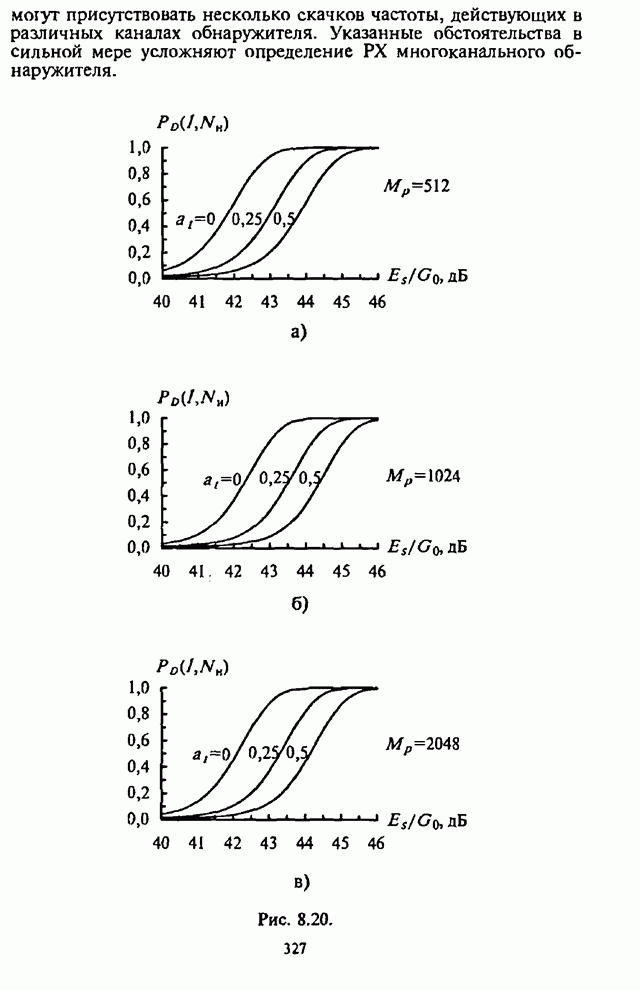
- 8.4.4. Влияние рассогласования по времени на обнаружение сигналов
- 8.5. Другие возможные типы обнаружителей сигналов с ППРЧ
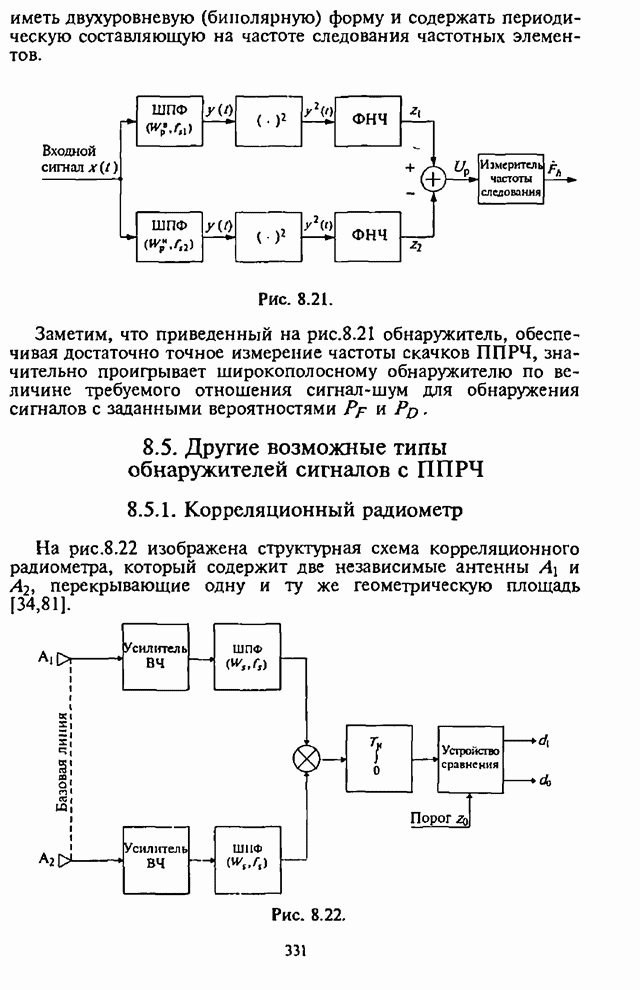
- 8.5.1. Корреляционный радиометр
- 8.5.2. Цифровой анализатор спектра
- 8.5.3. Метод вскрытия частотно-временной матрицы сигнала с ППРЧ
- Приложение П.8.1. Алгоритмы вычисления обобщенной Q-функции Маркума
- П.8.1.1. Постановка задачи
- П.8.1.2. Представление степенными рядами
- П.8.1.3. Представление в виде рядов Неймана
- П.8.1.4. Численное интегрирование
- П.8.1.5. Гауссовская аппроксимация
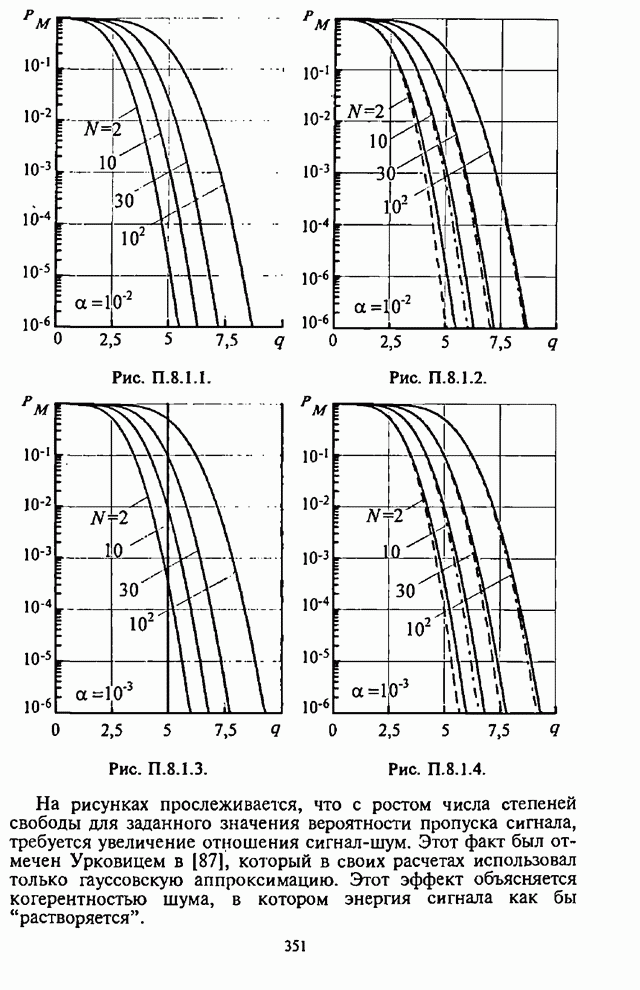
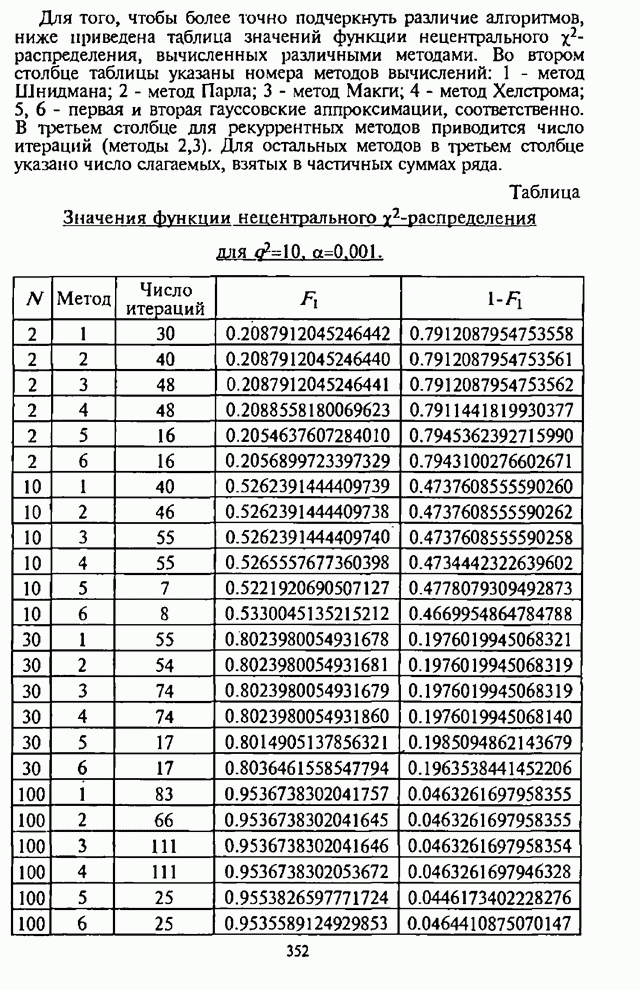
- П.8.1.6. Численные результаты
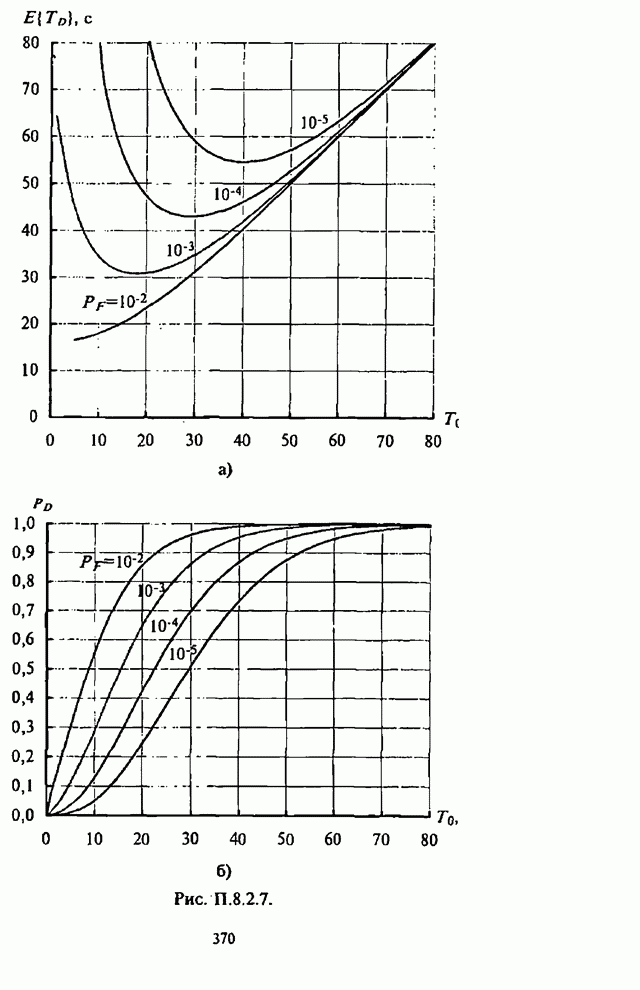
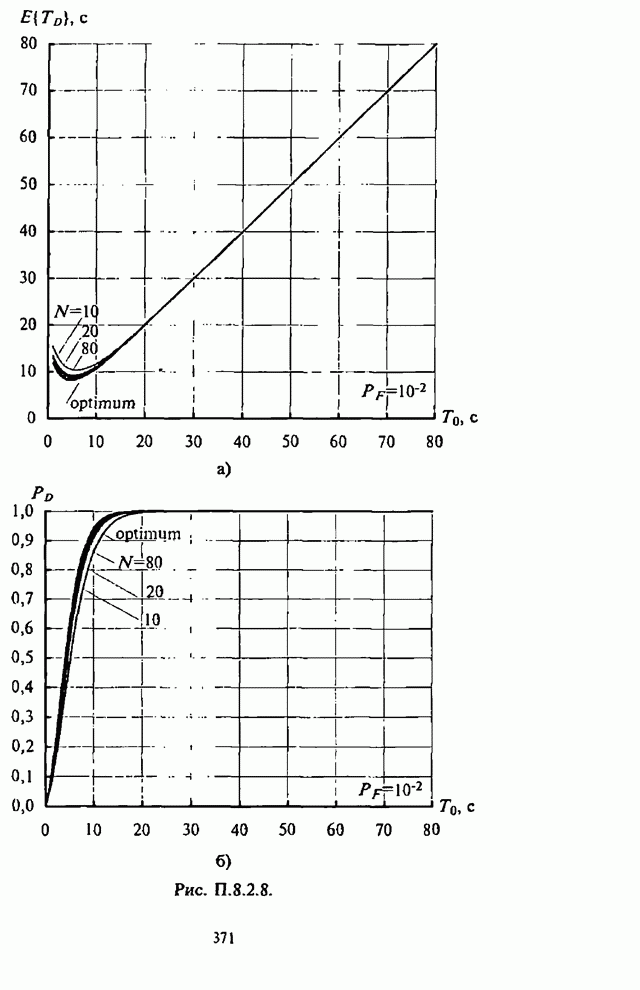
- Приложение П.8.2. Анализ вероятностно-временных характеристик алгоритмов обнаружения сигналов
- П.8.2.1. Вероятностно-временные характеристики основных видов обнаружителей
- П.8.2.2 Алгоритмы расчета вероятностно-временных характеристик основных видов обнаружителей
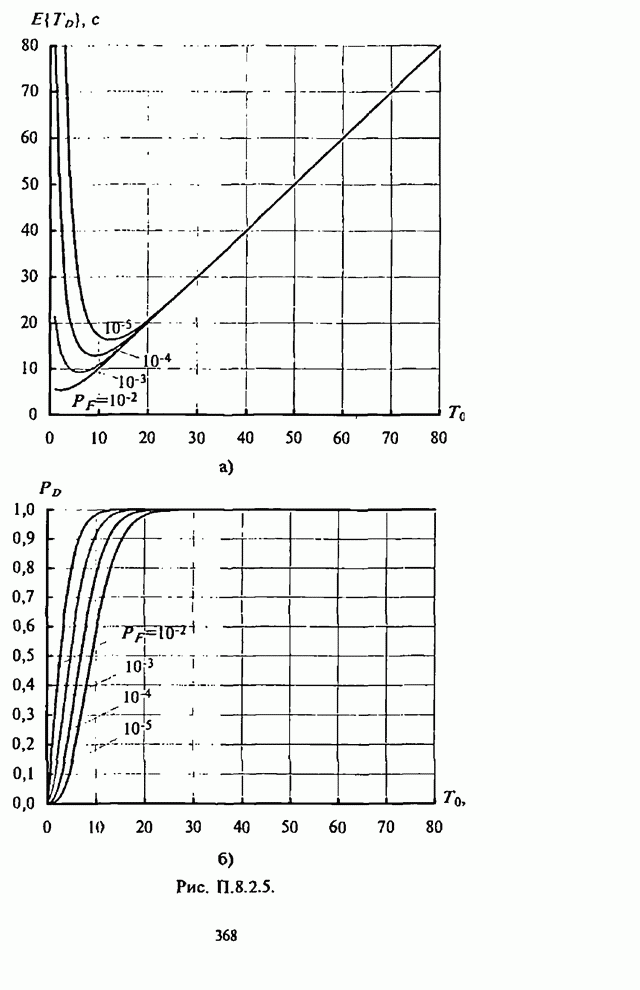
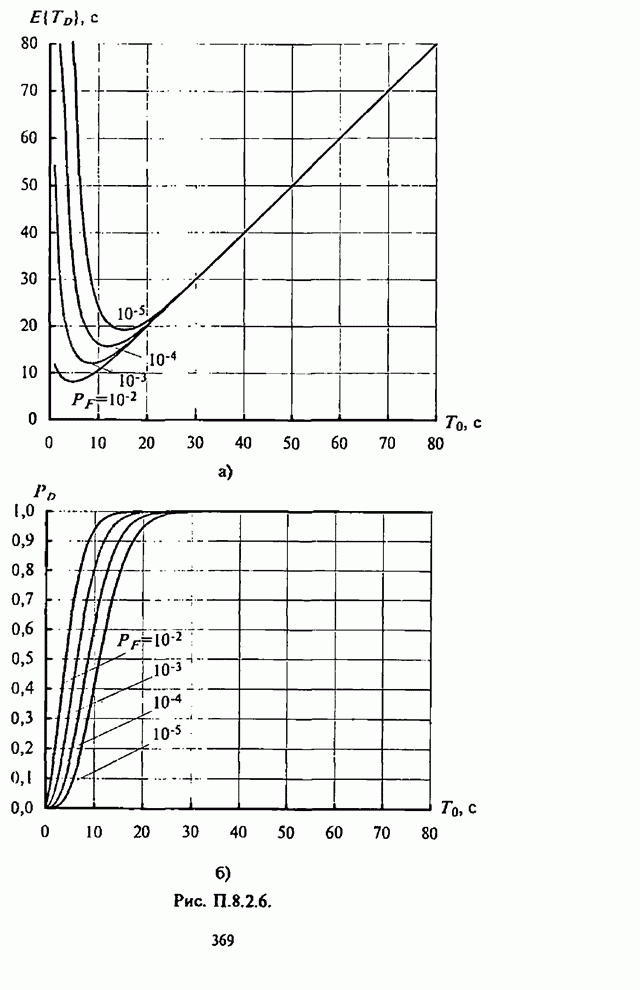
- П.8.2.3. Численные результаты
- СПИСОК ОСНОВНЫХ СОКРАЩЕНИЙ
- ОСНОВНЫЕ УСЛОВНЫЕ ОБОЗНАЧЕНИЯ
- СПИСОК ЛИТЕРАТУРЫ