| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
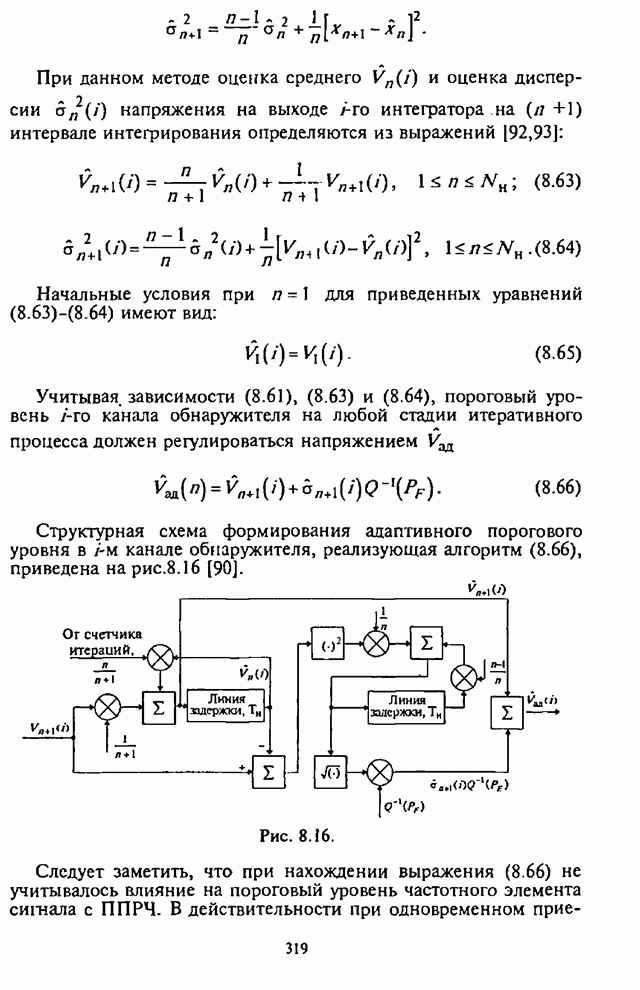
П.8.2.2 Алгоритмы расчета вероятностно-временных характеристик основных видов обнаружителей
П.8.2.2.1 Обнаружитель детерминированных сигналов
В данном случае на вход обнаружителя поступает случайный процесс
![]() , (П.8.2.20)
, (П.8.2.20)
где
![]() - АБГШ;
- АБГШ; ![]() при гипотезе
при гипотезе ![]() (
(![]() : сигнал присутствует) и
: сигнал присутствует) и ![]() при гипотезе
при гипотезе ![]() (
(![]() : сигнал отсутствует).
: сигнал отсутствует).
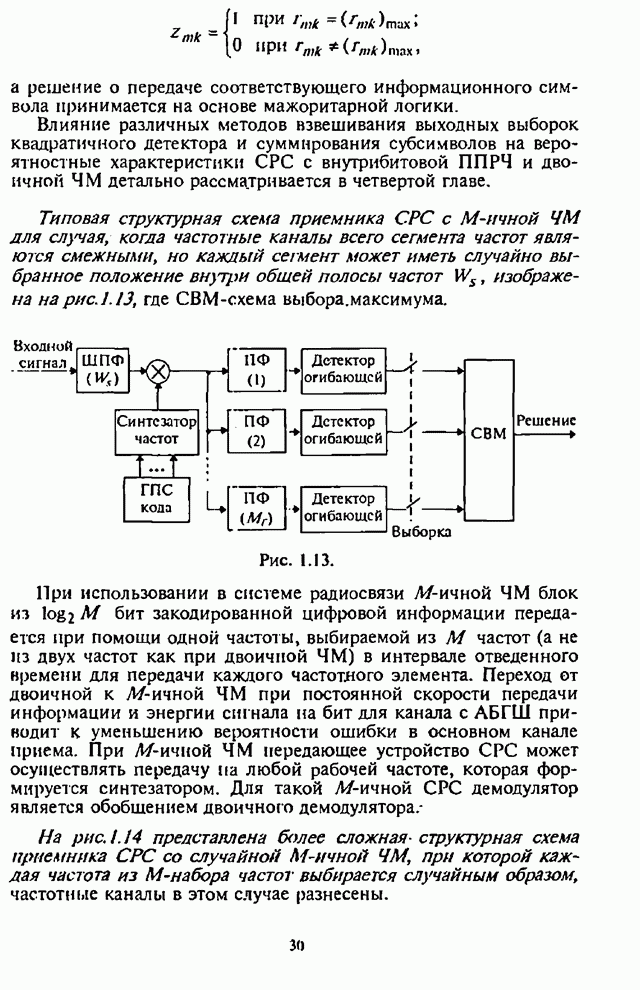
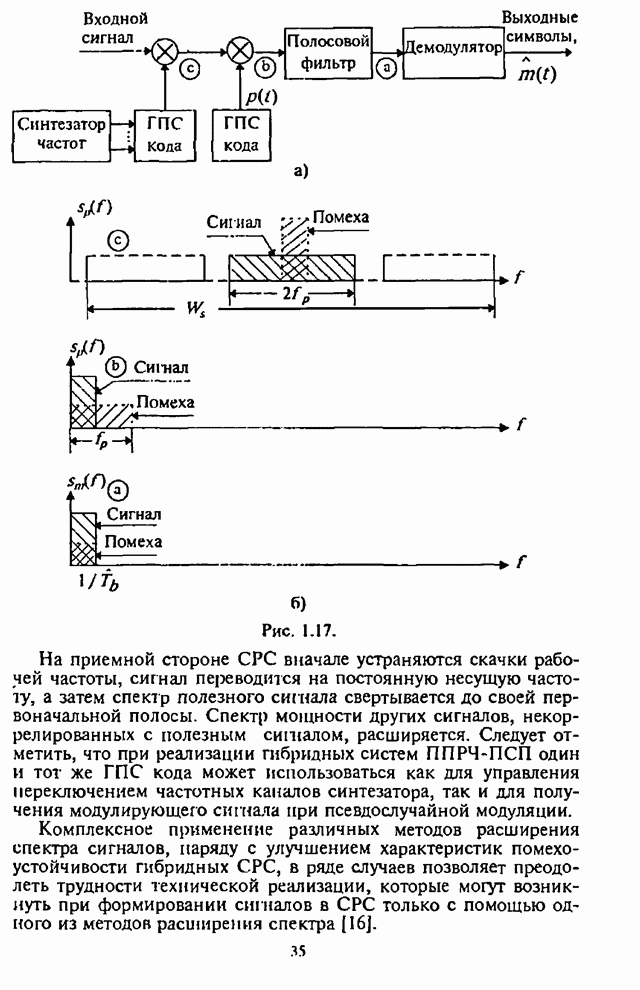
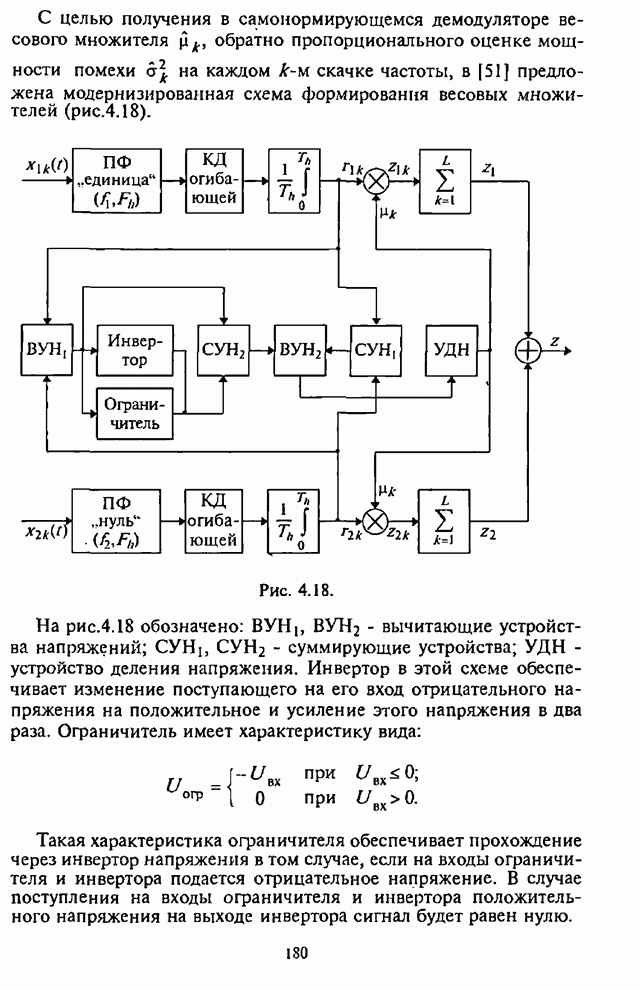
Оптимальный обнаружитель детерминированных сигналов может быть реализован на базе коррелятора или согласованного фильтра (рис.П.8.2.1,а,б, где обозначено: УС - устройство сравнения).

Рис. П.8.2.1.
Статистика обнаружителя имеет вид:
 (П.8.2.21)
(П.8.2.21)
Статистика
![]() имеет
гауссовское распределение с параметрами
имеет
гауссовское распределение с параметрами
![]() ; (П.8.2.22)
; (П.8.2.22)
 , (П.8.2.23)
, (П.8.2.23)
где
![]() - энергия
сигнала, накопленная за время
- энергия
сигнала, накопленная за время ![]() .
.
Отношение сигнал-шум
![]() , (П.8.2.24)
, (П.8.2.24)
где
![]() ;
; ![]() - мощность сигнала;
- мощность сигнала; ![]() - мощность АБГШ, ограниченного
полосой
- мощность АБГШ, ограниченного
полосой ![]() .
.
Вероятности ложной тревоги и обнаружения на одном шаге можно записать в виде:
 ; (П.8.2.25)
; (П.8.2.25)
 , (П.8.2.26)
, (П.8.2.26)
где
 ; (П.8.2.27)
; (П.8.2.27)
![]() -
нормированный порог, являющийся решением уравнения
-
нормированный порог, являющийся решением уравнения
 . (П.8.2.28)
. (П.8.2.28)
Определим
зависимость среднего времени ![]() , дисперсии
, дисперсии ![]() от длительности наблюдения на одном шаге
обнаружения
от длительности наблюдения на одном шаге
обнаружения ![]() при
заданных значениях
при
заданных значениях ![]() ,
,
![]() и
вероятности ложной тревоги
и
вероятности ложной тревоги ![]() . На основе (П.8.2.25)-(П.8.2.28) алгоритм
определения среднего времени до обнаружения рассчитывается в следующей последовательности.
. На основе (П.8.2.25)-(П.8.2.28) алгоритм
определения среднего времени до обнаружения рассчитывается в следующей последовательности.
1.
Задаются значения величин: ![]() - отношение сигнал-шум по мощности
- отношение сигнал-шум по мощности ![]() ;
; ![]() - шаг дискретизации во времени,
с;
- шаг дискретизации во времени,
с; ![]() - ширина
полосы, Гц; вероятность ложной тревоги
- ширина
полосы, Гц; вероятность ложной тревоги ![]() .
.
2.
Вычисляется текущее значение времени обнаружения на одном шаге ![]() ,
, ![]() ,
, ![]() с.
с.
3.
Для каждого ![]() вычисляется
значение нормированного порога исходя из уравнения (П.8.2.26),
вычисляется
значение нормированного порога исходя из уравнения (П.8.2.26), ![]() , где
, где ![]() . Для нахождения
. Для нахождения ![]() можно воспользоваться
аппроксимацией [48]
можно воспользоваться
аппроксимацией [48]

где
![]()

4.
Вычисляется отношение сигнал-шум ![]() и вероятность правильного обнаружения
и вероятность правильного обнаружения
 .
.
5.
Находятся среднее время ![]()
![]()
и его дисперсия
![]() .
.
П.8.2.2.2 Обнаружитель квазидетерминированных сигналов со случайной фазой
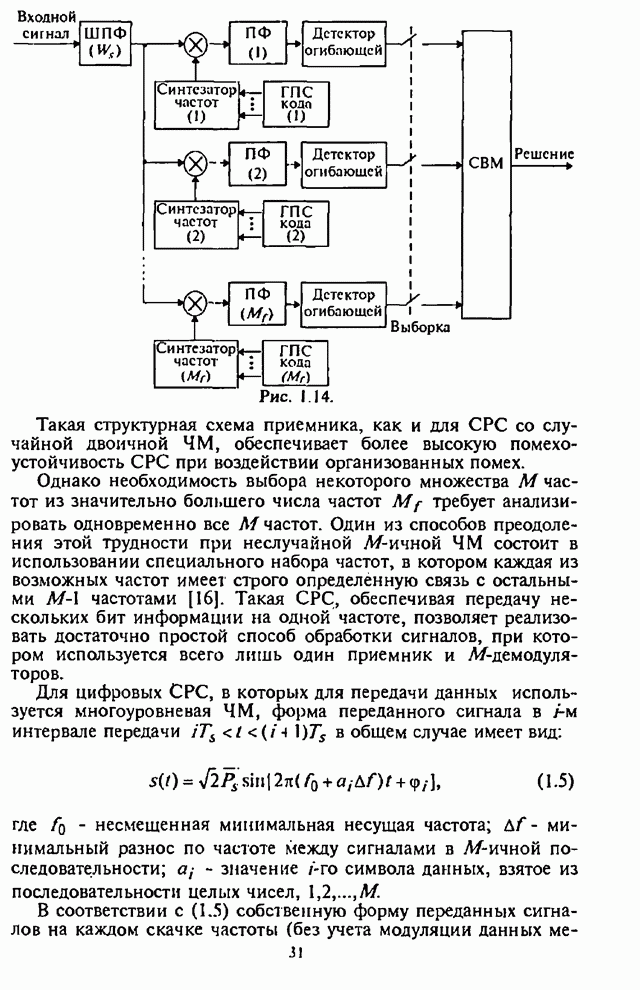
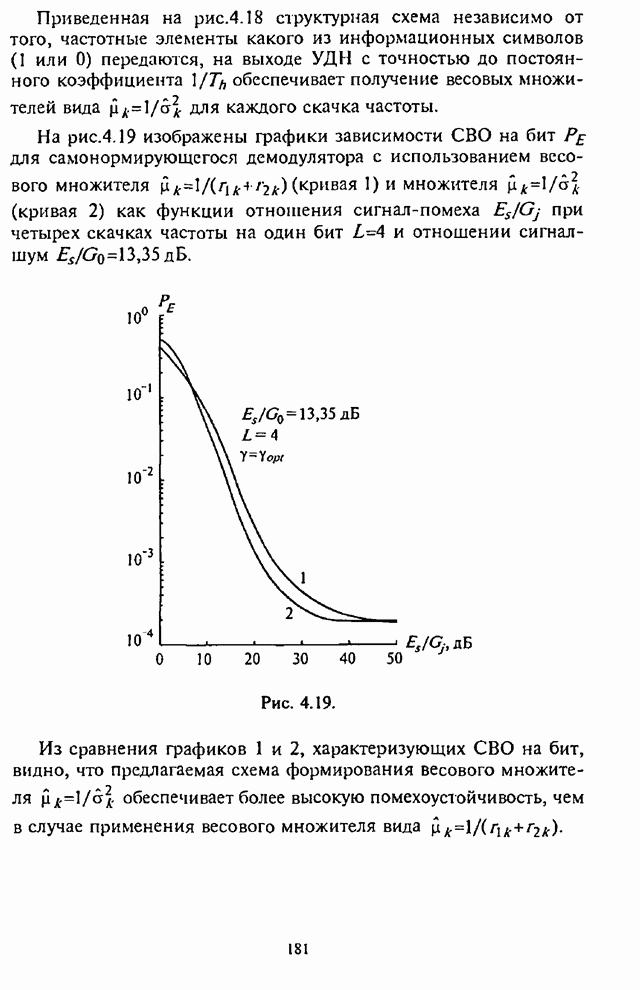
Структурная схема оптимального обнаружителя сигнала со случайной фазой, реализованного на базе коррелятора или согласованного фильтра, изображена на рис.П.8.2.2,а,б.

Рис. П.8.2.2.
Статистика на выходе обнаружителя при наличии шума и смеси сигнала с шумом распределена по закону Рэлея и обобщенному закону Рэлея, соответственно. Вероятность ложной тревоги определяется из выражения [90]
 , (П.8.2.29)
, (П.8.2.29)
а вероятность обнаружения
 . (П.8.3.30)
. (П.8.3.30)
Значение
нормированного порога ![]() находится из (П.8.2.29)
находится из (П.8.2.29)
![]() , (П.8.2.31)
, (П.8.2.31)
где
![]() . (П.8.2.32)
. (П.8.2.32)
Заменой
переменных ![]() выражение
(П.8.2.30) приводится к виду:
выражение
(П.8.2.30) приводится к виду:
 , (П.8.2.33)
, (П.8.2.33)
где
![]() - интегральная
функция вероятностей нецентрального
- интегральная
функция вероятностей нецентрального ![]() -распределения с двумя степенями свободы.
Используя (П.8.2.29)-(П.8.2.33), алгоритм расчета РХ обнаружителя проводится
следующим образом:
-распределения с двумя степенями свободы.
Используя (П.8.2.29)-(П.8.2.33), алгоритм расчета РХ обнаружителя проводится
следующим образом:
1.
Задаются значения величин: ![]() - шаг дискретизации во времени, с;
- шаг дискретизации во времени, с; ![]() - ширина полосы, Гц;
- ширина полосы, Гц; ![]() - отношение сигнал-шум
по мощности, а также вероятности ложных тревог
- отношение сигнал-шум
по мощности, а также вероятности ложных тревог ![]() .
.
2. При заданной вероятности ложной тревоги по формуле (П.8.2.31) вычисляется величина нормированного порога.
3.
Варьируются время наблюдения на одном шаге ![]() и
и ![]() .
.
4.
По формуле (П.8.2.33) вычисляется вероятность правильного обнаружения сигнала ![]() .
.
5. Вычисляется среднее время и дисперсия.
П. 8.2.2.3 Обнаружитель сигналов неизвестной структуры
Предельным
случаем априорной неопределенности относительно обнаруживаемых сигналов
является задача обнаружения стохастических сигналов на фоне аддитивной
гауссовской помехи ![]() ,
когда наблюдаемые реализации имеют вид
,
когда наблюдаемые реализации имеют вид
 (П.8.2.34)
(П.8.2.34)
где
![]() - случайный
гауссовский процесс.
- случайный
гауссовский процесс.
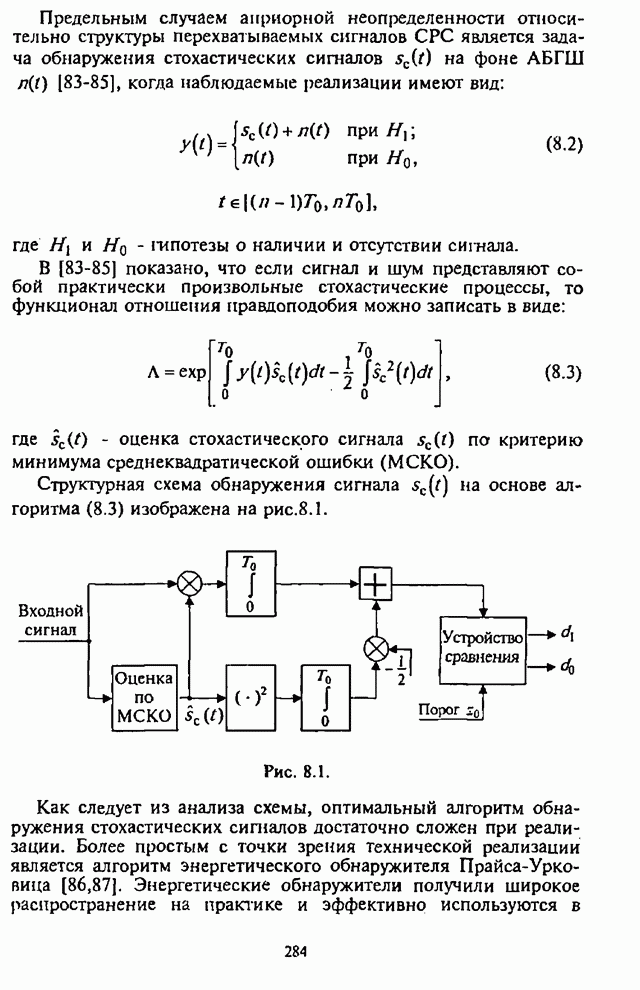
В [83] Кайлат показал, что функционал отношения правдоподобия при обнаружении стохастического сигнала в (П.8.2.34) в общем случае имеет вид:
 , (П.8.2.35)
, (П.8.2.35)
где
![]() -
(П.8.2.36)
-
(П.8.2.36)
оценка
случайного сигнала ![]() по
критерию минимума среднеквадратической ошибки (МСКО) в момент времени
по
критерию минимума среднеквадратической ошибки (МСКО) в момент времени ![]() на основе прошлых
значений
на основе прошлых
значений ![]()
![]() , в предположении, что
имеет место гипотеза
, в предположении, что
имеет место гипотеза ![]() .
.
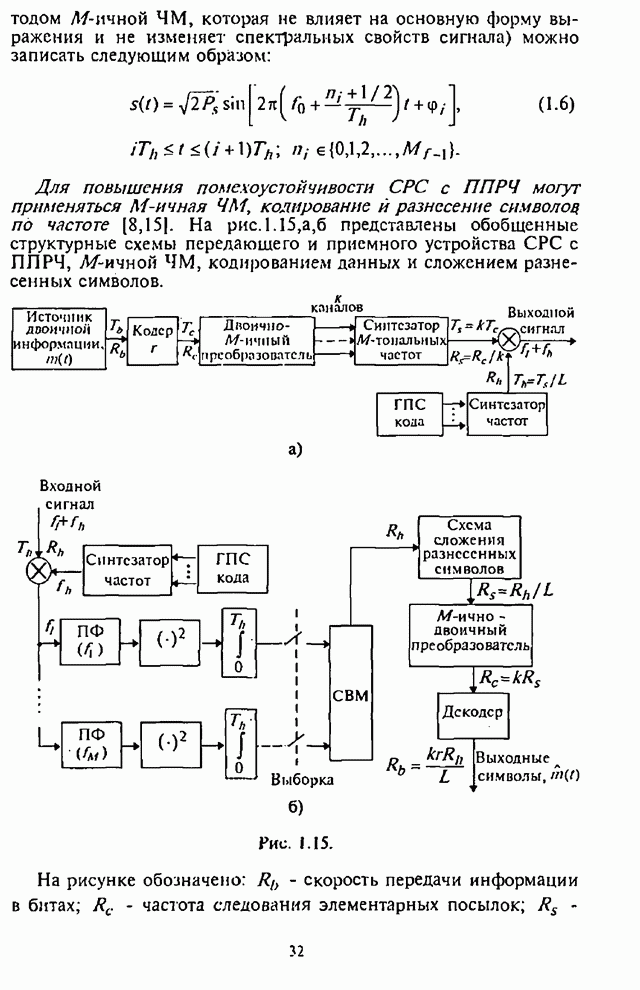
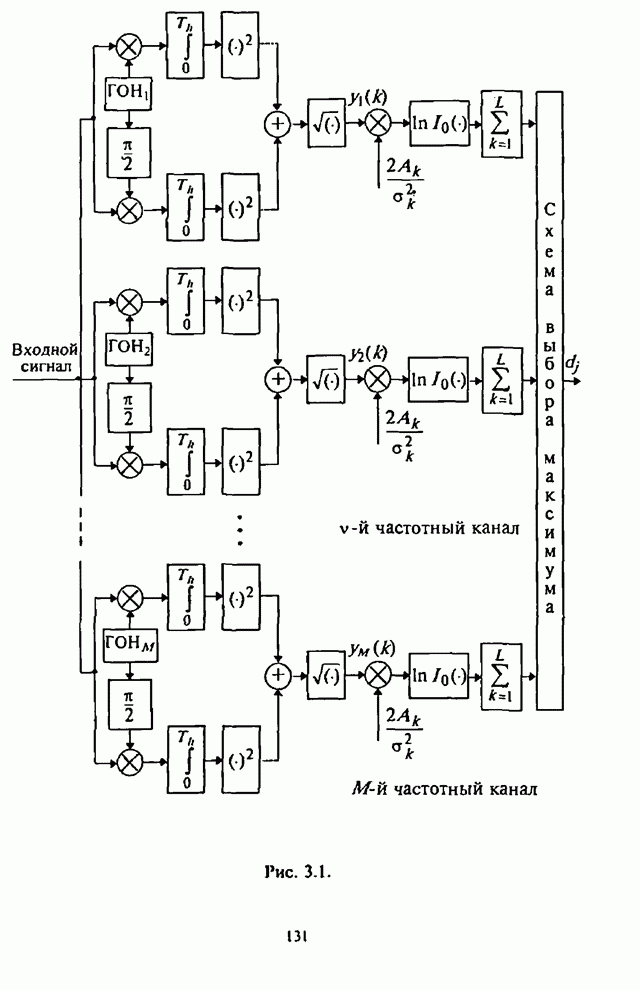
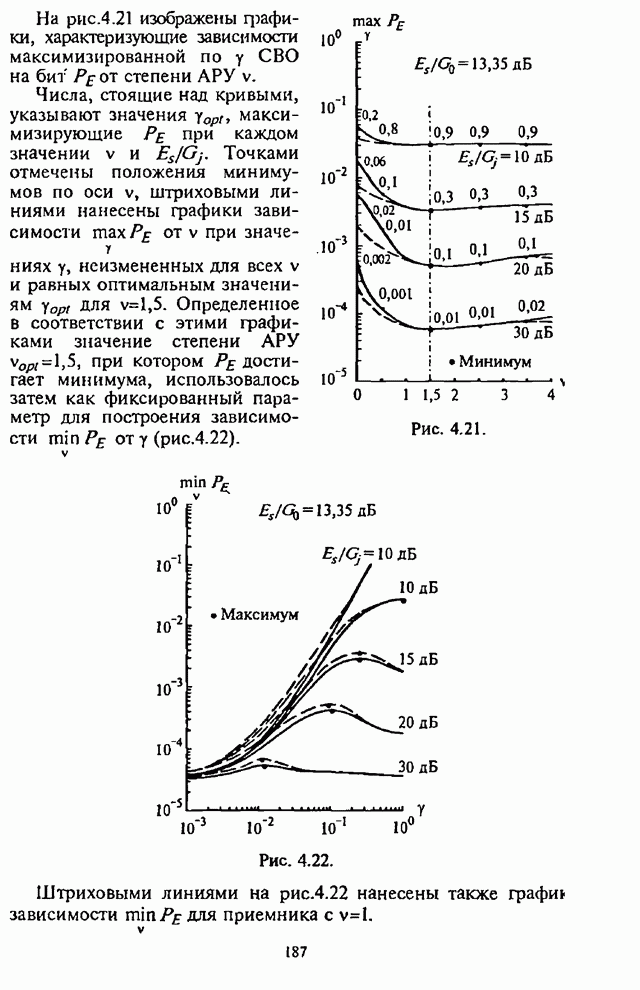
Как было показано выше, оптимальные алгоритмы обнаружения стохастических сигналов чрезвычайно трудоемки при практической реализации (см. рис.8.1). Более простым для реализации является энергетический обнаружитель Прайса-Урковица (рис.П.8.2.3) [86, 87].

Рис. П.8.2.3.
Нормированная статистика на выходе обнаружителя имеет вид:
 . (П.8.2.37)
. (П.8.2.37)
Вероятности
ложной тревоги ![]() и
обнаружения сигнала могут быть определены из выражений
и
обнаружения сигнала могут быть определены из выражений
![]() , (П.8.2.38)
, (П.8.2.38)
![]() , (П.8.2.39)
, (П.8.2.39)
где
![]() , и
, и ![]() , - функция
распределения для центрального и нецентрального
, - функция
распределения для центрального и нецентрального ![]() -распределения с
-распределения с ![]() степенями свободы и параметром
нецентральности
степенями свободы и параметром
нецентральности ![]() .
.
Значение порогового уровня находится как решение уравнения
![]() . (П.8.2.40)
. (П.8.2.40)
Для
решения данного уравнения можно использовать численные алгоритмы, в частности,
алгоритм деления отрезка пополам. Для ![]() целесообразно воспользоваться
аппроксимациями обратной функции для центрального
целесообразно воспользоваться
аппроксимациями обратной функции для центрального ![]() -распределения [48]
-распределения [48]
![]() , (П.8.2.41)
, (П.8.2.41)
 , (П.8.2.42)
, (П.8.2.42)
или более точной аппроксимацией Корниша-Фишера [109]
![]() , (П.8.2.43)
, (П.8.2.43)
где
![]() . После
вычисления порогового уровня
. После
вычисления порогового уровня ![]() вероятность обнаружения определяется из
выражения (П.8.2.39), где
вероятность обнаружения определяется из
выражения (П.8.2.39), где
 . (П.8.2.44)
. (П.8.2.44)
Из (П.8.2.38)-(П.8.2.44) следует алгоритм расчета характеристик обнаружителя сигналов неизвестной структуры.
1.
Для каждого ![]()
![]() вычисляются
вычисляются ![]() ;
; ![]() ;
; ![]() .
.
2.
Задается вероятность ложной тревоги ![]() ,
, ![]() . По заданной вероятности ложной тревоги
вычисляется
. По заданной вероятности ложной тревоги
вычисляется ![]() .
.
3.
По найденному значению ![]() по формулам (П.8.2.41)-(П.8.2.43)
определяется значение порогового уровня
по формулам (П.8.2.41)-(П.8.2.43)
определяется значение порогового уровня ![]() .
.
4.
Используя одну из процедур вычисления нецентрального ![]() -распределения, вычисляется
вероятность обнаружения
-распределения, вычисляется
вероятность обнаружения
![]() .
.
5.
Среднее время и дисперсия ![]() находятся по формулам (П.8.2.5) и
(П.8.2.10).
находятся по формулам (П.8.2.5) и
(П.8.2.10).
Алгоритм вычисления динамических характеристик при ограничении на число шагов обнаружения аналогичен рассмотренным ранее случаям, где в качестве выражений для среднего времени и дисперсии следует применять (П.8.2.15) и (П.8.2.18).
П.8.2.2.4. Обнаружители сигналов с постоянным уровнем ложной тревоги
В рассмотренных выше обнаружителях процедура обнаружения сигналов сводится к сравнению статистики, основанной на выборках входной смеси сигнала и помехи, с порогом. Однако, изменение интенсивности или закона распределения вероятностей помехи существенно ухудшает РХ обнаружителей, синтезированных по критерию максимума отношения правдоподобия. Так, например, изменение интенсивности помехи на 2 дБ приводит к изменению вероятности ложной тревоги в системе с фиксированным порогом на два порядка [110]. Поэтому возникает необходимость в специальных алгоритмах обработки с постоянным уровнем ложных тревог (ПУЛТ). Первоначально алгоритмы обработки с ПУЛТ появились для гауссовских помех с неизвестной мощностью. Стабилизация уровня ложной тревоги в этом случае сводится к оценке мощности помехи и установления соответствующего порога обнаружения.
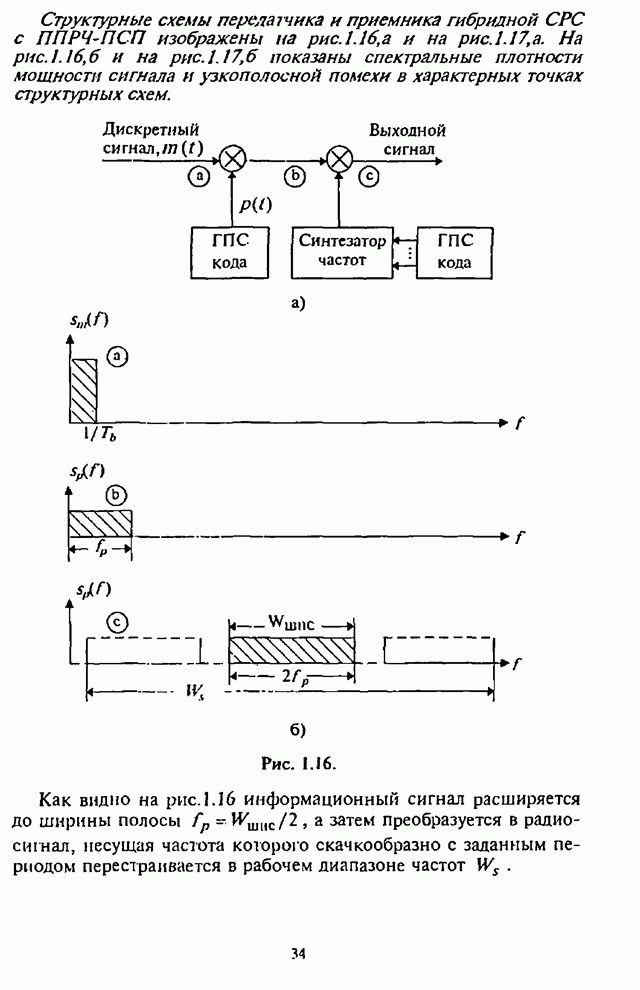
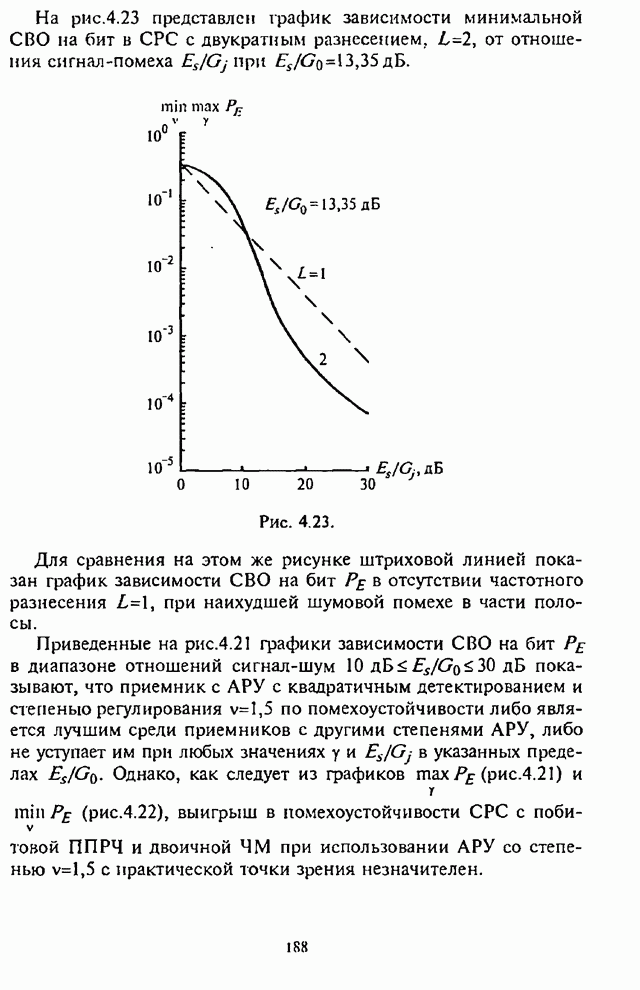
Структурная схема одного из вариантов такого обнаружителя изображена на рис.П.8.2.4.

Рис. П.8.2.4.
Она содержит линейный тракт приемника (ЛТП), квадратичный детектор (КД), линию задержки (ЛЗ), реализующую „скользящее окно", осредняющий сумматор, на выходе которого формируется сигнал, пропорциональный мощности шума, и пороговое устройство.
Величина
задержки между отводами ЛЗ приблизительно равна длительности принимаемого
сигнала. Сигнал с выхода центрального отвода ![]() сравнивается с произведением порогового
коэффициента
сравнивается с произведением порогового
коэффициента ![]() и
суммы
и
суммы ![]() .
Пороговый коэффициент
.
Пороговый коэффициент ![]() зависит от вероятности ложной тревоги и
величины „окна", а также числа отводов линии задержки. Правило принятия
гипотез имеет вид:
зависит от вероятности ложной тревоги и
величины „окна", а также числа отводов линии задержки. Правило принятия
гипотез имеет вид:
 (П.8.2.45)
(П.8.2.45)
Существуют различные комбинации обнаружителей данного типа [110,111]. Здесь ограничимся рассмотрением базового обнаружителя (рис.П.8.2.4). Приведем основные выражения для расчета вероятности ложной тревоги и обнаружения на одном шаге обнаружения.
Если на вход обнаружителя поступает только гауссовский шум, то статистика на выходе КД имеет плотность распределения вероятности
 , (П.8.2.46)
, (П.8.2.46)
где
![]() - средняя
мощность шума на входе детектора.
- средняя
мощность шума на входе детектора.
Если на вход детектора поступает смесь сигнала с шумом, то плотность распределения квадрата огибающей на выходе детектора имеет вид:
 , (П.8.2.47)
, (П.8.2.47)
где
![]() - амплитуда
сигнала,
- амплитуда
сигнала, ![]() -
отношение сигнал-шум. Обозначим через
-
отношение сигнал-шум. Обозначим через ![]() случайную величину на выходе
случайную величину на выходе ![]() -го отвода, не
совпадающего с центральным, а через
-го отвода, не
совпадающего с центральным, а через ![]() - на выходе центрального отвода, то
- на выходе центрального отвода, то ![]() имеет центральное
имеет центральное ![]() -распределение с двумя
степенями свободы, а
-распределение с двумя
степенями свободы, а ![]() -
центральное
-
центральное ![]() -распределение
при отсутствии сигнала и нецентральное
-распределение
при отсутствии сигнала и нецентральное ![]() -распределение с параметром
нецентральности
-распределение с параметром
нецентральности ![]() и
двумя степенями свободы при наличии сигнала. Так как величины на отводах ЛЗ независимы,
то случайная величина на выходе сумматора имеет центральное
и
двумя степенями свободы при наличии сигнала. Так как величины на отводах ЛЗ независимы,
то случайная величина на выходе сумматора имеет центральное ![]() -распределение с
-распределение с ![]() степенями свободы. Ее
плотность определяется из выражения
степенями свободы. Ее
плотность определяется из выражения
 , (П.8.2.48)
, (П.8.2.48)
где
![]() -
гамма-функция.
-
гамма-функция.
Вероятность ложной тревоги
 , (П.8.2.49)
, (П.8.2.49)
где
случайная величина ![]() имеет
при отсутствии сигнала центральное
имеет
при отсутствии сигнала центральное ![]() -распределение с
-распределение с ![]() и
и ![]() степенями свободы. Плотность
распределения вероятностей случайной величины
степенями свободы. Плотность
распределения вероятностей случайной величины ![]() определяется выражением [48]
определяется выражением [48]
 , (П.8.2.50)
, (П.8.2.50)
где
![]() -
бета-функция.
-
бета-функция.
Из (П.8.2.50) с учетом (П.8.2.49) получим выражение для вероятности ложной тревоги
 . (П.8.2.51)
. (П.8.2.51)
Вероятность
обнаружения также находится из (П.8.2.49) при условии, что ![]() имеет нецентральное
имеет нецентральное ![]() -распределение с
параметром нецентральности
-распределение с
параметром нецентральности ![]() и
и ![]() , a
, a ![]() имеет центральное
имеет центральное ![]() -распределение. Случайная
величина
-распределение. Случайная
величина
![]() (П.8.2.52)
(П.8.2.52)
в
данном случае имеет так называемое нецентральное ![]() -распределение со степенями свободы
-распределение со степенями свободы ![]() , параметром
нецентральности
, параметром
нецентральности ![]() и
плотностью распределения [48,112]
и
плотностью распределения [48,112]
 . (П8.2.53)
. (П8.2.53)
Вероятность обнаружения может быть представлена следующим образом:
 . (П.8.3.54)
. (П.8.3.54)
После подстановки (П.8.2.53) в (П.8.2.54) и интегрирования с учетом свойств бета-функции [48] получим выражение для вероятности обнаружения в виде ряда
 . (П.8.2.55)
. (П.8.2.55)
Формула
(П.8.2.55) устанавливает функциональную зависимость между вероятностью
обнаружения и величиной порогового множителя ![]() , который определяется через вероятность
ложной тревоги как решение уравнения (П.8.2.51). Заметим, что время расчета можно
сократить, если использовать рекуррентные формулы для вычисления функции
распределения [48].Выражение для вероятности обнаружения в этом случае можно
записать в виде:
, который определяется через вероятность
ложной тревоги как решение уравнения (П.8.2.51). Заметим, что время расчета можно
сократить, если использовать рекуррентные формулы для вычисления функции
распределения [48].Выражение для вероятности обнаружения в этом случае можно
записать в виде:
![]() , (П.8.2.56)
, (П.8.2.56)
где
 (П.8.2.57)
(П.8.2.57)
Выражения
(П.8.2.55), (П.8.2.56) и (П.8.2.57) позволяют рассчитать вероятность
обнаружения как функцию от отношения сигнал-шум при фиксированных вероятностях
ложных тревог ![]() и
числа отводов
и
числа отводов ![]() в
линии задержки.
в
линии задержки.
В
предельном случае при ![]() имеем
имеем ![]() -распределение с двумя степенями свободы.
Откуда следует, что пороговый коэффициент
-распределение с двумя степенями свободы.
Откуда следует, что пороговый коэффициент
![]() , (П.8.2.58)
, (П.8.2.58)
а вероятность обнаружения
![]() , (П.8.2.59)
, (П.8.2.59)
где
![]() - функция
распределения для
- функция
распределения для ![]() с
с
![]() степенями
свободы и параметром нецентральности
степенями
свободы и параметром нецентральности ![]() , определяемая (П.8.2.44). Из (П.8.2.55)-(П.8.2.56)
следует алгоритм расчета вероятностно-временных характеристик обнаружителей с
постоянным уровнем ложной тревоги.
, определяемая (П.8.2.44). Из (П.8.2.55)-(П.8.2.56)
следует алгоритм расчета вероятностно-временных характеристик обнаружителей с
постоянным уровнем ложной тревоги.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие
- Введение
- Глава 1. Системы радиосвязи с расширением спектра сигналов методом псевдослучайной перестройки рабочей частоты: общие принципы
- 1.1. Краткая характеристика расширения спектра сигналов методом ППРЧ
- 1.1.1. Основные принципы и методы расширения спектра сигналов
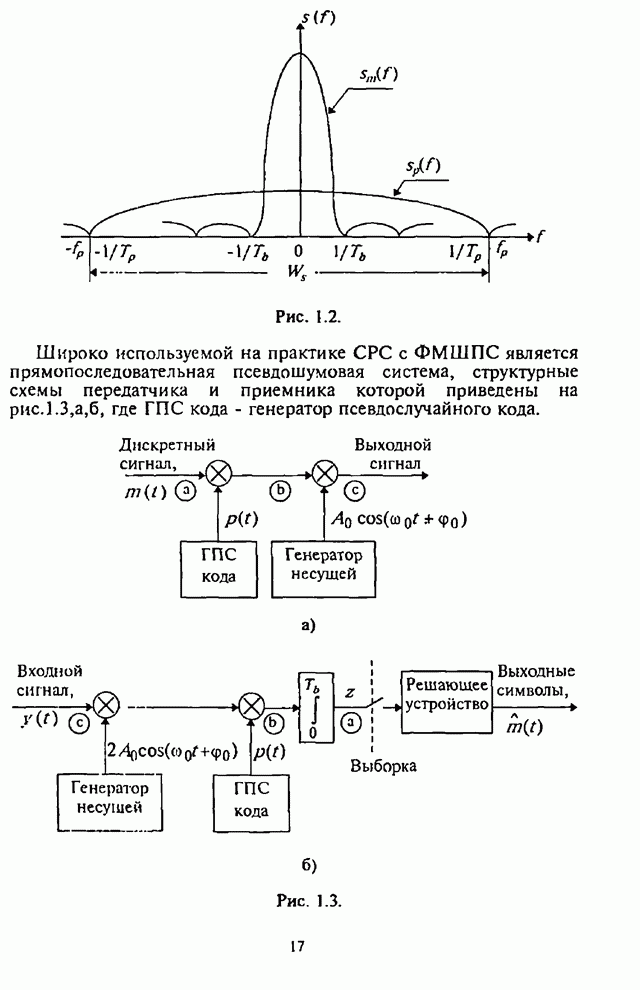
- 1.1.2. Метод псевдослучайной перестройки рабочей частоты
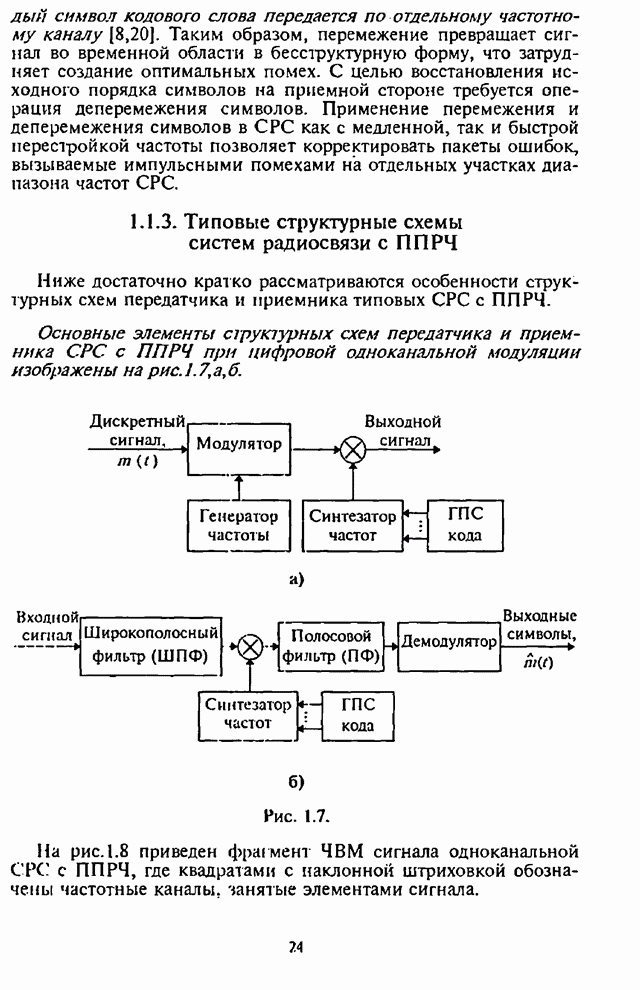
- 1.1.3. Типовые структурные схемы систем радиосвязи с ППРЧ
- 1.2. Коэффициент расширения спектра сигнала и запас помехоустойчивости системы радиосвязи с ППРЧ
- 1.3. Общая характеристика помехозащищенности систем радиосвязи с ППРЧ
- 1.3.1. Помехоустойчивость систем радиосвязи с ППРЧ
- 1.3.2. Скрытность сигналов систем радиосвязи с ППРЧ
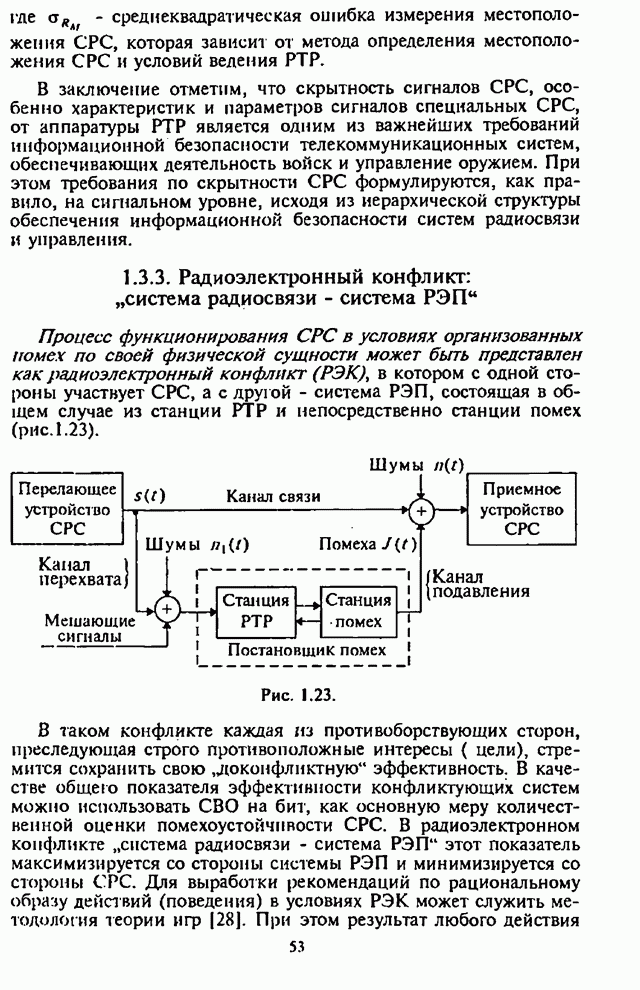
- 1.3.3. Радиоэлектронный конфликт: «система радиосвязи — система РЭП»
- 1.4. Модели и краткая характеристика основных видов помех
- Глава 2. Помехоустойчивость типовых систем радиосвязи с ППРЧ и частотной манипуляцией
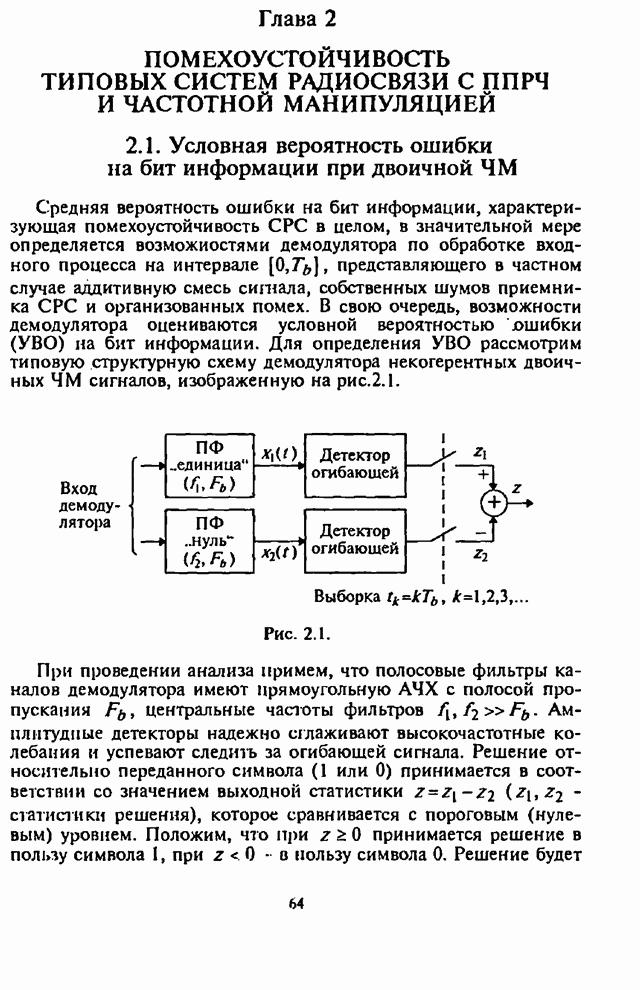
- 2.1. Условная вероятность ошибки на бит информации при двоичной ЧМ
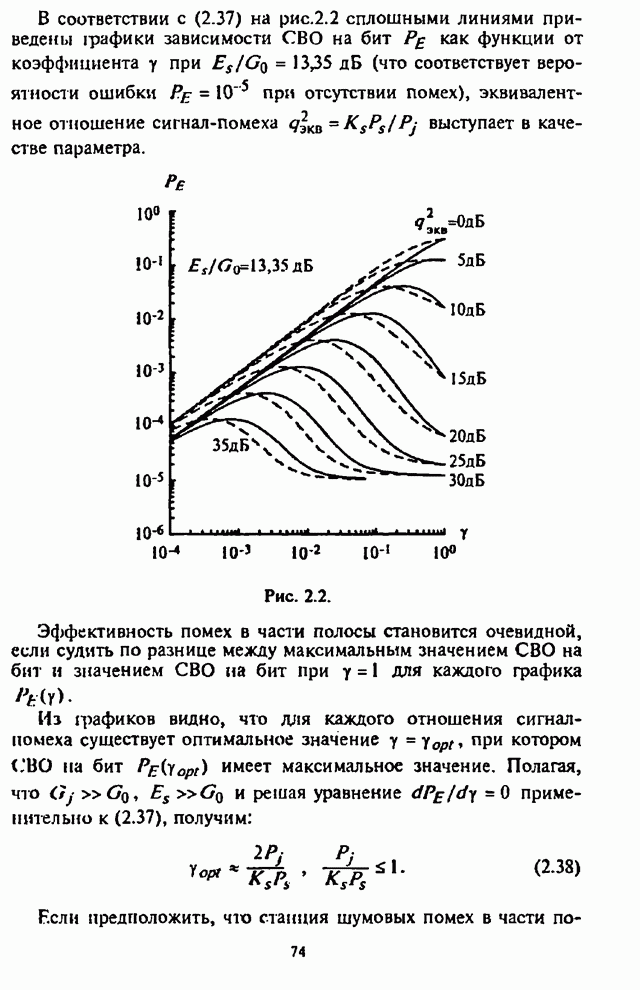
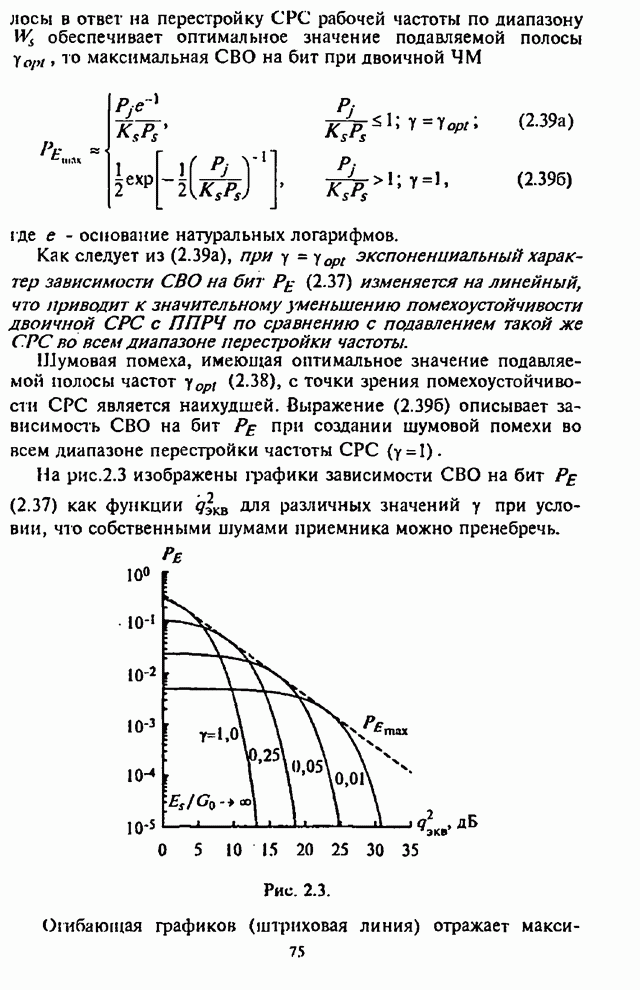
- 2.2. Оценка воздействия шумовой помехи в части полосы на системы радиосвязи с ППРЧ и неслучайной ЧМ
- 2.3. Оценка воздействия шумовой помехи в части полосы на системы радиосвязи с ППРЧ и случайной двоичной ЧМ
- 2.4. Оценка воздействия ответных помех на системы радиосвязи с ППРЧ и ЧМ
- 2.4.1. Оценка временных возможностей станции ответных помех
- 2.4.2. Оценка воздействия ответных шумовых помех на системы радиосвязи с ППРЧ и ЧМ
- 2.4.3. Оценка воздействия ответных гармонических помех на системы радиосвязи с ППРЧ и ЧМ
- 2.5. Помехоустойчивость систем радиосвязи с ППРЧ, двоичной ЧМ и блоковым кодированием
- Глава 3. Синтез и анализ эффективности адаптивных алгоритмов различения сигналов с ППРЧ, частотной модуляцией и разнесением символов по частоте
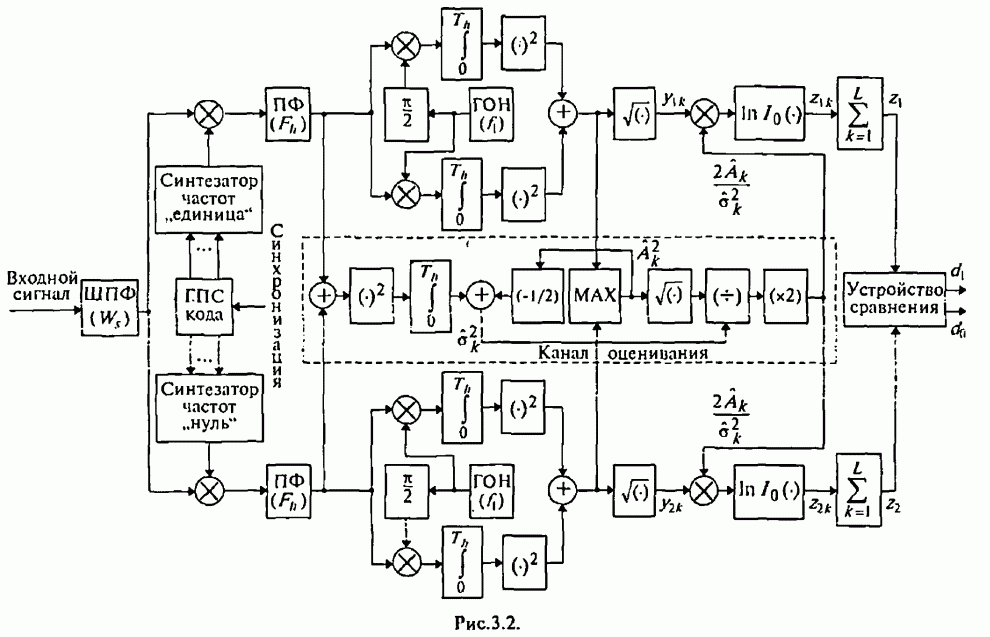
- 3.1. Синтез оптимального адаптивного алгоритма различения сигналов с внутрисимвольной ППРЧ и ЧМ
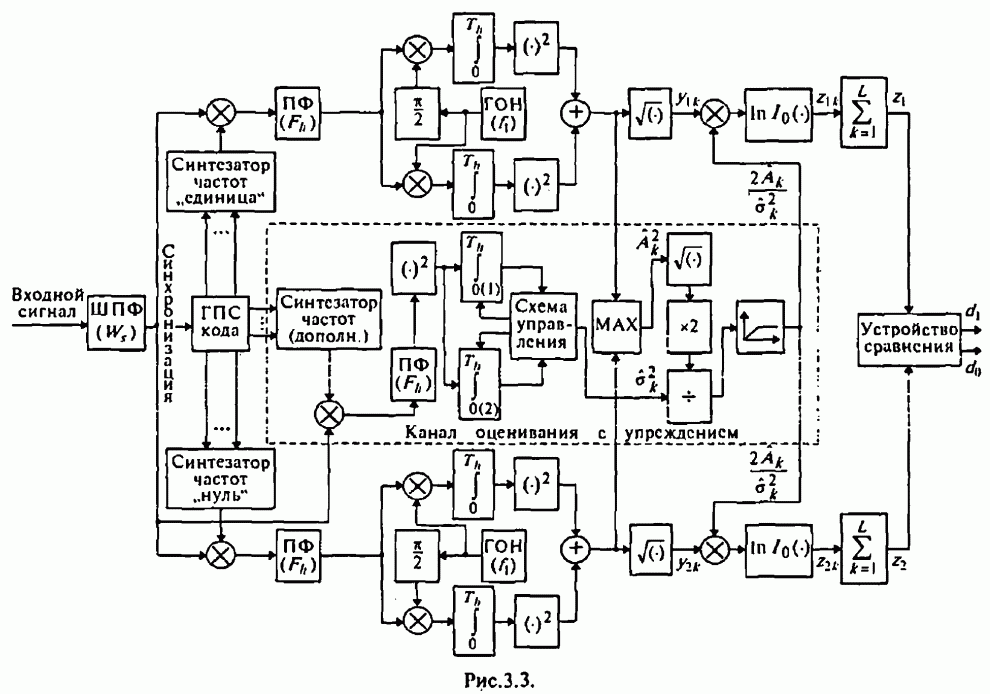
- 3.2. Квазиоптимальный адаптивный алгоритм различения сигналов с внутрисимвольной ППРЧ и двоичной ЧМ
- 3.3. Оценка помехоустойчивости синтезированного адаптивного алгоритма различения сигналов с внутрисимвольной ППРЧ и двоичной ЧМ
- 3.3.1. Случай «слабых» сигналов
- 3.3.2. Случай «сильных» сигналов
- Глава 4. Помехоустойчивость адаптивных алгоритмов демодуляции сигналов с внутрибитовой ППРЧ и двоичной частотной манипуляцией
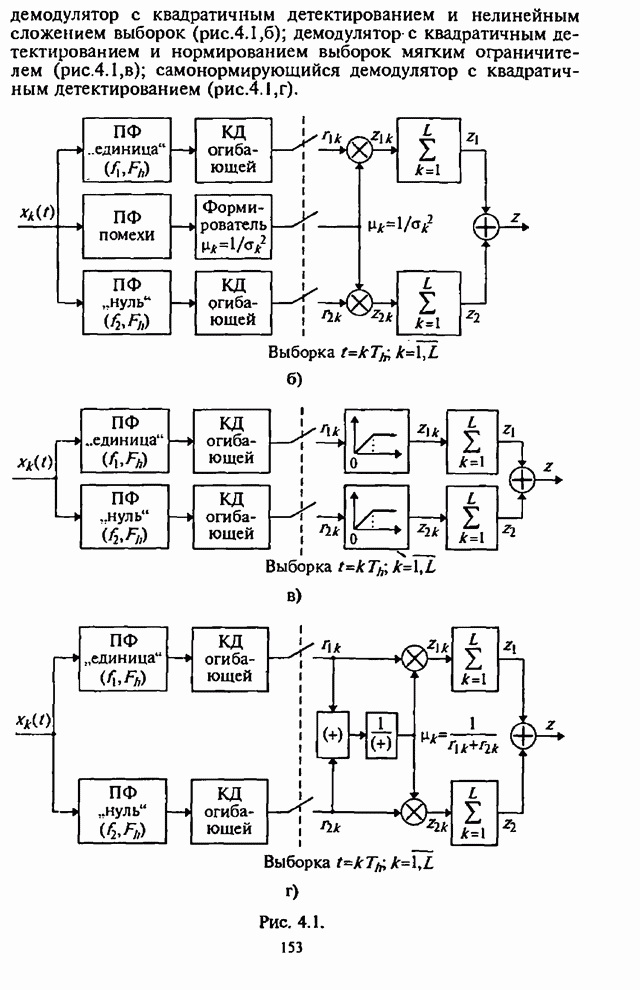
- 4.1. Структурные схемы демодуляторов
- 4.2. Помехоустойчивость демодулятора с линейным сложением выборок
- 4.3. Помехоустойчивость демодулятора с нелинейным сложением выборок
- 4.4. Помехоустойчивость демодулятора с мягким ограничителем
- 4.5. Помехоустойчивость самонормирующегося демодулятора
- 4.6. Влияние адаптивной регулировки усиления на помехоустойчивость СРС
- 4.7. Сравнительный анализ помехоустойчивости демодуляторов сигналов с внутрибитовой ППРЧ и двоичной ЧМ
- Глава 5. Помехоустойчивость систем радиосвязи с ППРЧ при совместном применении частотной модуляции, разнесения символов по частоте и блокового кодирования
- 5.1. Помехоустойчивость систем радиосвязи с ППРЧ при M-ичной ЧМ и L-кратным разнесении символов по частоте
- 5.1.1. Условная вероятность ошибки на бит информации
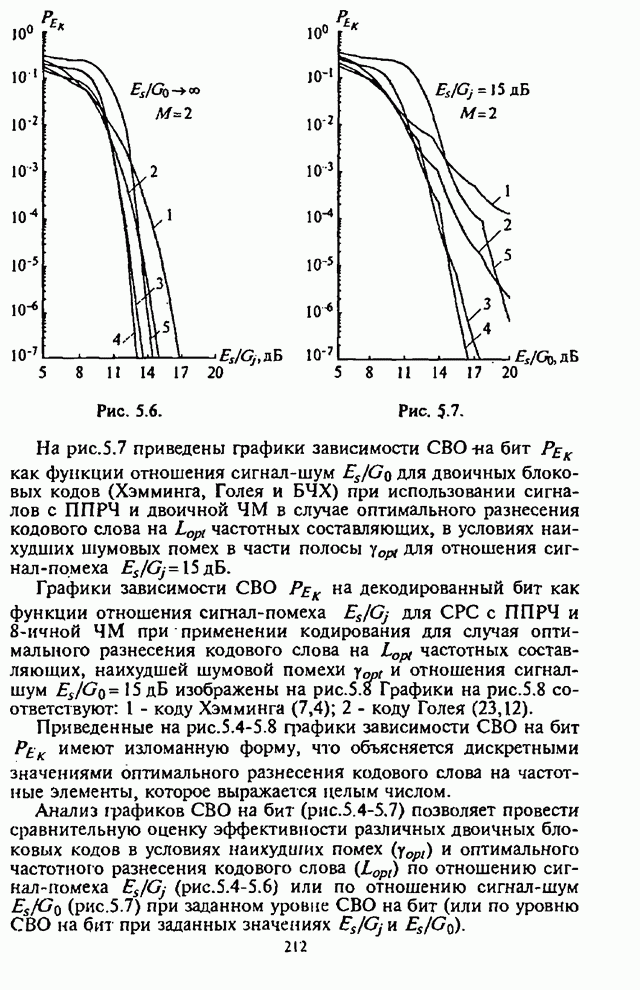
- 5.1.2. Анализ средней вероятности ошибки на бит информации
- 5.2. Помехоустойчивость систем радиосвязи с ППРЧ, M-ичной ЧМ, блоковым кодированием и L-кратным частотным разнесением кодовых слов
- 5.2.1. Структурная схема системы радиосвязи
- 5.2.2. Средняя вероятность ошибки на бит информации
- 5.2.3. Анализ средней вероятности ошибки на бит информации
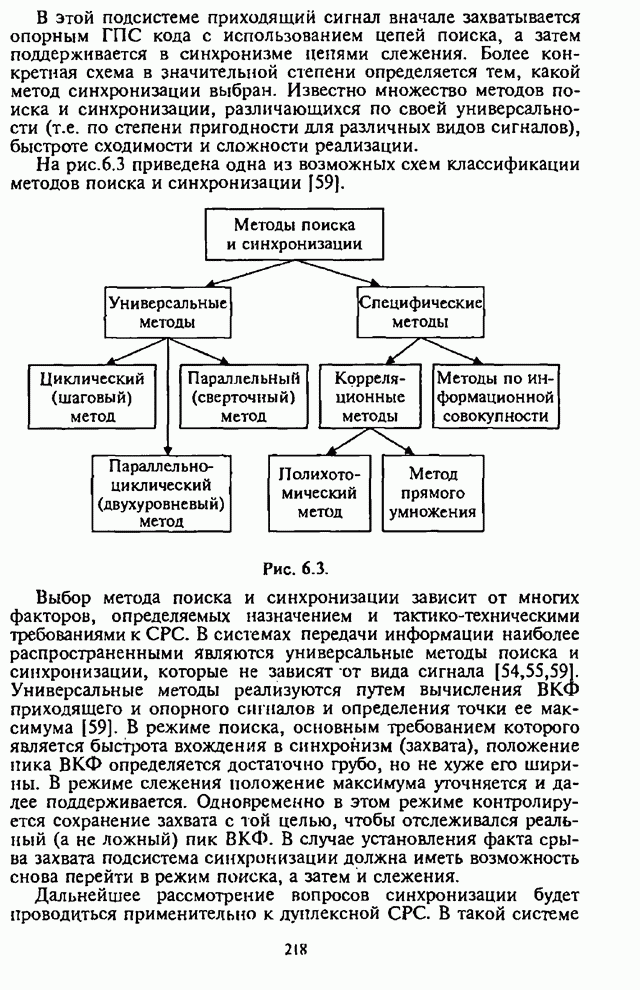
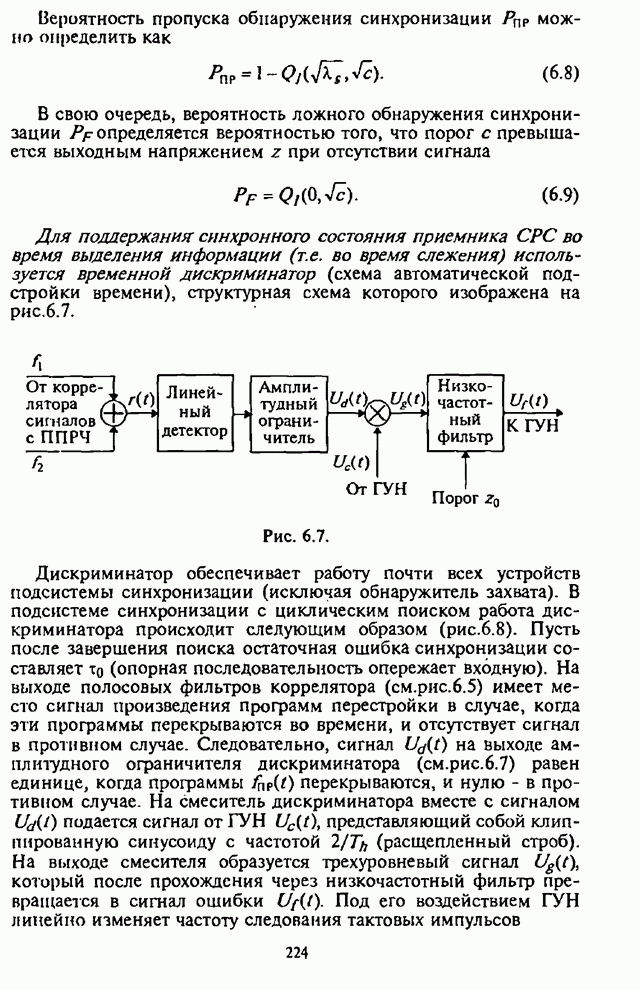
- Глава 6. Синхронизация в системах радиосвязи с псевдослучайной перестройкой рабочей частоты
- 6.1. Назначение подсистемы синхронизации
- 6.2. Описательная модель подсистемы синхронизации
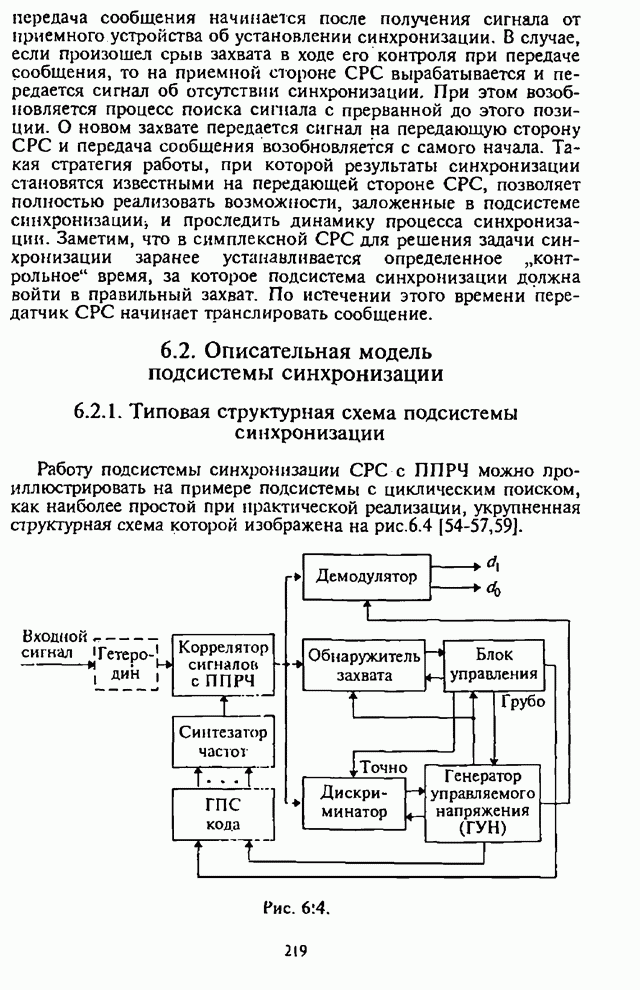
- 6.2.1. Типовая структурная схема подсистемы синхронизации
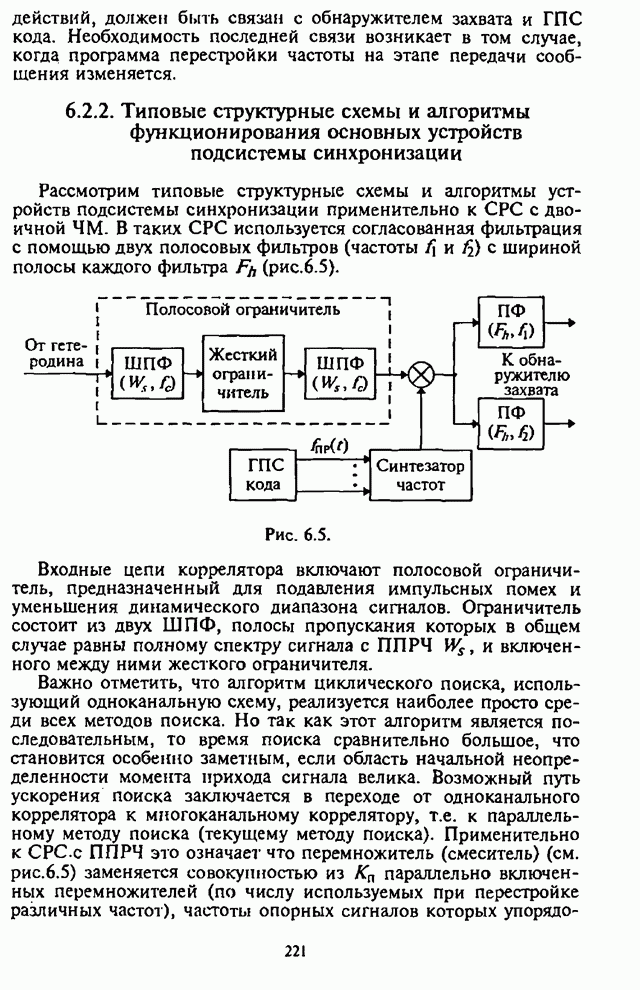
- 6.2.2. Типовые структурные схемы и алгоритмы функционирования основных устройств подсистемы синхронизации
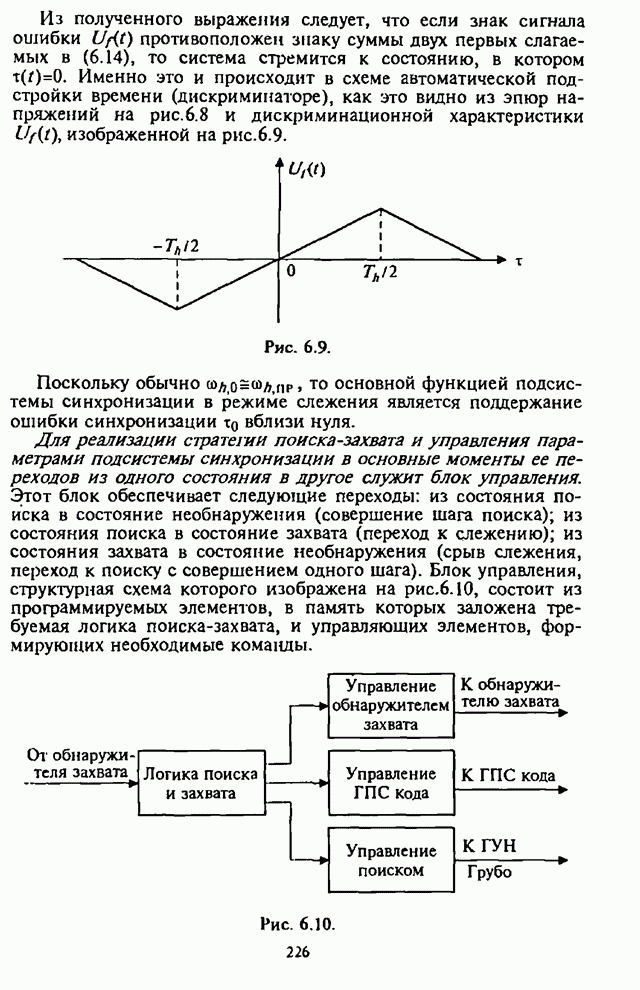
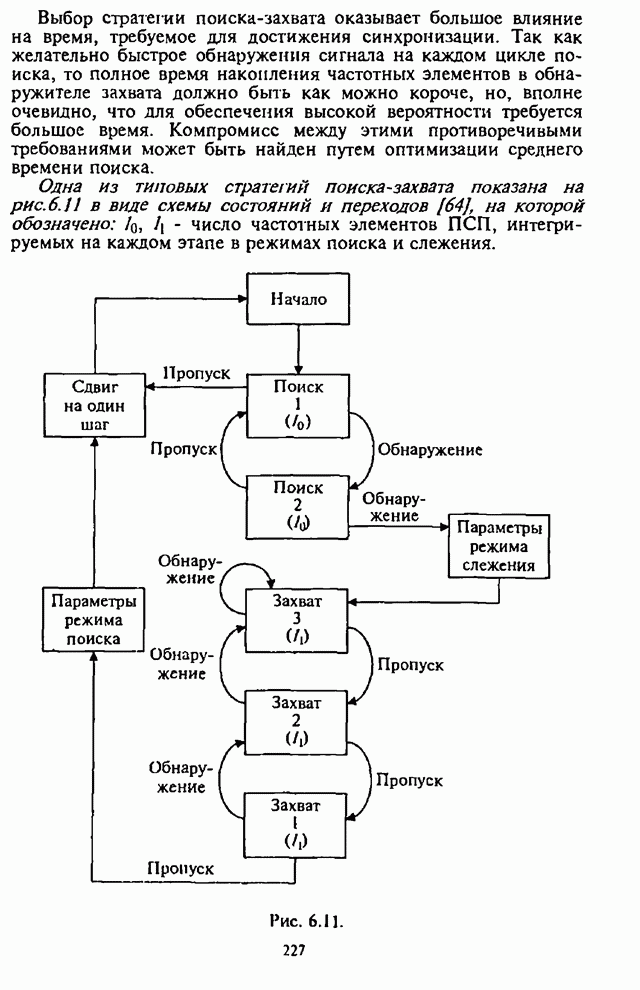
- 6.3. Показатели и оценка эффективности циклических процедур поиска
- Приложение П.6.1. Верхняя граница среднего нормированного времени поиска
- Приложение П.6.2. Верхняя граница вероятности правильного обнаружения
- Глава 7. Адаптивные антенные решетки в системах радиосвязи с псевдослучайной перестройкой рабочей частоты
- 7.1. Влияние сигналов с ППРЧ на характеристики адаптивной антенной решетки
- 7.2. Максиминный алгоритм обработки сигналов и помех
- 7.3. Реализация и возможности максиминного алгоритма
- 7.4. Модернизация максиминного алгоритма
- 7.4.1. Параметрическая обработка
- 7.4.2. Спектральная обработка
- 7.4.3. Обработка с упреждением
- Глава 8. Обнаружение сигналов с псевдослучайной перестройкой рабочей частоты
- 8.1. Обнаружение сигналов неизвестной структуры
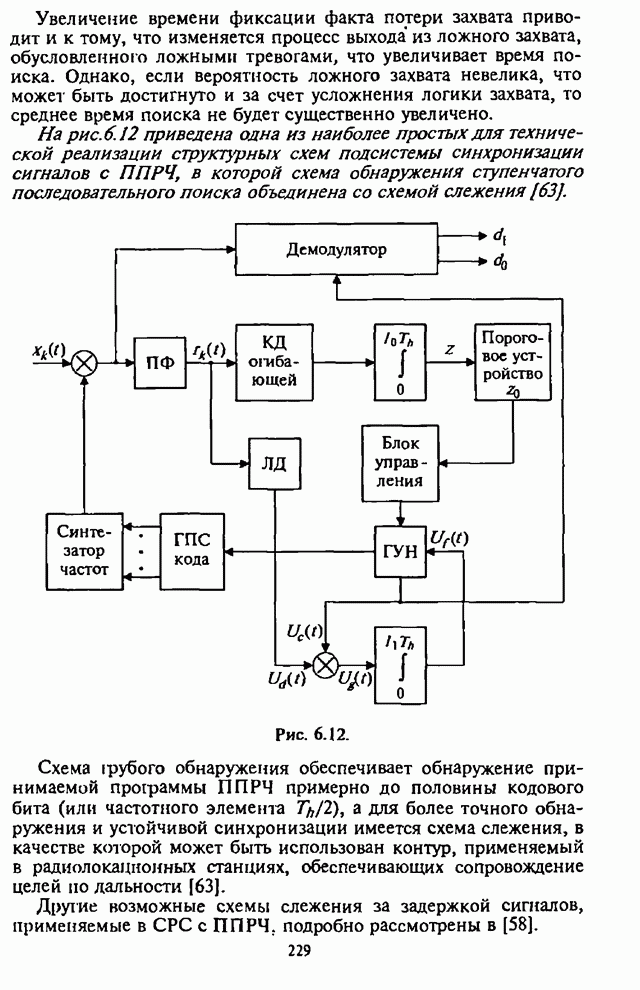
- 8.2. Широкополосный энергетический обнаружитель
- 8.3. Многоканальные энергетические обнаружители
- 8.3.1. Квазиоптимальный многоканальный обнаружитель
- 8.3.2. Многоканальный обнаружитель типа сумматора с блоком фильтров
- 8.3.3. Модель обнаружителя типа сумматора с блоком фильтров при перехвате сигналов с медленной ППРЧ
- 8.3.4. Многоканальный обнаружитель типа сумматора с блоком фильтров в части полосы
- 8.3.5. Рассогласование по времени и частоте между характеристиками сигнала с ППРЧ и параметрами обнаружителя
- 8.4. Многоканальный адаптивный энергетический обнаружитель в условиях воздействия мешающих сигналов
- 8.4.1. Структурная схема многоканального адаптивного энергетического обнаружителя с регулировкой порогового уровня
- 8.4.2. Вероятность ложной тревоги и адаптивная регулировка порогового уровня
- 8.4.3. Вероятность обнаружения
- 8.4.4. Влияние рассогласования по времени на обнаружение сигналов
- 8.5. Другие возможные типы обнаружителей сигналов с ППРЧ
- 8.5.1. Корреляционный радиометр
- 8.5.2. Цифровой анализатор спектра
- 8.5.3. Метод вскрытия частотно-временной матрицы сигнала с ППРЧ
- Приложение П.8.1. Алгоритмы вычисления обобщенной Q-функции Маркума
- П.8.1.1. Постановка задачи
- П.8.1.2. Представление степенными рядами
- П.8.1.3. Представление в виде рядов Неймана
- П.8.1.4. Численное интегрирование
- П.8.1.5. Гауссовская аппроксимация
- П.8.1.6. Численные результаты
- Приложение П.8.2. Анализ вероятностно-временных характеристик алгоритмов обнаружения сигналов
- П.8.2.1. Вероятностно-временные характеристики основных видов обнаружителей
- П.8.2.2 Алгоритмы расчета вероятностно-временных характеристик основных видов обнаружителей
- П.8.2.3. Численные результаты
- СПИСОК ОСНОВНЫХ СОКРАЩЕНИЙ
- ОСНОВНЫЕ УСЛОВНЫЕ ОБОЗНАЧЕНИЯ
- СПИСОК ЛИТЕРАТУРЫ