| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Приложение П.8.1. Алгоритмы вычисления обобщенной Q-функции Маркума
П.8.1.1. Постановка задачи
При
обнаружении сигналов в гауссовском шуме с равномерной спектральной плотностью
мощности в пределах рассматриваемой полосы частот статистика, по которой
принимается решение, имеет нецентральное ![]() -распределение. При этом параметр
нецентральности равен удвоенному отношению сигнал-шум
-распределение. При этом параметр
нецентральности равен удвоенному отношению сигнал-шум ![]() , число степеней свободы равно
удвоенному произведению длительности наблюдения на ширину полосы пропускания
входных цепей обнаружителя
, число степеней свободы равно
удвоенному произведению длительности наблюдения на ширину полосы пропускания
входных цепей обнаружителя ![]() . В отсутствии сигнала статистика имеет
центральное
. В отсутствии сигнала статистика имеет
центральное ![]() -распределение.
Поэтому для расчета вероятностей ложной тревоги и обнаружения сигналов
требуется вычислять интегралы от плотности вероятностей
-распределение.
Поэтому для расчета вероятностей ложной тревоги и обнаружения сигналов
требуется вычислять интегралы от плотности вероятностей ![]() -распределения с
-распределения с ![]() степенями свободы,
которое определяется следующим образом. Если
степенями свободы,
которое определяется следующим образом. Если ![]() - независимые нормально распределенные
случайные величины с параметрами
- независимые нормально распределенные
случайные величины с параметрами ![]() , соответственно, то распределение
случайной величины
, соответственно, то распределение
случайной величины
![]() (П.8.1.1)
(П.8.1.1)
называется
нецентральным ![]() -распределением
с
-распределением
с ![]() степенями
свободы и параметром нецентральности
степенями
свободы и параметром нецентральности
![]() . (П.8.1.2)
. (П.8.1.2)
При
![]() распределение
называется центральным
распределение
называется центральным ![]() -распределением.
-распределением.
Классические
алгоритмы расчета нецентрального ![]() -распределения, применяемые в
математической статистике, становятся малоэффективными при тех значениях
параметров, которые имеют место в задачах обнаружения. Поэтому в настоящее
время не ослабевает интерес к разработке эффективных алгоритмов расчета функции
нецентрального
-распределения, применяемые в
математической статистике, становятся малоэффективными при тех значениях
параметров, которые имеют место в задачах обнаружения. Поэтому в настоящее
время не ослабевает интерес к разработке эффективных алгоритмов расчета функции
нецентрального ![]() -распределения
с высокой точностью, о чем свидетельствует ряд публикаций [87,98-106]. При этом
расчет рабочих характеристик обнаружителей выделен в специфическую задачу,
связанную с вычислением обобщенной
-распределения
с высокой точностью, о чем свидетельствует ряд публикаций [87,98-106]. При этом
расчет рабочих характеристик обнаружителей выделен в специфическую задачу,
связанную с вычислением обобщенной ![]() -функции Маркума или
-функции Маркума или ![]() -функции. Алгоритмы расчета
указанных функций используют разложение в степенные ряды [100,101] или ряды по
функциям Бесселя (ряды Неймана) [102,103], численное интегрирование, основанное
на методе перевала вычисления контурных интегралов [105,106], а также различные
варианты гауссовской аппроксимации.
-функции. Алгоритмы расчета
указанных функций используют разложение в степенные ряды [100,101] или ряды по
функциям Бесселя (ряды Неймана) [102,103], численное интегрирование, основанное
на методе перевала вычисления контурных интегралов [105,106], а также различные
варианты гауссовской аппроксимации.
Ниже
приводятся систематизация разрозненных подходов к расчету распределения ![]() , модификация
алгоритмов, анализ вычислительной устойчивости и границ применимости, сравнение
результатов, полученных по различным алгоритмам.
, модификация
алгоритмов, анализ вычислительной устойчивости и границ применимости, сравнение
результатов, полученных по различным алгоритмам.
Как
известно [87,98,99], рабочие характеристики энергетических обнаружителей:
вероятности ![]() -
ложного обнаружения,
-
ложного обнаружения, ![]() -
обнаружения и
-
обнаружения и ![]() -
пропуска сигнала выражаются через интегральные функции центрального и
нецентрального
-
пропуска сигнала выражаются через интегральные функции центрального и
нецентрального ![]() -распределения
-распределения
![]() , (П.8.1.3)
, (П.8.1.3)
где
 - (П.8.1.4)
- (П.8.1.4)
интегральная
функция центрального ![]() -распределения;
-распределения;
 -
(П.8.1.5)
-
(П.8.1.5)
интегральная
функция нецентрального ![]() -распределения;
-распределения; ![]() - порог обнаружения;
- порог обнаружения; ![]() - число степеней
свободы (
- число степеней
свободы (![]() ,
, ![]() - время,
- время, ![]() - ширина полосы).
- ширина полосы).
В
классическом варианте нецентральное ![]() -распределение выражается через
центральное. Действительно, плотность вероятностей для нецентрального
-распределение выражается через
центральное. Действительно, плотность вероятностей для нецентрального ![]() -распределения с учетом
представления функции Бесселя в виде степенного ряда
-распределения с учетом
представления функции Бесселя в виде степенного ряда
 (П.8.1.6)
(П.8.1.6)
запишется следующим образом
 , (П.8.1.7)
, (П.8.1.7)
где
 -
(П.8.1.8)
-
(П.8.1.8)
плотность
вероятностей центрального ![]() -распрсделения. После интегрирования
(П.8.1.7) получим выражение для функции распределения
-распрсделения. После интегрирования
(П.8.1.7) получим выражение для функции распределения
 , (П.8.1.9)
, (П.8.1.9)
где
для четных ![]()
![]() . (П.8.1.10)
. (П.8.1.10)
Таким
образом, после подстановки (П.8.1.10) в (П.8.1.9) получим выражение для ![]() в виде степенного ряда
в виде степенного ряда
![]() . (П.8.1.11)
. (П.8.1.11)
Исторически
сложилось, что наряду с распространенным в математической статистике
центральным и нецентральным ![]() -распределением в задачах обнаружения
рассматриваются обобщенная
-распределением в задачах обнаружения
рассматриваются обобщенная ![]() -функция Маркума и
-функция Маркума и ![]() - функция, которые с помощью
замены переменных сводятся к распределению
- функция, которые с помощью
замены переменных сводятся к распределению ![]() . Для этих функций имеют место следующие
интегральные представления [100-102]:
. Для этих функций имеют место следующие
интегральные представления [100-102]:
 , (П.8.1.12)
, (П.8.1.12)
где
![]() и
и ![]() - параметры;
- параметры;
 (П.8.1.13)
(П.8.1.13)
обозначает
вероятность некогерентного обнаружения ![]() импульсов;
импульсов; ![]() - отношение сигнал-шум для одного
импульса;
- отношение сигнал-шум для одного
импульса; ![]() -
нормированный порог обнаружения.
-
нормированный порог обнаружения.
Между указанными функциями существует взаимосвязь:
 (П.8.1.14)
(П.8.1.14)
Таким образом, имея расчетные формулы для одной из функций, можно рассчитать другие функции, а, следовательно, и рабочие характеристики обнаружителей.
Для
расчета обобщенной ![]() -функции
Маркума хорошо известно представление в виде ряда Неймана [102]:
-функции
Маркума хорошо известно представление в виде ряда Неймана [102]:
 ; (П.8.1.15)
; (П.8.1.15)
 . (П.8.1.16)
. (П.8.1.16)
Представления через степенные ряды (П.8.1.11) и ряды Неймана (П.1.15), (П.1.16) являются основой для построения целого ряда эффективных вычислительных алгоритмов.
Для удобства сравнения с результатами, опубликованными в первоисточниках, сохраним обозначения, используемые в них.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие
- Введение
- Глава 1. Системы радиосвязи с расширением спектра сигналов методом псевдослучайной перестройки рабочей частоты: общие принципы
- 1.1. Краткая характеристика расширения спектра сигналов методом ППРЧ
- 1.1.1. Основные принципы и методы расширения спектра сигналов
- 1.1.2. Метод псевдослучайной перестройки рабочей частоты
- 1.1.3. Типовые структурные схемы систем радиосвязи с ППРЧ
- 1.2. Коэффициент расширения спектра сигнала и запас помехоустойчивости системы радиосвязи с ППРЧ
- 1.3. Общая характеристика помехозащищенности систем радиосвязи с ППРЧ
- 1.3.1. Помехоустойчивость систем радиосвязи с ППРЧ
- 1.3.2. Скрытность сигналов систем радиосвязи с ППРЧ
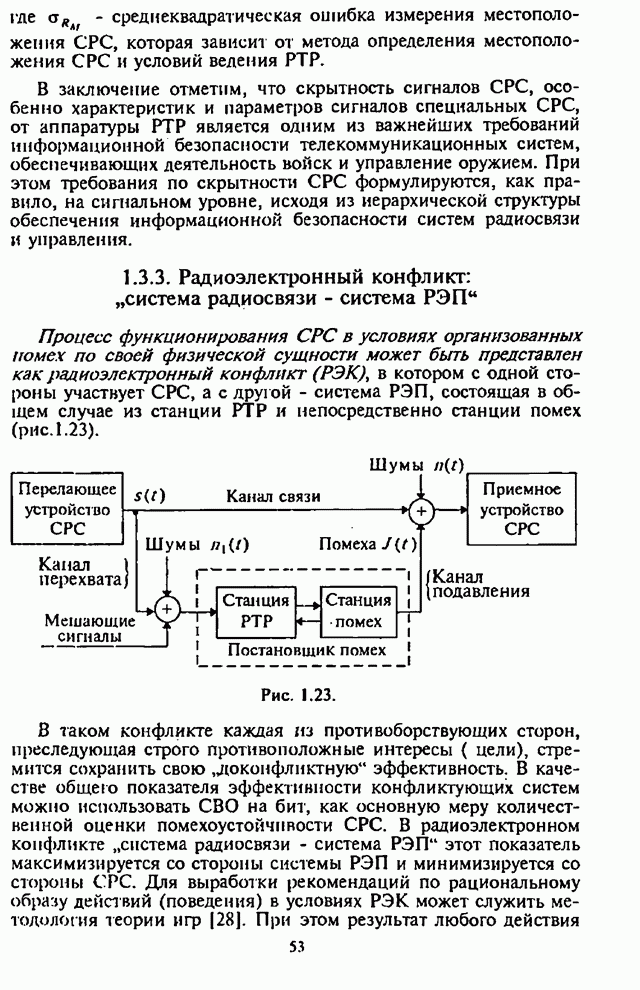
- 1.3.3. Радиоэлектронный конфликт: «система радиосвязи — система РЭП»
- 1.4. Модели и краткая характеристика основных видов помех
- Глава 2. Помехоустойчивость типовых систем радиосвязи с ППРЧ и частотной манипуляцией
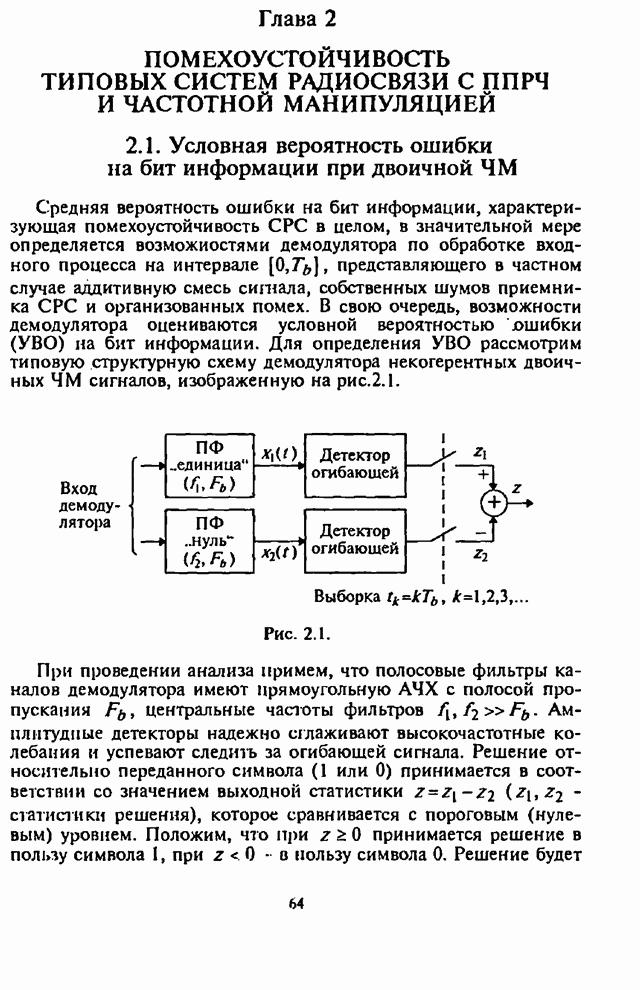
- 2.1. Условная вероятность ошибки на бит информации при двоичной ЧМ
- 2.2. Оценка воздействия шумовой помехи в части полосы на системы радиосвязи с ППРЧ и неслучайной ЧМ
- 2.3. Оценка воздействия шумовой помехи в части полосы на системы радиосвязи с ППРЧ и случайной двоичной ЧМ
- 2.4. Оценка воздействия ответных помех на системы радиосвязи с ППРЧ и ЧМ
- 2.4.1. Оценка временных возможностей станции ответных помех
- 2.4.2. Оценка воздействия ответных шумовых помех на системы радиосвязи с ППРЧ и ЧМ
- 2.4.3. Оценка воздействия ответных гармонических помех на системы радиосвязи с ППРЧ и ЧМ
- 2.5. Помехоустойчивость систем радиосвязи с ППРЧ, двоичной ЧМ и блоковым кодированием
- Глава 3. Синтез и анализ эффективности адаптивных алгоритмов различения сигналов с ППРЧ, частотной модуляцией и разнесением символов по частоте
- 3.1. Синтез оптимального адаптивного алгоритма различения сигналов с внутрисимвольной ППРЧ и ЧМ
- 3.2. Квазиоптимальный адаптивный алгоритм различения сигналов с внутрисимвольной ППРЧ и двоичной ЧМ
- 3.3. Оценка помехоустойчивости синтезированного адаптивного алгоритма различения сигналов с внутрисимвольной ППРЧ и двоичной ЧМ
- 3.3.1. Случай «слабых» сигналов
- 3.3.2. Случай «сильных» сигналов
- Глава 4. Помехоустойчивость адаптивных алгоритмов демодуляции сигналов с внутрибитовой ППРЧ и двоичной частотной манипуляцией
- 4.1. Структурные схемы демодуляторов
- 4.2. Помехоустойчивость демодулятора с линейным сложением выборок
- 4.3. Помехоустойчивость демодулятора с нелинейным сложением выборок
- 4.4. Помехоустойчивость демодулятора с мягким ограничителем
- 4.5. Помехоустойчивость самонормирующегося демодулятора
- 4.6. Влияние адаптивной регулировки усиления на помехоустойчивость СРС
- 4.7. Сравнительный анализ помехоустойчивости демодуляторов сигналов с внутрибитовой ППРЧ и двоичной ЧМ
- Глава 5. Помехоустойчивость систем радиосвязи с ППРЧ при совместном применении частотной модуляции, разнесения символов по частоте и блокового кодирования
- 5.1. Помехоустойчивость систем радиосвязи с ППРЧ при M-ичной ЧМ и L-кратным разнесении символов по частоте
- 5.1.1. Условная вероятность ошибки на бит информации
- 5.1.2. Анализ средней вероятности ошибки на бит информации
- 5.2. Помехоустойчивость систем радиосвязи с ППРЧ, M-ичной ЧМ, блоковым кодированием и L-кратным частотным разнесением кодовых слов
- 5.2.1. Структурная схема системы радиосвязи
- 5.2.2. Средняя вероятность ошибки на бит информации
- 5.2.3. Анализ средней вероятности ошибки на бит информации
- Глава 6. Синхронизация в системах радиосвязи с псевдослучайной перестройкой рабочей частоты
- 6.1. Назначение подсистемы синхронизации
- 6.2. Описательная модель подсистемы синхронизации
- 6.2.1. Типовая структурная схема подсистемы синхронизации
- 6.2.2. Типовые структурные схемы и алгоритмы функционирования основных устройств подсистемы синхронизации
- 6.3. Показатели и оценка эффективности циклических процедур поиска
- Приложение П.6.1. Верхняя граница среднего нормированного времени поиска
- Приложение П.6.2. Верхняя граница вероятности правильного обнаружения
- Глава 7. Адаптивные антенные решетки в системах радиосвязи с псевдослучайной перестройкой рабочей частоты
- 7.1. Влияние сигналов с ППРЧ на характеристики адаптивной антенной решетки
- 7.2. Максиминный алгоритм обработки сигналов и помех
- 7.3. Реализация и возможности максиминного алгоритма
- 7.4. Модернизация максиминного алгоритма
- 7.4.1. Параметрическая обработка
- 7.4.2. Спектральная обработка
- 7.4.3. Обработка с упреждением
- Глава 8. Обнаружение сигналов с псевдослучайной перестройкой рабочей частоты
- 8.1. Обнаружение сигналов неизвестной структуры
- 8.2. Широкополосный энергетический обнаружитель
- 8.3. Многоканальные энергетические обнаружители
- 8.3.1. Квазиоптимальный многоканальный обнаружитель
- 8.3.2. Многоканальный обнаружитель типа сумматора с блоком фильтров
- 8.3.3. Модель обнаружителя типа сумматора с блоком фильтров при перехвате сигналов с медленной ППРЧ
- 8.3.4. Многоканальный обнаружитель типа сумматора с блоком фильтров в части полосы
- 8.3.5. Рассогласование по времени и частоте между характеристиками сигнала с ППРЧ и параметрами обнаружителя
- 8.4. Многоканальный адаптивный энергетический обнаружитель в условиях воздействия мешающих сигналов
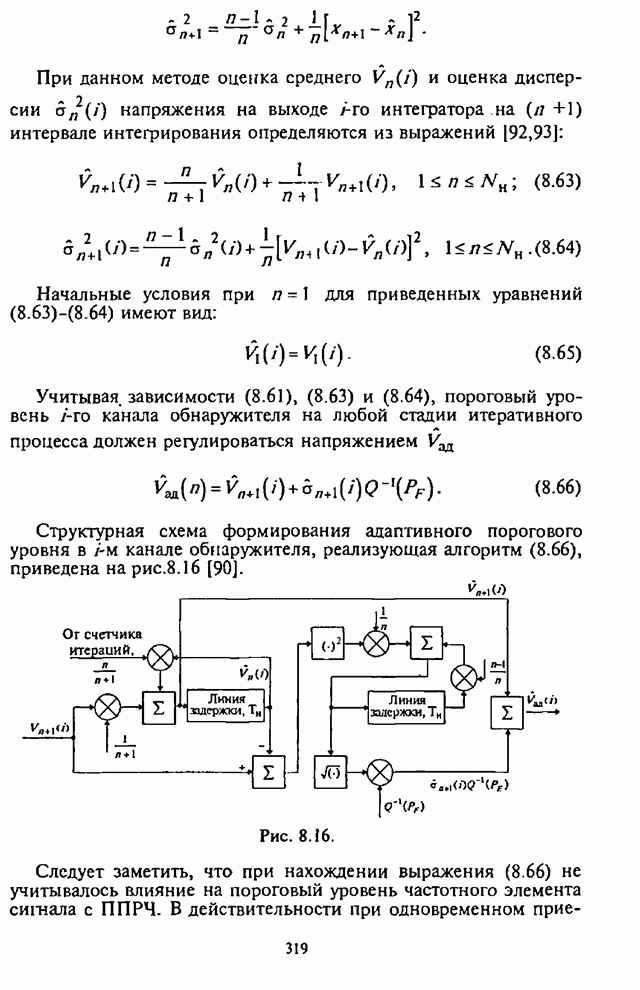
- 8.4.1. Структурная схема многоканального адаптивного энергетического обнаружителя с регулировкой порогового уровня
- 8.4.2. Вероятность ложной тревоги и адаптивная регулировка порогового уровня
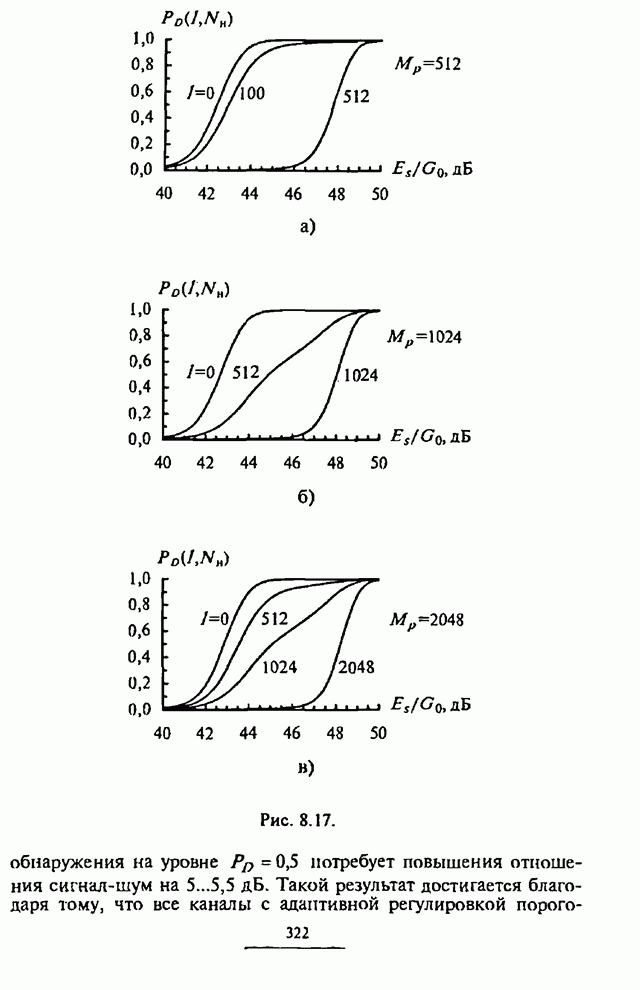
- 8.4.3. Вероятность обнаружения
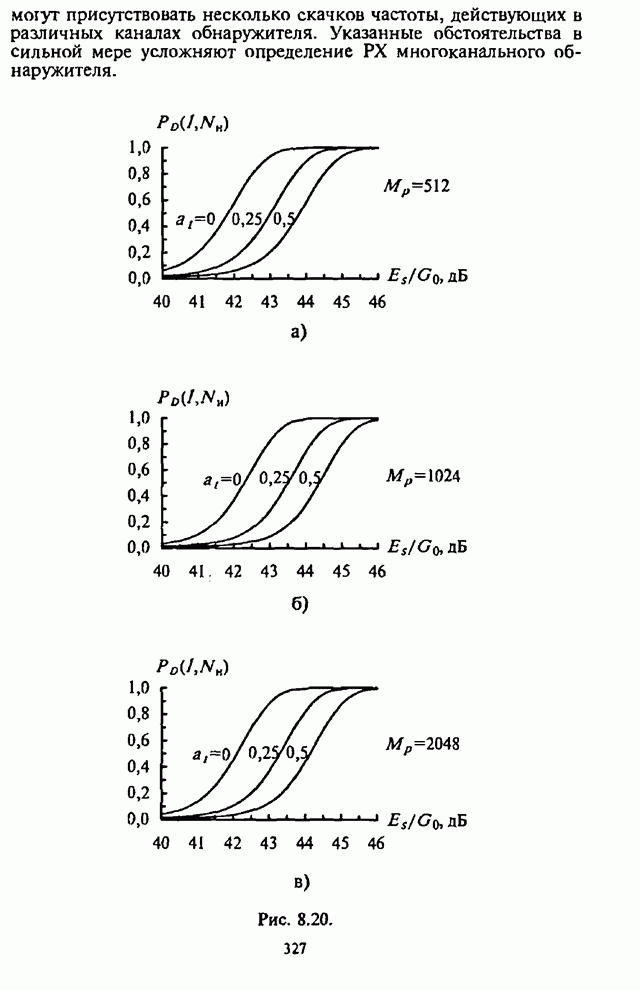
- 8.4.4. Влияние рассогласования по времени на обнаружение сигналов
- 8.5. Другие возможные типы обнаружителей сигналов с ППРЧ
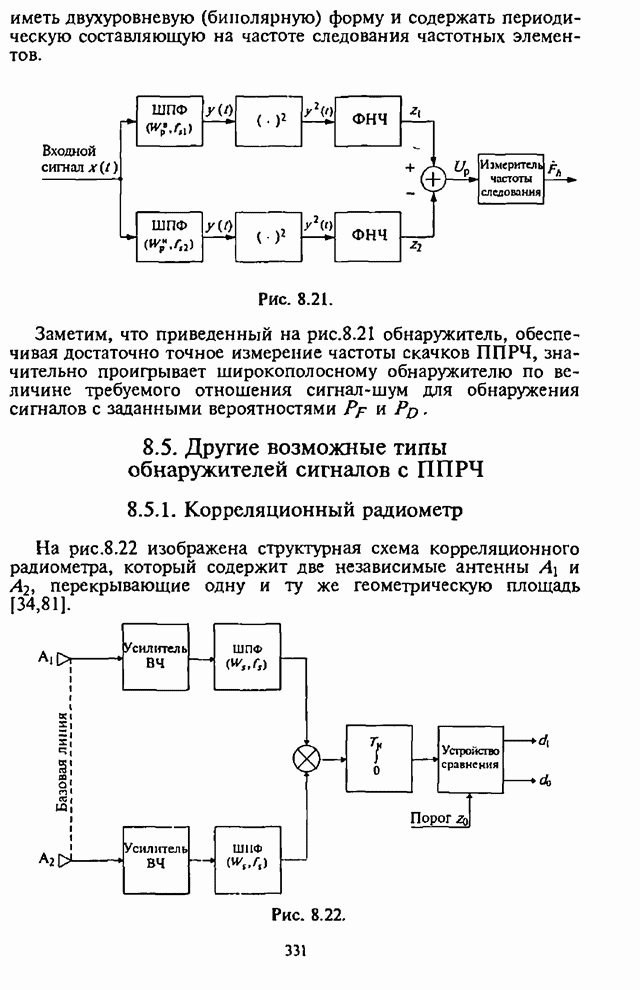
- 8.5.1. Корреляционный радиометр
- 8.5.2. Цифровой анализатор спектра
- 8.5.3. Метод вскрытия частотно-временной матрицы сигнала с ППРЧ
- Приложение П.8.1. Алгоритмы вычисления обобщенной Q-функции Маркума
- П.8.1.1. Постановка задачи
- П.8.1.2. Представление степенными рядами
- П.8.1.3. Представление в виде рядов Неймана
- П.8.1.4. Численное интегрирование
- П.8.1.5. Гауссовская аппроксимация
- П.8.1.6. Численные результаты
- Приложение П.8.2. Анализ вероятностно-временных характеристик алгоритмов обнаружения сигналов
- П.8.2.1. Вероятностно-временные характеристики основных видов обнаружителей
- П.8.2.2 Алгоритмы расчета вероятностно-временных характеристик основных видов обнаружителей
- П.8.2.3. Численные результаты
- СПИСОК ОСНОВНЫХ СОКРАЩЕНИЙ
- ОСНОВНЫЕ УСЛОВНЫЕ ОБОЗНАЧЕНИЯ
- СПИСОК ЛИТЕРАТУРЫ