| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
3.3.1. Случай «слабых» сигналов
Для слабых сигналов и достаточно точного измерения параметров
![]() и
и ![]() , когда
, когда ![]() , алгоритм (3.20) можно
представить в виде:
, алгоритм (3.20) можно
представить в виде:
 (3.38)
(3.38)
Входящие в (3.38) величины ![]() и
и ![]() запишем следующим образом:
запишем следующим образом:
 ; (3.39а)
; (3.39а)
![]() (3.39б)
(3.39б)
где ![]() - нормированные независимые гауссовские переменные
с нулевым средним и дисперсией, равной
- нормированные независимые гауссовские переменные
с нулевым средним и дисперсией, равной
![]() ;
; ![]() ;
;
![]() ;
; ![]() ;
;
![]() - статистически независимые гауссовские случайные
величины со средним значением, равным нулю, и дисперсиями:
- статистически независимые гауссовские случайные
величины со средним значением, равным нулю, и дисперсиями:

![]() и
и ![]() - величины, характеризующие элементы сигнала;
- величины, характеризующие элементы сигнала; ![]() - мощность помехи на
- мощность помехи на ![]() скачке частоты, определяемая
из выражения (3.4).
скачке частоты, определяемая
из выражения (3.4).
Как видно из (3.39а), нормированные ![]() , содержащие элементы полезного
сигнала, распределены по закону
, содержащие элементы полезного
сигнала, распределены по закону ![]() с двумя степенями свободы и параметром нецентральности
с двумя степенями свободы и параметром нецентральности ![]() , а нормированные величины
, а нормированные величины ![]() (3.39б), в которых отсутствует полезный сигнал, имеют
центральное
(3.39б), в которых отсутствует полезный сигнал, имеют
центральное ![]() - распределение с двумя
степенями свободы.
- распределение с двумя
степенями свободы.
Для случая сильной шумовой помехи
в части
полосы влиянием частотных элементов,
пораженных этой помехой, на результирующий
(суммарный) сигнал можно пренебречь. Заметим, что случай подавления
помехой всех ![]() субсимволов не рассматривается,
так как это полностью нарушает работоспособность СРС. В практических устройствах
обработки, как правило, осуществляется отключение частотных каналов,
подавленных сильной помехой.
субсимволов не рассматривается,
так как это полностью нарушает работоспособность СРС. В практических устройствах
обработки, как правило, осуществляется отключение частотных каналов,
подавленных сильной помехой.
Учитывая, что сомножитель ![]() в оставшихся субсимволах,
подвергнувшихся воздействию помехи, принимает примерно одно и тоже значение,
распределение случайной величины
в оставшихся субсимволах,
подвергнувшихся воздействию помехи, принимает примерно одно и тоже значение,
распределение случайной величины
 (3.40а)
(3.40а)
можно аппроксимировать нецентральным ![]() - распределением
с
- распределением
с ![]() степенями свободы и параметром нецентральности.
степенями свободы и параметром нецентральности.
![]() .
.
Случайная величина ![]() , в которой отсутствует полезный сигнал,
распределяется по закону центрального
, в которой отсутствует полезный сигнал,
распределяется по закону центрального ![]() - распределения с
- распределения с ![]() степенями свободы
степенями свободы
 (3.40б)
(3.40б)
В обшем случае УВО на бит определяется из выражения
 (3.41)
(3.41)
где ![]() ,
, ![]() - функции плотности распределения вероятностей
случайных величин
- функции плотности распределения вероятностей
случайных величин ![]() и
и ![]() соответственно.
соответственно.
В соответствии с [48] функции плотности распределения
вероятностей ![]() и
и ![]() имеют вид:
имеют вид:


где ![]() - модифицированная функция Бесселя первого рода
порядка
- модифицированная функция Бесселя первого рода
порядка ![]() ;
; ![]() - гамма-функция.
- гамма-функция.
Для получения УВО в виде конечной суммы представим внутренний интеграл в (3.41) в виде [48].
 (3.42a)
(3.42a)
а функцию ![]() как
как
 (3.42б)
(3.42б)
Используя (3.42а) и (3.42б), в соответствии с (3.41) получим выражение для УВО на бит [44]
 (3.43)
(3.43)
Применяя свойства гамма-функции [48,49]
![]()
преобразуем (3.43) к виду:
 (3.44)
(3.44)
где ![]() .
.
Бесконечный ряд в (3.44) представляет собой вырожденную пшергеометрическую функцию [48,49]
![]()
которую можно выразить следующим образом:
![]() (3.45)
(3.45)
где ![]() - обобщенный полином Лагерра
- обобщенный полином Лагерра ![]() [48].
[48].
После подстановки (3.45) в (3.44) получим выражение для УВО на
бит ![]() в виде конечной суммы при
условии, что
в виде конечной суммы при
условии, что ![]() [44]
[44]
 (3.46)
(3.46)
Учитывая (3.37), СВО на бит ![]() системы радиосвязи с внутрисимвольной ППРЧ и
синтезированным алгоритмом (3.38) определяется из выражения
системы радиосвязи с внутрисимвольной ППРЧ и
синтезированным алгоритмом (3.38) определяется из выражения
![]() (3.47)
(3.47)
где 
Из анализа уравнений (3.46) и (3.47) следует, что при выбранной модели слабых
сигналов, когда подавленные сильной помехой в части полосы субсимволы
исключены из рассмотрения, УВО на бит ![]() и, следовательно, СВО на бит
и, следовательно, СВО на бит ![]() в явном виде не зависят от отношения сигнал-помеха
в явном виде не зависят от отношения сигнал-помеха ![]() . Такая зависимость проявляется
опосредованно через величину подавляемой помехой части диапазона
. Такая зависимость проявляется
опосредованно через величину подавляемой помехой части диапазона ![]() ичисло субсимволов
ичисло субсимволов ![]() , подверженных
воздействию помехи.
, подверженных
воздействию помехи.
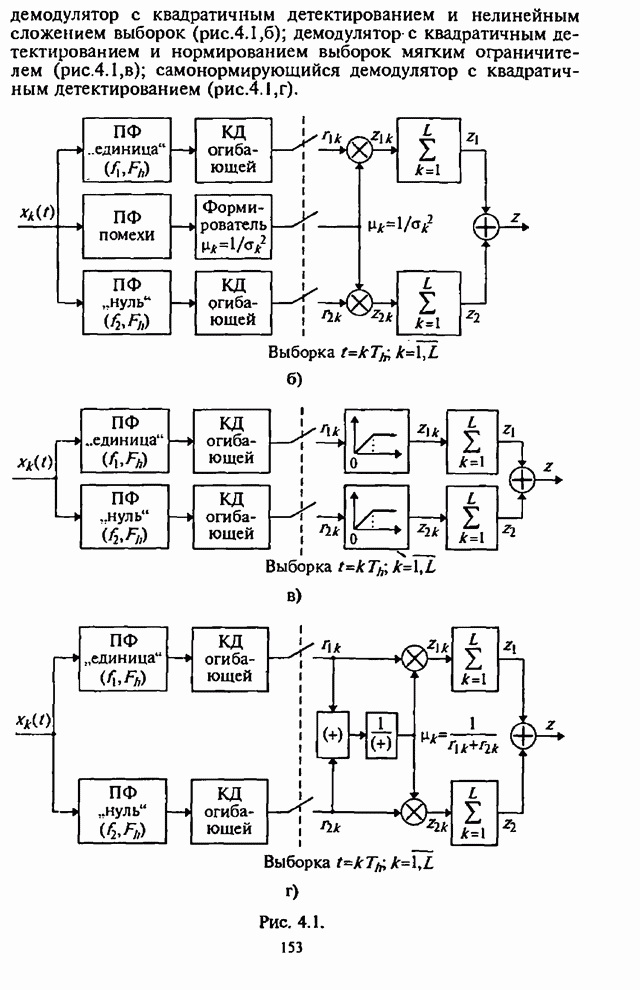
В [11] оценивается помехоустойчивость СРС с внутрисимвольной
ППРЧ и двоичной ЧМ, в которой для демодуляции сигналов используется алгоритм,
реализуемый с помощью квадратичного детектирования и нелинейного сложения
выборок, пронормированных весовым множителем вида ![]() . При анализе помехоустойчивости такой СРС
в [11] предполагается: 1) амплитуды субсимволов
. При анализе помехоустойчивости такой СРС
в [11] предполагается: 1) амплитуды субсимволов ![]() на разных частотах равны между
собой; 2) измерение мощности помехи
на разных частотах равны между
собой; 2) измерение мощности помехи ![]() осуществляется «идеально» без
ошибок на каждом
осуществляется «идеально» без
ошибок на каждом ![]() скачке
частоты.
скачке
частоты.
Для случая сильной шумовой помехи полученное в [11] выражение для УВО на бит имеет вид:
 ,
, ![]() (3.48)
(3.48)
Из (3.46) и (3.48) видно, что выражения для УВО на бит
при одном и том же параметре нецентральности ![]() отличаются только числом степеней свободы, которое при
отличаются только числом степеней свободы, которое при ![]() больше в (3.48).
больше в (3.48).
Проведем анализ влияния числа степеней свободы на УВО на бит. Для решения данной задачи воспользуемся гауссовской ап-проссимацией. При таком допущении УВО на бит определяется из выражения
 (3.49)
(3.49)
где ![]() - функция Лапласа,
- функция Лапласа, 
![]() - математическое ожидание
разности статистик
- математическое ожидание
разности статистик ![]() с точностью до множителя, не
влияющего на УВО,
с точностью до множителя, не
влияющего на УВО,
![]() ;
;
![]() - дисперсия разности статистик
- дисперсия разности статистик![]() :
:
![]() .
.
Анализ (3.49) показывает, что при большем числе
степеней свободы, когда ![]() , аргумент функции Лапласа
, аргумент функции Лапласа ![]() , где
, где ![]() . Следовательно, УВО на бит
(3.46) меньше аналогичной вероятности (3.48), так как
. Следовательно, УВО на бит
(3.46) меньше аналогичной вероятности (3.48), так как ![]() . Таким образом, в случае аппроксимации статистик
решения
. Таким образом, в случае аппроксимации статистик
решения ![]() и
и ![]() нормальным законом
распределения при сильной шумовой помехе и точном измерении амплитуды
субсимволов
нормальным законом
распределения при сильной шумовой помехе и точном измерении амплитуды
субсимволов ![]() и дисперсии шумовой помехи
и дисперсии шумовой помехи ![]() синтезированный квазиоптимальный алгоритм, как и
следовало ожидать, эффективнее эвристического алгоритма различения сигналов с внутрисимвольной
ППРЧ [11], а выражение (3.47) характеризует нижнюю границу СВО на бит
информации.
синтезированный квазиоптимальный алгоритм, как и
следовало ожидать, эффективнее эвристического алгоритма различения сигналов с внутрисимвольной
ППРЧ [11], а выражение (3.47) характеризует нижнюю границу СВО на бит
информации.
Заметим, что, когда влиянием собственных шумов
приемника СРС пренебречь нельзя, УВО на бит ![]() при слабом сигнале и точном измерении параметров
при слабом сигнале и точном измерении параметров ![]() и
и ![]() может быть получена из выражения (3.46) путем замены в
нем
может быть получена из выражения (3.46) путем замены в
нем ![]() на
на ![]() . В этом случае СВО на бит
. В этом случае СВО на бит ![]() имеет вид [11]:
имеет вид [11]:
 (3.50)
(3.50)
где параметр нецентральности ![]() определяется из выражения
определяется из выражения

При принятых выше допущениях оценка помехоустойчивости
СРС с внутрисимвольной ППРЧ и синтезированным квазиоптимальным алгоритмом
полиостью совпадает с оценкой помехоустойчивости СРС с внярисимвольной ППРЧ,
квадратичным детектированием и нелинейным сложением субсимволов при «идеальном»
измерении мощности помехи. Дальнейший анализ зависимости СВО на бит ![]() (3.50) детально изложен в
четвертой главе.
(3.50) детально изложен в
четвертой главе.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие
- Введение
- Глава 1. Системы радиосвязи с расширением спектра сигналов методом псевдослучайной перестройки рабочей частоты: общие принципы
- 1.1. Краткая характеристика расширения спектра сигналов методом ППРЧ
- 1.1.1. Основные принципы и методы расширения спектра сигналов
- 1.1.2. Метод псевдослучайной перестройки рабочей частоты
- 1.1.3. Типовые структурные схемы систем радиосвязи с ППРЧ
- 1.2. Коэффициент расширения спектра сигнала и запас помехоустойчивости системы радиосвязи с ППРЧ
- 1.3. Общая характеристика помехозащищенности систем радиосвязи с ППРЧ
- 1.3.1. Помехоустойчивость систем радиосвязи с ППРЧ
- 1.3.2. Скрытность сигналов систем радиосвязи с ППРЧ
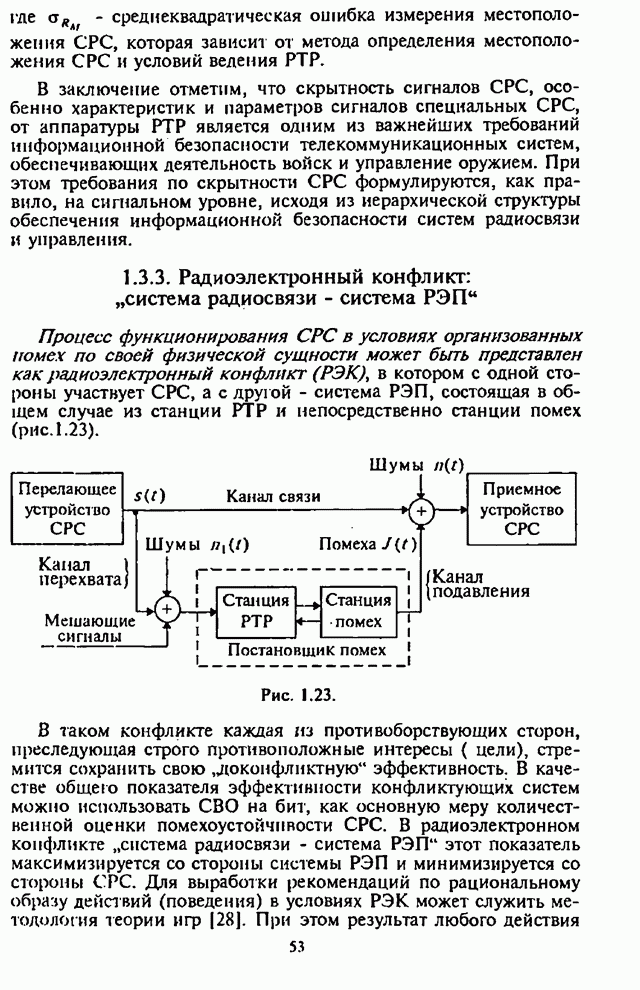
- 1.3.3. Радиоэлектронный конфликт: «система радиосвязи — система РЭП»
- 1.4. Модели и краткая характеристика основных видов помех
- Глава 2. Помехоустойчивость типовых систем радиосвязи с ППРЧ и частотной манипуляцией
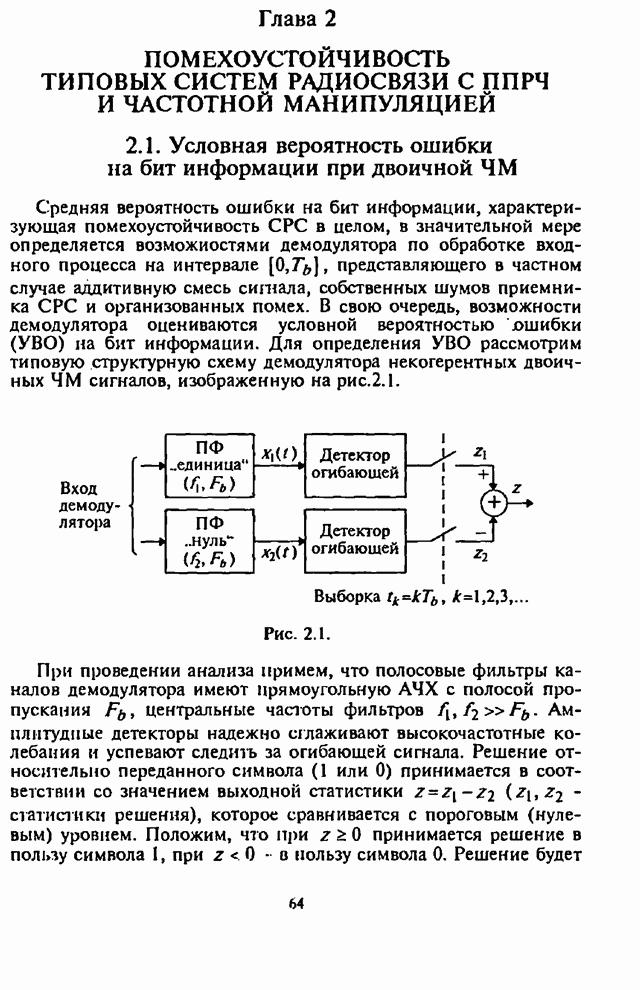
- 2.1. Условная вероятность ошибки на бит информации при двоичной ЧМ
- 2.2. Оценка воздействия шумовой помехи в части полосы на системы радиосвязи с ППРЧ и неслучайной ЧМ
- 2.3. Оценка воздействия шумовой помехи в части полосы на системы радиосвязи с ППРЧ и случайной двоичной ЧМ
- 2.4. Оценка воздействия ответных помех на системы радиосвязи с ППРЧ и ЧМ
- 2.4.1. Оценка временных возможностей станции ответных помех
- 2.4.2. Оценка воздействия ответных шумовых помех на системы радиосвязи с ППРЧ и ЧМ
- 2.4.3. Оценка воздействия ответных гармонических помех на системы радиосвязи с ППРЧ и ЧМ
- 2.5. Помехоустойчивость систем радиосвязи с ППРЧ, двоичной ЧМ и блоковым кодированием
- Глава 3. Синтез и анализ эффективности адаптивных алгоритмов различения сигналов с ППРЧ, частотной модуляцией и разнесением символов по частоте
- 3.1. Синтез оптимального адаптивного алгоритма различения сигналов с внутрисимвольной ППРЧ и ЧМ
- 3.2. Квазиоптимальный адаптивный алгоритм различения сигналов с внутрисимвольной ППРЧ и двоичной ЧМ
- 3.3. Оценка помехоустойчивости синтезированного адаптивного алгоритма различения сигналов с внутрисимвольной ППРЧ и двоичной ЧМ
- 3.3.1. Случай «слабых» сигналов
- 3.3.2. Случай «сильных» сигналов
- Глава 4. Помехоустойчивость адаптивных алгоритмов демодуляции сигналов с внутрибитовой ППРЧ и двоичной частотной манипуляцией
- 4.1. Структурные схемы демодуляторов
- 4.2. Помехоустойчивость демодулятора с линейным сложением выборок
- 4.3. Помехоустойчивость демодулятора с нелинейным сложением выборок
- 4.4. Помехоустойчивость демодулятора с мягким ограничителем
- 4.5. Помехоустойчивость самонормирующегося демодулятора
- 4.6. Влияние адаптивной регулировки усиления на помехоустойчивость СРС
- 4.7. Сравнительный анализ помехоустойчивости демодуляторов сигналов с внутрибитовой ППРЧ и двоичной ЧМ
- Глава 5. Помехоустойчивость систем радиосвязи с ППРЧ при совместном применении частотной модуляции, разнесения символов по частоте и блокового кодирования
- 5.1. Помехоустойчивость систем радиосвязи с ППРЧ при M-ичной ЧМ и L-кратным разнесении символов по частоте
- 5.1.1. Условная вероятность ошибки на бит информации
- 5.1.2. Анализ средней вероятности ошибки на бит информации
- 5.2. Помехоустойчивость систем радиосвязи с ППРЧ, M-ичной ЧМ, блоковым кодированием и L-кратным частотным разнесением кодовых слов
- 5.2.1. Структурная схема системы радиосвязи
- 5.2.2. Средняя вероятность ошибки на бит информации
- 5.2.3. Анализ средней вероятности ошибки на бит информации
- Глава 6. Синхронизация в системах радиосвязи с псевдослучайной перестройкой рабочей частоты
- 6.1. Назначение подсистемы синхронизации
- 6.2. Описательная модель подсистемы синхронизации
- 6.2.1. Типовая структурная схема подсистемы синхронизации
- 6.2.2. Типовые структурные схемы и алгоритмы функционирования основных устройств подсистемы синхронизации
- 6.3. Показатели и оценка эффективности циклических процедур поиска
- Приложение П.6.1. Верхняя граница среднего нормированного времени поиска
- Приложение П.6.2. Верхняя граница вероятности правильного обнаружения
- Глава 7. Адаптивные антенные решетки в системах радиосвязи с псевдослучайной перестройкой рабочей частоты
- 7.1. Влияние сигналов с ППРЧ на характеристики адаптивной антенной решетки
- 7.2. Максиминный алгоритм обработки сигналов и помех
- 7.3. Реализация и возможности максиминного алгоритма
- 7.4. Модернизация максиминного алгоритма
- 7.4.1. Параметрическая обработка
- 7.4.2. Спектральная обработка
- 7.4.3. Обработка с упреждением
- Глава 8. Обнаружение сигналов с псевдослучайной перестройкой рабочей частоты
- 8.1. Обнаружение сигналов неизвестной структуры
- 8.2. Широкополосный энергетический обнаружитель
- 8.3. Многоканальные энергетические обнаружители
- 8.3.1. Квазиоптимальный многоканальный обнаружитель
- 8.3.2. Многоканальный обнаружитель типа сумматора с блоком фильтров
- 8.3.3. Модель обнаружителя типа сумматора с блоком фильтров при перехвате сигналов с медленной ППРЧ
- 8.3.4. Многоканальный обнаружитель типа сумматора с блоком фильтров в части полосы
- 8.3.5. Рассогласование по времени и частоте между характеристиками сигнала с ППРЧ и параметрами обнаружителя
- 8.4. Многоканальный адаптивный энергетический обнаружитель в условиях воздействия мешающих сигналов
- 8.4.1. Структурная схема многоканального адаптивного энергетического обнаружителя с регулировкой порогового уровня
- 8.4.2. Вероятность ложной тревоги и адаптивная регулировка порогового уровня
- 8.4.3. Вероятность обнаружения
- 8.4.4. Влияние рассогласования по времени на обнаружение сигналов
- 8.5. Другие возможные типы обнаружителей сигналов с ППРЧ
- 8.5.1. Корреляционный радиометр
- 8.5.2. Цифровой анализатор спектра
- 8.5.3. Метод вскрытия частотно-временной матрицы сигнала с ППРЧ
- Приложение П.8.1. Алгоритмы вычисления обобщенной Q-функции Маркума
- П.8.1.1. Постановка задачи
- П.8.1.2. Представление степенными рядами
- П.8.1.3. Представление в виде рядов Неймана
- П.8.1.4. Численное интегрирование
- П.8.1.5. Гауссовская аппроксимация
- П.8.1.6. Численные результаты
- Приложение П.8.2. Анализ вероятностно-временных характеристик алгоритмов обнаружения сигналов
- П.8.2.1. Вероятностно-временные характеристики основных видов обнаружителей
- П.8.2.2 Алгоритмы расчета вероятностно-временных характеристик основных видов обнаружителей
- П.8.2.3. Численные результаты
- СПИСОК ОСНОВНЫХ СОКРАЩЕНИЙ
- ОСНОВНЫЕ УСЛОВНЫЕ ОБОЗНАЧЕНИЯ
- СПИСОК ЛИТЕРАТУРЫ