| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
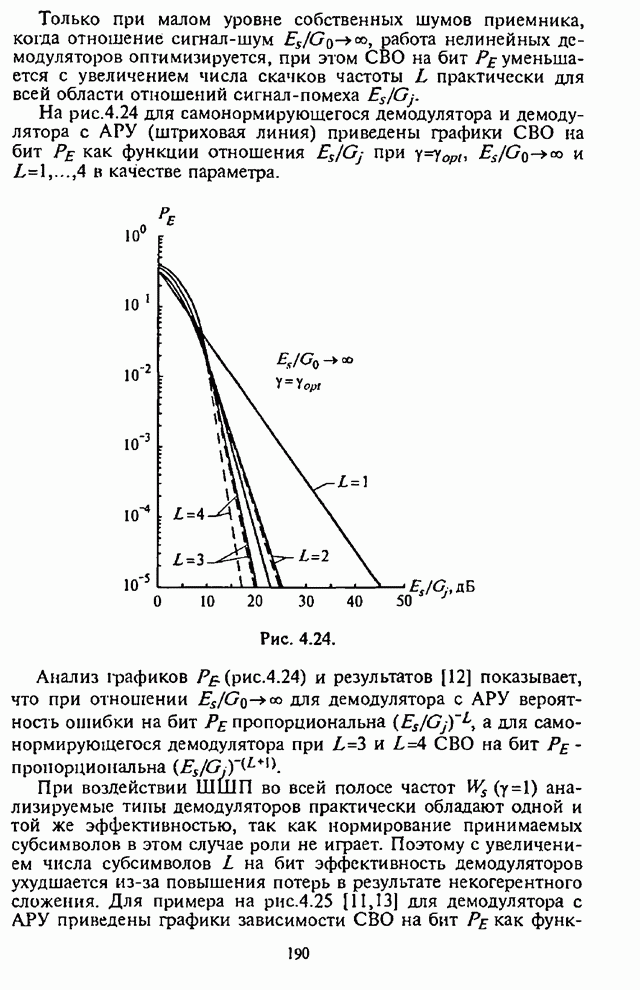
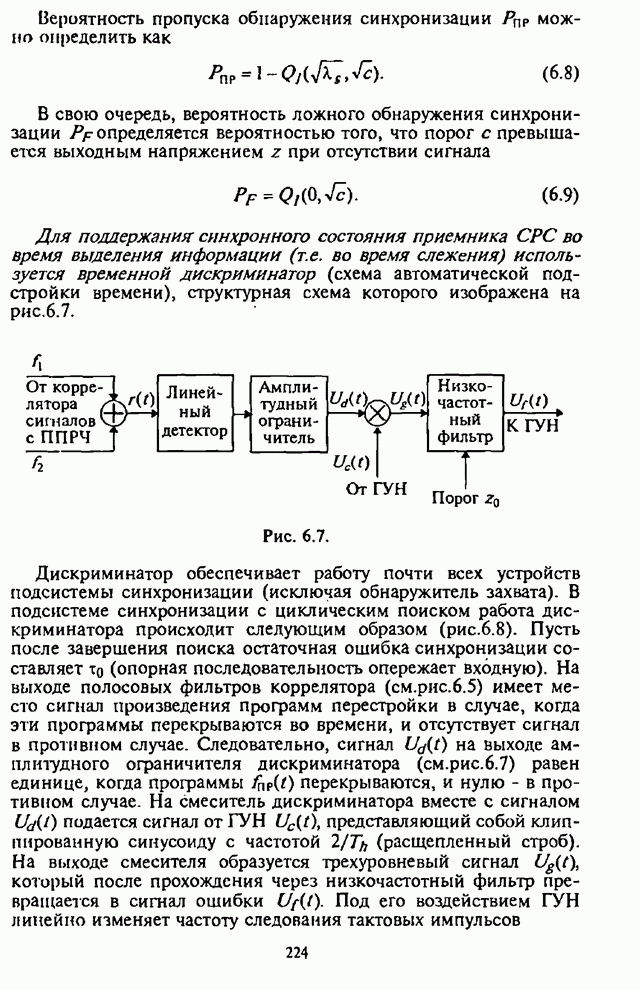
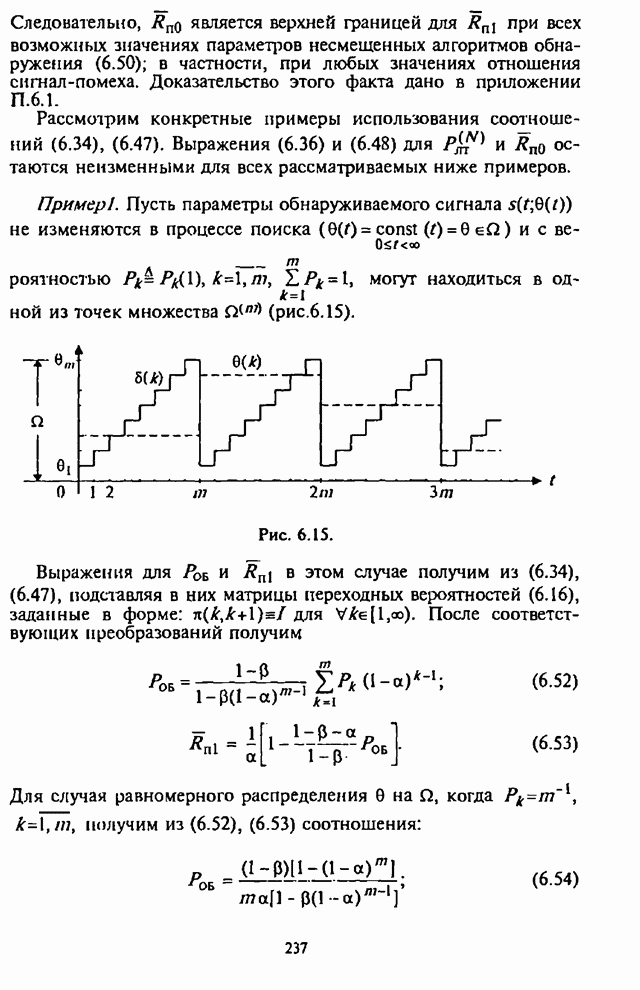
5.1.2. Анализ средней вероятности ошибки на бит информации
В соответствии с изложенным, оставляя в (5.4) только
главный член, соответствующий ![]() , и учитывая (5.10), получим приближенное
выражение для СВО на бит
, и учитывая (5.10), получим приближенное
выражение для СВО на бит ![]() для приемника СРС с АРУ при
для приемника СРС с АРУ при ![]() и
и ![]() [53]:
[53]:
 (5.12)
(5.12)
где
![]() (5.13)
(5.13)
Учитывая пропорциональность параметров ![]() и
и ![]() , оптимальное значение
, оптимальное значение ![]() , при котором шумовая
помеха в части полосы является наихудшей, а СВО на бит
, при котором шумовая
помеха в части полосы является наихудшей, а СВО на бит ![]() будет максимальной, находится
путем решения уравнения
будет максимальной, находится
путем решения уравнения ![]() . Используя уравнение
. Используя уравнение ![]() и (5.12), можно получить
выражение вида:
и (5.12), можно получить
выражение вида:
 (5.14)
(5.14)
где ![]() - множитель, заключенный в
квадратные скобки в формуле (5.12).
- множитель, заключенный в
квадратные скобки в формуле (5.12).
Положим, что решением уравнения (5.14) является ![]() . Тогда, с учетом (5.13) имеем:
. Тогда, с учетом (5.13) имеем:
 (5.15)
(5.15)
где ![]() - постоянная величина,
которую далее еще необходимо определить.
- постоянная величина,
которую далее еще необходимо определить.
Подставляя (5.15) в (5.12), получим максимальное значение СВО на бит
 (5.16)
(5.16)
где ![]() .
.
Конкретные значения параметра ![]() для любых значностей передачи
для любых значностей передачи
![]() определяются на основе решения
уравнений, подобных (5.14). Эти уравнения являются трансцендентными и решаются
численными методами. В случае
определяются на основе решения
уравнений, подобных (5.14). Эти уравнения являются трансцендентными и решаются
численными методами. В случае ![]() и
и ![]() путем решения уравнения
(5.14) с учетом функции
путем решения уравнения
(5.14) с учетом функции ![]() получим
получим ![]() . Следовательно,
. Следовательно,
 (5.17)
(5.17)
и
 (5.18)
(5.18)
Следуя приведенному выше подходу и используя формулу
обобщенной помехоустойчивости СРС с ППРЧ при ![]() -ичной ЧМ и
-ичной ЧМ и ![]() -кратном разнесении символов (5.5),
приведем результаты некоторых частных конфликтов СРС с ППРЧ и станции шумовой
помехи в части полосы для наихудшего случая (
-кратном разнесении символов (5.5),
приведем результаты некоторых частных конфликтов СРС с ППРЧ и станции шумовой
помехи в части полосы для наихудшего случая (![]() ) и малых собственных шумов приемника СРС
[32,53]:
) и малых собственных шумов приемника СРС
[32,53]:
при ![]() и
и ![]()
![]() (5.19)
(5.19)
во всем диапазоне отношений сигнал-помеха ![]() ;
;
при любой значности передачи ![]() и
и
![]()
 (5.20)
(5.20)
где
![]() .
.
Значения параметров ![]() и
и ![]() полученные в [32] для
полученные в [32] для ![]() , приведены и табл.5.1 (см.
табл.2.1 во 2-й главе).
, приведены и табл.5.1 (см.
табл.2.1 во 2-й главе).
Таблица
5.1. Значения параметров ![]() и
и ![]()
|
|
2 |
4 |
8 |
16 |
|
|
2,00 |
1,19 |
0,93 |
0,87 |
|
|
0,3679 |
0,2329 |
0,1954 |
0,1803 |
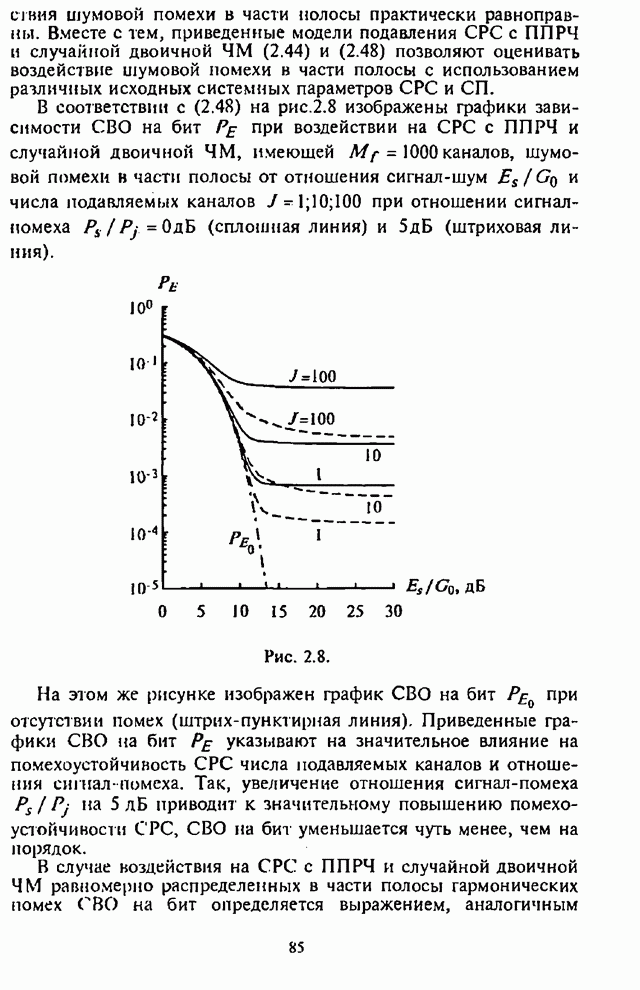
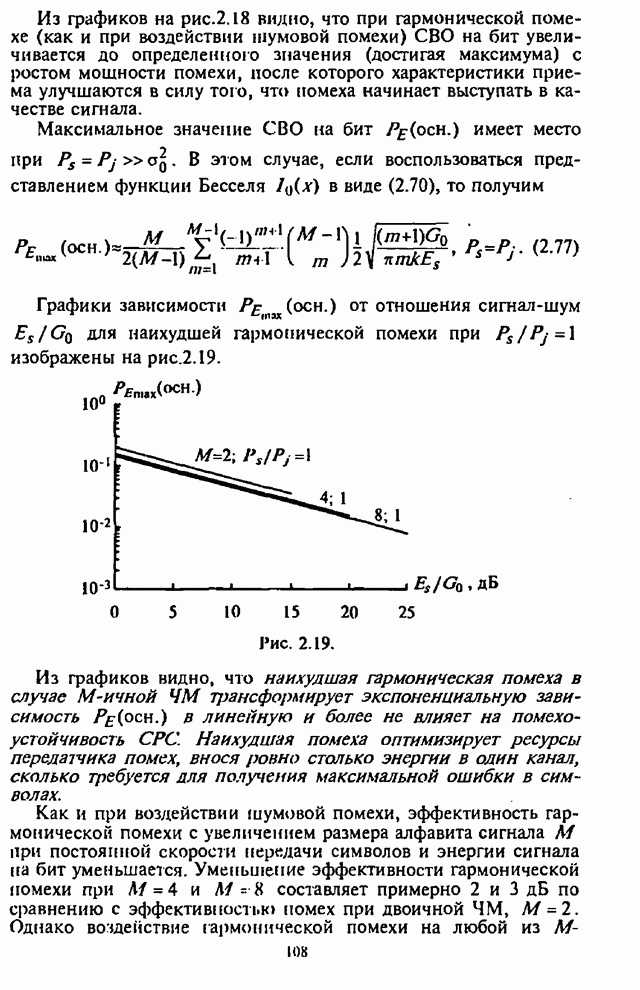
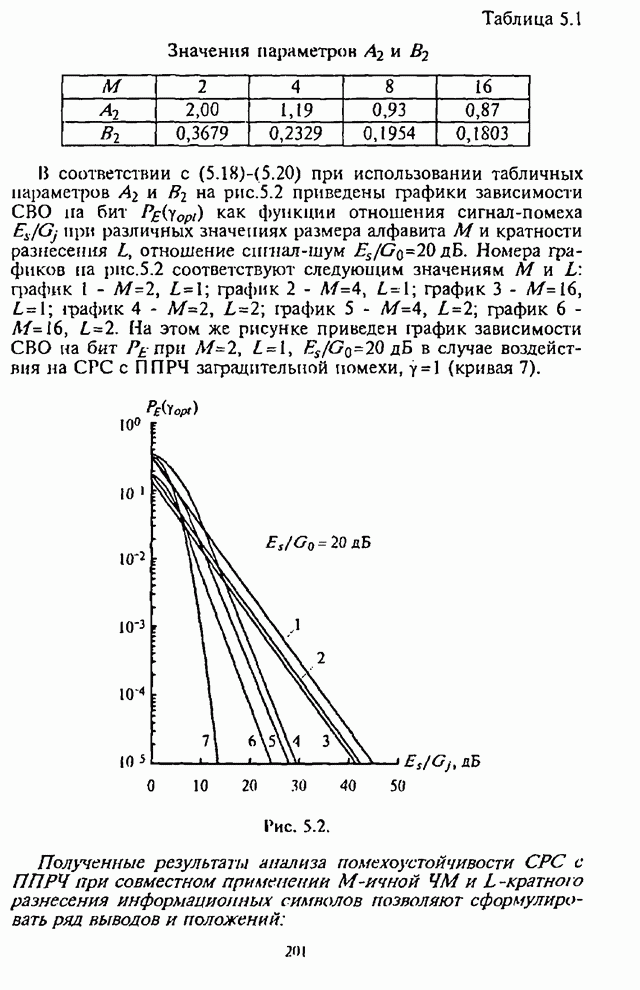
в соответствии с (5.18)-(5.20) при использовании
табличных параметров ![]() и
и
![]() на рис.5.2
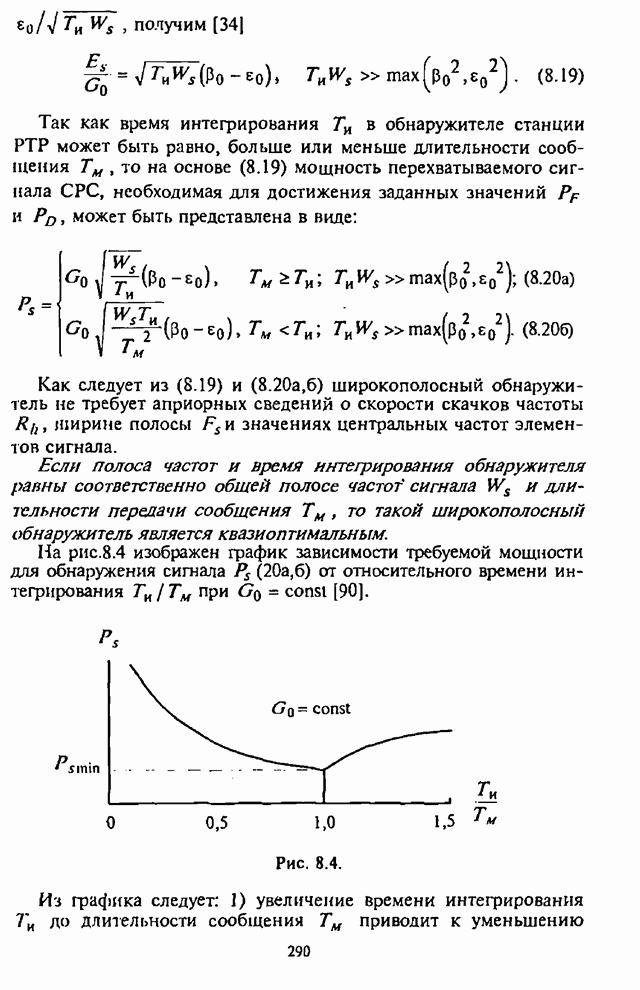
приведены графики зависимости СВО
па бит
на рис.5.2
приведены графики зависимости СВО
па бит ![]() как функции отношения
сигнал-помеха
как функции отношения
сигнал-помеха ![]() при различных значениях
размера алфавита
при различных значениях
размера алфавита ![]() и кратности разнесения
и кратности разнесения ![]() , отношение сигнал-шум
, отношение сигнал-шум ![]() . Номера графиков на рис.5.2
соответствуют следующим значениям
. Номера графиков на рис.5.2
соответствуют следующим значениям ![]() и
и ![]() : график 1 -
: график 1 - ![]() ,
, ![]() ; график 2 -
; график 2 - ![]() ,
, ![]() ; график 3 -
; график 3 - ![]() ,
, ![]() ; график 4 -
; график 4 - ![]() ,
, ![]() ; график 5 -
; график 5 - ![]() ,
, ![]() ; график 6 -
; график 6 - ![]() ,
, ![]() . На этом же рисунке приведен график
зависимости СВО
на бит
. На этом же рисунке приведен график
зависимости СВО
на бит ![]() при
при ![]() ,
, ![]() ,
, ![]() в случае воздействия на СРС с ППРЧ заградительной помехи,
в случае воздействия на СРС с ППРЧ заградительной помехи, ![]() (кривая 7).
(кривая 7).

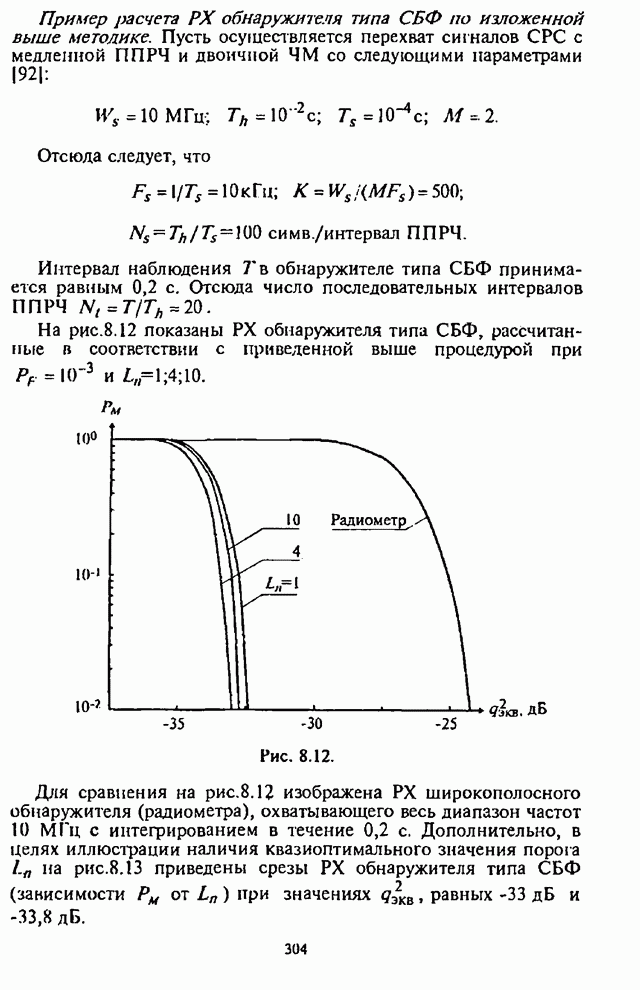
Рис. 5.2.
Полученные результаты анализа помехоустойчивости
СРС с
ППРЧ при совместном применении ![]() -ичной
ЧМ и
-ичной
ЧМ и
![]() -кратного разнесений информационных символов позволяют сформулировать ряд выводов и положений:
-кратного разнесений информационных символов позволяют сформулировать ряд выводов и положений:
1) увеличение размера алфавита передачи с ![]() до
до ![]() при
при ![]() и с
и с ![]() до
до ![]() также при
также при ![]() приводит к уменьшению
порогового значения отношения сигнал-помеха
приводит к уменьшению
порогового значения отношения сигнал-помеха ![]() соответственно на 2,05дБ и
3,10дБ, повышая тем самым помехоустойчивость СРС; 2) при увеличении размера
алфавита
соответственно на 2,05дБ и
3,10дБ, повышая тем самым помехоустойчивость СРС; 2) при увеличении размера
алфавита ![]() дифференциальный прирост
помехоустойчивости СРС постепенно снижается. Учитывая малый прирост
помехоустойчивости СРС и усложнение при этом технической реализации
аппаратуры, целесообразно, по всей видимости, признать
дифференциальный прирост
помехоустойчивости СРС постепенно снижается. Учитывая малый прирост
помехоустойчивости СРС и усложнение при этом технической реализации
аппаратуры, целесообразно, по всей видимости, признать ![]() предельным значением размера
алфавита передачи, выбираемого с целью повышения помехоустойчивости СРС в
условиях действия шумовой помехи в части полосы; 3) увеличение размера алфавита
передачи с
предельным значением размера
алфавита передачи, выбираемого с целью повышения помехоустойчивости СРС в
условиях действия шумовой помехи в части полосы; 3) увеличение размера алфавита
передачи с ![]() д о
д о
![]() при 2-кратном разнесении
символов по частоте (
при 2-кратном разнесении
символов по частоте (![]() ) приводит к повышению
помехоустойчивости СРС на 2,38дБ по пороговому значению отношения сигнал-помеха
) приводит к повышению
помехоустойчивости СРС на 2,38дБ по пороговому значению отношения сигнал-помеха
![]() . Однако это повышение помехоустойчивости СРС значительно
меньше, чем при увеличении кратности разнесения с
. Однако это повышение помехоустойчивости СРС значительно
меньше, чем при увеличении кратности разнесения с ![]() до
до ![]() при
при ![]() практически во всем рабочем
диапазоне отношений сигнал-помеха
практически во всем рабочем
диапазоне отношений сигнал-помеха ![]() , но несколько больше, чем
повышение помехоустойчивости за счет увеличения размера алфавита передачи с
, но несколько больше, чем
повышение помехоустойчивости за счет увеличения размера алфавита передачи с ![]() до
до ![]() при
при ![]() , которое составляет, как
указано выше, 2,05дБ.
, которое составляет, как
указано выше, 2,05дБ.
Последнее замечание в п.3 позволяет, не проводя
сравнительно трудоемких вычислений и используя результаты, полученные для СРС с
![]() и различными значениями
и различными значениями ![]() , ориентировочно оценить предполагаемый выигрыш по помехоустойчивости
за счет увеличения размера алфавита передачи до
, ориентировочно оценить предполагаемый выигрыш по помехоустойчивости
за счет увеличения размера алфавита передачи до ![]() при
при ![]() . Так, если выигрыш по
помехоустойчивости СРС с
. Так, если выигрыш по
помехоустойчивости СРС с ![]() при переходе от
при переходе от ![]() к
к ![]() несколько меньше, чем
соответствующий выигрыш СРС с
несколько меньше, чем
соответствующий выигрыш СРС с ![]() , то можно ожидать, что прирост
помехоустойчивости будет сохранять такую же тенденцию и дальше при
, то можно ожидать, что прирост
помехоустойчивости будет сохранять такую же тенденцию и дальше при ![]() . Поэтому помехоустойчивость СРС
с 2-кратным частотным разнесением символа не будет завышена, если примем, что
ее выигрыш при переходе от размера алфавита
. Поэтому помехоустойчивость СРС
с 2-кратным частотным разнесением символа не будет завышена, если примем, что
ее выигрыш при переходе от размера алфавита ![]() к
к ![]() такой же, как и СРС с
такой же, как и СРС с ![]() , т.е. 1,05дБ. В
результате получаем, что увеличение размера алфавита передачи с
, т.е. 1,05дБ. В
результате получаем, что увеличение размера алфавита передачи с ![]() до
до ![]() в СРС с 2-кратным разнесением
символа по частоте приведет к повышению помехоустойчивости, приблизительно
равному
в СРС с 2-кратным разнесением
символа по частоте приведет к повышению помехоустойчивости, приблизительно
равному ![]() по
пороговому значению отношения сигнал-помеха. В соответствии с этим на рис.5.2
приведен график зависимости СВО на бит
по
пороговому значению отношения сигнал-помеха. В соответствии с этим на рис.5.2
приведен график зависимости СВО на бит ![]() для СРС с ППРЧ при 16-ичной ЧМ
и
для СРС с ППРЧ при 16-ичной ЧМ
и ![]() (кривая
6).
(кривая
6).
Приведенный на рис.5.2 график СВО на бит ![]() (кривая 7) для СРС с
ППРЧ при
(кривая 7) для СРС с
ППРЧ при ![]() и
и ![]() в условиях заградительной
помехи (
в условиях заградительной
помехи (![]() )
показывает, что результат оптимизации ширины полосы
)
показывает, что результат оптимизации ширины полосы
(![]() ), в которой создается помеха, оказывается
весьма значительным. Средняя вероятность ошибки на бит
), в которой создается помеха, оказывается
весьма значительным. Средняя вероятность ошибки на бит ![]() в большей части диапазона отношений сигнал-помеха
в большей части диапазона отношений сигнал-помеха ![]() резко увеличивается, особенно
для СРС, не использующей частотного разнесения информационных символов. Однако
оптимальные стратегии (
резко увеличивается, особенно
для СРС, не использующей частотного разнесения информационных символов. Однако
оптимальные стратегии (![]() ) в
станции шумовой помехи в части
полосы могут быть осуществлены при условии, что системе
РЭП известны
такие параметры как диапазон перестройки
) в
станции шумовой помехи в части
полосы могут быть осуществлены при условии, что системе
РЭП известны
такие параметры как диапазон перестройки ![]() (который может
быть известен и заранее), мощность сигнала
(который может
быть известен и заранее), мощность сигнала
![]() и помехи
и помехи
![]() в
месте расположения подавляемой СРС
и др. Неизбежно возникающие при этом
ошибки естественно приводят к ухудшению эффективности станции помех и,
следовательно, повышению помехоустойчивости СРС. Кроме того, из графика СВО на
бит
в
месте расположения подавляемой СРС
и др. Неизбежно возникающие при этом
ошибки естественно приводят к ухудшению эффективности станции помех и,
следовательно, повышению помехоустойчивости СРС. Кроме того, из графика СВО на
бит ![]() (см.рис.5.2,
кривая 7) следует, что при малых отношениях сигнал-помеха
(см.рис.5.2,
кривая 7) следует, что при малых отношениях сигнал-помеха ![]() наиболее целесообразной
стратегией системы РЭП против СРС с ППРЧ является создание заградительной
шумовой помехи.
наиболее целесообразной
стратегией системы РЭП против СРС с ППРЧ является создание заградительной
шумовой помехи.
Таким образом, совместное применение в СРС с ППРЧ
многопозиционной передачи (![]() -ичной ЧМ) и внутрисимвольного частотного
разнесения (внутрисимвольной перестройки) способно значительно повысить
помехоустойчивость СРС в условиях воздействия наихудшей шумовой помехи в части
полосы.
-ичной ЧМ) и внутрисимвольного частотного
разнесения (внутрисимвольной перестройки) способно значительно повысить
помехоустойчивость СРС в условиях воздействия наихудшей шумовой помехи в части
полосы.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие
- Введение
- Глава 1. Системы радиосвязи с расширением спектра сигналов методом псевдослучайной перестройки рабочей частоты: общие принципы
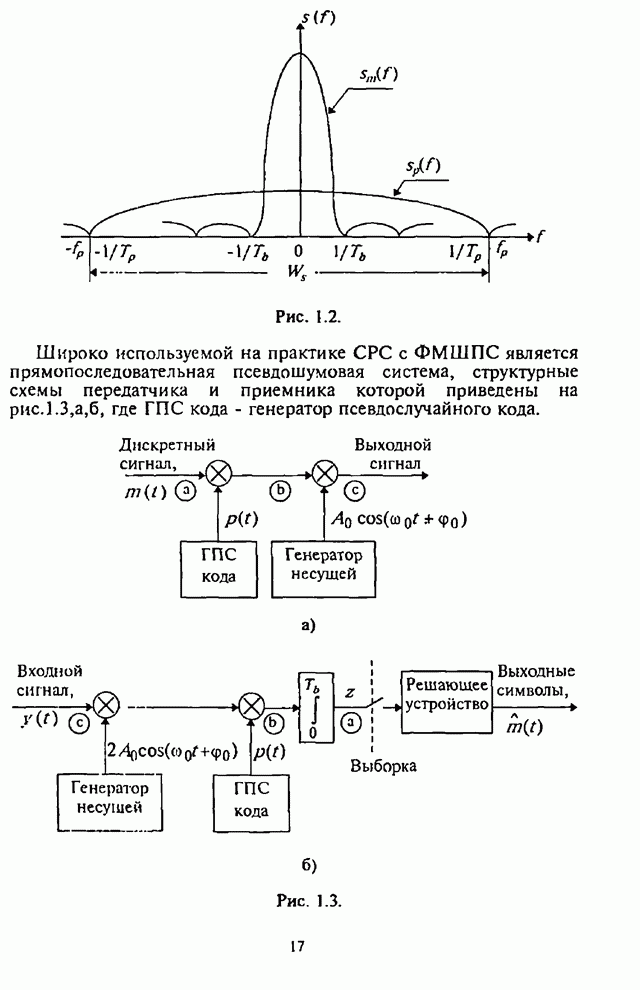
- 1.1. Краткая характеристика расширения спектра сигналов методом ППРЧ
- 1.1.1. Основные принципы и методы расширения спектра сигналов
- 1.1.2. Метод псевдослучайной перестройки рабочей частоты
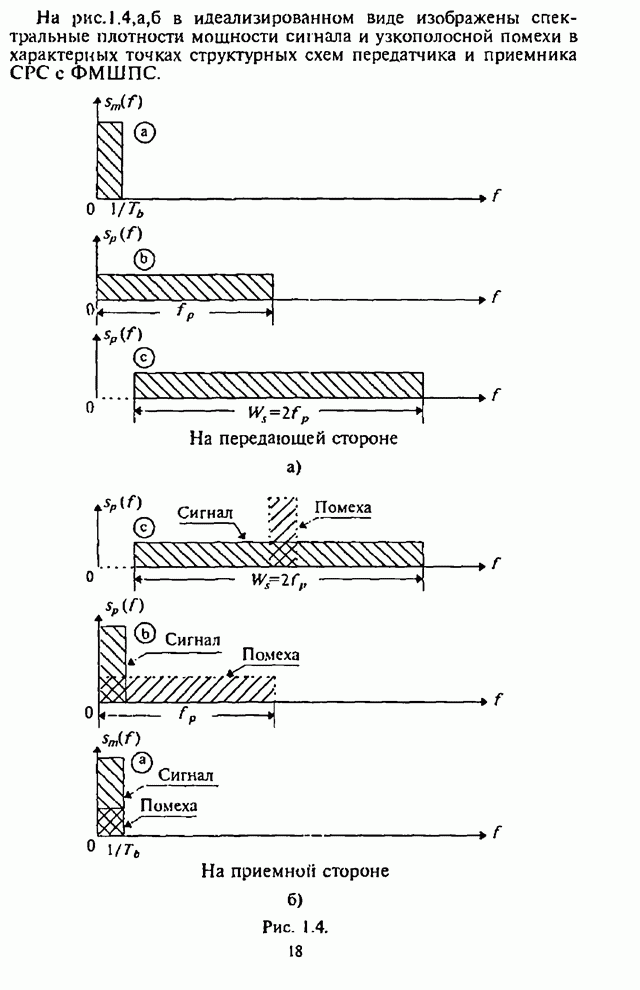
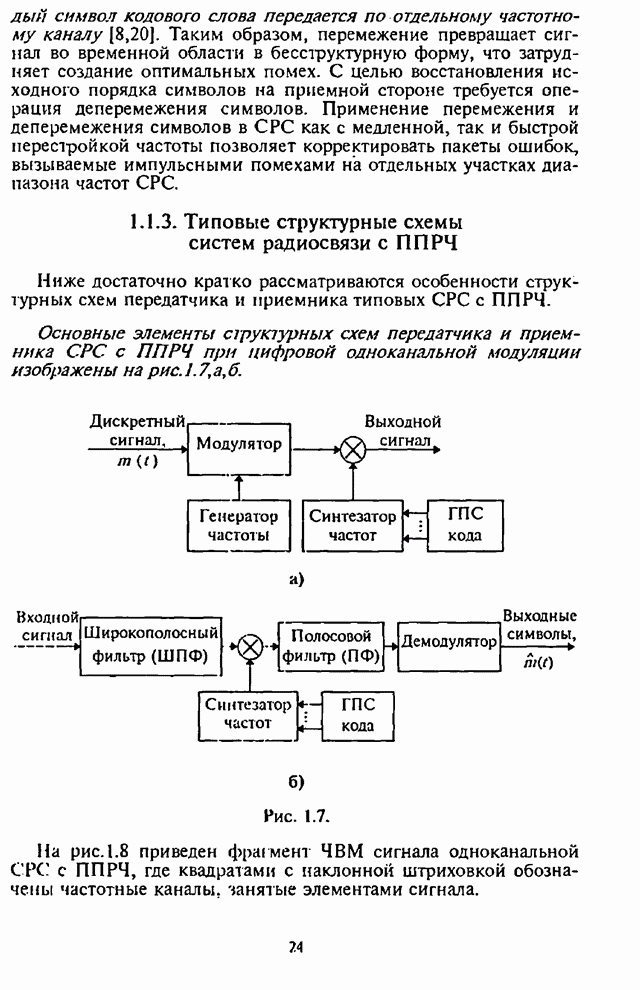
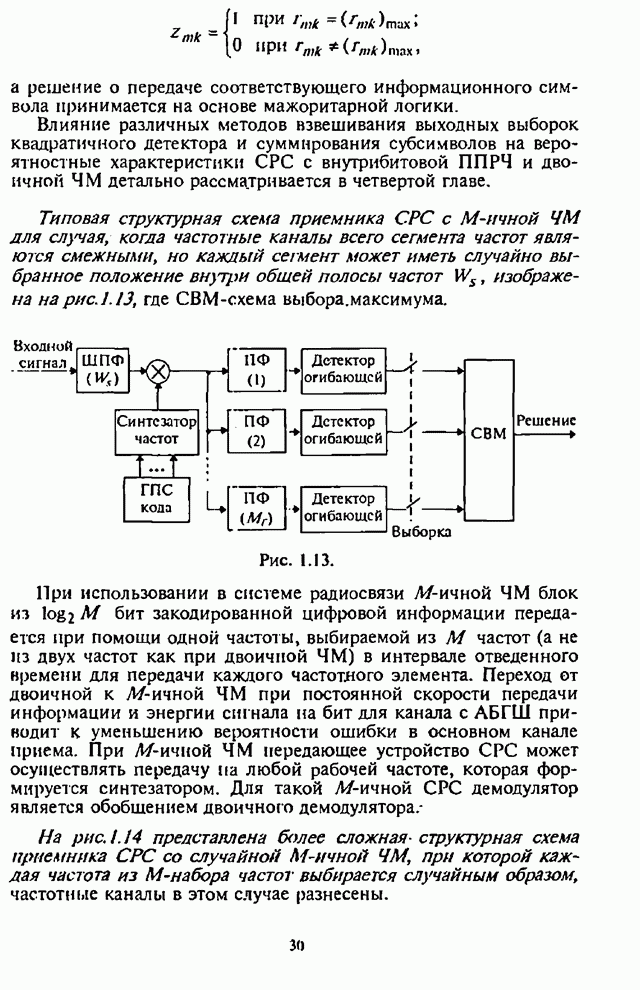
- 1.1.3. Типовые структурные схемы систем радиосвязи с ППРЧ
- 1.2. Коэффициент расширения спектра сигнала и запас помехоустойчивости системы радиосвязи с ППРЧ
- 1.3. Общая характеристика помехозащищенности систем радиосвязи с ППРЧ
- 1.3.1. Помехоустойчивость систем радиосвязи с ППРЧ
- 1.3.2. Скрытность сигналов систем радиосвязи с ППРЧ
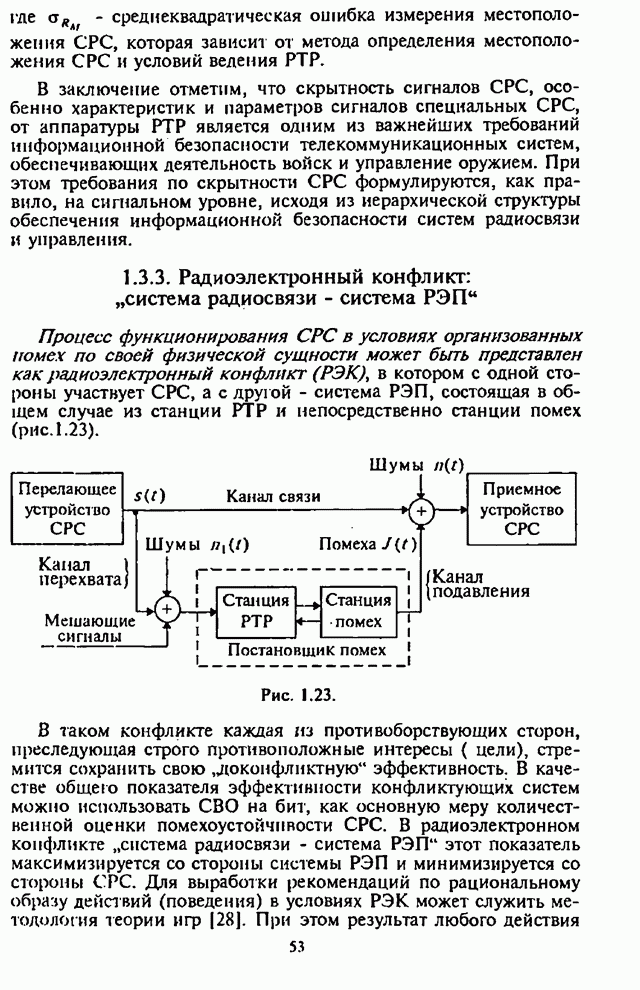
- 1.3.3. Радиоэлектронный конфликт: «система радиосвязи — система РЭП»
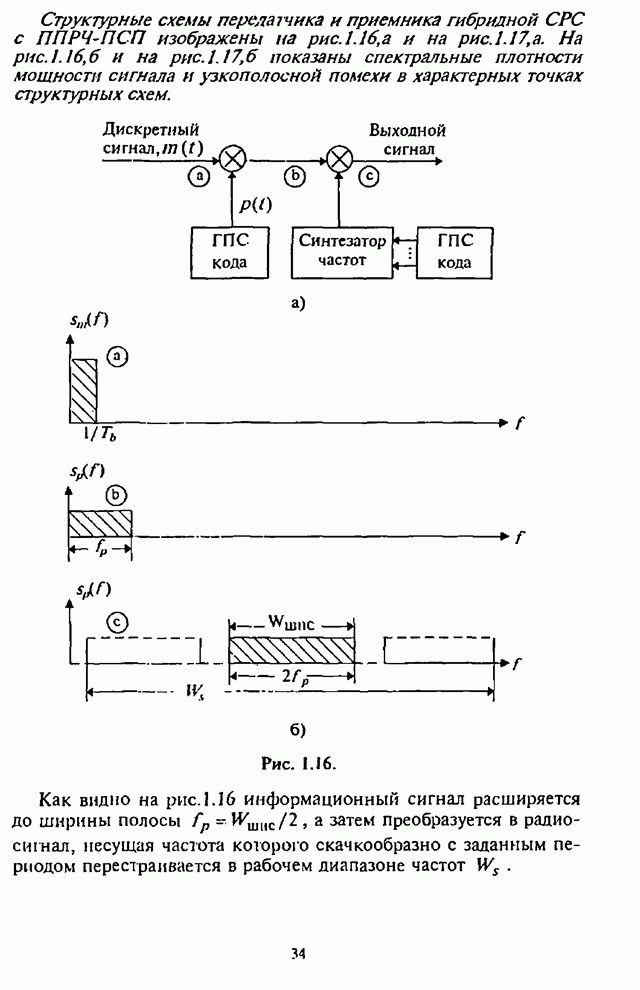
- 1.4. Модели и краткая характеристика основных видов помех
- Глава 2. Помехоустойчивость типовых систем радиосвязи с ППРЧ и частотной манипуляцией
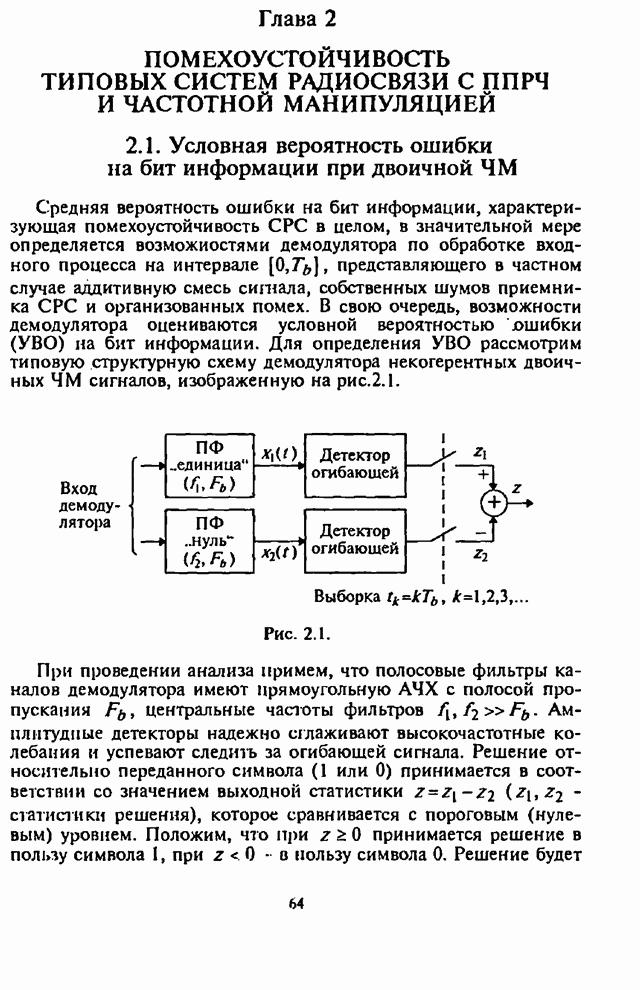
- 2.1. Условная вероятность ошибки на бит информации при двоичной ЧМ
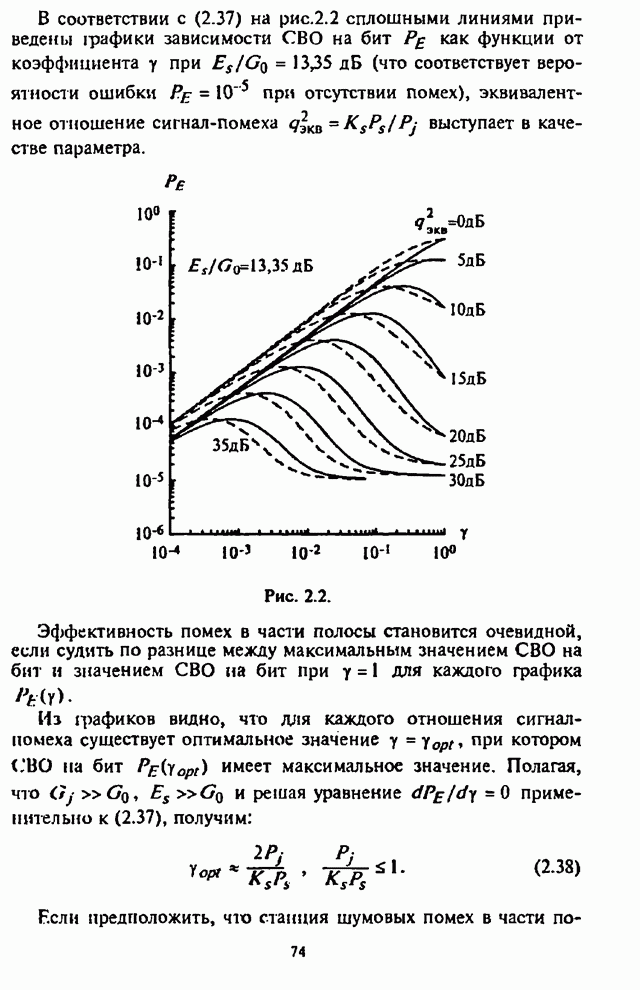
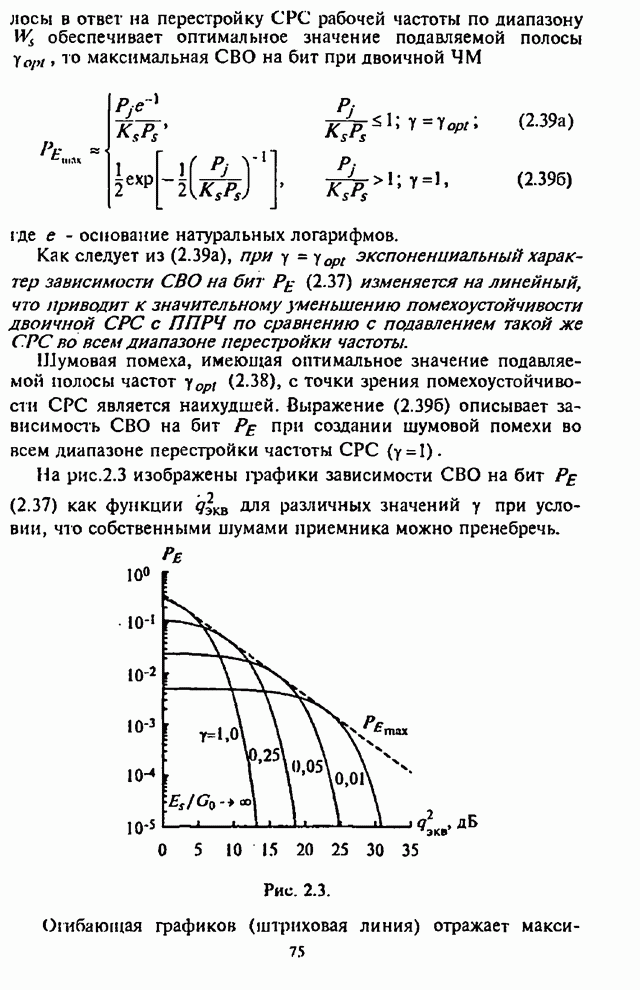
- 2.2. Оценка воздействия шумовой помехи в части полосы на системы радиосвязи с ППРЧ и неслучайной ЧМ
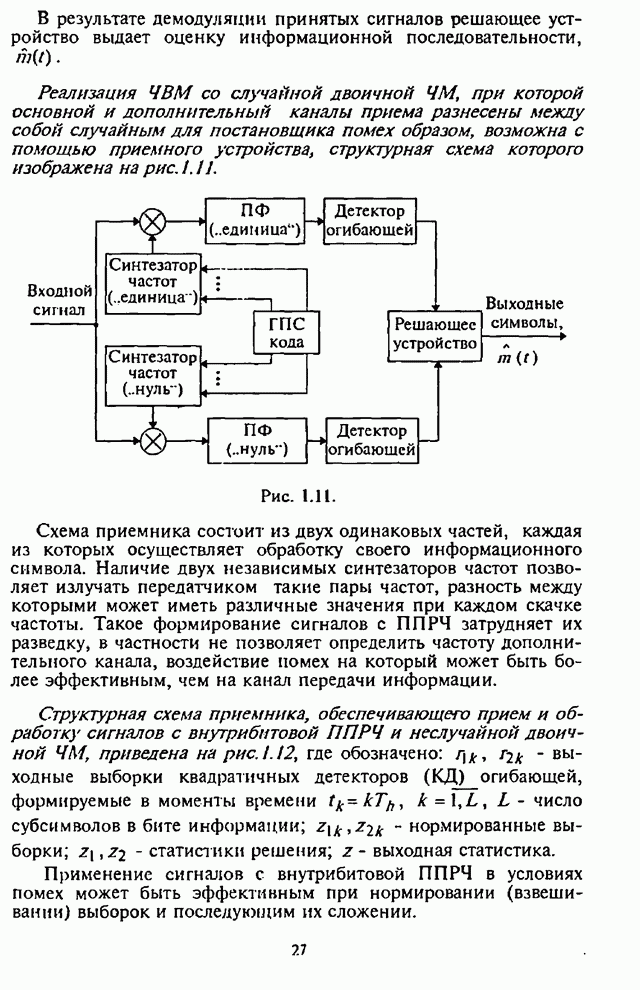
- 2.3. Оценка воздействия шумовой помехи в части полосы на системы радиосвязи с ППРЧ и случайной двоичной ЧМ
- 2.4. Оценка воздействия ответных помех на системы радиосвязи с ППРЧ и ЧМ
- 2.4.1. Оценка временных возможностей станции ответных помех
- 2.4.2. Оценка воздействия ответных шумовых помех на системы радиосвязи с ППРЧ и ЧМ
- 2.4.3. Оценка воздействия ответных гармонических помех на системы радиосвязи с ППРЧ и ЧМ
- 2.5. Помехоустойчивость систем радиосвязи с ППРЧ, двоичной ЧМ и блоковым кодированием
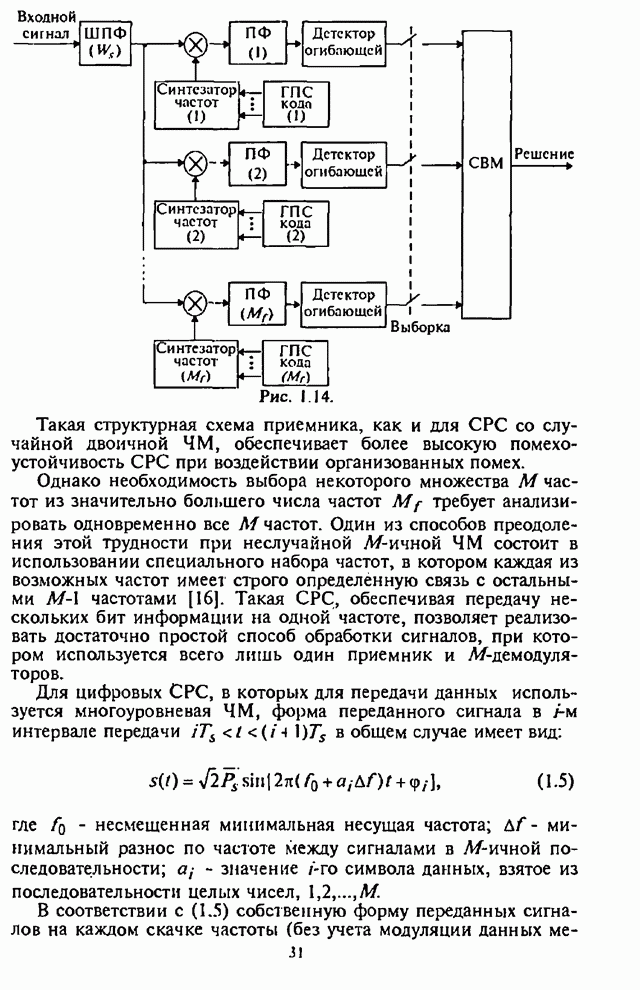
- Глава 3. Синтез и анализ эффективности адаптивных алгоритмов различения сигналов с ППРЧ, частотной модуляцией и разнесением символов по частоте
- 3.1. Синтез оптимального адаптивного алгоритма различения сигналов с внутрисимвольной ППРЧ и ЧМ
- 3.2. Квазиоптимальный адаптивный алгоритм различения сигналов с внутрисимвольной ППРЧ и двоичной ЧМ
- 3.3. Оценка помехоустойчивости синтезированного адаптивного алгоритма различения сигналов с внутрисимвольной ППРЧ и двоичной ЧМ
- 3.3.1. Случай «слабых» сигналов
- 3.3.2. Случай «сильных» сигналов
- Глава 4. Помехоустойчивость адаптивных алгоритмов демодуляции сигналов с внутрибитовой ППРЧ и двоичной частотной манипуляцией
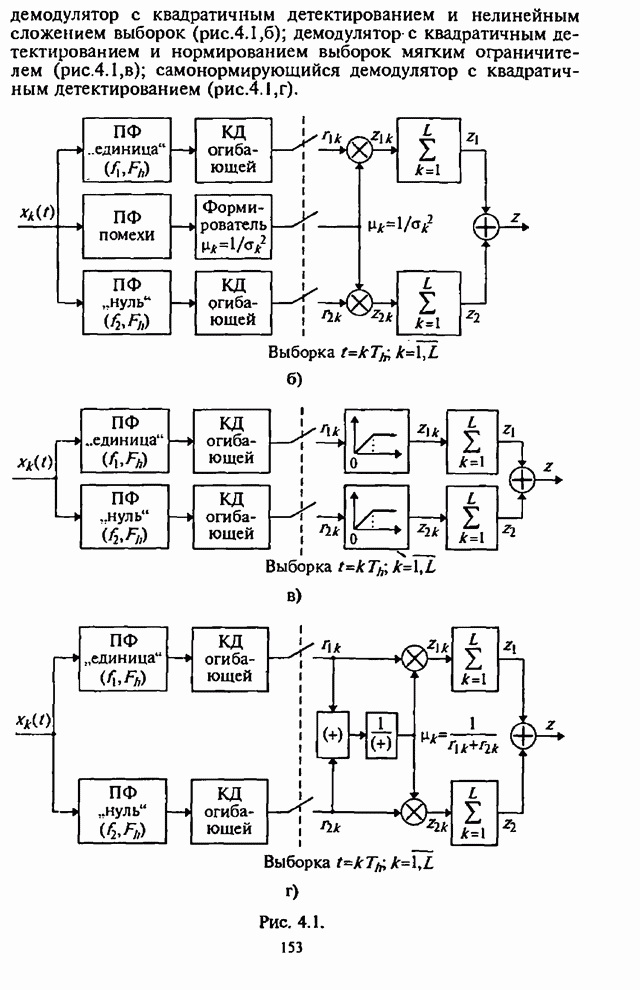
- 4.1. Структурные схемы демодуляторов
- 4.2. Помехоустойчивость демодулятора с линейным сложением выборок
- 4.3. Помехоустойчивость демодулятора с нелинейным сложением выборок
- 4.4. Помехоустойчивость демодулятора с мягким ограничителем
- 4.5. Помехоустойчивость самонормирующегося демодулятора
- 4.6. Влияние адаптивной регулировки усиления на помехоустойчивость СРС
- 4.7. Сравнительный анализ помехоустойчивости демодуляторов сигналов с внутрибитовой ППРЧ и двоичной ЧМ
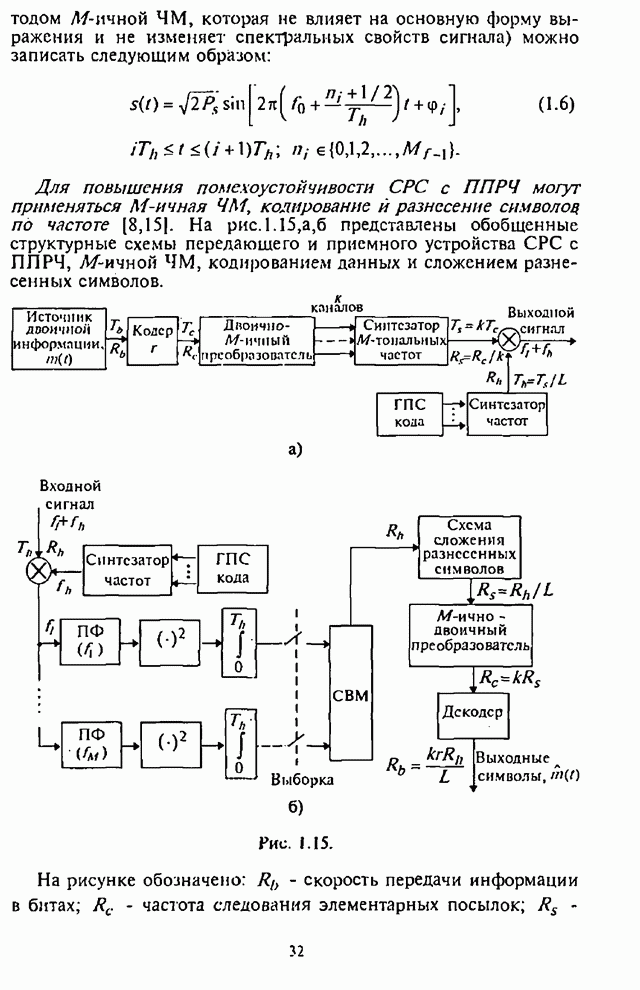
- Глава 5. Помехоустойчивость систем радиосвязи с ППРЧ при совместном применении частотной модуляции, разнесения символов по частоте и блокового кодирования
- 5.1. Помехоустойчивость систем радиосвязи с ППРЧ при M-ичной ЧМ и L-кратным разнесении символов по частоте
- 5.1.1. Условная вероятность ошибки на бит информации
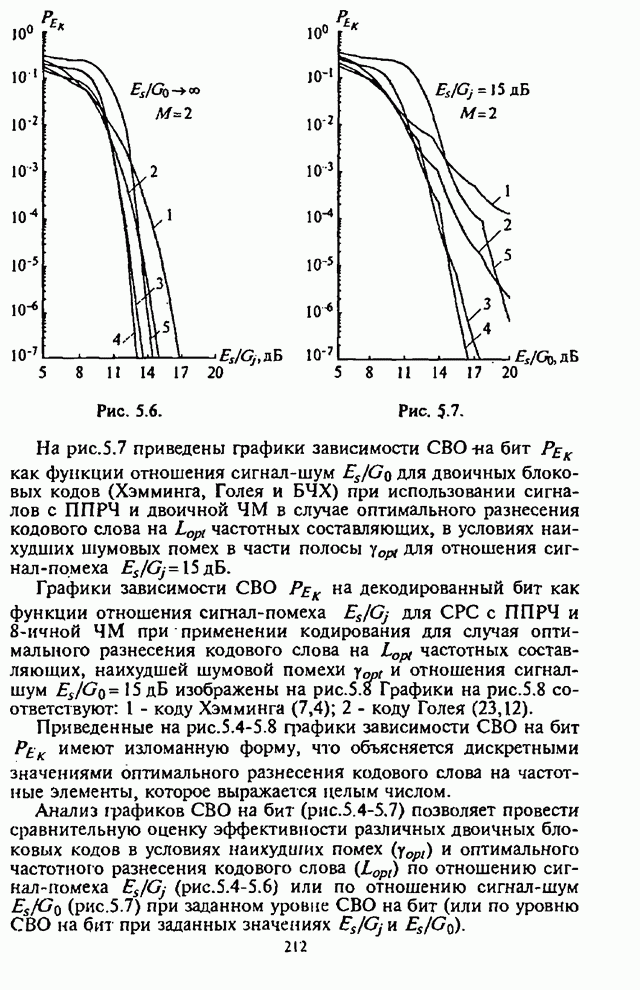
- 5.1.2. Анализ средней вероятности ошибки на бит информации
- 5.2. Помехоустойчивость систем радиосвязи с ППРЧ, M-ичной ЧМ, блоковым кодированием и L-кратным частотным разнесением кодовых слов
- 5.2.1. Структурная схема системы радиосвязи
- 5.2.2. Средняя вероятность ошибки на бит информации
- 5.2.3. Анализ средней вероятности ошибки на бит информации
- Глава 6. Синхронизация в системах радиосвязи с псевдослучайной перестройкой рабочей частоты
- 6.1. Назначение подсистемы синхронизации
- 6.2. Описательная модель подсистемы синхронизации
- 6.2.1. Типовая структурная схема подсистемы синхронизации
- 6.2.2. Типовые структурные схемы и алгоритмы функционирования основных устройств подсистемы синхронизации
- 6.3. Показатели и оценка эффективности циклических процедур поиска
- Приложение П.6.1. Верхняя граница среднего нормированного времени поиска
- Приложение П.6.2. Верхняя граница вероятности правильного обнаружения
- Глава 7. Адаптивные антенные решетки в системах радиосвязи с псевдослучайной перестройкой рабочей частоты
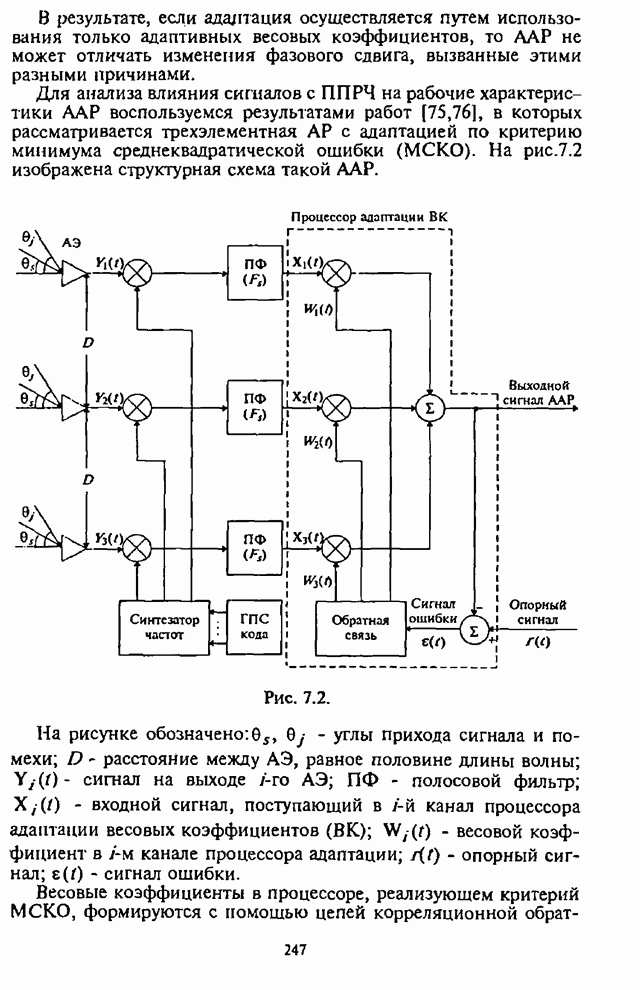
- 7.1. Влияние сигналов с ППРЧ на характеристики адаптивной антенной решетки
- 7.2. Максиминный алгоритм обработки сигналов и помех
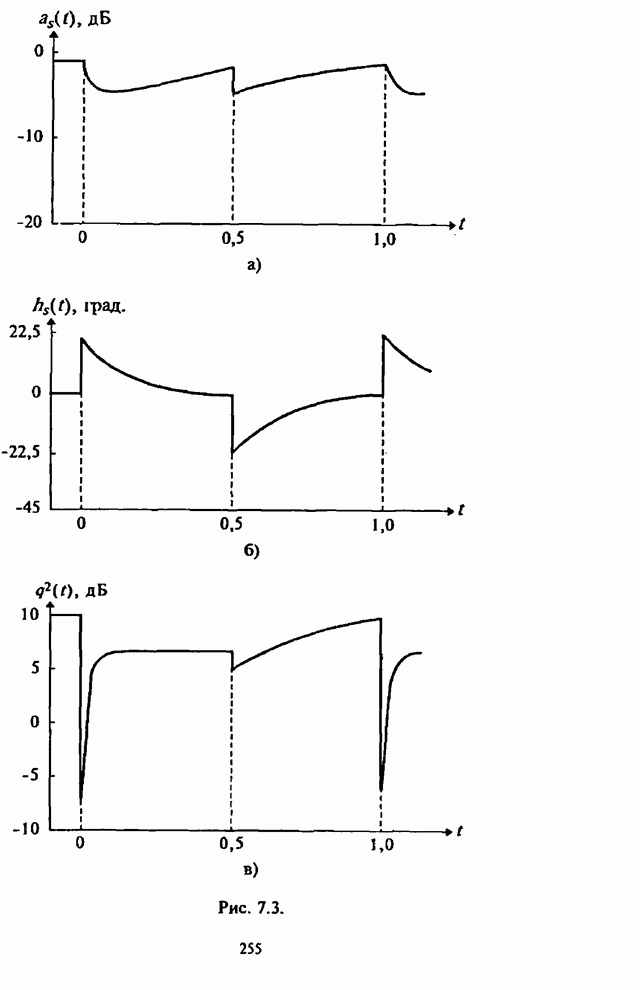
- 7.3. Реализация и возможности максиминного алгоритма
- 7.4. Модернизация максиминного алгоритма
- 7.4.1. Параметрическая обработка
- 7.4.2. Спектральная обработка
- 7.4.3. Обработка с упреждением
- Глава 8. Обнаружение сигналов с псевдослучайной перестройкой рабочей частоты
- 8.1. Обнаружение сигналов неизвестной структуры
- 8.2. Широкополосный энергетический обнаружитель
- 8.3. Многоканальные энергетические обнаружители
- 8.3.1. Квазиоптимальный многоканальный обнаружитель
- 8.3.2. Многоканальный обнаружитель типа сумматора с блоком фильтров
- 8.3.3. Модель обнаружителя типа сумматора с блоком фильтров при перехвате сигналов с медленной ППРЧ
- 8.3.4. Многоканальный обнаружитель типа сумматора с блоком фильтров в части полосы
- 8.3.5. Рассогласование по времени и частоте между характеристиками сигнала с ППРЧ и параметрами обнаружителя
- 8.4. Многоканальный адаптивный энергетический обнаружитель в условиях воздействия мешающих сигналов
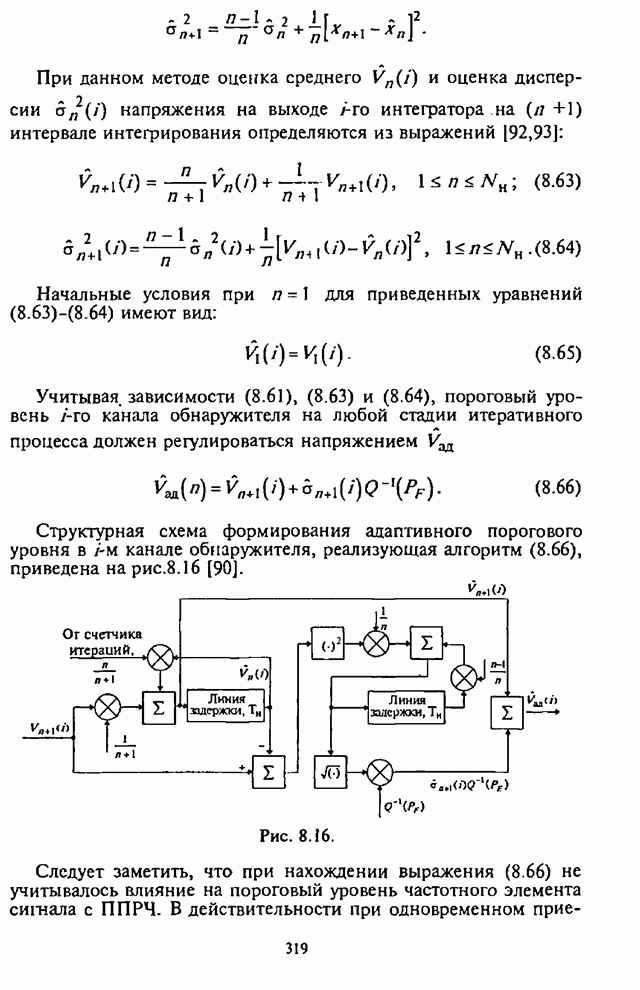
- 8.4.1. Структурная схема многоканального адаптивного энергетического обнаружителя с регулировкой порогового уровня
- 8.4.2. Вероятность ложной тревоги и адаптивная регулировка порогового уровня
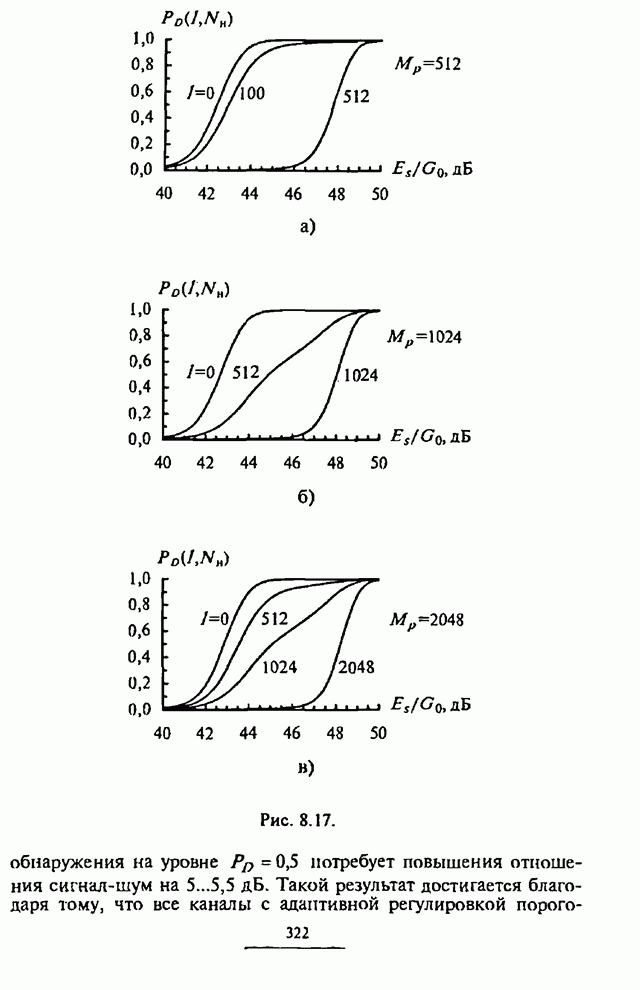
- 8.4.3. Вероятность обнаружения
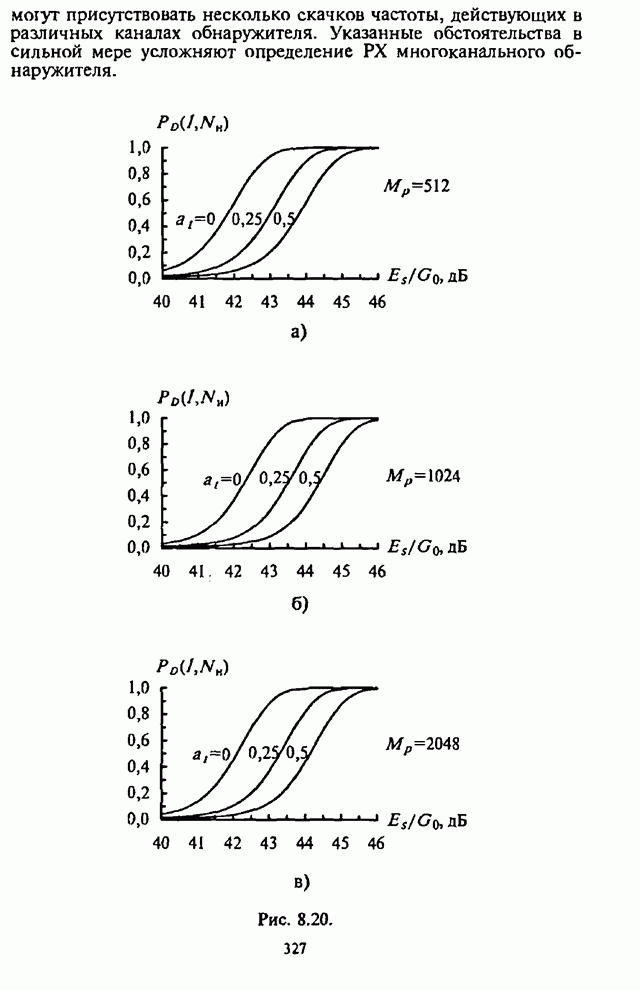
- 8.4.4. Влияние рассогласования по времени на обнаружение сигналов
- 8.5. Другие возможные типы обнаружителей сигналов с ППРЧ
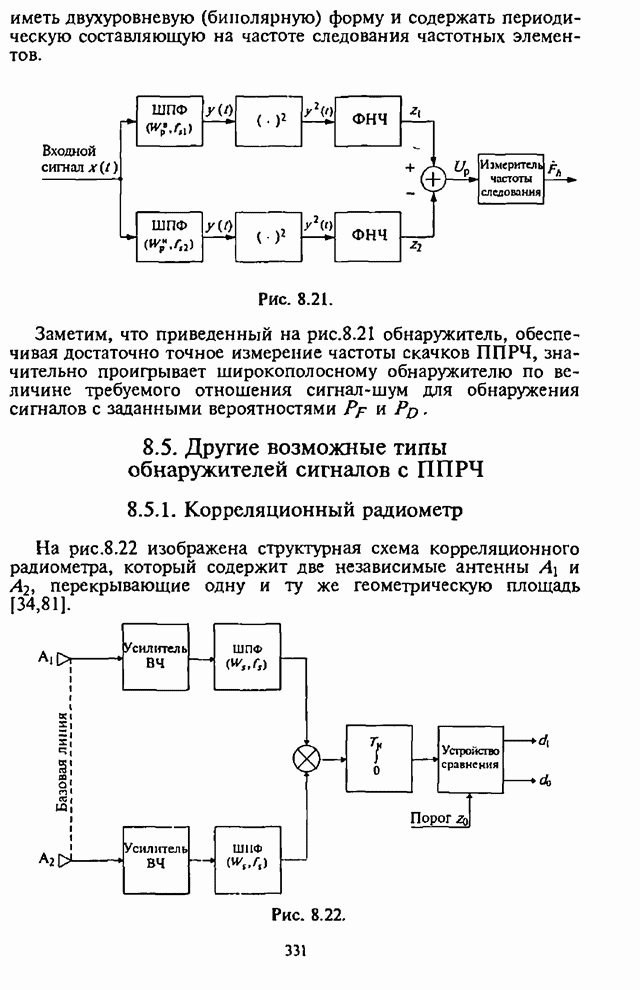
- 8.5.1. Корреляционный радиометр
- 8.5.2. Цифровой анализатор спектра
- 8.5.3. Метод вскрытия частотно-временной матрицы сигнала с ППРЧ
- Приложение П.8.1. Алгоритмы вычисления обобщенной Q-функции Маркума
- П.8.1.1. Постановка задачи
- П.8.1.2. Представление степенными рядами
- П.8.1.3. Представление в виде рядов Неймана
- П.8.1.4. Численное интегрирование
- П.8.1.5. Гауссовская аппроксимация
- П.8.1.6. Численные результаты
- Приложение П.8.2. Анализ вероятностно-временных характеристик алгоритмов обнаружения сигналов
- П.8.2.1. Вероятностно-временные характеристики основных видов обнаружителей
- П.8.2.2 Алгоритмы расчета вероятностно-временных характеристик основных видов обнаружителей
- П.8.2.3. Численные результаты
- СПИСОК ОСНОВНЫХ СОКРАЩЕНИЙ
- ОСНОВНЫЕ УСЛОВНЫЕ ОБОЗНАЧЕНИЯ
- СПИСОК ЛИТЕРАТУРЫ