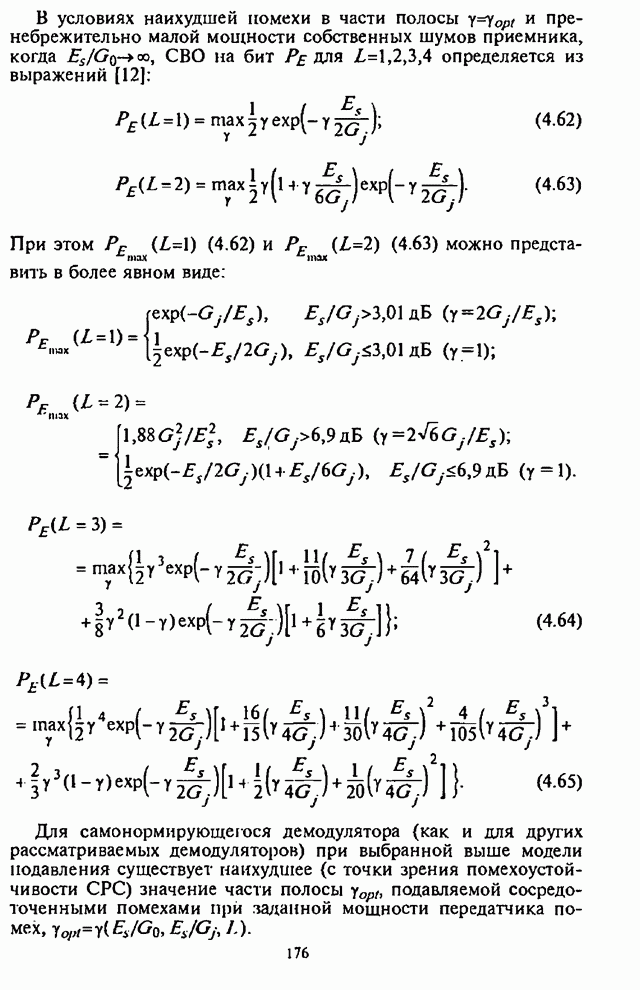| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
П.8.1.6. Численные результаты
Рассмотренные алгоритмы реализованы в виде программ на языке Turbo-Pascal для персональных ЭВМ и проведены численные расчеты. Вычислительные эксперименты показывают, что все методы, за исключением второй гауссовской аппроксимации, дают весьма близкие результаты.
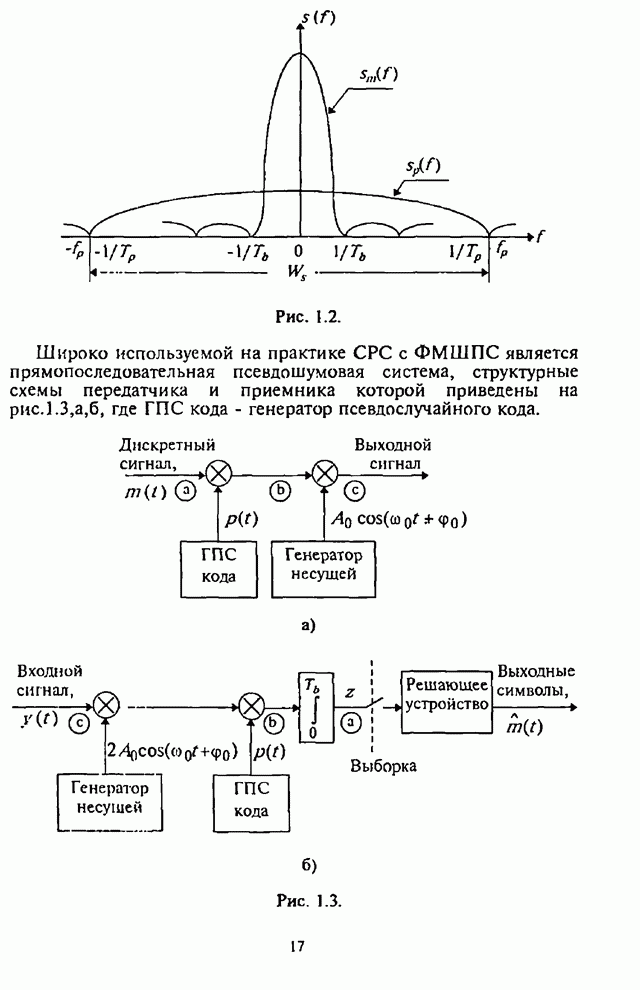
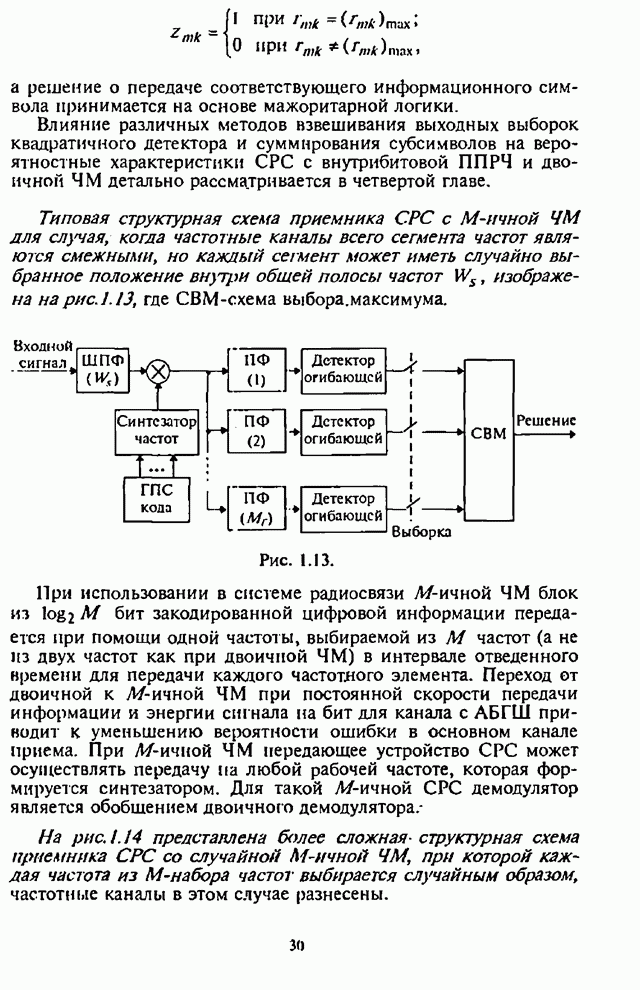
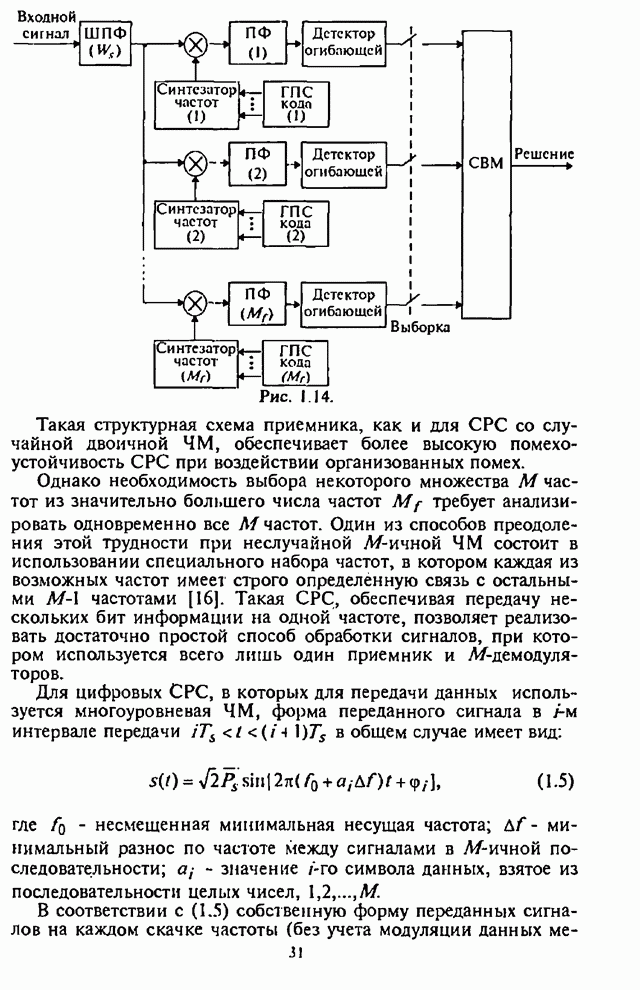
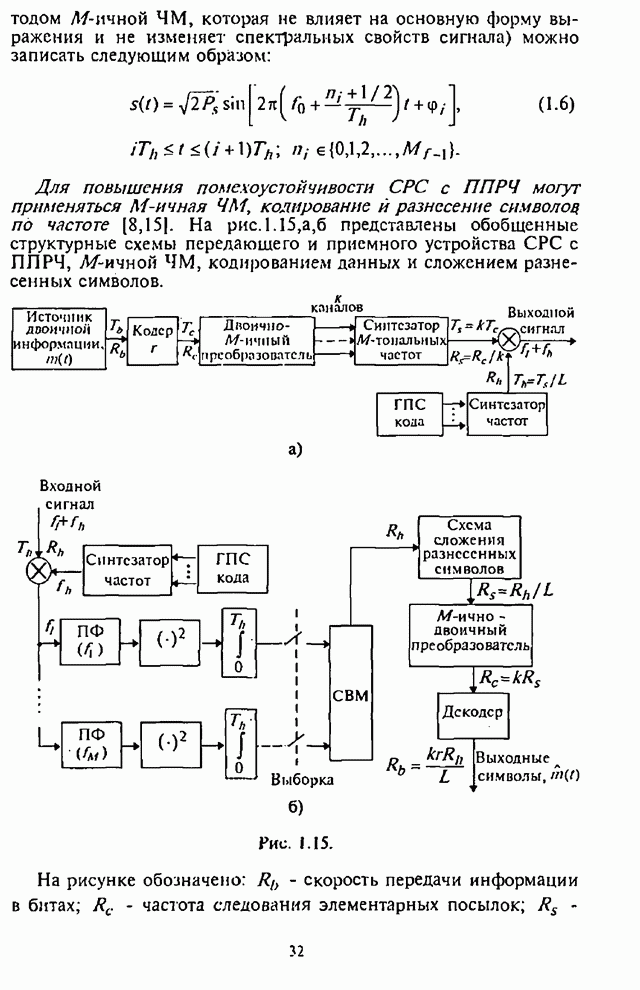
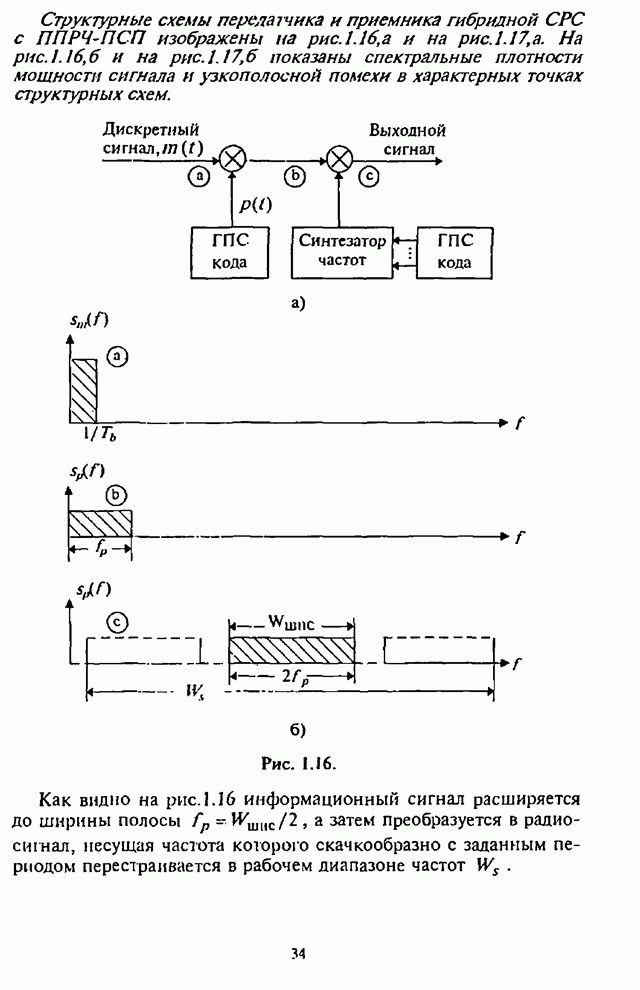
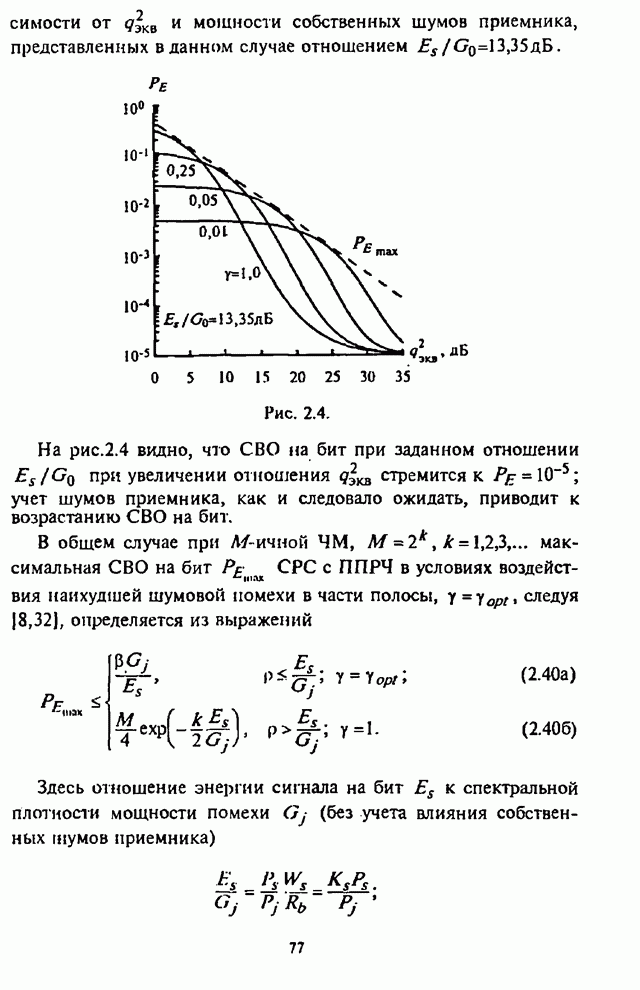
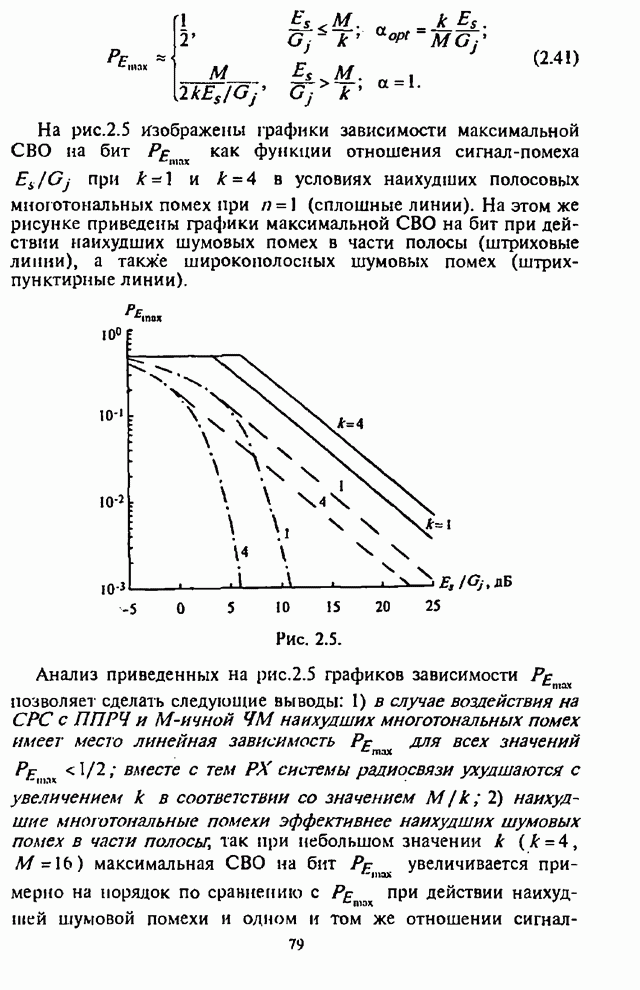
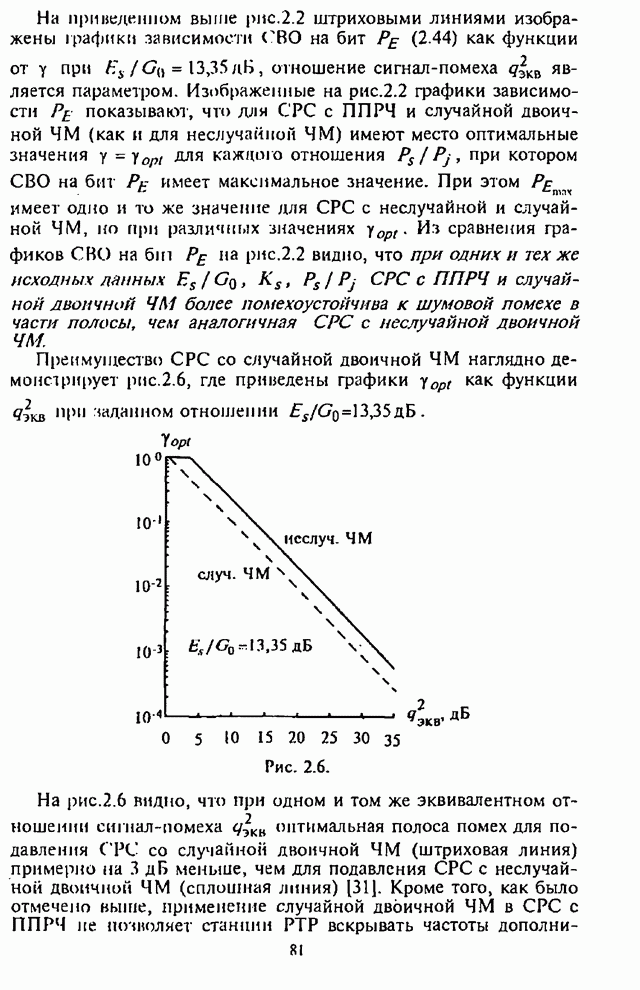
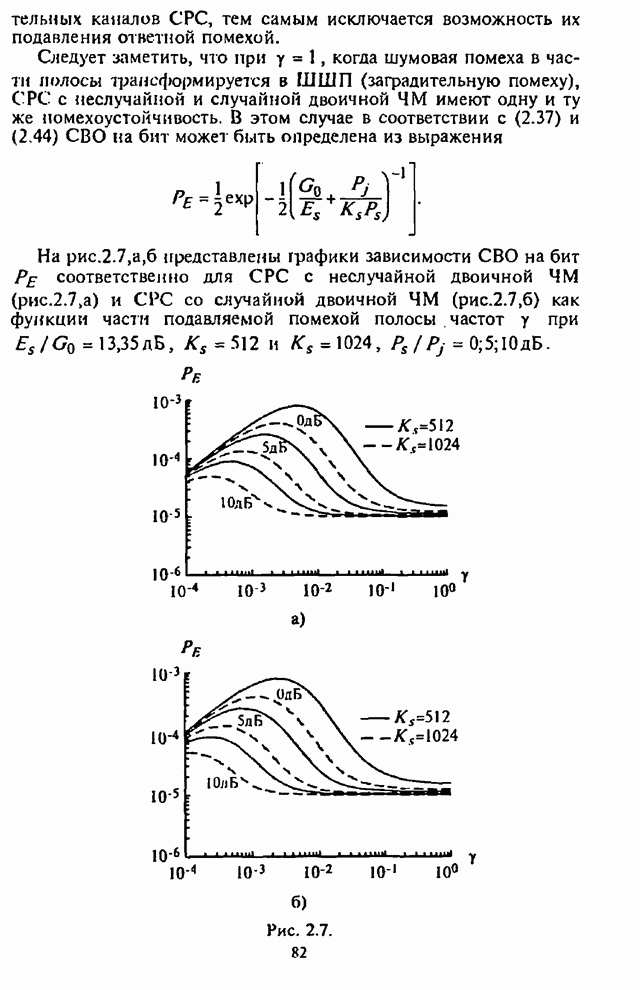
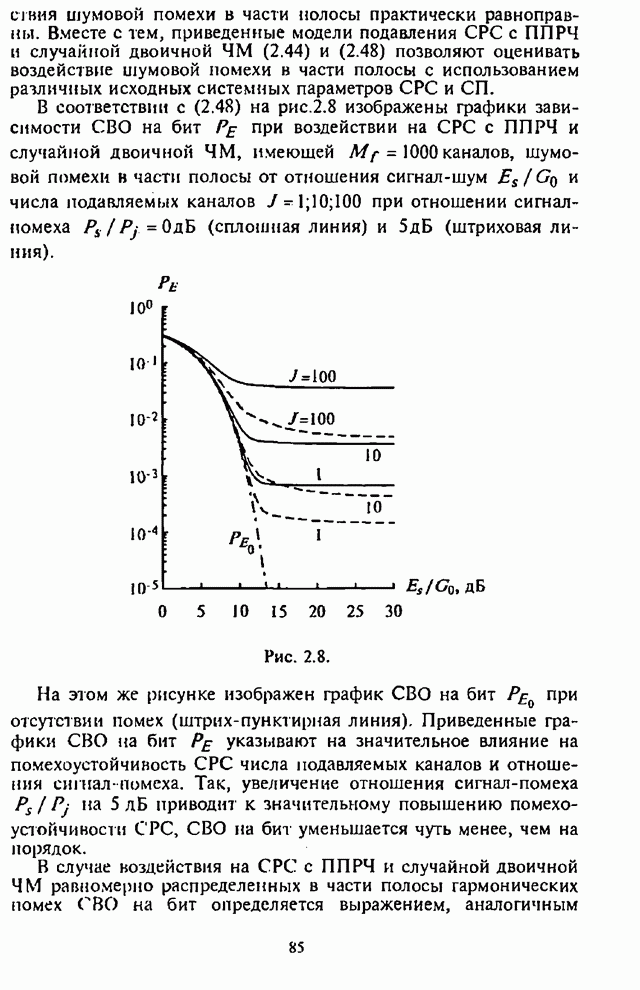
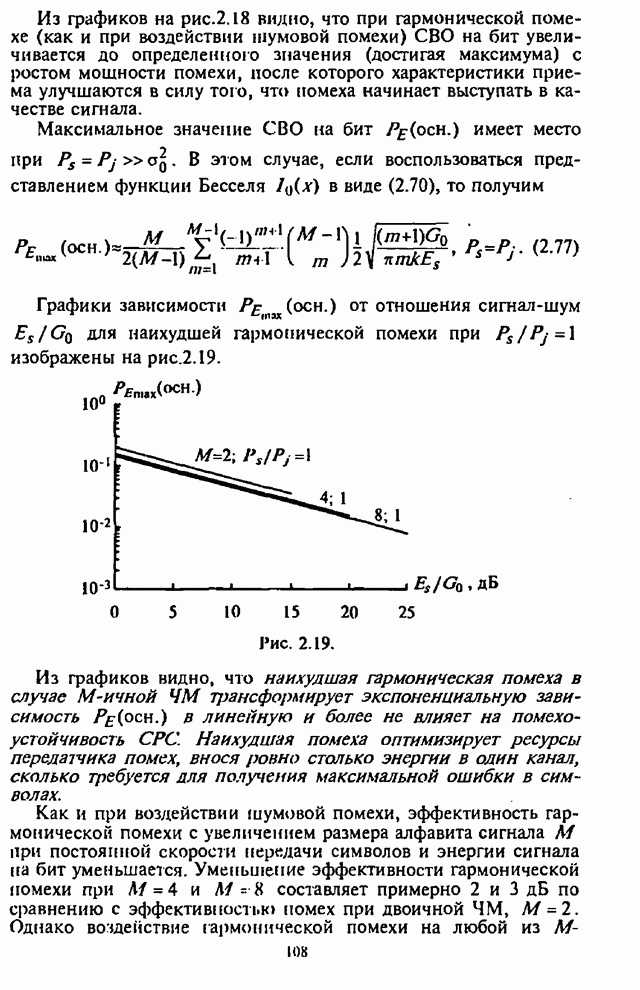
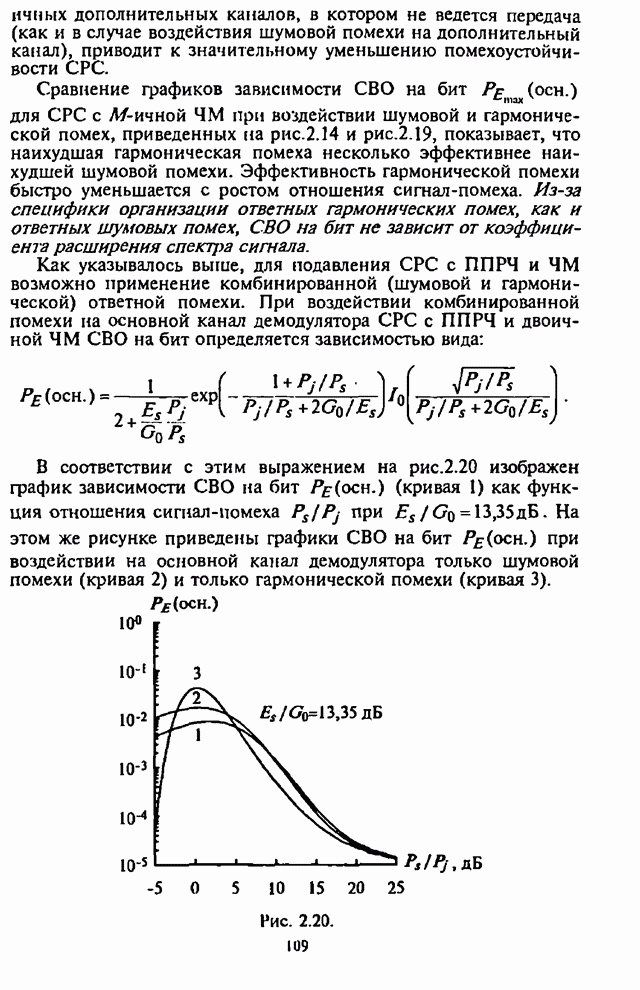
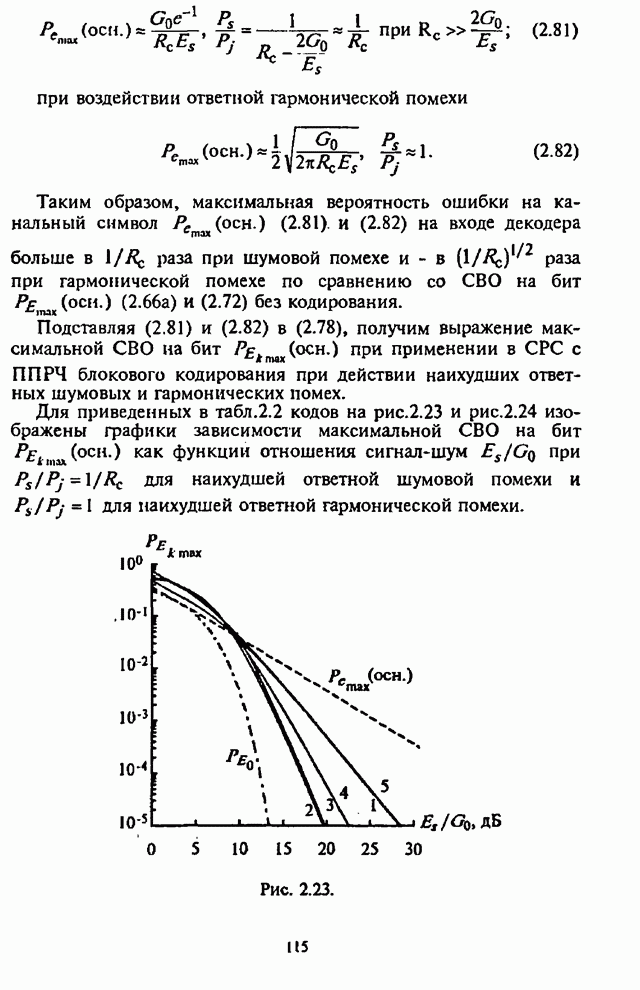
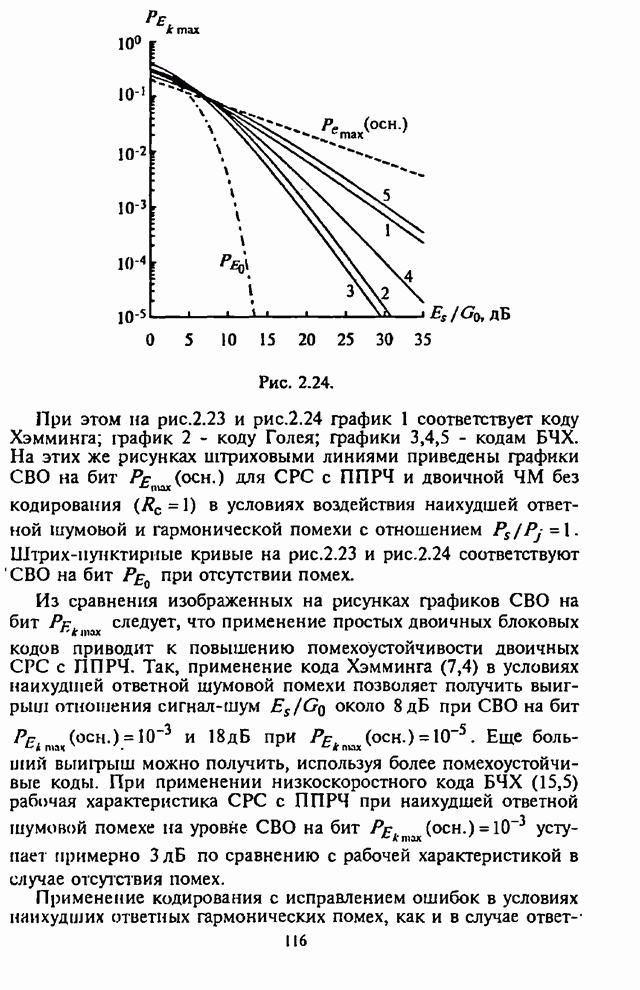
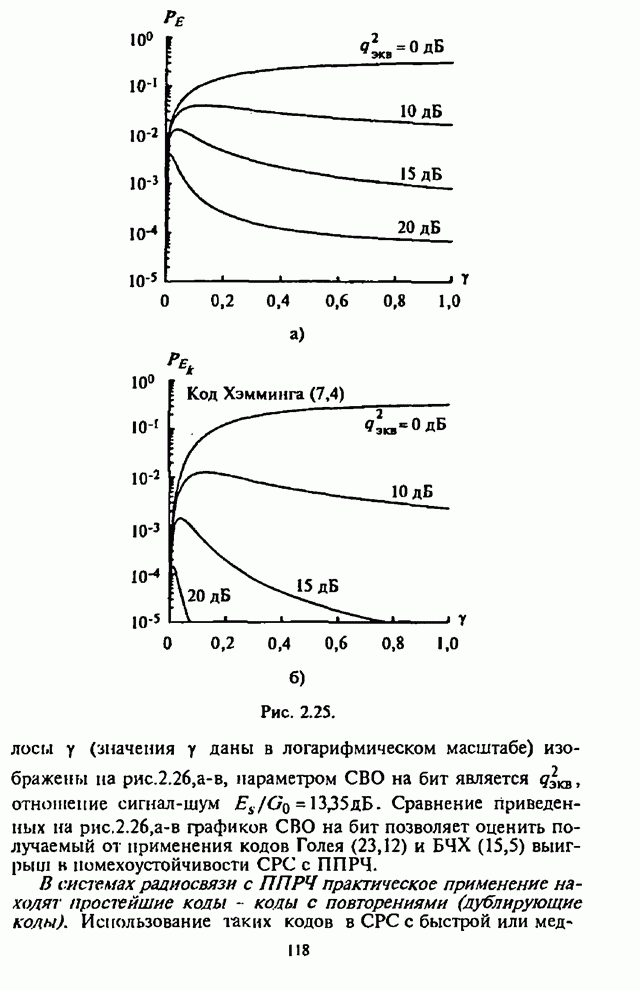
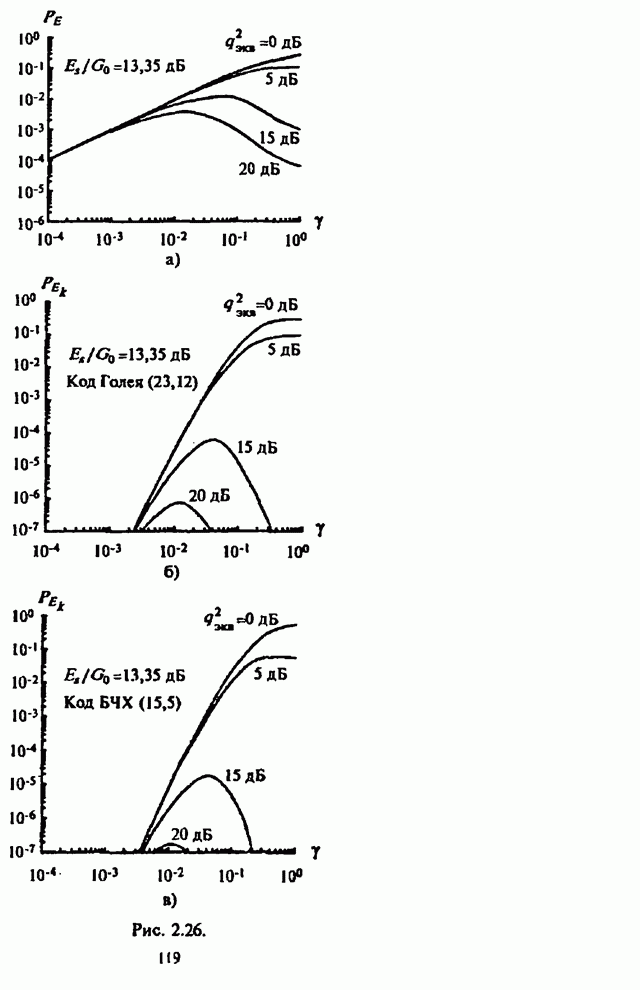
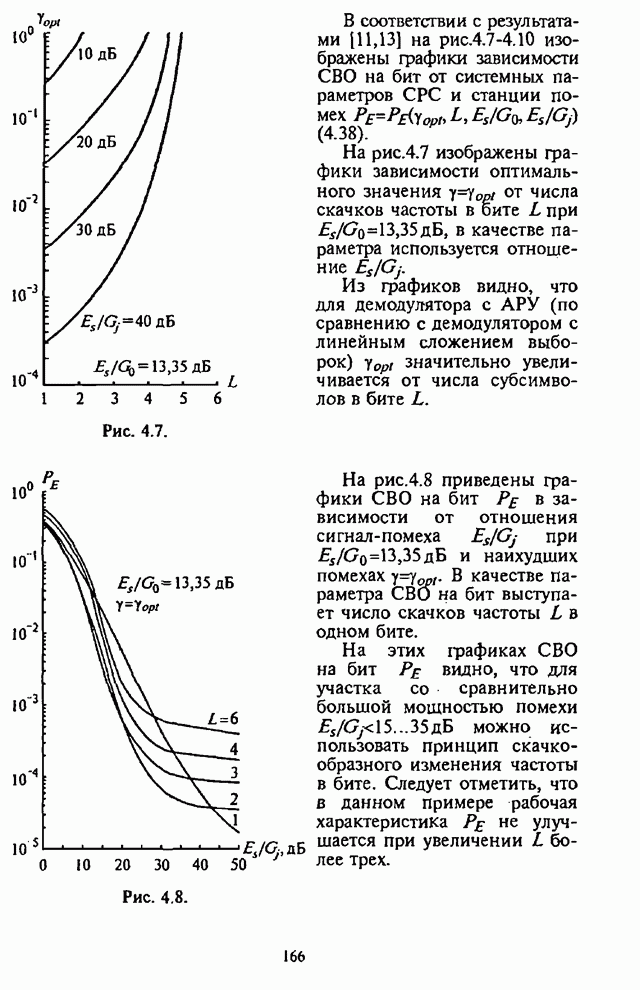
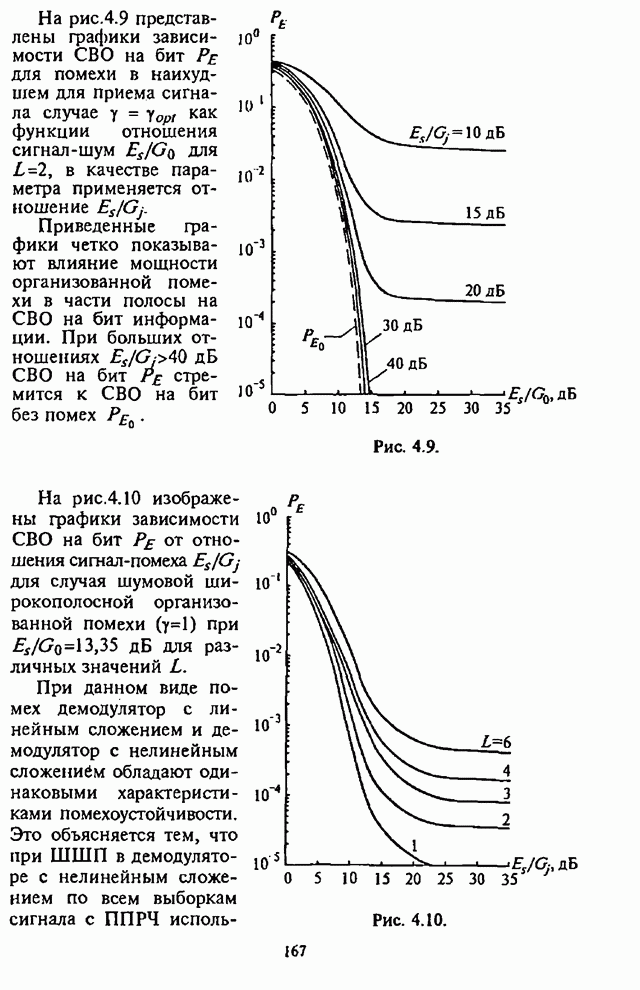
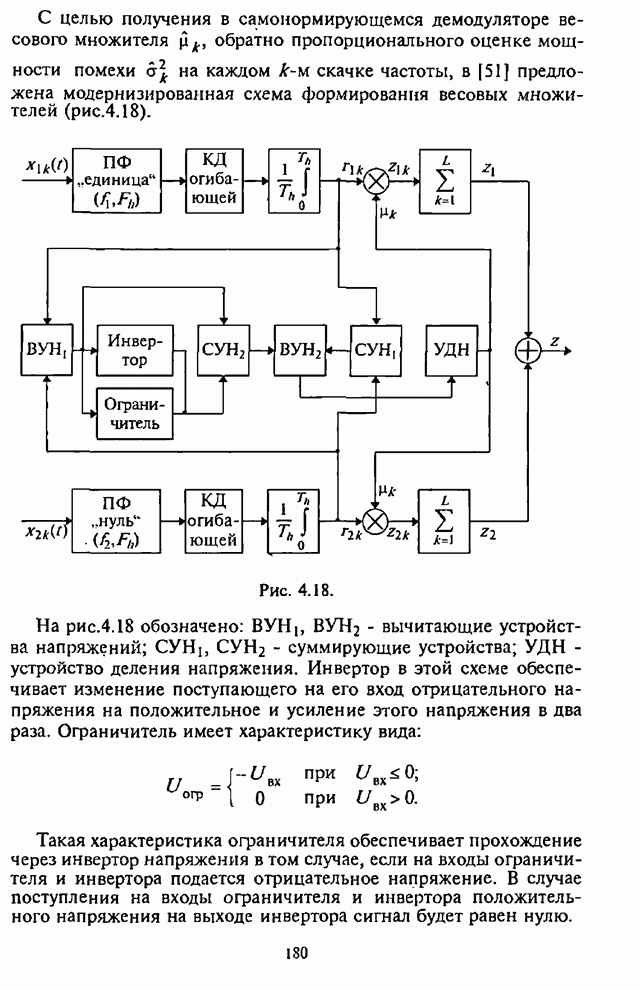
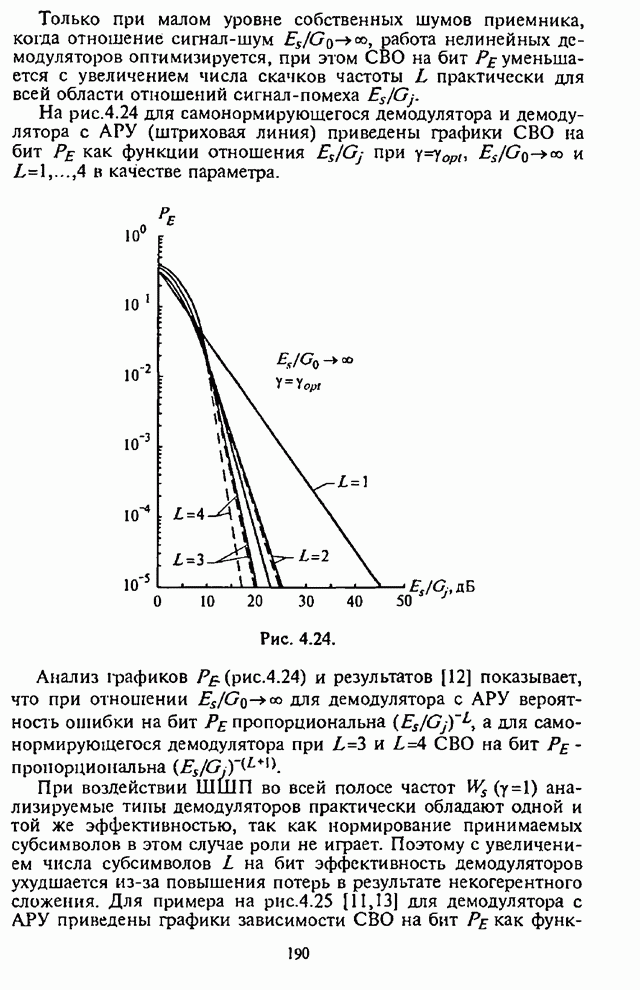
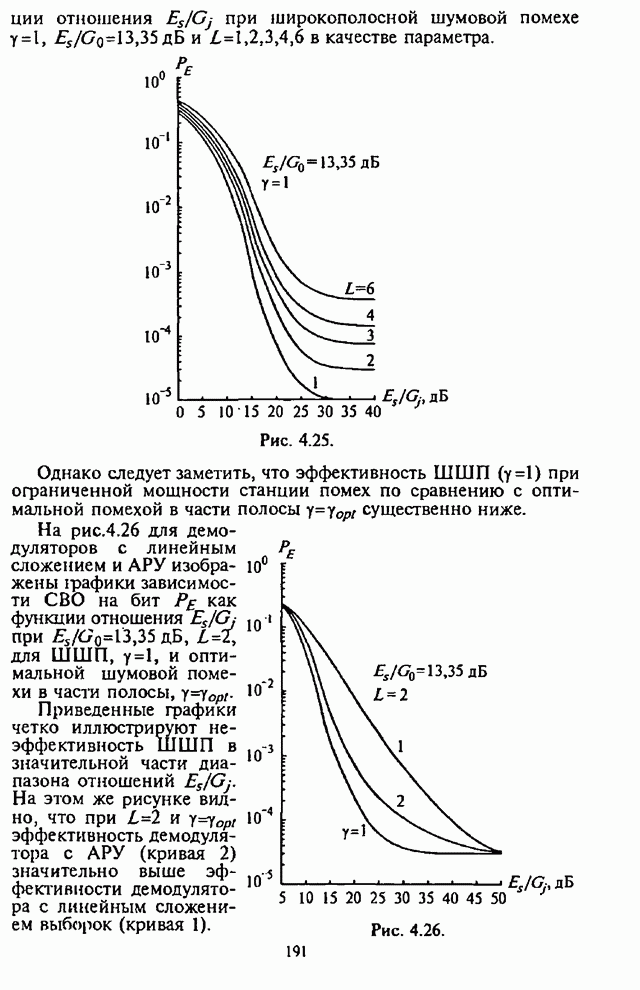
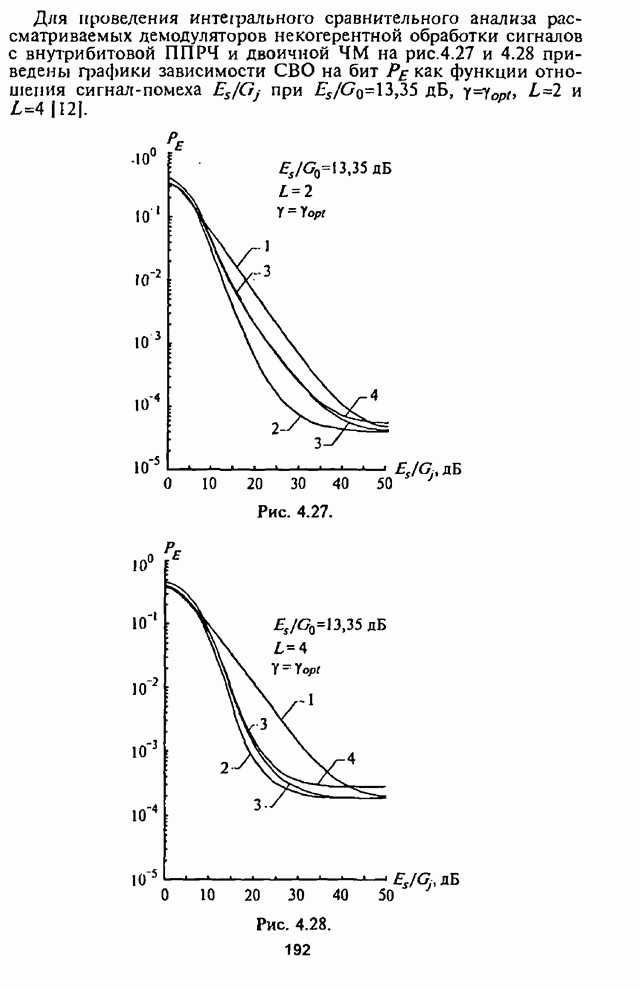
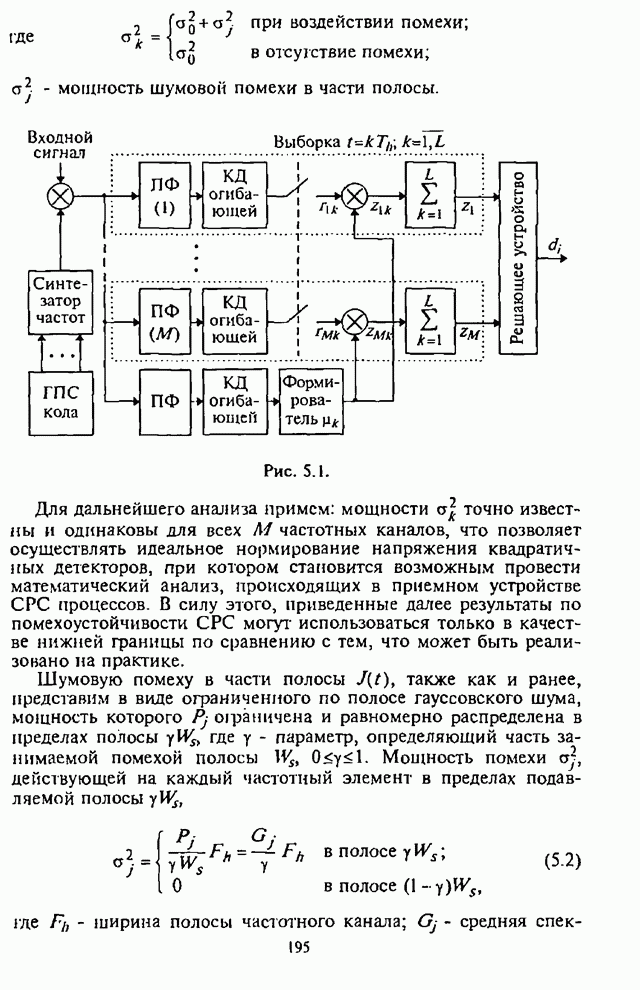
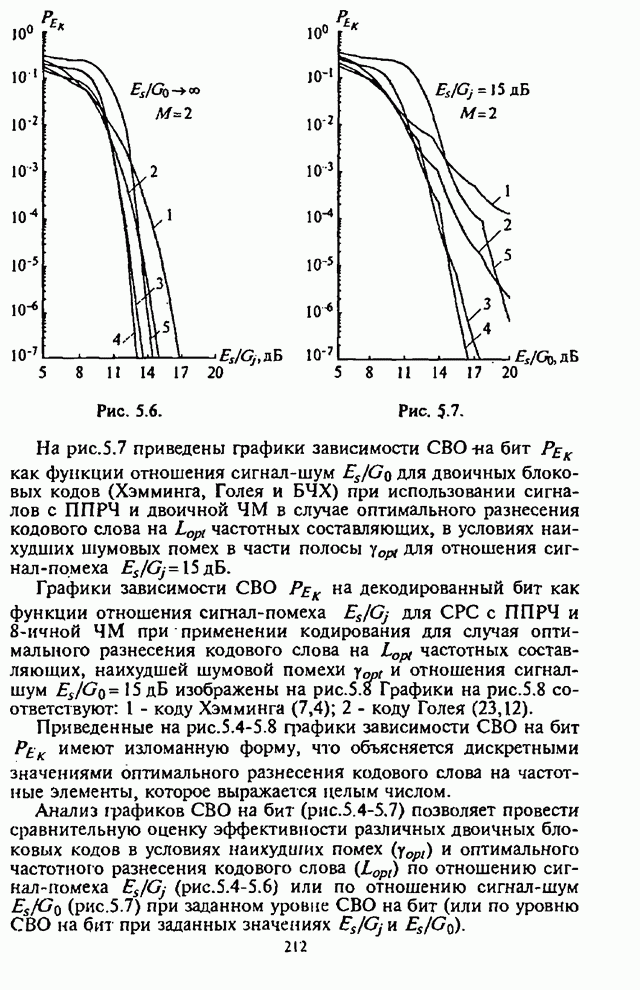
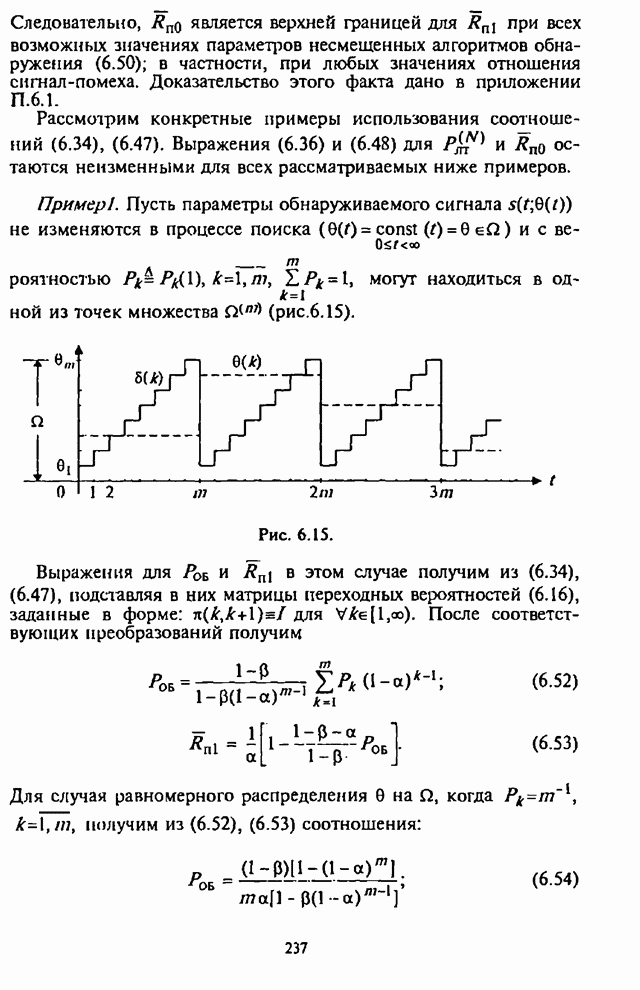
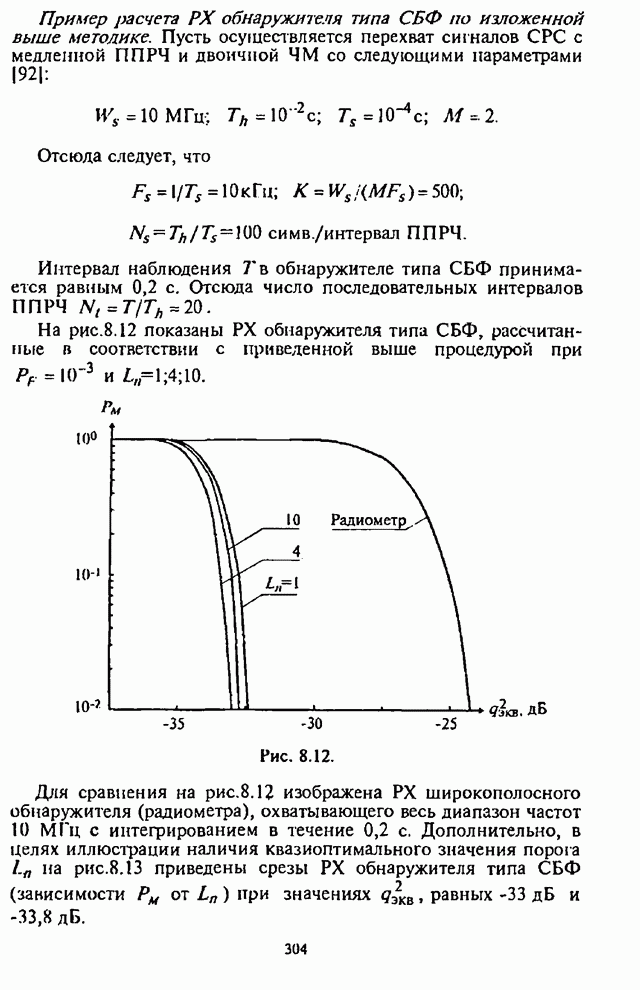
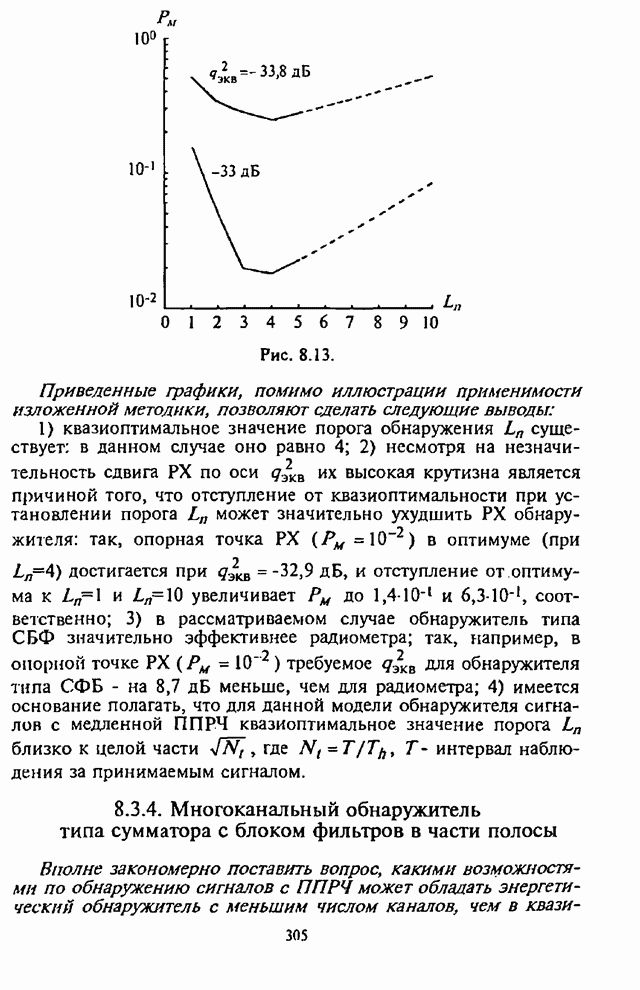
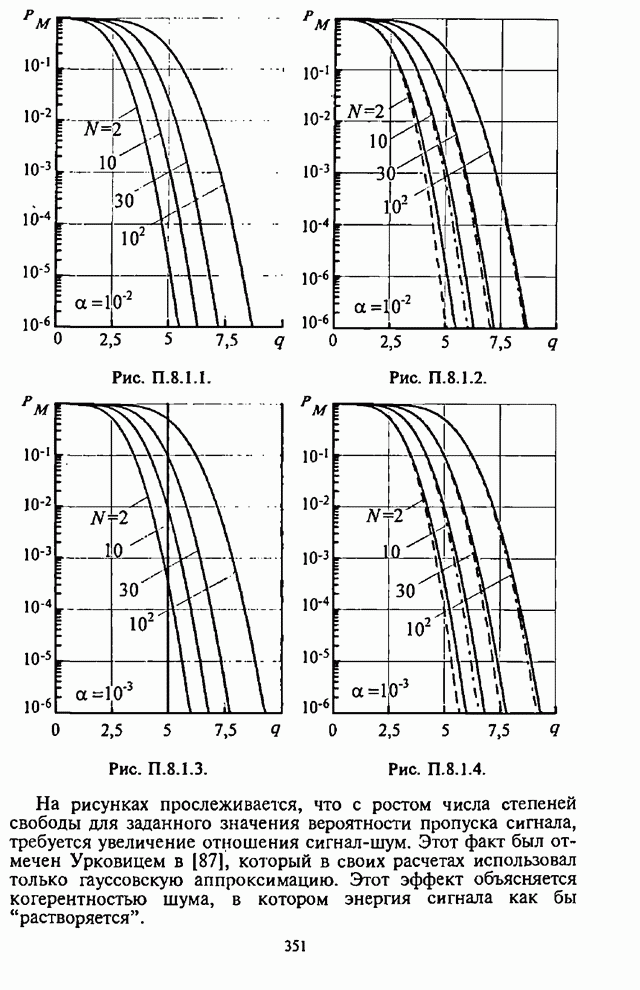
На рис.П.8.1.1-П.8.1.4 представлены зависимости вероятности пропуска сигнала от отношения сигнал-шум при различных значениях числа степеней свободы и при фиксированном значении вероятности ложной тревоги. На рис.П.8.1.1, П.8.1.3 показаны результаты, полученные методом Парла, другие методы дают практически такие же значения. Несколько отличаются результаты, полученные с помощью второй гауссовской аппроксимации (рис.П.8.1.2, П.8.1.4; сплошная линия соответствует первой гауссовской аппроксимации, штриховая - второй).

Рис. П.8.1.1.

Рис. П.8.1.2.

Рис. П.8.1.3.

Рис. П.8.1.4.
На рисунках прослеживается, что с ростом числа степеней свободы для заданного значения вероятности пропуска сигнала, требуется увеличение отношения сигнал-шум. Этот факт был отмечен Урковицем в [87], который в своих расчетах использовал только гауссовскую аппроксимацию. Этот эффект объясняется когерентностью шума, в котором энергия сигнала как бы "растворяется".
Для
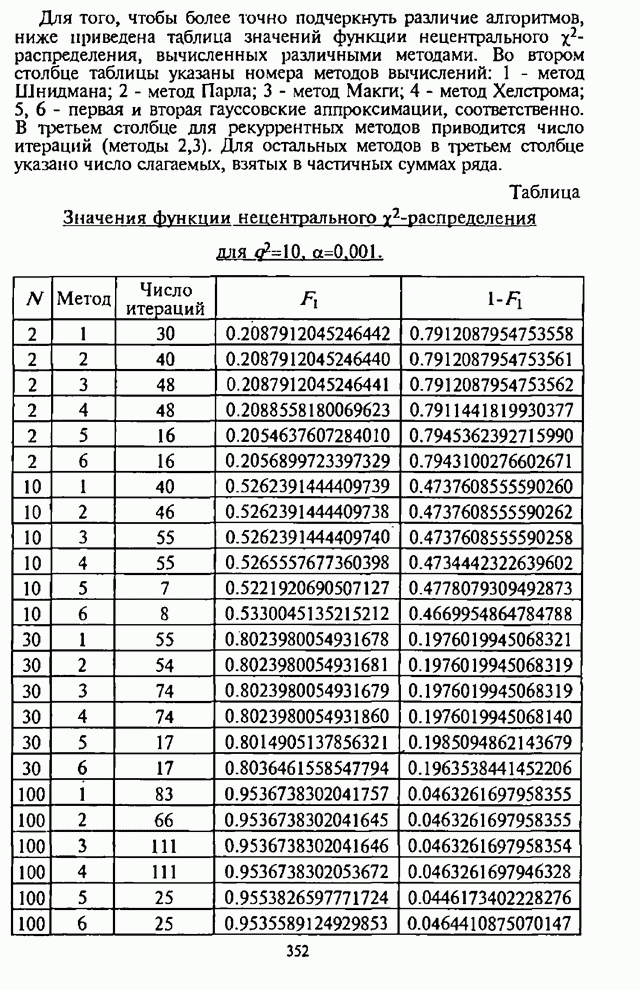
того, чтобы более точно подчеркнуть различие алгоритмов, ниже приведена таблица
значений функции нецентрального ![]() -распределения, вычисленных различными
методами. Во втором столбце таблицы указаны номера методов вычислений: 1 -
метод Шнидмана; 2 - метод Парла; 3 - метод Макги; 4 - метод Хелстрома; 5, 6 -
первая и вторая гауссовские аппроксимации, соответственно. В третьем столбце
для рекуррентных методов приводится число итераций (методы 2,3). Для остальных
методов в третьем столбце указано число слагаемых, взятых в частичных суммах
ряда.
-распределения, вычисленных различными
методами. Во втором столбце таблицы указаны номера методов вычислений: 1 -
метод Шнидмана; 2 - метод Парла; 3 - метод Макги; 4 - метод Хелстрома; 5, 6 -
первая и вторая гауссовские аппроксимации, соответственно. В третьем столбце
для рекуррентных методов приводится число итераций (методы 2,3). Для остальных
методов в третьем столбце указано число слагаемых, взятых в частичных суммах
ряда.
Таблица.
Значения функции нецентрального ![]() -распределения для
-распределения для ![]() .
.
|
N |
Метод |
Число итераций |
|
|
|
2 |
1 |
30 |
0.2087912045246442 |
0.7912087954753558 |
|
2 |
2 |
40 |
0.2087912045246440 |
0.7912087954753561 |
|
2 |
3 |
48 |
0.2087912045246441 |
0.7912087954753562 |
|
2 |
4 |
48 |
0.2088558180069623 |
0.7911441819930377 |
|
2 |
5 |
16 |
0.2054637607284010 |
0.7945362392715990 |
|
2 |
6 |
16 |
0.2056899723397329 |
0.7943100276602671 |
|
10 |
1 |
40 |
0.5262391444409739 |
0.4737608555590260 |
|
10 |
2 |
46 |
0.5262391444409738 |
0.4737608555590262 |
|
10 |
3 |
55 |
0.5262391444409740 |
0.4737608555590258 |
|
10 |
4 |
55 |
0.5265557677360398 |
0.4734442322639602 |
|
10 |
5 |
7 |
0.5221920690507127 |
0.4778079309492873 |
|
10 |
6 |
8 |
0.5330045135215212 |
0.4669954864784788 |
|
30 |
1 |
55 |
0.8023980054931678 |
0.1976019945068321 |
|
30 |
2 |
54 |
0.8023980054931681 |
0.1976019945068319 |
|
30 |
3 |
74 |
0.8023980054931679 |
0.1976019945068319 |
|
30 |
4 |
74 |
0.8023980054931860 |
0.1976019945068140 |
|
30 |
5 |
17 |
0.8014905137856321 |
0.1985094862143679 |
|
30 |
6 |
17 |
0.8036461558547794 |
0.1963538441452206 |
|
100 |
1 |
83 |
0.9536738302041757 |
0.0463261697958355 |
|
100 |
2 |
66 |
0.9536738302041645 |
0.0463261697958355 |
|
100 |
3 |
111 |
0.9536738302041646 |
0.0463261697958354 |
|
100 |
4 |
111 |
0.9536738302053672 |
0.0463261697946328 |
|
100 |
5 |
25 |
0.9553826597771724 |
0.0446173402228276 |
|
100 |
6 |
25 |
0.9535589124929853 |
0.0464410875070147 |
Сравнительный
анализ результатов показывает, что при малых значениях числа степеней свободы
малоэффективными являются гауссовская аппроксимация и метод Хелстрома. При
увеличении ![]() ,
несмотря на одинаковую точность вычислений, метод Парла остается более
эффективным из-за меньших затрат машинного времени.
,
несмотря на одинаковую точность вычислений, метод Парла остается более
эффективным из-за меньших затрат машинного времени.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие
- Введение
- Глава 1. Системы радиосвязи с расширением спектра сигналов методом псевдослучайной перестройки рабочей частоты: общие принципы
- 1.1. Краткая характеристика расширения спектра сигналов методом ППРЧ
- 1.1.1. Основные принципы и методы расширения спектра сигналов
- 1.1.2. Метод псевдослучайной перестройки рабочей частоты
- 1.1.3. Типовые структурные схемы систем радиосвязи с ППРЧ
- 1.2. Коэффициент расширения спектра сигнала и запас помехоустойчивости системы радиосвязи с ППРЧ
- 1.3. Общая характеристика помехозащищенности систем радиосвязи с ППРЧ
- 1.3.1. Помехоустойчивость систем радиосвязи с ППРЧ
- 1.3.2. Скрытность сигналов систем радиосвязи с ППРЧ
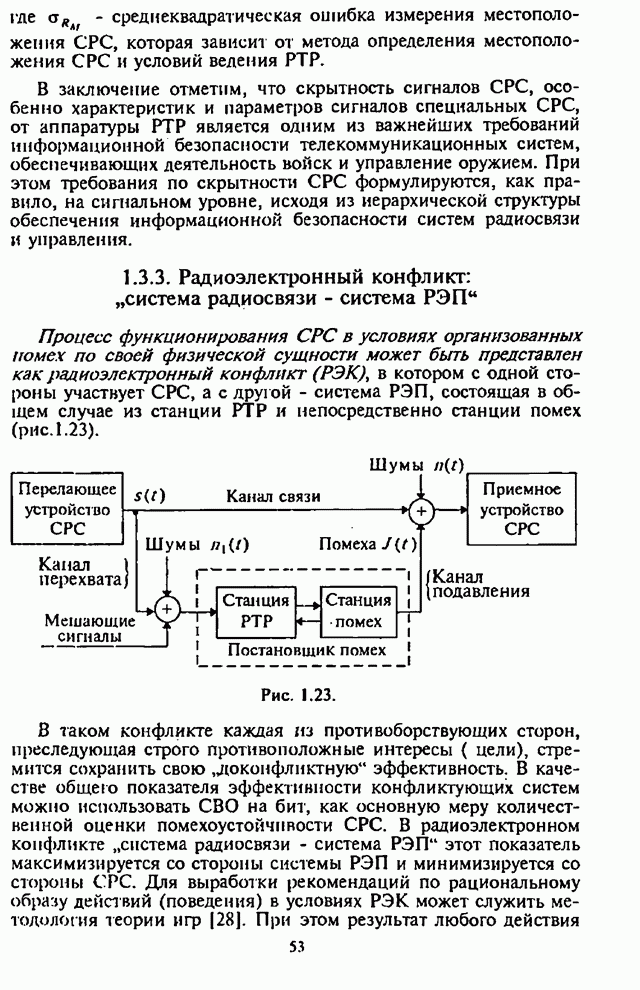
- 1.3.3. Радиоэлектронный конфликт: «система радиосвязи — система РЭП»
- 1.4. Модели и краткая характеристика основных видов помех
- Глава 2. Помехоустойчивость типовых систем радиосвязи с ППРЧ и частотной манипуляцией
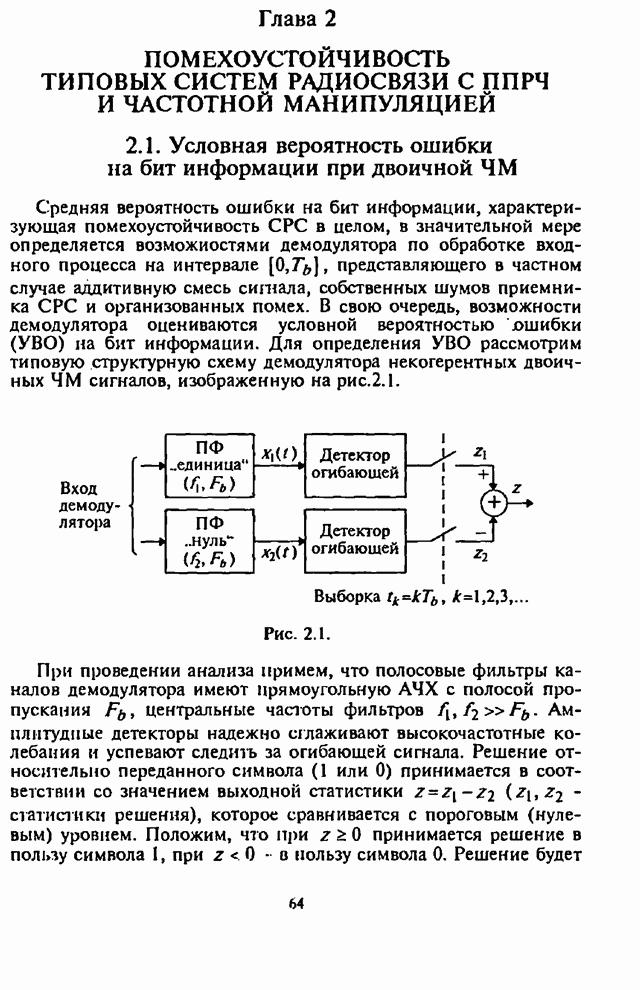
- 2.1. Условная вероятность ошибки на бит информации при двоичной ЧМ
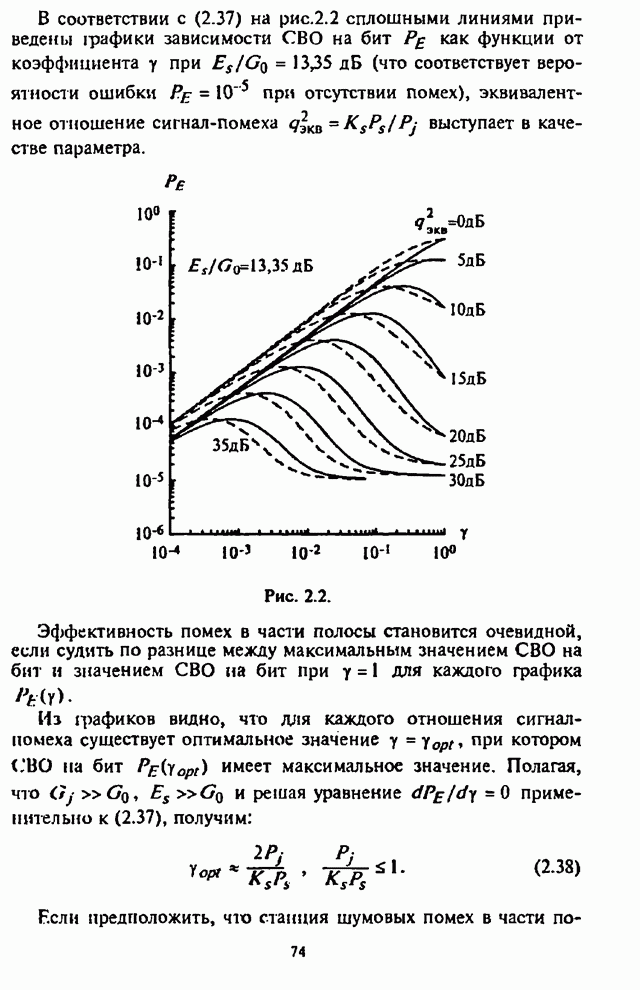
- 2.2. Оценка воздействия шумовой помехи в части полосы на системы радиосвязи с ППРЧ и неслучайной ЧМ
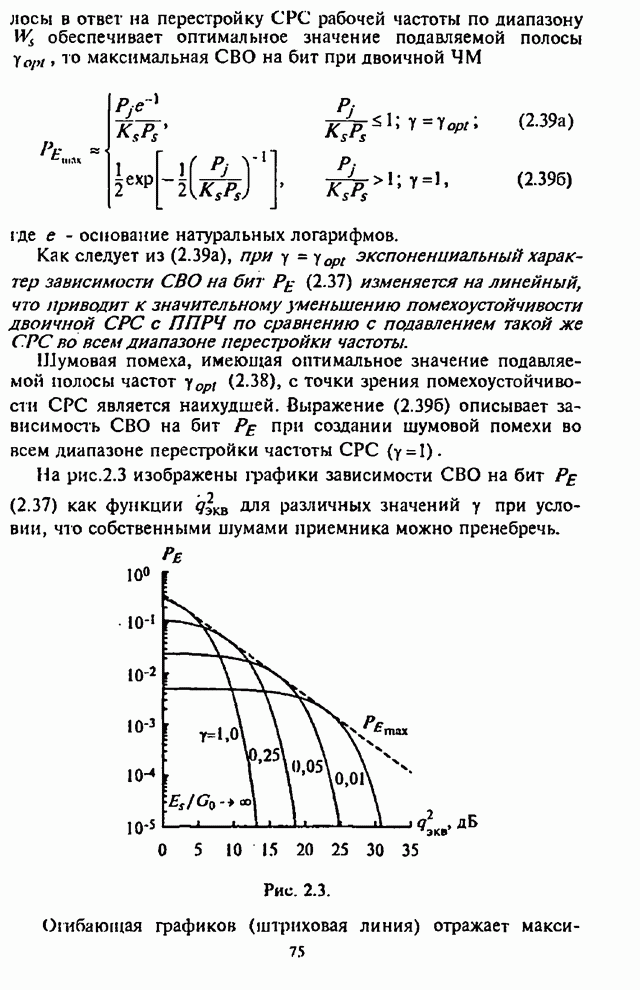
- 2.3. Оценка воздействия шумовой помехи в части полосы на системы радиосвязи с ППРЧ и случайной двоичной ЧМ
- 2.4. Оценка воздействия ответных помех на системы радиосвязи с ППРЧ и ЧМ
- 2.4.1. Оценка временных возможностей станции ответных помех
- 2.4.2. Оценка воздействия ответных шумовых помех на системы радиосвязи с ППРЧ и ЧМ
- 2.4.3. Оценка воздействия ответных гармонических помех на системы радиосвязи с ППРЧ и ЧМ
- 2.5. Помехоустойчивость систем радиосвязи с ППРЧ, двоичной ЧМ и блоковым кодированием
- Глава 3. Синтез и анализ эффективности адаптивных алгоритмов различения сигналов с ППРЧ, частотной модуляцией и разнесением символов по частоте
- 3.1. Синтез оптимального адаптивного алгоритма различения сигналов с внутрисимвольной ППРЧ и ЧМ
- 3.2. Квазиоптимальный адаптивный алгоритм различения сигналов с внутрисимвольной ППРЧ и двоичной ЧМ
- 3.3. Оценка помехоустойчивости синтезированного адаптивного алгоритма различения сигналов с внутрисимвольной ППРЧ и двоичной ЧМ
- 3.3.1. Случай «слабых» сигналов
- 3.3.2. Случай «сильных» сигналов
- Глава 4. Помехоустойчивость адаптивных алгоритмов демодуляции сигналов с внутрибитовой ППРЧ и двоичной частотной манипуляцией
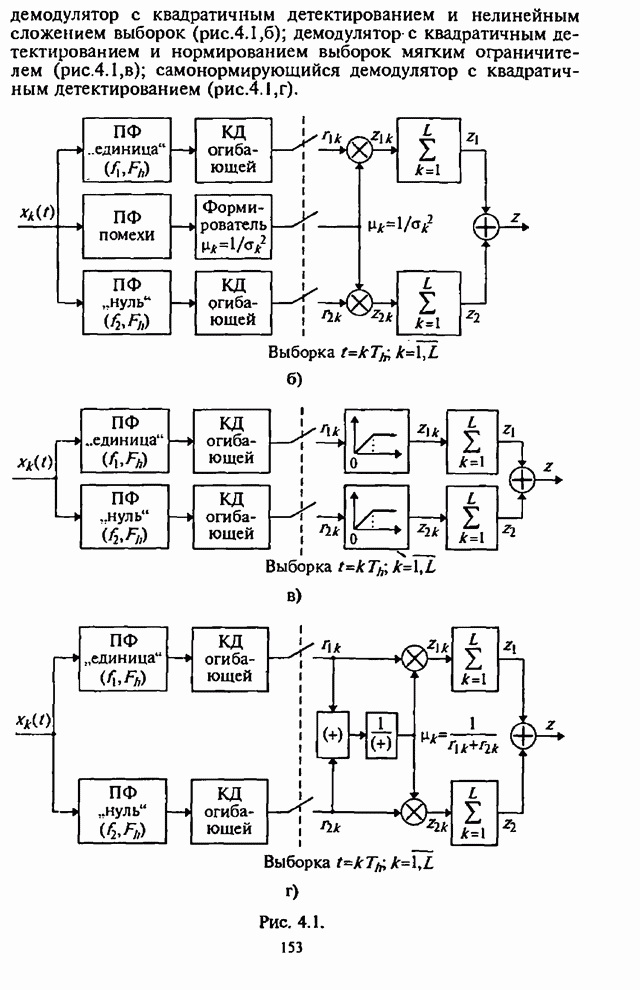
- 4.1. Структурные схемы демодуляторов
- 4.2. Помехоустойчивость демодулятора с линейным сложением выборок
- 4.3. Помехоустойчивость демодулятора с нелинейным сложением выборок
- 4.4. Помехоустойчивость демодулятора с мягким ограничителем
- 4.5. Помехоустойчивость самонормирующегося демодулятора
- 4.6. Влияние адаптивной регулировки усиления на помехоустойчивость СРС
- 4.7. Сравнительный анализ помехоустойчивости демодуляторов сигналов с внутрибитовой ППРЧ и двоичной ЧМ
- Глава 5. Помехоустойчивость систем радиосвязи с ППРЧ при совместном применении частотной модуляции, разнесения символов по частоте и блокового кодирования
- 5.1. Помехоустойчивость систем радиосвязи с ППРЧ при M-ичной ЧМ и L-кратным разнесении символов по частоте
- 5.1.1. Условная вероятность ошибки на бит информации
- 5.1.2. Анализ средней вероятности ошибки на бит информации
- 5.2. Помехоустойчивость систем радиосвязи с ППРЧ, M-ичной ЧМ, блоковым кодированием и L-кратным частотным разнесением кодовых слов
- 5.2.1. Структурная схема системы радиосвязи
- 5.2.2. Средняя вероятность ошибки на бит информации
- 5.2.3. Анализ средней вероятности ошибки на бит информации
- Глава 6. Синхронизация в системах радиосвязи с псевдослучайной перестройкой рабочей частоты
- 6.1. Назначение подсистемы синхронизации
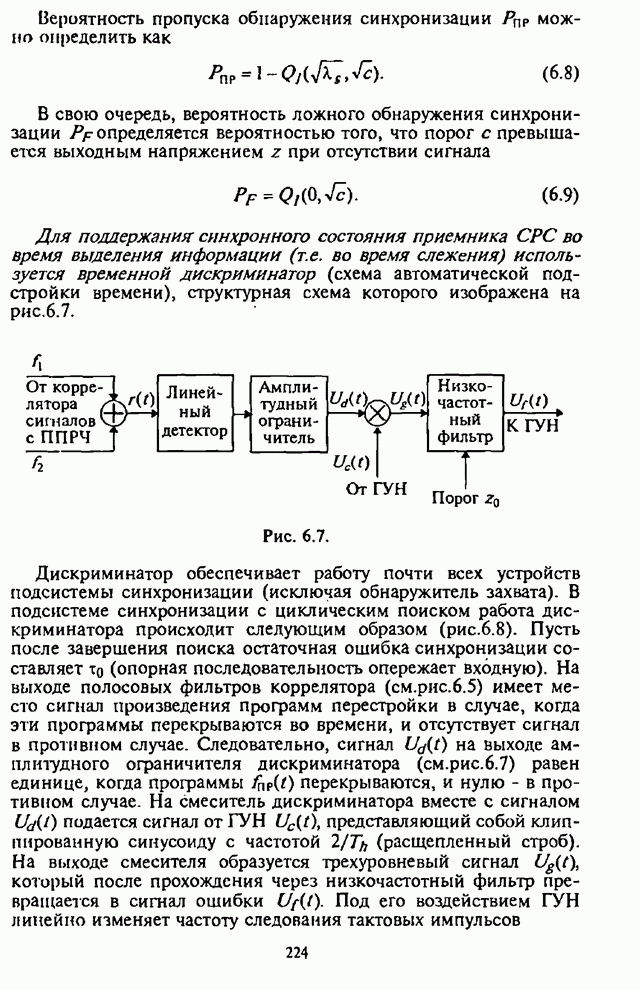
- 6.2. Описательная модель подсистемы синхронизации
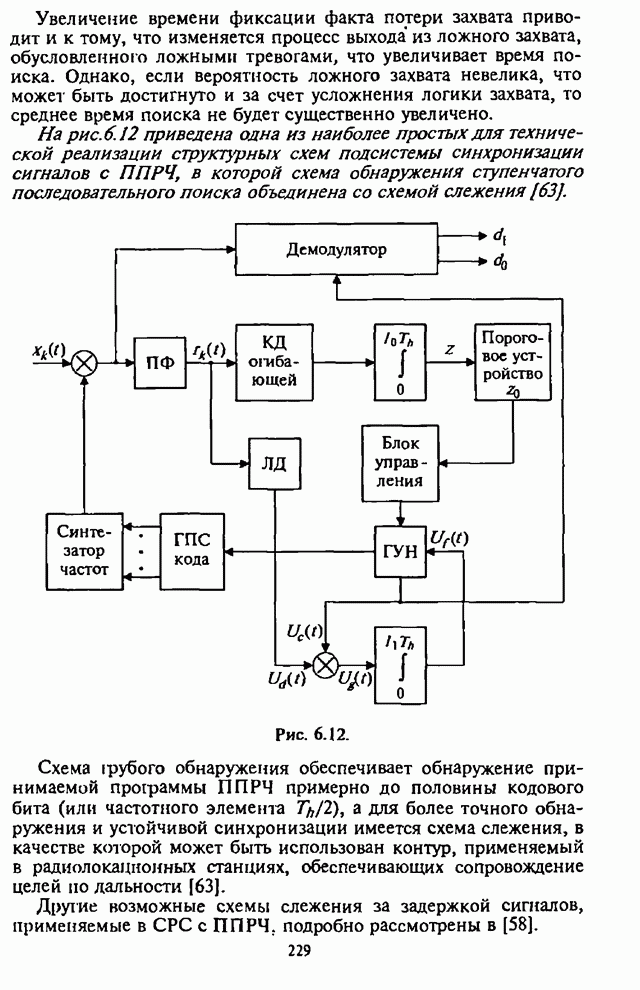
- 6.2.1. Типовая структурная схема подсистемы синхронизации
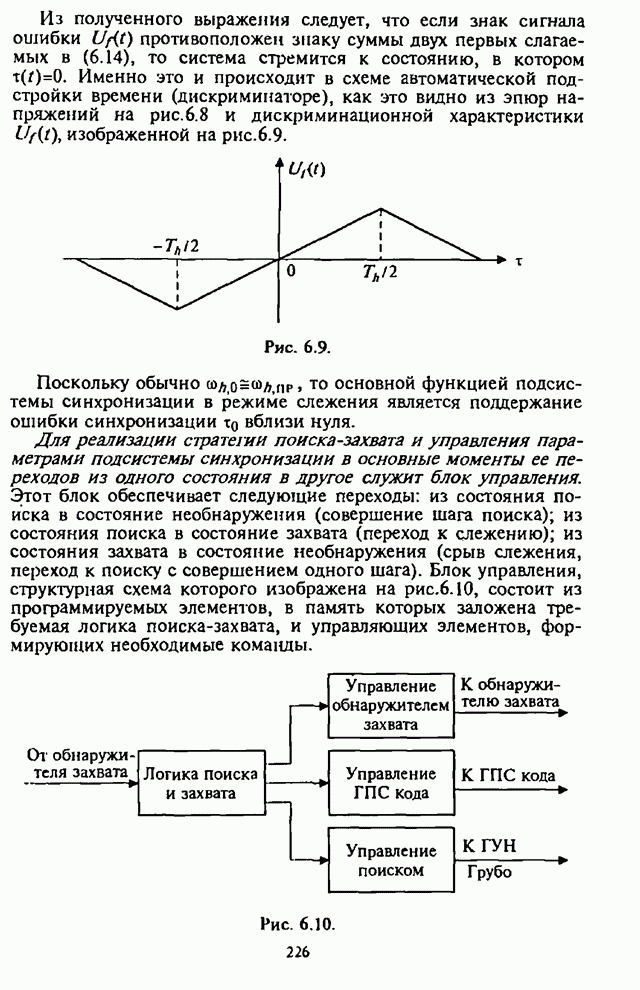
- 6.2.2. Типовые структурные схемы и алгоритмы функционирования основных устройств подсистемы синхронизации
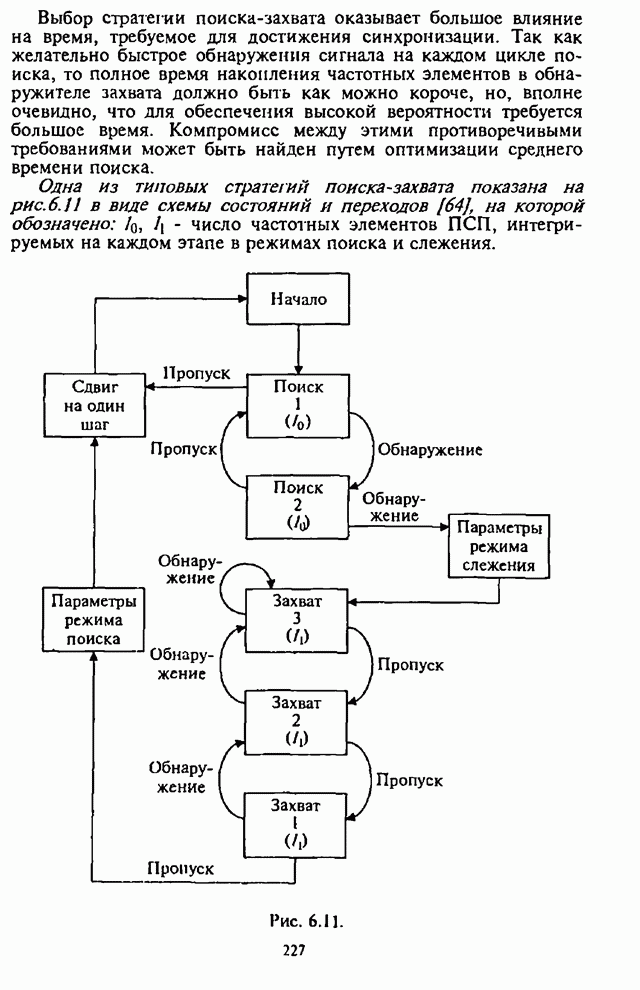
- 6.3. Показатели и оценка эффективности циклических процедур поиска
- Приложение П.6.1. Верхняя граница среднего нормированного времени поиска
- Приложение П.6.2. Верхняя граница вероятности правильного обнаружения
- Глава 7. Адаптивные антенные решетки в системах радиосвязи с псевдослучайной перестройкой рабочей частоты
- 7.1. Влияние сигналов с ППРЧ на характеристики адаптивной антенной решетки
- 7.2. Максиминный алгоритм обработки сигналов и помех
- 7.3. Реализация и возможности максиминного алгоритма
- 7.4. Модернизация максиминного алгоритма
- 7.4.1. Параметрическая обработка
- 7.4.2. Спектральная обработка
- 7.4.3. Обработка с упреждением
- Глава 8. Обнаружение сигналов с псевдослучайной перестройкой рабочей частоты
- 8.1. Обнаружение сигналов неизвестной структуры
- 8.2. Широкополосный энергетический обнаружитель
- 8.3. Многоканальные энергетические обнаружители
- 8.3.1. Квазиоптимальный многоканальный обнаружитель
- 8.3.2. Многоканальный обнаружитель типа сумматора с блоком фильтров
- 8.3.3. Модель обнаружителя типа сумматора с блоком фильтров при перехвате сигналов с медленной ППРЧ
- 8.3.4. Многоканальный обнаружитель типа сумматора с блоком фильтров в части полосы
- 8.3.5. Рассогласование по времени и частоте между характеристиками сигнала с ППРЧ и параметрами обнаружителя
- 8.4. Многоканальный адаптивный энергетический обнаружитель в условиях воздействия мешающих сигналов
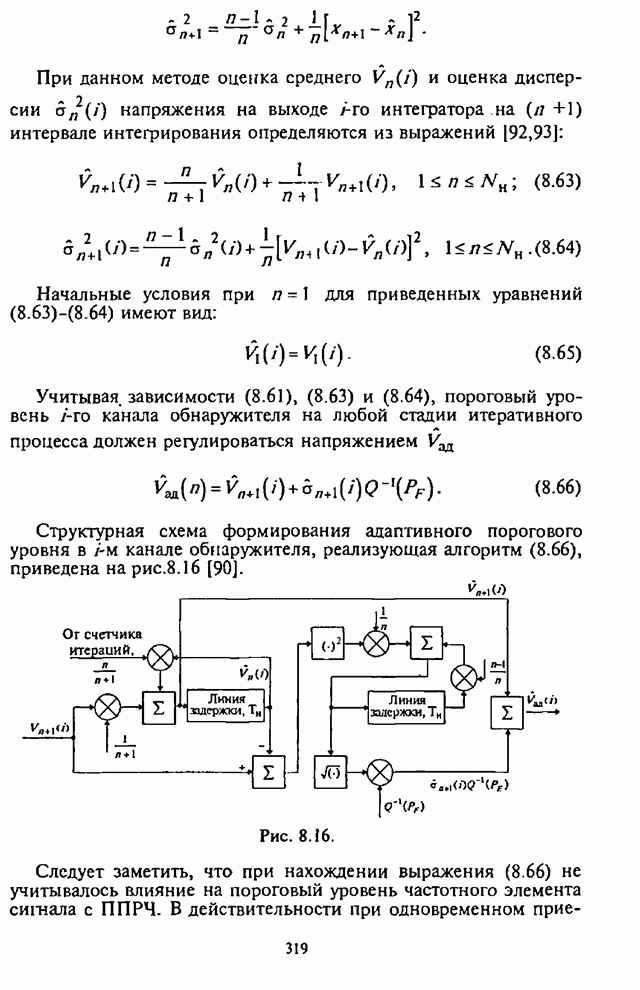
- 8.4.1. Структурная схема многоканального адаптивного энергетического обнаружителя с регулировкой порогового уровня
- 8.4.2. Вероятность ложной тревоги и адаптивная регулировка порогового уровня
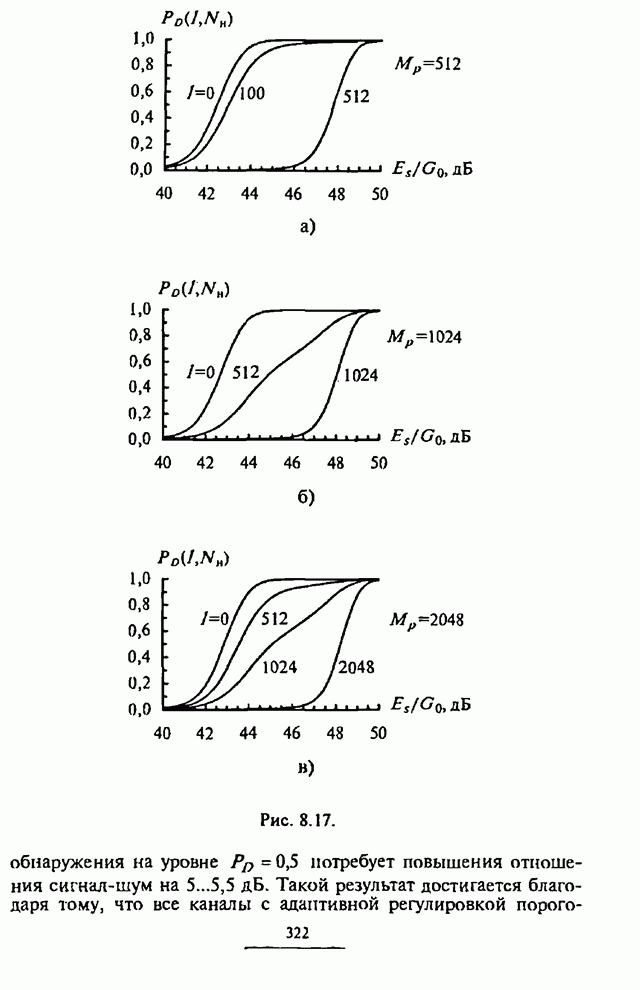
- 8.4.3. Вероятность обнаружения
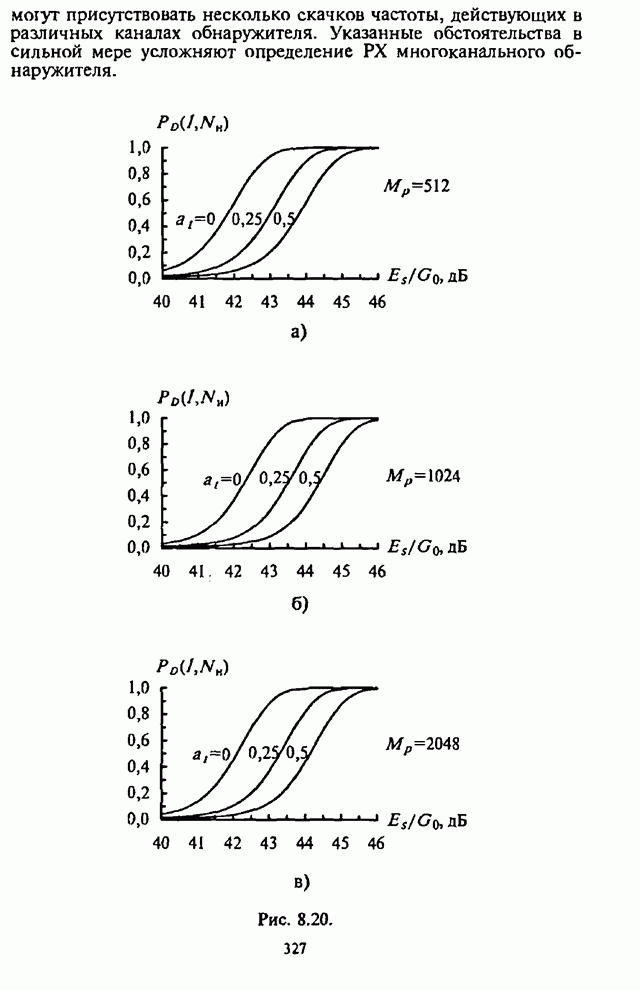
- 8.4.4. Влияние рассогласования по времени на обнаружение сигналов
- 8.5. Другие возможные типы обнаружителей сигналов с ППРЧ
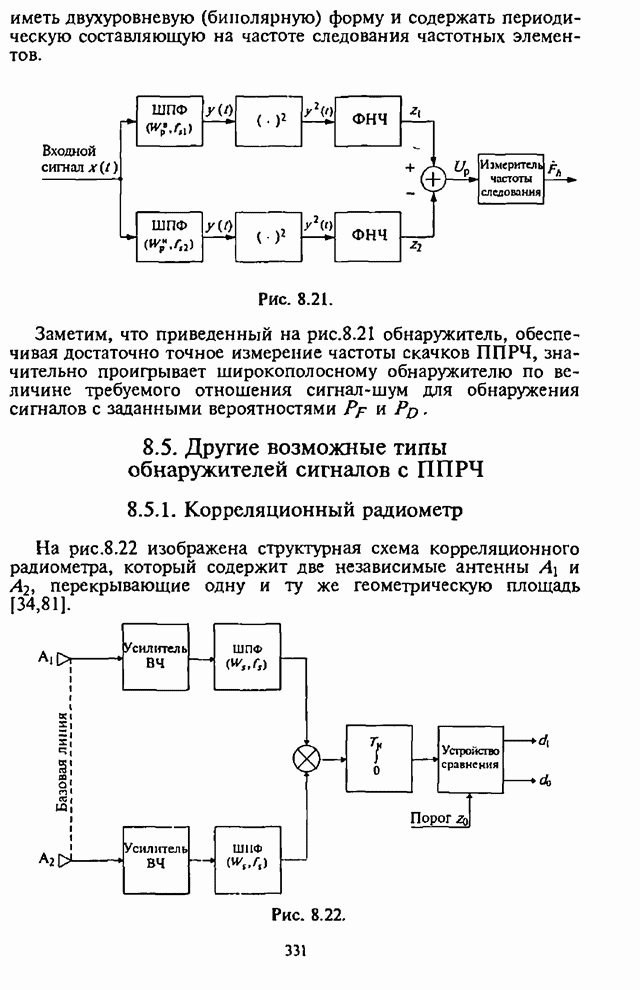
- 8.5.1. Корреляционный радиометр
- 8.5.2. Цифровой анализатор спектра
- 8.5.3. Метод вскрытия частотно-временной матрицы сигнала с ППРЧ
- Приложение П.8.1. Алгоритмы вычисления обобщенной Q-функции Маркума
- П.8.1.1. Постановка задачи
- П.8.1.2. Представление степенными рядами
- П.8.1.3. Представление в виде рядов Неймана
- П.8.1.4. Численное интегрирование
- П.8.1.5. Гауссовская аппроксимация
- П.8.1.6. Численные результаты
- Приложение П.8.2. Анализ вероятностно-временных характеристик алгоритмов обнаружения сигналов
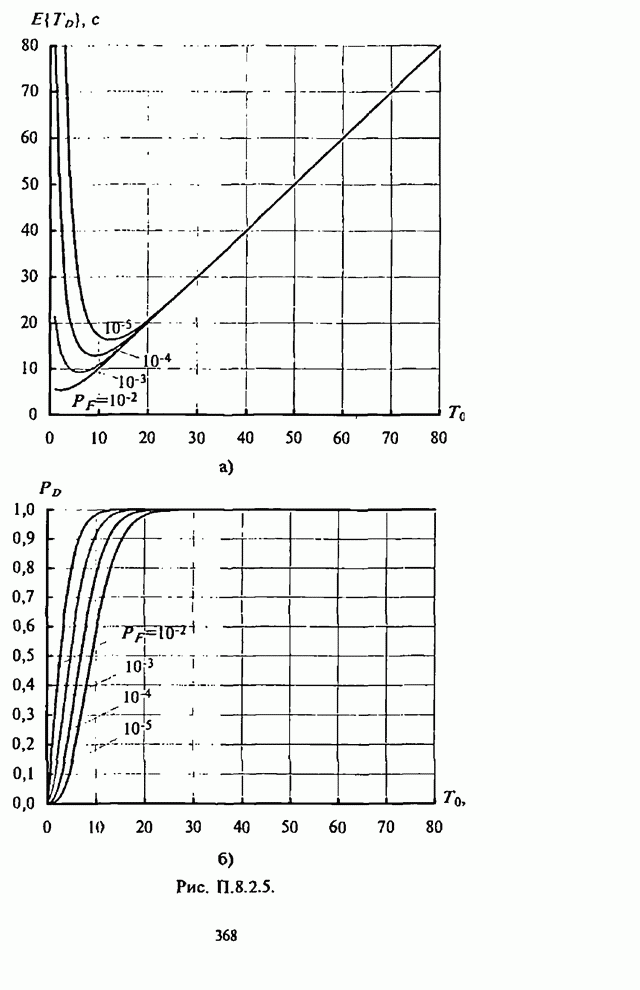
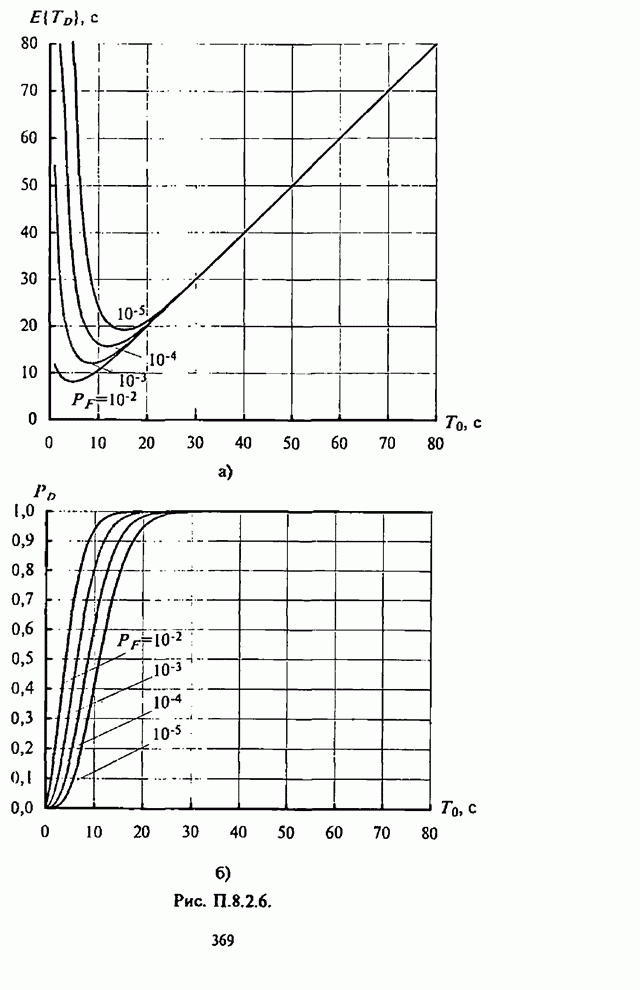
- П.8.2.1. Вероятностно-временные характеристики основных видов обнаружителей
- П.8.2.2 Алгоритмы расчета вероятностно-временных характеристик основных видов обнаружителей
- П.8.2.3. Численные результаты
- СПИСОК ОСНОВНЫХ СОКРАЩЕНИЙ
- ОСНОВНЫЕ УСЛОВНЫЕ ОБОЗНАЧЕНИЯ
- СПИСОК ЛИТЕРАТУРЫ