| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
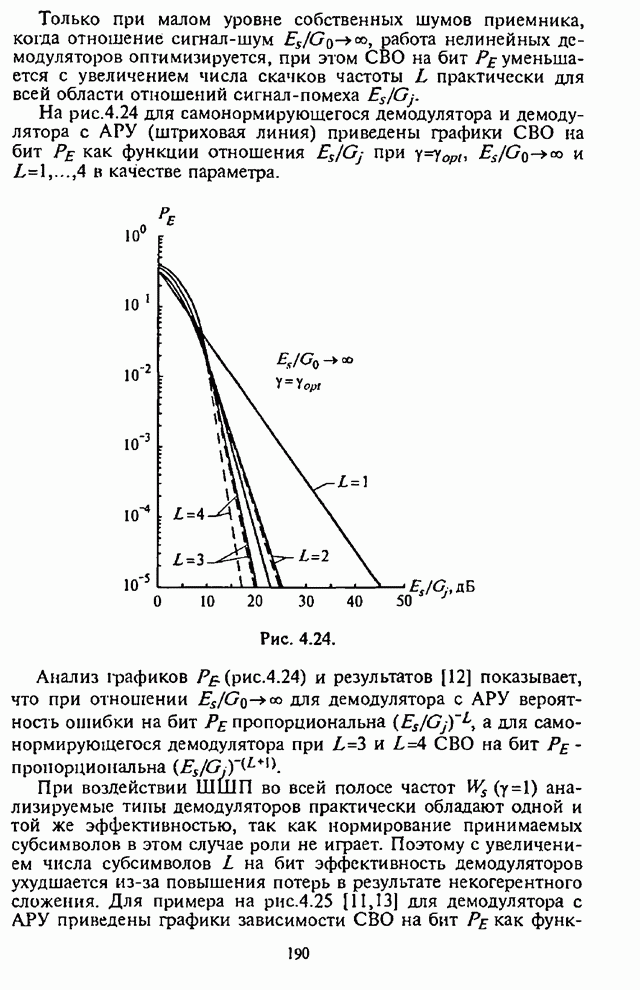
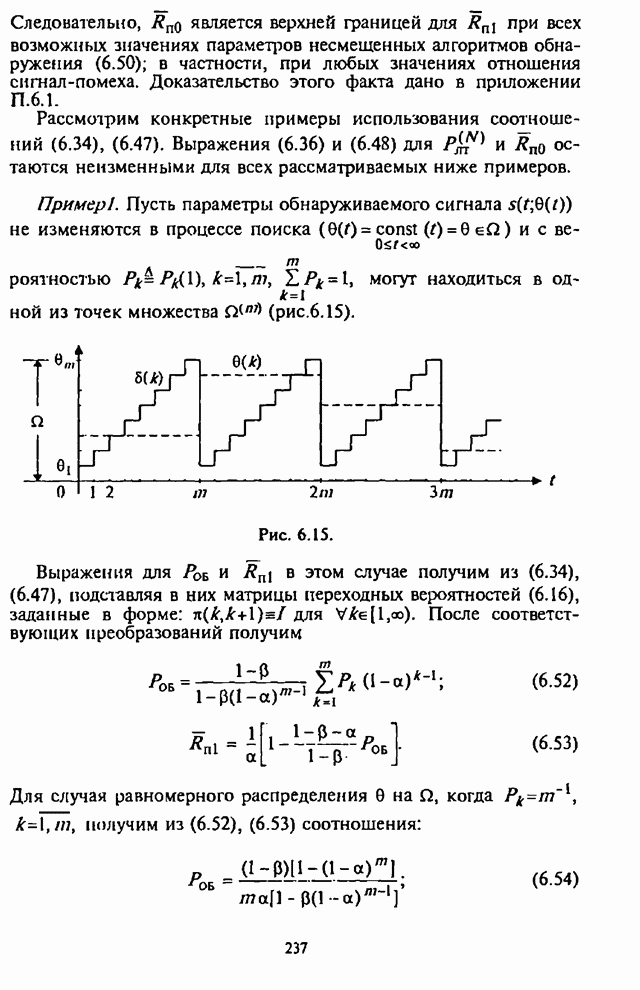
8.4.2. Вероятность ложной тревоги и адаптивная регулировка порогового уровня
В
случае аппроксимации выходной статистики ![]() гауссовским распределением вероятность
того, что собственные шумы превысят пороговый уровень
гауссовским распределением вероятность
того, что собственные шумы превысят пороговый уровень ![]() при одном наблюдении
определяется зависимостью, аналогичной (8.13), при замене в ней
при одном наблюдении
определяется зависимостью, аналогичной (8.13), при замене в ней ![]() на
на ![]()
 . (8.55)
. (8.55)
Полная
вероятность ложной тревоги ![]() , т.е. вероятность ложной тревоги
многоканального обнаружителя в целом зависит от выбранного правила принятия
решения. Рассмотрим простую ситуацию, при которой предполагается, что частотный
элемент сигнала присутствует в любом интервале интегрирования
, т.е. вероятность ложной тревоги
многоканального обнаружителя в целом зависит от выбранного правила принятия
решения. Рассмотрим простую ситуацию, при которой предполагается, что частотный
элемент сигнала присутствует в любом интервале интегрирования ![]() , если превышается
порог
, если превышается
порог ![]() только
в одном из
только
в одном из ![]() каналов.
Вероятность такой ситуации определяется формулой Бернулли
каналов.
Вероятность такой ситуации определяется формулой Бернулли
![]() . (8.56)
. (8.56)
Выше,
при описании структурной схемы обнаружителя указывалось, что необходимо
учитывать ![]() интервалов
интегрирования. Примем, что наличие сигнала фиксируется, если наблюдается
единственное превышение порога в каждом из
интервалов
интегрирования. Примем, что наличие сигнала фиксируется, если наблюдается
единственное превышение порога в каждом из ![]() интервалов интегрирования. При таком
правиле принятия решения полная вероятность ложной тревоги обнаружителя равна
вероятности того, что было точно
интервалов интегрирования. При таком
правиле принятия решения полная вероятность ложной тревоги обнаружителя равна
вероятности того, что было точно ![]() превышений порогового уровня
превышений порогового уровня ![]() в предыдущих
в предыдущих ![]() интервалах
интегрирования, и что имеет место единичное превышение порогового уровня в
интервалах
интегрирования, и что имеет место единичное превышение порогового уровня в ![]() -м интервале.
Вероятность такого события соответствует полной вероятности ложной тревоги
многоканального обнаружителя и может быть определена с использованием так
называемого "скользящего окна" [88,93]
-м интервале.
Вероятность такого события соответствует полной вероятности ложной тревоги
многоканального обнаружителя и может быть определена с использованием так
называемого "скользящего окна" [88,93]
 (8.57)
(8.57)
Выше
отмечалось, что обязательным условием функционирования многоканального
энергетического обнаружителя при воздействии на него узкополосных помех
является адаптивная регулировка порогового уровня, обеспечивающая равенство
вероятности ложной тревоги. В случае действия узкополосной помехи в ![]() -м канале вероятность
ложной тревоги по аналогии с (8.55) определяется формулой [90,93]
-м канале вероятность
ложной тревоги по аналогии с (8.55) определяется формулой [90,93]
 , (8.58)
, (8.58)
где
![]() - порог в
- порог в ![]() -м канале.
-м канале.
Для
определения порогового уровня при заданной вероятности ![]() воспользуемся, как и ранее,
функцией
воспользуемся, как и ранее,
функцией ![]() ,
обратной к функции
,
обратной к функции ![]() .
Применяя обратную функцию к правой и левой частям выражения (8.55), для случая
отсутствия узкополосной помехи в
.
Применяя обратную функцию к правой и левой частям выражения (8.55), для случая
отсутствия узкополосной помехи в ![]() -м канале получим
-м канале получим
 . (8.59)
. (8.59)
Пороговый
уровень ![]() на
основе (8.59) должен устанавливаться в соответствии с равенством
на
основе (8.59) должен устанавливаться в соответствии с равенством
![]() . (8.60)
. (8.60)
Используя
обратную функцию ![]() применительно
к выражению для вероятности
применительно
к выражению для вероятности ![]() (8.58) в случае присутствия в
(8.58) в случае присутствия в ![]() -м канале узкополосной
помехи, получим, что пороговый уровень должен регулироваться в соответствии с
формулой:
-м канале узкополосной
помехи, получим, что пороговый уровень должен регулироваться в соответствии с
формулой:
![]() . (8.61)
. (8.61)
При
этом вероятность ![]() для
каждого
для
каждого ![]() -го
канала должна определяться из условия обеспечения требуемой полной вероятности
ложной тревоги многоканального энергетического обнаружителя
-го
канала должна определяться из условия обеспечения требуемой полной вероятности
ложной тревоги многоканального энергетического обнаружителя ![]() (8.57). Из (8.61) следует, что
для адаптивной регулировки порогового уровня в каждом из каналов обнаружителя
требуется знание среднего значения
(8.57). Из (8.61) следует, что
для адаптивной регулировки порогового уровня в каждом из каналов обнаружителя
требуется знание среднего значения ![]() (8.53) и дисперсии
(8.53) и дисперсии ![]() (8.54) статистики
(8.54) статистики ![]() в случае присутствия
узкополосной помехи. С этой целью представим нормированное напряжение на выходе
интегратора
в случае присутствия
узкополосной помехи. С этой целью представим нормированное напряжение на выходе
интегратора ![]() -го
канала при действии узкополосной помехи в виде:
-го
канала при действии узкополосной помехи в виде:
 , (8.62)
, (8.62)
где
![]() - сигнал на
выходе полосового фильтра
- сигнал на
выходе полосового фильтра ![]() -го канала во время
-го канала во время ![]() -го интервала интегрирования.
-го интервала интегрирования.
Наиболее
приемлемым методом определения рекуррентной статистической оценки ![]() является итеративный
метод, при котором оценка уточняется на каждом интервале интегрирования по
формулам:
является итеративный
метод, при котором оценка уточняется на каждом интервале интегрирования по
формулам:

При
данном методе оценка среднего ![]() и оценка дисперсии
и оценка дисперсии ![]() напряжения на выходе
напряжения на выходе ![]() -го интегратора на
-го интегратора на ![]() интервале
интегрирования определяются из выражений [92,93]:
интервале
интегрирования определяются из выражений [92,93]:
![]() ; (8.63)
; (8.63)
![]() . (8.64)
. (8.64)
Начальные
условия при ![]() для
приведенных уравнений (8.63)-(8.64) имеют вид:
для
приведенных уравнений (8.63)-(8.64) имеют вид:
![]() . (8.65)
. (8.65)
Учитывая,
зависимости (8.61), (8.63) и (8.64), пороговый уровень ![]() -го канала обнаружителя на любой
стадии итеративного процесса должен регулироваться напряжением
-го канала обнаружителя на любой
стадии итеративного процесса должен регулироваться напряжением ![]()
![]() . (8.66)
. (8.66)
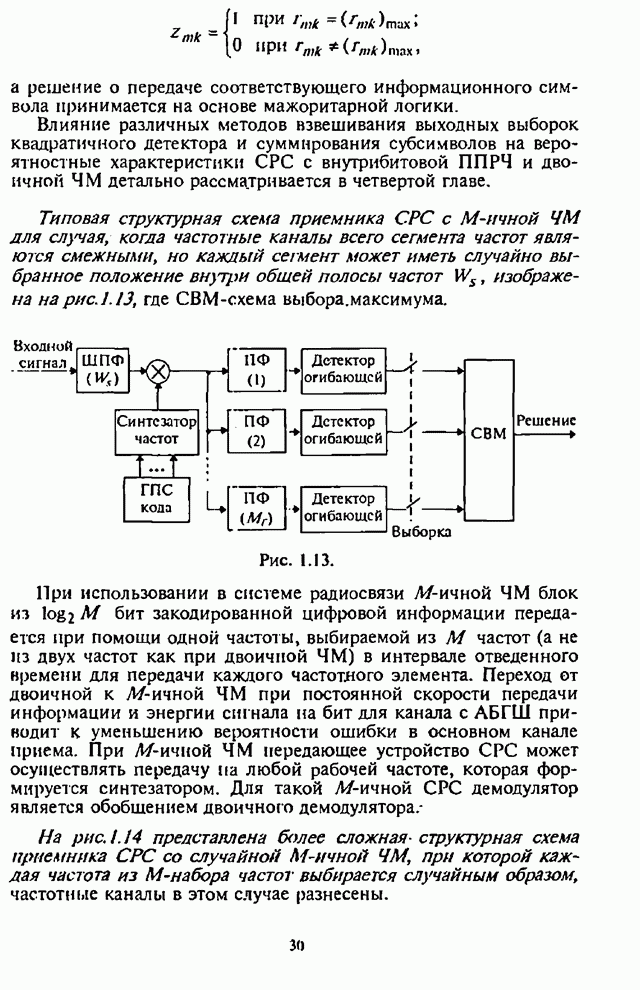
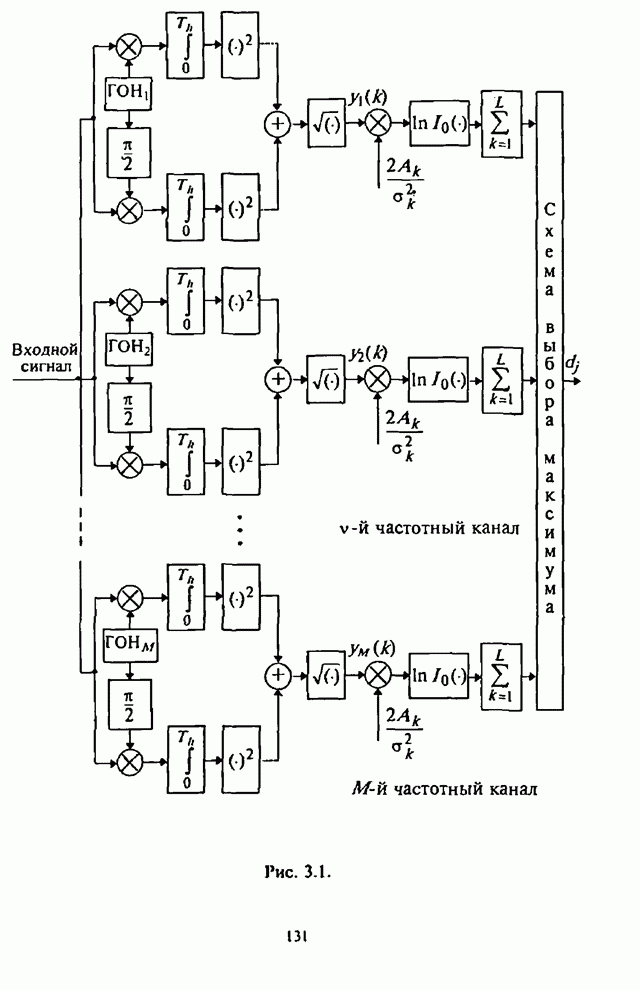
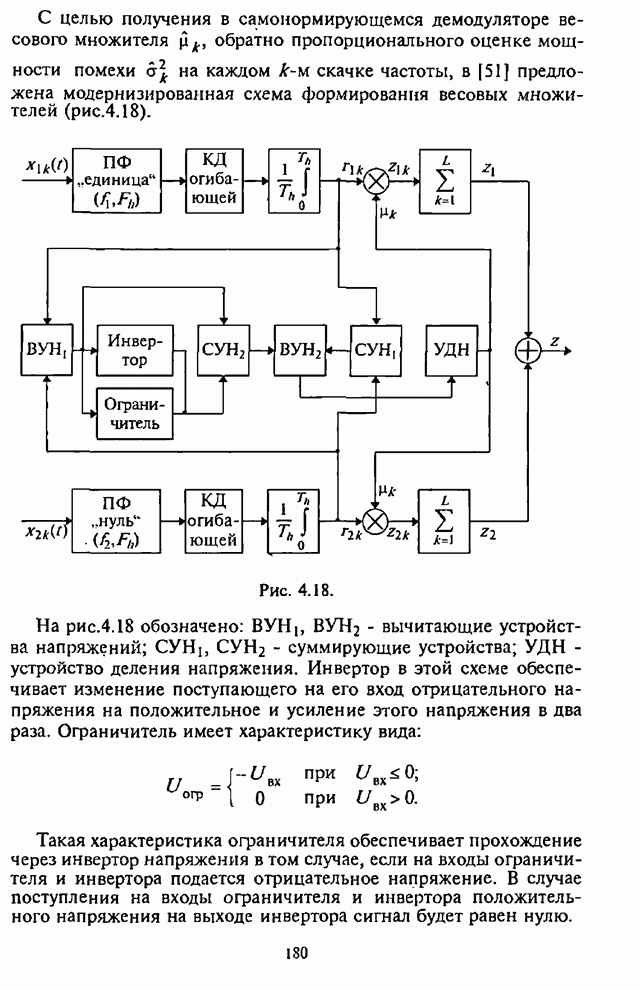
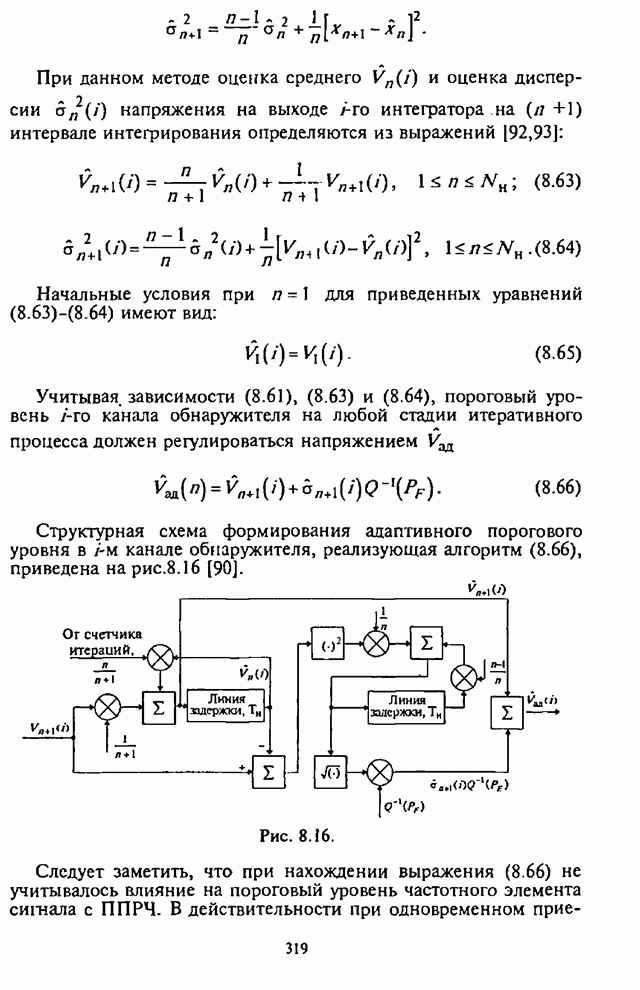
Структурная
схема формирования адаптивного порогового уровня в ![]() -м канале обнаружителя, реализующая
алгоритм (8.66), приведена на рис.8.16 [90].
-м канале обнаружителя, реализующая
алгоритм (8.66), приведена на рис.8.16 [90].

Рис. 8.16.
Следует
заметить, что при нахождении выражения (8.66) не учитывалось влияние на
пороговый уровень частотного элемента сигнала с ППРЧ. В действительности при
одновременном приеме сигнала и узкополосной помехи пороговый уровень в ![]() -м канале будет
отличаться от значения порога, определяемого формулой (8.66). Однако, учитывая,
как указывалось выше, что время воздействия узкополосной помехи значительно
больше длительности частотного элемента сигнала, то в процессе адаптации
статистические оценки среднего значения и дисперсии напряжения на выходе
-м канале будет
отличаться от значения порога, определяемого формулой (8.66). Однако, учитывая,
как указывалось выше, что время воздействия узкополосной помехи значительно
больше длительности частотного элемента сигнала, то в процессе адаптации
статистические оценки среднего значения и дисперсии напряжения на выходе ![]() -го интегратора (8.62)
будут сходиться к оцениваемым параметрам.
-го интегратора (8.62)
будут сходиться к оцениваемым параметрам.
В
общем случае для устранения влияния узкополосных помех на энергетический
обнаружитель можно применять фильтры подавления помех, расположив их до
квадратичных детекторов. При этом могут быть использованы: аналоговые
режекторные фильтры; устройства, осуществляющие режекцию в спектральной области
с использованием преобразования Фурье; адаптивные цифровые фильтры [94-96]. При
этом пороговый уровень ![]() в каждом канале определяется из выражения
(8.60).
в каждом канале определяется из выражения
(8.60).
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие
- Введение
- Глава 1. Системы радиосвязи с расширением спектра сигналов методом псевдослучайной перестройки рабочей частоты: общие принципы
- 1.1. Краткая характеристика расширения спектра сигналов методом ППРЧ
- 1.1.1. Основные принципы и методы расширения спектра сигналов
- 1.1.2. Метод псевдослучайной перестройки рабочей частоты
- 1.1.3. Типовые структурные схемы систем радиосвязи с ППРЧ
- 1.2. Коэффициент расширения спектра сигнала и запас помехоустойчивости системы радиосвязи с ППРЧ
- 1.3. Общая характеристика помехозащищенности систем радиосвязи с ППРЧ
- 1.3.1. Помехоустойчивость систем радиосвязи с ППРЧ
- 1.3.2. Скрытность сигналов систем радиосвязи с ППРЧ
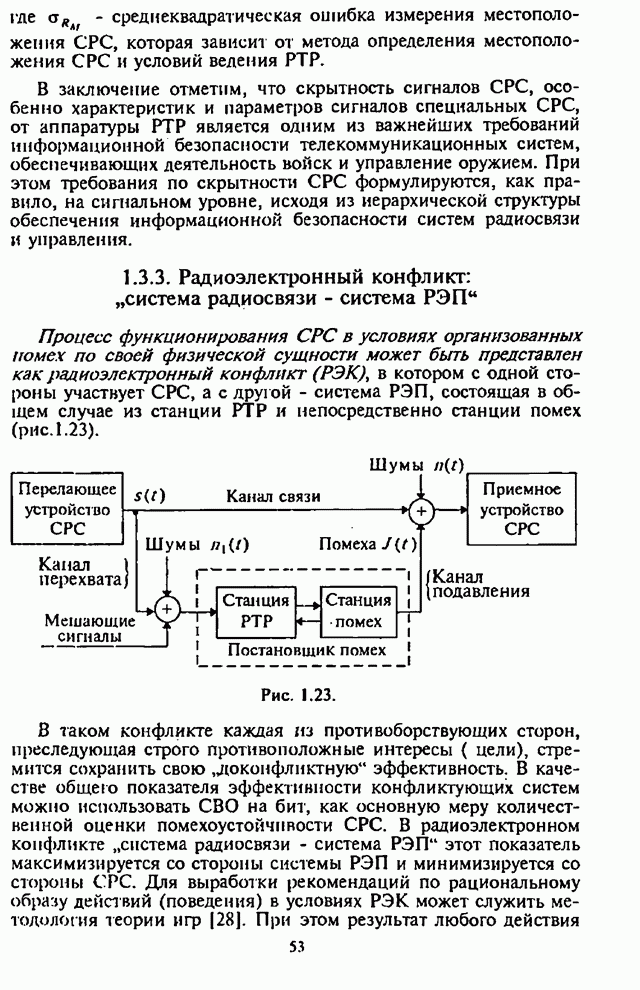
- 1.3.3. Радиоэлектронный конфликт: «система радиосвязи — система РЭП»
- 1.4. Модели и краткая характеристика основных видов помех
- Глава 2. Помехоустойчивость типовых систем радиосвязи с ППРЧ и частотной манипуляцией
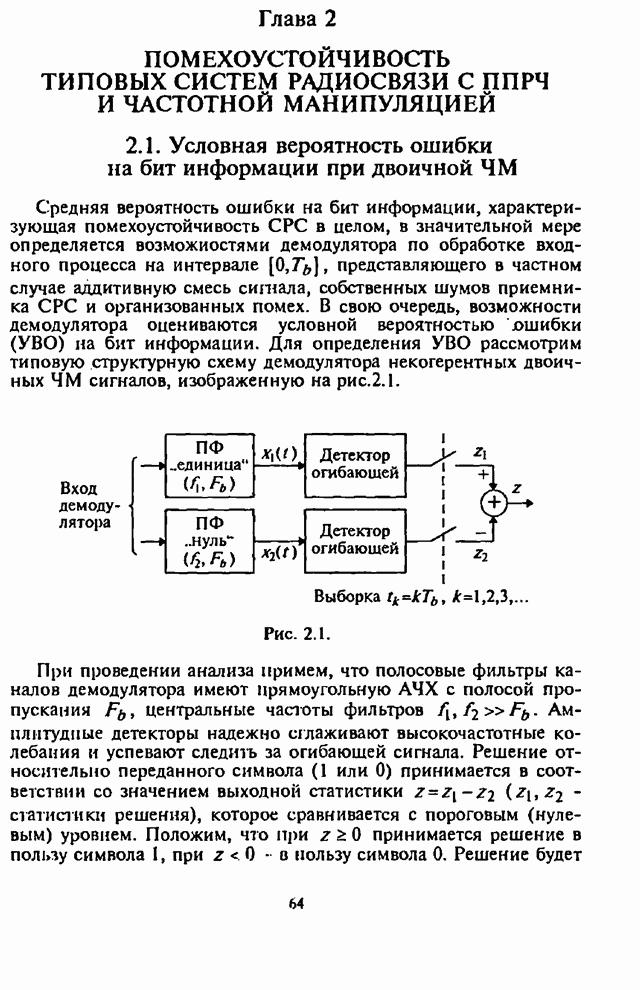
- 2.1. Условная вероятность ошибки на бит информации при двоичной ЧМ
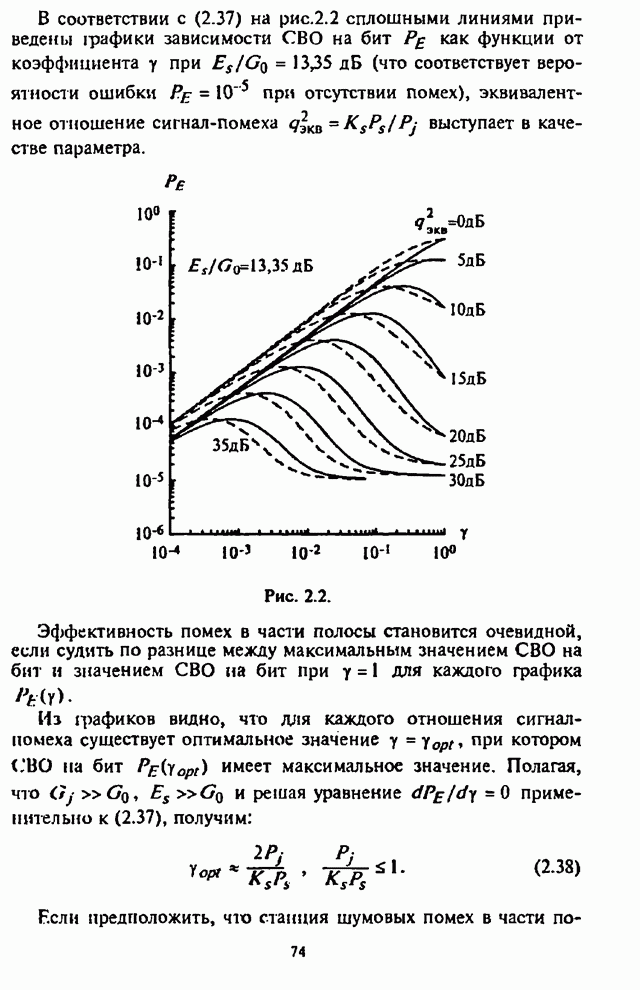
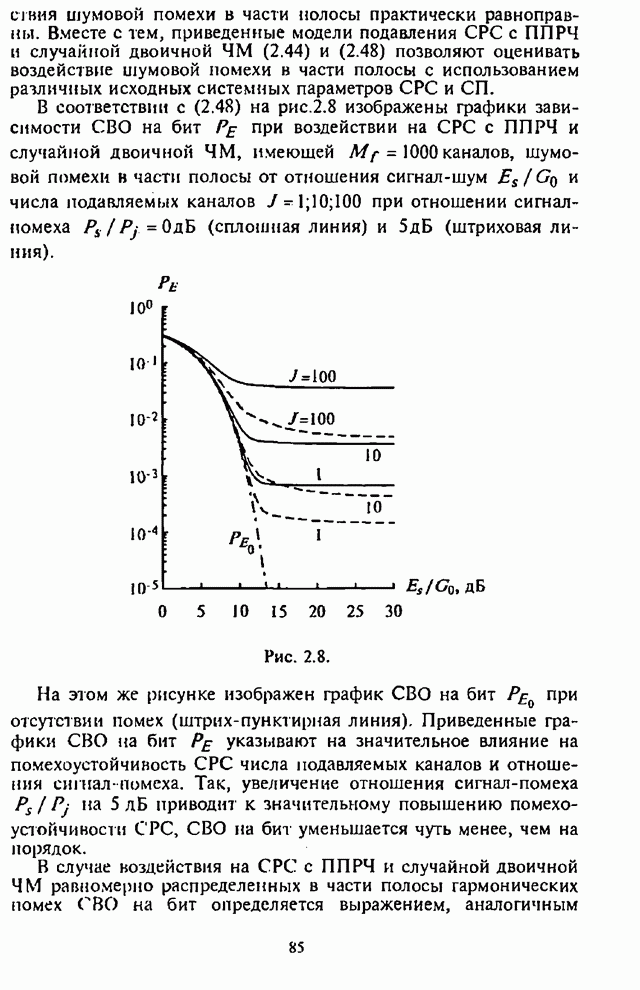
- 2.2. Оценка воздействия шумовой помехи в части полосы на системы радиосвязи с ППРЧ и неслучайной ЧМ
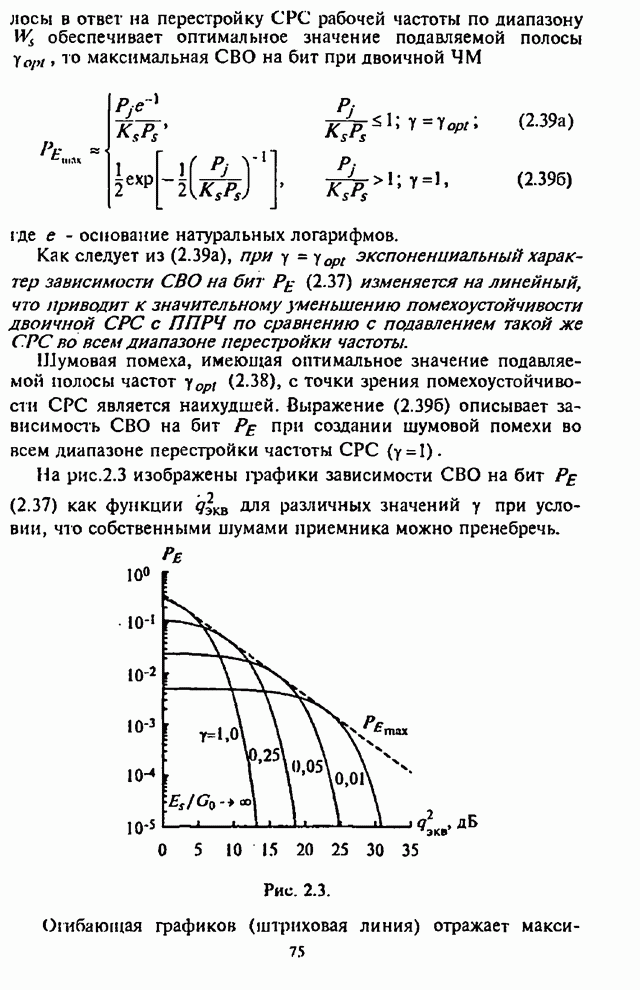
- 2.3. Оценка воздействия шумовой помехи в части полосы на системы радиосвязи с ППРЧ и случайной двоичной ЧМ
- 2.4. Оценка воздействия ответных помех на системы радиосвязи с ППРЧ и ЧМ
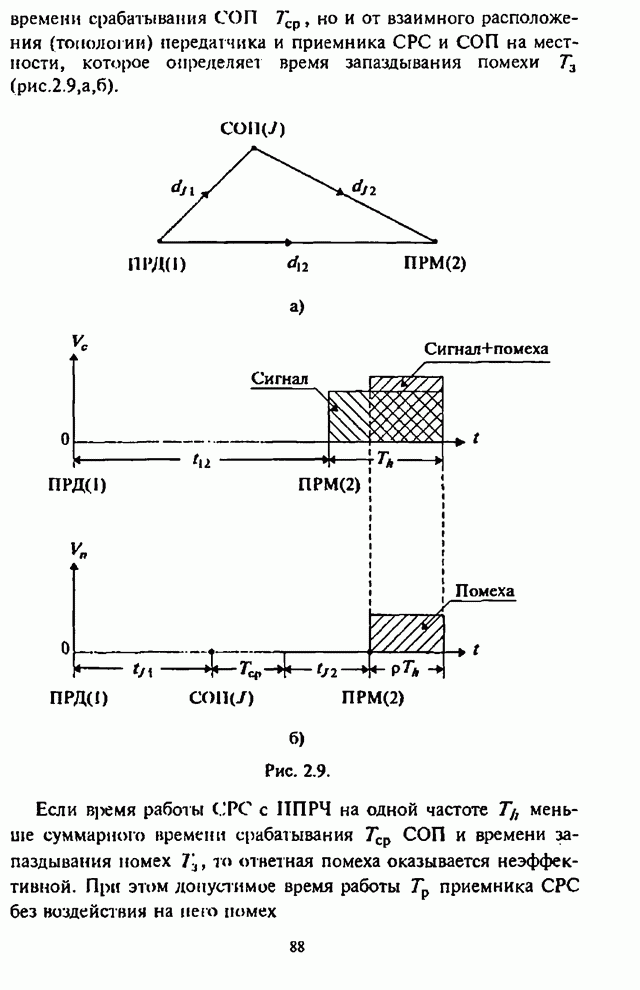
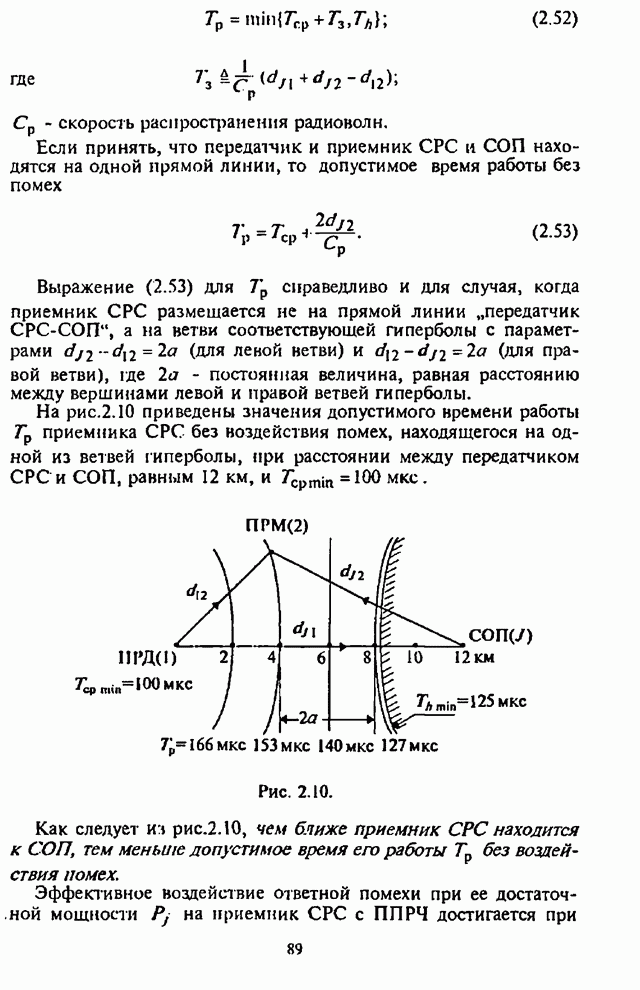
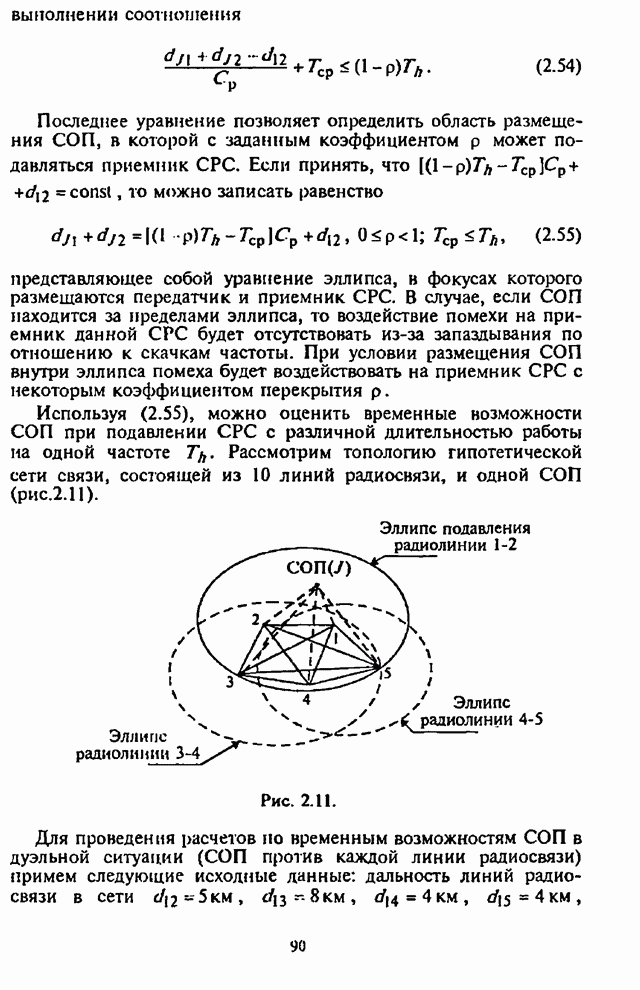
- 2.4.1. Оценка временных возможностей станции ответных помех
- 2.4.2. Оценка воздействия ответных шумовых помех на системы радиосвязи с ППРЧ и ЧМ
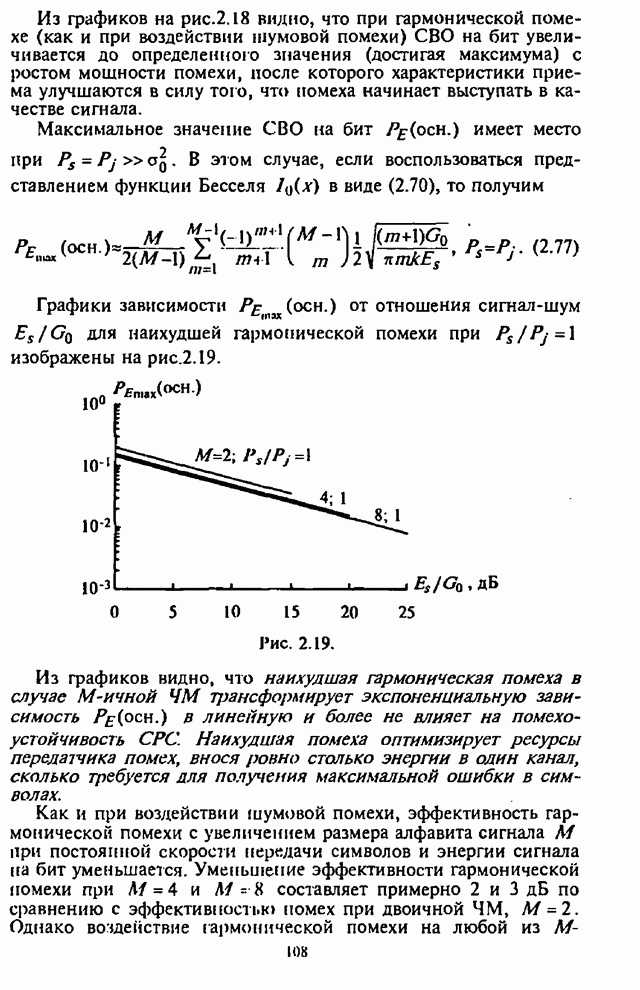
- 2.4.3. Оценка воздействия ответных гармонических помех на системы радиосвязи с ППРЧ и ЧМ
- 2.5. Помехоустойчивость систем радиосвязи с ППРЧ, двоичной ЧМ и блоковым кодированием
- Глава 3. Синтез и анализ эффективности адаптивных алгоритмов различения сигналов с ППРЧ, частотной модуляцией и разнесением символов по частоте
- 3.1. Синтез оптимального адаптивного алгоритма различения сигналов с внутрисимвольной ППРЧ и ЧМ
- 3.2. Квазиоптимальный адаптивный алгоритм различения сигналов с внутрисимвольной ППРЧ и двоичной ЧМ
- 3.3. Оценка помехоустойчивости синтезированного адаптивного алгоритма различения сигналов с внутрисимвольной ППРЧ и двоичной ЧМ
- 3.3.1. Случай «слабых» сигналов
- 3.3.2. Случай «сильных» сигналов
- Глава 4. Помехоустойчивость адаптивных алгоритмов демодуляции сигналов с внутрибитовой ППРЧ и двоичной частотной манипуляцией
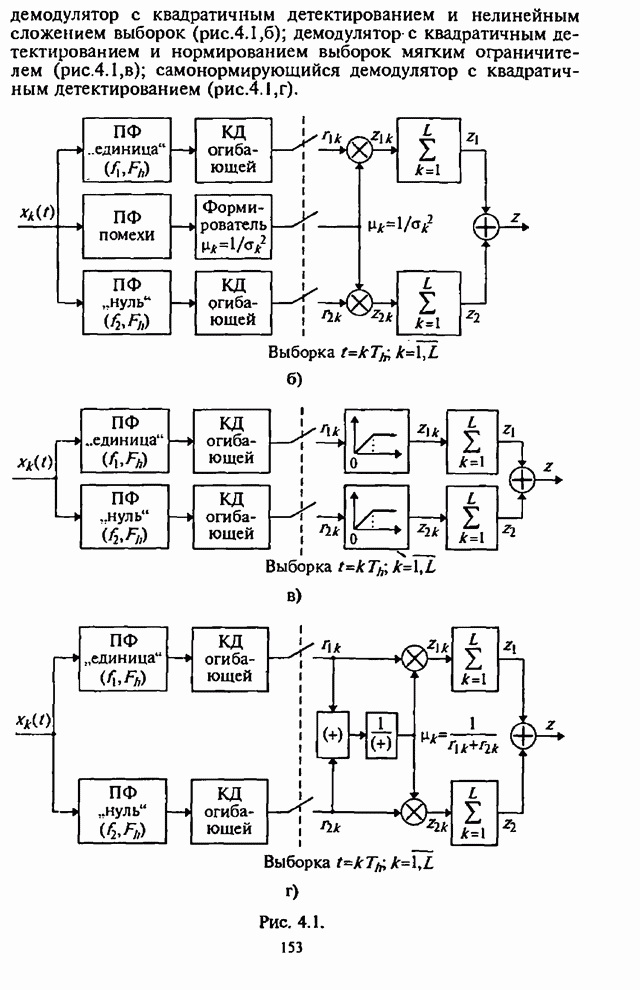
- 4.1. Структурные схемы демодуляторов
- 4.2. Помехоустойчивость демодулятора с линейным сложением выборок
- 4.3. Помехоустойчивость демодулятора с нелинейным сложением выборок
- 4.4. Помехоустойчивость демодулятора с мягким ограничителем
- 4.5. Помехоустойчивость самонормирующегося демодулятора
- 4.6. Влияние адаптивной регулировки усиления на помехоустойчивость СРС
- 4.7. Сравнительный анализ помехоустойчивости демодуляторов сигналов с внутрибитовой ППРЧ и двоичной ЧМ
- Глава 5. Помехоустойчивость систем радиосвязи с ППРЧ при совместном применении частотной модуляции, разнесения символов по частоте и блокового кодирования
- 5.1. Помехоустойчивость систем радиосвязи с ППРЧ при M-ичной ЧМ и L-кратным разнесении символов по частоте
- 5.1.1. Условная вероятность ошибки на бит информации
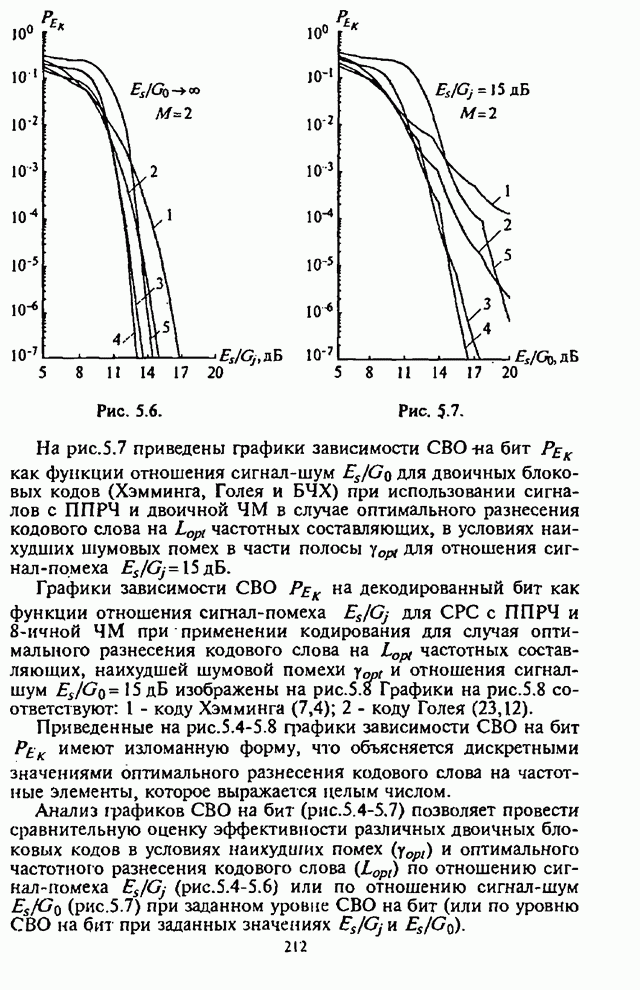
- 5.1.2. Анализ средней вероятности ошибки на бит информации
- 5.2. Помехоустойчивость систем радиосвязи с ППРЧ, M-ичной ЧМ, блоковым кодированием и L-кратным частотным разнесением кодовых слов
- 5.2.1. Структурная схема системы радиосвязи
- 5.2.2. Средняя вероятность ошибки на бит информации
- 5.2.3. Анализ средней вероятности ошибки на бит информации
- Глава 6. Синхронизация в системах радиосвязи с псевдослучайной перестройкой рабочей частоты
- 6.1. Назначение подсистемы синхронизации
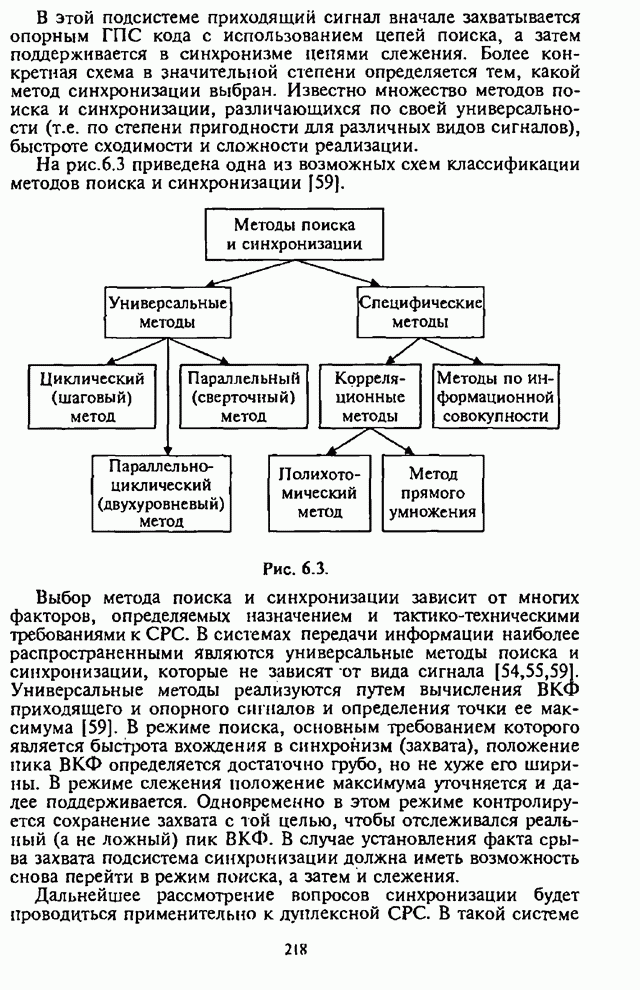
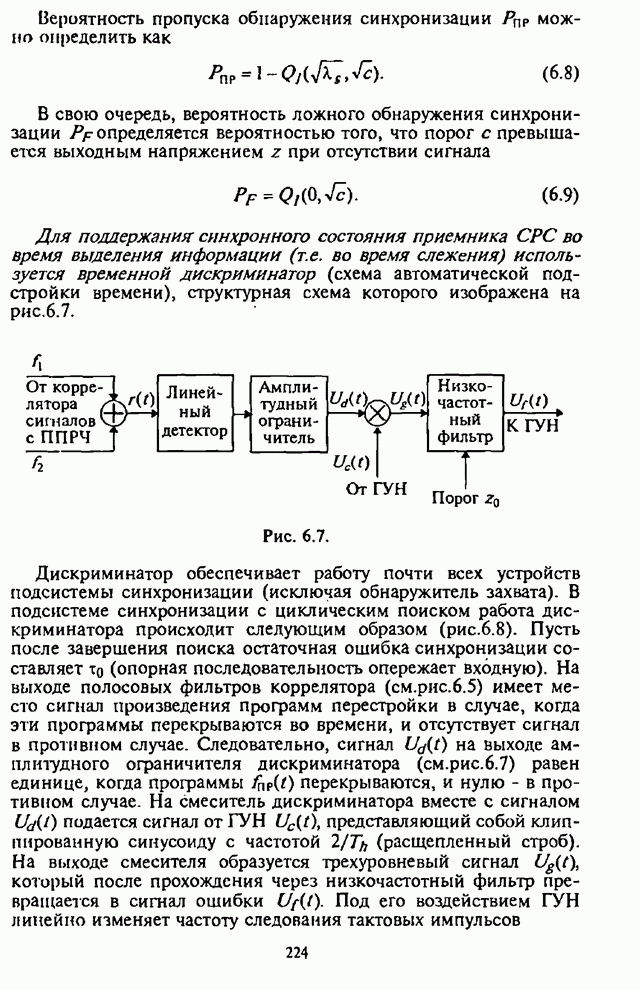
- 6.2. Описательная модель подсистемы синхронизации
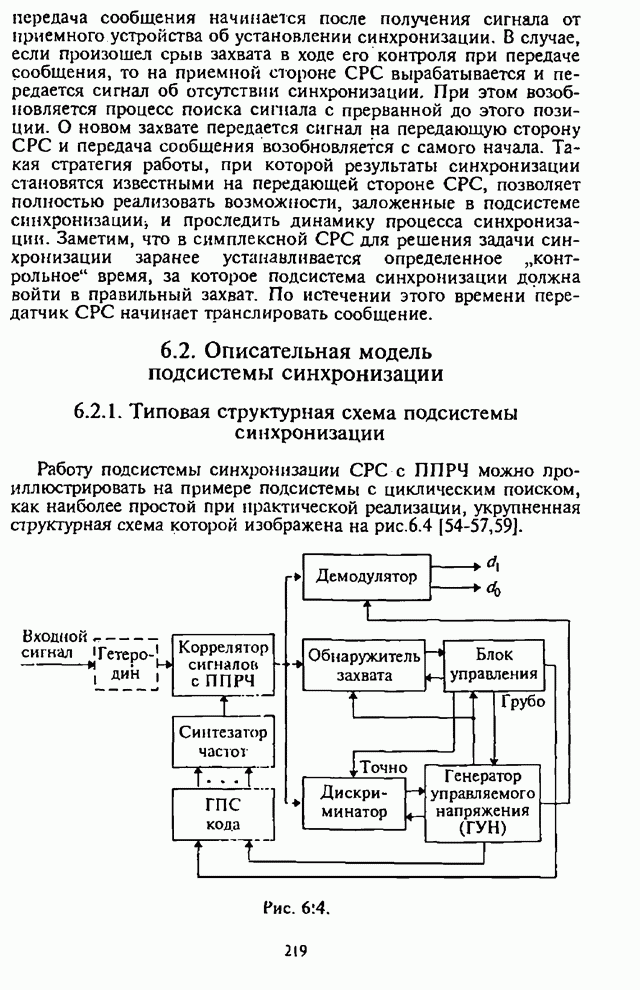
- 6.2.1. Типовая структурная схема подсистемы синхронизации
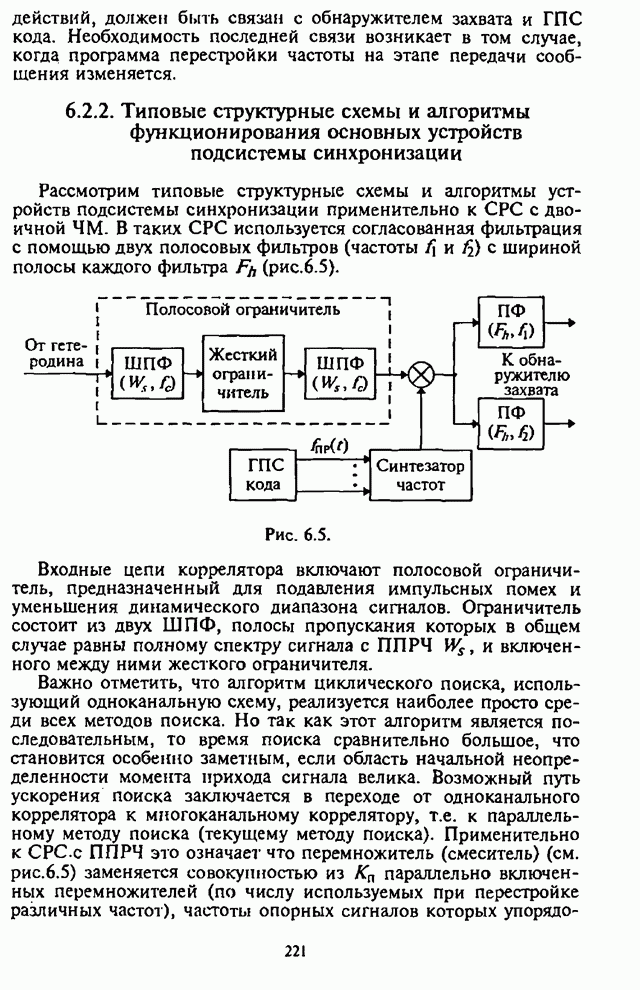
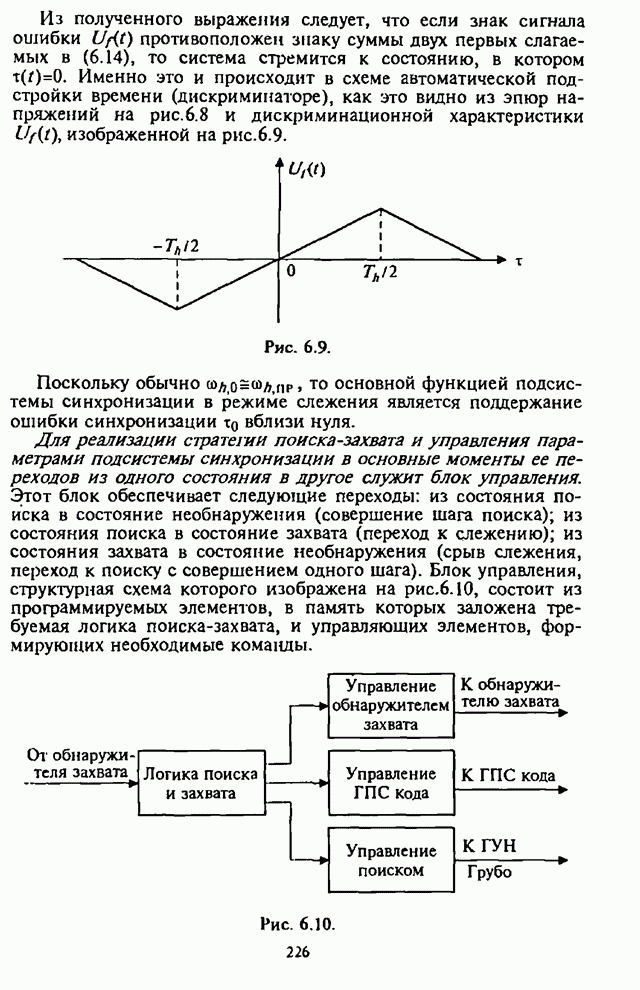
- 6.2.2. Типовые структурные схемы и алгоритмы функционирования основных устройств подсистемы синхронизации
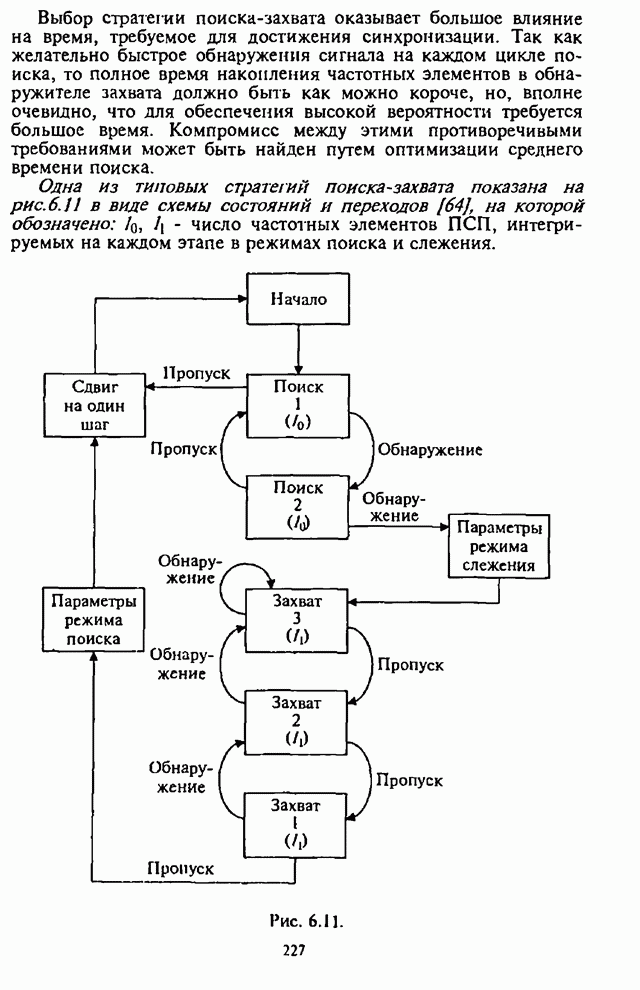
- 6.3. Показатели и оценка эффективности циклических процедур поиска
- Приложение П.6.1. Верхняя граница среднего нормированного времени поиска
- Приложение П.6.2. Верхняя граница вероятности правильного обнаружения
- Глава 7. Адаптивные антенные решетки в системах радиосвязи с псевдослучайной перестройкой рабочей частоты
- 7.1. Влияние сигналов с ППРЧ на характеристики адаптивной антенной решетки
- 7.2. Максиминный алгоритм обработки сигналов и помех
- 7.3. Реализация и возможности максиминного алгоритма
- 7.4. Модернизация максиминного алгоритма
- 7.4.1. Параметрическая обработка
- 7.4.2. Спектральная обработка
- 7.4.3. Обработка с упреждением
- Глава 8. Обнаружение сигналов с псевдослучайной перестройкой рабочей частоты
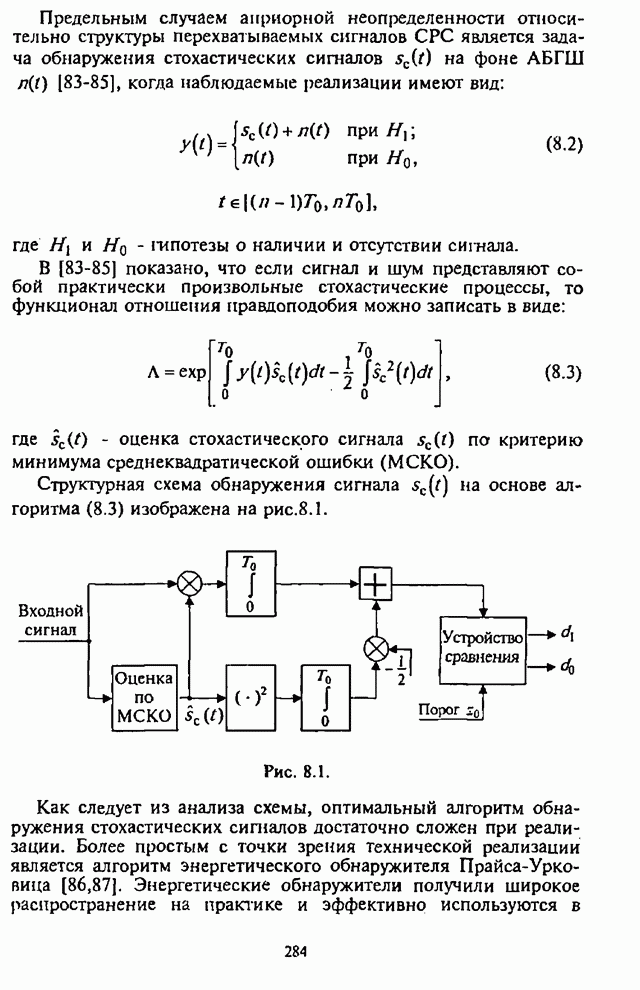
- 8.1. Обнаружение сигналов неизвестной структуры
- 8.2. Широкополосный энергетический обнаружитель
- 8.3. Многоканальные энергетические обнаружители
- 8.3.1. Квазиоптимальный многоканальный обнаружитель
- 8.3.2. Многоканальный обнаружитель типа сумматора с блоком фильтров
- 8.3.3. Модель обнаружителя типа сумматора с блоком фильтров при перехвате сигналов с медленной ППРЧ
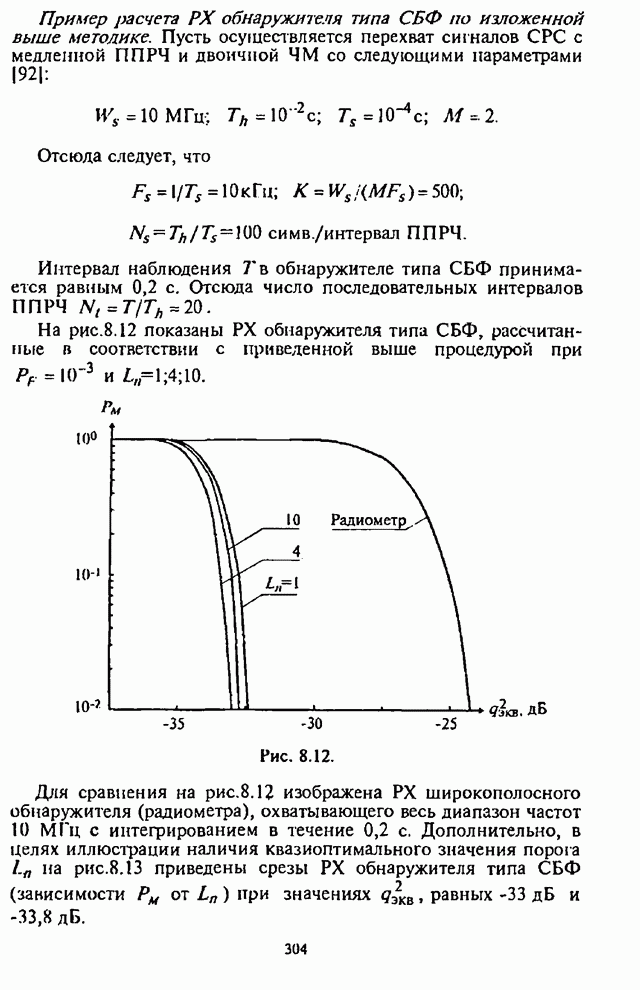
- 8.3.4. Многоканальный обнаружитель типа сумматора с блоком фильтров в части полосы
- 8.3.5. Рассогласование по времени и частоте между характеристиками сигнала с ППРЧ и параметрами обнаружителя
- 8.4. Многоканальный адаптивный энергетический обнаружитель в условиях воздействия мешающих сигналов
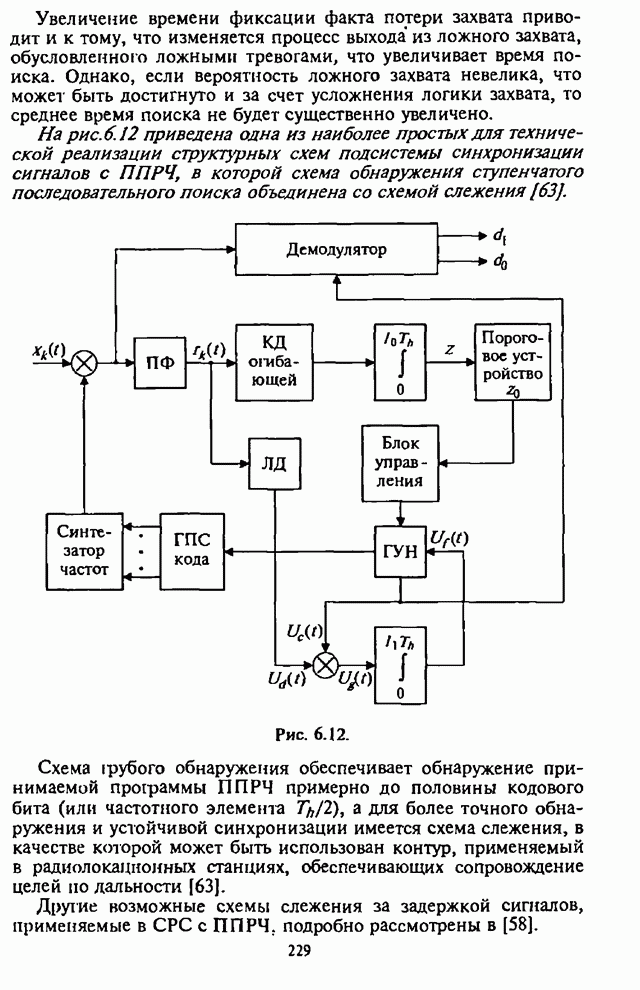
- 8.4.1. Структурная схема многоканального адаптивного энергетического обнаружителя с регулировкой порогового уровня
- 8.4.2. Вероятность ложной тревоги и адаптивная регулировка порогового уровня
- 8.4.3. Вероятность обнаружения
- 8.4.4. Влияние рассогласования по времени на обнаружение сигналов
- 8.5. Другие возможные типы обнаружителей сигналов с ППРЧ
- 8.5.1. Корреляционный радиометр
- 8.5.2. Цифровой анализатор спектра
- 8.5.3. Метод вскрытия частотно-временной матрицы сигнала с ППРЧ
- Приложение П.8.1. Алгоритмы вычисления обобщенной Q-функции Маркума
- П.8.1.1. Постановка задачи
- П.8.1.2. Представление степенными рядами
- П.8.1.3. Представление в виде рядов Неймана
- П.8.1.4. Численное интегрирование
- П.8.1.5. Гауссовская аппроксимация
- П.8.1.6. Численные результаты
- Приложение П.8.2. Анализ вероятностно-временных характеристик алгоритмов обнаружения сигналов
- П.8.2.1. Вероятностно-временные характеристики основных видов обнаружителей
- П.8.2.2 Алгоритмы расчета вероятностно-временных характеристик основных видов обнаружителей
- П.8.2.3. Численные результаты
- СПИСОК ОСНОВНЫХ СОКРАЩЕНИЙ
- ОСНОВНЫЕ УСЛОВНЫЕ ОБОЗНАЧЕНИЯ
- СПИСОК ЛИТЕРАТУРЫ