| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 8. Плоская деформация
В случае плоской деформации расчет несколько осложняется. Однако применение методов теории функций комплексного переменного (см., например, хорошо известную монографию Н. И. Мусхелишвили [6]) или метода Вестергаарда [7] позволяет прийти к аналогичным результатам. Сингулярность вблизи конца трещины дается формулой, аналогичной первой из (6.5), а именно

где

Для иллюстрации можно снова воспользоваться рис. 7, но уже с условиями на бесконечности

Отметим, что коэффициент интенсивности для компоненты  тот же, что для
тот же, что для  и справедлива асимптотическая формула
и справедлива асимптотическая формула

Отсюда следует, что отношение  стремится к единице при изменении аргумента вдоль оси
стремится к единице при изменении аргумента вдоль оси  Для другого пути (если он существует) предел, возможно, будет иным.
Для другого пути (если он существует) предел, возможно, будет иным.
Мы не приводим формулу для перемещения, которая аналогична второй из (6.5) (с другим множителем). Для получения связи между  следует повторить рассуждения для антиплоского случая. В итоге получим
следует повторить рассуждения для антиплоского случая. В итоге получим

(для традиционных обозначений модуля Юнга  и коэффициента Пуассона
и коэффициента Пуассона 
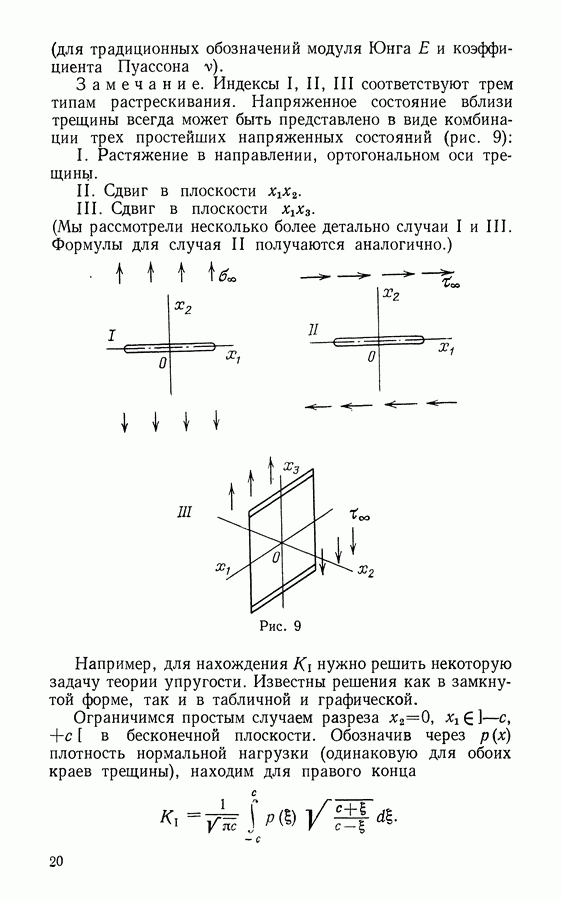
Замечание. Индексы  соответствуют трем типам растрескивания. Напряженное состояние вблизи трещины всегда может быть представлено в виде комбинации трех простейших напряженных состояний (рис. 9):
соответствуют трем типам растрескивания. Напряженное состояние вблизи трещины всегда может быть представлено в виде комбинации трех простейших напряженных состояний (рис. 9):
I. Растяжение в направлении, ортогональном оси трещины.
II. Сдвиг в плоскости  .
.
III. Сдвиг в плоскости  (Мы рассмотрели несколько более детально случаи
(Мы рассмотрели несколько более детально случаи  Формулы для случая
Формулы для случая  получаются аналогично.)
получаются аналогично.)

Рис. 9
Например, для нахождения  нужно решить некоторую задачу теории упругости. Известны решения как в замкнутой форме, так и в табличной и графической.
нужно решить некоторую задачу теории упругости. Известны решения как в замкнутой форме, так и в табличной и графической.
Ограничимся простым случаем разреза  в бесконечной плоскости. Обозначив через
в бесконечной плоскости. Обозначив через  плотность нормальной нагрузки (одинаковую для обоих краев трещины), находим для правого конца
плотность нормальной нагрузки (одинаковую для обоих краев трещины), находим для правого конца

Если  четная функция, то значение коэффициента интенсивности для обоих краев трещины будет
четная функция, то значение коэффициента интенсивности для обоих краев трещины будет

Рассмотрим отдельно два случая.
1. Случай, когда растяжение равно нулю на трещине и а на бесконечности. Заменив нулевое растяжение на трещине величиной и положив  получим из (8.2) результат, аналогичный (8.1)
получим из (8.2) результат, аналогичный (8.1)


Рис. 10
2. Случай, когда две силы, равные и противоположно направленные, приложены в середине, как на рис. 10. Интеграл тогда сводится к  и
и

Пусть теперь  силы имеют величину
силы имеют величину  Трещина длиной
Трещина длиной  будет устойчива и ее длина определяется соотношением
будет устойчива и ее длина определяется соотношением

Для скальных пород и для грунтов значение прочности  может рассматриваться как пренебрежимо малое, откуда следует, что длина устойчивой трещины будет
может рассматриваться как пренебрежимо малое, откуда следует, что длина устойчивой трещины будет

Эти простые рассуждения использовались С. А. Христиановичем как исходные предпосылки для построения теории разрушения угольных пластов в шахтах.
Теория, которую мы рассматриваем, справедлива лишь для размеров зон пластичности, малых по сравнению с длиной трещины. Следует отметить, что размерность К есть  где
где  сила,
сила,  длина.
длина.
Размер пластической зоны зависит также от величины предела текучести  Из
Из  можно образовать лишь
можно образовать лишь
одну комбинацию с размерностью длины, а именно

которая и дает (с точностью до безразмерного множителя) размер пластической зоны, изображенной на рис. 6.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- Глава 1. ОСНОВНЫЕ ПОНЯТИЯ
- § 1. Твердое тело
- § 2. Уравнения состояния
- § 3. Ползучесть, усталость, пластичность
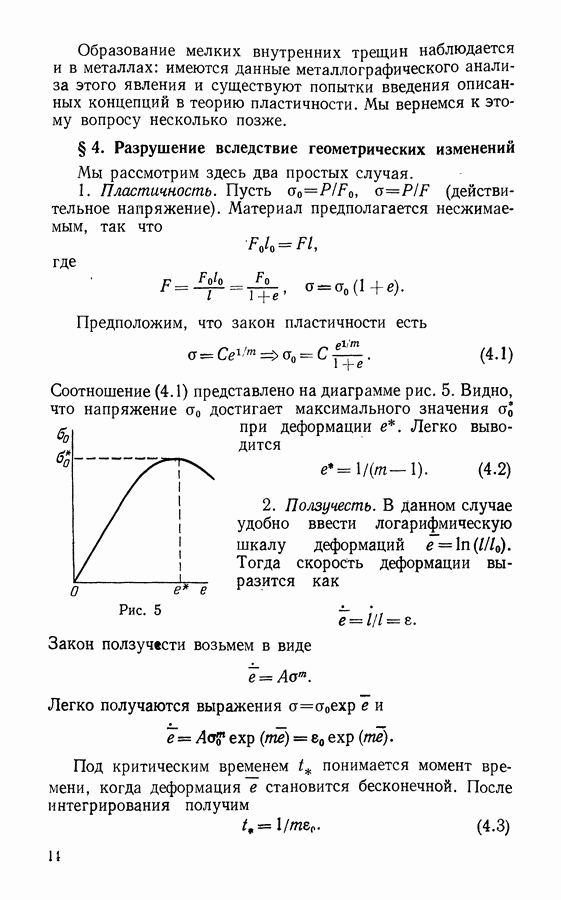
- § 4. Разрушение вследствие геометрических изменений
- Глава 2. МЕХАНИКА РАСПРОСТРАНЕНИЯ ТРЕЩИН
- § 5. Теория Гриффитса
- § 6. Антиплоская деформация
- § 7. Работа продвижения трещины
- § 8. Плоская деформация
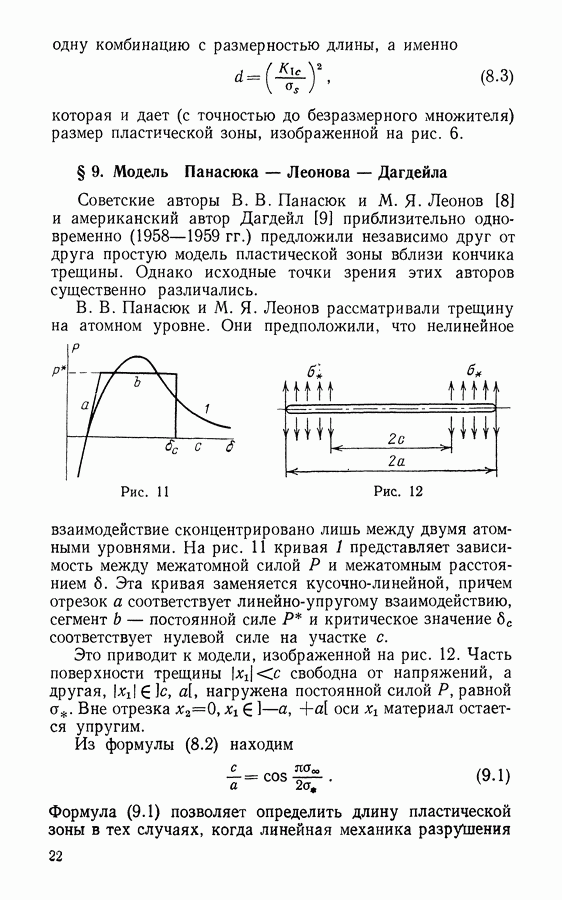
- § 9. Модель Панасюка — Леонова — Дагдейла
- § 10. Интеграл Райса — Черепанова
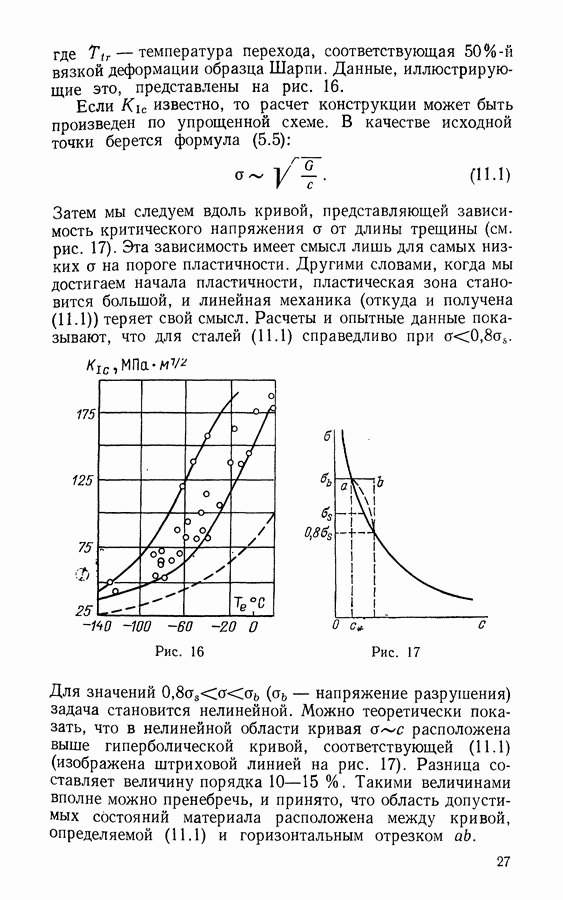
- § 11. Выводы главы 2
- Глава 3. ПОЛЗУЧЕСТЬ И РАЗРУШЕНИЕ МЕТАЛЛОВ ПРИ ВЫСОКИХ ТЕМПЕРАТУРАХ
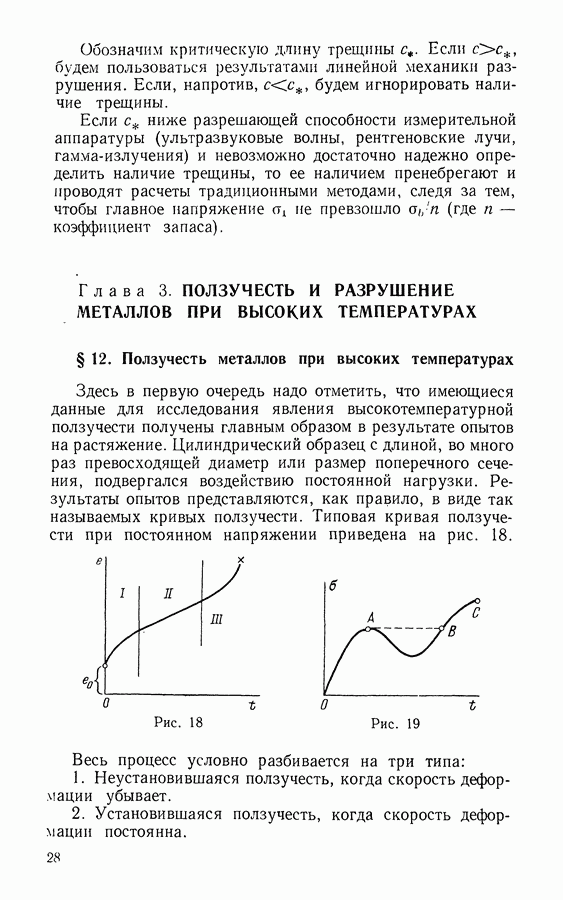
- § 12. Ползучесть металлов при высоких температурах
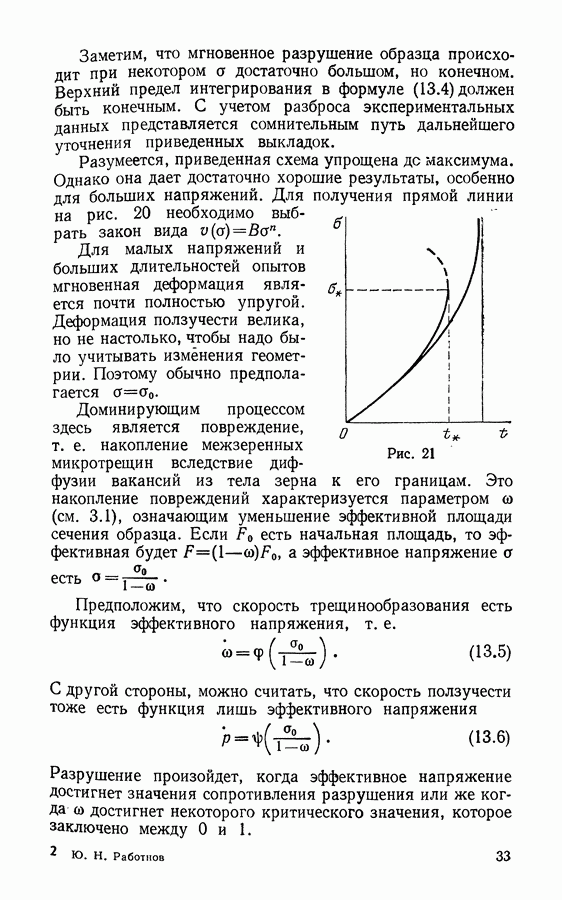
- § 13. Разрушение при растяжении
- § 14. Сложное напряженное состояние
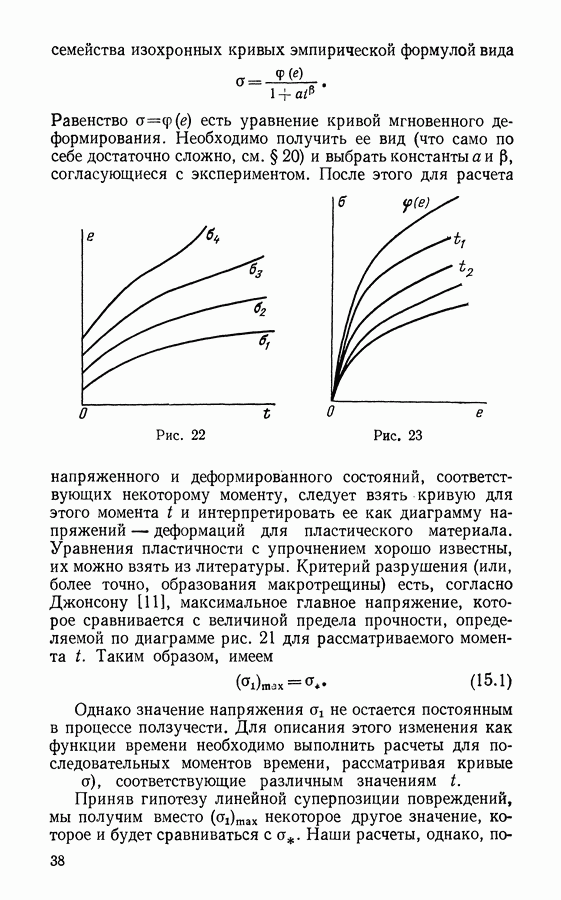
- § 15. Техническая теория. Изохронные кривые ползучести
- § 16. Разрушение при кратковременной ползучести
- § 17. Концентрация напряжений
- Глава 4. ЛИНЕЙНАЯ И НЕЛИНЕЙНАЯ НАСЛЕДСТВЕННОСТЬ
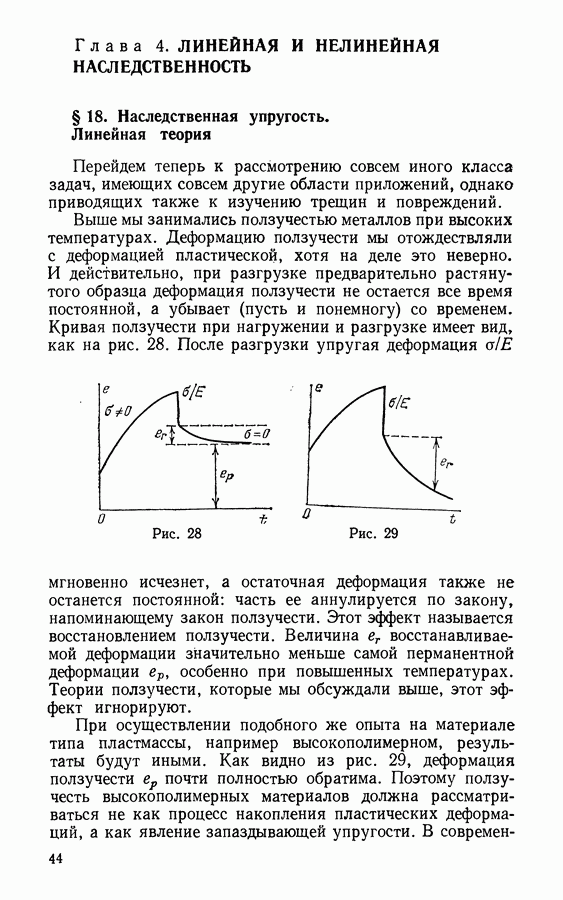
- § 18. Наследственная упругость. Линейная теория
- § 19. Задача о росте трещины
- § 20. Нелинейная наследственность
- Глава 5. МЕХАНИКА КОМПОЗИТНЫХ МАТЕРИАЛОВ
- § 21. Композиты волокнистого строения
- § 22. Слоистые упругие композиты
- § 23. Предельное состояние пластической композитной структуры
- § 24. Прочность слоистых композитов
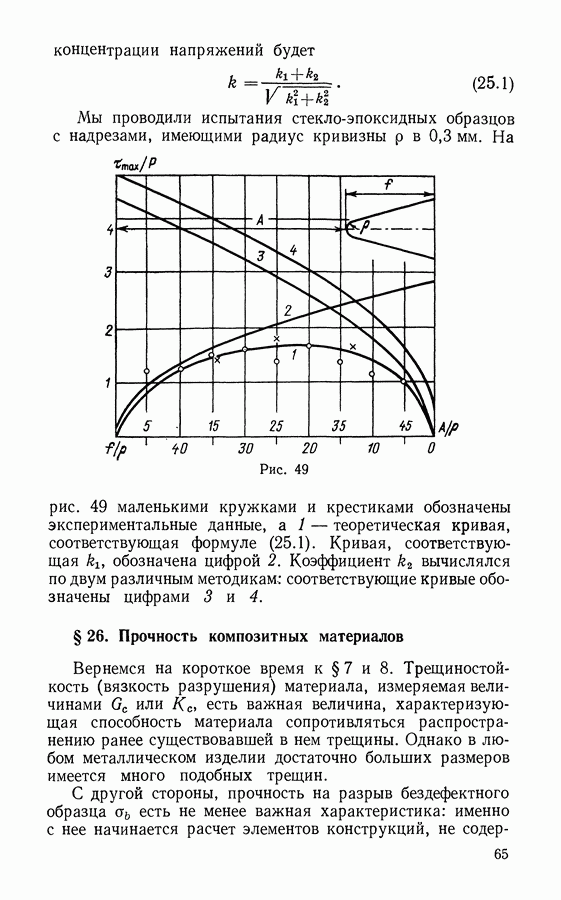
- § 25. Концентрация напряжений в композитах
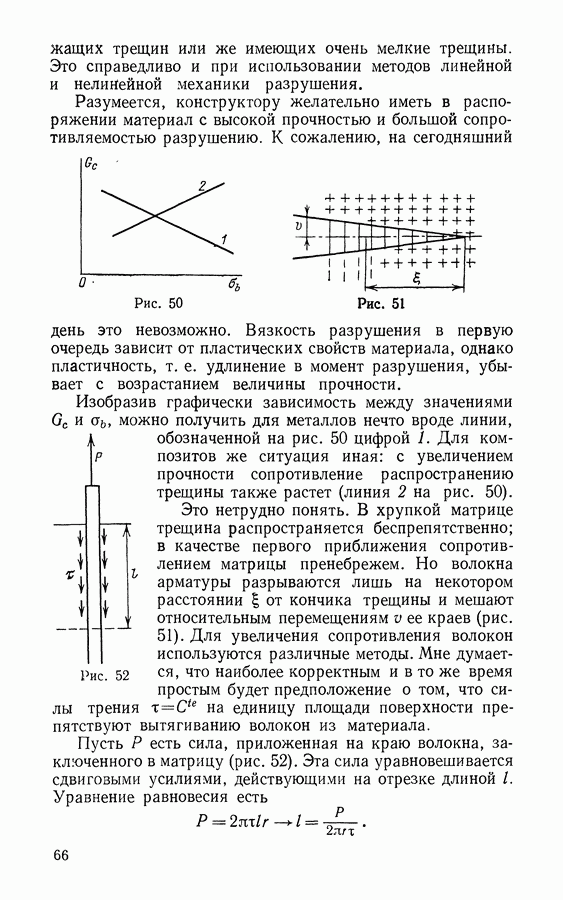
- § 26. Прочность композитных материалов
- ЗАКЛЮЧЕНИЕ