| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 9. Модель Панасюка — Леонова — Дагдейла
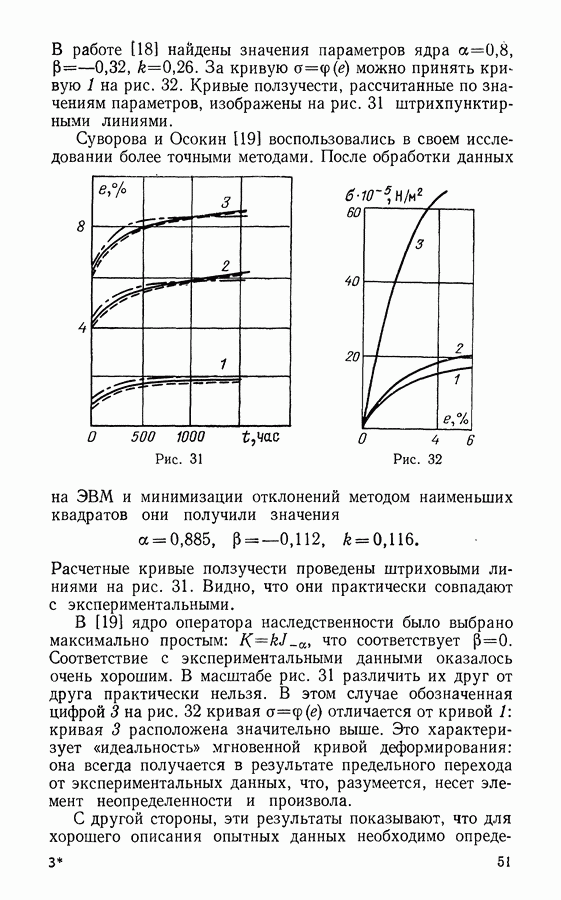
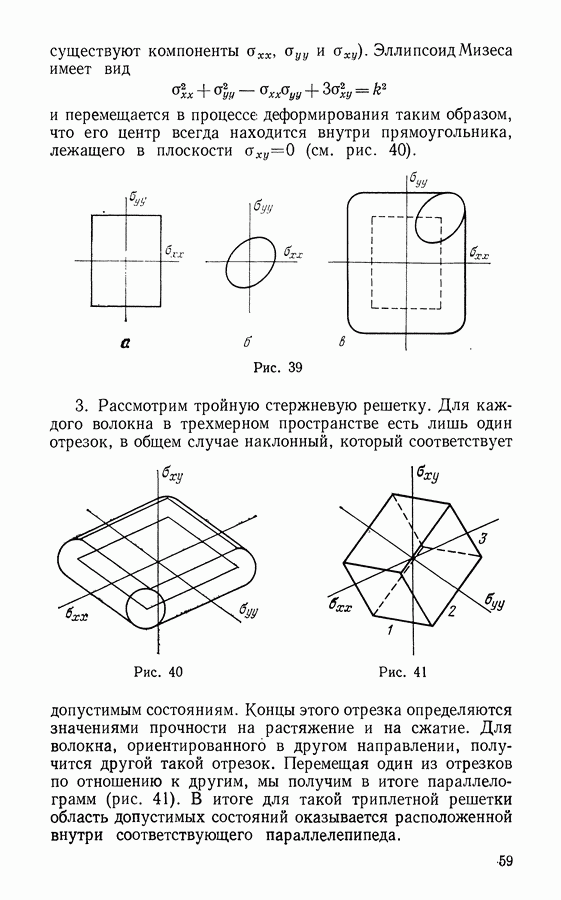
Советские авторы В. В. Панасюк и М. Я. Леонов [8] и американский автор Дагдейл [9] приблизительно одновременно (1958-1959 гг.) предложили независимо друг от друга простую модель пластической зоны вблизи кончика трещины. Однако исходные точки зрения этих авторов существенно различались.
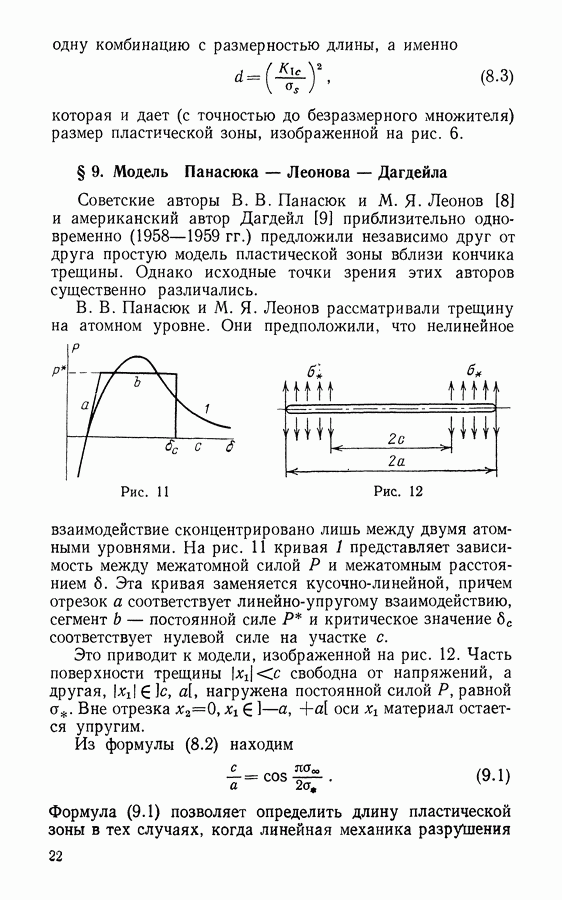
В. В. Панасюк и М. Я. Леонов рассматривали трещину на атомном уровне. Они предположили, что нелинейное взаимодействие сконцентрировано лишь между двумя атомными уровнями. На рис. 11 кривая 1 представляет зависимость между межатомной силой  и межатомным расстоянием
и межатомным расстоянием  Эта кривая заменяется кусочно-линейной, причем отрезок а соответствует линейно-упругому взаимодействию, сегмент
Эта кривая заменяется кусочно-линейной, причем отрезок а соответствует линейно-упругому взаимодействию, сегмент  постоянной силе
постоянной силе  и критическое значение
и критическое значение  соответствует нулевой силе на участке с.
соответствует нулевой силе на участке с.

Рис. 11

Рис. 12
Это приводит к модели, изображенной на рис. 12. Часть поверхности трещины  свободна от напряжений, а другая,
свободна от напряжений, а другая,  нагружена постоянной силой
нагружена постоянной силой  равной Вне отрезка
равной Вне отрезка  оси
оси  материал остается упругим.
материал остается упругим.
Из формулы (8.2) находим

Формула (9.1) позволяет определить длину пластической зоны в тех случаях, когда линейная механика разрушения
бессильна. Величина  может быть достаточно большой, и она стремится к бесконечности при о- а. Напротив, для разлагая косинус в ряд и оставляя два первых члена ряда, получим
может быть достаточно большой, и она стремится к бесконечности при о- а. Напротив, для разлагая косинус в ряд и оставляя два первых члена ряда, получим

Дагдейл получил те же результаты, исследуя напряженное состояние в тонкой плите, содержащей треш,ину, длина которой во много раз превосходит толщину плиты. В этом случае легко можно построить точное решение упруго-пластической задачи. Граница пластической зоны образуется из прямолинейных отрезков  а пластическое течение происходит в плоскостях, составляющих угол
а пластическое течение происходит в плоскостях, составляющих угол  с границей плиты (рис. 13). Формальный аспект расчета тот же, что и в двух рассмотренных выше случаях.
с границей плиты (рис. 13). Формальный аспект расчета тот же, что и в двух рассмотренных выше случаях.

Рис. 13
Можно указать на множество публикаций, касаюшихся решения упруго-пластической задачи для тела с трещинами. Для случая плоской деформации ситуация сходна с изображенной на рис. 6, но не на рис. 12, что подтверждается многими известными численными решениями данной задачи.
Относительно самих решений следует указать на один их общий недостаток. Деформации в пластической зоне являются очень большими, порядка 100% для мягкой стали. Таким образом, здесь можно воспользоваться теорией пластичности больших деформаций и вращений, либо же учесть изменения геометрии, выписав граничные условия на деформированной границе. Можно также оперировать уравнениями линейной теории упругости совместно с уравнениями теории малых пластических деформаций, что приводит к игнорированию нелинейно-геометрического характера задачи.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- Глава 1. ОСНОВНЫЕ ПОНЯТИЯ
- § 1. Твердое тело
- § 2. Уравнения состояния
- § 3. Ползучесть, усталость, пластичность
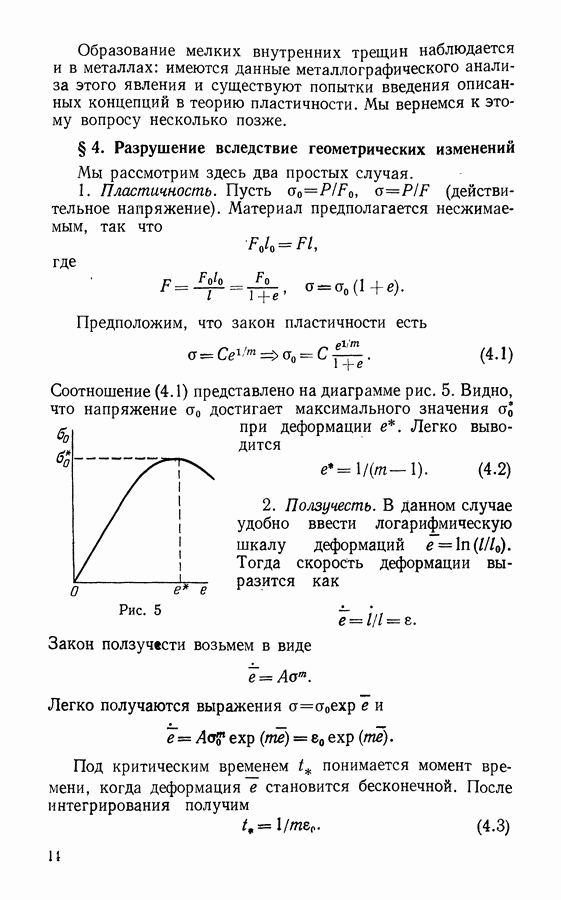
- § 4. Разрушение вследствие геометрических изменений
- Глава 2. МЕХАНИКА РАСПРОСТРАНЕНИЯ ТРЕЩИН
- § 5. Теория Гриффитса
- § 6. Антиплоская деформация
- § 7. Работа продвижения трещины
- § 8. Плоская деформация
- § 9. Модель Панасюка — Леонова — Дагдейла
- § 10. Интеграл Райса — Черепанова
- § 11. Выводы главы 2
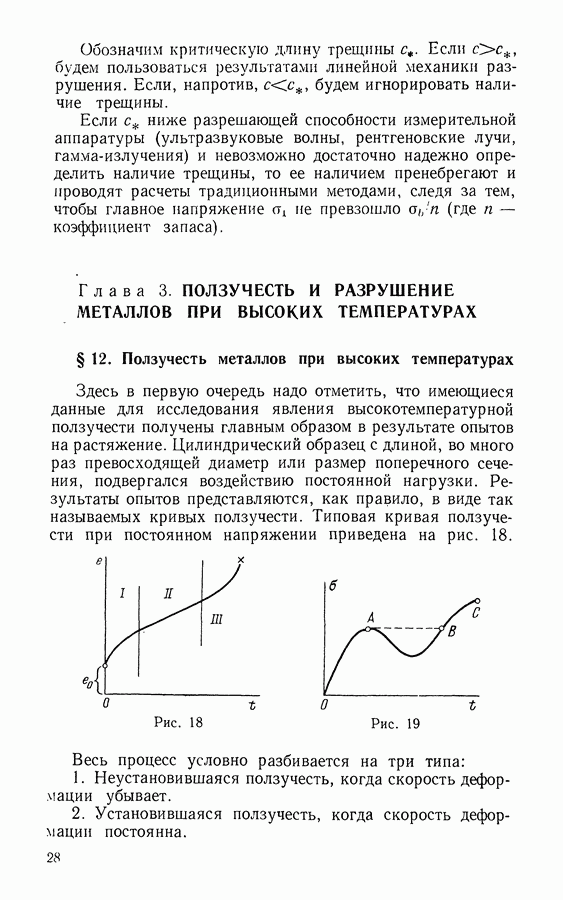
- Глава 3. ПОЛЗУЧЕСТЬ И РАЗРУШЕНИЕ МЕТАЛЛОВ ПРИ ВЫСОКИХ ТЕМПЕРАТУРАХ
- § 12. Ползучесть металлов при высоких температурах
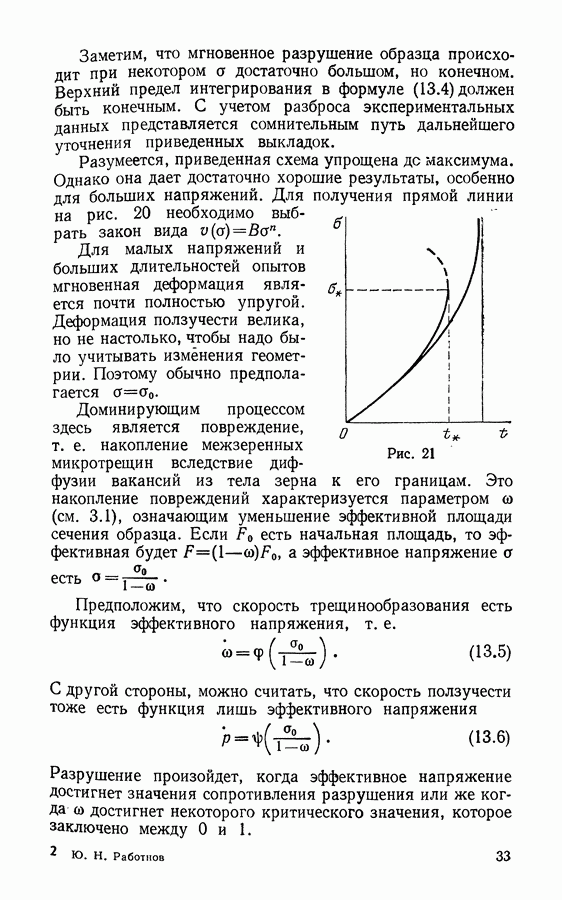
- § 13. Разрушение при растяжении
- § 14. Сложное напряженное состояние
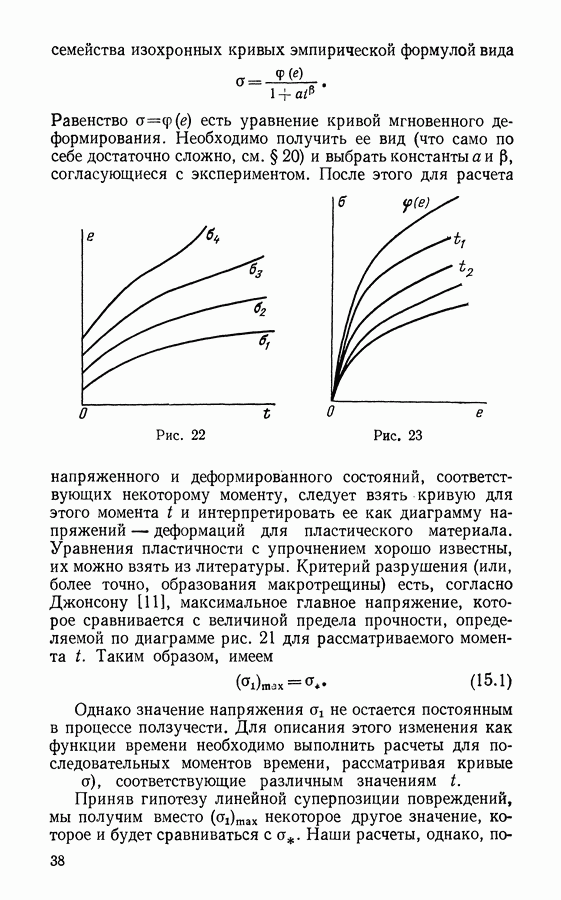
- § 15. Техническая теория. Изохронные кривые ползучести
- § 16. Разрушение при кратковременной ползучести
- § 17. Концентрация напряжений
- Глава 4. ЛИНЕЙНАЯ И НЕЛИНЕЙНАЯ НАСЛЕДСТВЕННОСТЬ
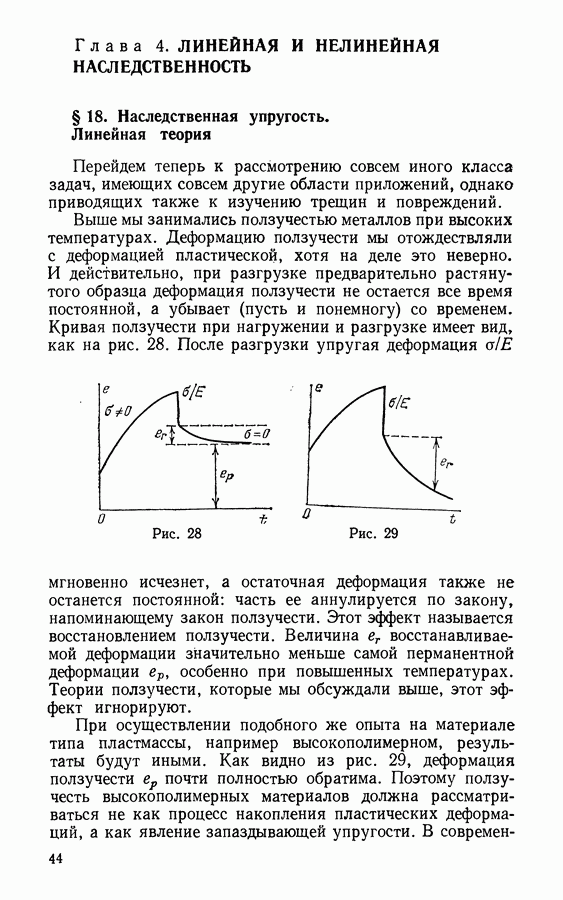
- § 18. Наследственная упругость. Линейная теория
- § 19. Задача о росте трещины
- § 20. Нелинейная наследственность
- Глава 5. МЕХАНИКА КОМПОЗИТНЫХ МАТЕРИАЛОВ
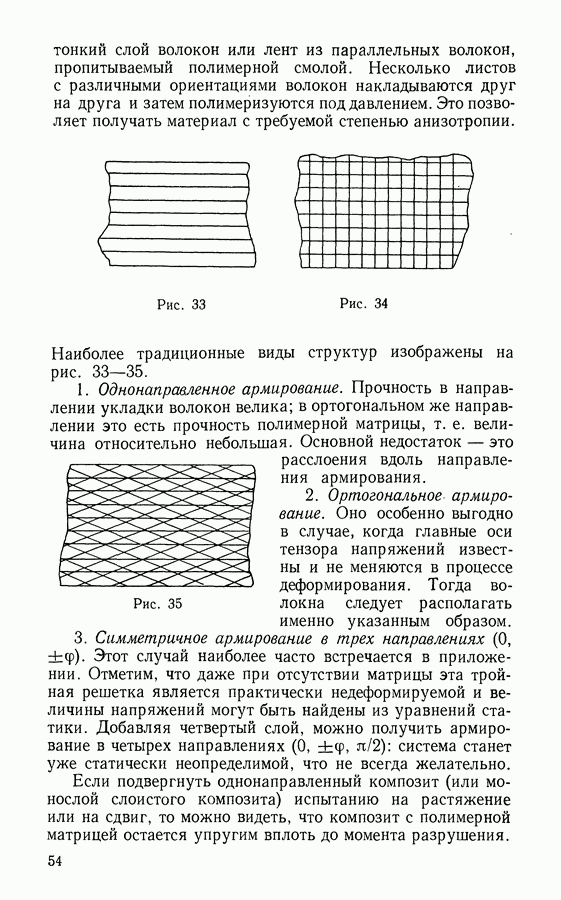
- § 21. Композиты волокнистого строения
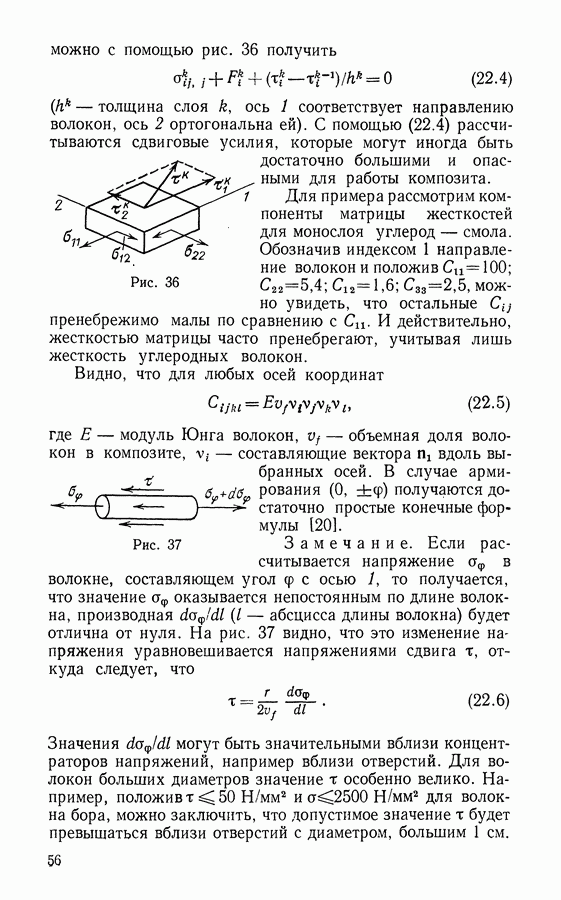
- § 22. Слоистые упругие композиты
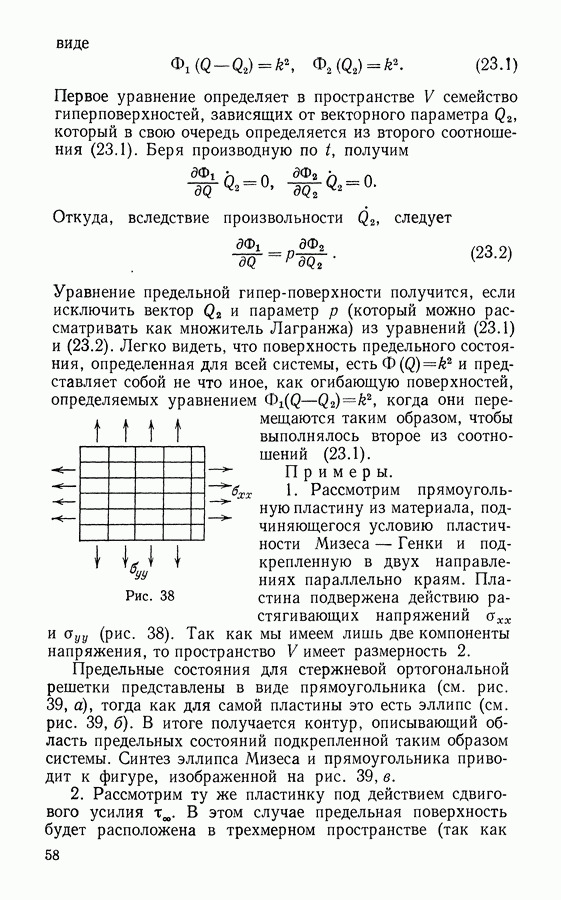
- § 23. Предельное состояние пластической композитной структуры
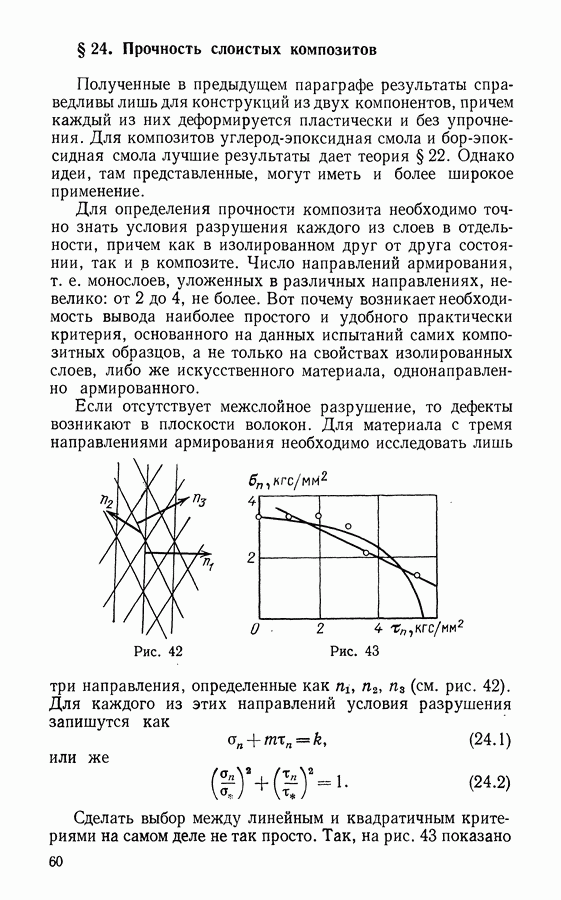
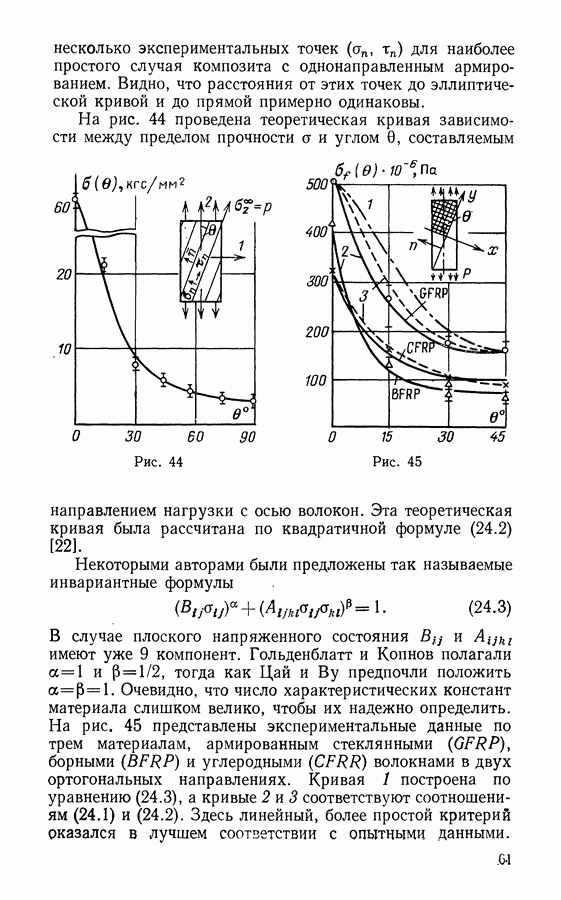
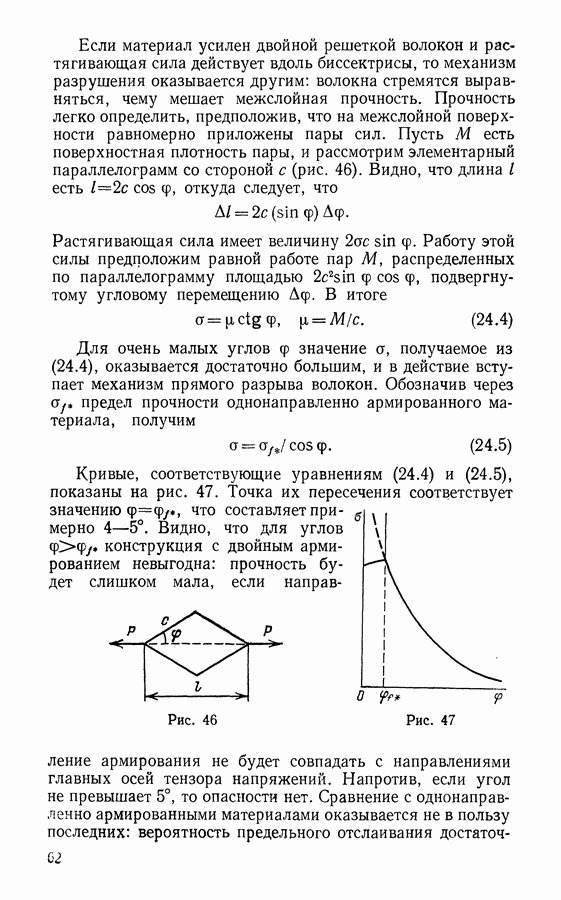
- § 24. Прочность слоистых композитов
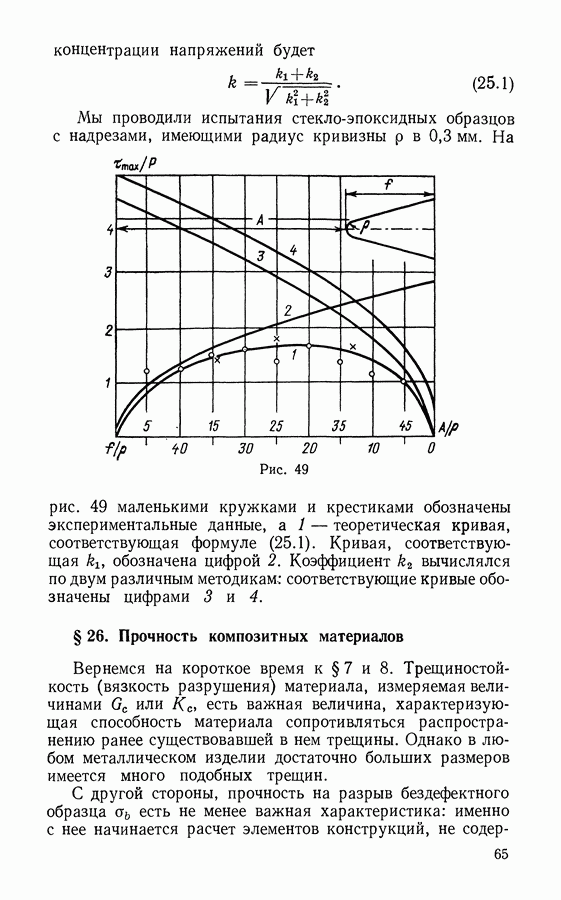
- § 25. Концентрация напряжений в композитах
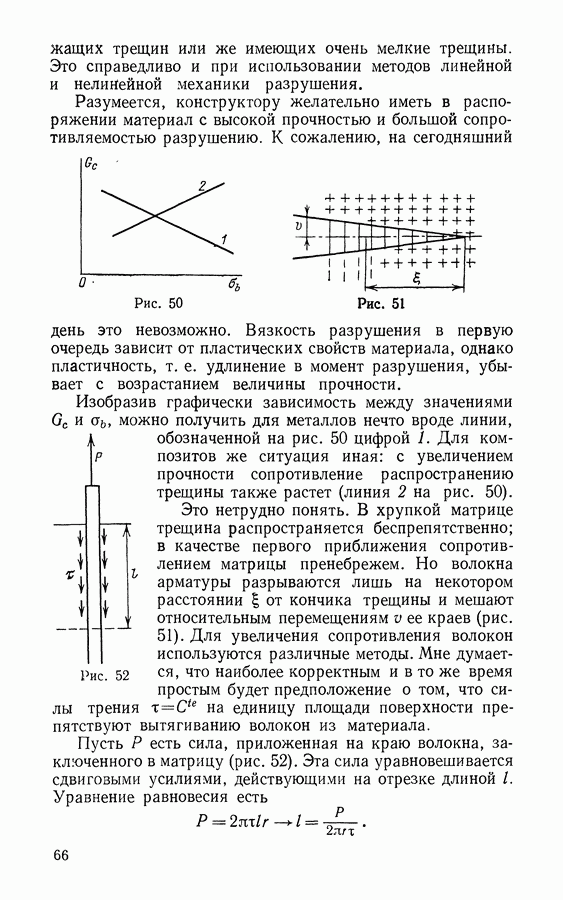
- § 26. Прочность композитных материалов
- ЗАКЛЮЧЕНИЕ