| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
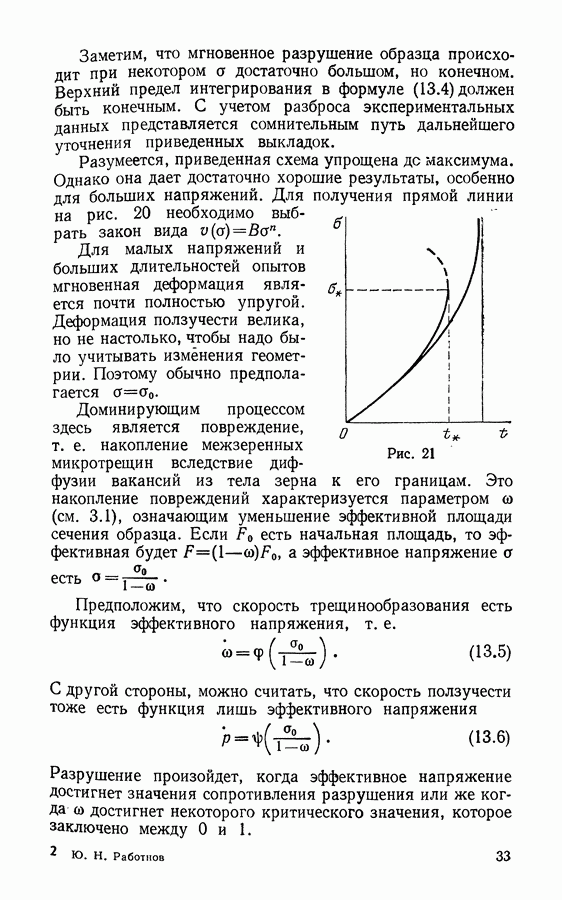
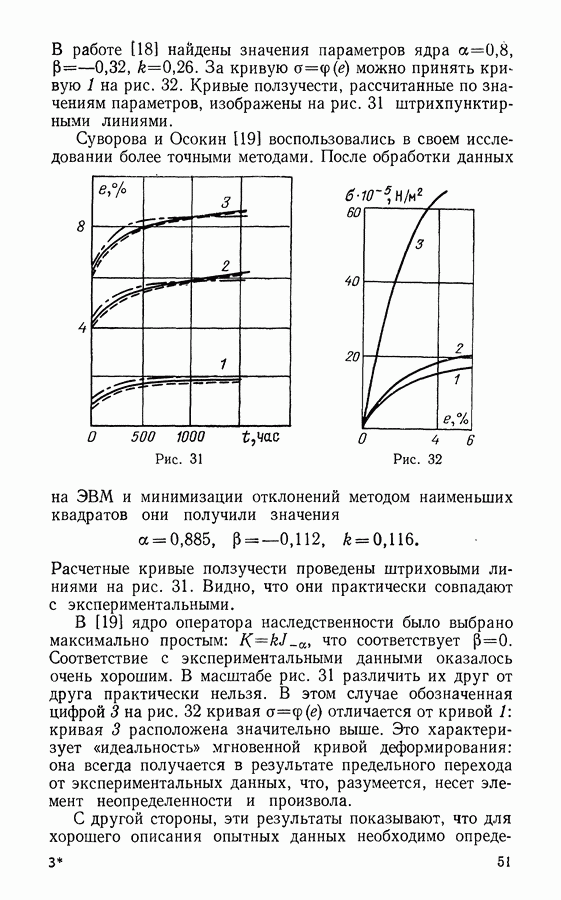
§ 23. Предельное состояние пластической композитной структуры
Предположим теперь, что как волокна, так и матрица могут деформироваться пластически и могут достигать состояния полной текучести  Мы будем рассматривать достаточно общий случай, когда структура 5 порядка
Мы будем рассматривать достаточно общий случай, когда структура 5 порядка  образована из
образована из  субструктур, имеющих некоторые общие элементы. Деформация элементов, одновременно принадлежащих ко многим субструктурам, будет, очевидно, всюду одинаковой (параллельное соединение структур). Вектор
субструктур, имеющих некоторые общие элементы. Деформация элементов, одновременно принадлежащих ко многим субструктурам, будет, очевидно, всюду одинаковой (параллельное соединение структур). Вектор  внутренних усилий в структуре
внутренних усилий в структуре  есть сумма внутренних векторов различных субструктур:
есть сумма внутренних векторов различных субструктур:

где каждый  принадлежит некоторому векторному конечномерному пространству V (не обязательно одному и тому же для всех).
принадлежит некоторому векторному конечномерному пространству V (не обязательно одному и тому же для всех).
Предположим, что все субструктуры имеют по крайней мере по нескольку общих элементов. Тогда, говоря об объединении субструктур  мы можем назвать это объединение
мы можем назвать это объединение  композитом [21]. Пластинки и оболочки с ребрами жесткости тоже могут являться примерами таких композитов.
композитом [21]. Пластинки и оболочки с ребрами жесткости тоже могут являться примерами таких композитов.
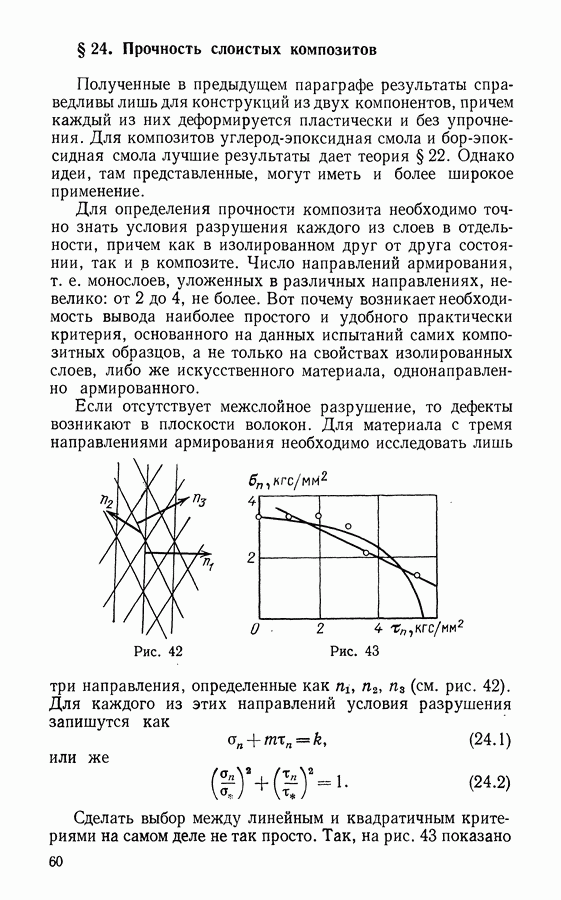
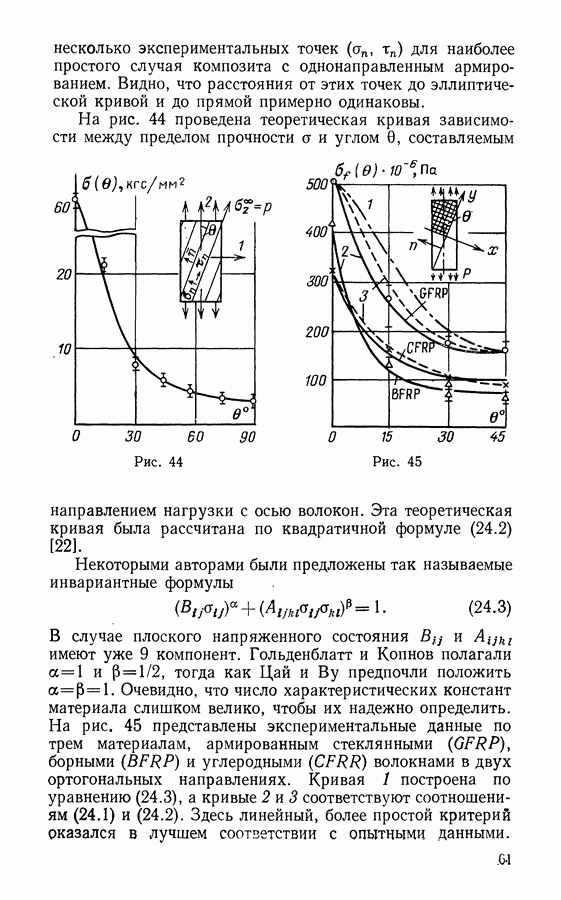
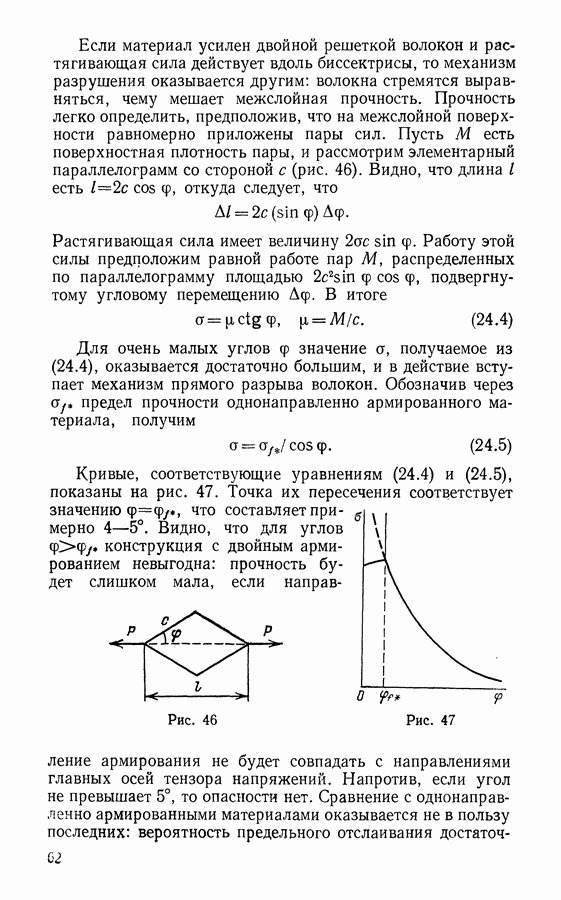
Рассмотрим подкрепленную ортогональной системой стержней пластину. Напряженное состояние в ней всегда представлено тремя компонентами усилий и тремя компонентами моментов. Что касается подкрепляющей решетки, то принимается, что система ортогональных стержней не препятствует сопротивлению тела ни сдвигу, ни кручению: соответствующая подсистема будет тогда иметь размерность 4 (два усилия и два момента). Аналогичным образом можно рассмотреть пластинки, армированные волокнами.
Предположим, что  состоит из двух частей
состоит из двух частей  Тогда
Тогда

В случае достижения каждой из подсистем предельного состояния будут выполняться два символических равенства

которые можно переписать в слегка модифицированном

Первое уравнение определяет в пространстве  семейство гиперповерхностей, зависящих от векторного параметра
семейство гиперповерхностей, зависящих от векторного параметра  который в свою очередь определяется из второго соотношения (23.1). Беря производную по
который в свою очередь определяется из второго соотношения (23.1). Беря производную по  получим
получим

Откуда, вследствие произвольности  следует
следует

Уравнение предельной гиперповерхности получится, если исключить вектор  и параметр
и параметр  (который можно рассматривать как множитель Лагранжа) из уравнений (23.1) и (23.2). Легко видеть, что поверхность предельного состояния, определенная для всей системы,
(который можно рассматривать как множитель Лагранжа) из уравнений (23.1) и (23.2). Легко видеть, что поверхность предельного состояния, определенная для всей системы,  представляет собой не что иное, как огибающую поверхностей, определяемых уравнением когда они перемещаются таким образом, чтобы выполнялось второе из соотношений (23.1).
представляет собой не что иное, как огибающую поверхностей, определяемых уравнением когда они перемещаются таким образом, чтобы выполнялось второе из соотношений (23.1).

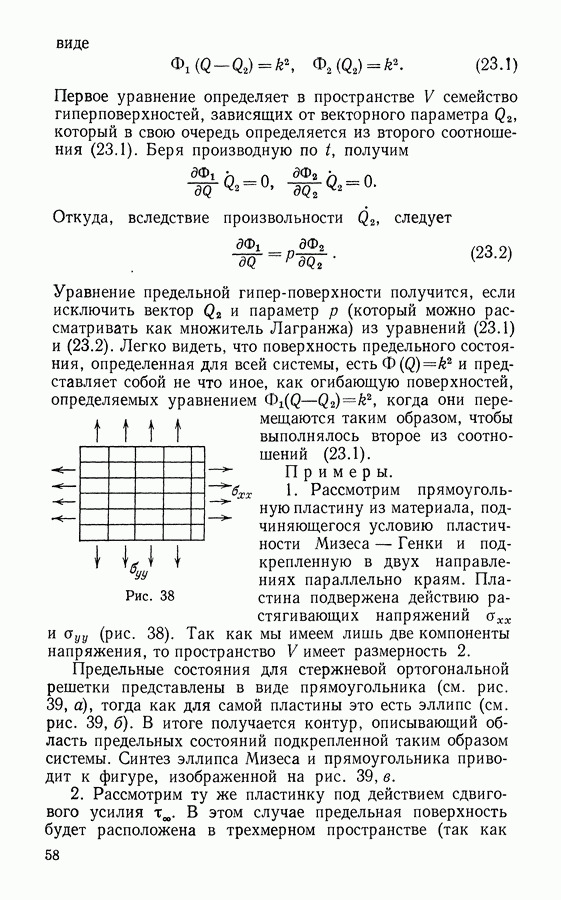
Рис. 38
Примеры.
1. Рассмотрим прямоугольную пластину из материала, подчиняющегося условию пластичности Мизеса — Генки и подкрепленную в двух направлениях параллельно краям. Пластина подвержена действию растягивающих напряжений  (рис. 38). Так как мы имеем лишь две компоненты напряжения, то пространство V имеет размерность 2.
(рис. 38). Так как мы имеем лишь две компоненты напряжения, то пространство V имеет размерность 2.
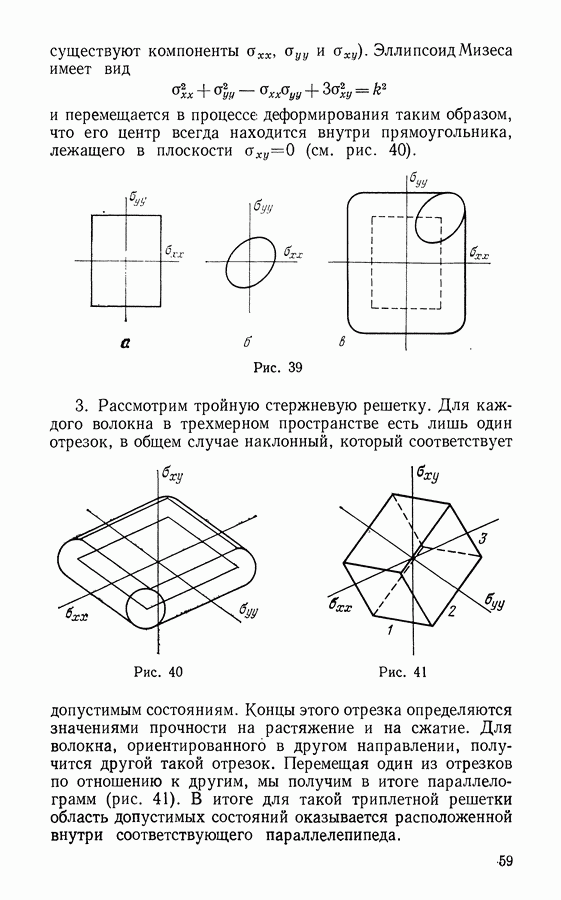
Предельные состояния для стержневой ортогональной решетки представлены в виде прямоугольника (см. рис. 39, а), тогда как для самой пластины это есть эллипс (см. рис. 39, б). В итоге получается контур, описывающий область предельных состояний подкрепленной таким образом системы. Синтез эллипса Мизеса и прямоугольника приводит к фигуре, изображенной на рис. 39, в.
2. Рассмотрим ту же пластинку под действием сдвигового усилия  В этом случае предельная поверхность будет расположена в трехмерном пространстве (так как
В этом случае предельная поверхность будет расположена в трехмерном пространстве (так как
существуют компоненты  Эллипсоид Мизеса имеет вид
Эллипсоид Мизеса имеет вид

и перемещается в процессе деформирования таким образом, что его центр всегда находится внутри прямоугольника, лежащего в плоскости  (см. рис. 40).
(см. рис. 40).

Рис. 39

Рис. 40

Рис. 41
3. Рассмотрим тройную стержневую решетку. Для каждого волокна в трехмерном пространстве есть лишь один отрезок, в общем случае наклонный, который соответствует допустимым состояниям. Концы этого отрезка определяются значениями прочности на растяжение и на сжатие. Для волокна, ориентированного в другом направлении, получится другой такой отрезок. Перемещая один из отрезков по отношению к другим, мы получим в итоге параллелограмм (рис. 41). В итоге для такой триплетной решетки область допустимых состояний оказывается расположенной внутри соответствующего параллелепипеда.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- Глава 1. ОСНОВНЫЕ ПОНЯТИЯ
- § 1. Твердое тело
- § 2. Уравнения состояния
- § 3. Ползучесть, усталость, пластичность
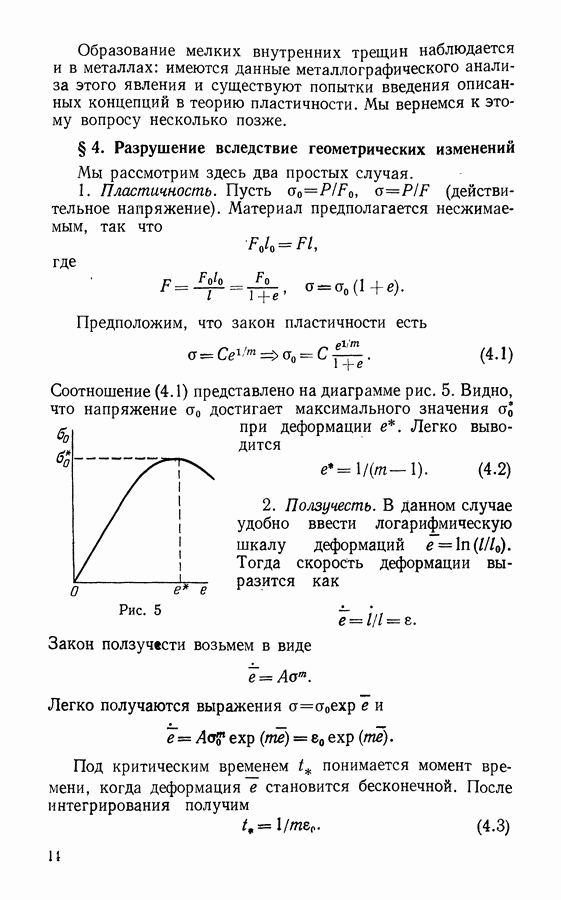
- § 4. Разрушение вследствие геометрических изменений
- Глава 2. МЕХАНИКА РАСПРОСТРАНЕНИЯ ТРЕЩИН
- § 5. Теория Гриффитса
- § 6. Антиплоская деформация
- § 7. Работа продвижения трещины
- § 8. Плоская деформация
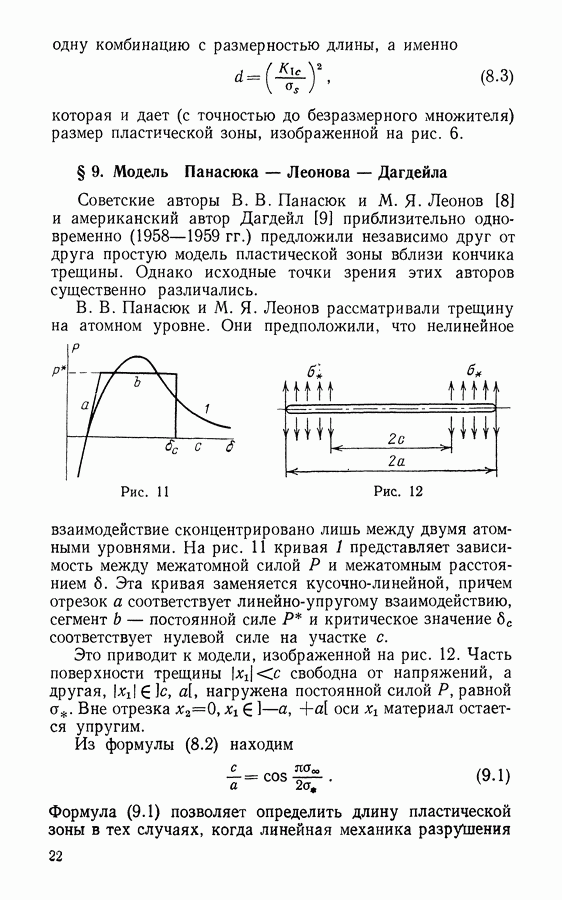
- § 9. Модель Панасюка — Леонова — Дагдейла
- § 10. Интеграл Райса — Черепанова
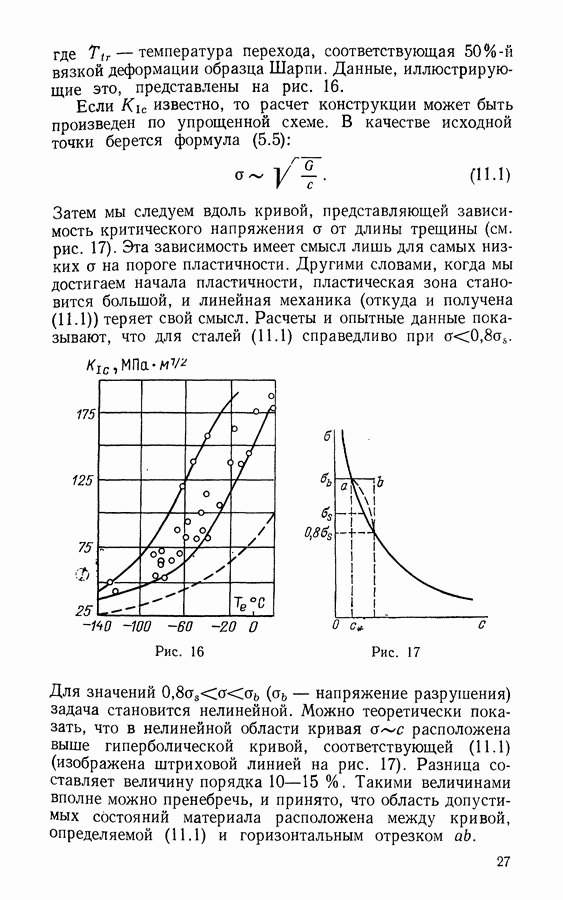
- § 11. Выводы главы 2
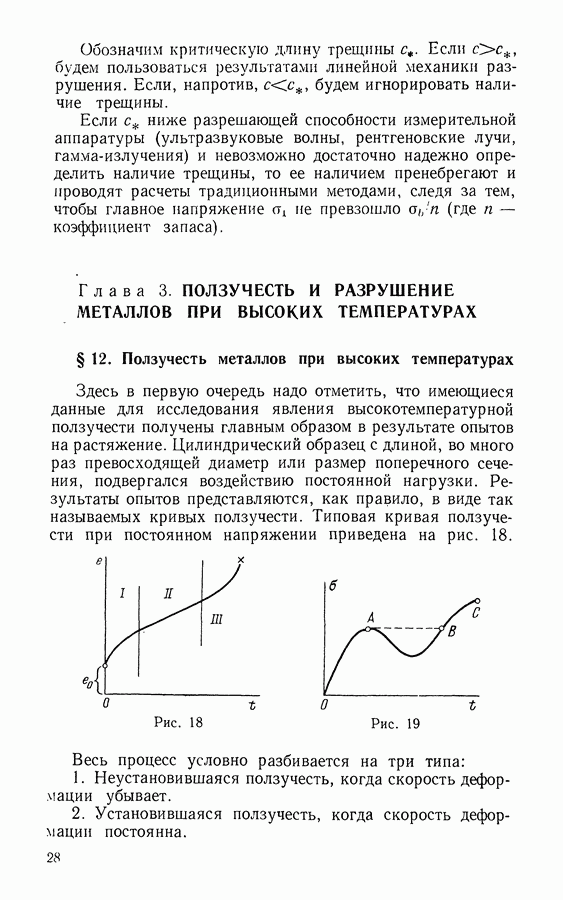
- Глава 3. ПОЛЗУЧЕСТЬ И РАЗРУШЕНИЕ МЕТАЛЛОВ ПРИ ВЫСОКИХ ТЕМПЕРАТУРАХ
- § 12. Ползучесть металлов при высоких температурах
- § 13. Разрушение при растяжении
- § 14. Сложное напряженное состояние
- § 15. Техническая теория. Изохронные кривые ползучести
- § 16. Разрушение при кратковременной ползучести
- § 17. Концентрация напряжений
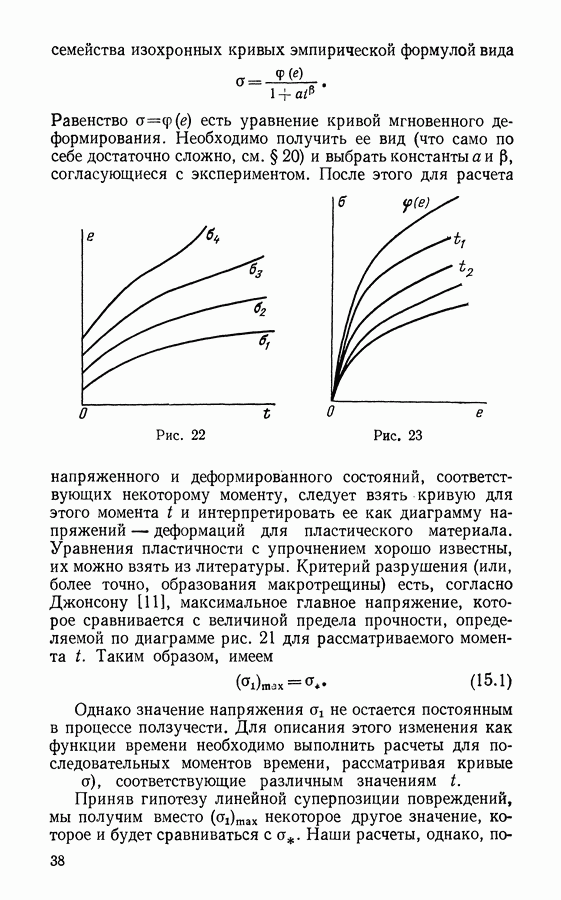
- Глава 4. ЛИНЕЙНАЯ И НЕЛИНЕЙНАЯ НАСЛЕДСТВЕННОСТЬ
- § 18. Наследственная упругость. Линейная теория
- § 19. Задача о росте трещины
- § 20. Нелинейная наследственность
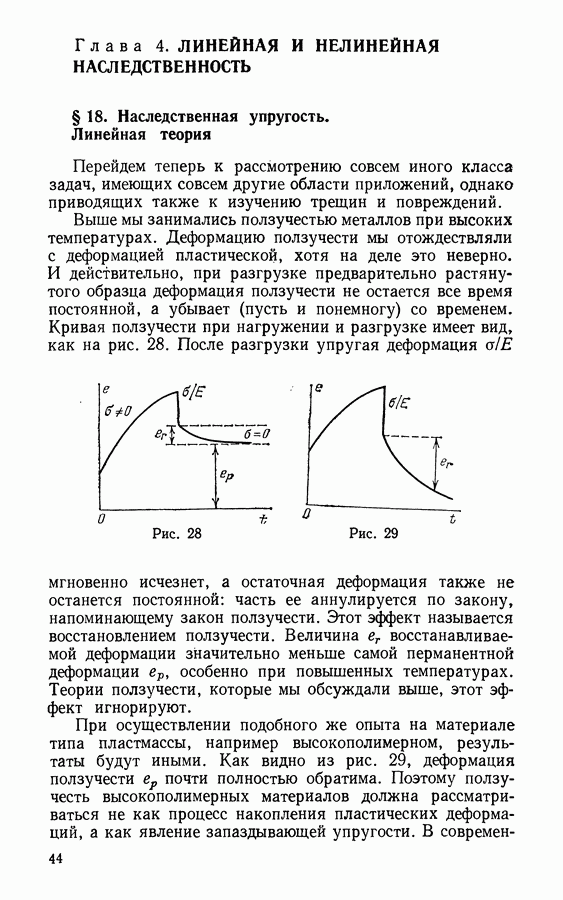
- Глава 5. МЕХАНИКА КОМПОЗИТНЫХ МАТЕРИАЛОВ
- § 21. Композиты волокнистого строения
- § 22. Слоистые упругие композиты
- § 23. Предельное состояние пластической композитной структуры
- § 24. Прочность слоистых композитов
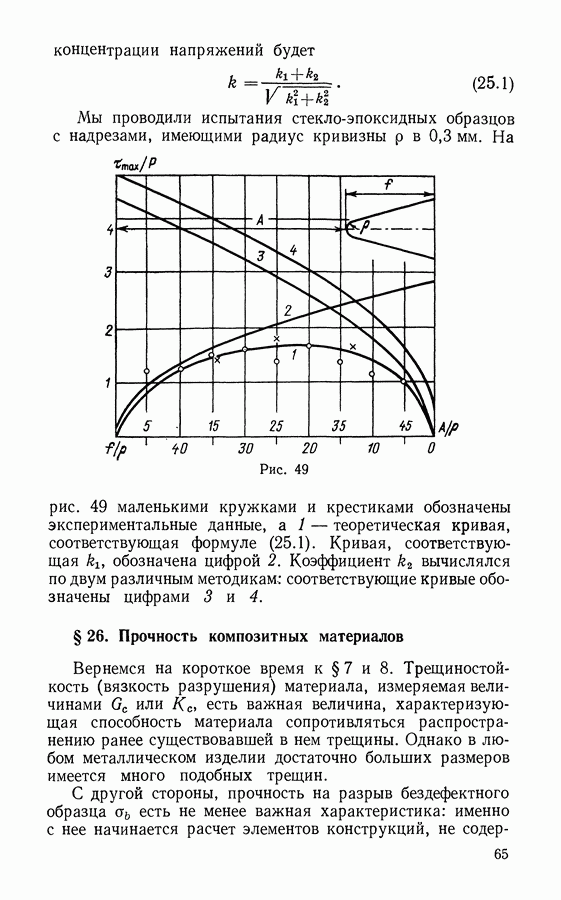
- § 25. Концентрация напряжений в композитах
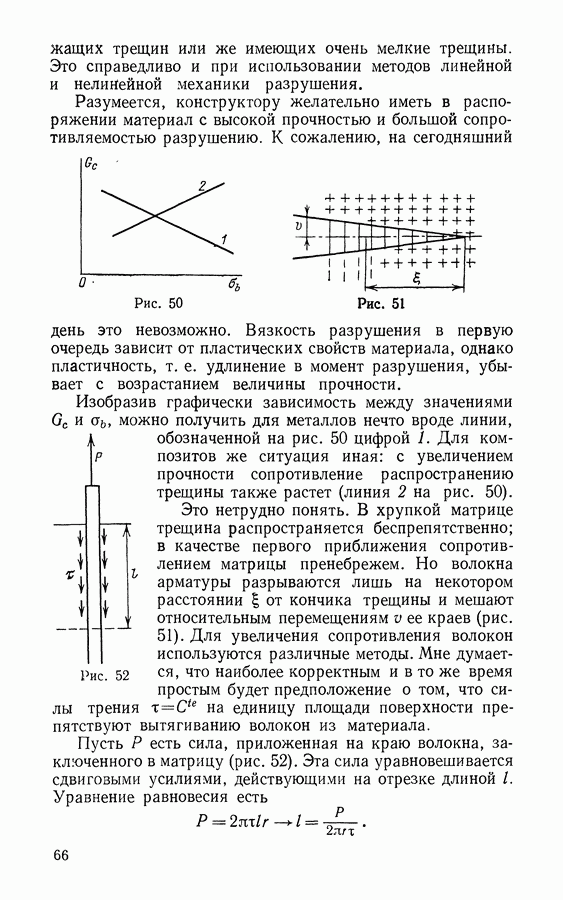
- § 26. Прочность композитных материалов
- ЗАКЛЮЧЕНИЕ