| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
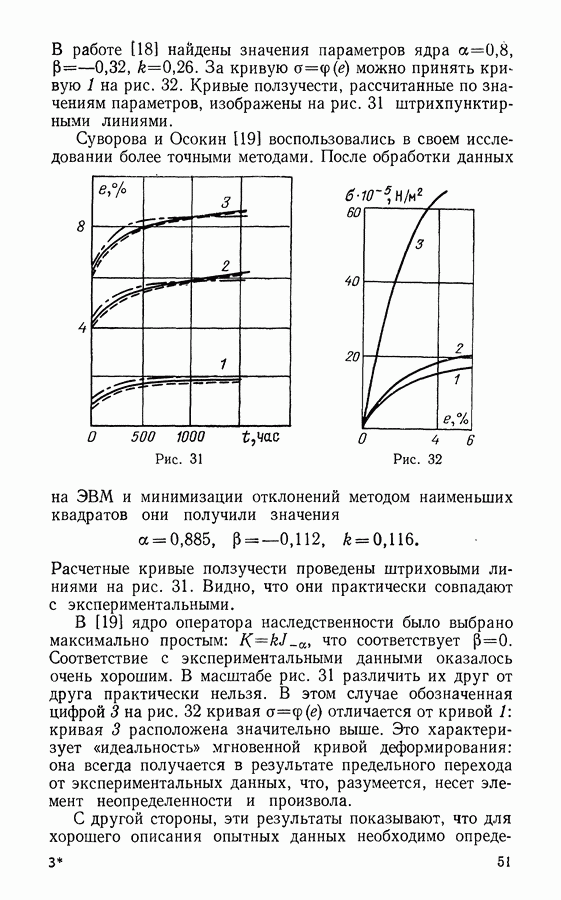
§ 10. Интеграл Райса — Черепанова
Пусть  есть плотность упругой энергии, зависящая от компонент тензора деформаций Утверждается, что интеграл
есть плотность упругой энергии, зависящая от компонент тензора деформаций Утверждается, что интеграл

(где  ) не зависит от пути интегрирования между точками
) не зависит от пути интегрирования между точками  и В 191.
и В 191.
Для доказательства необходимо показать, что этот интеграл обращается в нуль для любого замкнутого пути. С другой стороны, можно доказать, что если  взяты на разных сторонах трещины, то
взяты на разных сторонах трещины, то

Полная упругая энергия, содержащаяся в области 5 с границей  будет
будет

Пусть конец трещины продвинулся на расстояние А. Сила сопротивления оказывается равной  контур
контур  заменяется
заменяется  перемещения и становятся равными
перемещения и становятся равными  Заменив текущую координату
Заменив текущую координату  на
на  запишем (см. рис. 14)
запишем (см. рис. 14)

Рассматривая  как функцию А, получим
как функцию А, получим

что ведет к равенству (10.2), справедливому не только в случае упругого тела, подчиняющегося закону Гука, но и для любой среды, допускающей потенциал напряжений, т. е. функцию  такую, что
такую, что


Рис. 14
Такого рода зависимости лежат в основе теории пластичности Генки — Надаи, и концепция интеграла  может быть использована при наличии вблизи кончика трещины пластической зоны. Следует отметить, что теория Генки — Надаи справедлива с некоторой степенью приближения. Например, если материал в пластической зоне подчиняется закону теории пластического течения, то формула (10.2) становится, вообще говоря, неверной. То же самое происходит в случае движущейся трещины, так как за пластической зоной происходит разгрузка материала.
может быть использована при наличии вблизи кончика трещины пластической зоны. Следует отметить, что теория Генки — Надаи справедлива с некоторой степенью приближения. Например, если материал в пластической зоне подчиняется закону теории пластического течения, то формула (10.2) становится, вообще говоря, неверной. То же самое происходит в случае движущейся трещины, так как за пластической зоной происходит разгрузка материала.
Рассмотрим теперь два простых случая, иллюстрирующих прихменение формулы (10.2).
1. Закон упругости (или пластичности) вида

(Это уравнение, разумеется, может быть записано в тензорном виде — если учесть основные факторы, влияющие на поведение материала. Однако для нашей цели лишь показатель экспоненты а представляет интерес.)
Пусть деформация есть функция пространственной координаты  вида
вида

Тогда плотность упругой энергии есть (с точностью до множителя)

Для существования интеграла (10.1) необходимо, чтобы

или

В случае линейно-упругого тела имеем и особенности для деформации и напряжения будут одного типа, т. е. для малых 
В предельном случае материала без упрочнения имеем

Напряжение останется конечным, а деформация имеет сильную особенность, типа  для малых
для малых 
2. Раскрытие трещины  Мы возвращаемся к теории, представленной в § 9, и хотим рассчитать раскрытие трещины в точках
Мы возвращаемся к теории, представленной в § 9, и хотим рассчитать раскрытие трещины в точках 

Рис. 15
Пусть  где индексы + и — обозначают два берега трещины.
где индексы + и — обозначают два берега трещины.
Выбрав путь интегрирования, как на рис. 15, получим  и далее
и далее

Это можно записать и в виде

Структура этой формулы вытекает из анализа размерностей (как это было и в случае (8.2)).
В общем случае справедливо

где параметр  может быть рассчитан для реальной пластической зоны (необязательно для модели Леонова — Панасюка). Началу продвижения трещины соответствует критическое раскрытие трещины
может быть рассчитан для реальной пластической зоны (необязательно для модели Леонова — Панасюка). Началу продвижения трещины соответствует критическое раскрытие трещины  (в англо-американской терминологии:
(в англо-американской терминологии:  перемещение при раскрытии трещины). Для определения критического значения К, т. е.
перемещение при раскрытии трещины). Для определения критического значения К, т. е.  необходимо измерить
необходимо измерить  в момент начала движения трещины, что делается с помощью выражения, аналогичного (10.5).
в момент начала движения трещины, что делается с помощью выражения, аналогичного (10.5).
В большинстве практических случаев можно считать, что величина  пластической зоны имеет тот же порядок, что и толщина пластины. Отметим, что интегрирование соответствующей трехмерной задачи не может дать напряженного состояния в кончике трещины. Поэтому обычно
пластической зоны имеет тот же порядок, что и толщина пластины. Отметим, что интегрирование соответствующей трехмерной задачи не может дать напряженного состояния в кончике трещины. Поэтому обычно  определяется экспериментальным путем. При этом, естественно, результат зависит от формы образца и от условий опыта.
определяется экспериментальным путем. При этом, естественно, результат зависит от формы образца и от условий опыта.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- Глава 1. ОСНОВНЫЕ ПОНЯТИЯ
- § 1. Твердое тело
- § 2. Уравнения состояния
- § 3. Ползучесть, усталость, пластичность
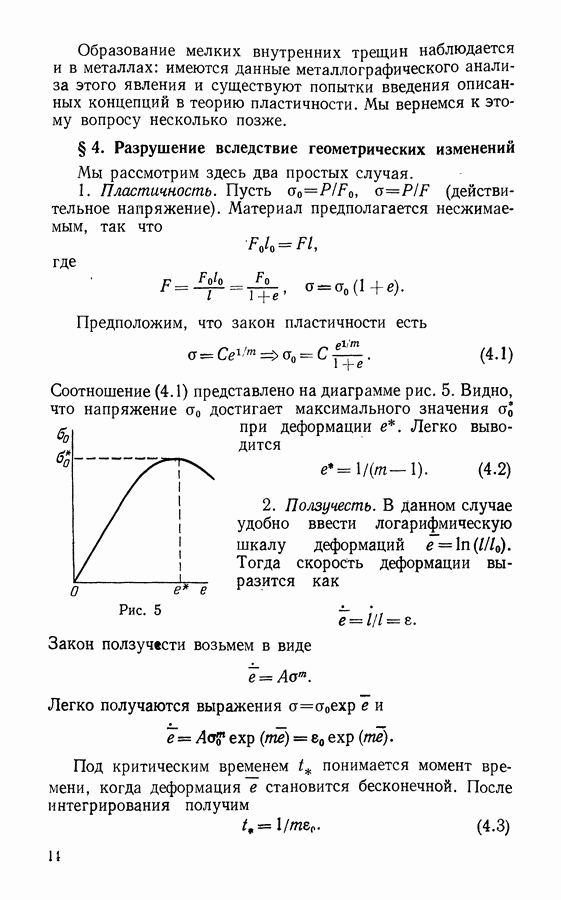
- § 4. Разрушение вследствие геометрических изменений
- Глава 2. МЕХАНИКА РАСПРОСТРАНЕНИЯ ТРЕЩИН
- § 5. Теория Гриффитса
- § 6. Антиплоская деформация
- § 7. Работа продвижения трещины
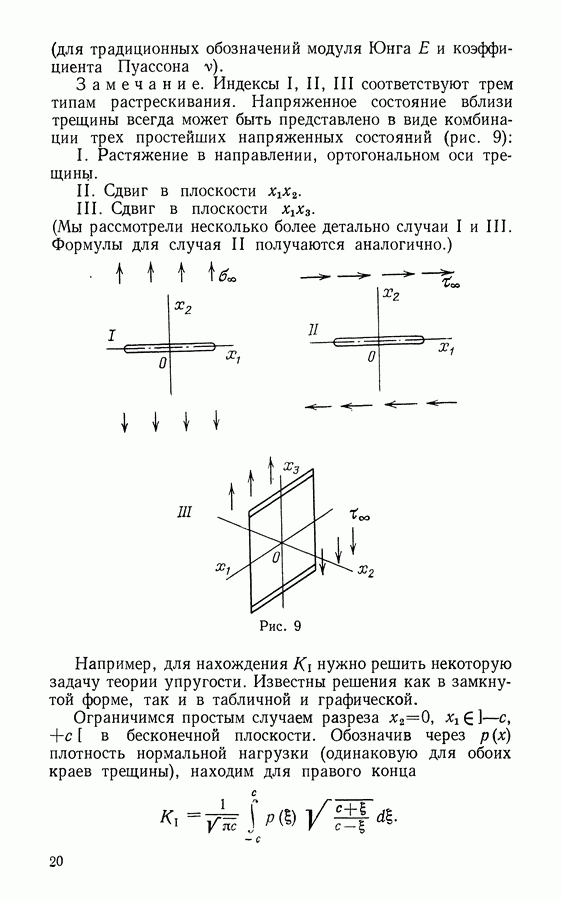
- § 8. Плоская деформация
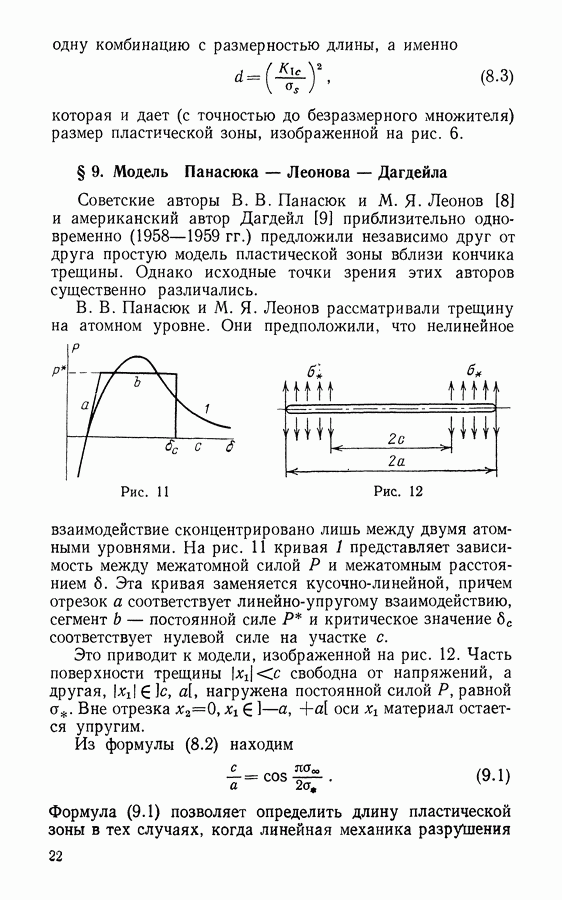
- § 9. Модель Панасюка — Леонова — Дагдейла
- § 10. Интеграл Райса — Черепанова
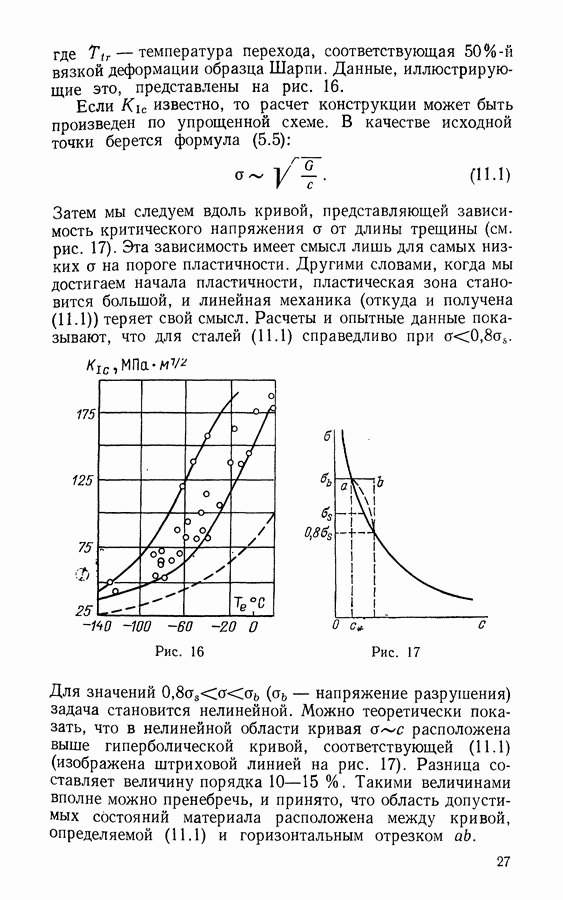
- § 11. Выводы главы 2
- Глава 3. ПОЛЗУЧЕСТЬ И РАЗРУШЕНИЕ МЕТАЛЛОВ ПРИ ВЫСОКИХ ТЕМПЕРАТУРАХ
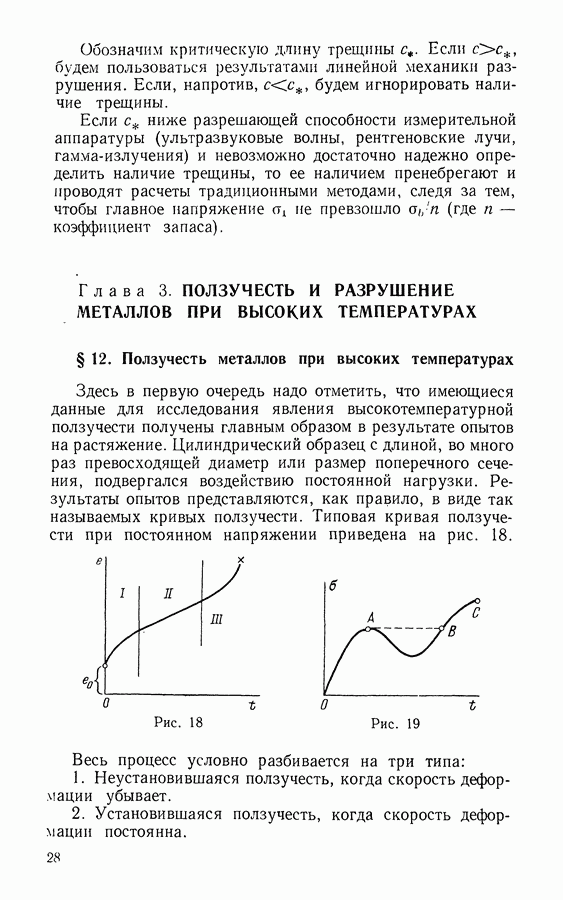
- § 12. Ползучесть металлов при высоких температурах
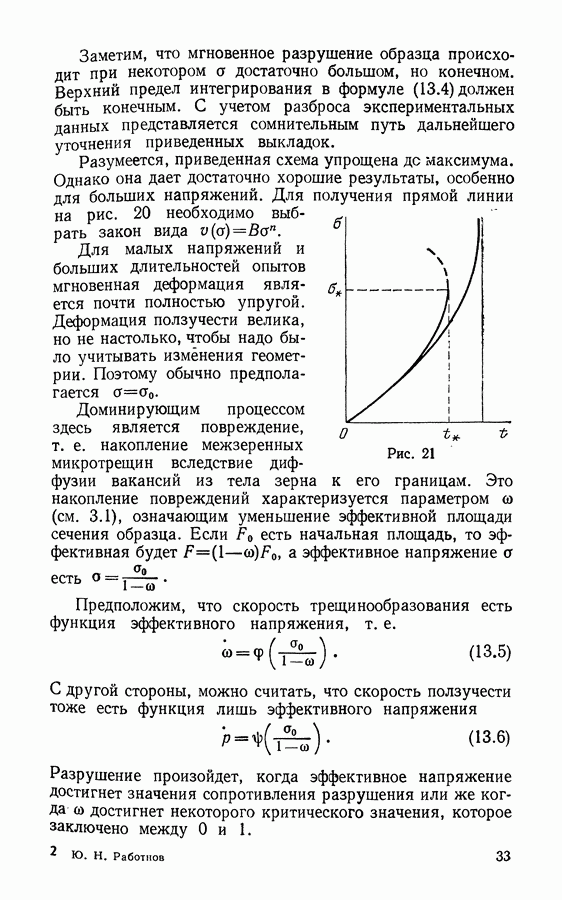
- § 13. Разрушение при растяжении
- § 14. Сложное напряженное состояние
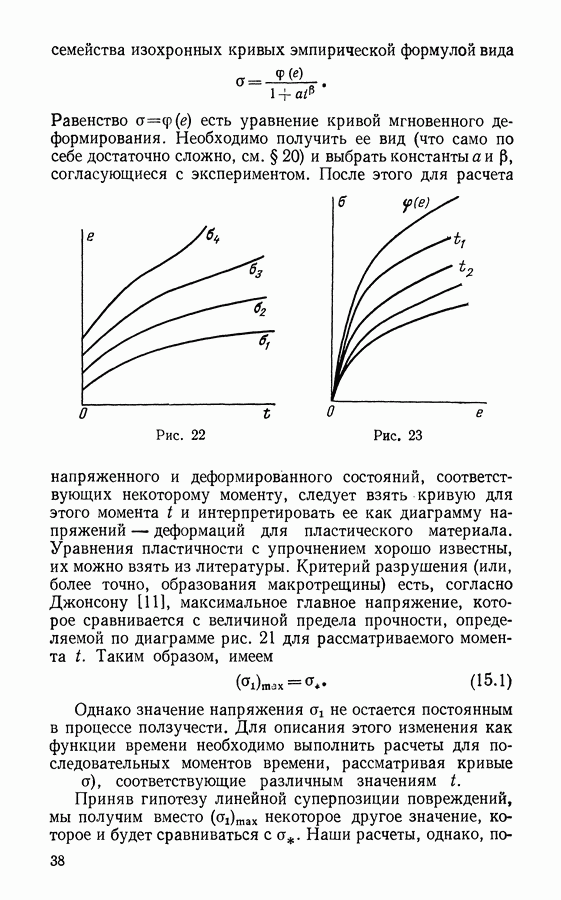
- § 15. Техническая теория. Изохронные кривые ползучести
- § 16. Разрушение при кратковременной ползучести
- § 17. Концентрация напряжений
- Глава 4. ЛИНЕЙНАЯ И НЕЛИНЕЙНАЯ НАСЛЕДСТВЕННОСТЬ
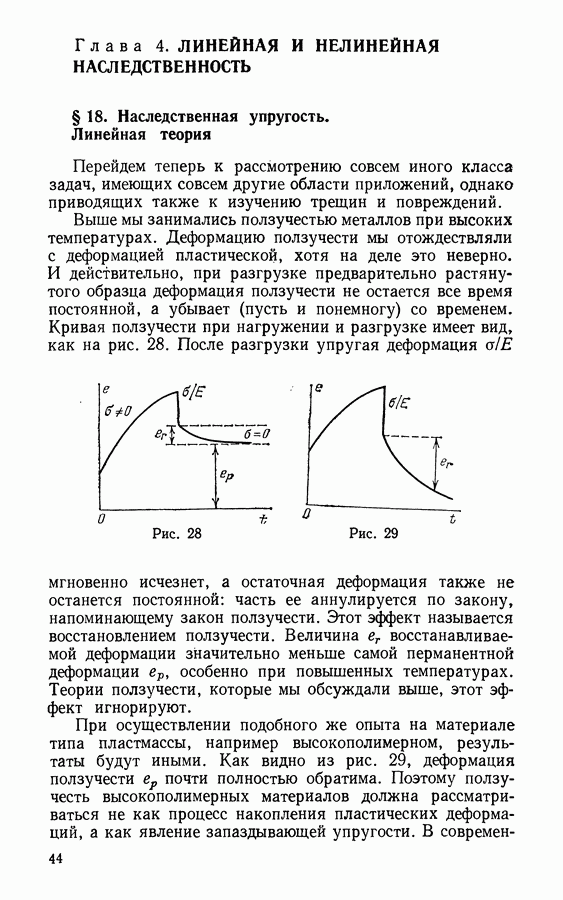
- § 18. Наследственная упругость. Линейная теория
- § 19. Задача о росте трещины
- § 20. Нелинейная наследственность
- Глава 5. МЕХАНИКА КОМПОЗИТНЫХ МАТЕРИАЛОВ
- § 21. Композиты волокнистого строения
- § 22. Слоистые упругие композиты
- § 23. Предельное состояние пластической композитной структуры
- § 24. Прочность слоистых композитов
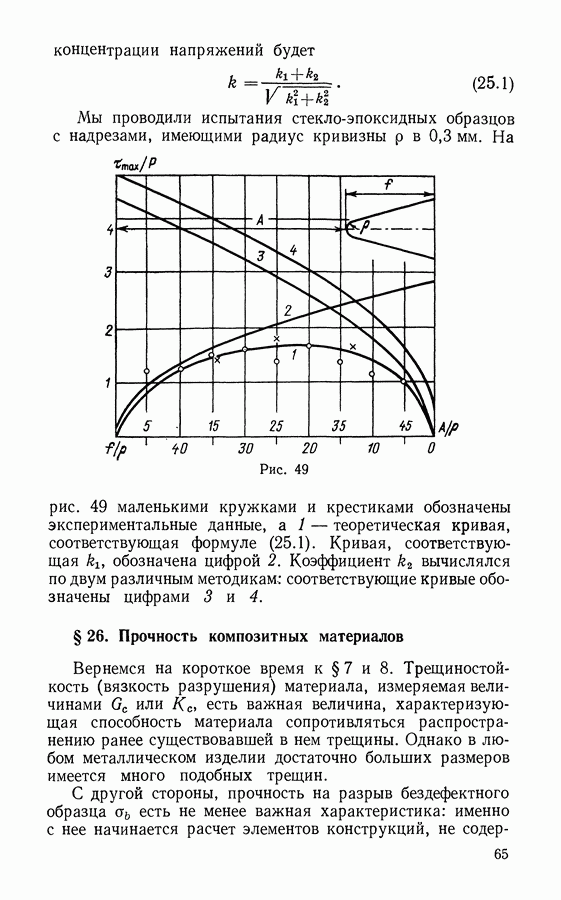
- § 25. Концентрация напряжений в композитах
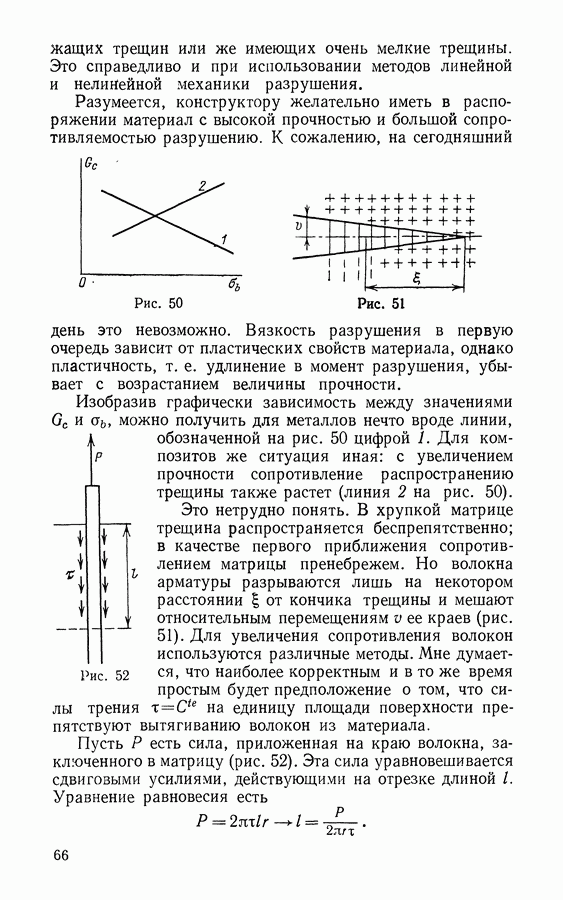
- § 26. Прочность композитных материалов
- ЗАКЛЮЧЕНИЕ