| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Глава 4. ЛИНЕЙНАЯ И НЕЛИНЕЙНАЯ НАСЛЕДСТВЕННОСТЬ
§ 18. Наследственная упругость. Линейная теория
Перейдем теперь к рассмотрению совсем иного класса задач, имеющих совсем другие области приложений, однако приводящих также к изучению трещин и повреждений.
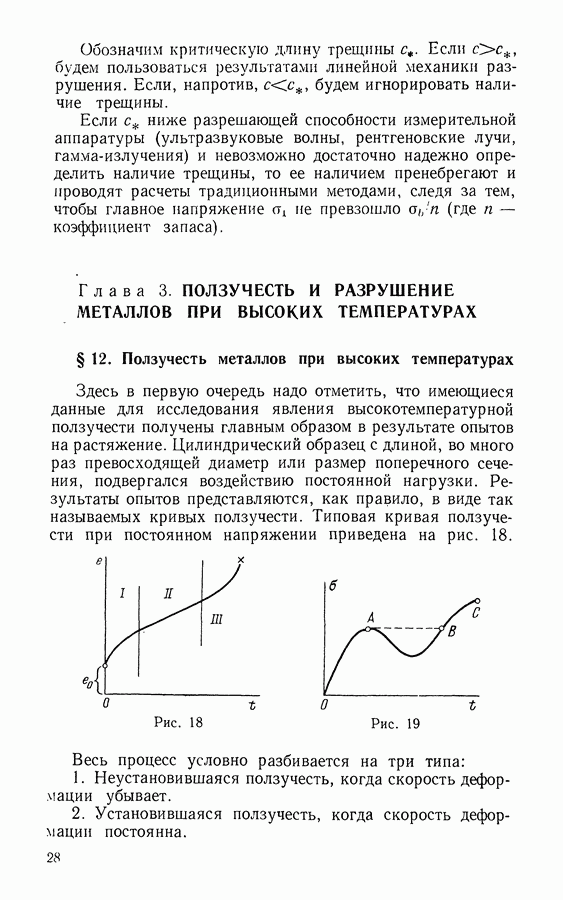
Выше мы занимались ползучестью металлов при высоких температурах. Деформацию ползучести мы отождествляли с деформацией пластической, хотя на деле это неверно. И действительно, при разгрузке предварительно растянутого образца деформация ползучести не остается все время постоянной, а убывает (пусть и понемногу) со временем. Кривая ползучести при нагружении и разгрузке имеет вид, как на рис. 28.

Рис. 28

Рис. 29
После разгрузки упругая деформация  мгновенно исчезнет, а остаточная деформация также не останется постоянной: часть ее аннулируется по закону, напоминающему закон ползучести. Этот эффект называется восстановлением ползучести. Величина
мгновенно исчезнет, а остаточная деформация также не останется постоянной: часть ее аннулируется по закону, напоминающему закон ползучести. Этот эффект называется восстановлением ползучести. Величина  восстанавливаемой деформации значительно меньше самой перманентной деформации
восстанавливаемой деформации значительно меньше самой перманентной деформации  особенно при повышенных температурах. Теории ползучести, которые мы обсуждали выше, этот эффект игнорируют.
особенно при повышенных температурах. Теории ползучести, которые мы обсуждали выше, этот эффект игнорируют.
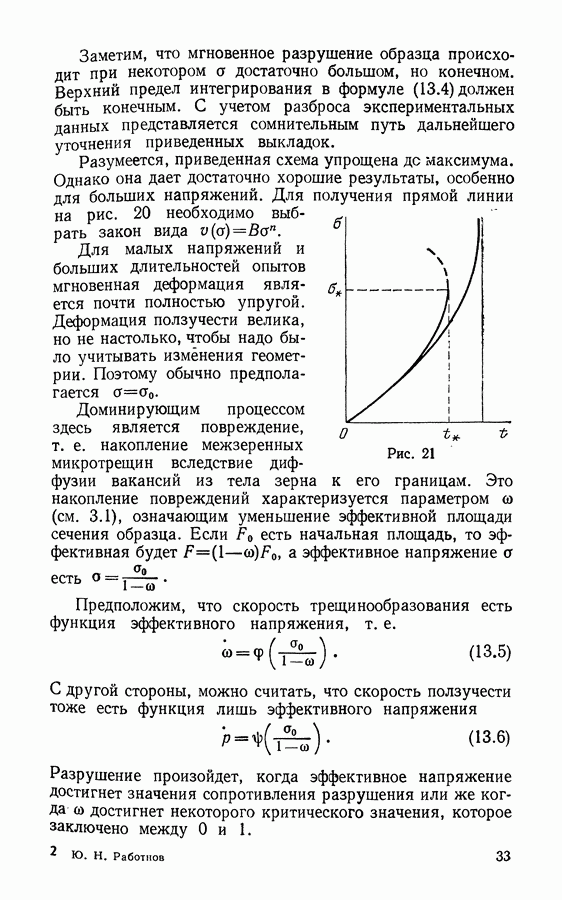
При осуществлении подобного же опыта на материале типа пластмассы, например высокополимерном, результаты будут иными. Как видно из рис. 29, деформация ползучести  почти полностью обратима. Поэтому ползучесть высокополимерных материалов должна рассматриваться не как процесс накопления пластических деформаций, а как явление запаздывающей упругости. В
почти полностью обратима. Поэтому ползучесть высокополимерных материалов должна рассматриваться не как процесс накопления пластических деформаций, а как явление запаздывающей упругости. В
современной литературе этот класс явлений называют вязко-упругостью. Но предпочтительней является термин, введенный Вито Вольтерра: наследственная упругость.
В рамках линейной теории определяющее соотношение наследственной теории запишется в виде

где К есть оператор Вольтерра, определяемый как

Если из (18.1) определять а, то в момент 

где  есть резольвентный оператор, соответствующий
есть резольвентный оператор, соответствующий
Раскладывая выражение  в формальный ряд (аналогично разложению
в формальный ряд (аналогично разложению  при
при  проблема сходимости требует специального изучения), получим ряд Неймана для резольвенты уравнения Вольтерра.
проблема сходимости требует специального изучения), получим ряд Неймана для резольвенты уравнения Вольтерра.
Для уточнения возможностей оперирования с ядром К была построена алгебра операторов, используемых в теории Вольтерра.
Отметим важное тождество [14]

(с особенностью при  Оно используется при решении всех уравнений вида
Оно используется при решении всех уравнений вида

Можно сказать, что любой такой оператор К порождает семейство операторов зависящих от одного параметра к,
В приложениях уравнение Вольтерра тесно связано с оператором Абеля (назовем его  ), определяемым как
), определяемым как

(где  есть гамма-функция Эйлера). Назовем такие операторы экспоненциальными операторами с индексом а
есть гамма-функция Эйлера). Назовем такие операторы экспоненциальными операторами с индексом а
и запишем

Мы берем а из области а  что как раз соответствует практическим случаям. Ядро этого оператора имеет слабую особенность (характеризуемую как при
что как раз соответствует практическим случаям. Ядро этого оператора имеет слабую особенность (характеризуемую как при  стремится к
стремится к  при
при  (если выполняется
(если выполняется  ).
).
В этих условиях можно воспользоваться принципом соответствия, сформулированным Вольтерра. Он состоит в том, что для решения любой задачи наследственной упругости следует решить прежде всего аналогичную задачу классической упругости. В решении будут содержаться различные комбинации упругих постоянных, причем в виде рациональных выражений. Тогда, если операторы, описывающие свойства материала, принадлежат к указанному классу операторов  то можно использовать (18,2) для расшифровки результата, заменив в нем упругие постоянные на операторы. Ситуация слегка осложняется, если упругие константы входят в решение не в алгебраическом виде. Следует отметить, что применение к интегральному уравнению Вольтерра преобразования Лапласа приводит к тем же результатам.
то можно использовать (18,2) для расшифровки результата, заменив в нем упругие постоянные на операторы. Ситуация слегка осложняется, если упругие константы входят в решение не в алгебраическом виде. Следует отметить, что применение к интегральному уравнению Вольтерра преобразования Лапласа приводит к тем же результатам.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- Глава 1. ОСНОВНЫЕ ПОНЯТИЯ
- § 1. Твердое тело
- § 2. Уравнения состояния
- § 3. Ползучесть, усталость, пластичность
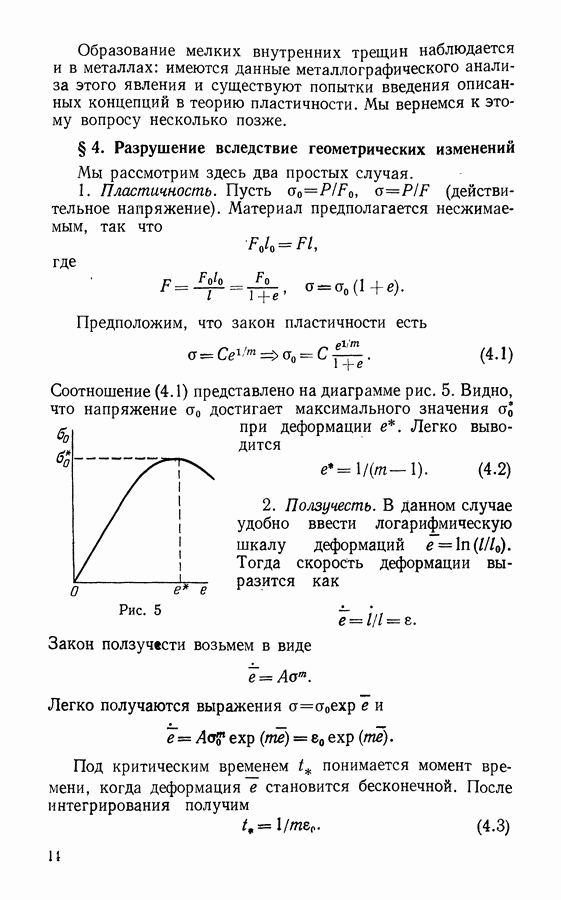
- § 4. Разрушение вследствие геометрических изменений
- Глава 2. МЕХАНИКА РАСПРОСТРАНЕНИЯ ТРЕЩИН
- § 5. Теория Гриффитса
- § 6. Антиплоская деформация
- § 7. Работа продвижения трещины
- § 8. Плоская деформация
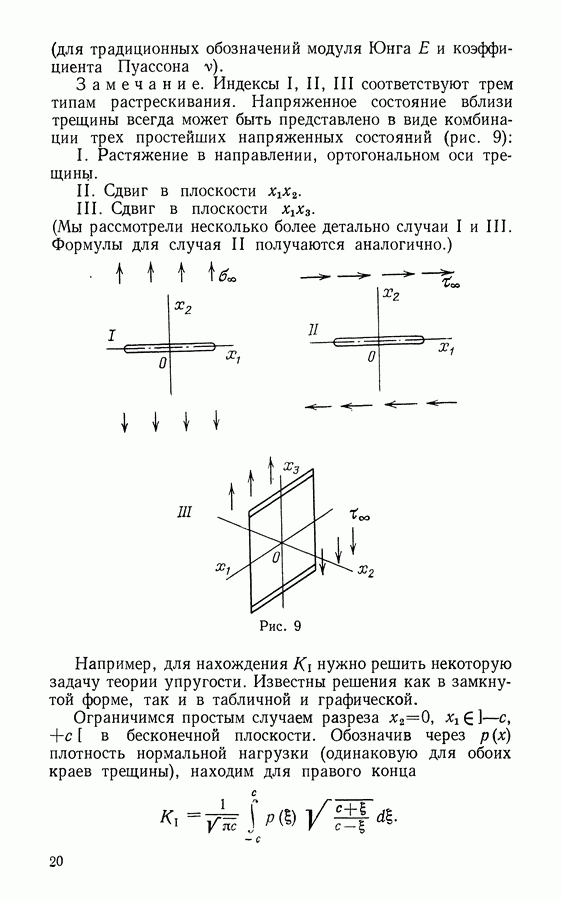
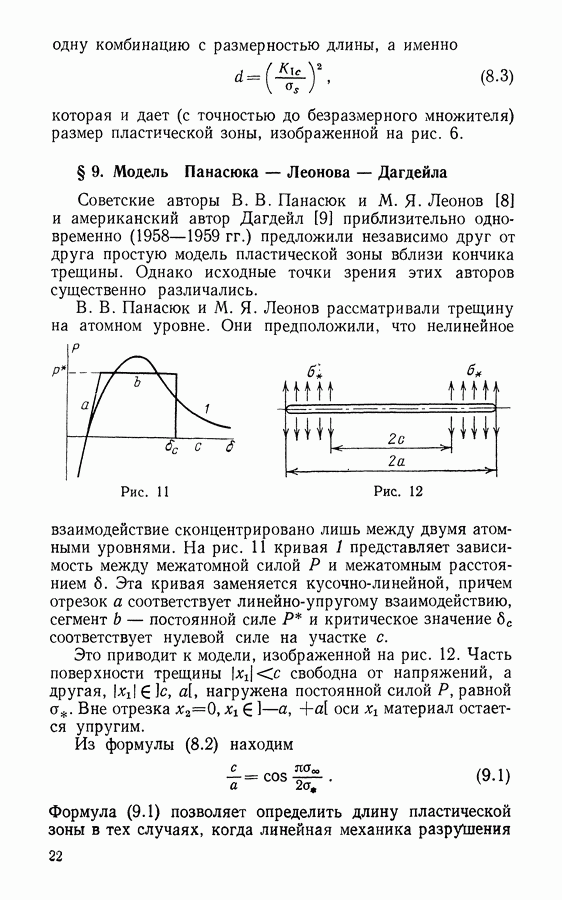
- § 9. Модель Панасюка — Леонова — Дагдейла
- § 10. Интеграл Райса — Черепанова
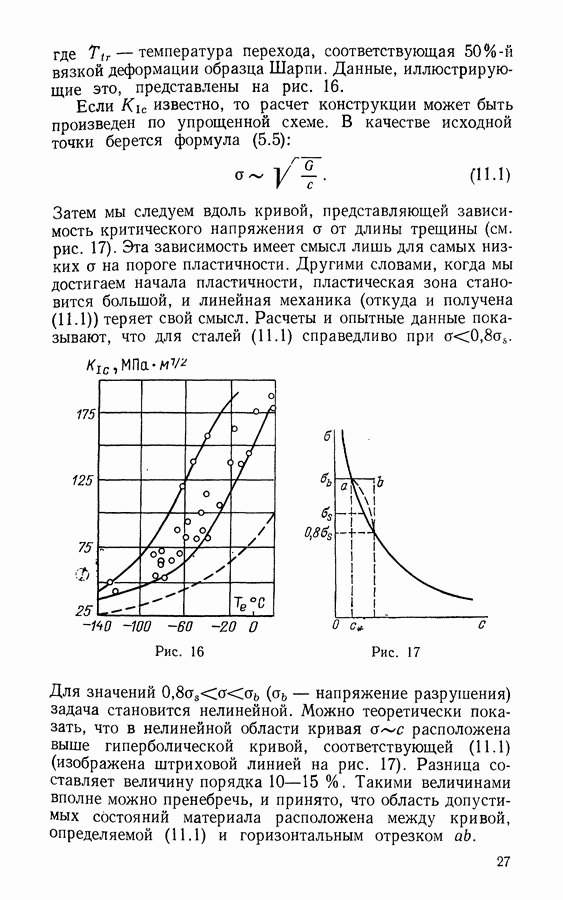
- § 11. Выводы главы 2
- Глава 3. ПОЛЗУЧЕСТЬ И РАЗРУШЕНИЕ МЕТАЛЛОВ ПРИ ВЫСОКИХ ТЕМПЕРАТУРАХ
- § 12. Ползучесть металлов при высоких температурах
- § 13. Разрушение при растяжении
- § 14. Сложное напряженное состояние
- § 15. Техническая теория. Изохронные кривые ползучести
- § 16. Разрушение при кратковременной ползучести
- § 17. Концентрация напряжений
- Глава 4. ЛИНЕЙНАЯ И НЕЛИНЕЙНАЯ НАСЛЕДСТВЕННОСТЬ
- § 18. Наследственная упругость. Линейная теория
- § 19. Задача о росте трещины
- § 20. Нелинейная наследственность
- Глава 5. МЕХАНИКА КОМПОЗИТНЫХ МАТЕРИАЛОВ
- § 21. Композиты волокнистого строения
- § 22. Слоистые упругие композиты
- § 23. Предельное состояние пластической композитной структуры
- § 24. Прочность слоистых композитов
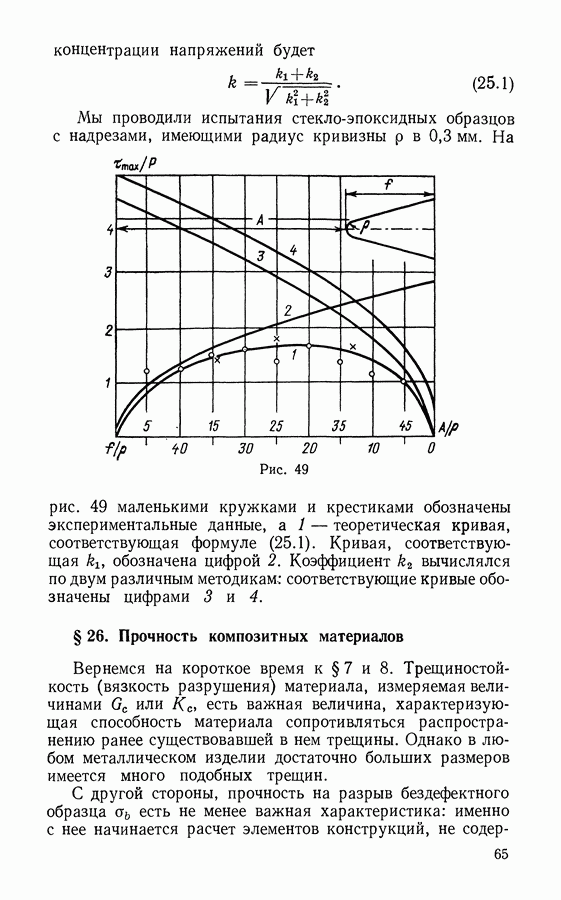
- § 25. Концентрация напряжений в композитах
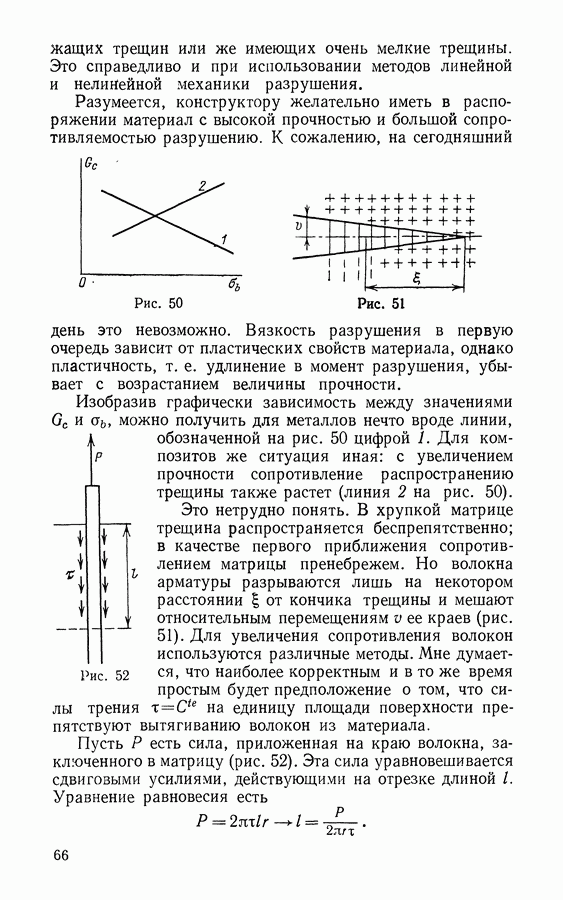
- § 26. Прочность композитных материалов
- ЗАКЛЮЧЕНИЕ