| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
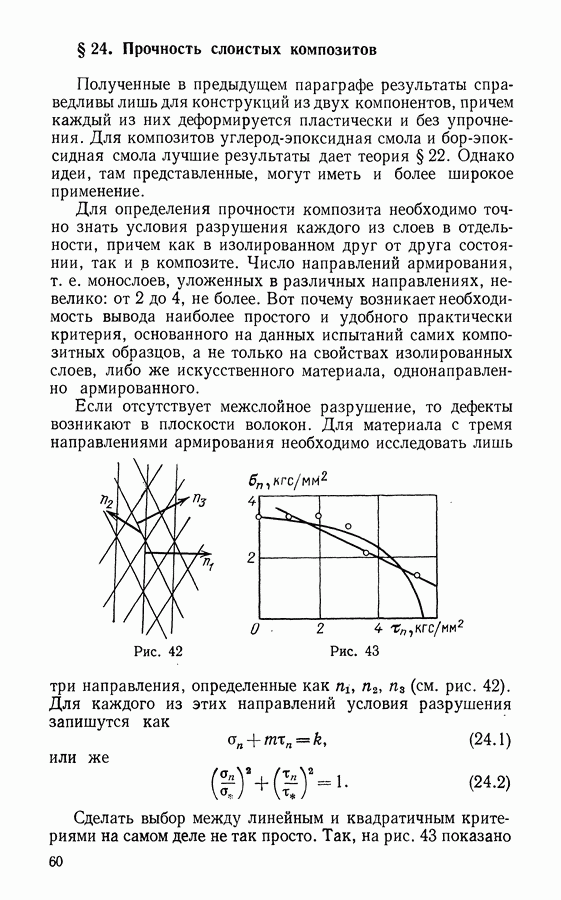
§ 13. Разрушение при растяжении
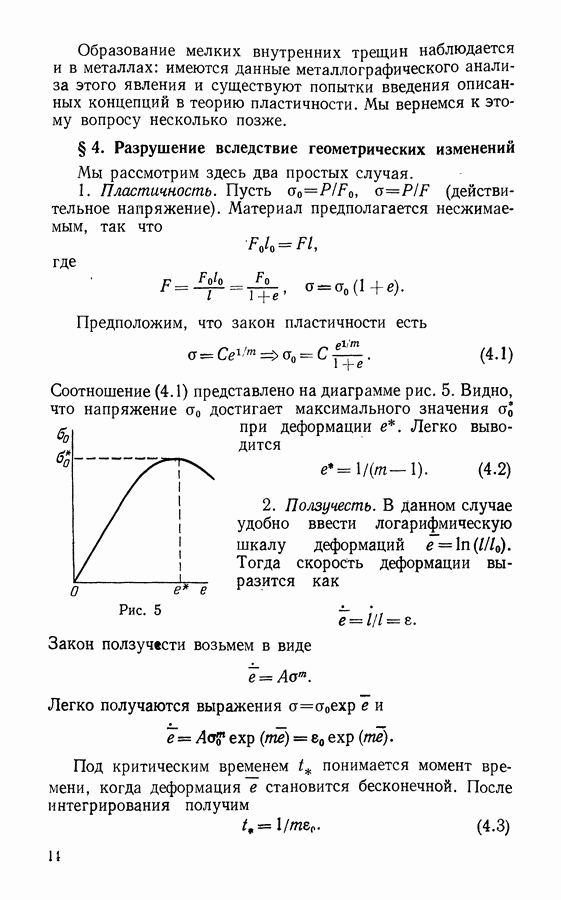
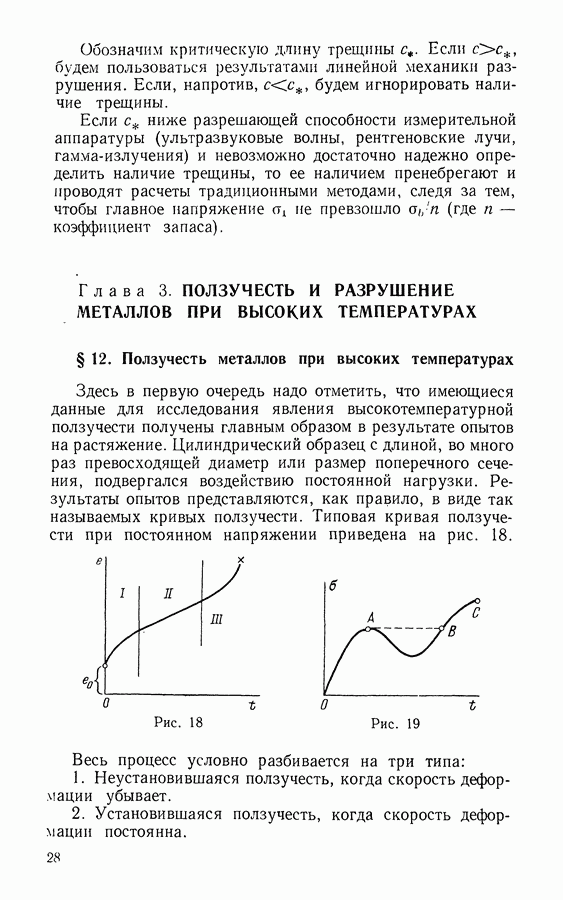
Маленький крестик на кривой ползучести (см. рис. 18) соответствует моменту разрушения образца. Деформация  в момент разрушения может быть как большой, так и малой — это зависит от материала, условий эксперимента, температуры, величины нагрузки.
в момент разрушения может быть как большой, так и малой — это зависит от материала, условий эксперимента, температуры, величины нагрузки.
Отбросив в сторону эти аспекты (мало изученные в общей постановке), рассмотрим экспериментальную
программу исследования величины сопротивления материала как функции времени. Пусть некоторое число идентичных образцов подвергается в течение длительного времени нагружению напряжениями растяжения  различной величины, и в каждом случае измеряется время до разрушения
различной величины, и в каждом случае измеряется время до разрушения  На плоскости
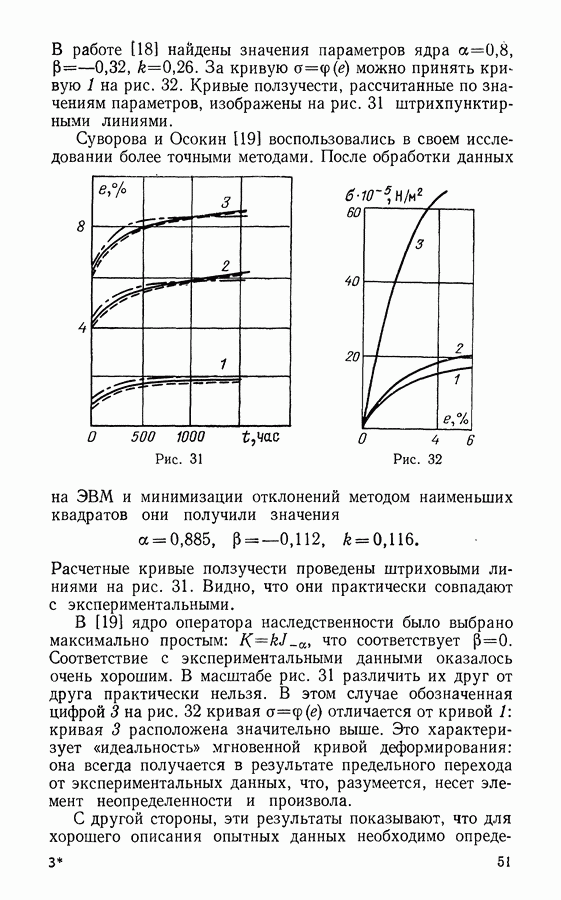
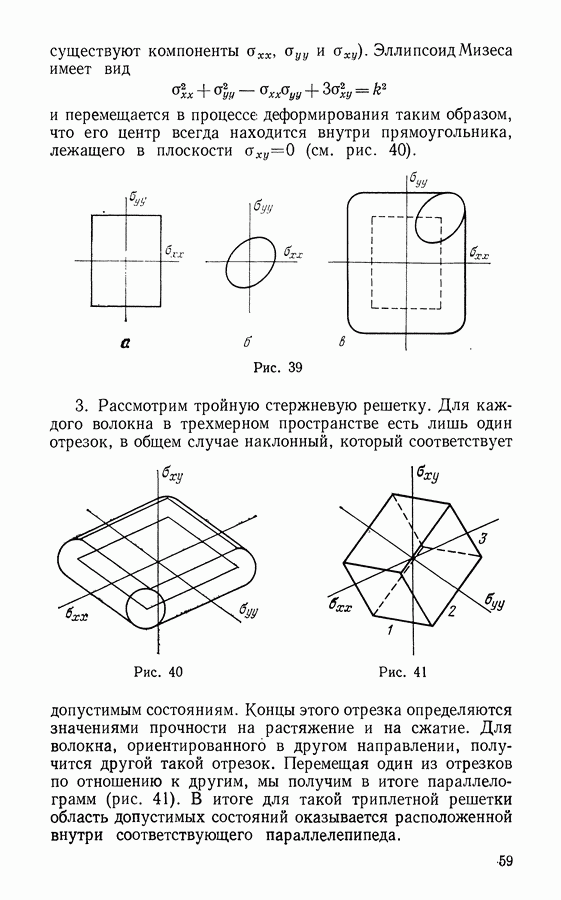
На плоскости  можно, таким образом, построить кривую, называемую кривой длительной прочности. Удобнее представлять ее в логарифмических координатах, как на рис. 20. Эта кривая состоит из двух почти линейных участков: первый из них (участок 1) соответствует явлению вязкого разрушения, а второй (участок 2) — хрупкого. Измерив полную деформацию после разрушения, можно видеть, что при вязком разрушении удлинение довольно существенно, а при хрупком оно мало.
можно, таким образом, построить кривую, называемую кривой длительной прочности. Удобнее представлять ее в логарифмических координатах, как на рис. 20. Эта кривая состоит из двух почти линейных участков: первый из них (участок 1) соответствует явлению вязкого разрушения, а второй (участок 2) — хрупкого. Измерив полную деформацию после разрушения, можно видеть, что при вязком разрушении удлинение довольно существенно, а при хрупком оно мало.
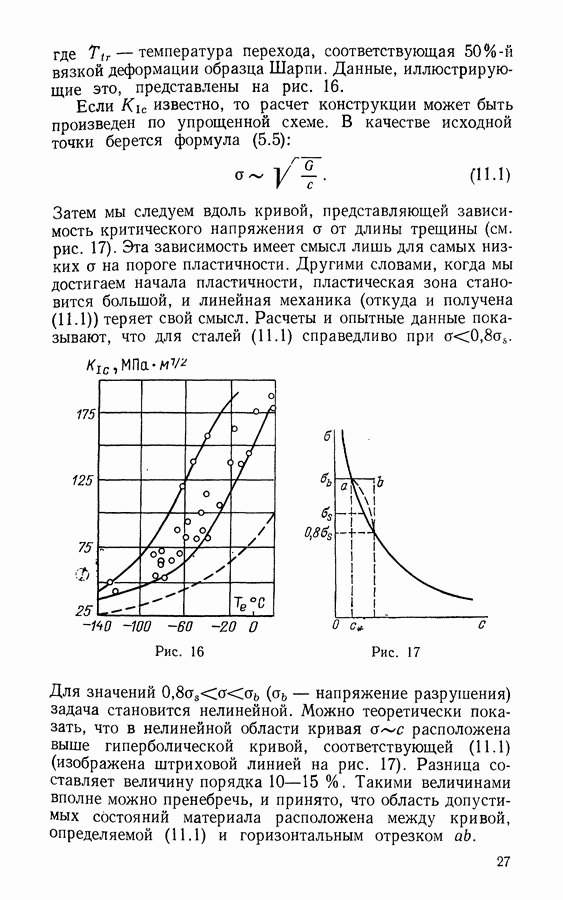
Разумеется, на реальных диаграммах угловая точка должна быть заменена участком плавного перехода.

Рис. 20
Интересные результаты дают опыты на свинцовых образцах при лабораторной температуре. При приложении существенной нагрузки образец ломался за несколько секунд с деформацией порядка  Снижение величины нагрузки в два раза приводило к разрушению за несколько дней, причем к хрупкому, с полной деформацией
Снижение величины нагрузки в два раза приводило к разрушению за несколько дней, причем к хрупкому, с полной деформацией  Это ясно показывает, что в каждом из случаев внутренние механизмы явления различны.
Это ясно показывает, что в каждом из случаев внутренние механизмы явления различны.
Рассмотрим более подробно процесс вязкого разрушения. Вследствие больших деформаций можно пренебречь упругой частью, а также деформацией, накопленной на первом этапе ползучести.
Запишем для скорости деформации

Из-за наличия больших деформаций выберем логарифмический масштаб  для измерения степени деформирования. Таким образом,
для измерения степени деформирования. Таким образом,

Обозначим традиционно через  условное напряжение, т. е. величину силы растяжения, деленную на величину
условное напряжение, т. е. величину силы растяжения, деленную на величину
начальной площади сечения образца (на рис. 20 в качестве координаты использовано  Со). Для реального напряже
Со). Для реального напряже  получим
получим

или, учитывая условие сохранения объема,

Взяв производную по времени, запишем

Внеся  в (13.1), придем к дифференциальному уравнению
в (13.1), придем к дифференциальному уравнению

Если член в скобках равен нулю, то величина о должна быть бесконечной — это мы и примем за наступление разрушения. Таким образом, необходимо найти решение  уравнения
уравнения

После интегрирования, учтя, что  имеем
имеем

В плоскости  это есть кривая, изображенная на рис. 21. Видно, что при
это есть кривая, изображенная на рис. 21. Видно, что при  скорость деформации стремится к бесконечности. Величина 4 называется временем до разрушения.
скорость деформации стремится к бесконечности. Величина 4 называется временем до разрушения.
Если пренебречь мгновенной пластической деформацией, то из (13.3) следует

И значение интеграла остается конечным при отоо. Соответствующая кривая изображена штриховой линией на рис. 21.
Долговечность материала рассчитанная по (13.4) для  будет больше, чем величина
будет больше, чем величина  получающаяся из (13.3) для хотя разница и не так уж велика.
получающаяся из (13.3) для хотя разница и не так уж велика.
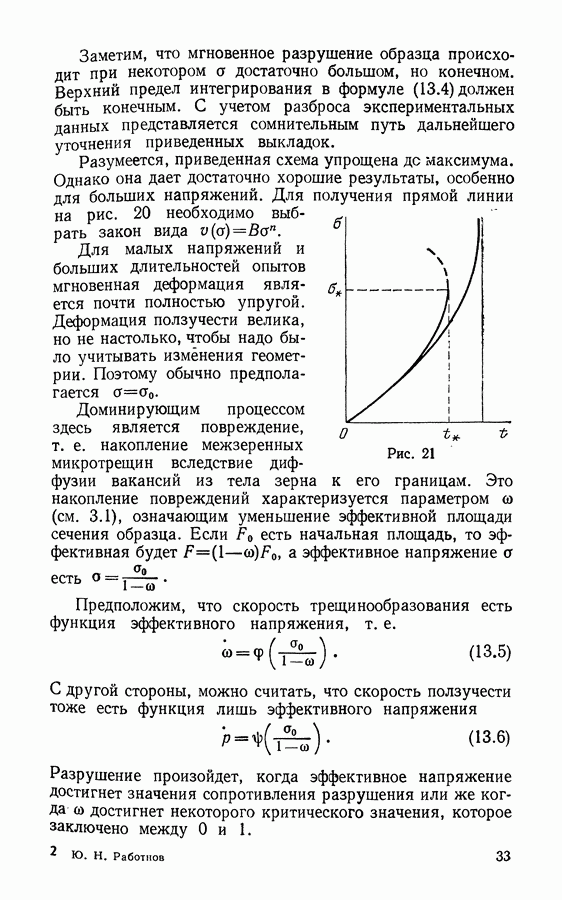
Заметим, что мгновенное разрушение образца происходит при некотором а достаточно большом, но конечном. Верхний предел интегрирования в формуле (13.4) должен быть конечным. С учетом разброса экспериментальных данных представляется сомнительным путь дальнейшего уточнения приведенных выкладок.
Разумеется, приведенная схема упрощена  максимума. Однако она дает достаточно хорошие результаты, особенно для больших напряжений. Для получения прямой линии на рис. 20 необходимо выбрать закон вида
максимума. Однако она дает достаточно хорошие результаты, особенно для больших напряжений. Для получения прямой линии на рис. 20 необходимо выбрать закон вида 
Для малых напряжений и больших длительностей опытов мгновенная деформация является почти полностью упругой. Деформация ползучести велика, но не настолько, чтобы надо было учитывать изменения геометрии. Поэтому обычно предполагается 

Рис. 21
Доминирующим процессом здесь является повреждение, т. е. накопление межзеренных микротрещин вследствие диффузии вакансий из тела зерна к его границам. Это накопление повреждений характеризуется параметром о (см. 3.1), означающим уменьшение эффективной площади сечения образца. Если  есть начальная площадь, то эффективная будет
есть начальная площадь, то эффективная будет  а эффективное напряжение а есть
а эффективное напряжение а есть 
Предположим, что скорость трещинообразования есть функция эффективного напряжения, т. е.

С другой стороны, можно считать, что скорость ползучести тоже есть функция лишь эффективного напряжения

Разрушение произойдет, когда эффективное напряжение достигнет значения сопротивления разрушения или же когда О) достигнет некоторого критического значения, которое заключено между О и 1.
с учетом разброса опытных данных невозможно получить точное значение этой критической точки, и проста предполагают, что в момент отрыва  Выбирая функцию
Выбирая функцию  как
как  можно проинтегрировать (13.5) способом разделения переменных. Интегрируя по со от О до 1, получим оценку времени до разрушения
можно проинтегрировать (13.5) способом разделения переменных. Интегрируя по со от О до 1, получим оценку времени до разрушения

которая соответствует участку 2 прямой в логарифмических координатах (см. рис. 20).
Промежуточная область может рассматриваться как сочетающая влияния растрескивания, значительной деформаций ползучести, а также геометрических изменений площади сечения, которыми уже нельзя пренебречь (см. ссылку [10]).
Выше не учитывался фактор упрочнения. Если же учесть его, то уравнение запишется:

Ограничимся здесь частным случаем, а именно когда функции  в уравнениях (13.5) и (13.6) одинаковы с точностью до постоянного множителя. Тогда
в уравнениях (13.5) и (13.6) одинаковы с точностью до постоянного множителя. Тогда

или

где  деформация в момент разрушения. Тогда уравнение ползучести будет выглядеть как
деформация в момент разрушения. Тогда уравнение ползучести будет выглядеть как

Форма его аналогична форме (12.4) с той разницей, что  во втором члене больше не является параметром упрочнения; это есть упрочнение на первой стадии и растрескивание на третьей.
во втором члене больше не является параметром упрочнения; это есть упрочнение на первой стадии и растрескивание на третьей.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- Глава 1. ОСНОВНЫЕ ПОНЯТИЯ
- § 1. Твердое тело
- § 2. Уравнения состояния
- § 3. Ползучесть, усталость, пластичность
- § 4. Разрушение вследствие геометрических изменений
- Глава 2. МЕХАНИКА РАСПРОСТРАНЕНИЯ ТРЕЩИН
- § 5. Теория Гриффитса
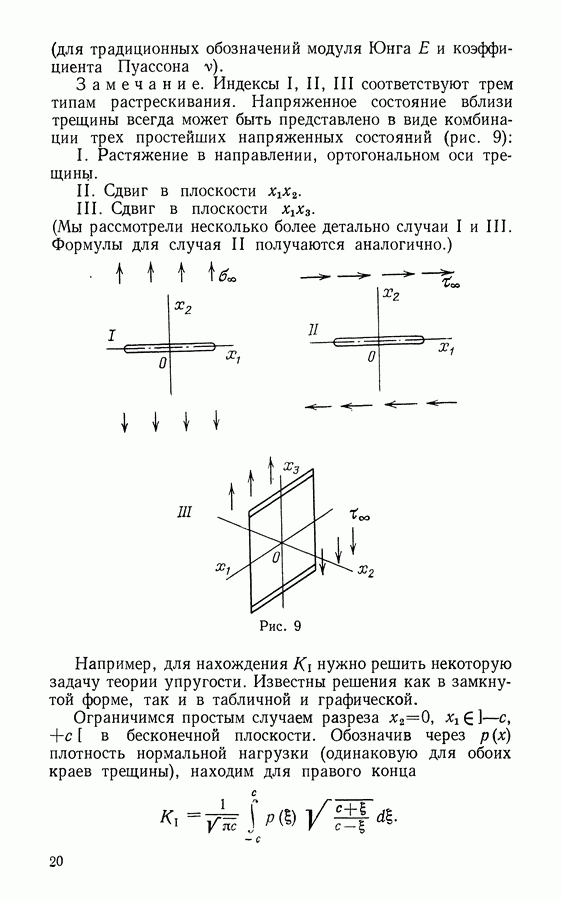
- § 6. Антиплоская деформация
- § 7. Работа продвижения трещины
- § 8. Плоская деформация
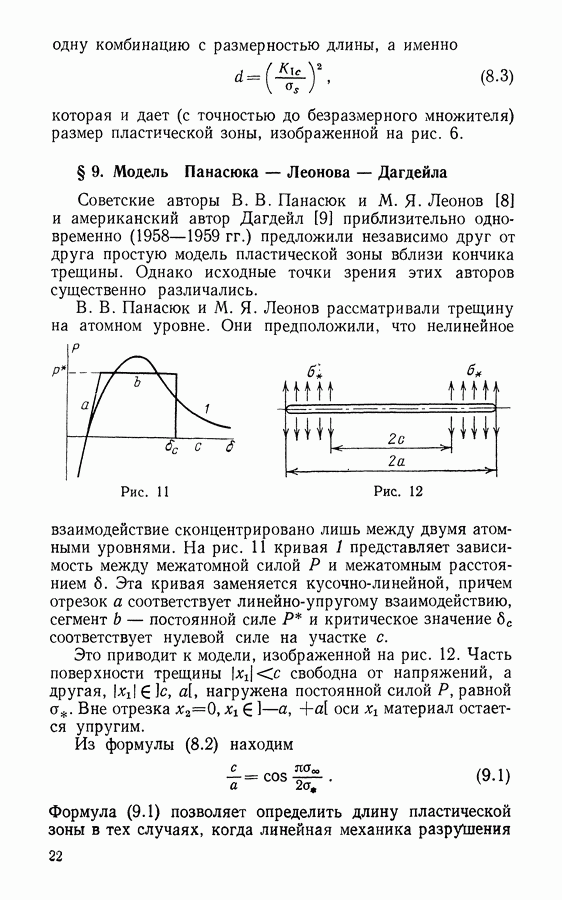
- § 9. Модель Панасюка — Леонова — Дагдейла
- § 10. Интеграл Райса — Черепанова
- § 11. Выводы главы 2
- Глава 3. ПОЛЗУЧЕСТЬ И РАЗРУШЕНИЕ МЕТАЛЛОВ ПРИ ВЫСОКИХ ТЕМПЕРАТУРАХ
- § 12. Ползучесть металлов при высоких температурах
- § 13. Разрушение при растяжении
- § 14. Сложное напряженное состояние
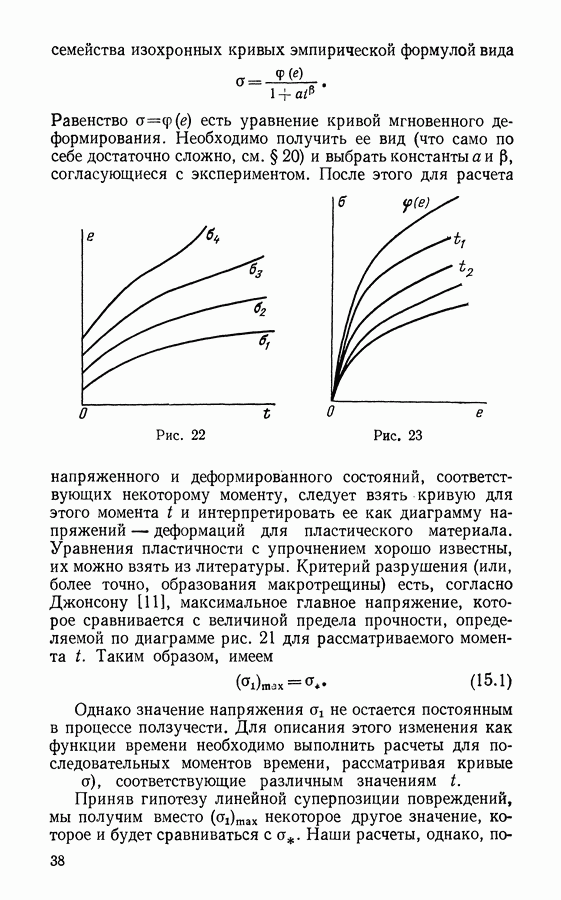
- § 15. Техническая теория. Изохронные кривые ползучести
- § 16. Разрушение при кратковременной ползучести
- § 17. Концентрация напряжений
- Глава 4. ЛИНЕЙНАЯ И НЕЛИНЕЙНАЯ НАСЛЕДСТВЕННОСТЬ
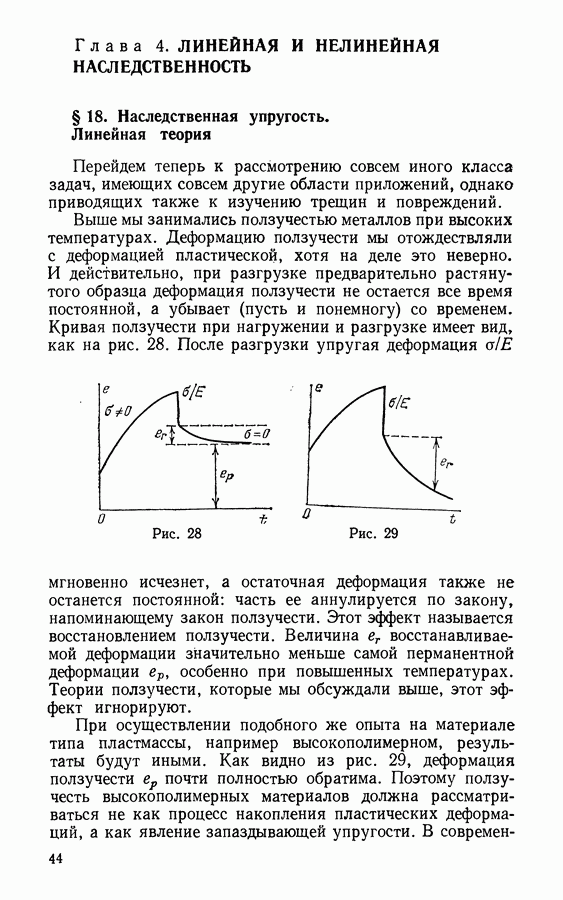
- § 18. Наследственная упругость. Линейная теория
- § 19. Задача о росте трещины
- § 20. Нелинейная наследственность
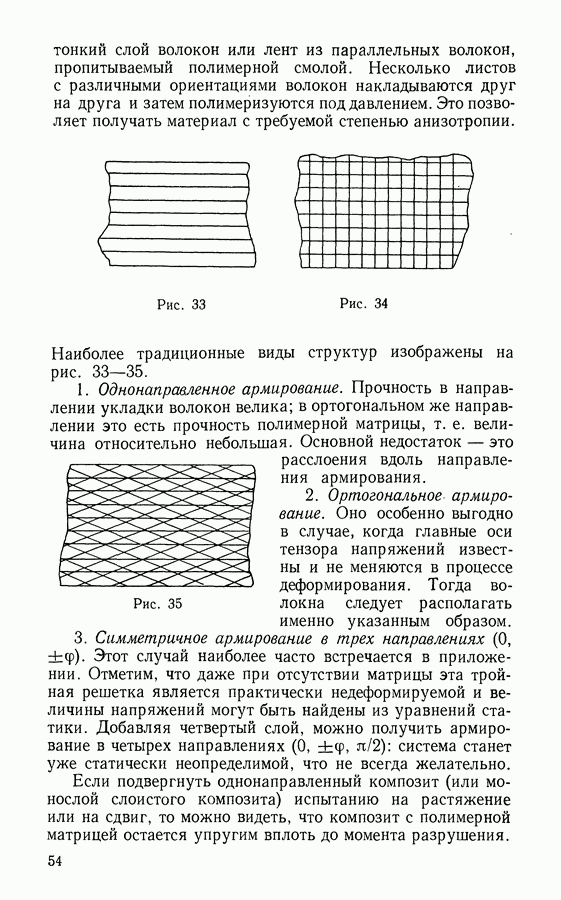
- Глава 5. МЕХАНИКА КОМПОЗИТНЫХ МАТЕРИАЛОВ
- § 21. Композиты волокнистого строения
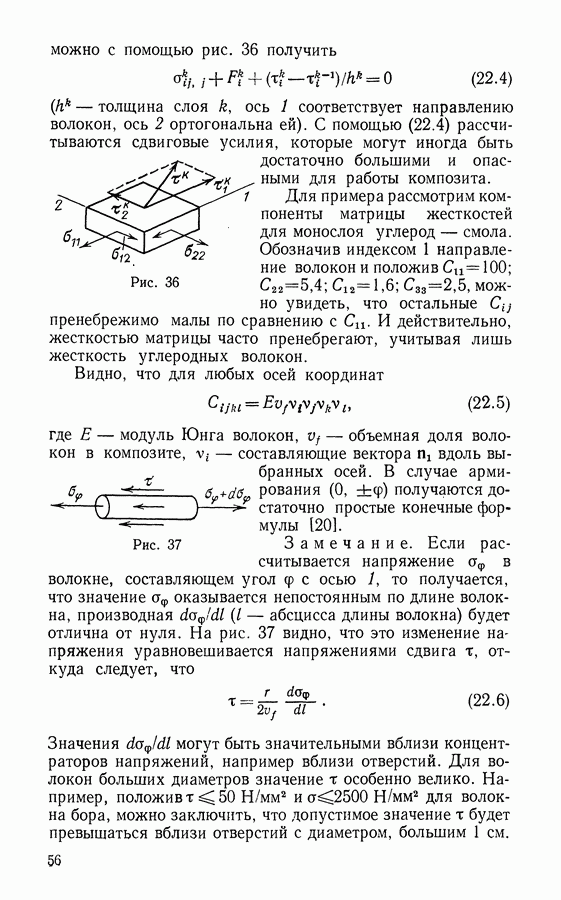
- § 22. Слоистые упругие композиты
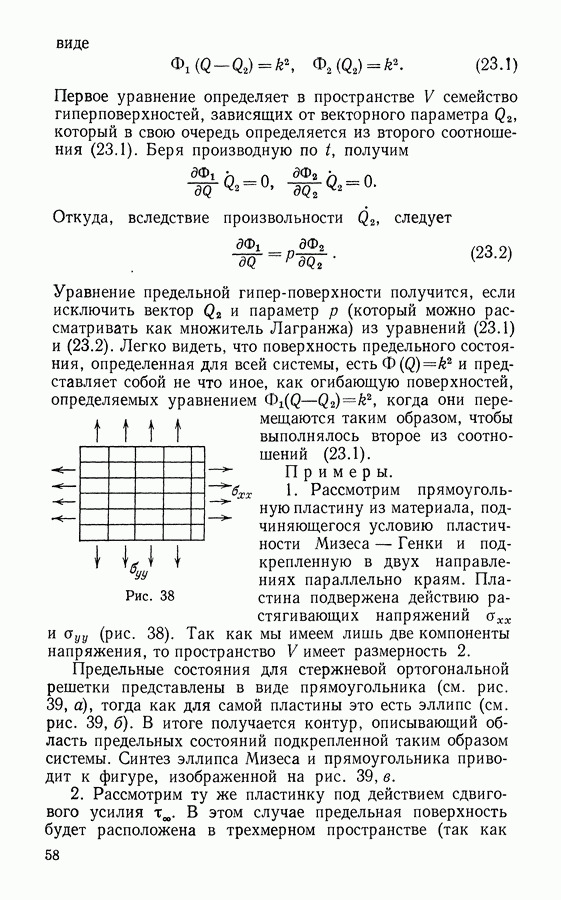
- § 23. Предельное состояние пластической композитной структуры
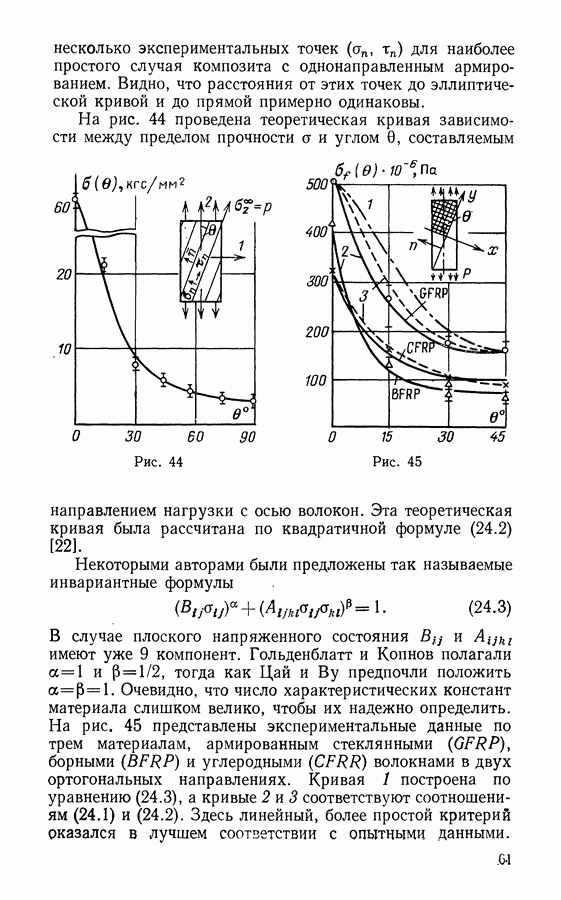
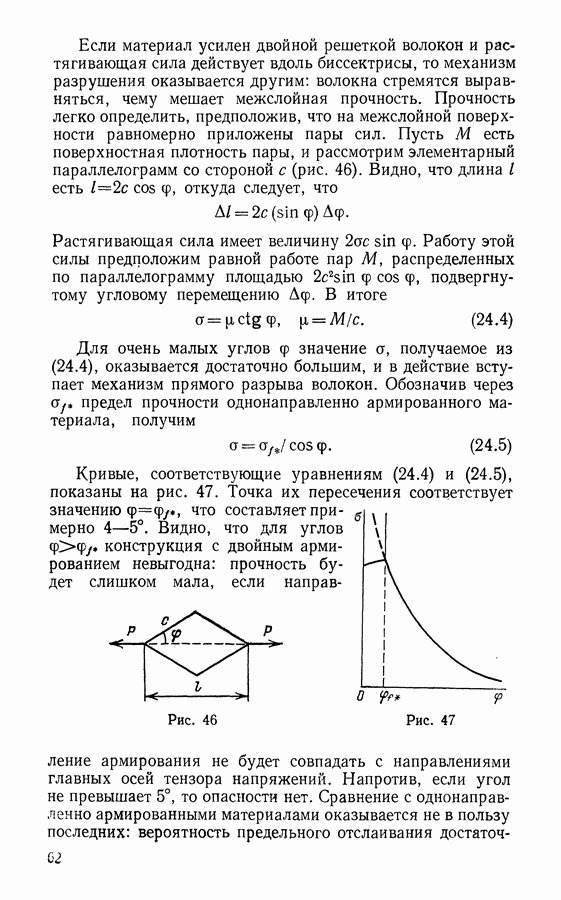
- § 24. Прочность слоистых композитов
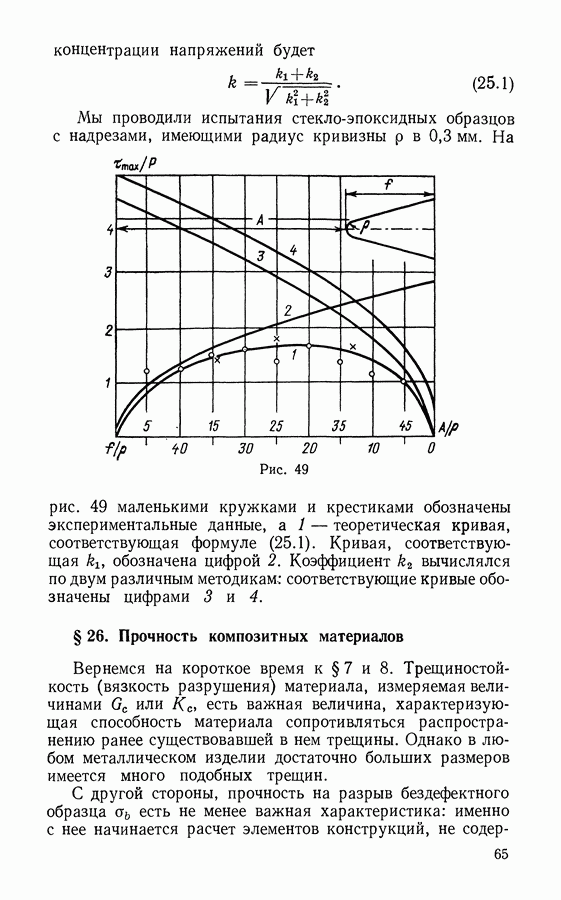
- § 25. Концентрация напряжений в композитах
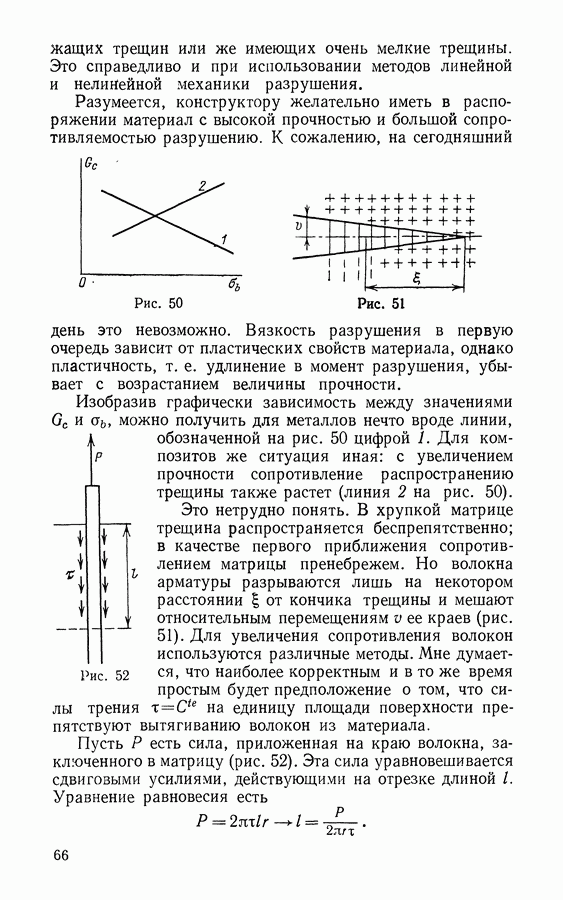
- § 26. Прочность композитных материалов
- ЗАКЛЮЧЕНИЕ