| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 19. Задача о росте трещины
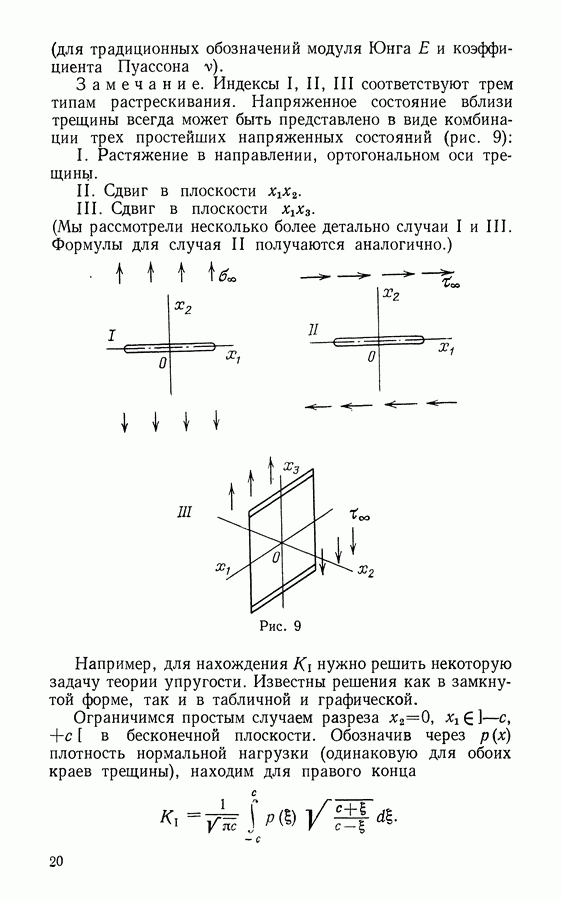
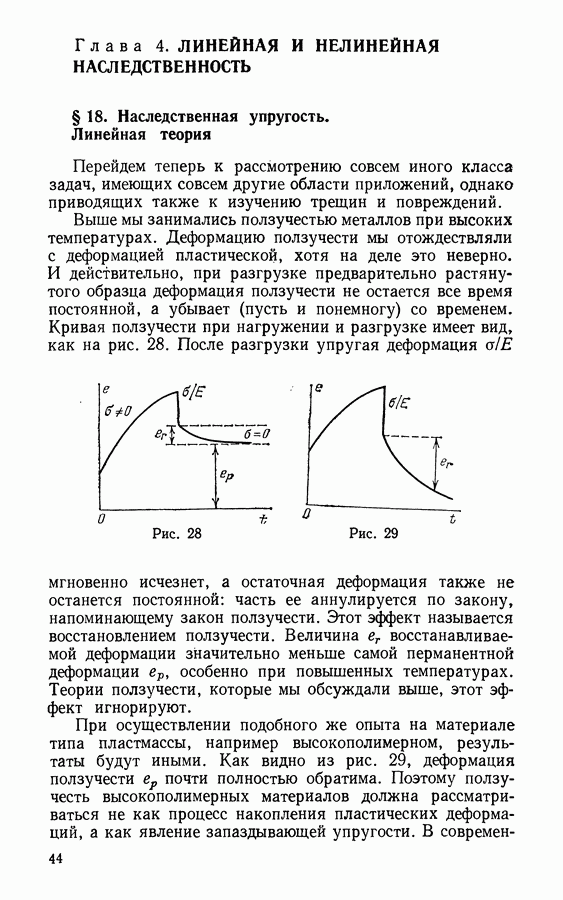
Принцип Вольтерра, изложенный в предьщущем параграфе, применим в общем случае лишь к задачам, где тип краевых условий считается неизменным. К примеру, с помощью этого принципа не удается решить задачу о движущемся штампе, где перемещение точки границы известна лишь в тот короткий период, когда штамп находится вблизи нее. Можно, однако, указать и случаи, где принцип действует: среди прочих задача Герца, или же задача о движении трещин.
Запишем основные уравнения плоской задачи в виде

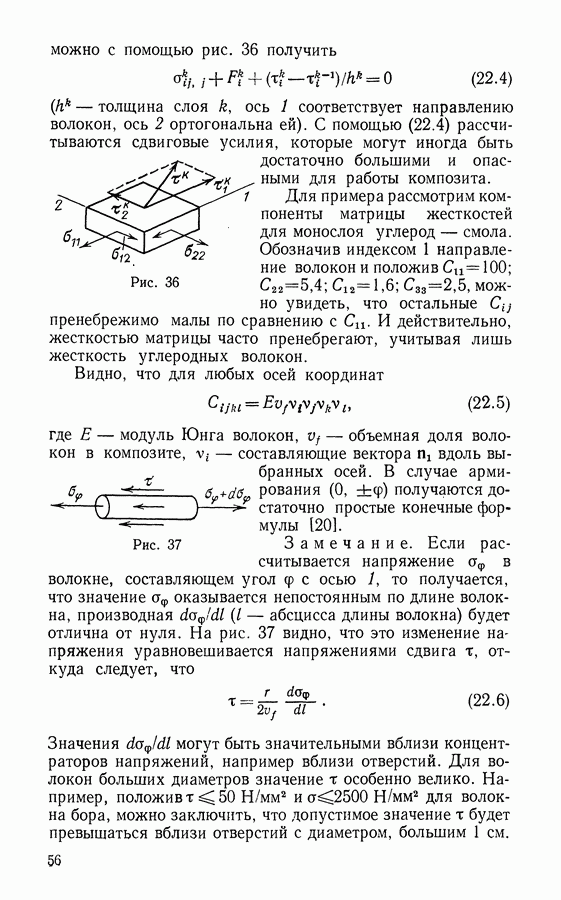
Черточки над  означают, что упругие константы заменены здесь операторами вида
означают, что упругие константы заменены здесь операторами вида  . Положив
. Положив

получим на прямой 

Таким образом, методика решения плоской задачи наследственной упругости не отличается от методики решения классической упругой задачи. Здесь длина трещины  предполагалась функцией времени. Распределение напряжений остается таким же, как в уже изученных случаях (см. § 8).
предполагалась функцией времени. Распределение напряжений остается таким же, как в уже изученных случаях (см. § 8).
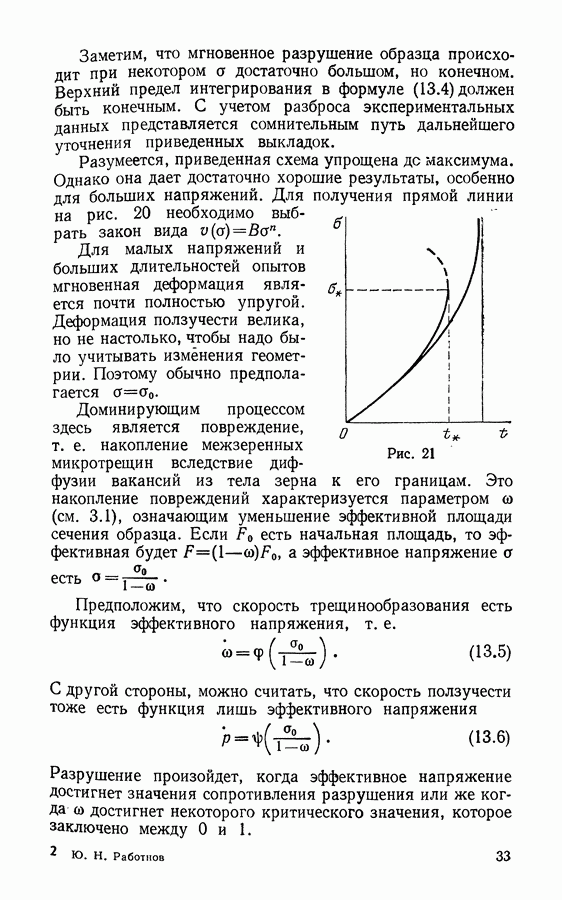
В работах ряда советских физиков указывалось на возможность появления ультрамикроскопических трещин в тонких пленках некоторых полимерных материалов. Методы, основанные на измерении дисперсии рентгеновских лучей, позволили оценить величину длины этих микротрещин, которая оказалась лежащей в пределах от 100 до 1000 А  При нагружении материала концентрация этих трещин со временем увеличивается, и при достижении концентрацией величины приблизительно
При нагружении материала концентрация этих трещин со временем увеличивается, и при достижении концентрацией величины приблизительно  микротрещин на см появляется макротрещина. Распространяется эта видимая глазу трещина достаточно быстро, что приводит к разрушению образца. Этот механизм разрушения отличается от описанного нами в гл. 2.
микротрещин на см появляется макротрещина. Распространяется эта видимая глазу трещина достаточно быстро, что приводит к разрушению образца. Этот механизм разрушения отличается от описанного нами в гл. 2.
В линейной механике разрушения предполагается, что материал остается упругим и неповрежденным повсюду, кроме небольшой зоны вблизи кончика трещины. Предположим теперь, напротив, что процесс растрескивания, заключающийся в образовании микротрещин, происходит во всем теле, содержащем трещину. Скорость движения управляется условием достижения на кончике трещины критического значения плотности микротрещины  . Что касается процесса образования микротрещин, то предположим, что скорость их накопления есть функция первого» инварианта напряжений, т. е.
. Что касается процесса образования микротрещин, то предположим, что скорость их накопления есть функция первого» инварианта напряжений, т. е.

Ограничимся здесь случаем, когда эта функция линейна.. Всегда можно определить критическое значение  такое, что это уравнение примет вид
такое, что это уравнение примет вид

Разумеется, можно оперировать и нелинейной функцией  но тогда решение можно получить лишь с помощью численных методов. Поэтому выбор здесь уравнения (19.2) продиктован лишь желанием получить замкнутое решение.
но тогда решение можно получить лишь с помощью численных методов. Поэтому выбор здесь уравнения (19.2) продиктован лишь желанием получить замкнутое решение.
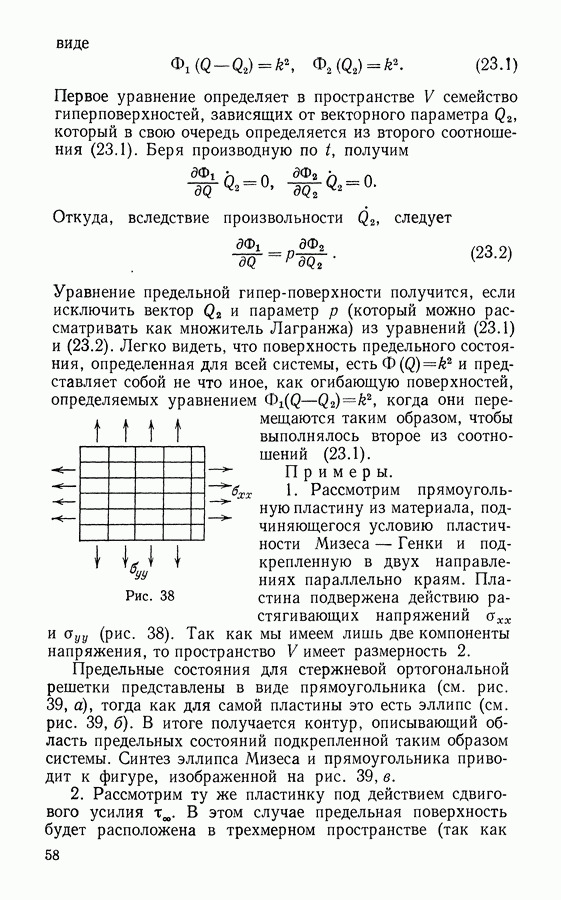
приведем известный результат для плоского напряженного состояния при 

Трещина, представленная на рис. 30, имеет в момент  длину
длину  а в текущий момент
а в текущий момент  длину
длину  Значение
Значение  В момент
В момент  для точки с абсциссой
для точки с абсциссой  будет согласно (19.2)
будет согласно (19.2)


Рис. 30
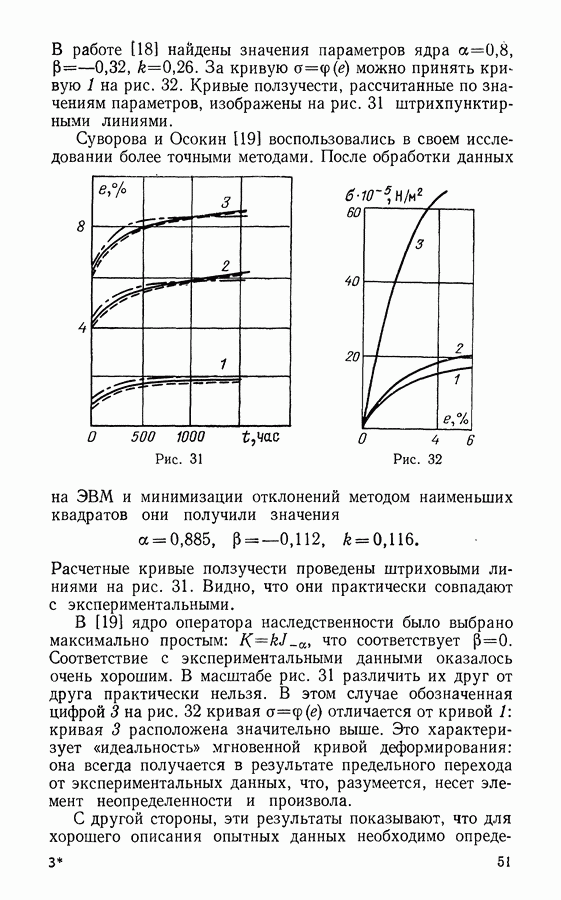
Внесем (19.3) в (19.2) и проинтегрируем. Полагая  придем к уравнению Абеля
придем к уравнению Абеля

решение которого будет

| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- Глава 1. ОСНОВНЫЕ ПОНЯТИЯ
- § 1. Твердое тело
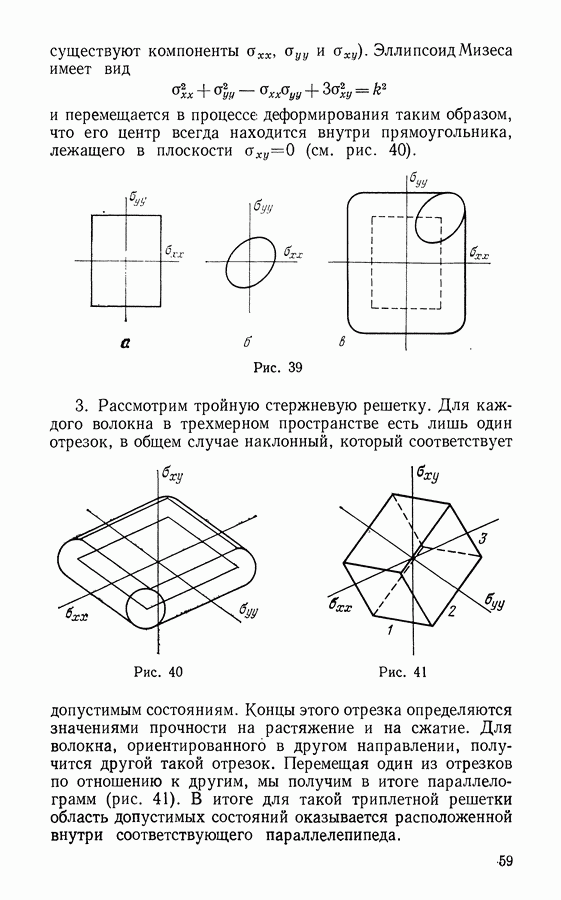
- § 2. Уравнения состояния
- § 3. Ползучесть, усталость, пластичность
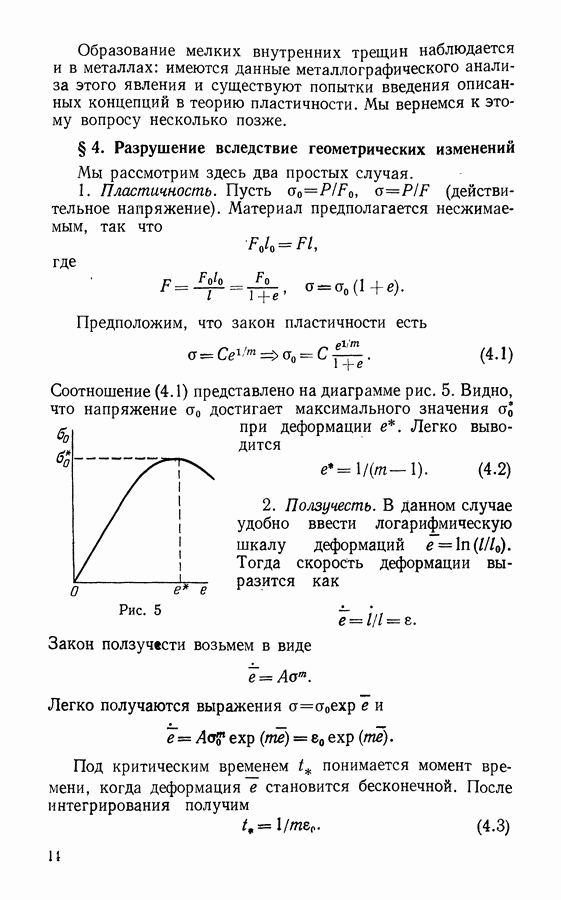
- § 4. Разрушение вследствие геометрических изменений
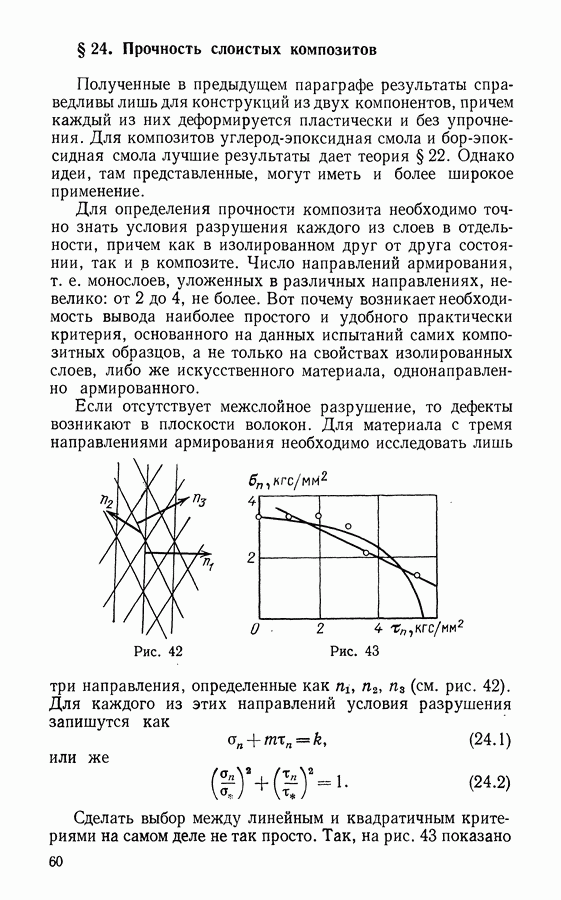
- Глава 2. МЕХАНИКА РАСПРОСТРАНЕНИЯ ТРЕЩИН
- § 5. Теория Гриффитса
- § 6. Антиплоская деформация
- § 7. Работа продвижения трещины
- § 8. Плоская деформация
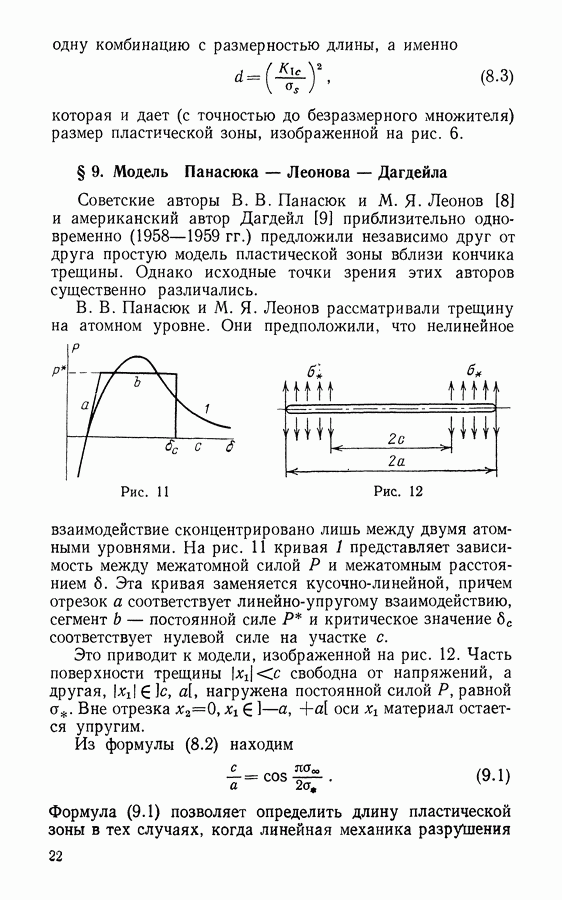
- § 9. Модель Панасюка — Леонова — Дагдейла
- § 10. Интеграл Райса — Черепанова
- § 11. Выводы главы 2
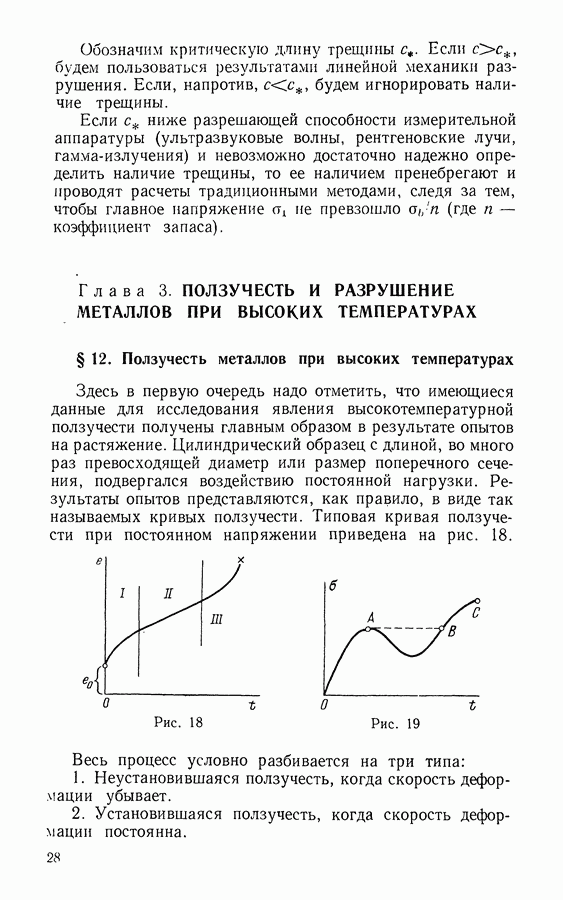
- Глава 3. ПОЛЗУЧЕСТЬ И РАЗРУШЕНИЕ МЕТАЛЛОВ ПРИ ВЫСОКИХ ТЕМПЕРАТУРАХ
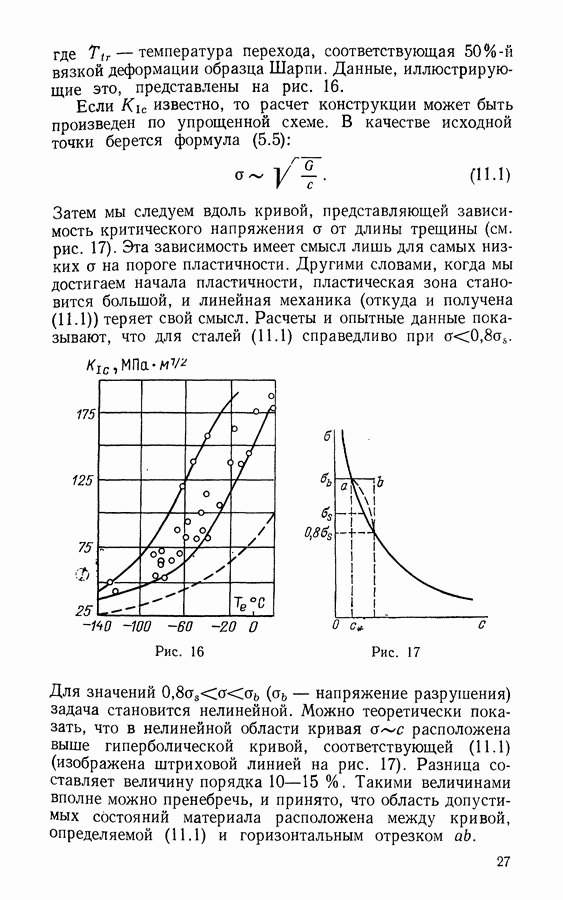
- § 12. Ползучесть металлов при высоких температурах
- § 13. Разрушение при растяжении
- § 14. Сложное напряженное состояние
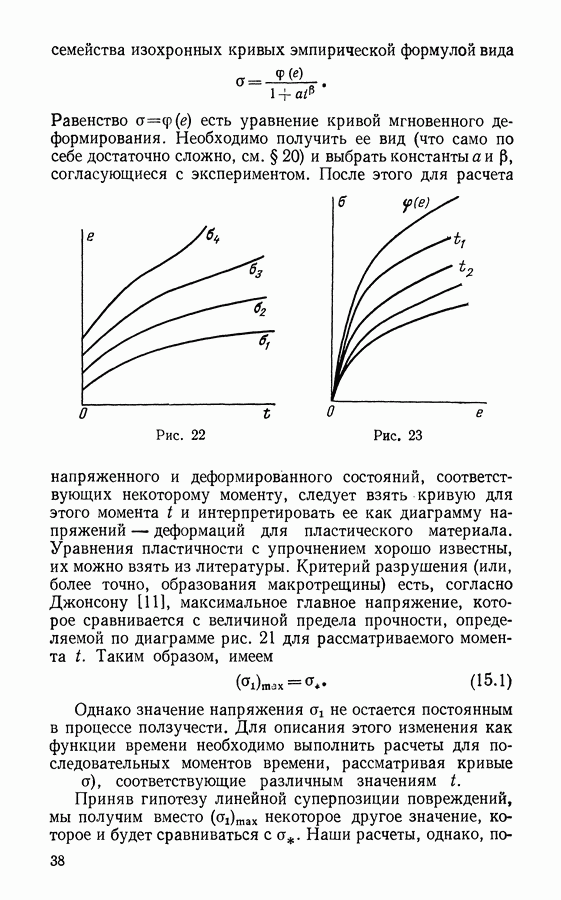
- § 15. Техническая теория. Изохронные кривые ползучести
- § 16. Разрушение при кратковременной ползучести
- § 17. Концентрация напряжений
- Глава 4. ЛИНЕЙНАЯ И НЕЛИНЕЙНАЯ НАСЛЕДСТВЕННОСТЬ
- § 18. Наследственная упругость. Линейная теория
- § 19. Задача о росте трещины
- § 20. Нелинейная наследственность
- Глава 5. МЕХАНИКА КОМПОЗИТНЫХ МАТЕРИАЛОВ
- § 21. Композиты волокнистого строения
- § 22. Слоистые упругие композиты
- § 23. Предельное состояние пластической композитной структуры
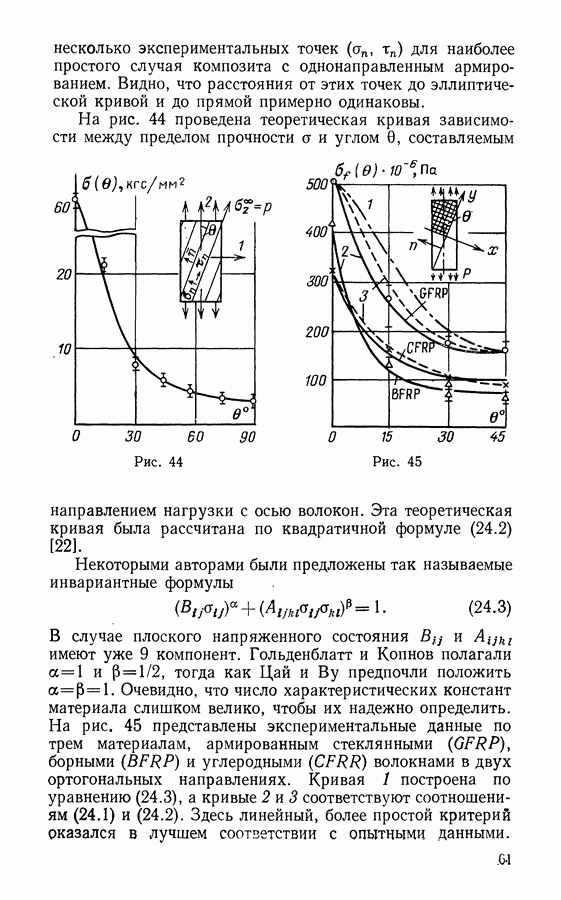
- § 24. Прочность слоистых композитов
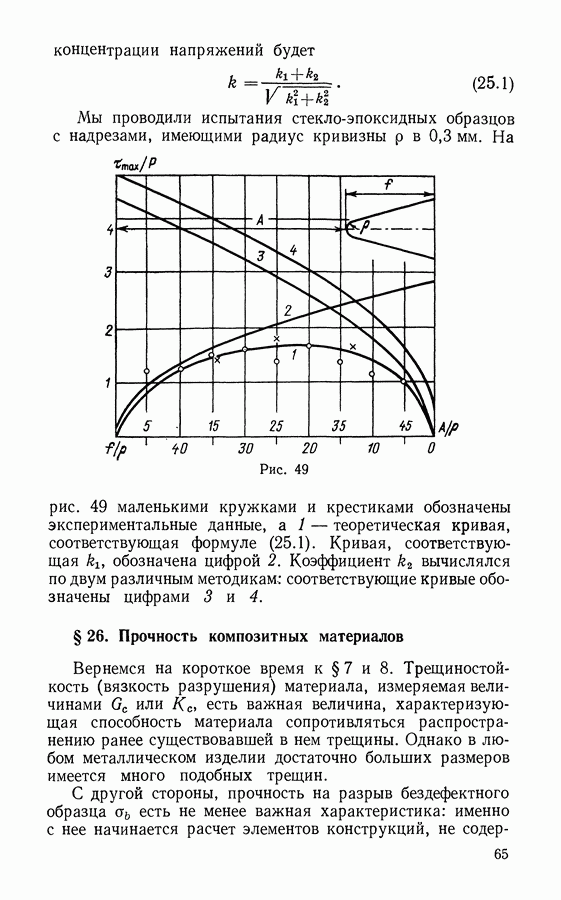
- § 25. Концентрация напряжений в композитах
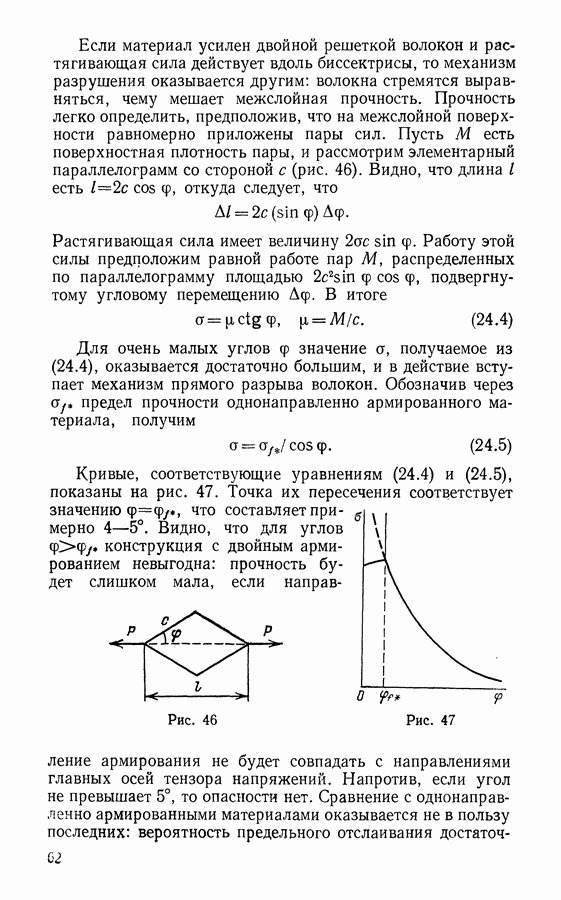
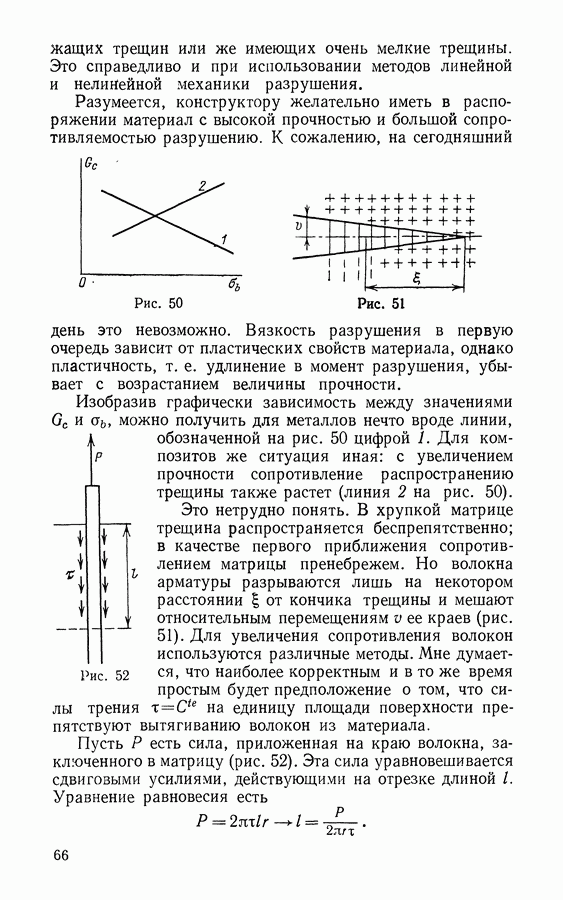
- § 26. Прочность композитных материалов
- ЗАКЛЮЧЕНИЕ