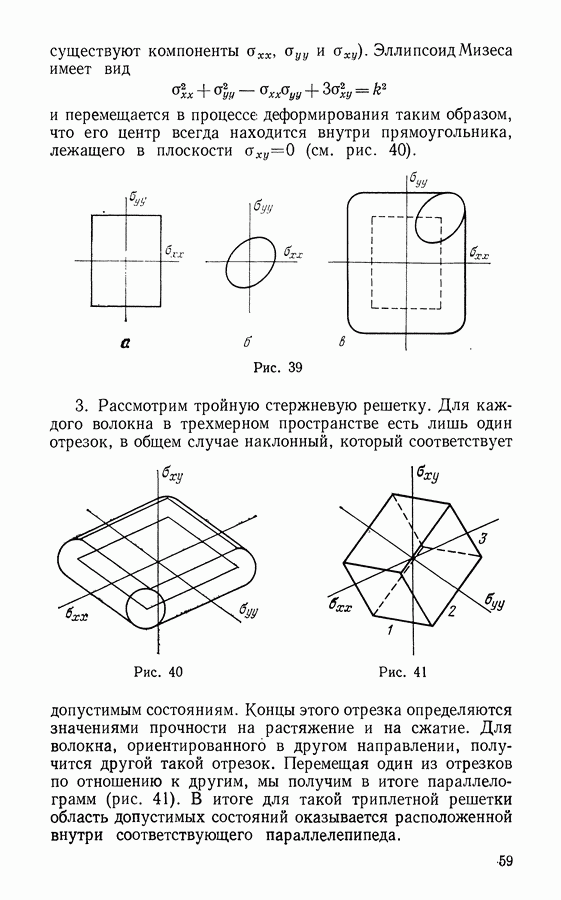
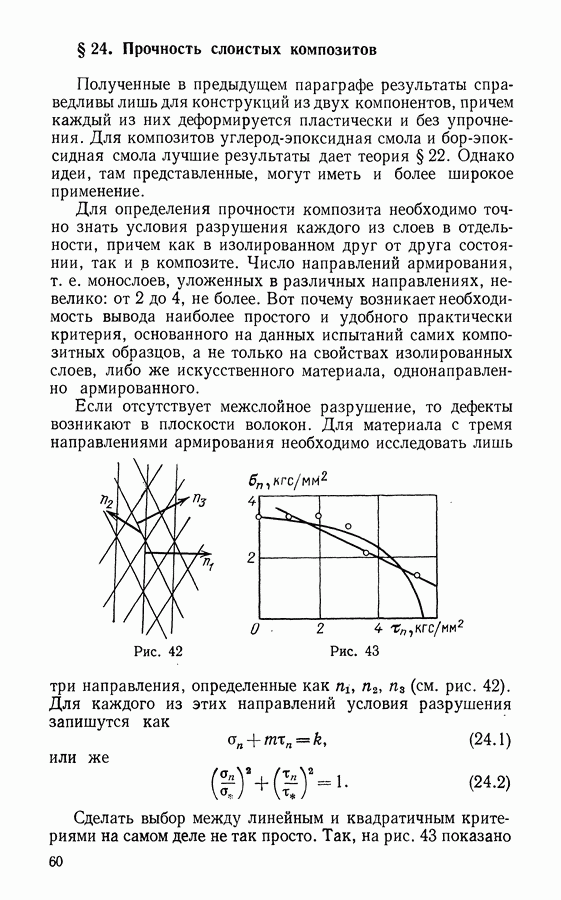
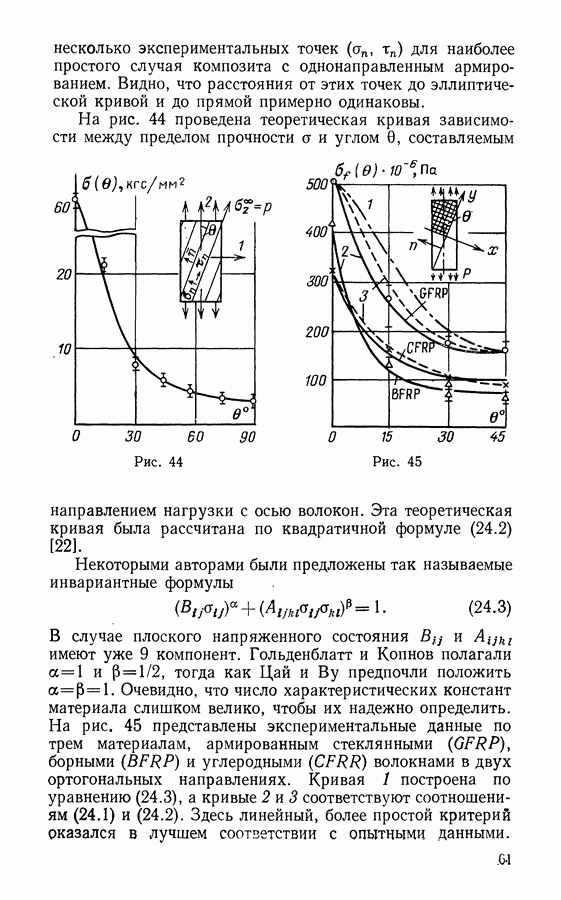
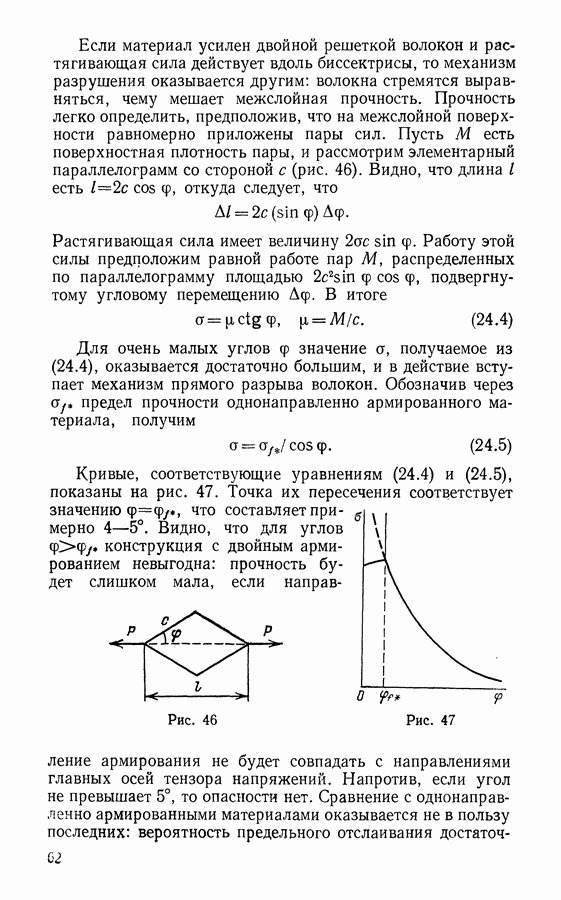
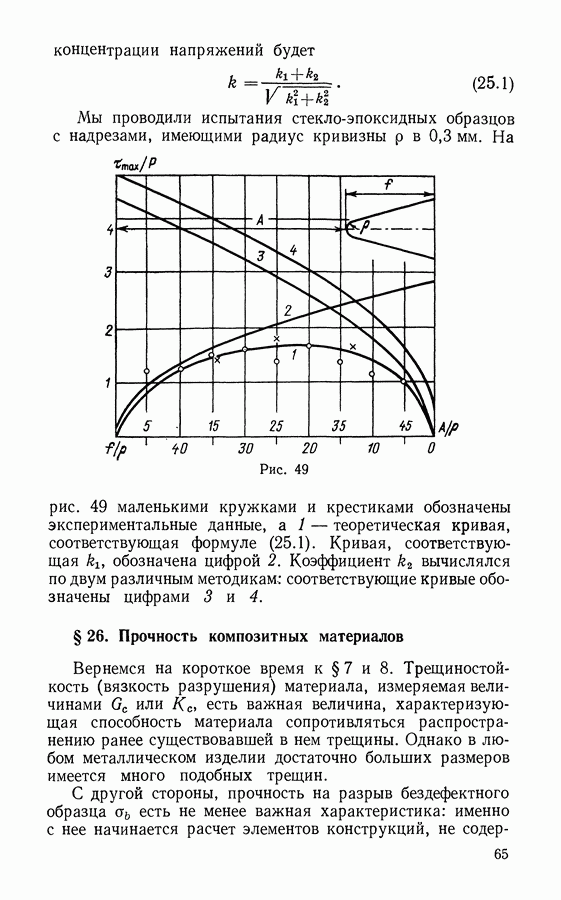
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 26. Прочность композитных материалов
Вернемся на короткое время к § 7 и 8. Трещиностойкость (вязкость разрушения) материала, измеряемая величинами  или
или  есть важная величина, характеризующая способность материала сопротивляться распространению ранее существовавшей в нем трещины. Однако в любом металлическом изделии достаточно больших размеров имеется много подобных трещин.
есть важная величина, характеризующая способность материала сопротивляться распространению ранее существовавшей в нем трещины. Однако в любом металлическом изделии достаточно больших размеров имеется много подобных трещин.
С другой стороны, прочность на разрыв бездефектного образца  есть не менее важная характеристика: именно с нее начинается расчет элементов конструкций, не
есть не менее важная характеристика: именно с нее начинается расчет элементов конструкций, не
содержащих трещин или же имеющих очень мелкие трещины. Это справедливо и при использовании методов линейной и нелинейной механики разрушения.
Разумеется, конструктору желательно иметь в распоряжении материал с высокой прочностью и большой сопротивляемостью разрушению. К сожалению, на сегодняшний день это невозможно. Вязкость разрушения в первую очередь зависит от пластических свойств материала, однако пластичность, т. е. удлинение в момент разрушения, убывает с возрастанием величины прочности.

Рис. 50

Рис. 51

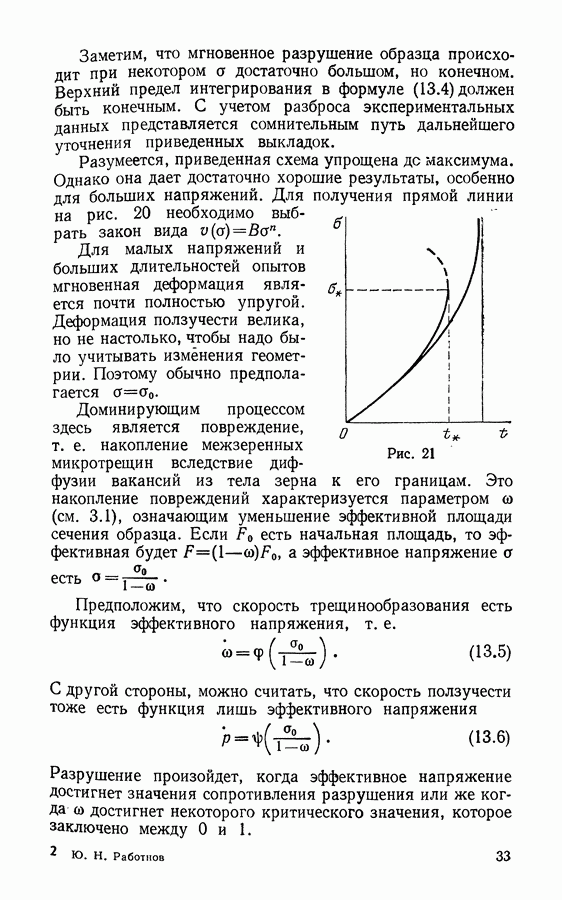
Рис. 52
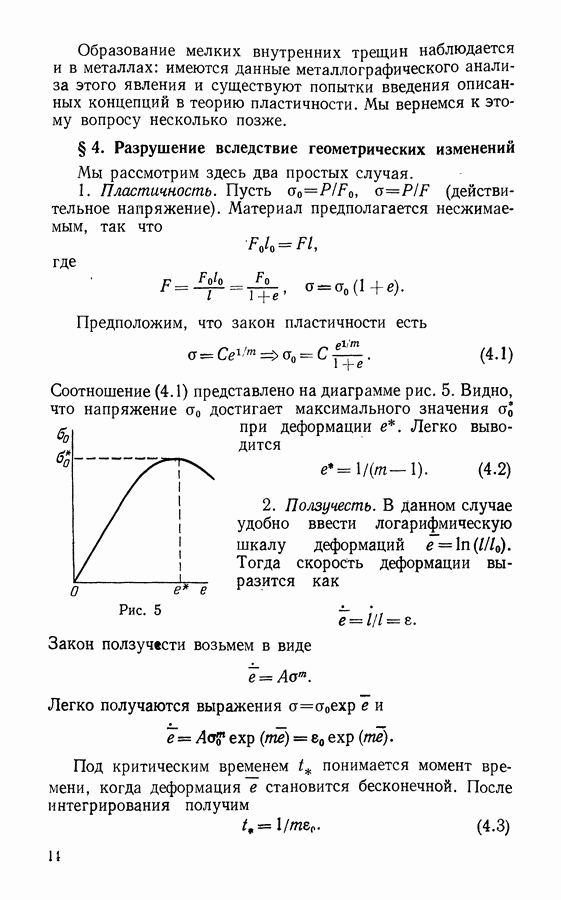
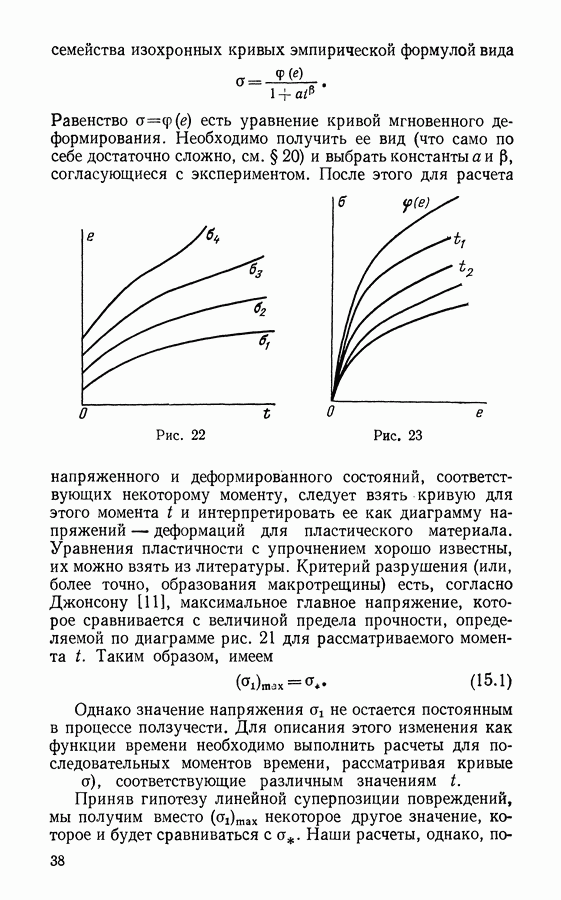
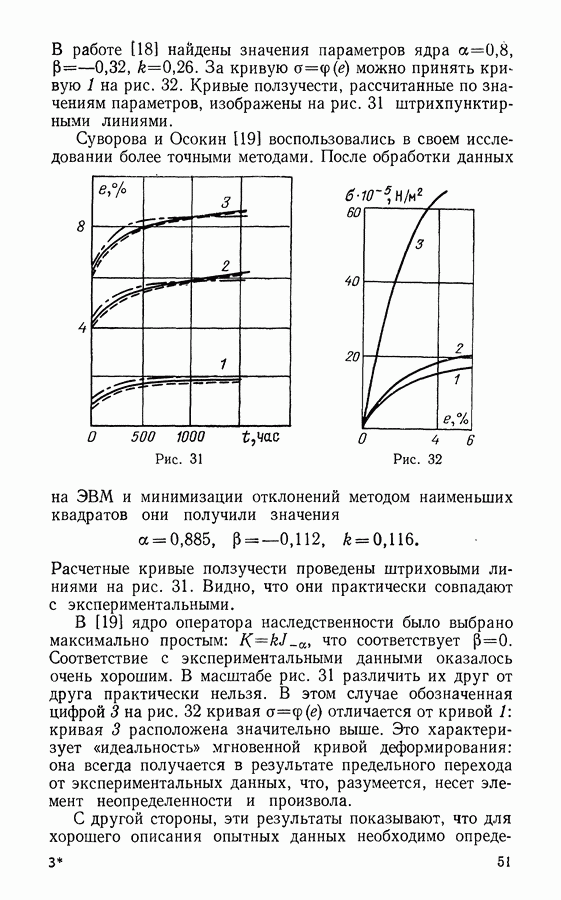
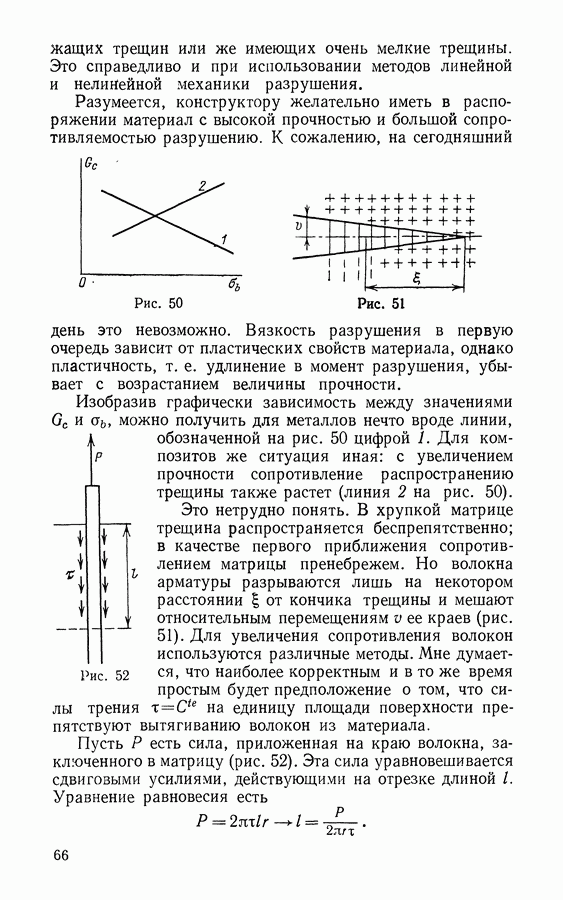
Изобразив графически зависимость между значениями  можно получить для металлов нечто вроде линии, обозначенной на рис. 50 цифрой 1. Для композитов же ситуация иная: с увеличением прочности сопротивление распространению трещины также растет (линия 2 на рис. 50).
можно получить для металлов нечто вроде линии, обозначенной на рис. 50 цифрой 1. Для композитов же ситуация иная: с увеличением прочности сопротивление распространению трещины также растет (линия 2 на рис. 50).
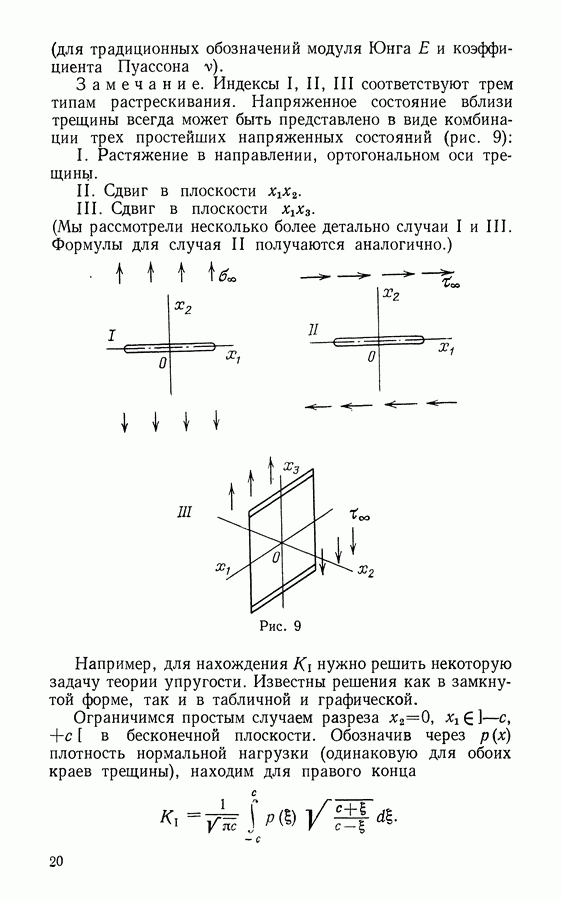
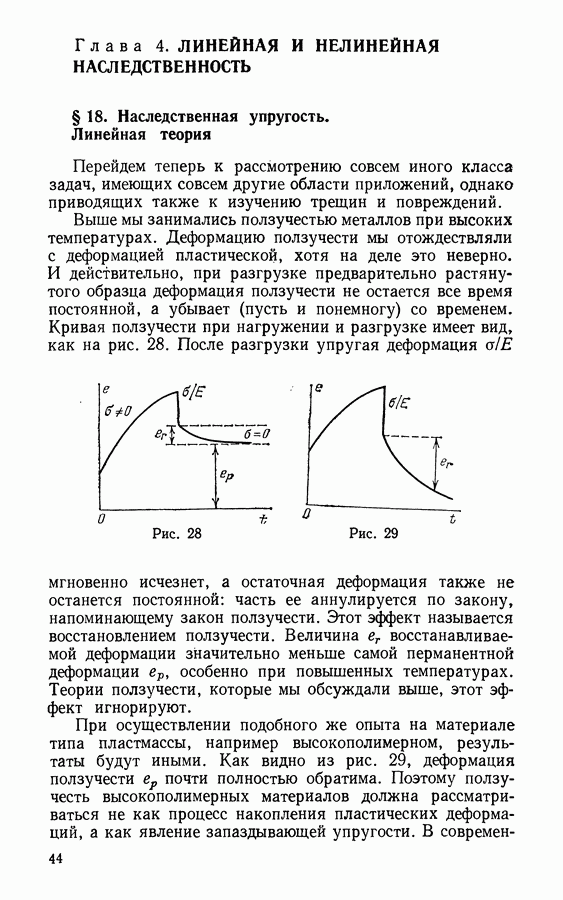
Это нетрудно понять. В хрупкой матрице трещина распространяется беспрепятственно; в качестве первого приближения сопротивлением матрицы пренебрежем. Но волокна арматуры разрываются лишь на некотором расстоянии I от кончика трещины и мешают относительным перемещениям  ее краев (рис. 51). Для увеличения сопротивления волокон используются различные методы. Мне думается, что наиболее корректным и в то же время простым будет предположение о том, что силы трения на единицу площади поверхности препятствуют вытягиванию волокон из материала.
ее краев (рис. 51). Для увеличения сопротивления волокон используются различные методы. Мне думается, что наиболее корректным и в то же время простым будет предположение о том, что силы трения на единицу площади поверхности препятствуют вытягиванию волокон из материала.
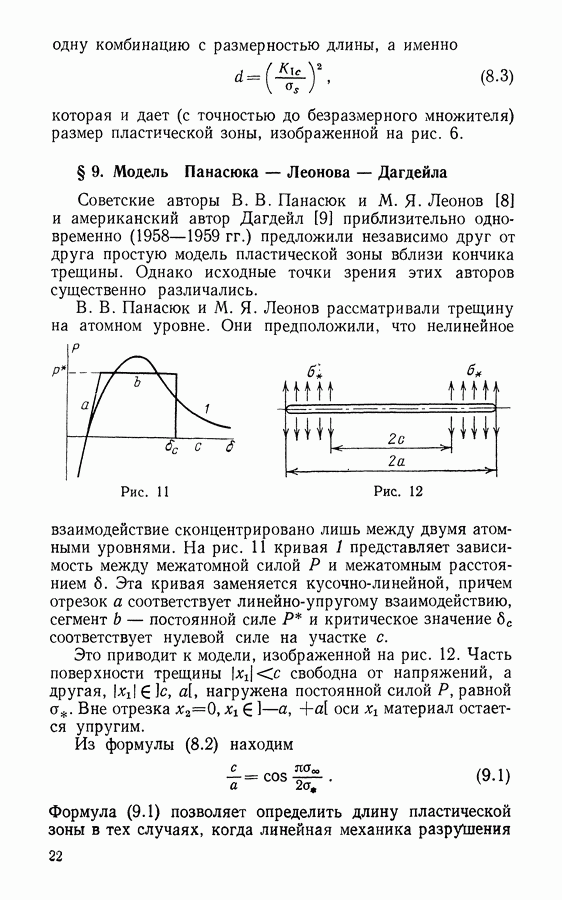
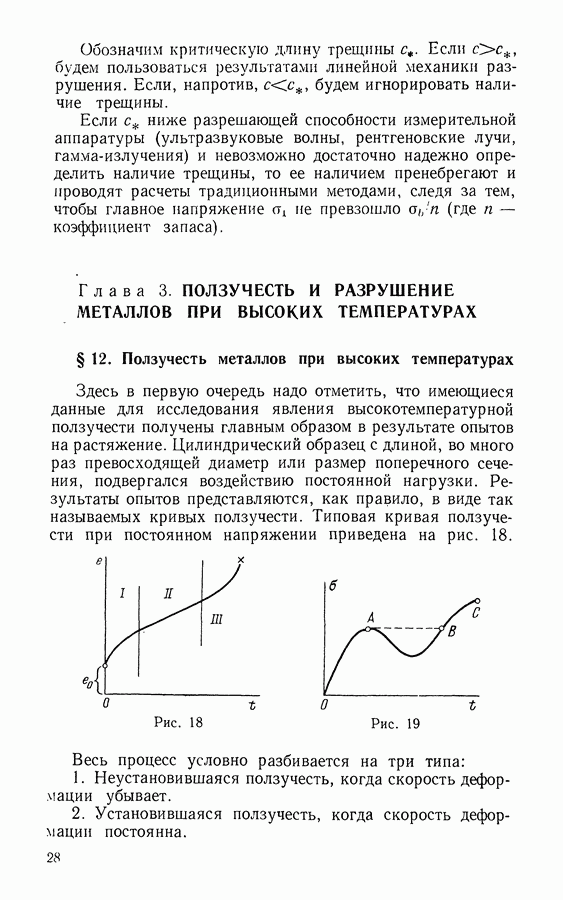
Пусть  есть сила, приложенная на краю волокна, заключенного в матрицу (рис. 52). Эта сила уравновешивается сдвиговыми усилиями, действующими на отрезке длиной
есть сила, приложенная на краю волокна, заключенного в матрицу (рис. 52). Эта сила уравновешивается сдвиговыми усилиями, действующими на отрезке длиной  Уравнение равновесия есть
Уравнение равновесия есть

Тогда удлинение элемента волокна длиной I будет (в направлении оси 

Если а есть среднее напряжение композита, то

где  есть объемная плотность содержания волокон в материале. Обращаясь к предыдущему соотношению, можно видеть, что связь между напряжением в зоне вокруг кончика трещины и относительным перемещением ее границ будет
есть объемная плотность содержания волокон в материале. Обращаясь к предыдущему соотношению, можно видеть, что связь между напряжением в зоне вокруг кончика трещины и относительным перемещением ее границ будет

Положим теперь (где  расстояние до кончика трещины), и вычислим интеграл Райса — Черепанова. Получим
расстояние до кончика трещины), и вычислим интеграл Райса — Черепанова. Получим

Предполагается, что движение трещины начинается при достижении величиной  значения прочности на разрыв волокон. Положив
значения прочности на разрыв волокон. Положив  получим
получим

Из (26.3) следует, что сопротивление распространению трещины возрастает вместе с прочностью волокна и объемной плотностью содержания арматуры в материале. Однако это не говорит о наличии простого произведения, линейного по каждому из факторов. С другой стороны, сила сцепления  равная сопротивлению матрицы сдвигу, не должна быть слишком велика.
равная сопротивлению матрицы сдвигу, не должна быть слишком велика.
Эта теория применима лишь к ортогонально армированным материалам, содержащим трещины, распространяющиеся вдоль направлений армирования. В противном случае ситуация существенно осложняется.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- Глава 1. ОСНОВНЫЕ ПОНЯТИЯ
- § 1. Твердое тело
- § 2. Уравнения состояния
- § 3. Ползучесть, усталость, пластичность
- § 4. Разрушение вследствие геометрических изменений
- Глава 2. МЕХАНИКА РАСПРОСТРАНЕНИЯ ТРЕЩИН
- § 5. Теория Гриффитса
- § 6. Антиплоская деформация
- § 7. Работа продвижения трещины
- § 8. Плоская деформация
- § 9. Модель Панасюка — Леонова — Дагдейла
- § 10. Интеграл Райса — Черепанова
- § 11. Выводы главы 2
- Глава 3. ПОЛЗУЧЕСТЬ И РАЗРУШЕНИЕ МЕТАЛЛОВ ПРИ ВЫСОКИХ ТЕМПЕРАТУРАХ
- § 12. Ползучесть металлов при высоких температурах
- § 13. Разрушение при растяжении
- § 14. Сложное напряженное состояние
- § 15. Техническая теория. Изохронные кривые ползучести
- § 16. Разрушение при кратковременной ползучести
- § 17. Концентрация напряжений
- Глава 4. ЛИНЕЙНАЯ И НЕЛИНЕЙНАЯ НАСЛЕДСТВЕННОСТЬ
- § 18. Наследственная упругость. Линейная теория
- § 19. Задача о росте трещины
- § 20. Нелинейная наследственность
- Глава 5. МЕХАНИКА КОМПОЗИТНЫХ МАТЕРИАЛОВ
- § 21. Композиты волокнистого строения
- § 22. Слоистые упругие композиты
- § 23. Предельное состояние пластической композитной структуры
- § 24. Прочность слоистых композитов
- § 25. Концентрация напряжений в композитах
- § 26. Прочность композитных материалов
- ЗАКЛЮЧЕНИЕ