| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Глава 3. ПОЛЗУЧЕСТЬ И РАЗРУШЕНИЕ МЕТАЛЛОВ ПРИ ВЫСОКИХ ТЕМПЕРАТУРАХ
§ 12. Ползучесть металлов при высоких температурах
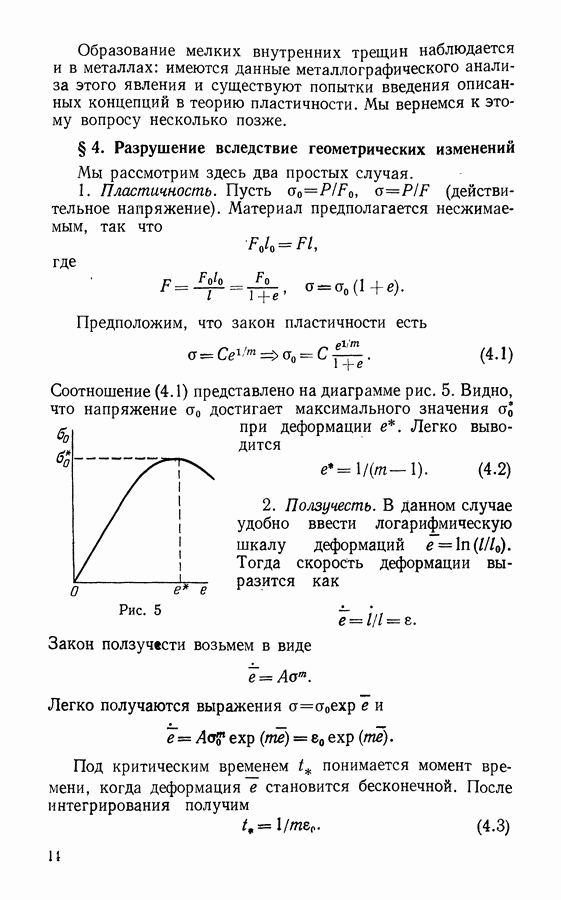
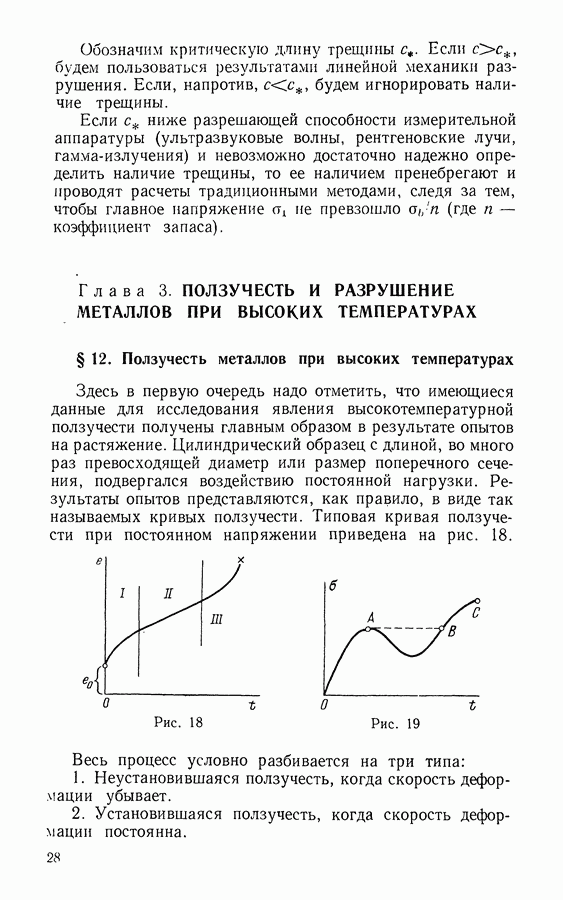
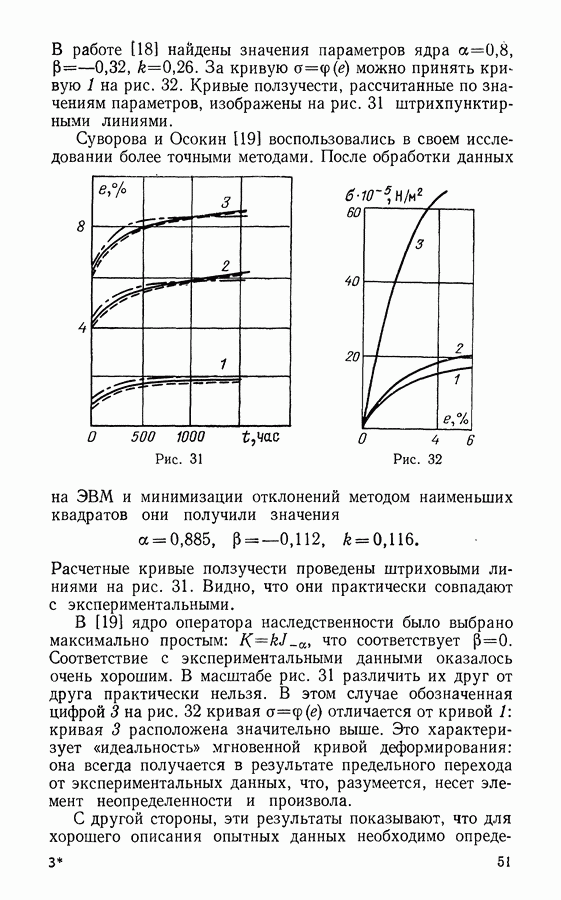
Здесь в первую очередь надо отметить, что имеющиеся данные для исследования явления высокотемпературной ползучести получены главным образом в результате опытов на растяжение. Цилиндрический образец с длиной, во много раз превосходящей диаметр или размер поперечного сечения, подвергался воздействию постоянной нагрузки. Результаты опытов представляются, как правило, в виде так называемых кривых ползучести. Типовая кривая ползучести при постоянном напряжении приведена на рис. 18.

Рис. 18

Рис. 19
Весь процесс условно разбивается на три типа:
1. Неустановившаяся ползучесть, когда скорость деформации убывает.
2. Установившаяся ползучесть, когда скорость деформации постоянна.
3. Ускоряющаяся ползучесть, предшествующая разрушению.
Введение понятия «высокой температуры» существенным образом зависит от температуры плавления заданного материала. Например, так как температура плавления свинца примерно  то ползучесть при «лабораторной температуре» в районе
то ползучесть при «лабораторной температуре» в районе  уже можно рассматривать как феномен «высокой температуры».
уже можно рассматривать как феномен «высокой температуры».
Пусть  мгновенная деформация, включающая в себя в общем случае упругий и пластический члены:
мгновенная деформация, включающая в себя в общем случае упругий и пластический члены:

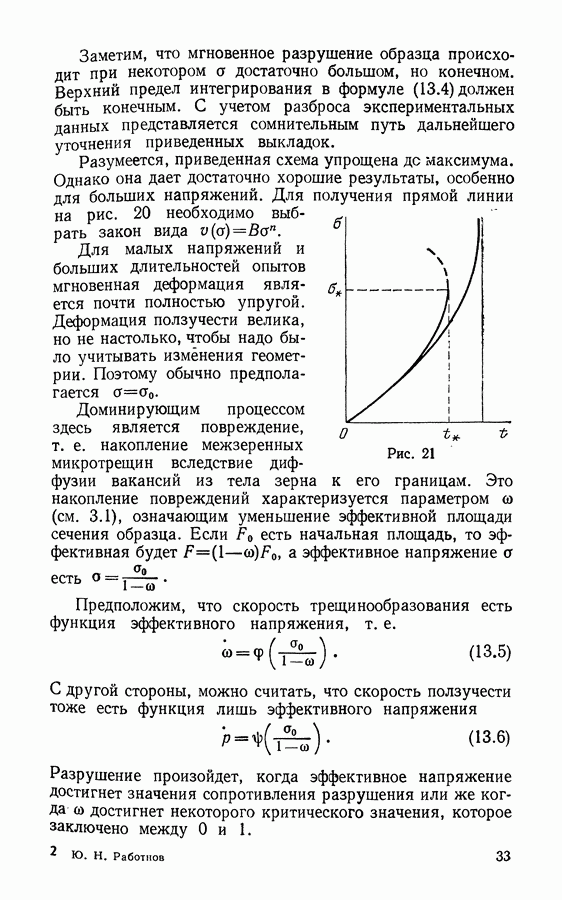
где  максимальное значение напряжения во временном интервале, предшествующем рассматриваемому моменту. Поведение напряжения как функции времени иллюстрируется диаграммой на рис. 19.
максимальное значение напряжения во временном интервале, предшествующем рассматриваемому моменту. Поведение напряжения как функции времени иллюстрируется диаграммой на рис. 19.
Для участков  и
и  кривой можно записать
кривой можно записать

 есть монотонная возрастающая функция).
есть монотонная возрастающая функция).
Мгновенная деформация зависит лишь от текущей величины напряжения.
Но для участка между  уже выполняется равенство
уже выполняется равенство

так как пластическая деформация, соответствующая точке  остается неизменной.
остается неизменной.
На втором этапе ползучести скорость есть функция лишь напряжения и температуры. Эта зависимость изучалась многими авторами и для большого числа материалов. В большинстве случаев она нелинейна. Предлагались различные виды зависимости

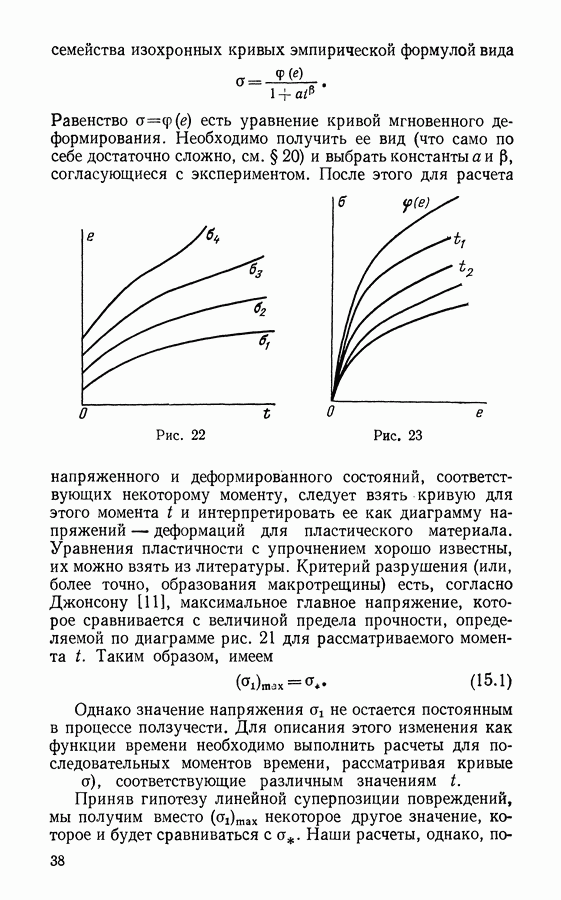
Вторая из этих формул имеет тот недостаток, что дает отличную от нуля скорость ползучести при  Третья достаточно мало отличается от второй при больших а, но для малых а дает удовлетворительный результат
Третья достаточно мало отличается от второй при больших а, но для малых а дает удовлетворительный результат

 первых стадии ползучести могут быть описаны с помощью так называемой теории упрочнения. Здесь
первых стадии ползучести могут быть описаны с помощью так называемой теории упрочнения. Здесь
предполагается, что скорость деформации зависит не только от напряжения а, но и от параметра упрочнения.
Если  есть полная деформация, а о — мгновенная из формулы (12.1), то
есть полная деформация, а о — мгновенная из формулы (12.1), то

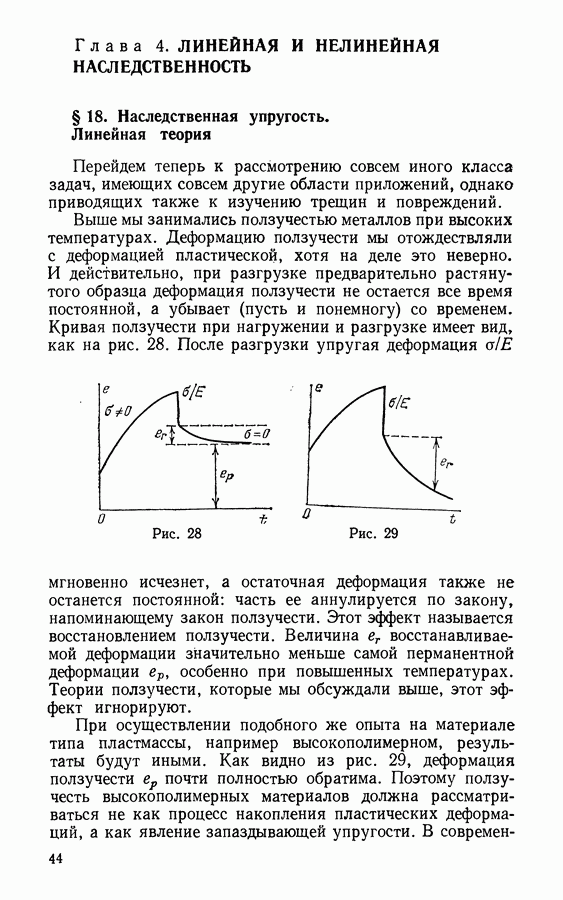
для деформации ползучести  Заметим, что следует различать пластическую деформацию ползучести
Заметим, что следует различать пластическую деформацию ползучести  и мгновенную пластическую дормацию
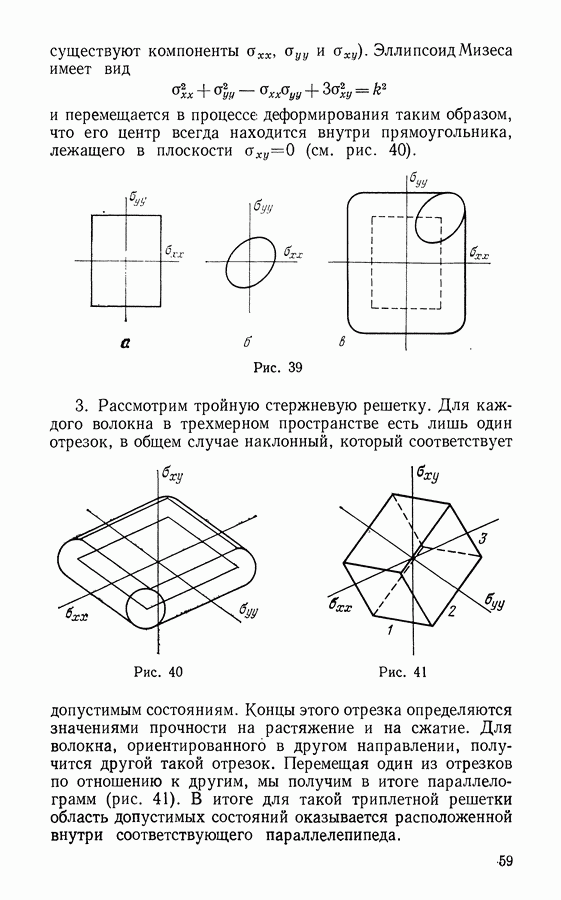
и мгновенную пластическую дормацию  Хотя обе они являются деформациями пластическими, но их свойства с металлургической точки зрения сильно различаются. (В англо-американской терминологии: грубое скольжение для существенных скольжений, происходящих даже между параллельными достаточно удаленными плоскостями, и малое скольжение для скольжений ползучести, самих по себе почти минимальных, но проявляющихся при глобальном деформировании материала.)
Хотя обе они являются деформациями пластическими, но их свойства с металлургической точки зрения сильно различаются. (В англо-американской терминологии: грубое скольжение для существенных скольжений, происходящих даже между параллельными достаточно удаленными плоскостями, и малое скольжение для скольжений ползучести, самих по себе почти минимальных, но проявляющихся при глобальном деформировании материала.)
Это объясняет различные роли, которые они исполняют в уравнении состояния.
Запишем теперь

Наиболее простая гипотеза состоит в принятии за параметр  самой деформации ползучести, т. е.
самой деформации ползучести, т. е.  Тогда мы придем к так называемому уравнению Людвига и Надаи, позволяющему почти с достаточной точностью описать результаты опытов, даже для нагружений по «произвольному» закону.
Тогда мы придем к так называемому уравнению Людвига и Надаи, позволяющему почти с достаточной точностью описать результаты опытов, даже для нагружений по «произвольному» закону.
С другой стороны, можно в качестве параметра упрочнения выбрать

означающий работу, рассеянную в процессе ползучести.
Обобщение на трехмерный случай очевидно.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- Глава 1. ОСНОВНЫЕ ПОНЯТИЯ
- § 1. Твердое тело
- § 2. Уравнения состояния
- § 3. Ползучесть, усталость, пластичность
- § 4. Разрушение вследствие геометрических изменений
- Глава 2. МЕХАНИКА РАСПРОСТРАНЕНИЯ ТРЕЩИН
- § 5. Теория Гриффитса
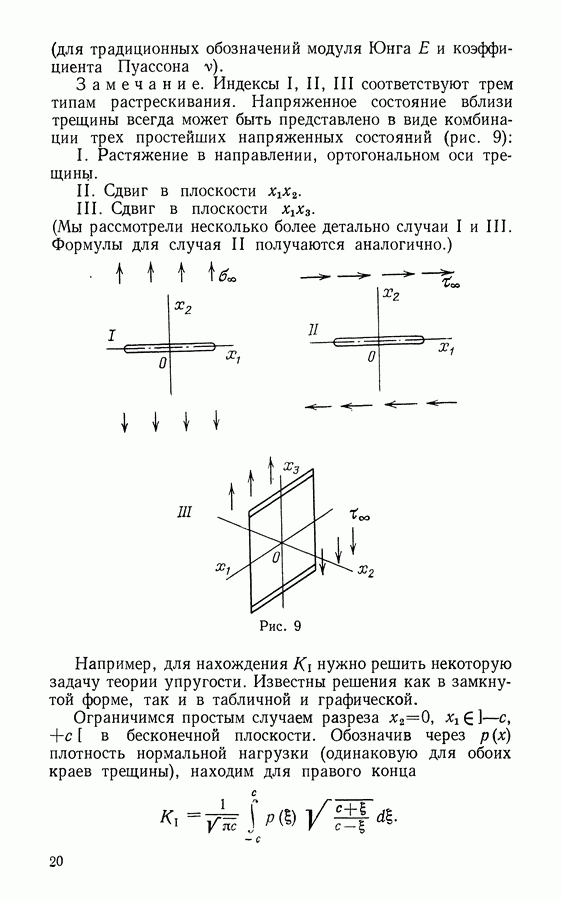
- § 6. Антиплоская деформация
- § 7. Работа продвижения трещины
- § 8. Плоская деформация
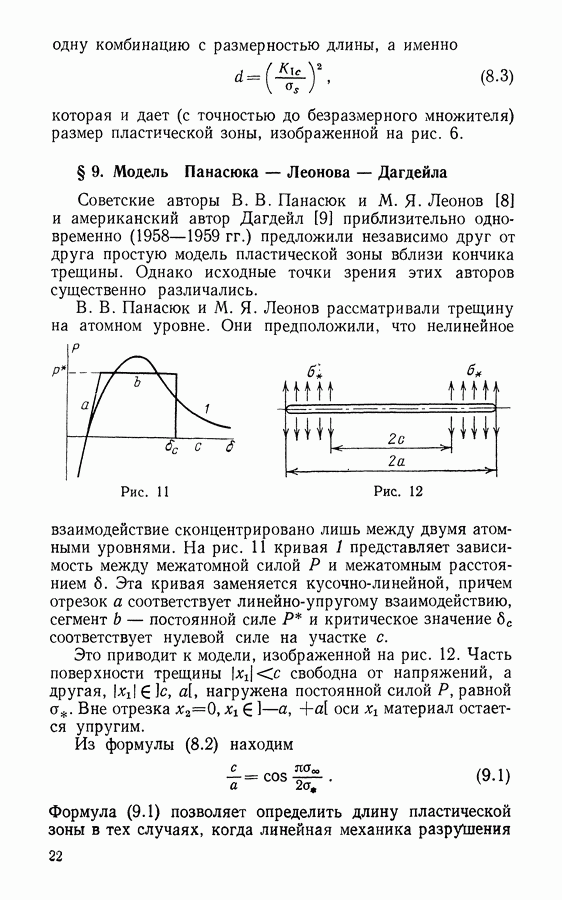
- § 9. Модель Панасюка — Леонова — Дагдейла
- § 10. Интеграл Райса — Черепанова
- § 11. Выводы главы 2
- Глава 3. ПОЛЗУЧЕСТЬ И РАЗРУШЕНИЕ МЕТАЛЛОВ ПРИ ВЫСОКИХ ТЕМПЕРАТУРАХ
- § 12. Ползучесть металлов при высоких температурах
- § 13. Разрушение при растяжении
- § 14. Сложное напряженное состояние
- § 15. Техническая теория. Изохронные кривые ползучести
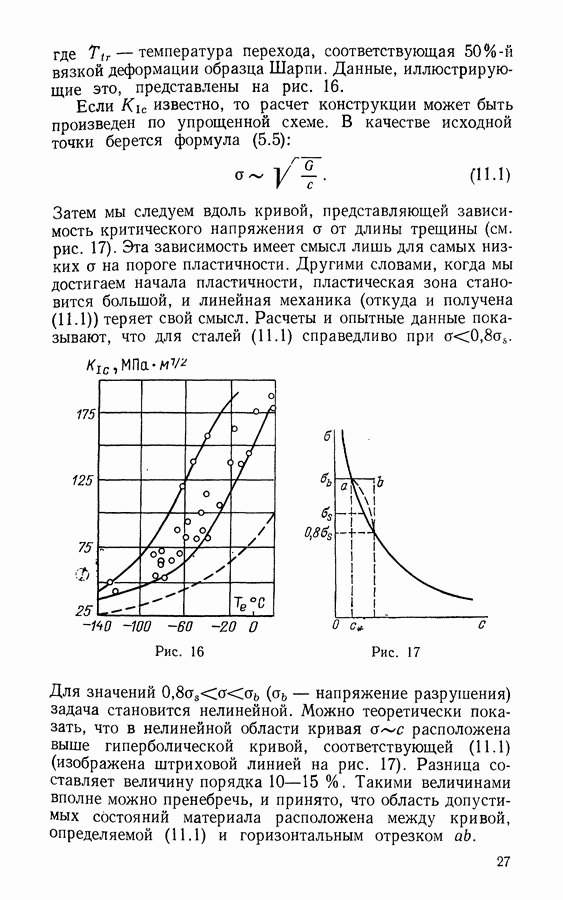
- § 16. Разрушение при кратковременной ползучести
- § 17. Концентрация напряжений
- Глава 4. ЛИНЕЙНАЯ И НЕЛИНЕЙНАЯ НАСЛЕДСТВЕННОСТЬ
- § 18. Наследственная упругость. Линейная теория
- § 19. Задача о росте трещины
- § 20. Нелинейная наследственность
- Глава 5. МЕХАНИКА КОМПОЗИТНЫХ МАТЕРИАЛОВ
- § 21. Композиты волокнистого строения
- § 22. Слоистые упругие композиты
- § 23. Предельное состояние пластической композитной структуры
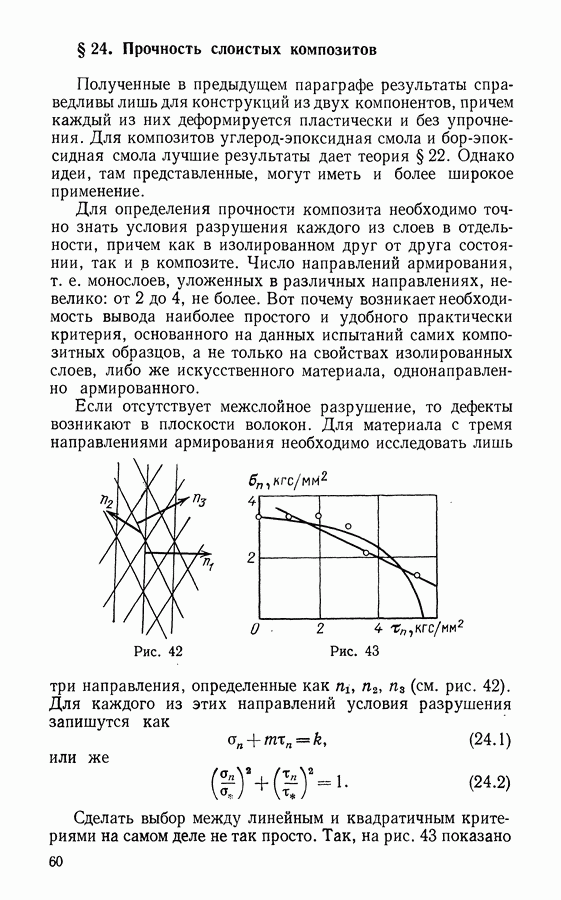
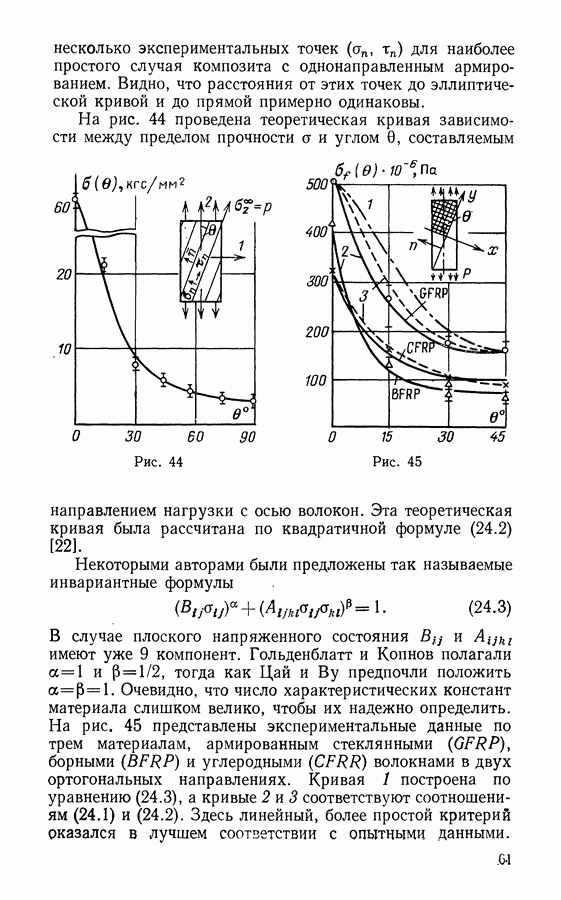
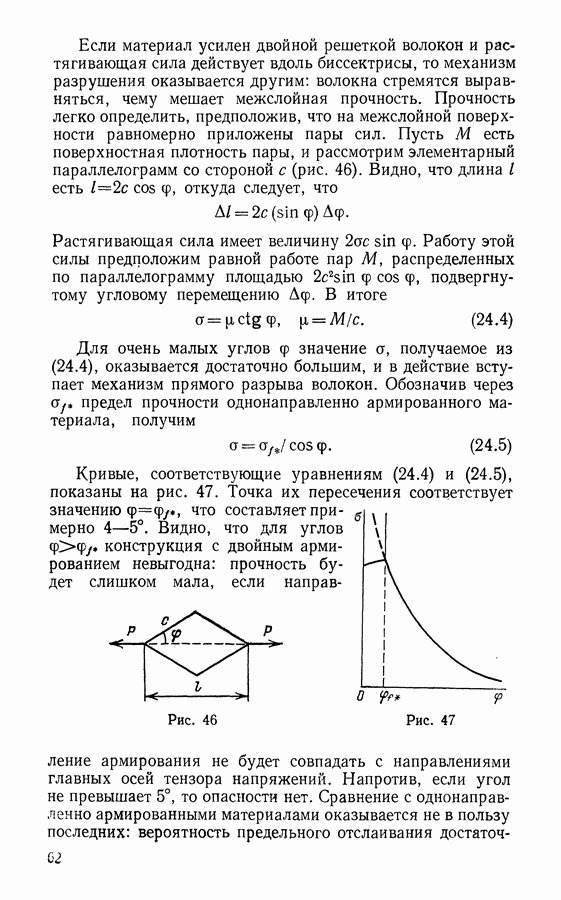
- § 24. Прочность слоистых композитов
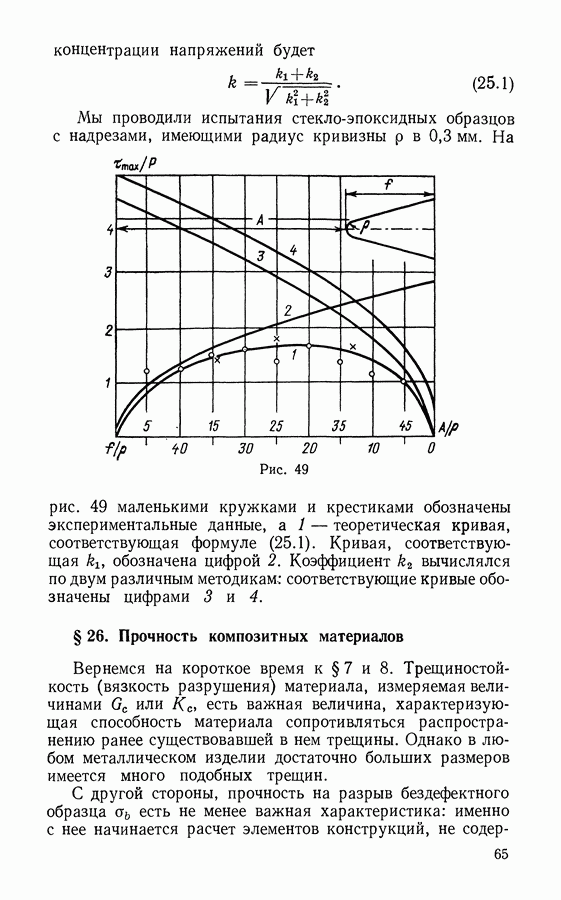
- § 25. Концентрация напряжений в композитах
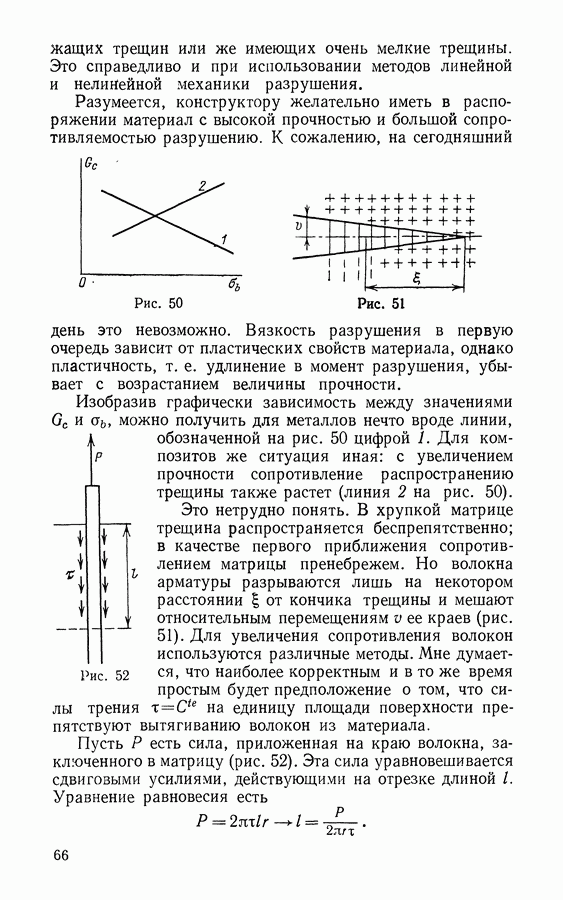
- § 26. Прочность композитных материалов
- ЗАКЛЮЧЕНИЕ