| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Глава 2. МЕХАНИКА РАСПРОСТРАНЕНИЯ ТРЕЩИН
§ 5. Теория Гриффитса
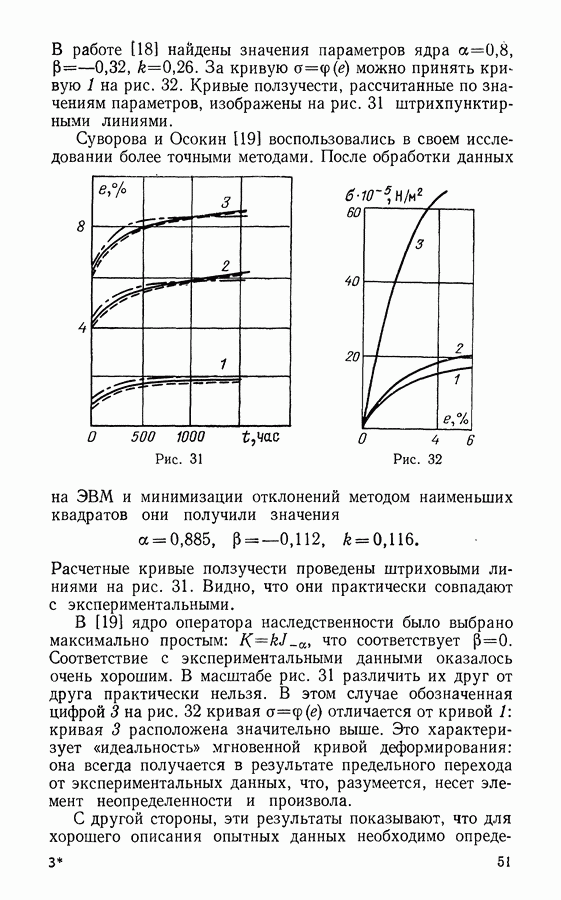
Хорошо известно, что теоретическая прочность твердых тел, рассчитанная по той или иной атомистической модели, во много раз превосходит реальную прочность (в сотни или даже тысячи раз). Гриффитс (1920) первым предложил объяснение этого факта: он предположил, что любое реальное тело содержит маленькие трещинки, которые могут либо увеличиваться под нагрузкой, либо же случайным образом оставаться такими же.
Анализ размерностей позволяет «на пальцах» получить результат Гриффитса. Рассмотрим часть тела, подверженную усилиям растяжения и находящуюся в условиях однородной деформации. Напряжение описывается одной компонентой а, модуль упругости есть  упругая энергия на единицу объема есть
упругая энергия на единицу объема есть

Здесь опущен множитель 1/2, как, впрочем, и все другие безразмерные множители ниже.
Предположим, что наше тело содержит лишь круговую трещину радиуса  Вокруг трещины происходит разгрузка. С точностью до безразмерного коэффициента полная энергия будет (так как объем имеет размер куба с ребром
Вокруг трещины происходит разгрузка. С точностью до безразмерного коэффициента полная энергия будет (так как объем имеет размер куба с ребром  Изменение упругой энергии тогда будет (с точностью до безразмерного множителя)
Изменение упругой энергии тогда будет (с точностью до безразмерного множителя)

Если размер трещины станет  то вариация упругой энергии (с точностью до безразмерного множителя) будет
то вариация упругой энергии (с точностью до безразмерного множителя) будет

Это уменьшение упругой энергии может быть компенсировано увеличением поверхностной энергии

Если уравнение энергетического баланса содержит лишь эти два члена, то приравнивая (5.3) и (5.4), получим (с точностью до безразмерного множителя) формулу Гриффитса

Коэффициент С не может быть, разумеется, определен лишь на основе анализа размерностей.
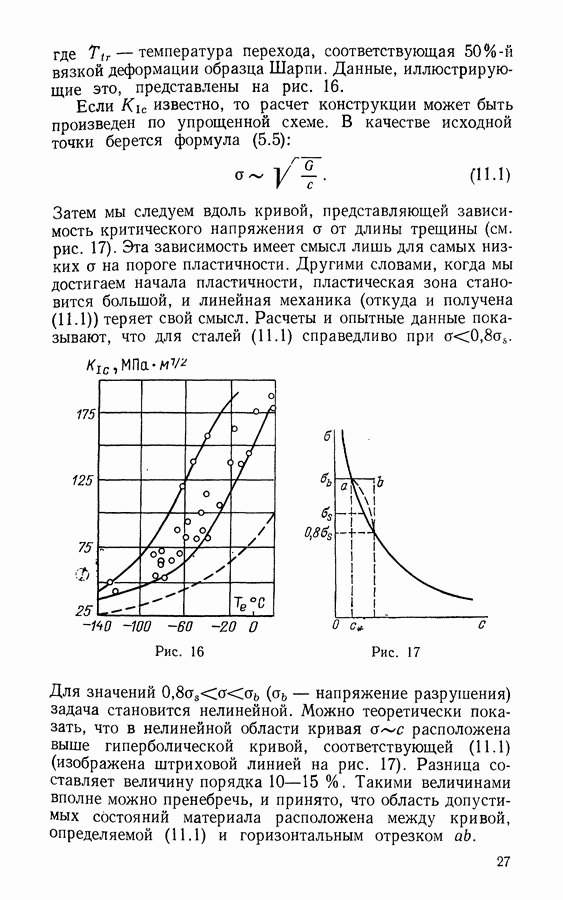
Для стекла значение у, входящего в (5.5), оказывается достаточно близким к значениям, получаемым различными физическими методами. Напротив, для металлов величина у из (5.5) оказывается на 3 порядка больше, чем определяемая поверхностной энергией.

Рис. 6
Объяснение данному факту было дано Дж. Ирвином и Е. О. Орованом. И действительно, перед кончиком трещины расположена пластическая зона (см. рис. 6). Распространение трещины сопровождается работой пластической деформации. Пусть  есть величина этой работы на единицу длины трещины и на единичное ее приращение. Величина
есть величина этой работы на единицу длины трещины и на единичное ее приращение. Величина  имеет размерность силы на единицу длины, и поэтому называется силой сопротивления распространению трещины. Если глубина пластической зоны
имеет размерность силы на единицу длины, и поэтому называется силой сопротивления распространению трещины. Если глубина пластической зоны  мала, т. е. то результаты анализа размерностей справедливы и справедлива формула (5.5), где у заменяется на
мала, т. е. то результаты анализа размерностей справедливы и справедлива формула (5.5), где у заменяется на 
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- Глава 1. ОСНОВНЫЕ ПОНЯТИЯ
- § 1. Твердое тело
- § 2. Уравнения состояния
- § 3. Ползучесть, усталость, пластичность
- § 4. Разрушение вследствие геометрических изменений
- Глава 2. МЕХАНИКА РАСПРОСТРАНЕНИЯ ТРЕЩИН
- § 5. Теория Гриффитса
- § 6. Антиплоская деформация
- § 7. Работа продвижения трещины
- § 8. Плоская деформация
- § 9. Модель Панасюка — Леонова — Дагдейла
- § 10. Интеграл Райса — Черепанова
- § 11. Выводы главы 2
- Глава 3. ПОЛЗУЧЕСТЬ И РАЗРУШЕНИЕ МЕТАЛЛОВ ПРИ ВЫСОКИХ ТЕМПЕРАТУРАХ
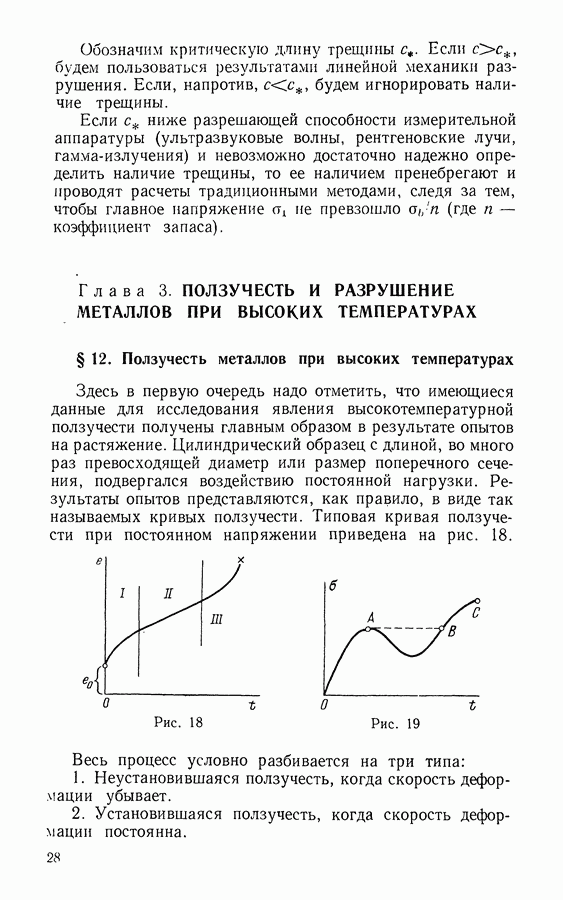
- § 12. Ползучесть металлов при высоких температурах
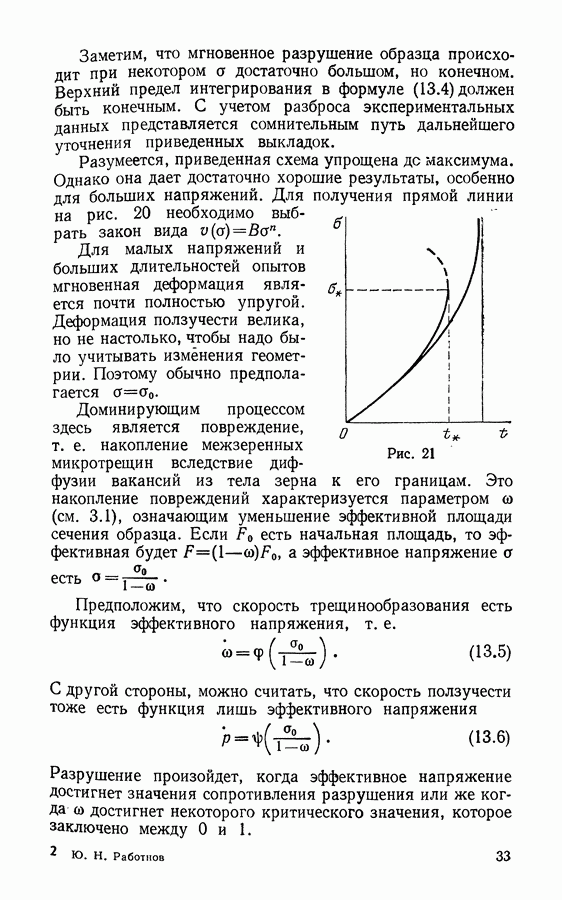
- § 13. Разрушение при растяжении
- § 14. Сложное напряженное состояние
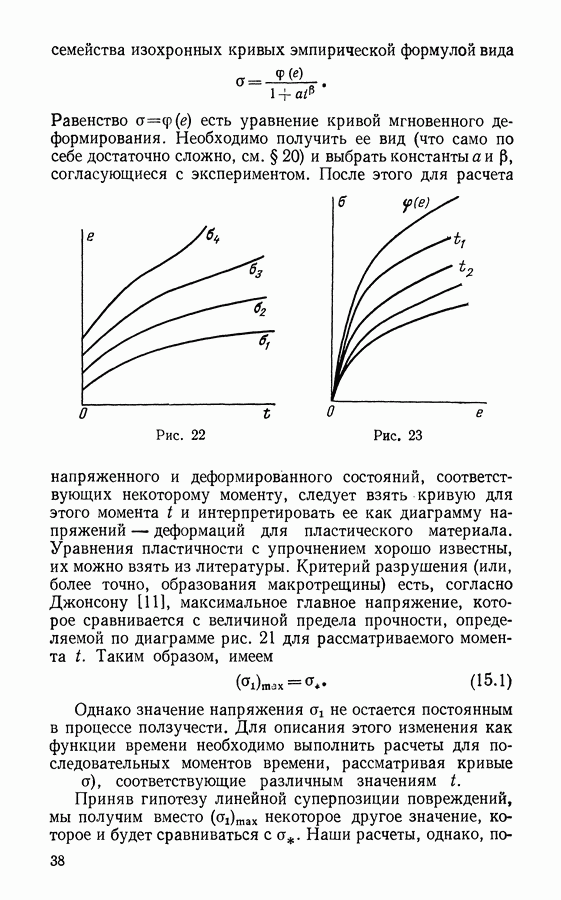
- § 15. Техническая теория. Изохронные кривые ползучести
- § 16. Разрушение при кратковременной ползучести
- § 17. Концентрация напряжений
- Глава 4. ЛИНЕЙНАЯ И НЕЛИНЕЙНАЯ НАСЛЕДСТВЕННОСТЬ
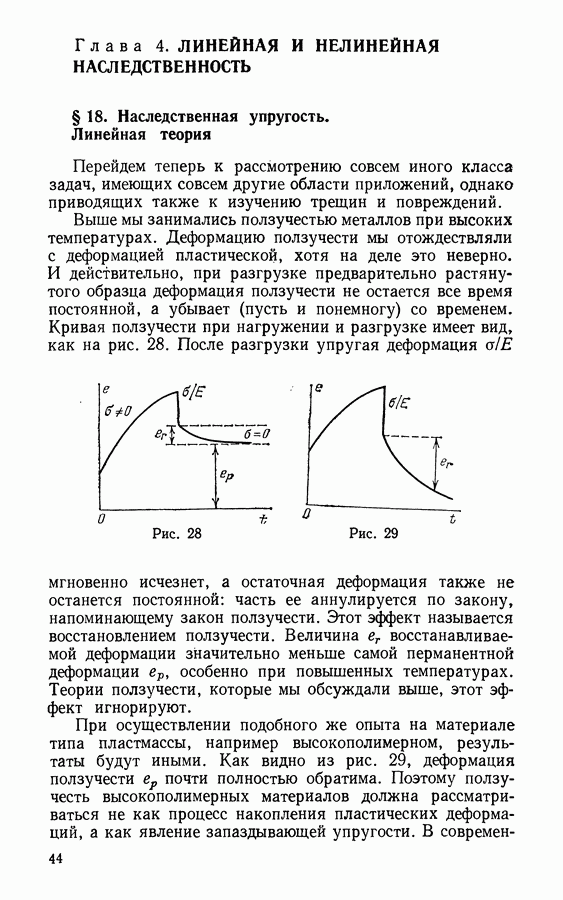
- § 18. Наследственная упругость. Линейная теория
- § 19. Задача о росте трещины
- § 20. Нелинейная наследственность
- Глава 5. МЕХАНИКА КОМПОЗИТНЫХ МАТЕРИАЛОВ
- § 21. Композиты волокнистого строения
- § 22. Слоистые упругие композиты
- § 23. Предельное состояние пластической композитной структуры
- § 24. Прочность слоистых композитов
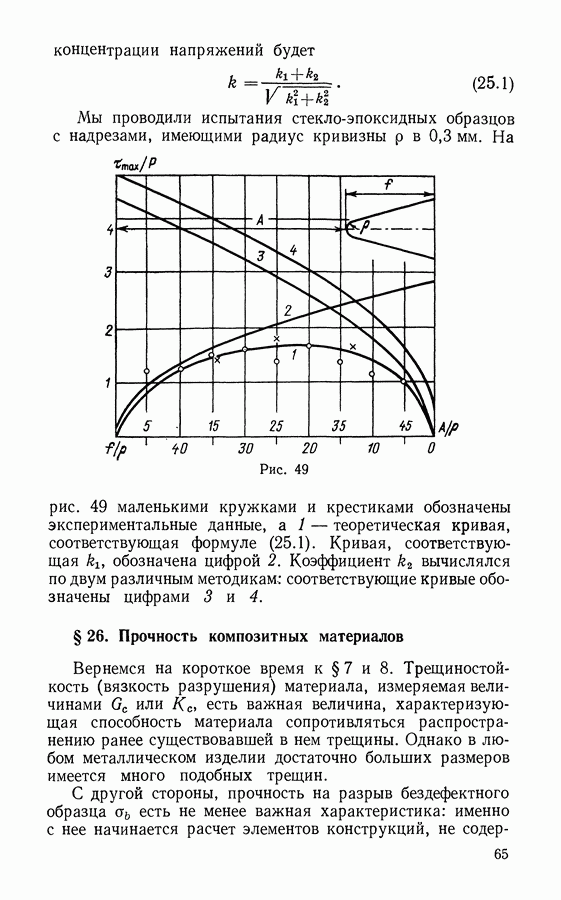
- § 25. Концентрация напряжений в композитах
- § 26. Прочность композитных материалов
- ЗАКЛЮЧЕНИЕ