| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 20. Нелинейная наследственность
Поведение большинства полимеров является нелинейным, и напряжения в общем случае не будут достаточно малыми. Следуя идее Фреше, Вольтерра предложил записать уравнение состояния в виде 

(интегралы Стилтьеса). Эта идея была забыта на протяжении полувека, и лишь в 60-х годах ею стали пользоваться для интерпретации опытных данных. Одной из первых публикаций в этом направлении явилась работа [15], где соотношение (20.1) использовалось для описания ползучести полипропилена. Немного позднее Финдли с сотрудниками начал публикацию серии исследований по данной теме [16].
Отметим, что во всех этих работах рассматривались материалы, поведение которых не слишком отличалось от линейного. Приняв, что закон ползучести при растяжении и сжатии один и тот же, авторы удерживали в формальном ряде (20.1) лишь два члена и описывали поведение материала с помощью двух ядер 
Обратная формула, выражающая а как функционал от  имеет структуру, аналогичную (20.1), однако с расчетной точки зрения она не столь удобна.
имеет структуру, аналогичную (20.1), однако с расчетной точки зрения она не столь удобна.
В принципе испытания на ползучесть при постоянной нагрузке позволяют построить оба ядра  Однако вследствие вида матрицы системы линейных уравнений, из которых определяются
Однако вследствие вида матрицы системы линейных уравнений, из которых определяются  результаты часто оказываются неустойчивыми [17].
результаты часто оказываются неустойчивыми [17].
С другой стороны, точное описание ползучести с помощью трех ядер часто невозможно, если деформации не являются малыми: кривая мгновенного деформирования не может быть удовлетворительно описана полиномом третьей степени. Если же увеличивать число членов в разложении (20.1), расчетные трудности резко возрастают. Вот почему мы рассмотрим здесь упрощенную теорию, основанную на гипотезе, что все ядра (20,1) имеют одну структуру, т. е.

Положим теперь 

и перепишем (20.1) в виде

Формальный ряд (20.4) определяет  как функцию
как функцию  Предположив возможности ее обращения, запишем
Предположив возможности ее обращения, запишем

или

т. е. основное уравнение теории нелинейной наследственности.
Обобщение на неодномерный случай не представляет труда. Вводятся модифицированные напряжения

и предполагается существование потенциала  как функции
как функции  такого, что
такого, что

Для линейной наследственности в случае изотропного тела получим 

где коэффициент Пуассона есть просто постоянный множитель, а не оператор. Это допущение часто используется в линейной теории из-за трудностей экспериментального определения данных для построения оператора 
В случае нелинейной теории мы не располагаем достаточным числом экспериментальных данных, чтобы подтвердить или опровергнуть гипотезу (20.6).
Вернемся вновь к одномерному случаю. Пусть в уравнении (20.5).
Тогда

где есть хорошо известная функция времени. Уравнение (20.7) описывает семейство изохронных кривых ползучести, которые подобны друг другу. На это подобие уже указывалось в § 15. Уравнение  определяет мгновенную кривую «напряжения — деформации», кривую, которую в действительности получить невозможно, так как скорость деформации есть всегда величина конечная. Мы будем рассматривать эту кривую как некую идеальную, воображаемую. Это можно сделать, выбрав определенным образом форму ядра оператора
определяет мгновенную кривую «напряжения — деформации», кривую, которую в действительности получить невозможно, так как скорость деформации есть всегда величина конечная. Мы будем рассматривать эту кривую как некую идеальную, воображаемую. Это можно сделать, выбрав определенным образом форму ядра оператора  к примеру
к примеру 
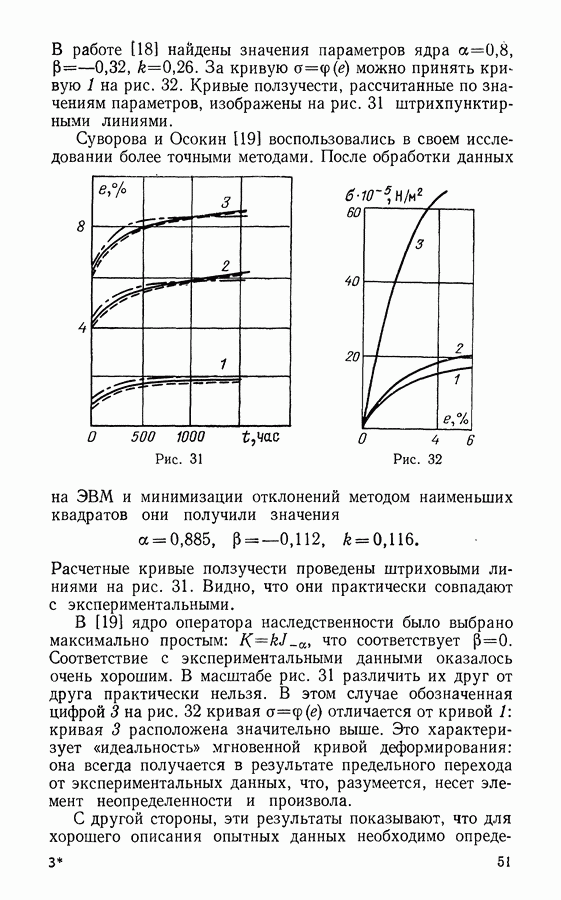
На рис. 31 представлены кривые ползучести пластического материала, армированного стекловолокнами (сплошные линии). Линии 1, 2,3 соответствуют значениям растягивающего напряжения в 8,1, 12,2 и  Ядро оператора К выбрано в виде
Ядро оператора К выбрано в виде

в работе [18] найдены значения параметров ядра  За кривую
За кривую  можно принять кривую 1 на рис. 32. Кривые ползучести, рассчитанные по значениям параметров, изображены на рис. 31 штрихпунктирными линиями.
можно принять кривую 1 на рис. 32. Кривые ползучести, рассчитанные по значениям параметров, изображены на рис. 31 штрихпунктирными линиями.
Суворова и Осокин [19] воспользовались в своем исследовании более точными методами. данных

Рис. 31

Рис. 32
После обработкина ЭВМ и минимизации отклонений методом наименьших квадратов они получили значения

Расчетные кривые ползучести проведены штриховыми линиями на рис. 31. Видно, что они практически совпадают с экспериментальными.
В [19] ядро оператора наследственности было выбрано максимально простым: что соответствует 
Соответствие с экспериментальными данными оказалось очень хорошим. В масштабе рис. 31 различить их друг от друга практически нельзя. В этом случае обозначенная цифрой 3 на рис. 32 кривая  отличается от кривой 1: кривая 3 расположена значительно выше. Это характеризует «идеальность» мгновенной кривой деформирования: она всегда получается в результате предельного перехода от экспериментальных данных, что, разумеется, несет элемент неопределенности и произвола.
отличается от кривой 1: кривая 3 расположена значительно выше. Это характеризует «идеальность» мгновенной кривой деформирования: она всегда получается в результате предельного перехода от экспериментальных данных, что, разумеется, несет элемент неопределенности и произвола.
С другой стороны, эти результаты показывают, что для хорошего описания опытных данных необходимо
определить значения лишь двух констант, а не трех. Так, выбрав произвольно  мы затем определили (
мы затем определили ( Суворова и Осокин положили и затем нашли
Суворова и Осокин положили и затем нашли  Соответствие между теорией и экспериментом было, тем не менее, хорошим.
Соответствие между теорией и экспериментом было, тем не менее, хорошим.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- Глава 1. ОСНОВНЫЕ ПОНЯТИЯ
- § 1. Твердое тело
- § 2. Уравнения состояния
- § 3. Ползучесть, усталость, пластичность
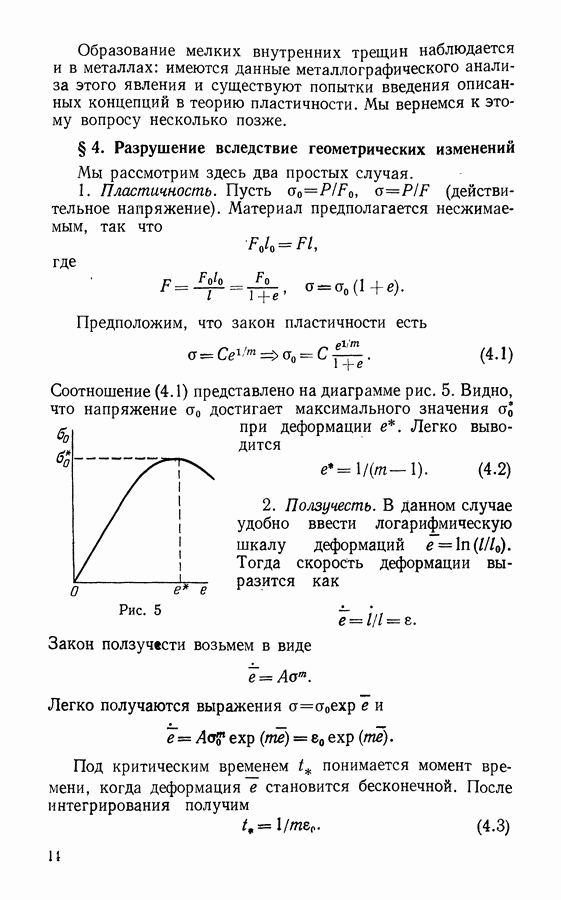
- § 4. Разрушение вследствие геометрических изменений
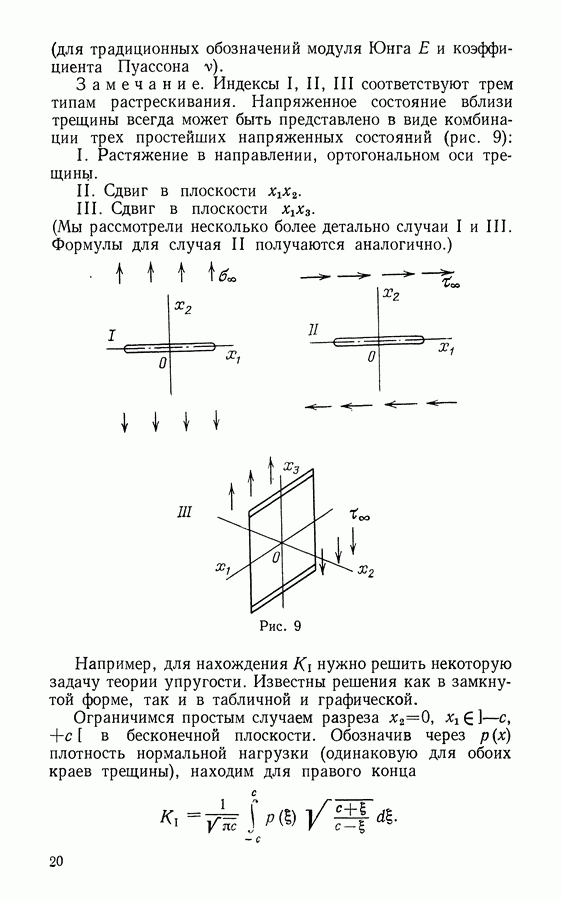
- Глава 2. МЕХАНИКА РАСПРОСТРАНЕНИЯ ТРЕЩИН
- § 5. Теория Гриффитса
- § 6. Антиплоская деформация
- § 7. Работа продвижения трещины
- § 8. Плоская деформация
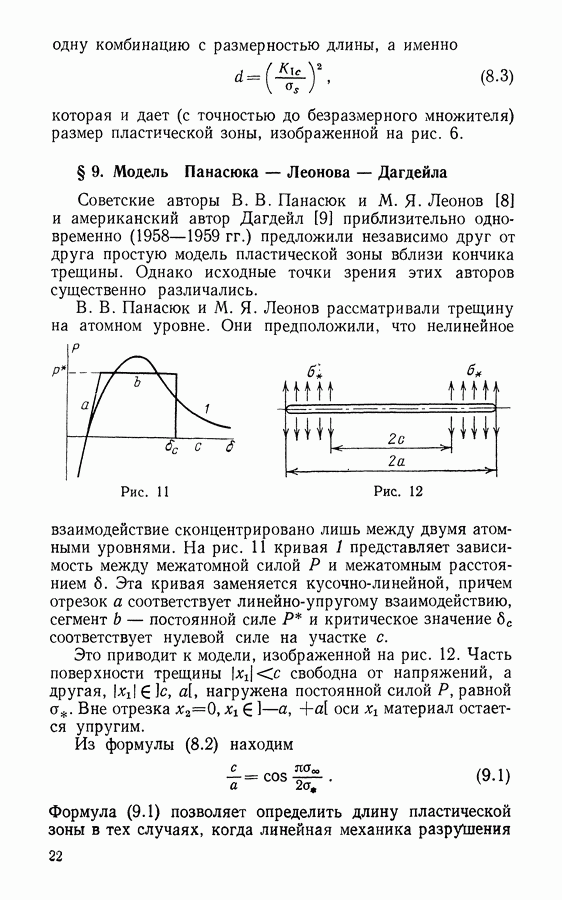
- § 9. Модель Панасюка — Леонова — Дагдейла
- § 10. Интеграл Райса — Черепанова
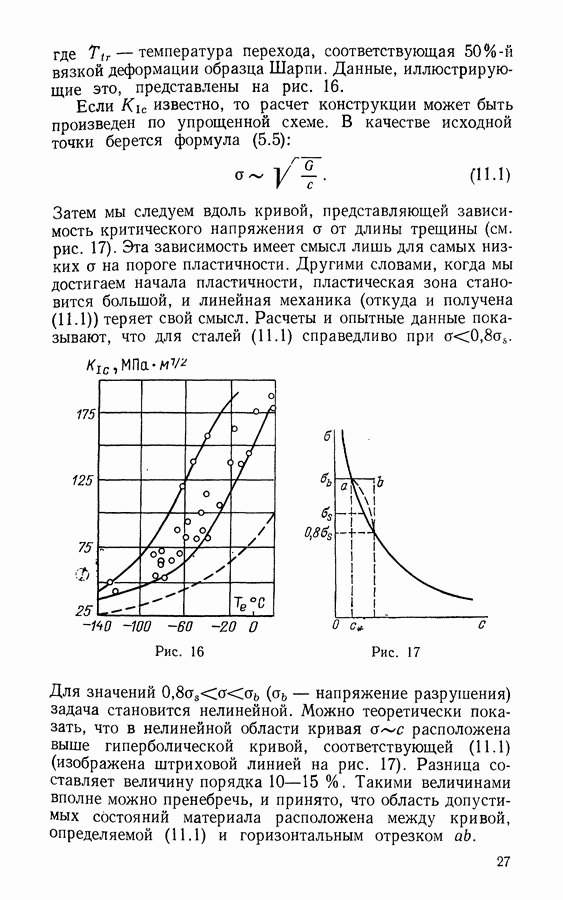
- § 11. Выводы главы 2
- Глава 3. ПОЛЗУЧЕСТЬ И РАЗРУШЕНИЕ МЕТАЛЛОВ ПРИ ВЫСОКИХ ТЕМПЕРАТУРАХ
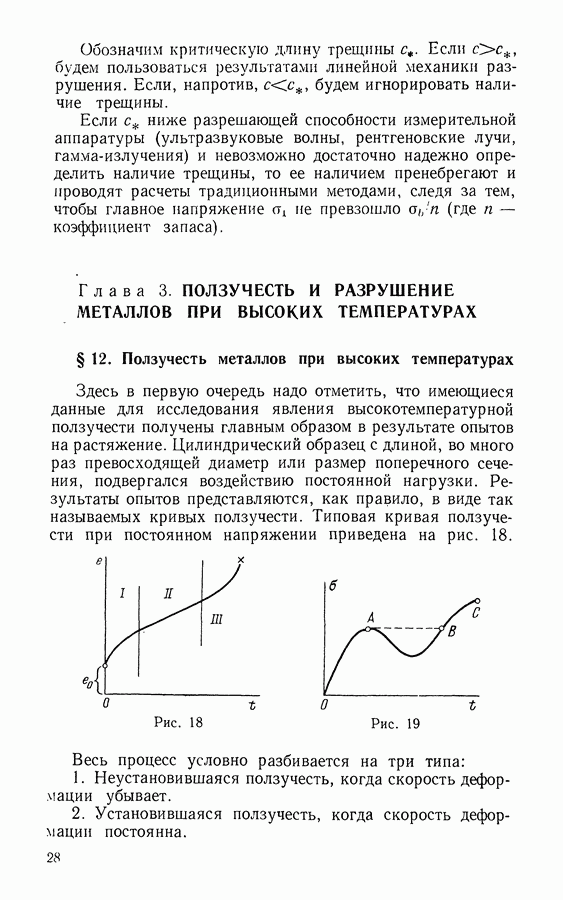
- § 12. Ползучесть металлов при высоких температурах
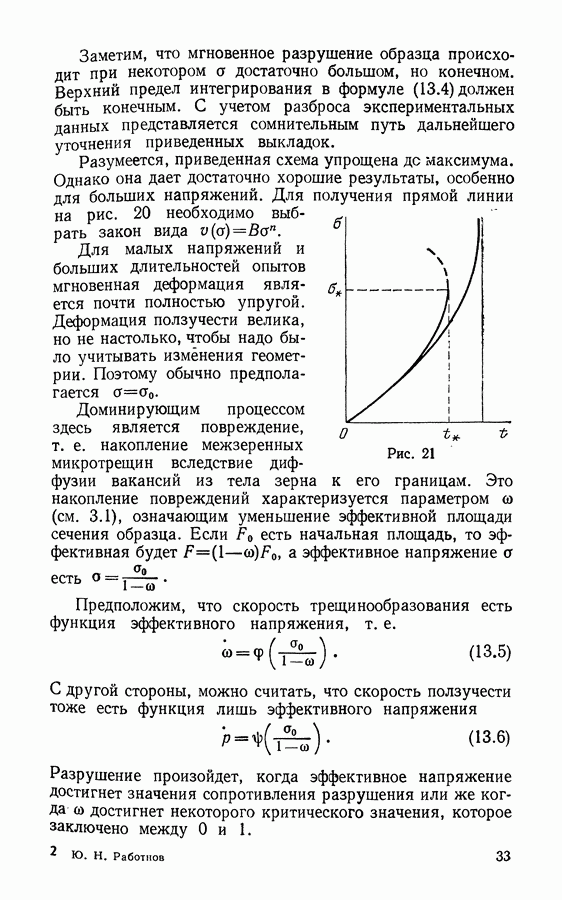
- § 13. Разрушение при растяжении
- § 14. Сложное напряженное состояние
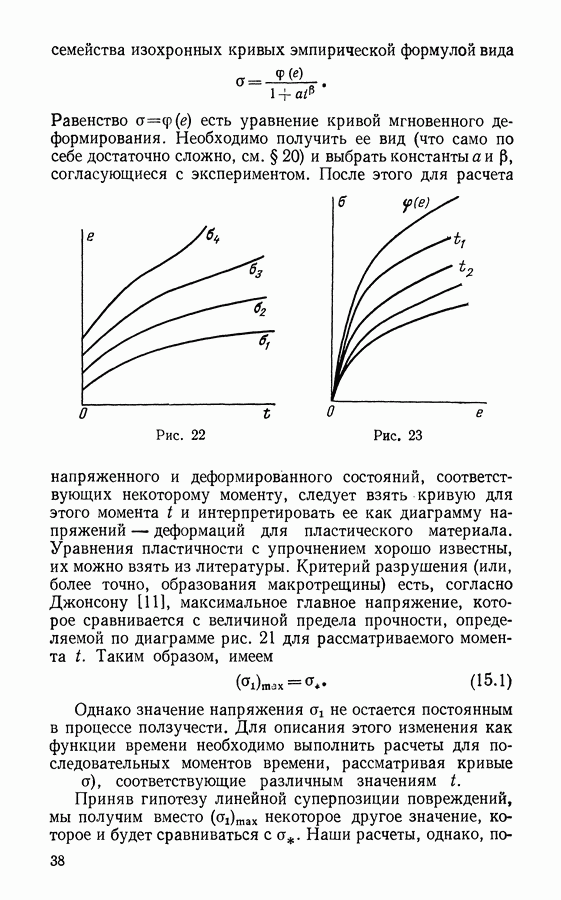
- § 15. Техническая теория. Изохронные кривые ползучести
- § 16. Разрушение при кратковременной ползучести
- § 17. Концентрация напряжений
- Глава 4. ЛИНЕЙНАЯ И НЕЛИНЕЙНАЯ НАСЛЕДСТВЕННОСТЬ
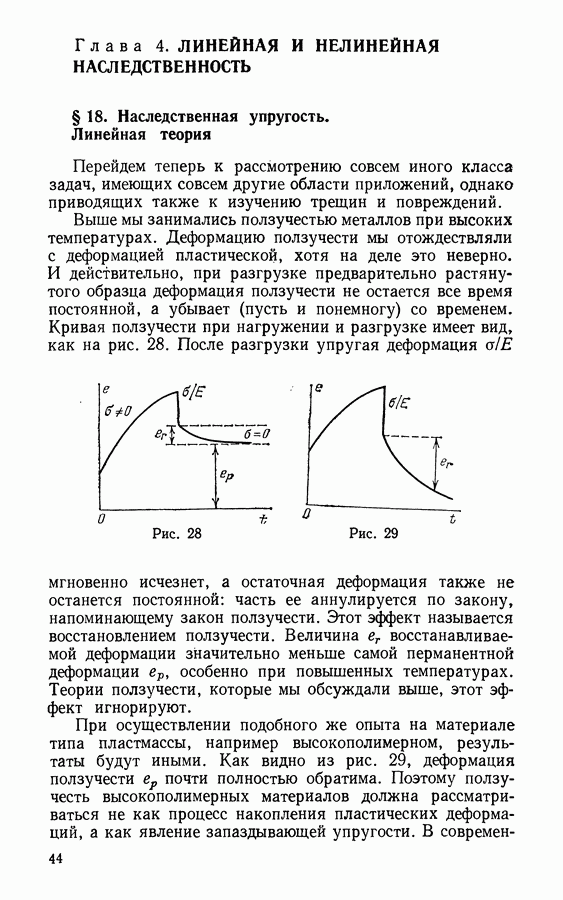
- § 18. Наследственная упругость. Линейная теория
- § 19. Задача о росте трещины
- § 20. Нелинейная наследственность
- Глава 5. МЕХАНИКА КОМПОЗИТНЫХ МАТЕРИАЛОВ
- § 21. Композиты волокнистого строения
- § 22. Слоистые упругие композиты
- § 23. Предельное состояние пластической композитной структуры
- § 24. Прочность слоистых композитов
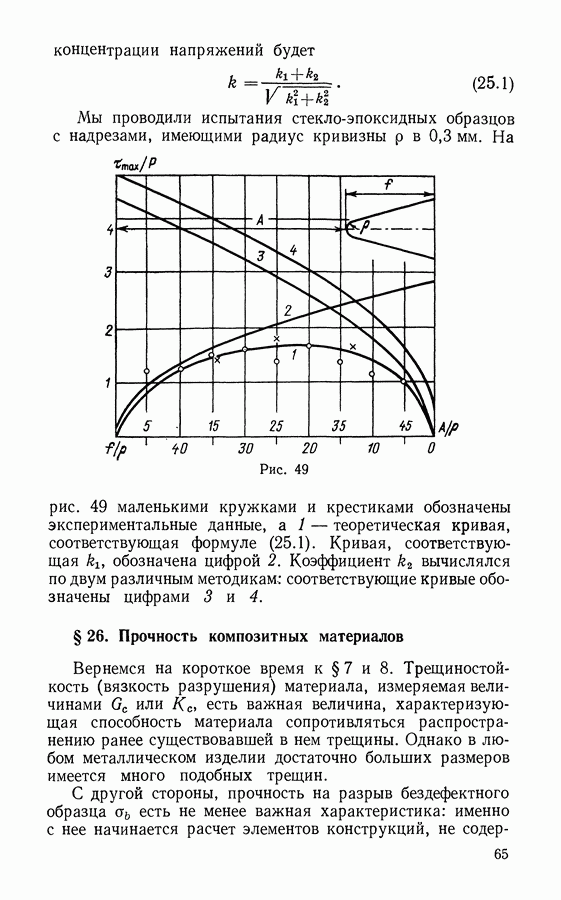
- § 25. Концентрация напряжений в композитах
- § 26. Прочность композитных материалов
- ЗАКЛЮЧЕНИЕ