| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 11. Выводы главы 2
Мы не хотим настаивать на применении практических методов или на экспериментальном определении прочности. Отметим лишь, что нелинейная механика может быть применена здесь лишь в редких случаях.
Для мягких сталей со значительной прочностью значение  (рассчитанное или измеренное) может быть того же порядка, что и величины линейных размеров образца. Для получения достаточно надежного значения
(рассчитанное или измеренное) может быть того же порядка, что и величины линейных размеров образца. Для получения достаточно надежного значения  необходимо, таким образом, выбирать громоздкие образцы, что сопряжено с трудностями как их изготовления, так и испытания.
необходимо, таким образом, выбирать громоздкие образцы, что сопряжено с трудностями как их изготовления, так и испытания.
Этим и объясняется большой интерес к развитию методов, основанных на  -интеграле, например на
-интеграле, например на 
Заметим, что  с понижением температуры убывает, хотя
с понижением температуры убывает, хотя  растет с убыванием температуры. В итоге пластическая зона становится более узкой, и появляется возможность определения
растет с убыванием температуры. В итоге пластическая зона становится более узкой, и появляется возможность определения  на образцах достаточно малых размеров.
на образцах достаточно малых размеров.
Для перлитных сталей  есть функция температурного превышения
есть функция температурного превышения

где  температура перехода, соответствующая
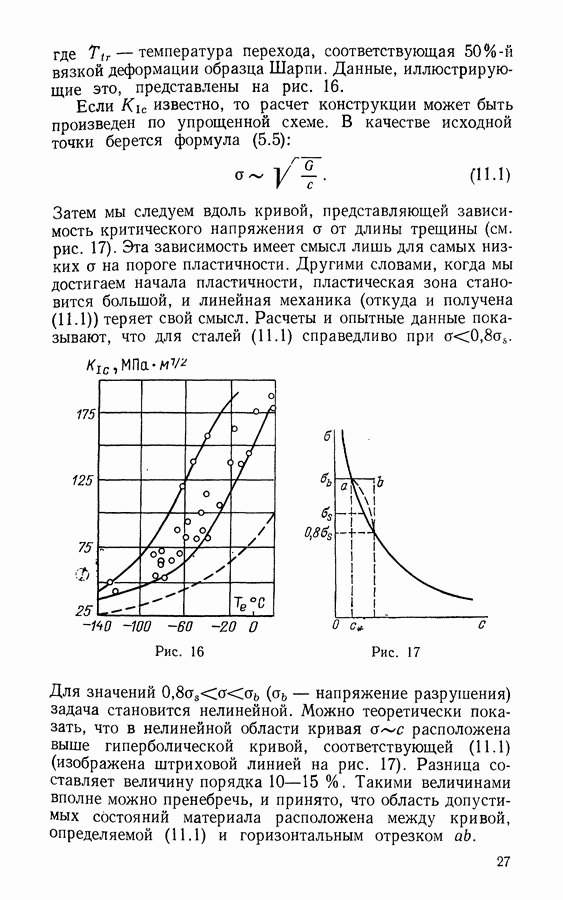
температура перехода, соответствующая  вязкой деформации образца Шарпи. Данные, иллюстрирующие это, представлены на рис. 16.
вязкой деформации образца Шарпи. Данные, иллюстрирующие это, представлены на рис. 16.
Если  известно, то расчет конструкции может быть произведен по упрощенной схеме. В качестве исходной точки берется формула (5.5):
известно, то расчет конструкции может быть произведен по упрощенной схеме. В качестве исходной точки берется формула (5.5):

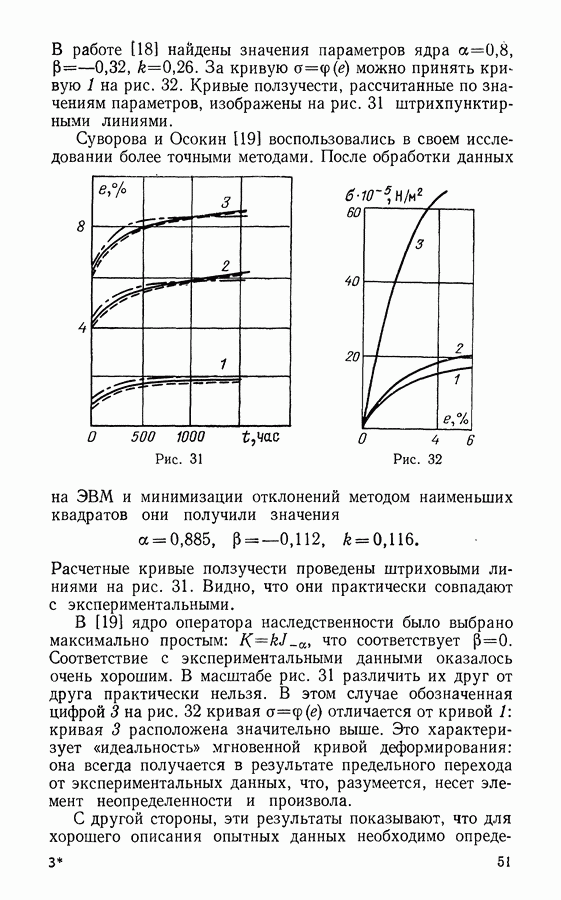
Затем мы следуем вдоль кривой, представляющей зависимость критического напряжения а от длины трещины (см. рис. 17). Эта зависимость имеет смысл лишь для самых низких а на пороге пластичности. Другими словами, когда мы достигаем начала пластичности, пластическая зона становится большой, и линейная механика (откуда и получена  теряет свой смысл. Расчеты и опытные данные показывают, что для сталей (11.1) справедливо при
теряет свой смысл. Расчеты и опытные данные показывают, что для сталей (11.1) справедливо при 

Рис. 16

Рис. 17
Для значений  напряжение разрушения) задача становится нелинейной. Можно теоретически показать, что в нелинейной области кривая
напряжение разрушения) задача становится нелинейной. Можно теоретически показать, что в нелинейной области кривая  расположена выше гиперболической кривой, соответствующей (11.1) (изображена штриховой линией на рис. 17). Разница составляет величину порядка
расположена выше гиперболической кривой, соответствующей (11.1) (изображена штриховой линией на рис. 17). Разница составляет величину порядка  Такими величинами вполне можно пренебречь, и принято, что область допустимых состояний материала расположена между кривой, определяемой (11.1) и гооизонтальным отрезком
Такими величинами вполне можно пренебречь, и принято, что область допустимых состояний материала расположена между кривой, определяемой (11.1) и гооизонтальным отрезком 
Обозначим критическую длину трещины с. Если будем пользоваться результатами линейной механики разрушения. Если, напротив, будем игнорировать наличие трещины.
Если с ниже разрешающей способности измерительной аппаратуры (ультразвуковые волны, рентгеновские лучи, гамма-излучения) и невозможно достаточно надежно определить наличие трещины, то ее наличием пренебрегают и проводят расчеты традиционными методами, следя за тем, чтобы главное напряжение  не превзошло
не превзошло  (где
(где  - коэффициент запаса).
- коэффициент запаса).
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- Глава 1. ОСНОВНЫЕ ПОНЯТИЯ
- § 1. Твердое тело
- § 2. Уравнения состояния
- § 3. Ползучесть, усталость, пластичность
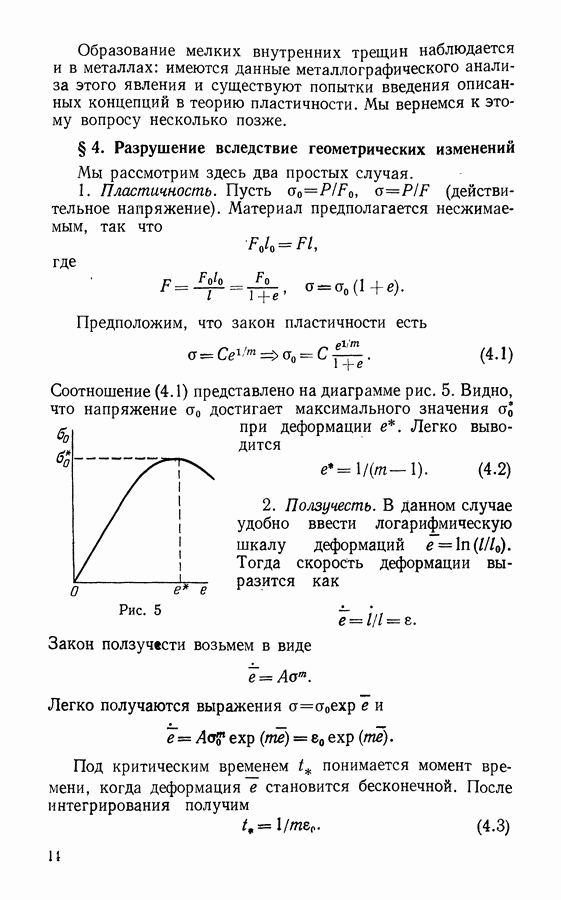
- § 4. Разрушение вследствие геометрических изменений
- Глава 2. МЕХАНИКА РАСПРОСТРАНЕНИЯ ТРЕЩИН
- § 5. Теория Гриффитса
- § 6. Антиплоская деформация
- § 7. Работа продвижения трещины
- § 8. Плоская деформация
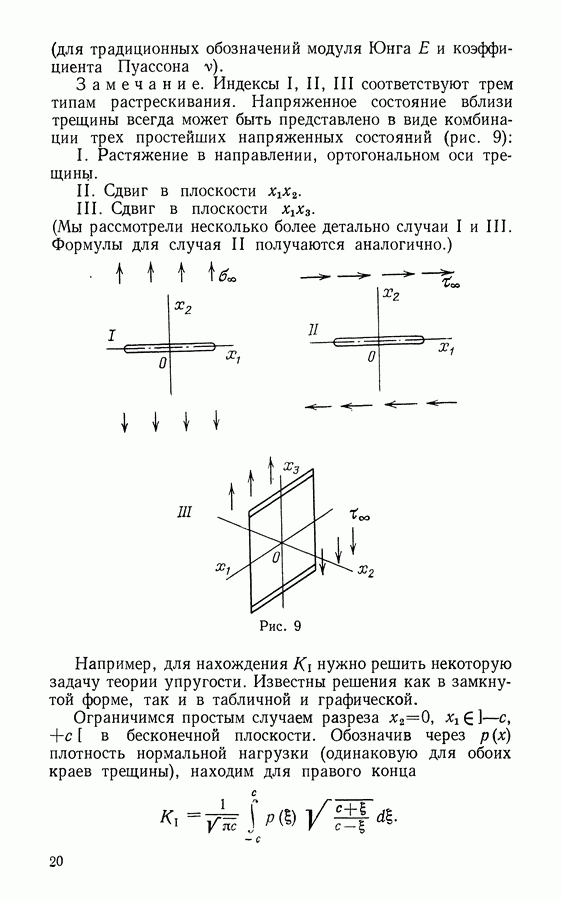
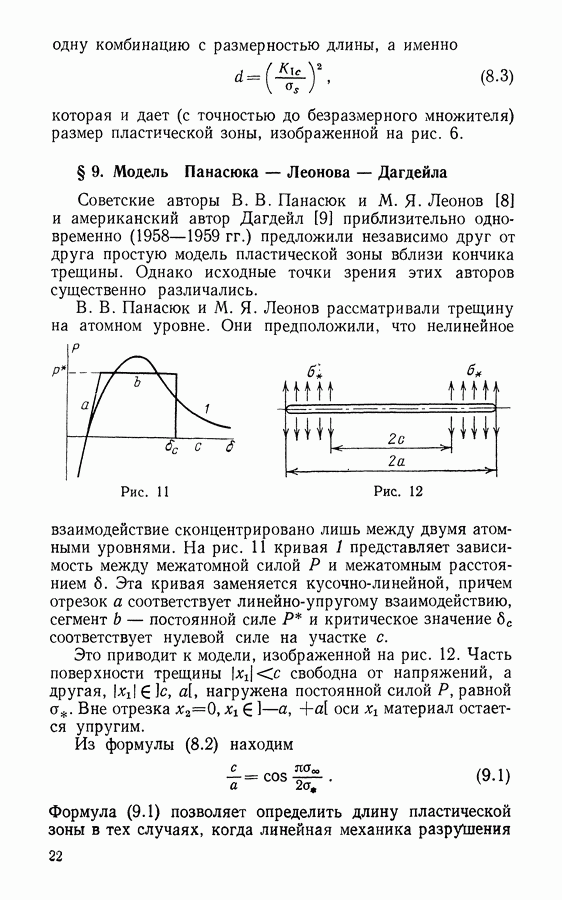
- § 9. Модель Панасюка — Леонова — Дагдейла
- § 10. Интеграл Райса — Черепанова
- § 11. Выводы главы 2
- Глава 3. ПОЛЗУЧЕСТЬ И РАЗРУШЕНИЕ МЕТАЛЛОВ ПРИ ВЫСОКИХ ТЕМПЕРАТУРАХ
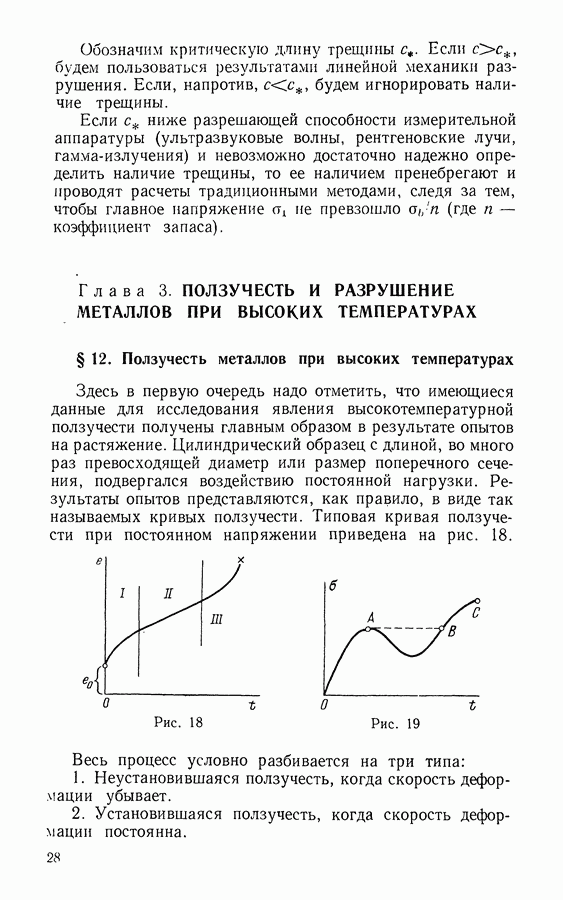
- § 12. Ползучесть металлов при высоких температурах
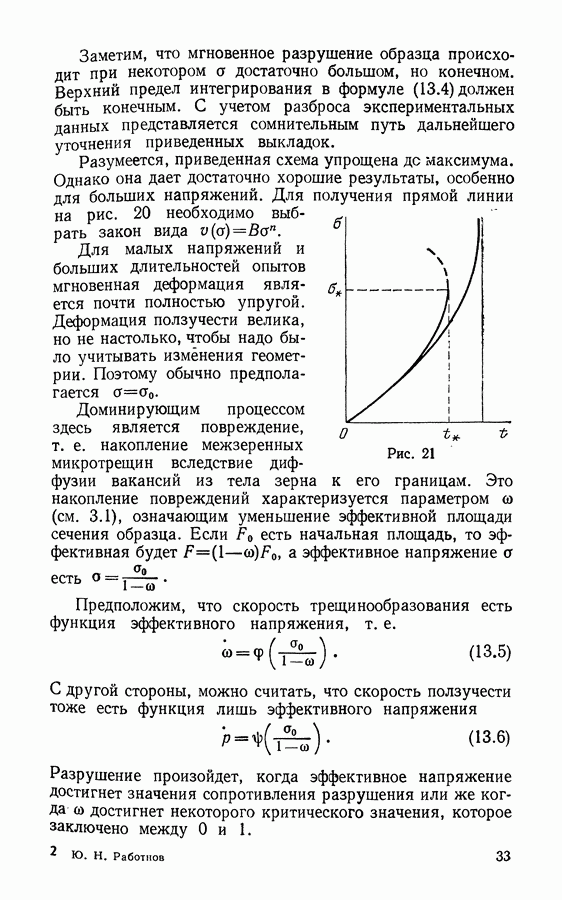
- § 13. Разрушение при растяжении
- § 14. Сложное напряженное состояние
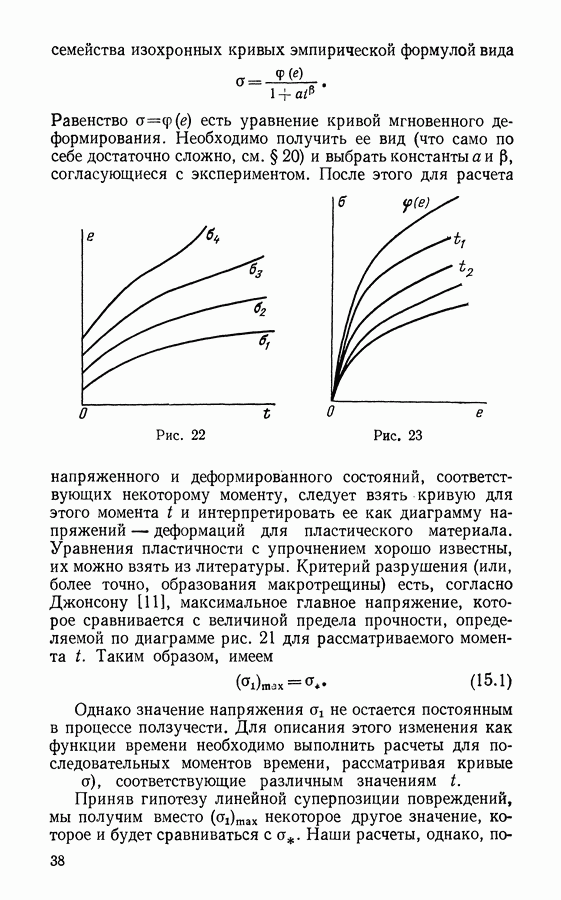
- § 15. Техническая теория. Изохронные кривые ползучести
- § 16. Разрушение при кратковременной ползучести
- § 17. Концентрация напряжений
- Глава 4. ЛИНЕЙНАЯ И НЕЛИНЕЙНАЯ НАСЛЕДСТВЕННОСТЬ
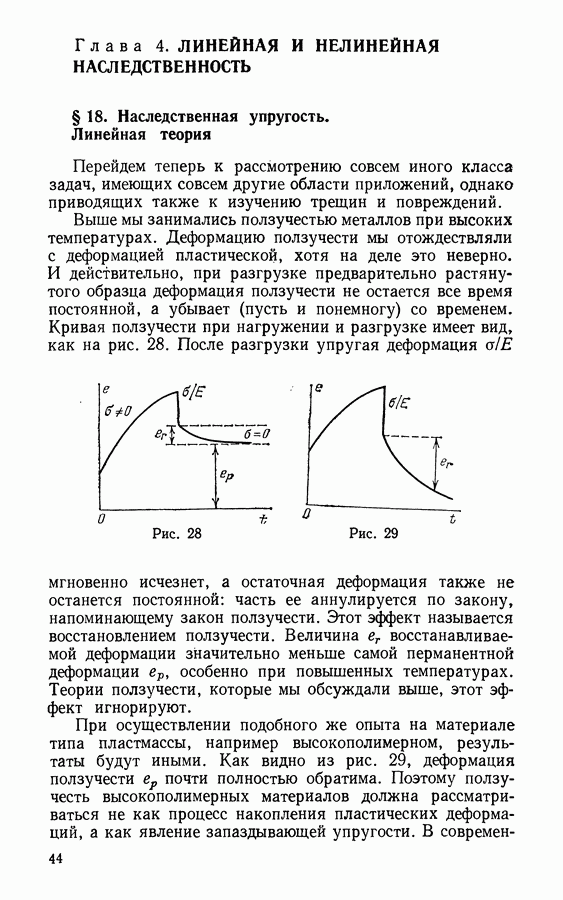
- § 18. Наследственная упругость. Линейная теория
- § 19. Задача о росте трещины
- § 20. Нелинейная наследственность
- Глава 5. МЕХАНИКА КОМПОЗИТНЫХ МАТЕРИАЛОВ
- § 21. Композиты волокнистого строения
- § 22. Слоистые упругие композиты
- § 23. Предельное состояние пластической композитной структуры
- § 24. Прочность слоистых композитов
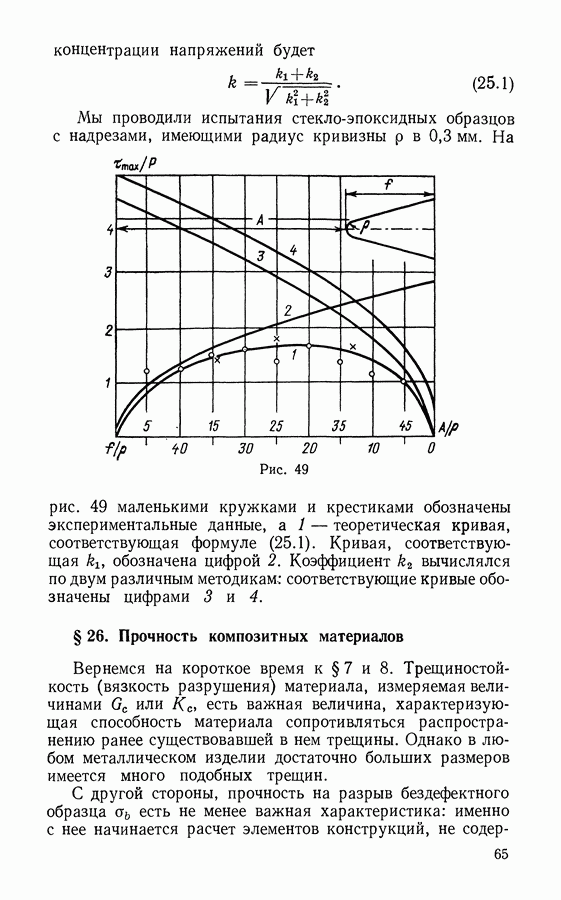
- § 25. Концентрация напряжений в композитах
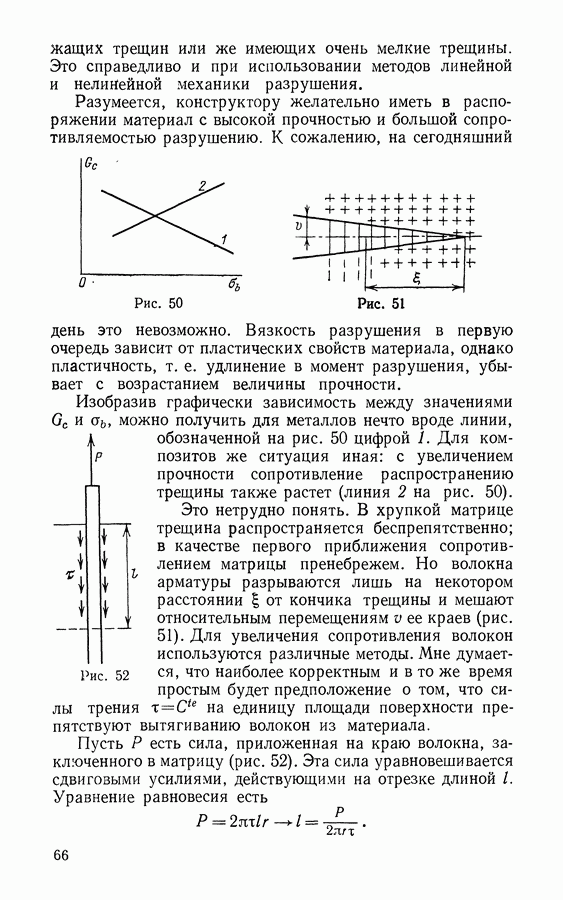
- § 26. Прочность композитных материалов
- ЗАКЛЮЧЕНИЕ