| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Газообразное состояние. Газовые законы
Бели энергия притяжения между молекулами меньше их кинетической энергии, то совокупность таких молекул будет существовать в виде газа. Индивидуальное вещество в газообразном состоянии характеризуется следующими величинами: Р — давлением; Т или t — температурой, измеряемой в градусах Кельвина или Цельсия; V — объемом; m — массой всего газа; М — молярной массой. Газовые законы устанавливают взаимосвязь между этими величинами. При этом используется простейшая модель газообразного состояния веществ — идеальный газ, которая основана на следующих допущениях: 1) между частицами газа отсутствуют силы взаимодействия; 2) сами частицы представляют собой материальные точки.
Вначале были установлены газовые законы, справедливые для постоянной массы данного газа (т.е.  ), и, кроме того, одна из оставшихся величин, (Р, V, Т) также поддерживается постоянной.
), и, кроме того, одна из оставшихся величин, (Р, V, Т) также поддерживается постоянной.
1. T=const (изотермический процесс).
Взаимосвязь между изменением Р и V выражается законом Бойля—Мариотта
 (4.1)
(4.1)
2. P=const (изобарический процесс).
Взаимосвязь между изменением V и t выражается законом Гей-Люссака

где а — коэффициент удельного объемного расширения, равный для всех газов  . Бели это значение подставить в уравнение (4.2) и температуру выражать в шкале Кельвина, то закон Гей-Люссака запишется так:
. Бели это значение подставить в уравнение (4.2) и температуру выражать в шкале Кельвина, то закон Гей-Люссака запишется так:
 (4.3)
(4.3)
3. V=const (изохорический процесс).
Взаимосвязь между  выражается законом Шарля
выражается законом Шарля

где  . В более удобной форме закон Шарля можно записать так:
. В более удобной форме закон Шарля можно записать так:
 (4.4)
(4.4)
На основе трёх частных законов можно легко вывести объединенный газовый закон (вывод — см. [Кузьменко, 1977, с. 112]), который выглядит следующим образом:
 (4.5)
(4.5)
Подчеркнем, что объединенный газовый закон, как и частные законы, справедлив только для постоянной массы данного газа.
Уравнение Клапейрона—Менделеева.
После того как было установлено экспериментально, что 1 моль любого газа при нормальных условиях  занимает объем
занимает объем  объединенный газовый закон для одного моля любого газа стали записывать так:
объединенный газовый закон для одного моля любого газа стали записывать так:

где R — универсальная газовая постоянная.
Действительно, объединенный газовый закон для любой постоянной массы газа (а значит, и для одного моля газа) имеет вид (4.5), но и для одного моля газа const имеет одно и то же значение для всех реальных газов при таких условиях, при которых они ведут себя как идеальный газ. Обозначив эту постоянную R, получим уравнение (4.6).
Газовая постоянная равна работе расширения 1 моля идеального газа при нагревании на 1 К при постоянном давлении.
Чтобы найти численное значение R, необходимо знать, какой объем занимает газ при каких-либо определенных значениях Р и Т. Проще всего считать условия нормальными, тогда

и в единицах СИ  .
.
Как будут меняться левая и правая части уравнения (4.6), если у нас будет не один, a v молей? Левая часть уравнения увеличивается в v раз, так как v молей займут в v раз больший объем, а правая часть не изменится (R — постоянная величина, а Т не зависит от числа молей). Чтобы уравнение (4.6) было справедливо для молей, надо умножить правую часть на 

где  число молей равно общей массе газа, деленной на молярную массу. Подставляя это значение в уравнение (4.7), получим
число молей равно общей массе газа, деленной на молярную массу. Подставляя это значение в уравнение (4.7), получим

Уравнение идеального газа в форме (4.7) и (4.8) называется уравнением Клапейрона—Менделеева, оно выражает взаимосвязь между всеми величинами, характеризующими газ, а поэтому является наиболее общим в приближении модели идеального газа.
Из уравнения Клапейрона—Менделеева можно вывести ряд простых, но важных следствий.
1) Многие газовые реакции происходят при постоянных температуре и давлении.
При этих условиях
 (4.9)
(4.9)
Уравнение (4.9) есть не что иное как закон Авогадро, который утверждает, что в равных объемах газов при постоянных температуре и давлении содержится одинаковое число молекул.
2) Другое интересное следствие касается плотности газов. Из уравнения (4.8) следует, что
 (4.10)
(4.10)
при постоянных давлении и температуре. Это означает, что при этих условиях плотность газа определяется только его молярной массой. Такой результат позволяет ввести понятие относительной плотности одного газа по другому:

(см. § 1). Эта величина показывает, во сколько раз первый газ тяжелее второго при одинаковых условиях.
3) Бели реакция происходит в замкнутом сосуде  ) при постоянной температуре, то
) при постоянной температуре, то
 (4.12)
(4.12)
Это соотношение означает, что в замкнутом сосуде при заданных условиях давление зависит только от общего числа молекул газов.
В заключение рассмотрим важное для многих задач понятие средней молярной массы смеси газов. Напомним, что для одного вещества молярная масса равна отношению массы к числу молей:

Точно такое же соотношение справедливо для смеси газов:

Поскольку газы в смеси всегда находятся при одинаковых условиях, то к ним применим закон Авогадро (4.9), и определение средней молярной массы можно переписать, заменив число молей на объем:

Рекомендуемая литература: [Кузьменко, 1977, гл. 4), [Третъяков, § 13], [Фримантл, т. 1, гл. 3], [Хомчепко, 1993, 1.11, 3.7].
| << Предыдущий параграф | Следующий параграф >> |
- ВВЕДЕНИЕ
- Глава I. ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ХИМИИ
- § 1. Предмет химии. Важнейшие понятия и законы химии
- Основные стехиометрические законы химии
- ЗАДАЧИ И УПРАЖНЕНИЯ
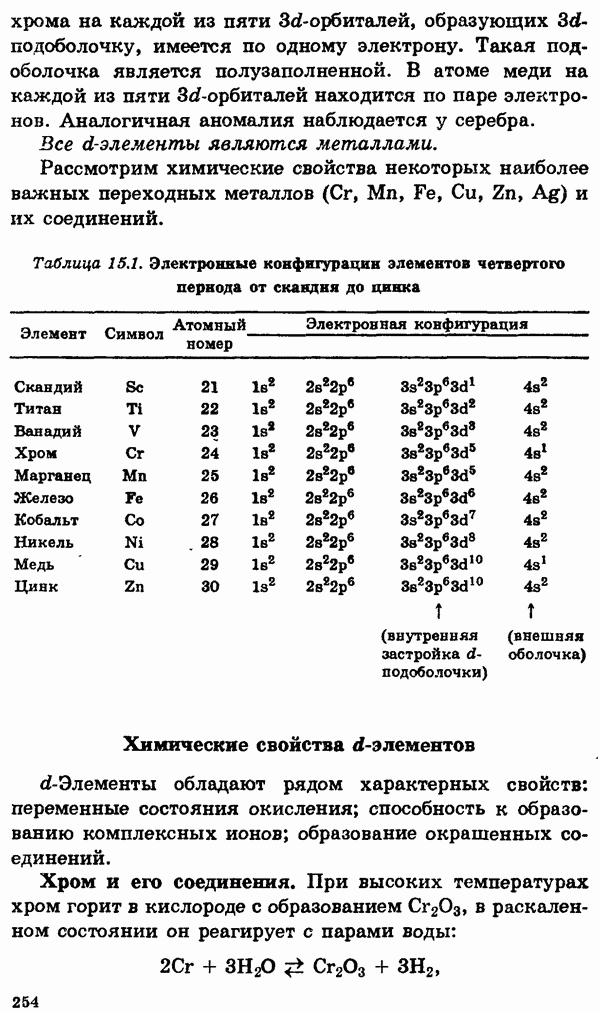
- § 2. Строение атома
- Электронные конфигурации атомов
- Ядро атома и радиоактивные превращения
- ЗАДАЧИ И УПРАЖНЕНИЯ
- § 3. Строение молекул. Химическая связь. Валентность элементов
- ЗАДАЧИ И УПРАЖНЕНИЯ
- § 4. Агрегатные состояния вещества
- Характерные свойства газов, жидкостей и твердых тел
- Газообразное состояние. Газовые законы
- ЗАДАЧИ И УПРАЖНЕНИЯ
- § 5. Закономерности протекания химических реакций
- Химическая кинетика
- Химическое равновесие
- ЗАДАЧИ И УПРАЖНЕНИЯ
- § 6. Растворы. Электролитическая диссоциация. Гидролиз солей
- Электролиты и электролитическая диссоциация
- Гидролиз солей
- ЗАДАЧИ И УПРАЖНЕНИЯ
- § 7. Классификация химических реакций. Окислительно-восстановительные процессы. Электролиз
- Окислительно-восстановительные реакции
- Электролиз
- ЗАДАЧИ И УПРАЖНЕНИЯ
- Глава II. НЕОРГАНИЧЕСКАЯ ХИМИЯ
- § 8. Номенклатура, классификация неорганических веществ. Свойства и способы получения
- Оксиды
- Основания (гидроксиды металлов)
- Кислоты
- Соли
- § 9. Водород. Галогены и их соединения
- Галогены и их соединения
- ЗАДАЧИ И УПРАЖНЕНИЯ
- § 10. Подгруппа кислорода
- Сера и ее соединения
- ЗАДАЧИ И УПРАЖНЕНИЯ
- § 11. Подгруппа азота
- Фосфор и его соединения
- ЗАДАЧИ И УПРАЖНЕНИЯ
- § 12. Подгруппа углерода
- Углерод и его соединения
- Кремний и его соединения
- ЗАДАЧИ И УПРАЖНЕНИЯ
- § 13. Свойства s-элементов (щелочных и щелочноземельных металлов) и их соединений
- ЗАДАЧИ И УПРАЖНЕНИЯ
- § 14. Алюминий — типичный р-металл
- Соединения алюминия и их свойства
- ЗАДАЧИ И УПРАЖНЕНИЯ
- § 15. Главные переходные металлы (d-элементы) и их соединения
- Химические свойства d-элементов
- ЗАДАЧИ И УПРАЖНЕНИЯ
- § 16. Задачи для повторения по неорганической химии
- Глава III. ОРГАНИЧЕСКАЯ ХИМИЯ
- § 17. Основные понятия и закономерности в органической химии. Предмет органической химии
- Классификация и номенклатура органических соединений
- Изомерия органических соединений
- Взаимное влияние атомов в молекуле и реакционная способность органических соединений
- Общая характеристика органических реакций
- ЗАДАЧИ И УПРАЖНЕНИЯ
- § 18. Предельные (насыщенные) углеводороды
- Циклоалканы
- ЗАДАЧИ И УПРАЖНЕНИЯ
- § 19. Алкены. Диеновые углеводороды
- Диеновые углеводороды (алкадиены)
- ЗАДАЧИ И УПРАЖНЕНИЯ
- § 20. Алкины
- ЗАДАЧИ И УПРАЖНЕНИЯ
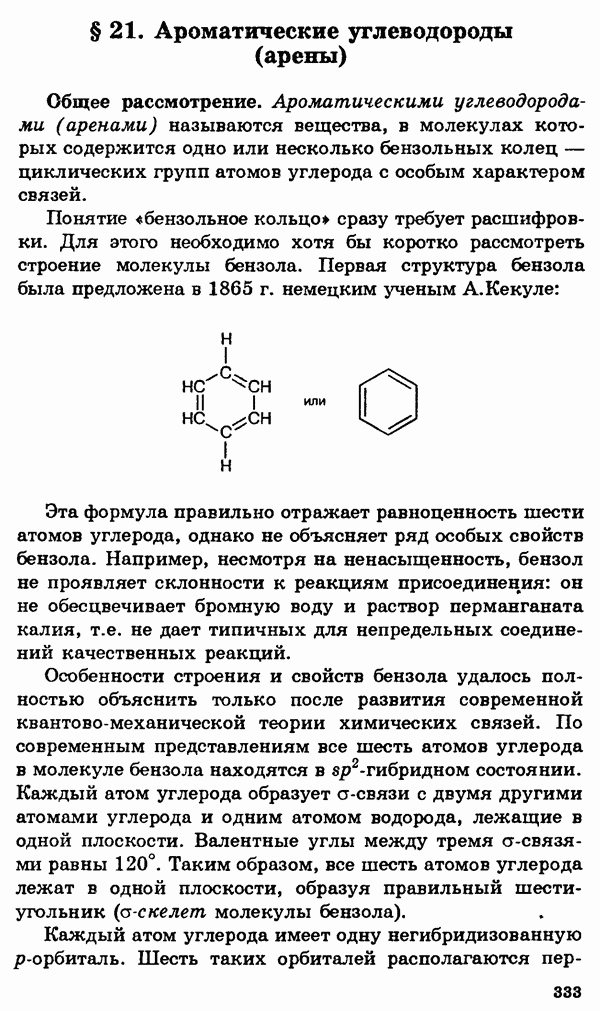
- § 21. Ароматические углеводороды (арены)
- ЗАДАЧИ И УПРАЖНЕНИЯ
- § 22. Спирты и фенолы
- Многоатомные спирты
- Фенолы
- ЗАДАЧИ И УПРАЖНЕНИЯ
- § 23. Карбонильные соединения — альдегиды и кетоны
- ЗАДАЧИ И УПРАЖНЕНИЯ
- § 24. Карбоновые кислоты. Сложные эфиры. Жиры
- Сложные эфиры. Жиры
- ЗАДАЧИ И УПРАЖНЕНИЯ
- Глава 4. ОСНОВНЫЕ ПРИЕМЫ РЕШЕНИЯ ЗАДАЧ
- Определение молекулярной формулы веществ
- Определение состава и разделение смесей
- Задачи на газовые законы
- Способы выражения концентрации растворов
- Ионные реакции в растворах
- Задачи на окислительно-восстановительные реакции
- Разные задачи
- ПРОГРАММА ПО ХИМИИ ДЛЯ ПОСТУПАЮЩИХ В УНИВЕРСИТЕТЫ
- ОТВЕТЫ
- Рекомендуемая литература