| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
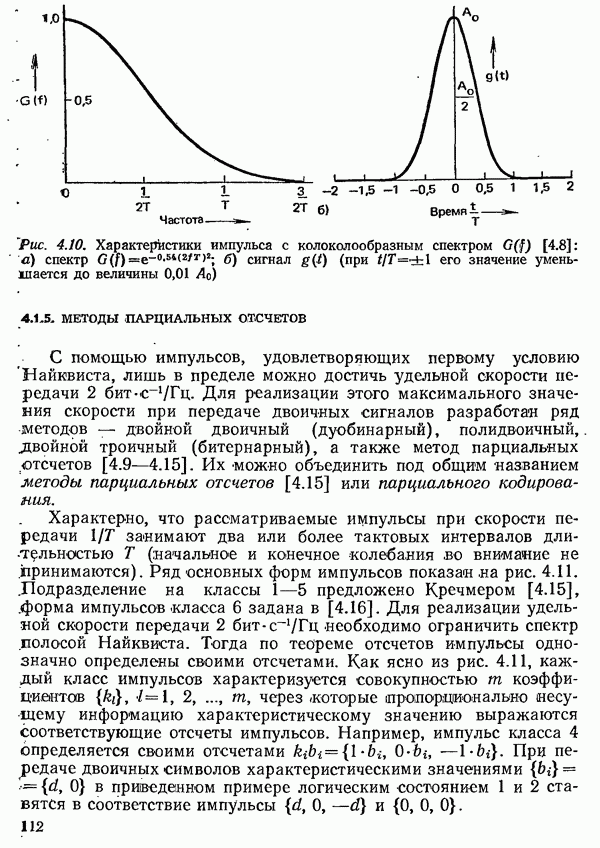
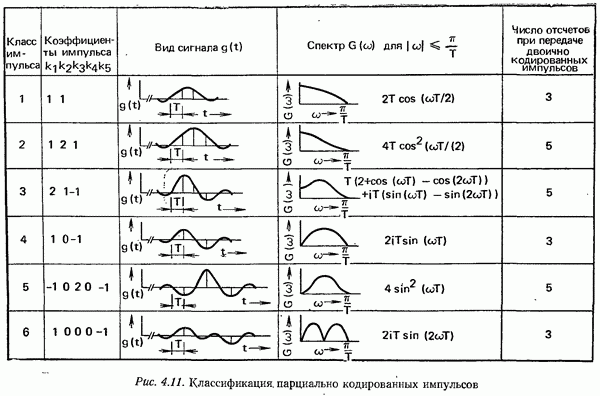
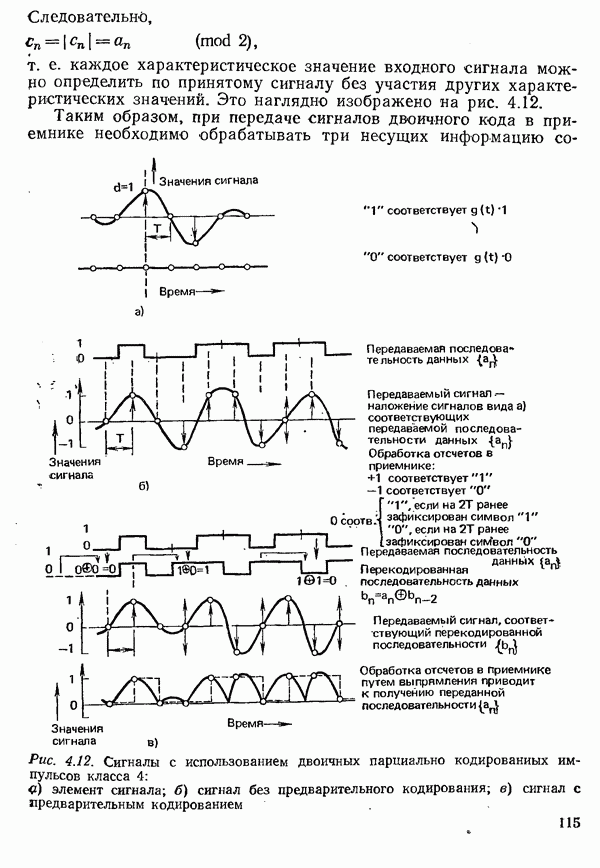
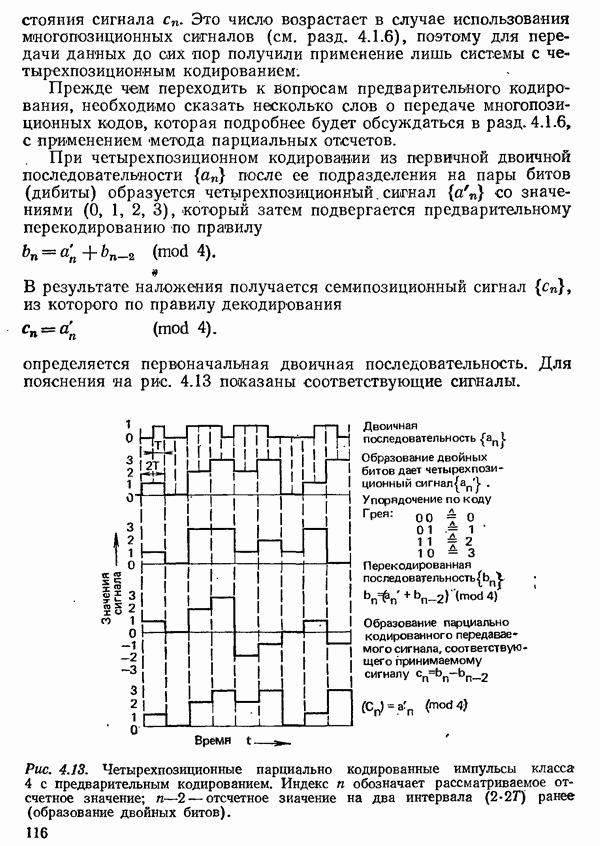
2.4.4. КАНАЛЬНОЕ КОДИРОВАНИЕ
Канальное кодирование имеет целью так преобразовать с введением избыточности кодовые комбинации, выдаваемые кодером источника, чтобы возникающие в линии связи ошибки обнаруживались в приемнике и могли бы быть исправлены (см. рис. 2.10).
2.4.4.1. ОСНОВНЫЕ ПРИНЦИПЫ ЗАЩИТЫ ОТ ОШИБОК
У рассмотренных в разд. 2.4.3.2 равномерных кодов для кодирования источника были использованы в качестве кодовых комбинаций все (или почти  возможные двоичные наборы (минимальное расстояние Хемминга
возможные двоичные наборы (минимальное расстояние Хемминга  . Поэтому при ошибке в одной или нескольких позициях получается другая используемая
. Поэтому при ошибке в одной или нескольких позициях получается другая используемая
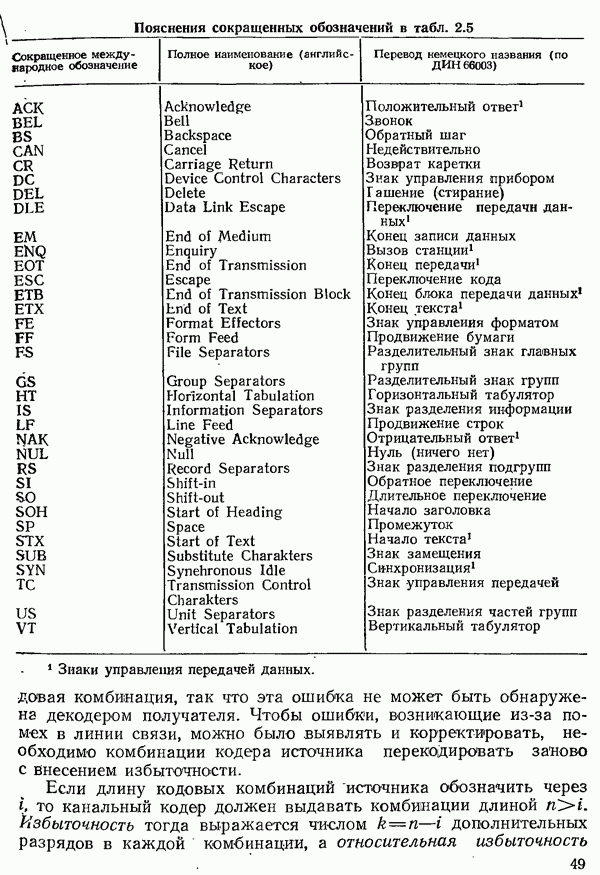
Таблица 2.5. (см. скан) Семиэлементный код по  (в международном варианте соответствует коду
(в международном варианте соответствует коду  и алфавиту № 5 МККТТ; девять знаков, которые в немецком варианте отличаются от указанных международных стандартов, заключены в прямоугольные скобки)
и алфавиту № 5 МККТТ; девять знаков, которые в немецком варианте отличаются от указанных международных стандартов, заключены в прямоугольные скобки)
Пояснения сокращенных обозначений в табл. 2.5 (см. скан)
кодовая комбинация, так что эта ошибка не может быть обнаружена декодером получателя. Чтобы ошибки, возникающие из-за помех в линии связи, можно было выявлять и корректировать, необходимо комбинации кодера источника перекодировать заново с внесением избыточности.
Если длину кодовых комбинаций источника обозначить через I, то канальный кодер должен выдавать комбинации длиной  Избыточность тогда выражается числом
Избыточность тогда выражается числом  дополнительных разрядов в каждой комбинации, а относительная избыточность
дополнительных разрядов в каждой комбинации, а относительная избыточность
есть  Отношение
Отношение  называют также скоростью передачи кода.
называют также скоростью передачи кода.
Объем  -элементного двоичного кода на (выходе канального кодера составляет
-элементного двоичного кода на (выходе канального кодера составляет  так что достаточно малого числа
так что достаточно малого числа  дополнительных разрядов, чтобы многократно увеличить объем кода по сравнению с первоначальным. Из нового множества
дополнительных разрядов, чтобы многократно увеличить объем кода по сравнению с первоначальным. Из нового множества  кодовых комбинаций выбирают подмножество из
кодовых комбинаций выбирают подмножество из  комбинаций так, чтобы минимальное расстояние
комбинаций так, чтобы минимальное расстояние  между ними было возможно больше, и приводят эти кодовые комбинации в соответствие первоначальным.
между ними было возможно больше, и приводят эти кодовые комбинации в соответствие первоначальным.  остальные комбинации
остальные комбинации  -элементного кода называются запрещенными. Комбинация
-элементного кода называются запрещенными. Комбинация  -элементного кода только тогда может перейти в другую комбинацию, когда в ней ошибочны
-элементного кода только тогда может перейти в другую комбинацию, когда в ней ошибочны  битов. Поэтому ошибка обнаруживается в декодере с уверенностью тогда, когда наивысшее число ошибочных битов в кодовой комбинации
битов. Поэтому ошибка обнаруживается в декодере с уверенностью тогда, когда наивысшее число ошибочных битов в кодовой комбинации  Для выявления ошибок необходимо, таким образом, чтобы минимальное расстояние
Для выявления ошибок необходимо, таким образом, чтобы минимальное расстояние  Если желательно корректировать ошибки, то при декодировании, как правило, поступают по принципу «максимального сходства»: если принята ошибочная и, следовательно, запрещенная комбинация, то считается правильней та комбинация, которая меньше всего отличается от принятой. Чтобы это решение, называемое коррекцией ошибок, было правильным и не приводило к некоторой другой комбинации, отличной от посланной, при минимальном расстоянии
Если желательно корректировать ошибки, то при декодировании, как правило, поступают по принципу «максимального сходства»: если принята ошибочная и, следовательно, запрещенная комбинация, то считается правильней та комбинация, которая меньше всего отличается от принятой. Чтобы это решение, называемое коррекцией ошибок, было правильным и не приводило к некоторой другой комбинации, отличной от посланной, при минимальном расстоянии  допускается ошибка не более чем в
допускается ошибка не более чем в  знаках, причем должно быть
знаках, причем должно быть  Уже для коррекции однократной ошибки
Уже для коррекции однократной ошибки  в кодовой комбинации требуется расстояние
в кодовой комбинации требуется расстояние  Так как
Так как  всегда четное число, то расстояние
всегда четное число, то расстояние  должно быть нечетным, если требуется однозначное и полное декодирование по принципу сходства. Если расстояние
должно быть нечетным, если требуется однозначное и полное декодирование по принципу сходства. Если расстояние  четное число, то имеются запрещенные комбинации, которые одинаково удалены от более чем одной комбинации.
четное число, то имеются запрещенные комбинации, которые одинаково удалены от более чем одной комбинации.
2.4.4.2. НЕКОТОРЫЕ ПРИМЕРЫ КОДОВ С ОБНАРУЖЕНИЕМ И ИСПРАВЛЕНИЕМ ОШИБОК
Для обнаружения ошибок, в особенности при коротких кодовых комбинациях, представляют практический интерес равновесные коды. При этом в качестве комбинаций в  -элементном коде выбирают все наборы с одинаковым весом
-элементном коде выбирают все наборы с одинаковым весом  их количество
их количество 

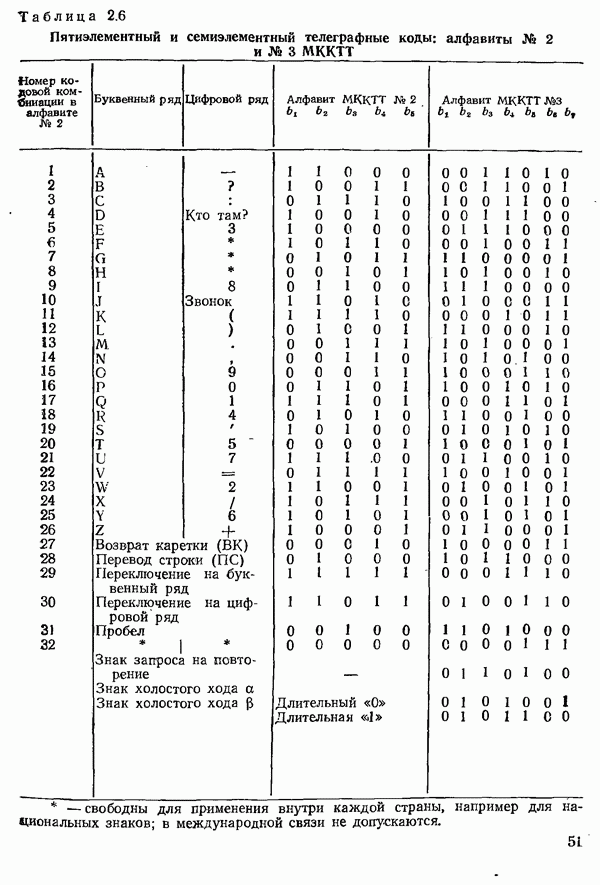
Все прочие комбинации  -элементного кода рассматриваются как запрещенные или - бессмысленные. Примером может служить алфавит № 3 МККТТ [2.26] (табл. 2.6) с семью двоичными
-элементного кода рассматриваются как запрещенные или - бессмысленные. Примером может служить алфавит № 3 МККТТ [2.26] (табл. 2.6) с семью двоичными

(кликните для просмотра скана)
элементами в каждой комбинации, выступающий в качестве кода, исправляющего ошибки, который поставлен в соответствие  -эле-ментному алфавиту № 2. Из общего числа 27—128 возможных двоичных наборов в качестве кодовых комбинаций используются те, которые содержат по три символа 1 и четыре символа 0. Таким образом, этот код содержит
-эле-ментному алфавиту № 2. Из общего числа 27—128 возможных двоичных наборов в качестве кодовых комбинаций используются те, которые содержат по три символа 1 и четыре символа 0. Таким образом, этот код содержит  комбинаций. Из них 32 имеют то же значение, что и комбинации алфавита № 2, а остальные три служат в качестве знаков холостого хода
комбинаций. Из них 32 имеют то же значение, что и комбинации алфавита № 2, а остальные три служат в качестве знаков холостого хода  и запроса на повторение
и запроса на повторение  (практическое применение кода рассмотрено в томе 2, разд. 10.4.1). Хотя у равновесного кода минимальное расстояние
(практическое применение кода рассмотрено в томе 2, разд. 10.4.1). Хотя у равновесного кода минимальное расстояние  однако могут быть обнаружены кроме простых ошибок также и все кратные искажения одинакового направления, т. е. превращения. 0 в 1 или 1 в 0, из-за связанного с этим изменениявеса. Остаются необнаруженными только искажения четной кратности (практически, прежде всего, двукратные), при которых в каждой комбинации возникает одинаковое число переходов как 0 в 1, так и 1 в 0.
однако могут быть обнаружены кроме простых ошибок также и все кратные искажения одинакового направления, т. е. превращения. 0 в 1 или 1 в 0, из-за связанного с этим изменениявеса. Остаются необнаруженными только искажения четной кратности (практически, прежде всего, двукратные), при которых в каждой комбинации возникает одинаковое число переходов как 0 в 1, так и 1 в 0.
Если при преобразовании  -элементного алфавита № 2 в
-элементного алфавита № 2 в  -эле-ментный равновесный код не составляет труда установить для большинства комбинаций систематическое правило перекодирования, упрощающее реализацию кодера, то соответствие между равновесными кодовыми комбинациями и заданными комбинациями остается, в принципе, еще произвольным (списочное кодирование). В противоположность этому все другие рассмотренные здесь примеры касаются алгебраических кодов. У них к каждой комбинации заданного
-эле-ментный равновесный код не составляет труда установить для большинства комбинаций систематическое правило перекодирования, упрощающее реализацию кодера, то соответствие между равновесными кодовыми комбинациями и заданными комбинациями остается, в принципе, еще произвольным (списочное кодирование). В противоположность этому все другие рассмотренные здесь примеры касаются алгебраических кодов. У них к каждой комбинации заданного  -позиционного кода присоединено
-позиционного кода присоединено  избыточных двоичных элементов, которые могут быть рассчитаны по алгебраическим правилам на основе
избыточных двоичных элементов, которые могут быть рассчитаны по алгебраическим правилам на основе  информационных элементов данной комбинации.
информационных элементов данной комбинации.
В простейшем случае к заданной кодовой комбинации добавляется знак контроля по четности таким образом, что вес новой кодовой комбинации всегда четный либо всегда нечетный. Минимальное расстояние  т.е., как уже пояснялось, обнаруживаются простые (одиночные) ошибки. Для каналов с малой вероятностью ошибок достаточно и такого метода их обнаружения, если только малы длины кодовых комбинаций (например, 10). Из-за простоты кодирования (и декодирования) контроль по четности часто проводится в кодере источника, где, например, к комбинациям алфавита № 5, состоящим из семи знаков, добавляется еще один, восьмой [2.24] (см. разд. 2.4.3.2).
т.е., как уже пояснялось, обнаруживаются простые (одиночные) ошибки. Для каналов с малой вероятностью ошибок достаточно и такого метода их обнаружения, если только малы длины кодовых комбинаций (например, 10). Из-за простоты кодирования (и декодирования) контроль по четности часто проводится в кодере источника, где, например, к комбинациям алфавита № 5, состоящим из семи знаков, добавляется еще один, восьмой [2.24] (см. разд. 2.4.3.2).
Кроме рассмотренных выше простых примеров в многочисленных теоретических исследованиях с применением методов теории групп разработаны алгебраические коды, которые пригодны как для обнаружения, так и для исправления ошибок, в том числе
пакетов ошибок [2.12, 2.27-2.37]. Однако в рамках этого раздела нет возможности остановиться на этих вопросах подробнее.
Для эффективного распознавания ошибок отри малой избыточности применяются кодовые комбинации большей длины (например, от 100 до 1000 бит). Независимо от частных свойств таких. блочных кодов, например их объема, количество k проверочных, символов определяется тем, с какой вероятностью при любой-, плотности и распределении ошибок, в том числе и для пакетов ошибок, одна ошибка остается необнаруженной. Эта вероятность имеет порядок  так что к блоку стремятся присоединить большее число проверочных символов (например, от 10 до 20), однако при этом, вследствие большей длины кодовой комбинации, относительная избыточность еще остается умеренной.
так что к блоку стремятся присоединить большее число проверочных символов (например, от 10 до 20), однако при этом, вследствие большей длины кодовой комбинации, относительная избыточность еще остается умеренной.
Для коррекции ошибок кодовые комбинации имеют, в общем, намного меньшую длину, например от 10 до 100 бит, а относительная избыточность лежит в пределах примерно от  до 0,7. Однако декодирование блочных кодов с исправлением - ошибок связано со сравнительно высокими затратами. Иначе обстоит дело для сверточных кодов, у которых «скользящим образом» из информационных бит, проходящих по регистру сдвига, образуются проверочные биты, используемые на приемной стороне для коррекции ошибок. Такие методы рассматриваются в томе 2, разд.
до 0,7. Однако декодирование блочных кодов с исправлением - ошибок связано со сравнительно высокими затратами. Иначе обстоит дело для сверточных кодов, у которых «скользящим образом» из информационных бит, проходящих по регистру сдвига, образуются проверочные биты, используемые на приемной стороне для коррекции ошибок. Такие методы рассматриваются в томе 2, разд. 
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ К РУССКОМУ ИЗДАНИЮ
- 1. Обзор
- 1.1. ОБРАБОТКА И ТЕЛЕОБРАБОТКА ДАННЫХ
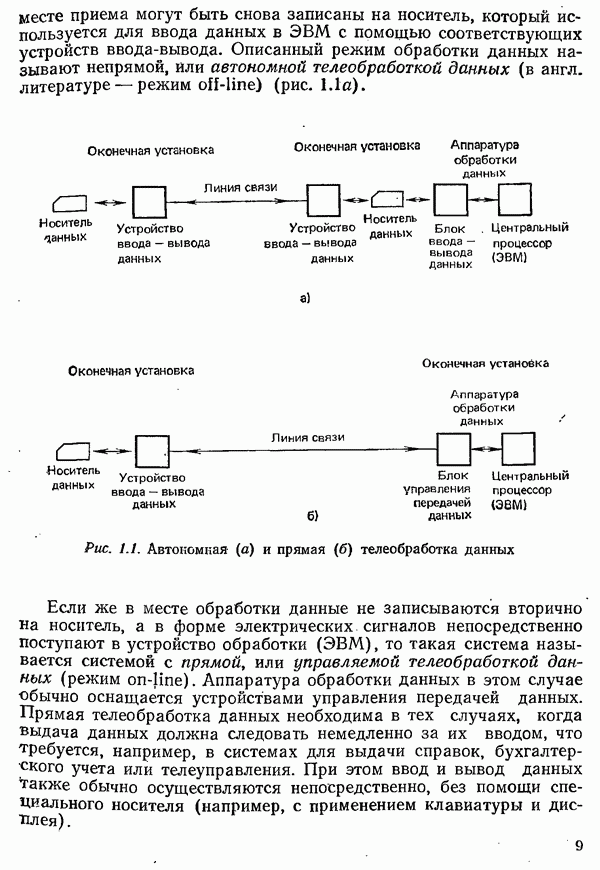
- 1.2. АВТОНОМНАЯ И УПРАВЛЯЕМАЯ ТЕЛЕОБРАБОТКА ДАННЫХ
- 1.3. КЛАССИФИКАЦИЯ СИСТЕМ ТЕЛЕОБРАБОТКИ ДАННЫХ
- 1.4. СТРУКТУРА СИСТЕМ ТЕЛЕОБРАБОТКИ ДАННЫХ
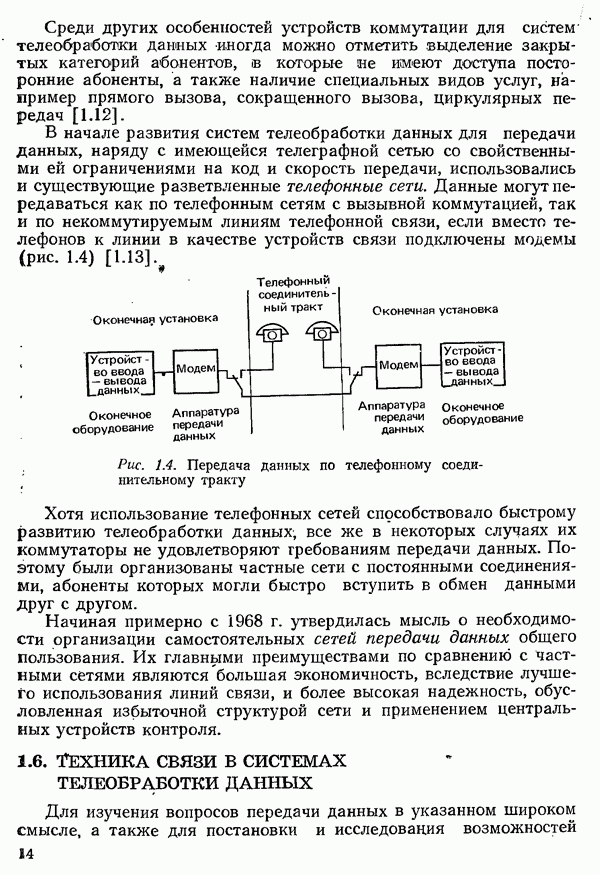
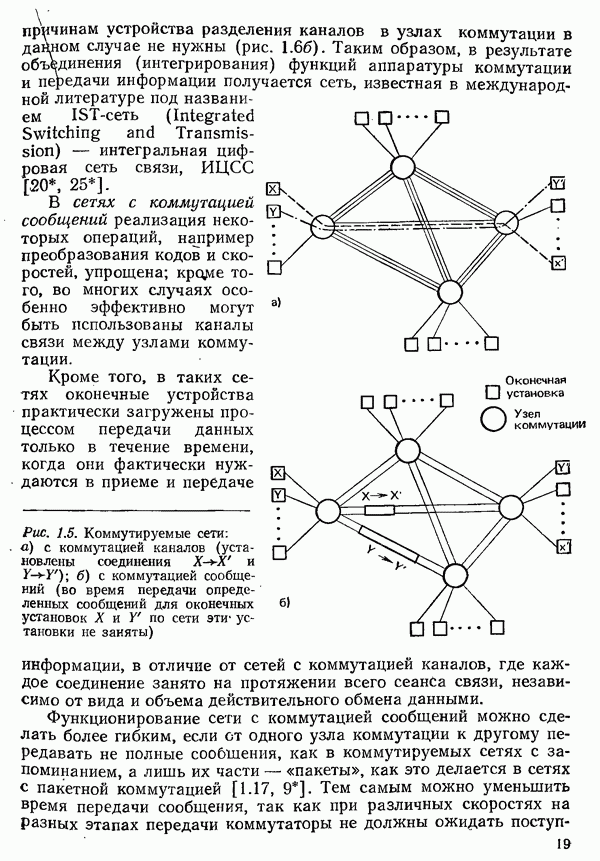
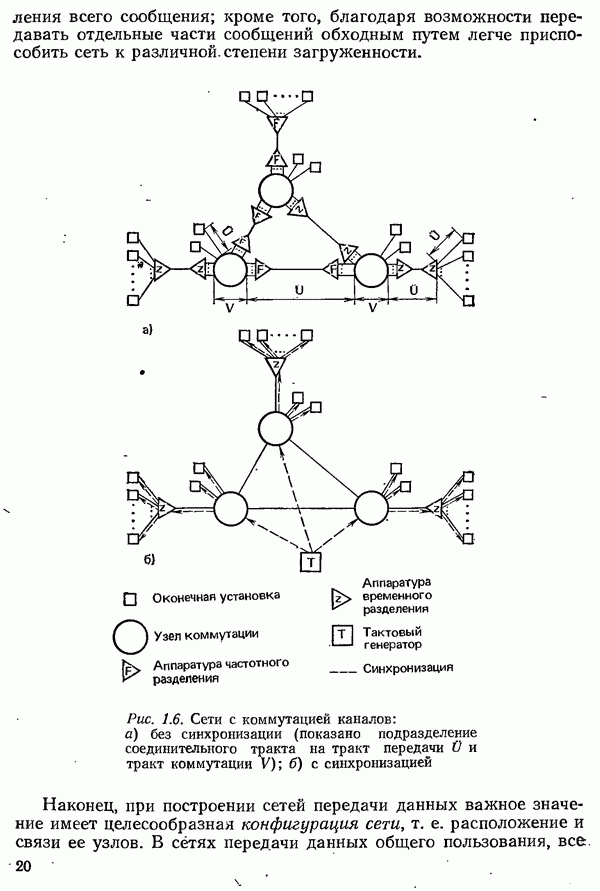
- 1.5. ТРЕБОВАНИЯ К ТЕХНИКЕ СВЯЗИ И КОММУТАЦИИ В СИСТЕМАХ ТЕЛЕОБРАБОТКИ ДАННЫХ
- 1.6. ТЕХНИКА СВЯЗИ В СИСТЕМАХ ТЕЛЕОБРАБОТКИ ДАННЫХ
- 2. Основные понятия техники связи
- 2.2. СИГНАЛЫ
- 2.2.2. ДИСКРЕТИЗАЦИЯ, КВАНТОВАНИЕ, ВЛИЯНИЕ ШУМОВ
- 2.2.3. СВОЙСТВА ПЕРВИЧНЫХ СИГНАЛОВ ДЛЯ ПЕРЕДАЧИ ДАННЫХ
- 2.2.3.2. ВРЕМЕННЫЕ СООТНОШЕНИЯ МЕЖДУ СИГНАЛАМИ
- 2.2.4. РЕЖИМЫ РАБОТЫ ПРИ ПЕРЕДАЧЕ СИГНАЛОВ
- 2.3. НЕКОТОРЫЕ ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ИНФОРМАЦИИ
- 2.3.2. ПЕРЕДАННАЯ ИНФОРМАЦИЯ. ПРОПУСКНАЯ СПОСОБНОСТЬ КАНАЛА СВЯЗИ
- 2.4. КОДИРОВАНИЕ
- 2.4.3. КОДИРОВАНИЕ ИСТОЧНИКА
- 2.4.4. КАНАЛЬНОЕ КОДИРОВАНИЕ
- 3. Каналы связи
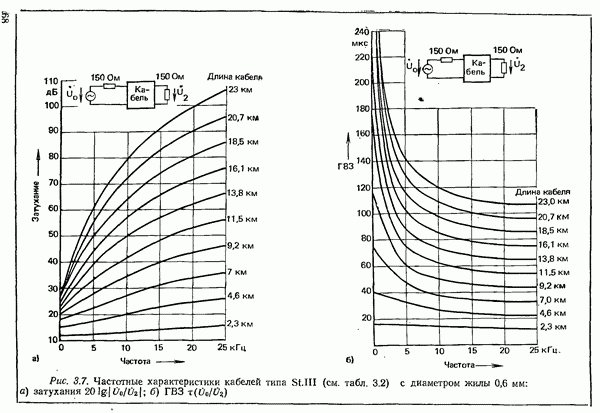
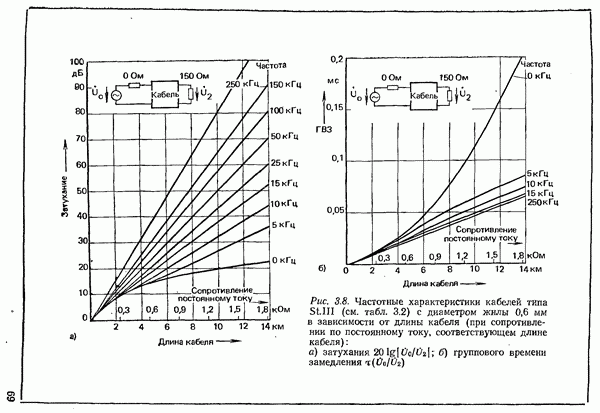
- 3.1. КАНАЛЫ БЛИЖНЕЙ СВЯЗИ
- 3.1.1.1. СВОЙСТВА И ПАРАМЕТРЫ ПРОВОДНЫХ ЛИНИЙ СВЯЗИ
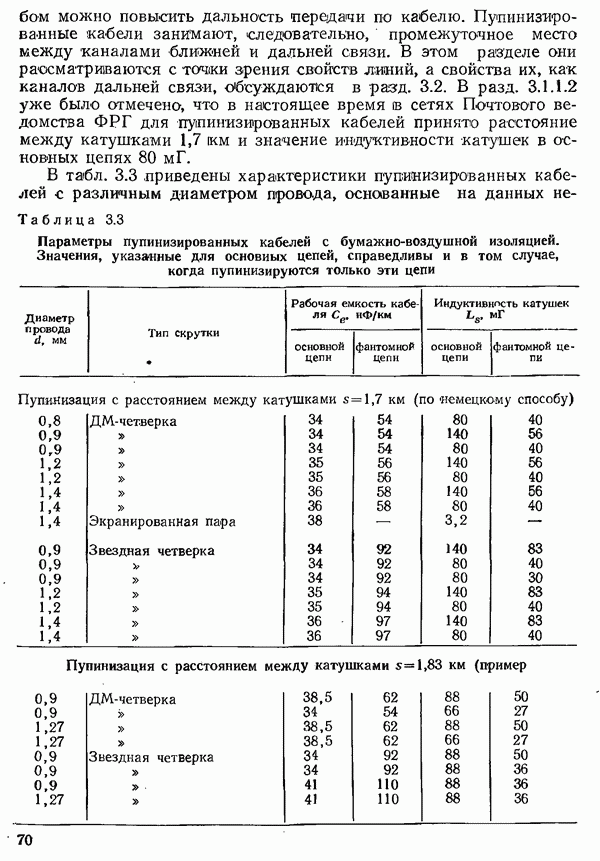
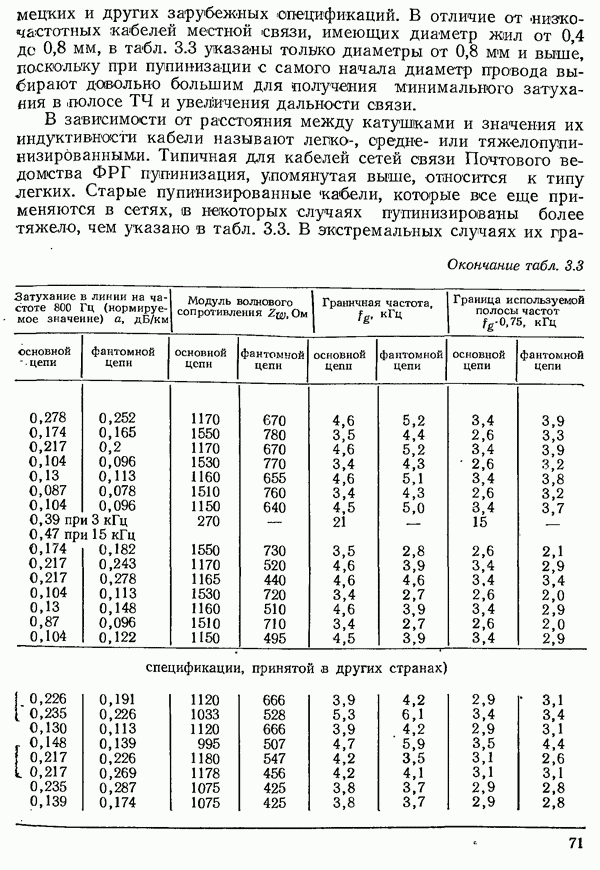
- 3.1.1.2. УМЕНЬШЕНИЕ ЗАТУХАНИЯ ПУТЕМ УВЕЛИЧЕНИЯ ИНДУКТИВНОСТИ. ПУПИНИЗАЦИЯ
- 3.1.2. ХАРАКТЕРИСТИКИ ПАР ЖИЛ НИЗКОЧАСТОТНЫХ КАБЕЛЕЙ
- 3.1.3. ХАРАКТЕРИСТИКИ ПАР ЖИЛ ПУПИЯИЗИРОВАННЫХ КАБЕЛЕЙ
- 3.1.4. ПЕРЕХОДНЫЕ ПОМЕХИ В КАБЕЛЯХ
- 3.1.5. НАПРЯЖЕНИЯ ШУМОВ НА ПАРАХ ШИЛ КАБЕЛЕЙ
- 3.2. КАНАЛЫ ДАЛЬНЕЙ СВЯЗИ
- 3.2.2. КАНАЛЫ ТОНАЛЬНОЙ ЧАСТОТЫ
- 3.2.3. СОЕДИНИТЕЛЬНЫЕ ТРАКТЫ НА ОСНОВЕ ПЕРВИЧНЫХ ГРУПП КАНАЛОВ
- 4. Методы передачи данных
- 4.1.1. СИГНАЛЫ И СПЕКТРЫ
- 4.1.2. РЯД ФУРЬЕ
- 4.1.3. ИСКАЖЕНИЯ ФОРМЫ ИМПУЛЬСОВ ПРИ ОГРАНИЧЕНИИ ПОЛОСЫ ЧАСТОТ
- 4.1.4. УСЛОВИЯ НАЙКВИСТА
- 4.1.5. МЕТОДЫ ПАРЦИАЛЬНЫХ ОТСЧЕТОВ
- 4.1.6. ПЕРЕДАЧА МНОГОПОЗИЦИОННЫХ СИГНАЛОВ
- 4.2. МЕТОДЫ ПЕРЕДАЧИ В ПЕРВИЧНОЙ ПОЛОСЕ ЧАСТОТ
- 4.2.1. МЕТОДЫ С ПРИМЕНЕНИЕМ ДВУПОЛЯРНЫХ И ОДНОПОЛЯРНЫХ ИМПУЛЬСОВ
- 4.2.2. БИПОЛЯРНЫЙ МЕТОД
- 4.2.3. ПСЕВДОТРОИЧНЫЕ МЕТОДЫ
- 4.2.4. МЕТОДЫ С ПРИМЕНЕНИЕМ БИПОЛЯРНЫХ КОДОВ ВЫСОКОЙ ПЛОТНОСТИ
- 4.2.5. ДВУХФАЗНЫЙ МЕТОД. ИЛИ МЕТОД РАСЩЕПЛЕНИЯ ФАЗЫ
- 4.2.6. ДВУХФАЗНО-КОДОВЫЙ МЕТОД
- 4.2.7. МЕТОДЫ ПАРЦИАЛЬНЫХ ОТСЧЕТОВ
- 4.3. МЕТОДЫ ПЕРЕДАЧИ С ПРИМЕНЕНИЕМ МОДУЛЯЦИИ
- 4.3.1. АМПЛИТУДНАЯ МОДУЛЯЦИЯ
- 4.3.1.2. АМПЛИТУДНАЯ МОДУЛЯЦИЯ С ОДНОЙ БОКОВОЙ ПОЛОСОЙ И С ЧАСТИЧНО ПОДАВЛЕННОЙ БОКОВОЙ ПОЛОСОЙ
- 4.3.1.3. КВАДРАТУРНАЯ АМПЛИТУДНАЯ МОДУЛЯЦИЯ
- 4.3.1.4. УДЕЛЬНАЯ СКОРОСТЬ ПЕРЕДАЧИ ПРИ АМПЛИТУДНОЙ МОДУЛЯЦИИ
- 4.3.2. ЧАСТОТНАЯ МОДУЛЯЦИЯ
- 4.3.2.1. УДЕЛЬНАЯ СКОРОСТЬ ПЕРЕДАЧИ ПРИ ЧАСТОТНОЙ МОДУЛЯЦИИ
- 4.3.3. ФАЗОВАЯ МОДУЛЯЦИЯ
- 4.4. ВОССТАНОВЛЕНИЕ ТАКТОВ И НЕСУЩЕЙ
- 4.4.2. ВОССТАНОВЛЕНИЕ ЧАСТОТЫ И ФАЗЫ НЕСУЩЕЙ
- 4.5. ВЕРОЯТНОСТЬ ОШИБКИ ПРИ НАЛИЧИИ ПОМЕХ
- 4.5.1. ВЕРОЯТНОСТЬ ОШИБКИ ПРИ УЧЕТЕ ТОЛЬКО ШУМА В КАНАЛЕ СВЯЗИ
- 4.5.2. ВЕРОЯТНОСТЬ ОШИБКИ С УЧЕТОМ ЛИНЕЙНЫХ ИСКАЖЕНИЙ
- 4.5.3. ВЕРОЯТНОСТЬ ОШИБКИ С УЧЕТОМ ПРОЦЕССОВ МОДУЛЯЦИИ И ДЕМОДУЛЯЦИИ
- 5. Учет свойств реальных каналов связи при передаче данных
- 5.2. ВЛИЯНИЕ ХАРАКТЕРИСТИК КАНАЛОВ СВЯЗИ НА ПЕРЕДАЧУ ДАННЫХ
- 5.2.2. СДВИГИ ЧАСТОТЫ
- 5.2.3. ФАЗОВОЕ ДРОЖАНИЕ
- 5.2.4. ВЛИЯНИЕ РЕАЛЬНЫХ ПОМЕХ
- 5.3. КОРРЕКЦИЯ ПРИНИМАЕМОГО СИГНАЛА ДАННЫХ
- 5.3.1. КОРРЕКЦИЯ ПРИНИМАЕМОГО СИГНАЛА ДАННЫХ В ЧАСТОТНОЙ ОБЛАСТИ
- 5.3.1.1. КОМПРОМИССНЫЙ КОРРЕКТОР
- 5.3.1.2. НАСТРАИВАЕМЫЙ ЧАСТОТНЫЙ КОРРЕКТОР СИГНАЛОВ ДАННЫХ
- 5.3.2. КОРРЕКЦИЯ ПРИНИМАЕМОГО СИГНАЛА ДАННЫХ ВО ВРЕМЕННОЙ ОБЛАСТИ
- 5.3.2.2. КРИТЕРИИ НАСТРОЙКИ КОРРЕКТОРА ВО ВРЕМЕННОЙ ОБЛАСТИ
- 5.3.2.3. АВТОМАТИЧЕСКАЯ НАСТРОЙКА ТРАНСВЕРСАЛЬНОГО КОРРЕКТИРУЮЩЕГО ФИЛЬТРА
- 5.3.2.4. РЕКУРСИВНЫЙ КОРРЕКТОР
- 5.3.2.5. СХОДИМОСТЬ НАСТРОЙКИ КОРРЕКТОРА
- 5.3.2.6. КОРРЕКТОР ДЛЯ СПЕЦИАЛЬНЫХ МЕТОДОВ ПЕРЕДАЧИ
- 6. Основы коммутации данных
- 6.1.2. МЕТОДЫ КОММУТАЦИИ
- 6.1.3. СПОСОБЫ КОММУТАЦИИ КАНАЛОВ
- 6.1.4. СИГНАЛИЗАЦИЯ
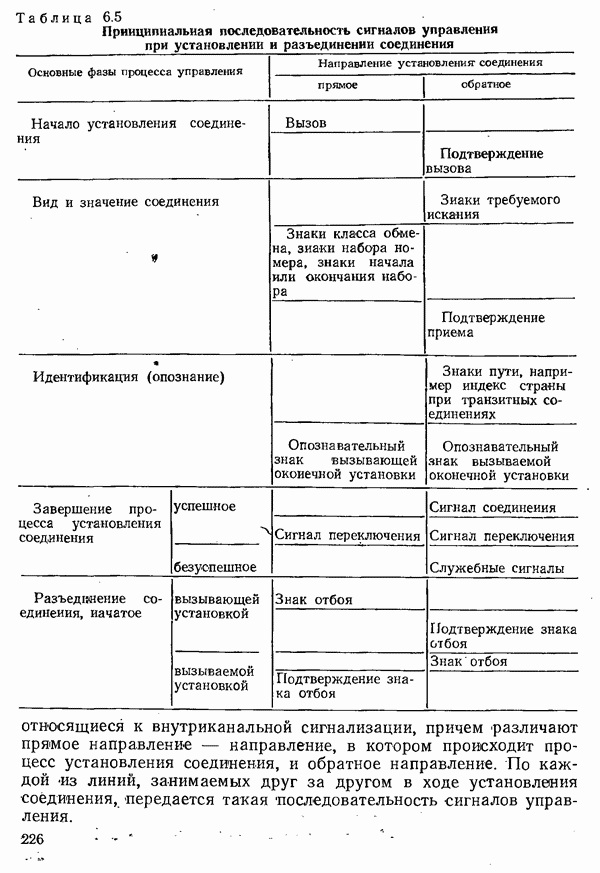
- 6.1.5. УПРАВЛЕНИЕ ПРОЦЕССАМИ СОЕДИНЕНИЯ И РАЗЪЕДИНЕНИЯ
- 6.1.6. ПОДРАЗДЕЛЕНИЕ ЦЕПЕЙ КОММУТАЦИИ КАНАЛОВ
- 6.1.7. ДОПОЛНИТЕЛЬНЫЕ ЗАДАЧИ КОММУТАЦИОННЫХ УСТРОЙСТВ
- 6.2. АНАЛИЗ СИСТЕМ КОММУТАЦИИ НА ОСНОВЕ ТЕОРИИ ТЕЛЕТРАФИКА
- 6.2.2. СИСТЕМЫ С ПОТЕРЯМИ
- 6.2.3. СИСТЕМЫ С ОЖИДАНИЕМ
- 6.2.4. ИЗМЕРЕНИЯ НАГРУЗКИ
- СПИСОК ЛИТЕРАТУРЫ