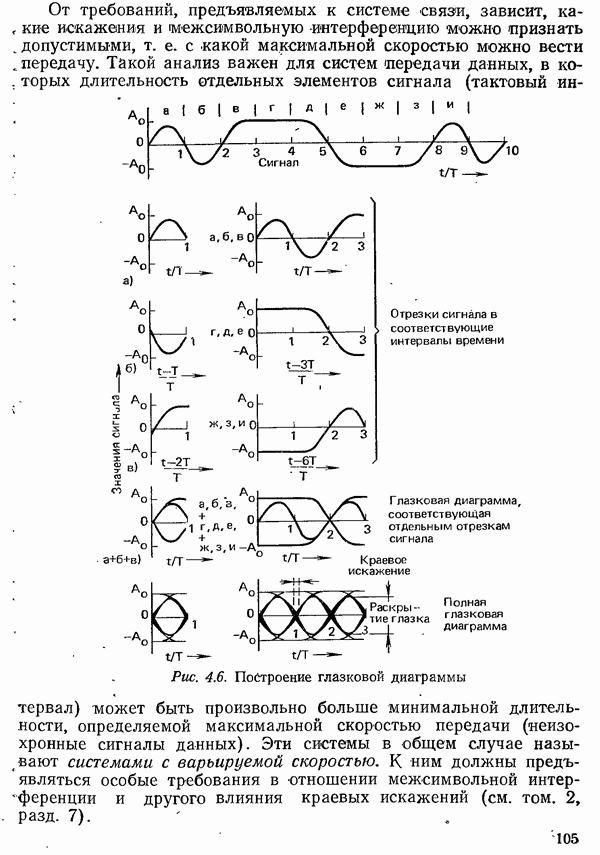
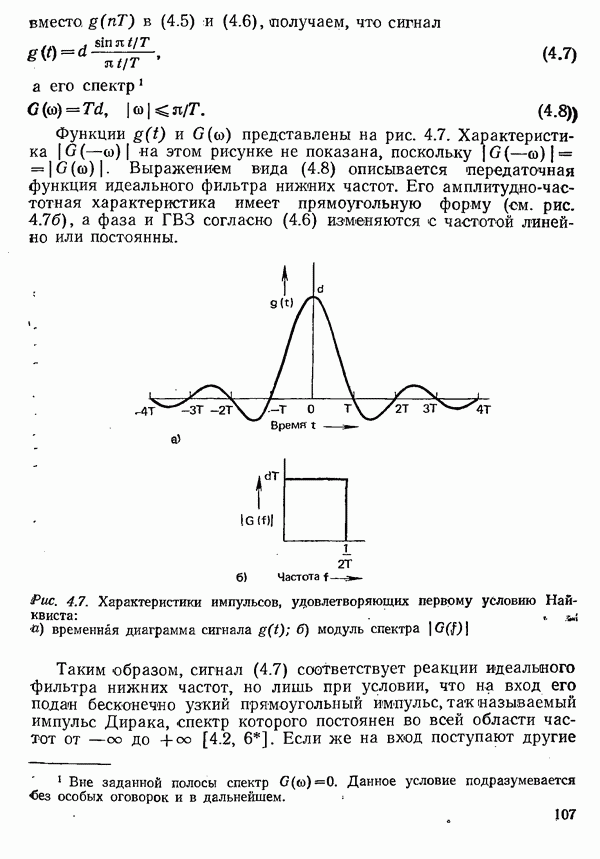
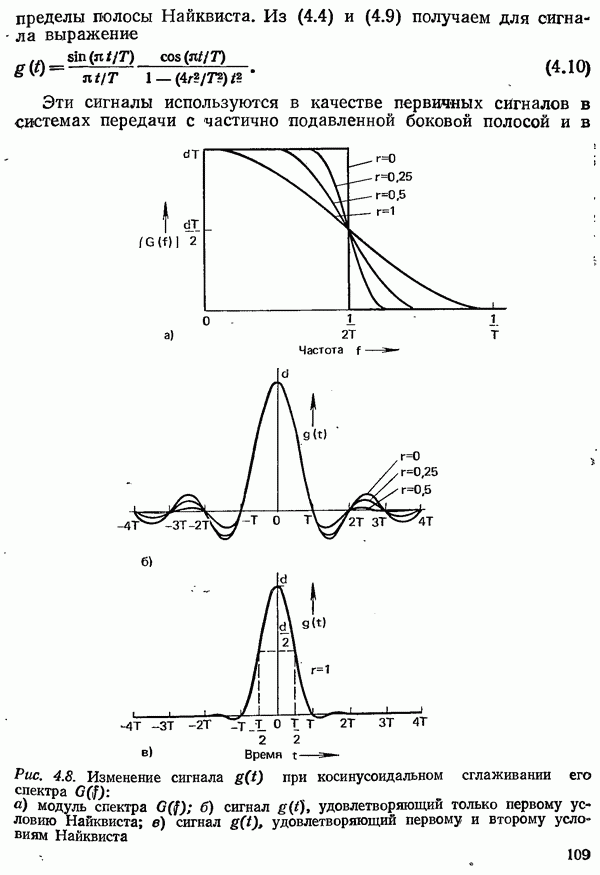
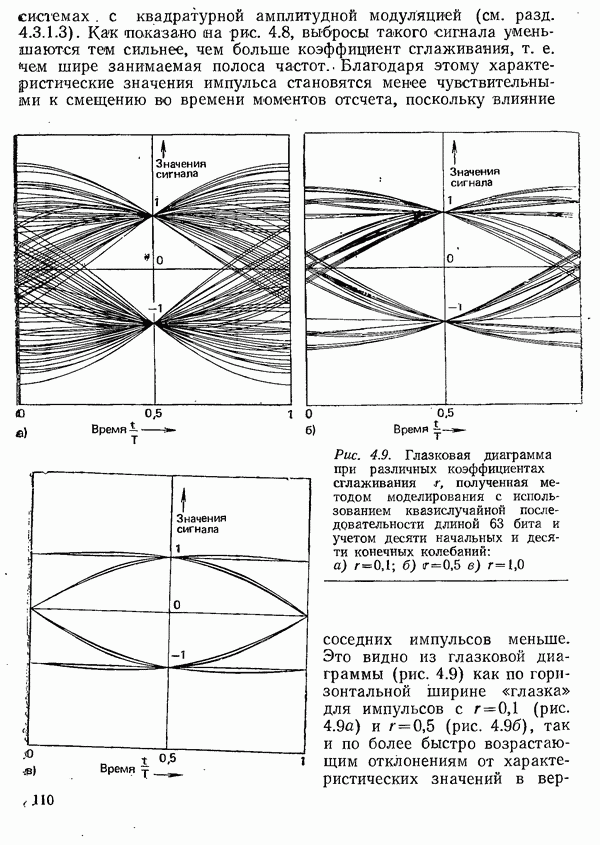
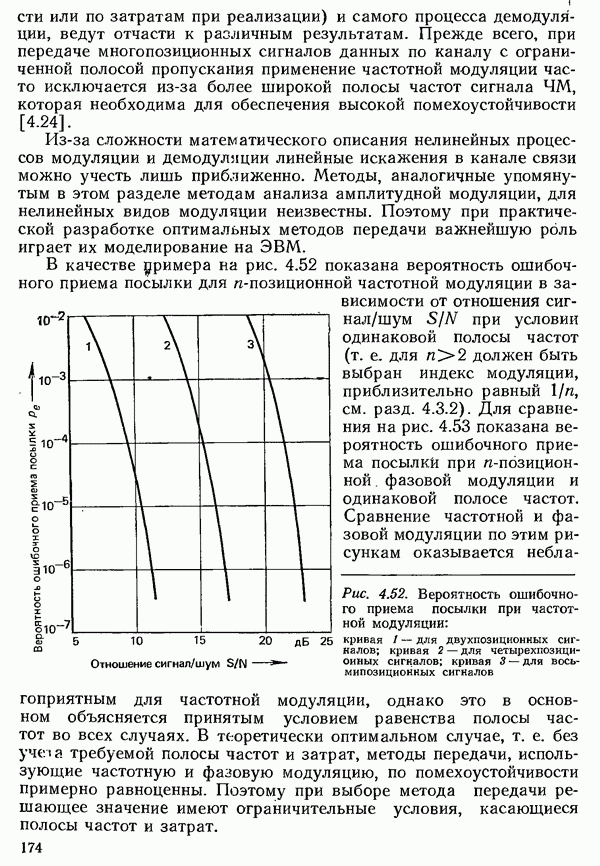
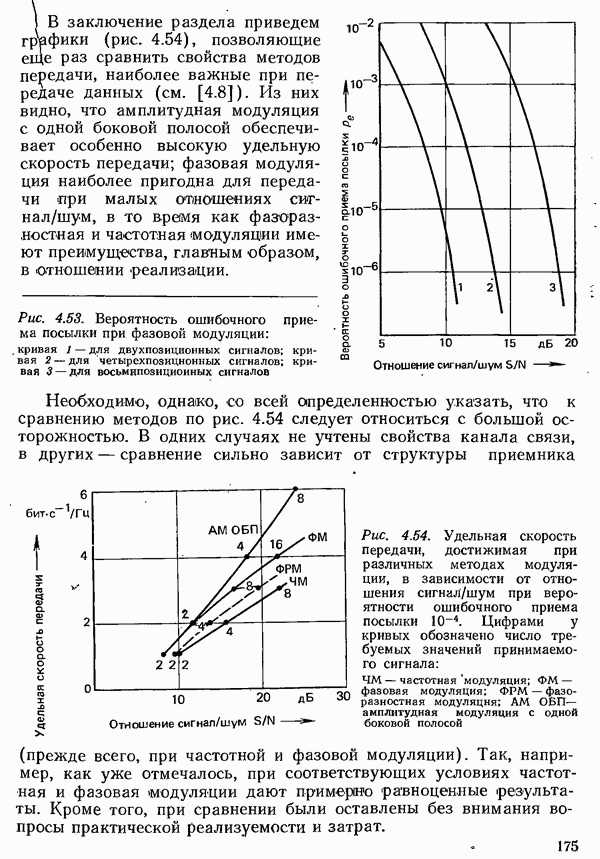
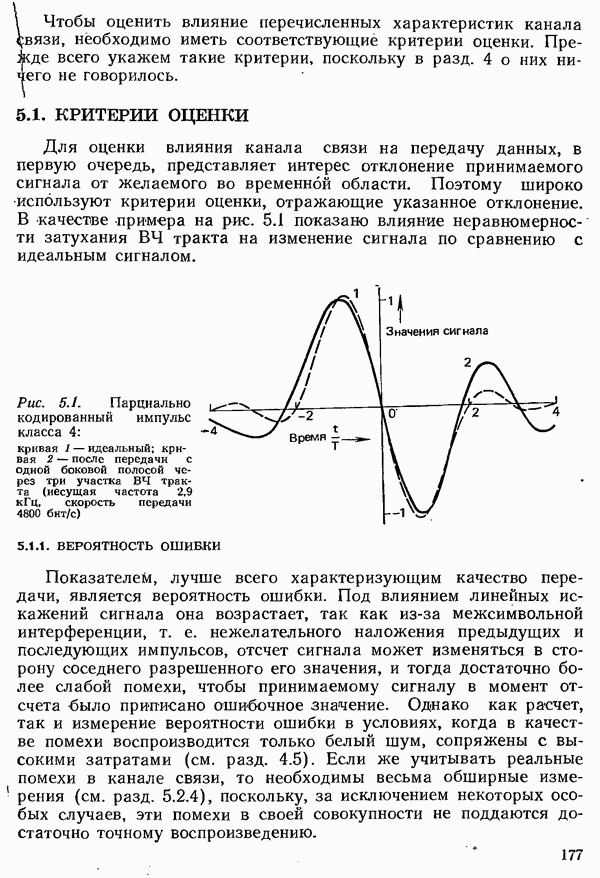
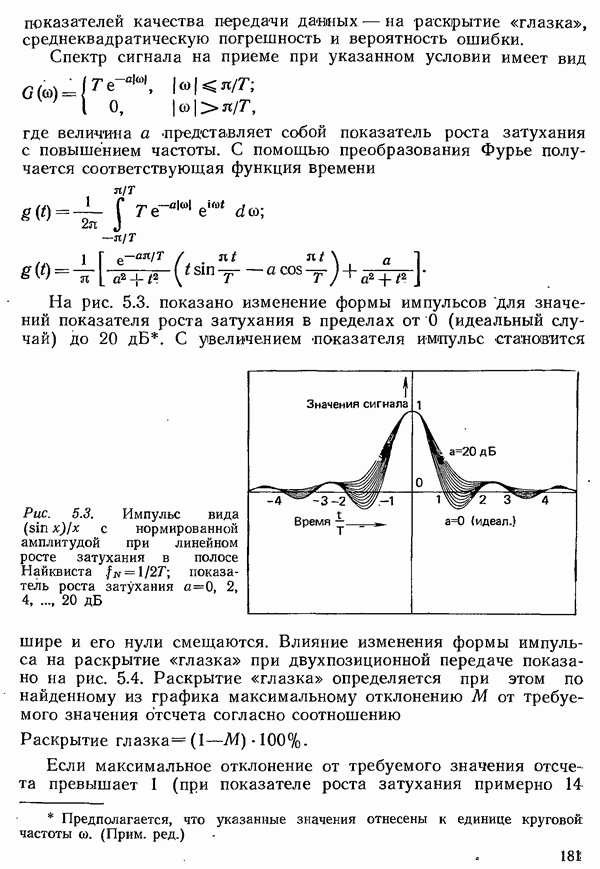
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
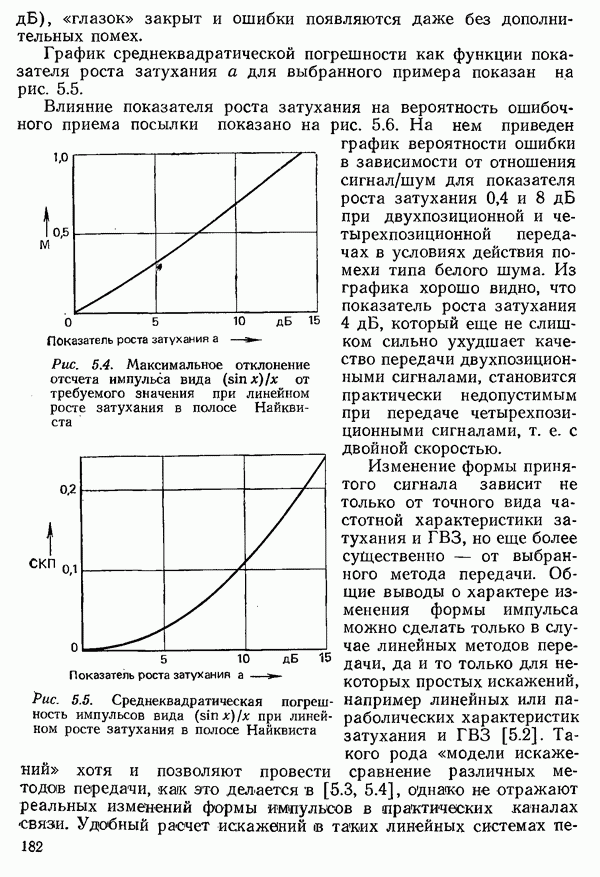
4.3.2. ЧАСТОТНАЯ МОДУЛЯЦИЯ
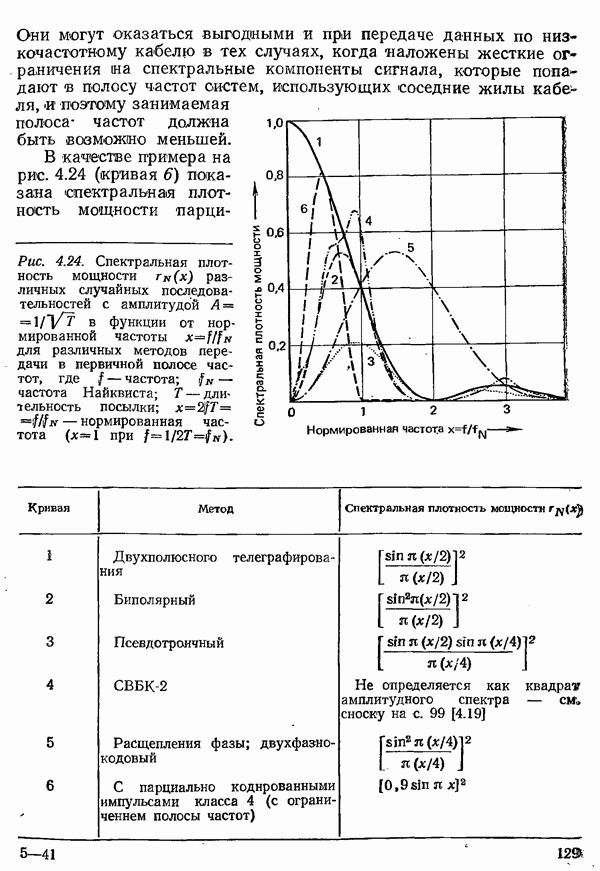
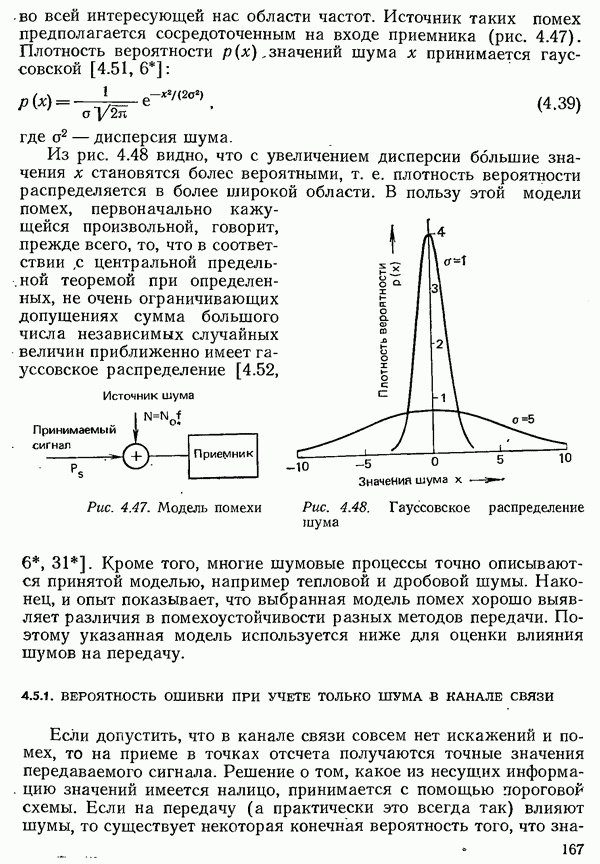
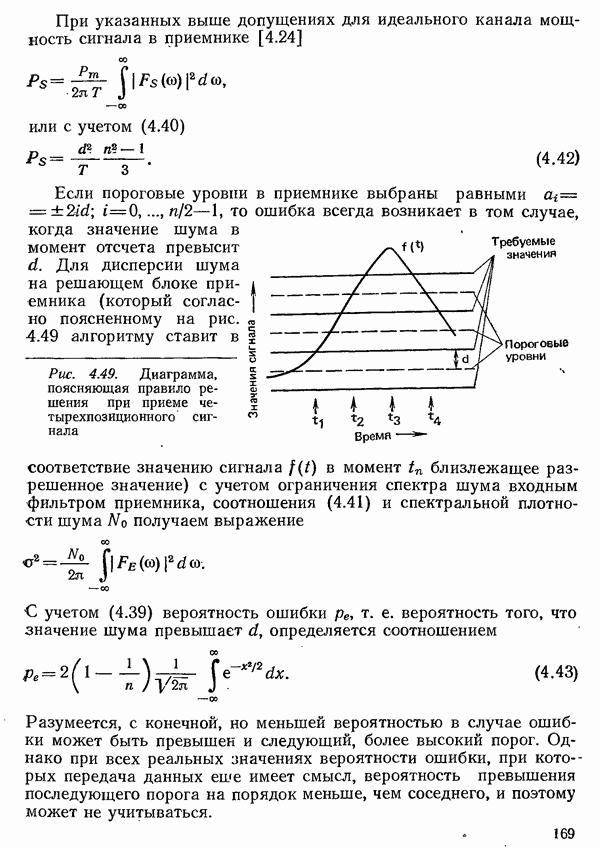
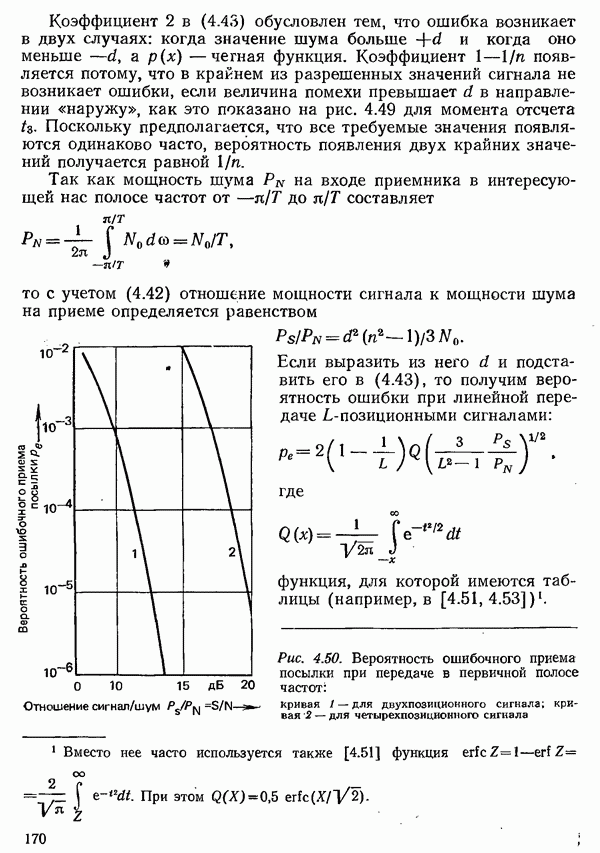
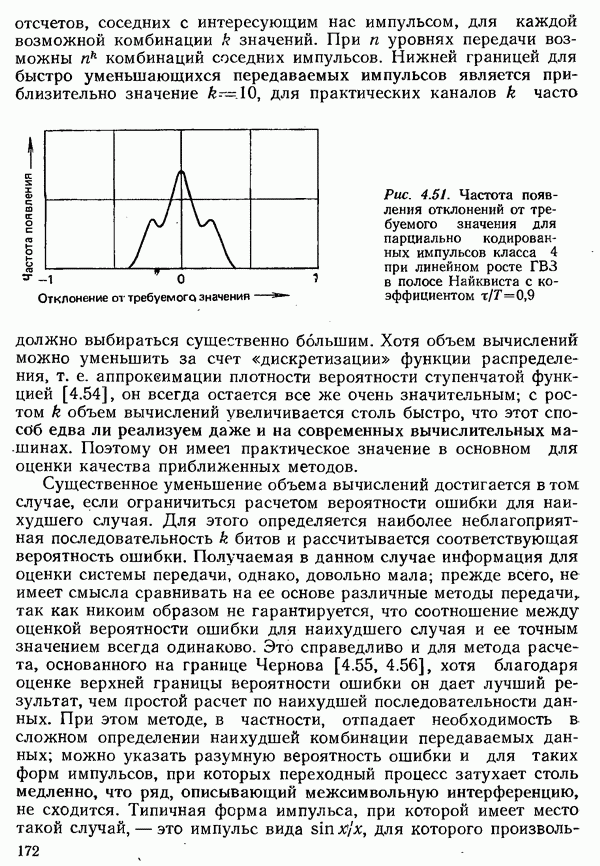
Частотная модуляция применяется, прежде всего, для передачи данных с низкими и средними скоростями, так как системы с частотной модуляцией реализуются с меньшими затратами, чем с амплитудной или фазовой модуляцией. Однако в системах с частотной модуляцией повышение удельной скорости передачи составляет более сложную проблему.
Чтобы показать отличие частотной модуляции от амплитудной, рассмотрим вначале некоторые общие положения. Модулированный сигнал  с амплитудой А и несущей частотой
с амплитудой А и несущей частотой  описывается выражением
описывается выражением

Отсюда мгновенная частота этого модулированного колебания 
При модуляции первичным сигналом  с учетом коэффициента пропорциональности
с учетом коэффициента пропорциональности  получаем
получаем

Из записанных соотношений следует, что частотномодулированный сигнал описывается выражением

Из (4.23) ясно, что частотномодулированный сигнал не получается из первичного сигнала путем простого линейного преобразования, как при амплитудной модуляции, а связан с ним нелинейной зависимостью. Поэтому при расчете спектра следует непосредственно рассматривать высокочастотный сигнал.
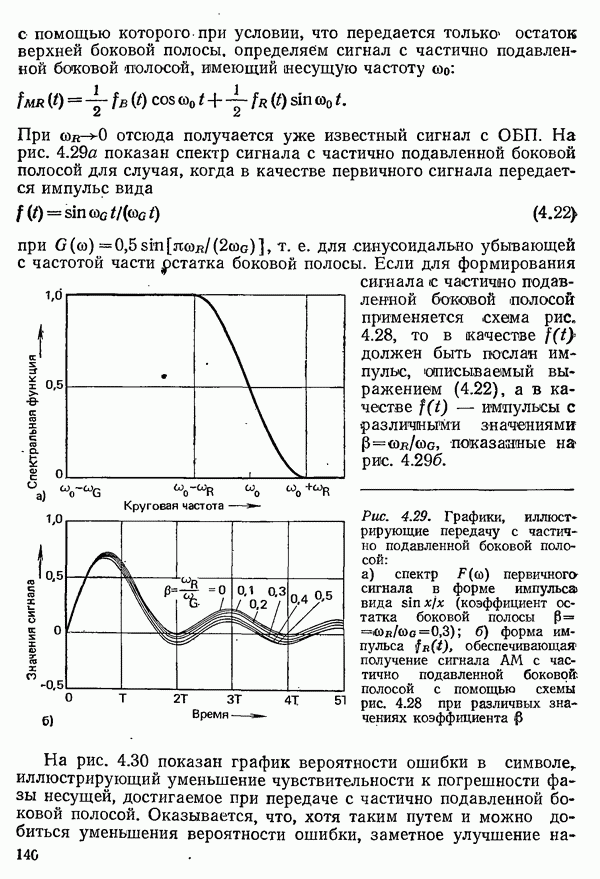
Можно привести расчет спектра для произвольного первичного сигнала Однако он сложен и не требуется для систем, применяемых при передаче данных. В системах, о которых здесь идет речь, для скачкообразного переключения частоты несущего колебания в модуляторе используется непосредственно сигнал данных
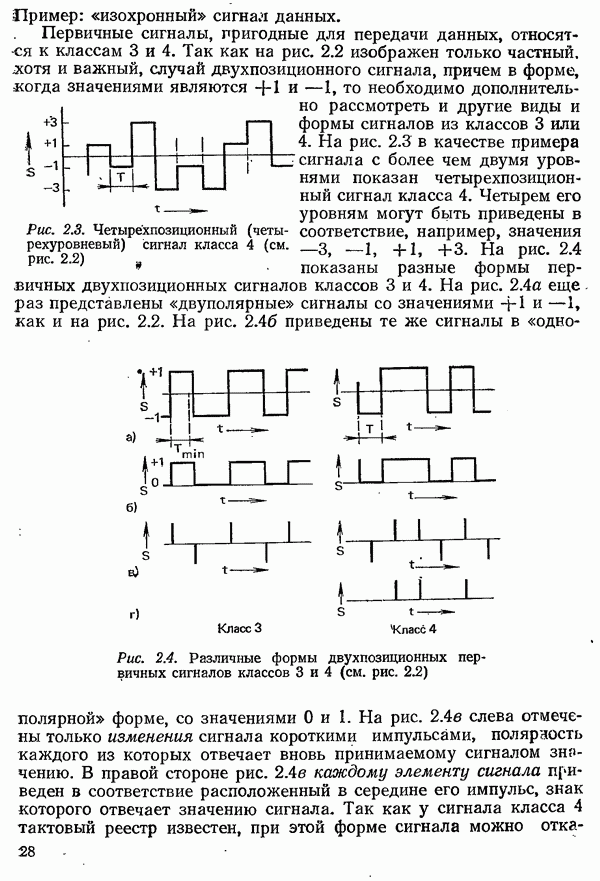
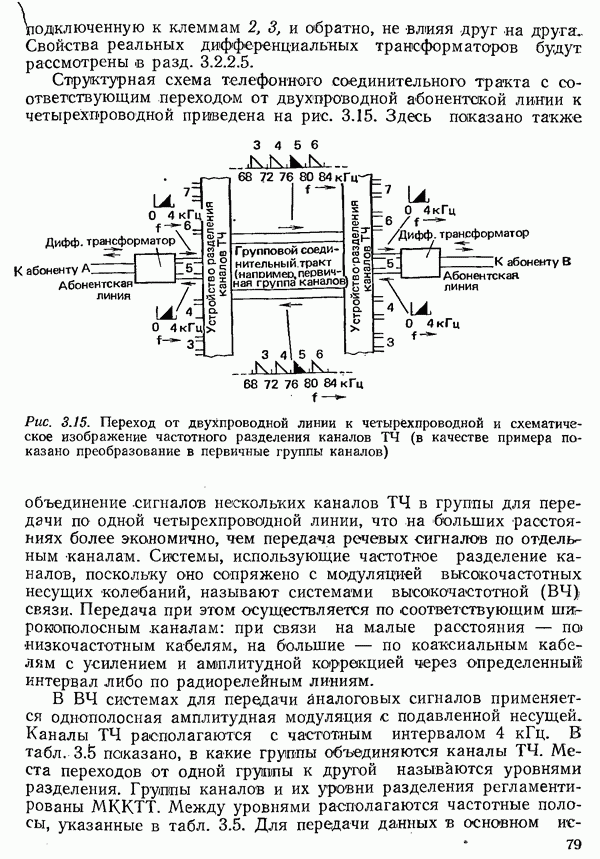
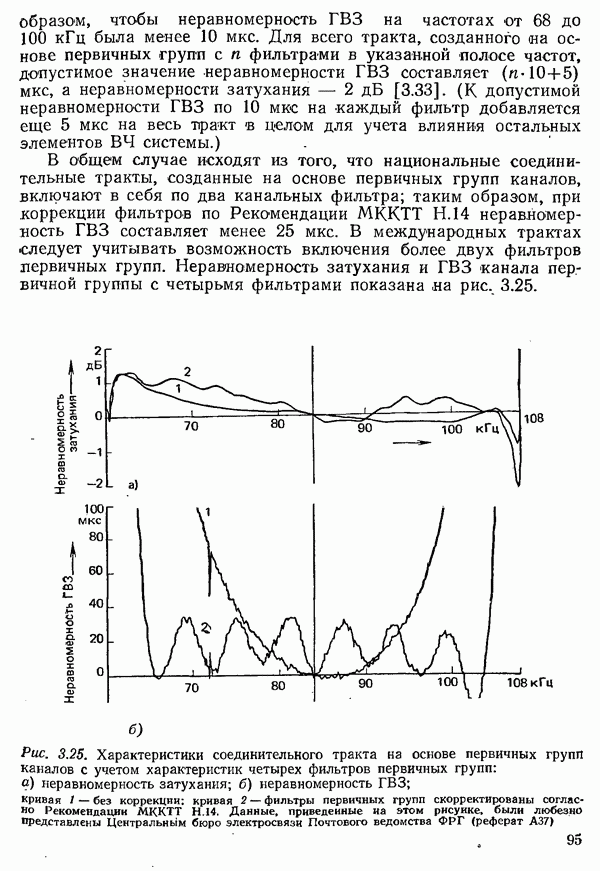
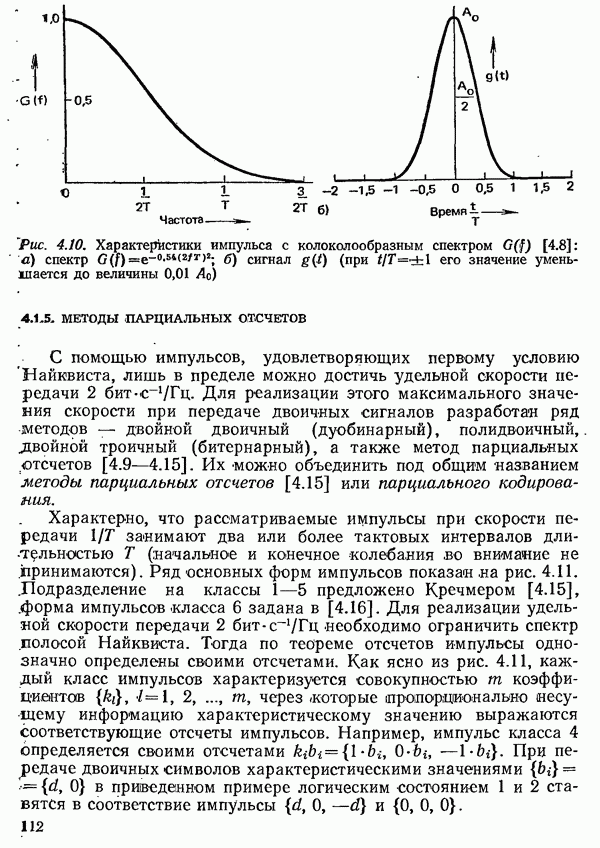
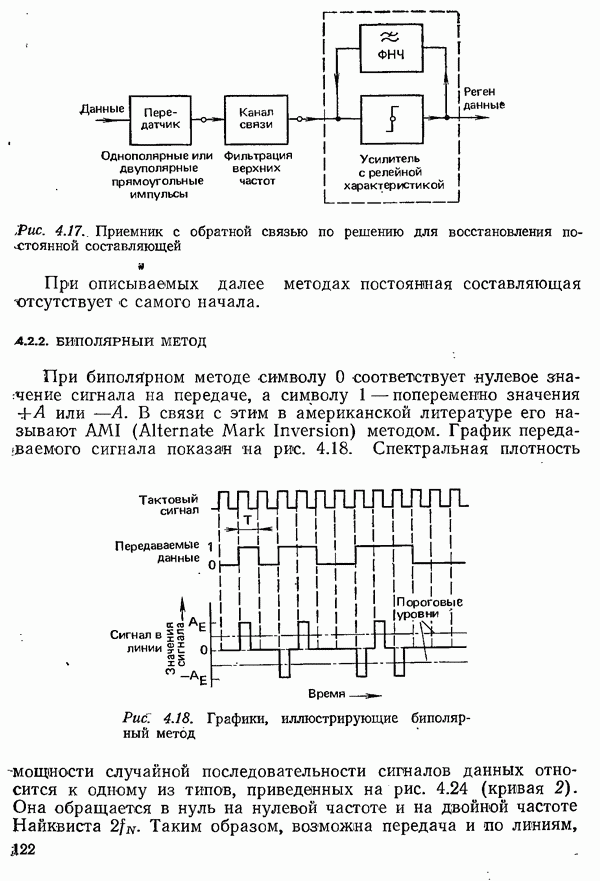
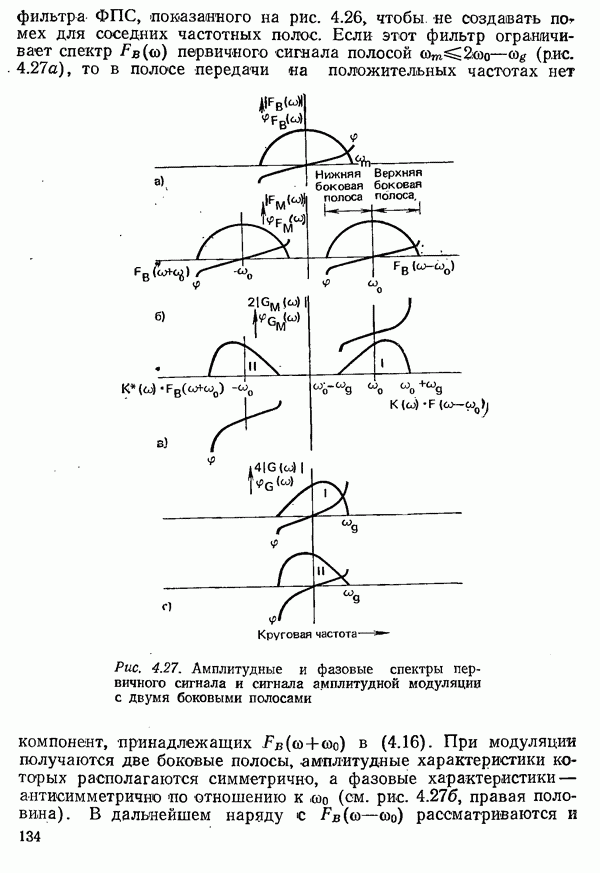
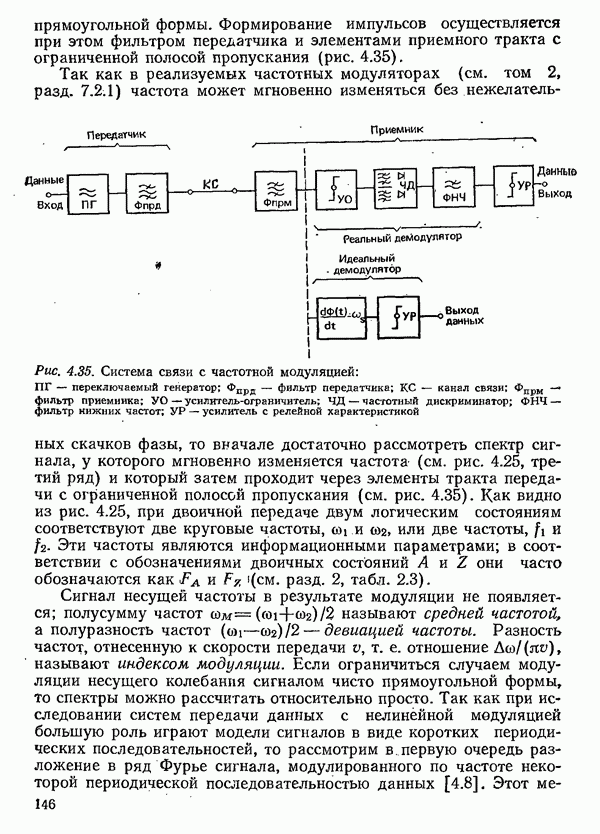
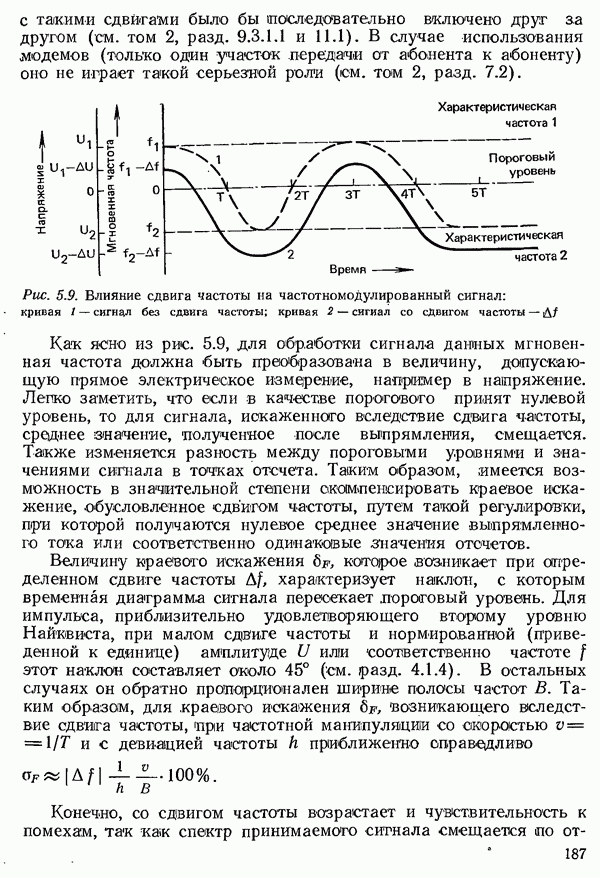
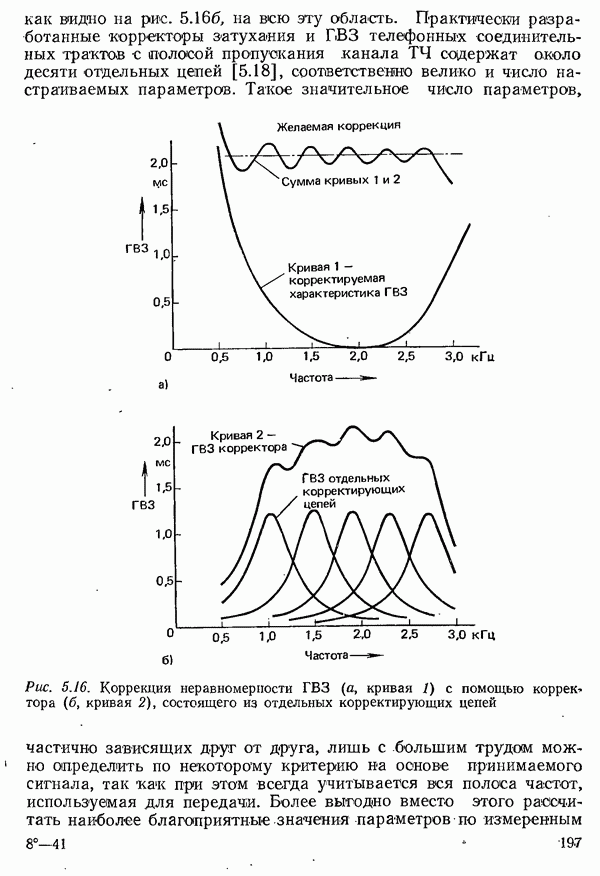
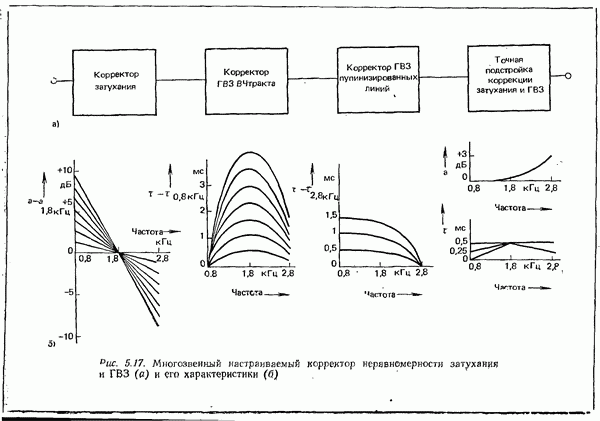
прямоугольной формы. Формирование импульсов осуществляется при этом фильтром передатчика и элементами приемного тракта с ограниченной полосой пропускания (рис. 4.35).

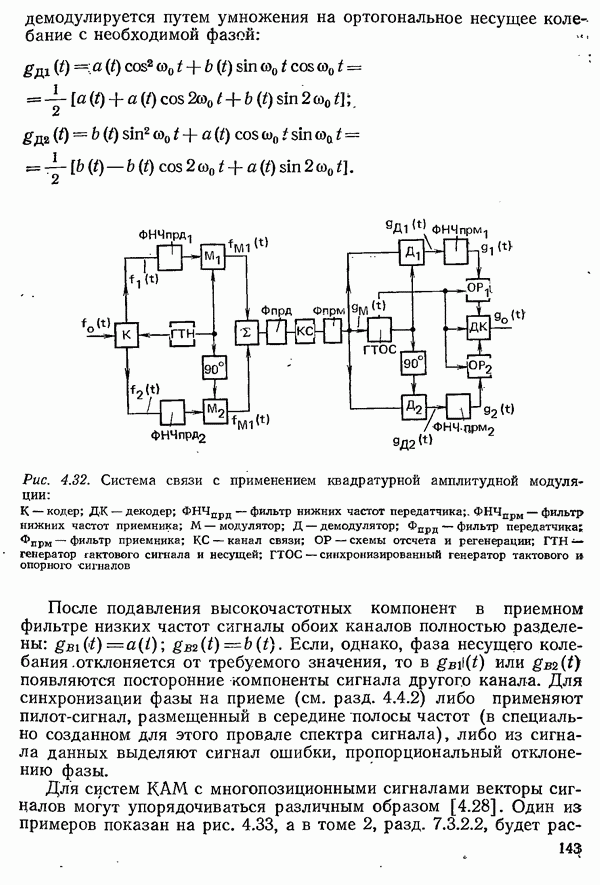
Рис. 4.35. Система связи с частотной модуляцией:  переключаемый генератор; Фпрд — фильтр передатчика;
переключаемый генератор; Фпрд — фильтр передатчика;  канал связи; Фпрм — фильтр приемника; УО — усилитель-ограничитель;
канал связи; Фпрм — фильтр приемника; УО — усилитель-ограничитель;  частотный дискриминатор;
частотный дискриминатор;  фильтр нижних частот;
фильтр нижних частот;  усилитель с релейной характеристикой
усилитель с релейной характеристикой
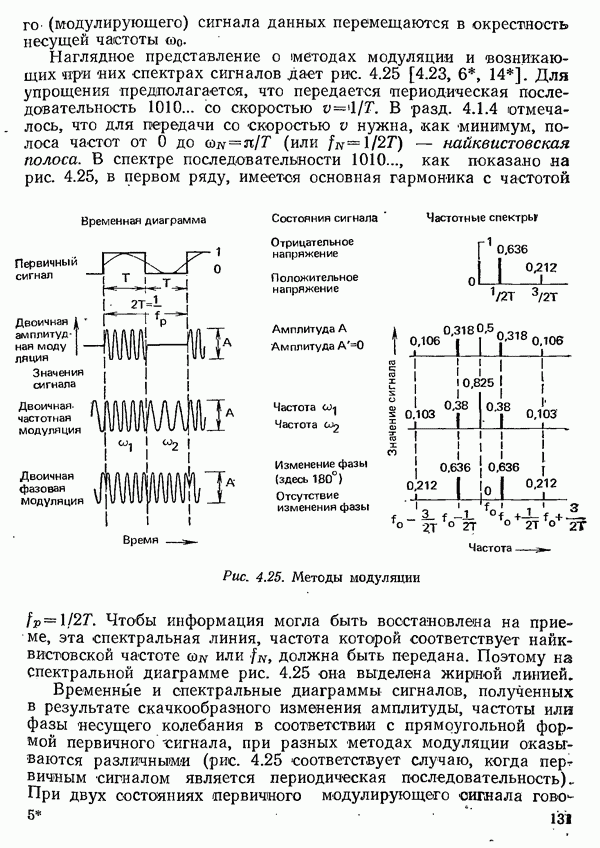
Так как в реализуемых частотных модуляторах (см. том 2, разд. 7.2.1) частота может мгновенно изменяться без нежелательных скачков фазы, то вначале достаточно рассмотреть спектр сигнала, у которого мгновенно изменяется частота (см. рис. 4.25, третий ряд) и который затем проходит через элементы тракта передачи с ограниченной полосой пропускания (см. рис. 4.35). Как видно из рис. 4.25, при двоичной передаче двум логическим состояниям соответствуют две круговые частоты,  и юг, или две частоты, и
и юг, или две частоты, и  Эти частоты являются информационными параметрами; в соответствии с обозначениями двоичных состояний
Эти частоты являются информационными параметрами; в соответствии с обозначениями двоичных состояний  они часто обозначаются как
они часто обозначаются как  и
и  разд. 2, табл. 2.3).
разд. 2, табл. 2.3).
Сигнал несущей частоты в результате модуляции не появляется; полусумму частот  называют средней частотой, а полуразность частот
называют средней частотой, а полуразность частот  девиацией частоты. Разность частот, отнесенную к скорости передачи
девиацией частоты. Разность частот, отнесенную к скорости передачи  е. отношение
е. отношение  называют индексом модуляции. Если ограничиться случаем модуляции несущего колебания сигналом чисто прямоугольной формы, То спектры можно рассчитать относительно просто. Так как при исследовании систем передачи данных с нелинейной модуляцией большую роль играют модели сигналов в виде коротких периодических последовательностей, то рассмотрим в первую очередь разложение в ряд Фурье сигнала, модулированного по частоте некоторой периодической последовательностью данных [4.8]. Этот
называют индексом модуляции. Если ограничиться случаем модуляции несущего колебания сигналом чисто прямоугольной формы, То спектры можно рассчитать относительно просто. Так как при исследовании систем передачи данных с нелинейной модуляцией большую роль играют модели сигналов в виде коротких периодических последовательностей, то рассмотрим в первую очередь разложение в ряд Фурье сигнала, модулированного по частоте некоторой периодической последовательностью данных [4.8]. Этот
метод применим и для сигналов, модулированных по фазе [4.29]. Частотномодулированпый сигнал можно представить в виде

или как вещественную часть функции

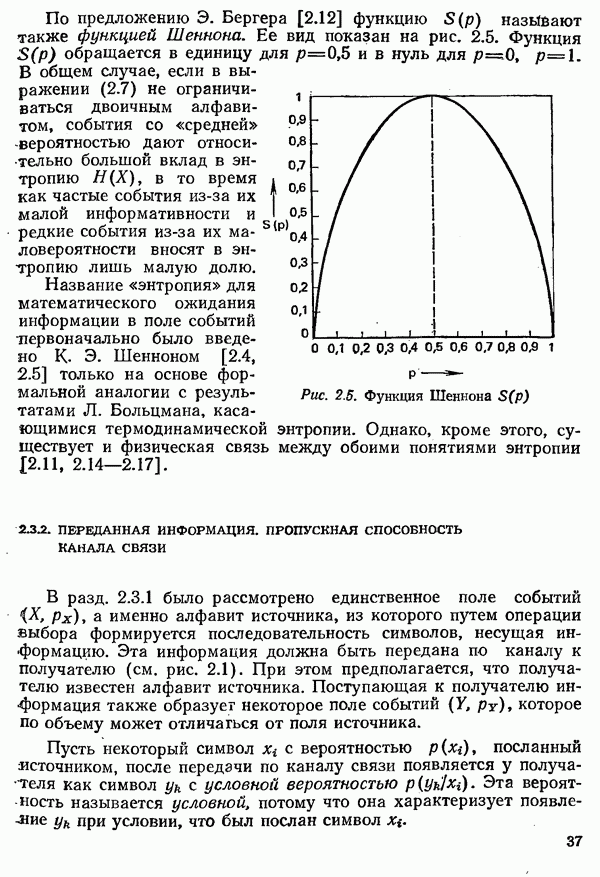
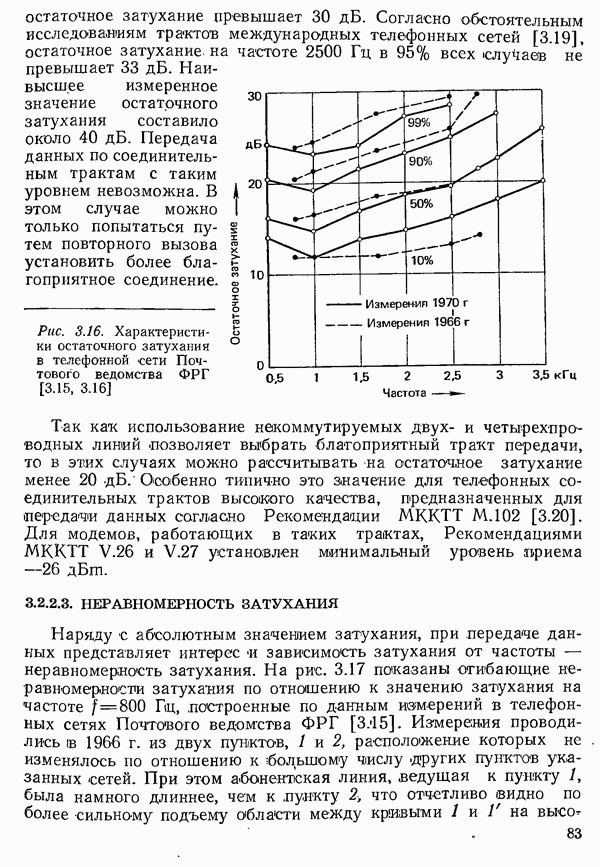
На рис. 4.36 в ряду  показана некоторая периодическая последовательность данных, а в ряду «б» — фазовая характеристика модулированного сигнала при условии
показана некоторая периодическая последовательность данных, а в ряду «б» — фазовая характеристика модулированного сигнала при условии  поскольку постоянный фазовый сдвиг можно не принимать во внимание.
поскольку постоянный фазовый сдвиг можно не принимать во внимание.

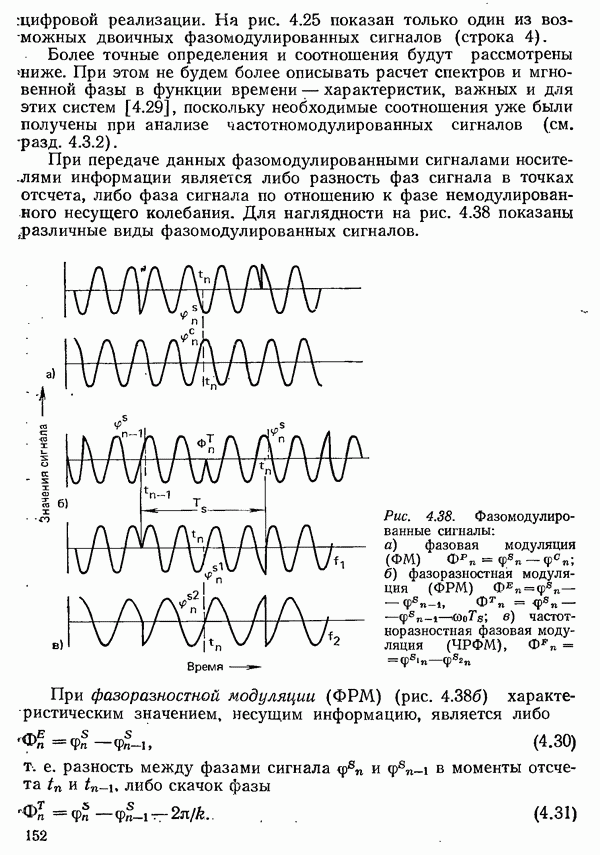
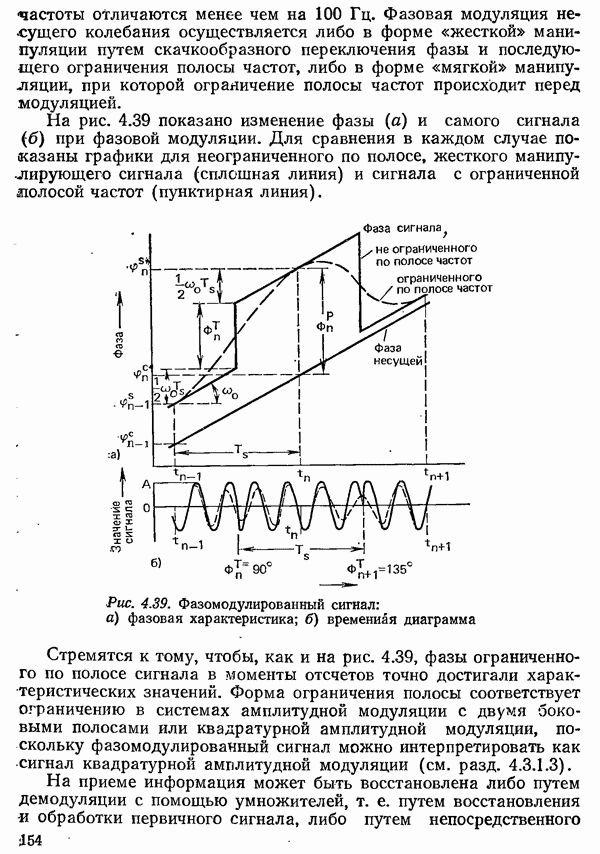
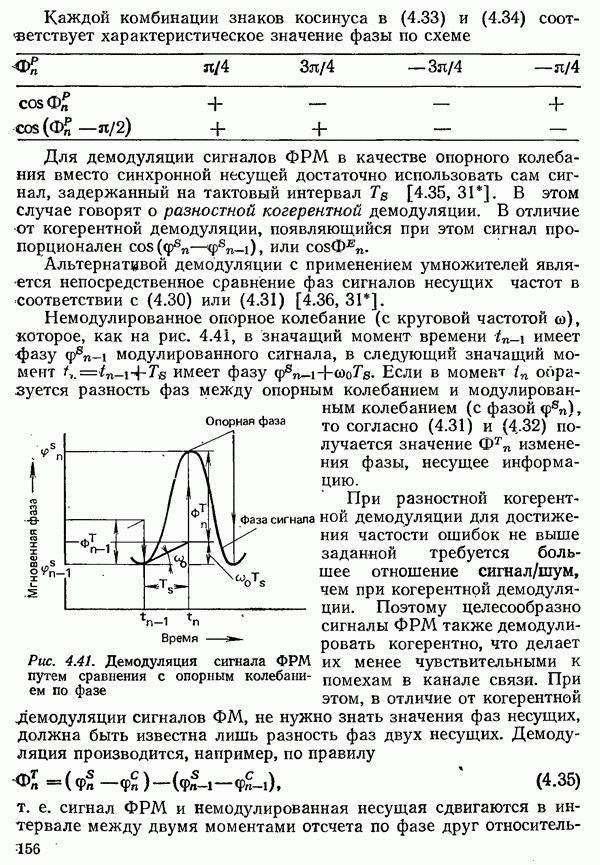
Рис. 4.36. Фазовая характеристика периодического частотно-модулиронанного сигнала данных:
а) сигнал данных с «жесткой» манипуляцией; б) фазовая характеристика этого сигнала; в) периодическая компонента фазовой характеристики
По отношению к фазе  несущего колебания с так называемой средневзвешенной частотой
несущего колебания с так называемой средневзвешенной частотой  фаза
фаза  имеет периодическую составляющую
имеет периодическую составляющую  Поэтому можно записать
Поэтому можно записать

Определяя теперь коэффициенты разложения сигнала с фазой  в ряд Фурье (см. разд. 4.1.2), получаем
в ряд Фурье (см. разд. 4.1.2), получаем

Интеграл в (4.24) вычисляется просто, поскольку  как видно из рис. 4.36, представляет собой кусочно-линейную функцию времени. Для периодической последовательности данных с периодом
как видно из рис. 4.36, представляет собой кусочно-линейную функцию времени. Для периодической последовательности данных с периодом  (на рис. 4.36 она принята симметричной относительно точки
(на рис. 4.36 она принята симметричной относительно точки  при
при  -позиционном скачкообразном переключении частот
-позиционном скачкообразном переключении частот  с тактовым интервалом
с тактовым интервалом  получаем средневзвешенную частоту
получаем средневзвешенную частоту

и коэффициенты Фурье

где

и

Отсюда получаем ряд Фурье для частотномодулированного сигнала:

Учитывая разложение (4.25), а также амплитудно-частотную  и фазо-частотную характеристики
и фазо-частотную характеристики  фильтров приемника и передатчика (см. рис. 4.35), получаем спектральное представление ограниченного по полосе частотномодулированного сигнала на выходе фильтра приемника:
фильтров приемника и передатчика (см. рис. 4.35), получаем спектральное представление ограниченного по полосе частотномодулированного сигнала на выходе фильтра приемника:

Для демодуляции принятый сигнал ограничивается по амплитуде усилителем-ограничителем (см. рис. 4.35). Тогда информация содержится только во временных интервалах между переходами через нуль и может быть затем преобразована в легко измеряемые электрические величины (например, напряжения) с помощью демодуляторов, описанных в разд. 7.2, том 2.
Все эти демодуляторы работают некогерентно и приближенно измеряют мгновенную частоту. Можно было бы построить системы с когерентной демодуляцией, однако из-за высоких затрат они не применяются. Для точного измерения мгновенной частоты необходим идеальный демодулятор (см. нижнюю часть рис. 4.35). Для пояснения этого представим сигнал (4.26) в общем виде:

Отсюда получим [4.8]

где с учетом (4.26) квадратурные компоненты

Фаза сигнала (4.27) с учетом (4.28)

С помощью (4.28) и (4.29) можно также определить фазомодулированный сигнал по его спектру.
Для мгновенной частоты частотномодулированного сигнала из; (4.29) получаем

Демодулированный первичный сигнал может быть найден как разность между мгновенной и средневзвешенной частотами:

Используя полученное таким образом выражение для демодулированного сигнала, можно при моделировании системы совместно определить оптимальные характеристики фильтров передатчика и приемника [4.30].
Вопрос, об оптимизации системы с точки зрения ее чувствительности к помехам решается, однако, не так просто, как в случаелинейной системы модуляции, где наиболее благоприятно равное участие полосовых фильтров передатчика и приемника в формировании импульсов (см. разд. 4.5). В данном случае благоприятнее неодинаковое ограничение полосы частот в передатчике и приемнике [4.32]. Поэтому при восстановлении первичного сигнала следует принимать во внимание индекс модуляции и ограничение полосы частот в демодуляторе, в том числе и влияние низкочастотных фильтров, предназначенных для подавления компонент несущей частоты. Общая оптимизация системы возможна лишь на. основе моделирования во временной области. Его, однако, целесообразно проводить только для расчета переходных процессов [4.31]. Оптимизация в отношении чувствительности к помехам потребовала бы при моделировании больших затрат времени на вычисления.
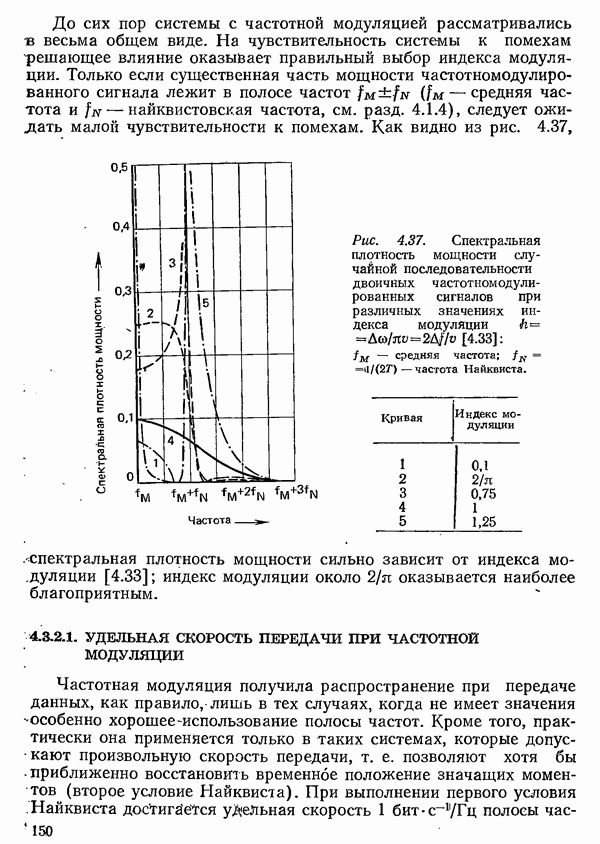
До сих пор системы с частотной модуляцией рассматривались в весьма общем виде. На чувствительность системы к помехам решающее влияние оказывает правильный выбор индекса модуляции. Только если существенная часть мощности частотномодулированного сигнала лежит в полосе частот  - средняя частота и
- средняя частота и  найквистовская частота, см. разд. 4.1.4), следует ожидать малой чувствительности к помехам.
найквистовская частота, см. разд. 4.1.4), следует ожидать малой чувствительности к помехам.

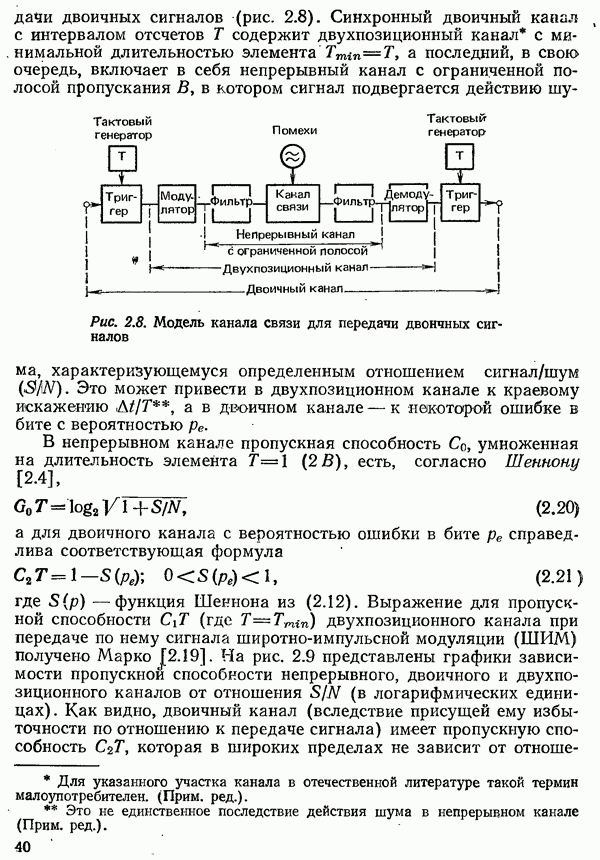
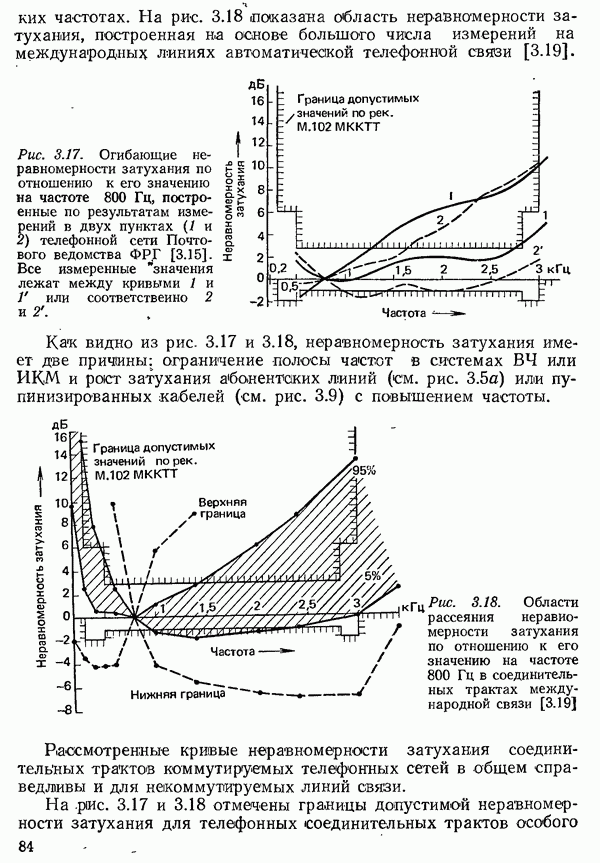
Рис. 4.37. Спектральная плотность мощности случайной последовательности двоичных частотномодулированных сигналов при различных значениях индекса модуляции  [4.33]:
[4.33]:  средняя частота;
средняя частота;  частота Найквиста.
частота Найквиста.

Как видно из рис. 4.37, спектральная плотность мощности сильно зависит от индекса модуляции [4.33]; индекс модуляции около  оказывается наиболее благоприятным.
оказывается наиболее благоприятным.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ К РУССКОМУ ИЗДАНИЮ
- 1. Обзор
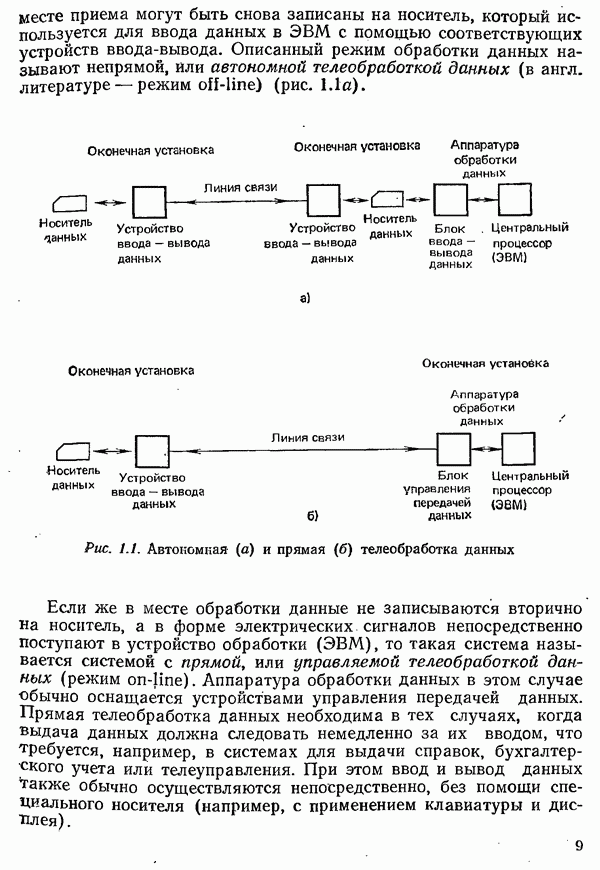
- 1.1. ОБРАБОТКА И ТЕЛЕОБРАБОТКА ДАННЫХ
- 1.2. АВТОНОМНАЯ И УПРАВЛЯЕМАЯ ТЕЛЕОБРАБОТКА ДАННЫХ
- 1.3. КЛАССИФИКАЦИЯ СИСТЕМ ТЕЛЕОБРАБОТКИ ДАННЫХ
- 1.4. СТРУКТУРА СИСТЕМ ТЕЛЕОБРАБОТКИ ДАННЫХ
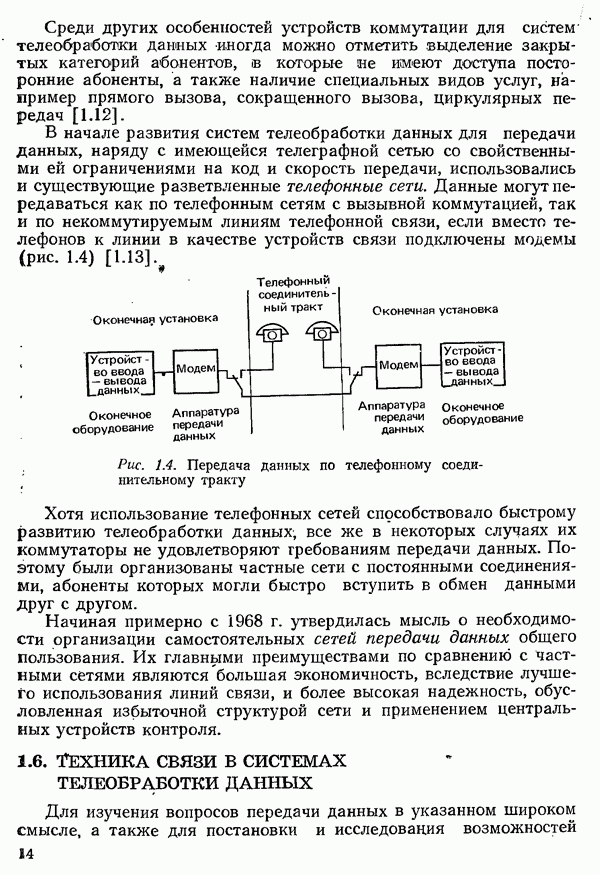
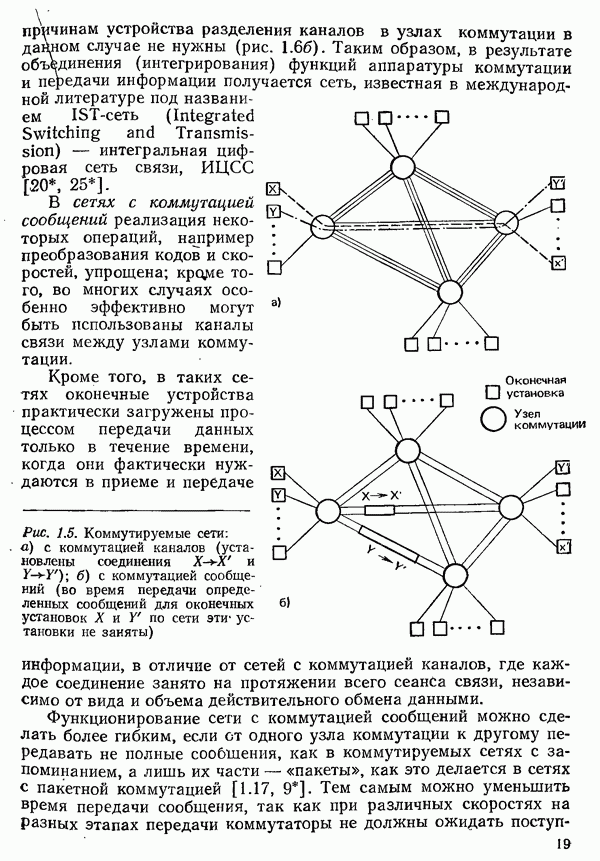
- 1.5. ТРЕБОВАНИЯ К ТЕХНИКЕ СВЯЗИ И КОММУТАЦИИ В СИСТЕМАХ ТЕЛЕОБРАБОТКИ ДАННЫХ
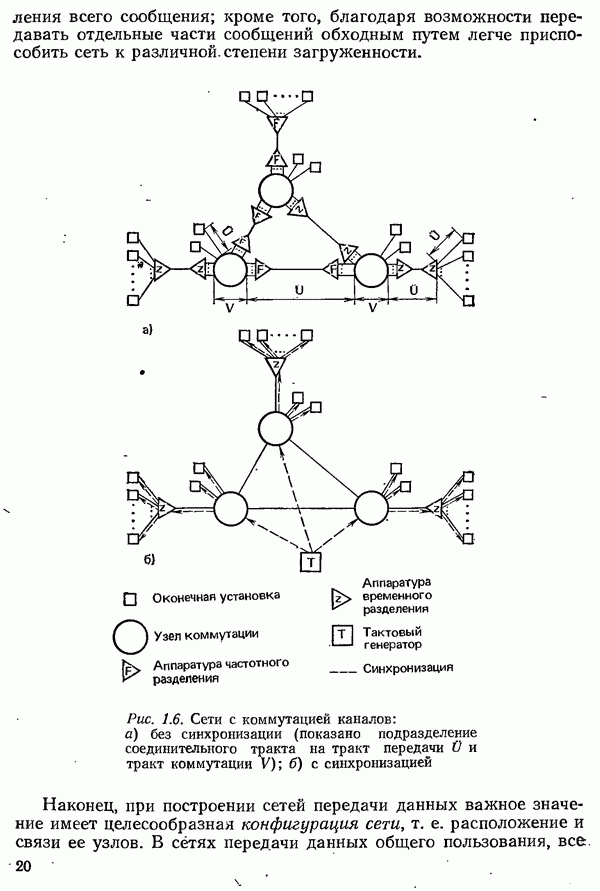
- 1.6. ТЕХНИКА СВЯЗИ В СИСТЕМАХ ТЕЛЕОБРАБОТКИ ДАННЫХ
- 2. Основные понятия техники связи
- 2.2. СИГНАЛЫ
- 2.2.2. ДИСКРЕТИЗАЦИЯ, КВАНТОВАНИЕ, ВЛИЯНИЕ ШУМОВ
- 2.2.3. СВОЙСТВА ПЕРВИЧНЫХ СИГНАЛОВ ДЛЯ ПЕРЕДАЧИ ДАННЫХ
- 2.2.3.2. ВРЕМЕННЫЕ СООТНОШЕНИЯ МЕЖДУ СИГНАЛАМИ
- 2.2.4. РЕЖИМЫ РАБОТЫ ПРИ ПЕРЕДАЧЕ СИГНАЛОВ
- 2.3. НЕКОТОРЫЕ ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ИНФОРМАЦИИ
- 2.3.2. ПЕРЕДАННАЯ ИНФОРМАЦИЯ. ПРОПУСКНАЯ СПОСОБНОСТЬ КАНАЛА СВЯЗИ
- 2.4. КОДИРОВАНИЕ
- 2.4.3. КОДИРОВАНИЕ ИСТОЧНИКА
- 2.4.4. КАНАЛЬНОЕ КОДИРОВАНИЕ
- 3. Каналы связи
- 3.1. КАНАЛЫ БЛИЖНЕЙ СВЯЗИ
- 3.1.1.1. СВОЙСТВА И ПАРАМЕТРЫ ПРОВОДНЫХ ЛИНИЙ СВЯЗИ
- 3.1.1.2. УМЕНЬШЕНИЕ ЗАТУХАНИЯ ПУТЕМ УВЕЛИЧЕНИЯ ИНДУКТИВНОСТИ. ПУПИНИЗАЦИЯ
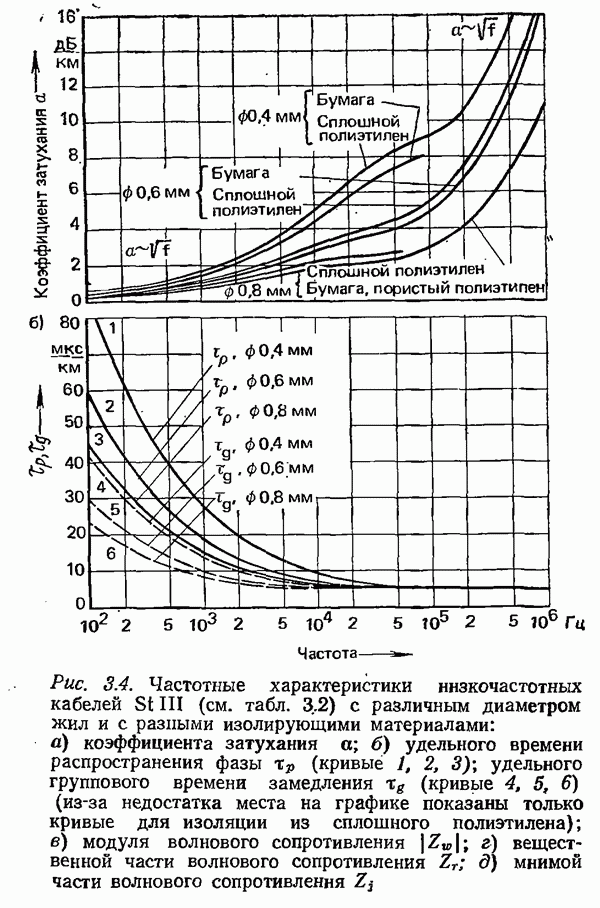
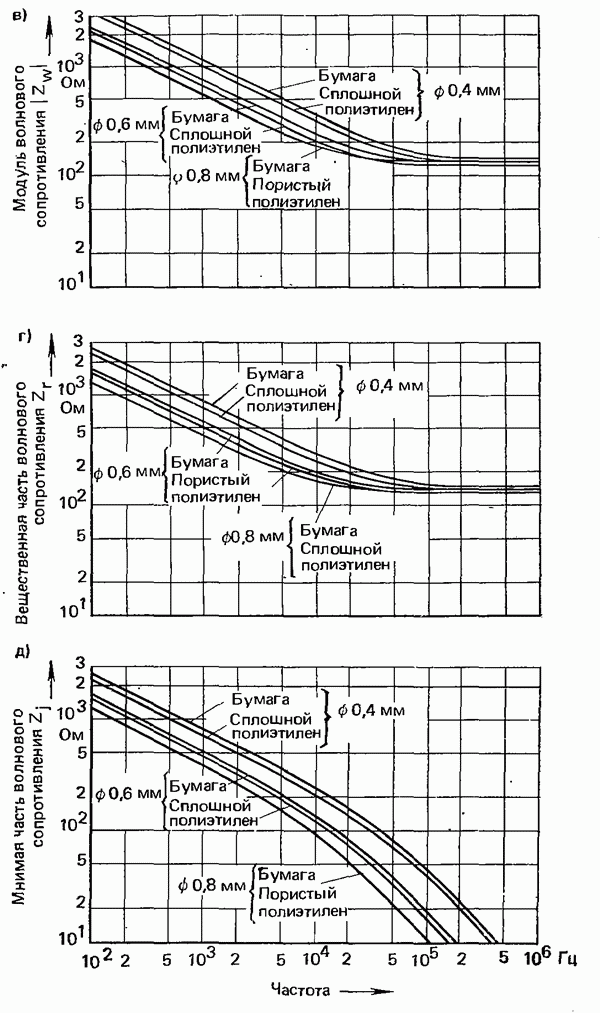
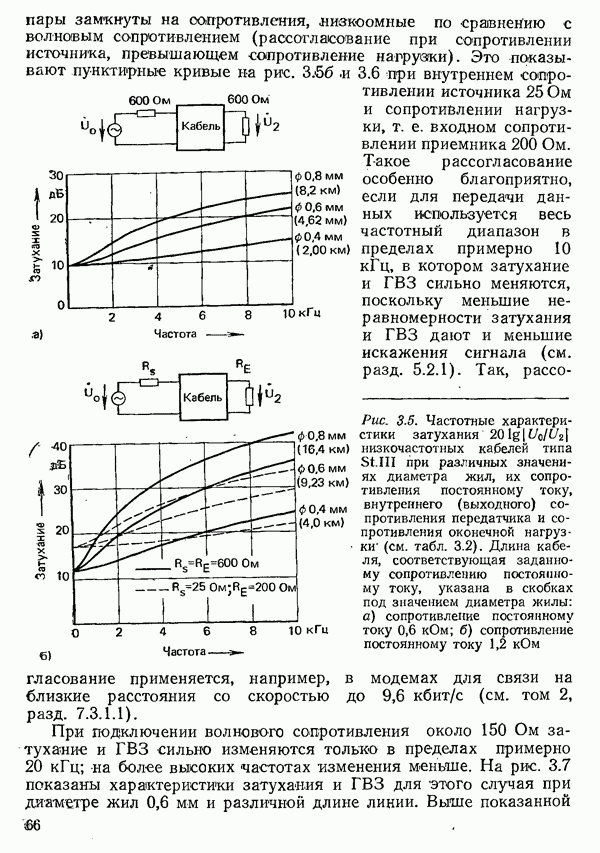
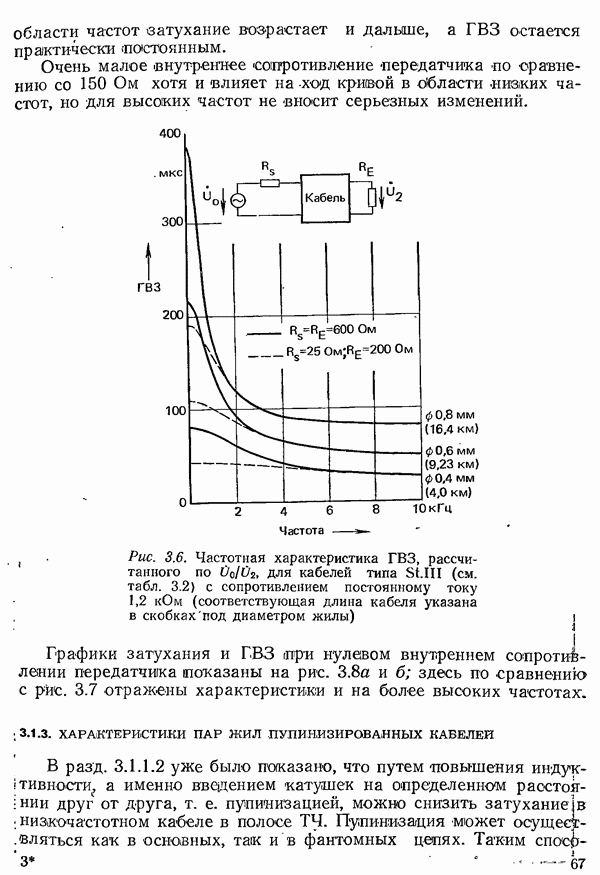
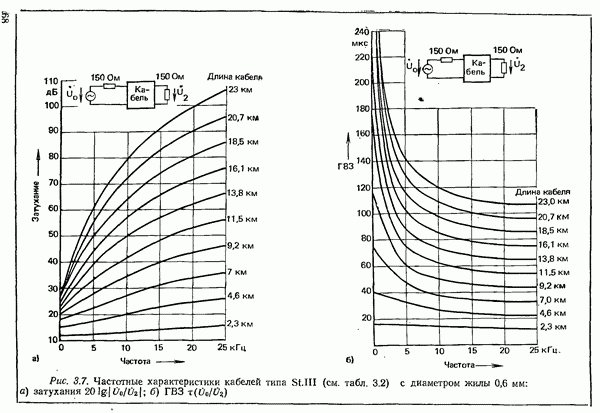
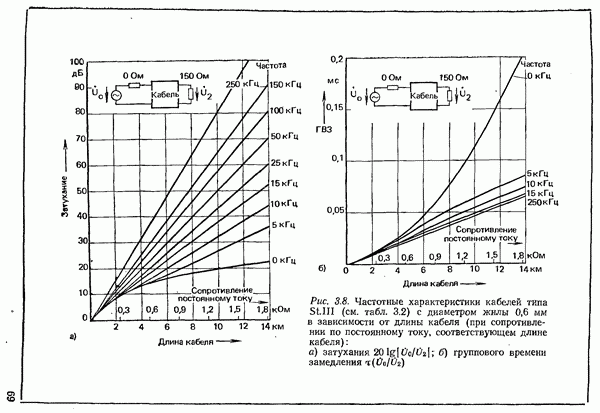
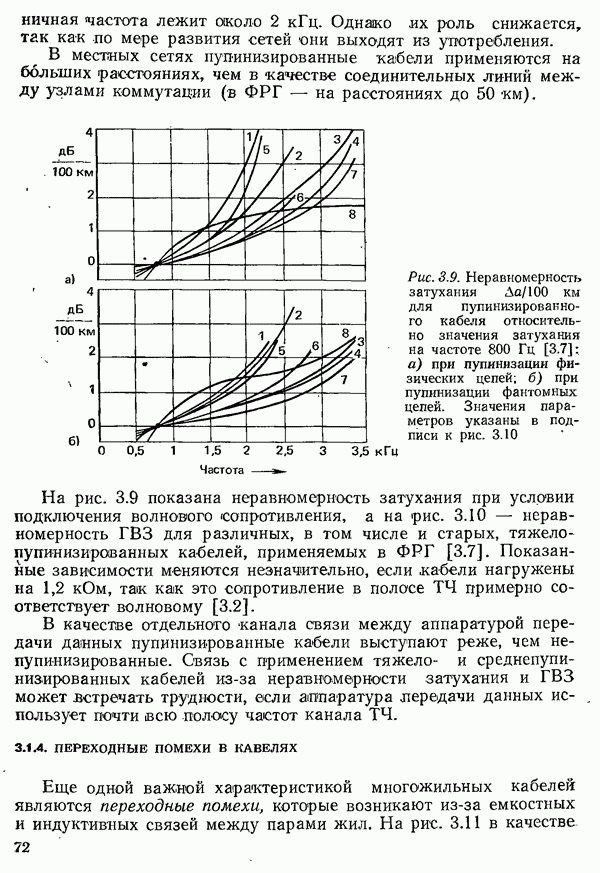
- 3.1.2. ХАРАКТЕРИСТИКИ ПАР ЖИЛ НИЗКОЧАСТОТНЫХ КАБЕЛЕЙ
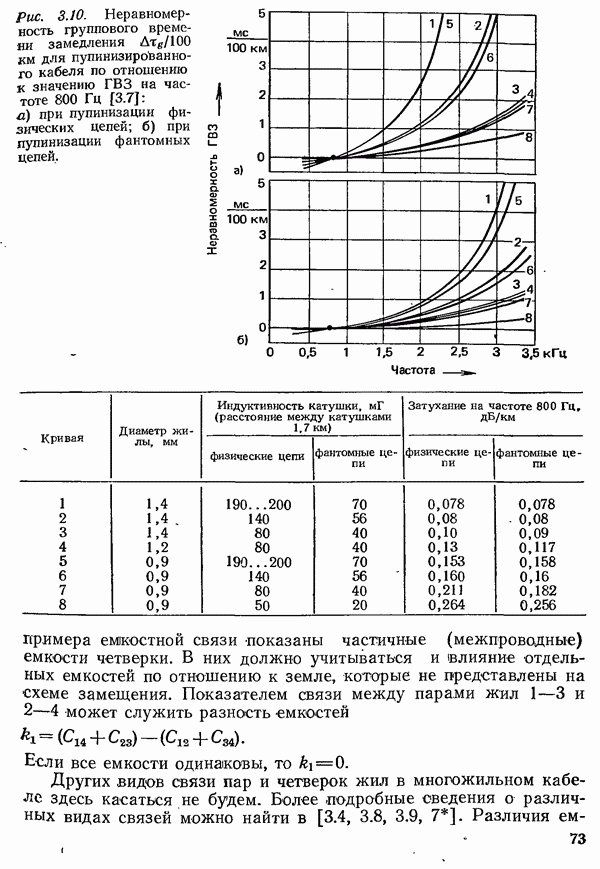
- 3.1.3. ХАРАКТЕРИСТИКИ ПАР ЖИЛ ПУПИЯИЗИРОВАННЫХ КАБЕЛЕЙ
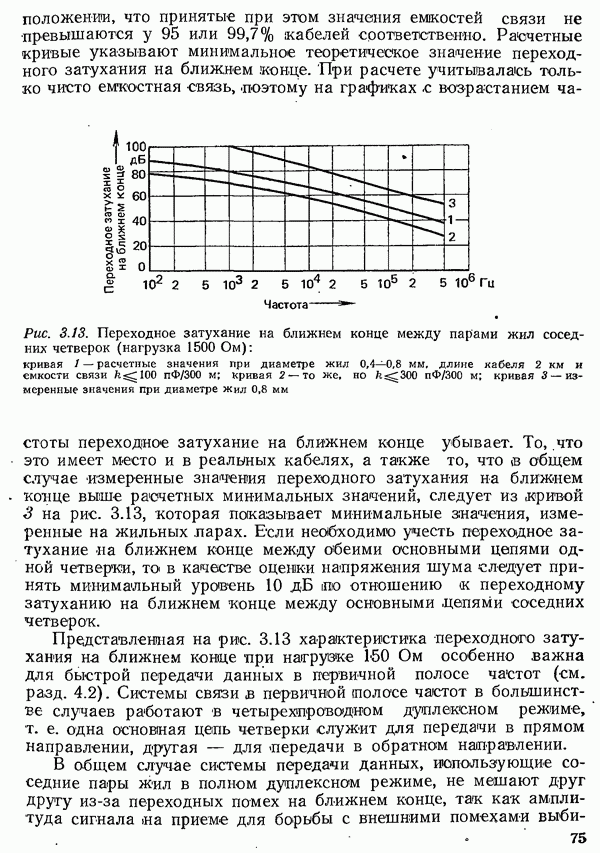
- 3.1.4. ПЕРЕХОДНЫЕ ПОМЕХИ В КАБЕЛЯХ
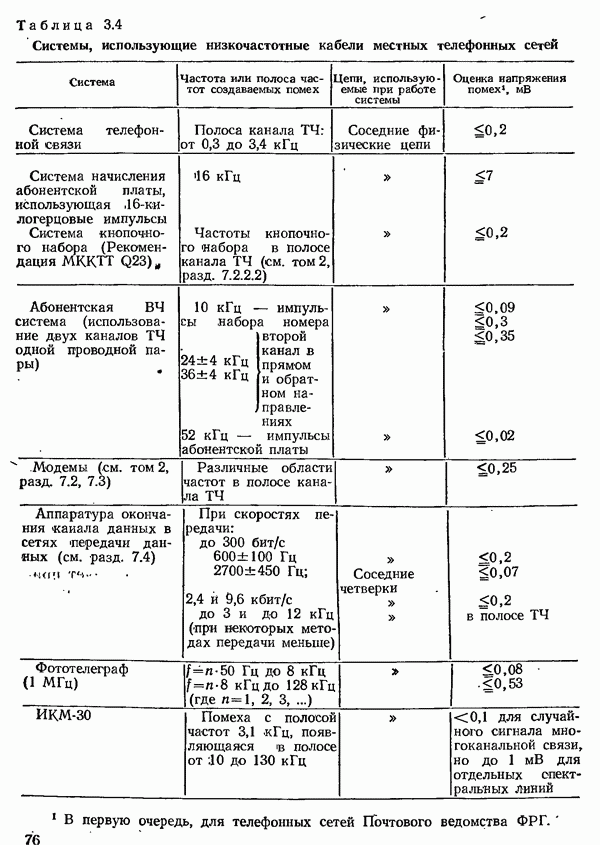
- 3.1.5. НАПРЯЖЕНИЯ ШУМОВ НА ПАРАХ ШИЛ КАБЕЛЕЙ
- 3.2. КАНАЛЫ ДАЛЬНЕЙ СВЯЗИ
- 3.2.2. КАНАЛЫ ТОНАЛЬНОЙ ЧАСТОТЫ
- 3.2.3. СОЕДИНИТЕЛЬНЫЕ ТРАКТЫ НА ОСНОВЕ ПЕРВИЧНЫХ ГРУПП КАНАЛОВ
- 4. Методы передачи данных
- 4.1.1. СИГНАЛЫ И СПЕКТРЫ
- 4.1.2. РЯД ФУРЬЕ
- 4.1.3. ИСКАЖЕНИЯ ФОРМЫ ИМПУЛЬСОВ ПРИ ОГРАНИЧЕНИИ ПОЛОСЫ ЧАСТОТ
- 4.1.4. УСЛОВИЯ НАЙКВИСТА
- 4.1.5. МЕТОДЫ ПАРЦИАЛЬНЫХ ОТСЧЕТОВ
- 4.1.6. ПЕРЕДАЧА МНОГОПОЗИЦИОННЫХ СИГНАЛОВ
- 4.2. МЕТОДЫ ПЕРЕДАЧИ В ПЕРВИЧНОЙ ПОЛОСЕ ЧАСТОТ
- 4.2.1. МЕТОДЫ С ПРИМЕНЕНИЕМ ДВУПОЛЯРНЫХ И ОДНОПОЛЯРНЫХ ИМПУЛЬСОВ
- 4.2.2. БИПОЛЯРНЫЙ МЕТОД
- 4.2.3. ПСЕВДОТРОИЧНЫЕ МЕТОДЫ
- 4.2.4. МЕТОДЫ С ПРИМЕНЕНИЕМ БИПОЛЯРНЫХ КОДОВ ВЫСОКОЙ ПЛОТНОСТИ
- 4.2.5. ДВУХФАЗНЫЙ МЕТОД. ИЛИ МЕТОД РАСЩЕПЛЕНИЯ ФАЗЫ
- 4.2.6. ДВУХФАЗНО-КОДОВЫЙ МЕТОД
- 4.2.7. МЕТОДЫ ПАРЦИАЛЬНЫХ ОТСЧЕТОВ
- 4.3. МЕТОДЫ ПЕРЕДАЧИ С ПРИМЕНЕНИЕМ МОДУЛЯЦИИ
- 4.3.1. АМПЛИТУДНАЯ МОДУЛЯЦИЯ
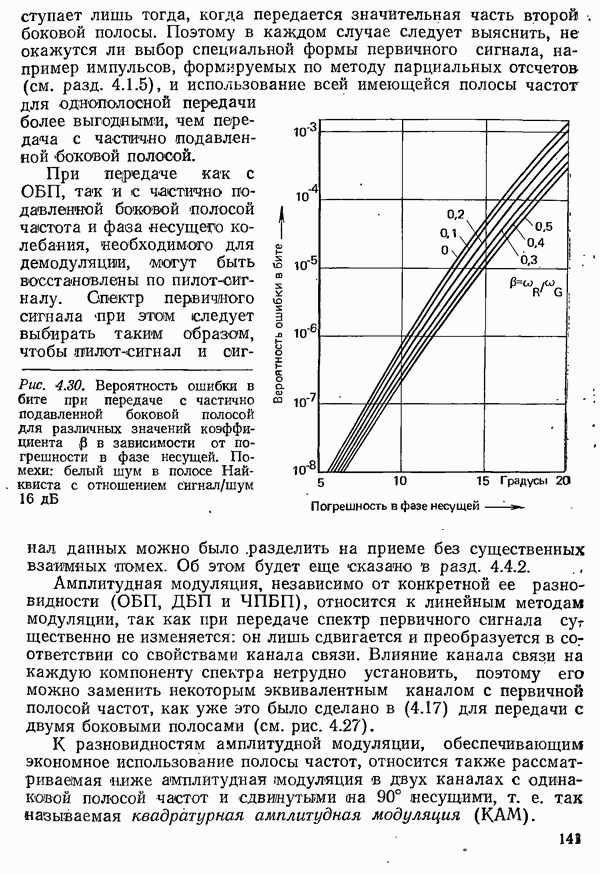
- 4.3.1.2. АМПЛИТУДНАЯ МОДУЛЯЦИЯ С ОДНОЙ БОКОВОЙ ПОЛОСОЙ И С ЧАСТИЧНО ПОДАВЛЕННОЙ БОКОВОЙ ПОЛОСОЙ
- 4.3.1.3. КВАДРАТУРНАЯ АМПЛИТУДНАЯ МОДУЛЯЦИЯ
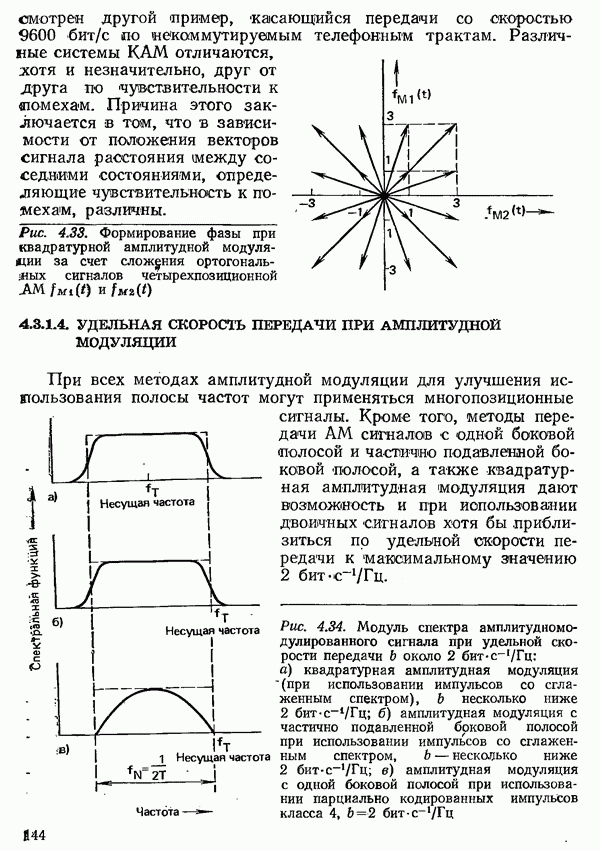
- 4.3.1.4. УДЕЛЬНАЯ СКОРОСТЬ ПЕРЕДАЧИ ПРИ АМПЛИТУДНОЙ МОДУЛЯЦИИ
- 4.3.2. ЧАСТОТНАЯ МОДУЛЯЦИЯ
- 4.3.2.1. УДЕЛЬНАЯ СКОРОСТЬ ПЕРЕДАЧИ ПРИ ЧАСТОТНОЙ МОДУЛЯЦИИ
- 4.3.3. ФАЗОВАЯ МОДУЛЯЦИЯ
- 4.4. ВОССТАНОВЛЕНИЕ ТАКТОВ И НЕСУЩЕЙ
- 4.4.2. ВОССТАНОВЛЕНИЕ ЧАСТОТЫ И ФАЗЫ НЕСУЩЕЙ
- 4.5. ВЕРОЯТНОСТЬ ОШИБКИ ПРИ НАЛИЧИИ ПОМЕХ
- 4.5.1. ВЕРОЯТНОСТЬ ОШИБКИ ПРИ УЧЕТЕ ТОЛЬКО ШУМА В КАНАЛЕ СВЯЗИ
- 4.5.2. ВЕРОЯТНОСТЬ ОШИБКИ С УЧЕТОМ ЛИНЕЙНЫХ ИСКАЖЕНИЙ
- 4.5.3. ВЕРОЯТНОСТЬ ОШИБКИ С УЧЕТОМ ПРОЦЕССОВ МОДУЛЯЦИИ И ДЕМОДУЛЯЦИИ
- 5. Учет свойств реальных каналов связи при передаче данных
- 5.2. ВЛИЯНИЕ ХАРАКТЕРИСТИК КАНАЛОВ СВЯЗИ НА ПЕРЕДАЧУ ДАННЫХ
- 5.2.2. СДВИГИ ЧАСТОТЫ
- 5.2.3. ФАЗОВОЕ ДРОЖАНИЕ
- 5.2.4. ВЛИЯНИЕ РЕАЛЬНЫХ ПОМЕХ
- 5.3. КОРРЕКЦИЯ ПРИНИМАЕМОГО СИГНАЛА ДАННЫХ
- 5.3.1. КОРРЕКЦИЯ ПРИНИМАЕМОГО СИГНАЛА ДАННЫХ В ЧАСТОТНОЙ ОБЛАСТИ
- 5.3.1.1. КОМПРОМИССНЫЙ КОРРЕКТОР
- 5.3.1.2. НАСТРАИВАЕМЫЙ ЧАСТОТНЫЙ КОРРЕКТОР СИГНАЛОВ ДАННЫХ
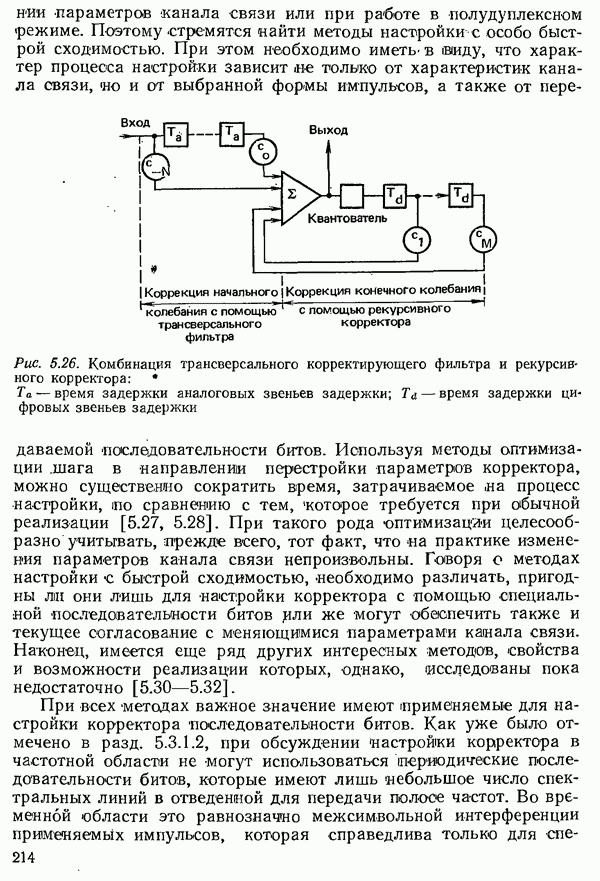
- 5.3.2. КОРРЕКЦИЯ ПРИНИМАЕМОГО СИГНАЛА ДАННЫХ ВО ВРЕМЕННОЙ ОБЛАСТИ
- 5.3.2.2. КРИТЕРИИ НАСТРОЙКИ КОРРЕКТОРА ВО ВРЕМЕННОЙ ОБЛАСТИ
- 5.3.2.3. АВТОМАТИЧЕСКАЯ НАСТРОЙКА ТРАНСВЕРСАЛЬНОГО КОРРЕКТИРУЮЩЕГО ФИЛЬТРА
- 5.3.2.4. РЕКУРСИВНЫЙ КОРРЕКТОР
- 5.3.2.5. СХОДИМОСТЬ НАСТРОЙКИ КОРРЕКТОРА
- 5.3.2.6. КОРРЕКТОР ДЛЯ СПЕЦИАЛЬНЫХ МЕТОДОВ ПЕРЕДАЧИ
- 6. Основы коммутации данных
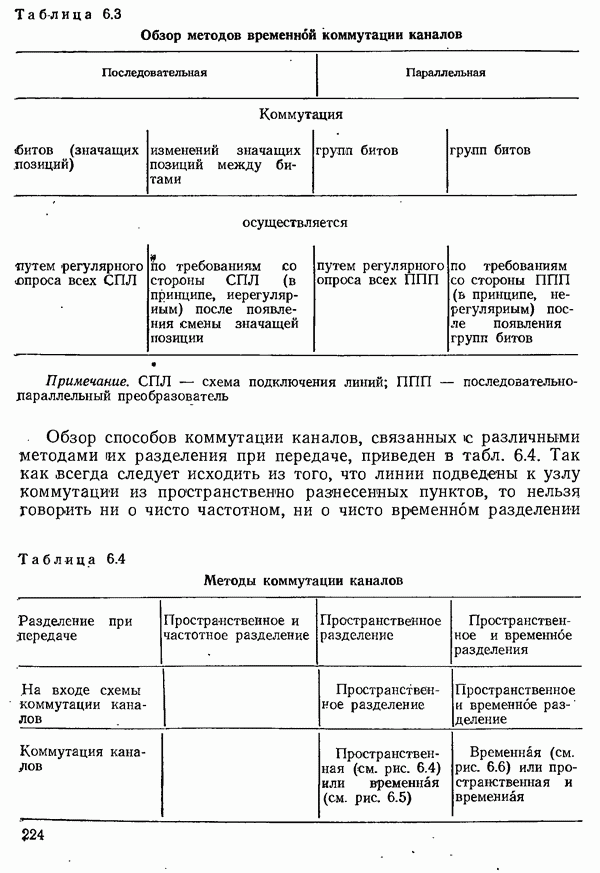
- 6.1.2. МЕТОДЫ КОММУТАЦИИ
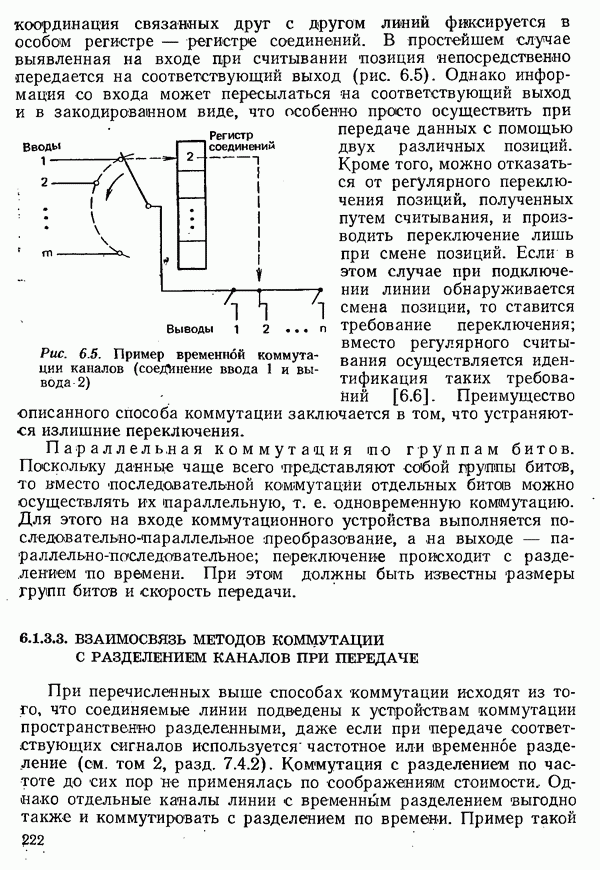
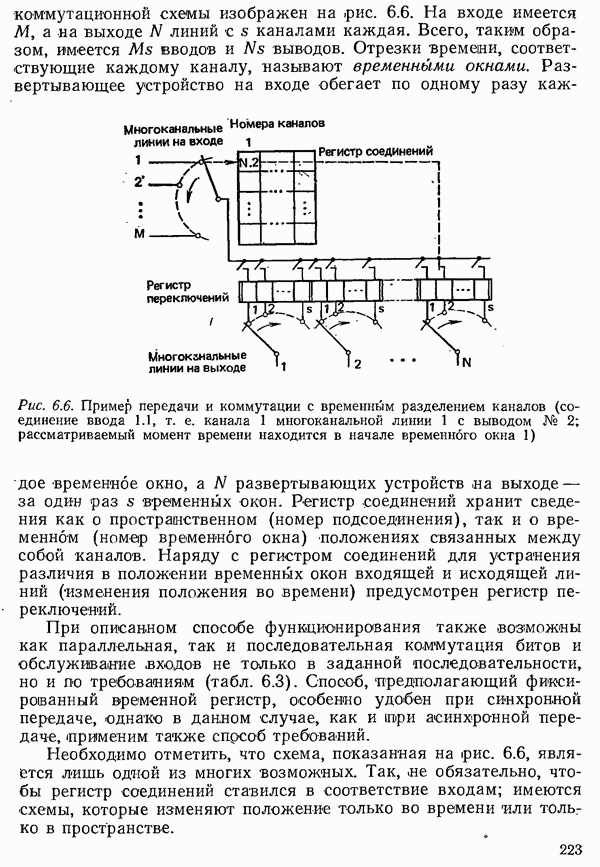
- 6.1.3. СПОСОБЫ КОММУТАЦИИ КАНАЛОВ
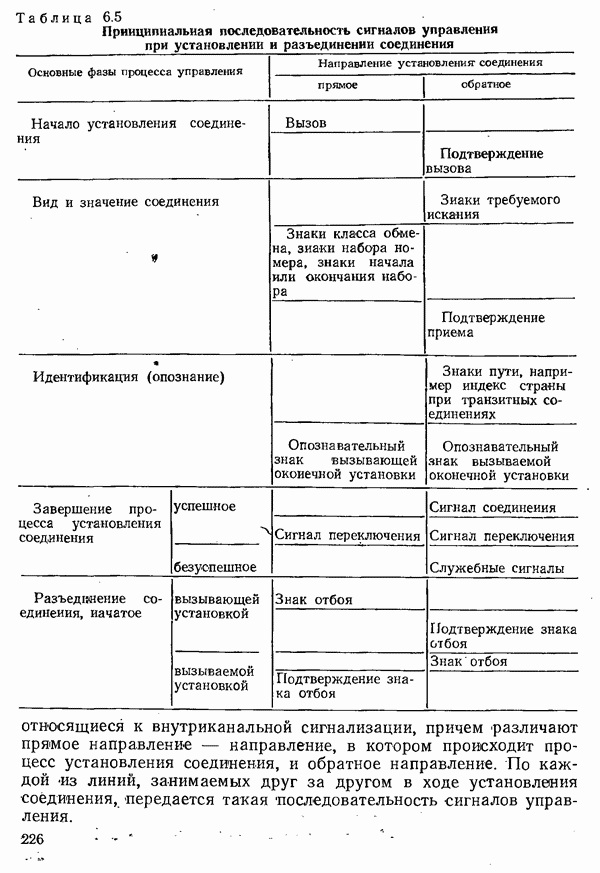
- 6.1.4. СИГНАЛИЗАЦИЯ
- 6.1.5. УПРАВЛЕНИЕ ПРОЦЕССАМИ СОЕДИНЕНИЯ И РАЗЪЕДИНЕНИЯ
- 6.1.6. ПОДРАЗДЕЛЕНИЕ ЦЕПЕЙ КОММУТАЦИИ КАНАЛОВ
- 6.1.7. ДОПОЛНИТЕЛЬНЫЕ ЗАДАЧИ КОММУТАЦИОННЫХ УСТРОЙСТВ
- 6.2. АНАЛИЗ СИСТЕМ КОММУТАЦИИ НА ОСНОВЕ ТЕОРИИ ТЕЛЕТРАФИКА
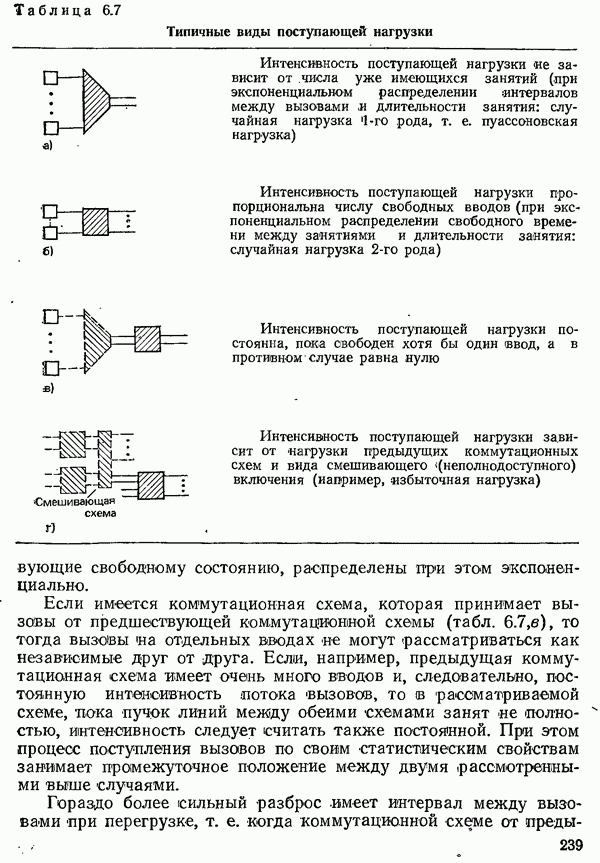
- 6.2.2. СИСТЕМЫ С ПОТЕРЯМИ
- 6.2.3. СИСТЕМЫ С ОЖИДАНИЕМ
- 6.2.4. ИЗМЕРЕНИЯ НАГРУЗКИ
- СПИСОК ЛИТЕРАТУРЫ