| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
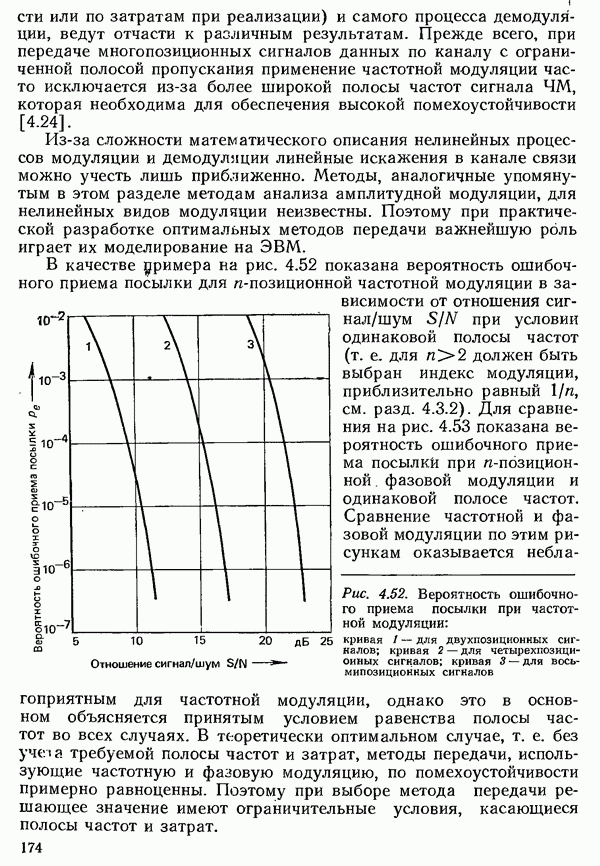
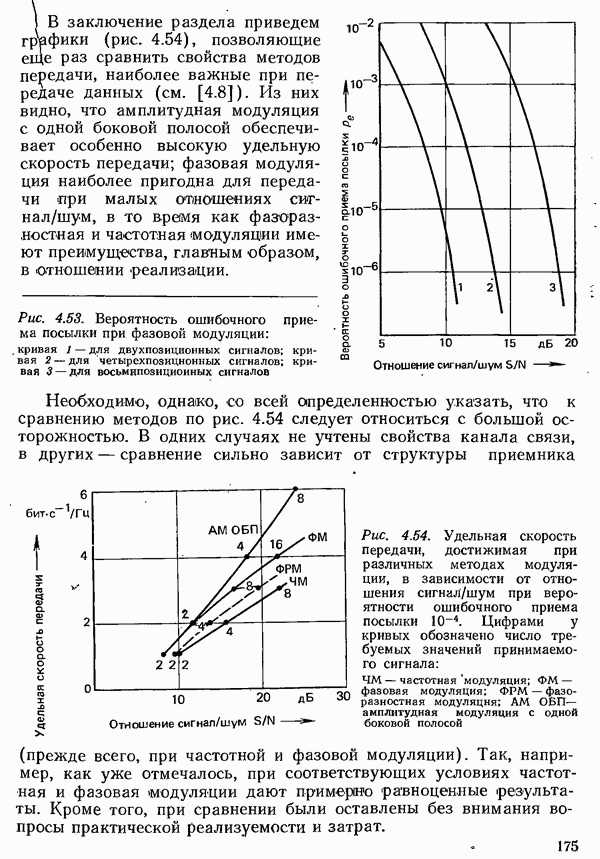
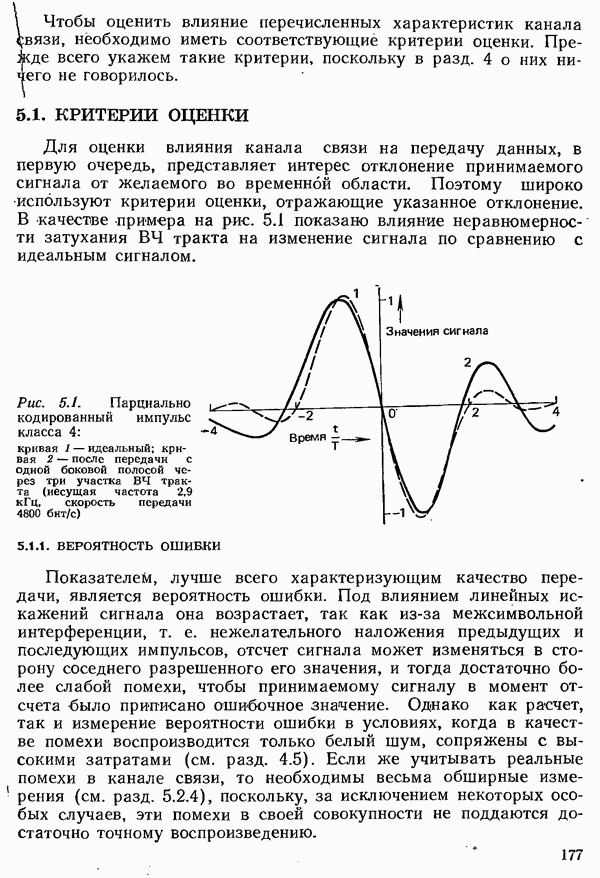
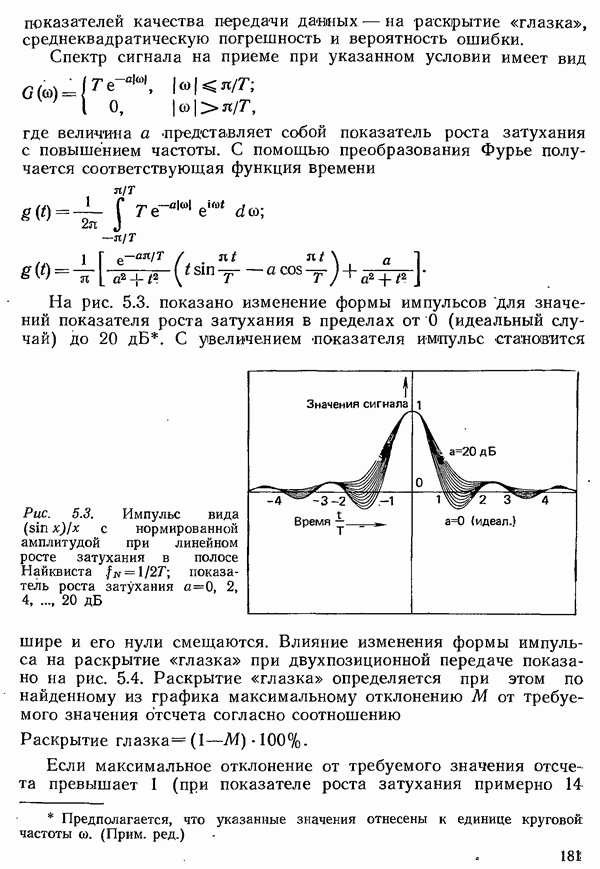
4.5.2. ВЕРОЯТНОСТЬ ОШИБКИ С УЧЕТОМ ЛИНЕЙНЫХ ИСКАЖЕНИЙ
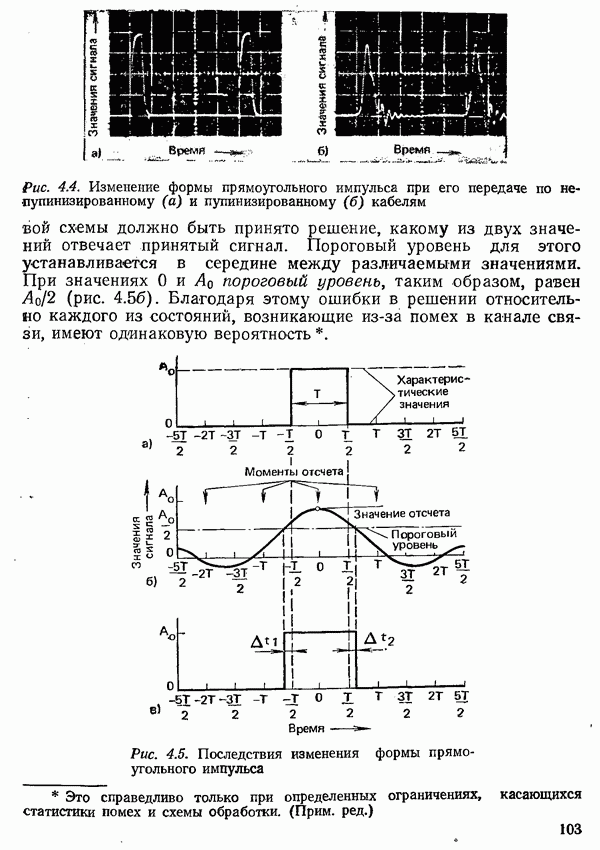
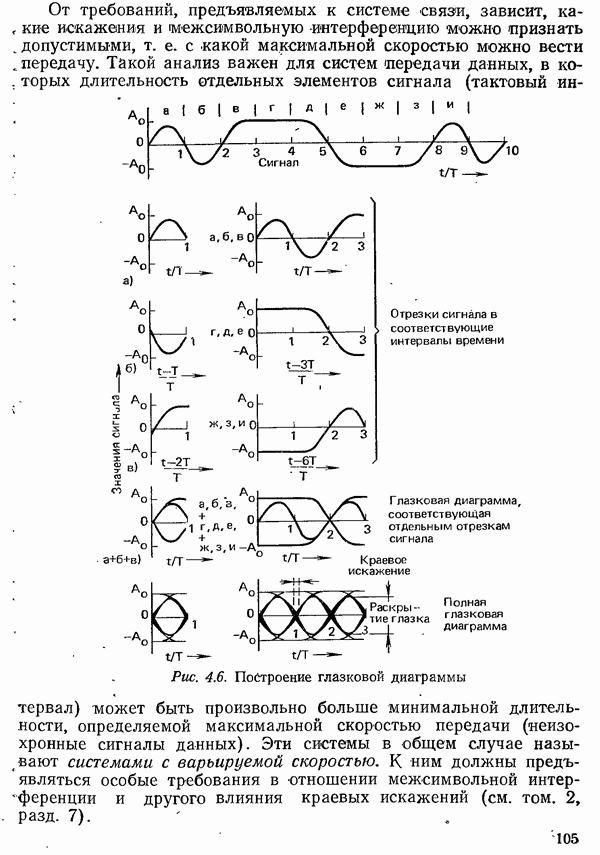
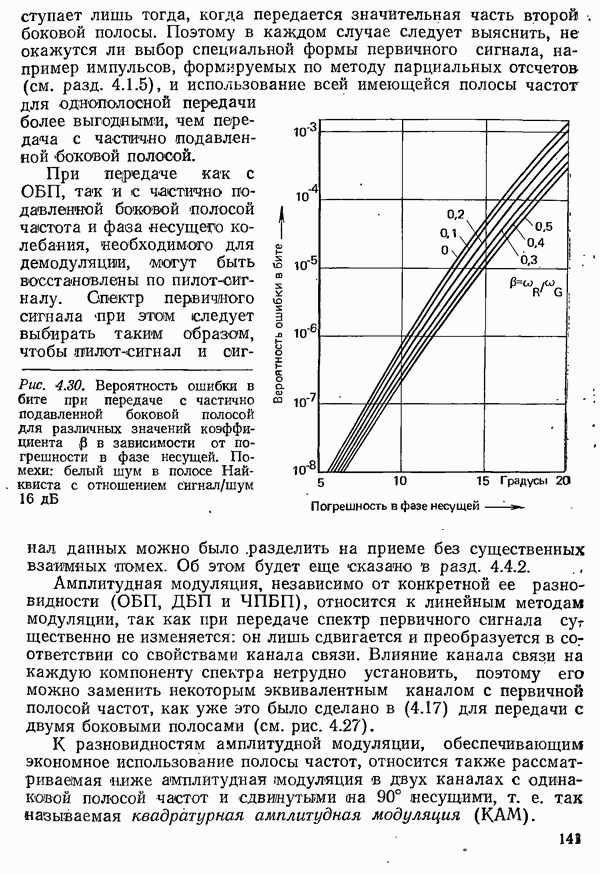
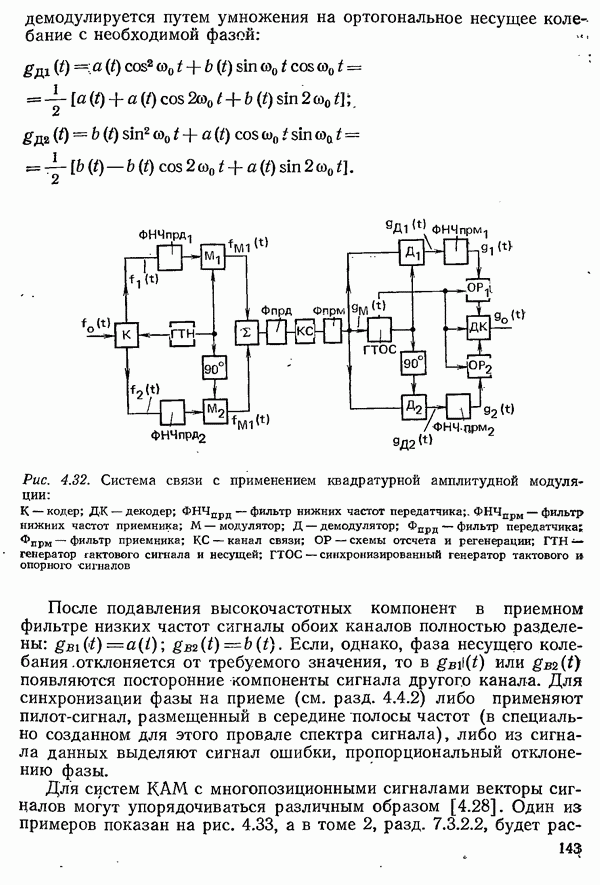
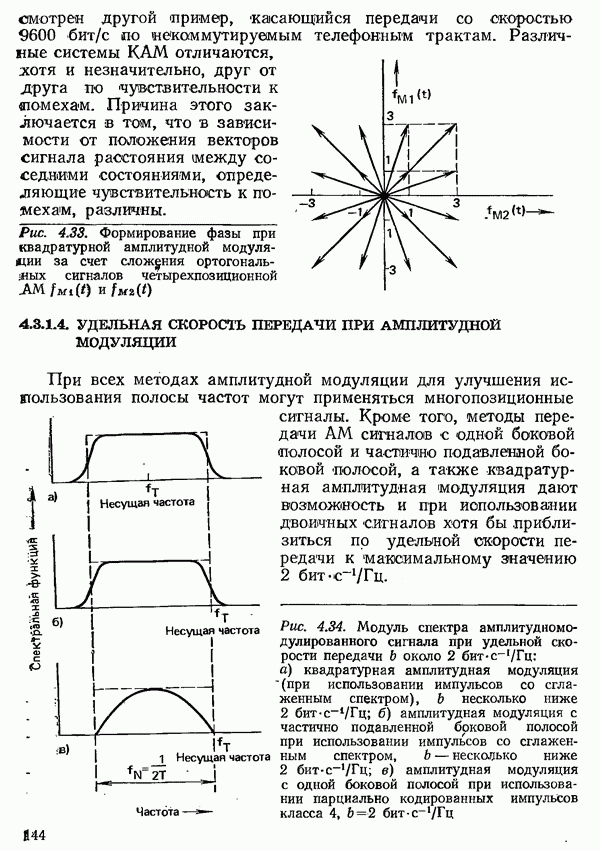
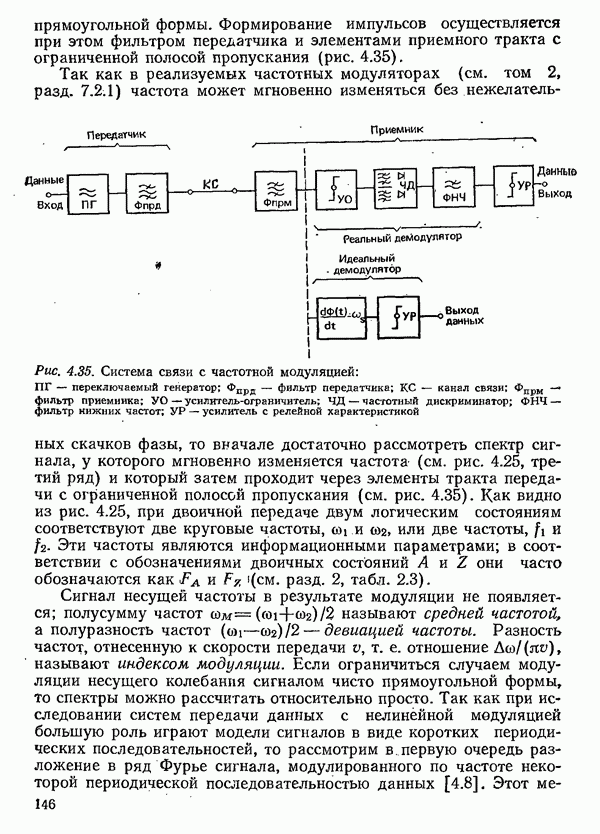
При расчете вероятности ошибки в рамках модели помех до сих пор учитывалось лишь влияние аддитивного шума. Чтобы рассчитать вероятность ошибки во всей системе передачи, необходимо учесть влияние и всех других мешающих факторов, имеющихся в канале связи. Особенно зажны линейные искажения, которые, как было отмечено в разд. 5.2, вызывают межсимвольную интерференцию. Она ведет к повышению вероятности ошибки, так как даже при отсутствии шума сигнал в точках отсчета не принимает требуемых значений, и, следовательно, уже более малое значение шума, чем то, что соответствует разности между требуемым значением и пороговым уровнем, может вести к ошибке.
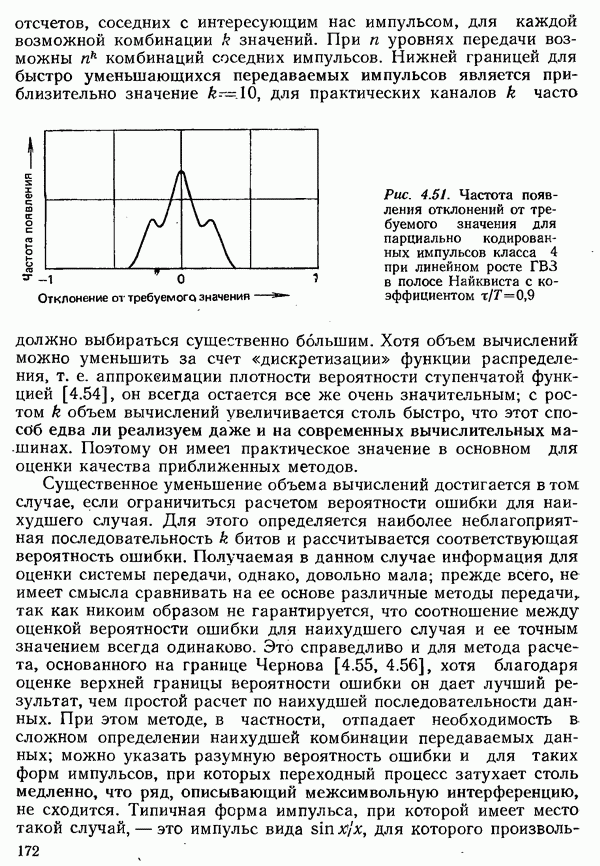
Так же, как и шум, межсимвольную интерференцию следует рассматривать как случайный процесс. Однако для нее не удается построить столь же простую вероятностную модель, как для шума; характеризующее ее распределение вероятностей должно быть найдено с учетом свойств исследуемого канала связи и метода передачи. Как правило, распределение вероятностей, описывающее межсимвольную интерференцию, не может быть приближенно заменено распределением Гаусса. На рис. 4.51 в качестве примера показано распределение искажений, вызванных межсимвольной интерференцией, для случая, когда двухпозиционный парциально кодированный сигнал передается по каналу с линейно возрастающей величиной ГВЗ.
Трудности точного анализа влияния межсимвольной интерференции на вероятность ошибки послужили стимулом к разработке весьма разнообразных приближенных методов. Первая мысль, которая напрашивается, — рассчитать вклад в вероятность ошибки 
отсчетов, соседних с интересующим нас импульсом, для каждой возможной комбинации  значений. При
значений. При  уровнях передачи возможны
уровнях передачи возможны  комбинаций соседних импульсов. Нижней границей для быстро уменьшающихся передаваемых импульсов является приблизительно значение
комбинаций соседних импульсов. Нижней границей для быстро уменьшающихся передаваемых импульсов является приблизительно значение  для практических каналов
для практических каналов  часто должно выбираться существенно большим.
часто должно выбираться существенно большим.

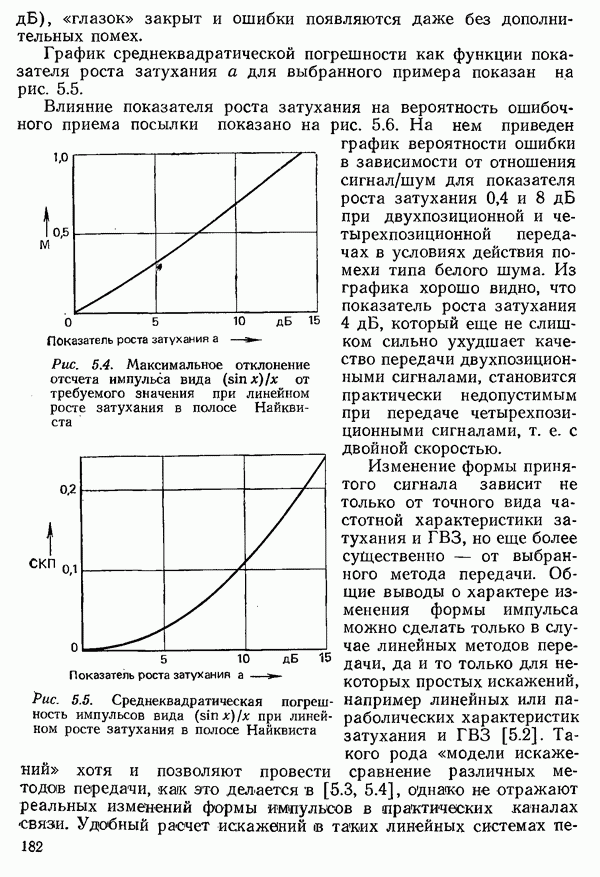
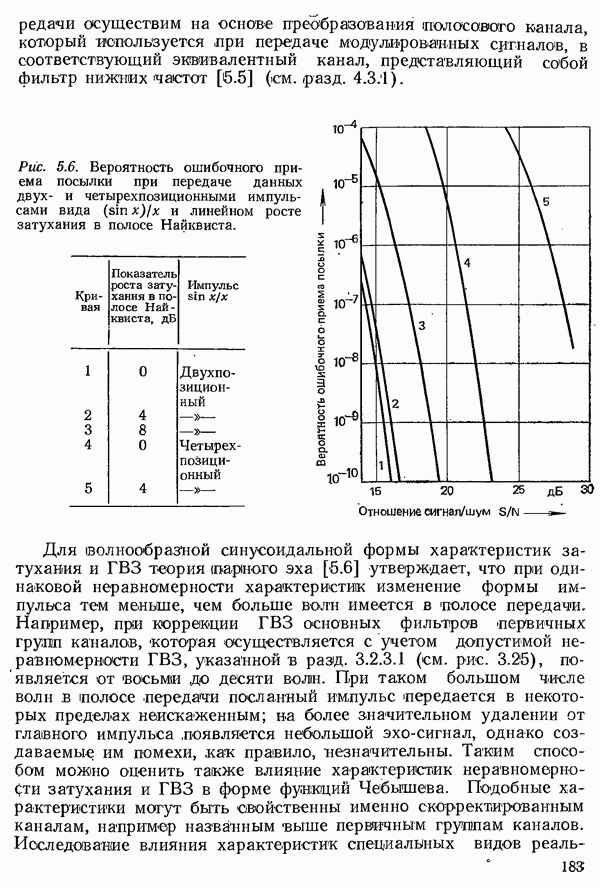
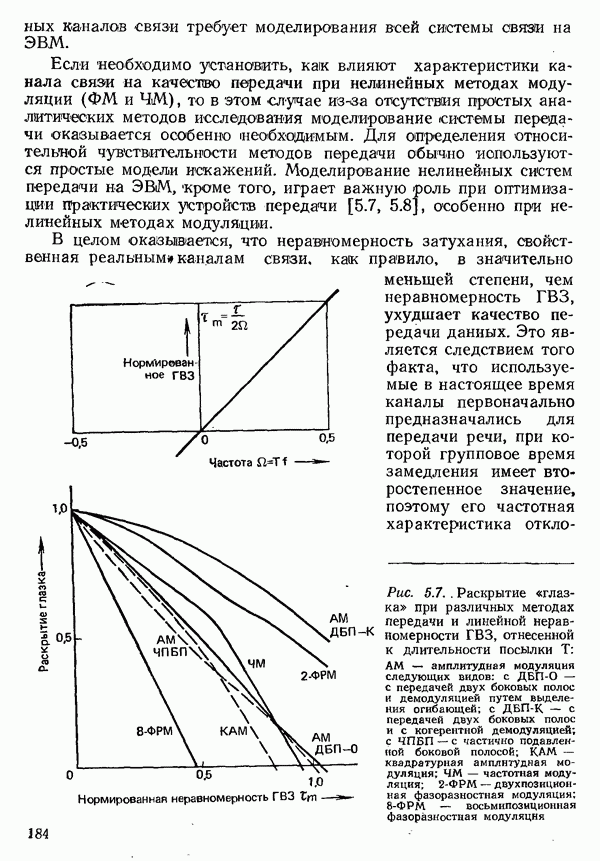
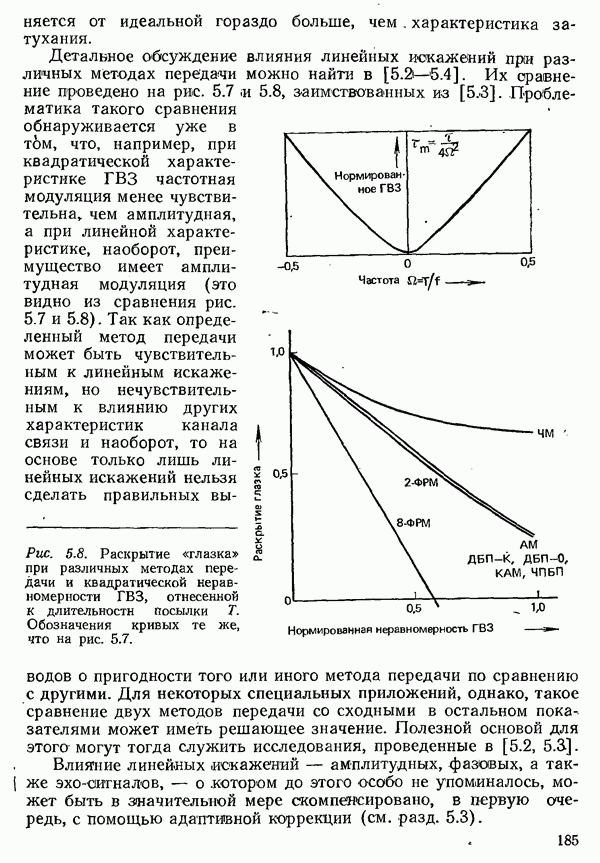
Рис. 4.51. Частота появления отклонений от требуемого значения для парциально кодированных импульсов класса 4 при линейном росте ГВЗ в полосе Найквиста с коэффициентом 
Хотя объем вычислений можно уменьшить за счет «дискретизации» функции распределения, т. е. аппрокеимации плотности вероятности ступенчатой функцией [4.54], он всегда остается все же очень значительным; с ростом  объем вычислений увеличивается столь быстро, что этот способ едва ли реализуем даже и на современных вычислительных машинах. Поэтому он имеет практическое значение в основном для оценки качества приближенных методов.
объем вычислений увеличивается столь быстро, что этот способ едва ли реализуем даже и на современных вычислительных машинах. Поэтому он имеет практическое значение в основном для оценки качества приближенных методов.
Существенное уменьшение объема вычислений достигается в том случае, если ограничиться расчетом вероятности ошибки для наихудшего случая. Для этого определяется наиболее неблагоприятная последовательность  битов и рассчитывается соответствующая вероятность ошибки. Получаемая в данном случае информация для оценки системы передачи, однако, довольно мала; прежде всего, не имеет смысла сравнивать на ее основе различные методы передачи, так как никоим образом не гарантируется, что соотношение между оценкой вероятности ошибки для наихудшего случая и ее точным значением всегда одинаково Это справедливо и для метода расчета, основанного на границе Чернова [4.55, 4.56], хотя благодаря оценке верхней границы вероятности ошибки он дает лучший результат, чем простой расчет по наихудшей последовательности данных. При этом методе, в частности, отпадает необходимость в сложном определении наихудшей комбинации передаваемых данных; можно указать разумную вероятность ошибки и для таких форм импульсов, при которых переходный процесс затухает столь медленно, что ряд, описывающий межсимвольную интерференцию, не сходится. Типичная форма импульса, при которой имеет место такой случай, — это импульс вида
битов и рассчитывается соответствующая вероятность ошибки. Получаемая в данном случае информация для оценки системы передачи, однако, довольно мала; прежде всего, не имеет смысла сравнивать на ее основе различные методы передачи, так как никоим образом не гарантируется, что соотношение между оценкой вероятности ошибки для наихудшего случая и ее точным значением всегда одинаково Это справедливо и для метода расчета, основанного на границе Чернова [4.55, 4.56], хотя благодаря оценке верхней границы вероятности ошибки он дает лучший результат, чем простой расчет по наихудшей последовательности данных. При этом методе, в частности, отпадает необходимость в сложном определении наихудшей комбинации передаваемых данных; можно указать разумную вероятность ошибки и для таких форм импульсов, при которых переходный процесс затухает столь медленно, что ряд, описывающий межсимвольную интерференцию, не сходится. Типичная форма импульса, при которой имеет место такой случай, — это импульс вида  для которого
для которого
произвольно малая погрешность момента отсчета теоретически уже ведет к ошибке, так как члены получающегося ряда отсчетных значений уменьшаются как  и ряд не сходится.
и ряд не сходится.
Расчет вероятности ошибки, достаточно точный и для сравнения сходных методов передачи или оптимизации систем передачи, может быть осуществлен с помощью разложений в ряды [4.57-4.64]. На этих методах, применяемых в последнее время и требующих несколько более сложного математического аппарата, мы, однако, не будем останавливаться. Их основное значение заключается в том, что при сравнительно умеренных затратах они позволяют получить точное представление о влиянии различных параметров на качество передачи.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ К РУССКОМУ ИЗДАНИЮ
- 1. Обзор
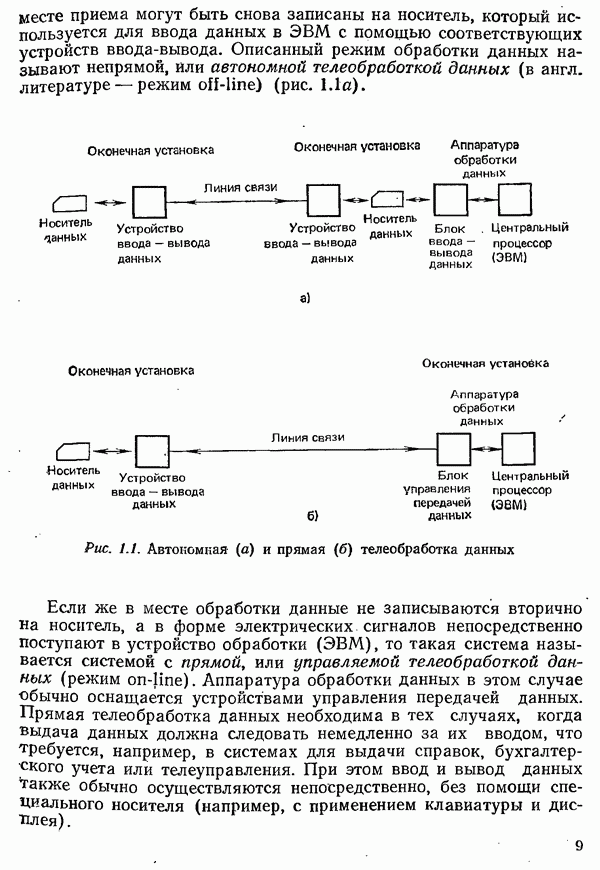
- 1.1. ОБРАБОТКА И ТЕЛЕОБРАБОТКА ДАННЫХ
- 1.2. АВТОНОМНАЯ И УПРАВЛЯЕМАЯ ТЕЛЕОБРАБОТКА ДАННЫХ
- 1.3. КЛАССИФИКАЦИЯ СИСТЕМ ТЕЛЕОБРАБОТКИ ДАННЫХ
- 1.4. СТРУКТУРА СИСТЕМ ТЕЛЕОБРАБОТКИ ДАННЫХ
- 1.5. ТРЕБОВАНИЯ К ТЕХНИКЕ СВЯЗИ И КОММУТАЦИИ В СИСТЕМАХ ТЕЛЕОБРАБОТКИ ДАННЫХ
- 1.6. ТЕХНИКА СВЯЗИ В СИСТЕМАХ ТЕЛЕОБРАБОТКИ ДАННЫХ
- 2. Основные понятия техники связи
- 2.2. СИГНАЛЫ
- 2.2.2. ДИСКРЕТИЗАЦИЯ, КВАНТОВАНИЕ, ВЛИЯНИЕ ШУМОВ
- 2.2.3. СВОЙСТВА ПЕРВИЧНЫХ СИГНАЛОВ ДЛЯ ПЕРЕДАЧИ ДАННЫХ
- 2.2.3.2. ВРЕМЕННЫЕ СООТНОШЕНИЯ МЕЖДУ СИГНАЛАМИ
- 2.2.4. РЕЖИМЫ РАБОТЫ ПРИ ПЕРЕДАЧЕ СИГНАЛОВ
- 2.3. НЕКОТОРЫЕ ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ИНФОРМАЦИИ
- 2.3.2. ПЕРЕДАННАЯ ИНФОРМАЦИЯ. ПРОПУСКНАЯ СПОСОБНОСТЬ КАНАЛА СВЯЗИ
- 2.4. КОДИРОВАНИЕ
- 2.4.3. КОДИРОВАНИЕ ИСТОЧНИКА
- 2.4.4. КАНАЛЬНОЕ КОДИРОВАНИЕ
- 3. Каналы связи
- 3.1. КАНАЛЫ БЛИЖНЕЙ СВЯЗИ
- 3.1.1.1. СВОЙСТВА И ПАРАМЕТРЫ ПРОВОДНЫХ ЛИНИЙ СВЯЗИ
- 3.1.1.2. УМЕНЬШЕНИЕ ЗАТУХАНИЯ ПУТЕМ УВЕЛИЧЕНИЯ ИНДУКТИВНОСТИ. ПУПИНИЗАЦИЯ
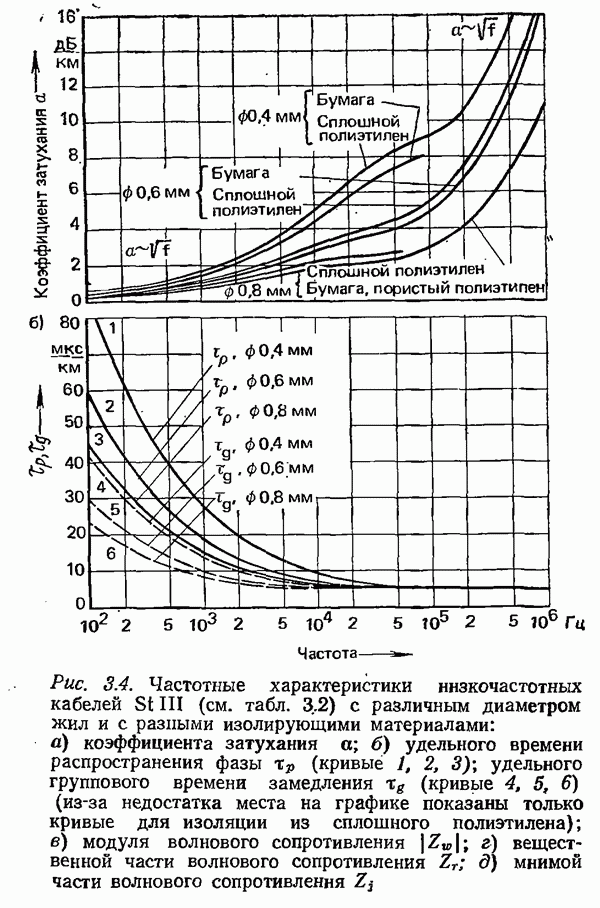
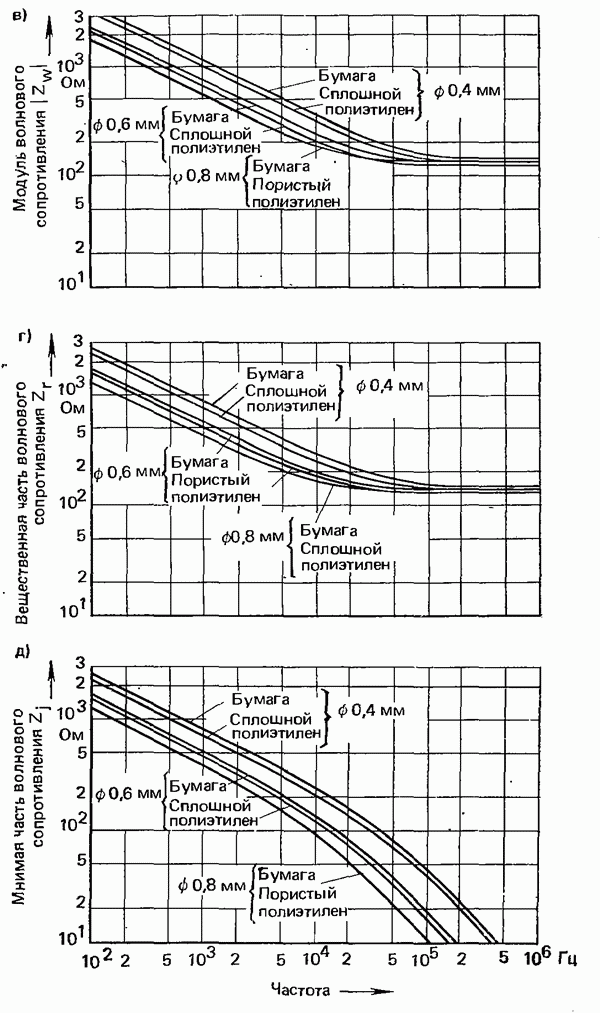
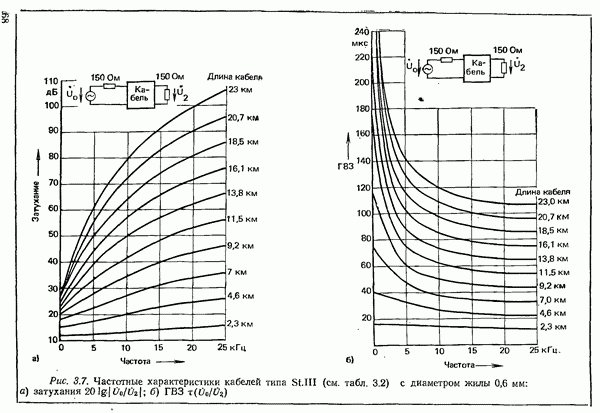
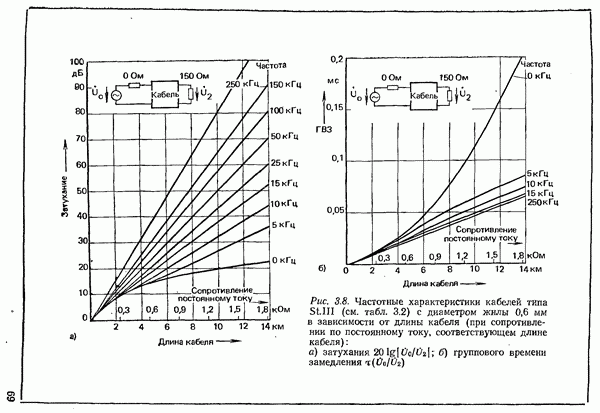
- 3.1.2. ХАРАКТЕРИСТИКИ ПАР ЖИЛ НИЗКОЧАСТОТНЫХ КАБЕЛЕЙ
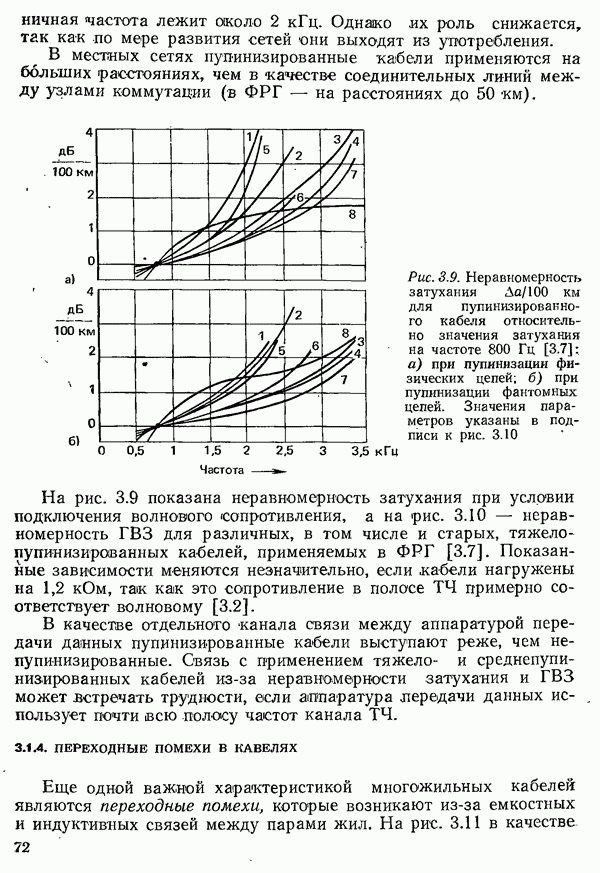
- 3.1.3. ХАРАКТЕРИСТИКИ ПАР ЖИЛ ПУПИЯИЗИРОВАННЫХ КАБЕЛЕЙ
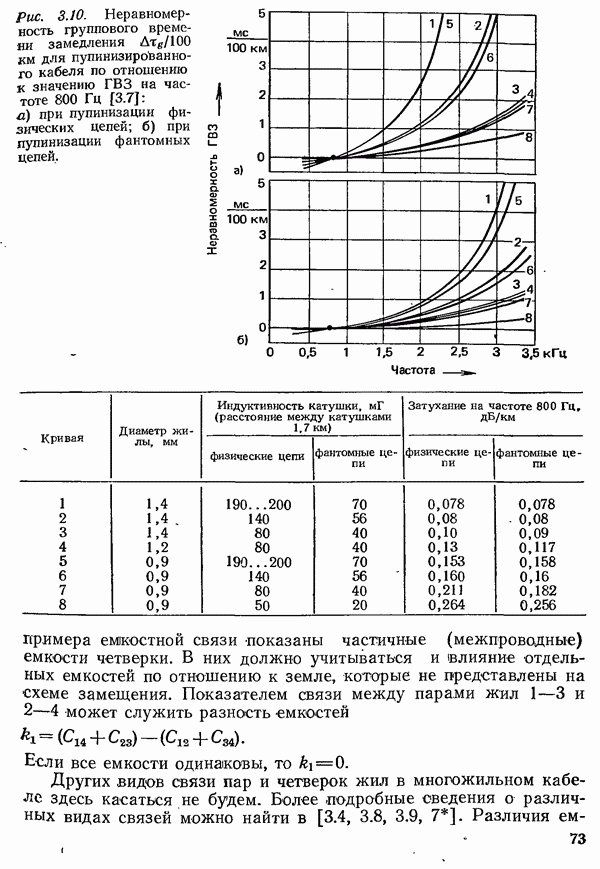
- 3.1.4. ПЕРЕХОДНЫЕ ПОМЕХИ В КАБЕЛЯХ
- 3.1.5. НАПРЯЖЕНИЯ ШУМОВ НА ПАРАХ ШИЛ КАБЕЛЕЙ
- 3.2. КАНАЛЫ ДАЛЬНЕЙ СВЯЗИ
- 3.2.2. КАНАЛЫ ТОНАЛЬНОЙ ЧАСТОТЫ
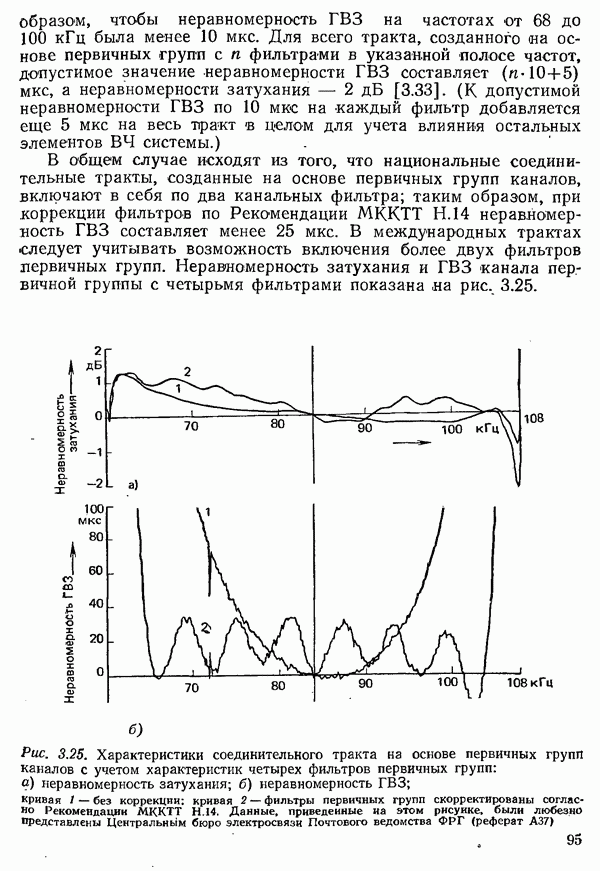
- 3.2.3. СОЕДИНИТЕЛЬНЫЕ ТРАКТЫ НА ОСНОВЕ ПЕРВИЧНЫХ ГРУПП КАНАЛОВ
- 4. Методы передачи данных
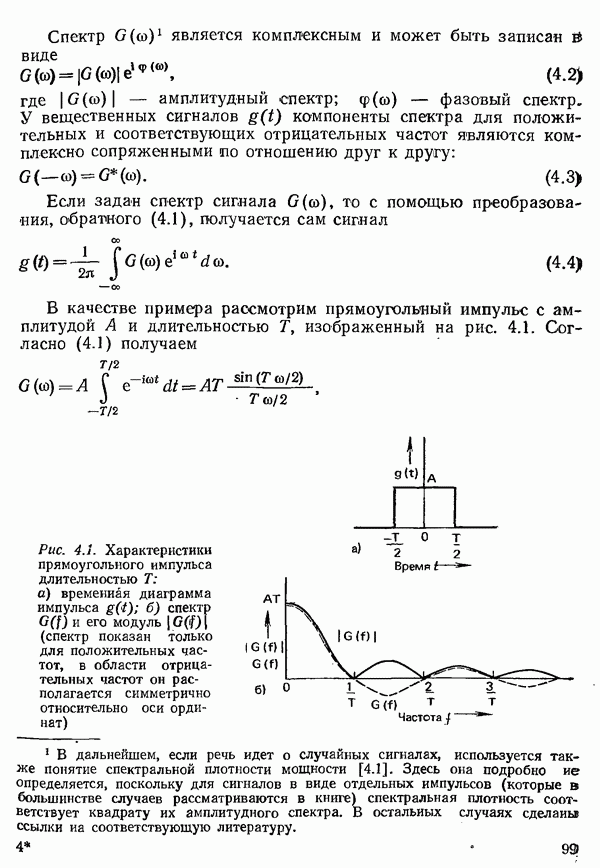
- 4.1.1. СИГНАЛЫ И СПЕКТРЫ
- 4.1.2. РЯД ФУРЬЕ
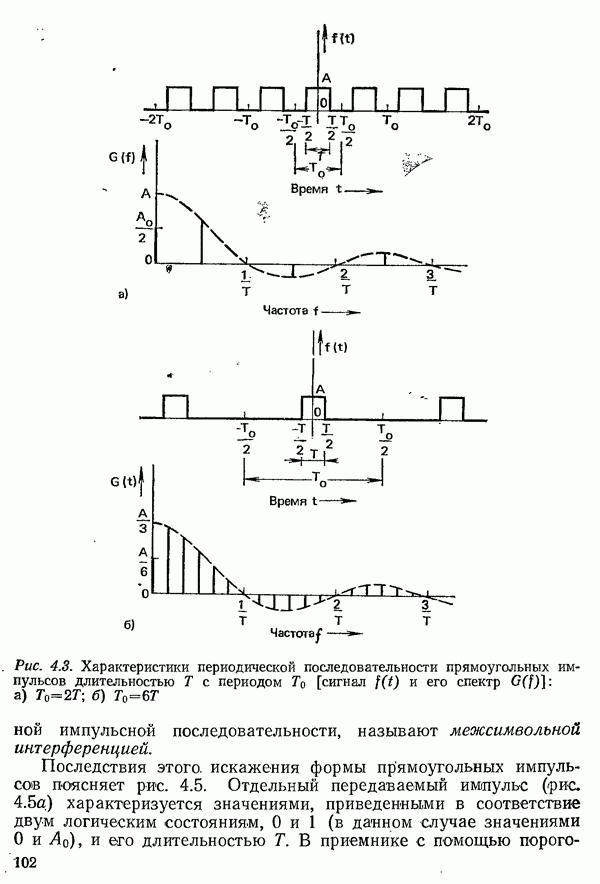
- 4.1.3. ИСКАЖЕНИЯ ФОРМЫ ИМПУЛЬСОВ ПРИ ОГРАНИЧЕНИИ ПОЛОСЫ ЧАСТОТ
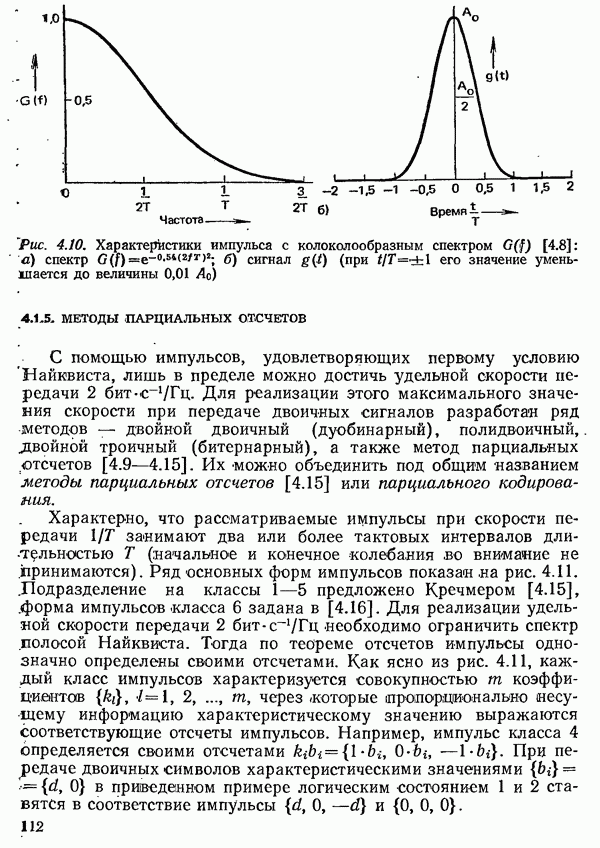
- 4.1.4. УСЛОВИЯ НАЙКВИСТА
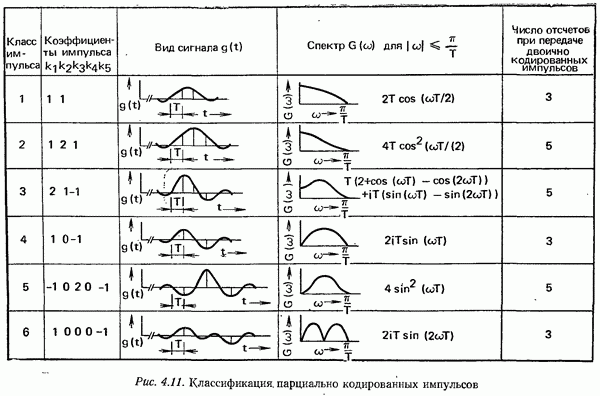
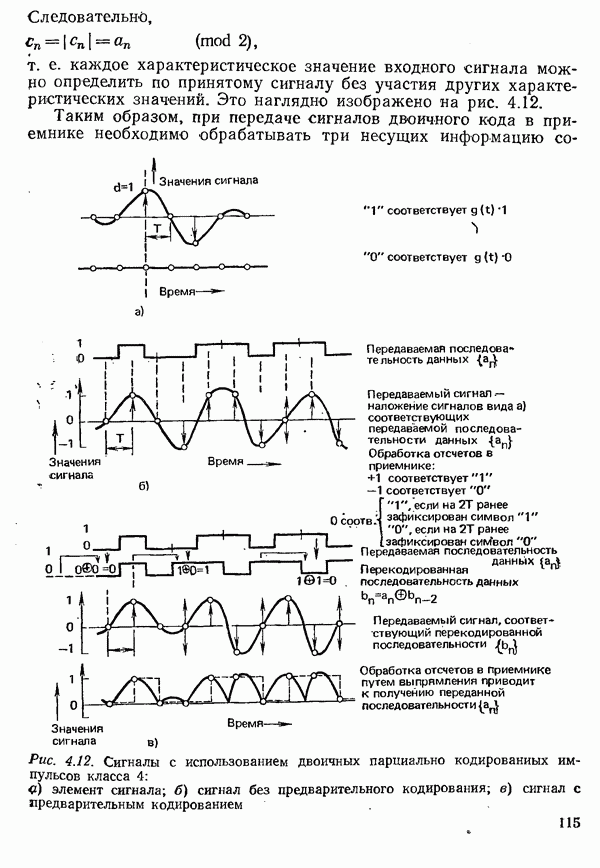
- 4.1.5. МЕТОДЫ ПАРЦИАЛЬНЫХ ОТСЧЕТОВ
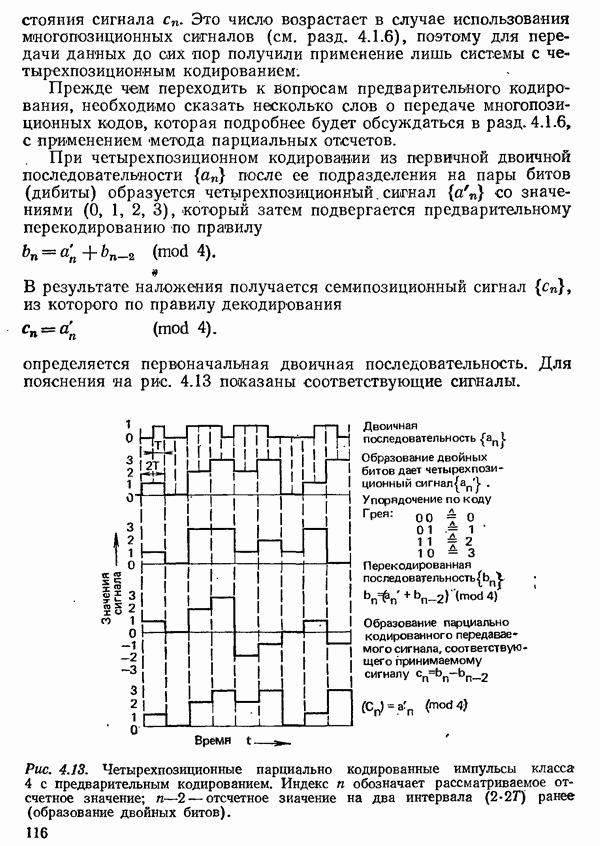
- 4.1.6. ПЕРЕДАЧА МНОГОПОЗИЦИОННЫХ СИГНАЛОВ
- 4.2. МЕТОДЫ ПЕРЕДАЧИ В ПЕРВИЧНОЙ ПОЛОСЕ ЧАСТОТ
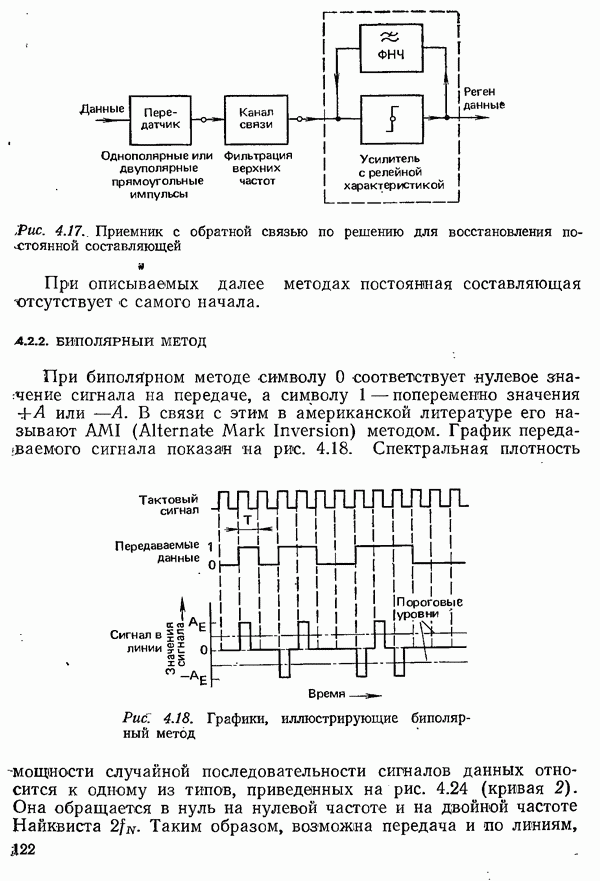
- 4.2.1. МЕТОДЫ С ПРИМЕНЕНИЕМ ДВУПОЛЯРНЫХ И ОДНОПОЛЯРНЫХ ИМПУЛЬСОВ
- 4.2.2. БИПОЛЯРНЫЙ МЕТОД
- 4.2.3. ПСЕВДОТРОИЧНЫЕ МЕТОДЫ
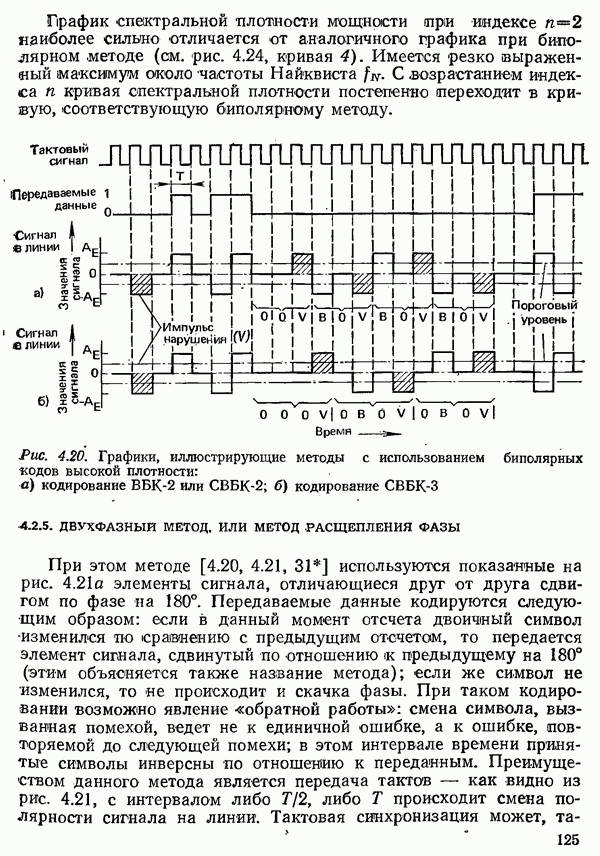
- 4.2.4. МЕТОДЫ С ПРИМЕНЕНИЕМ БИПОЛЯРНЫХ КОДОВ ВЫСОКОЙ ПЛОТНОСТИ
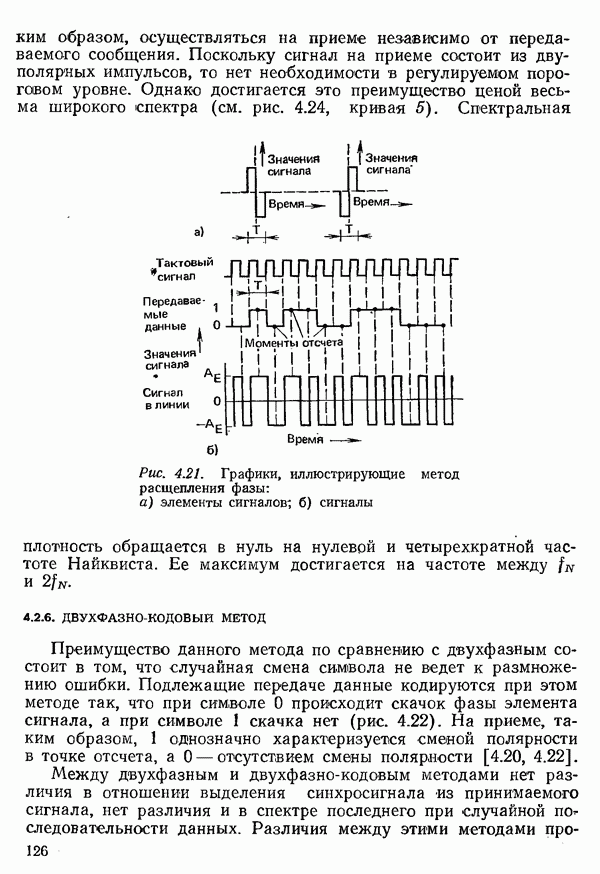
- 4.2.5. ДВУХФАЗНЫЙ МЕТОД. ИЛИ МЕТОД РАСЩЕПЛЕНИЯ ФАЗЫ
- 4.2.6. ДВУХФАЗНО-КОДОВЫЙ МЕТОД
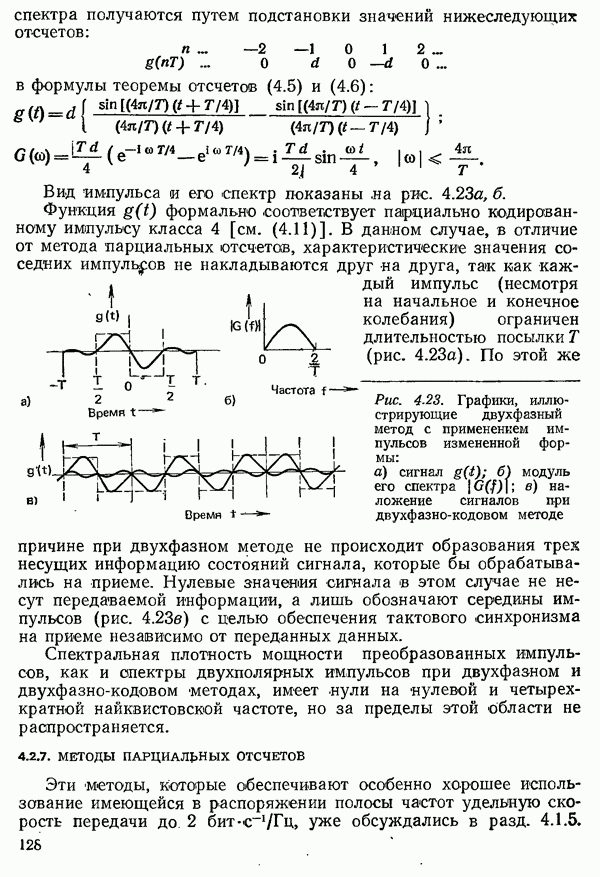
- 4.2.7. МЕТОДЫ ПАРЦИАЛЬНЫХ ОТСЧЕТОВ
- 4.3. МЕТОДЫ ПЕРЕДАЧИ С ПРИМЕНЕНИЕМ МОДУЛЯЦИИ
- 4.3.1. АМПЛИТУДНАЯ МОДУЛЯЦИЯ
- 4.3.1.2. АМПЛИТУДНАЯ МОДУЛЯЦИЯ С ОДНОЙ БОКОВОЙ ПОЛОСОЙ И С ЧАСТИЧНО ПОДАВЛЕННОЙ БОКОВОЙ ПОЛОСОЙ
- 4.3.1.3. КВАДРАТУРНАЯ АМПЛИТУДНАЯ МОДУЛЯЦИЯ
- 4.3.1.4. УДЕЛЬНАЯ СКОРОСТЬ ПЕРЕДАЧИ ПРИ АМПЛИТУДНОЙ МОДУЛЯЦИИ
- 4.3.2. ЧАСТОТНАЯ МОДУЛЯЦИЯ
- 4.3.2.1. УДЕЛЬНАЯ СКОРОСТЬ ПЕРЕДАЧИ ПРИ ЧАСТОТНОЙ МОДУЛЯЦИИ
- 4.3.3. ФАЗОВАЯ МОДУЛЯЦИЯ
- 4.4. ВОССТАНОВЛЕНИЕ ТАКТОВ И НЕСУЩЕЙ
- 4.4.2. ВОССТАНОВЛЕНИЕ ЧАСТОТЫ И ФАЗЫ НЕСУЩЕЙ
- 4.5. ВЕРОЯТНОСТЬ ОШИБКИ ПРИ НАЛИЧИИ ПОМЕХ
- 4.5.1. ВЕРОЯТНОСТЬ ОШИБКИ ПРИ УЧЕТЕ ТОЛЬКО ШУМА В КАНАЛЕ СВЯЗИ
- 4.5.2. ВЕРОЯТНОСТЬ ОШИБКИ С УЧЕТОМ ЛИНЕЙНЫХ ИСКАЖЕНИЙ
- 4.5.3. ВЕРОЯТНОСТЬ ОШИБКИ С УЧЕТОМ ПРОЦЕССОВ МОДУЛЯЦИИ И ДЕМОДУЛЯЦИИ
- 5. Учет свойств реальных каналов связи при передаче данных
- 5.2. ВЛИЯНИЕ ХАРАКТЕРИСТИК КАНАЛОВ СВЯЗИ НА ПЕРЕДАЧУ ДАННЫХ
- 5.2.2. СДВИГИ ЧАСТОТЫ
- 5.2.3. ФАЗОВОЕ ДРОЖАНИЕ
- 5.2.4. ВЛИЯНИЕ РЕАЛЬНЫХ ПОМЕХ
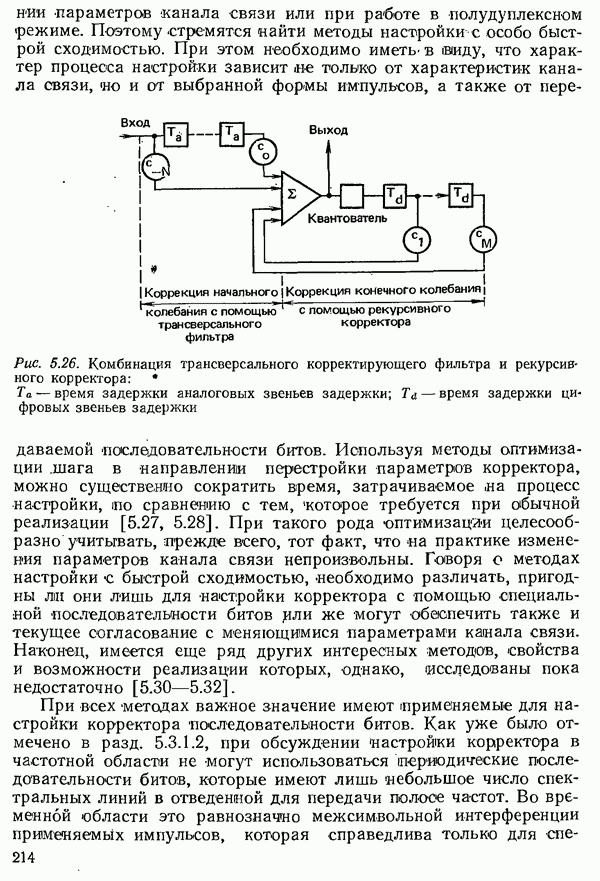
- 5.3. КОРРЕКЦИЯ ПРИНИМАЕМОГО СИГНАЛА ДАННЫХ
- 5.3.1. КОРРЕКЦИЯ ПРИНИМАЕМОГО СИГНАЛА ДАННЫХ В ЧАСТОТНОЙ ОБЛАСТИ
- 5.3.1.1. КОМПРОМИССНЫЙ КОРРЕКТОР
- 5.3.1.2. НАСТРАИВАЕМЫЙ ЧАСТОТНЫЙ КОРРЕКТОР СИГНАЛОВ ДАННЫХ
- 5.3.2. КОРРЕКЦИЯ ПРИНИМАЕМОГО СИГНАЛА ДАННЫХ ВО ВРЕМЕННОЙ ОБЛАСТИ
- 5.3.2.2. КРИТЕРИИ НАСТРОЙКИ КОРРЕКТОРА ВО ВРЕМЕННОЙ ОБЛАСТИ
- 5.3.2.3. АВТОМАТИЧЕСКАЯ НАСТРОЙКА ТРАНСВЕРСАЛЬНОГО КОРРЕКТИРУЮЩЕГО ФИЛЬТРА
- 5.3.2.4. РЕКУРСИВНЫЙ КОРРЕКТОР
- 5.3.2.5. СХОДИМОСТЬ НАСТРОЙКИ КОРРЕКТОРА
- 5.3.2.6. КОРРЕКТОР ДЛЯ СПЕЦИАЛЬНЫХ МЕТОДОВ ПЕРЕДАЧИ
- 6. Основы коммутации данных
- 6.1.2. МЕТОДЫ КОММУТАЦИИ
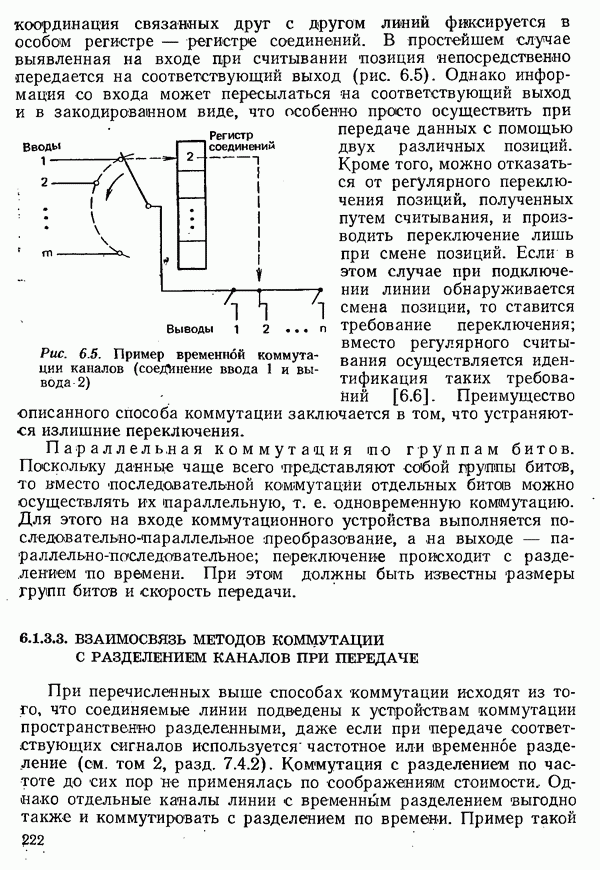
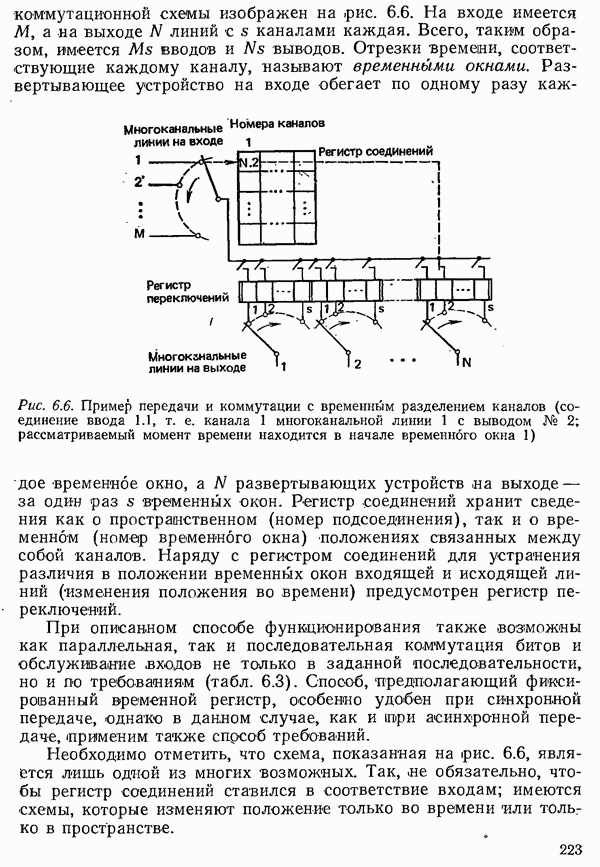
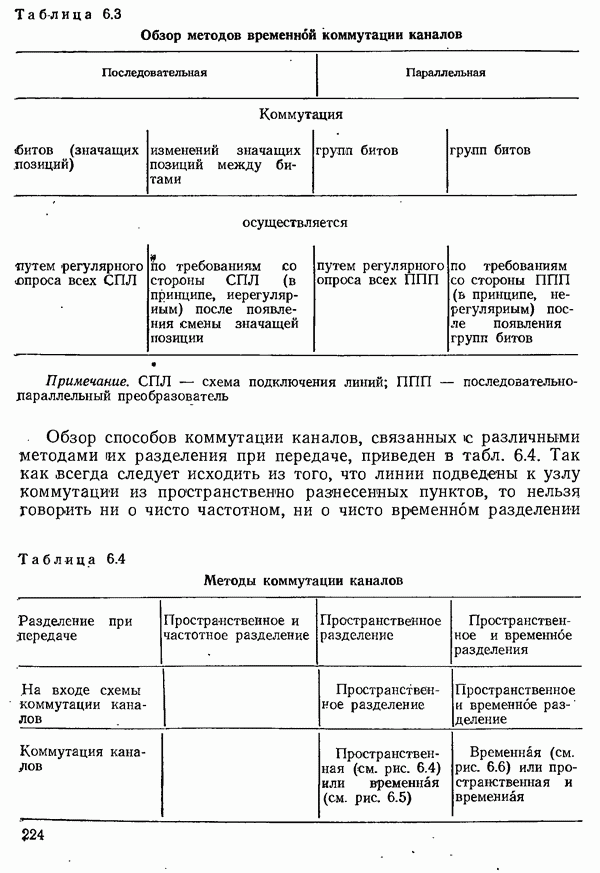
- 6.1.3. СПОСОБЫ КОММУТАЦИИ КАНАЛОВ
- 6.1.4. СИГНАЛИЗАЦИЯ
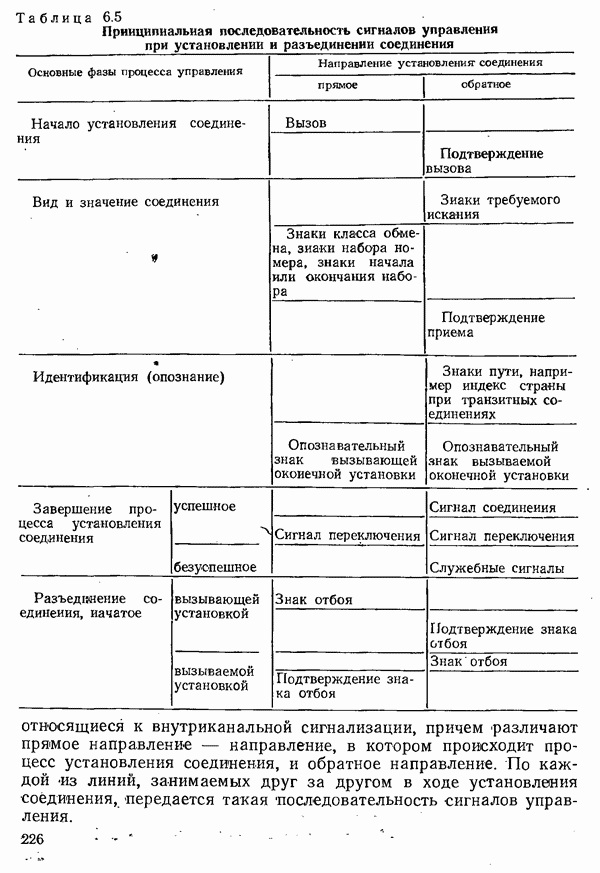
- 6.1.5. УПРАВЛЕНИЕ ПРОЦЕССАМИ СОЕДИНЕНИЯ И РАЗЪЕДИНЕНИЯ
- 6.1.6. ПОДРАЗДЕЛЕНИЕ ЦЕПЕЙ КОММУТАЦИИ КАНАЛОВ
- 6.1.7. ДОПОЛНИТЕЛЬНЫЕ ЗАДАЧИ КОММУТАЦИОННЫХ УСТРОЙСТВ
- 6.2. АНАЛИЗ СИСТЕМ КОММУТАЦИИ НА ОСНОВЕ ТЕОРИИ ТЕЛЕТРАФИКА
- 6.2.2. СИСТЕМЫ С ПОТЕРЯМИ
- 6.2.3. СИСТЕМЫ С ОЖИДАНИЕМ
- 6.2.4. ИЗМЕРЕНИЯ НАГРУЗКИ
- СПИСОК ЛИТЕРАТУРЫ