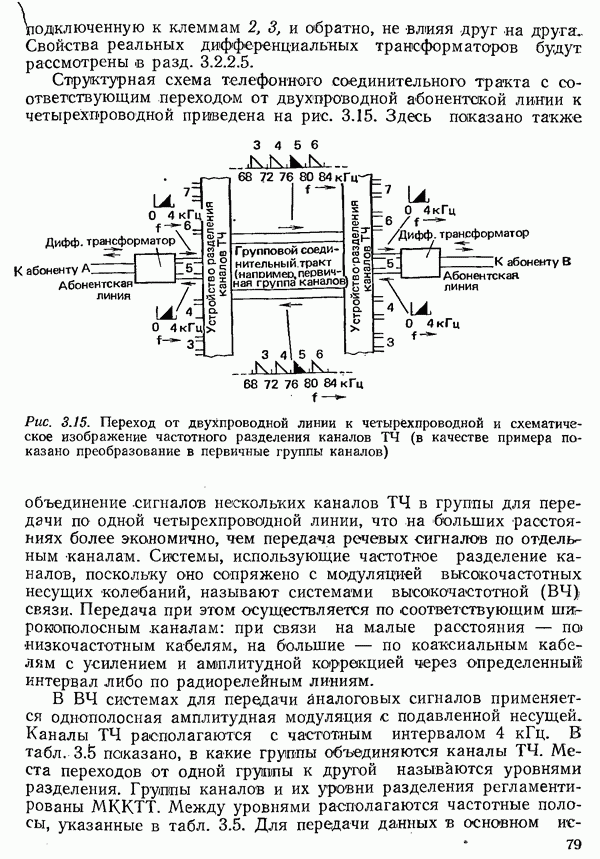
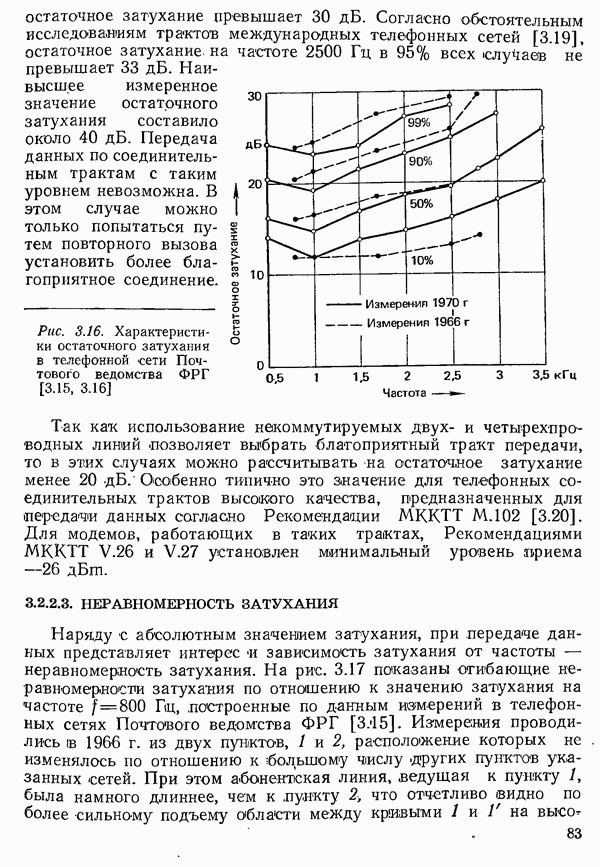
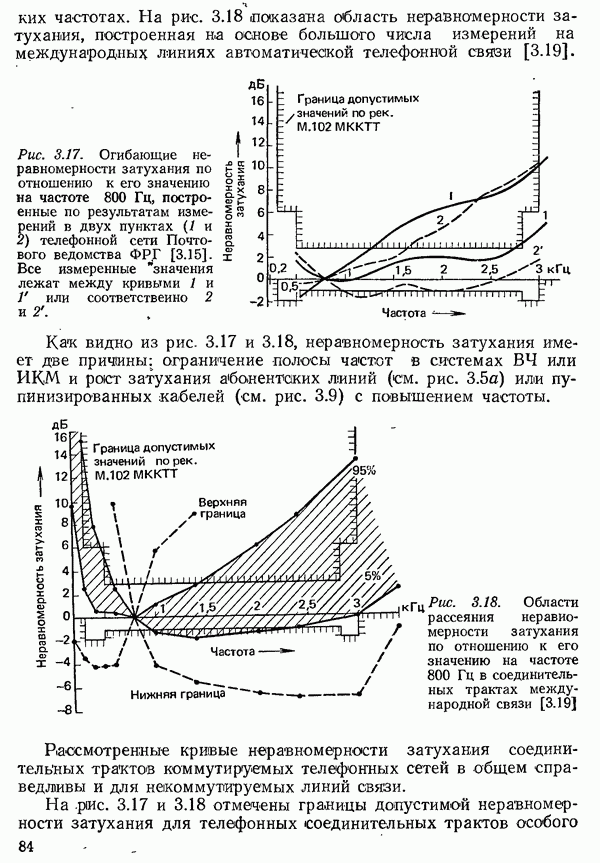
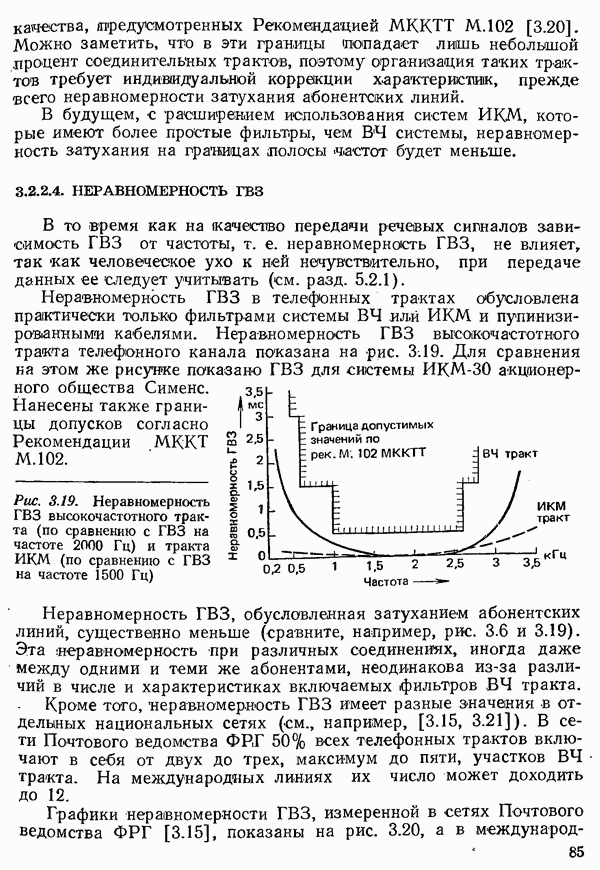
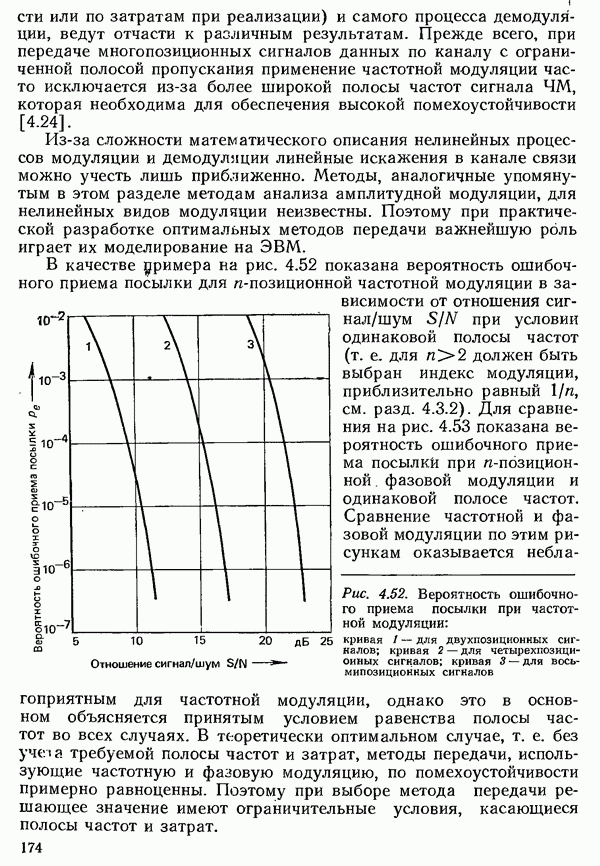
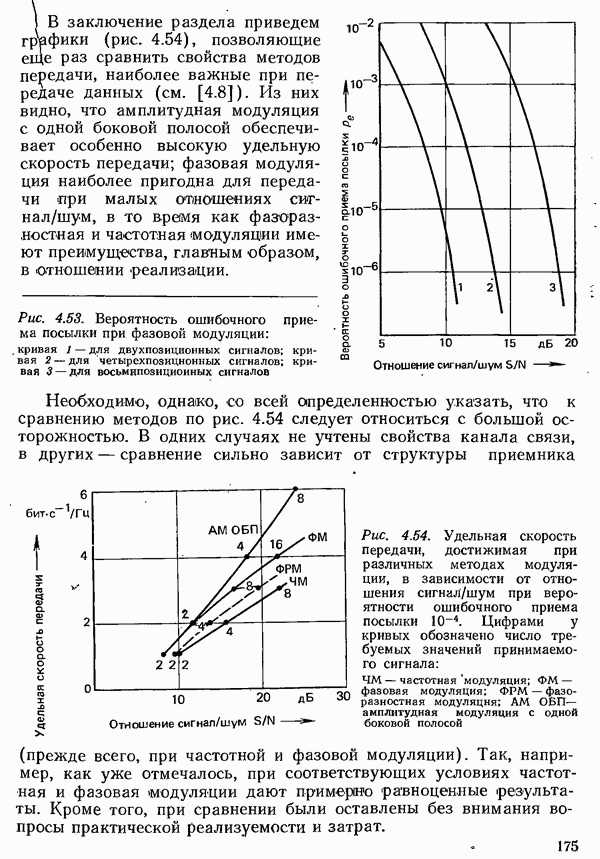
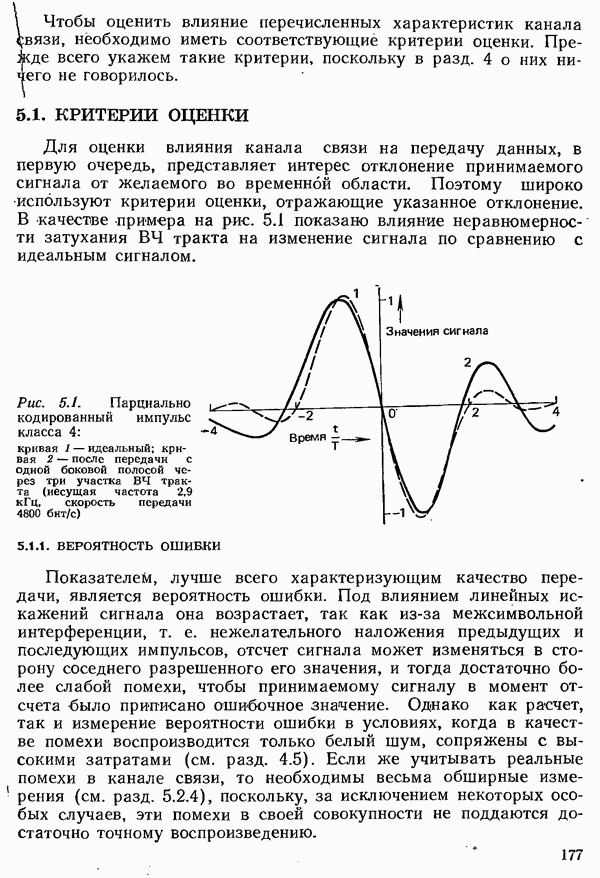
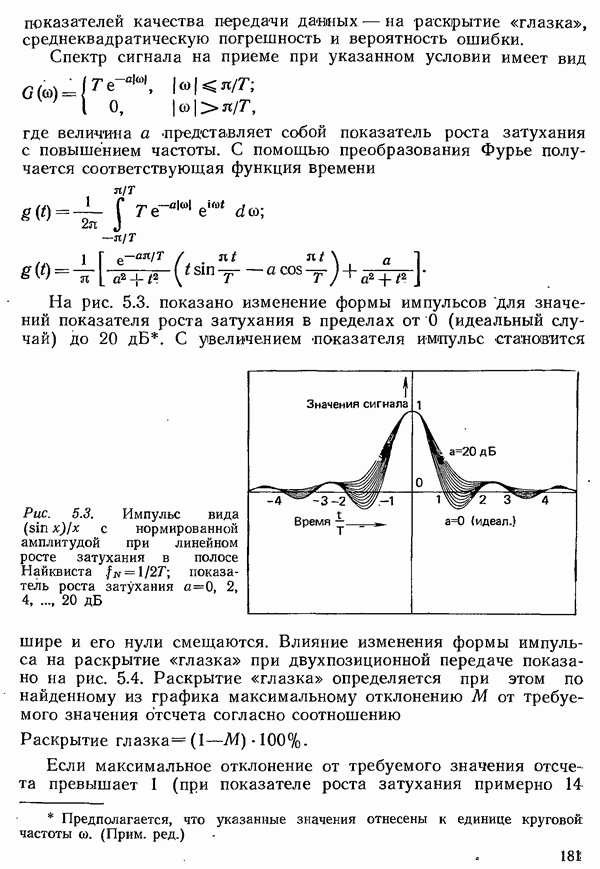
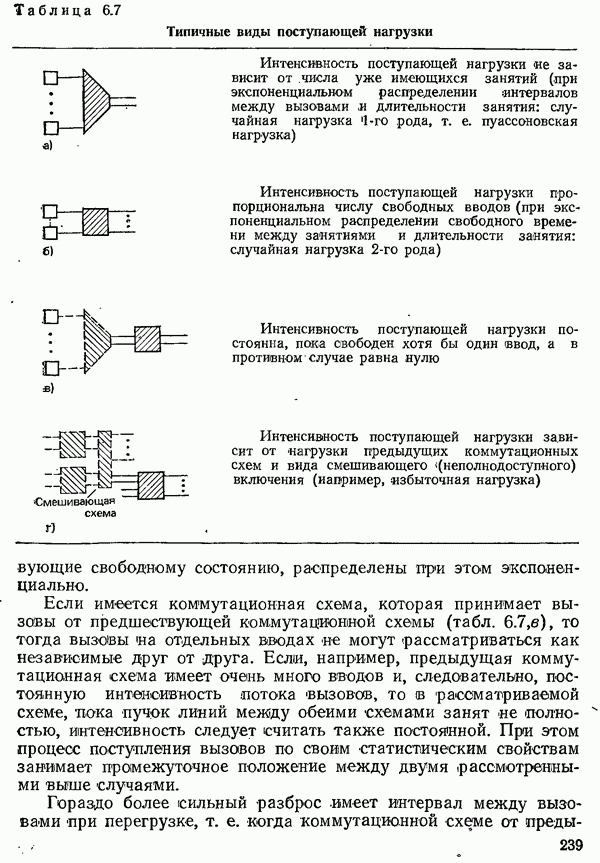
| << Предыдущий параграф | Следующий параграф >> |
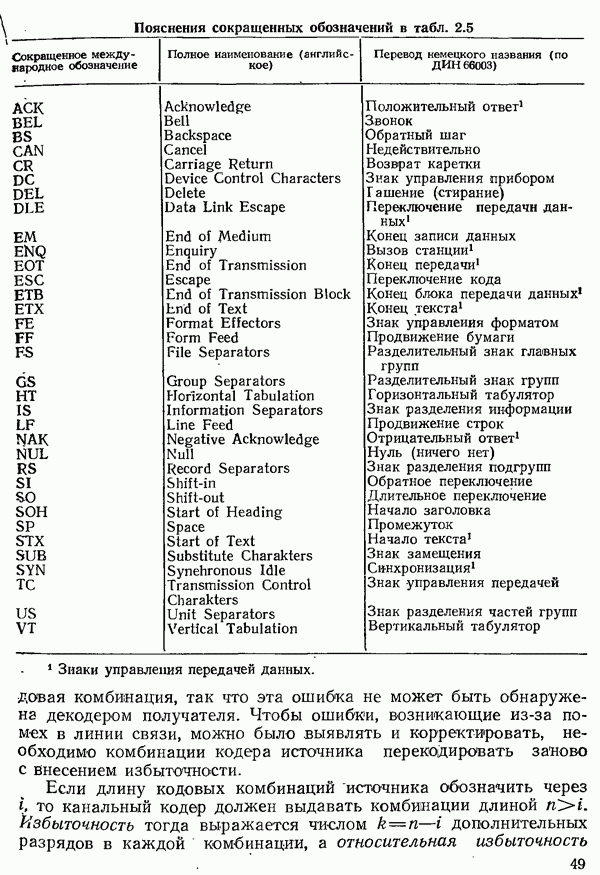
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
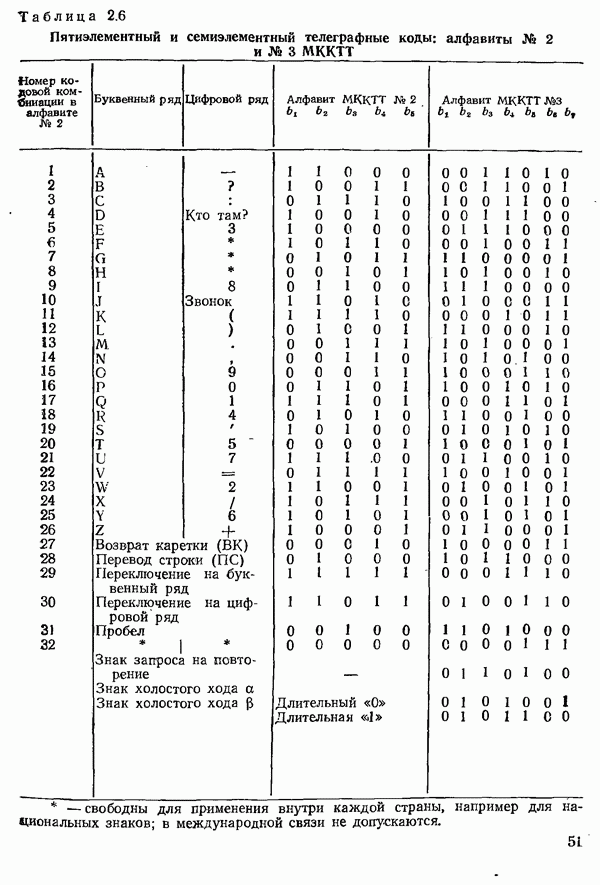
4.1.4. УСЛОВИЯ НАЙКВИСТА
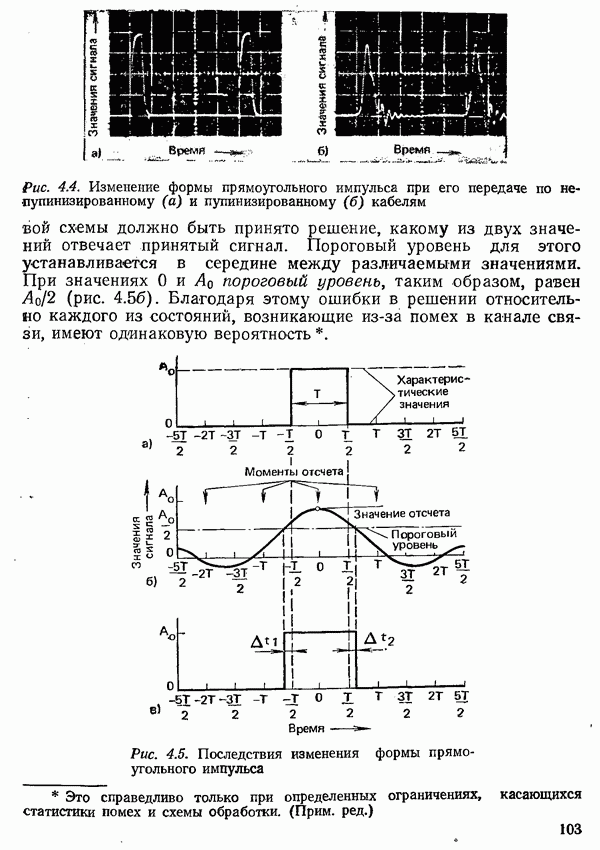
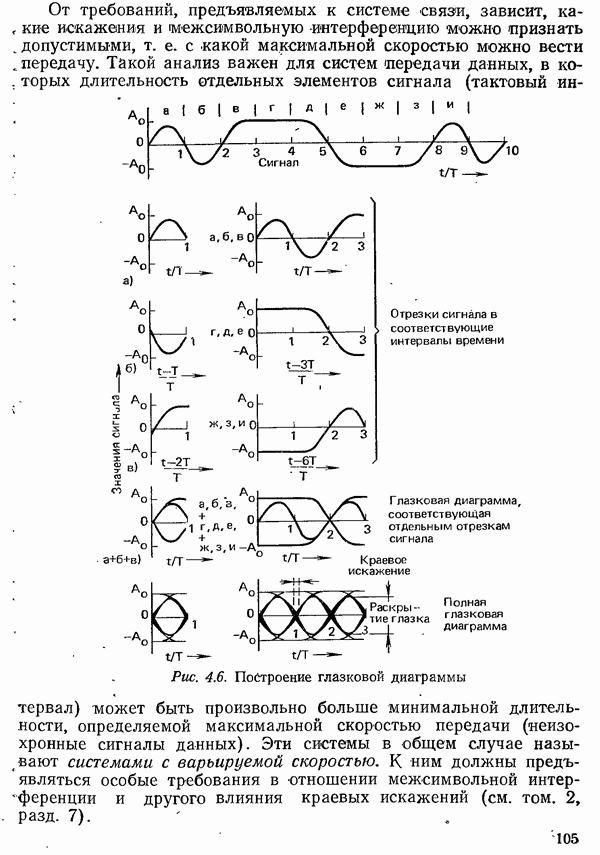
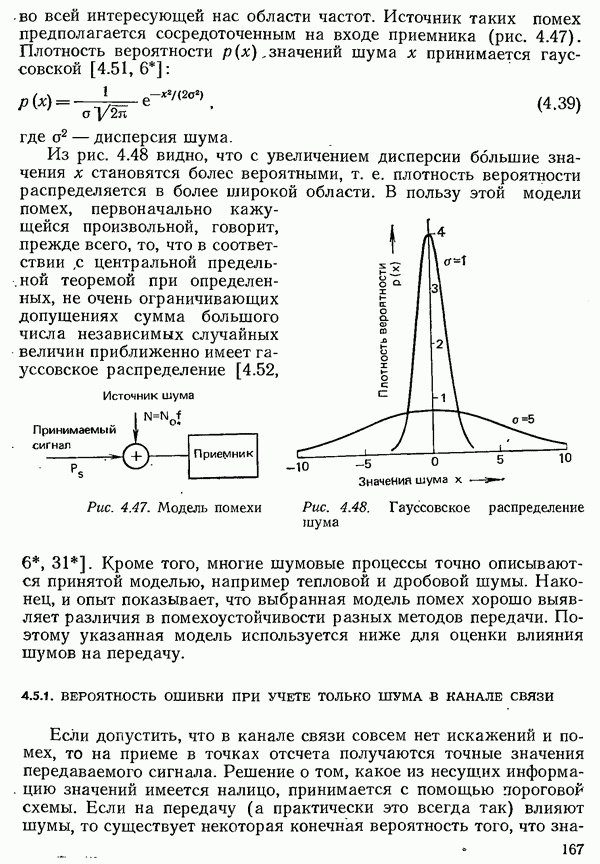
Для обеспечения определенной скорости передачи воздействие соседних импульсов не должно проявляться лишь в моменты отсчетов, отстоящих друг от друга на интервал  когда снимается информация; при этом условии получается передача без межсимвольяой интерференции и с минимальной вероятностью ошибки, Поскольку последняя зависит только от отклонений характеристических значений, учитываемых при решении, от порогового уровня (см. рис. 4.5). Это условие, называют первым условием Найквиста [4.3]. Оно выполняется для импульса, который только в некоторый момент отсчета имеет отличное от нуля характеристическое значение и нулевые значения (во всех остальных отсчетных точках.
когда снимается информация; при этом условии получается передача без межсимвольяой интерференции и с минимальной вероятностью ошибки, Поскольку последняя зависит только от отклонений характеристических значений, учитываемых при решении, от порогового уровня (см. рис. 4.5). Это условие, называют первым условием Найквиста [4.3]. Оно выполняется для импульса, который только в некоторый момент отсчета имеет отличное от нуля характеристическое значение и нулевые значения (во всех остальных отсчетных точках.
Первое условие Найквиста касается лишь отсчетов сигнала в дискретных точках  Сигнал как функция непрерывного времени
Сигнал как функция непрерывного времени  однозначно определяется своими отсчетами
однозначно определяется своими отсчетами  взятыми с интервалом
взятыми с интервалом  если его преобразование Фурье
если его преобразование Фурье  отлично от нуля лишь в полосе частот
отлично от нуля лишь в полосе частот  Это утверждение называют теоремой отсчетов, или теоремой Шеннона [4.4].
Это утверждение называют теоремой отсчетов, или теоремой Шеннона [4.4].
Из теоремы отсчетов следует, что сигнал

а его спектр

Область частот  или соответственно
или соответственно  называют полосой Найквиста, частоту
называют полосой Найквиста, частоту  частотой Найквиста, а интервал времени
частотой Найквиста, а интервал времени  интервалом Найквиста.
интервалом Найквиста.
В соответствии с первым условием Найквиста отсчеты сигнала можно представить в таком виде:

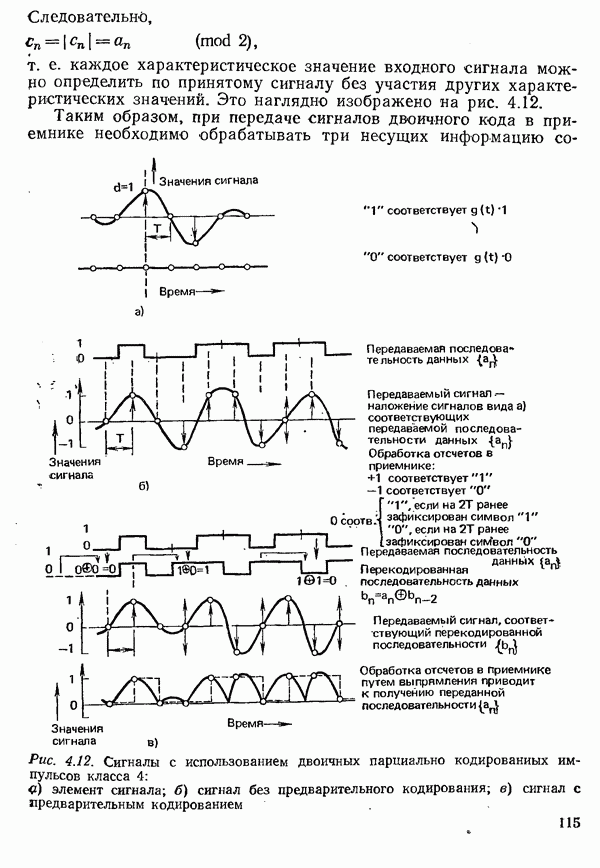
Характеристическое значение  указанное в таблице, несет информацию, содержащуюся в сигнале. Подставив это значение
указанное в таблице, несет информацию, содержащуюся в сигнале. Подставив это значение
вместо,  в (4.5) и (4.6), получаем, что сигнал
в (4.5) и (4.6), получаем, что сигнал

а его спектр 1

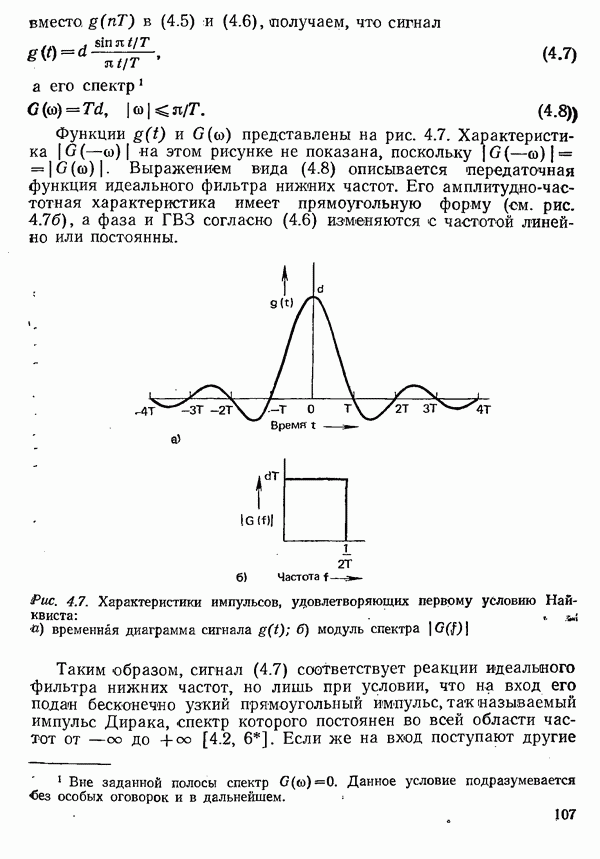
Функции  представлены на рис. 4.7. Характеристика
представлены на рис. 4.7. Характеристика  на этом рисунке не показана, поскольку
на этом рисунке не показана, поскольку  Выражением вида (4.8) описывается передаточная функция идеального фильтра нижних частот. Его амплитудно-частотная характеристика имеет прямоугольную форму (см. рис. 4.76), а фаза и ГВЗ согласно (4.6) изменяются с частотой линейно или постоянны.
Выражением вида (4.8) описывается передаточная функция идеального фильтра нижних частот. Его амплитудно-частотная характеристика имеет прямоугольную форму (см. рис. 4.76), а фаза и ГВЗ согласно (4.6) изменяются с частотой линейно или постоянны.

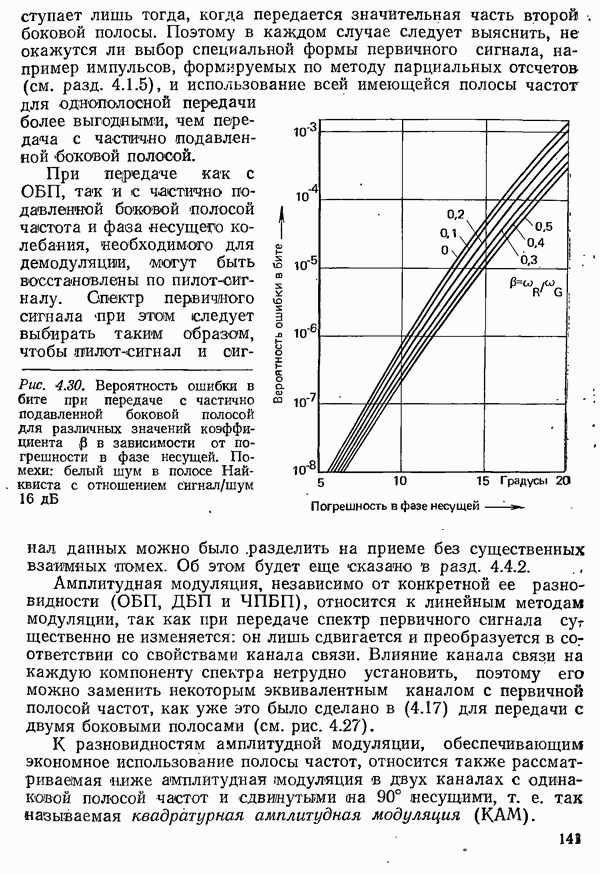
Рис. 4.7. Характеристики импульсов, удовлетворяющих первому условию Найквиста:  временная диаграмма сигнала
временная диаграмма сигнала  модуль спектра
модуль спектра 
Таким образом, сигнал (4 7) соответствует реакции идеального фильтра нижних частот, но лишь при условии, что на вход его подан бесконечно узкий прямоугольный импульс, так называемый импульс Дирака, спектр которого постоянен во всей области частот от  . Если же на вход поступают другие
. Если же на вход поступают другие
импульсы, то их спектр следует учитывать в (4.8). Это справедливо и для дальнейшего изложения.
Независимо от сказанного выше реализация сигналов, удовлетворяющих первому условию Найквиста, встречает трудности, так как сигналы, спектр которых сосредоточен в ограниченной полосе частот, имеют длительность во времени от  до
до  Такие, сигналы не могут появиться на приеме, поскольку в силу принципа причинности требуют появления сигнала на передаче в момент
Такие, сигналы не могут появиться на приеме, поскольку в силу принципа причинности требуют появления сигнала на передаче в момент  Столь же нереальна, в принципе, и интерпретация
Столь же нереальна, в принципе, и интерпретация  в форме (4.6) как частотной характеристики некоторого фильтра, в частности, потому, что функция вида (4.7) нереализуема, а к фильтру предъявляется условие
в форме (4.6) как частотной характеристики некоторого фильтра, в частности, потому, что функция вида (4.7) нереализуема, а к фильтру предъявляется условие  при
при 
Даже если бы импульс в форме функции  был бы реализуем, его нельзя было бы использовать, поскольку он потребовал бы очень точного соблюдения моментов отсчета. При самом незначительном их отклонении ряд для возникающих при этом измененных отсчетов не сходится, т. е. они дают столь большую» межеимвольную интерференцию, что характеристические значения становятся ошибочными. Тогда при любой последовательности импульсов вида
был бы реализуем, его нельзя было бы использовать, поскольку он потребовал бы очень точного соблюдения моментов отсчета. При самом незначительном их отклонении ряд для возникающих при этом измененных отсчетов не сходится, т. е. они дают столь большую» межеимвольную интерференцию, что характеристические значения становятся ошибочными. Тогда при любой последовательности импульсов вида  восстановление информации невозможно. Несмотря на это, такой импульс используют при теоретическом анализе для оценки предельных значений.
восстановление информации невозможно. Несмотря на это, такой импульс используют при теоретическом анализе для оценки предельных значений.
В дальнейшем рассматриваются только импульсы, которые реализуемы, по крайней мере, приближенно [4.5]. Рассматриваемые импульсы идеализированы, т. е. длятся от  до
до  как и элементарный импульс вида
как и элементарный импульс вида  Однако, как будет рассмотрено в этом разделе, они могут быть ограничены конечным интервалом путем замены точного спектра приближенным.
Однако, как будет рассмотрено в этом разделе, они могут быть ограничены конечным интервалом путем замены точного спектра приближенным.
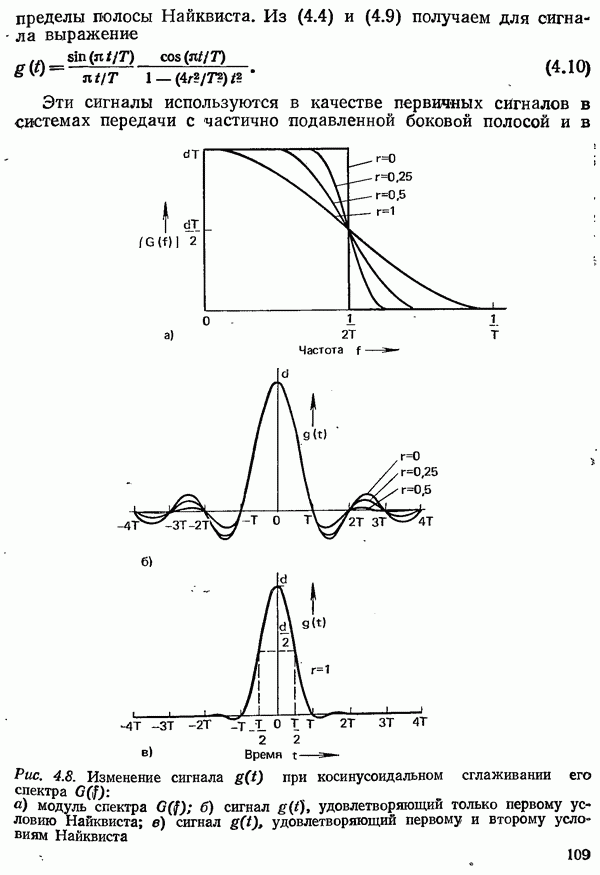
В результате сглаживания прямоугольной формы спектра по косинусоидальному закону  получается сигнал, который, как и элементарный импульс
получается сигнал, который, как и элементарный импульс  удовлетворяет первому условию Найквиста [4.6]. Спектр вместо прямоугольной приобретает форму
удовлетворяет первому условию Найквиста [4.6]. Спектр вместо прямоугольной приобретает форму

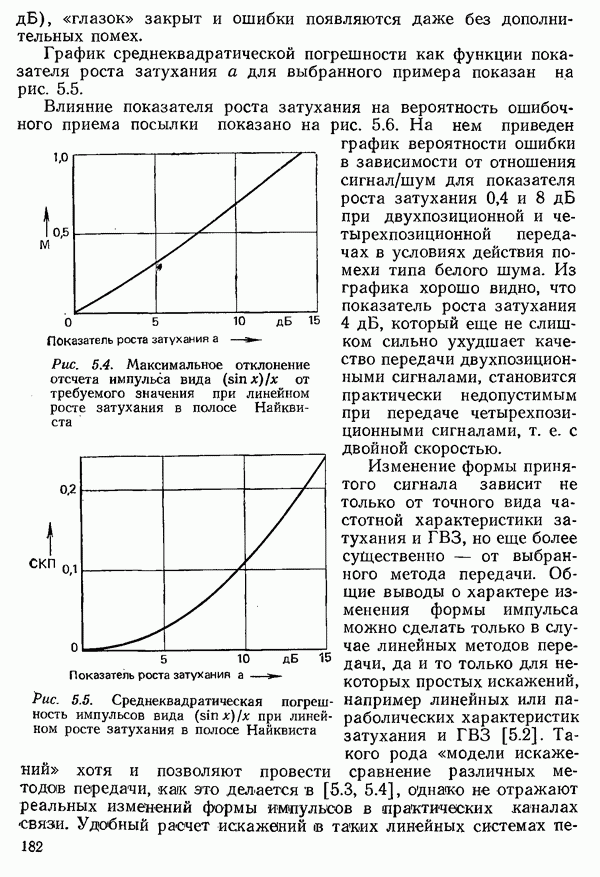
показанную на рис. 4.8а.
В равенстве (4.9) коэффициент сглаживания  задается в пределах
задается в пределах  так что спектр может быть максимум на 100% шире полосы Найквиста. [Для
так что спектр может быть максимум на 100% шире полосы Найквиста. [Для  справедливо (4.8)]. Новый сигнал, хотя и удовлетворяет первому условию Найквиста, однако уже не определяется однозначно своими отсчетами
справедливо (4.8)]. Новый сигнал, хотя и удовлетворяет первому условию Найквиста, однако уже не определяется однозначно своими отсчетами  поскольку его спектр, вопреки требованию теоремы отсчетов, выходит за
поскольку его спектр, вопреки требованию теоремы отсчетов, выходит за
пределы полосы Найквиста. Из (4.4) и (4.9) получаем для сигнала выражение

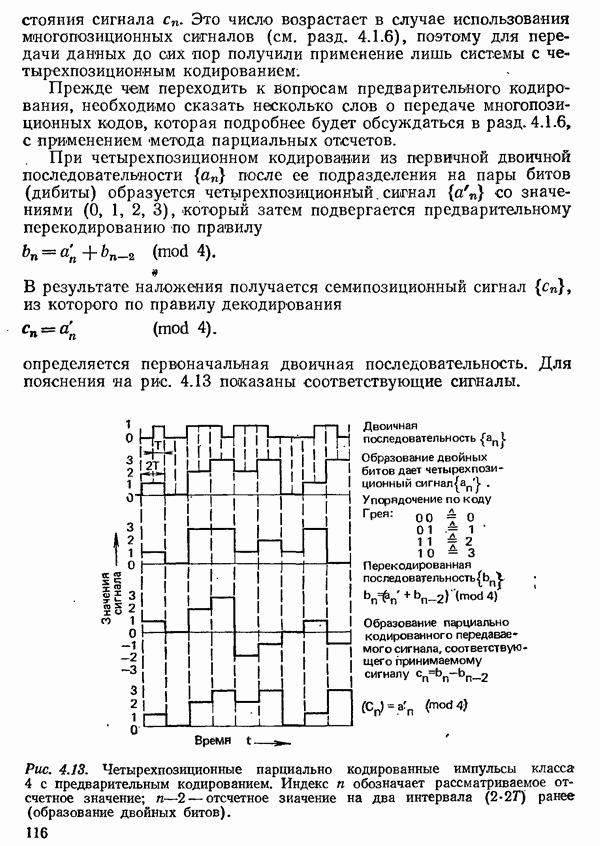
Эти сигналы используются в качестве первичных сигналов в системах передачи с частично подавленной боковой полосой и в
Рис. 4.8. (см. скан) Изменение сигнала  при косинусоидальном сглаживании его спектра
при косинусоидальном сглаживании его спектра  а) модуль спектра
а) модуль спектра  сигнал
сигнал  удовлетворяющий только первому условию Найквиста; в) сигнал
удовлетворяющий только первому условию Найквиста; в) сигнал  удовлетворяющий первому и второму условиям Найквиста
удовлетворяющий первому и второму условиям Найквиста
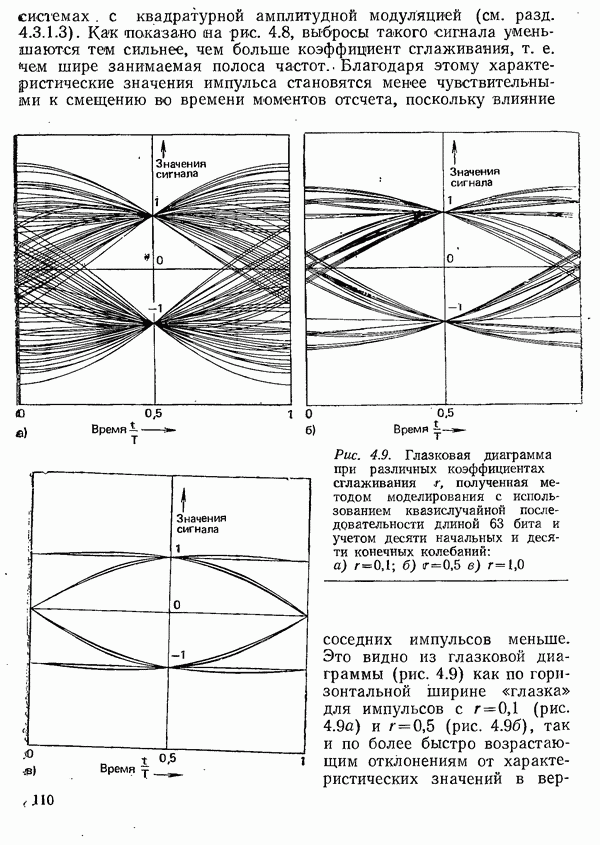
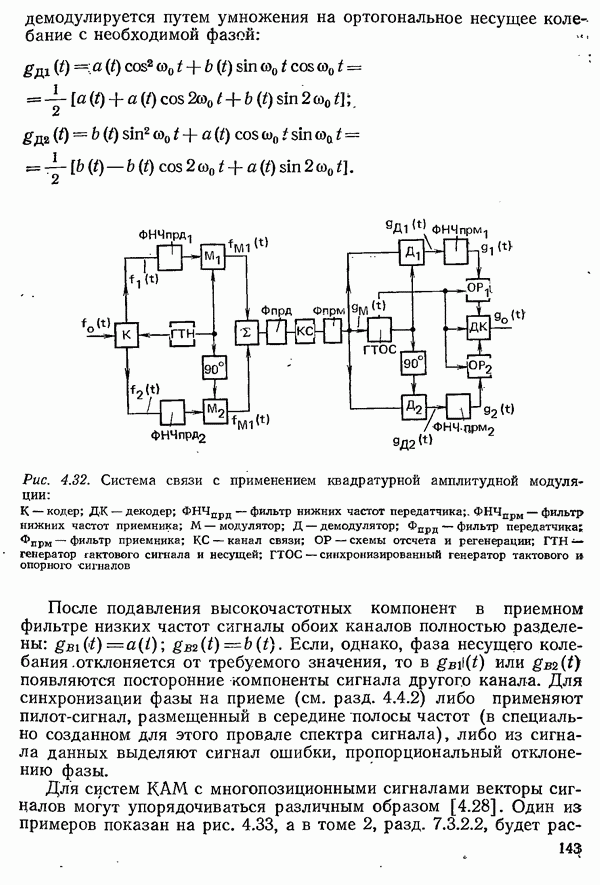
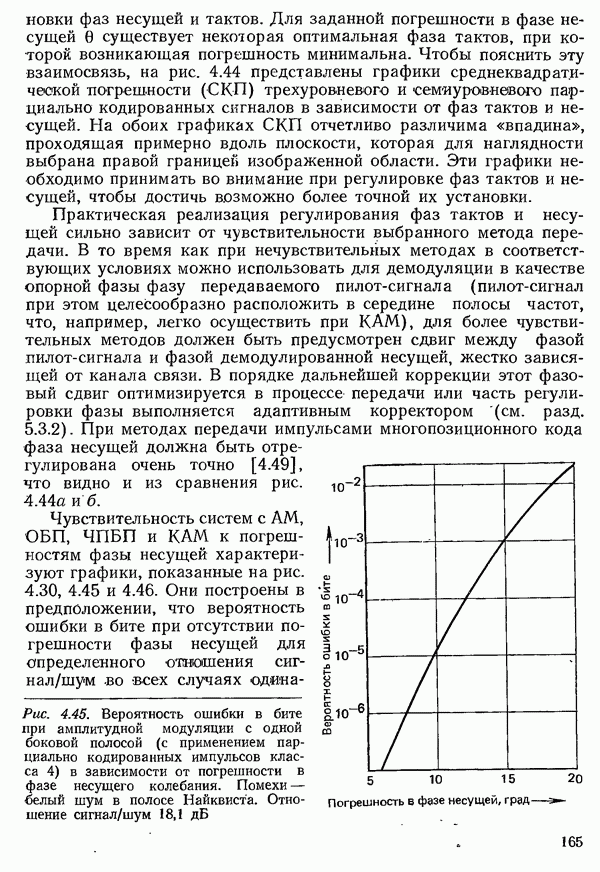
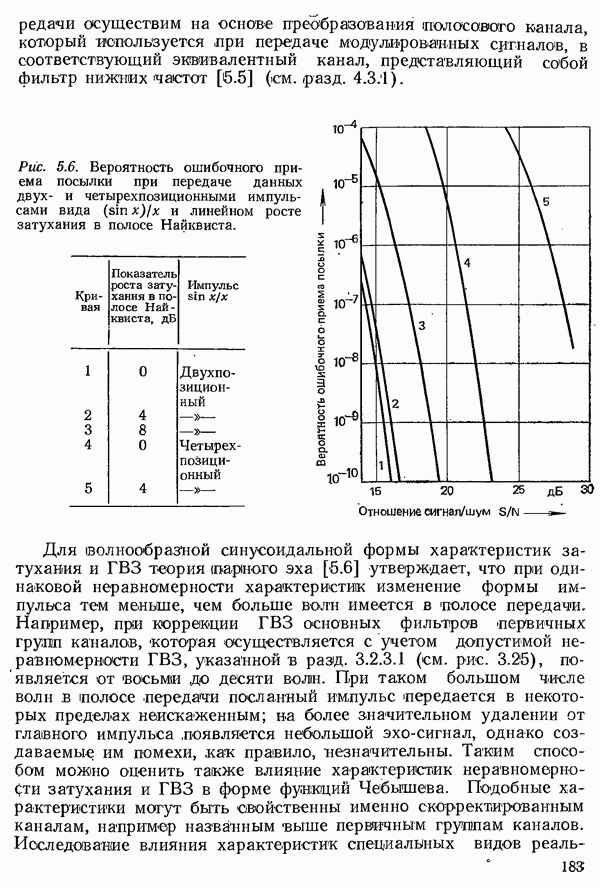
системах с квадратурной амплитудной модуляцией (см. разд. 4.3.1.3). Как показано на рис. 4.8, выбросы такого сигнала уменьшаются тем сильнее, чем больше коэффициент сглаживания, т. е. <чем шире занимаемая полоса частот.. Благодаря этому характеристические значения импульса становятся менее чувствительными к смещению во времени моментов отсчета, поскольку влияние соседних импульсов меньше. Это видно из глазковой диаграммы (рис. 4.9) как по горизонтальной ширине «глазка» для импульсов с  (рис. 4.9а) и
(рис. 4.9а) и  (рис. 4.96), так и по более быстро возрастающим отклонениям от характеристических значений в
(рис. 4.96), так и по более быстро возрастающим отклонениям от характеристических значений в


Рис. 4.9. Глазковая диаграмма при различных коэффициентах сглаживания  полученная методом моделирования с использованием квазислучайной последовательности длиной 63 бита и учетом десяти начальных и десяти конечных колебаний: а)
полученная методом моделирования с использованием квазислучайной последовательности длиной 63 бита и учетом десяти начальных и десяти конечных колебаний: а) 
вертикальном направлении при отклонениях от оптимальной точки отсчета.
При  импульс содержит дополнительную нулевую точку между моментами отсчета, так что не только значения сигнала в точках отсчета, но и мгновенные значения в середине между этими точками могут быть определены без искажений. Кроме того, за время
импульс содержит дополнительную нулевую точку между моментами отсчета, так что не только значения сигнала в точках отсчета, но и мгновенные значения в середине между этими точками могут быть определены без искажений. Кроме того, за время  максимальное значение
максимальное значение  главного импульса падает наполовину, до значения
главного импульса падает наполовину, до значения  (см. рис. 4.8).
(см. рис. 4.8).
Этот импульсный сигнал удовлетворяет второму условию Найквиста [4.6], которое требует, чтобы вне интервала  центром в точке отсчета) имели место нули при
центром в точке отсчета) имели место нули при  где
где  а значения сигнала при удалении на
а значения сигнала при удалении на  от точки отсчета составляли половину максимального значения.
от точки отсчета составляли половину максимального значения.
Таким образом, с помощью этого импульса в приемнике можно определить первоначальную длительность переданного импульса, т. е. избежать краевых искажений, что видно и из глазковой диаграммы на рис. 4.9в. Диаграмма указывает также на некритичность к отклонениям от оптимальных моментов отсчета.
Для передачи двоичных сигналов со скоростью  в полосе частот
в полосе частот  удельная скорость передачи, т. е. скорость передачи в расчете на единицу полосы частот, составляет,
удельная скорость передачи, т. е. скорость передачи в расчете на единицу полосы частот, составляет, 

Так как коэффициент сглаживания  лежит между нулем и единицей, удельная скорость передачи здесь меньше 2 — это теоретический максимум, достигаемый только для импульса вида
лежит между нулем и единицей, удельная скорость передачи здесь меньше 2 — это теоретический максимум, достигаемый только для импульса вида 
Малые коэффициенты сглаживания, обеспечивающие высокую удельную скорость передачи, из-за требований к точности моментов отсчета трудно реализуемы. Из литературы [4.7] известны, например, системы с коэффициентом сглаживания 0,16, которому соответствует удельная скорость передачи  Сигналы с такими коэффициентами используются в устройствах передачи со скоростью 9600 бит/с по некоммутируемым трактам с полосой частот канала ТЧ (см. том 2, разд. 7.3).
Сигналы с такими коэффициентами используются в устройствах передачи со скоростью 9600 бит/с по некоммутируемым трактам с полосой частот канала ТЧ (см. том 2, разд. 7.3).
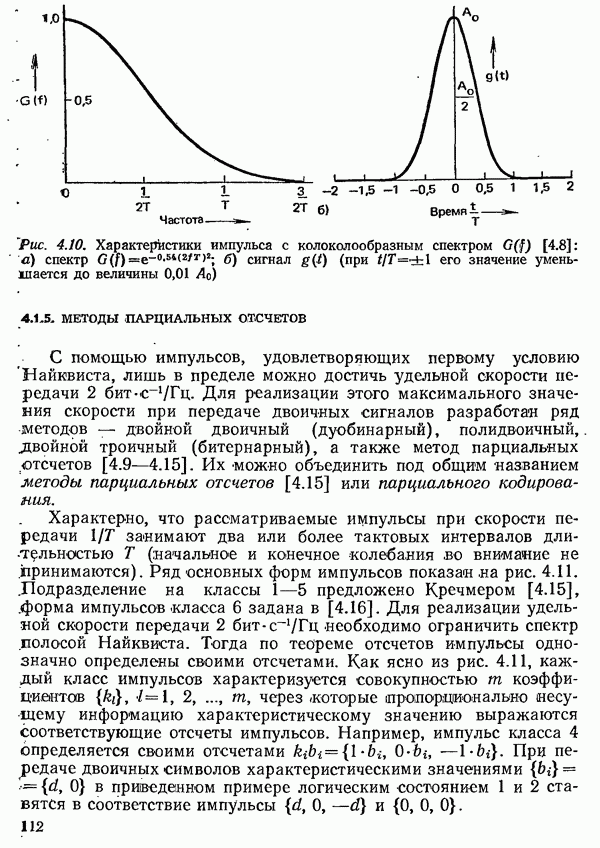
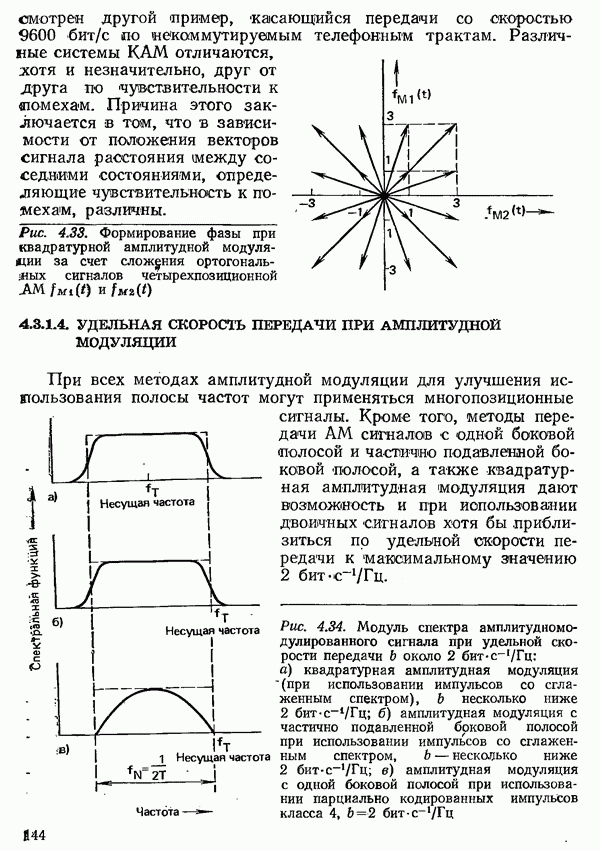
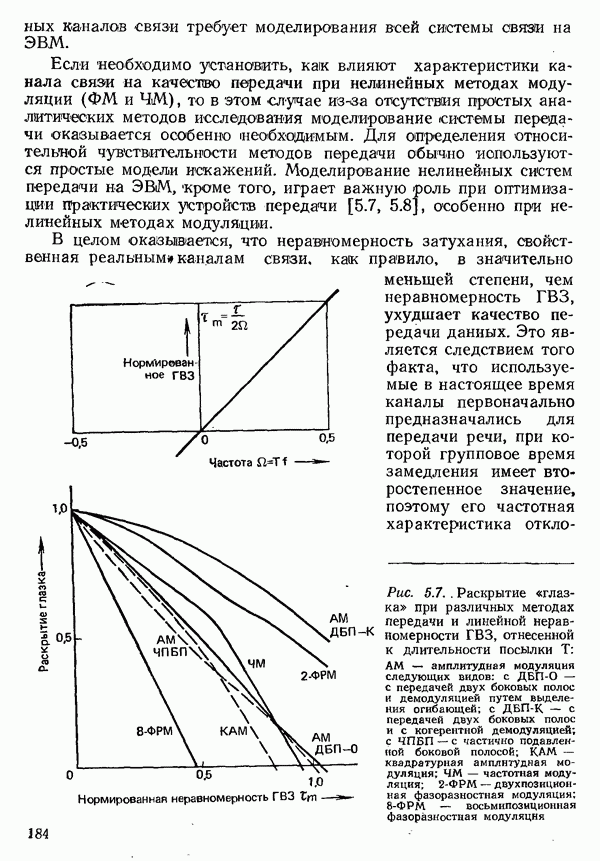
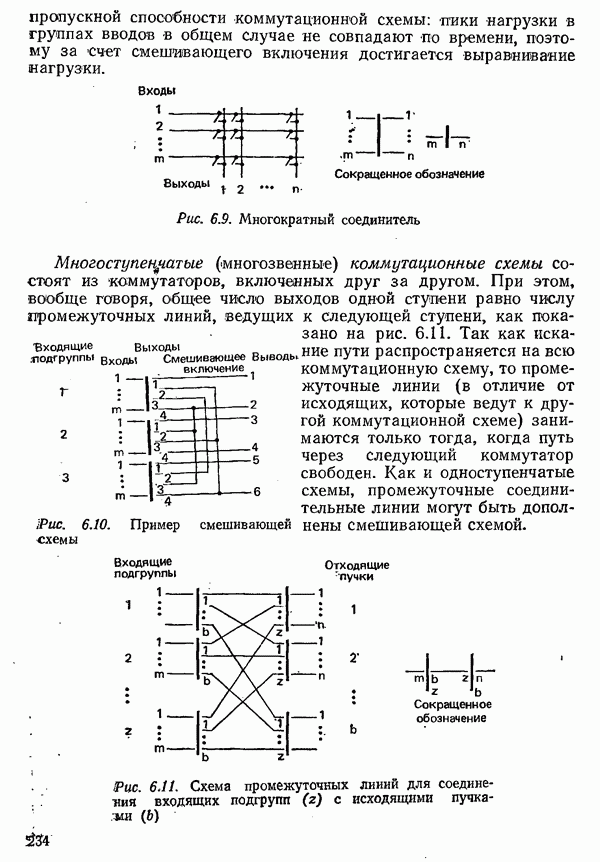
Конечно, можно использовать импульсы другой формы, удовлетворяющие первому или второму условиям Найквиста лишь приближенно. При этом, однако, требуется более широкая полоса частот, чем для «сглаженных», как описано выше, импульсов. Примером может служить импульс, показанный на рис. 4.10 [4.8]. Как видно, практически его спектр занимает частоты до  и спадает очень быстро. Такого рода импульсы можно применять, например, для передачи в первичной полосе частот (разд. 4.2), поскольку в этом случае удельная скорость передачи не играет такой большой роли.
и спадает очень быстро. Такого рода импульсы можно применять, например, для передачи в первичной полосе частот (разд. 4.2), поскольку в этом случае удельная скорость передачи не играет такой большой роли.

Рис. 4.10. Характеристики импульса с колоколообразным спектром  а) спектр
а) спектр  сигнал
сигнал  его значение уменьшается до величины
его значение уменьшается до величины 
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ К РУССКОМУ ИЗДАНИЮ
- 1. Обзор
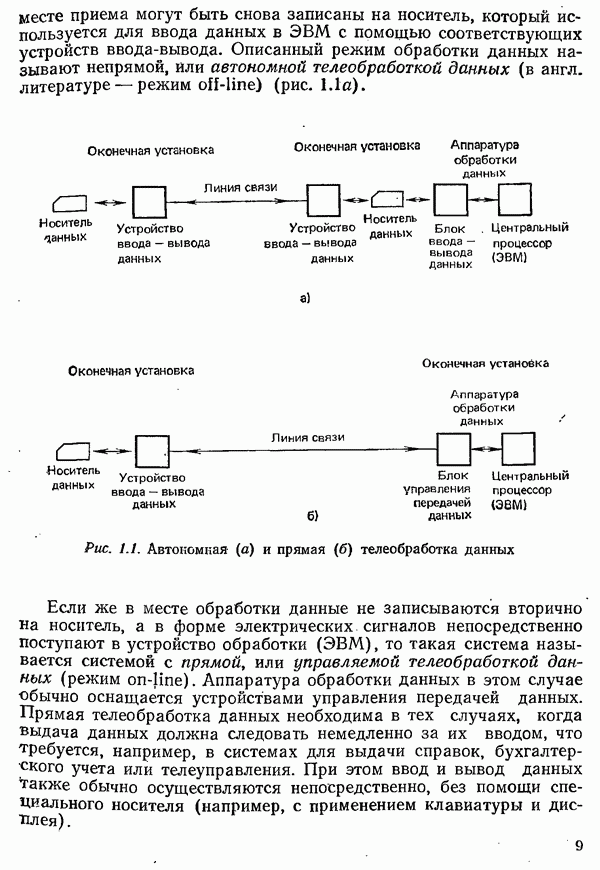
- 1.1. ОБРАБОТКА И ТЕЛЕОБРАБОТКА ДАННЫХ
- 1.2. АВТОНОМНАЯ И УПРАВЛЯЕМАЯ ТЕЛЕОБРАБОТКА ДАННЫХ
- 1.3. КЛАССИФИКАЦИЯ СИСТЕМ ТЕЛЕОБРАБОТКИ ДАННЫХ
- 1.4. СТРУКТУРА СИСТЕМ ТЕЛЕОБРАБОТКИ ДАННЫХ
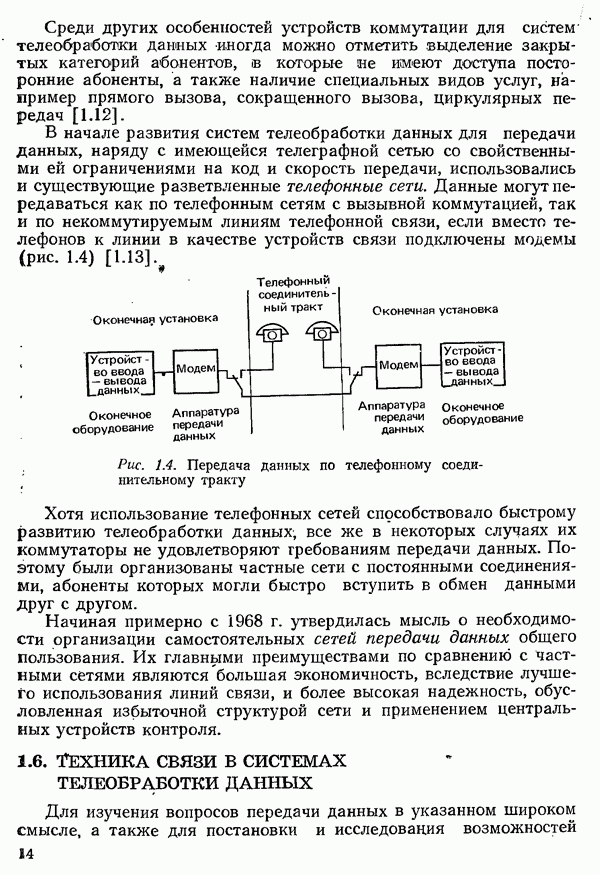
- 1.5. ТРЕБОВАНИЯ К ТЕХНИКЕ СВЯЗИ И КОММУТАЦИИ В СИСТЕМАХ ТЕЛЕОБРАБОТКИ ДАННЫХ
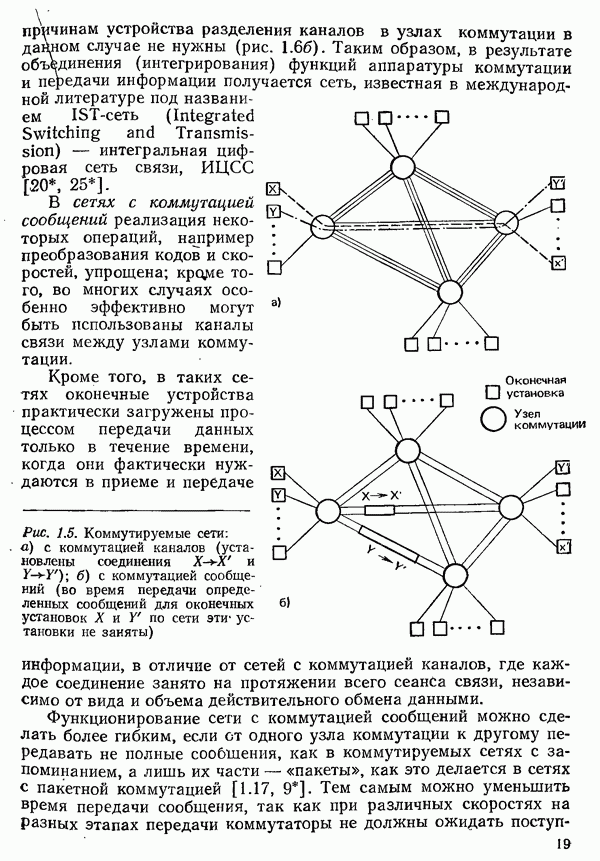
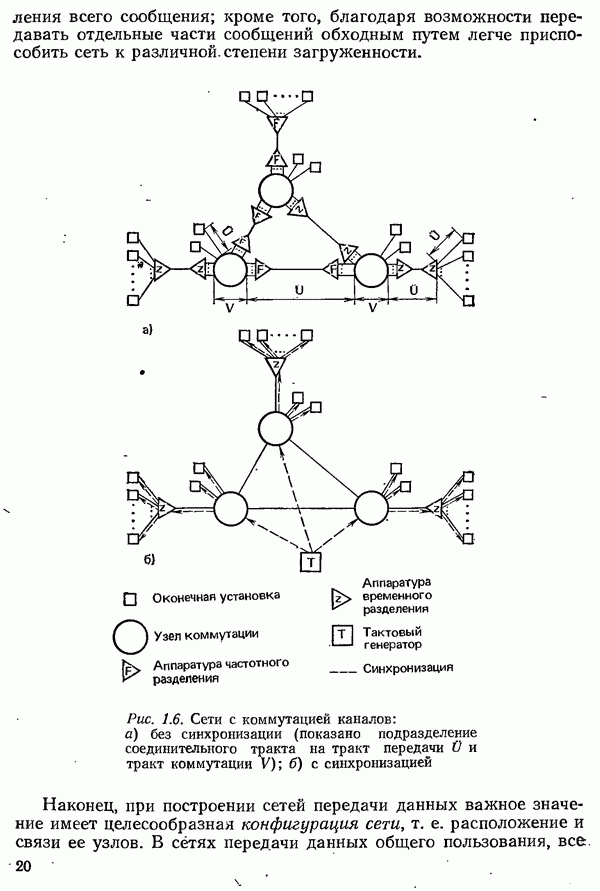
- 1.6. ТЕХНИКА СВЯЗИ В СИСТЕМАХ ТЕЛЕОБРАБОТКИ ДАННЫХ
- 2. Основные понятия техники связи
- 2.2. СИГНАЛЫ
- 2.2.2. ДИСКРЕТИЗАЦИЯ, КВАНТОВАНИЕ, ВЛИЯНИЕ ШУМОВ
- 2.2.3. СВОЙСТВА ПЕРВИЧНЫХ СИГНАЛОВ ДЛЯ ПЕРЕДАЧИ ДАННЫХ
- 2.2.3.2. ВРЕМЕННЫЕ СООТНОШЕНИЯ МЕЖДУ СИГНАЛАМИ
- 2.2.4. РЕЖИМЫ РАБОТЫ ПРИ ПЕРЕДАЧЕ СИГНАЛОВ
- 2.3. НЕКОТОРЫЕ ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ИНФОРМАЦИИ
- 2.3.2. ПЕРЕДАННАЯ ИНФОРМАЦИЯ. ПРОПУСКНАЯ СПОСОБНОСТЬ КАНАЛА СВЯЗИ
- 2.4. КОДИРОВАНИЕ
- 2.4.3. КОДИРОВАНИЕ ИСТОЧНИКА
- 2.4.4. КАНАЛЬНОЕ КОДИРОВАНИЕ
- 3. Каналы связи
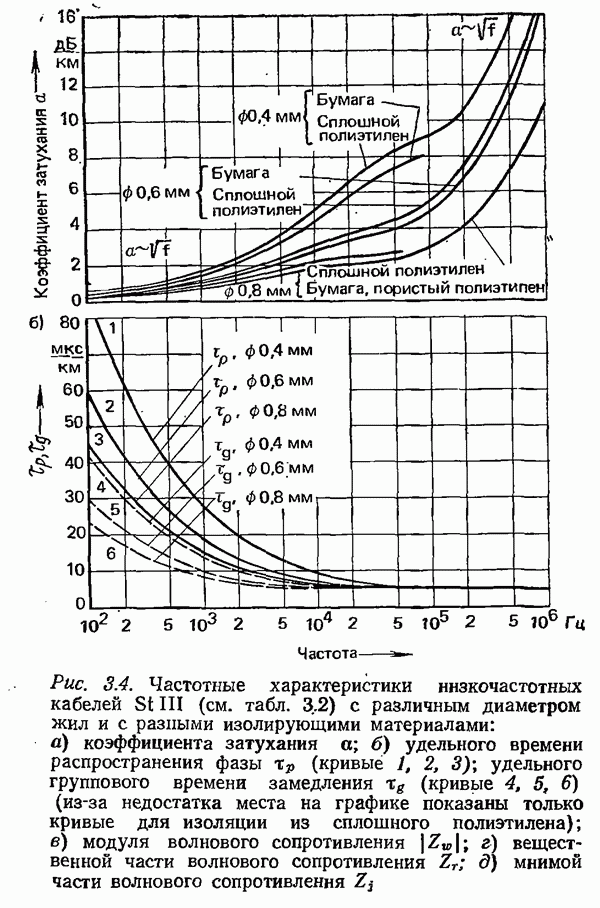
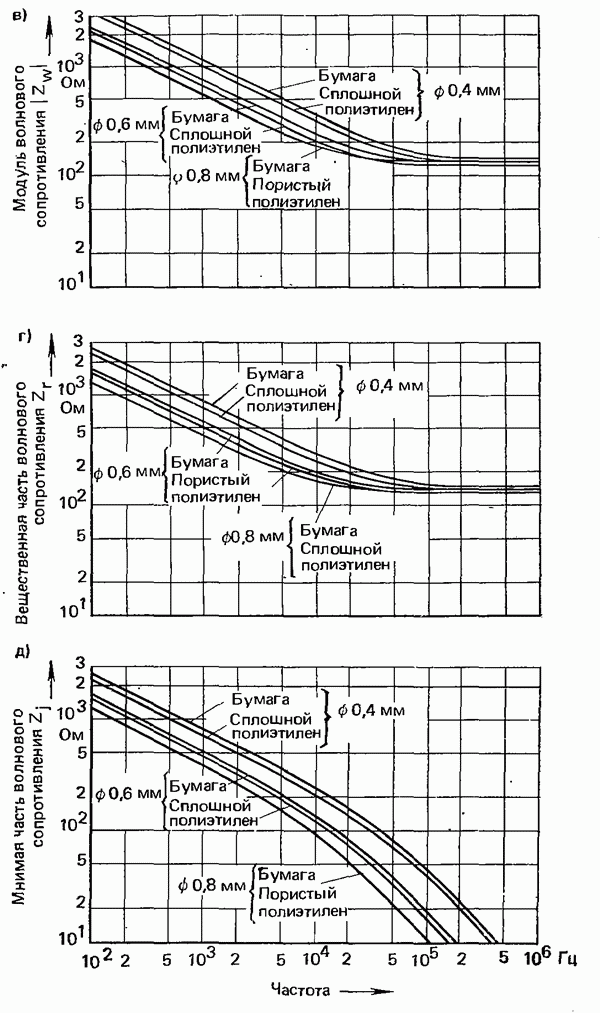
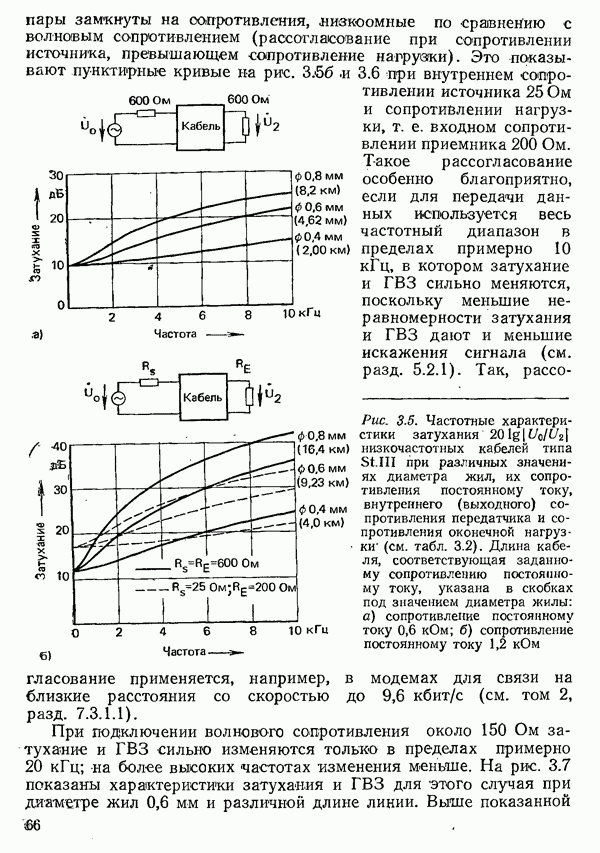
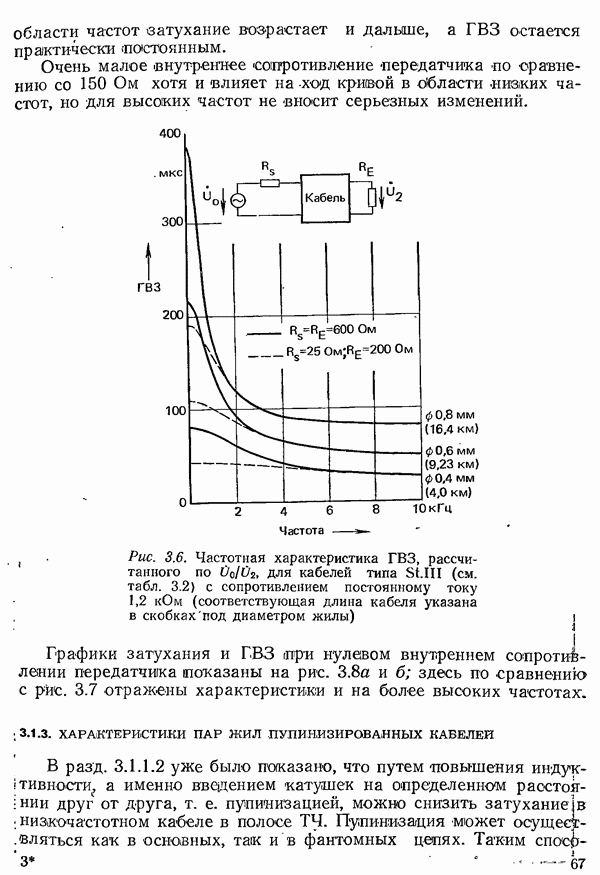
- 3.1. КАНАЛЫ БЛИЖНЕЙ СВЯЗИ
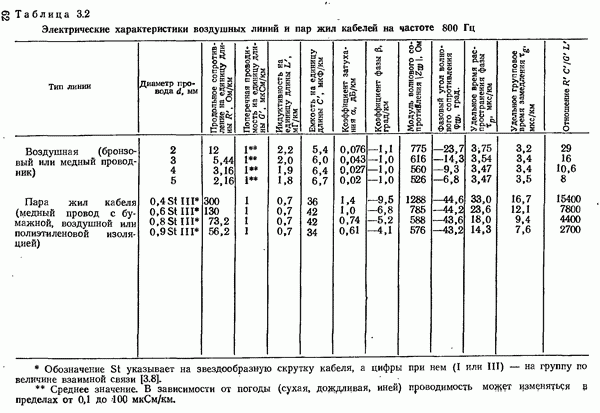
- 3.1.1.1. СВОЙСТВА И ПАРАМЕТРЫ ПРОВОДНЫХ ЛИНИЙ СВЯЗИ
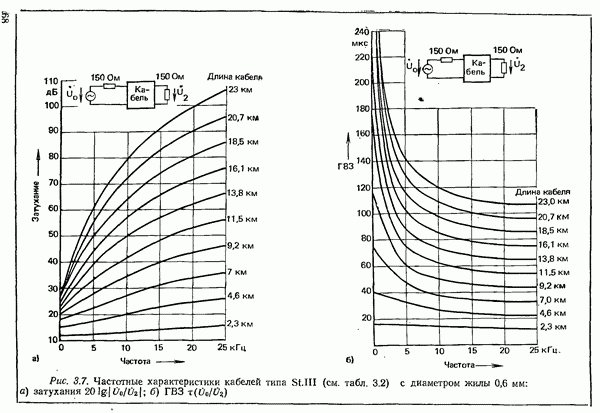
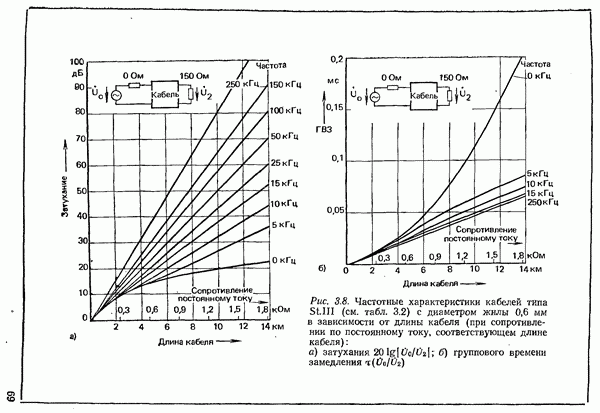
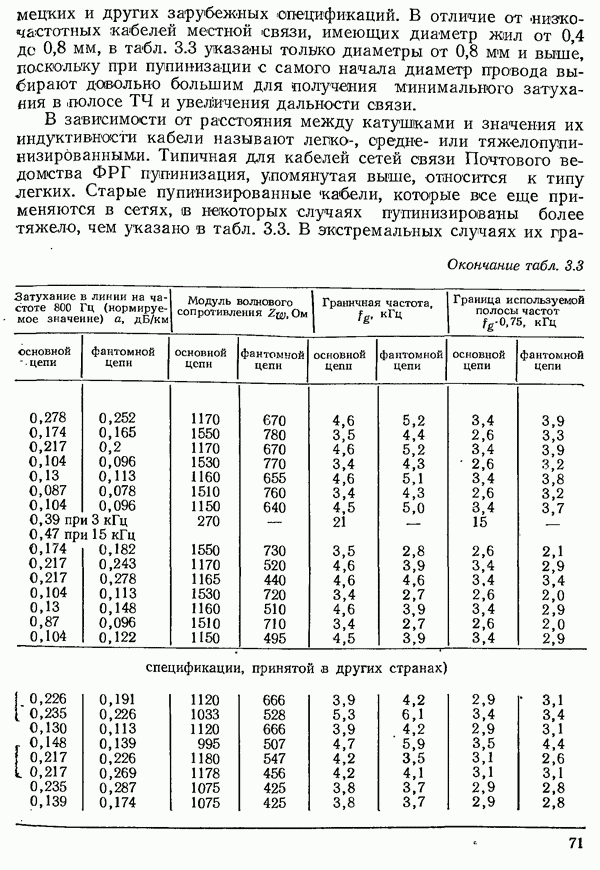
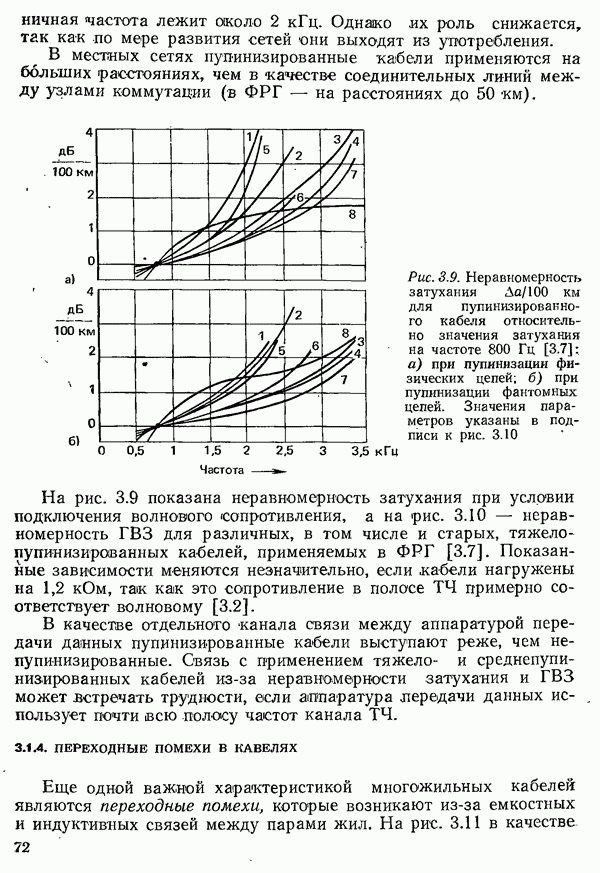
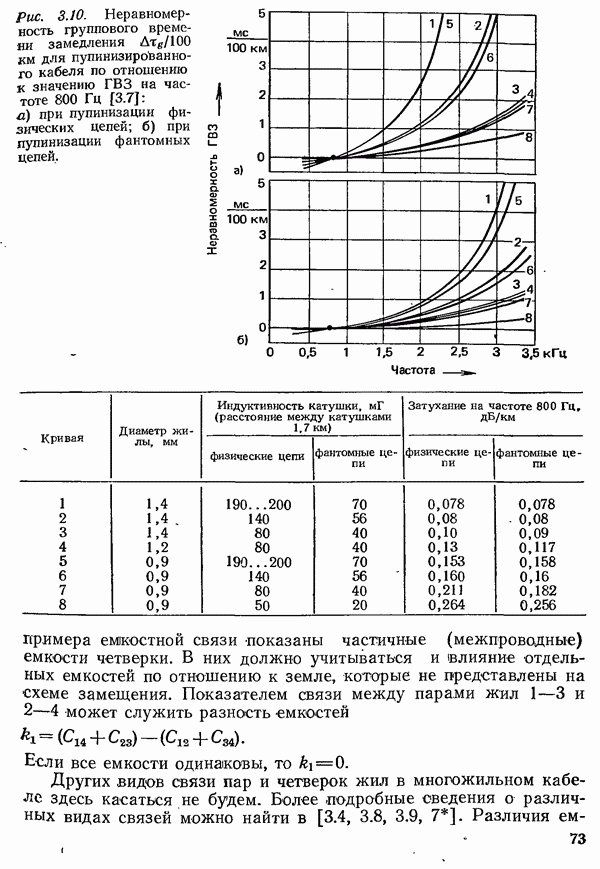
- 3.1.1.2. УМЕНЬШЕНИЕ ЗАТУХАНИЯ ПУТЕМ УВЕЛИЧЕНИЯ ИНДУКТИВНОСТИ. ПУПИНИЗАЦИЯ
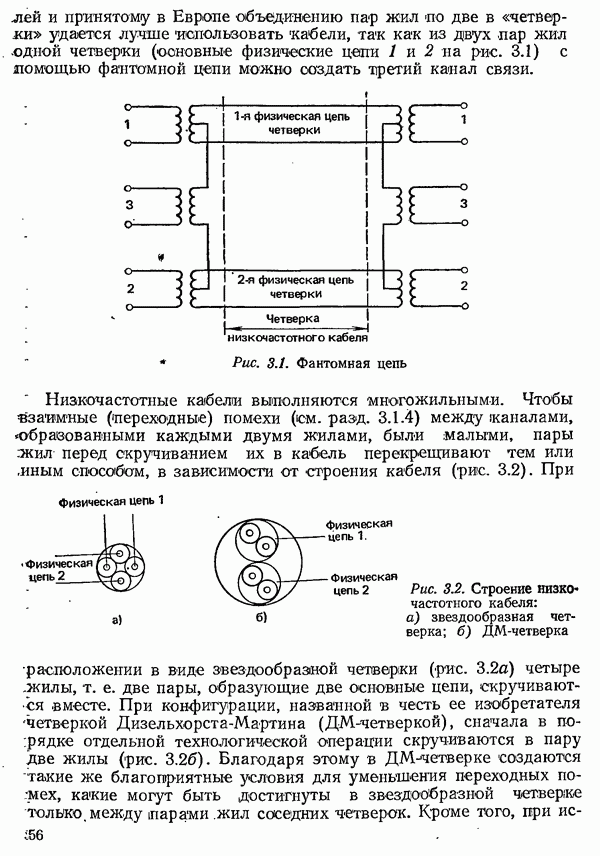
- 3.1.2. ХАРАКТЕРИСТИКИ ПАР ЖИЛ НИЗКОЧАСТОТНЫХ КАБЕЛЕЙ
- 3.1.3. ХАРАКТЕРИСТИКИ ПАР ЖИЛ ПУПИЯИЗИРОВАННЫХ КАБЕЛЕЙ
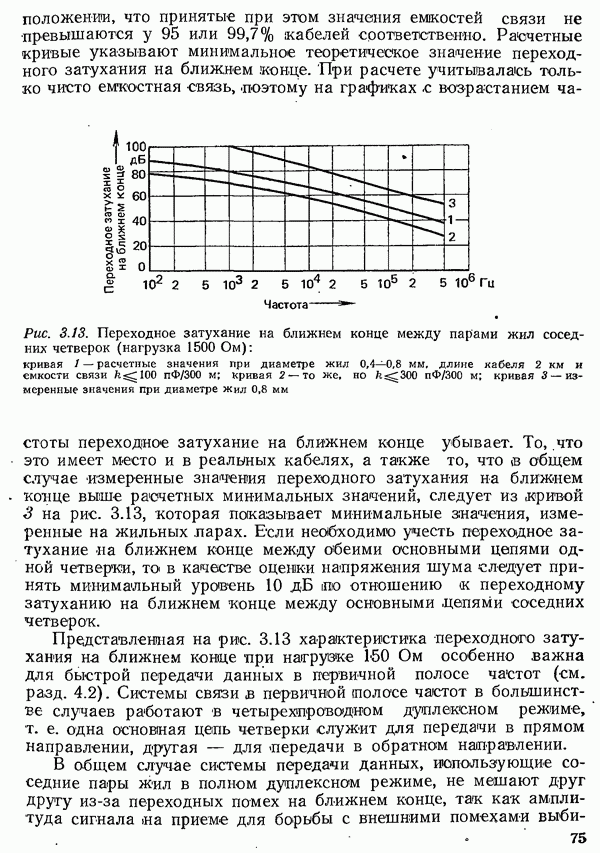
- 3.1.4. ПЕРЕХОДНЫЕ ПОМЕХИ В КАБЕЛЯХ
- 3.1.5. НАПРЯЖЕНИЯ ШУМОВ НА ПАРАХ ШИЛ КАБЕЛЕЙ
- 3.2. КАНАЛЫ ДАЛЬНЕЙ СВЯЗИ
- 3.2.2. КАНАЛЫ ТОНАЛЬНОЙ ЧАСТОТЫ
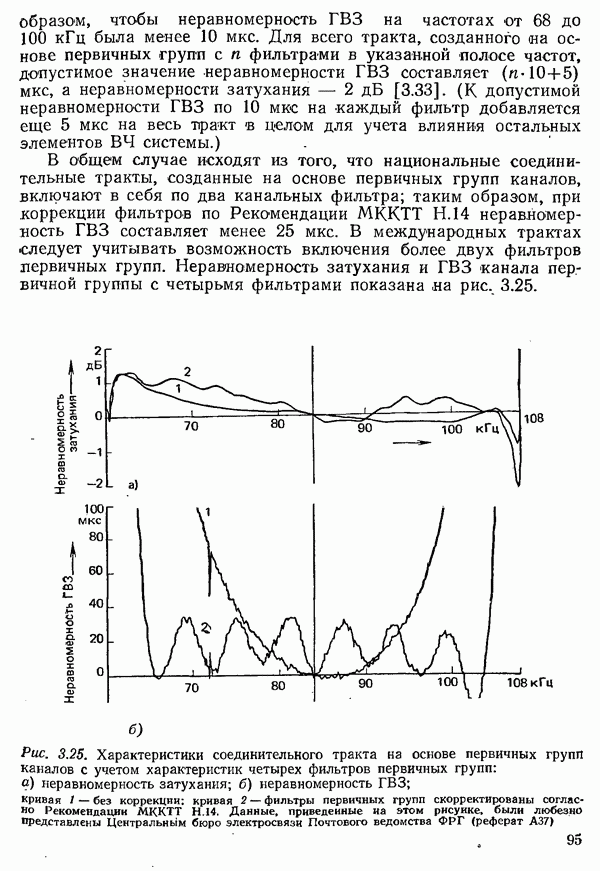
- 3.2.3. СОЕДИНИТЕЛЬНЫЕ ТРАКТЫ НА ОСНОВЕ ПЕРВИЧНЫХ ГРУПП КАНАЛОВ
- 4. Методы передачи данных
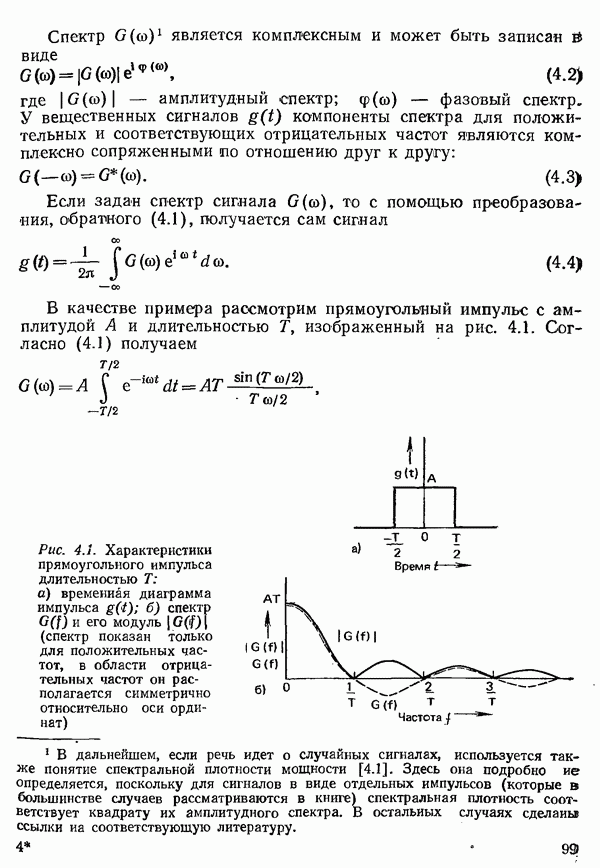
- 4.1.1. СИГНАЛЫ И СПЕКТРЫ
- 4.1.2. РЯД ФУРЬЕ
- 4.1.3. ИСКАЖЕНИЯ ФОРМЫ ИМПУЛЬСОВ ПРИ ОГРАНИЧЕНИИ ПОЛОСЫ ЧАСТОТ
- 4.1.4. УСЛОВИЯ НАЙКВИСТА
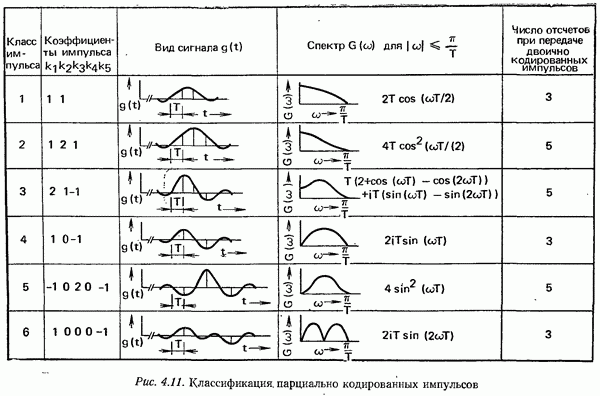
- 4.1.5. МЕТОДЫ ПАРЦИАЛЬНЫХ ОТСЧЕТОВ
- 4.1.6. ПЕРЕДАЧА МНОГОПОЗИЦИОННЫХ СИГНАЛОВ
- 4.2. МЕТОДЫ ПЕРЕДАЧИ В ПЕРВИЧНОЙ ПОЛОСЕ ЧАСТОТ
- 4.2.1. МЕТОДЫ С ПРИМЕНЕНИЕМ ДВУПОЛЯРНЫХ И ОДНОПОЛЯРНЫХ ИМПУЛЬСОВ
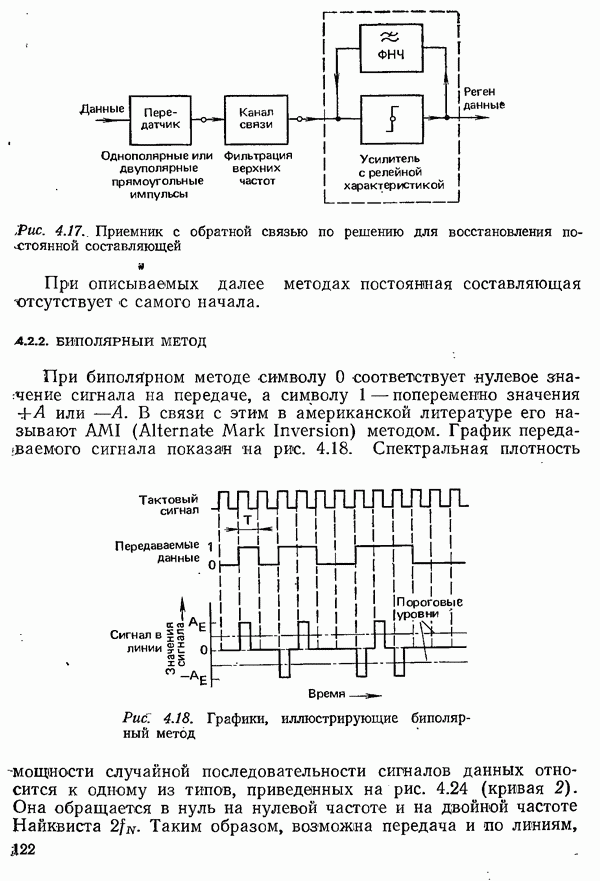
- 4.2.2. БИПОЛЯРНЫЙ МЕТОД
- 4.2.3. ПСЕВДОТРОИЧНЫЕ МЕТОДЫ
- 4.2.4. МЕТОДЫ С ПРИМЕНЕНИЕМ БИПОЛЯРНЫХ КОДОВ ВЫСОКОЙ ПЛОТНОСТИ
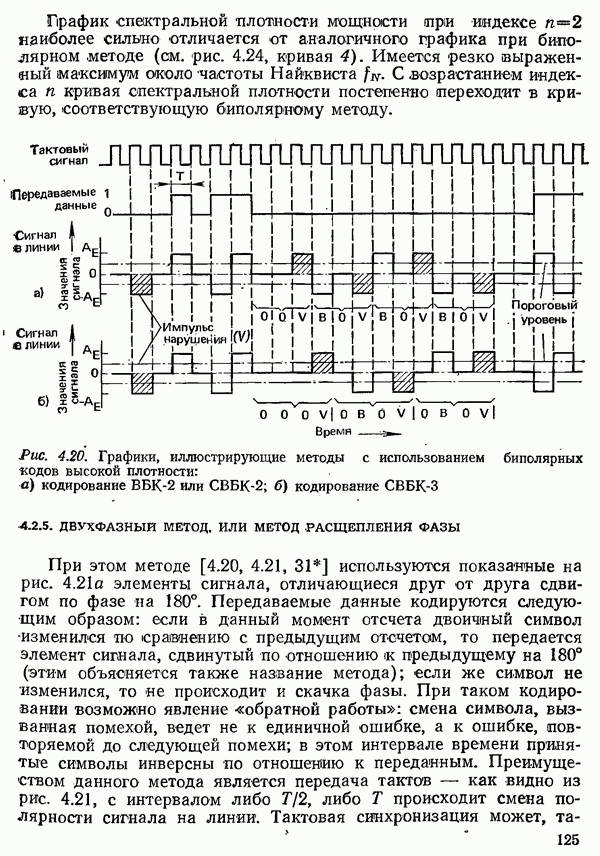
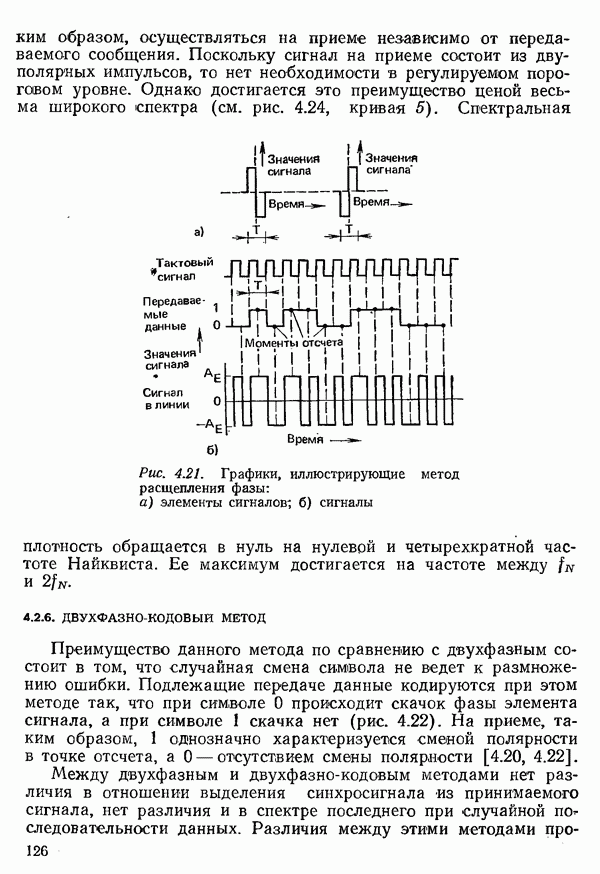
- 4.2.5. ДВУХФАЗНЫЙ МЕТОД. ИЛИ МЕТОД РАСЩЕПЛЕНИЯ ФАЗЫ
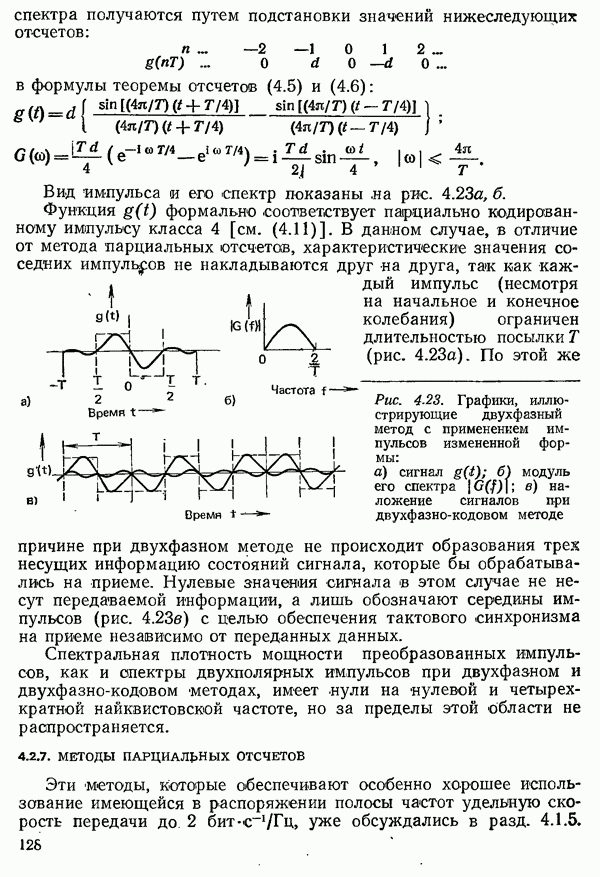
- 4.2.6. ДВУХФАЗНО-КОДОВЫЙ МЕТОД
- 4.2.7. МЕТОДЫ ПАРЦИАЛЬНЫХ ОТСЧЕТОВ
- 4.3. МЕТОДЫ ПЕРЕДАЧИ С ПРИМЕНЕНИЕМ МОДУЛЯЦИИ
- 4.3.1. АМПЛИТУДНАЯ МОДУЛЯЦИЯ
- 4.3.1.2. АМПЛИТУДНАЯ МОДУЛЯЦИЯ С ОДНОЙ БОКОВОЙ ПОЛОСОЙ И С ЧАСТИЧНО ПОДАВЛЕННОЙ БОКОВОЙ ПОЛОСОЙ
- 4.3.1.3. КВАДРАТУРНАЯ АМПЛИТУДНАЯ МОДУЛЯЦИЯ
- 4.3.1.4. УДЕЛЬНАЯ СКОРОСТЬ ПЕРЕДАЧИ ПРИ АМПЛИТУДНОЙ МОДУЛЯЦИИ
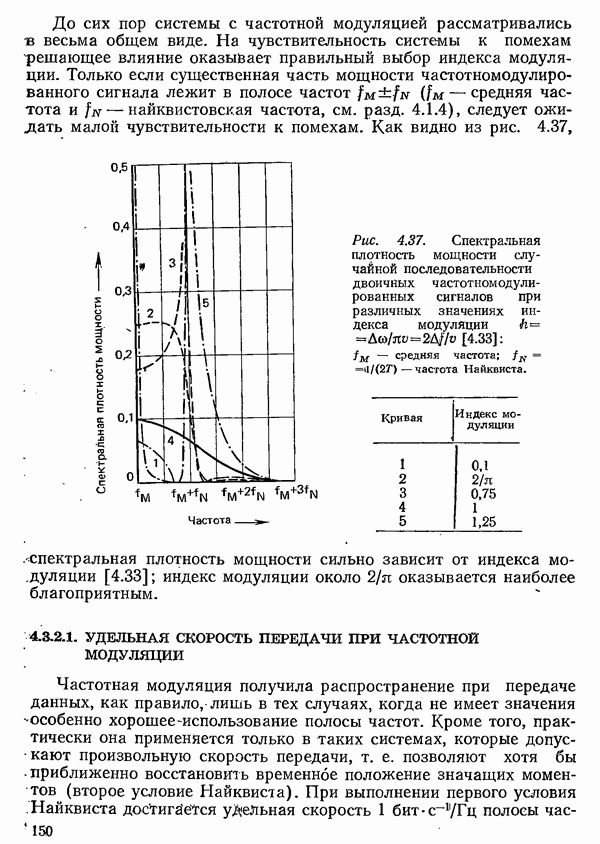
- 4.3.2. ЧАСТОТНАЯ МОДУЛЯЦИЯ
- 4.3.2.1. УДЕЛЬНАЯ СКОРОСТЬ ПЕРЕДАЧИ ПРИ ЧАСТОТНОЙ МОДУЛЯЦИИ
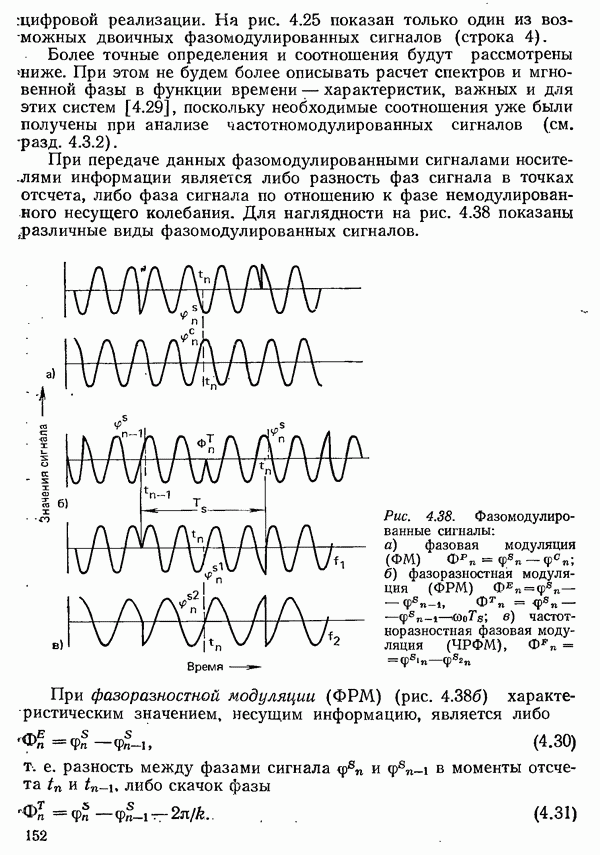
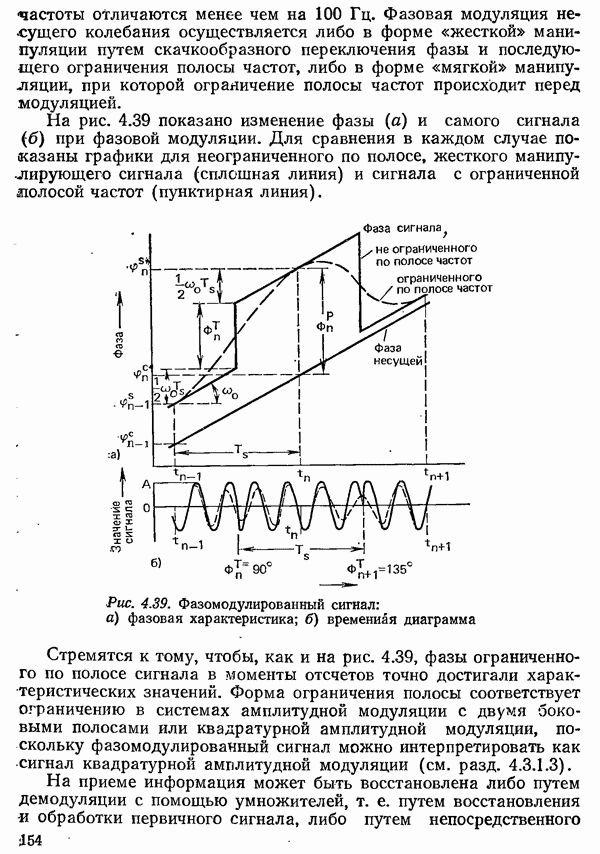
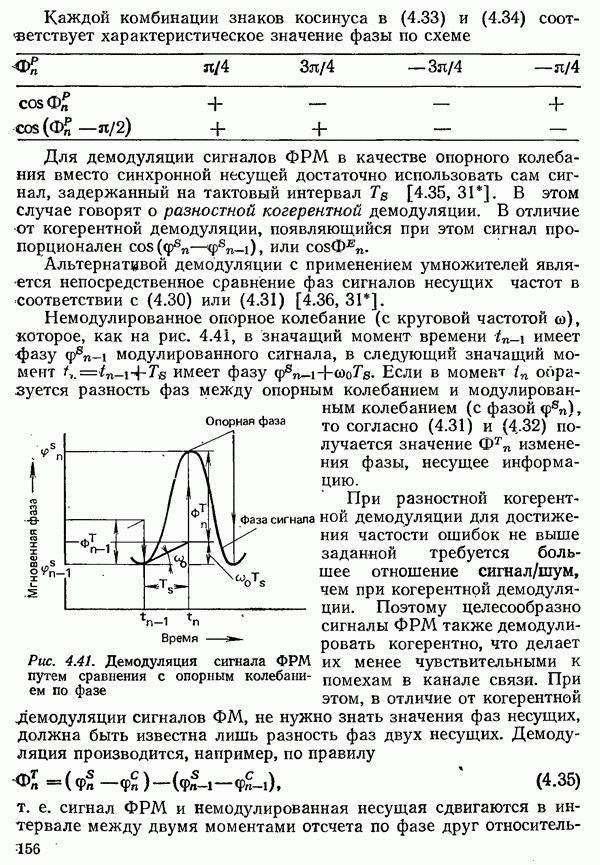
- 4.3.3. ФАЗОВАЯ МОДУЛЯЦИЯ
- 4.4. ВОССТАНОВЛЕНИЕ ТАКТОВ И НЕСУЩЕЙ
- 4.4.2. ВОССТАНОВЛЕНИЕ ЧАСТОТЫ И ФАЗЫ НЕСУЩЕЙ
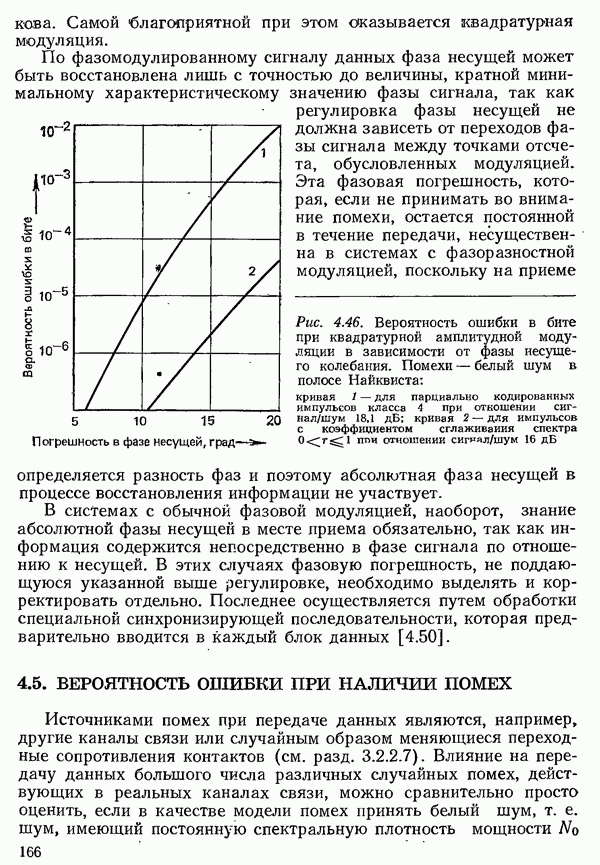
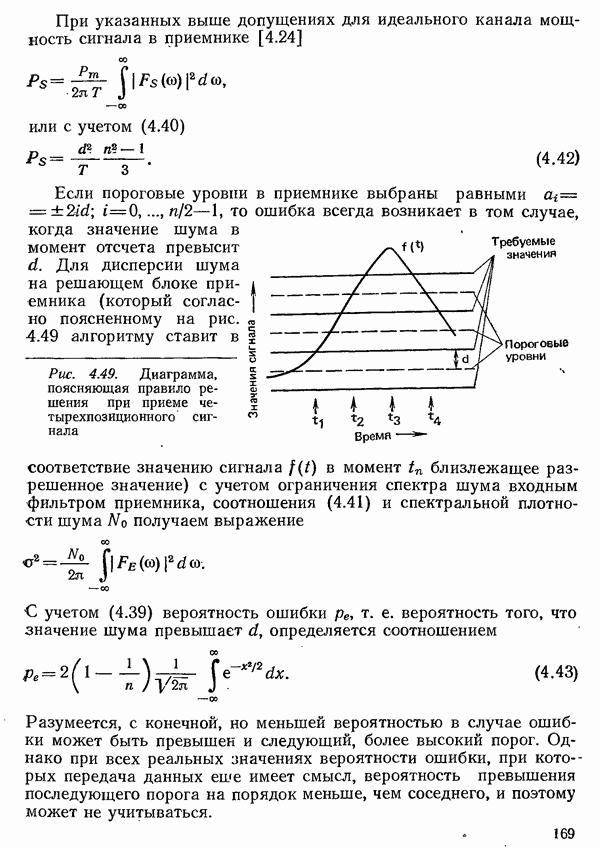
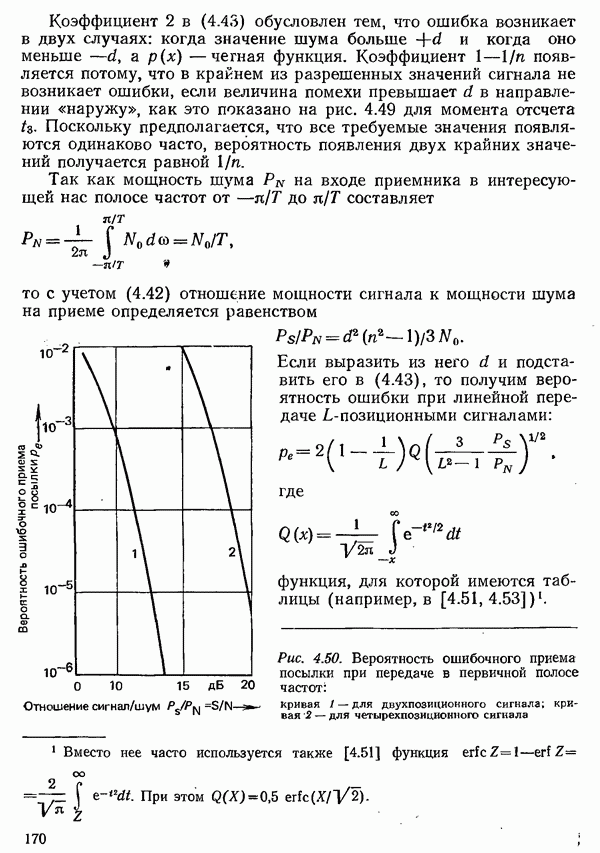
- 4.5. ВЕРОЯТНОСТЬ ОШИБКИ ПРИ НАЛИЧИИ ПОМЕХ
- 4.5.1. ВЕРОЯТНОСТЬ ОШИБКИ ПРИ УЧЕТЕ ТОЛЬКО ШУМА В КАНАЛЕ СВЯЗИ
- 4.5.2. ВЕРОЯТНОСТЬ ОШИБКИ С УЧЕТОМ ЛИНЕЙНЫХ ИСКАЖЕНИЙ
- 4.5.3. ВЕРОЯТНОСТЬ ОШИБКИ С УЧЕТОМ ПРОЦЕССОВ МОДУЛЯЦИИ И ДЕМОДУЛЯЦИИ
- 5. Учет свойств реальных каналов связи при передаче данных
- 5.2. ВЛИЯНИЕ ХАРАКТЕРИСТИК КАНАЛОВ СВЯЗИ НА ПЕРЕДАЧУ ДАННЫХ
- 5.2.2. СДВИГИ ЧАСТОТЫ
- 5.2.3. ФАЗОВОЕ ДРОЖАНИЕ
- 5.2.4. ВЛИЯНИЕ РЕАЛЬНЫХ ПОМЕХ
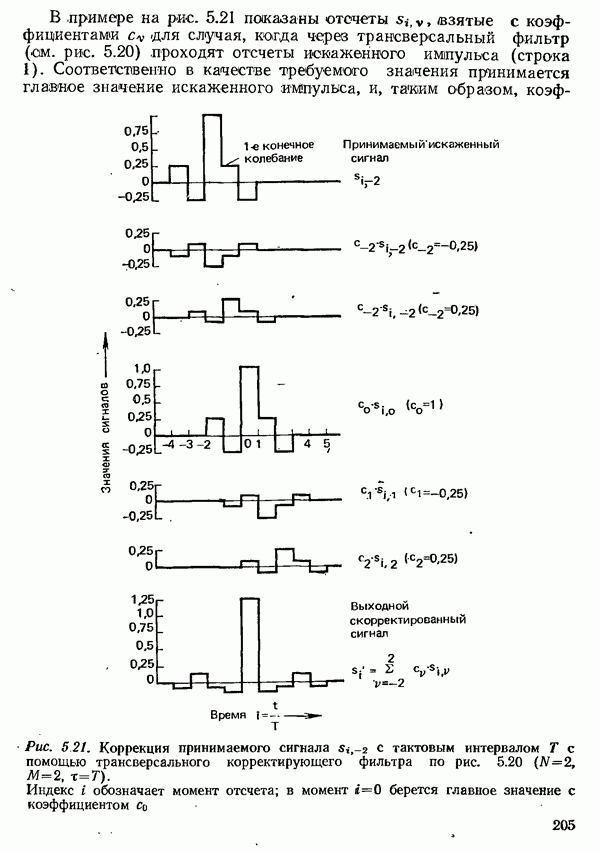
- 5.3. КОРРЕКЦИЯ ПРИНИМАЕМОГО СИГНАЛА ДАННЫХ
- 5.3.1. КОРРЕКЦИЯ ПРИНИМАЕМОГО СИГНАЛА ДАННЫХ В ЧАСТОТНОЙ ОБЛАСТИ
- 5.3.1.1. КОМПРОМИССНЫЙ КОРРЕКТОР
- 5.3.1.2. НАСТРАИВАЕМЫЙ ЧАСТОТНЫЙ КОРРЕКТОР СИГНАЛОВ ДАННЫХ
- 5.3.2. КОРРЕКЦИЯ ПРИНИМАЕМОГО СИГНАЛА ДАННЫХ ВО ВРЕМЕННОЙ ОБЛАСТИ
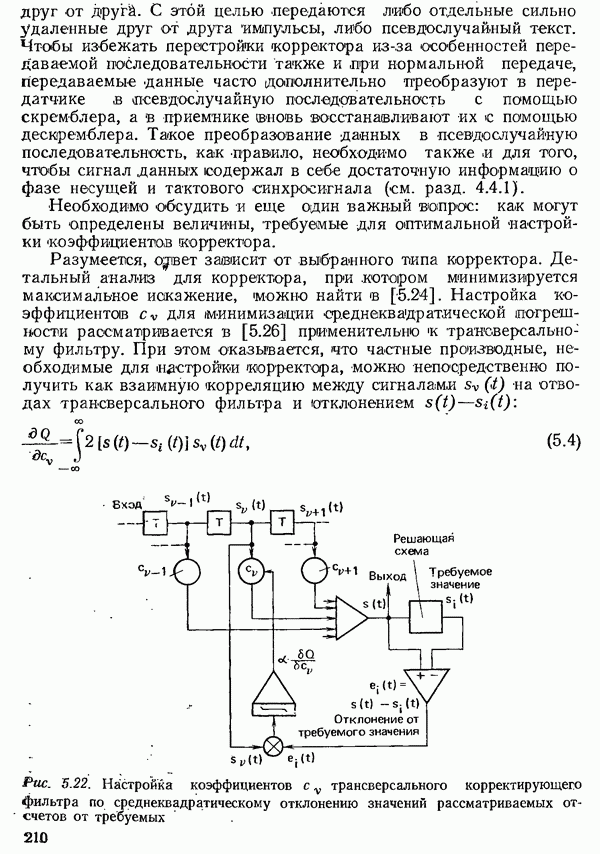
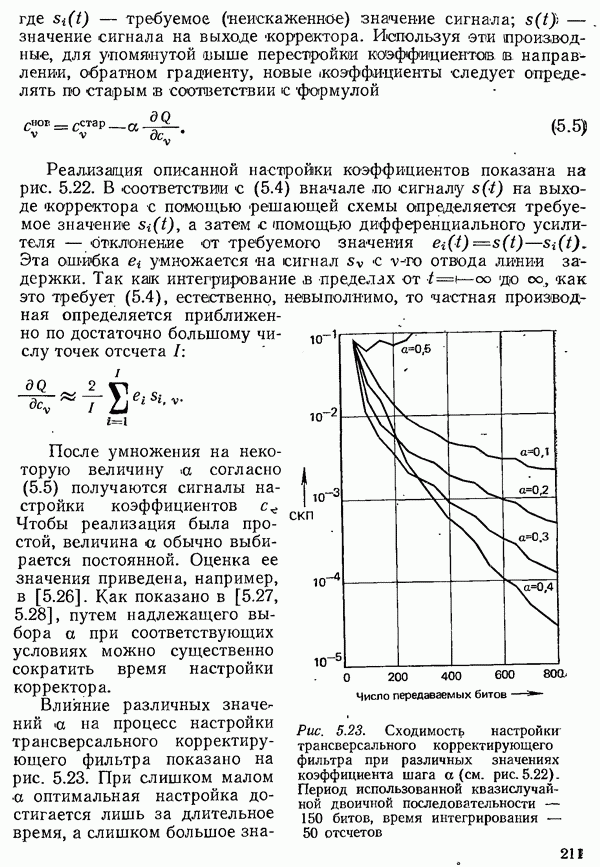
- 5.3.2.2. КРИТЕРИИ НАСТРОЙКИ КОРРЕКТОРА ВО ВРЕМЕННОЙ ОБЛАСТИ
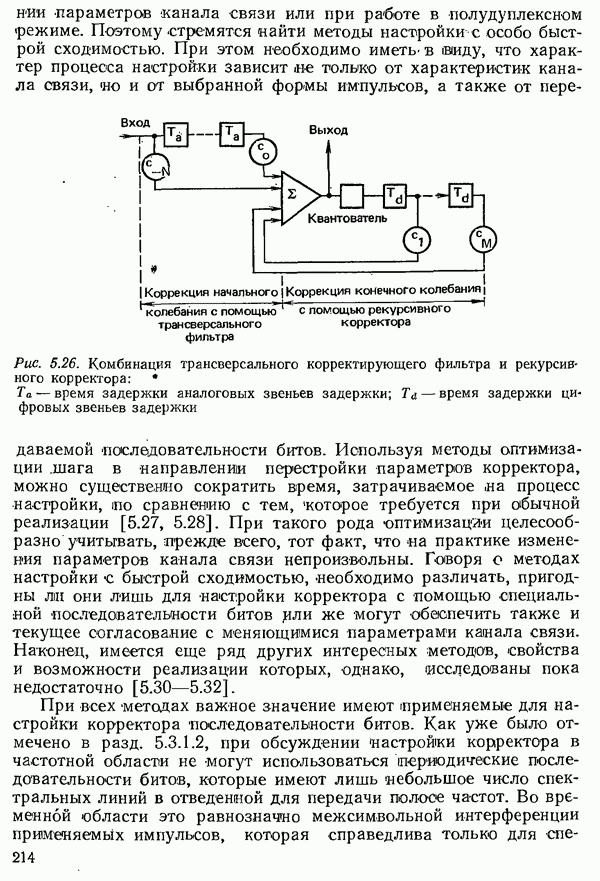
- 5.3.2.3. АВТОМАТИЧЕСКАЯ НАСТРОЙКА ТРАНСВЕРСАЛЬНОГО КОРРЕКТИРУЮЩЕГО ФИЛЬТРА
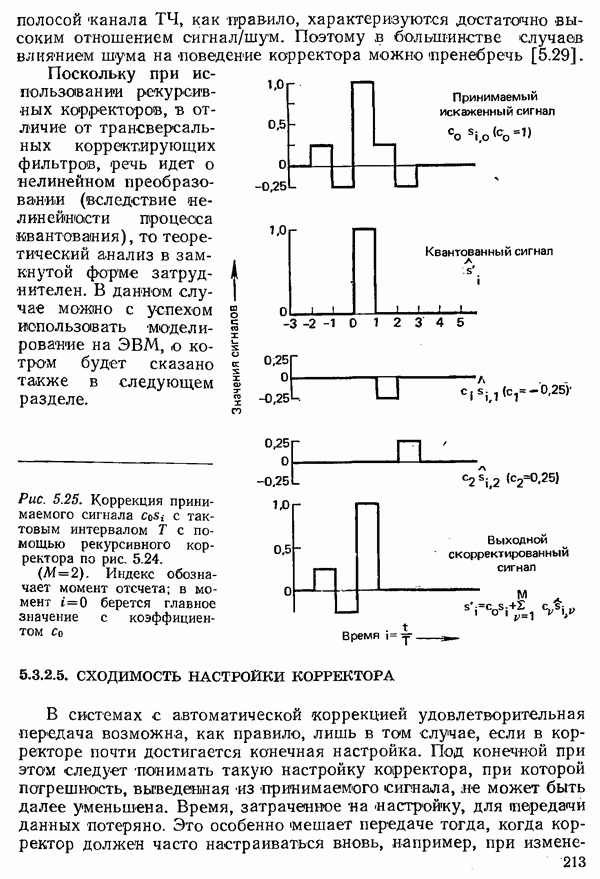
- 5.3.2.4. РЕКУРСИВНЫЙ КОРРЕКТОР
- 5.3.2.5. СХОДИМОСТЬ НАСТРОЙКИ КОРРЕКТОРА
- 5.3.2.6. КОРРЕКТОР ДЛЯ СПЕЦИАЛЬНЫХ МЕТОДОВ ПЕРЕДАЧИ
- 6. Основы коммутации данных
- 6.1.2. МЕТОДЫ КОММУТАЦИИ
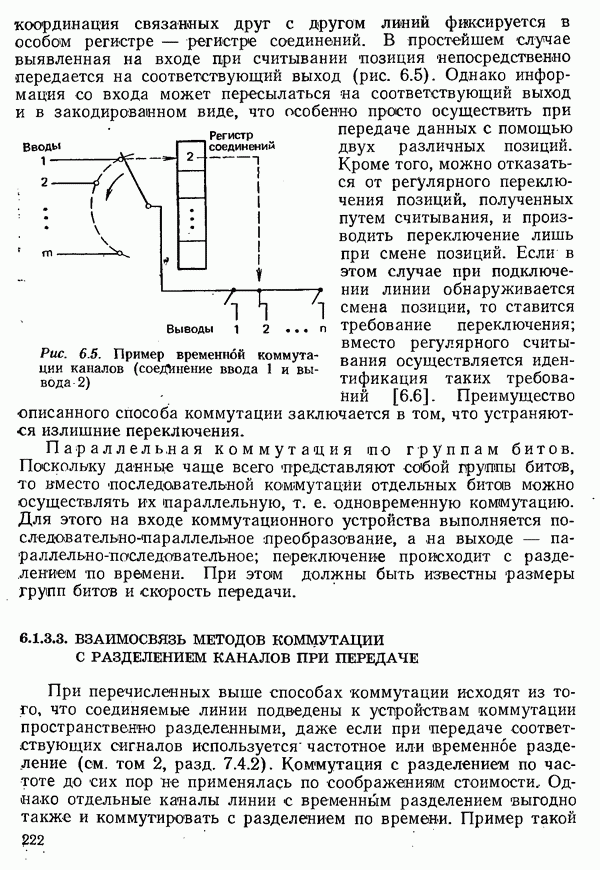
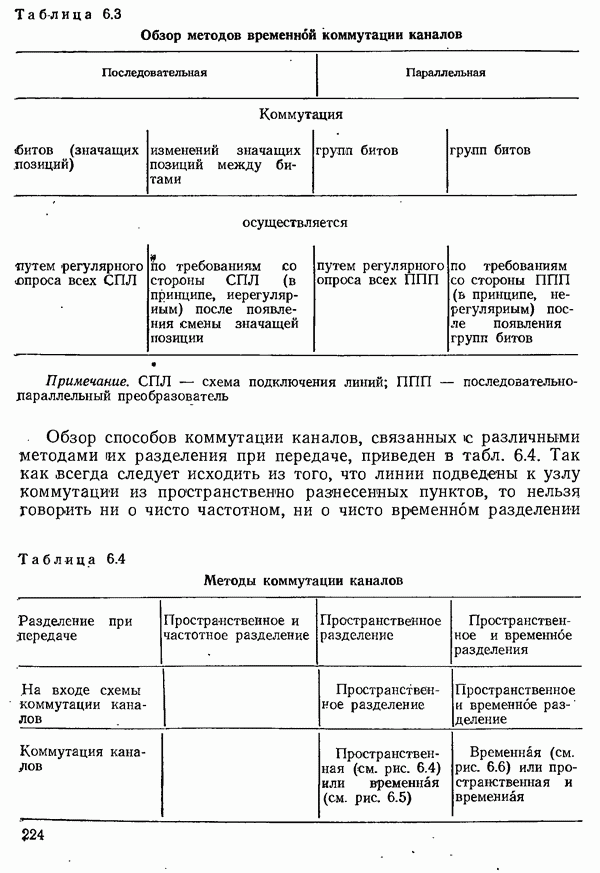
- 6.1.3. СПОСОБЫ КОММУТАЦИИ КАНАЛОВ
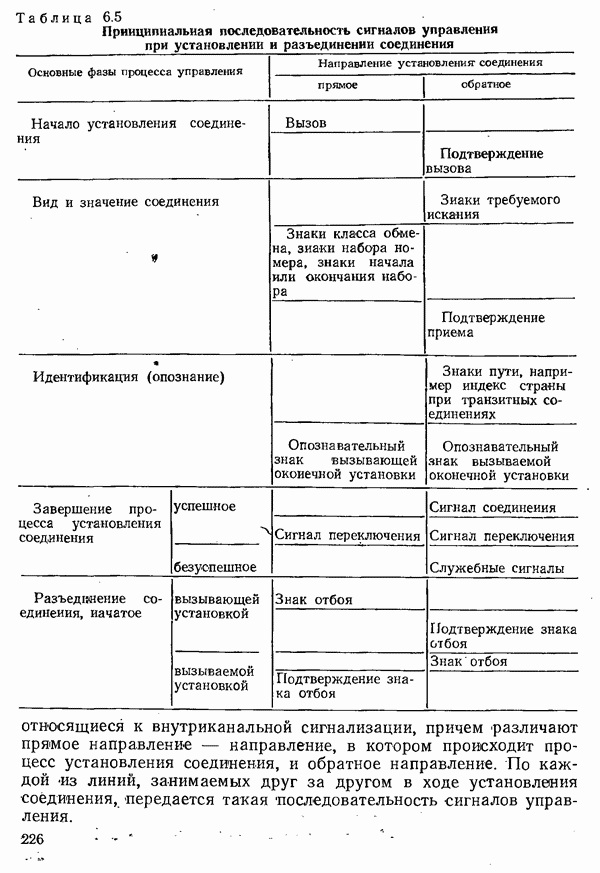
- 6.1.4. СИГНАЛИЗАЦИЯ
- 6.1.5. УПРАВЛЕНИЕ ПРОЦЕССАМИ СОЕДИНЕНИЯ И РАЗЪЕДИНЕНИЯ
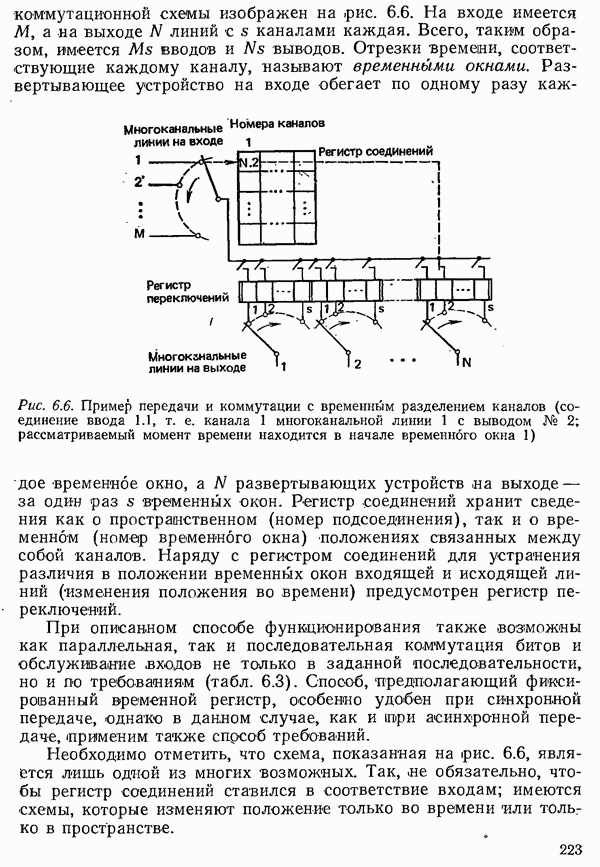
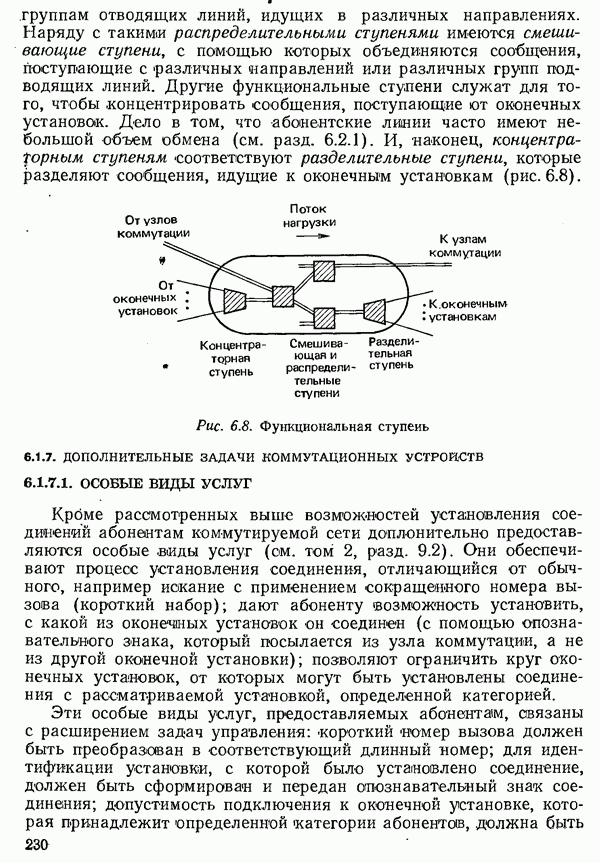
- 6.1.6. ПОДРАЗДЕЛЕНИЕ ЦЕПЕЙ КОММУТАЦИИ КАНАЛОВ
- 6.1.7. ДОПОЛНИТЕЛЬНЫЕ ЗАДАЧИ КОММУТАЦИОННЫХ УСТРОЙСТВ
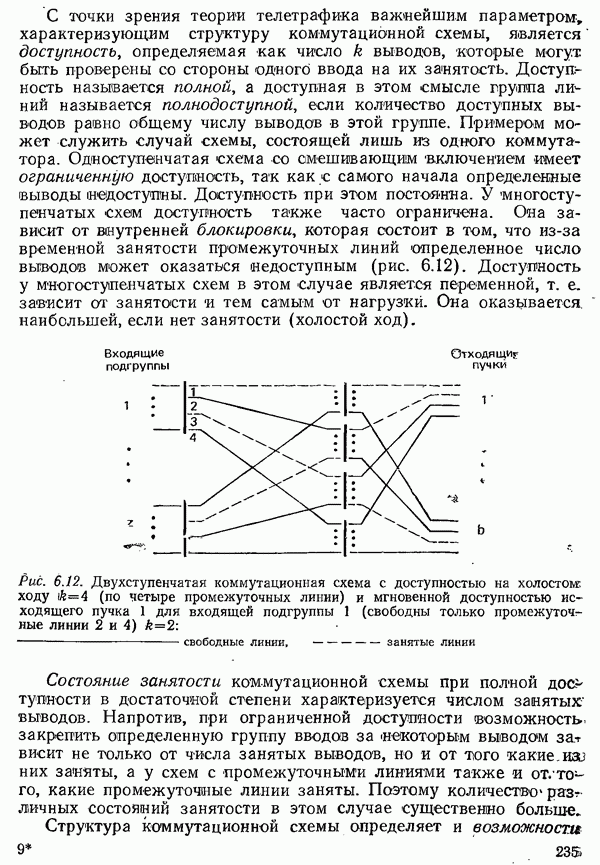
- 6.2. АНАЛИЗ СИСТЕМ КОММУТАЦИИ НА ОСНОВЕ ТЕОРИИ ТЕЛЕТРАФИКА
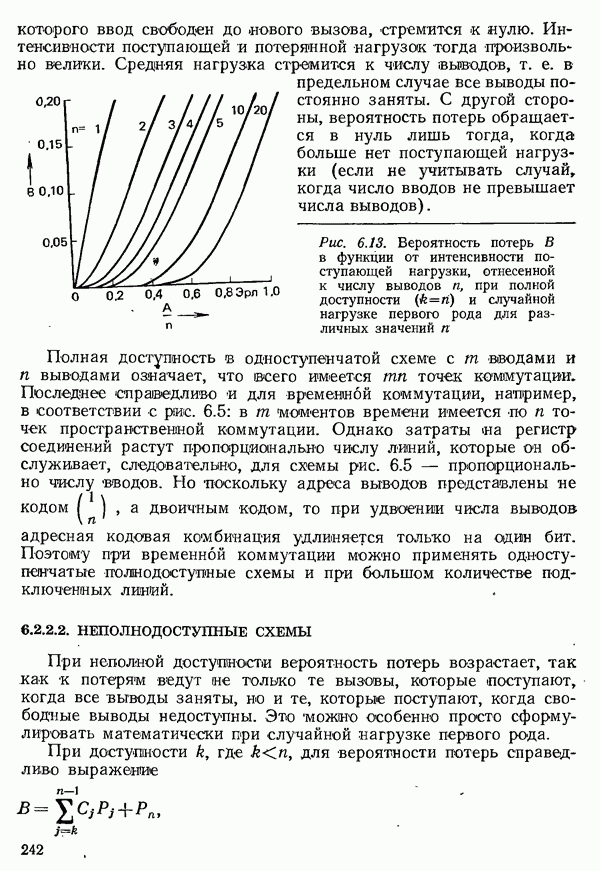
- 6.2.2. СИСТЕМЫ С ПОТЕРЯМИ
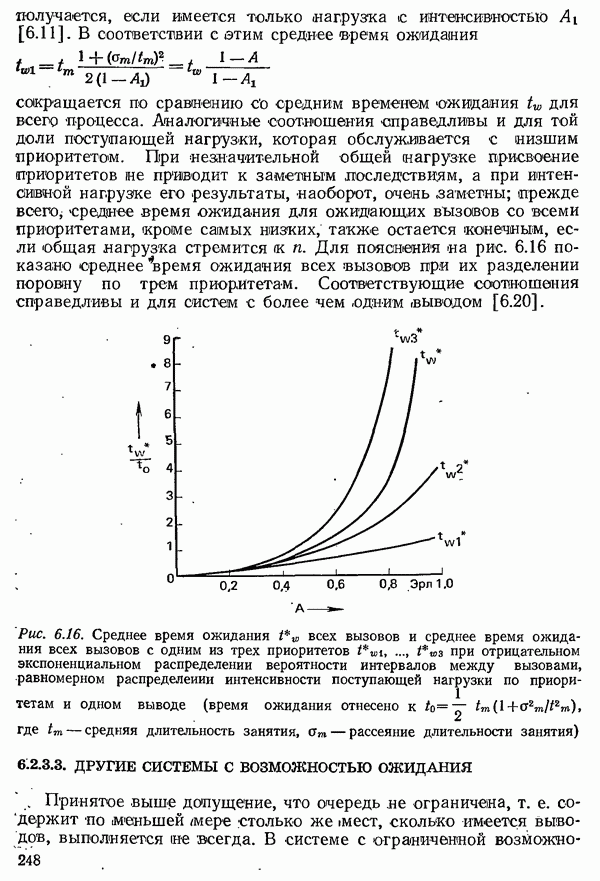
- 6.2.3. СИСТЕМЫ С ОЖИДАНИЕМ
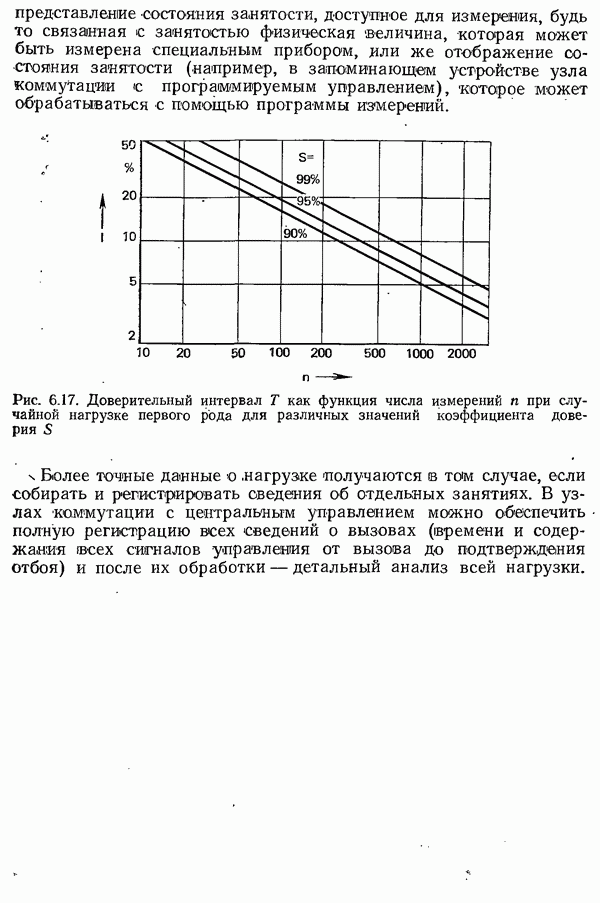
- 6.2.4. ИЗМЕРЕНИЯ НАГРУЗКИ
- СПИСОК ЛИТЕРАТУРЫ