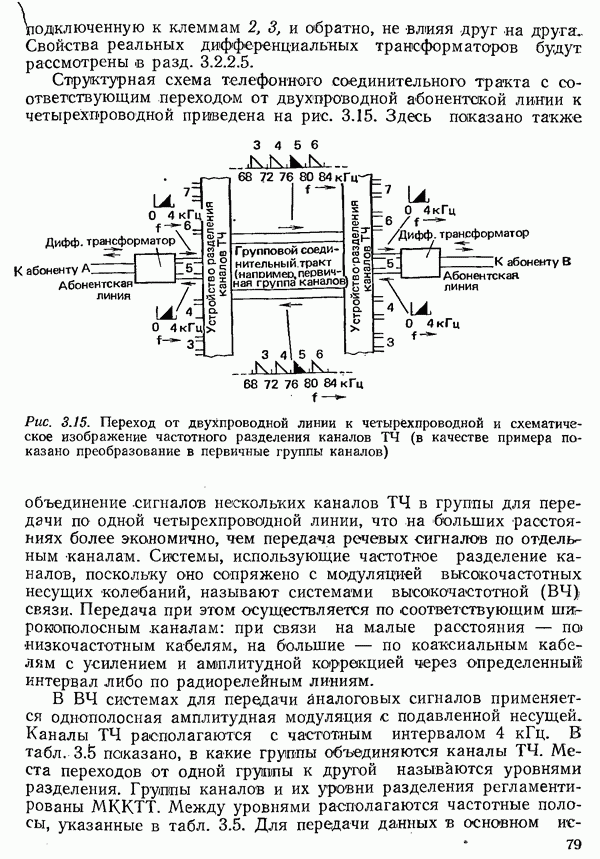
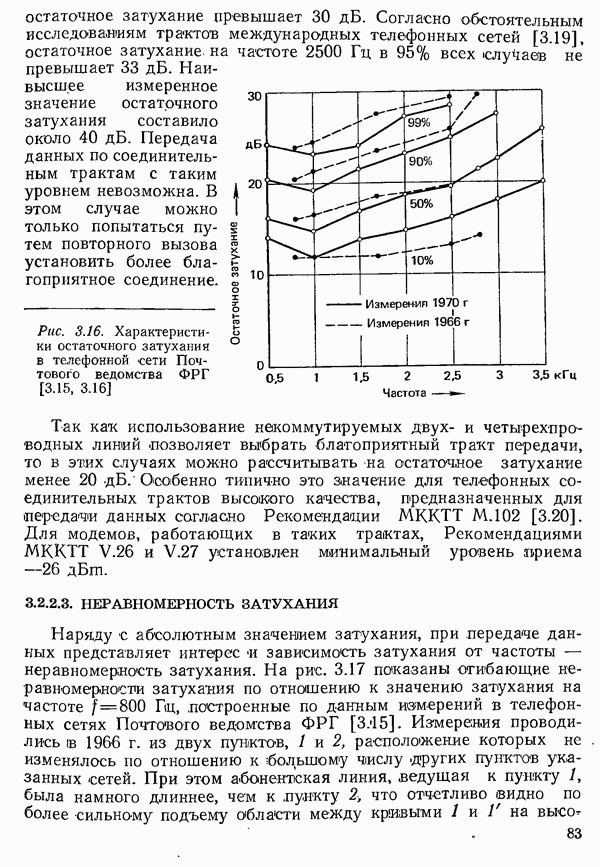
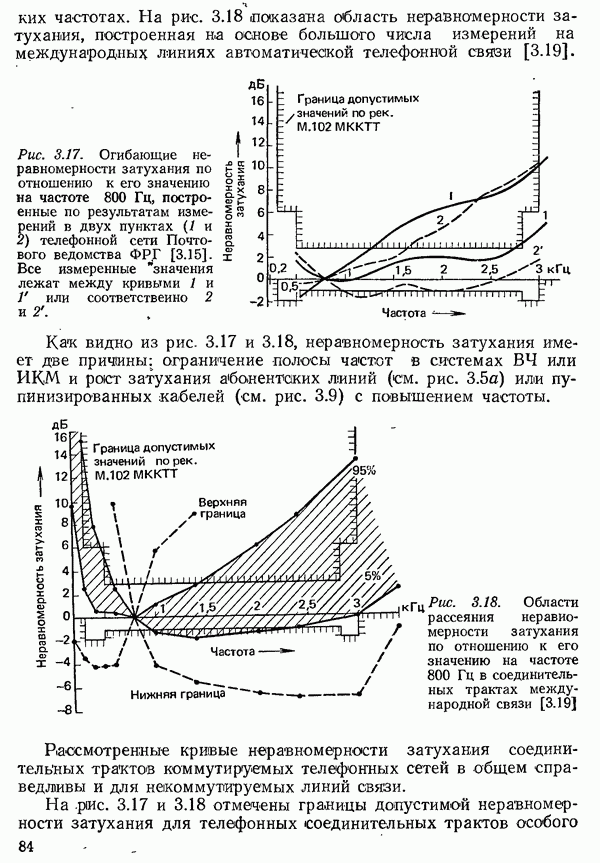
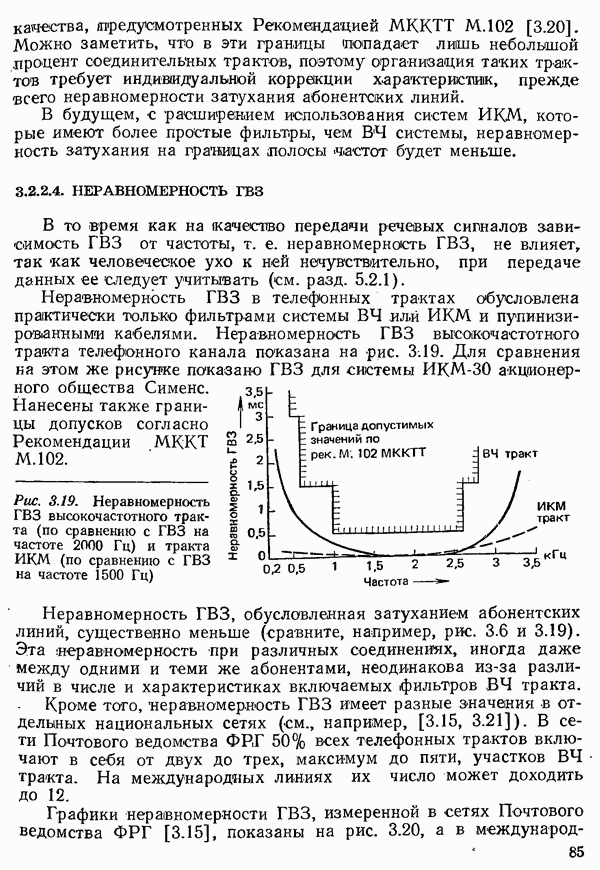
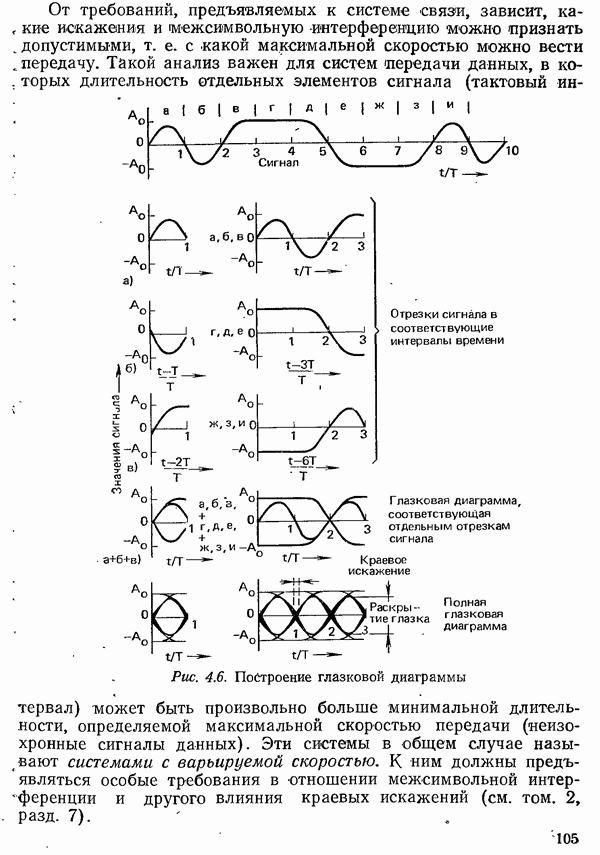
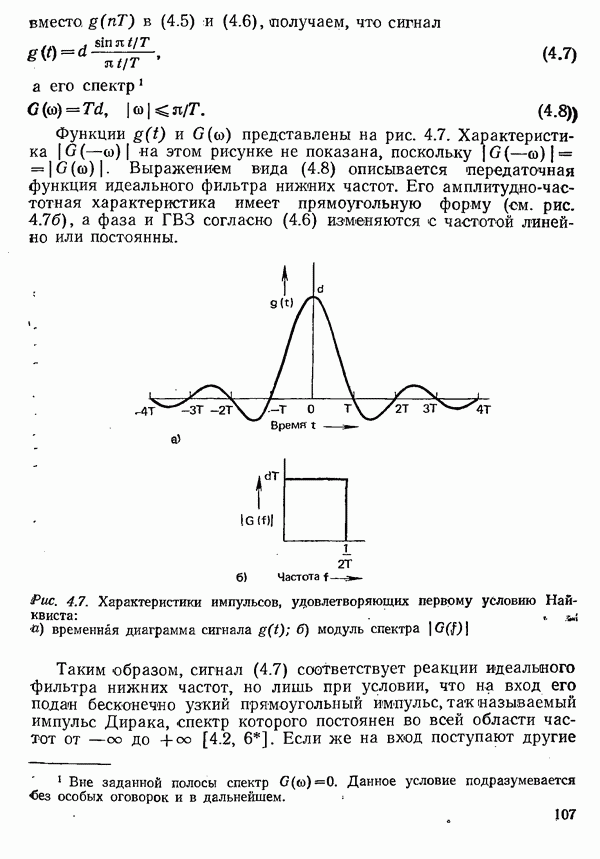
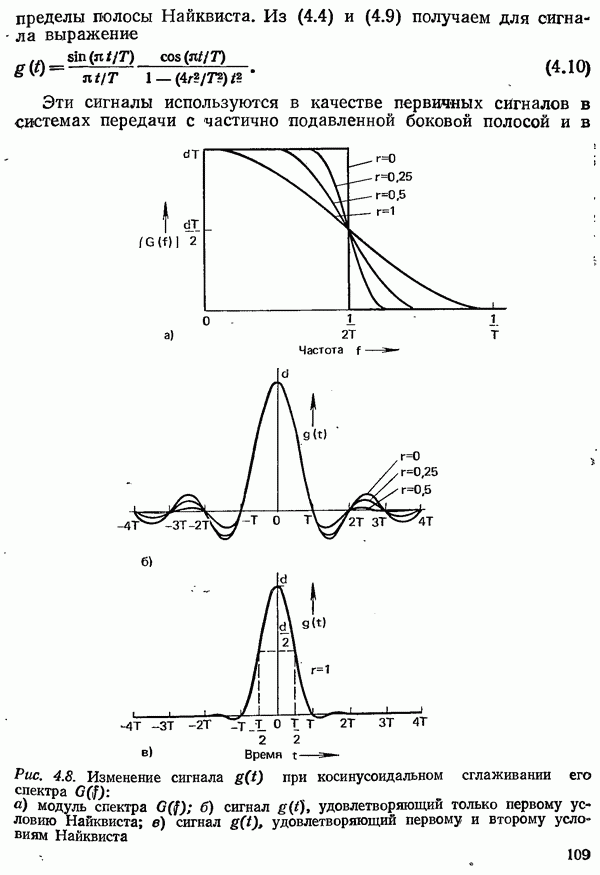
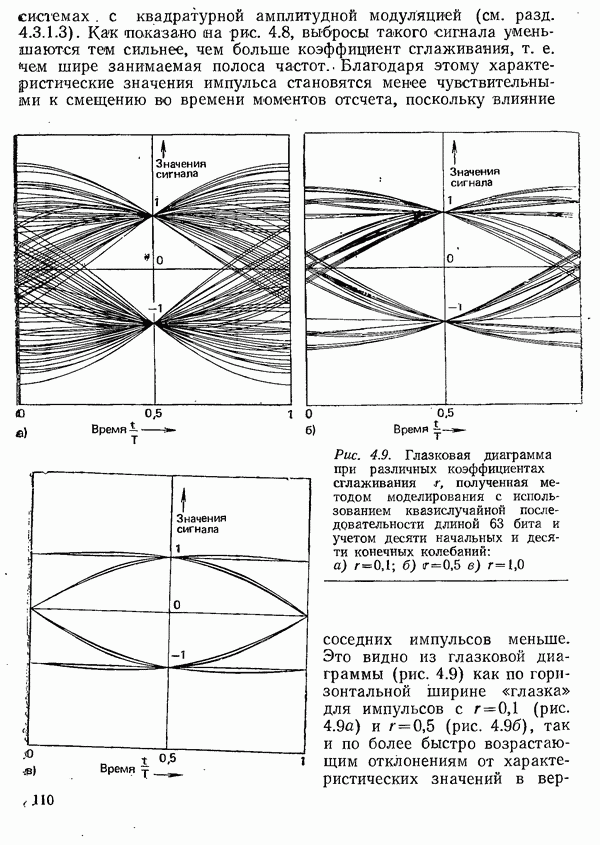
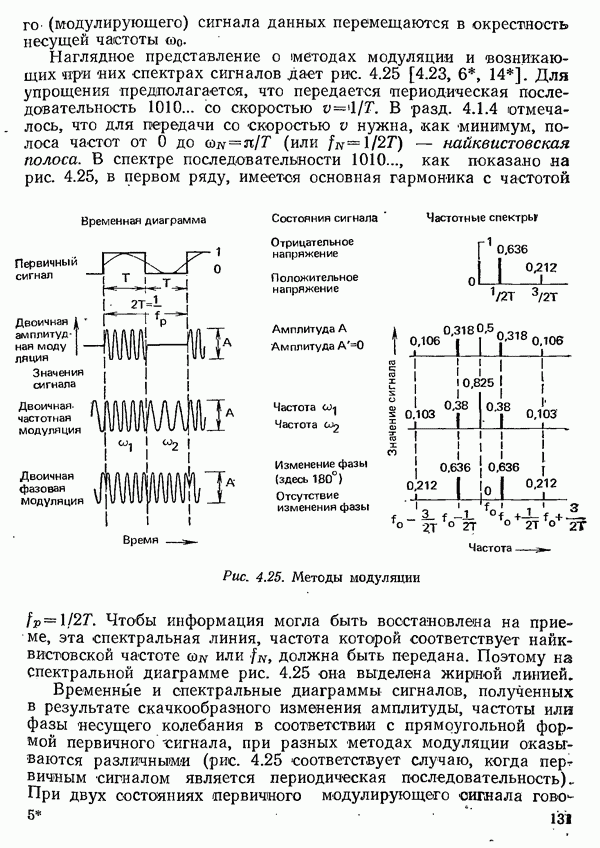
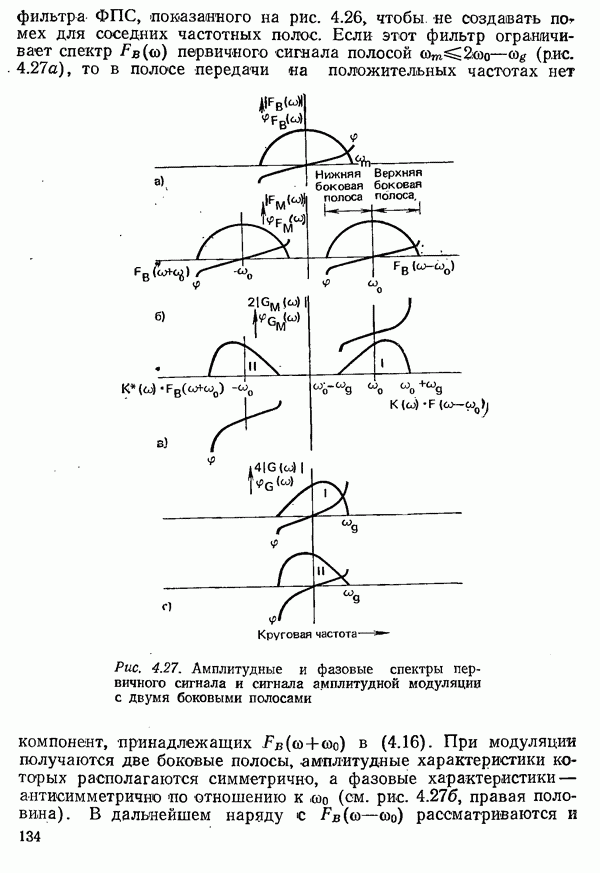
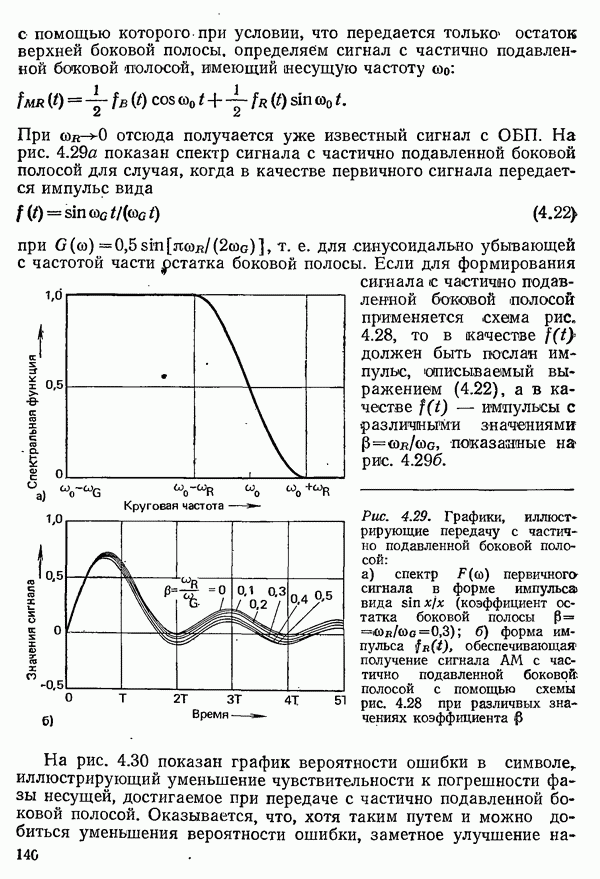
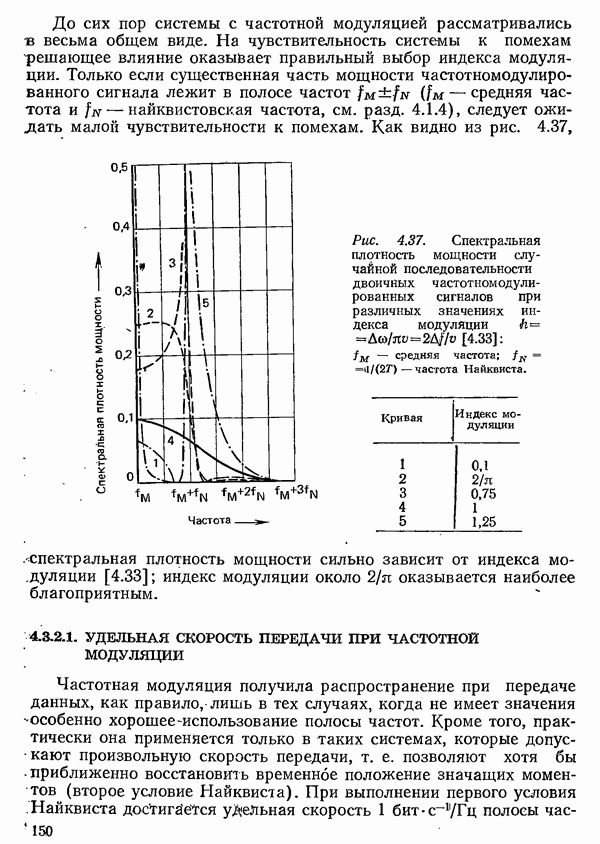
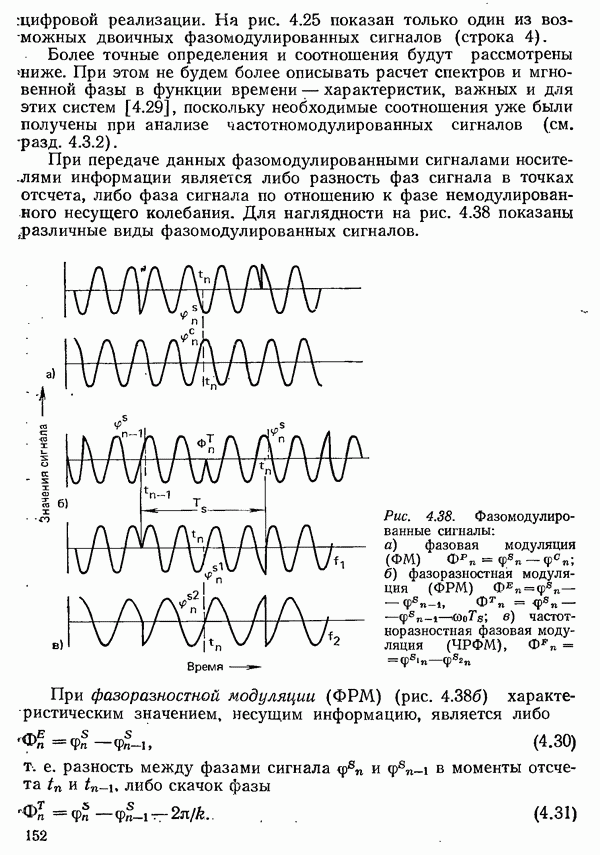
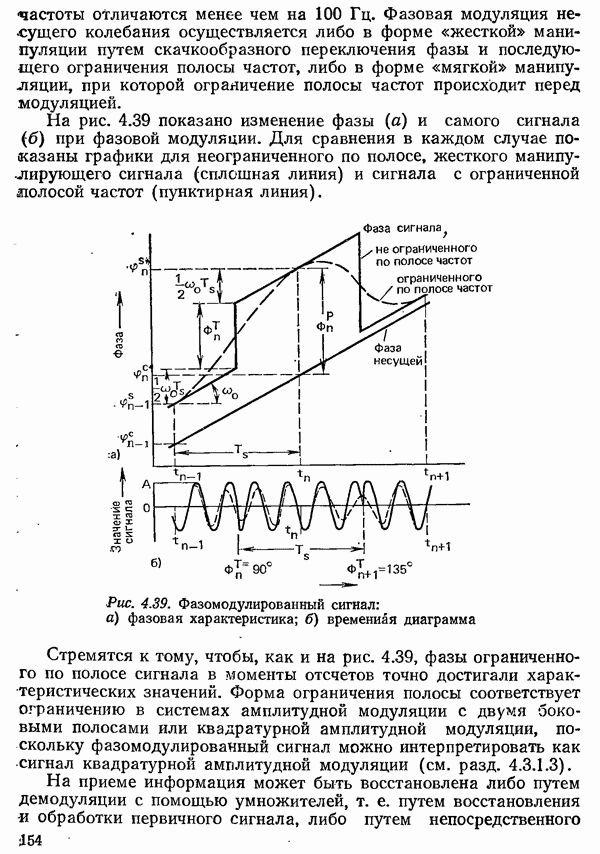
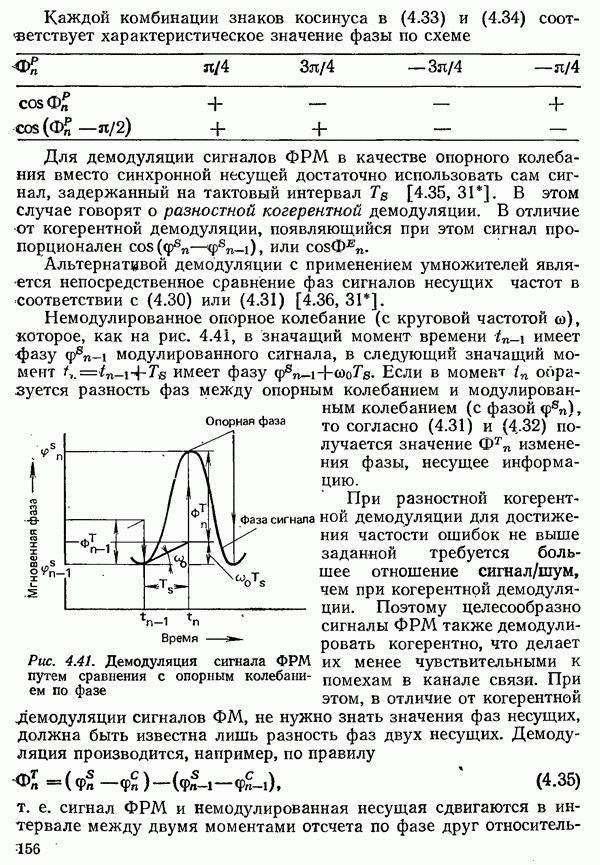
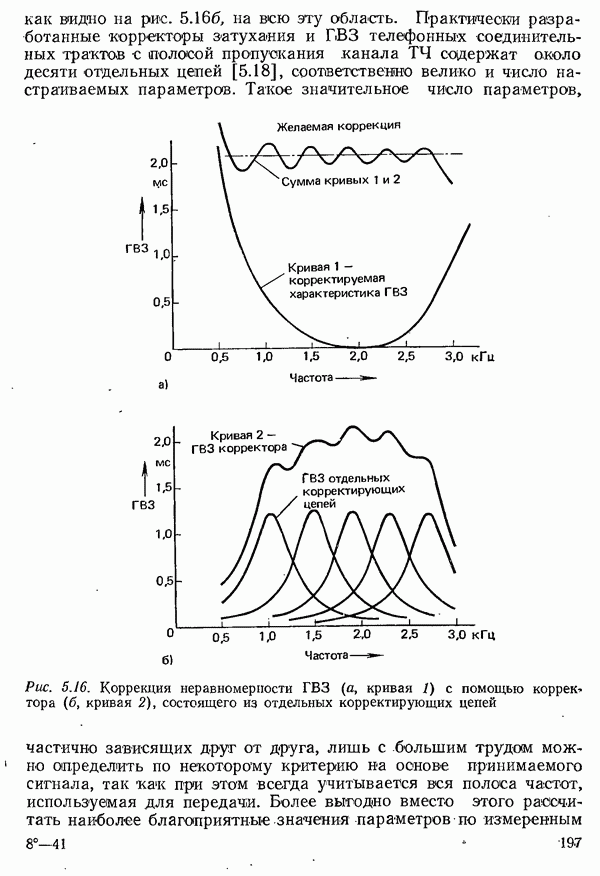
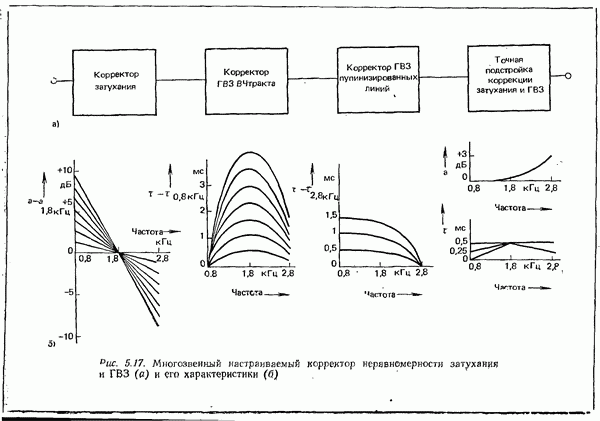
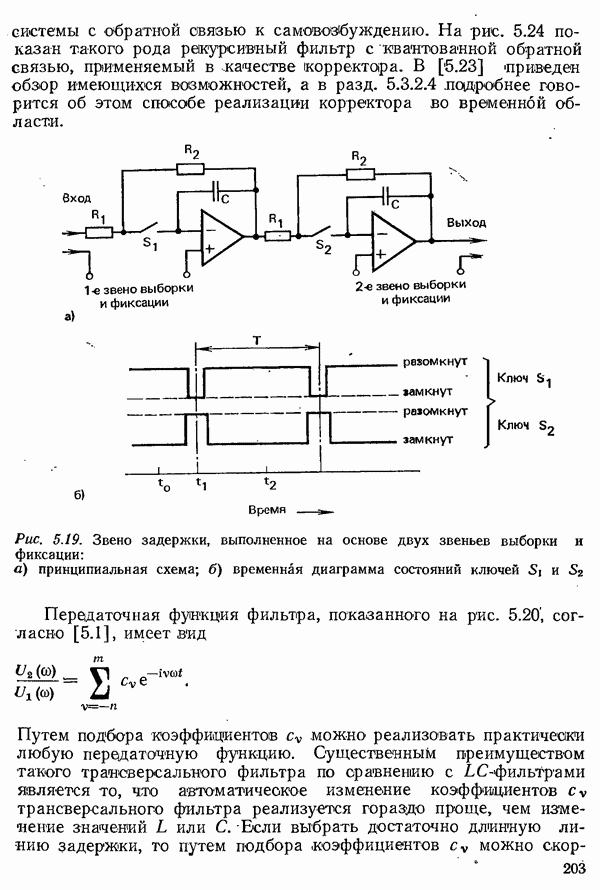
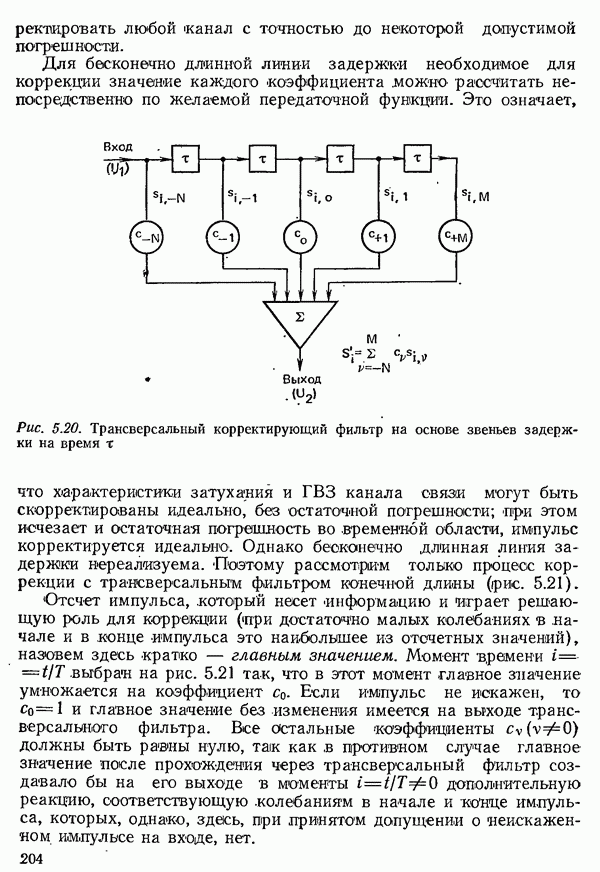
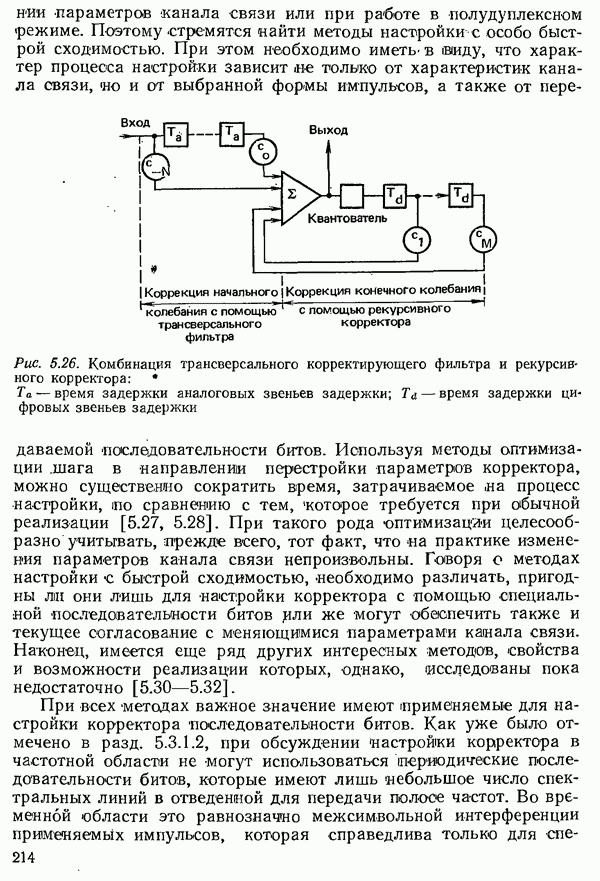
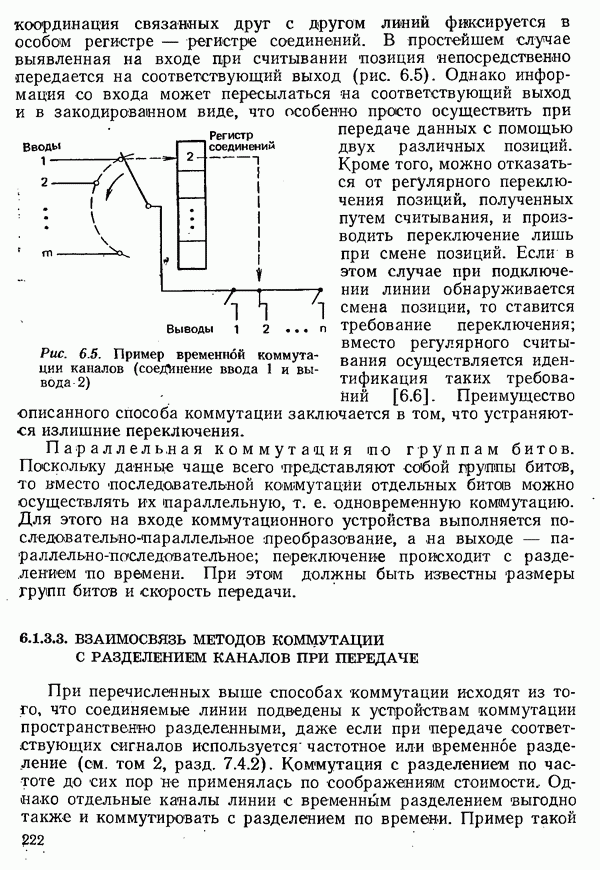
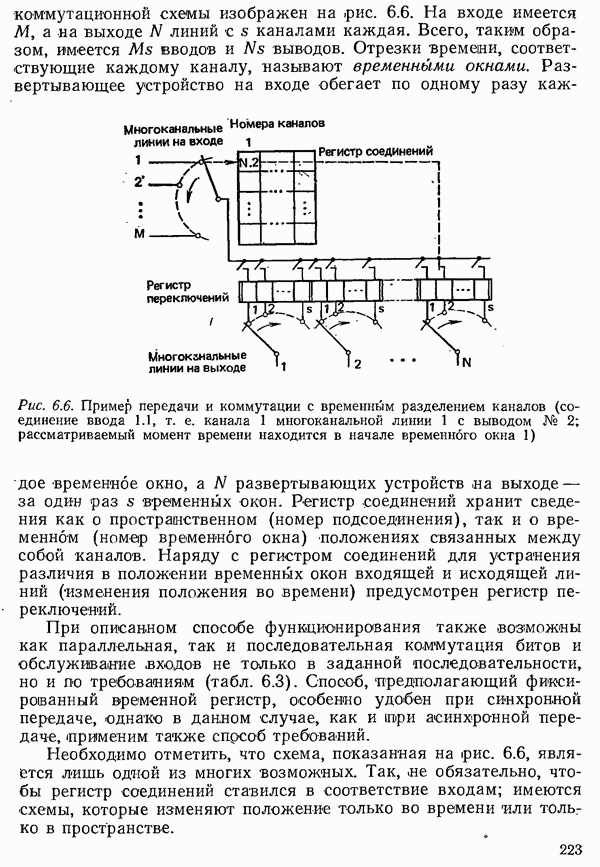
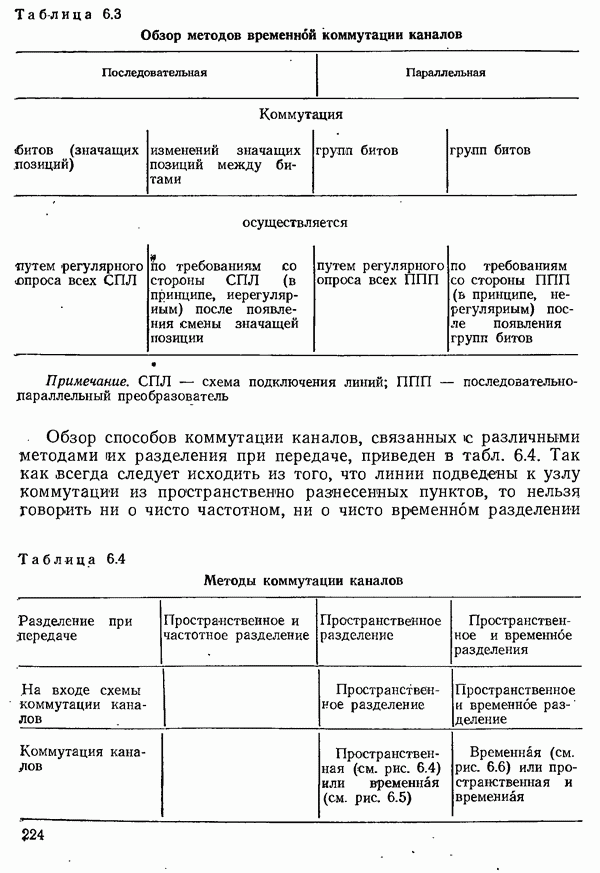
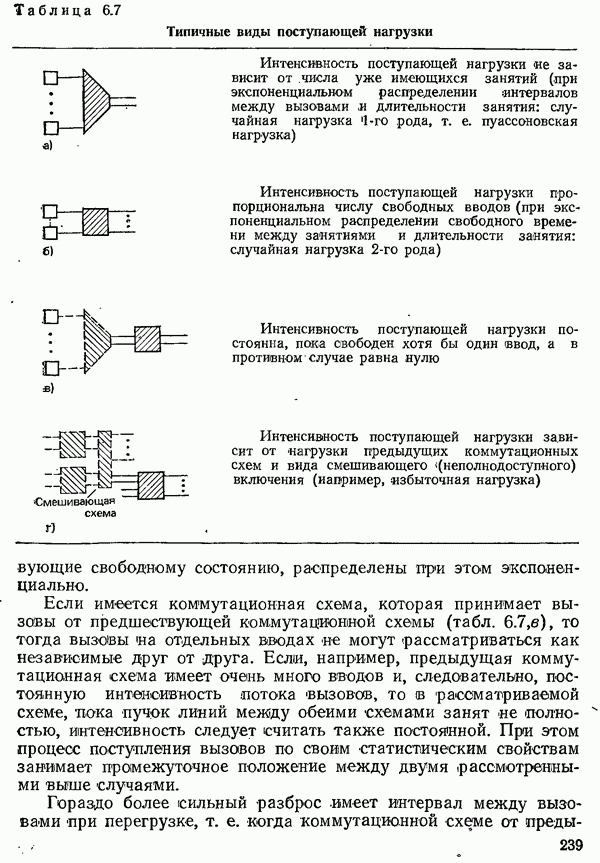
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
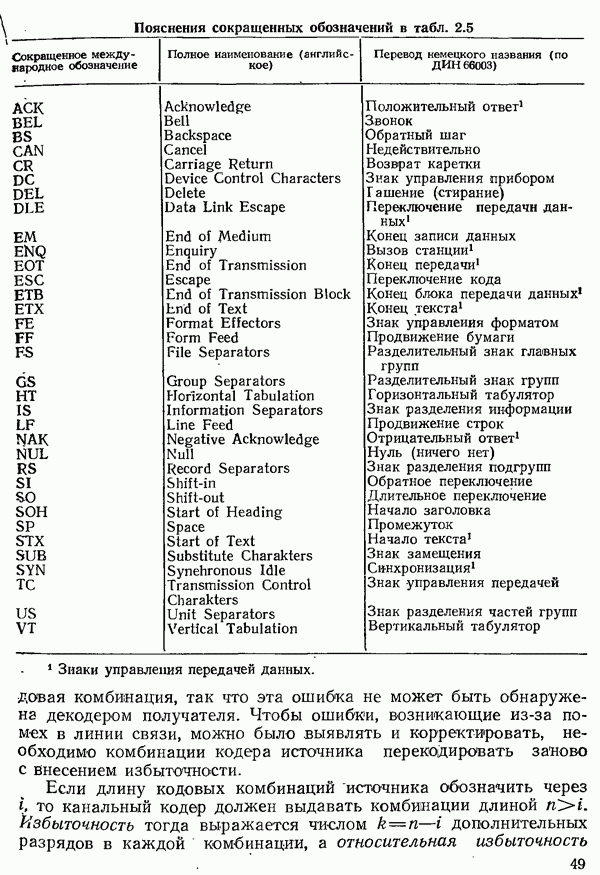
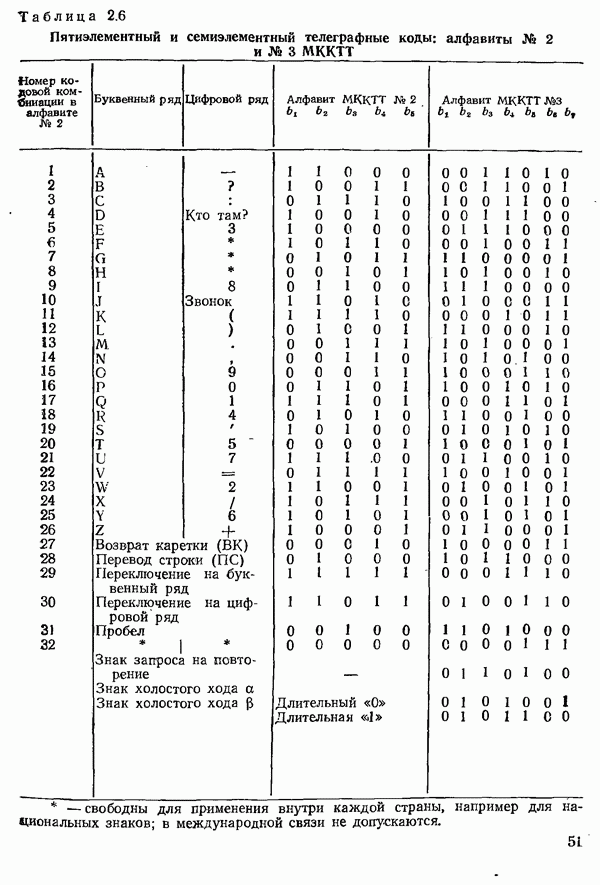
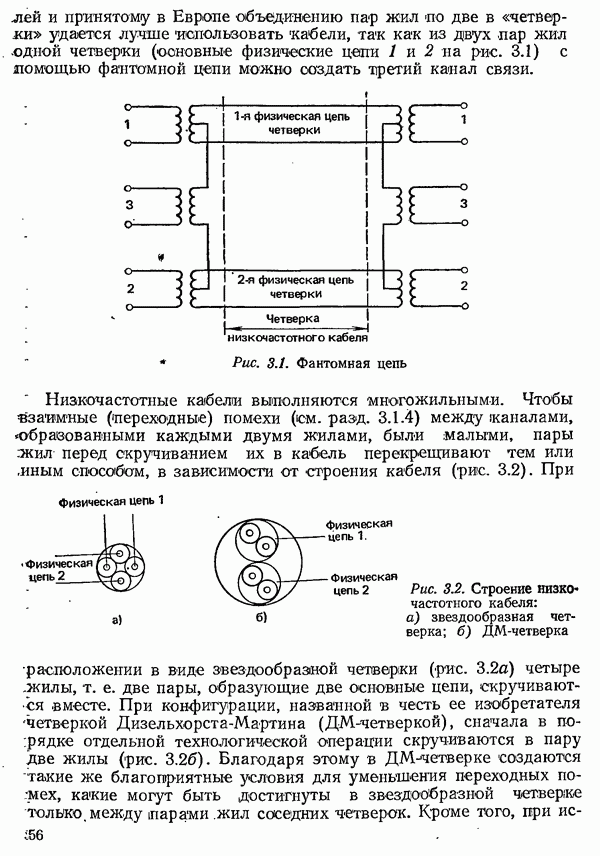
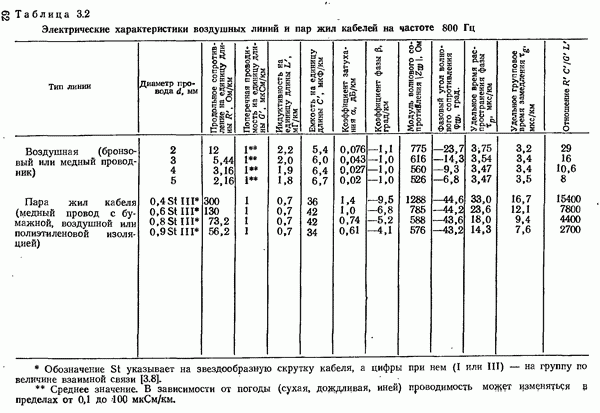
4.5.1. ВЕРОЯТНОСТЬ ОШИБКИ ПРИ УЧЕТЕ ТОЛЬКО ШУМА В КАНАЛЕ СВЯЗИ
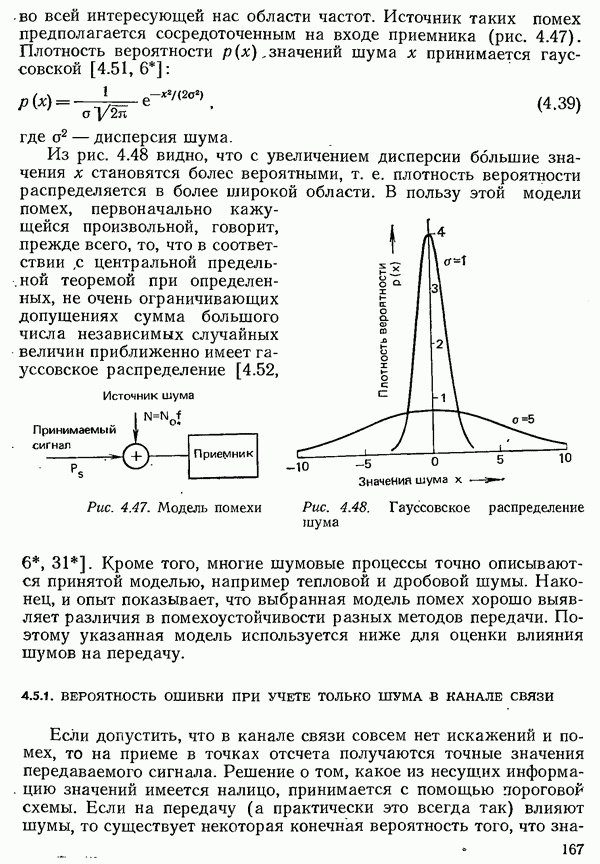
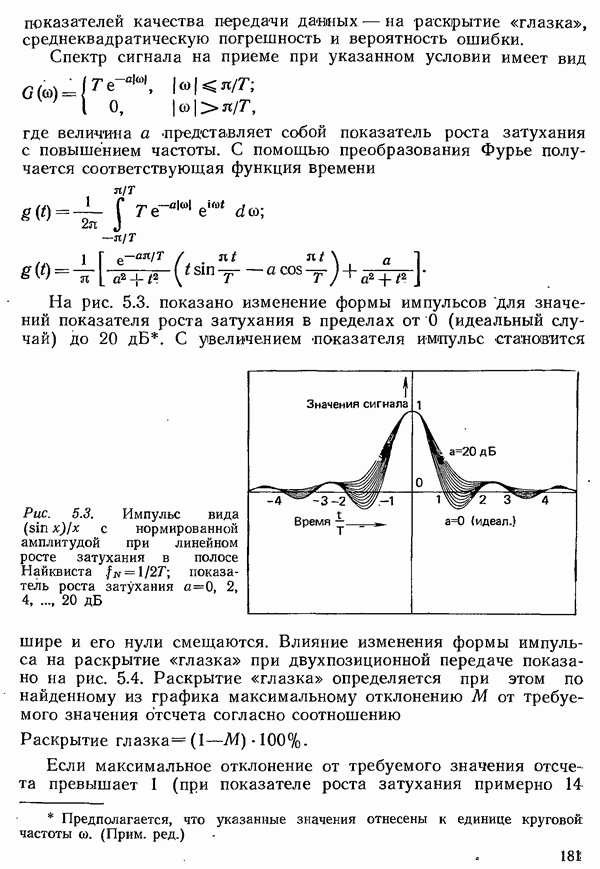
Если допустить, что в канале связи совсем нет искажений и помех, то на приеме в точках отсчета получаются точные значения передаваемого сигнала. Решение о том, какое из несущих информацию значений имеется налицо, принимается с помощью пороговой схемы. Если на передачу (а практически это всегда так) влияют шумы, то существует некоторая конечная вероятность того, что
значение сигнала изменится так, что приемник отождествит его с другим, отличным от посланного, состоянием сигнала, т. е. появится ошибка. Чтобы можно было установить, как велика вероятность такого рода ошибки в практической системе, целесообразно сначала исследовать систему передачи в первичной полосе частот.
Если передаются  различных уровней, которые могут принимать значения
различных уровней, которые могут принимать значения  и появляются одинаково часто, то средняя мощнссть
и появляются одинаково часто, то средняя мощнссть  ступенчатой функции времени, с помощью которой передаются данные, определяется выражением [4.53]
ступенчатой функции времени, с помощью которой передаются данные, определяется выражением [4.53]

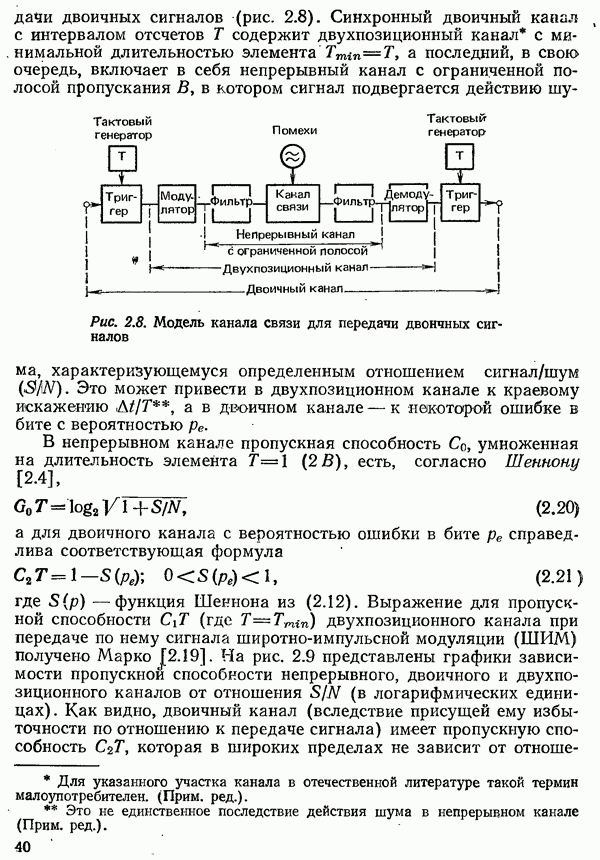
Чтобы ограничить передаваемую мощность используемой полосой частот канала связи, необходимо ограничить в передатчике бесконечно широкий спектр указанной функции времени. Одновременно желательно ограничение полосы и в приемнике с тем, чтобы сохранить малой мощность шума, пропорциональную полосе пропускания фильтра, установленного на приеме.
При последующем анализе системы передачи в первичной полосе частот будем предполагать, что ее общая передаточная функция имеет вид

т. е. имеет место прямоугольное ограничение полосы частот.
Как уже было отмечено выше, желательно иметь фильтры как на входе, так и на выходе канала связи. Поскольку, однако, общая передаточная функция  задана, ее разлагают на два сомножителя, один из которых
задана, ее разлагают на два сомножителя, один из которых  выражает передаточную функцию фильтра передатчика, а другой
выражает передаточную функцию фильтра передатчика, а другой  -фильтра приемника. При линейных методах передачи и при условии ограниченной мощности на входе канала оптимальным оказывается такое разложение, при котором фильтры передатчика и приемника имеют одинаковые по модулю передаточные функции [4.24]:
-фильтра приемника. При линейных методах передачи и при условии ограниченной мощности на входе канала оптимальным оказывается такое разложение, при котором фильтры передатчика и приемника имеют одинаковые по модулю передаточные функции [4.24]:

Фазовые характеристики фильтров при этом произвольны, за исключением одного условия — их сумма должна соответствовать передаточной функции  требуемой при выбранном методе передачи. При применении нелинейных методов модуляции — ЧМ и ФМ - найти оптимальное разложение не так просто [4.32].
требуемой при выбранном методе передачи. При применении нелинейных методов модуляции — ЧМ и ФМ - найти оптимальное разложение не так просто [4.32].
При указанных выше допущениях для идеального канала мощность сигнала в приемнике [4.24]

или с учетом (4.40)

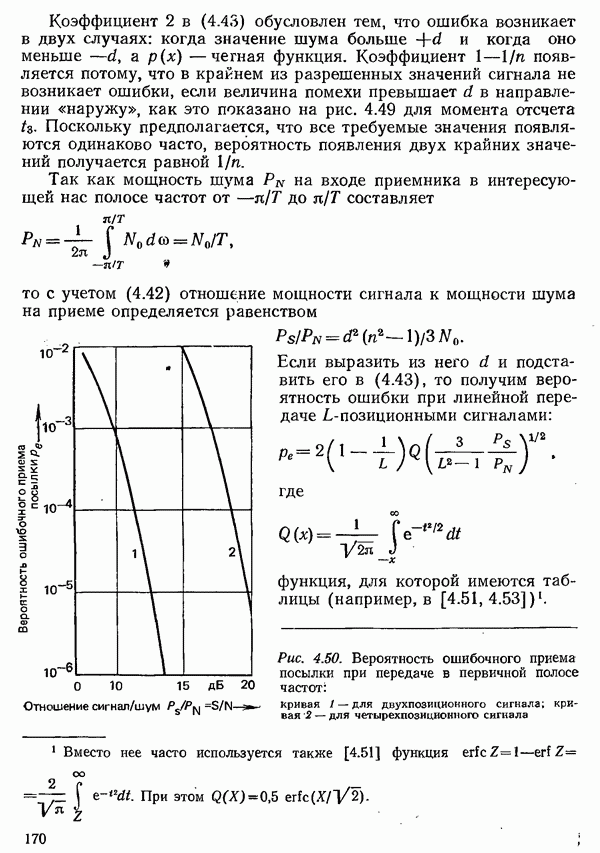
Если пороговые уровни в приемнике выбраны равными  то ошибка всегда возникает в том случае, когда значение шума в момент отсчета превысит
то ошибка всегда возникает в том случае, когда значение шума в момент отсчета превысит  .
.

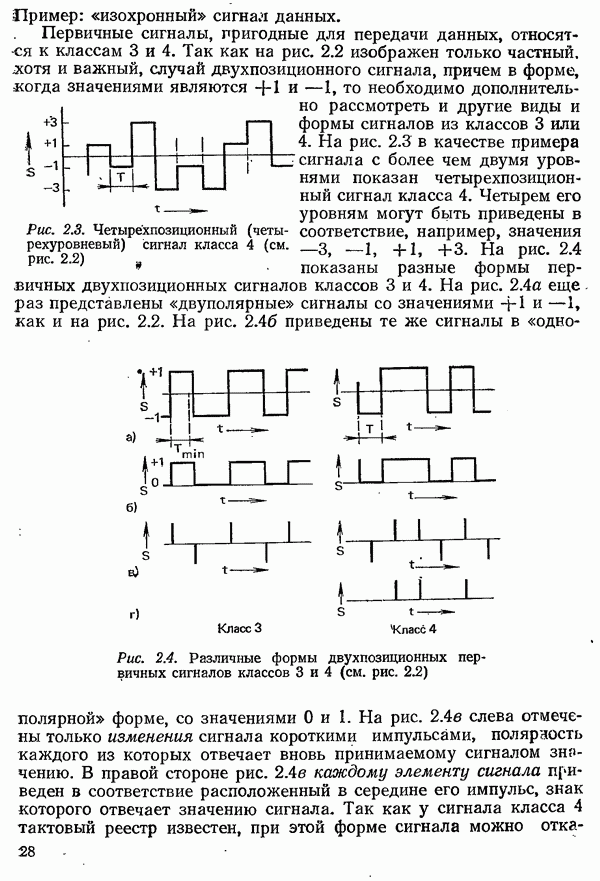
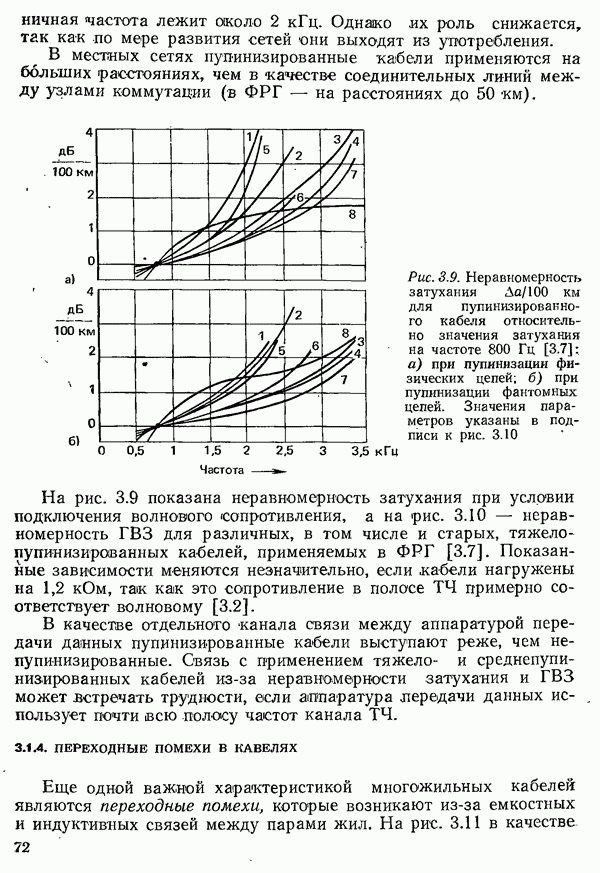
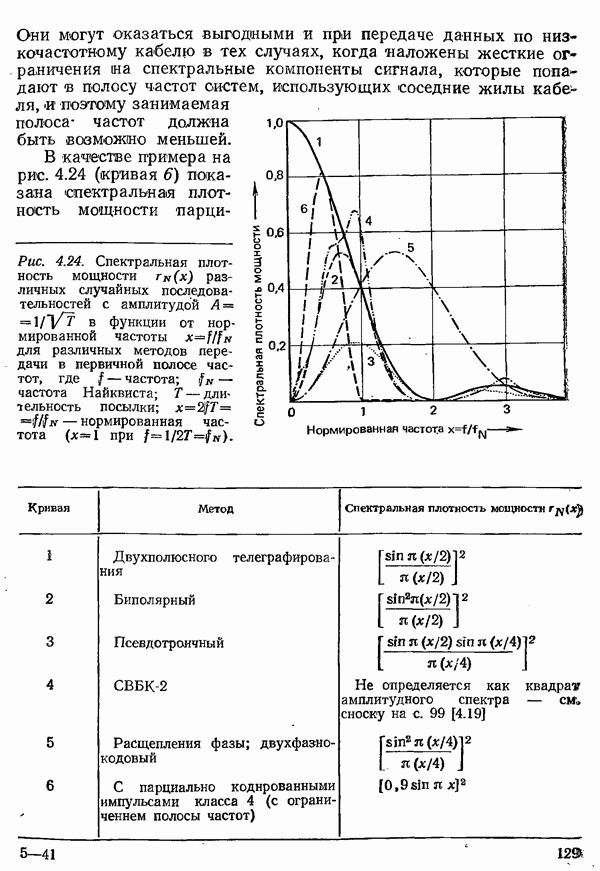
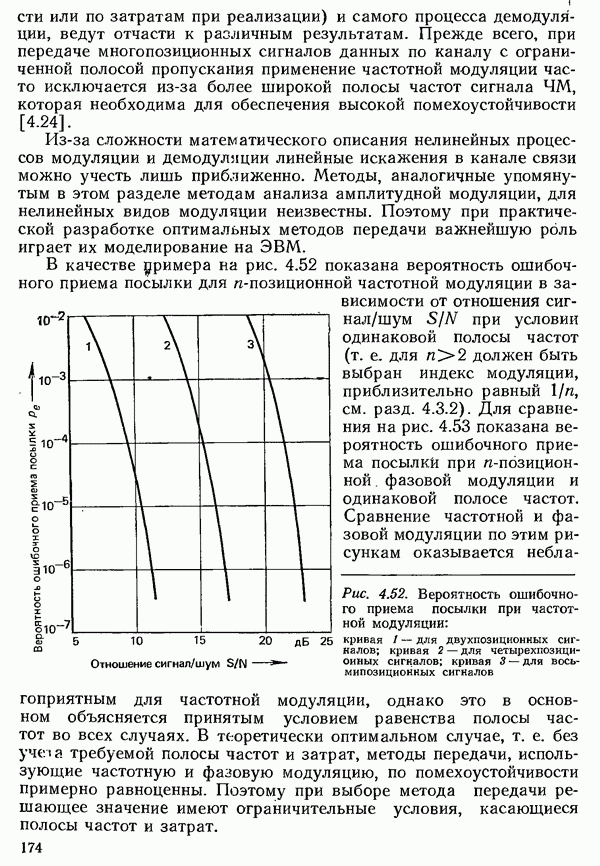
Рис. 4.49. Диаграмма, поясняющая правило решения при приеме четырехпозиционного сигнала
Для дисперсии шума на решающем блоке приемника (который согласно поясненному на рис. 4.49 алгоритму ставит в соответствие значению сигнала  в момент
в момент  близлежащее разрешенное значение) с учетом ограничения спектра шума входным фильтром приемника, соотношения (4.41) и спектральной плотности шума
близлежащее разрешенное значение) с учетом ограничения спектра шума входным фильтром приемника, соотношения (4.41) и спектральной плотности шума  получаем выражение
получаем выражение

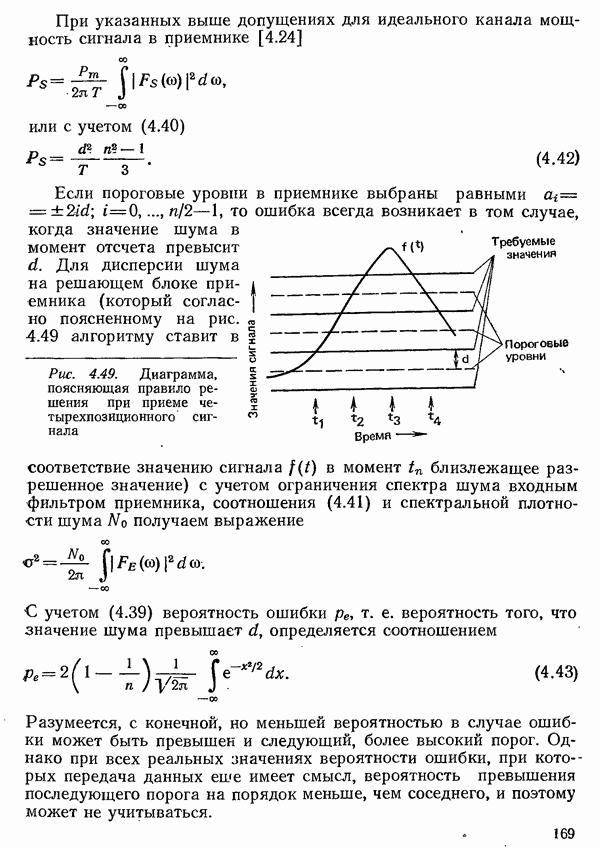
 учетом (4.39) вероятность ошибки
учетом (4.39) вероятность ошибки  е. вероятность того, что значение шума превышает
е. вероятность того, что значение шума превышает  определяется соотношением
определяется соотношением

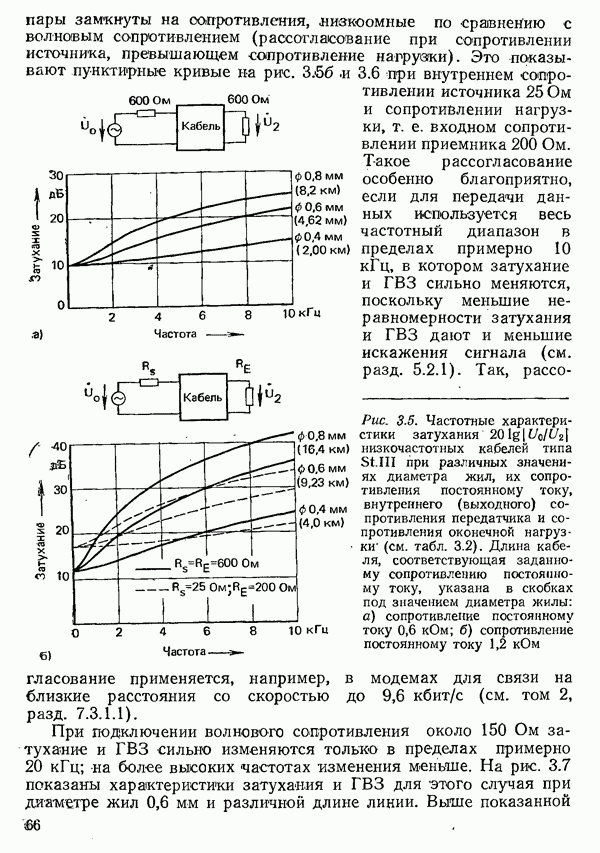
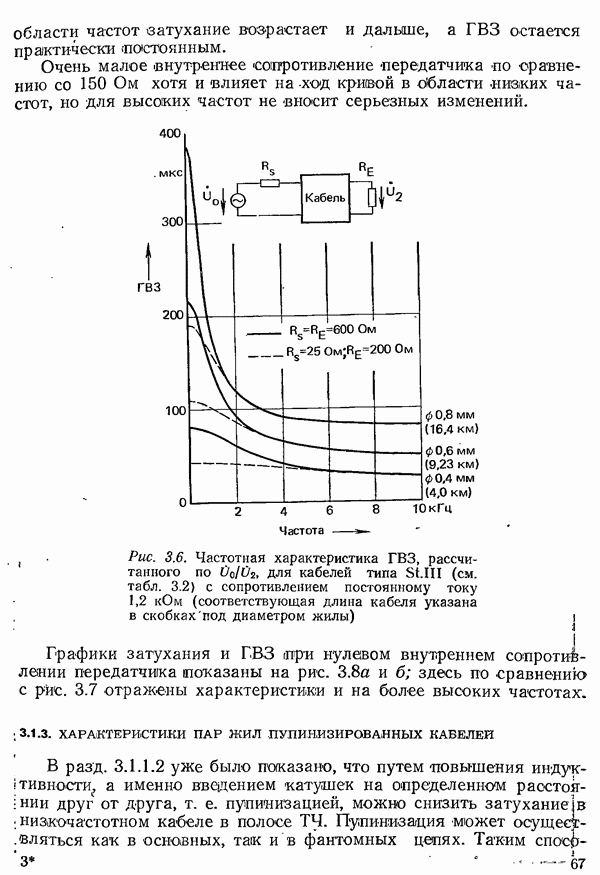
Разумеется, с конечной, но меньшей вероятностью в случае ошибки может быть превышен и следующий, более высокий порог. Однако при всех реальных значениях вероятности ошибки, при которых передача данных еще имеет смысл, вероятность превышения последующего порога на порядок меньше, чем соседнего, и поэтому может не учитываться.
Коэффициент 2 в (4.43) обусловлен тем, что ошибка возникает в двух случаях: когда значение шума больше  и когда оно меньше
и когда оно меньше  - четная функция. Коэффициент
- четная функция. Коэффициент  появляется потому, что в крайнем из разрешенных значений сигнала не возникает ошибки, если величина помехи превышает
появляется потому, что в крайнем из разрешенных значений сигнала не возникает ошибки, если величина помехи превышает  в направлении «наружу», как это показано на рис. 4.49 для момента отсчета
в направлении «наружу», как это показано на рис. 4.49 для момента отсчета  Поскольку предполагается, что все требуемые значения появляются одинаково часто, вероятность появления двух крайних значений получается равной
Поскольку предполагается, что все требуемые значения появляются одинаково часто, вероятность появления двух крайних значений получается равной 
Так как мощность шума  на входе приемника в интересующей нас полосе частот от
на входе приемника в интересующей нас полосе частот от  до
до  составляет
составляет

то с учетом (4.42) отношение мощности сигнала к мощности шума на приеме определяется равенством

Если выразить из него  и подставить его в (4.43), то получим вероятность ошибки при линейной передаче
и подставить его в (4.43), то получим вероятность ошибки при линейной передаче  -позиционными сигналами:
-позиционными сигналами:

где

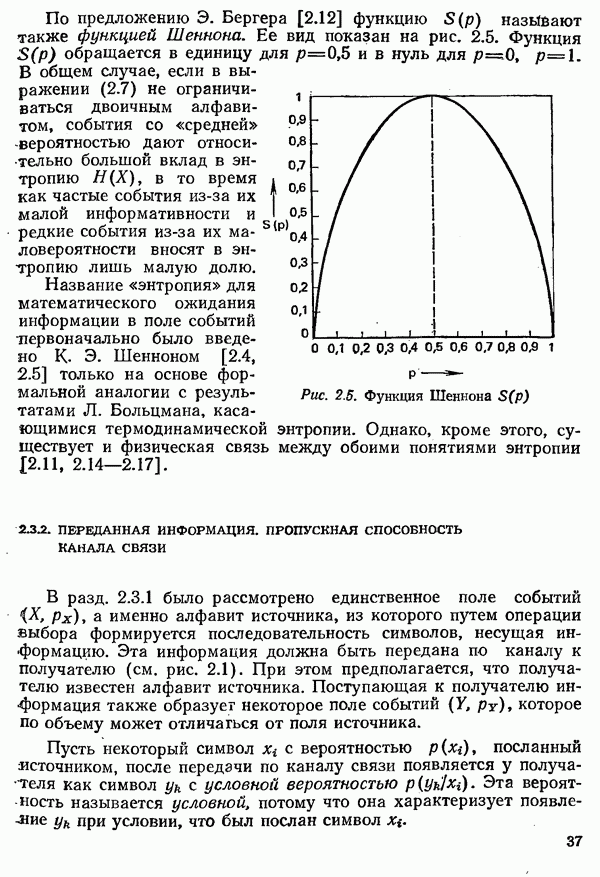
функция, для которой имеются таблицы (например, в [4.51, 4.53]).

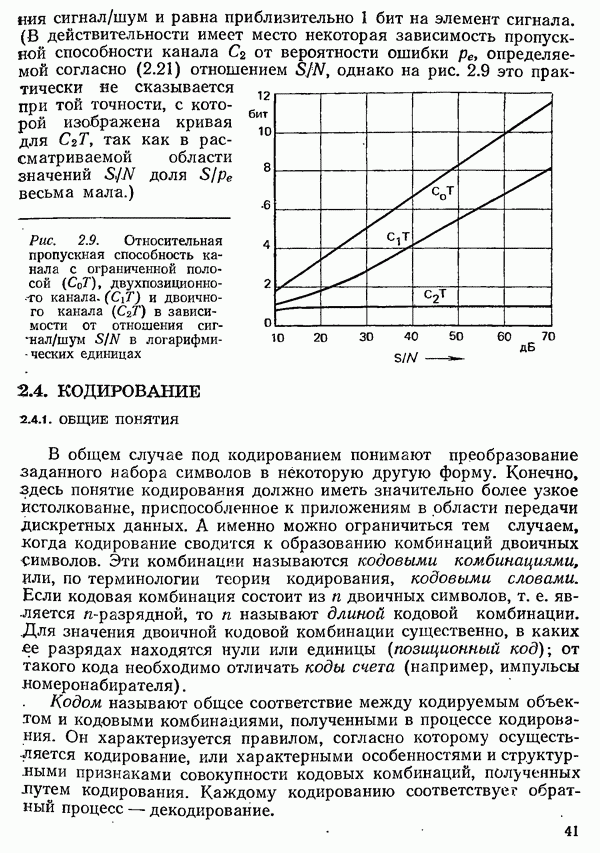
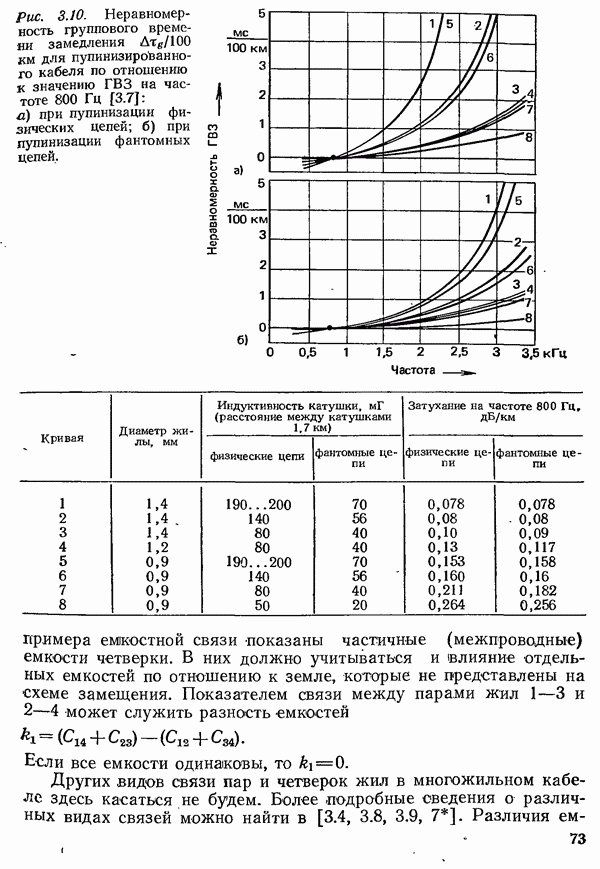
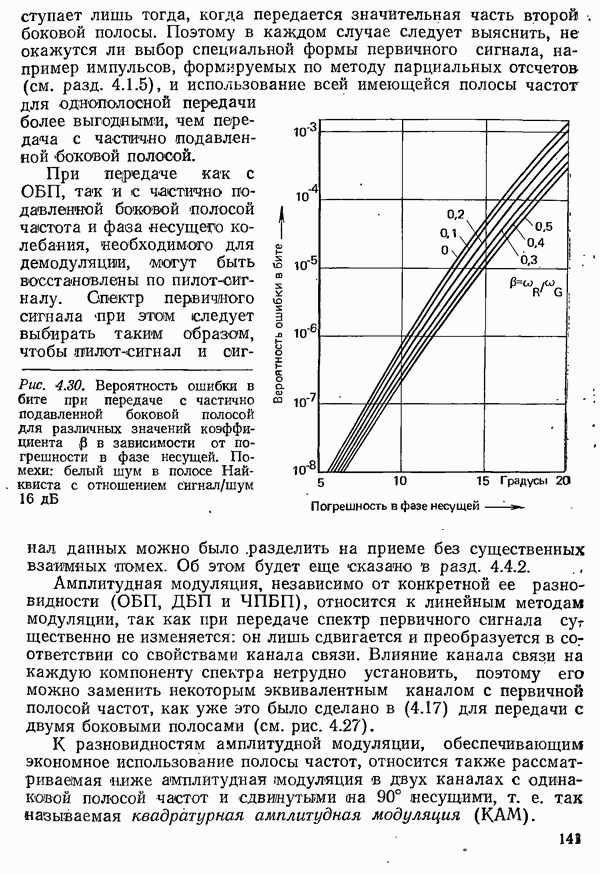
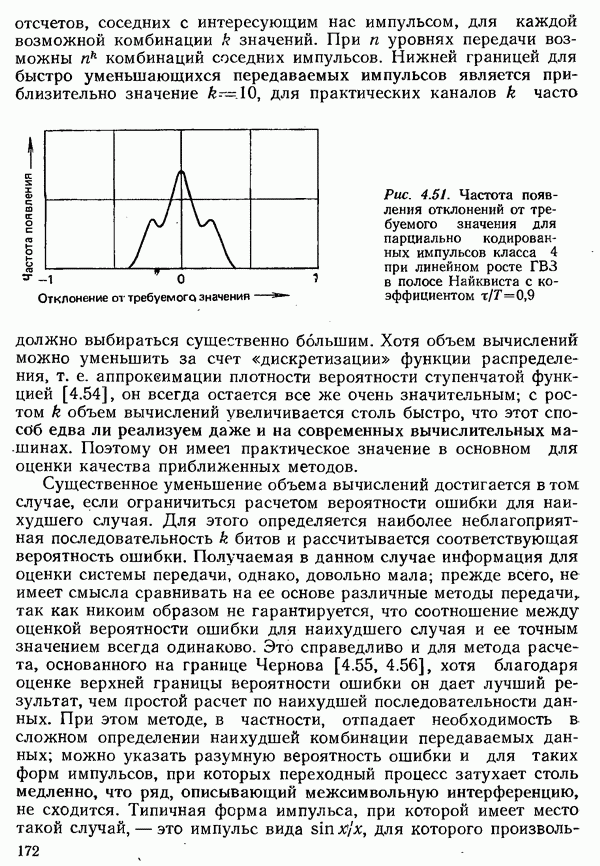
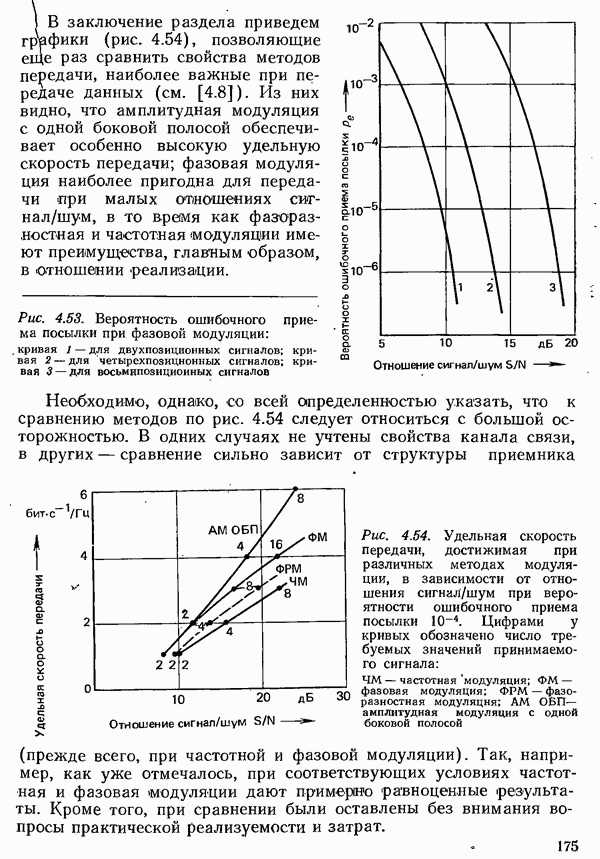
Рис. 4.50. Вероятность ошибочного приема посылки при передаче в первичной полосе частот: кривая 1 — для двухпозиционного сигнала; кривая 2 — для четырехпозиционного сигнала
Полученная формула выражает вероятность ошибочного приема одной посылки, т. е. ошибку на одном тактовом интервале. При двоичной передаче она совпадает с вероятностью ошибки в бите. При многопозиционной передаче вероятность ошибки  бите, зависит от вероятности ошибочного приема посылки и от применяемого кодирования (см. разд. 4.1.6). Поэтому в дальнейшем для многопозиционных сигналов указывается вероятность ошибочного приема посылки. Ее зависимость от отношения сига а
бите, зависит от вероятности ошибочного приема посылки и от применяемого кодирования (см. разд. 4.1.6). Поэтому в дальнейшем для многопозиционных сигналов указывается вероятность ошибочного приема посылки. Ее зависимость от отношения сига а  для двухпозиционных и четырехпозицио ноных сигналов показала на рис. 4.50.
для двухпозиционных и четырехпозицио ноных сигналов показала на рис. 4.50.
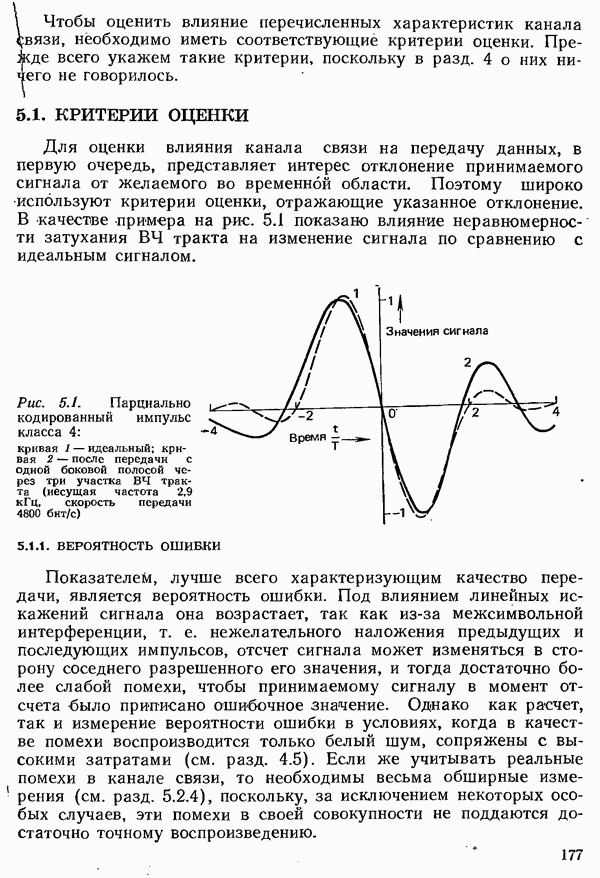
Часто, однако, представляет интерес не только вероятность ошибочного приема посылки при заданном отношении сигнал/шум, но и, наоборот, отношение сигнал/шум, при котором обеспечен прием с заданной вероятностью ошибки. Для этого случая получены простые и обычно достаточные по точности приближенные формулы 
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ К РУССКОМУ ИЗДАНИЮ
- 1. Обзор
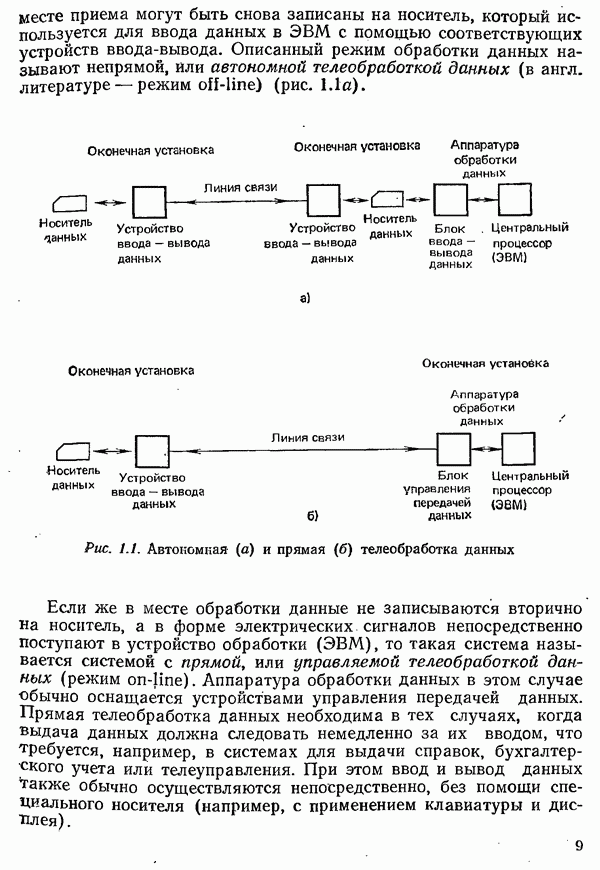
- 1.1. ОБРАБОТКА И ТЕЛЕОБРАБОТКА ДАННЫХ
- 1.2. АВТОНОМНАЯ И УПРАВЛЯЕМАЯ ТЕЛЕОБРАБОТКА ДАННЫХ
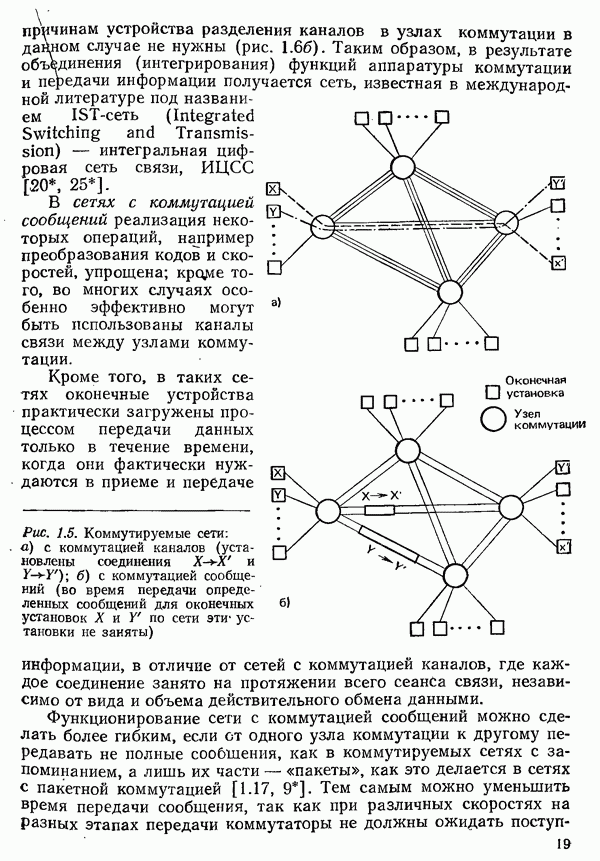
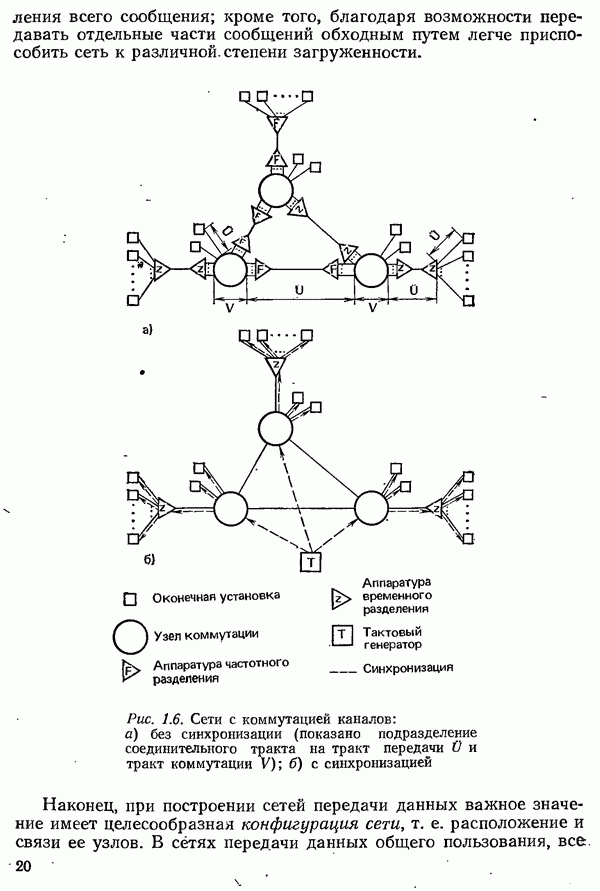
- 1.3. КЛАССИФИКАЦИЯ СИСТЕМ ТЕЛЕОБРАБОТКИ ДАННЫХ
- 1.4. СТРУКТУРА СИСТЕМ ТЕЛЕОБРАБОТКИ ДАННЫХ
- 1.5. ТРЕБОВАНИЯ К ТЕХНИКЕ СВЯЗИ И КОММУТАЦИИ В СИСТЕМАХ ТЕЛЕОБРАБОТКИ ДАННЫХ
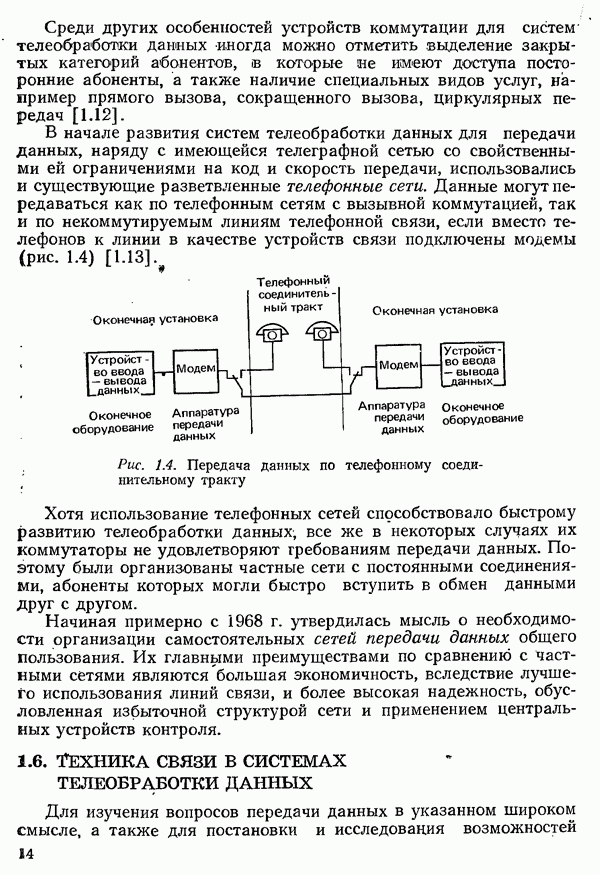
- 1.6. ТЕХНИКА СВЯЗИ В СИСТЕМАХ ТЕЛЕОБРАБОТКИ ДАННЫХ
- 2. Основные понятия техники связи
- 2.2. СИГНАЛЫ
- 2.2.2. ДИСКРЕТИЗАЦИЯ, КВАНТОВАНИЕ, ВЛИЯНИЕ ШУМОВ
- 2.2.3. СВОЙСТВА ПЕРВИЧНЫХ СИГНАЛОВ ДЛЯ ПЕРЕДАЧИ ДАННЫХ
- 2.2.3.2. ВРЕМЕННЫЕ СООТНОШЕНИЯ МЕЖДУ СИГНАЛАМИ
- 2.2.4. РЕЖИМЫ РАБОТЫ ПРИ ПЕРЕДАЧЕ СИГНАЛОВ
- 2.3. НЕКОТОРЫЕ ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ИНФОРМАЦИИ
- 2.3.2. ПЕРЕДАННАЯ ИНФОРМАЦИЯ. ПРОПУСКНАЯ СПОСОБНОСТЬ КАНАЛА СВЯЗИ
- 2.4. КОДИРОВАНИЕ
- 2.4.3. КОДИРОВАНИЕ ИСТОЧНИКА
- 2.4.4. КАНАЛЬНОЕ КОДИРОВАНИЕ
- 3. Каналы связи
- 3.1. КАНАЛЫ БЛИЖНЕЙ СВЯЗИ
- 3.1.1.1. СВОЙСТВА И ПАРАМЕТРЫ ПРОВОДНЫХ ЛИНИЙ СВЯЗИ
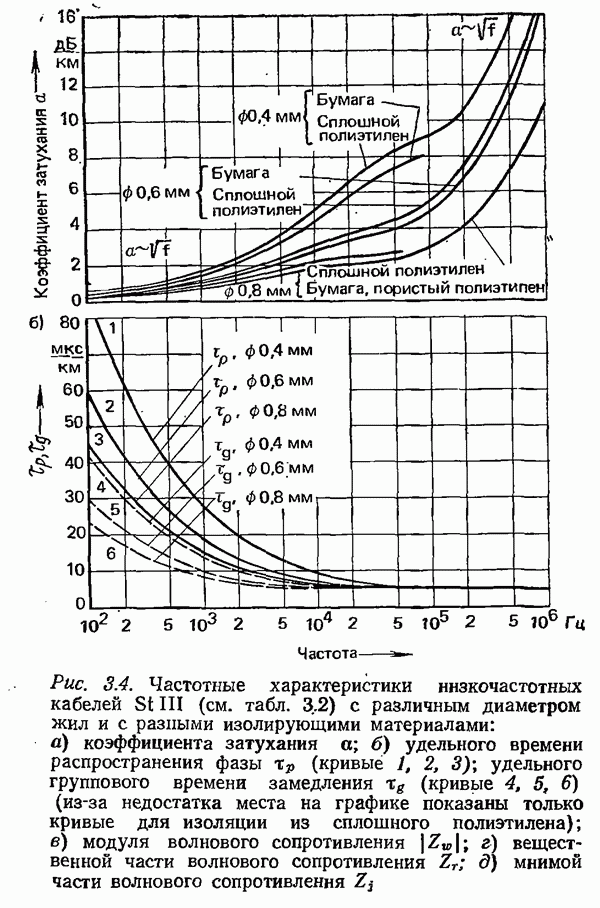
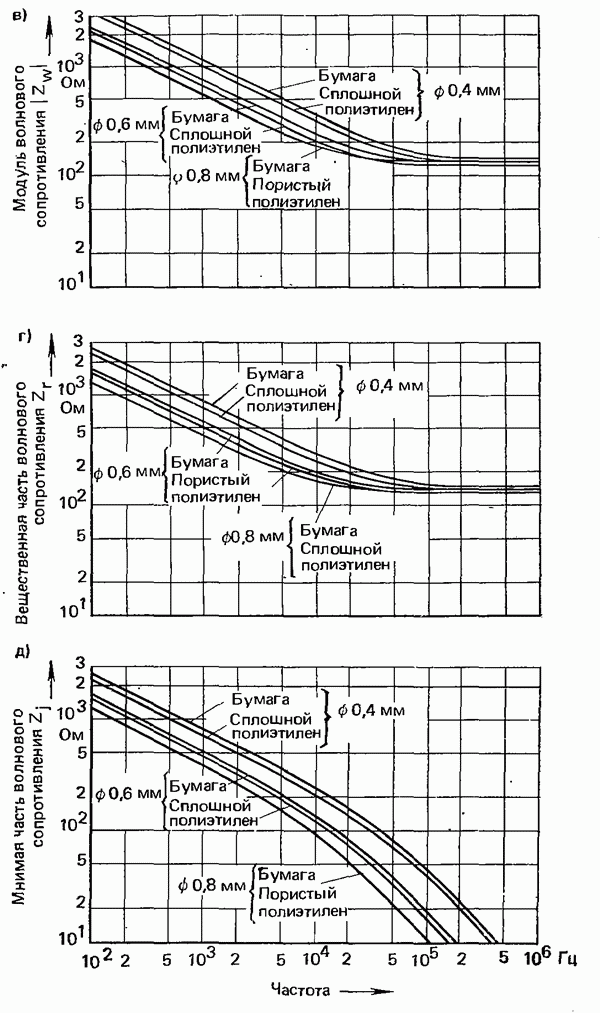
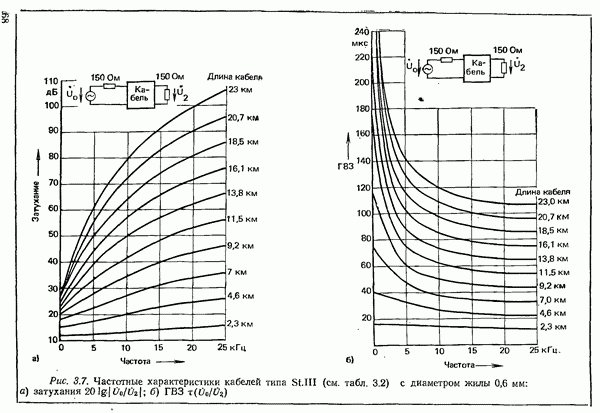
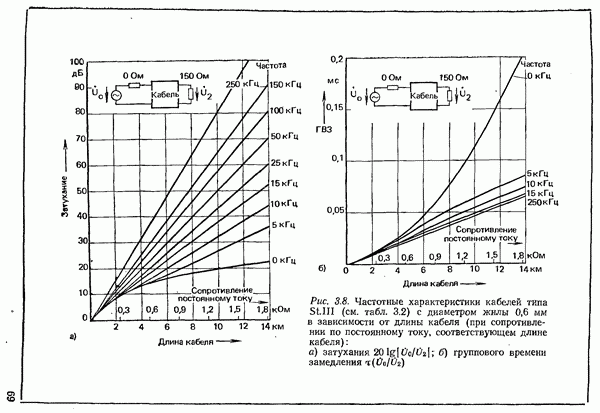
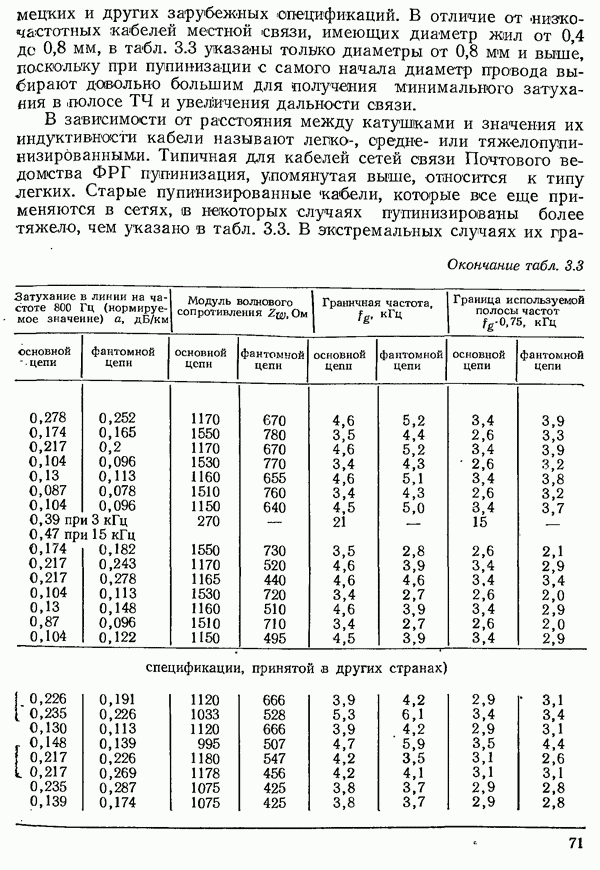
- 3.1.1.2. УМЕНЬШЕНИЕ ЗАТУХАНИЯ ПУТЕМ УВЕЛИЧЕНИЯ ИНДУКТИВНОСТИ. ПУПИНИЗАЦИЯ
- 3.1.2. ХАРАКТЕРИСТИКИ ПАР ЖИЛ НИЗКОЧАСТОТНЫХ КАБЕЛЕЙ
- 3.1.3. ХАРАКТЕРИСТИКИ ПАР ЖИЛ ПУПИЯИЗИРОВАННЫХ КАБЕЛЕЙ
- 3.1.4. ПЕРЕХОДНЫЕ ПОМЕХИ В КАБЕЛЯХ
- 3.1.5. НАПРЯЖЕНИЯ ШУМОВ НА ПАРАХ ШИЛ КАБЕЛЕЙ
- 3.2. КАНАЛЫ ДАЛЬНЕЙ СВЯЗИ
- 3.2.2. КАНАЛЫ ТОНАЛЬНОЙ ЧАСТОТЫ
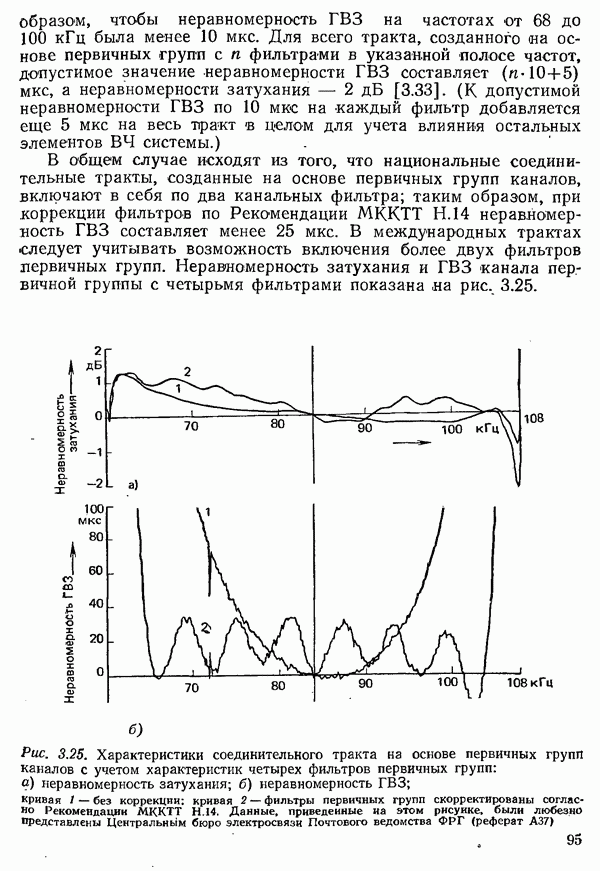
- 3.2.3. СОЕДИНИТЕЛЬНЫЕ ТРАКТЫ НА ОСНОВЕ ПЕРВИЧНЫХ ГРУПП КАНАЛОВ
- 4. Методы передачи данных
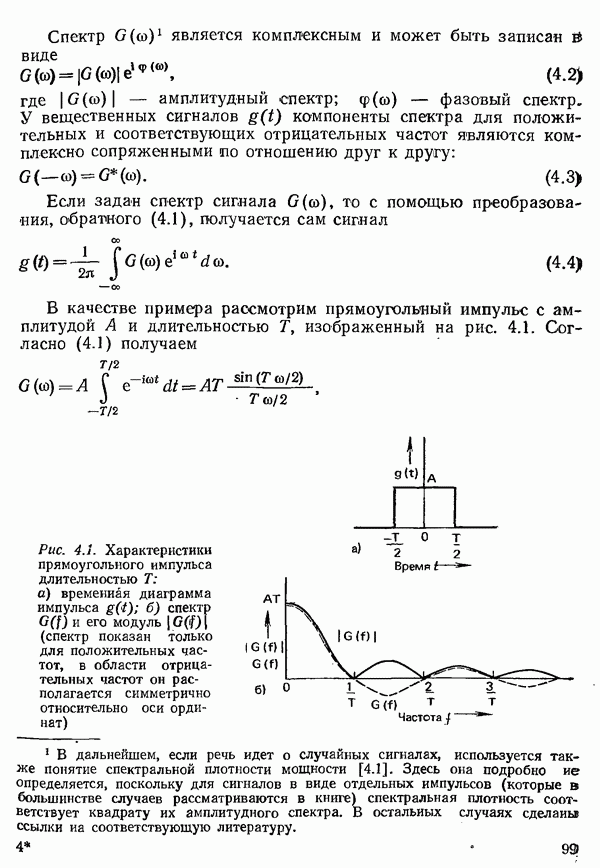
- 4.1.1. СИГНАЛЫ И СПЕКТРЫ
- 4.1.2. РЯД ФУРЬЕ
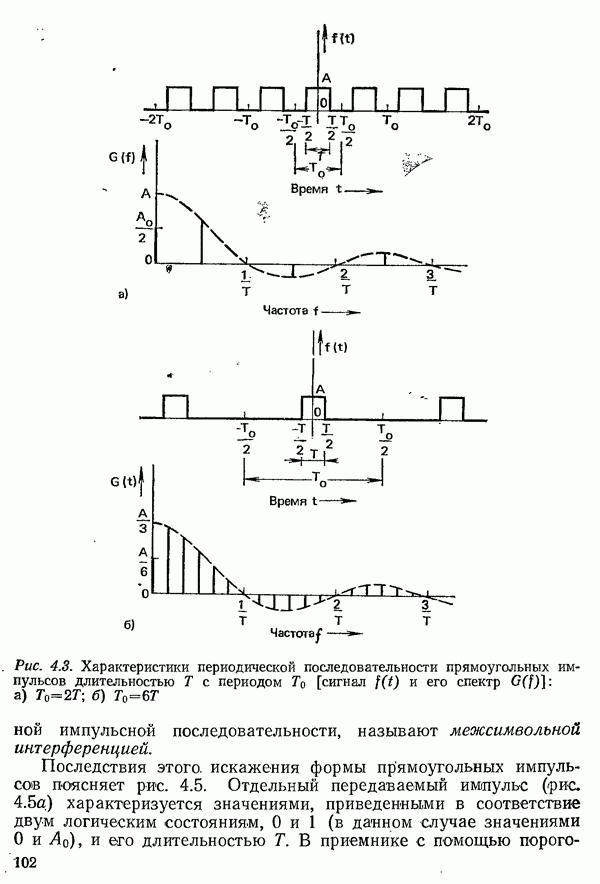
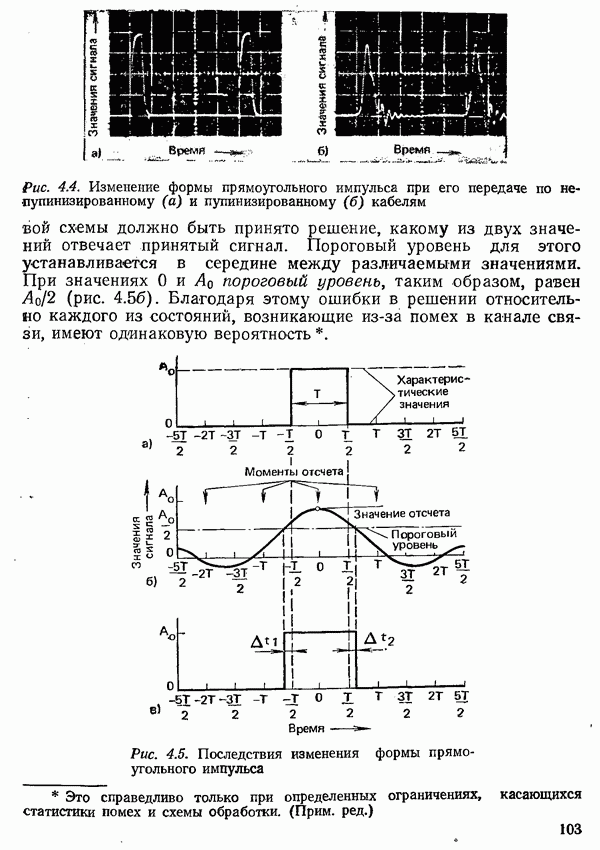
- 4.1.3. ИСКАЖЕНИЯ ФОРМЫ ИМПУЛЬСОВ ПРИ ОГРАНИЧЕНИИ ПОЛОСЫ ЧАСТОТ
- 4.1.4. УСЛОВИЯ НАЙКВИСТА
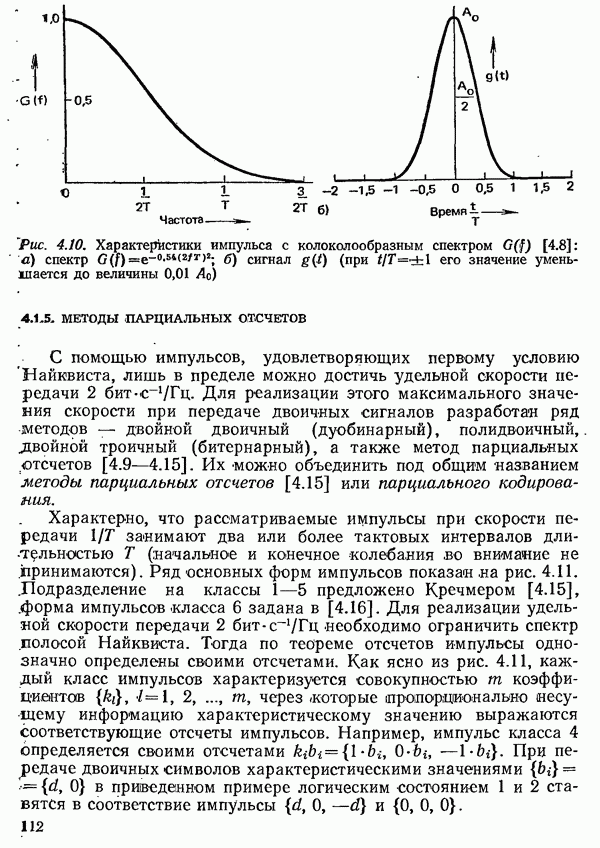
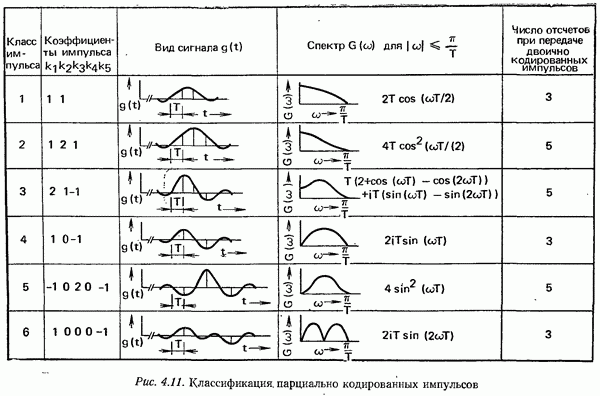
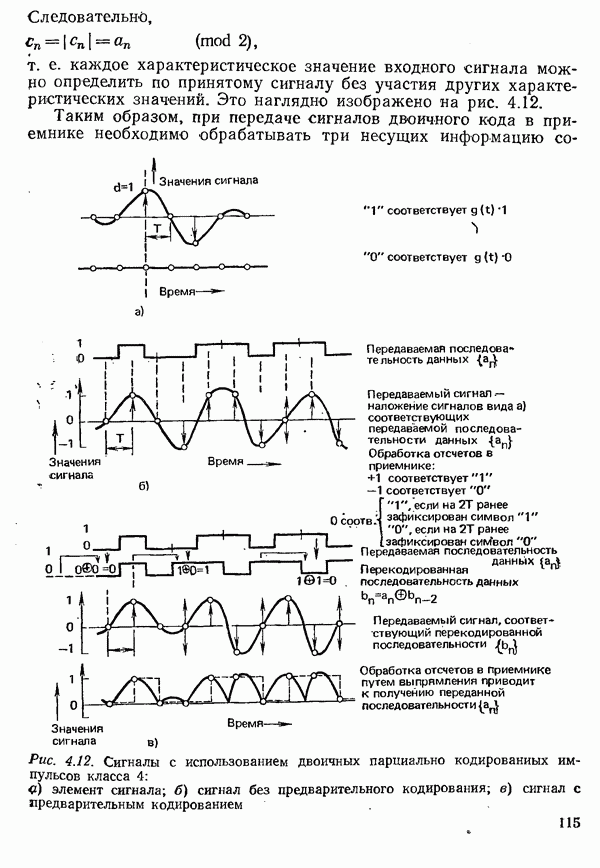
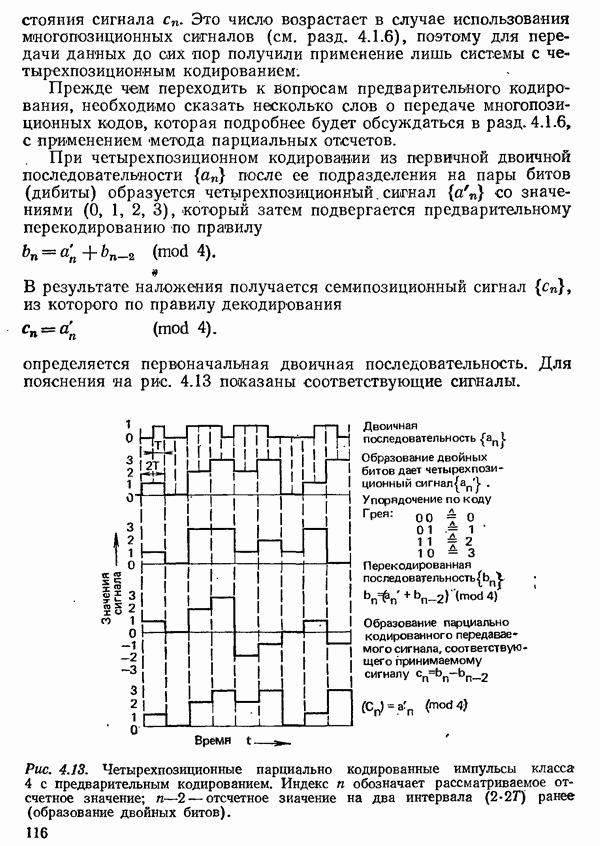
- 4.1.5. МЕТОДЫ ПАРЦИАЛЬНЫХ ОТСЧЕТОВ
- 4.1.6. ПЕРЕДАЧА МНОГОПОЗИЦИОННЫХ СИГНАЛОВ
- 4.2. МЕТОДЫ ПЕРЕДАЧИ В ПЕРВИЧНОЙ ПОЛОСЕ ЧАСТОТ
- 4.2.1. МЕТОДЫ С ПРИМЕНЕНИЕМ ДВУПОЛЯРНЫХ И ОДНОПОЛЯРНЫХ ИМПУЛЬСОВ
- 4.2.2. БИПОЛЯРНЫЙ МЕТОД
- 4.2.3. ПСЕВДОТРОИЧНЫЕ МЕТОДЫ
- 4.2.4. МЕТОДЫ С ПРИМЕНЕНИЕМ БИПОЛЯРНЫХ КОДОВ ВЫСОКОЙ ПЛОТНОСТИ
- 4.2.5. ДВУХФАЗНЫЙ МЕТОД. ИЛИ МЕТОД РАСЩЕПЛЕНИЯ ФАЗЫ
- 4.2.6. ДВУХФАЗНО-КОДОВЫЙ МЕТОД
- 4.2.7. МЕТОДЫ ПАРЦИАЛЬНЫХ ОТСЧЕТОВ
- 4.3. МЕТОДЫ ПЕРЕДАЧИ С ПРИМЕНЕНИЕМ МОДУЛЯЦИИ
- 4.3.1. АМПЛИТУДНАЯ МОДУЛЯЦИЯ
- 4.3.1.2. АМПЛИТУДНАЯ МОДУЛЯЦИЯ С ОДНОЙ БОКОВОЙ ПОЛОСОЙ И С ЧАСТИЧНО ПОДАВЛЕННОЙ БОКОВОЙ ПОЛОСОЙ
- 4.3.1.3. КВАДРАТУРНАЯ АМПЛИТУДНАЯ МОДУЛЯЦИЯ
- 4.3.1.4. УДЕЛЬНАЯ СКОРОСТЬ ПЕРЕДАЧИ ПРИ АМПЛИТУДНОЙ МОДУЛЯЦИИ
- 4.3.2. ЧАСТОТНАЯ МОДУЛЯЦИЯ
- 4.3.2.1. УДЕЛЬНАЯ СКОРОСТЬ ПЕРЕДАЧИ ПРИ ЧАСТОТНОЙ МОДУЛЯЦИИ
- 4.3.3. ФАЗОВАЯ МОДУЛЯЦИЯ
- 4.4. ВОССТАНОВЛЕНИЕ ТАКТОВ И НЕСУЩЕЙ
- 4.4.2. ВОССТАНОВЛЕНИЕ ЧАСТОТЫ И ФАЗЫ НЕСУЩЕЙ
- 4.5. ВЕРОЯТНОСТЬ ОШИБКИ ПРИ НАЛИЧИИ ПОМЕХ
- 4.5.1. ВЕРОЯТНОСТЬ ОШИБКИ ПРИ УЧЕТЕ ТОЛЬКО ШУМА В КАНАЛЕ СВЯЗИ
- 4.5.2. ВЕРОЯТНОСТЬ ОШИБКИ С УЧЕТОМ ЛИНЕЙНЫХ ИСКАЖЕНИЙ
- 4.5.3. ВЕРОЯТНОСТЬ ОШИБКИ С УЧЕТОМ ПРОЦЕССОВ МОДУЛЯЦИИ И ДЕМОДУЛЯЦИИ
- 5. Учет свойств реальных каналов связи при передаче данных
- 5.2. ВЛИЯНИЕ ХАРАКТЕРИСТИК КАНАЛОВ СВЯЗИ НА ПЕРЕДАЧУ ДАННЫХ
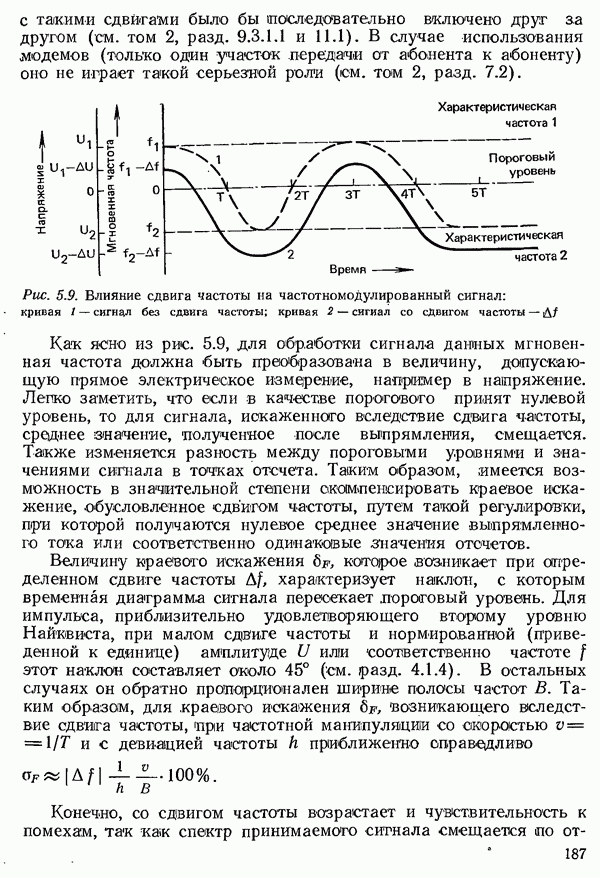
- 5.2.2. СДВИГИ ЧАСТОТЫ
- 5.2.3. ФАЗОВОЕ ДРОЖАНИЕ
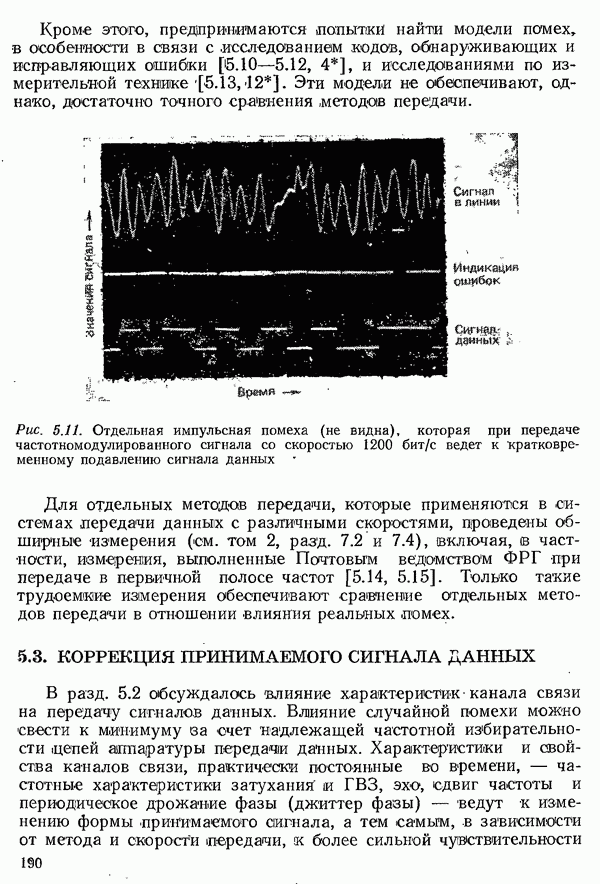
- 5.2.4. ВЛИЯНИЕ РЕАЛЬНЫХ ПОМЕХ
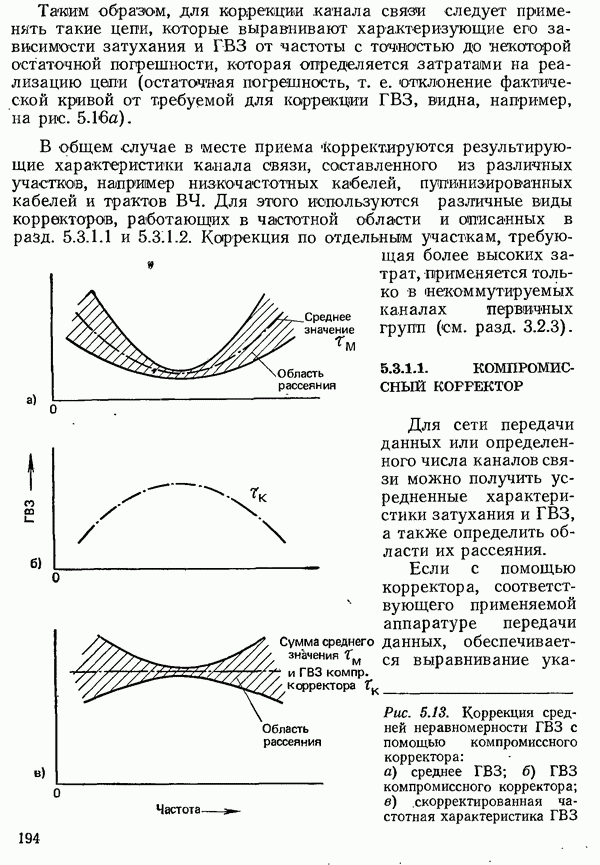
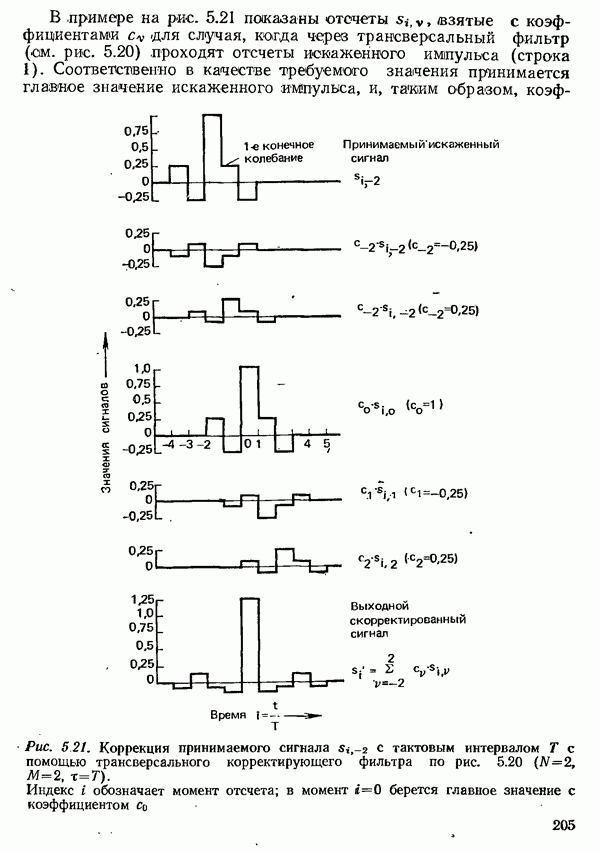
- 5.3. КОРРЕКЦИЯ ПРИНИМАЕМОГО СИГНАЛА ДАННЫХ
- 5.3.1. КОРРЕКЦИЯ ПРИНИМАЕМОГО СИГНАЛА ДАННЫХ В ЧАСТОТНОЙ ОБЛАСТИ
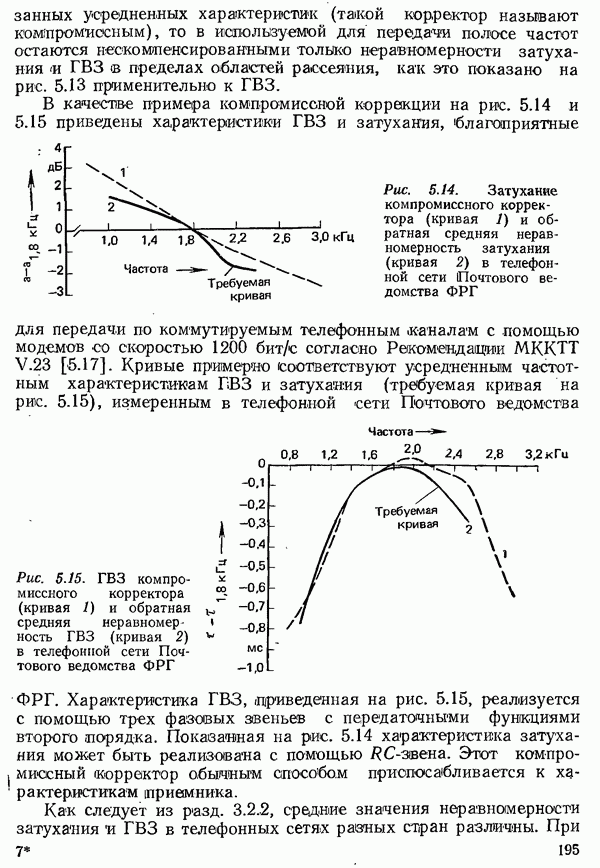
- 5.3.1.1. КОМПРОМИССНЫЙ КОРРЕКТОР
- 5.3.1.2. НАСТРАИВАЕМЫЙ ЧАСТОТНЫЙ КОРРЕКТОР СИГНАЛОВ ДАННЫХ
- 5.3.2. КОРРЕКЦИЯ ПРИНИМАЕМОГО СИГНАЛА ДАННЫХ ВО ВРЕМЕННОЙ ОБЛАСТИ
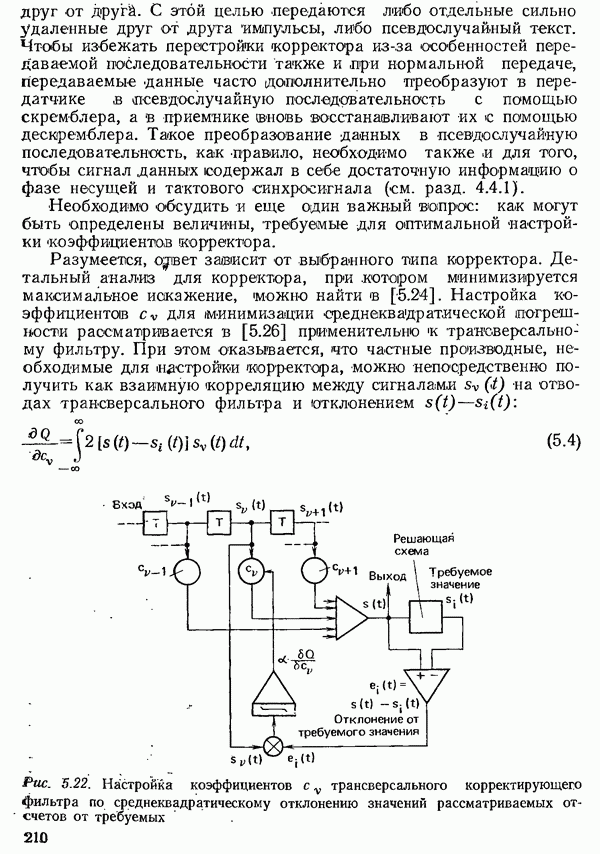
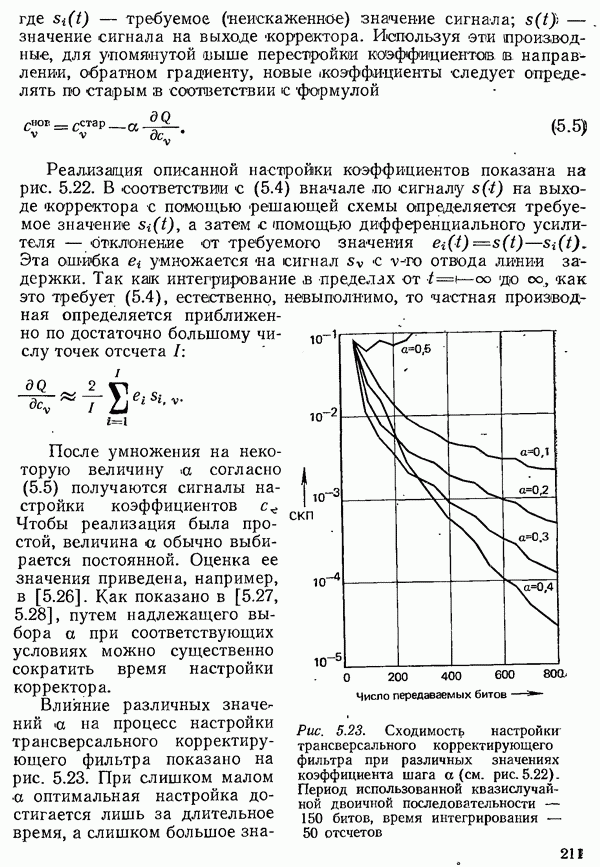
- 5.3.2.2. КРИТЕРИИ НАСТРОЙКИ КОРРЕКТОРА ВО ВРЕМЕННОЙ ОБЛАСТИ
- 5.3.2.3. АВТОМАТИЧЕСКАЯ НАСТРОЙКА ТРАНСВЕРСАЛЬНОГО КОРРЕКТИРУЮЩЕГО ФИЛЬТРА
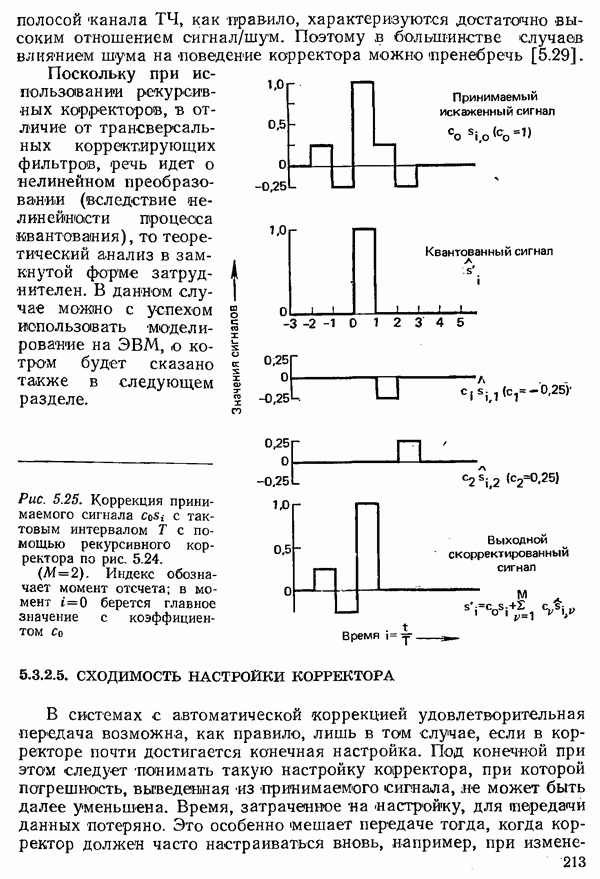
- 5.3.2.4. РЕКУРСИВНЫЙ КОРРЕКТОР
- 5.3.2.5. СХОДИМОСТЬ НАСТРОЙКИ КОРРЕКТОРА
- 5.3.2.6. КОРРЕКТОР ДЛЯ СПЕЦИАЛЬНЫХ МЕТОДОВ ПЕРЕДАЧИ
- 6. Основы коммутации данных
- 6.1.2. МЕТОДЫ КОММУТАЦИИ
- 6.1.3. СПОСОБЫ КОММУТАЦИИ КАНАЛОВ
- 6.1.4. СИГНАЛИЗАЦИЯ
- 6.1.5. УПРАВЛЕНИЕ ПРОЦЕССАМИ СОЕДИНЕНИЯ И РАЗЪЕДИНЕНИЯ
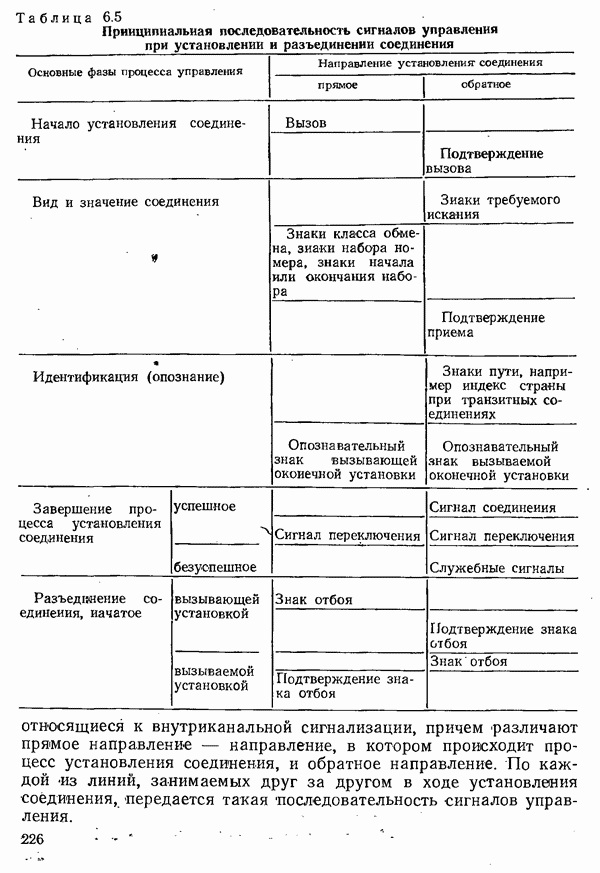
- 6.1.6. ПОДРАЗДЕЛЕНИЕ ЦЕПЕЙ КОММУТАЦИИ КАНАЛОВ
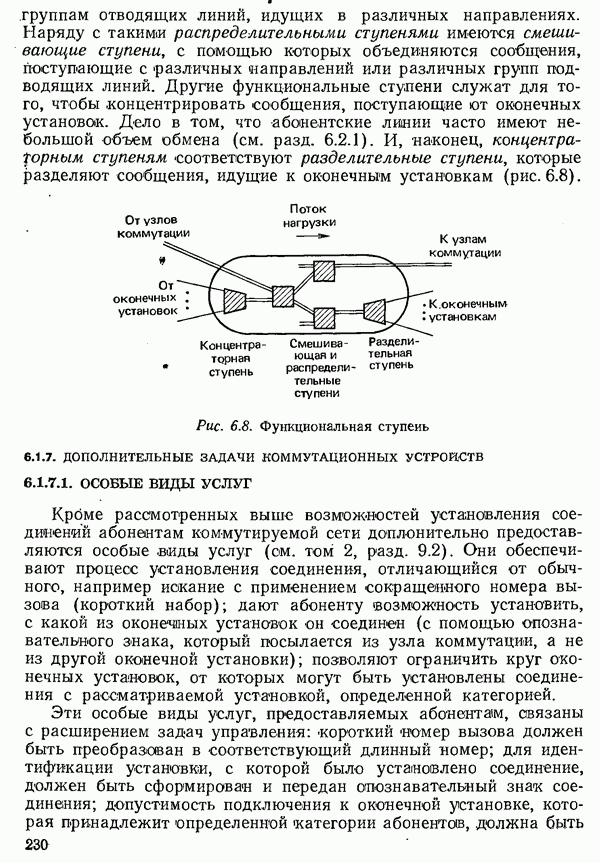
- 6.1.7. ДОПОЛНИТЕЛЬНЫЕ ЗАДАЧИ КОММУТАЦИОННЫХ УСТРОЙСТВ
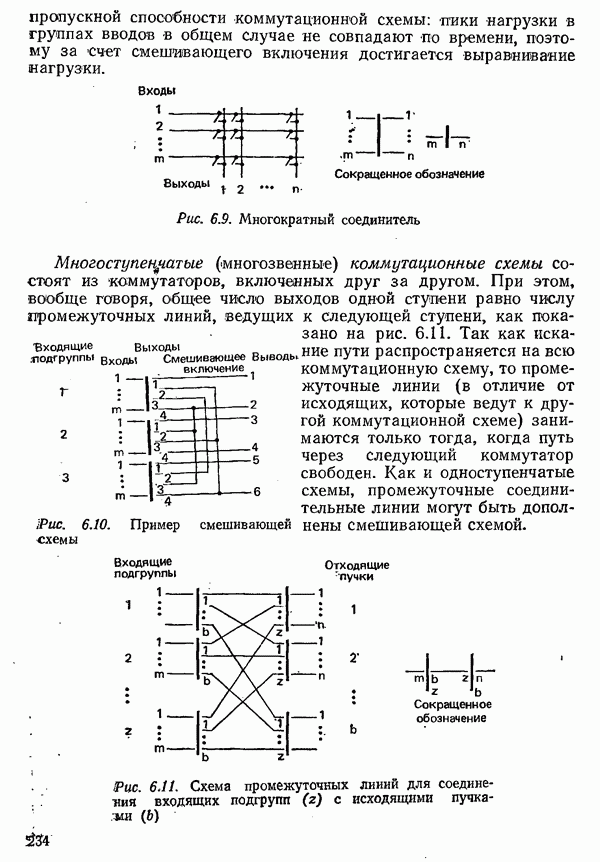
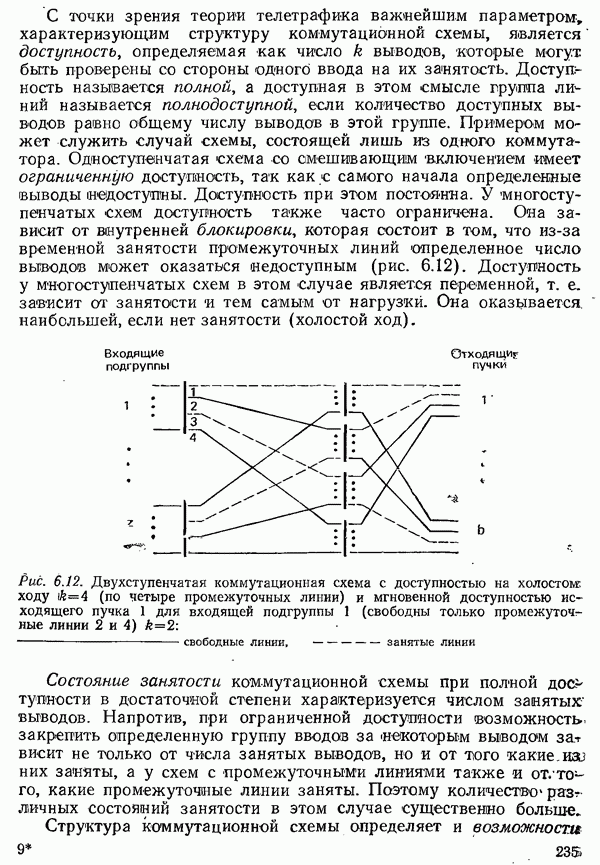
- 6.2. АНАЛИЗ СИСТЕМ КОММУТАЦИИ НА ОСНОВЕ ТЕОРИИ ТЕЛЕТРАФИКА
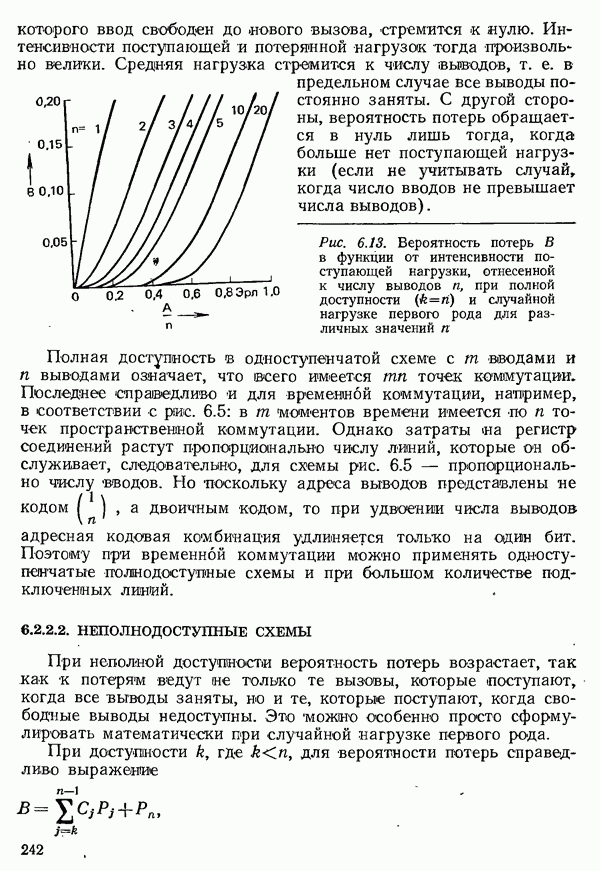
- 6.2.2. СИСТЕМЫ С ПОТЕРЯМИ
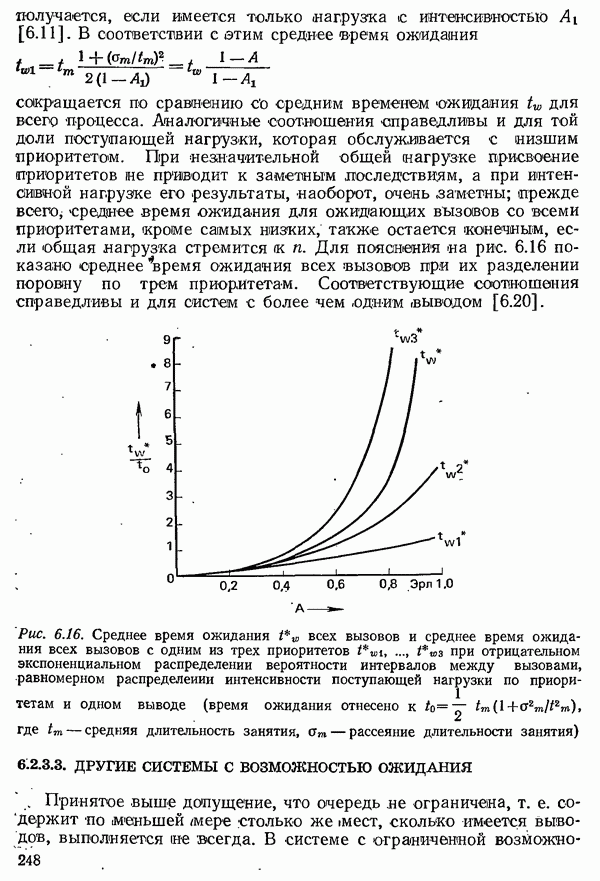
- 6.2.3. СИСТЕМЫ С ОЖИДАНИЕМ
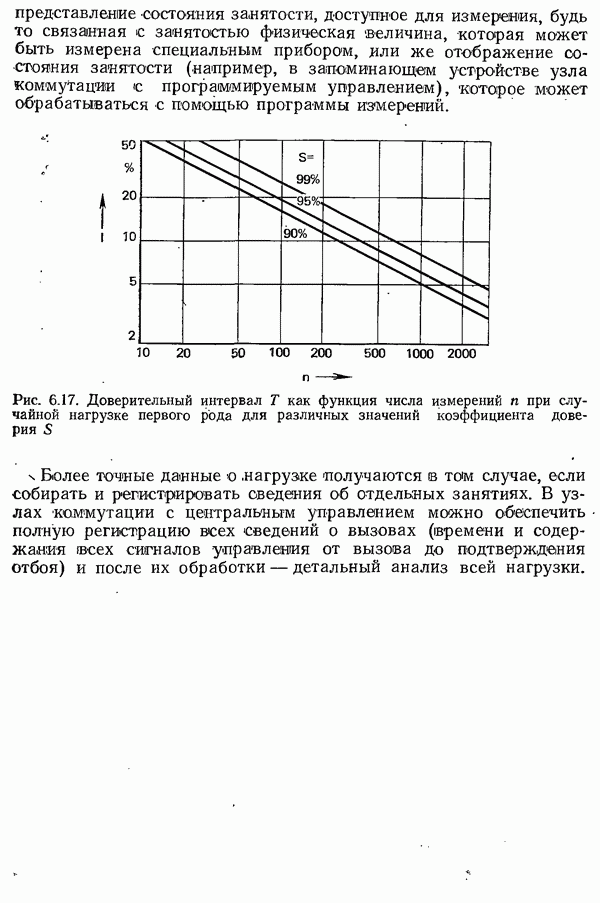
- 6.2.4. ИЗМЕРЕНИЯ НАГРУЗКИ
- СПИСОК ЛИТЕРАТУРЫ