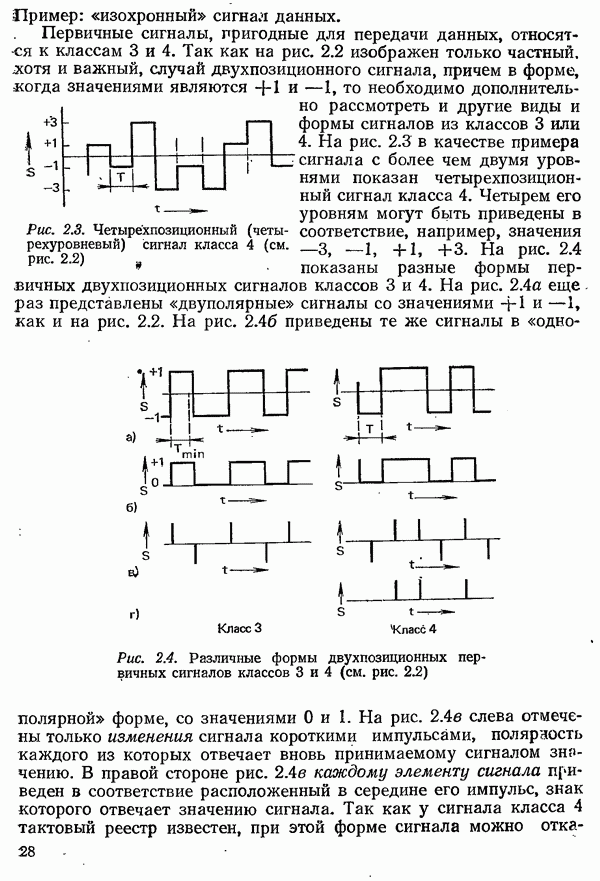
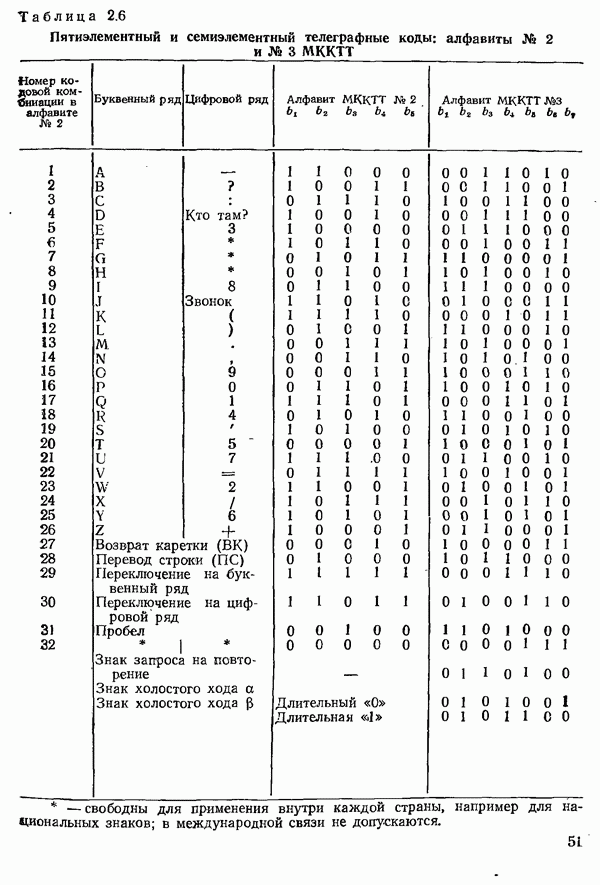
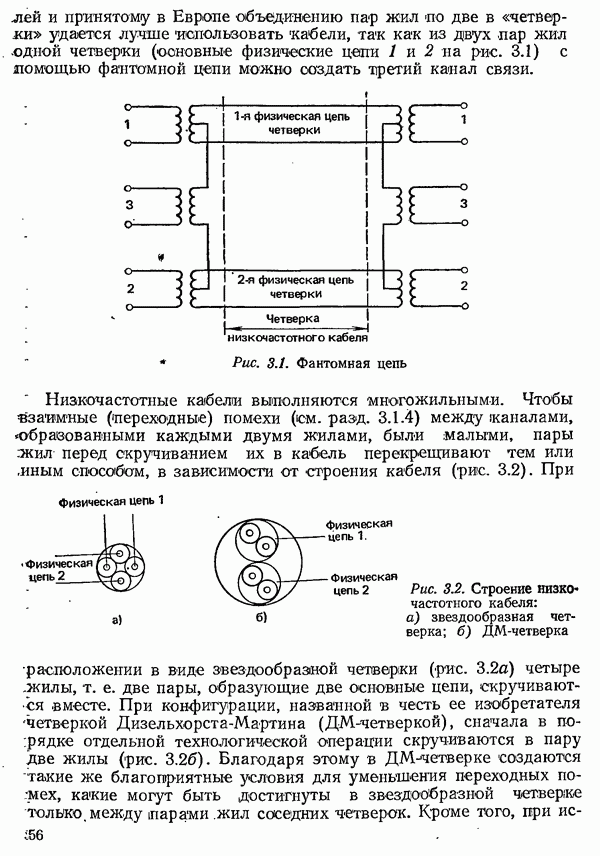
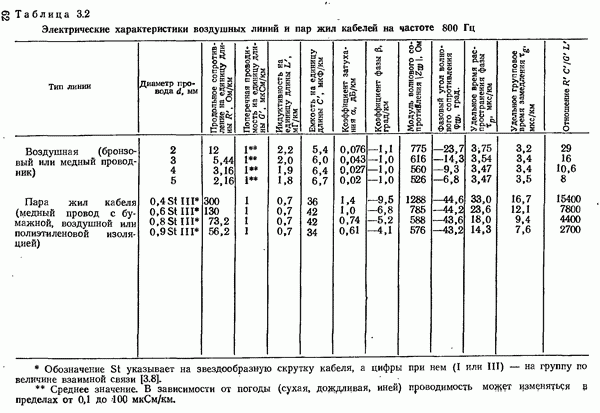
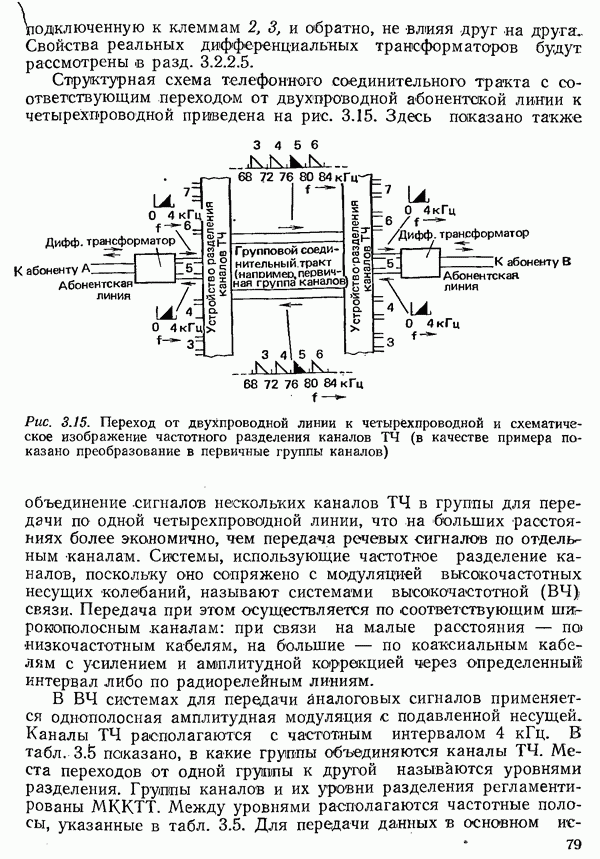
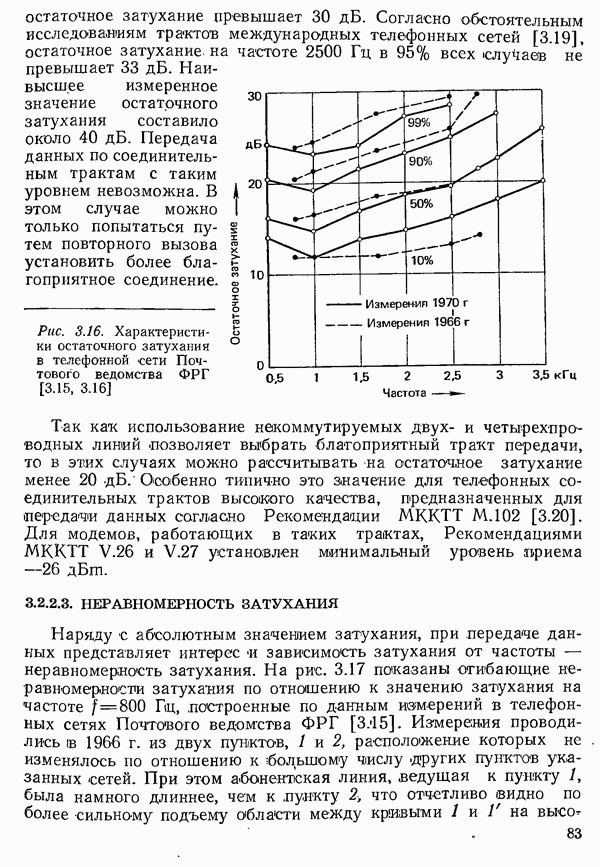
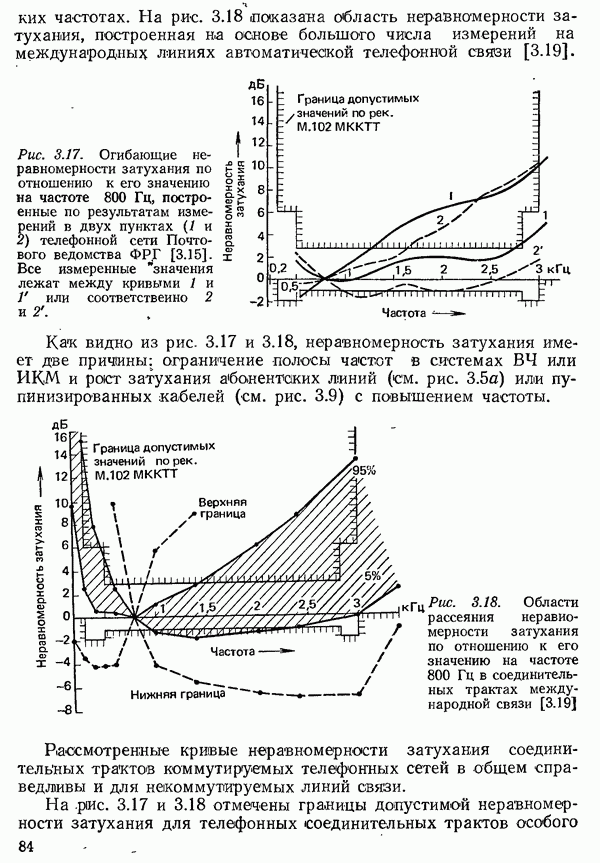
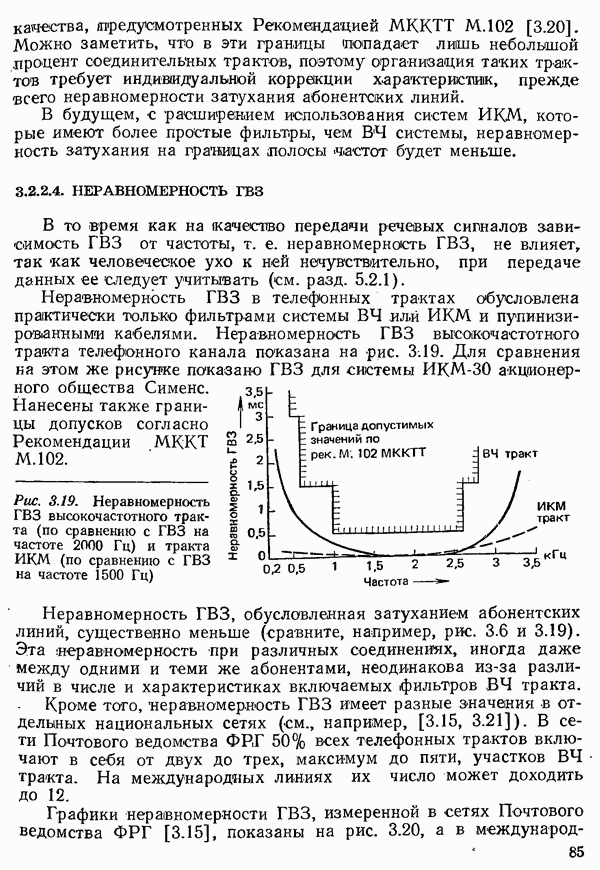
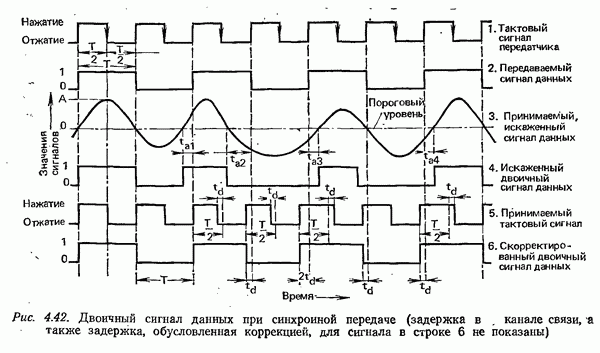
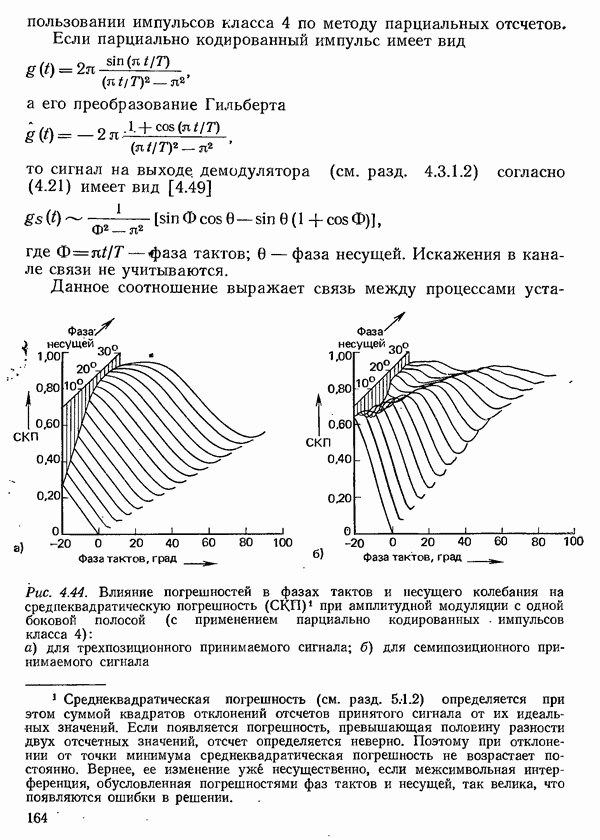
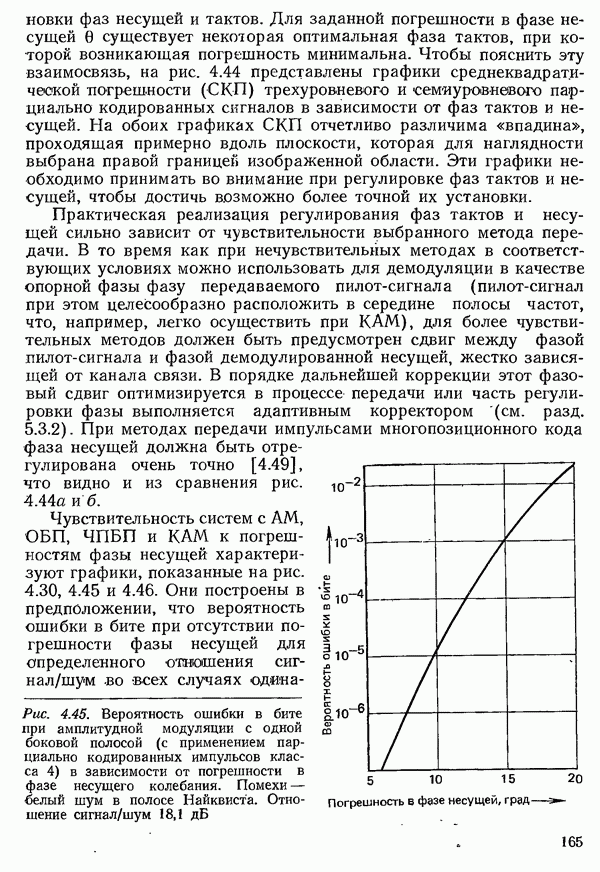
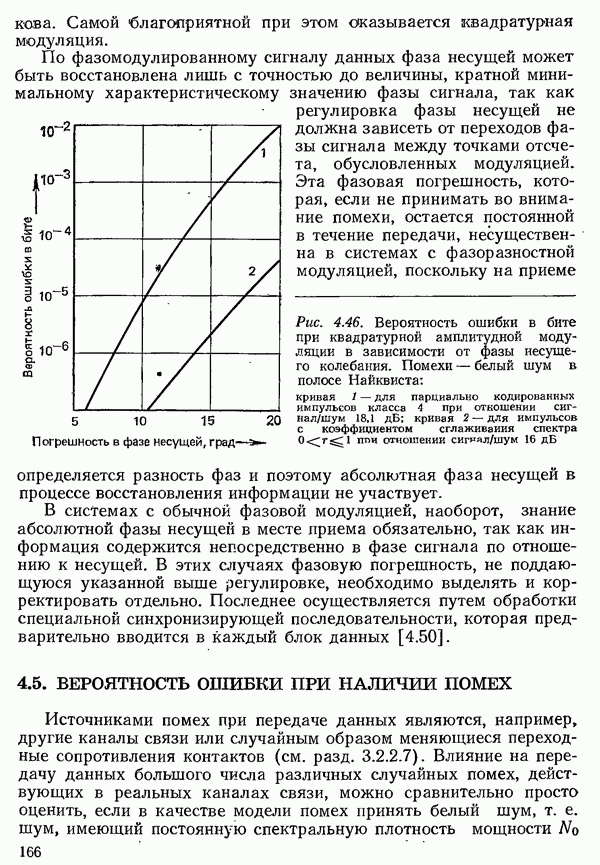
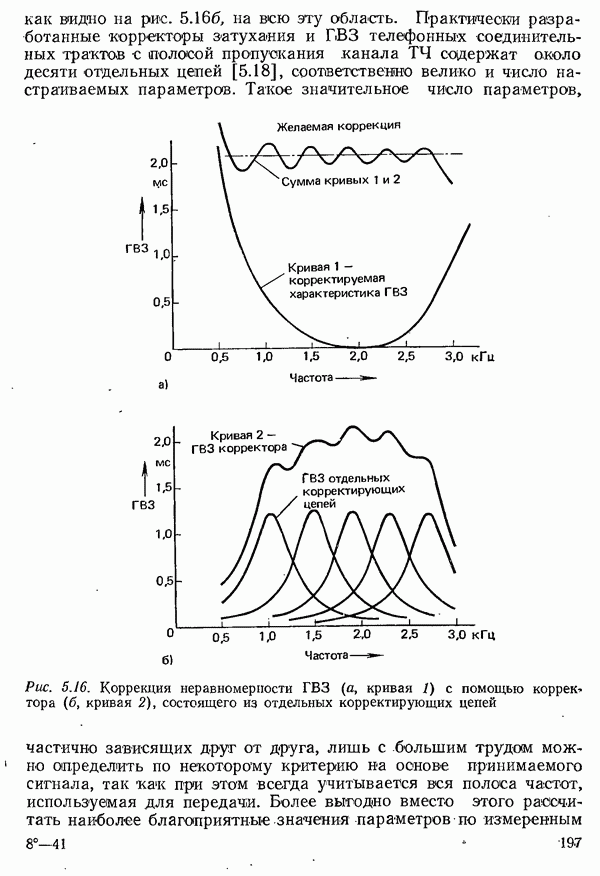
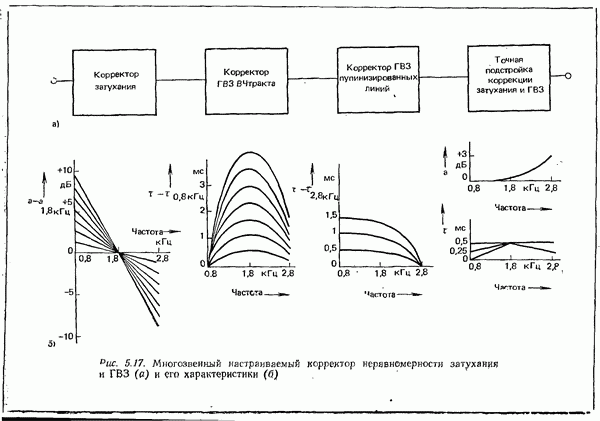
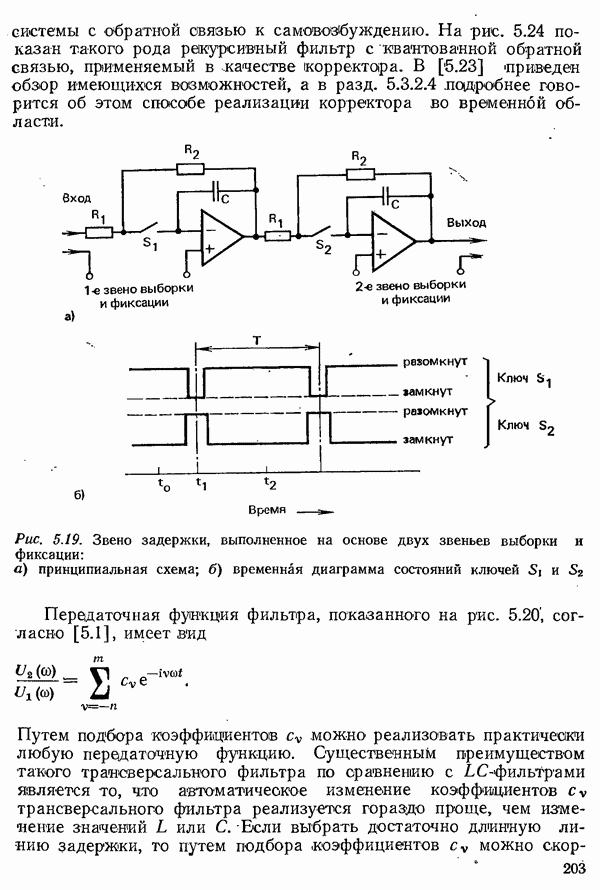
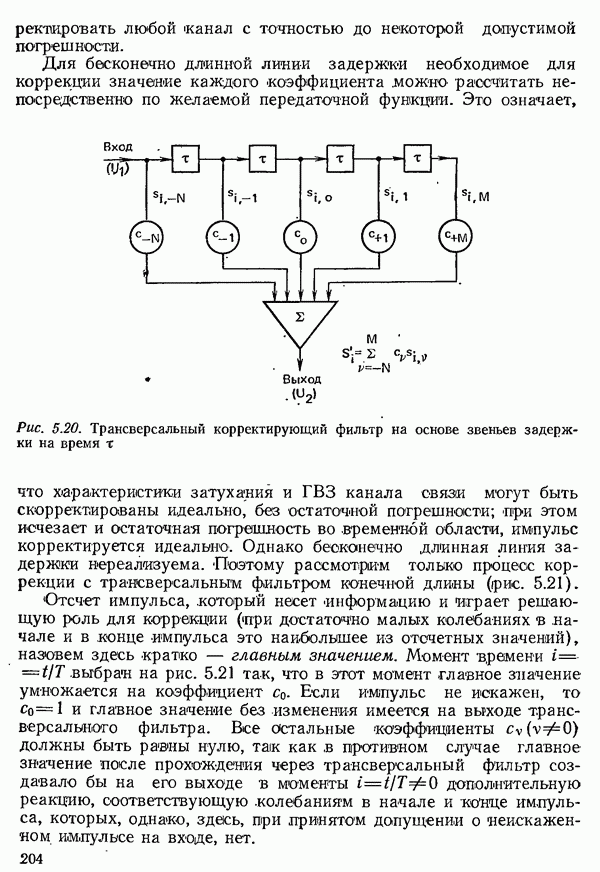
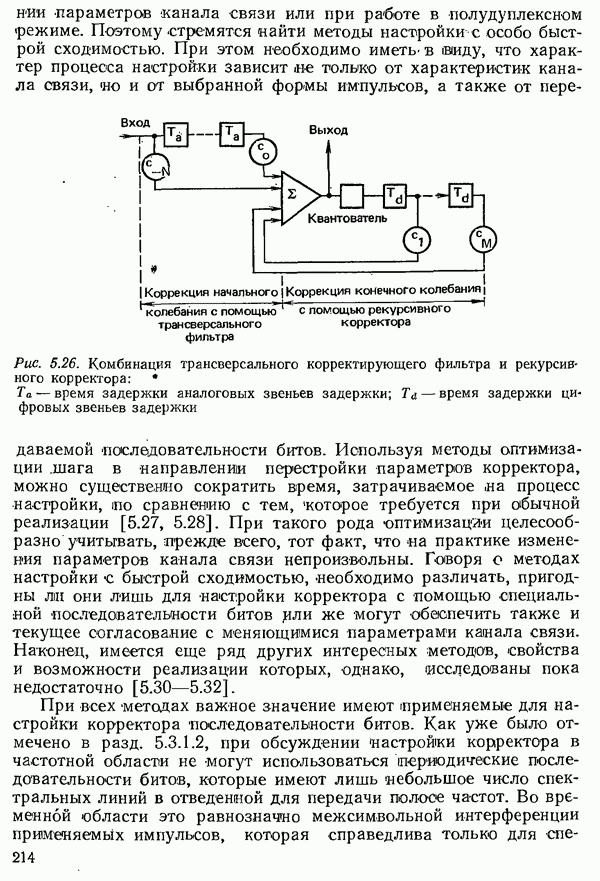
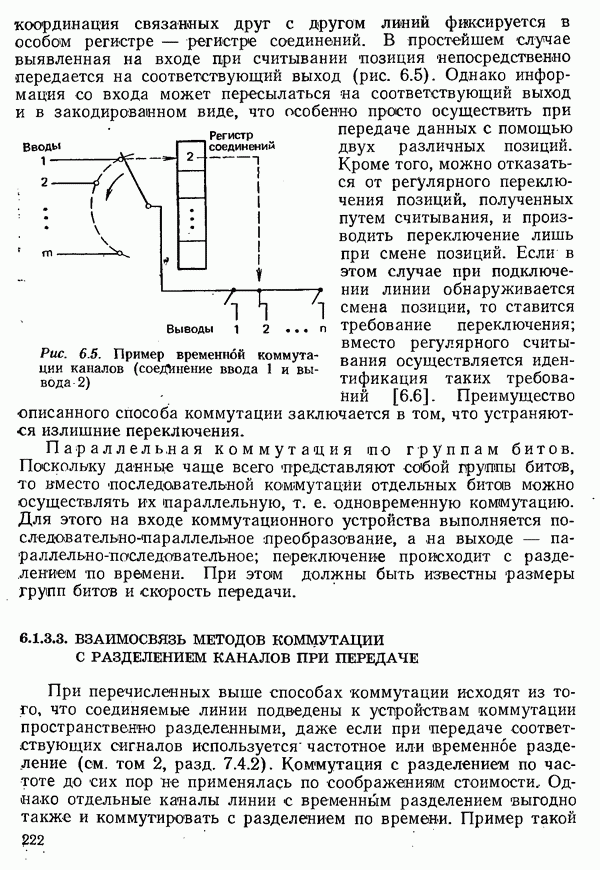
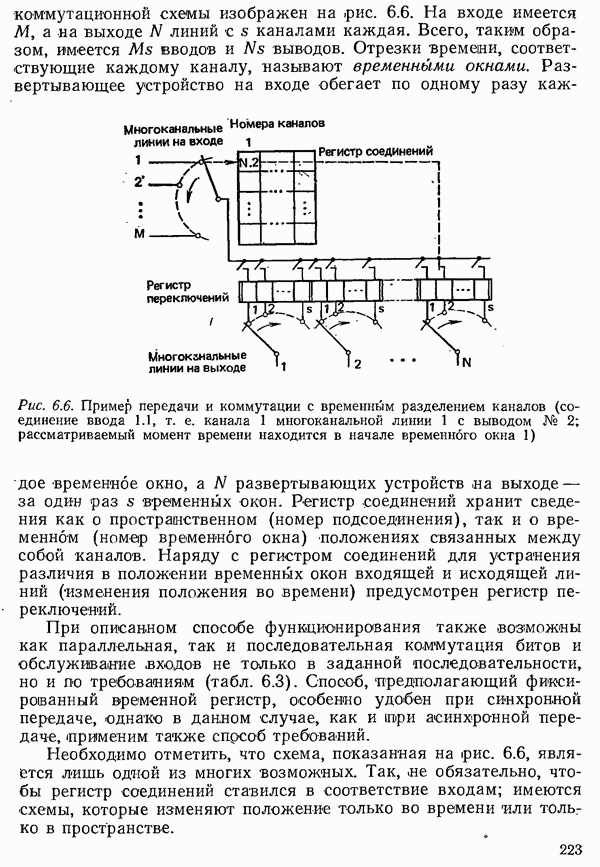
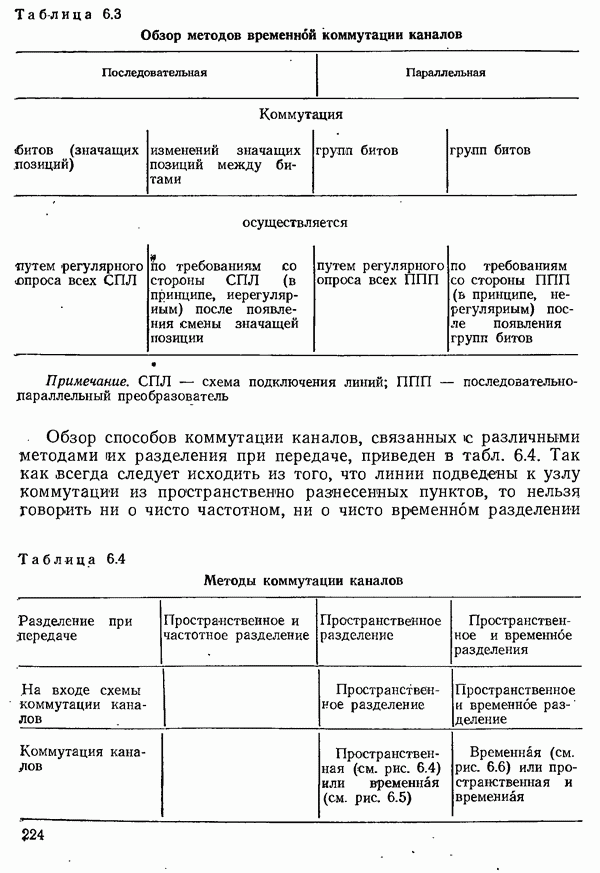
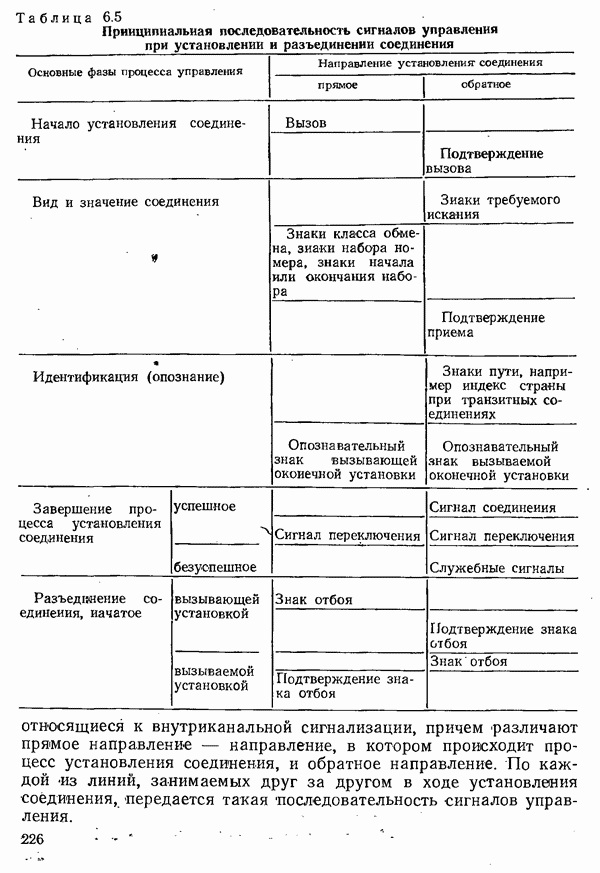
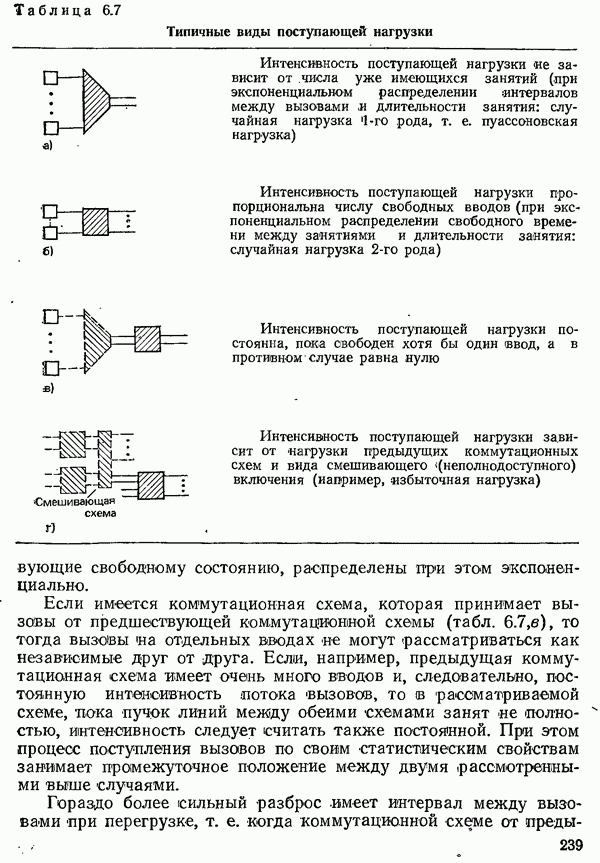
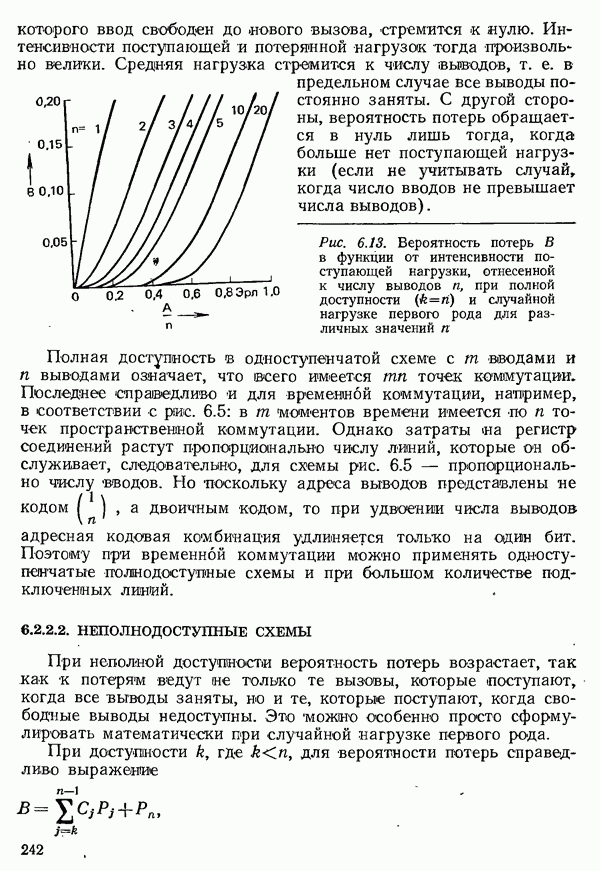
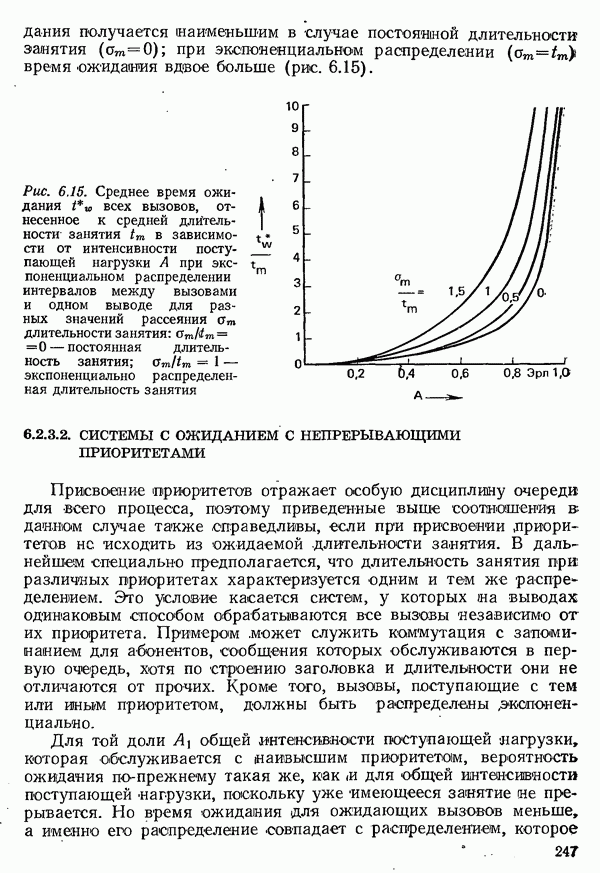
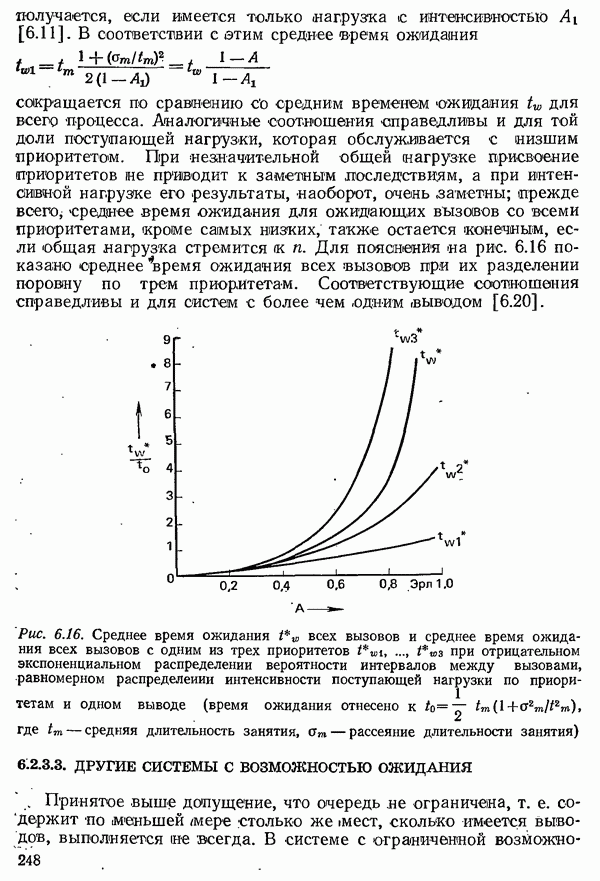
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
3.1.1.1. СВОЙСТВА И ПАРАМЕТРЫ ПРОВОДНЫХ ЛИНИЙ СВЯЗИ
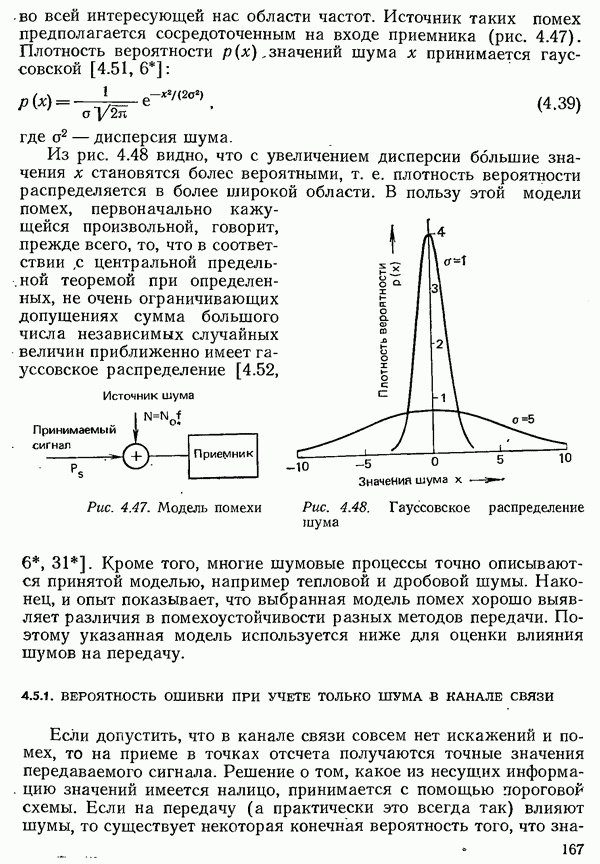
В этом разделе рассматриваются электрические свойства каналов ближней связи. Пара проводов, образующая канал, называется, как это принято в технике связи, линией.
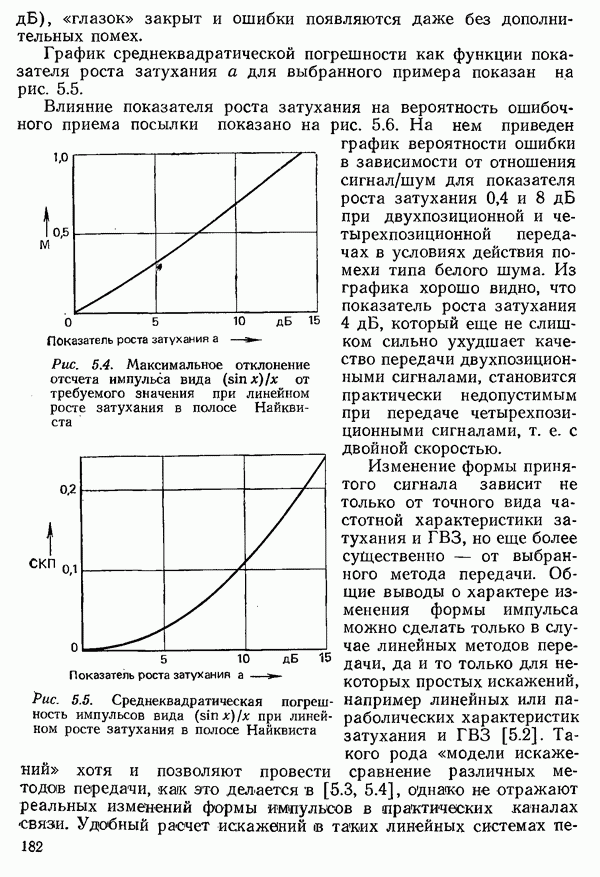
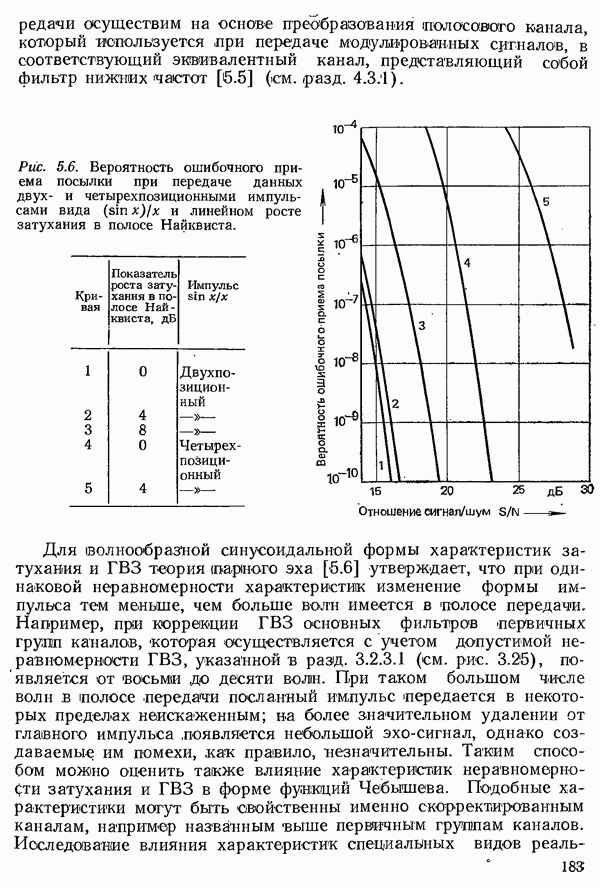
Электрические свойства линии длиной I характеризуются сопротивлением  и индуктивностью
и индуктивностью  которые измеряются на входе линии при коротком замыкании двух ее проводов на выходе, а также емкостью С и проводимостью
которые измеряются на входе линии при коротком замыкании двух ее проводов на выходе, а также емкостью С и проводимостью  между проводами. Частоту при этом следует выбирать так, чтобы длина волны была большой по сравнению с длиной линии
между проводами. Частоту при этом следует выбирать так, чтобы длина волны была большой по сравнению с длиной линии  . У однородных линий, которые только и будут здесь рассматриваться, перечисленные выше параметры распределены равномерно по всей длине линии. У кабелей связи измеряемые значения относят к единице длины проводов
. У однородных линий, которые только и будут здесь рассматриваться, перечисленные выше параметры распределены равномерно по всей длине линии. У кабелей связи измеряемые значения относят к единице длины проводов  и называют первичными параметрами линии:
и называют первичными параметрами линии:

Для описания свойств линии определенной длины I применительно к передаче данных должны быть рассчитаны, затухание и фазовый сдвиг или связанное с ним групповое время замедления в зависимости от частоты  или круговой частоты
или круговой частоты  (см. разд. 5.2). С этой целью линию представляют разделенной на бесконечно малые отрезки, для которых можно составить схему замещения.
(см. разд. 5.2). С этой целью линию представляют разделенной на бесконечно малые отрезки, для которых можно составить схему замещения.

Рис. 3.3. Схема замещения участка линии длиной 
На рис. 3.3 показана схема замещения бесконечно короткого отрезка линии. Исходя из
нее Томсон в 1855 г. вывел дифференциальные уравнения линии — телеграфные уравнения:

Эти уравнения позволяют рассчитать  и напряжение и на расстоянии
и напряжение и на расстоянии  от начала линии в зависимости от/времени
от начала линии в зависимости от/времени  Для понимания последующих рассуждений сначала рассмотрим бесконечно длинную линию.
Для понимания последующих рассуждений сначала рассмотрим бесконечно длинную линию.
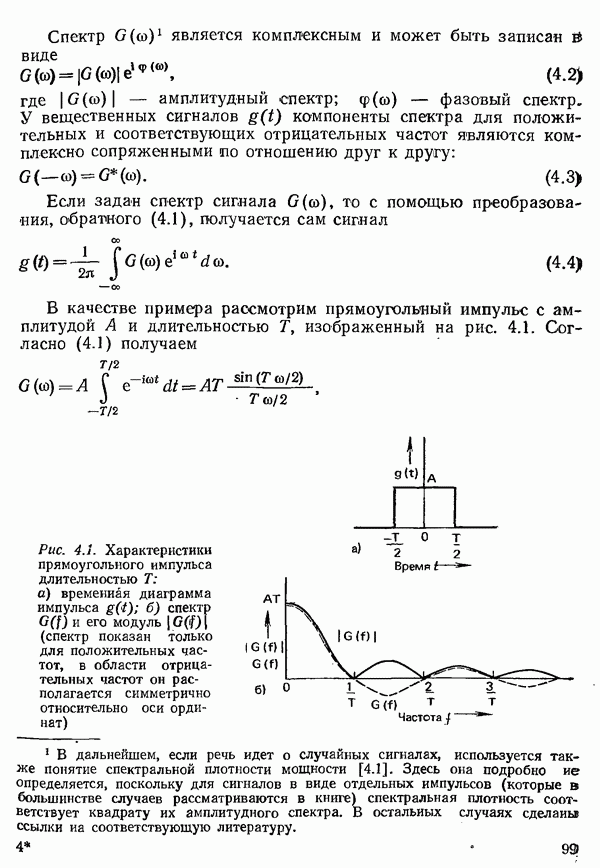
Для бесконечно длинной линии, возбуждаемой в ее начале синусоидальным колебанием  решение в комплексной форме записи имеет вид
решение в комплексной форме записи имеет вид

где  Выражение (3.2) описывает распространяющуюся от начала линии затухающую волну; величину у называют коэффициентом распространения.
Выражение (3.2) описывает распространяющуюся от начала линии затухающую волну; величину у называют коэффициентом распространения.
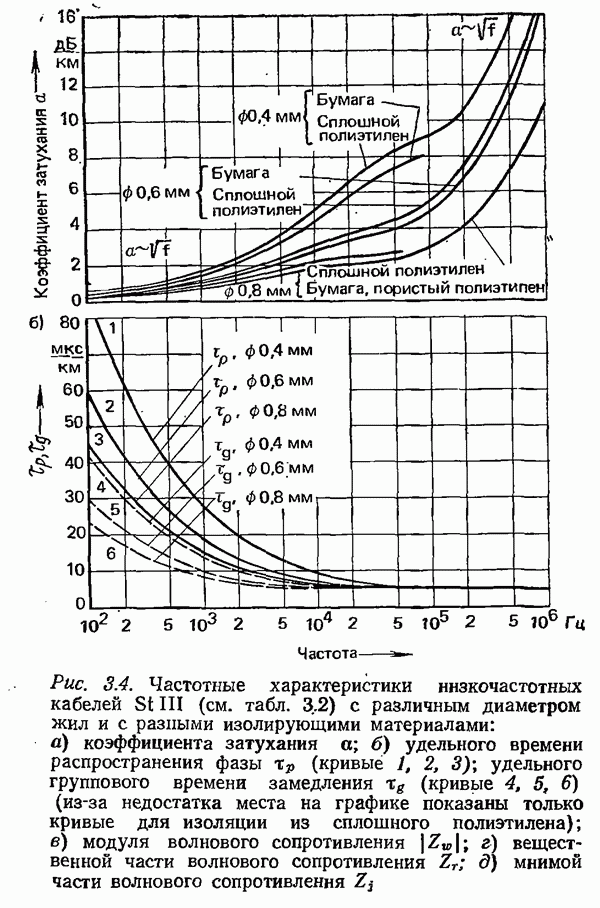
Величина а выражает коэффициент затухания, характеризующий уменьшение вдоль линии амплитуды напряжения или тока,  коэффициент фазы, определяющий фазовый сдвиг напряжения или тока вдоль линии. Через
коэффициент фазы, определяющий фазовый сдвиг напряжения или тока вдоль линии. Через  определяются фазовая скорость
определяются фазовая скорость  и групповая скорость
и групповая скорость  волны. Обратные величины характеризуют время пробега волны:
волны. Обратные величины характеризуют время пробега волны:  удельное время распространения фазы и
удельное время распространения фазы и  удельное групповое время замедления. Величины
удельное групповое время замедления. Величины  являются параметрами, отнесенными к длине линии, обычно в расчете на
являются параметрами, отнесенными к длине линии, обычно в расчете на  длины линии.
длины линии.
Величины  могут быть заданы как функции первичных параметров линии
могут быть заданы как функции первичных параметров линии  и круговой частоты
и круговой частоты  с которой изменяются ток и напряжение в начале линии:
с которой изменяются ток и напряжение в начале линии:

Величина

называется степенью затухания в линии длиной 
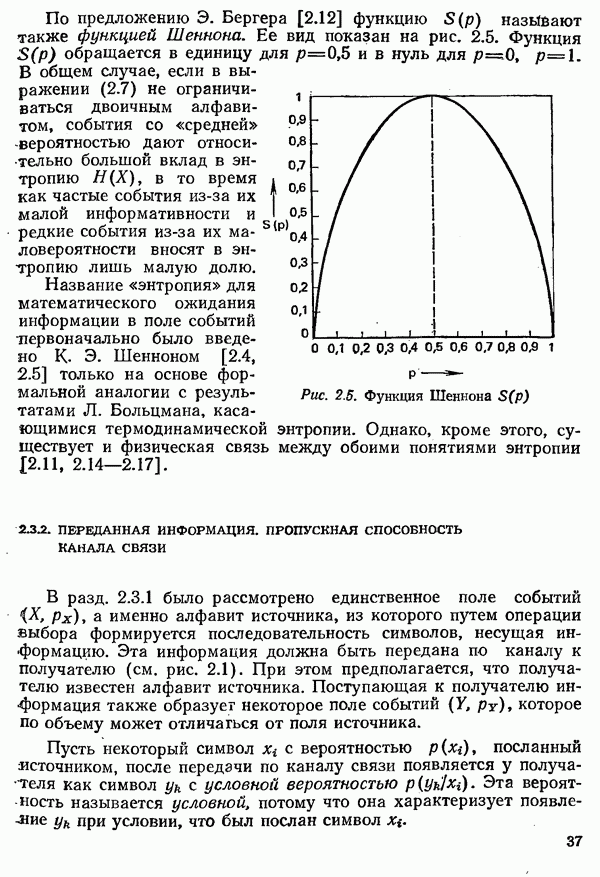
Логарифмы отношений двух величин одинаковой размерности часто встречаются в технике связи. Для отношения двух напряжений,  или двух мощностей,
или двух мощностей,  введено наименование степень затухания, вместо которого часто, в том числе и здесь далее, употребляется сокращенный термин затухание. При использовании десятичных логарифмов соответствующие единицы называются децибелами
введено наименование степень затухания, вместо которого часто, в том числе и здесь далее, употребляется сокращенный термин затухание. При использовании десятичных логарифмов соответствующие единицы называются децибелами  а при использовании менее употребительных ныне натуральных логарифмов — неперами
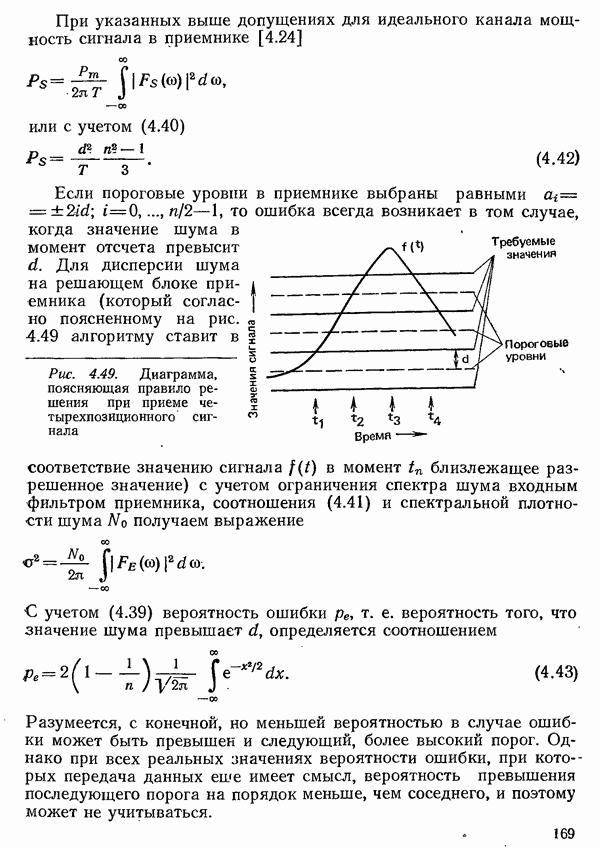
а при использовании менее употребительных ныне натуральных логарифмов — неперами 
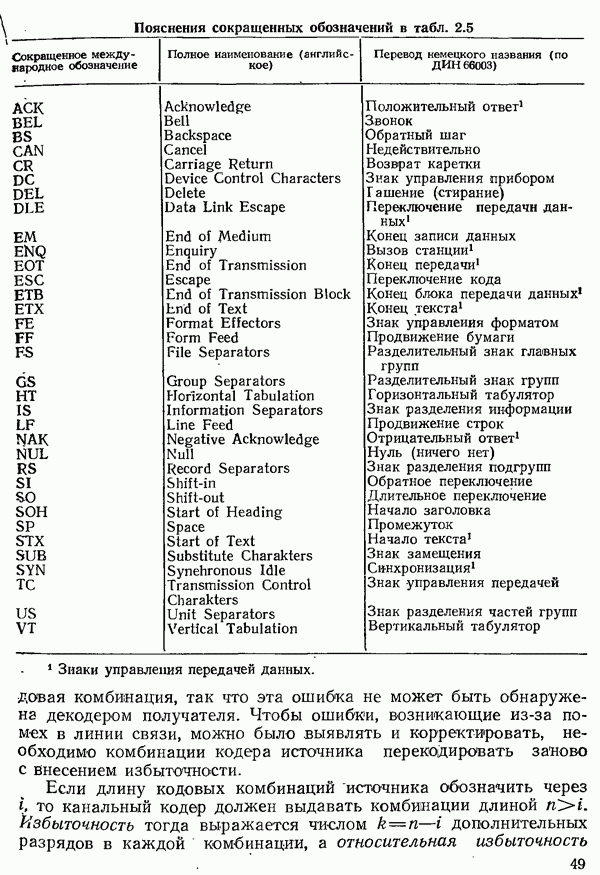
Таблица 3.1. Децибелы и неперы

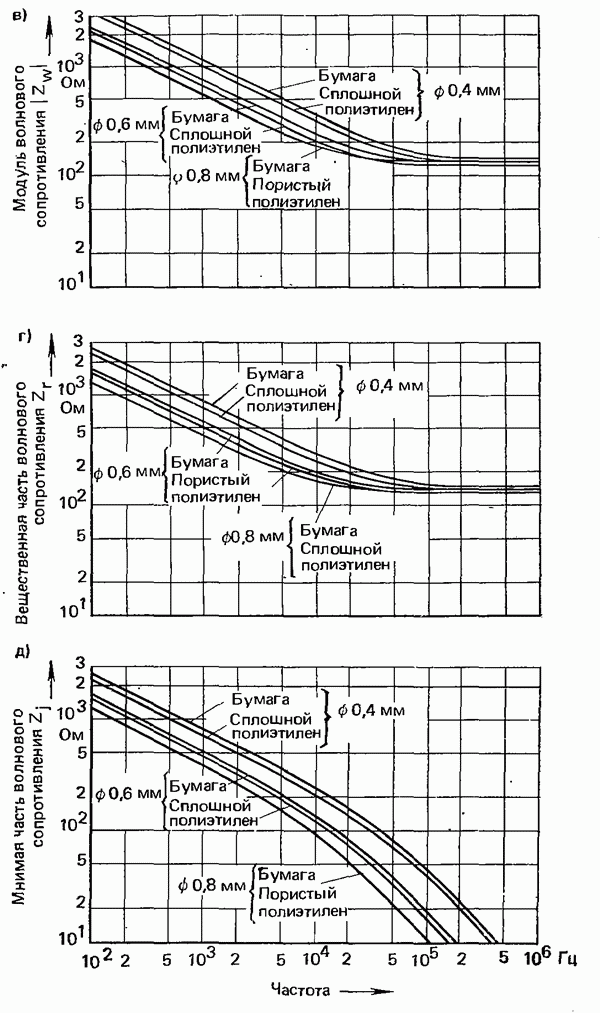
Наряду с коэффициентами затухания и фазы,  другой величиной, имеющей важное значение для описания свойств линии, является входное сопротивление бесконечно длинной линии
другой величиной, имеющей важное значение для описания свойств линии, является входное сопротивление бесконечно длинной линии 
Комплексное сопротивление  на входе бесконечно длинной линии называют ее волновым сопротивлением. Оно зависит от первичных параметров линии
на входе бесконечно длинной линии называют ее волновым сопротивлением. Оно зависит от первичных параметров линии  и от круговой частоты
и от круговой частоты  :
:

Его модуль

а фазовый угол

Смысл понятия волнового сопротивления становится ясным, если от рассмотрения бесконечно длинной линии перейти к линии конечной длины. Если линия конечной длины замкнута на некоторое сопротивление  то решение телеграфных уравнений (3.1)
то решение телеграфных уравнений (3.1)
для напряжения  и тока
и тока  на расстоянии
на расстоянии  от начала линии имеет вид
от начала линии имеет вид

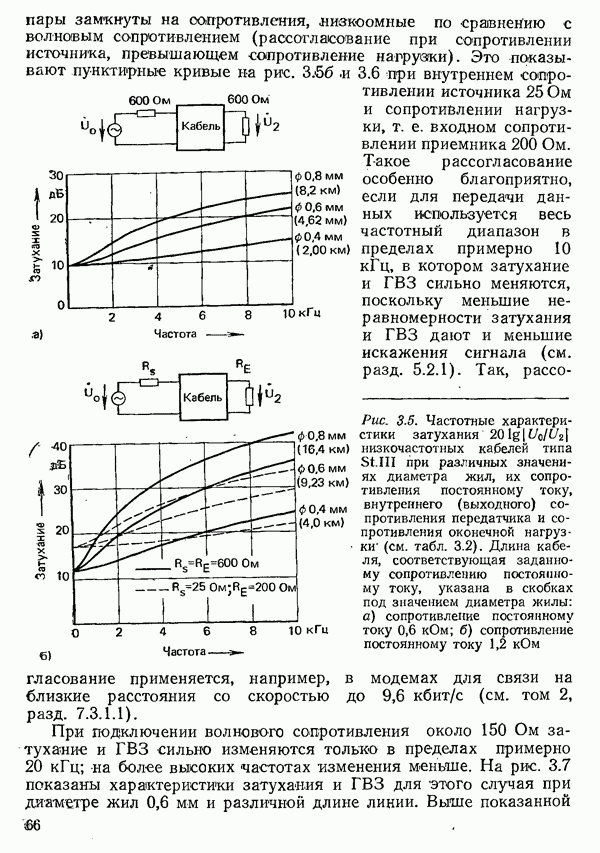
Первое слагаемое в (3.7), как и в решении для бесконечно длинной линии, описывает волну, распространяющуюся от начала к концу линии, а второе — волну в обратном направлении. Этой отраженной от конца волны, являющейся помехой для передачи сигналов, можно избежать лишь в том случае, если линия замкнута на волновое сопротивление, т. е. в 
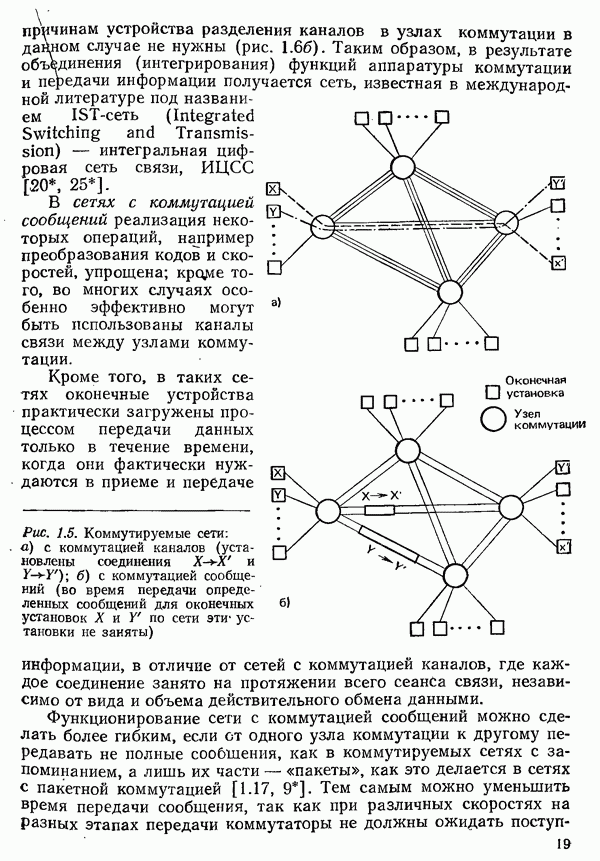
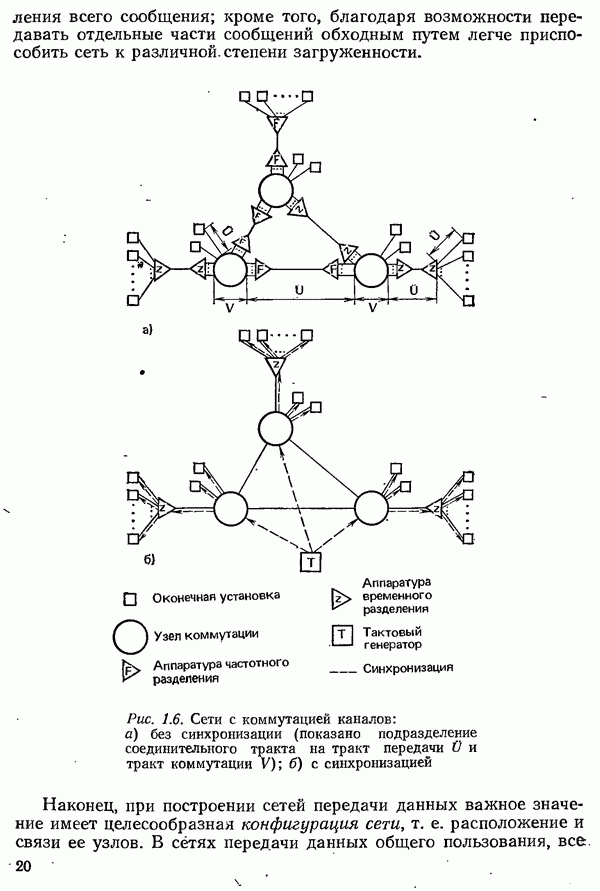
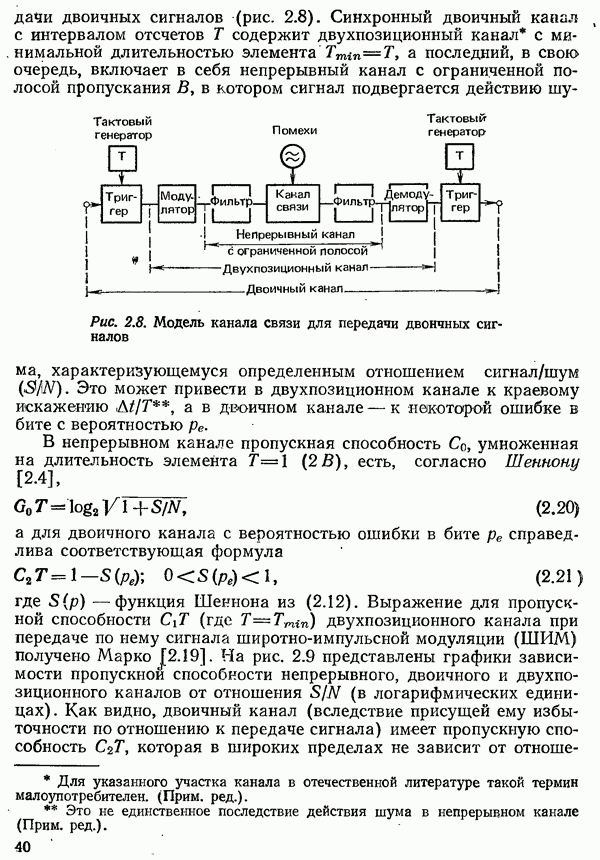
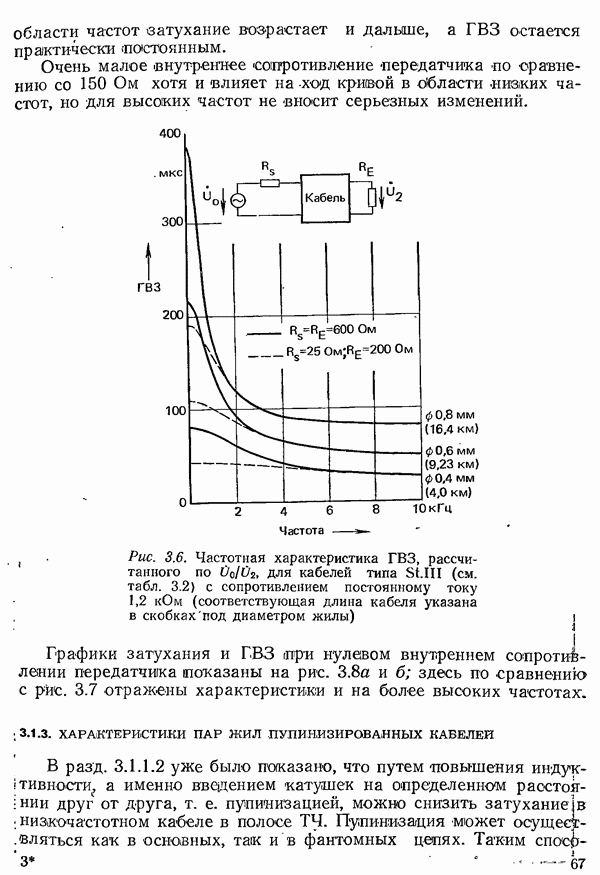
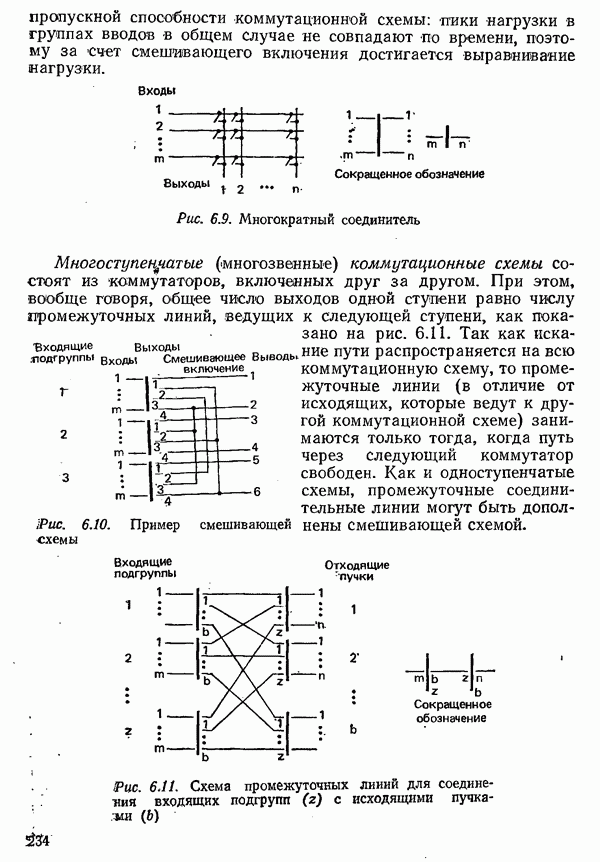
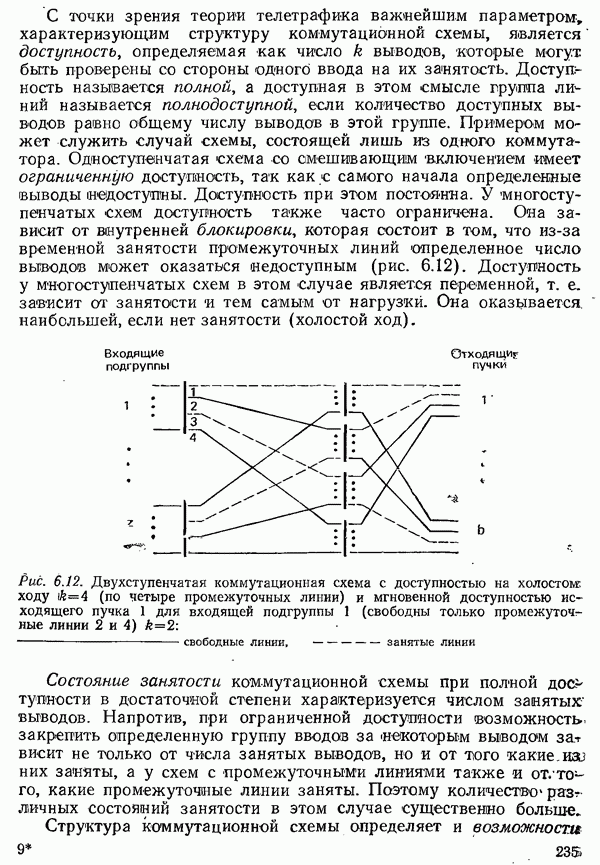
Предыдущие рассуждения относились к однородным линиям, для любого отрезка которых справедлива одна и та же схема замещения (см. рис. 3.3) с одинаковыми значениями первичных параметров  . В сетях последовательно включаются кабели с различными диаметрами проводов и, следовательно, с различными первичными параметрами, поэтому возможно многократное отражение. Их свойства по отношению к передаче сигналов при этом могут быть определены только путем расчетов или измерений для каждого отдельного случая.
. В сетях последовательно включаются кабели с различными диаметрами проводов и, следовательно, с различными первичными параметрами, поэтому возможно многократное отражение. Их свойства по отношению к передаче сигналов при этом могут быть определены только путем расчетов или измерений для каждого отдельного случая.
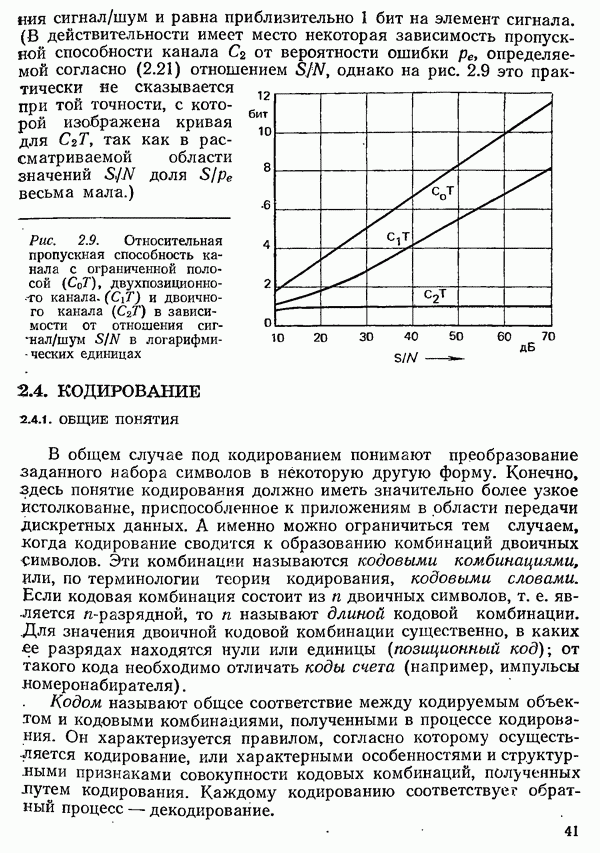
В области частот примерно от  и выше сопротивления
и выше сопротивления  индуктивности уже нельзя считать не зависящими от частоты. Здесь уже необходимо учитывать скин-эффект, который вызывает неравномерное распределение плотности тока но сечению пар проводников, а также эффекты, связанные с влиянием соседних пар и оболочки кабеля, например потери от вихревых токов.
индуктивности уже нельзя считать не зависящими от частоты. Здесь уже необходимо учитывать скин-эффект, который вызывает неравномерное распределение плотности тока но сечению пар проводников, а также эффекты, связанные с влиянием соседних пар и оболочки кабеля, например потери от вихревых токов.
Более подробно эти вопросы рассмотрены в  .
.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ К РУССКОМУ ИЗДАНИЮ
- 1. Обзор
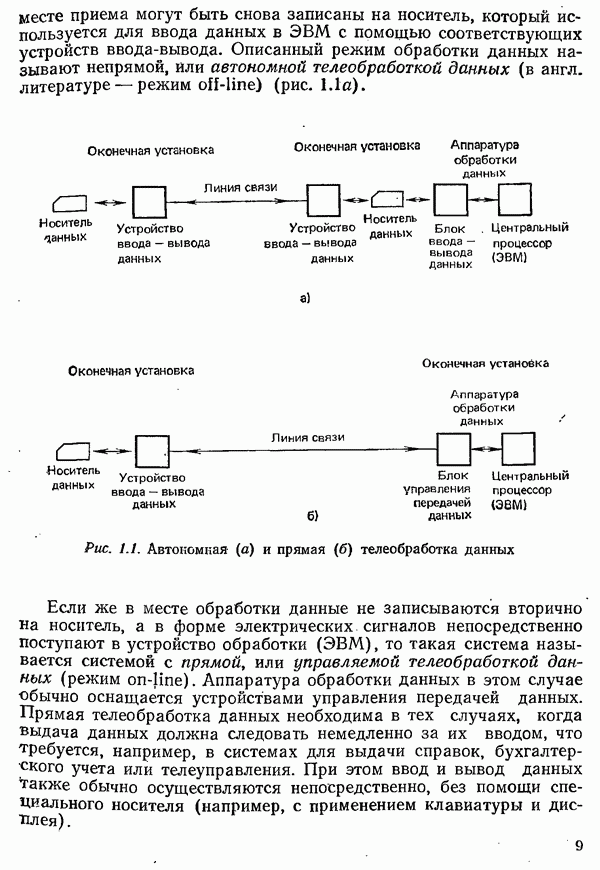
- 1.1. ОБРАБОТКА И ТЕЛЕОБРАБОТКА ДАННЫХ
- 1.2. АВТОНОМНАЯ И УПРАВЛЯЕМАЯ ТЕЛЕОБРАБОТКА ДАННЫХ
- 1.3. КЛАССИФИКАЦИЯ СИСТЕМ ТЕЛЕОБРАБОТКИ ДАННЫХ
- 1.4. СТРУКТУРА СИСТЕМ ТЕЛЕОБРАБОТКИ ДАННЫХ
- 1.5. ТРЕБОВАНИЯ К ТЕХНИКЕ СВЯЗИ И КОММУТАЦИИ В СИСТЕМАХ ТЕЛЕОБРАБОТКИ ДАННЫХ
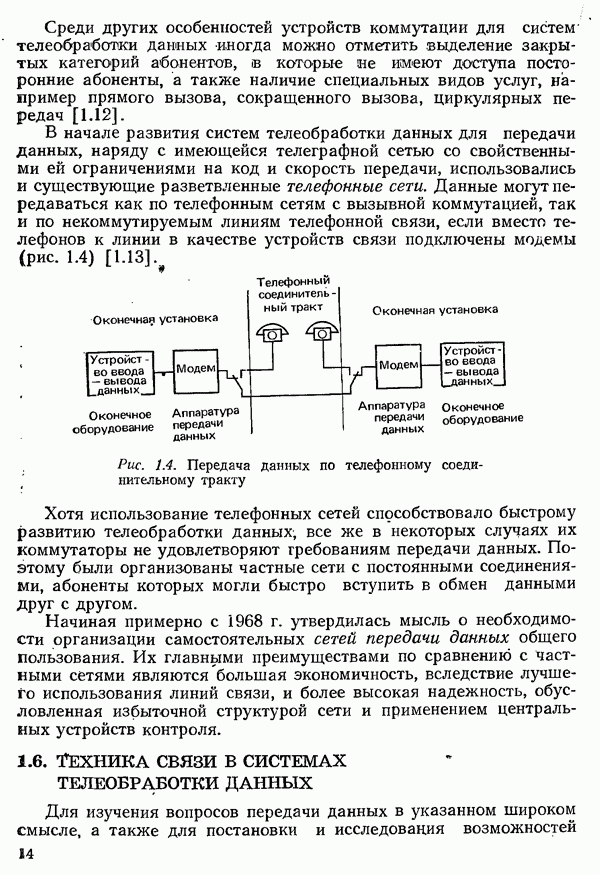
- 1.6. ТЕХНИКА СВЯЗИ В СИСТЕМАХ ТЕЛЕОБРАБОТКИ ДАННЫХ
- 2. Основные понятия техники связи
- 2.2. СИГНАЛЫ
- 2.2.2. ДИСКРЕТИЗАЦИЯ, КВАНТОВАНИЕ, ВЛИЯНИЕ ШУМОВ
- 2.2.3. СВОЙСТВА ПЕРВИЧНЫХ СИГНАЛОВ ДЛЯ ПЕРЕДАЧИ ДАННЫХ
- 2.2.3.2. ВРЕМЕННЫЕ СООТНОШЕНИЯ МЕЖДУ СИГНАЛАМИ
- 2.2.4. РЕЖИМЫ РАБОТЫ ПРИ ПЕРЕДАЧЕ СИГНАЛОВ
- 2.3. НЕКОТОРЫЕ ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ИНФОРМАЦИИ
- 2.3.2. ПЕРЕДАННАЯ ИНФОРМАЦИЯ. ПРОПУСКНАЯ СПОСОБНОСТЬ КАНАЛА СВЯЗИ
- 2.4. КОДИРОВАНИЕ
- 2.4.3. КОДИРОВАНИЕ ИСТОЧНИКА
- 2.4.4. КАНАЛЬНОЕ КОДИРОВАНИЕ
- 3. Каналы связи
- 3.1. КАНАЛЫ БЛИЖНЕЙ СВЯЗИ
- 3.1.1.1. СВОЙСТВА И ПАРАМЕТРЫ ПРОВОДНЫХ ЛИНИЙ СВЯЗИ
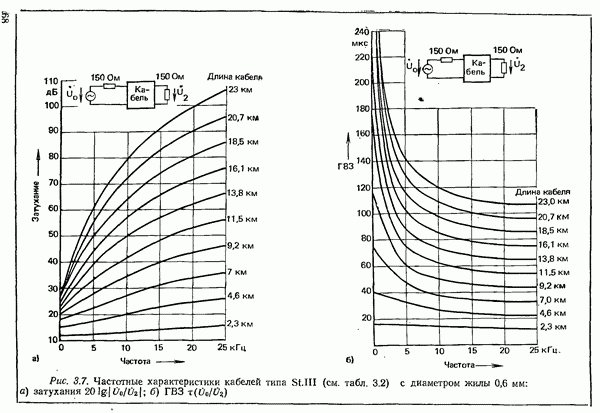
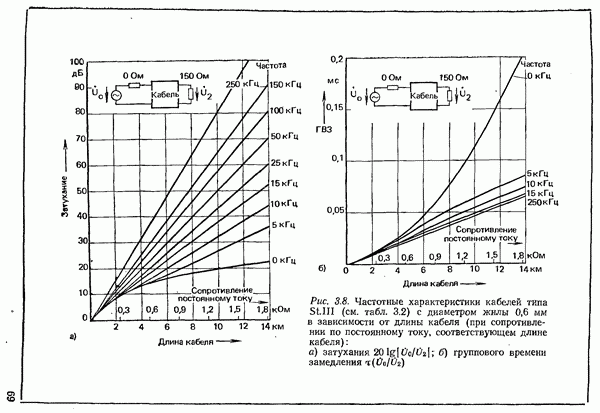
- 3.1.1.2. УМЕНЬШЕНИЕ ЗАТУХАНИЯ ПУТЕМ УВЕЛИЧЕНИЯ ИНДУКТИВНОСТИ. ПУПИНИЗАЦИЯ
- 3.1.2. ХАРАКТЕРИСТИКИ ПАР ЖИЛ НИЗКОЧАСТОТНЫХ КАБЕЛЕЙ
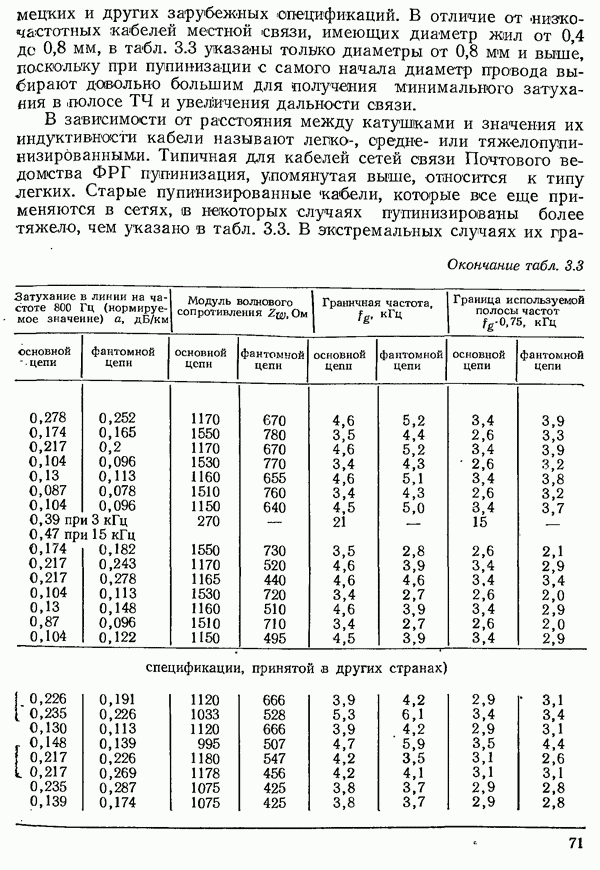
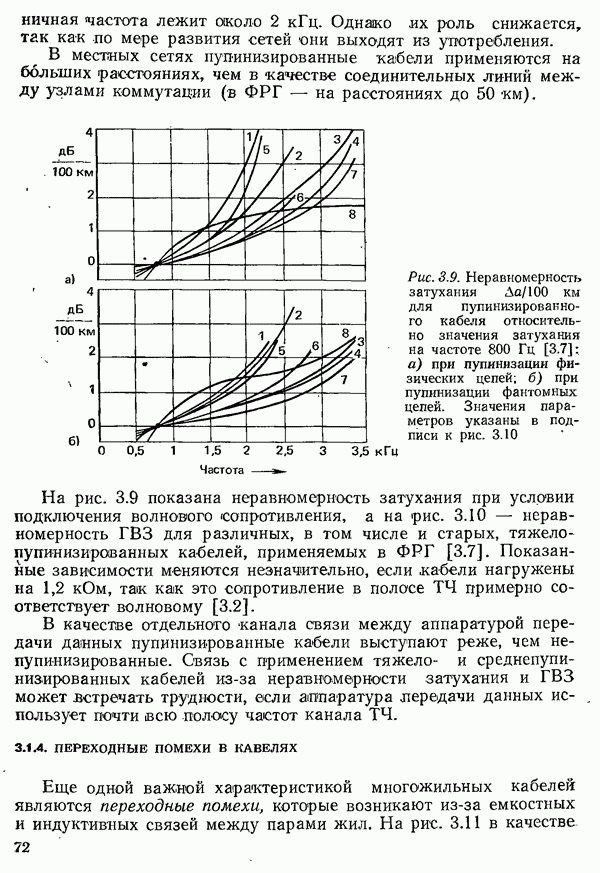
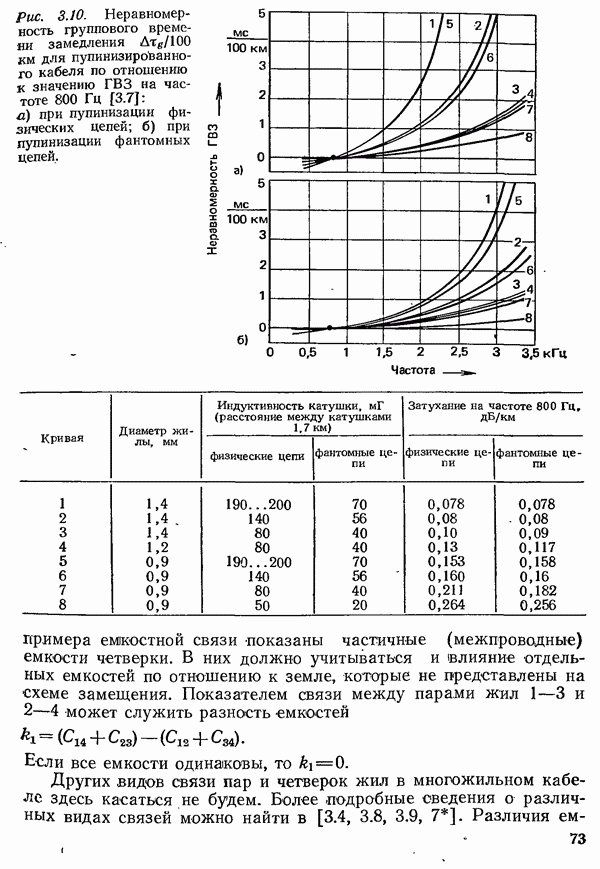
- 3.1.3. ХАРАКТЕРИСТИКИ ПАР ЖИЛ ПУПИЯИЗИРОВАННЫХ КАБЕЛЕЙ
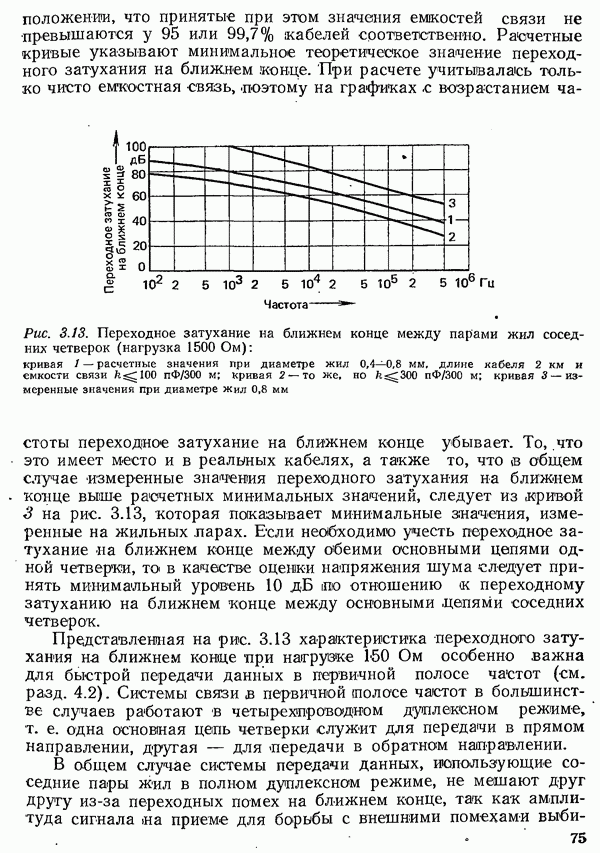
- 3.1.4. ПЕРЕХОДНЫЕ ПОМЕХИ В КАБЕЛЯХ
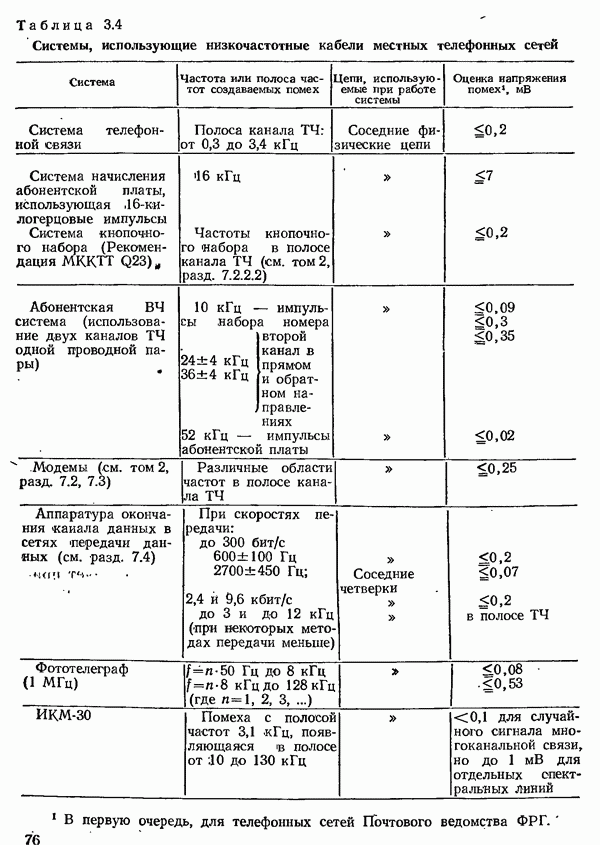
- 3.1.5. НАПРЯЖЕНИЯ ШУМОВ НА ПАРАХ ШИЛ КАБЕЛЕЙ
- 3.2. КАНАЛЫ ДАЛЬНЕЙ СВЯЗИ
- 3.2.2. КАНАЛЫ ТОНАЛЬНОЙ ЧАСТОТЫ
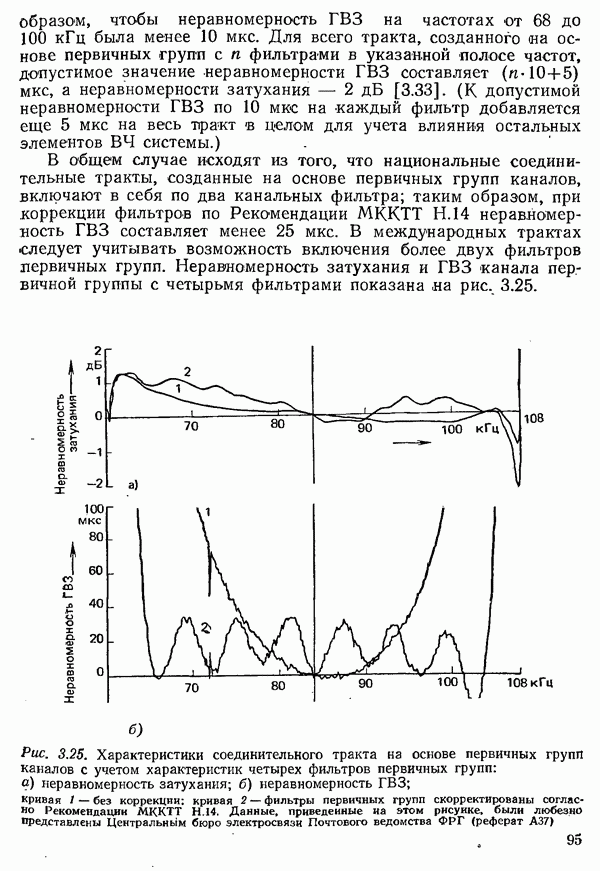
- 3.2.3. СОЕДИНИТЕЛЬНЫЕ ТРАКТЫ НА ОСНОВЕ ПЕРВИЧНЫХ ГРУПП КАНАЛОВ
- 4. Методы передачи данных
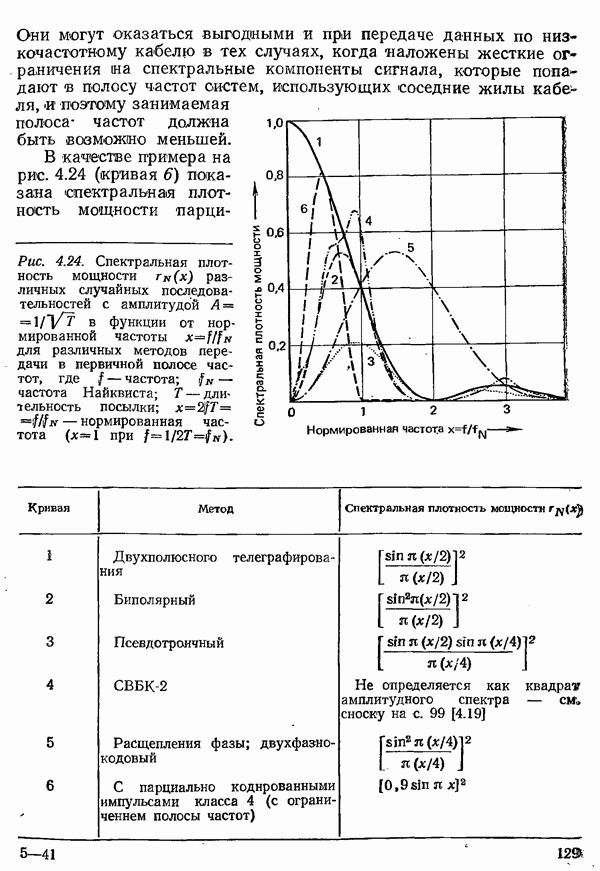
- 4.1.1. СИГНАЛЫ И СПЕКТРЫ
- 4.1.2. РЯД ФУРЬЕ
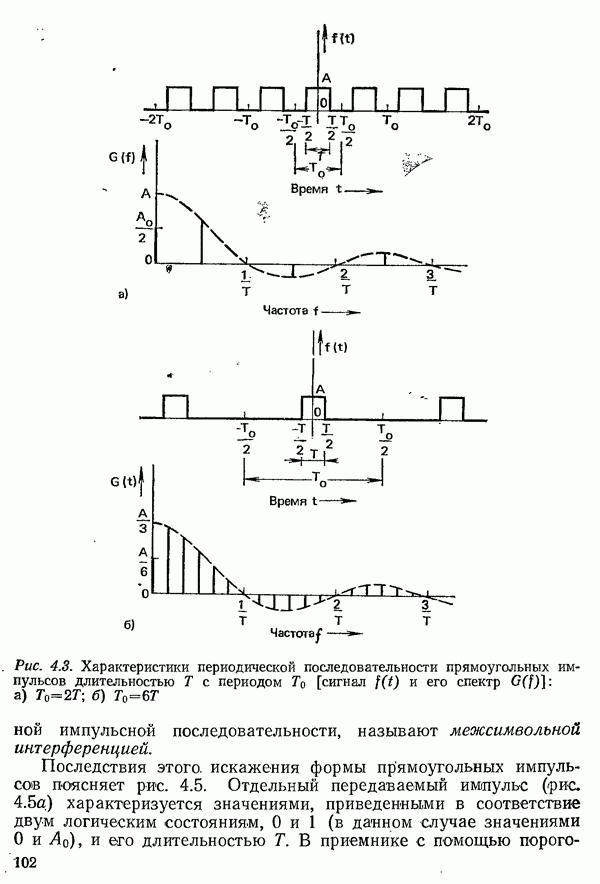
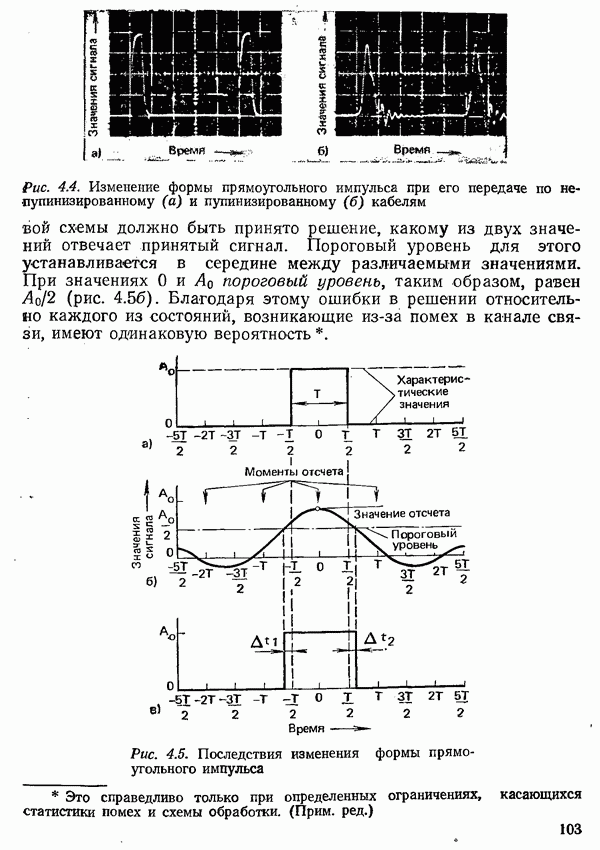
- 4.1.3. ИСКАЖЕНИЯ ФОРМЫ ИМПУЛЬСОВ ПРИ ОГРАНИЧЕНИИ ПОЛОСЫ ЧАСТОТ
- 4.1.4. УСЛОВИЯ НАЙКВИСТА
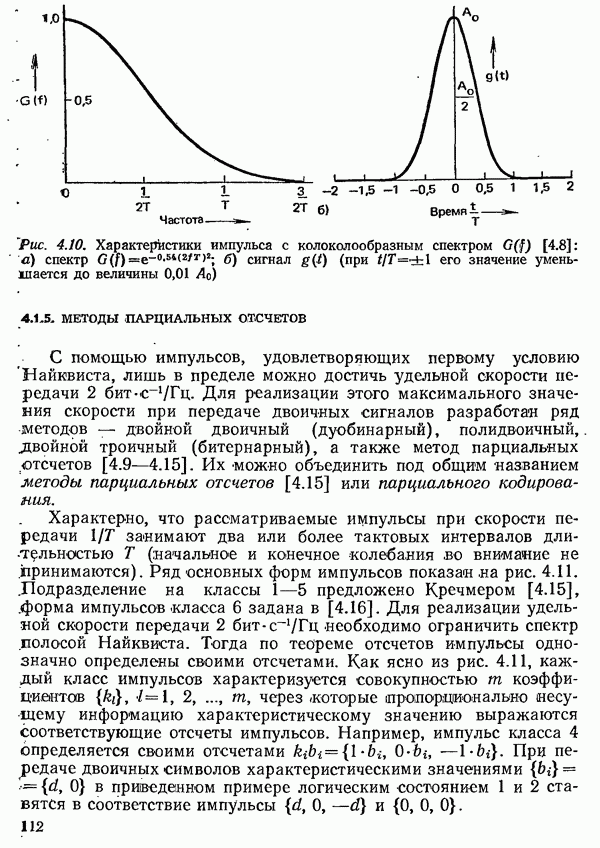
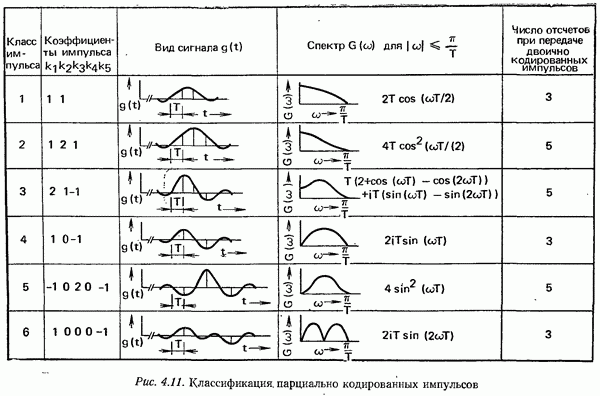
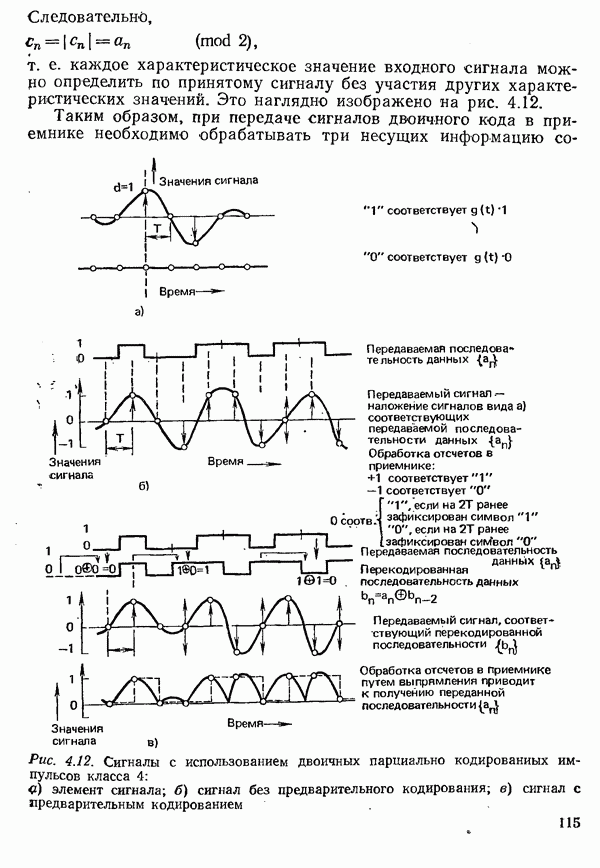
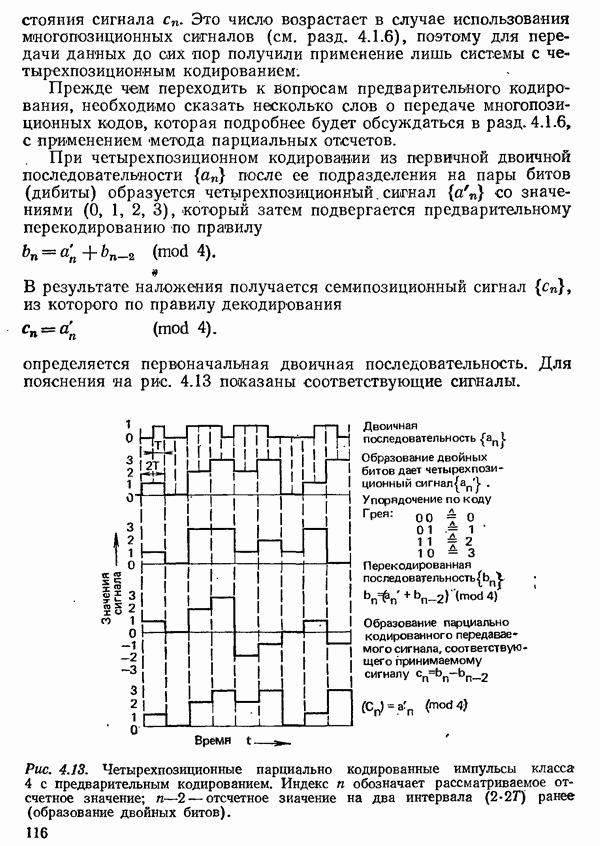
- 4.1.5. МЕТОДЫ ПАРЦИАЛЬНЫХ ОТСЧЕТОВ
- 4.1.6. ПЕРЕДАЧА МНОГОПОЗИЦИОННЫХ СИГНАЛОВ
- 4.2. МЕТОДЫ ПЕРЕДАЧИ В ПЕРВИЧНОЙ ПОЛОСЕ ЧАСТОТ
- 4.2.1. МЕТОДЫ С ПРИМЕНЕНИЕМ ДВУПОЛЯРНЫХ И ОДНОПОЛЯРНЫХ ИМПУЛЬСОВ
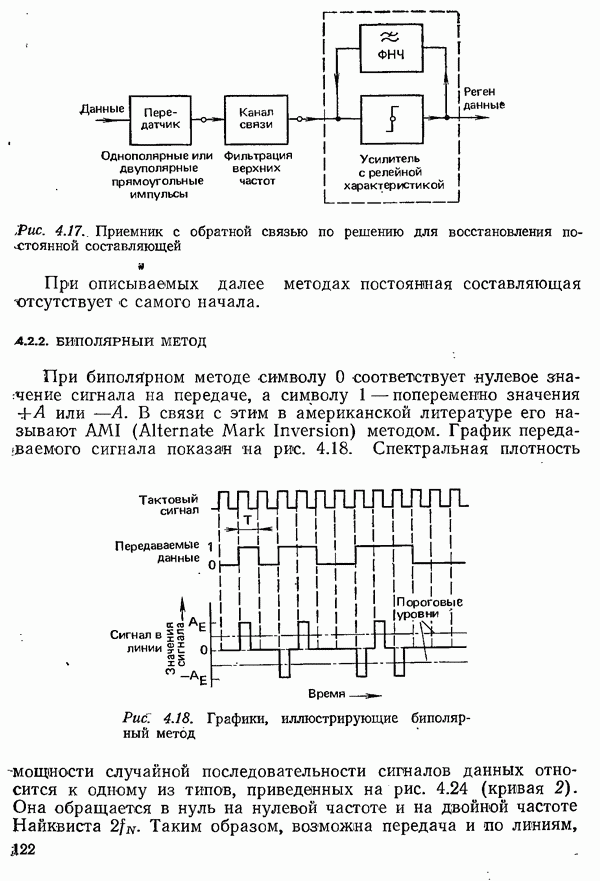
- 4.2.2. БИПОЛЯРНЫЙ МЕТОД
- 4.2.3. ПСЕВДОТРОИЧНЫЕ МЕТОДЫ
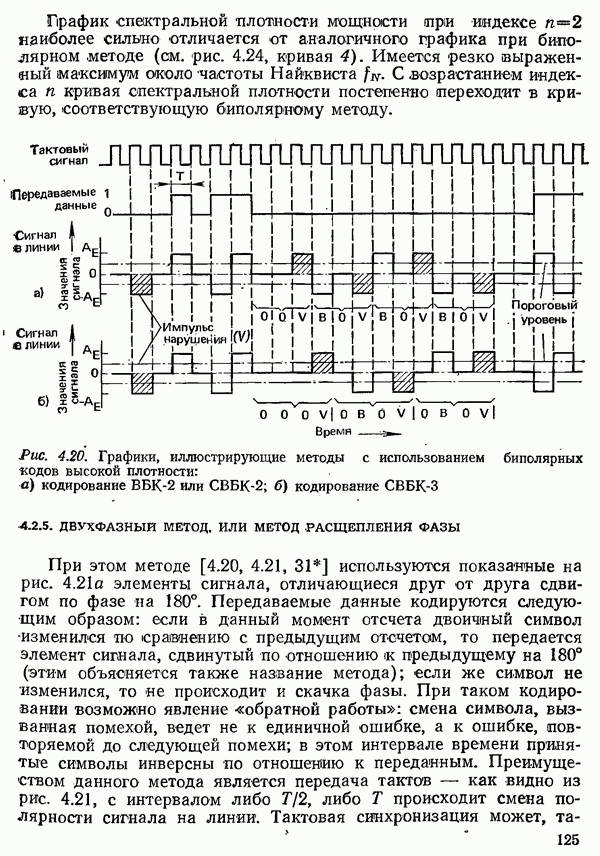
- 4.2.4. МЕТОДЫ С ПРИМЕНЕНИЕМ БИПОЛЯРНЫХ КОДОВ ВЫСОКОЙ ПЛОТНОСТИ
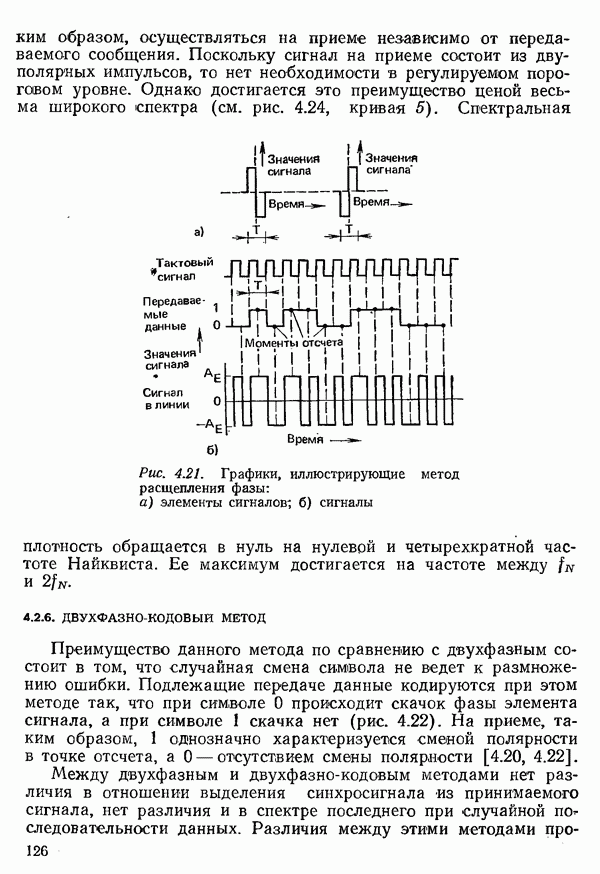
- 4.2.5. ДВУХФАЗНЫЙ МЕТОД. ИЛИ МЕТОД РАСЩЕПЛЕНИЯ ФАЗЫ
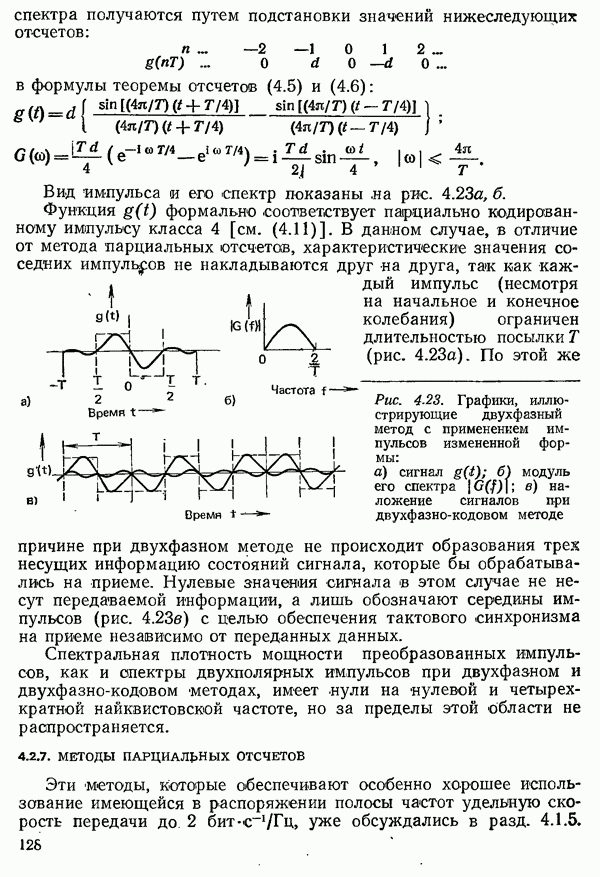
- 4.2.6. ДВУХФАЗНО-КОДОВЫЙ МЕТОД
- 4.2.7. МЕТОДЫ ПАРЦИАЛЬНЫХ ОТСЧЕТОВ
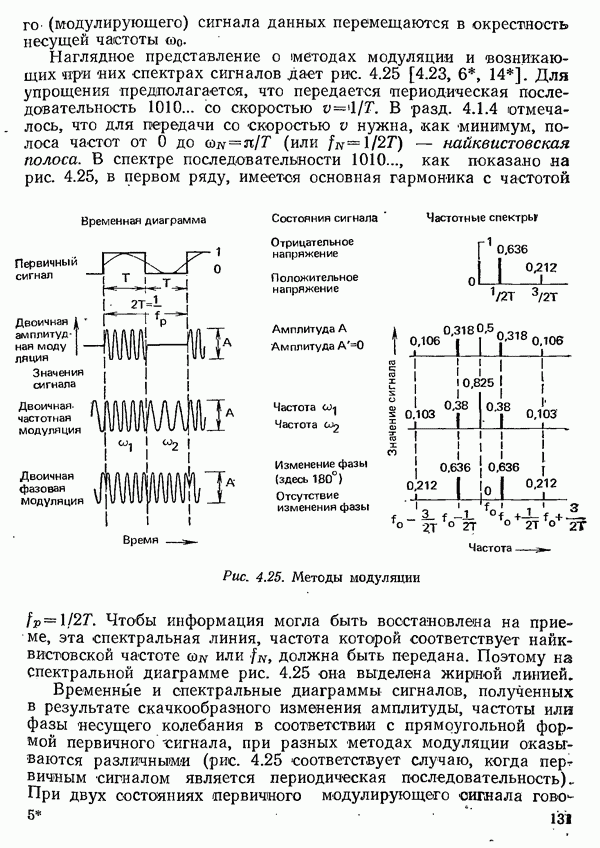
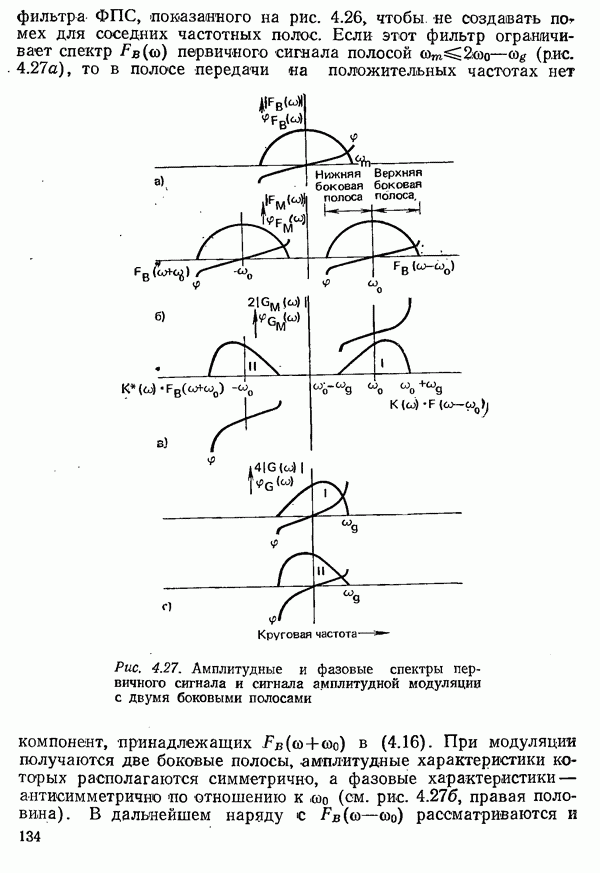
- 4.3. МЕТОДЫ ПЕРЕДАЧИ С ПРИМЕНЕНИЕМ МОДУЛЯЦИИ
- 4.3.1. АМПЛИТУДНАЯ МОДУЛЯЦИЯ
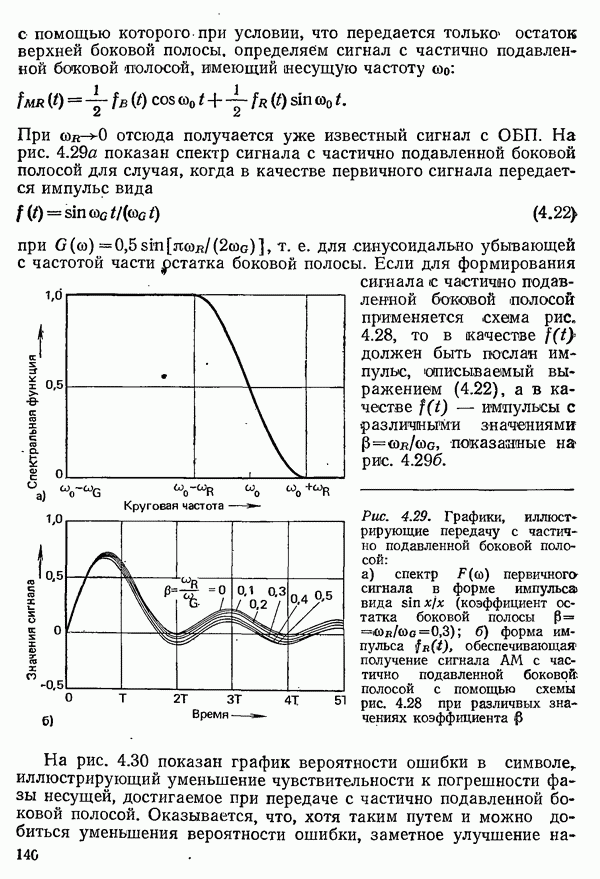
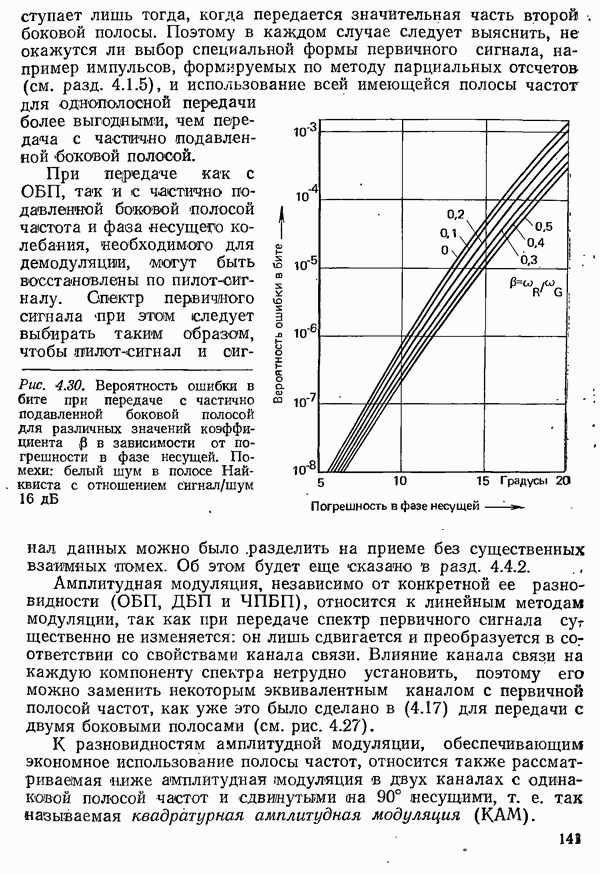
- 4.3.1.2. АМПЛИТУДНАЯ МОДУЛЯЦИЯ С ОДНОЙ БОКОВОЙ ПОЛОСОЙ И С ЧАСТИЧНО ПОДАВЛЕННОЙ БОКОВОЙ ПОЛОСОЙ
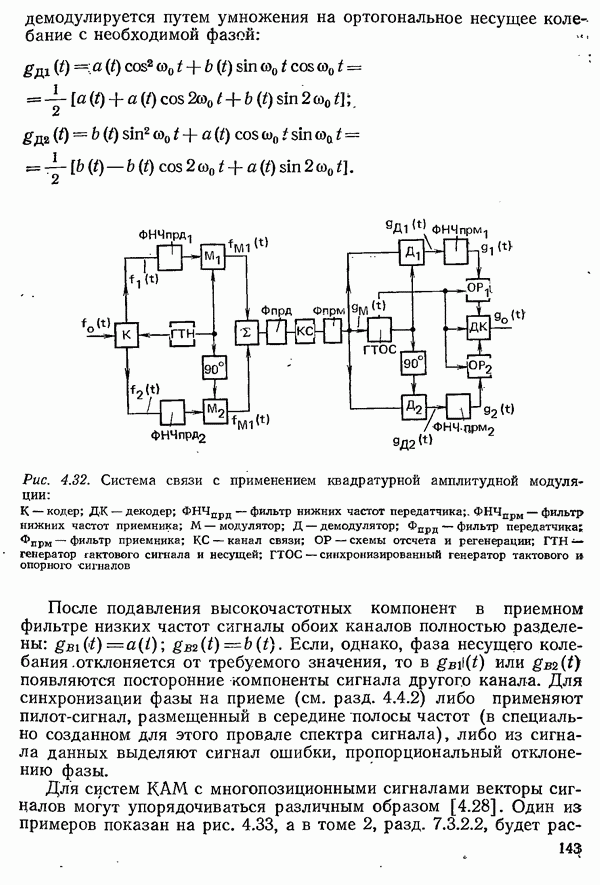
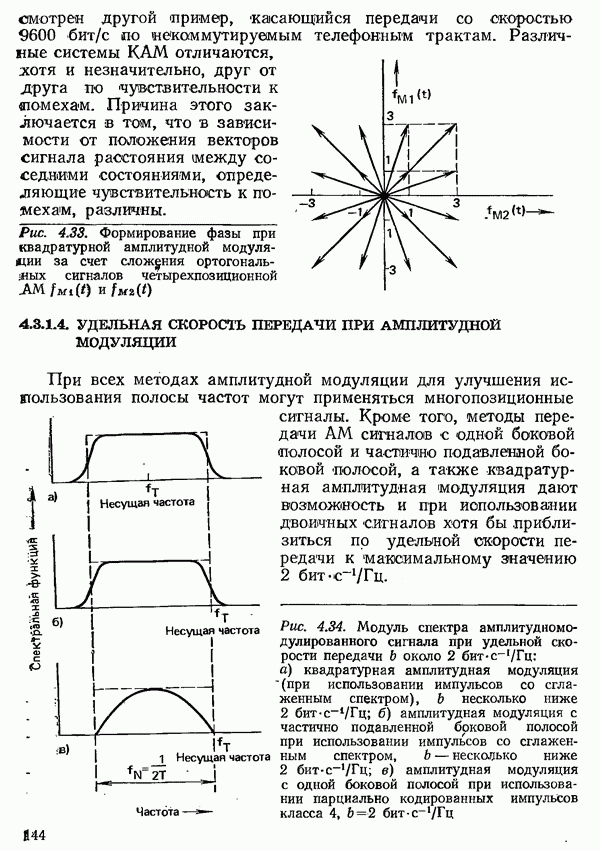
- 4.3.1.3. КВАДРАТУРНАЯ АМПЛИТУДНАЯ МОДУЛЯЦИЯ
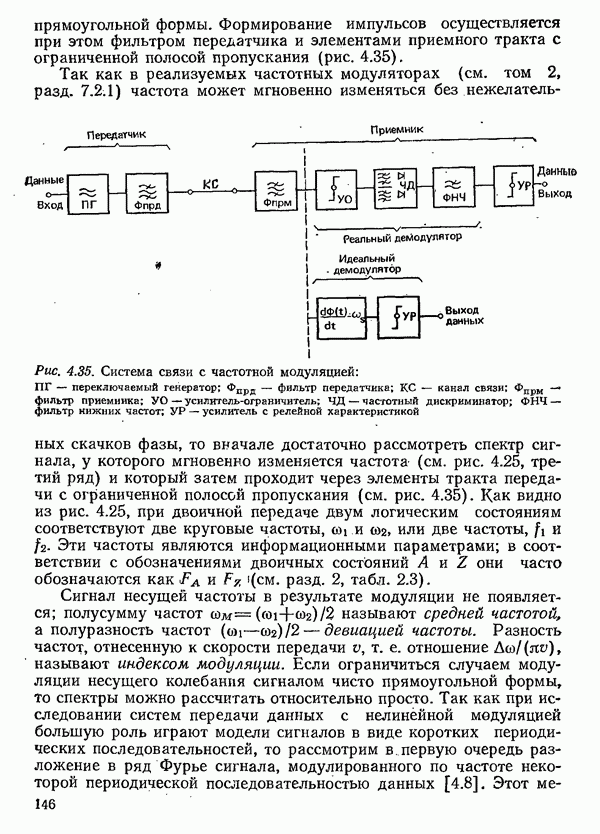
- 4.3.1.4. УДЕЛЬНАЯ СКОРОСТЬ ПЕРЕДАЧИ ПРИ АМПЛИТУДНОЙ МОДУЛЯЦИИ
- 4.3.2. ЧАСТОТНАЯ МОДУЛЯЦИЯ
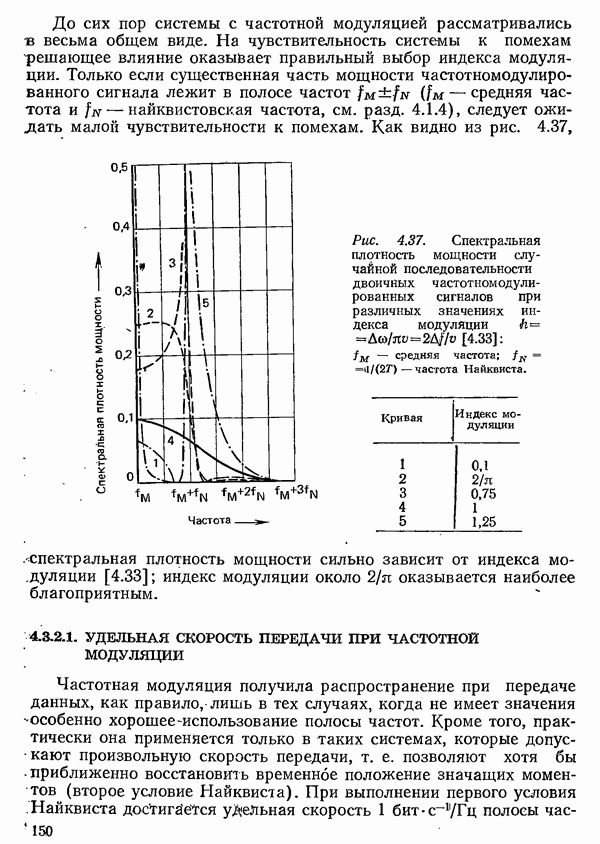
- 4.3.2.1. УДЕЛЬНАЯ СКОРОСТЬ ПЕРЕДАЧИ ПРИ ЧАСТОТНОЙ МОДУЛЯЦИИ
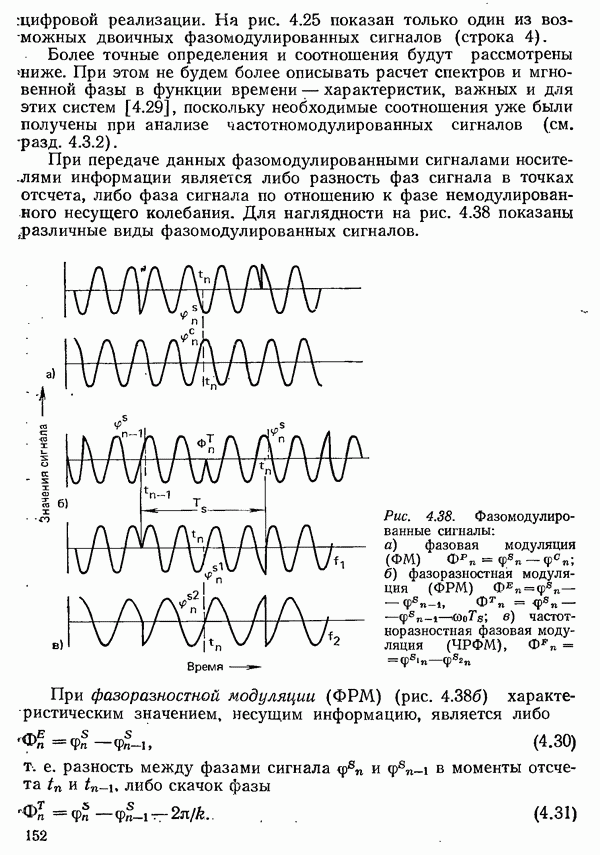
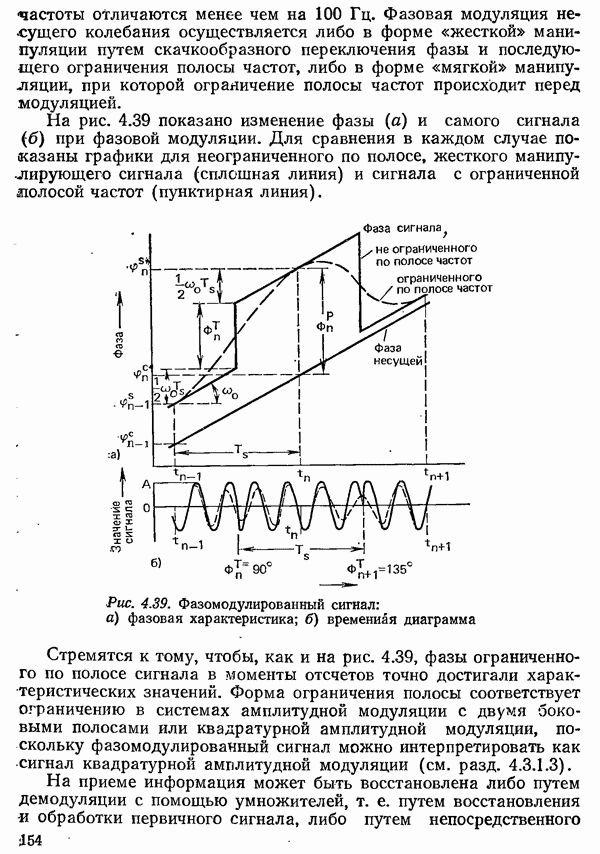
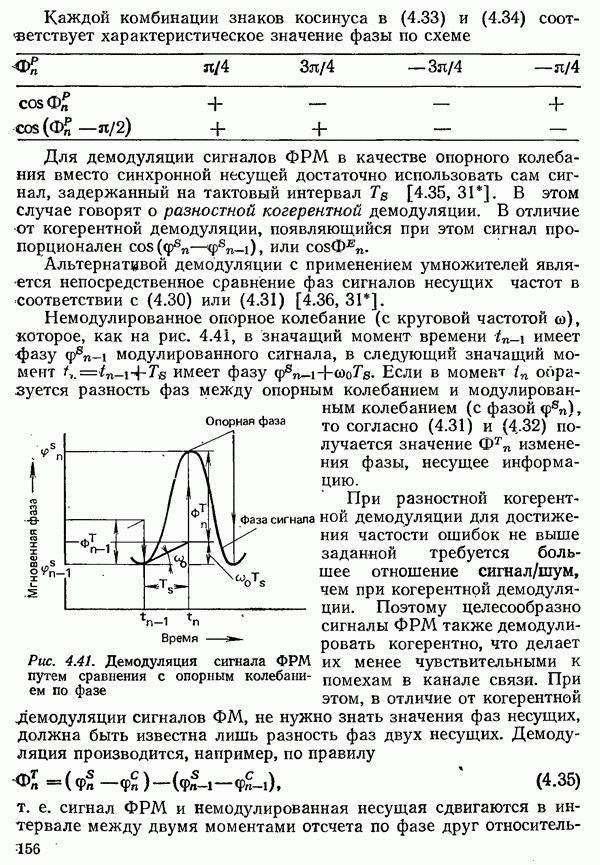
- 4.3.3. ФАЗОВАЯ МОДУЛЯЦИЯ
- 4.4. ВОССТАНОВЛЕНИЕ ТАКТОВ И НЕСУЩЕЙ
- 4.4.2. ВОССТАНОВЛЕНИЕ ЧАСТОТЫ И ФАЗЫ НЕСУЩЕЙ
- 4.5. ВЕРОЯТНОСТЬ ОШИБКИ ПРИ НАЛИЧИИ ПОМЕХ
- 4.5.1. ВЕРОЯТНОСТЬ ОШИБКИ ПРИ УЧЕТЕ ТОЛЬКО ШУМА В КАНАЛЕ СВЯЗИ
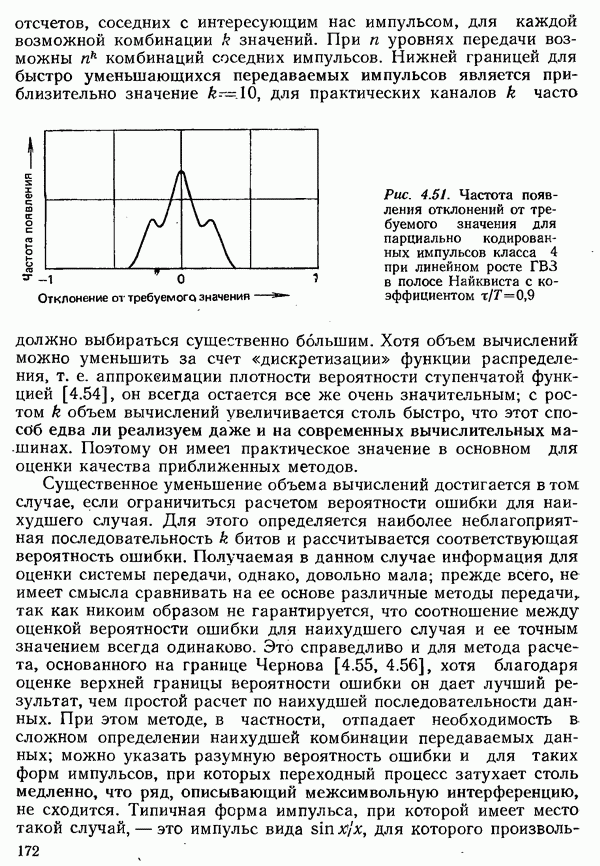
- 4.5.2. ВЕРОЯТНОСТЬ ОШИБКИ С УЧЕТОМ ЛИНЕЙНЫХ ИСКАЖЕНИЙ
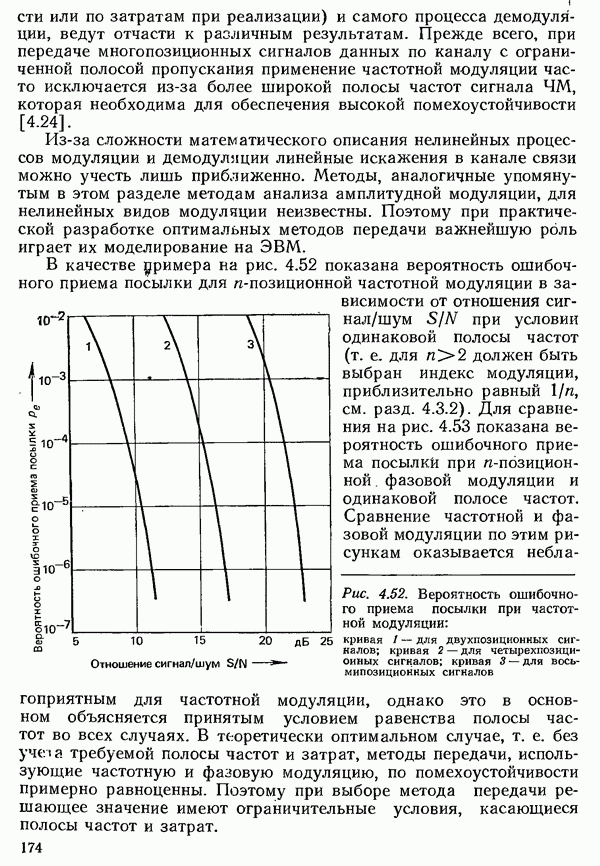
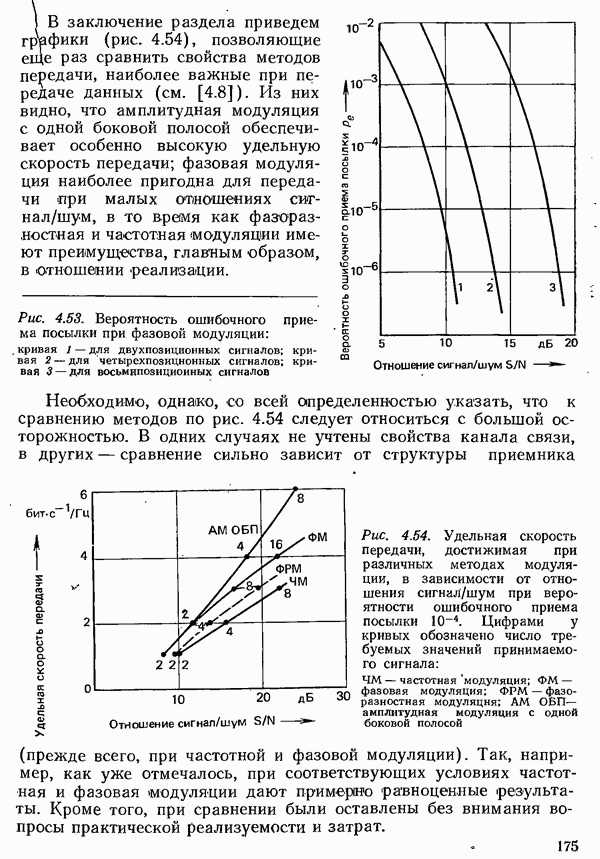
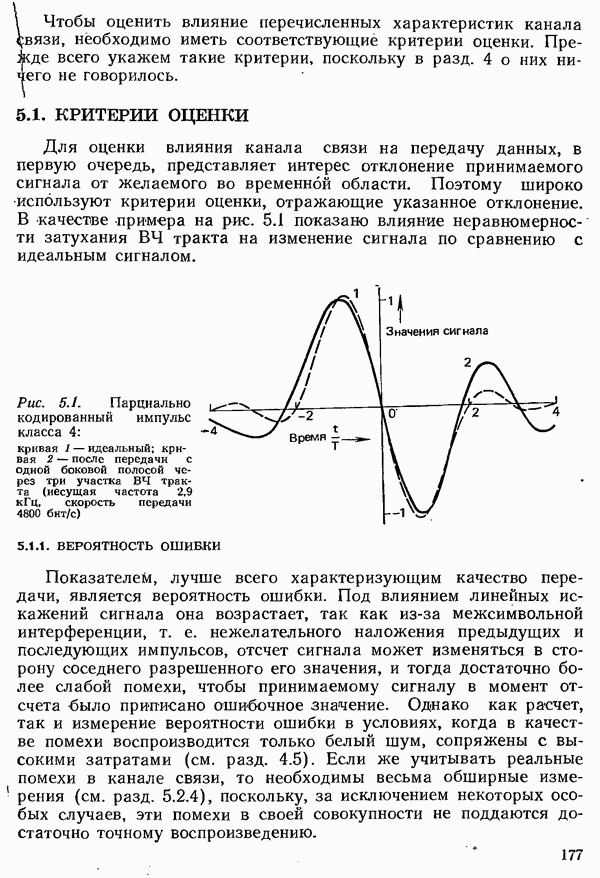
- 4.5.3. ВЕРОЯТНОСТЬ ОШИБКИ С УЧЕТОМ ПРОЦЕССОВ МОДУЛЯЦИИ И ДЕМОДУЛЯЦИИ
- 5. Учет свойств реальных каналов связи при передаче данных
- 5.2. ВЛИЯНИЕ ХАРАКТЕРИСТИК КАНАЛОВ СВЯЗИ НА ПЕРЕДАЧУ ДАННЫХ
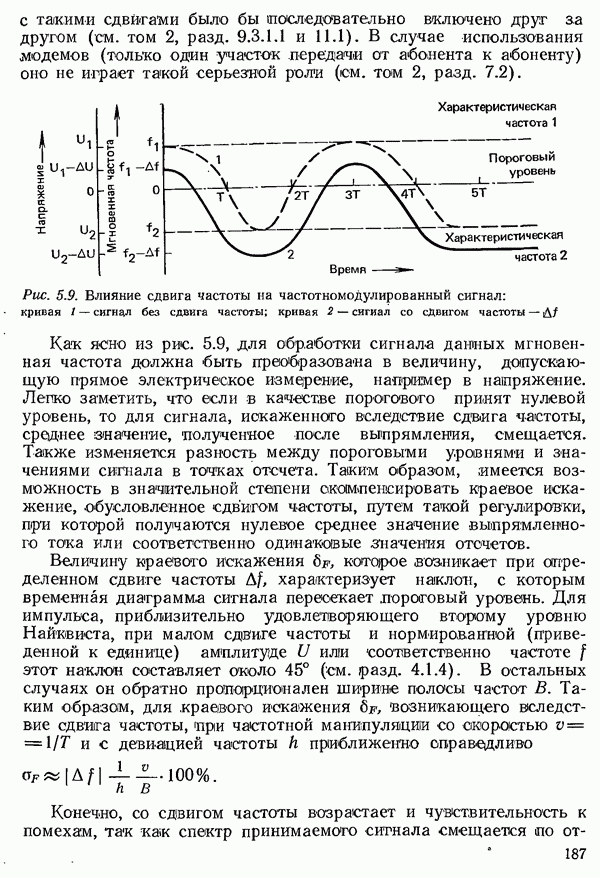
- 5.2.2. СДВИГИ ЧАСТОТЫ
- 5.2.3. ФАЗОВОЕ ДРОЖАНИЕ
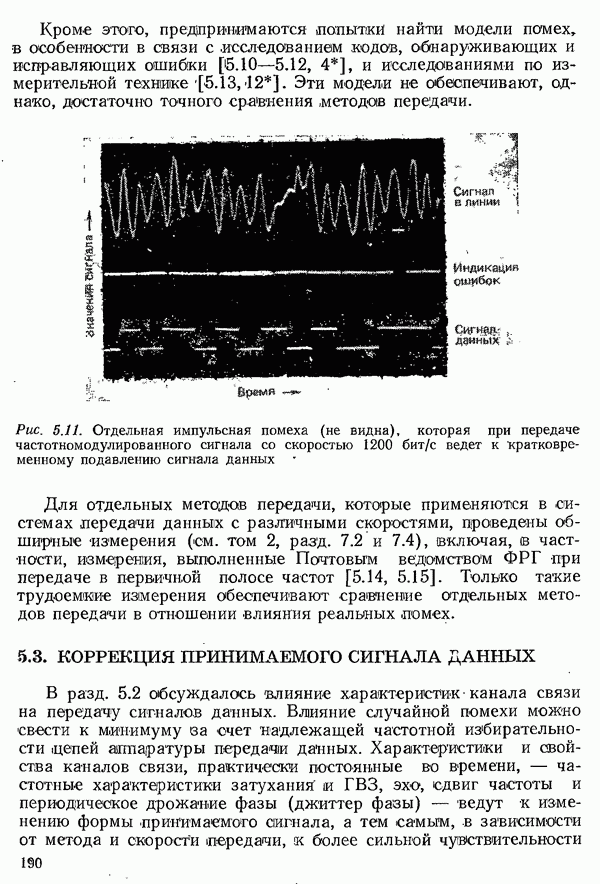
- 5.2.4. ВЛИЯНИЕ РЕАЛЬНЫХ ПОМЕХ
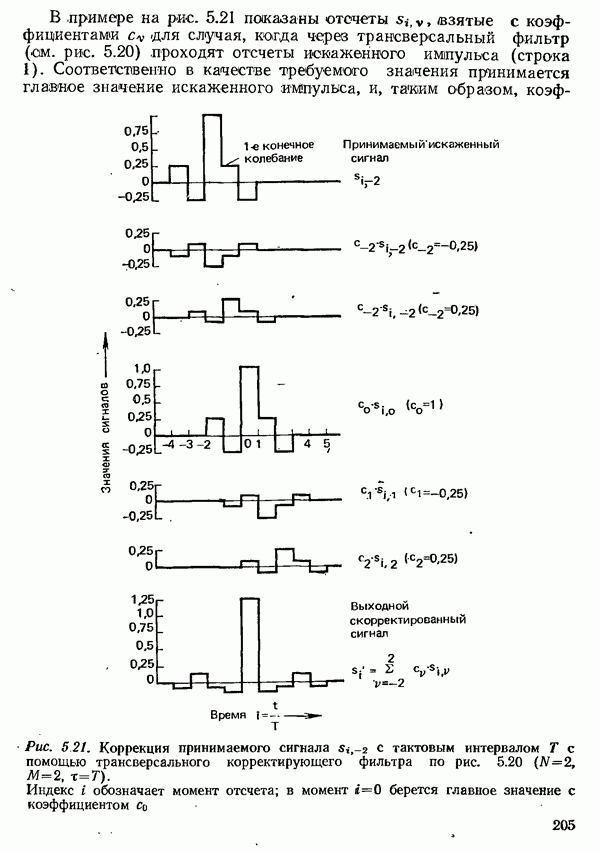
- 5.3. КОРРЕКЦИЯ ПРИНИМАЕМОГО СИГНАЛА ДАННЫХ
- 5.3.1. КОРРЕКЦИЯ ПРИНИМАЕМОГО СИГНАЛА ДАННЫХ В ЧАСТОТНОЙ ОБЛАСТИ
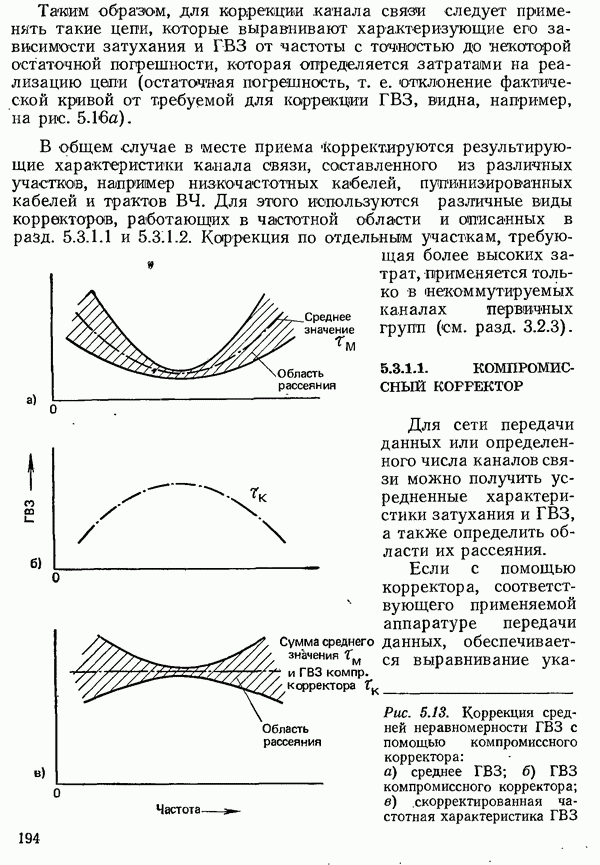
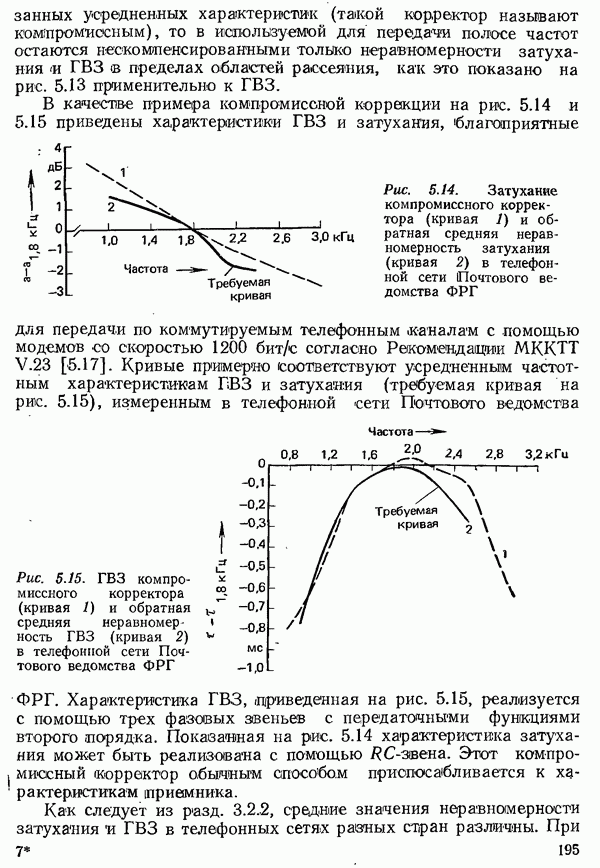
- 5.3.1.1. КОМПРОМИССНЫЙ КОРРЕКТОР
- 5.3.1.2. НАСТРАИВАЕМЫЙ ЧАСТОТНЫЙ КОРРЕКТОР СИГНАЛОВ ДАННЫХ
- 5.3.2. КОРРЕКЦИЯ ПРИНИМАЕМОГО СИГНАЛА ДАННЫХ ВО ВРЕМЕННОЙ ОБЛАСТИ
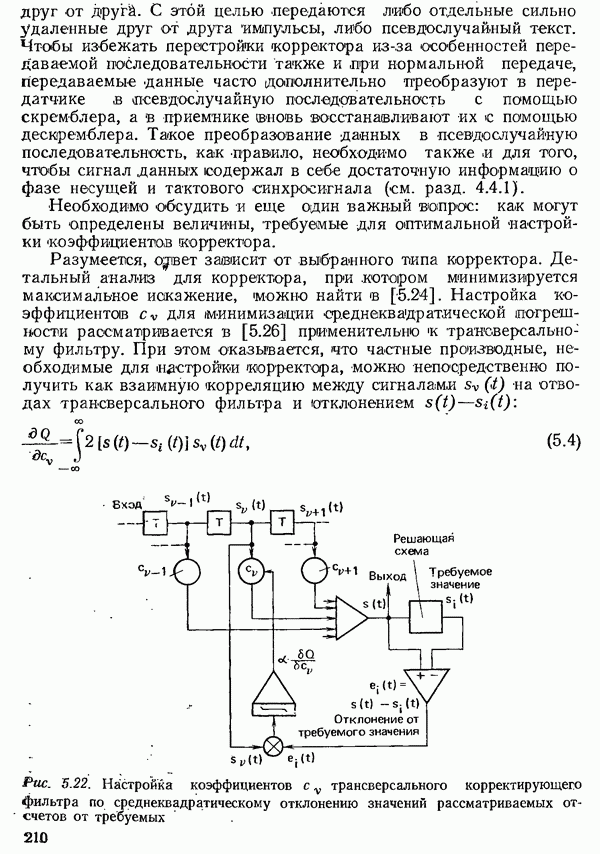
- 5.3.2.2. КРИТЕРИИ НАСТРОЙКИ КОРРЕКТОРА ВО ВРЕМЕННОЙ ОБЛАСТИ
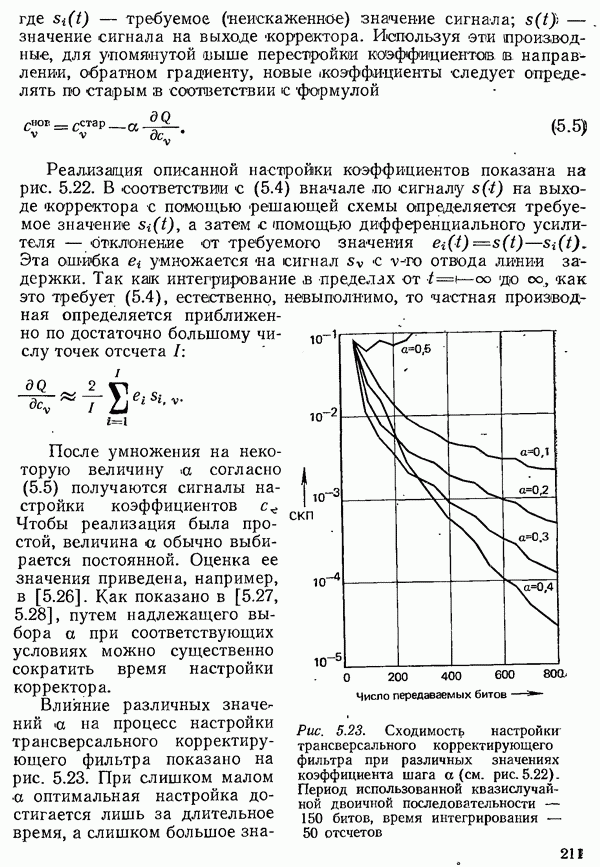
- 5.3.2.3. АВТОМАТИЧЕСКАЯ НАСТРОЙКА ТРАНСВЕРСАЛЬНОГО КОРРЕКТИРУЮЩЕГО ФИЛЬТРА
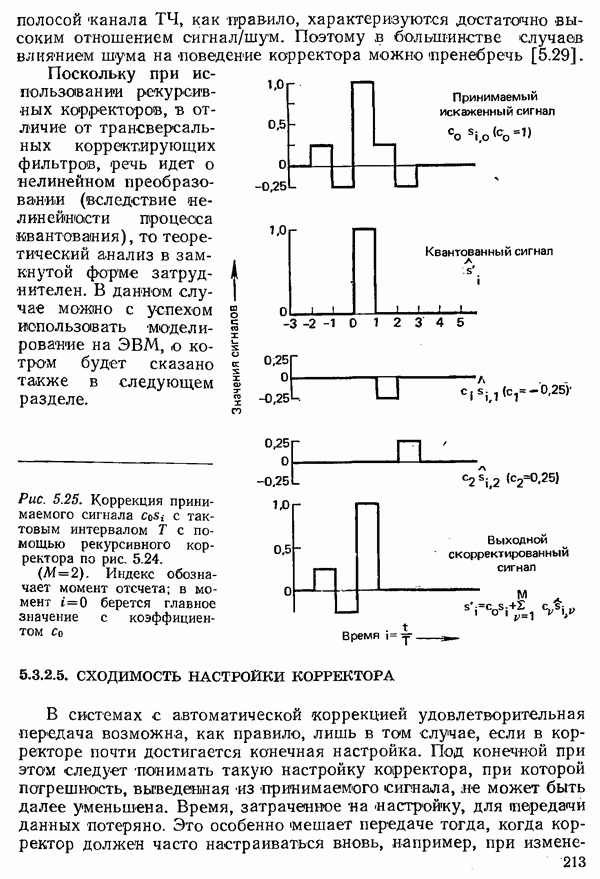
- 5.3.2.4. РЕКУРСИВНЫЙ КОРРЕКТОР
- 5.3.2.5. СХОДИМОСТЬ НАСТРОЙКИ КОРРЕКТОРА
- 5.3.2.6. КОРРЕКТОР ДЛЯ СПЕЦИАЛЬНЫХ МЕТОДОВ ПЕРЕДАЧИ
- 6. Основы коммутации данных
- 6.1.2. МЕТОДЫ КОММУТАЦИИ
- 6.1.3. СПОСОБЫ КОММУТАЦИИ КАНАЛОВ
- 6.1.4. СИГНАЛИЗАЦИЯ
- 6.1.5. УПРАВЛЕНИЕ ПРОЦЕССАМИ СОЕДИНЕНИЯ И РАЗЪЕДИНЕНИЯ
- 6.1.6. ПОДРАЗДЕЛЕНИЕ ЦЕПЕЙ КОММУТАЦИИ КАНАЛОВ
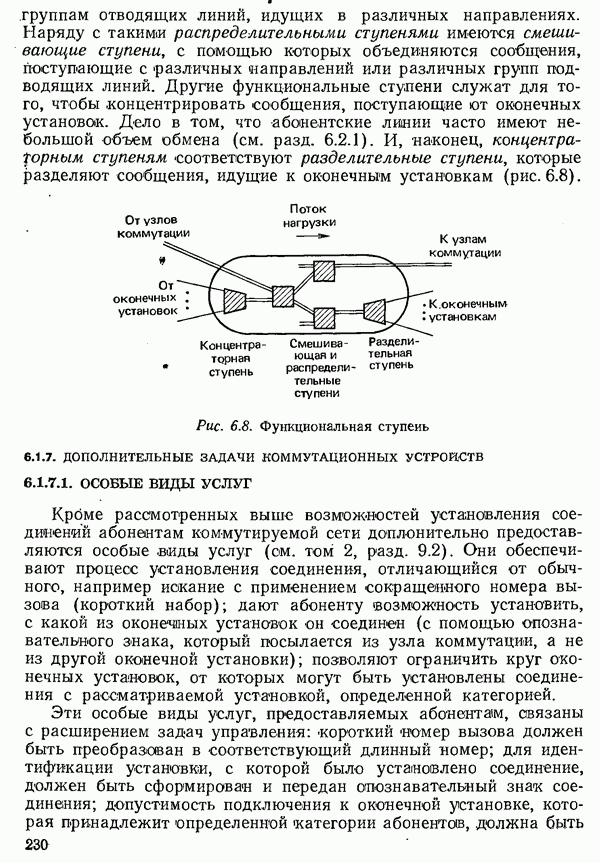
- 6.1.7. ДОПОЛНИТЕЛЬНЫЕ ЗАДАЧИ КОММУТАЦИОННЫХ УСТРОЙСТВ
- 6.2. АНАЛИЗ СИСТЕМ КОММУТАЦИИ НА ОСНОВЕ ТЕОРИИ ТЕЛЕТРАФИКА
- 6.2.2. СИСТЕМЫ С ПОТЕРЯМИ
- 6.2.3. СИСТЕМЫ С ОЖИДАНИЕМ
- 6.2.4. ИЗМЕРЕНИЯ НАГРУЗКИ
- СПИСОК ЛИТЕРАТУРЫ