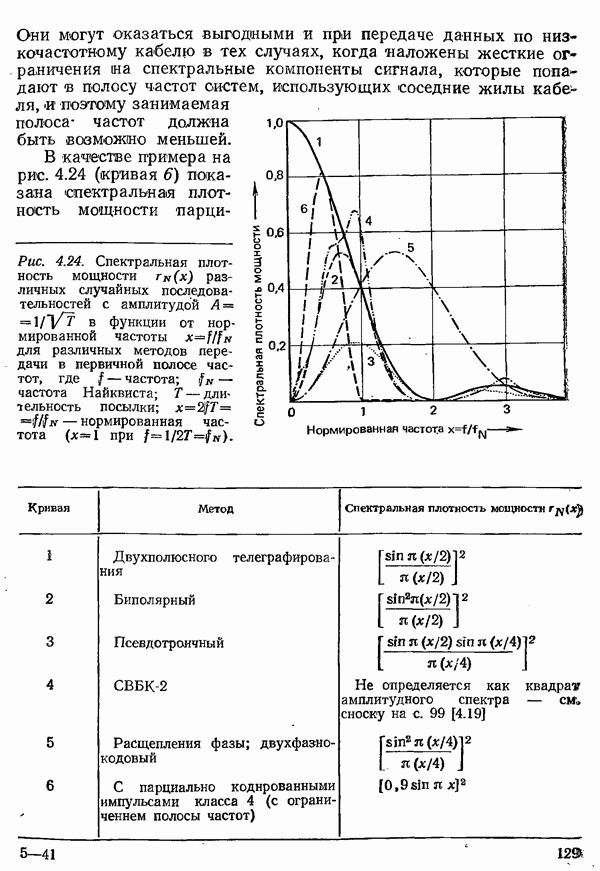
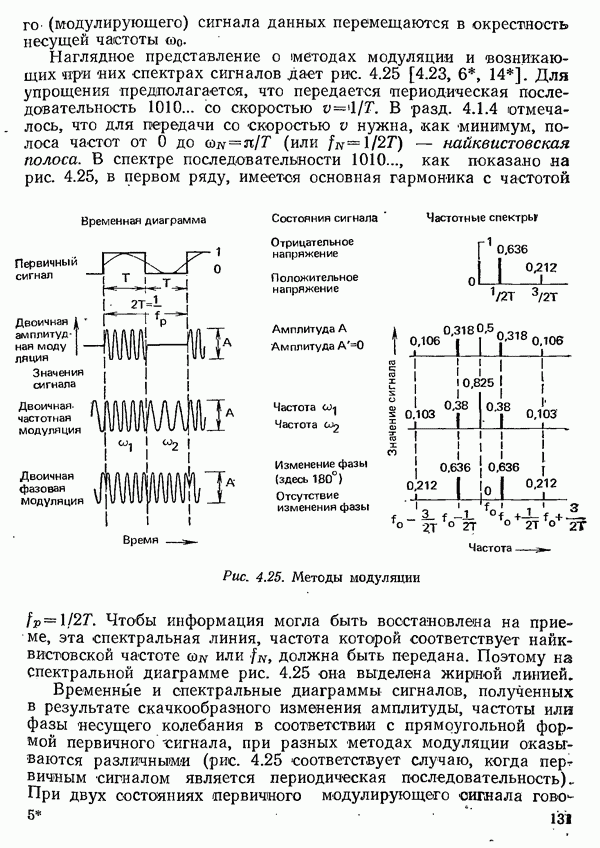
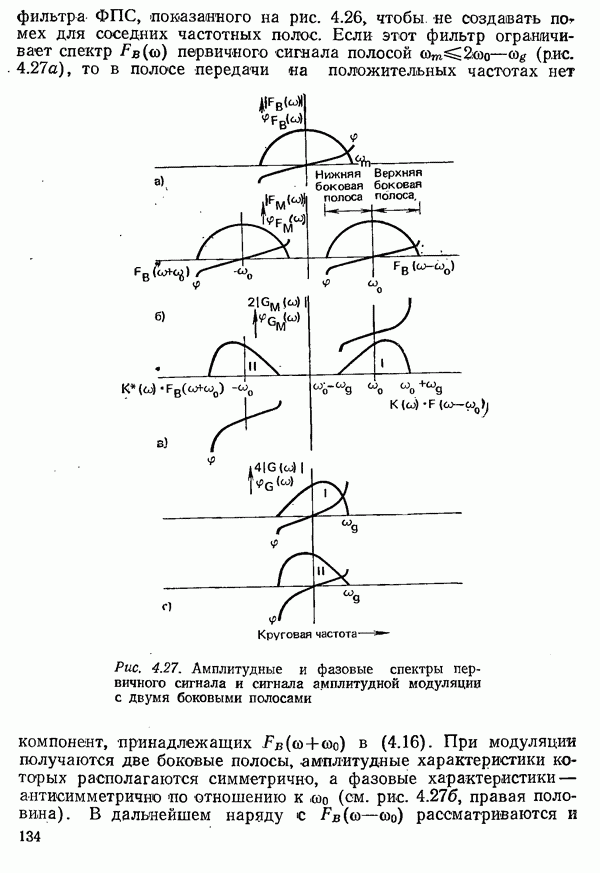
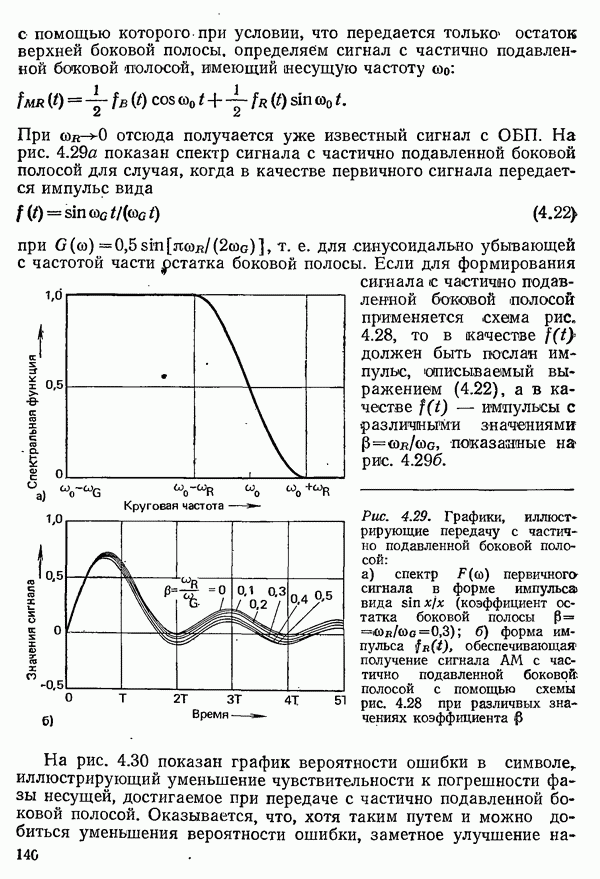
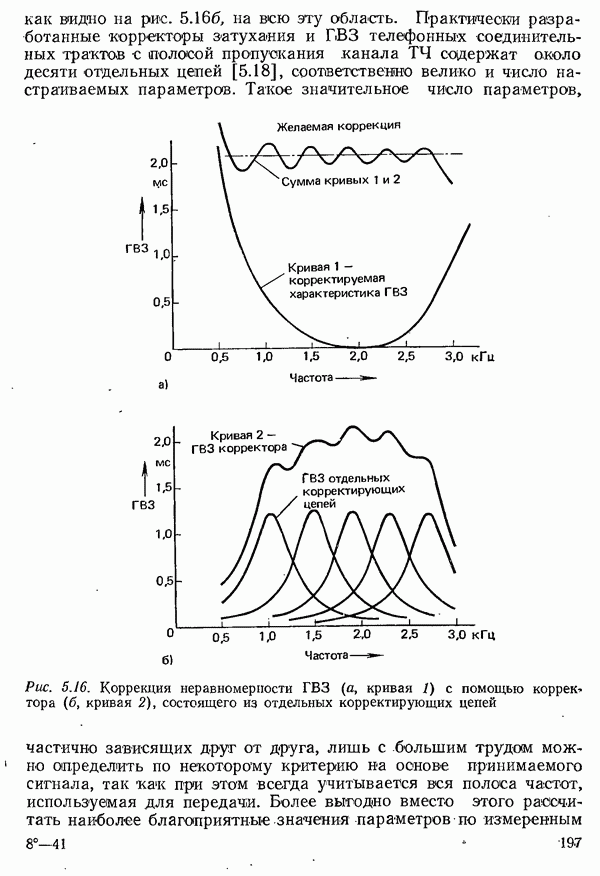
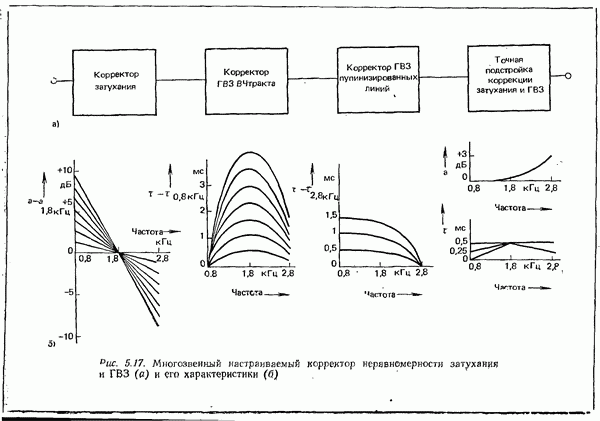
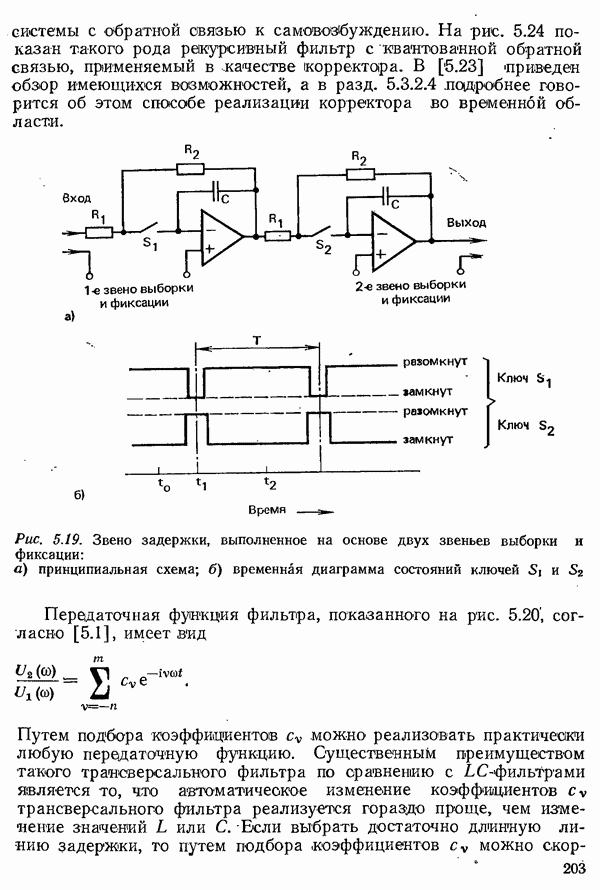
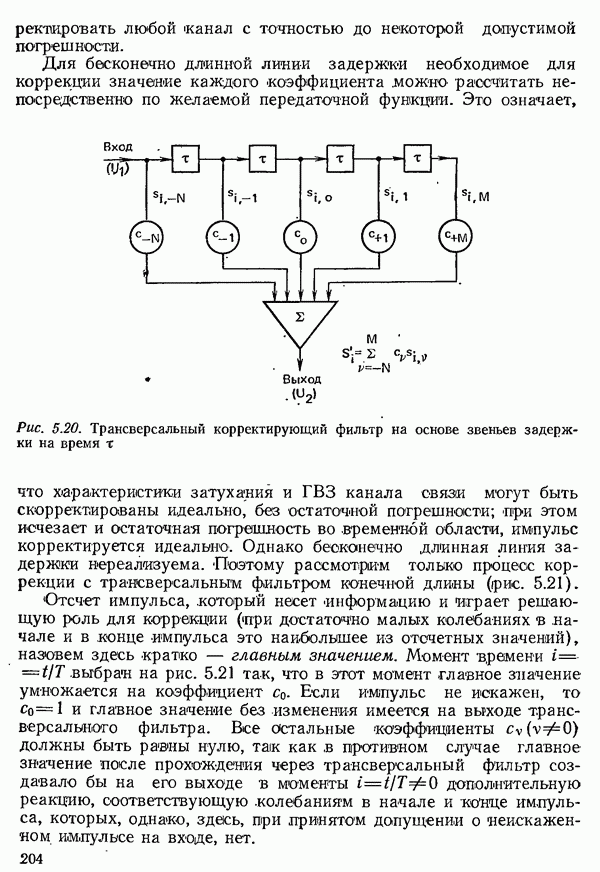
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
6.2.3. СИСТЕМЫ С ОЖИДАНИЕМ
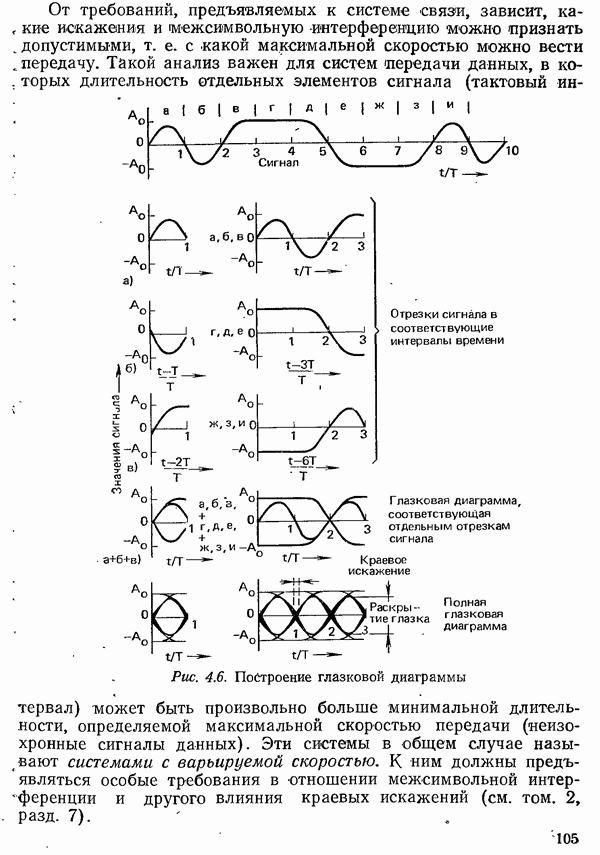
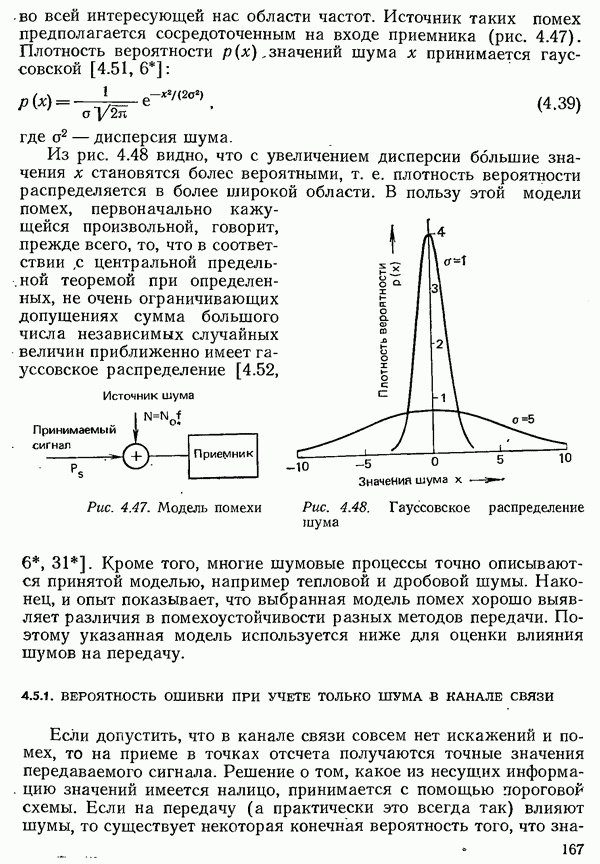
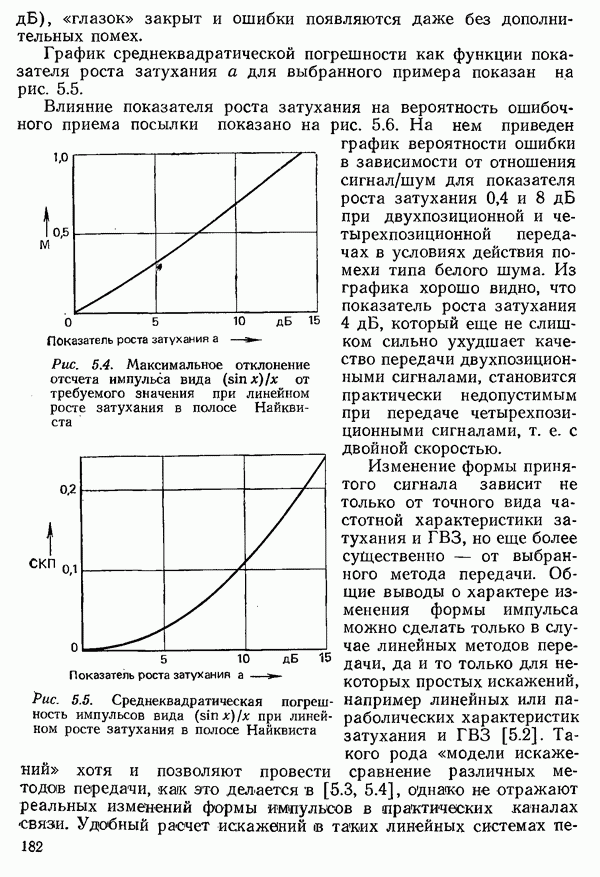
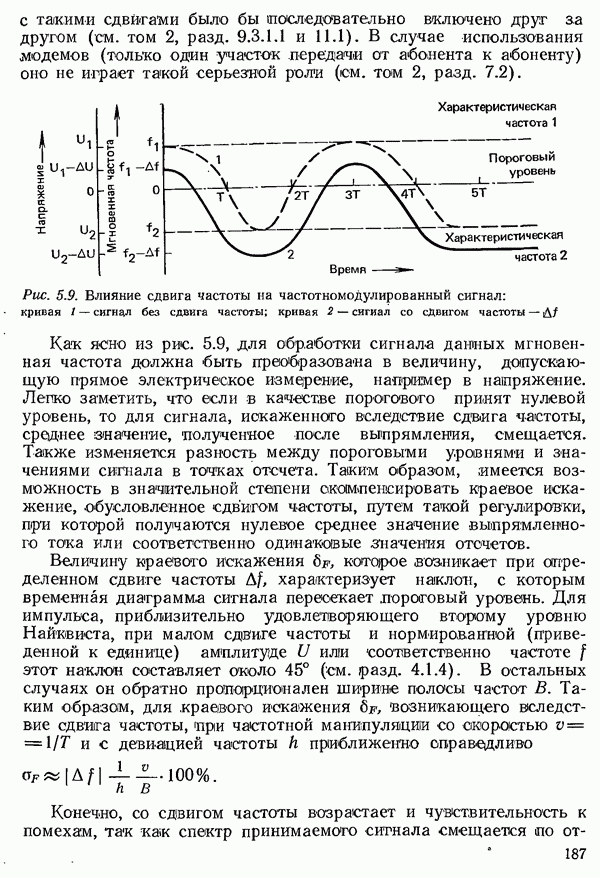
Определяющим показателем для оценки системы с ожиданием [6.17, 6.18] является вероятность того, что вызов должен ожидать обслуживания в течение времени, большего  е. вероятность превышения
е. вероятность превышения  (в частности, вероятность
(в частности, вероятность  того, что вызов вообще должен ожидать обслуживания). Другим важным показателем часто служит среднее время ожидания для всех вызовов
того, что вызов вообще должен ожидать обслуживания). Другим важным показателем часто служит среднее время ожидания для всех вызовов  или же среднее время ожидания обслуживания для ожидающих вызовов
или же среднее время ожидания обслуживания для ожидающих вызовов 
Два последних показателя связаны между собой соотношением

поскольку среднее время ожидания для всех вызовов складывается из указанных в формуле частей времени ожидания для ожидающих и неожидающих вызовов.
Размеры очереди определяются количеством ожидающих обслуживания вызовов. Его среднее значение  само по себе, конечно, не достаточное для определения размеров очереди, рассчитывается по среднему числу вызовов, поступающих в единицу времени,
само по себе, конечно, не достаточное для определения размеров очереди, рассчитывается по среднему числу вызовов, поступающих в единицу времени,  и среднему времени ожидания всех вызовов (поскольку все вызовы могут ожидать обслуживания сколь угодно долго и, следовательно, ни время ожидания, ни длина очереди не ограничены),
и среднему времени ожидания всех вызовов (поскольку все вызовы могут ожидать обслуживания сколь угодно долго и, следовательно, ни время ожидания, ни длина очереди не ограничены),

В таком виде соотношение справедливо для совокупности всех вызовов; если применяются приоритеты, то соответствующее соотношение справедливо для каждого приоритета 

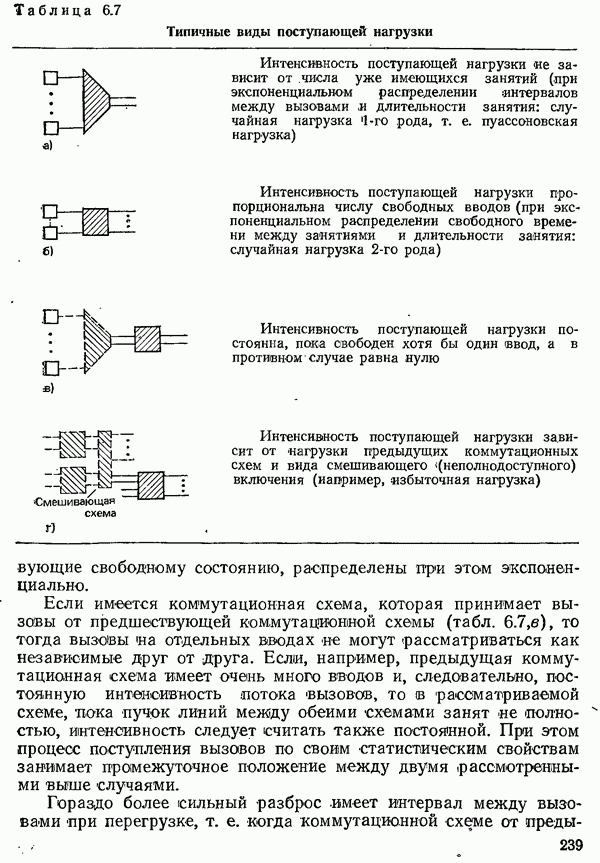
В дальнейшем будем исходить из того, что интенсивность поступающей нагрузки не зависит от состояния и интервалы между вызовами распределены по экспоненциальному закону. Рассмотрим вначале схемы с  выводами, а затем такие же схемы с одним выводом. В системах с ожиданием они играют большую роль, так как в общем случае доступ к центральным коммутационным устройствам осуществляется через систему с ожиданием. По той же причине особое значение имеет случай, когда длительность занятия постоянна. Системы с ожиданием, имеющие ограниченную доступность, напротив, здесь не рассматриваются, т. е. в дальнейшем предполагается полная доступность.
выводами, а затем такие же схемы с одним выводом. В системах с ожиданием они играют большую роль, так как в общем случае доступ к центральным коммутационным устройствам осуществляется через систему с ожиданием. По той же причине особое значение имеет случай, когда длительность занятия постоянна. Системы с ожиданием, имеющие ограниченную доступность, напротив, здесь не рассматриваются, т. е. в дальнейшем предполагается полная доступность.
6.2.3.1. СИСТЕМЫ С ОЖИДАНИЕМ БЕЗ ПРИОРИТЕТОВ
Используя тот же подход, что и при описании систем с потерями, рассмотрим систему со многими выводами, которая имеет случайную нагрузку. Пусть имеется только одна очередь и нет приоритетов. Предположим, что очередь и время ожидания не ограничены, а вызовы обрабатываются в порядке их поступления. Процесс является стационарным только в том случае, если вызовов поступает в среднем меньше, чем может быть обслужено с помощью  выводов, т. е. А должно быть меньше
выводов, т. е. А должно быть меньше 
Вероятность ожидания определяется вероятностью того, что вызов поступил и должен ждать, деленной на вероятность того, что вызов вообще поступает в тот же отрезок времени. При случайном обмене первого рода, используя вероятности состояний, получаем выражение

аналогичное формуле потерь Эрланга. Вероятность того, что все  выводов замяты и обслуживания ожидают
выводов замяты и обслуживания ожидают  вызовов,
вызовов,

а среднее число всех ожидающих вызовов

Вероятность  конечна и при очень малом обмене. Чем ближе значение интенсивности поступающей нагрузки к числу выводов, тем больше число ожидающих вызовов, в то время как вероятность ожидания, так же как и
конечна и при очень малом обмене. Чем ближе значение интенсивности поступающей нагрузки к числу выводов, тем больше число ожидающих вызовов, в то время как вероятность ожидания, так же как и  приближается к единице.
приближается к единице.
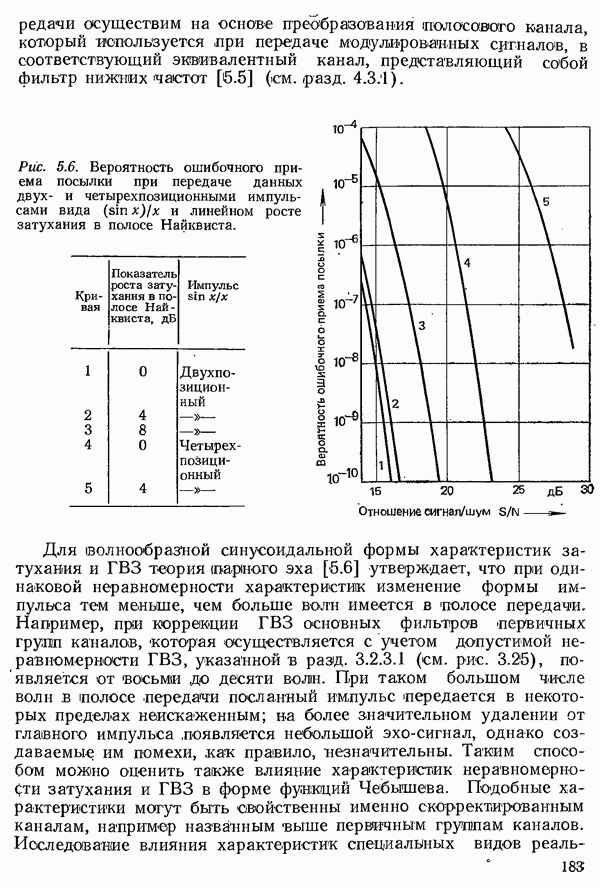
Вследствие экспоненциального распределения длительности занятия время ожидания имеет такое же распределение. Таким образом, вызов ожидает обработки в течение времени, большего  с вероятностью
с вероятностью

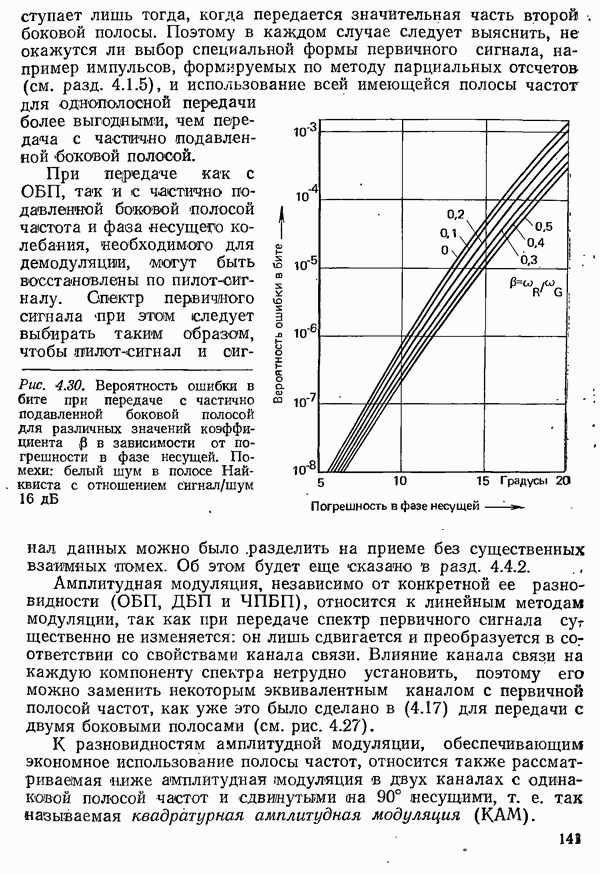
(рис. 6.14). Здесь  среднее время ожидания для ожидающих вызовов. И при очень малой интенсивности поступающей нагрузки значение не меньше
среднее время ожидания для ожидающих вызовов. И при очень малой интенсивности поступающей нагрузки значение не меньше  так как если вызов вообще ожидает, то в среднем он должен ждать до тех пор, пока вывод не освободится. Среднее время ожидания
так как если вызов вообще ожидает, то в среднем он должен ждать до тех пор, пока вывод не освободится. Среднее время ожидания  всех вызовов,
всех вызовов,

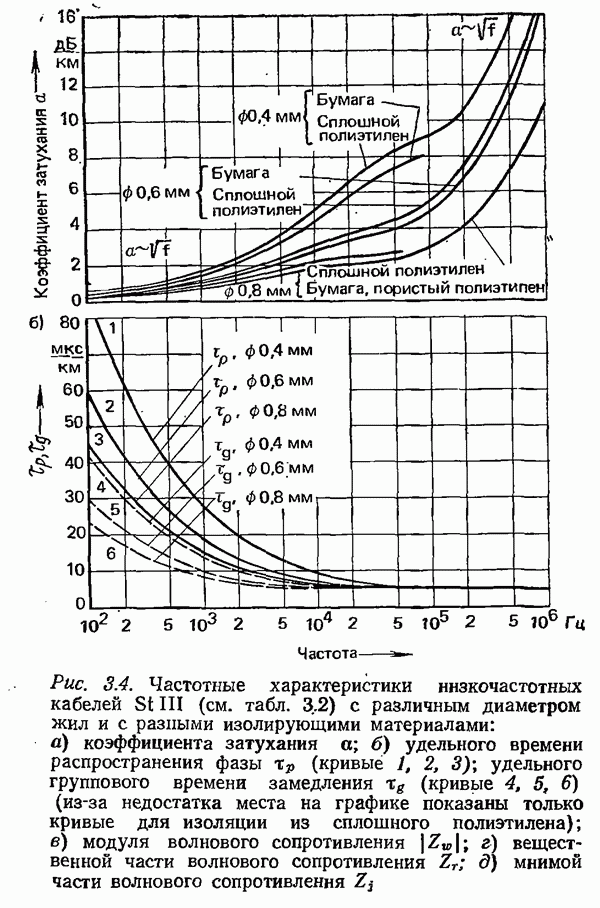
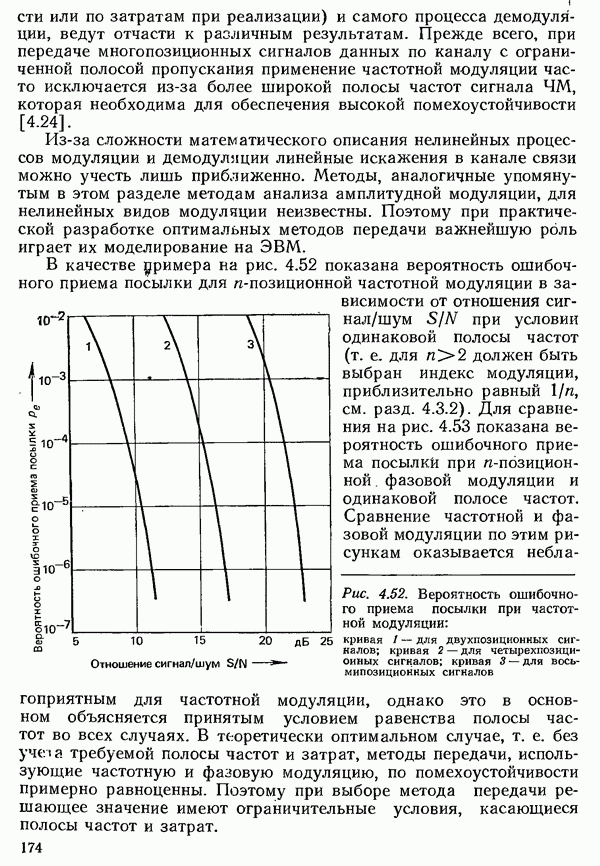
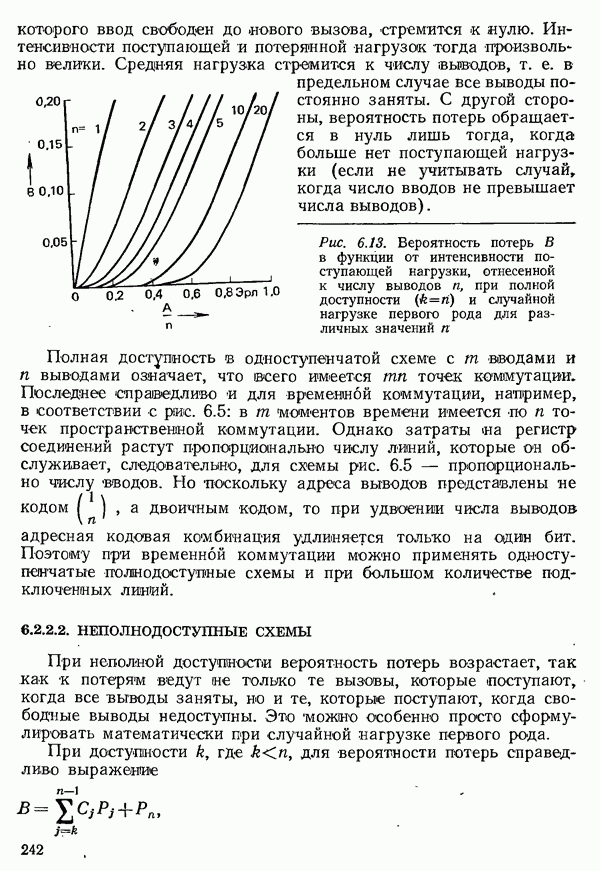
Рис. 6.14. Вероятность  того, что время ожидания больше
того, что время ожидания больше  в функции от
в функции от  для различного числа выводов
для различного числа выводов  при поступающей нагрузке А, отнесенной к числу выводов
при поступающей нагрузке А, отнесенной к числу выводов  равной
равной  полной доступности и случайной нагрузке первого рода
полной доступности и случайной нагрузке первого рода
(наоборот, при малых значениях интенсивности поступающей нагрузки, как и вероятность ожидания, весьма мало.
В рассмотренном выше примере предполагалось, что вызовы обслуживаются в порядке их поступления (первым поступил — первым обслужен). Это допущение оказывает влияние на распределение вероятностей времени ожидания. Однако до тех пор, пока ожидаемая длительность занятия не учитывается, вероятность ожидания и среднее время ожидания не зависят от дисциплины очереди. Это справедливо как для случайной нагрузки второго рода, так и для пуаоооновского процесса.
Влияние дисциплины очереди, прежде всего, проявляется при рассеянии времени ожидания. Для времени ожидания ,в качестве крайних случаев удобно было рассматривать постоянное и экспоненциально распределенное время ожидания. Для дисциплины очереди роль тких случаев играют обслуживание в порядке поступления вызовов и обслуживание на основе случайного выбора из очереди (случайность при этом означает, что если вывод освобождается, то каждый из ожидающих вызовов может быть выбран с одинаковой вероятностью). Случайный выбор приводит к тому, что время ожидания рассеивается сильнее, чем при обслуживании вызовов в порядке их поступления. Вероятность превышения для малых значений времени ожидания становится меньше, а для больших — больше [6.19].
Другая дисциплина очереди может быть связана с еще большим рассеянием времени ожидания; предельным случаем является обслуживание в порядке, противоположном поступлению вызовов (пришел последним — обслужен первым).
Для систем с ожиданием, имеющих один вывод, справедливы приведенные выше соотношения при  кроме того, следует отметить еще некоторые весьма общие свойства. Так, вероятность
кроме того, следует отметить еще некоторые весьма общие свойства. Так, вероятность  независимо от распределения длительности занятия и от дисциплины очереди предполагает, что в дисциплине очереди не учитывается ожидаемая в каждом случае длительность занятия и что интервалы между вызовами распределены экспоненциально. Напротив, вероятность превышения зависит как от распределения длительности занятия, так и от дисциплины очереди.
независимо от распределения длительности занятия и от дисциплины очереди предполагает, что в дисциплине очереди не учитывается ожидаемая в каждом случае длительность занятия и что интервалы между вызовами распределены экспоненциально. Напротив, вероятность превышения зависит как от распределения длительности занятия, так и от дисциплины очереди.
При тех же предположениях от дисциплины очереди не зависят также среднее число ожидающих вызовов и их среднее время ожидания. Распределение длительности занятия влияет на эти средние значения лишь постольку, поскольку они ведут к различным значениям рассеяния от длительности занятия:

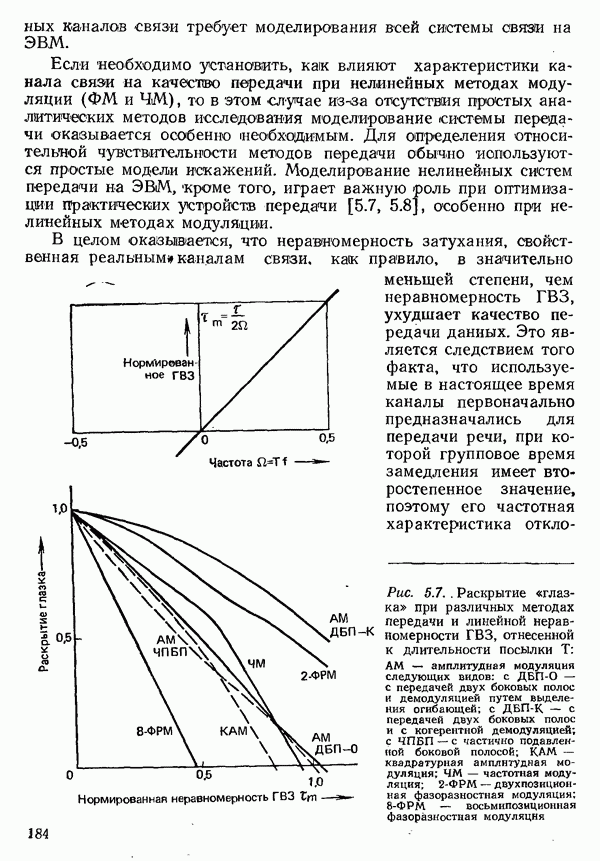
При одинаковых средних значениях длительности занятия и равной интенсивности поступающей нагрузки среднее время
ожидания получается наименьшим в случае постоянной длительности замятия  при экспоненциальном распределении
при экспоненциальном распределении  время ожидания вдвое больше (рис. 6.15).
время ожидания вдвое больше (рис. 6.15).

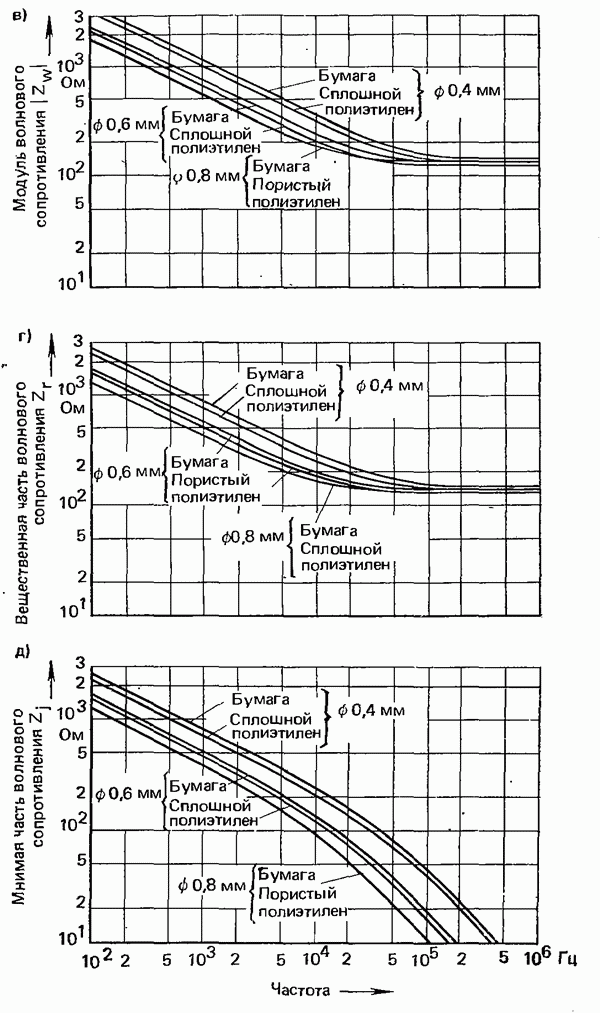
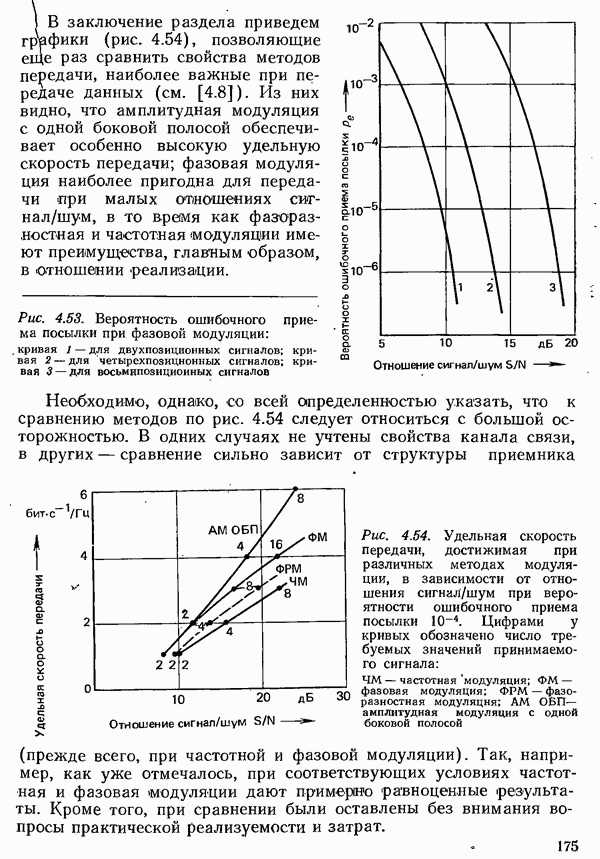
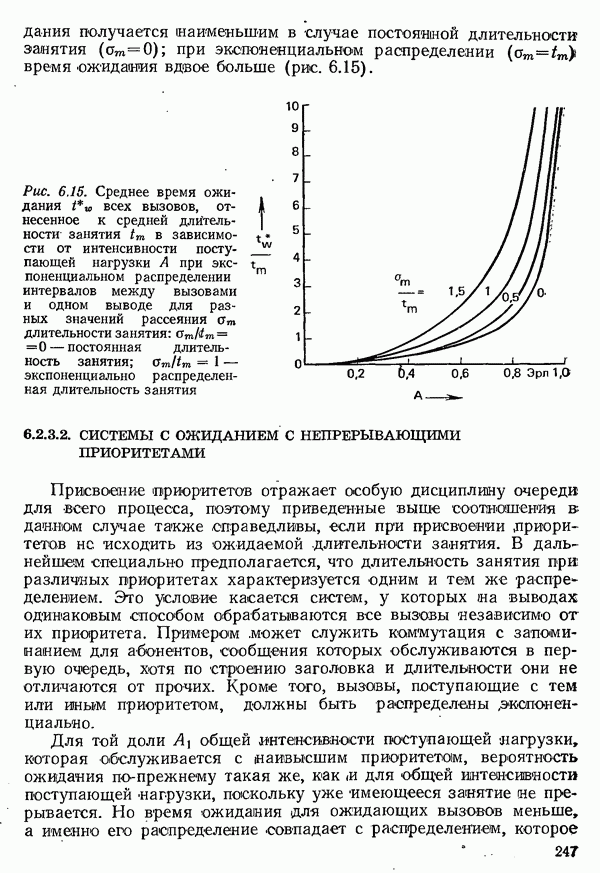
Рис. 6.15. Среднее время ожидания  всех вызовов, отнесенное к средней длительности занятия
всех вызовов, отнесенное к средней длительности занятия  в зависимости от интенсивности поступающей нагрузки А при экспоненциальном распределении интервалов между вызовами и одном выводе для разных значений рассеяния
в зависимости от интенсивности поступающей нагрузки А при экспоненциальном распределении интервалов между вызовами и одном выводе для разных значений рассеяния  длительности занятия:
длительности занятия:  постоянная длительность занятия;
постоянная длительность занятия;  экспоненциально распределенная длительность занятия
экспоненциально распределенная длительность занятия
6.2.3.2. СИСТЕМЫ С ОЖИДАНИЕМ С НЕПРЕРЫВАЮЩИМИ ПРИОРИТЕТАМИ
Присвоение приоритетов отражает особую дисциплину очереди для всего процесса, поэтому приведенные выше соотношения в данном случае также справедливы, если при присвоении приоритетов не исходить из ожидаемой длительности занятия. В дальнейшем специально предполагается, что длительность занятия при различных приоритетах характеризуется одним и тем же распределением. Это условие касается систем, у которых на выводах одинаковым способом обрабатываются все вызовы независимо от их приоритета. Примером может служить коммутация с запоминанием для абонентов, сообщения которых обслуживаются в первую очередь, хотя по строению заголовка и длительности они не отличаются от прочих. Кроме того, вызовы, поступающие с тем или иным приоритетом, должны быть распределены экспоненциально.
Для той доли А] общей интенсивности поступающей нагрузки, которая обслужив а ется с наивысшим приоритетом, вероятность ожидания по-прежнему такая же, как (и для общей интенсивности поступающей нагрузки, поскольку уже имеющееся занятие не прерывается. Но время ожидания для ожидающих вызовов меньше, а именно его распределение совпадает с распределением, которое
получается, если имеется только нагрузка с интенсивностью  . В соответствии с этим среднее время ожидания
. В соответствии с этим среднее время ожидания 

сокращается по сравнению со средним временем ожидания  для всего процесса. Аналогичные соотношения справедливы и для той доли поступающей нагрузки, которая обслуживается с низшим приоритетом. При незначительной общей нагрузке присвоение приоритетов не приводит к заметным последствиям, а при интенсивной нагрузке его результаты, наоборот, очень заметны; прежде всего, среднее время ожидания для ожидающих вызовов со всеми приоритетами, кроме самых низких, также остается конечным, если общая нагрузка стремится к
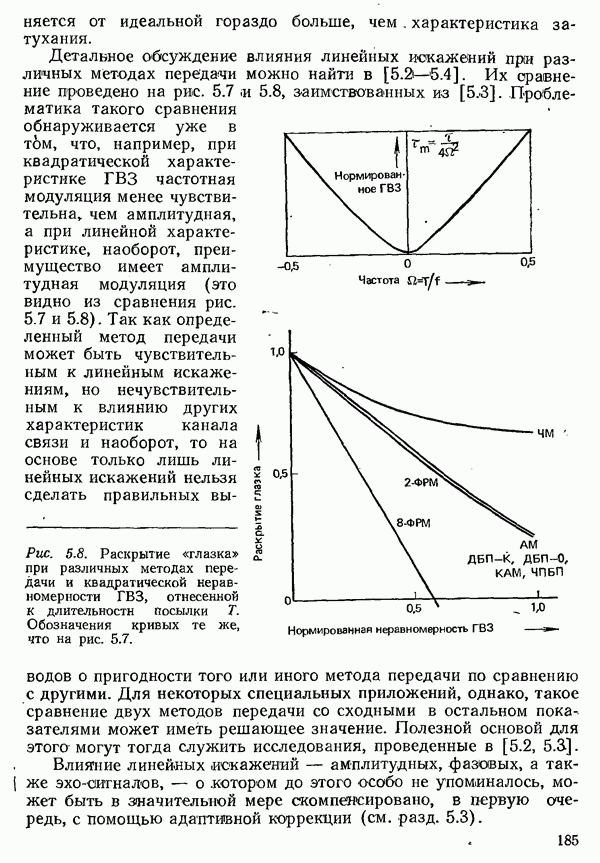
для всего процесса. Аналогичные соотношения справедливы и для той доли поступающей нагрузки, которая обслуживается с низшим приоритетом. При незначительной общей нагрузке присвоение приоритетов не приводит к заметным последствиям, а при интенсивной нагрузке его результаты, наоборот, очень заметны; прежде всего, среднее время ожидания для ожидающих вызовов со всеми приоритетами, кроме самых низких, также остается конечным, если общая нагрузка стремится к  Для пояснения на рис. 6.16 показано среднее время ожидания всех вызовов при их разделении поровну по трем приоритетам. Соответствующие соотношения справедливы и для систем с более чем одним выводом [6.20].
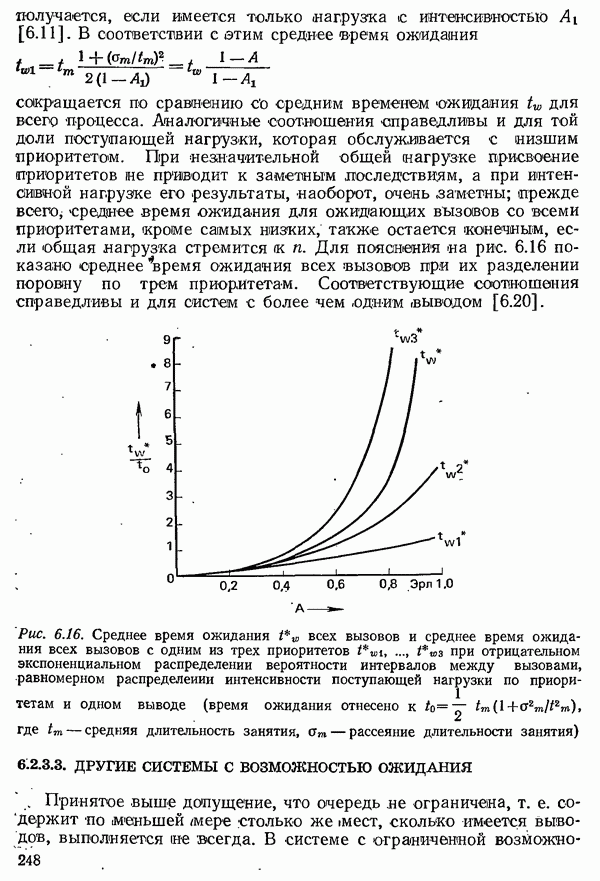
Для пояснения на рис. 6.16 показано среднее время ожидания всех вызовов при их разделении поровну по трем приоритетам. Соответствующие соотношения справедливы и для систем с более чем одним выводом [6.20].

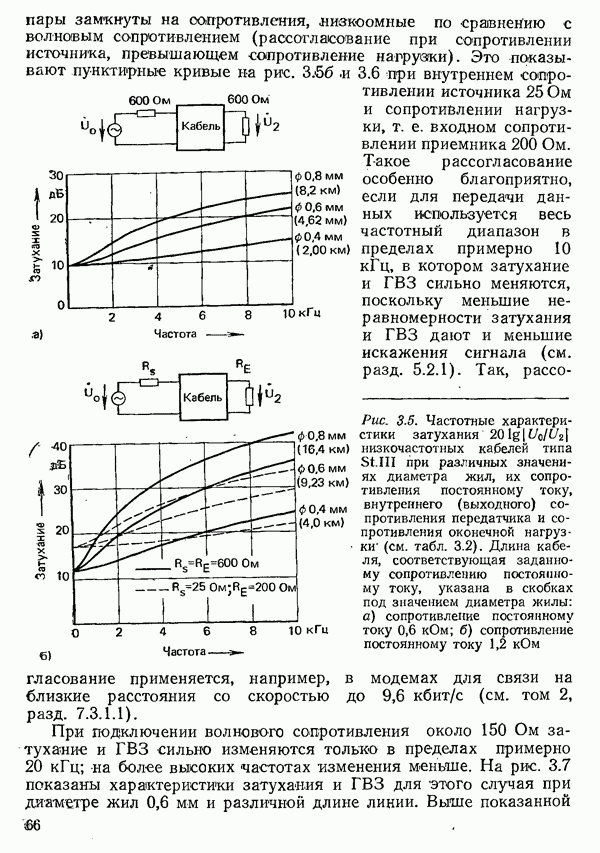
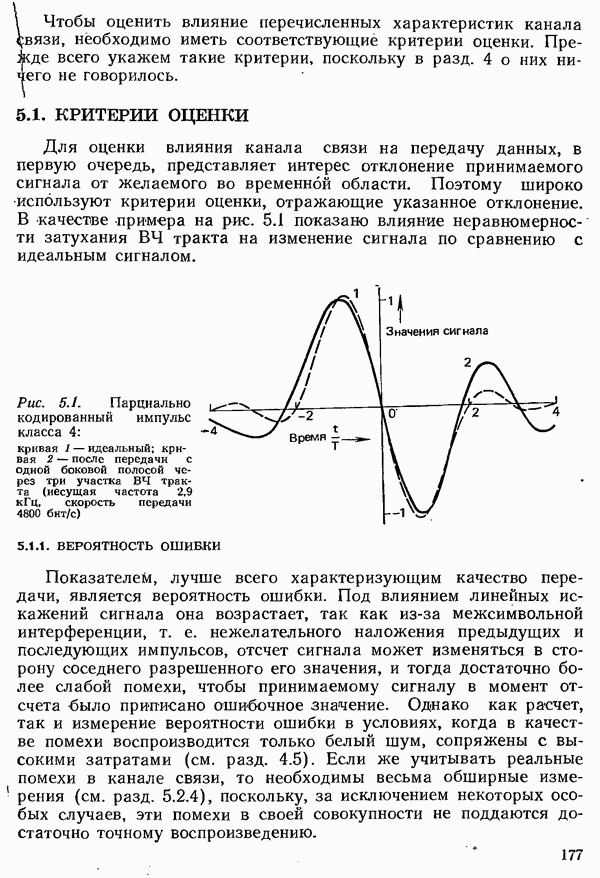
Рис. 6.16. Среднее время ожидания  всех вызовов и среднее время ожидания всех вызовов с одним из трех приоритетов
всех вызовов и среднее время ожидания всех вызовов с одним из трех приоритетов  при отрицательном экспоненциальном распределении вероятности интервалов между вызовами, равномерном распределении интенсивности поступающей нагрузки по приоритетам и одном выводе (время ожидания отнесено к
при отрицательном экспоненциальном распределении вероятности интервалов между вызовами, равномерном распределении интенсивности поступающей нагрузки по приоритетам и одном выводе (время ожидания отнесено к  где
где  средняя длительность занятия,
средняя длительность занятия,  рассеяние длительности занятия)
рассеяние длительности занятия)
6.2.3.3. ДРУГИЕ СИСТЕМЫ С ВОЗМОЖНОСТЬЮ ОЖИДАНИЯ
Принятое выше допущение, что очередь не ограничена, т. е. содержит по меньшей мере столько же мест, сколько имеется выводов, выполняется не всегда. В системе с ограниченной
возможностью ожидания вероятность потери меньвде, чем в чистой системе с потерями, а среднее время ожидания короче, чем в системе с ожиданием без ограничений.
Если в системе с различными приоритетами важно уменьшить не только среднее время ожидания для ожидающих вызовов с высокими приоритетами, но и вероятность ожидания, то занятия, имеющие более низкие приоритеты, должны прерываться. Вызовы с наивысшими приоритетами тогда обслуживаются так, как будто бы существует только эта часть нагрузки. Вероятность ожидания при этом снижается, и распределение ожидания внутри указанного приоритета определяется только значениями длительности занятия для вызовов с этим приоритетом.
С помощью некоторых других мероприятий можно минимизировать среднее время ожидания для всех вызовов, например, так, чтобы вызовы с кратчайшей ожидаемой длительностью занятия обслуживались с наивысшим приоритетам.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ К РУССКОМУ ИЗДАНИЮ
- 1. Обзор
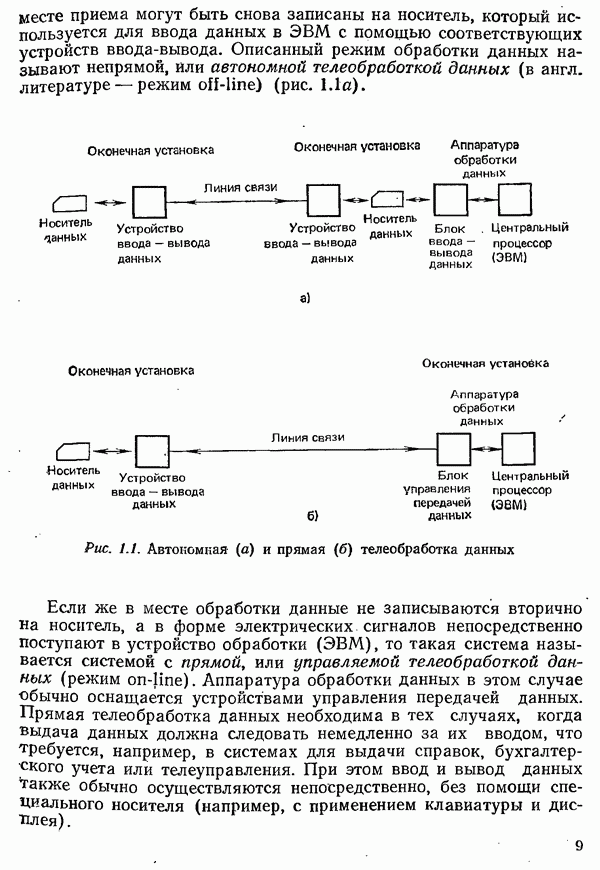
- 1.1. ОБРАБОТКА И ТЕЛЕОБРАБОТКА ДАННЫХ
- 1.2. АВТОНОМНАЯ И УПРАВЛЯЕМАЯ ТЕЛЕОБРАБОТКА ДАННЫХ
- 1.3. КЛАССИФИКАЦИЯ СИСТЕМ ТЕЛЕОБРАБОТКИ ДАННЫХ
- 1.4. СТРУКТУРА СИСТЕМ ТЕЛЕОБРАБОТКИ ДАННЫХ
- 1.5. ТРЕБОВАНИЯ К ТЕХНИКЕ СВЯЗИ И КОММУТАЦИИ В СИСТЕМАХ ТЕЛЕОБРАБОТКИ ДАННЫХ
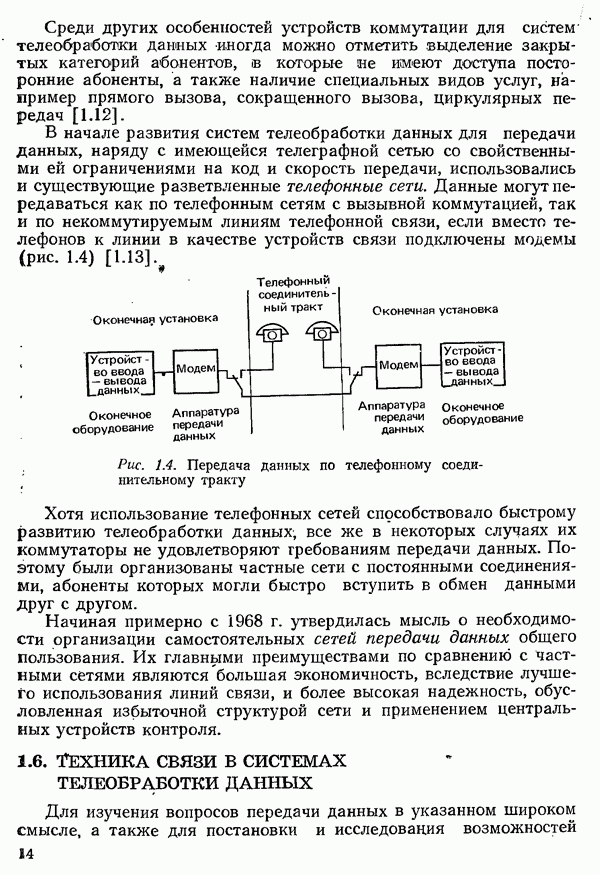
- 1.6. ТЕХНИКА СВЯЗИ В СИСТЕМАХ ТЕЛЕОБРАБОТКИ ДАННЫХ
- 2. Основные понятия техники связи
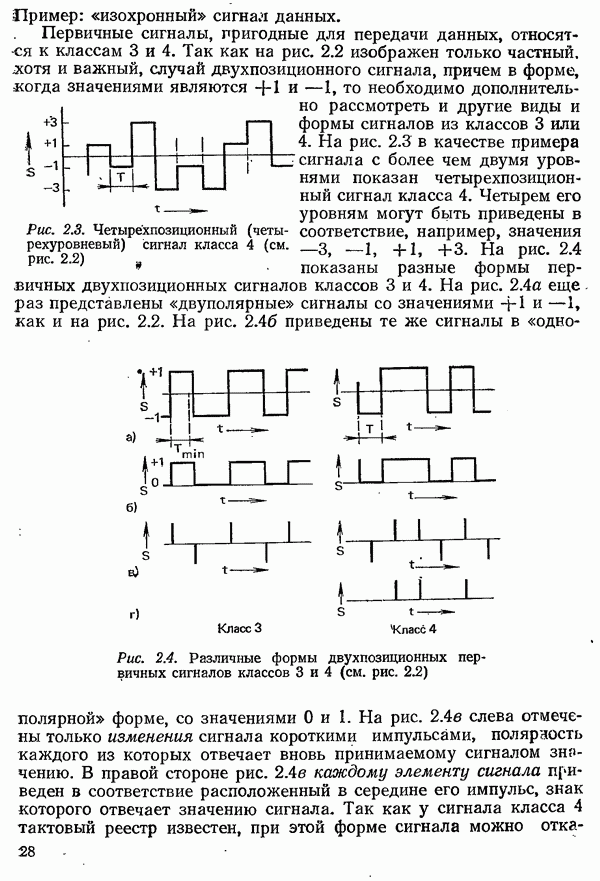
- 2.2. СИГНАЛЫ
- 2.2.2. ДИСКРЕТИЗАЦИЯ, КВАНТОВАНИЕ, ВЛИЯНИЕ ШУМОВ
- 2.2.3. СВОЙСТВА ПЕРВИЧНЫХ СИГНАЛОВ ДЛЯ ПЕРЕДАЧИ ДАННЫХ
- 2.2.3.2. ВРЕМЕННЫЕ СООТНОШЕНИЯ МЕЖДУ СИГНАЛАМИ
- 2.2.4. РЕЖИМЫ РАБОТЫ ПРИ ПЕРЕДАЧЕ СИГНАЛОВ
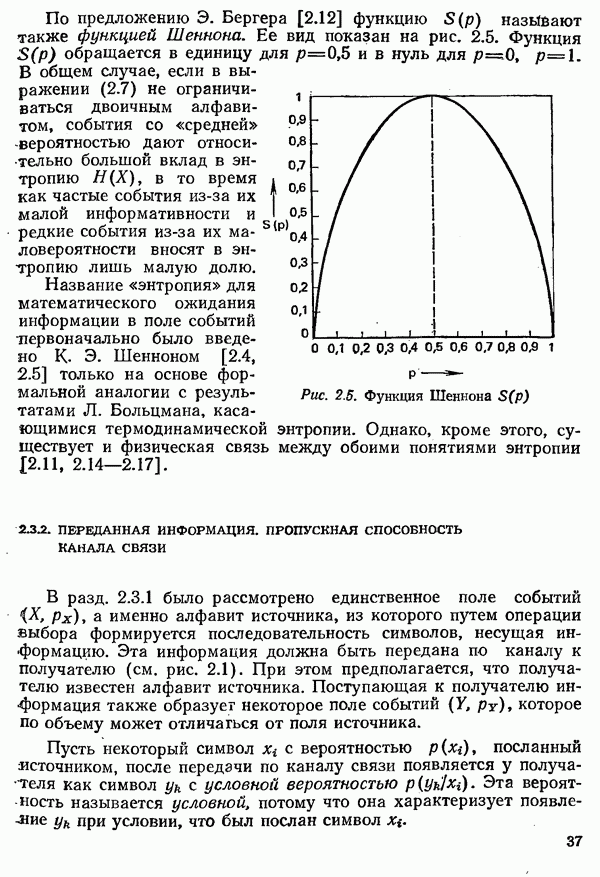
- 2.3. НЕКОТОРЫЕ ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ИНФОРМАЦИИ
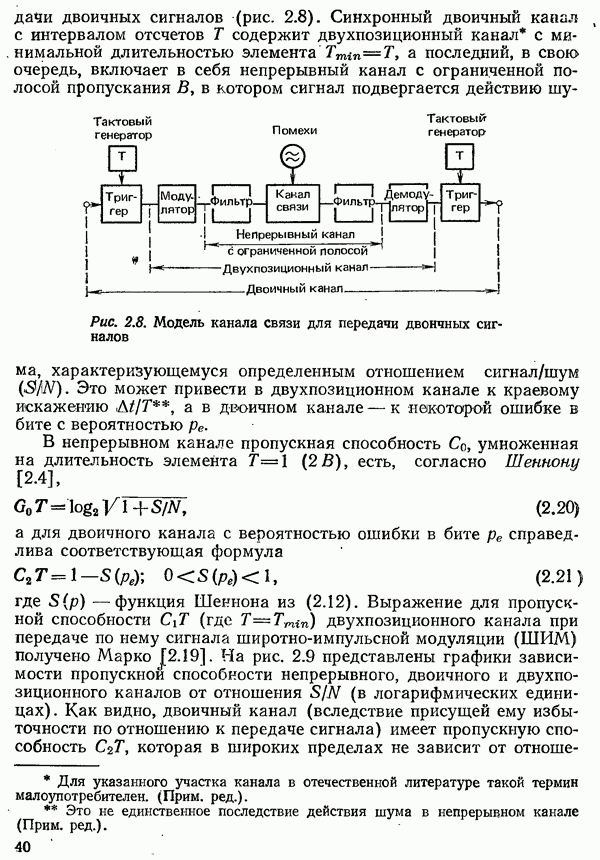
- 2.3.2. ПЕРЕДАННАЯ ИНФОРМАЦИЯ. ПРОПУСКНАЯ СПОСОБНОСТЬ КАНАЛА СВЯЗИ
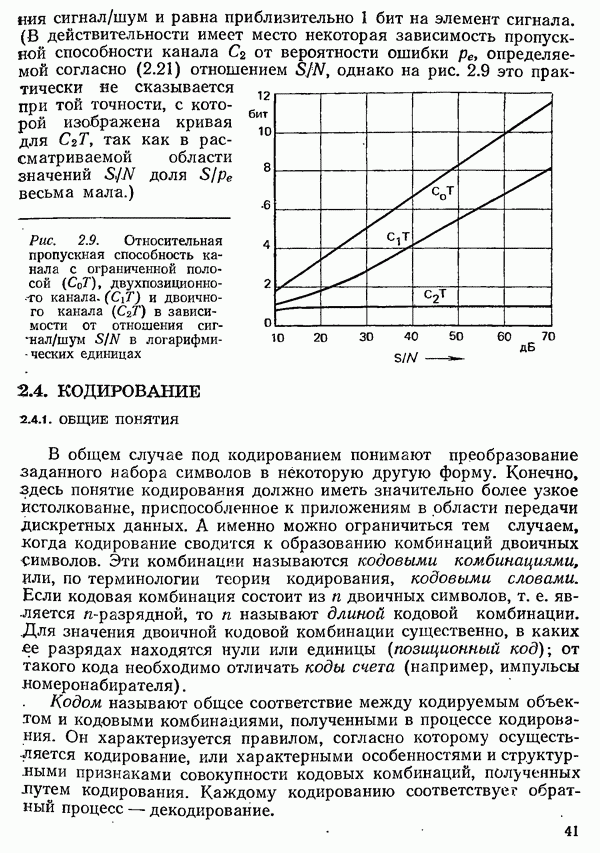
- 2.4. КОДИРОВАНИЕ
- 2.4.3. КОДИРОВАНИЕ ИСТОЧНИКА
- 2.4.4. КАНАЛЬНОЕ КОДИРОВАНИЕ
- 3. Каналы связи
- 3.1. КАНАЛЫ БЛИЖНЕЙ СВЯЗИ
- 3.1.1.1. СВОЙСТВА И ПАРАМЕТРЫ ПРОВОДНЫХ ЛИНИЙ СВЯЗИ
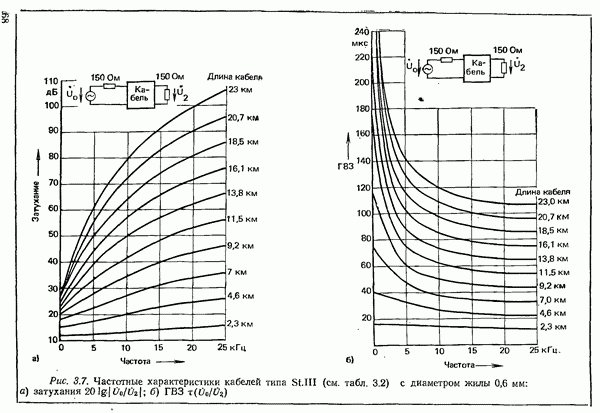
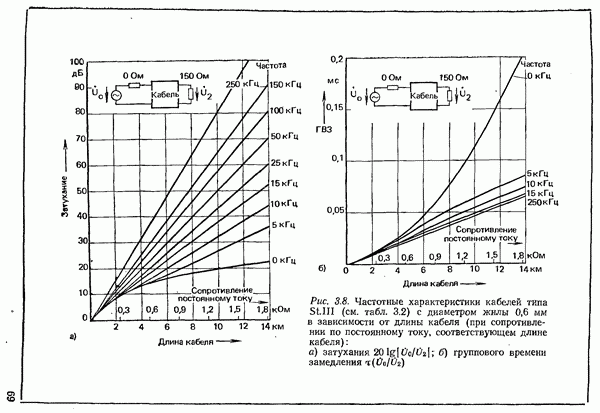
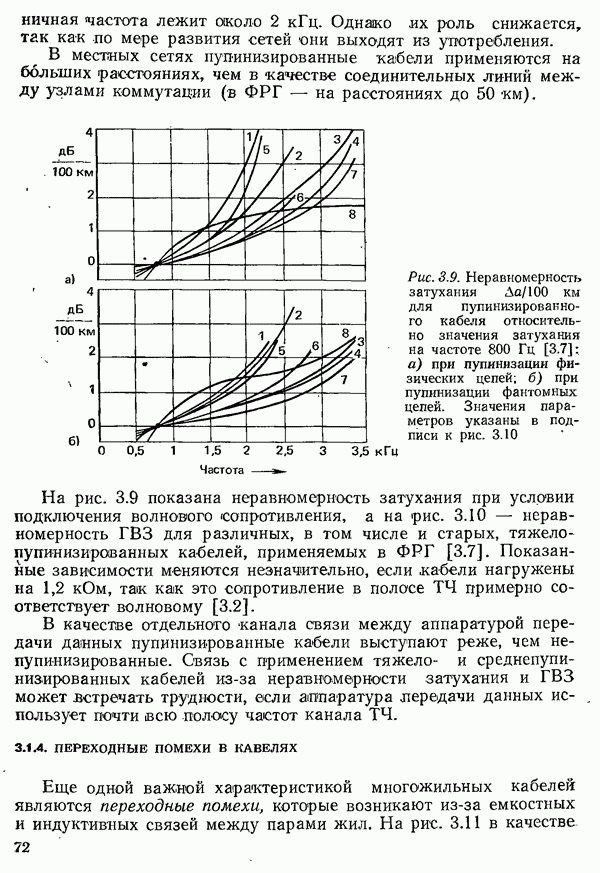
- 3.1.1.2. УМЕНЬШЕНИЕ ЗАТУХАНИЯ ПУТЕМ УВЕЛИЧЕНИЯ ИНДУКТИВНОСТИ. ПУПИНИЗАЦИЯ
- 3.1.2. ХАРАКТЕРИСТИКИ ПАР ЖИЛ НИЗКОЧАСТОТНЫХ КАБЕЛЕЙ
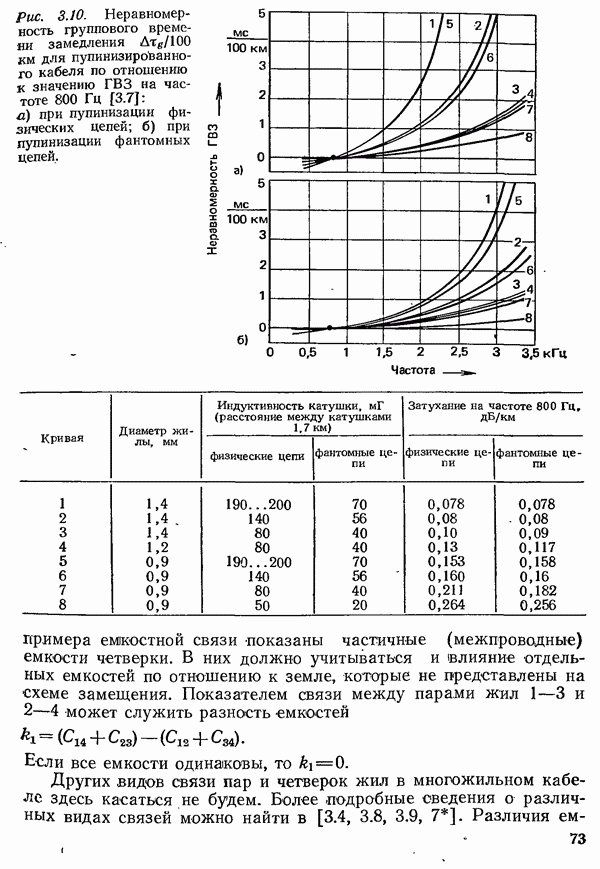
- 3.1.3. ХАРАКТЕРИСТИКИ ПАР ЖИЛ ПУПИЯИЗИРОВАННЫХ КАБЕЛЕЙ
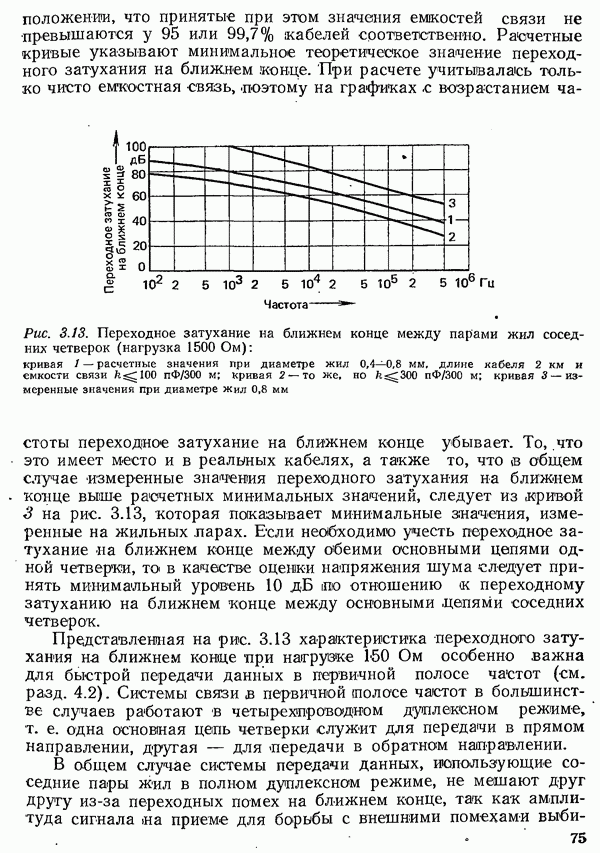
- 3.1.4. ПЕРЕХОДНЫЕ ПОМЕХИ В КАБЕЛЯХ
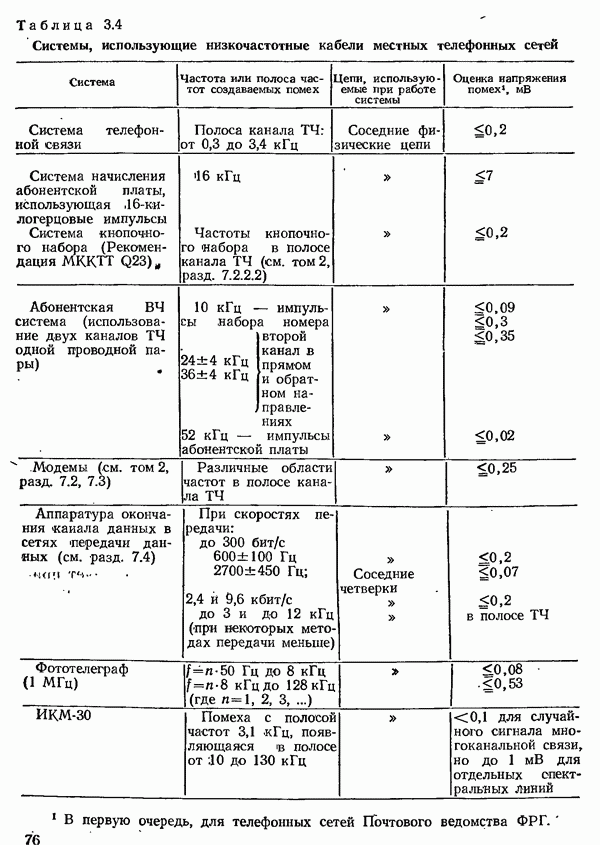
- 3.1.5. НАПРЯЖЕНИЯ ШУМОВ НА ПАРАХ ШИЛ КАБЕЛЕЙ
- 3.2. КАНАЛЫ ДАЛЬНЕЙ СВЯЗИ
- 3.2.2. КАНАЛЫ ТОНАЛЬНОЙ ЧАСТОТЫ
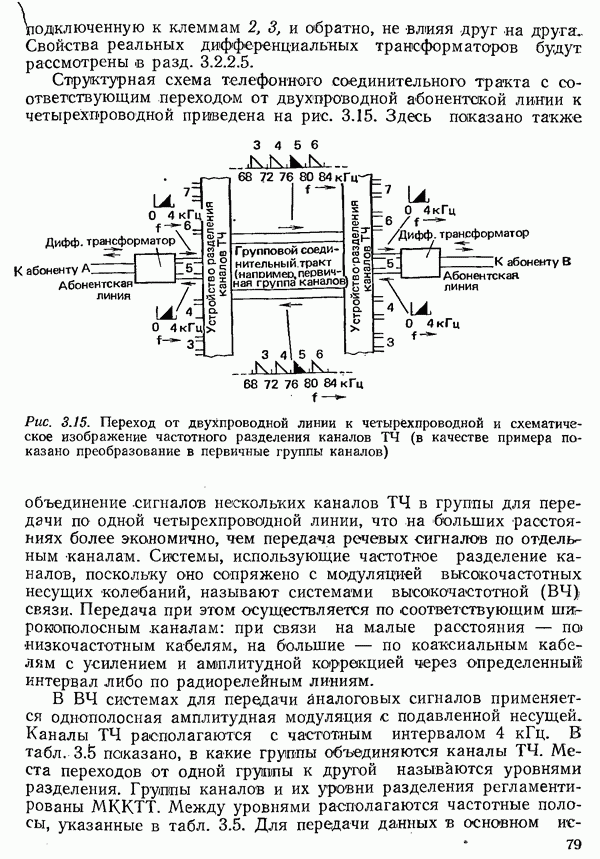
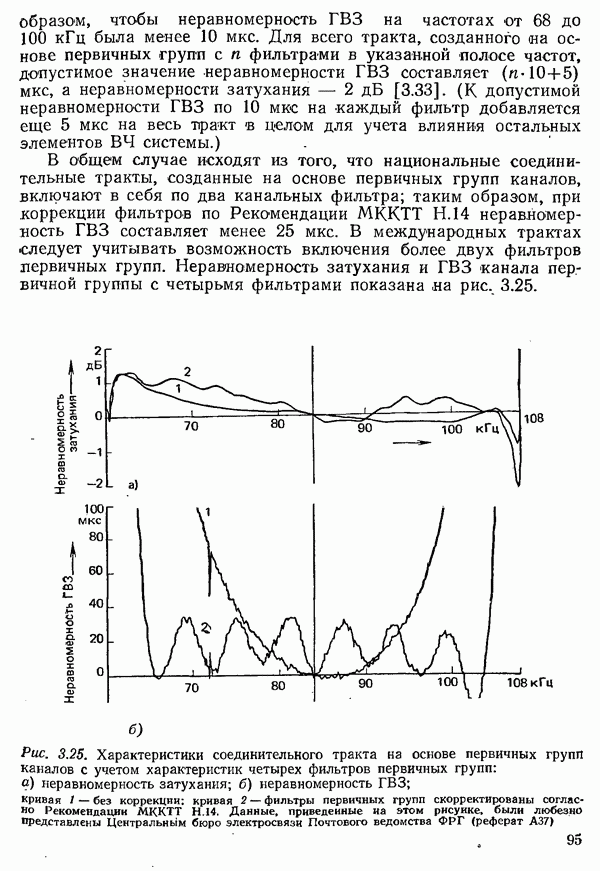
- 3.2.3. СОЕДИНИТЕЛЬНЫЕ ТРАКТЫ НА ОСНОВЕ ПЕРВИЧНЫХ ГРУПП КАНАЛОВ
- 4. Методы передачи данных
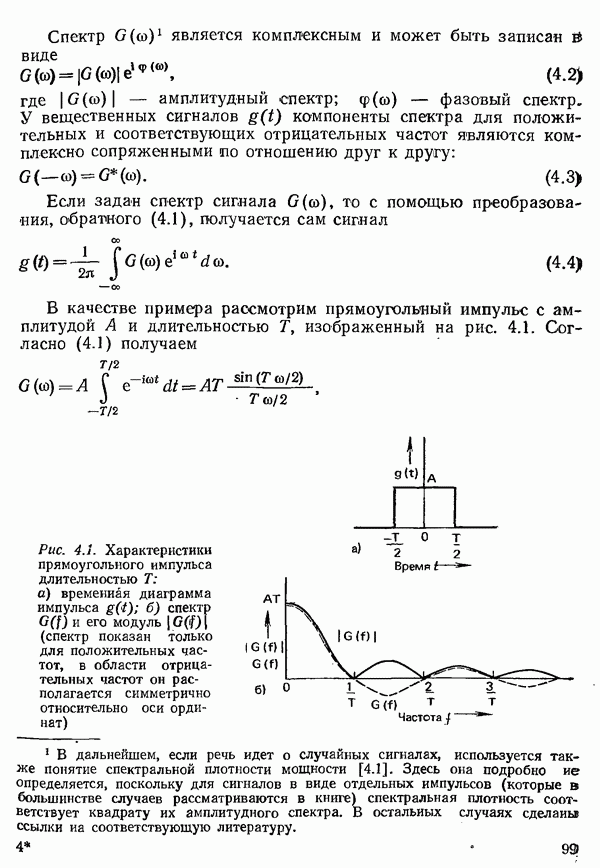
- 4.1.1. СИГНАЛЫ И СПЕКТРЫ
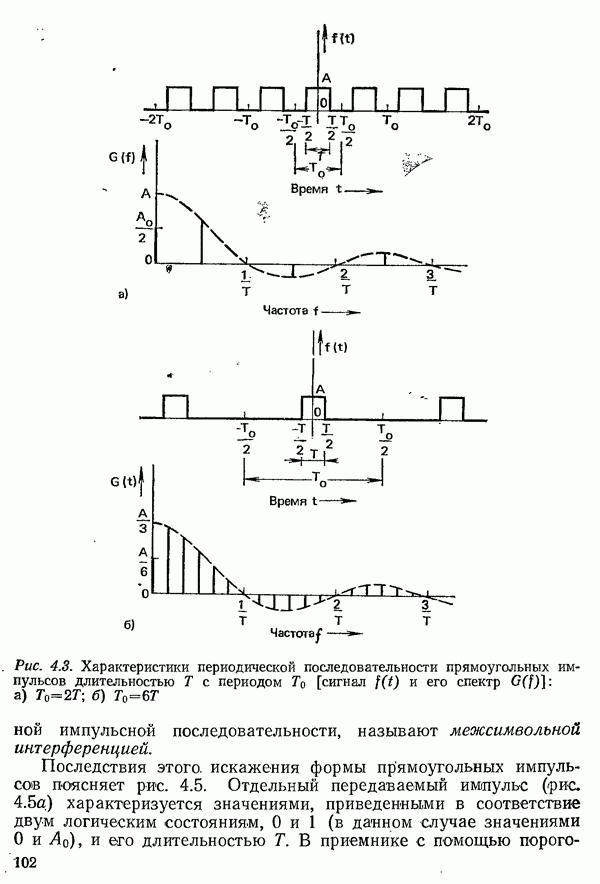
- 4.1.2. РЯД ФУРЬЕ
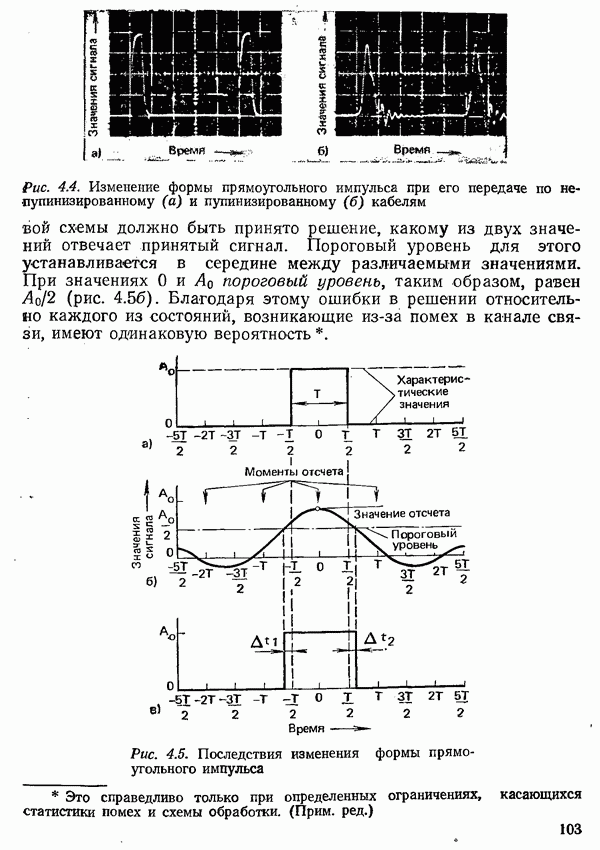
- 4.1.3. ИСКАЖЕНИЯ ФОРМЫ ИМПУЛЬСОВ ПРИ ОГРАНИЧЕНИИ ПОЛОСЫ ЧАСТОТ
- 4.1.4. УСЛОВИЯ НАЙКВИСТА
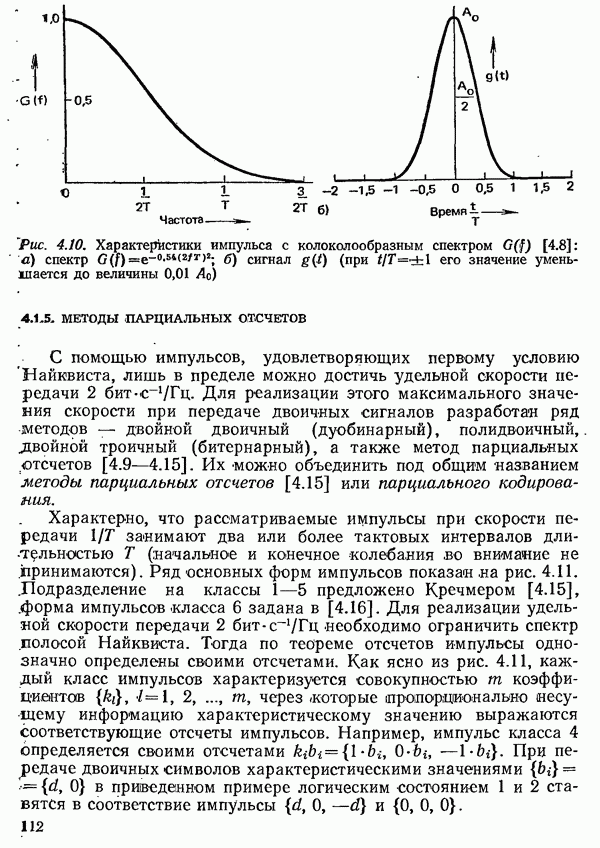
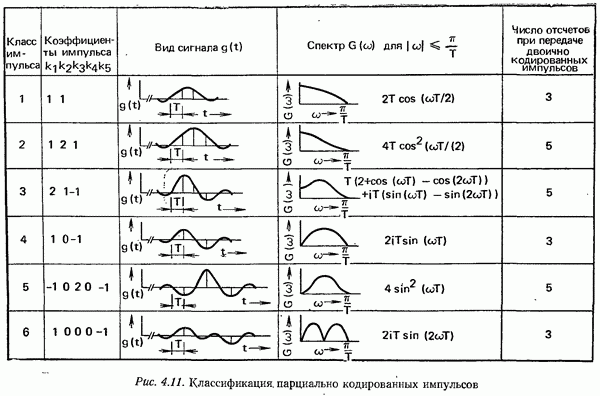
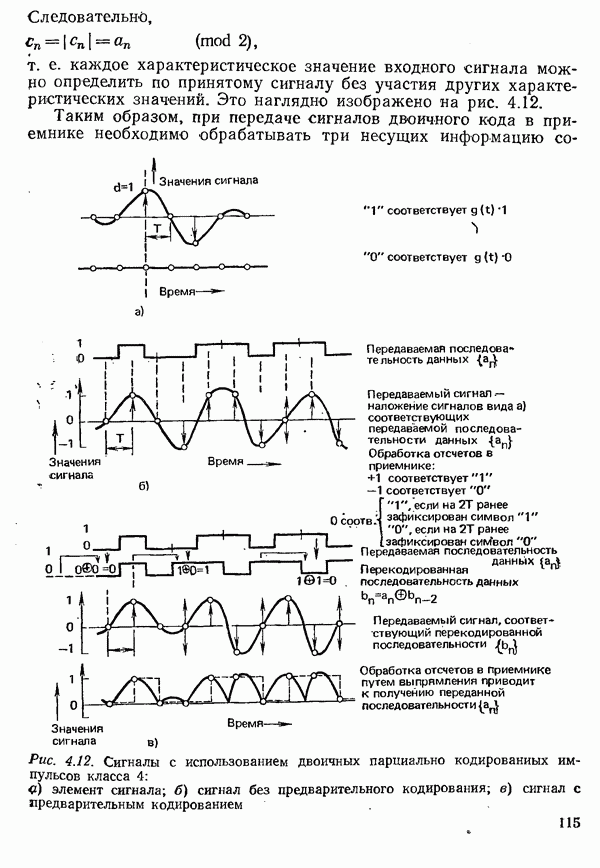
- 4.1.5. МЕТОДЫ ПАРЦИАЛЬНЫХ ОТСЧЕТОВ
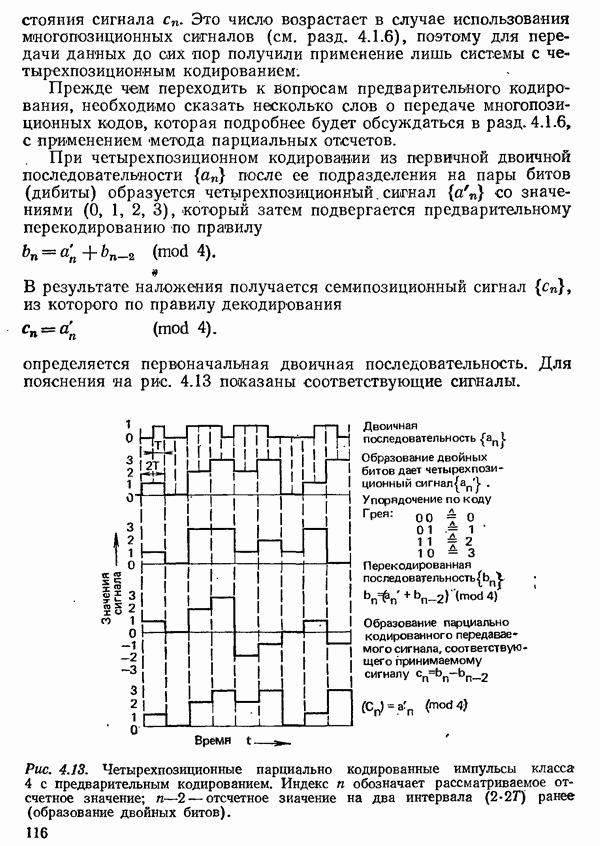
- 4.1.6. ПЕРЕДАЧА МНОГОПОЗИЦИОННЫХ СИГНАЛОВ
- 4.2. МЕТОДЫ ПЕРЕДАЧИ В ПЕРВИЧНОЙ ПОЛОСЕ ЧАСТОТ
- 4.2.1. МЕТОДЫ С ПРИМЕНЕНИЕМ ДВУПОЛЯРНЫХ И ОДНОПОЛЯРНЫХ ИМПУЛЬСОВ
- 4.2.2. БИПОЛЯРНЫЙ МЕТОД
- 4.2.3. ПСЕВДОТРОИЧНЫЕ МЕТОДЫ
- 4.2.4. МЕТОДЫ С ПРИМЕНЕНИЕМ БИПОЛЯРНЫХ КОДОВ ВЫСОКОЙ ПЛОТНОСТИ
- 4.2.5. ДВУХФАЗНЫЙ МЕТОД. ИЛИ МЕТОД РАСЩЕПЛЕНИЯ ФАЗЫ
- 4.2.6. ДВУХФАЗНО-КОДОВЫЙ МЕТОД
- 4.2.7. МЕТОДЫ ПАРЦИАЛЬНЫХ ОТСЧЕТОВ
- 4.3. МЕТОДЫ ПЕРЕДАЧИ С ПРИМЕНЕНИЕМ МОДУЛЯЦИИ
- 4.3.1. АМПЛИТУДНАЯ МОДУЛЯЦИЯ
- 4.3.1.2. АМПЛИТУДНАЯ МОДУЛЯЦИЯ С ОДНОЙ БОКОВОЙ ПОЛОСОЙ И С ЧАСТИЧНО ПОДАВЛЕННОЙ БОКОВОЙ ПОЛОСОЙ
- 4.3.1.3. КВАДРАТУРНАЯ АМПЛИТУДНАЯ МОДУЛЯЦИЯ
- 4.3.1.4. УДЕЛЬНАЯ СКОРОСТЬ ПЕРЕДАЧИ ПРИ АМПЛИТУДНОЙ МОДУЛЯЦИИ
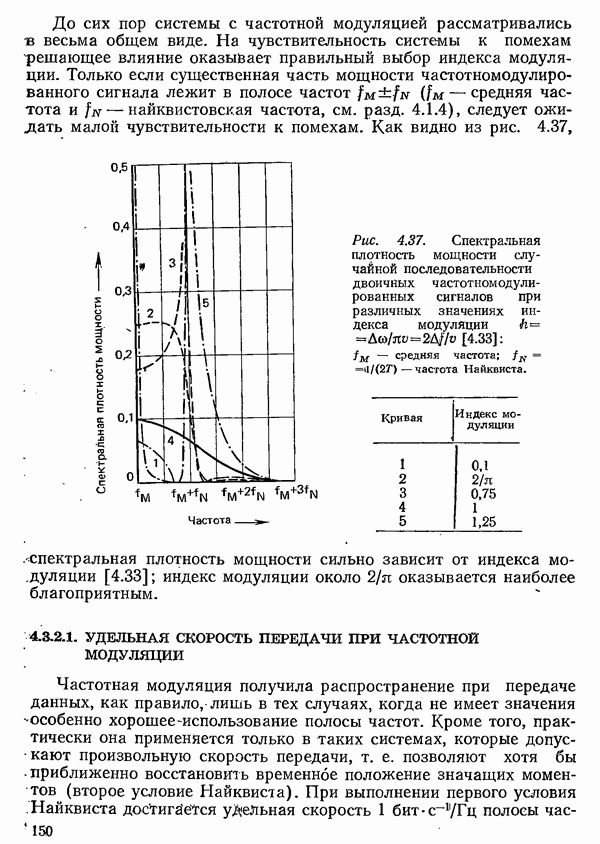
- 4.3.2. ЧАСТОТНАЯ МОДУЛЯЦИЯ
- 4.3.2.1. УДЕЛЬНАЯ СКОРОСТЬ ПЕРЕДАЧИ ПРИ ЧАСТОТНОЙ МОДУЛЯЦИИ
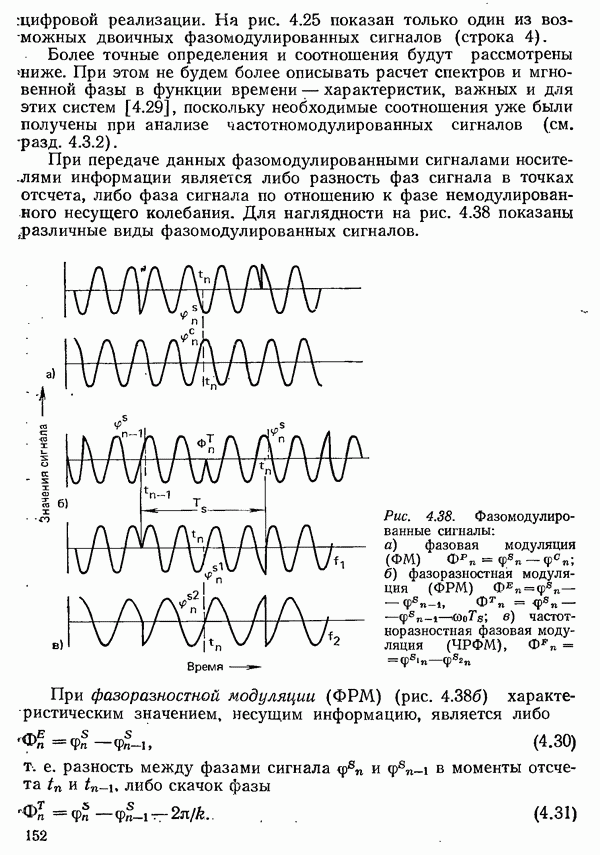
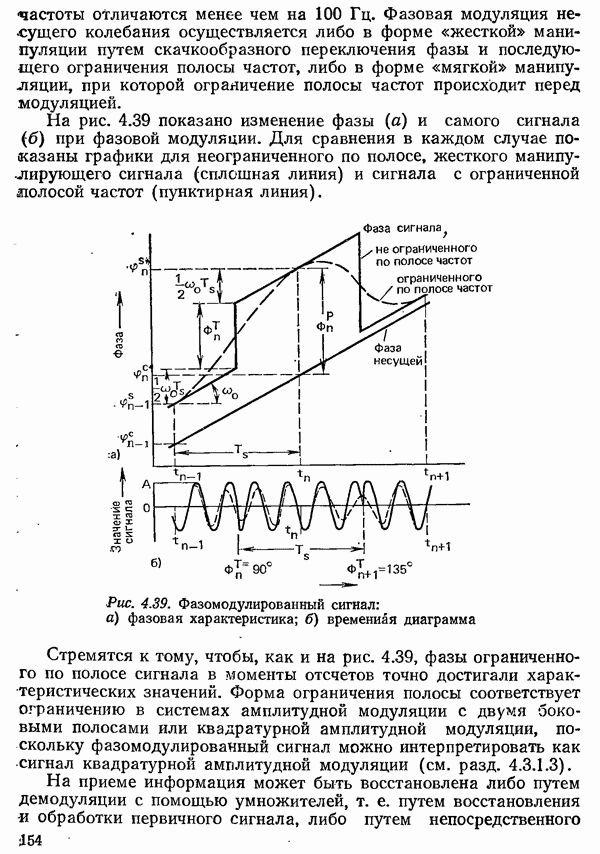
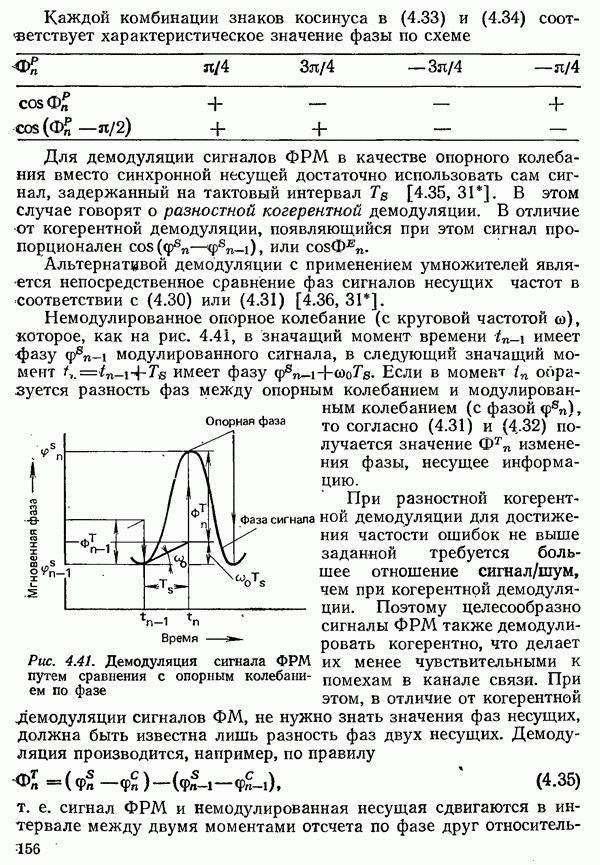
- 4.3.3. ФАЗОВАЯ МОДУЛЯЦИЯ
- 4.4. ВОССТАНОВЛЕНИЕ ТАКТОВ И НЕСУЩЕЙ
- 4.4.2. ВОССТАНОВЛЕНИЕ ЧАСТОТЫ И ФАЗЫ НЕСУЩЕЙ
- 4.5. ВЕРОЯТНОСТЬ ОШИБКИ ПРИ НАЛИЧИИ ПОМЕХ
- 4.5.1. ВЕРОЯТНОСТЬ ОШИБКИ ПРИ УЧЕТЕ ТОЛЬКО ШУМА В КАНАЛЕ СВЯЗИ
- 4.5.2. ВЕРОЯТНОСТЬ ОШИБКИ С УЧЕТОМ ЛИНЕЙНЫХ ИСКАЖЕНИЙ
- 4.5.3. ВЕРОЯТНОСТЬ ОШИБКИ С УЧЕТОМ ПРОЦЕССОВ МОДУЛЯЦИИ И ДЕМОДУЛЯЦИИ
- 5. Учет свойств реальных каналов связи при передаче данных
- 5.2. ВЛИЯНИЕ ХАРАКТЕРИСТИК КАНАЛОВ СВЯЗИ НА ПЕРЕДАЧУ ДАННЫХ
- 5.2.2. СДВИГИ ЧАСТОТЫ
- 5.2.3. ФАЗОВОЕ ДРОЖАНИЕ
- 5.2.4. ВЛИЯНИЕ РЕАЛЬНЫХ ПОМЕХ
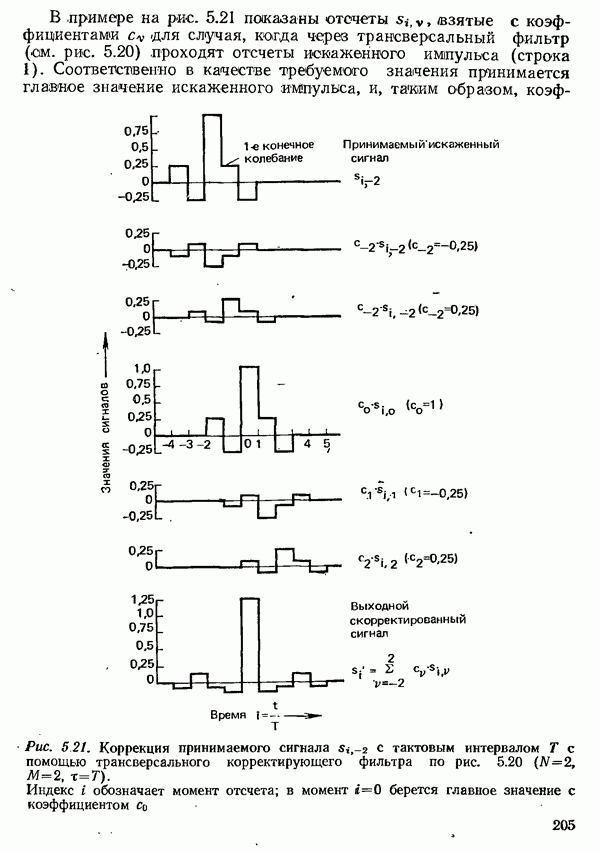
- 5.3. КОРРЕКЦИЯ ПРИНИМАЕМОГО СИГНАЛА ДАННЫХ
- 5.3.1. КОРРЕКЦИЯ ПРИНИМАЕМОГО СИГНАЛА ДАННЫХ В ЧАСТОТНОЙ ОБЛАСТИ
- 5.3.1.1. КОМПРОМИССНЫЙ КОРРЕКТОР
- 5.3.1.2. НАСТРАИВАЕМЫЙ ЧАСТОТНЫЙ КОРРЕКТОР СИГНАЛОВ ДАННЫХ
- 5.3.2. КОРРЕКЦИЯ ПРИНИМАЕМОГО СИГНАЛА ДАННЫХ ВО ВРЕМЕННОЙ ОБЛАСТИ
- 5.3.2.2. КРИТЕРИИ НАСТРОЙКИ КОРРЕКТОРА ВО ВРЕМЕННОЙ ОБЛАСТИ
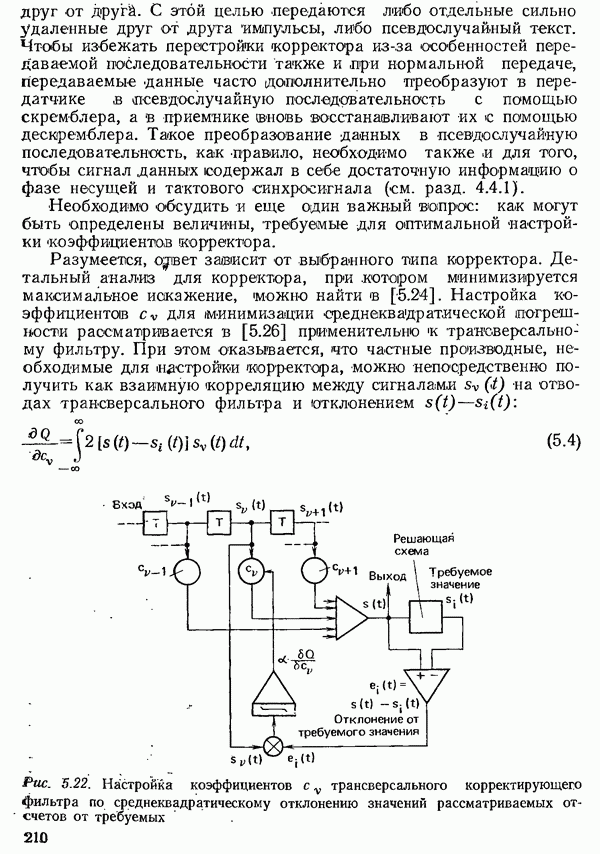
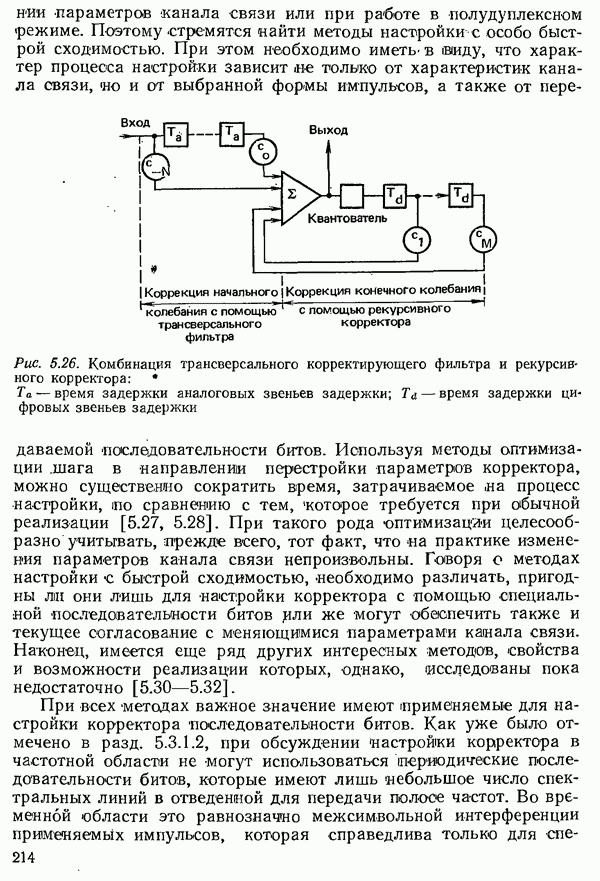
- 5.3.2.3. АВТОМАТИЧЕСКАЯ НАСТРОЙКА ТРАНСВЕРСАЛЬНОГО КОРРЕКТИРУЮЩЕГО ФИЛЬТРА
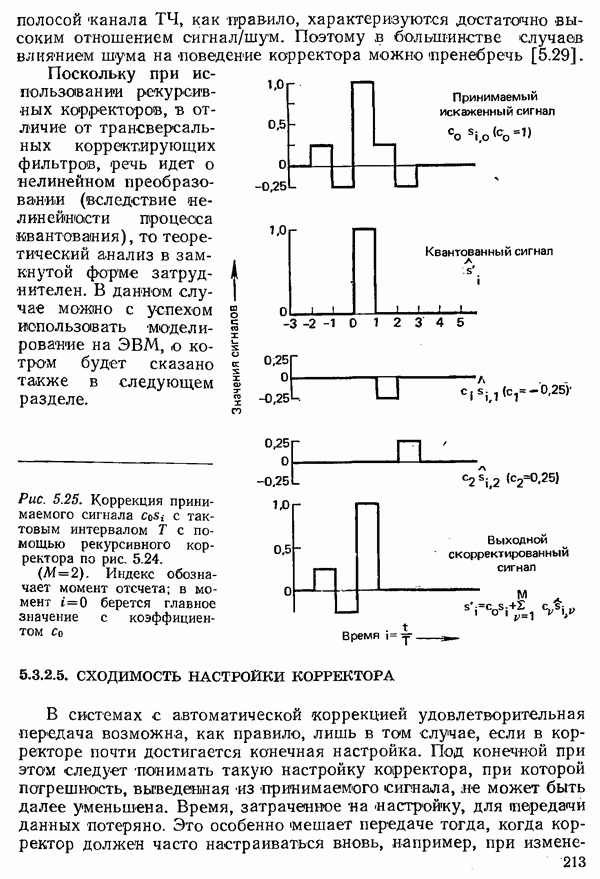
- 5.3.2.4. РЕКУРСИВНЫЙ КОРРЕКТОР
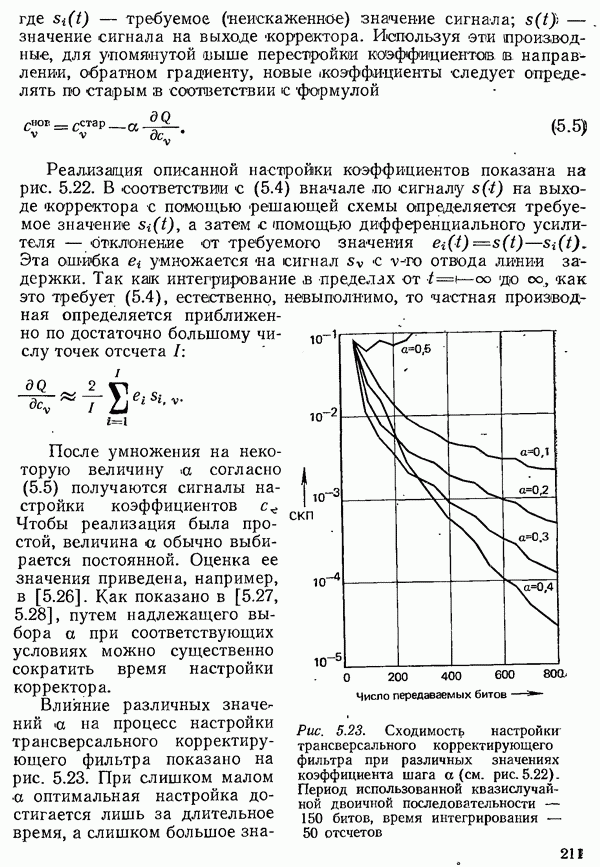
- 5.3.2.5. СХОДИМОСТЬ НАСТРОЙКИ КОРРЕКТОРА
- 5.3.2.6. КОРРЕКТОР ДЛЯ СПЕЦИАЛЬНЫХ МЕТОДОВ ПЕРЕДАЧИ
- 6. Основы коммутации данных
- 6.1.2. МЕТОДЫ КОММУТАЦИИ
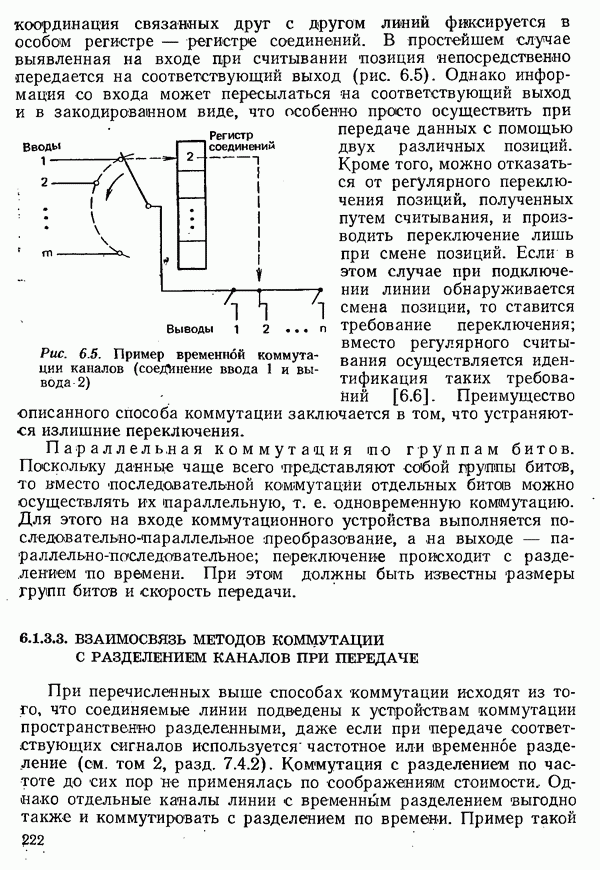
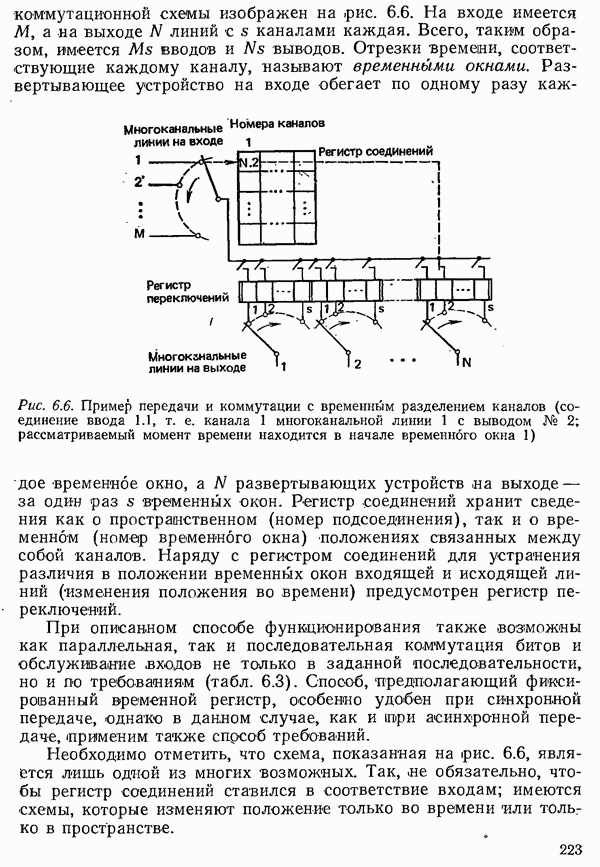
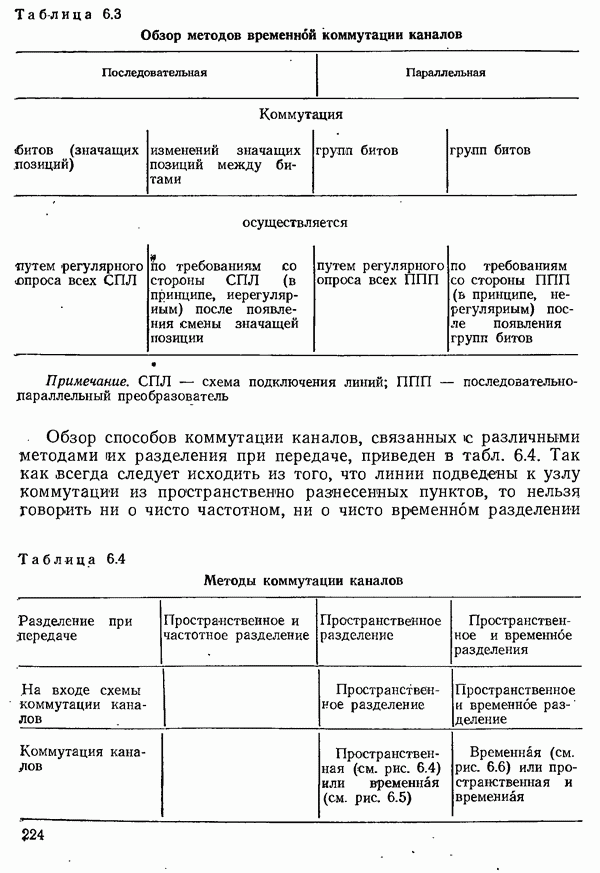
- 6.1.3. СПОСОБЫ КОММУТАЦИИ КАНАЛОВ
- 6.1.4. СИГНАЛИЗАЦИЯ
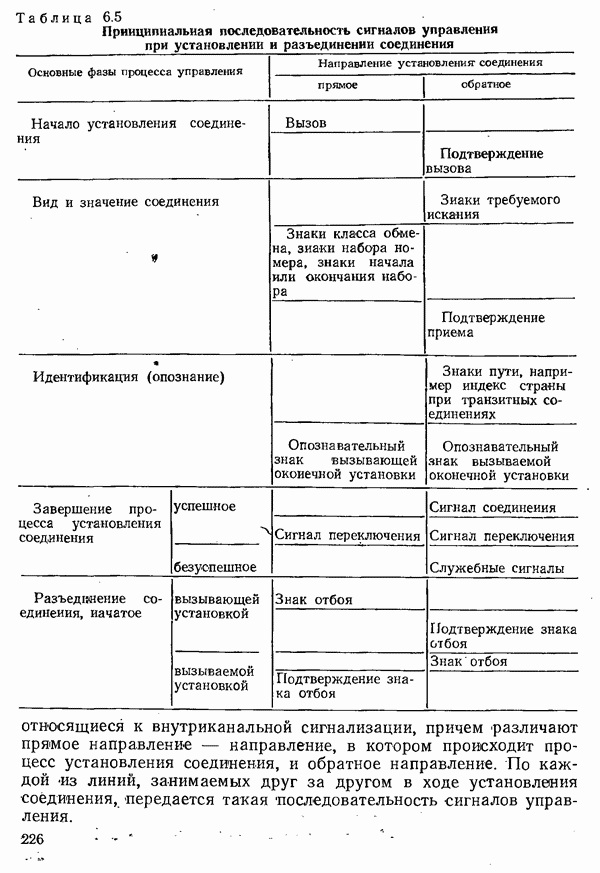
- 6.1.5. УПРАВЛЕНИЕ ПРОЦЕССАМИ СОЕДИНЕНИЯ И РАЗЪЕДИНЕНИЯ
- 6.1.6. ПОДРАЗДЕЛЕНИЕ ЦЕПЕЙ КОММУТАЦИИ КАНАЛОВ
- 6.1.7. ДОПОЛНИТЕЛЬНЫЕ ЗАДАЧИ КОММУТАЦИОННЫХ УСТРОЙСТВ
- 6.2. АНАЛИЗ СИСТЕМ КОММУТАЦИИ НА ОСНОВЕ ТЕОРИИ ТЕЛЕТРАФИКА
- 6.2.2. СИСТЕМЫ С ПОТЕРЯМИ
- 6.2.3. СИСТЕМЫ С ОЖИДАНИЕМ
- 6.2.4. ИЗМЕРЕНИЯ НАГРУЗКИ
- СПИСОК ЛИТЕРАТУРЫ