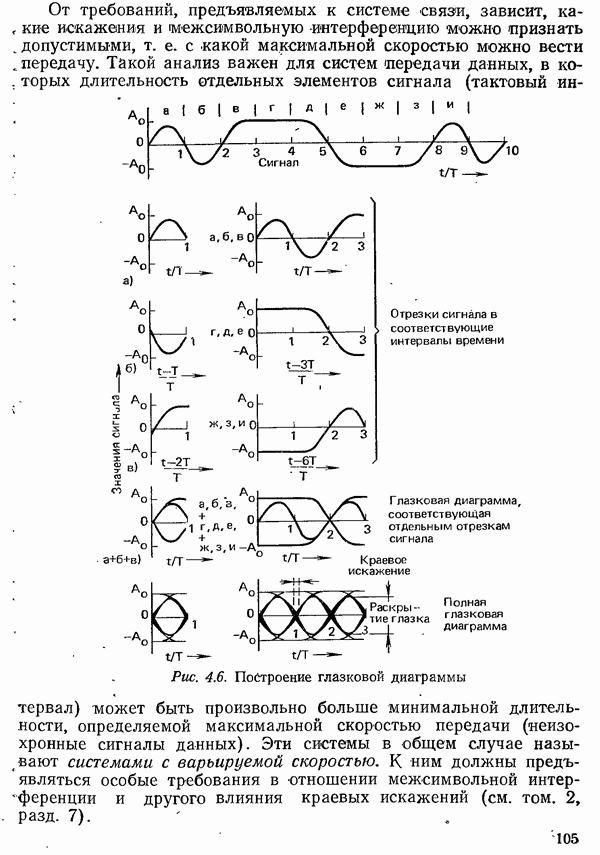
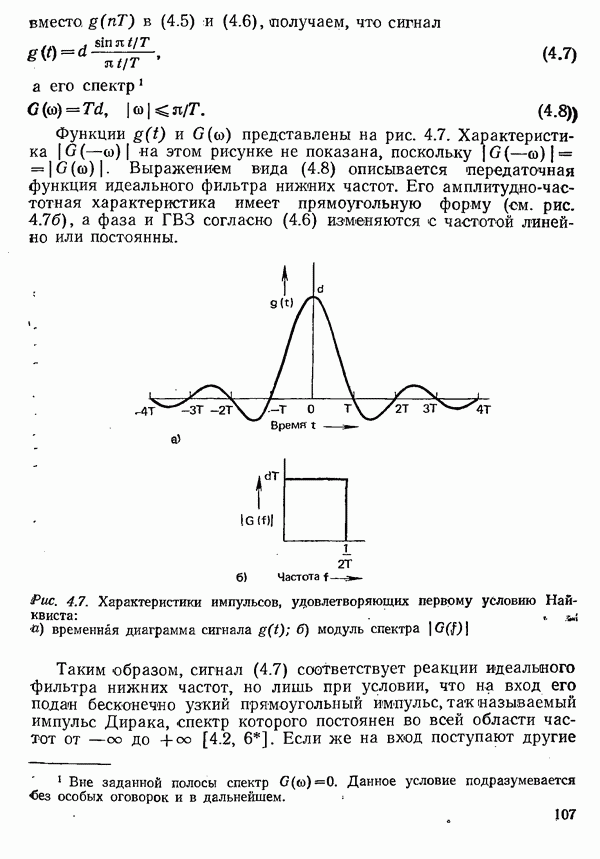
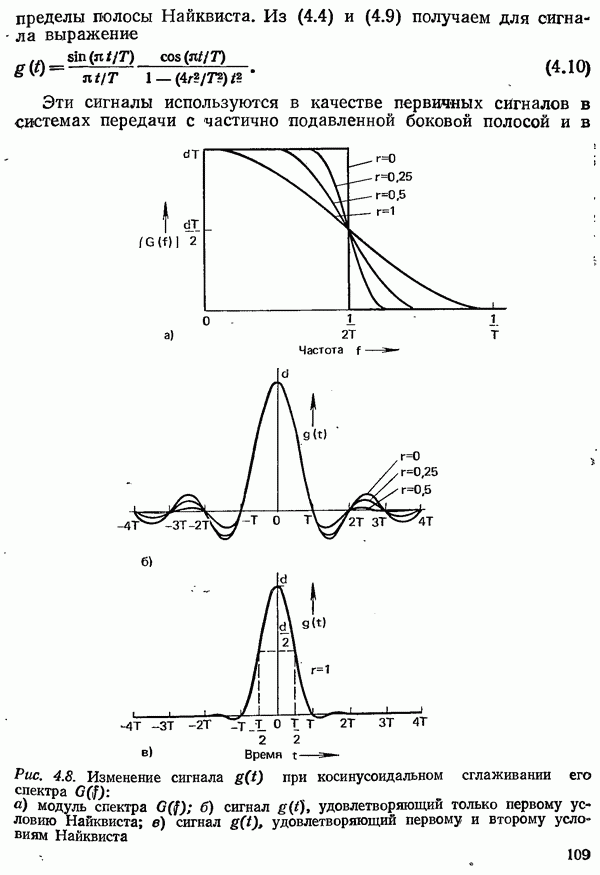
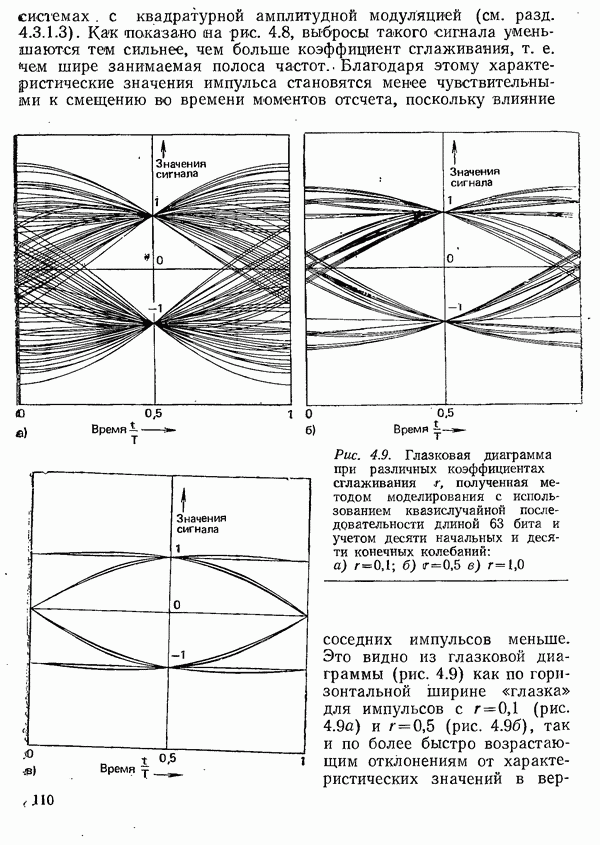
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
2.3.2. ПЕРЕДАННАЯ ИНФОРМАЦИЯ. ПРОПУСКНАЯ СПОСОБНОСТЬ КАНАЛА СВЯЗИ
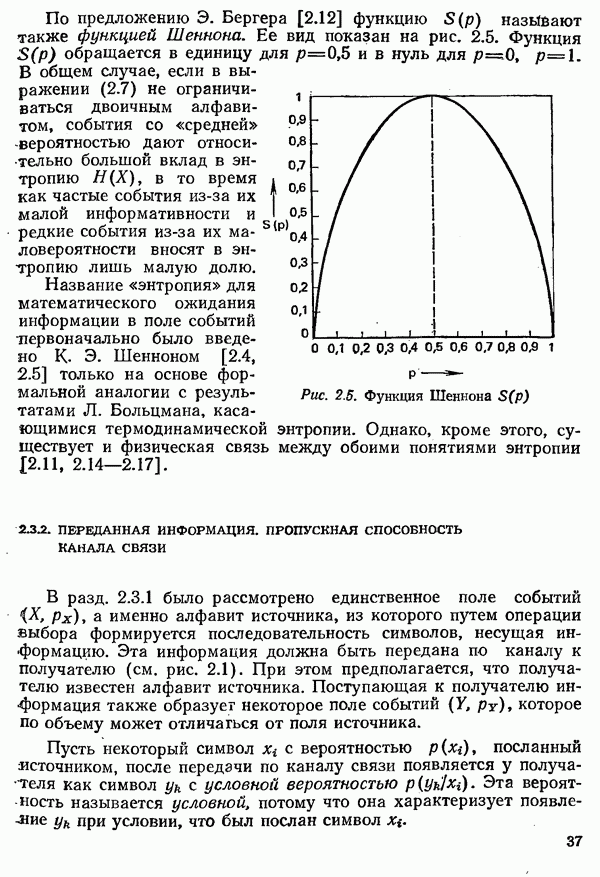
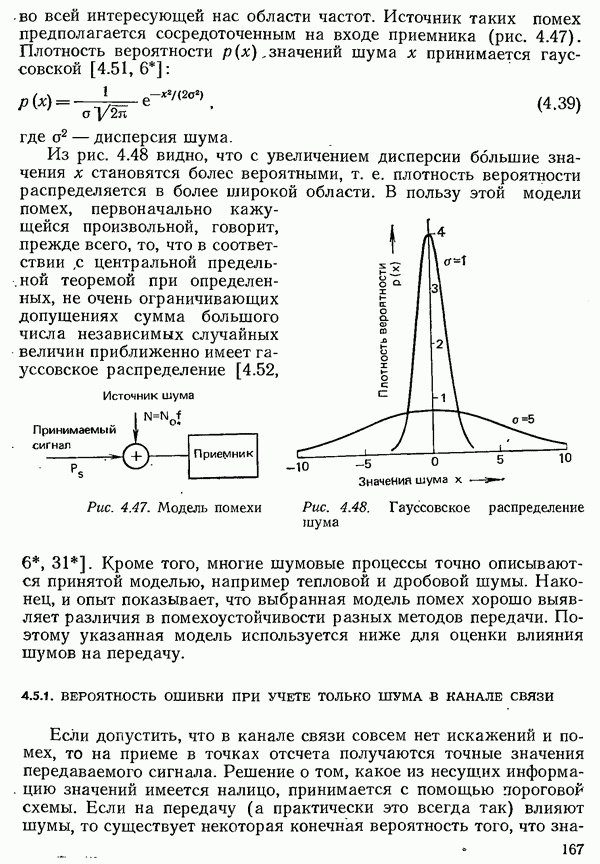
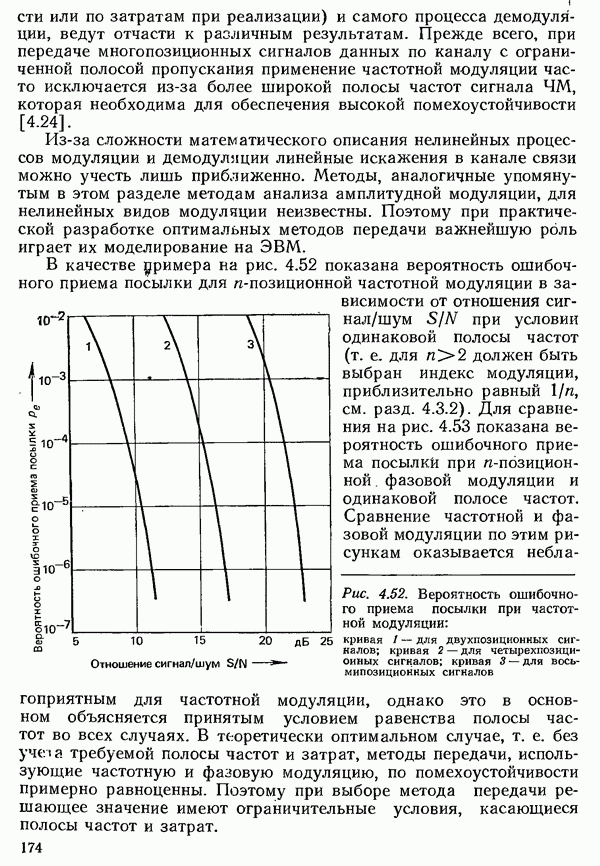
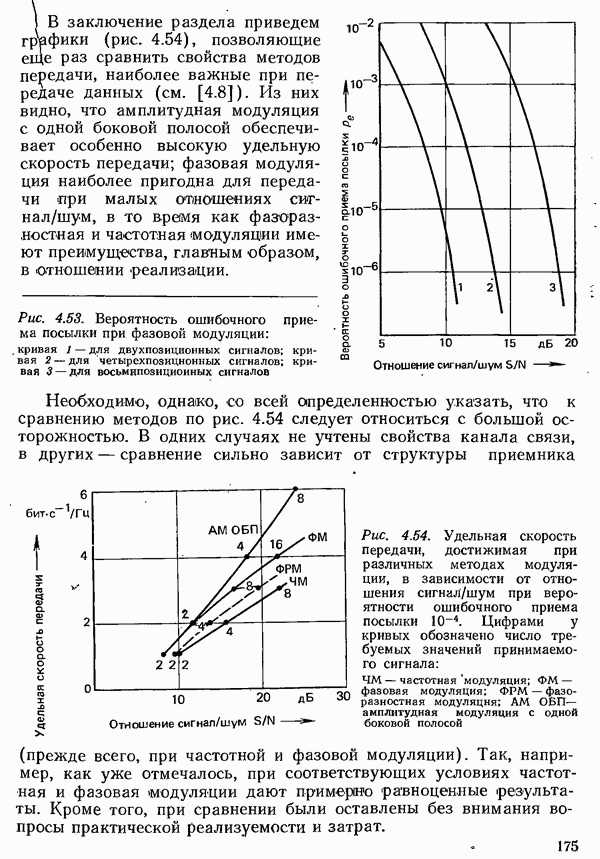
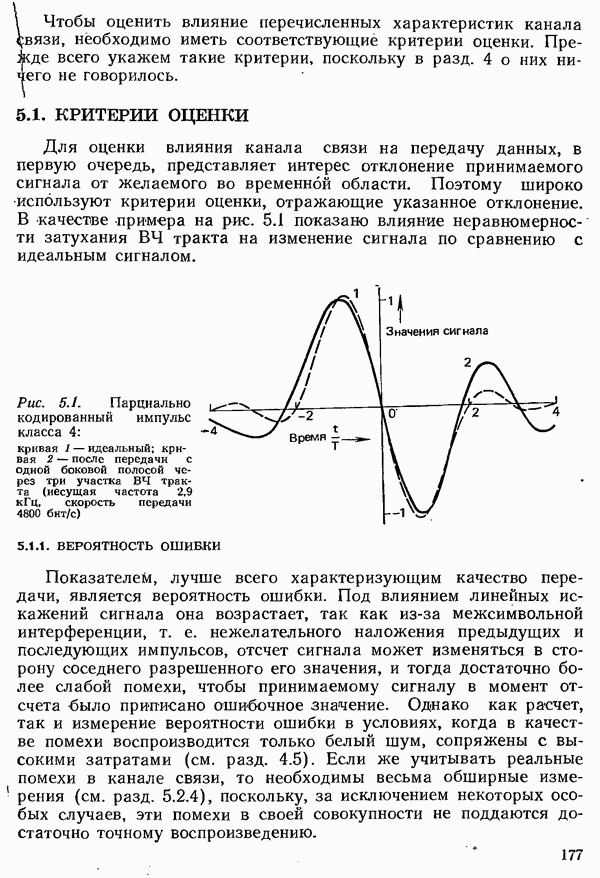
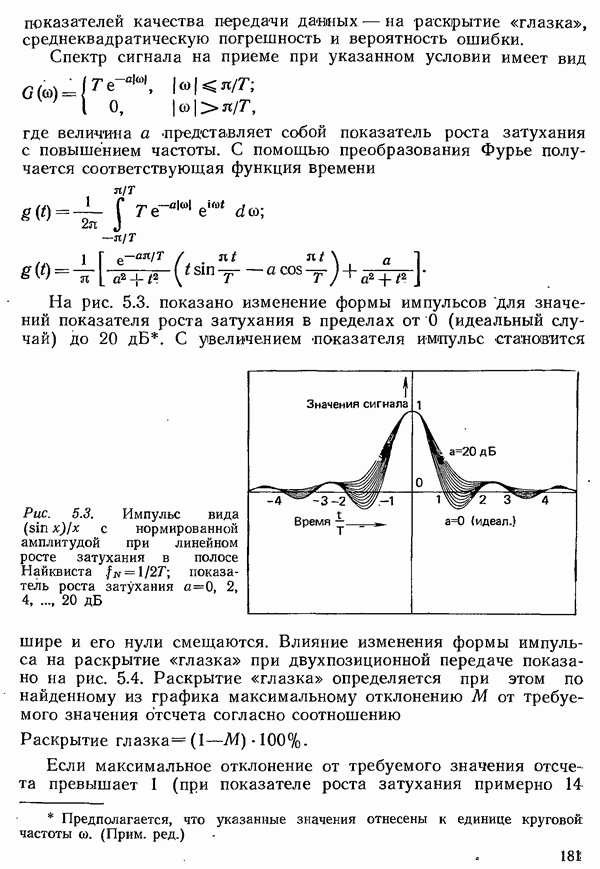
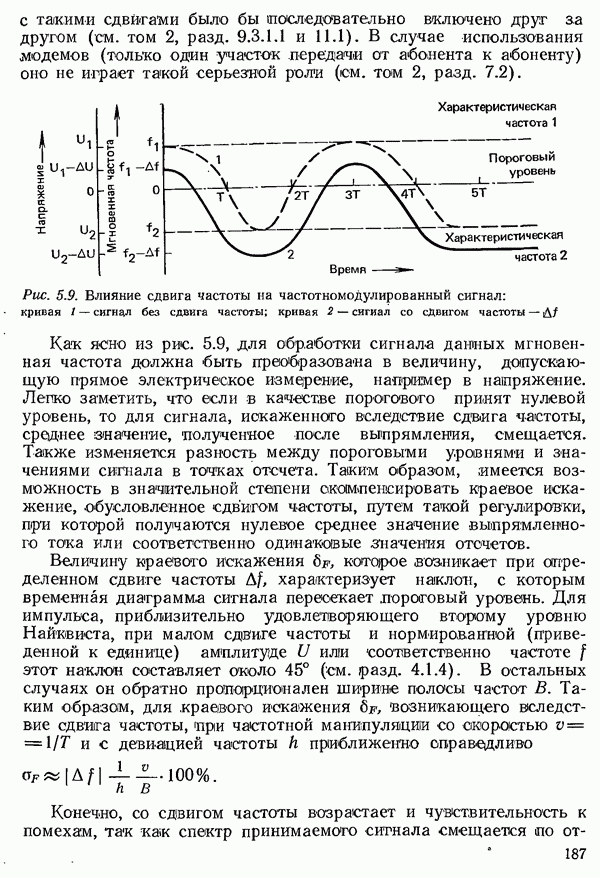
В разд. 2.3.1 было рассмотрено единственное поле событий  а именно алфавит источника, из которого путем операции выбора формируется последовательность символов, несущая информацию. Эта информация должна быть передана по каналу к получателю (см. рис. 2.1). При этом предполагается, что получателю известен алфавит источника. Поступающая к получателю информация также образует некоторое поле событий
а именно алфавит источника, из которого путем операции выбора формируется последовательность символов, несущая информацию. Эта информация должна быть передана по каналу к получателю (см. рис. 2.1). При этом предполагается, что получателю известен алфавит источника. Поступающая к получателю информация также образует некоторое поле событий  которое по объему может отличаться от поля источника.
которое по объему может отличаться от поля источника.
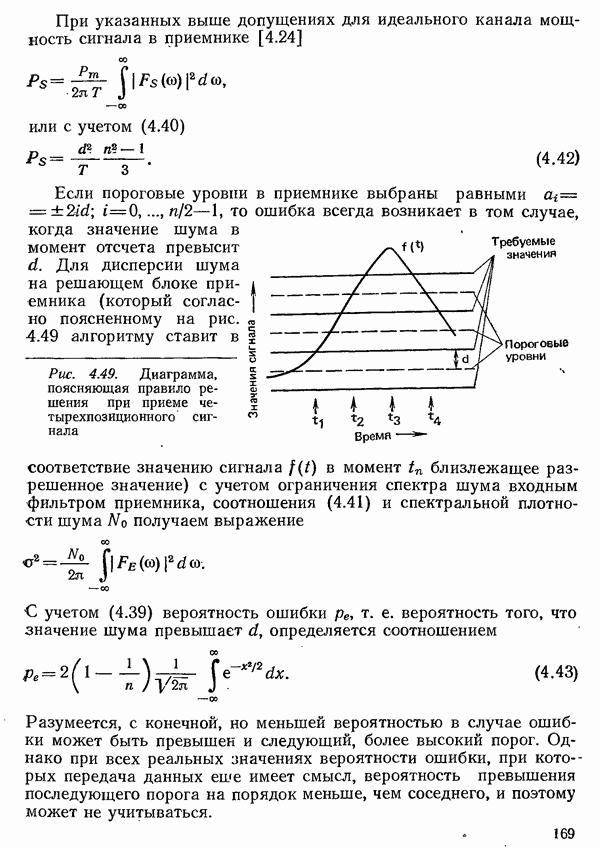
Пусть некоторый символ  с вероятностью
с вероятностью  посланный источником, после передачи по каналу связи появляется у получателя как символ
посланный источником, после передачи по каналу связи появляется у получателя как символ  с условной вероятностью
с условной вероятностью  Эта вероятность называется условной, потому что она характеризует появление
Эта вероятность называется условной, потому что она характеризует появление  при условии, что был послан символ
при условии, что был послан символ 
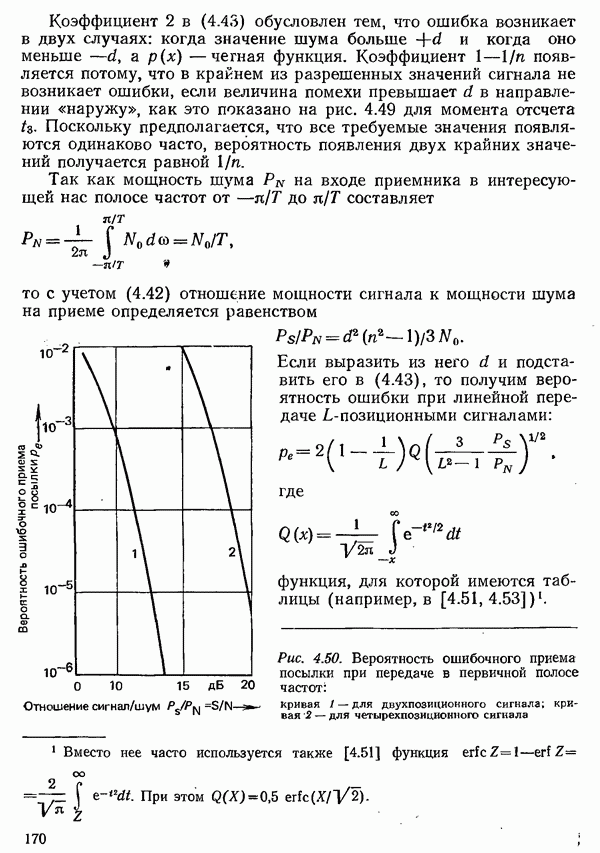
В соответствии с (2.6) теперь для пары событий  можно определить информацию
можно определить информацию

Это вытекает из того, что совместная вероятность  пары событий,
пары событий,  у может быть представлена как произведение вероятности события
у может быть представлена как произведение вероятности события  на вычисленную с учетом его появления условную вероятность
на вычисленную с учетом его появления условную вероятность  события
события 
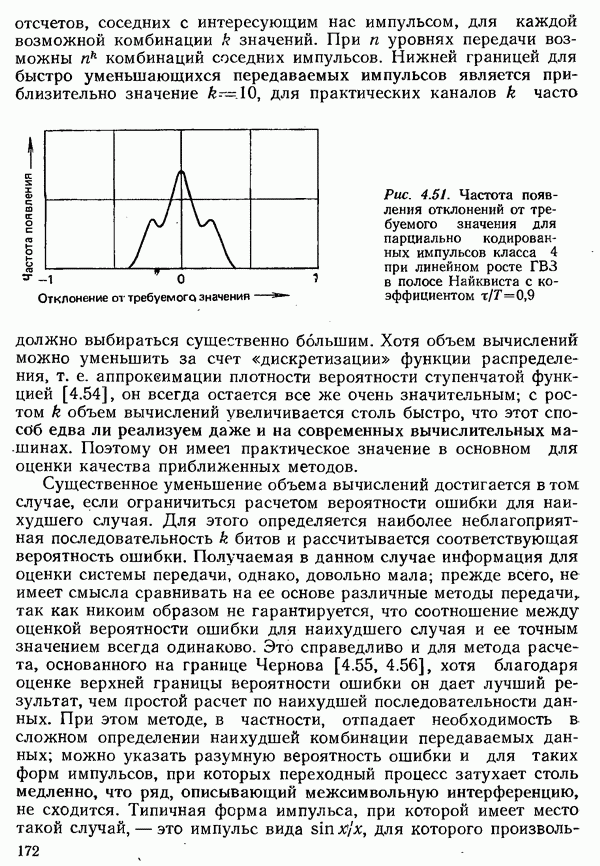
Порядок следования событий  можно изменить:
можно изменить:

так как ту же совместную вероятность  можно представить в виде произведения вероятности
можно представить в виде произведения вероятности  появления на приеме символа
появления на приеме символа  на вероятность
на вероятность  того, что был передан символ
того, что был передан символ  при условии,
при условии,  принят
принят 
Количествам информации (2.13) и (2.14) соответствуют математические ожидания информации, т. е. совместная энтропия

и

Условные энтропии  выражают степень «развязки» полей событий
выражают степень «развязки» полей событий  и
и  На рис. 2.6 это изображается по Схоутену [2.18] в виде двух пересекающихся кругов, причем левый круг представляет
На рис. 2.6 это изображается по Схоутену [2.18] в виде двух пересекающихся кругов, причем левый круг представляет  правый —
правый —  а жирно окантованная общая площадь - совместную энтропию
а жирно окантованная общая площадь - совместную энтропию 

Рис. 2.6. Диаграмма подразделения совместной энтропии  : обведенная жирной линией общая площадь — совместная энтропия
: обведенная жирной линией общая площадь — совместная энтропия  левый круг — энтропия
левый круг — энтропия  правый круг — энтропия
правый круг — энтропия 
При жесткой связи обоих полей событий (идеальная, свободная от шумов передача) оба круга одинаково велйки и совпадают друг с другом, так что заштрихованные площади  исчезают. Если, напротив, оба поля события полностью развязаны
исчезают. Если, напротив, оба поля события полностью развязаны
(например, из-за разрыва линии связи), то оба круга на рис. 2.6 располагаются отдельно друг от друга, т. е.

В общем случае круги накладываются друг на друга так, что имеется общая часть  (канал передачи с шумами).
(канал передачи с шумами).
Составляющие совместной энтропии имеют следующие названия и значение (рис. 2.6 и  потерянная часть посланной информации, которая не достигает приемника; она называется ненадежностью канала;
потерянная часть посланной информации, которая не достигает приемника; она называется ненадежностью канала;  та часть воспринимаемой приемником информации, которая не имеет отношения к переданной информации; она называется иррелевантной информацией или энтропией шума. Часть информации, поступившей на вход канала связи, которая достигает приемника,
та часть воспринимаемой приемником информации, которая не имеет отношения к переданной информации; она называется иррелевантной информацией или энтропией шума. Часть информации, поступившей на вход канала связи, которая достигает приемника,

выражает количество переданной полезной информации.

Рис. 2.7. Передача информации по каналу с шумом (представление по Е. Р. Бергеру)
Среднее количество информации, проходящее по каналу в секунду, называют скоростью передачи информации,  (единица измерения —
(единица измерения —  Она зависит от свойств канала и источника, однако при допущении всех возможных способов кодирования входного сигнала можно устранить зависимость
Она зависит от свойств канала и источника, однако при допущении всех возможных способов кодирования входного сигнала можно устранить зависимость  от свойств источника и получить максимальное значение скорости передачи информации
от свойств источника и получить максимальное значение скорости передачи информации  Оно называется пропускной способностью канала С и зависит от свойств канала.
Оно называется пропускной способностью канала С и зависит от свойств канала.
К. Э. Шеннон показал, что ненадежность канала И при наличии шума можно сделать сколь угодно малой за счет надлежащего кодирования, если скорость поступления информации на вход канала не превышает его пропускной способности.
Очень интересно сравнение пропускной способности каналов различных типов, которое было проведено  Марко [2.19]. Рассмотрим с этой целью следующую модель канала связи для
Марко [2.19]. Рассмотрим с этой целью следующую модель канала связи для
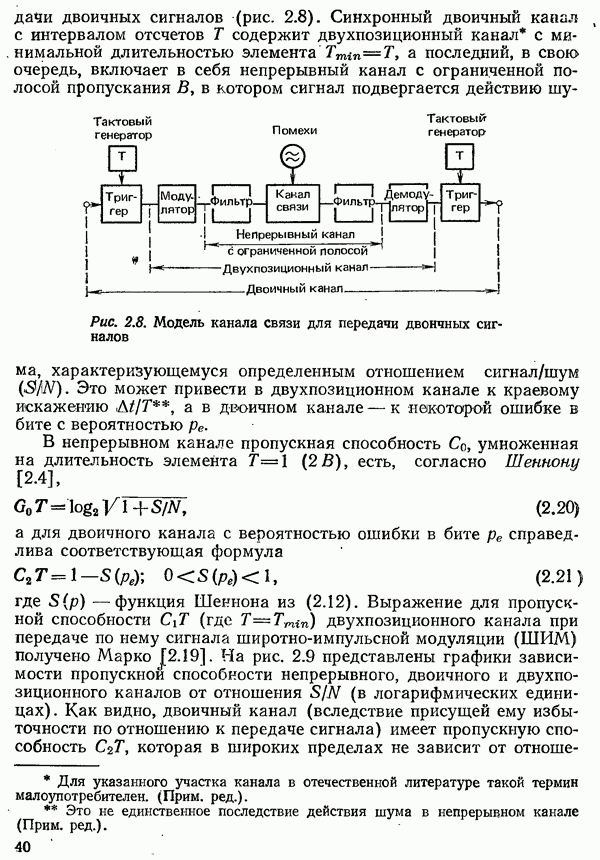
передачи двоичных сигналов (рис. 2.8). Синхронный двоичный канал с интервалом отсчетов  содержит двухпозиционный канал с минимальной длительностью элемента
содержит двухпозиционный канал с минимальной длительностью элемента  а последний, в свою очередь, включает в себя непрерывный канал с ограниченной полосой пропускания В, в котором сигнал подвергается действию шума, характеризующемуся определенным отношением сигнал/шум
а последний, в свою очередь, включает в себя непрерывный канал с ограниченной полосой пропускания В, в котором сигнал подвергается действию шума, характеризующемуся определенным отношением сигнал/шум 

Рис. 2.8. Модель канала связи для передачи двоичных сигналов
Это может привести в двухпозиционном канале к краевому искажению  а в двоичном канале — к некоторой ошибке в бите с вероятностью
а в двоичном канале — к некоторой ошибке в бите с вероятностью 
В непрерывном канале пропускная способность Со, умноженная на длительность элемента  есть, согласно Шеннону
есть, согласно Шеннону 

а для двоичного канала с вероятностью ошибки в бите  справедлива соответствующая формула
справедлива соответствующая формула

где  — функция Шеннона из (2.12). Выражение для пропускной способности
— функция Шеннона из (2.12). Выражение для пропускной способности  (где
(где  двухпозиционного канала при передаче по нему сигнала широтно-импульсной модуляции (ШИМ) получено Марко
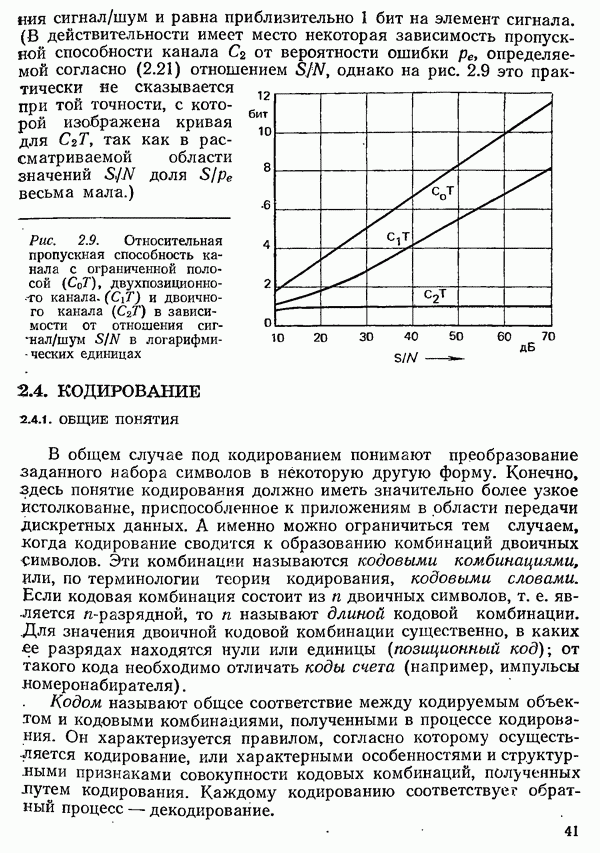
двухпозиционного канала при передаче по нему сигнала широтно-импульсной модуляции (ШИМ) получено Марко  На рис. 2.9 представлены графики зависимости пропускной способности непрерывного, двоичного и двухпозиционного каналов от отношения
На рис. 2.9 представлены графики зависимости пропускной способности непрерывного, двоичного и двухпозиционного каналов от отношения  (в логарифмических единицах). Как видно, двоичный канал (вследствие присущей ему избыточности по отношению к передаче сигнала) имеет пропускную способность
(в логарифмических единицах). Как видно, двоичный канал (вследствие присущей ему избыточности по отношению к передаче сигнала) имеет пропускную способность  которая в широких пределах не зависит от
которая в широких пределах не зависит от
отношения сигнал/шум и равна приблизительно 1 бит на элемент сигнала. (В действительности имеет место некоторая зависимость пропускной способности канала  от вероятности ошибки
от вероятности ошибки  определяемой согласно (2.21) отношением
определяемой согласно (2.21) отношением  однако на рис. 2.9 это практически не сказывается при той точности, с которой изображена кривая для
однако на рис. 2.9 это практически не сказывается при той точности, с которой изображена кривая для  так как в рассматриваемой области значений
так как в рассматриваемой области значений  доля
доля  весьма мала.)
весьма мала.)

Рис. 2.9. Относительная пропускная способность канала с ограниченной полосой  двухпозиционного канала.
двухпозиционного канала.  и двоичного канала
и двоичного канала  в зависимости от отношения сигнал/шум
в зависимости от отношения сигнал/шум  в логарифмических единицах
в логарифмических единицах
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ К РУССКОМУ ИЗДАНИЮ
- 1. Обзор
- 1.1. ОБРАБОТКА И ТЕЛЕОБРАБОТКА ДАННЫХ
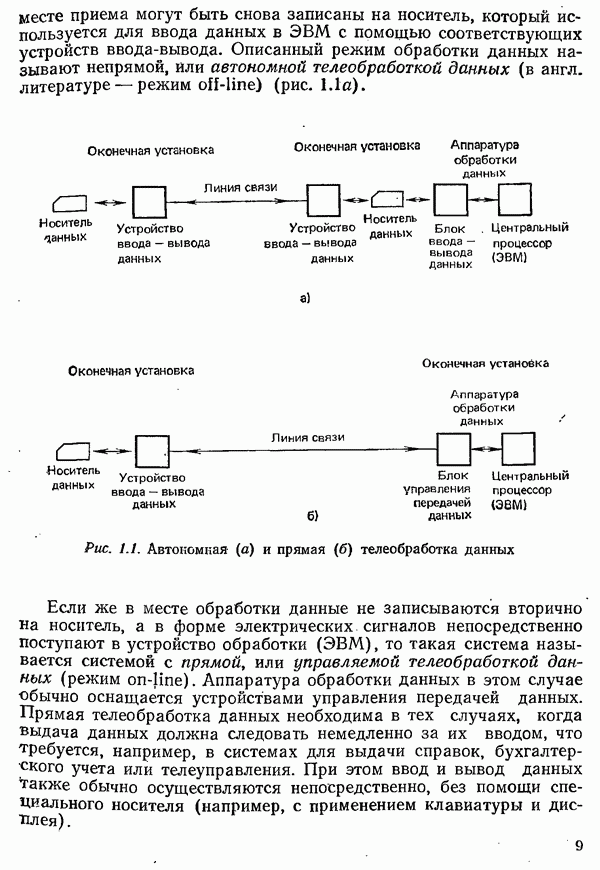
- 1.2. АВТОНОМНАЯ И УПРАВЛЯЕМАЯ ТЕЛЕОБРАБОТКА ДАННЫХ
- 1.3. КЛАССИФИКАЦИЯ СИСТЕМ ТЕЛЕОБРАБОТКИ ДАННЫХ
- 1.4. СТРУКТУРА СИСТЕМ ТЕЛЕОБРАБОТКИ ДАННЫХ
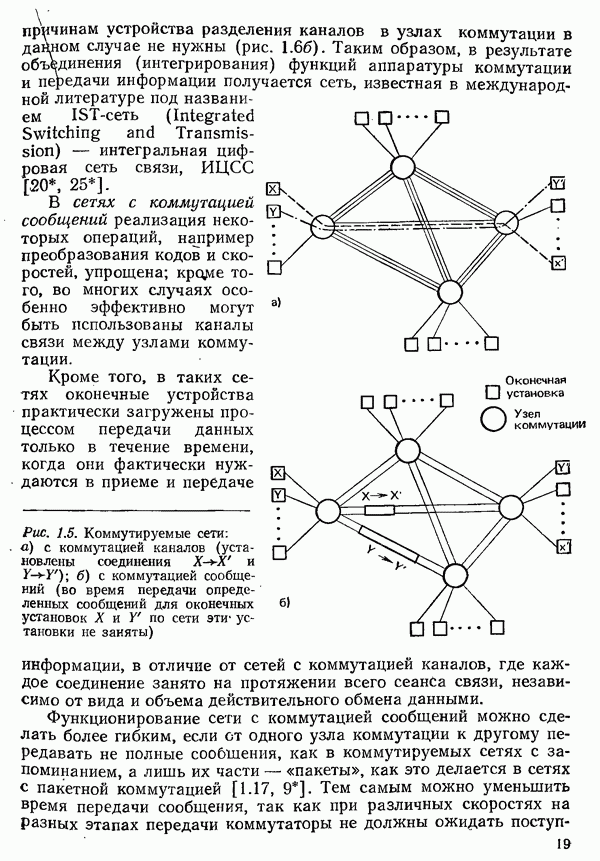
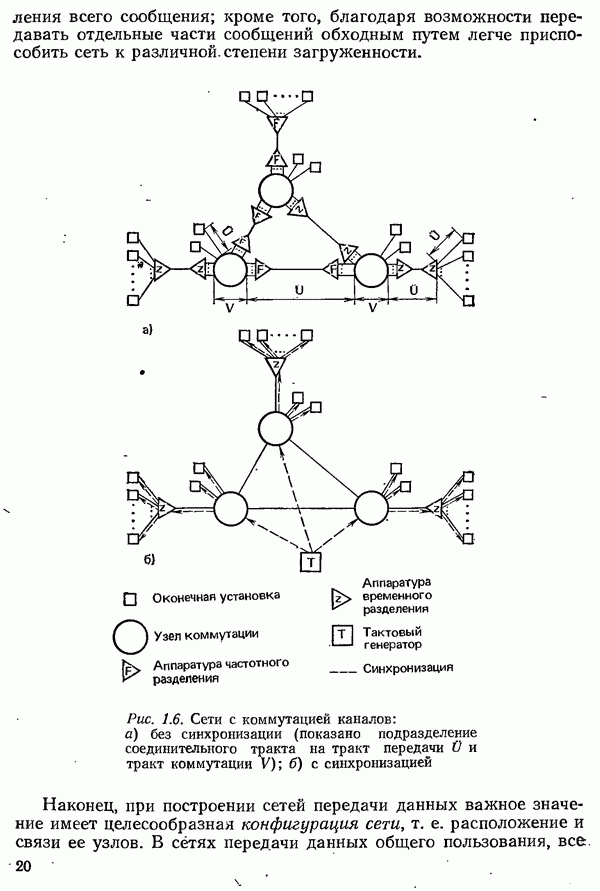
- 1.5. ТРЕБОВАНИЯ К ТЕХНИКЕ СВЯЗИ И КОММУТАЦИИ В СИСТЕМАХ ТЕЛЕОБРАБОТКИ ДАННЫХ
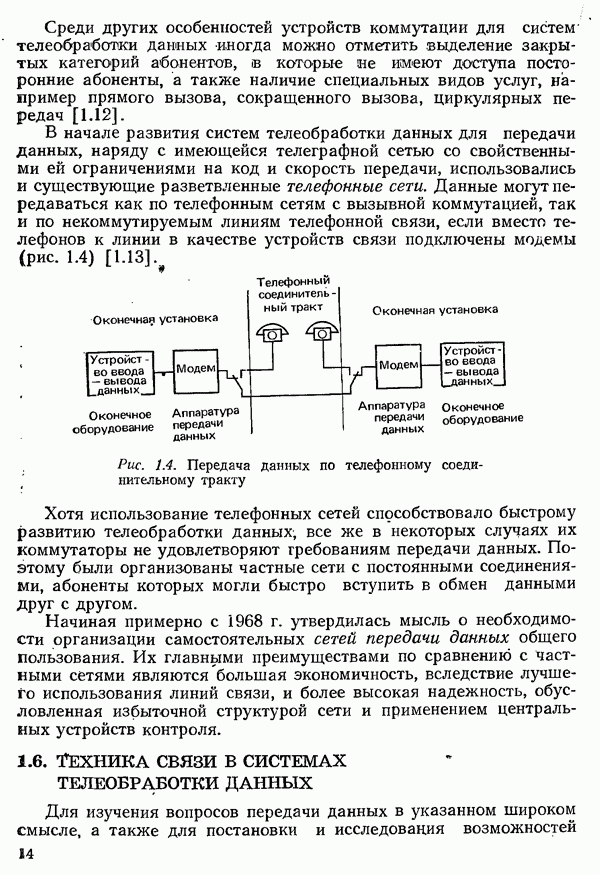
- 1.6. ТЕХНИКА СВЯЗИ В СИСТЕМАХ ТЕЛЕОБРАБОТКИ ДАННЫХ
- 2. Основные понятия техники связи
- 2.2. СИГНАЛЫ
- 2.2.2. ДИСКРЕТИЗАЦИЯ, КВАНТОВАНИЕ, ВЛИЯНИЕ ШУМОВ
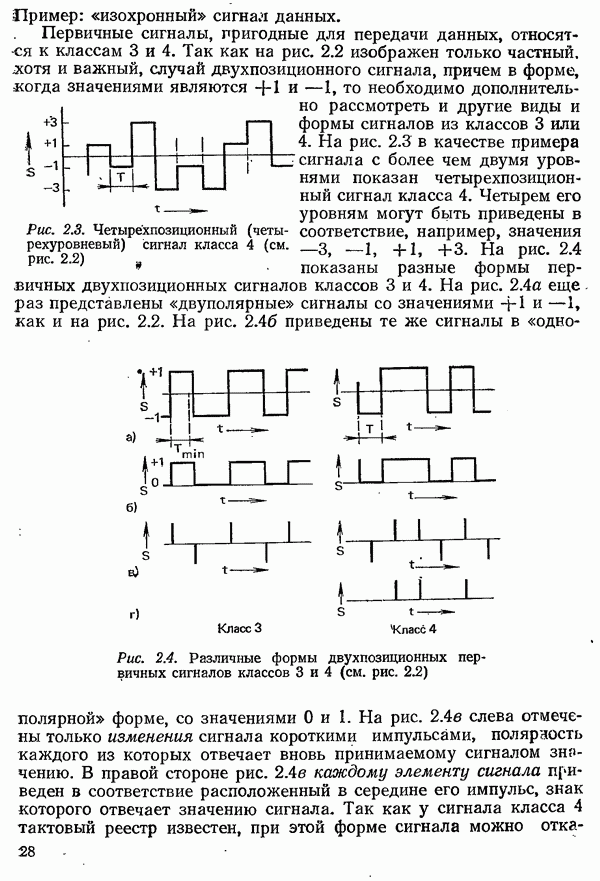
- 2.2.3. СВОЙСТВА ПЕРВИЧНЫХ СИГНАЛОВ ДЛЯ ПЕРЕДАЧИ ДАННЫХ
- 2.2.3.2. ВРЕМЕННЫЕ СООТНОШЕНИЯ МЕЖДУ СИГНАЛАМИ
- 2.2.4. РЕЖИМЫ РАБОТЫ ПРИ ПЕРЕДАЧЕ СИГНАЛОВ
- 2.3. НЕКОТОРЫЕ ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ИНФОРМАЦИИ
- 2.3.2. ПЕРЕДАННАЯ ИНФОРМАЦИЯ. ПРОПУСКНАЯ СПОСОБНОСТЬ КАНАЛА СВЯЗИ
- 2.4. КОДИРОВАНИЕ
- 2.4.3. КОДИРОВАНИЕ ИСТОЧНИКА
- 2.4.4. КАНАЛЬНОЕ КОДИРОВАНИЕ
- 3. Каналы связи
- 3.1. КАНАЛЫ БЛИЖНЕЙ СВЯЗИ
- 3.1.1.1. СВОЙСТВА И ПАРАМЕТРЫ ПРОВОДНЫХ ЛИНИЙ СВЯЗИ
- 3.1.1.2. УМЕНЬШЕНИЕ ЗАТУХАНИЯ ПУТЕМ УВЕЛИЧЕНИЯ ИНДУКТИВНОСТИ. ПУПИНИЗАЦИЯ
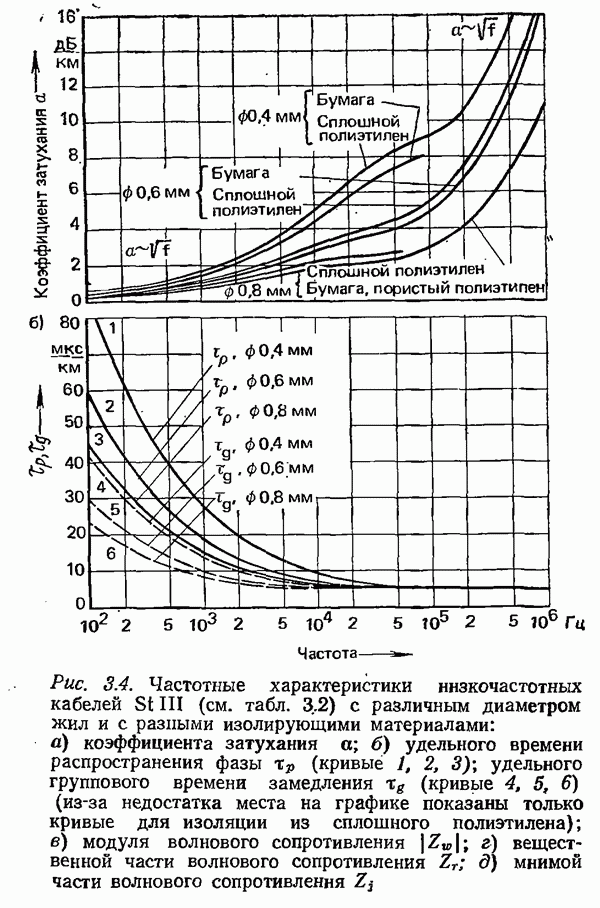
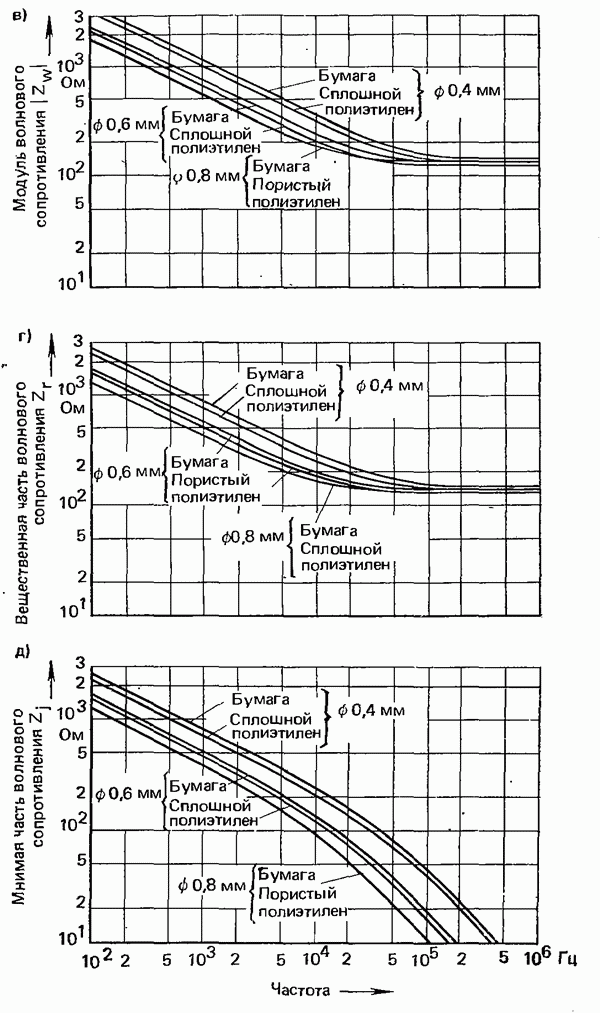
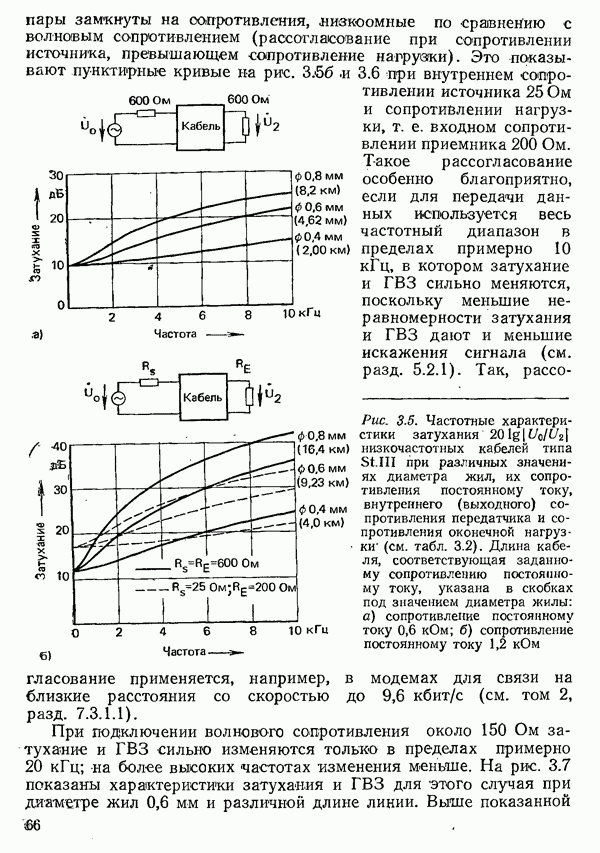
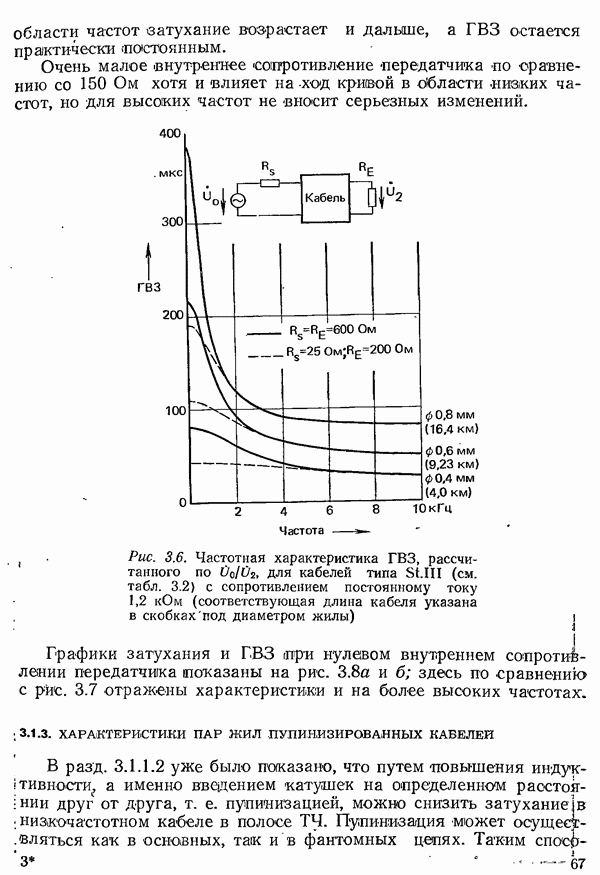
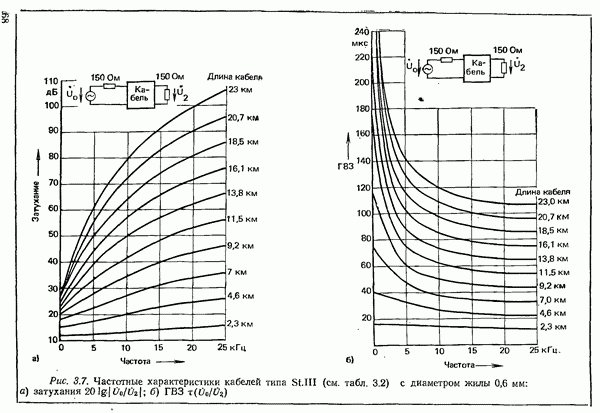
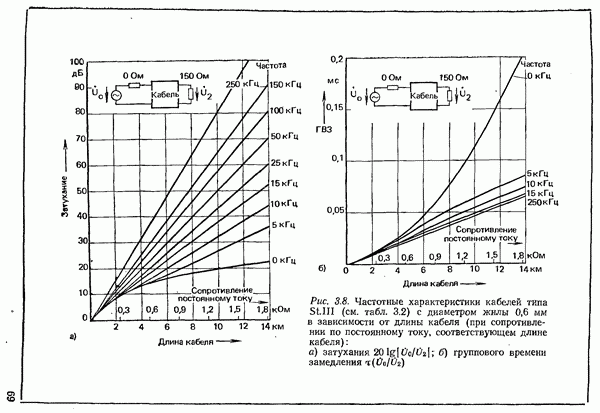
- 3.1.2. ХАРАКТЕРИСТИКИ ПАР ЖИЛ НИЗКОЧАСТОТНЫХ КАБЕЛЕЙ
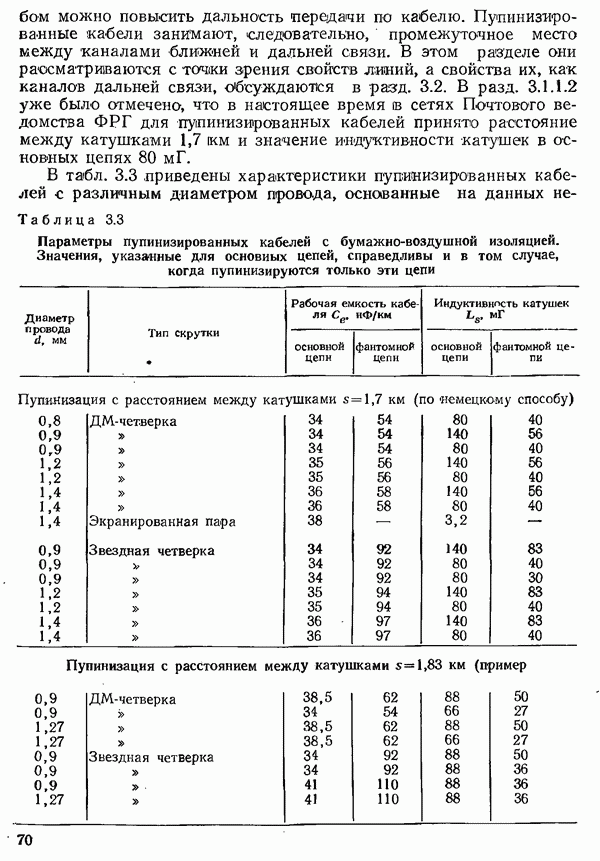
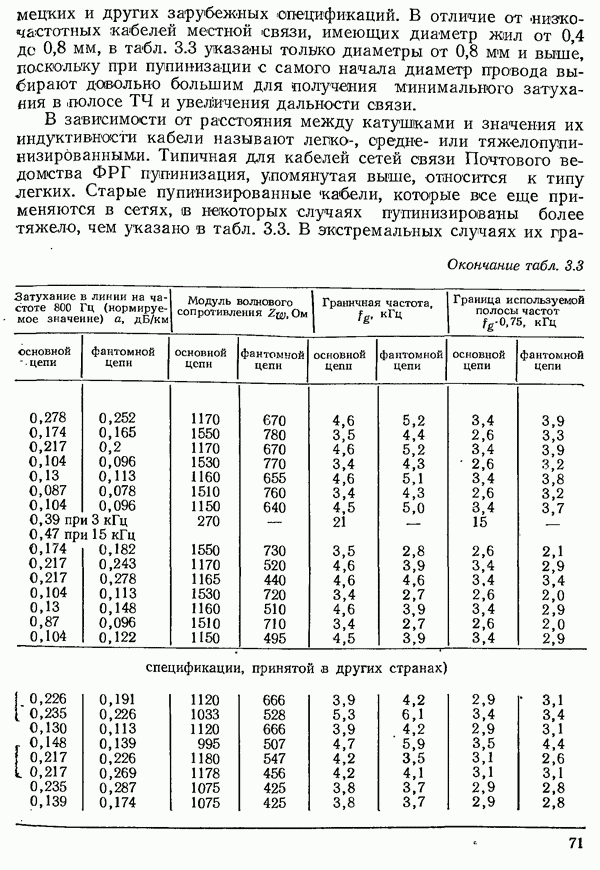
- 3.1.3. ХАРАКТЕРИСТИКИ ПАР ЖИЛ ПУПИЯИЗИРОВАННЫХ КАБЕЛЕЙ
- 3.1.4. ПЕРЕХОДНЫЕ ПОМЕХИ В КАБЕЛЯХ
- 3.1.5. НАПРЯЖЕНИЯ ШУМОВ НА ПАРАХ ШИЛ КАБЕЛЕЙ
- 3.2. КАНАЛЫ ДАЛЬНЕЙ СВЯЗИ
- 3.2.2. КАНАЛЫ ТОНАЛЬНОЙ ЧАСТОТЫ
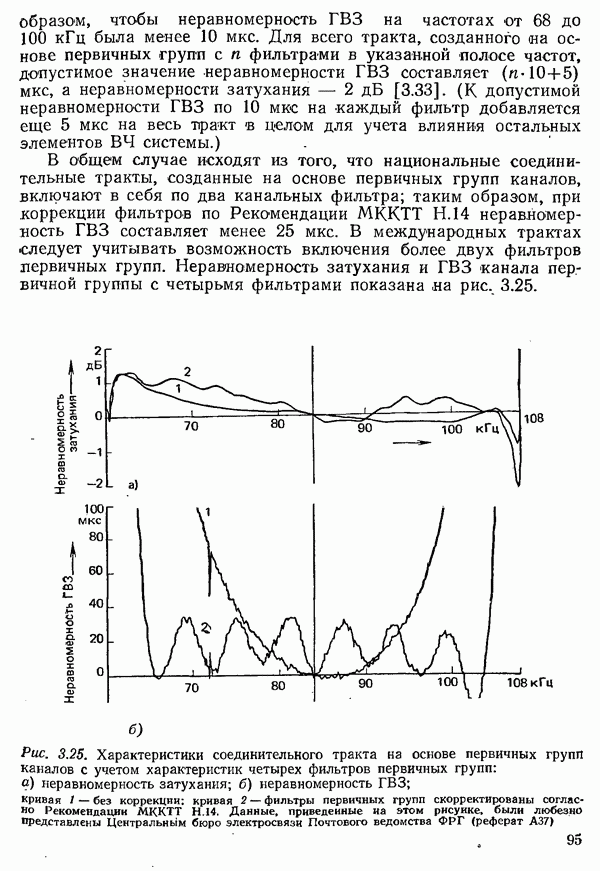
- 3.2.3. СОЕДИНИТЕЛЬНЫЕ ТРАКТЫ НА ОСНОВЕ ПЕРВИЧНЫХ ГРУПП КАНАЛОВ
- 4. Методы передачи данных
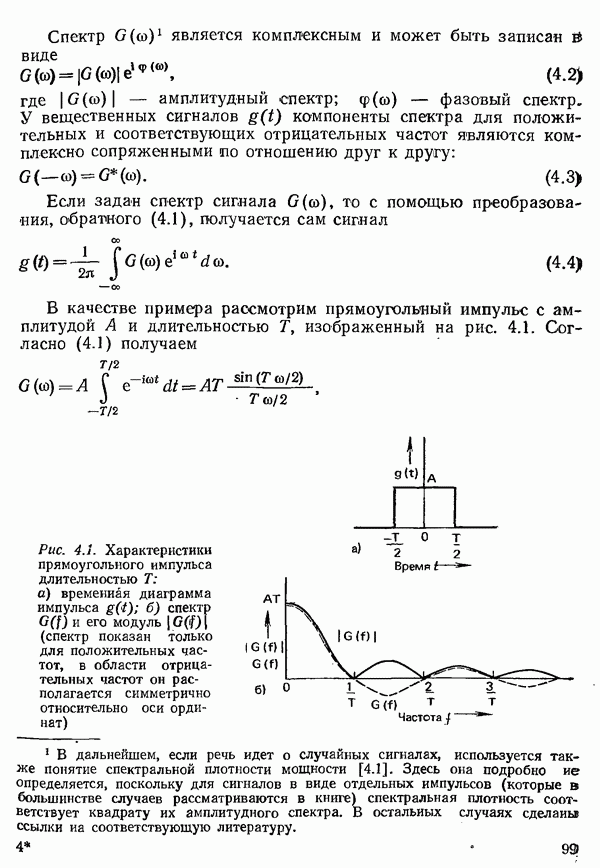
- 4.1.1. СИГНАЛЫ И СПЕКТРЫ
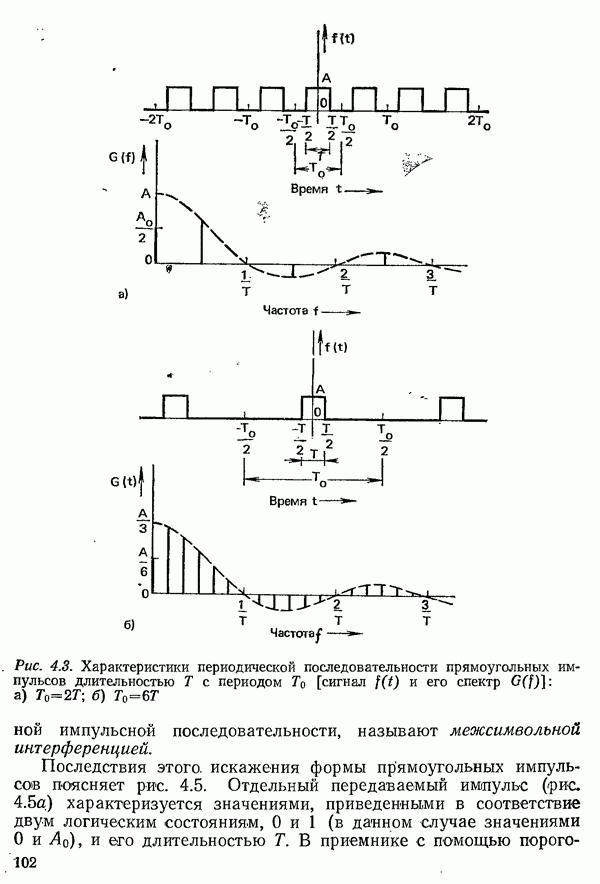
- 4.1.2. РЯД ФУРЬЕ
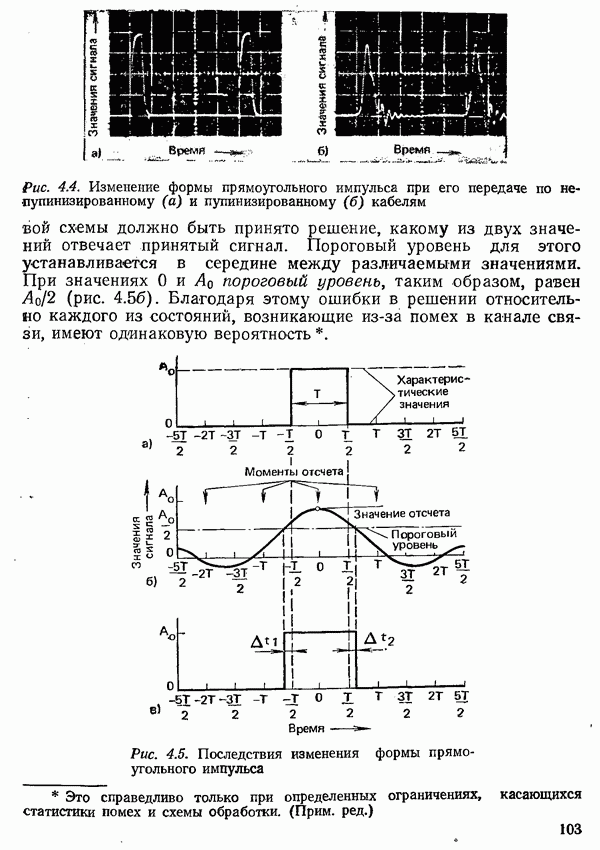
- 4.1.3. ИСКАЖЕНИЯ ФОРМЫ ИМПУЛЬСОВ ПРИ ОГРАНИЧЕНИИ ПОЛОСЫ ЧАСТОТ
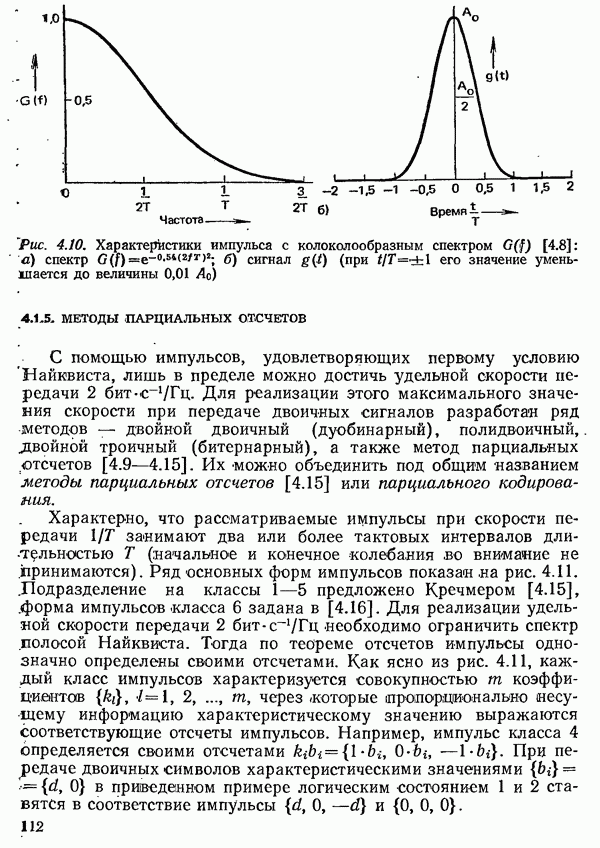
- 4.1.4. УСЛОВИЯ НАЙКВИСТА
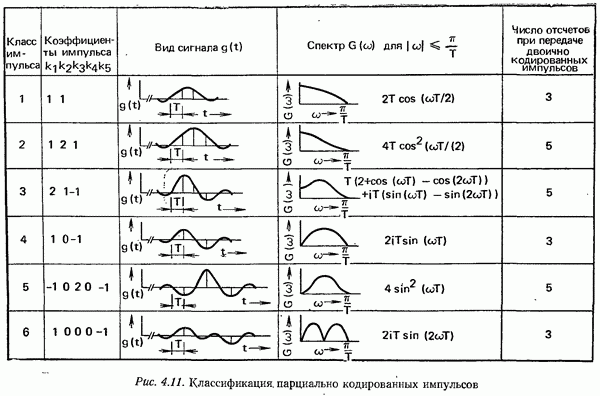
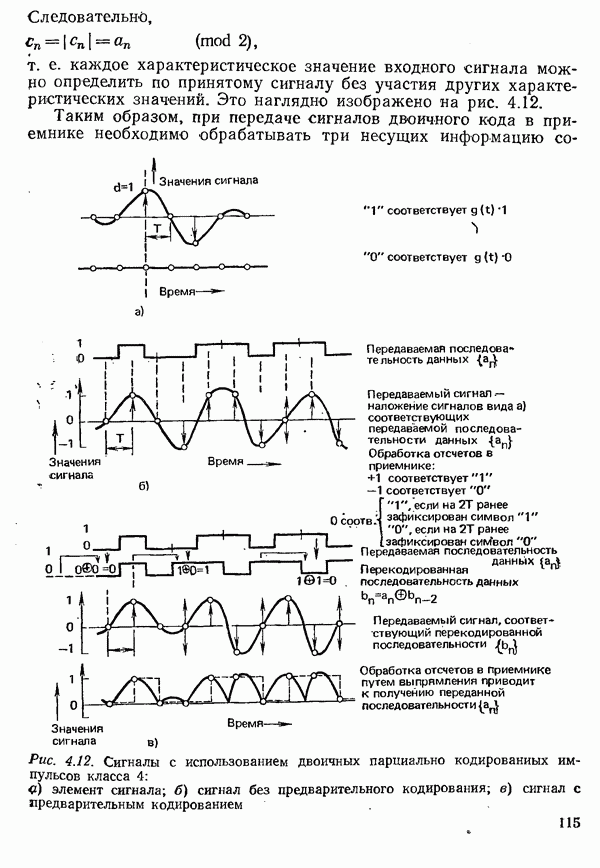
- 4.1.5. МЕТОДЫ ПАРЦИАЛЬНЫХ ОТСЧЕТОВ
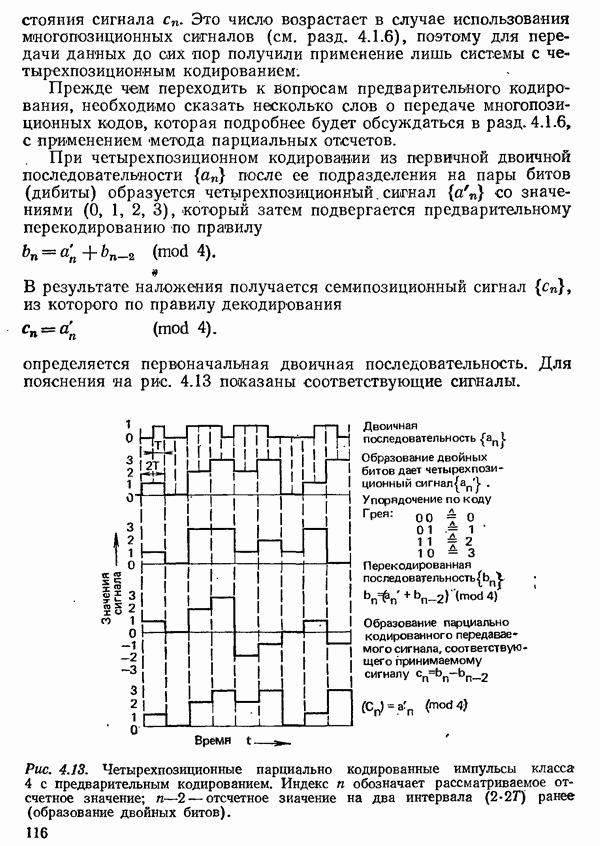
- 4.1.6. ПЕРЕДАЧА МНОГОПОЗИЦИОННЫХ СИГНАЛОВ
- 4.2. МЕТОДЫ ПЕРЕДАЧИ В ПЕРВИЧНОЙ ПОЛОСЕ ЧАСТОТ
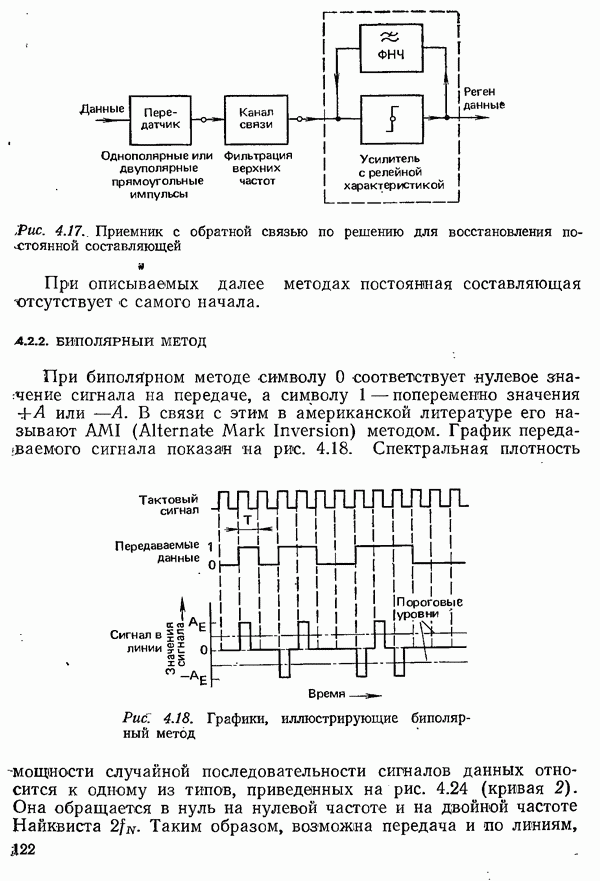
- 4.2.1. МЕТОДЫ С ПРИМЕНЕНИЕМ ДВУПОЛЯРНЫХ И ОДНОПОЛЯРНЫХ ИМПУЛЬСОВ
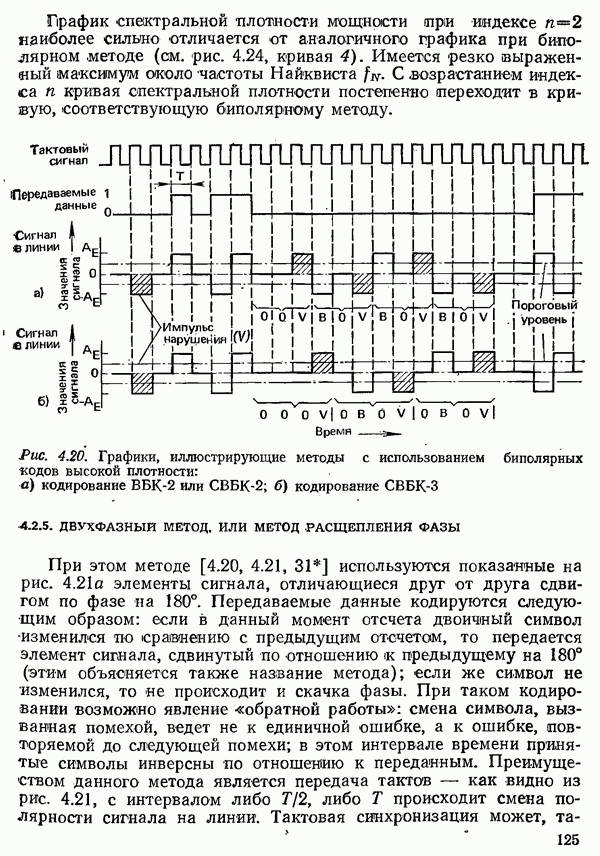
- 4.2.2. БИПОЛЯРНЫЙ МЕТОД
- 4.2.3. ПСЕВДОТРОИЧНЫЕ МЕТОДЫ
- 4.2.4. МЕТОДЫ С ПРИМЕНЕНИЕМ БИПОЛЯРНЫХ КОДОВ ВЫСОКОЙ ПЛОТНОСТИ
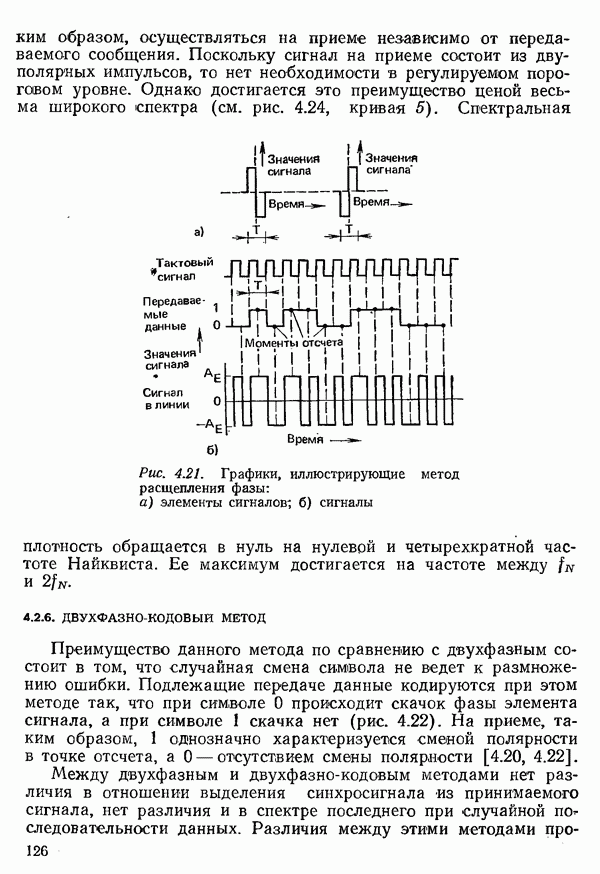
- 4.2.5. ДВУХФАЗНЫЙ МЕТОД. ИЛИ МЕТОД РАСЩЕПЛЕНИЯ ФАЗЫ
- 4.2.6. ДВУХФАЗНО-КОДОВЫЙ МЕТОД
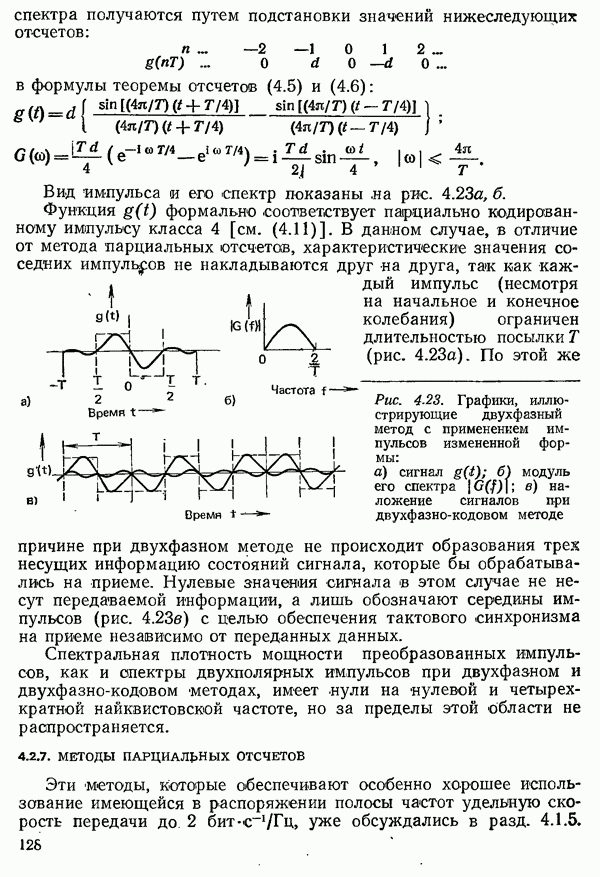
- 4.2.7. МЕТОДЫ ПАРЦИАЛЬНЫХ ОТСЧЕТОВ
- 4.3. МЕТОДЫ ПЕРЕДАЧИ С ПРИМЕНЕНИЕМ МОДУЛЯЦИИ
- 4.3.1. АМПЛИТУДНАЯ МОДУЛЯЦИЯ
- 4.3.1.2. АМПЛИТУДНАЯ МОДУЛЯЦИЯ С ОДНОЙ БОКОВОЙ ПОЛОСОЙ И С ЧАСТИЧНО ПОДАВЛЕННОЙ БОКОВОЙ ПОЛОСОЙ
- 4.3.1.3. КВАДРАТУРНАЯ АМПЛИТУДНАЯ МОДУЛЯЦИЯ
- 4.3.1.4. УДЕЛЬНАЯ СКОРОСТЬ ПЕРЕДАЧИ ПРИ АМПЛИТУДНОЙ МОДУЛЯЦИИ
- 4.3.2. ЧАСТОТНАЯ МОДУЛЯЦИЯ
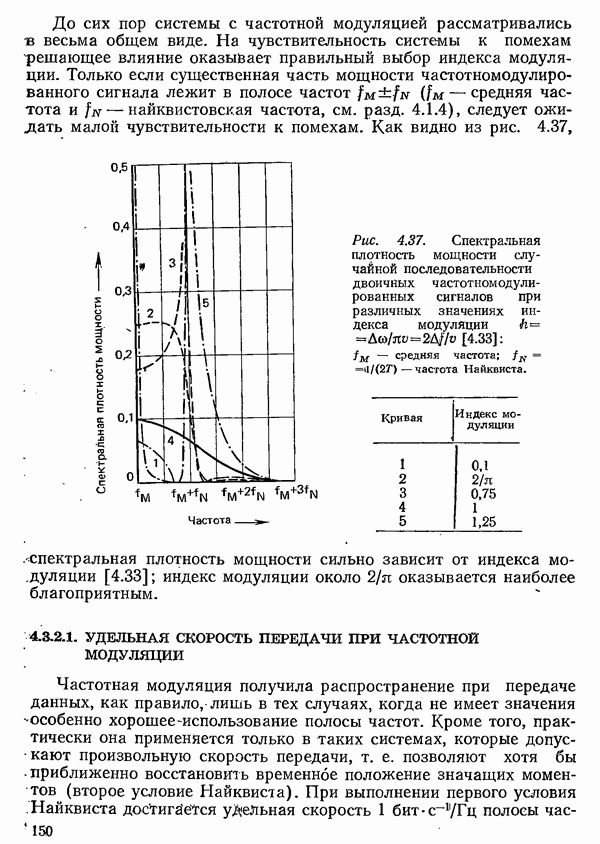
- 4.3.2.1. УДЕЛЬНАЯ СКОРОСТЬ ПЕРЕДАЧИ ПРИ ЧАСТОТНОЙ МОДУЛЯЦИИ
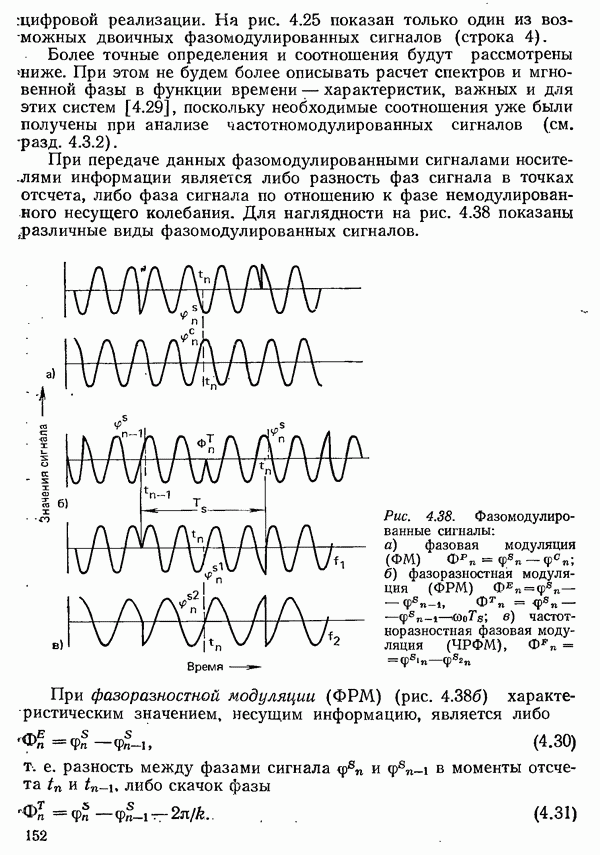
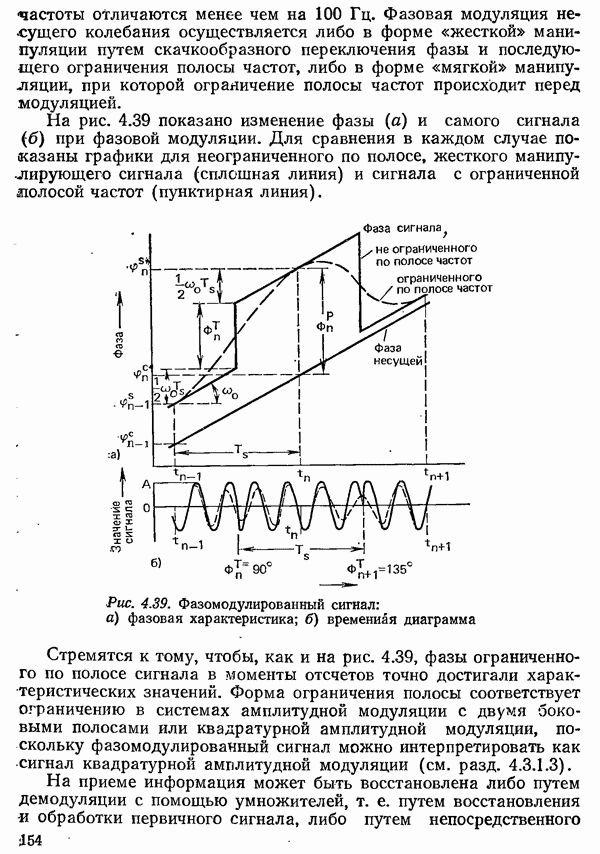
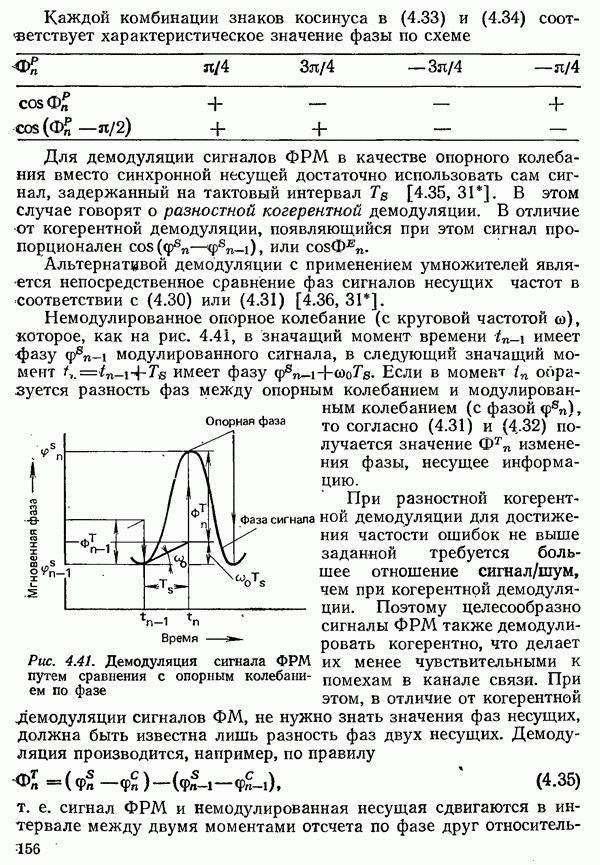
- 4.3.3. ФАЗОВАЯ МОДУЛЯЦИЯ
- 4.4. ВОССТАНОВЛЕНИЕ ТАКТОВ И НЕСУЩЕЙ
- 4.4.2. ВОССТАНОВЛЕНИЕ ЧАСТОТЫ И ФАЗЫ НЕСУЩЕЙ
- 4.5. ВЕРОЯТНОСТЬ ОШИБКИ ПРИ НАЛИЧИИ ПОМЕХ
- 4.5.1. ВЕРОЯТНОСТЬ ОШИБКИ ПРИ УЧЕТЕ ТОЛЬКО ШУМА В КАНАЛЕ СВЯЗИ
- 4.5.2. ВЕРОЯТНОСТЬ ОШИБКИ С УЧЕТОМ ЛИНЕЙНЫХ ИСКАЖЕНИЙ
- 4.5.3. ВЕРОЯТНОСТЬ ОШИБКИ С УЧЕТОМ ПРОЦЕССОВ МОДУЛЯЦИИ И ДЕМОДУЛЯЦИИ
- 5. Учет свойств реальных каналов связи при передаче данных
- 5.2. ВЛИЯНИЕ ХАРАКТЕРИСТИК КАНАЛОВ СВЯЗИ НА ПЕРЕДАЧУ ДАННЫХ
- 5.2.2. СДВИГИ ЧАСТОТЫ
- 5.2.3. ФАЗОВОЕ ДРОЖАНИЕ
- 5.2.4. ВЛИЯНИЕ РЕАЛЬНЫХ ПОМЕХ
- 5.3. КОРРЕКЦИЯ ПРИНИМАЕМОГО СИГНАЛА ДАННЫХ
- 5.3.1. КОРРЕКЦИЯ ПРИНИМАЕМОГО СИГНАЛА ДАННЫХ В ЧАСТОТНОЙ ОБЛАСТИ
- 5.3.1.1. КОМПРОМИССНЫЙ КОРРЕКТОР
- 5.3.1.2. НАСТРАИВАЕМЫЙ ЧАСТОТНЫЙ КОРРЕКТОР СИГНАЛОВ ДАННЫХ
- 5.3.2. КОРРЕКЦИЯ ПРИНИМАЕМОГО СИГНАЛА ДАННЫХ ВО ВРЕМЕННОЙ ОБЛАСТИ
- 5.3.2.2. КРИТЕРИИ НАСТРОЙКИ КОРРЕКТОРА ВО ВРЕМЕННОЙ ОБЛАСТИ
- 5.3.2.3. АВТОМАТИЧЕСКАЯ НАСТРОЙКА ТРАНСВЕРСАЛЬНОГО КОРРЕКТИРУЮЩЕГО ФИЛЬТРА
- 5.3.2.4. РЕКУРСИВНЫЙ КОРРЕКТОР
- 5.3.2.5. СХОДИМОСТЬ НАСТРОЙКИ КОРРЕКТОРА
- 5.3.2.6. КОРРЕКТОР ДЛЯ СПЕЦИАЛЬНЫХ МЕТОДОВ ПЕРЕДАЧИ
- 6. Основы коммутации данных
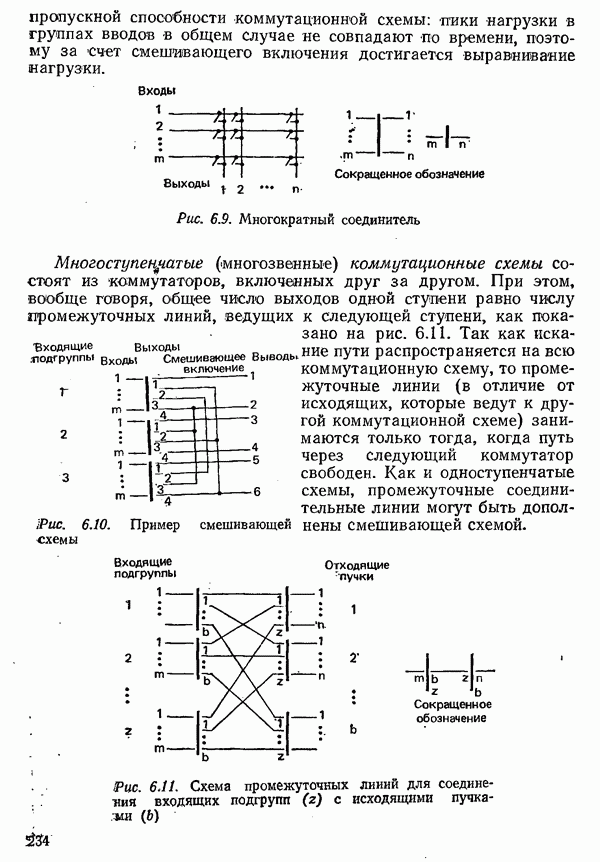
- 6.1.2. МЕТОДЫ КОММУТАЦИИ
- 6.1.3. СПОСОБЫ КОММУТАЦИИ КАНАЛОВ
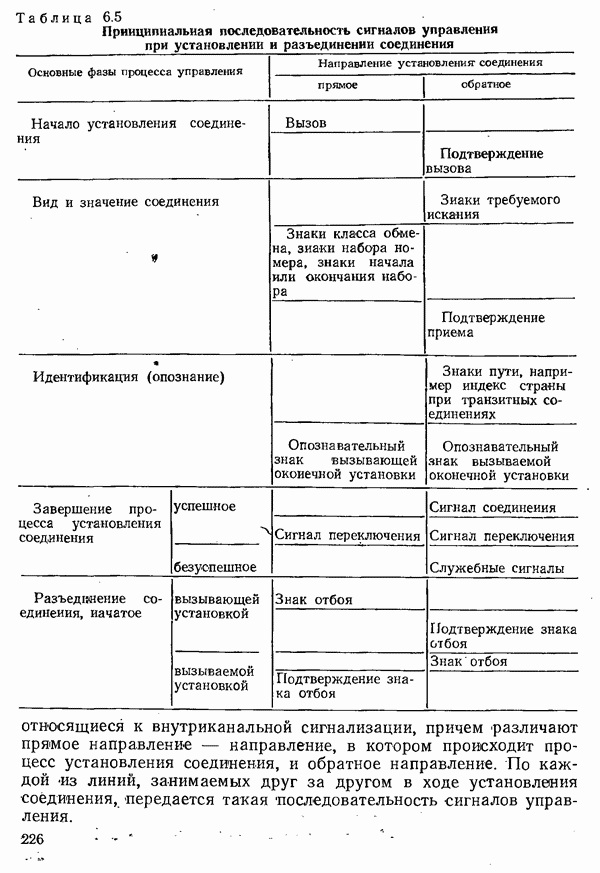
- 6.1.4. СИГНАЛИЗАЦИЯ
- 6.1.5. УПРАВЛЕНИЕ ПРОЦЕССАМИ СОЕДИНЕНИЯ И РАЗЪЕДИНЕНИЯ
- 6.1.6. ПОДРАЗДЕЛЕНИЕ ЦЕПЕЙ КОММУТАЦИИ КАНАЛОВ
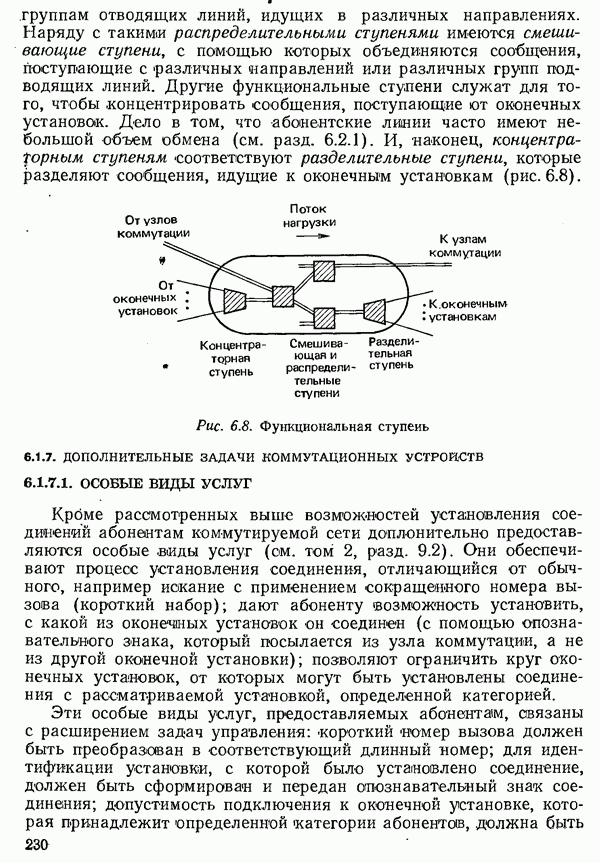
- 6.1.7. ДОПОЛНИТЕЛЬНЫЕ ЗАДАЧИ КОММУТАЦИОННЫХ УСТРОЙСТВ
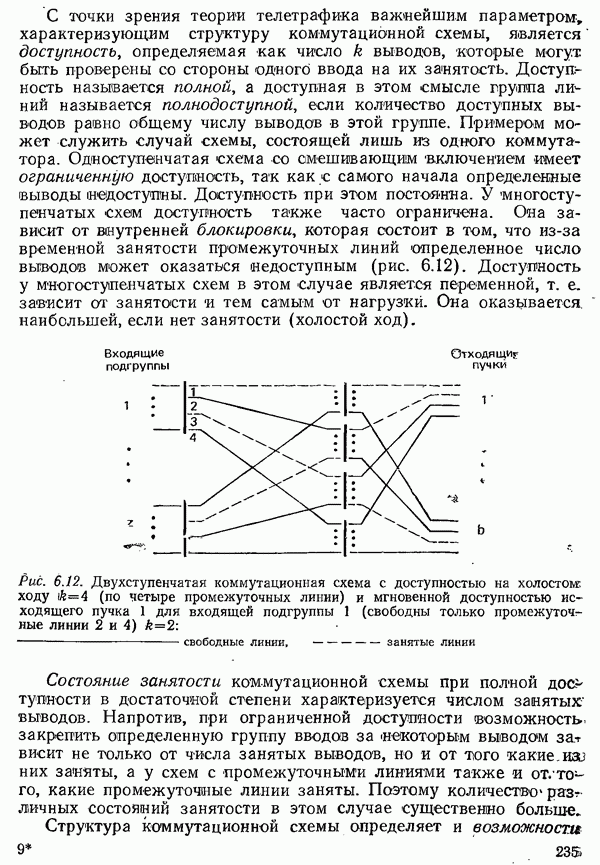
- 6.2. АНАЛИЗ СИСТЕМ КОММУТАЦИИ НА ОСНОВЕ ТЕОРИИ ТЕЛЕТРАФИКА
- 6.2.2. СИСТЕМЫ С ПОТЕРЯМИ
- 6.2.3. СИСТЕМЫ С ОЖИДАНИЕМ
- 6.2.4. ИЗМЕРЕНИЯ НАГРУЗКИ
- СПИСОК ЛИТЕРАТУРЫ