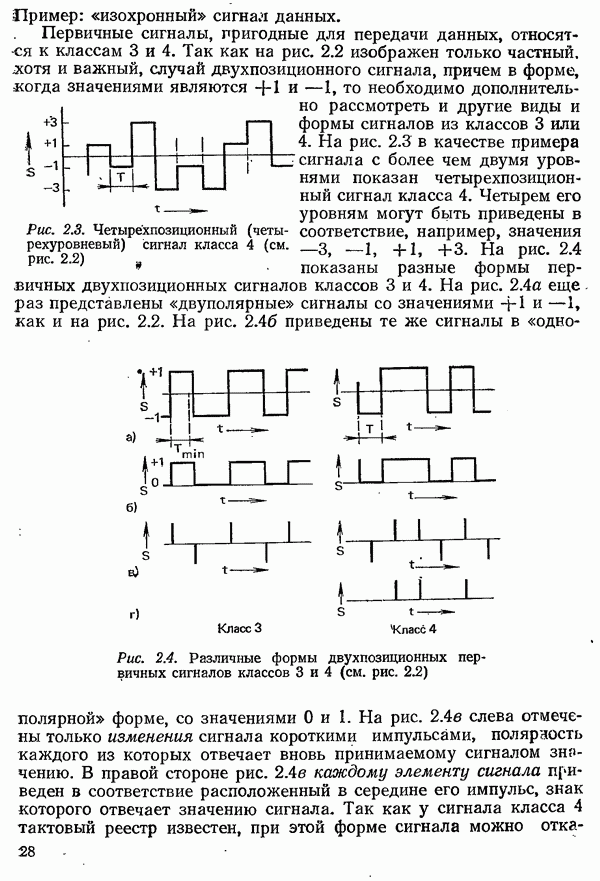
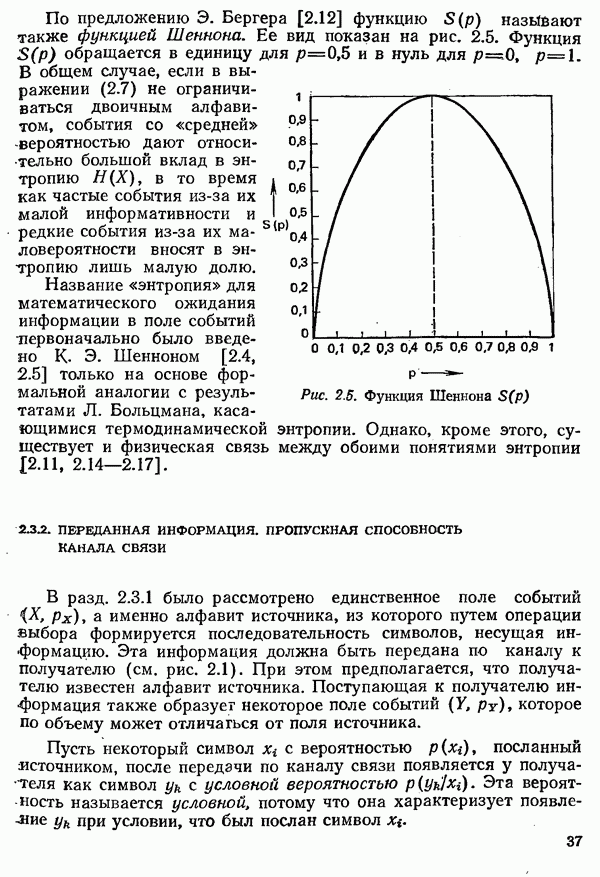
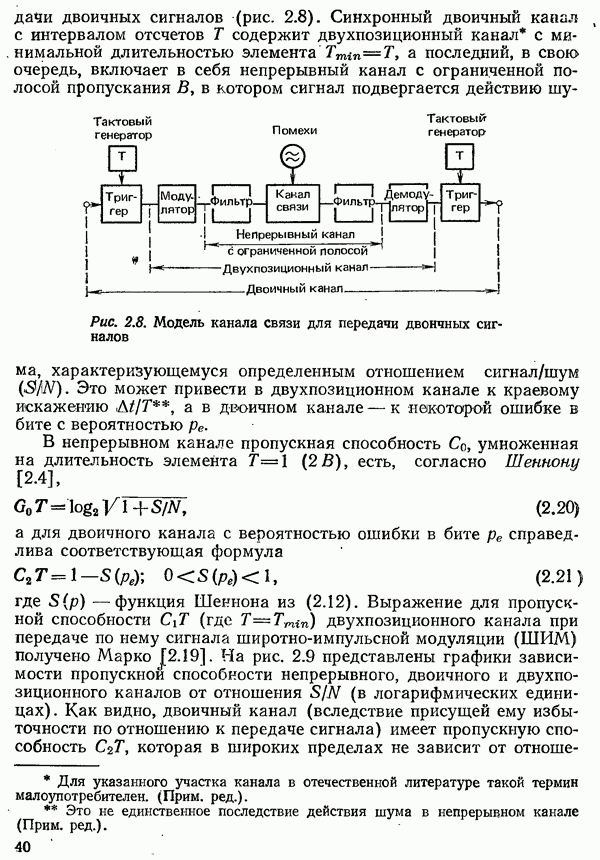
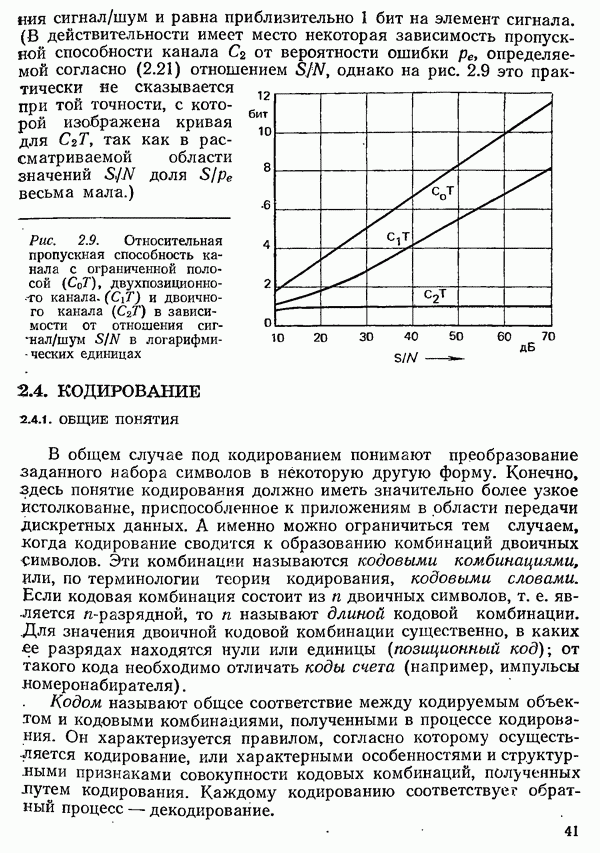
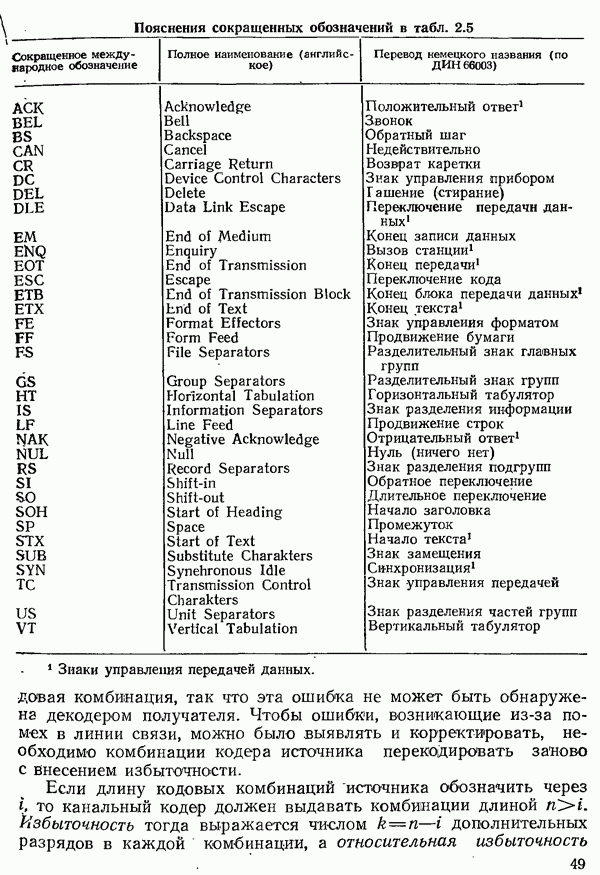
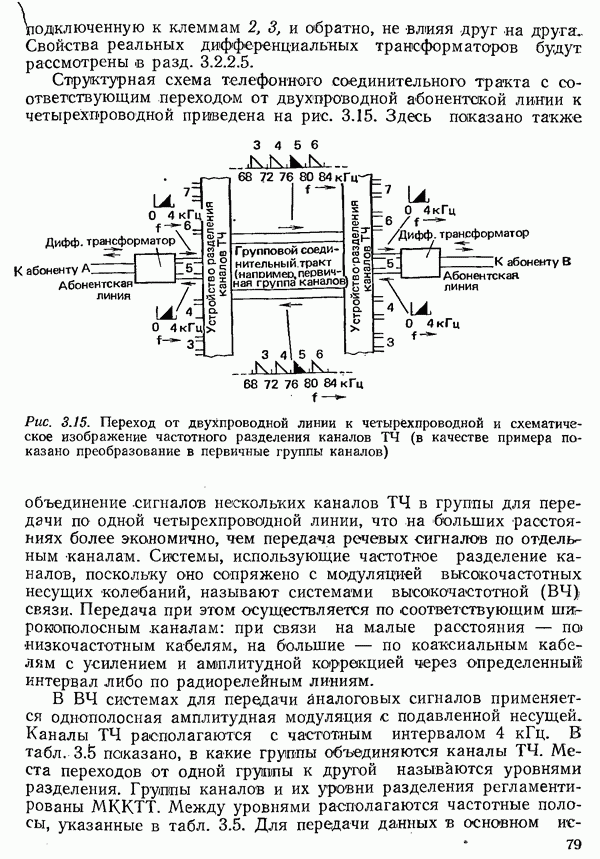
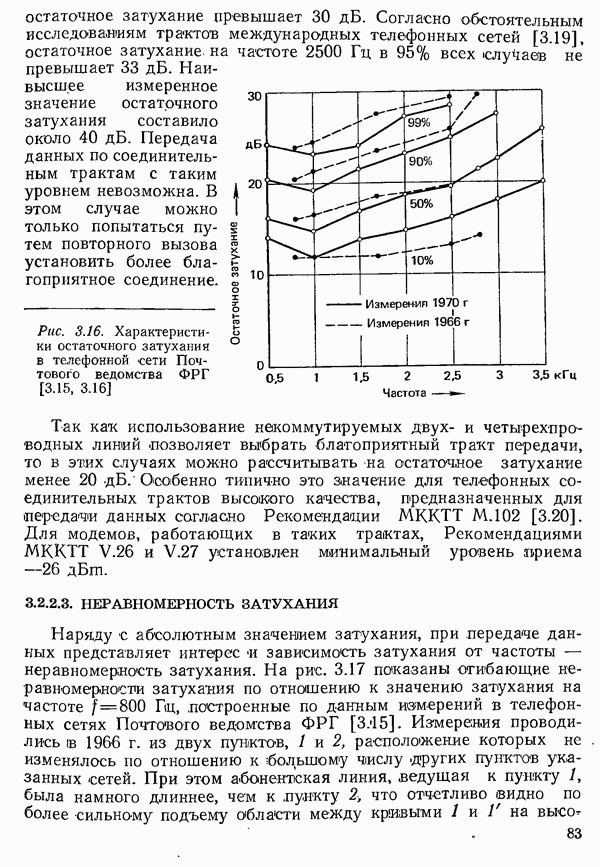
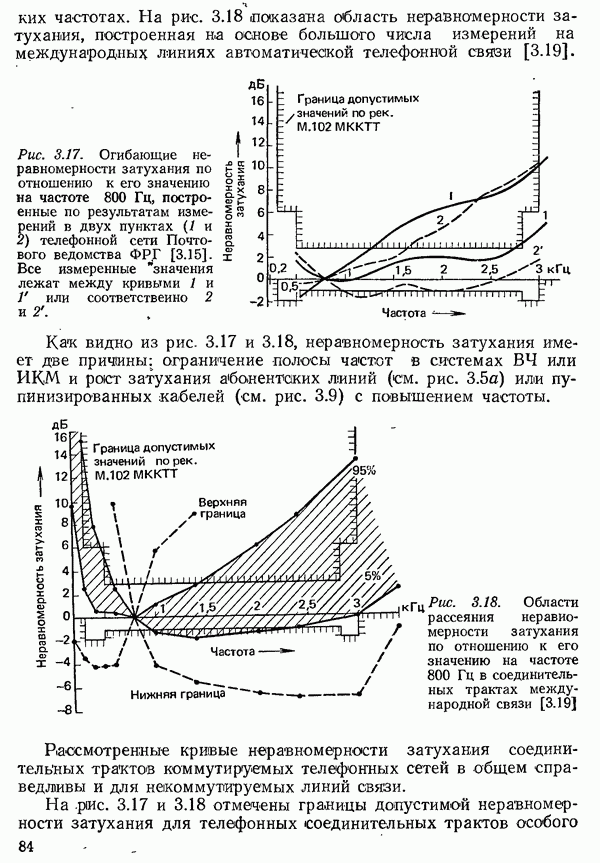
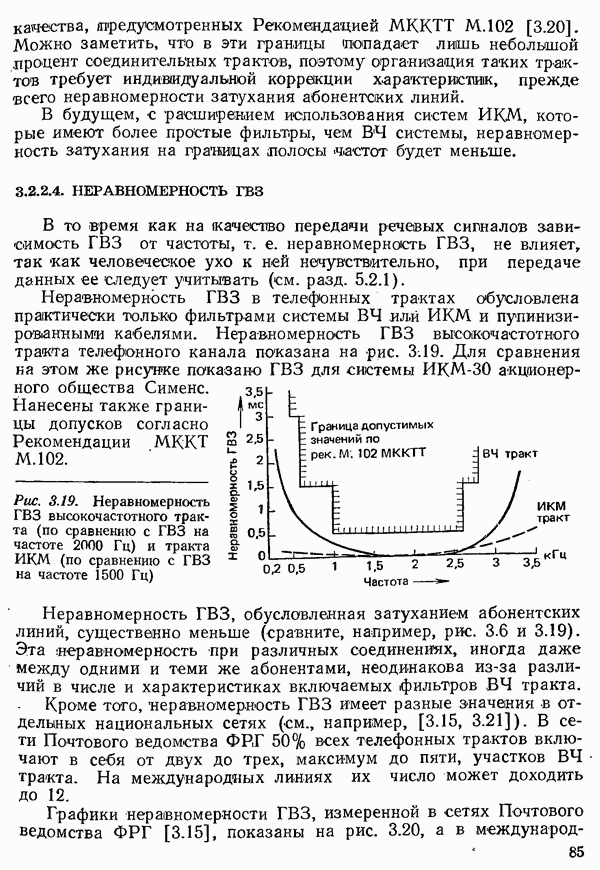
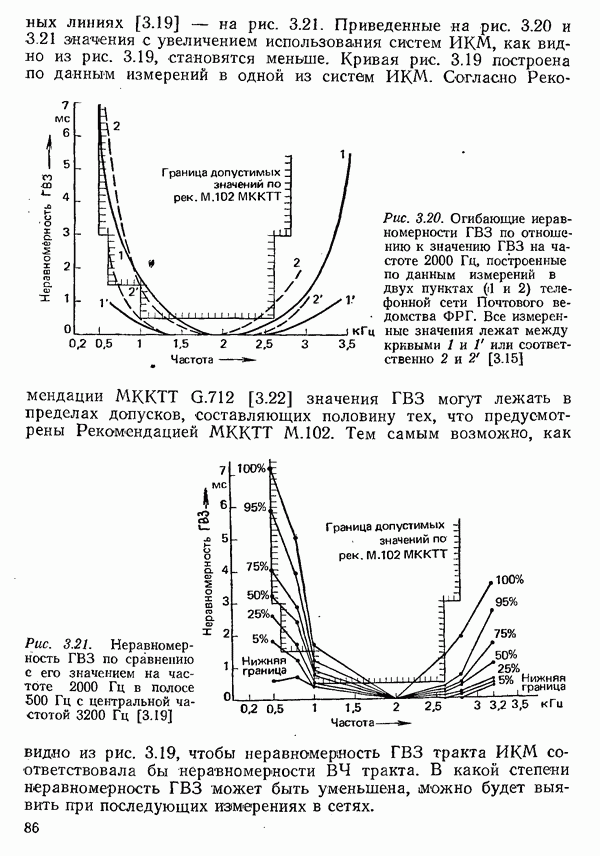
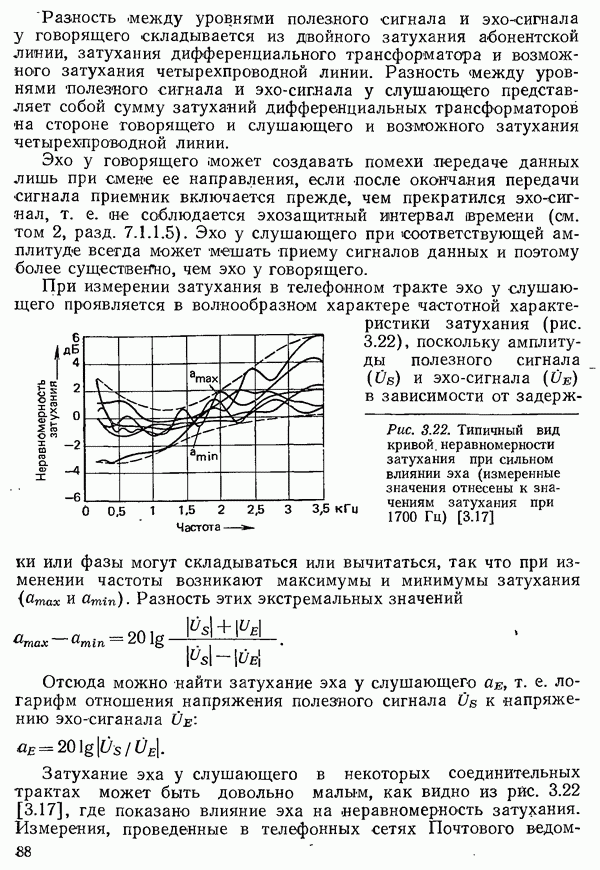
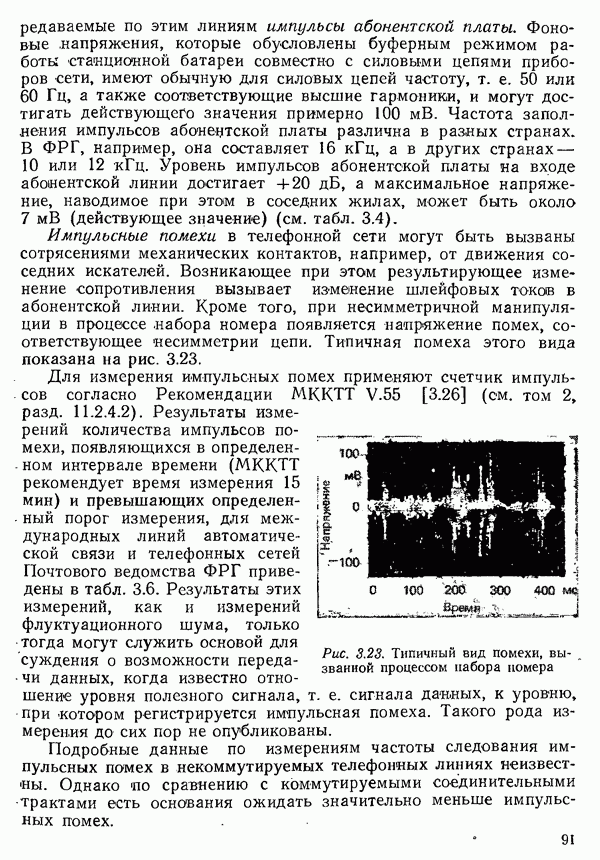
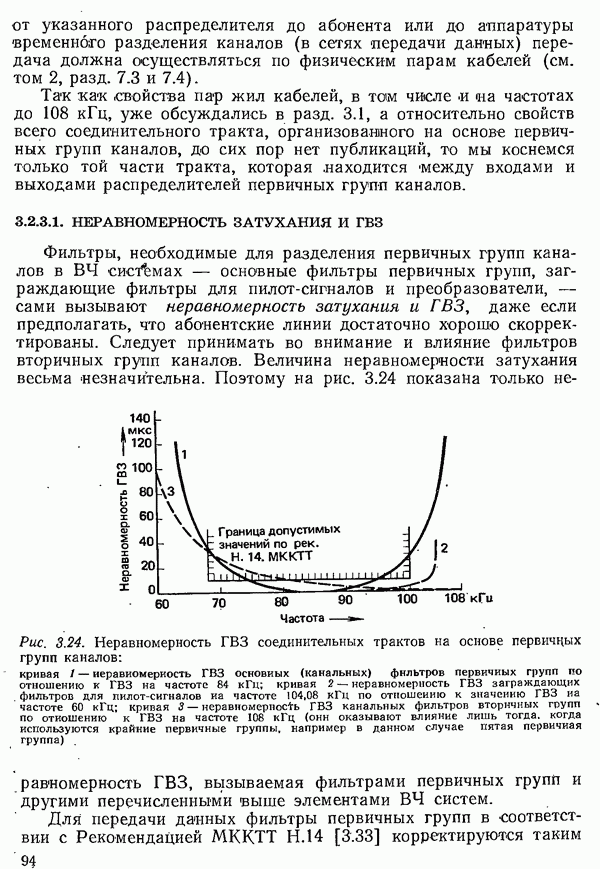
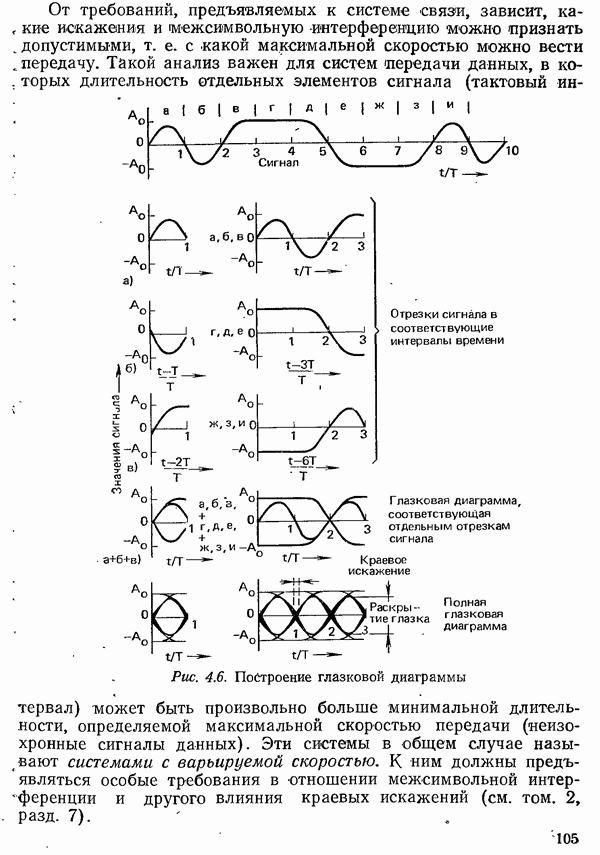
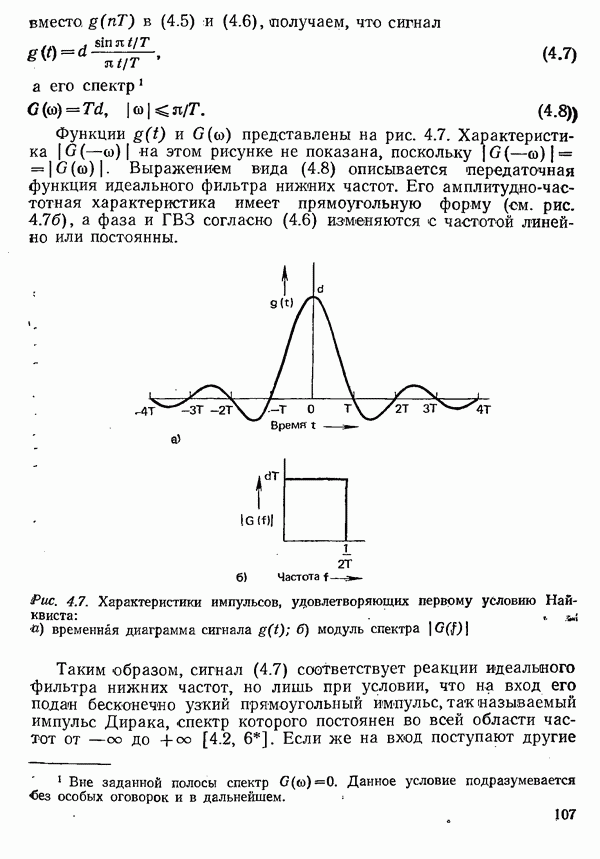
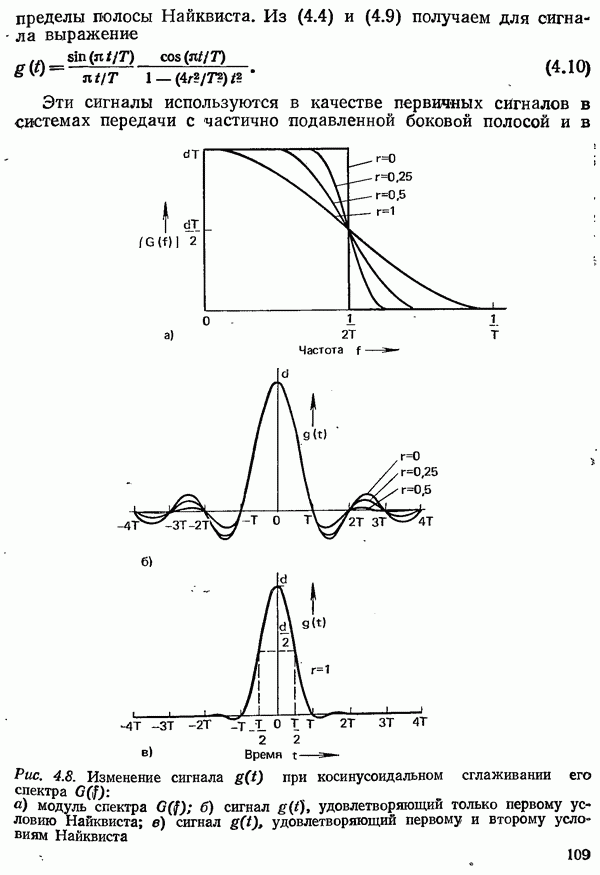
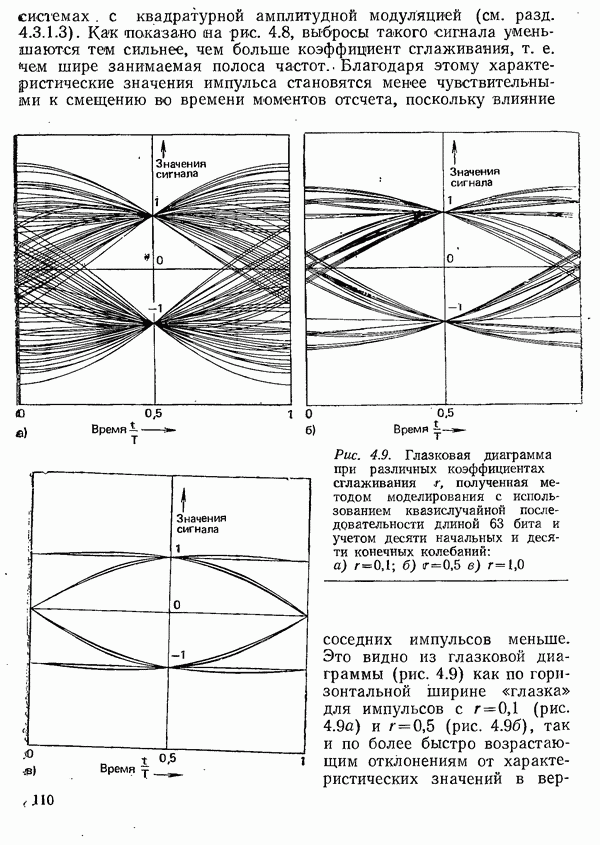
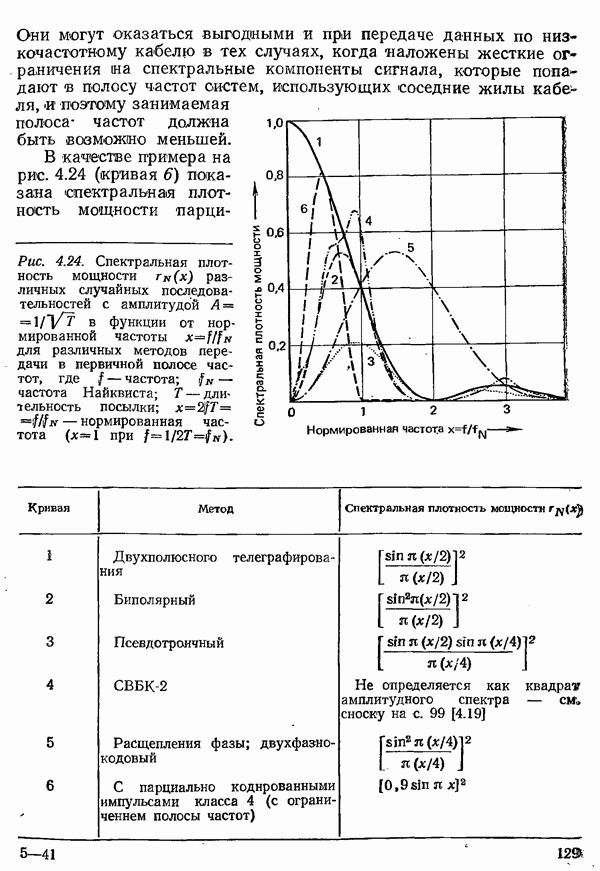
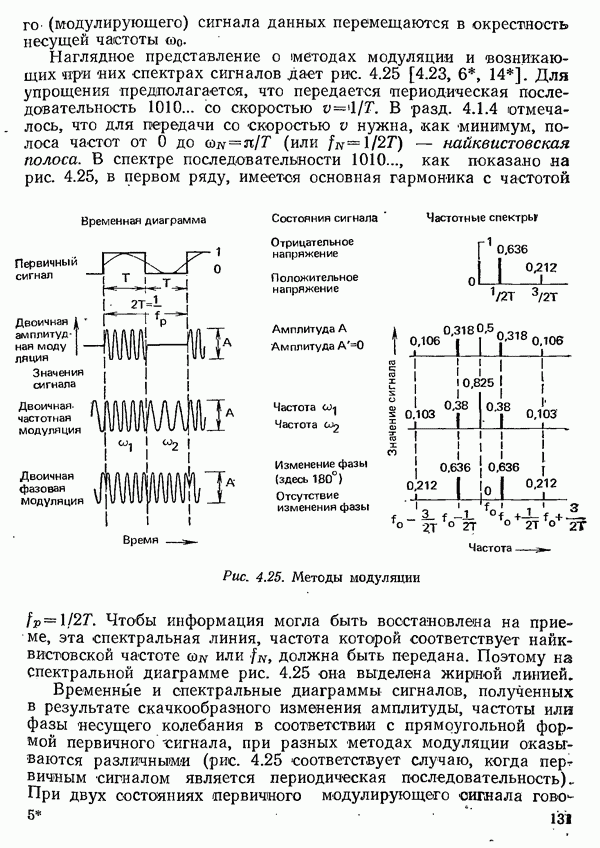
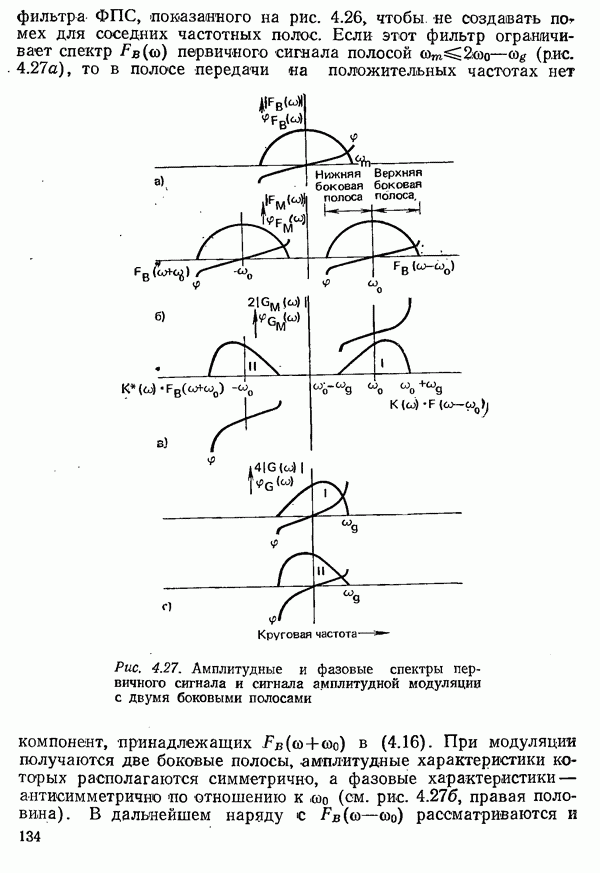
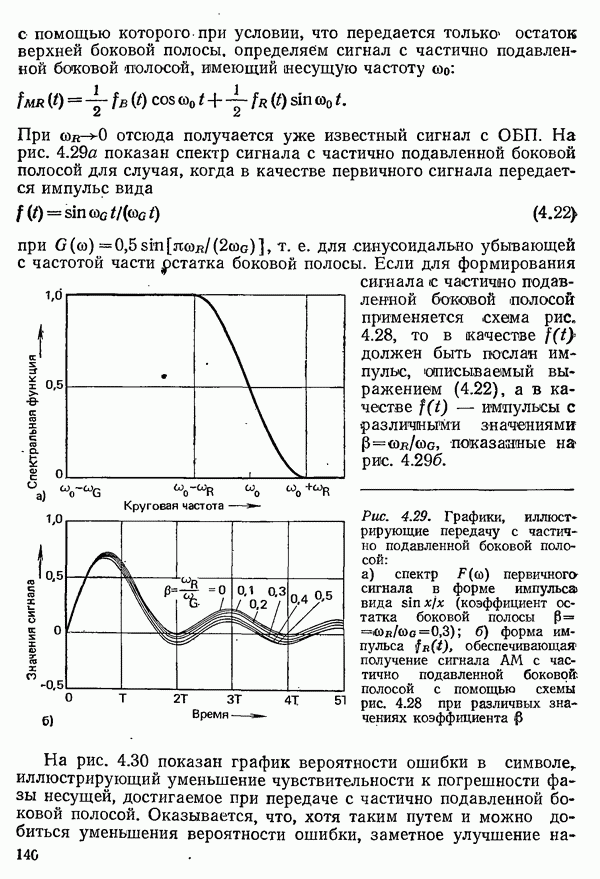
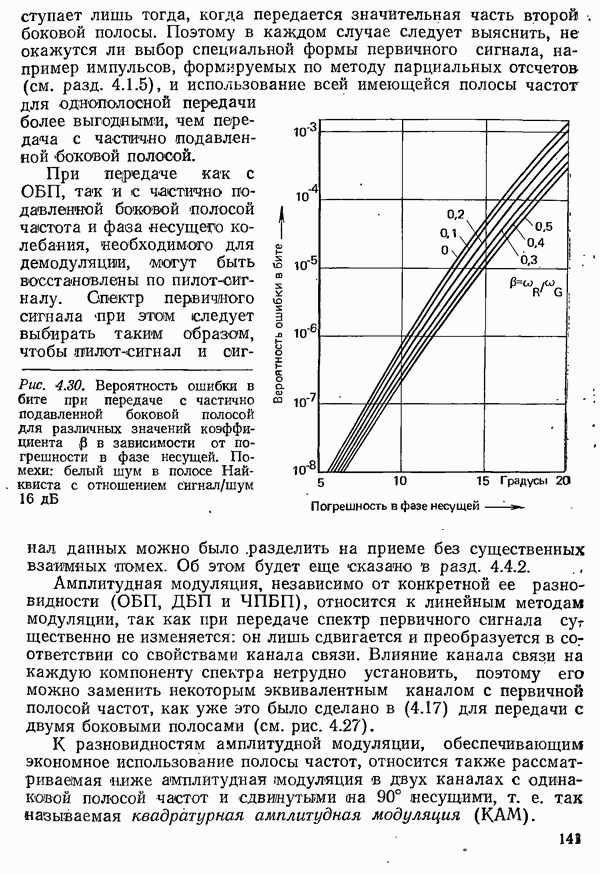
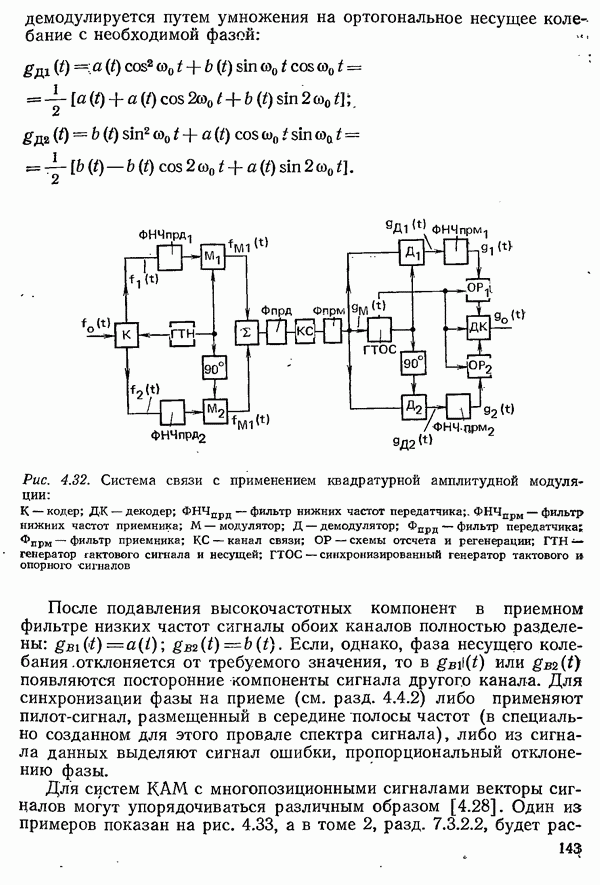
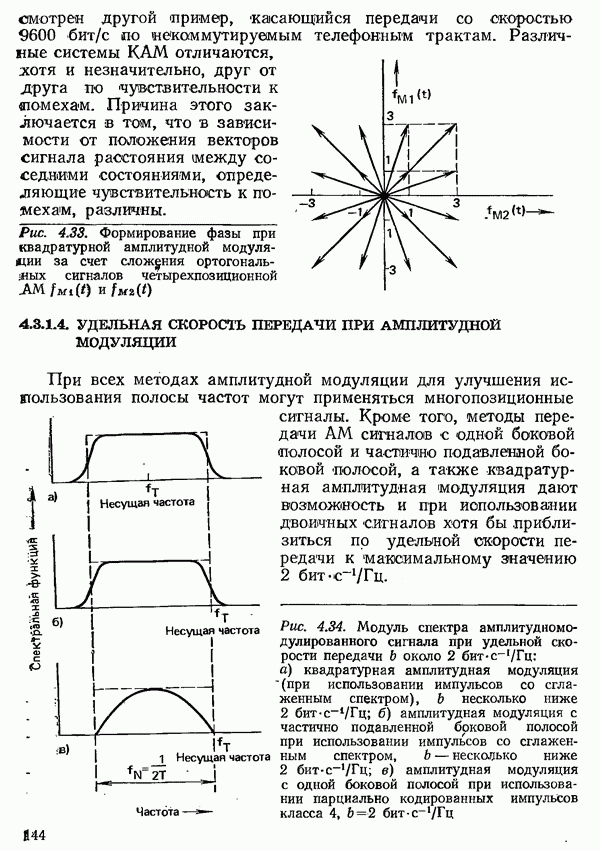
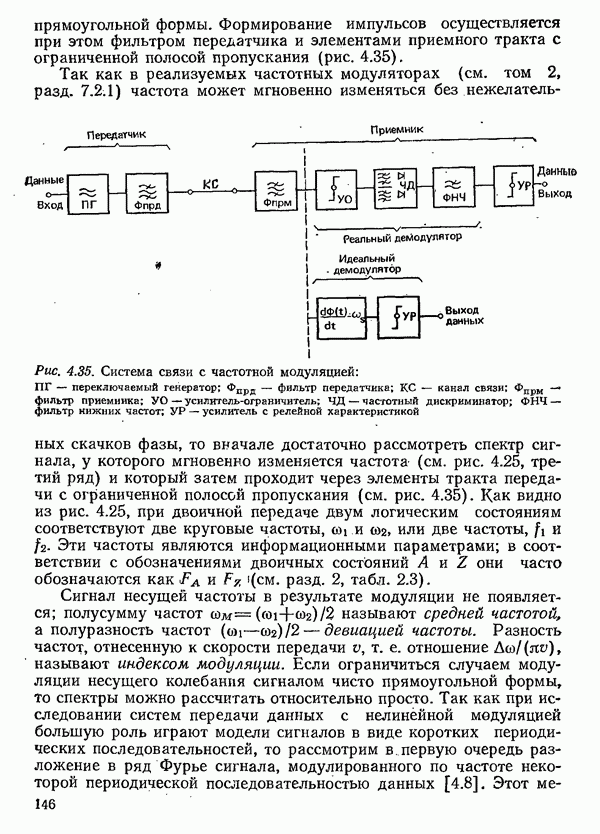
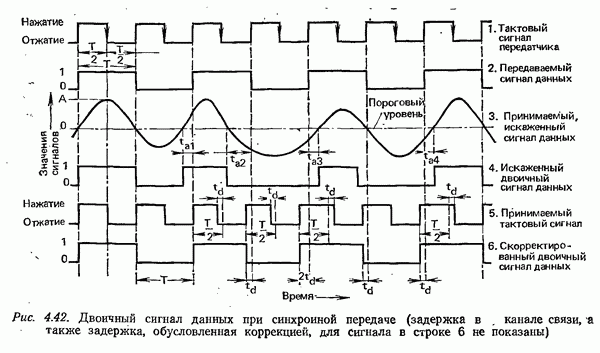
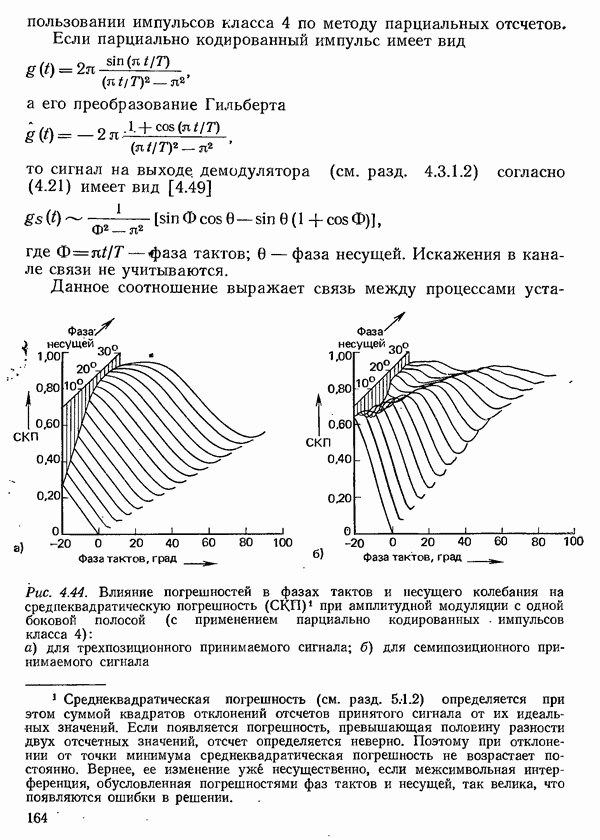
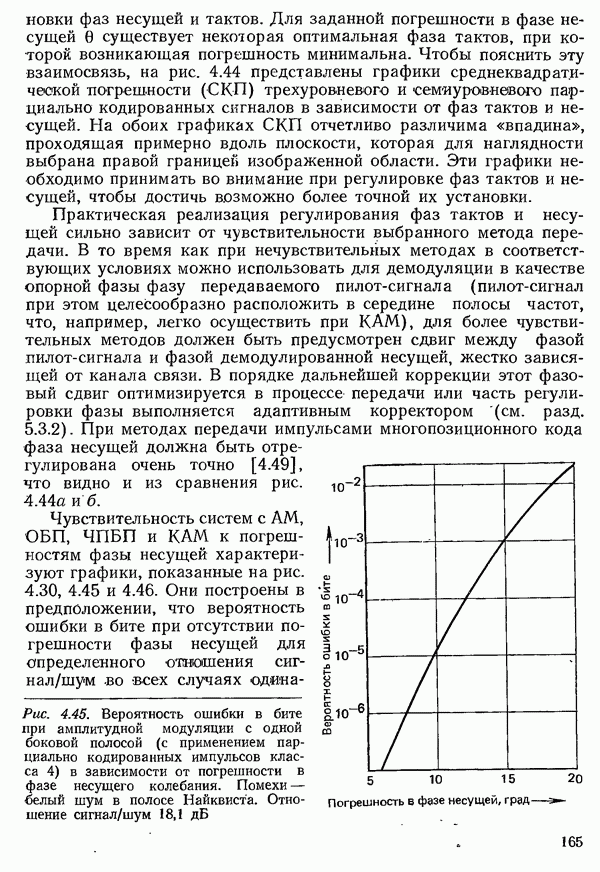
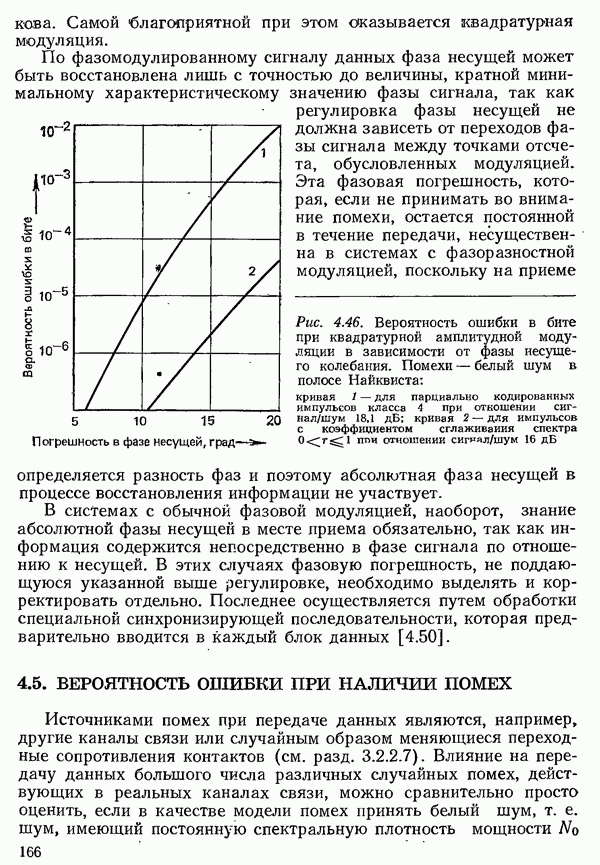
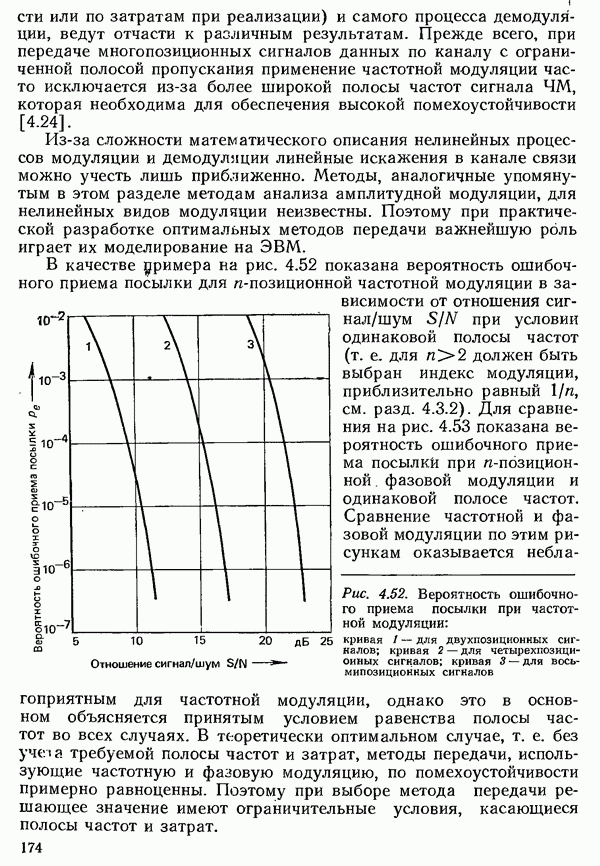
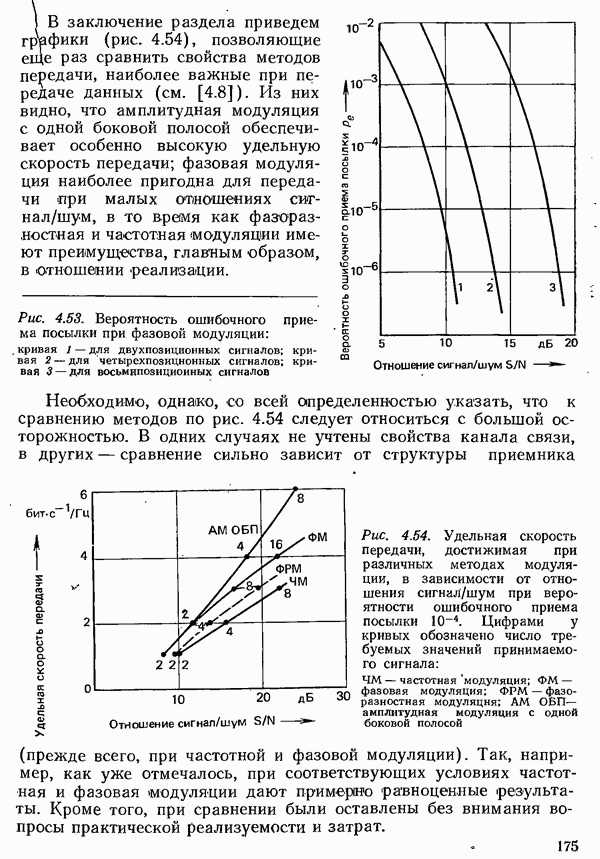
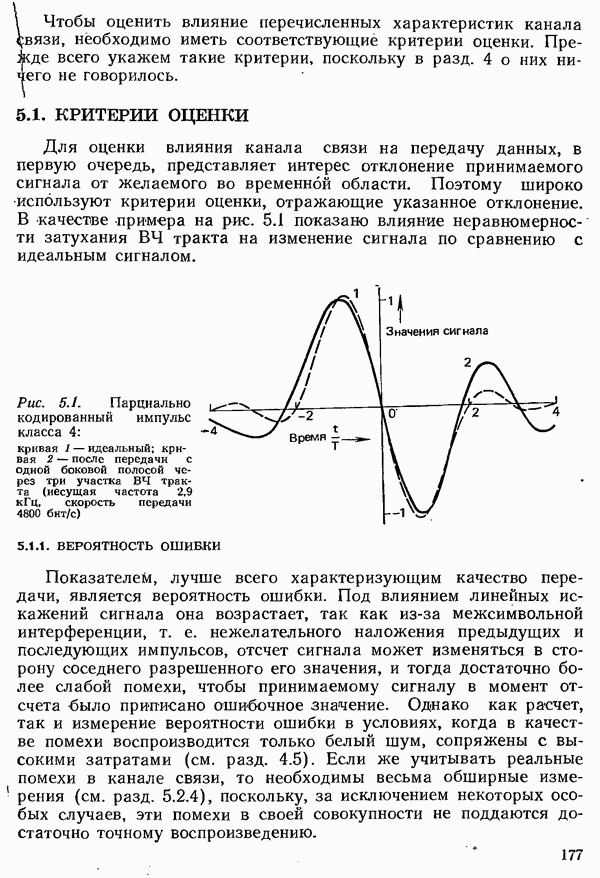
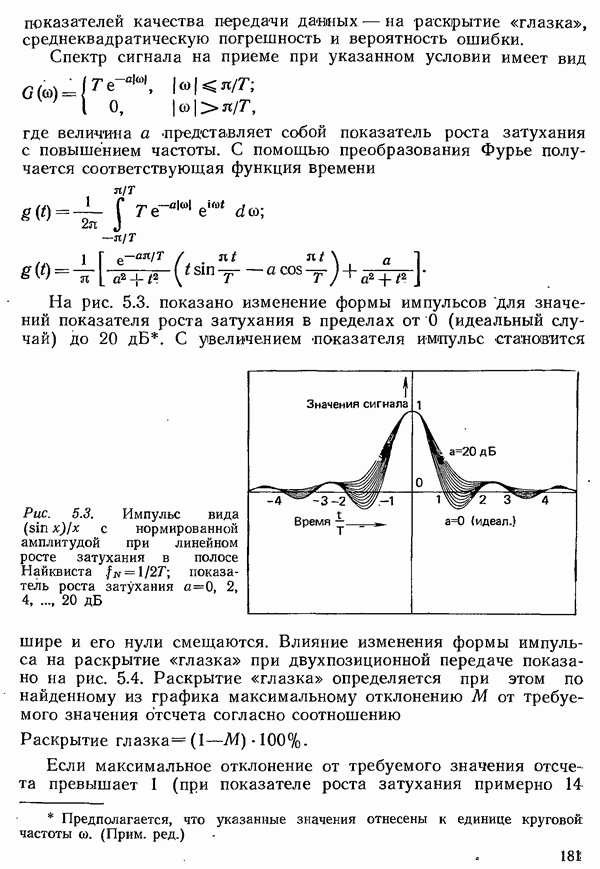
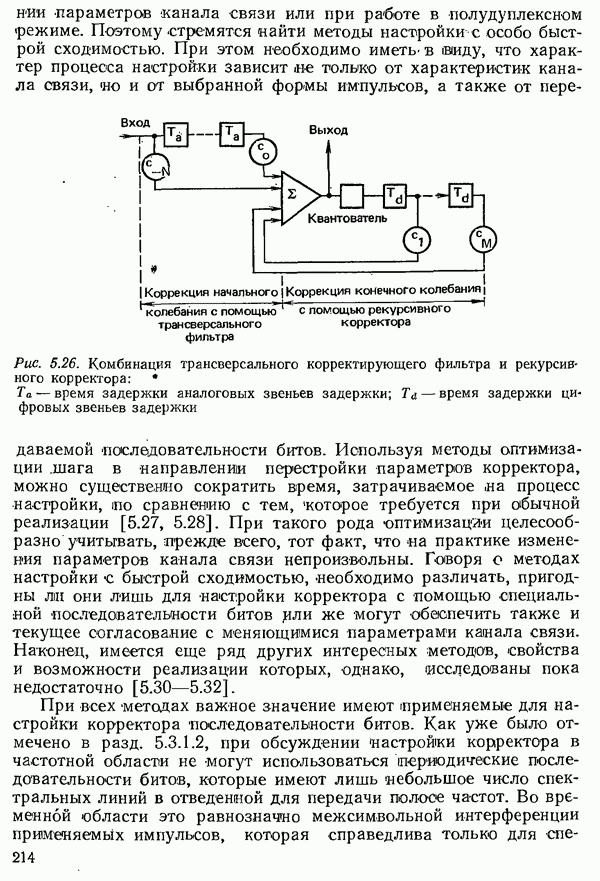
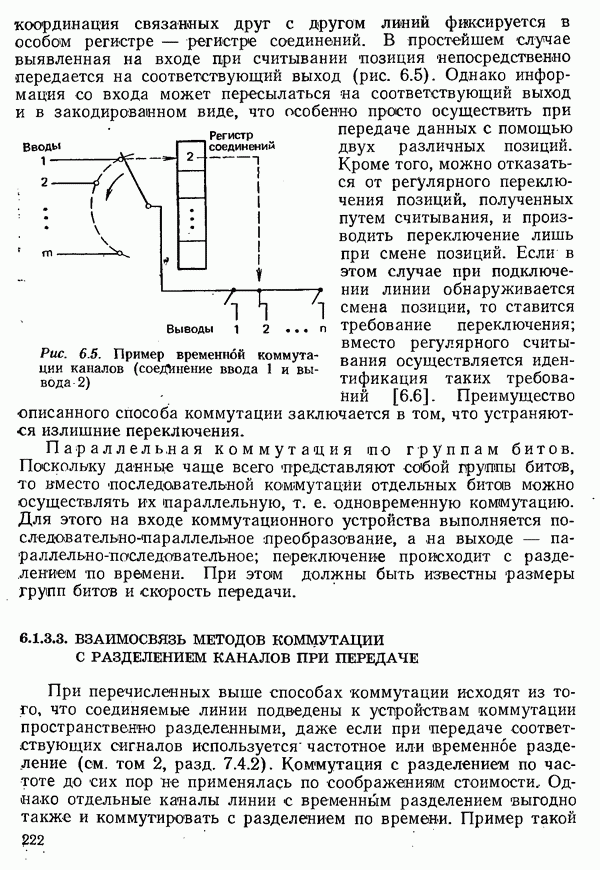
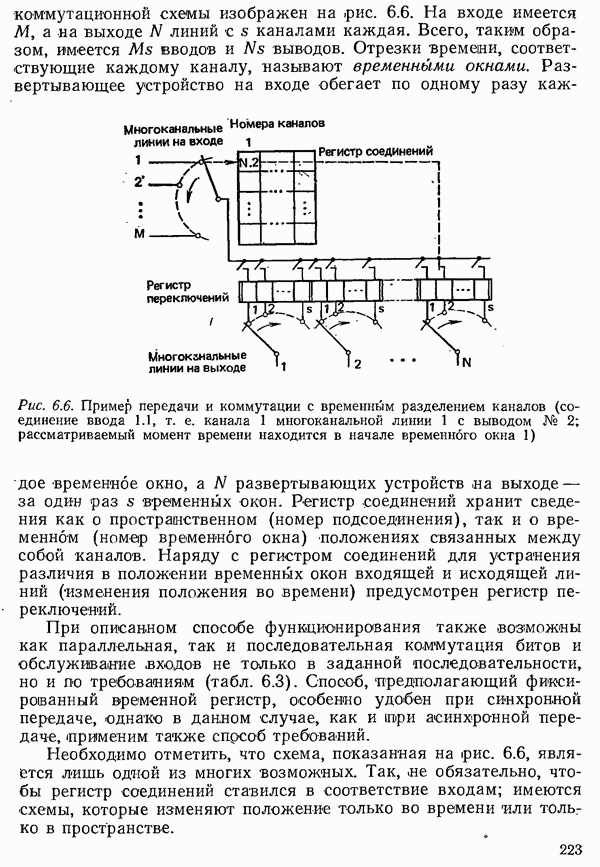
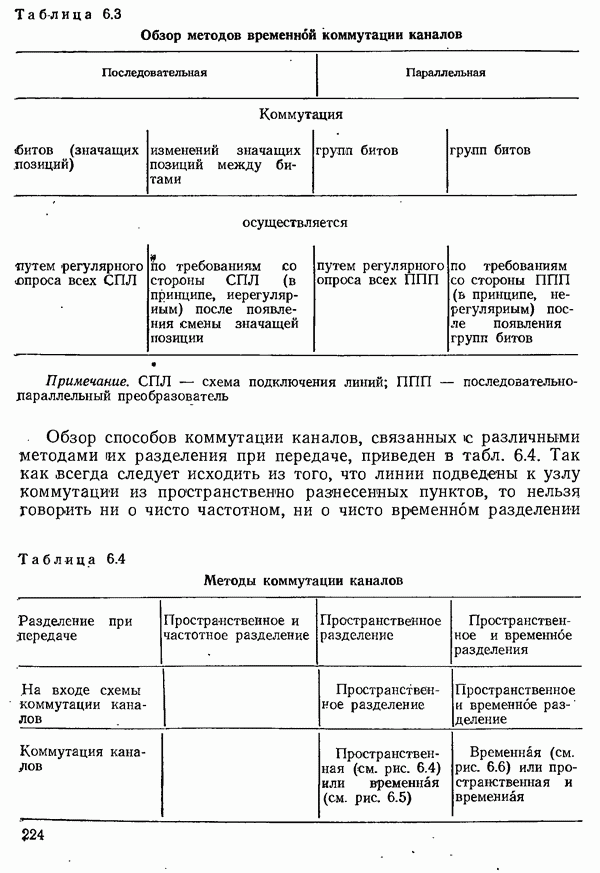
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
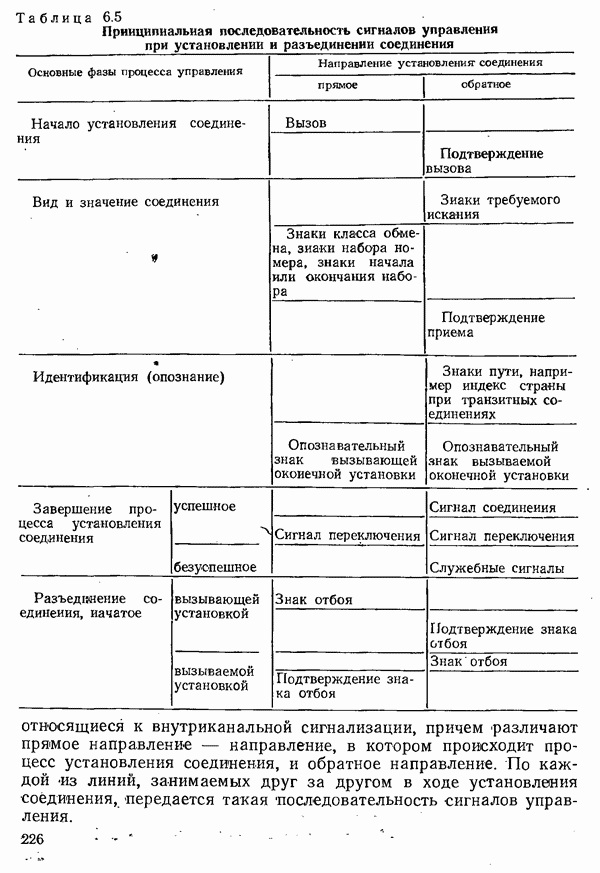
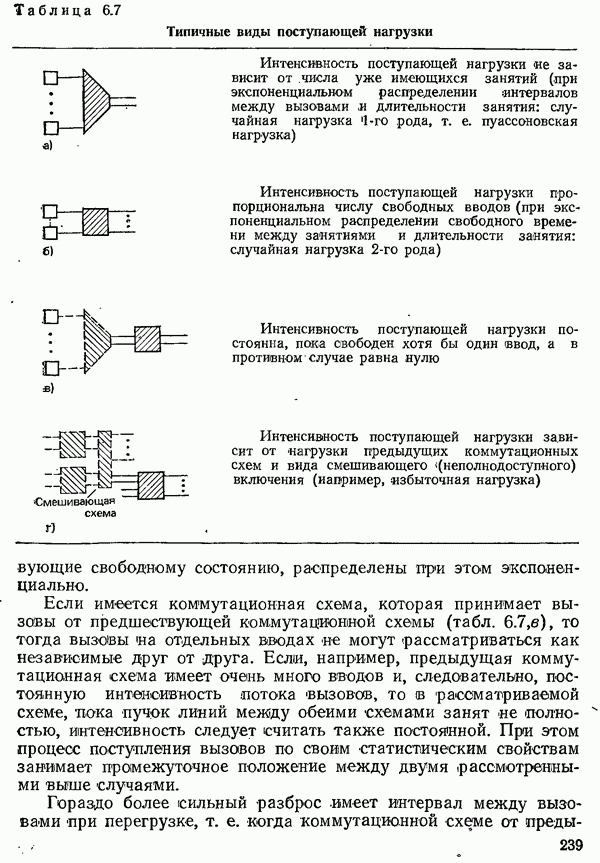
6.2.2. СИСТЕМЫ С ПОТЕРЯМИ
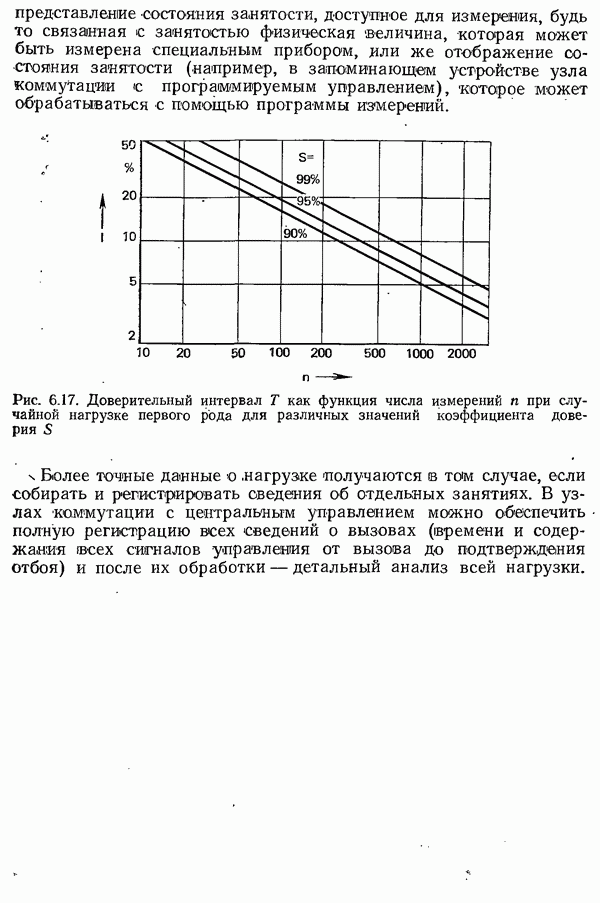
В системах с потерями важнейшим показателем пропускной способности коммутационной схемы является вероятность потерь

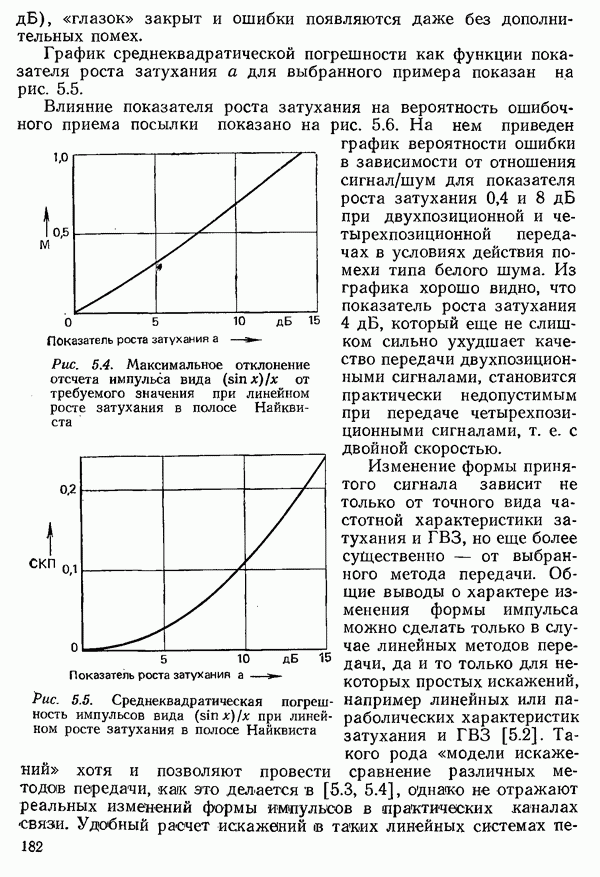
.Величина  т. е. разность между Средним количеством вызовов, поступающих за время
т. е. разность между Средним количеством вызовов, поступающих за время  (интенсивностью поступающей нагрузки), и средним количеством одновременно занятых в это время выводов, есть среднее число вызовов, теряемых за время
(интенсивностью поступающей нагрузки), и средним количеством одновременно занятых в это время выводов, есть среднее число вызовов, теряемых за время  Это число — интенсивность потерянной нагрузки — делится на интенсивность поступающей нагрузки, в результате чего получается вероятность потерь. Указание ее значения всегда должно доподняться сведениями о характеристиках рассматриваемой нагрузки (интенсивности поступающей напрузки и ее рода).
Это число — интенсивность потерянной нагрузки — делится на интенсивность поступающей нагрузки, в результате чего получается вероятность потерь. Указание ее значения всегда должно доподняться сведениями о характеристиках рассматриваемой нагрузки (интенсивности поступающей напрузки и ее рода).
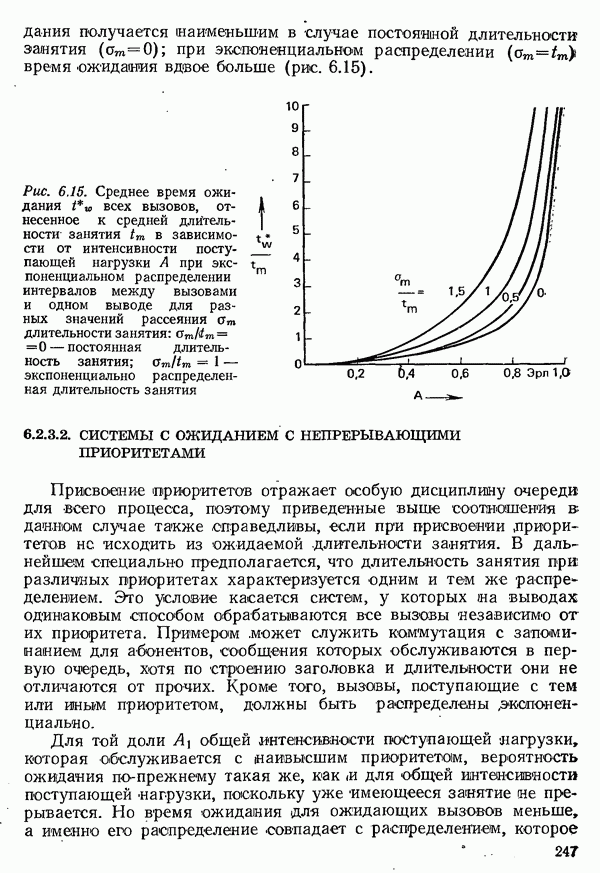
Важнейшим примером системы с потерями является коммутационная схема, которая в сети с коммутацией каналов располагается в тракте соединения между вызывающей и вызываемой оконечными установками, а освобождения соединительной линии, ведущей к следующему узлу коммутации, промежуточной или отводящей линии в рассматриваемом узле коммутации не ожидается. Остановимся далее только на простом в математическом отношении случае, когда длительность занятия имеет экспоненциальное распределение. Даже если определенная система телеобработки данных, которая обслуживается сетью передачи данных с коммутацией каналов, всегда требует соединений с одинаковой длительностью, то во всей коммутируемой сети следует рассчитывать на некоторый разброс значений длительности занятия.
6.2.2.1. ПОЛНОДОСТУПНЫЕ СХЕМЫ
Исследования по теории телетрафика, насколько это возможно, исходят из анализа состояний системы. При полной доступности важно не то, какие именно выводы заняты, а лишь каково их количество. Вероятность того, что из  выводов занято точно
выводов занято точно  обозначим
обозначим  Вызов ведет к потере в том случае, если он поступает в течение времени, когда все выводы заняты.
Вызов ведет к потере в том случае, если он поступает в течение времени, когда все выводы заняты.
При случайном обмене первого рода поступление вызовов постоянно, т. е. не зависит от состояния системы, поэтому вероятность потерь совпадает с вероятностью состояния  Таким образам,
Таким образам,

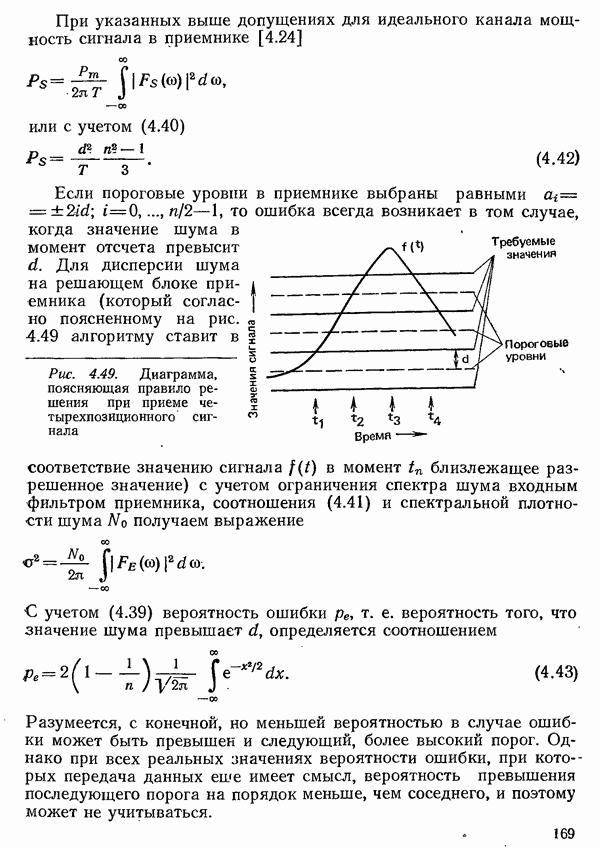
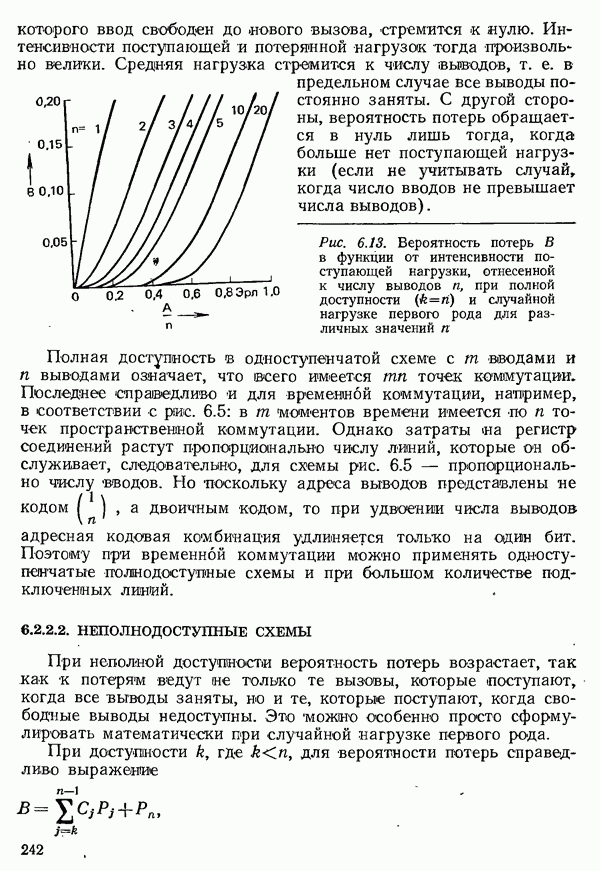
или, если выразить указанную вероятность через интенсивность поступающей нагрузки (рис. 6.13),

(формула потерь Эрланга), где 
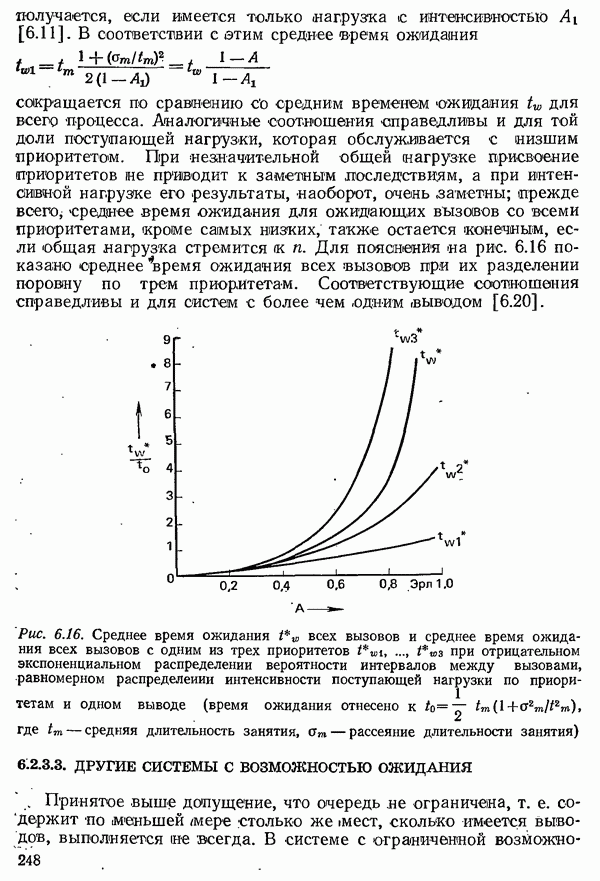
Вероятность потерь стремится к 1, если средний интервал между вызовами  или соответственно среднее время
или соответственно среднее время  в течение
в течение
которого ввод свободен до нового вызова, стремится к нулю. Интенсивности поступающей и потерянной нагрузок тогда произвольно велики. Средняя нагрузка стремится к числу выводов, т. е. в предельном случае все выводы постоянно заняты. С другой стороны, вероятность потерь обращается в нуль лишь тогда, когда больше нет поступающей нагрузки (если не учитывать случай, когда число вводов не превышает числа выводов).

Рис. 6.13. Вероятность потерь В в функции от интенсивности поступающей нагрузки, отнесенной к числу выводов  при полной доступности
при полной доступности  и случайной нагрузке первого рода для различных значений
и случайной нагрузке первого рода для различных значений 
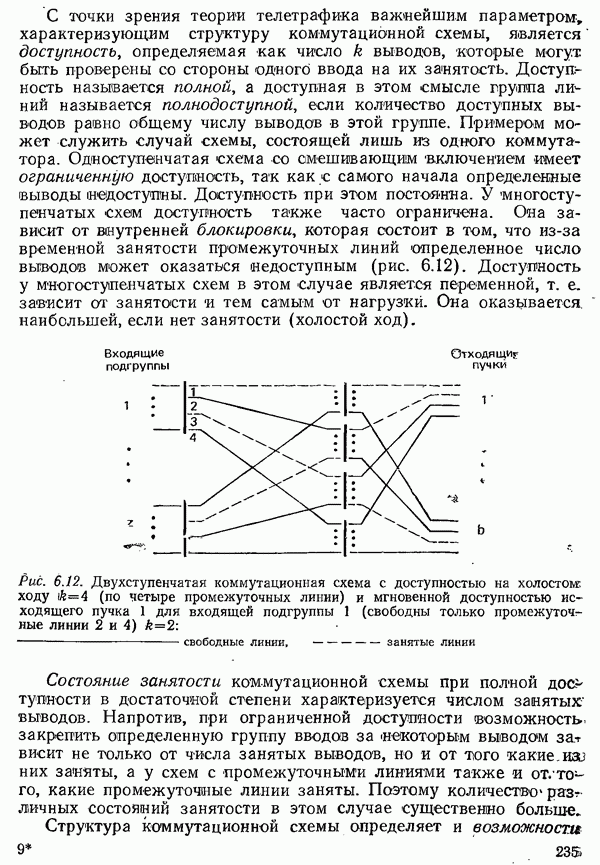
Полная доступность в одноступенчатой схеме с  вводами и
вводами и  выводами означает, что всего имеется
выводами означает, что всего имеется  точек коммутации. Последнее справедливо и для временной коммутации, например, в соответствии с рис. 6.5: в
точек коммутации. Последнее справедливо и для временной коммутации, например, в соответствии с рис. 6.5: в  моментов времени имеется по
моментов времени имеется по  точек пространственной коммутации. Однако затраты на регистр соединений растут пропорционально числу линий, которые он обслуживает, следовательно, для схемы рис. 6.5 — пропорционально числу вводов. Но поскольку адреса выводов представлены не кодом
точек пространственной коммутации. Однако затраты на регистр соединений растут пропорционально числу линий, которые он обслуживает, следовательно, для схемы рис. 6.5 — пропорционально числу вводов. Но поскольку адреса выводов представлены не кодом  а двоичным кодом, то при удвоении числа выводов адресная кодовая комбинация удлиняется только на один бит. Поэтому при временной коммутации можно применять одноступенчатые полнодоступные схемы и при большом количестве подключенных линий.
а двоичным кодом, то при удвоении числа выводов адресная кодовая комбинация удлиняется только на один бит. Поэтому при временной коммутации можно применять одноступенчатые полнодоступные схемы и при большом количестве подключенных линий.
6.2.2.2. НЕПОЛНОДОСТУПНЫЕ СХЕМЫ
При неполной доступности вероятность потерь возрастает, так как к потерям ведут не только те вызовы, которые поступают, когда все выводы заняты, но и те, которые поступают, когда свободные выводы недоступны. Это можно особенно просто сформулировать математически при случайной нагрузке первого рода.
При доступности  где
где  для вероятности потерь справедливо выражение
для вероятности потерь справедливо выражение

где  вероятность того, что состояние
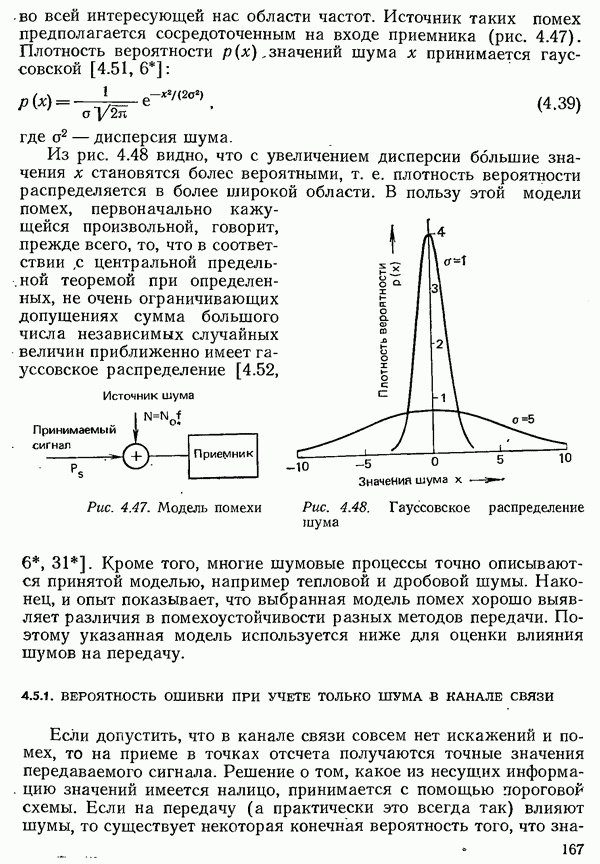
вероятность того, что состояние  выводов занято, т. е.
выводов занято, т. е.  выводов свободно) не может быть достигнуто ни одним выводом (вероятность блокировки). Вероятности
выводов свободно) не может быть достигнуто ни одним выводом (вероятность блокировки). Вероятности  при этом складываются из отдельных вероятностей различных возможностей того, что
при этом складываются из отдельных вероятностей различных возможностей того, что  выводов занято. При полной доступности величина
выводов занято. При полной доступности величина  обращается в нуль, таким образом получается приведенное выше соотношение:
обращается в нуль, таким образом получается приведенное выше соотношение:

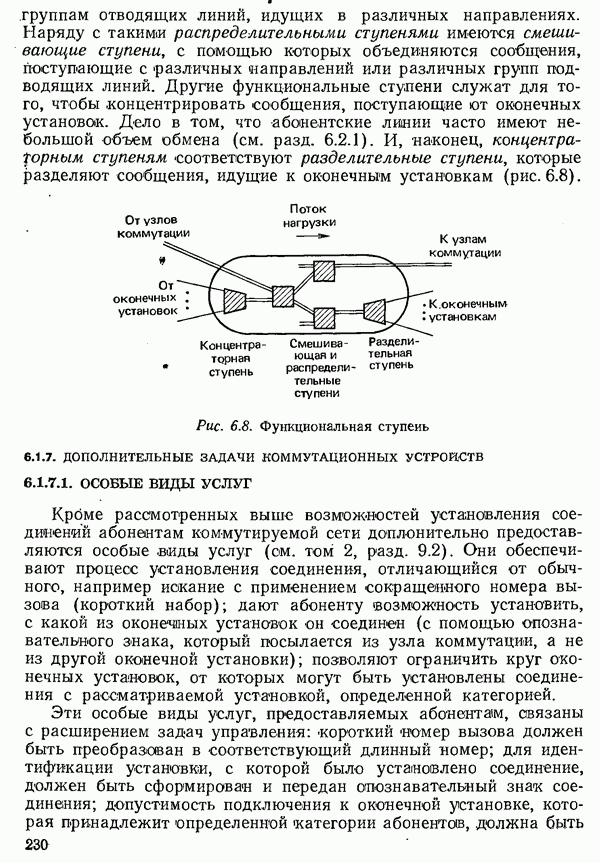
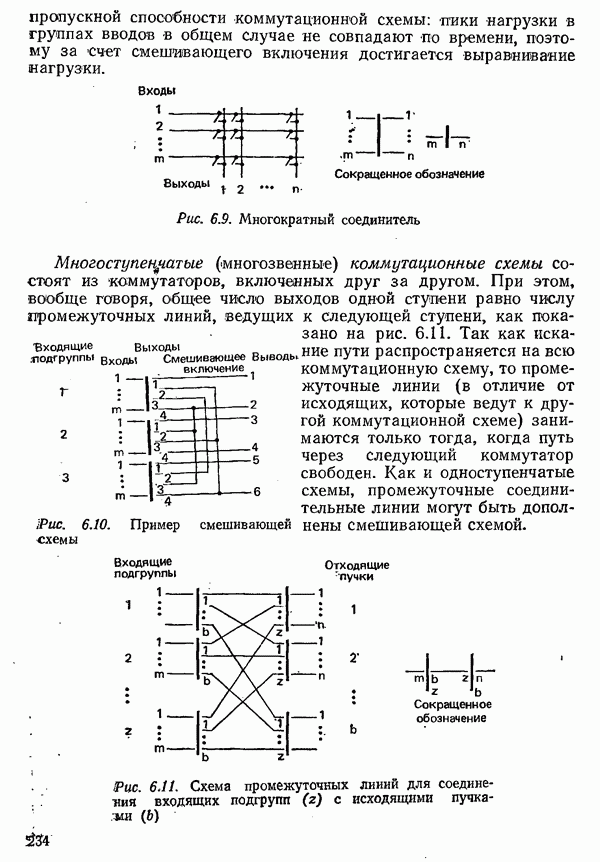
Простейшая одноступенчатая неполяодоступная схема является результатом подразделения вводов или соответственно поступающей нагрузки и выводов на подгруппы с полной доступностью. При подразделении на  подгрупп требуется в общей сложности
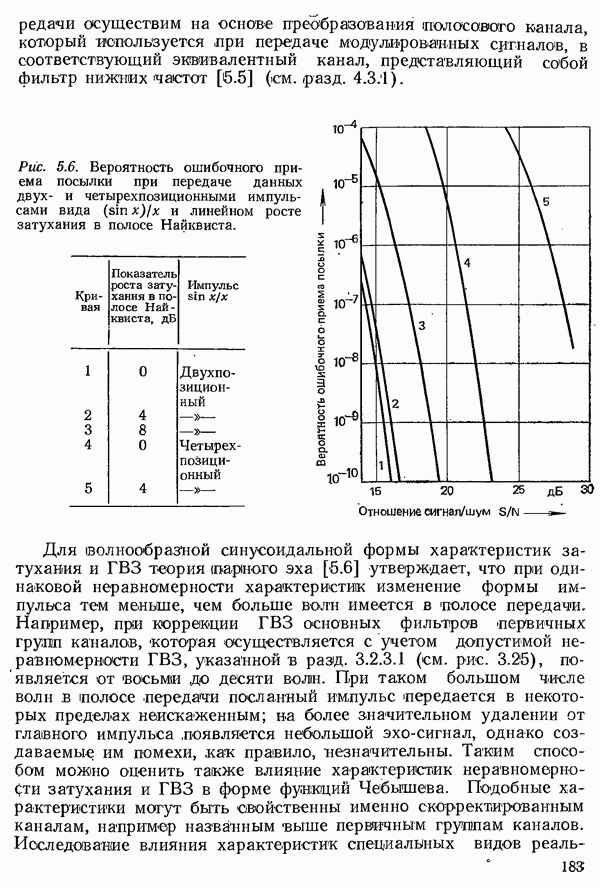
подгрупп требуется в общей сложности  точек коммутации. Однако вероятность потерь сильно возрастает, так как не происходит выравнивания «нагрузки между подгруппами. На рис. 6.13 приведены графики вероятностей потерь для больших пучков линий [6.16]; результат действия подразделения, например, на две одинаковые подгруппы, виден из сравнения вероятности потерь для
точек коммутации. Однако вероятность потерь сильно возрастает, так как не происходит выравнивания «нагрузки между подгруппами. На рис. 6.13 приведены графики вероятностей потерь для больших пучков линий [6.16]; результат действия подразделения, например, на две одинаковые подгруппы, виден из сравнения вероятности потерь для  выводов. При общей интенсивности поступающей нагрузки, равной
выводов. При общей интенсивности поступающей нагрузки, равной  неполном пучке из десяти отводящих линий (
неполном пучке из десяти отводящих линий ( на линию) вероятность потерь составляет около 4%, а при подразделении на два пучка по пять линий — около 11%.
на линию) вероятность потерь составляет около 4%, а при подразделении на два пучка по пять линий — около 11%.
В схемах со смешивающими ступенями (см. рис. 6.10) вероятность потерь меньше, чем при подразделениии на подгруппы. Однако расчет вероятностей состояний, а тем самым и вероятностей потерь составляет в данном случае, как и для других неполнодоступных схем, особую проблему из-за большого числа различных состояний.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ К РУССКОМУ ИЗДАНИЮ
- 1. Обзор
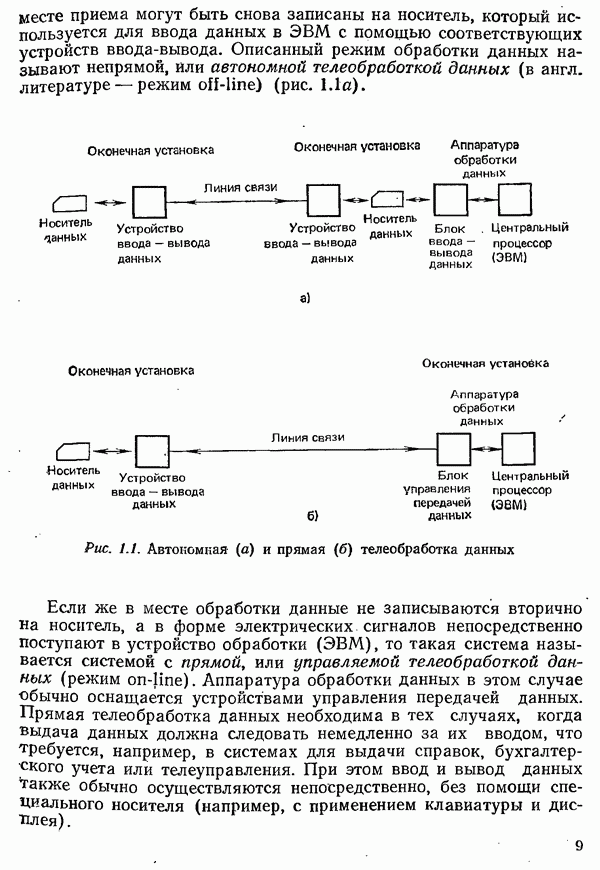
- 1.1. ОБРАБОТКА И ТЕЛЕОБРАБОТКА ДАННЫХ
- 1.2. АВТОНОМНАЯ И УПРАВЛЯЕМАЯ ТЕЛЕОБРАБОТКА ДАННЫХ
- 1.3. КЛАССИФИКАЦИЯ СИСТЕМ ТЕЛЕОБРАБОТКИ ДАННЫХ
- 1.4. СТРУКТУРА СИСТЕМ ТЕЛЕОБРАБОТКИ ДАННЫХ
- 1.5. ТРЕБОВАНИЯ К ТЕХНИКЕ СВЯЗИ И КОММУТАЦИИ В СИСТЕМАХ ТЕЛЕОБРАБОТКИ ДАННЫХ
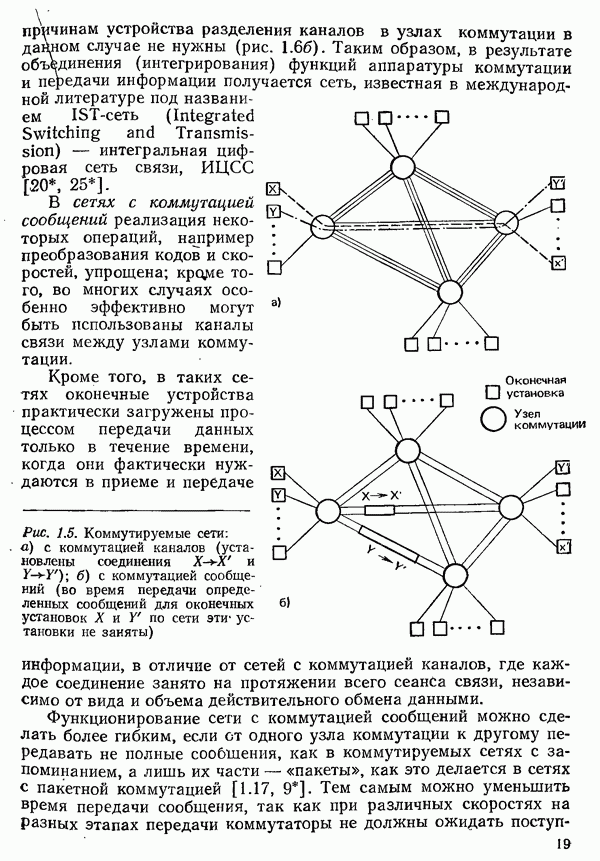
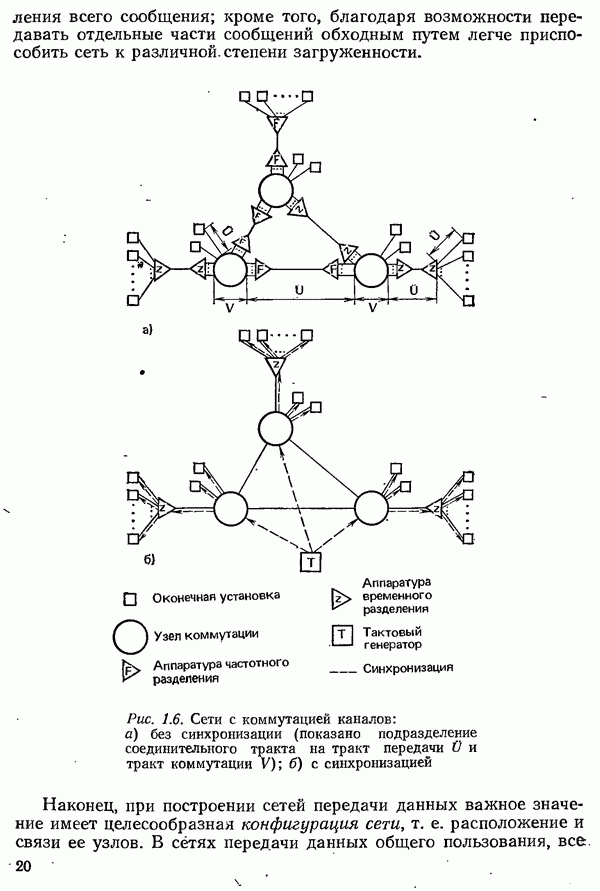
- 1.6. ТЕХНИКА СВЯЗИ В СИСТЕМАХ ТЕЛЕОБРАБОТКИ ДАННЫХ
- 2. Основные понятия техники связи
- 2.2. СИГНАЛЫ
- 2.2.2. ДИСКРЕТИЗАЦИЯ, КВАНТОВАНИЕ, ВЛИЯНИЕ ШУМОВ
- 2.2.3. СВОЙСТВА ПЕРВИЧНЫХ СИГНАЛОВ ДЛЯ ПЕРЕДАЧИ ДАННЫХ
- 2.2.3.2. ВРЕМЕННЫЕ СООТНОШЕНИЯ МЕЖДУ СИГНАЛАМИ
- 2.2.4. РЕЖИМЫ РАБОТЫ ПРИ ПЕРЕДАЧЕ СИГНАЛОВ
- 2.3. НЕКОТОРЫЕ ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ИНФОРМАЦИИ
- 2.3.2. ПЕРЕДАННАЯ ИНФОРМАЦИЯ. ПРОПУСКНАЯ СПОСОБНОСТЬ КАНАЛА СВЯЗИ
- 2.4. КОДИРОВАНИЕ
- 2.4.3. КОДИРОВАНИЕ ИСТОЧНИКА
- 2.4.4. КАНАЛЬНОЕ КОДИРОВАНИЕ
- 3. Каналы связи
- 3.1. КАНАЛЫ БЛИЖНЕЙ СВЯЗИ
- 3.1.1.1. СВОЙСТВА И ПАРАМЕТРЫ ПРОВОДНЫХ ЛИНИЙ СВЯЗИ
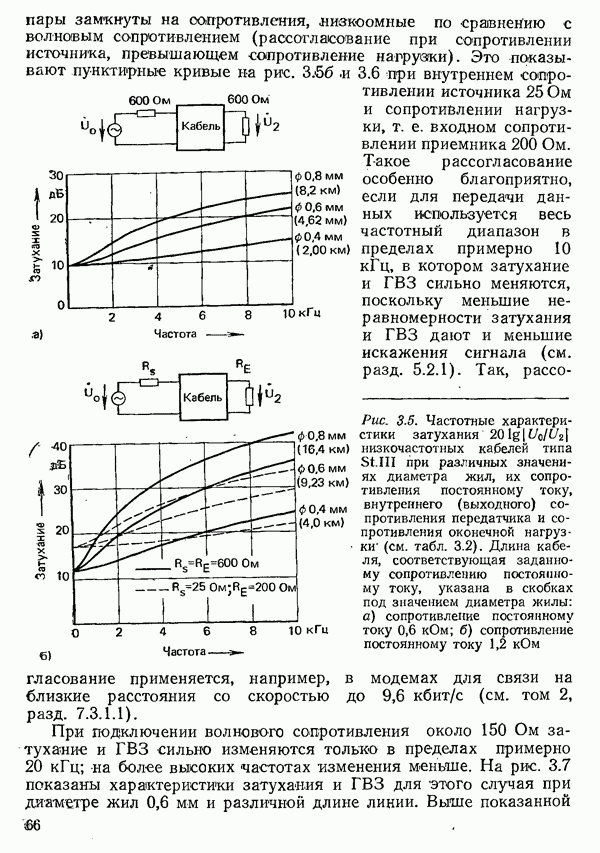
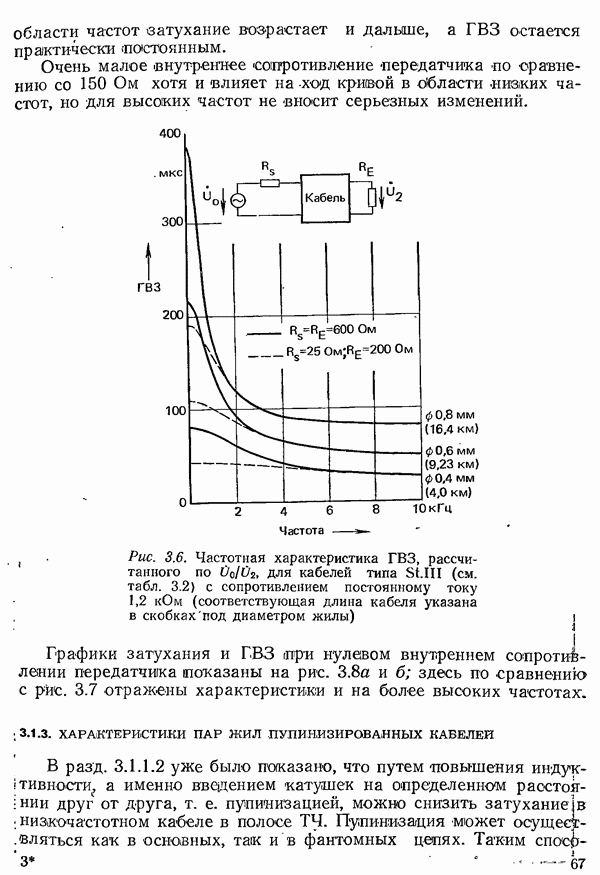
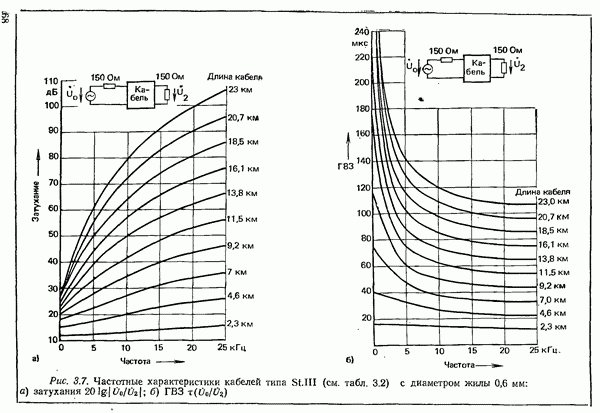
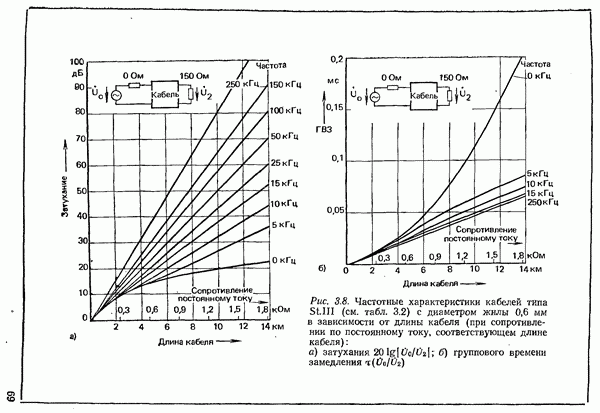
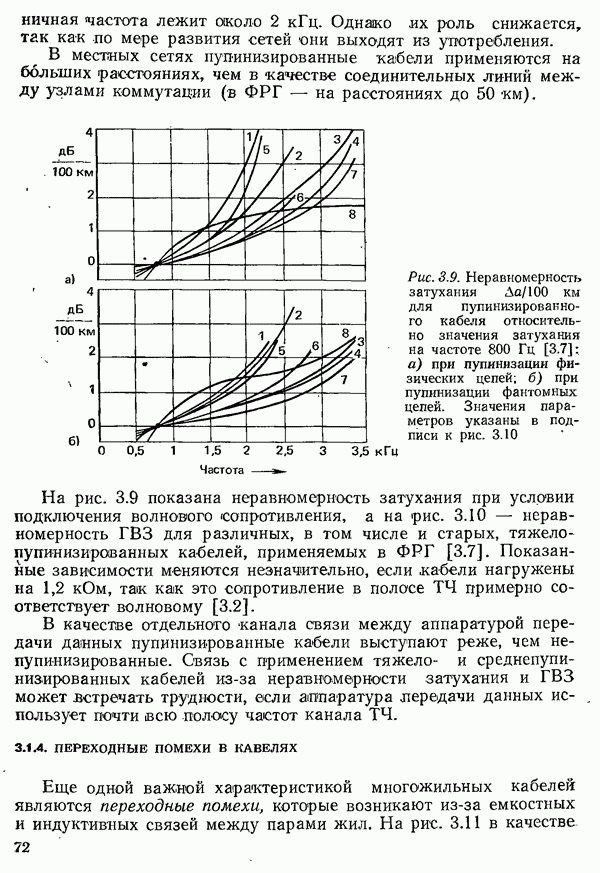
- 3.1.1.2. УМЕНЬШЕНИЕ ЗАТУХАНИЯ ПУТЕМ УВЕЛИЧЕНИЯ ИНДУКТИВНОСТИ. ПУПИНИЗАЦИЯ
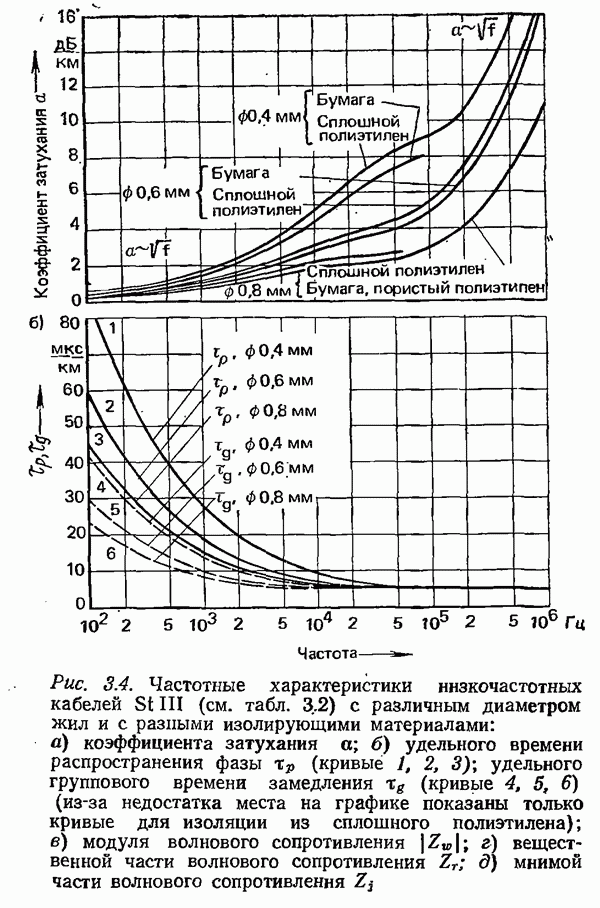
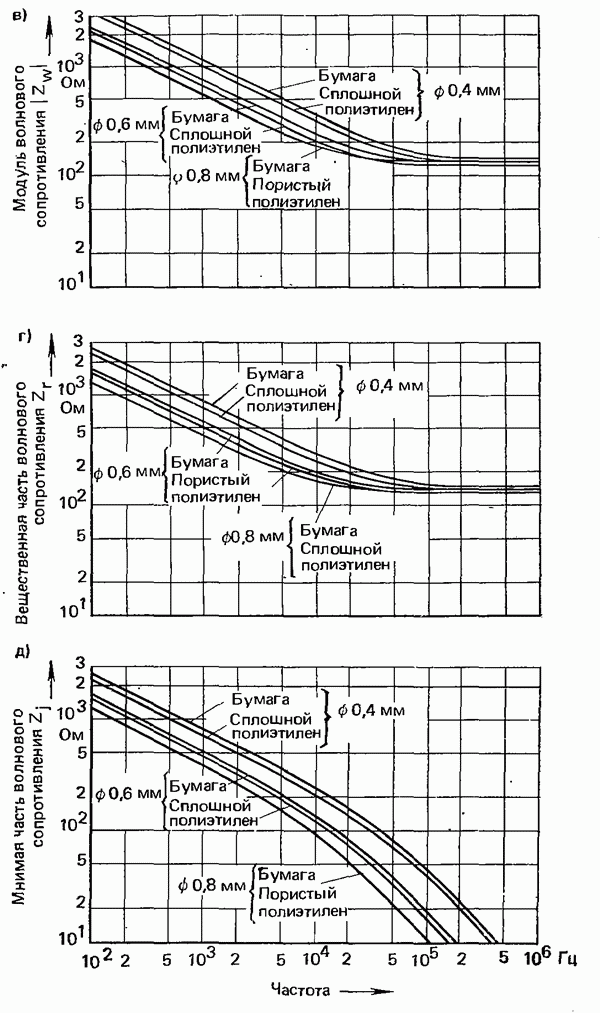
- 3.1.2. ХАРАКТЕРИСТИКИ ПАР ЖИЛ НИЗКОЧАСТОТНЫХ КАБЕЛЕЙ
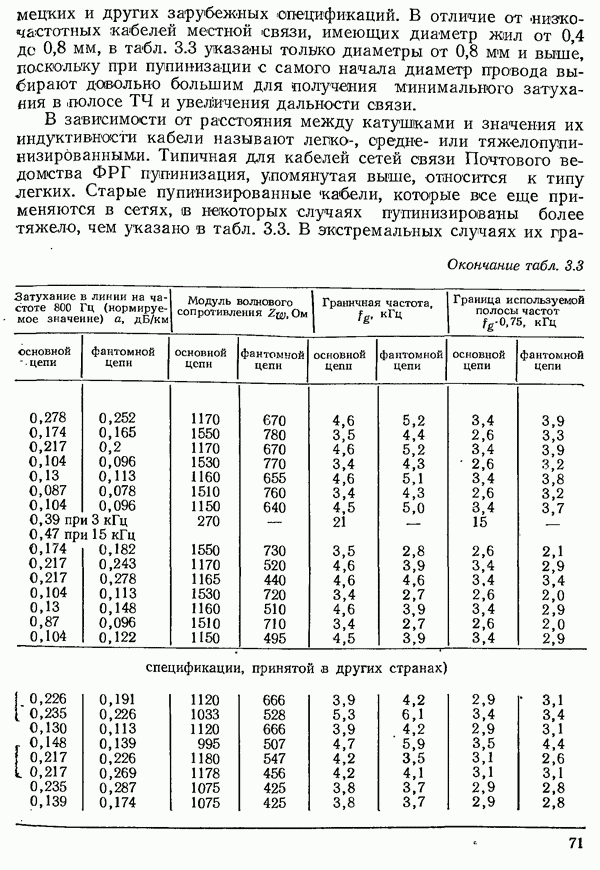
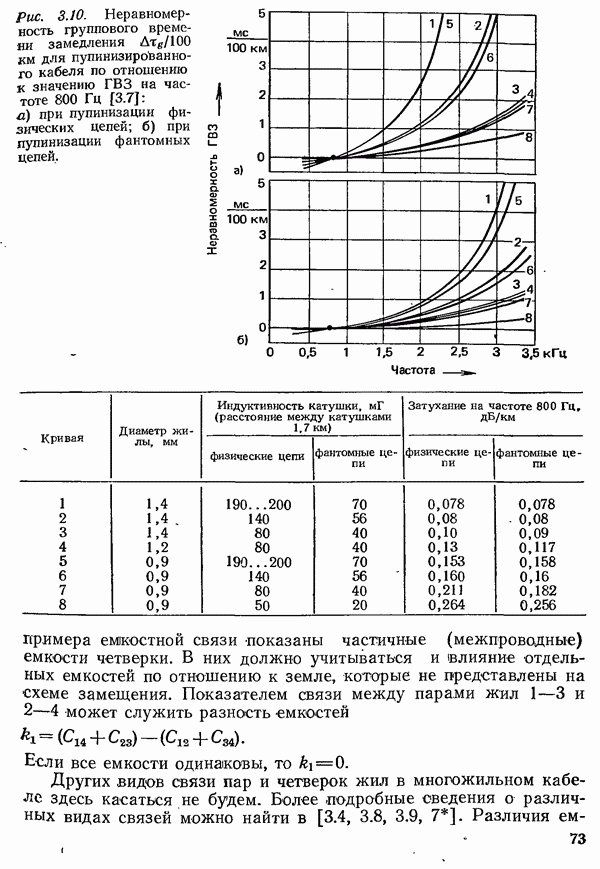
- 3.1.3. ХАРАКТЕРИСТИКИ ПАР ЖИЛ ПУПИЯИЗИРОВАННЫХ КАБЕЛЕЙ
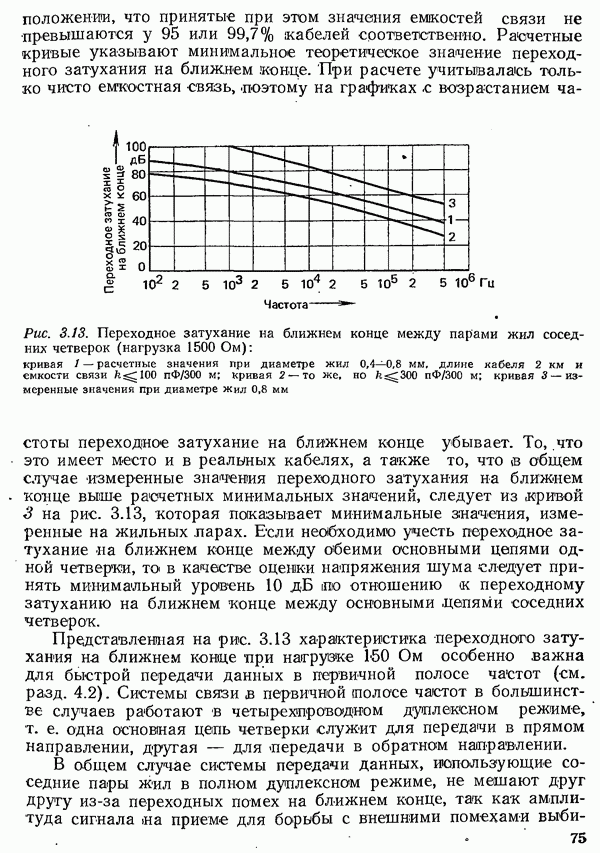
- 3.1.4. ПЕРЕХОДНЫЕ ПОМЕХИ В КАБЕЛЯХ
- 3.1.5. НАПРЯЖЕНИЯ ШУМОВ НА ПАРАХ ШИЛ КАБЕЛЕЙ
- 3.2. КАНАЛЫ ДАЛЬНЕЙ СВЯЗИ
- 3.2.2. КАНАЛЫ ТОНАЛЬНОЙ ЧАСТОТЫ
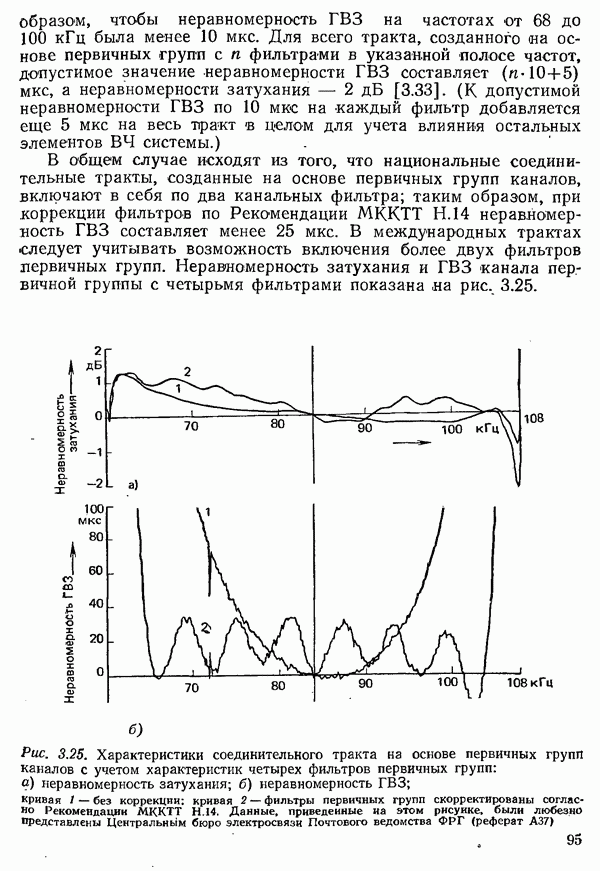
- 3.2.3. СОЕДИНИТЕЛЬНЫЕ ТРАКТЫ НА ОСНОВЕ ПЕРВИЧНЫХ ГРУПП КАНАЛОВ
- 4. Методы передачи данных
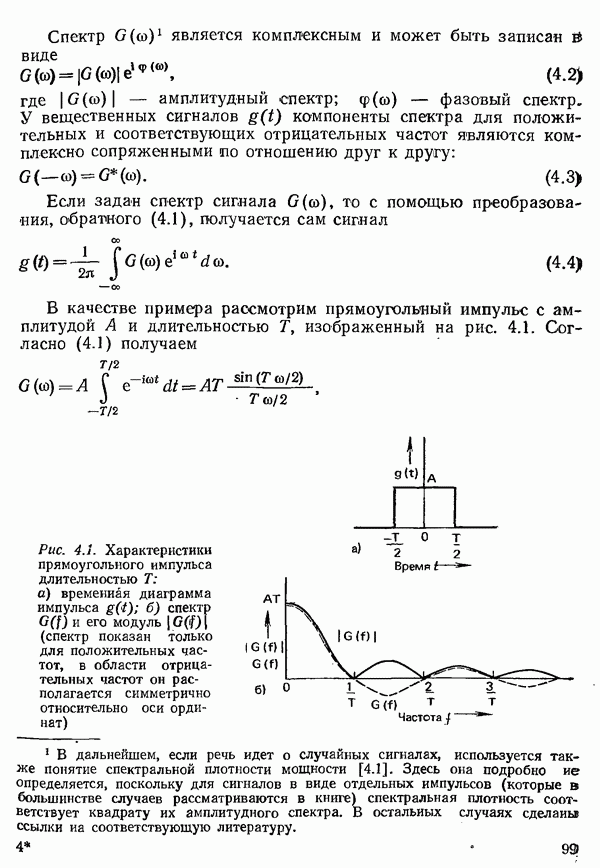
- 4.1.1. СИГНАЛЫ И СПЕКТРЫ
- 4.1.2. РЯД ФУРЬЕ
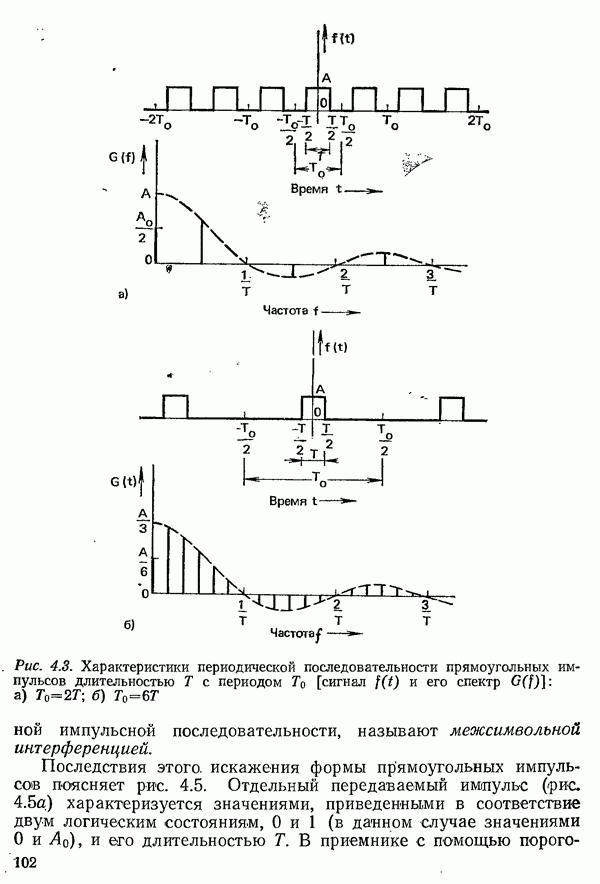
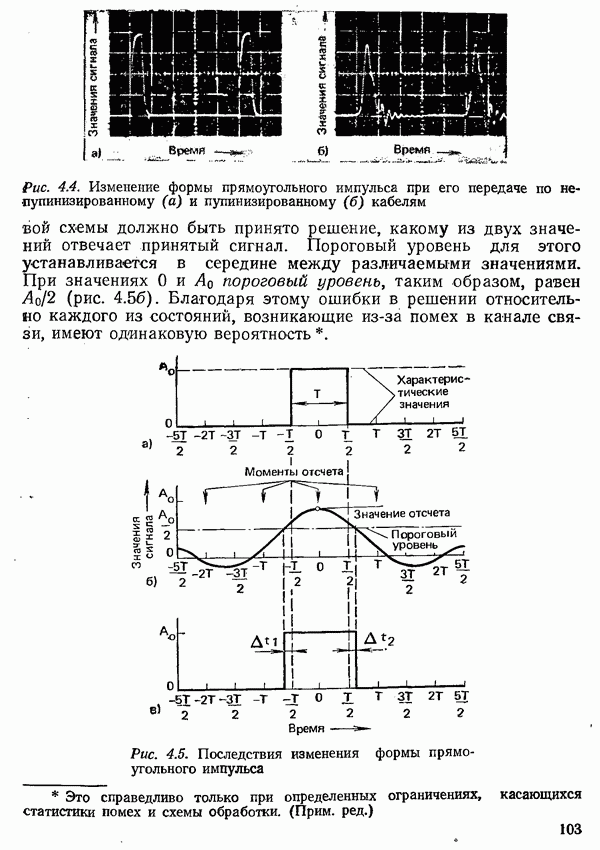
- 4.1.3. ИСКАЖЕНИЯ ФОРМЫ ИМПУЛЬСОВ ПРИ ОГРАНИЧЕНИИ ПОЛОСЫ ЧАСТОТ
- 4.1.4. УСЛОВИЯ НАЙКВИСТА
- 4.1.5. МЕТОДЫ ПАРЦИАЛЬНЫХ ОТСЧЕТОВ
- 4.1.6. ПЕРЕДАЧА МНОГОПОЗИЦИОННЫХ СИГНАЛОВ
- 4.2. МЕТОДЫ ПЕРЕДАЧИ В ПЕРВИЧНОЙ ПОЛОСЕ ЧАСТОТ
- 4.2.1. МЕТОДЫ С ПРИМЕНЕНИЕМ ДВУПОЛЯРНЫХ И ОДНОПОЛЯРНЫХ ИМПУЛЬСОВ
- 4.2.2. БИПОЛЯРНЫЙ МЕТОД
- 4.2.3. ПСЕВДОТРОИЧНЫЕ МЕТОДЫ
- 4.2.4. МЕТОДЫ С ПРИМЕНЕНИЕМ БИПОЛЯРНЫХ КОДОВ ВЫСОКОЙ ПЛОТНОСТИ
- 4.2.5. ДВУХФАЗНЫЙ МЕТОД. ИЛИ МЕТОД РАСЩЕПЛЕНИЯ ФАЗЫ
- 4.2.6. ДВУХФАЗНО-КОДОВЫЙ МЕТОД
- 4.2.7. МЕТОДЫ ПАРЦИАЛЬНЫХ ОТСЧЕТОВ
- 4.3. МЕТОДЫ ПЕРЕДАЧИ С ПРИМЕНЕНИЕМ МОДУЛЯЦИИ
- 4.3.1. АМПЛИТУДНАЯ МОДУЛЯЦИЯ
- 4.3.1.2. АМПЛИТУДНАЯ МОДУЛЯЦИЯ С ОДНОЙ БОКОВОЙ ПОЛОСОЙ И С ЧАСТИЧНО ПОДАВЛЕННОЙ БОКОВОЙ ПОЛОСОЙ
- 4.3.1.3. КВАДРАТУРНАЯ АМПЛИТУДНАЯ МОДУЛЯЦИЯ
- 4.3.1.4. УДЕЛЬНАЯ СКОРОСТЬ ПЕРЕДАЧИ ПРИ АМПЛИТУДНОЙ МОДУЛЯЦИИ
- 4.3.2. ЧАСТОТНАЯ МОДУЛЯЦИЯ
- 4.3.2.1. УДЕЛЬНАЯ СКОРОСТЬ ПЕРЕДАЧИ ПРИ ЧАСТОТНОЙ МОДУЛЯЦИИ
- 4.3.3. ФАЗОВАЯ МОДУЛЯЦИЯ
- 4.4. ВОССТАНОВЛЕНИЕ ТАКТОВ И НЕСУЩЕЙ
- 4.4.2. ВОССТАНОВЛЕНИЕ ЧАСТОТЫ И ФАЗЫ НЕСУЩЕЙ
- 4.5. ВЕРОЯТНОСТЬ ОШИБКИ ПРИ НАЛИЧИИ ПОМЕХ
- 4.5.1. ВЕРОЯТНОСТЬ ОШИБКИ ПРИ УЧЕТЕ ТОЛЬКО ШУМА В КАНАЛЕ СВЯЗИ
- 4.5.2. ВЕРОЯТНОСТЬ ОШИБКИ С УЧЕТОМ ЛИНЕЙНЫХ ИСКАЖЕНИЙ
- 4.5.3. ВЕРОЯТНОСТЬ ОШИБКИ С УЧЕТОМ ПРОЦЕССОВ МОДУЛЯЦИИ И ДЕМОДУЛЯЦИИ
- 5. Учет свойств реальных каналов связи при передаче данных
- 5.2. ВЛИЯНИЕ ХАРАКТЕРИСТИК КАНАЛОВ СВЯЗИ НА ПЕРЕДАЧУ ДАННЫХ
- 5.2.2. СДВИГИ ЧАСТОТЫ
- 5.2.3. ФАЗОВОЕ ДРОЖАНИЕ
- 5.2.4. ВЛИЯНИЕ РЕАЛЬНЫХ ПОМЕХ
- 5.3. КОРРЕКЦИЯ ПРИНИМАЕМОГО СИГНАЛА ДАННЫХ
- 5.3.1. КОРРЕКЦИЯ ПРИНИМАЕМОГО СИГНАЛА ДАННЫХ В ЧАСТОТНОЙ ОБЛАСТИ
- 5.3.1.1. КОМПРОМИССНЫЙ КОРРЕКТОР
- 5.3.1.2. НАСТРАИВАЕМЫЙ ЧАСТОТНЫЙ КОРРЕКТОР СИГНАЛОВ ДАННЫХ
- 5.3.2. КОРРЕКЦИЯ ПРИНИМАЕМОГО СИГНАЛА ДАННЫХ ВО ВРЕМЕННОЙ ОБЛАСТИ
- 5.3.2.2. КРИТЕРИИ НАСТРОЙКИ КОРРЕКТОРА ВО ВРЕМЕННОЙ ОБЛАСТИ
- 5.3.2.3. АВТОМАТИЧЕСКАЯ НАСТРОЙКА ТРАНСВЕРСАЛЬНОГО КОРРЕКТИРУЮЩЕГО ФИЛЬТРА
- 5.3.2.4. РЕКУРСИВНЫЙ КОРРЕКТОР
- 5.3.2.5. СХОДИМОСТЬ НАСТРОЙКИ КОРРЕКТОРА
- 5.3.2.6. КОРРЕКТОР ДЛЯ СПЕЦИАЛЬНЫХ МЕТОДОВ ПЕРЕДАЧИ
- 6. Основы коммутации данных
- 6.1.2. МЕТОДЫ КОММУТАЦИИ
- 6.1.3. СПОСОБЫ КОММУТАЦИИ КАНАЛОВ
- 6.1.4. СИГНАЛИЗАЦИЯ
- 6.1.5. УПРАВЛЕНИЕ ПРОЦЕССАМИ СОЕДИНЕНИЯ И РАЗЪЕДИНЕНИЯ
- 6.1.6. ПОДРАЗДЕЛЕНИЕ ЦЕПЕЙ КОММУТАЦИИ КАНАЛОВ
- 6.1.7. ДОПОЛНИТЕЛЬНЫЕ ЗАДАЧИ КОММУТАЦИОННЫХ УСТРОЙСТВ
- 6.2. АНАЛИЗ СИСТЕМ КОММУТАЦИИ НА ОСНОВЕ ТЕОРИИ ТЕЛЕТРАФИКА
- 6.2.2. СИСТЕМЫ С ПОТЕРЯМИ
- 6.2.3. СИСТЕМЫ С ОЖИДАНИЕМ
- 6.2.4. ИЗМЕРЕНИЯ НАГРУЗКИ
- СПИСОК ЛИТЕРАТУРЫ