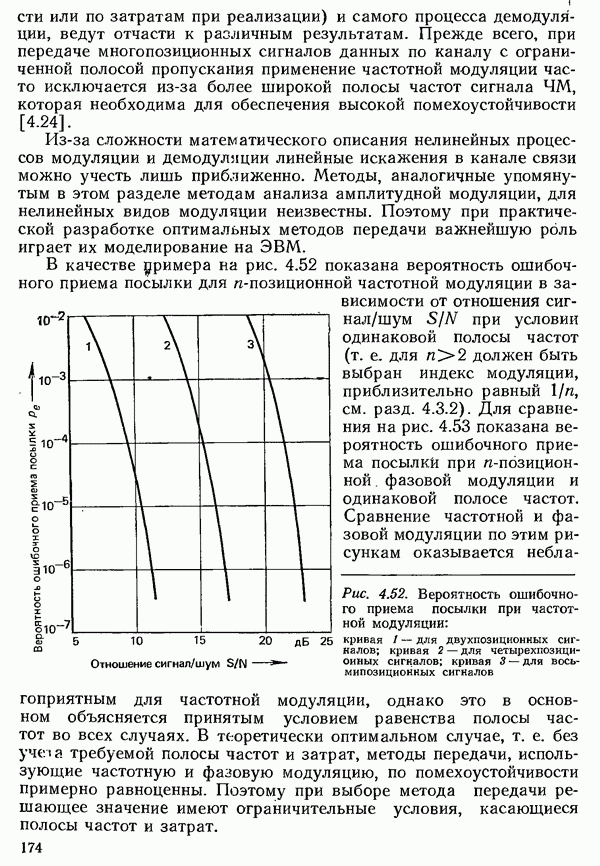
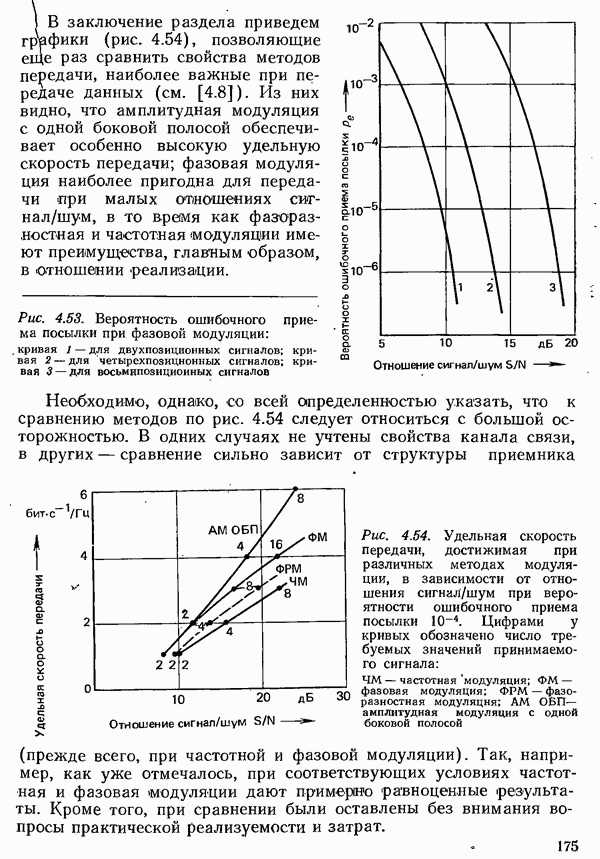
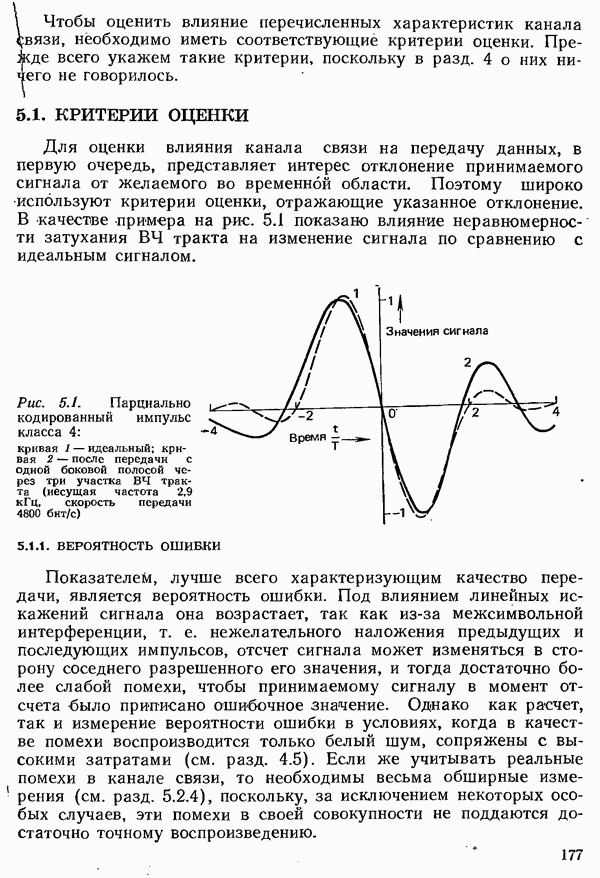
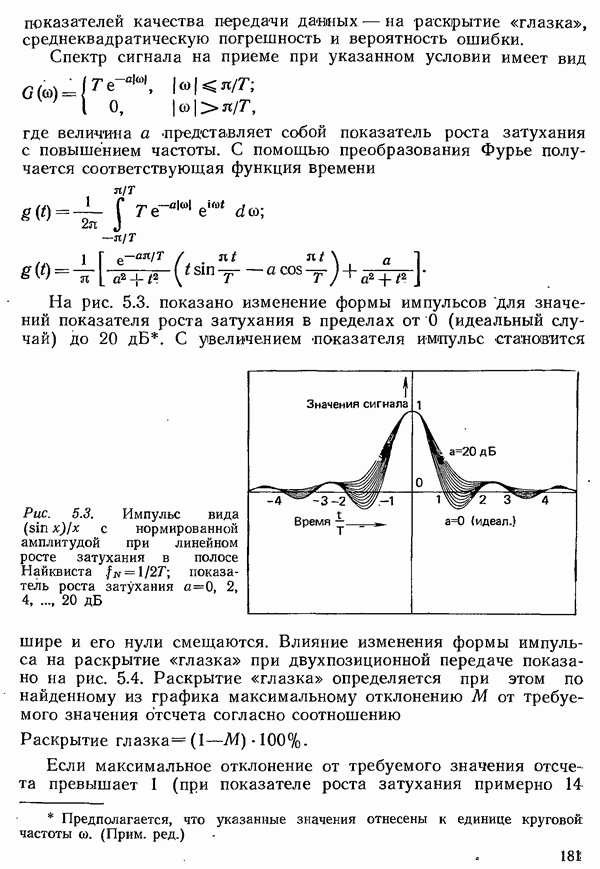
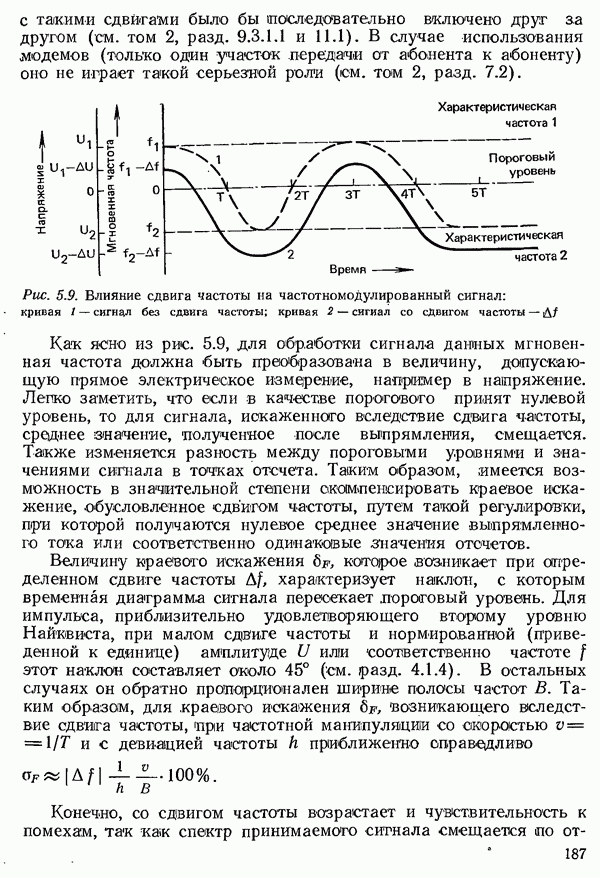
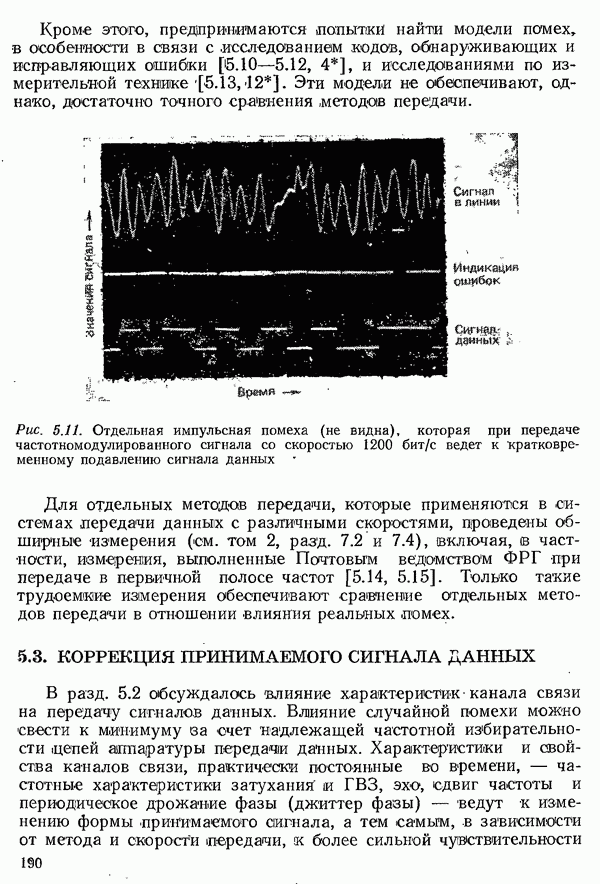
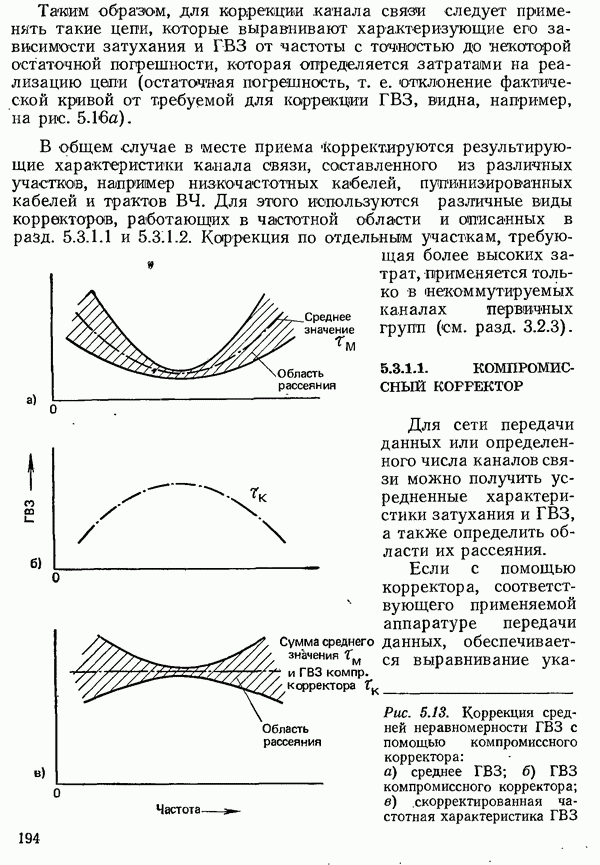
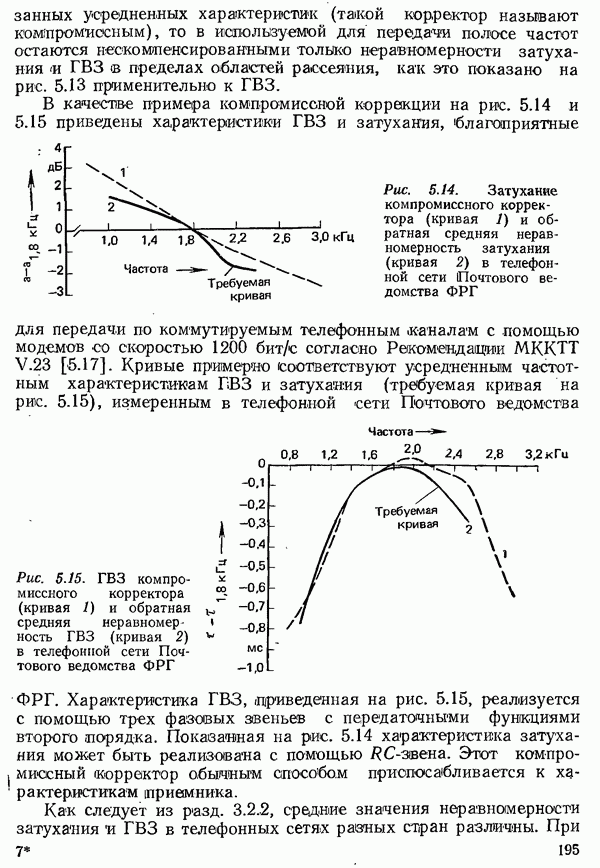
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
2.3. НЕКОТОРЫЕ ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ИНФОРМАЦИИ
2.3.1. ИНФОРМАЦИЯ, ЭНТРОПИЯ
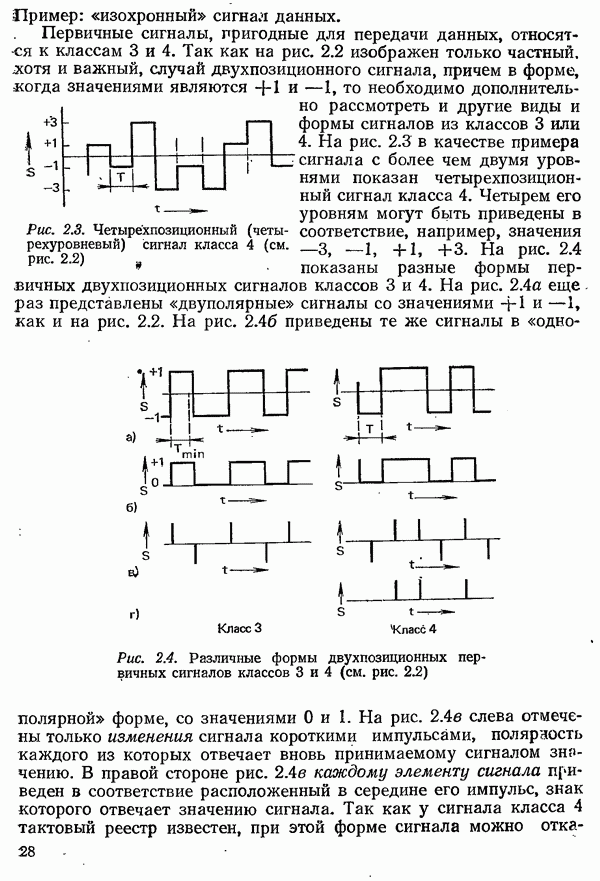
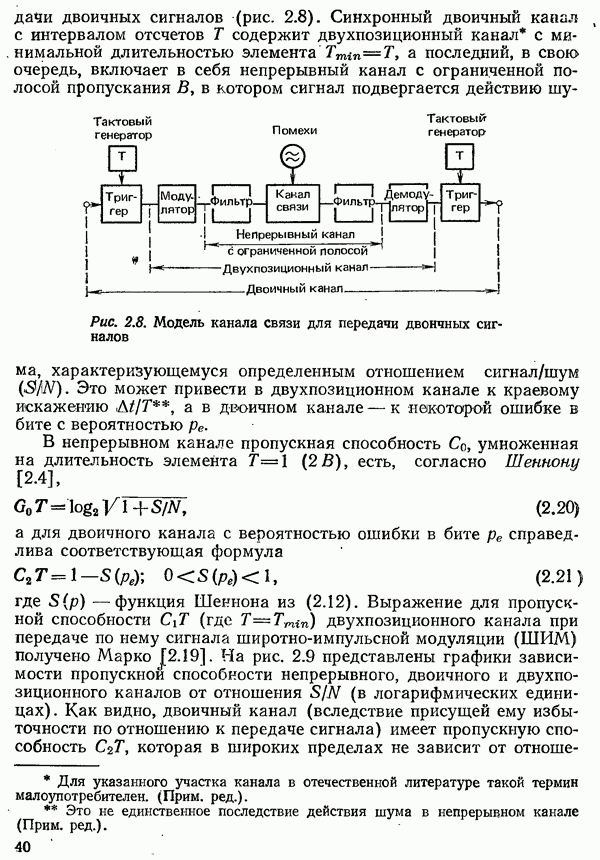
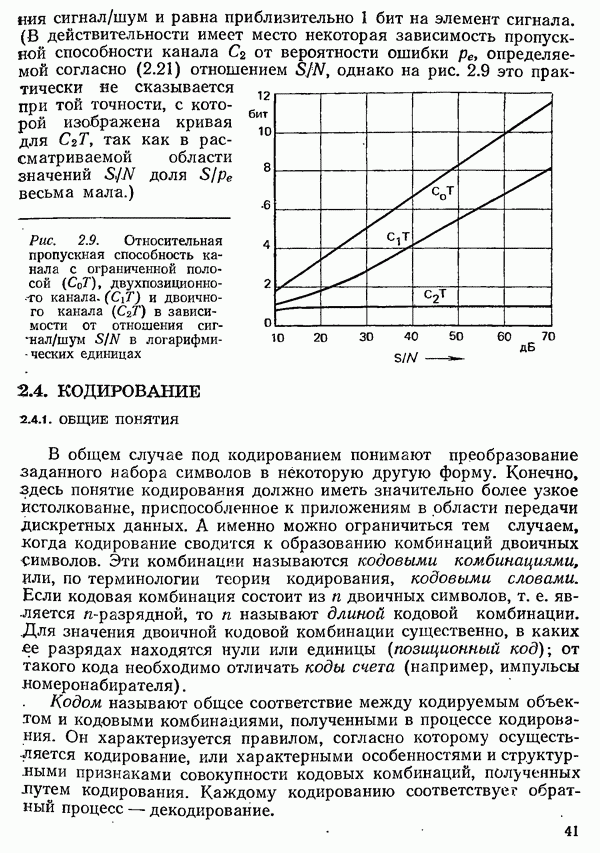
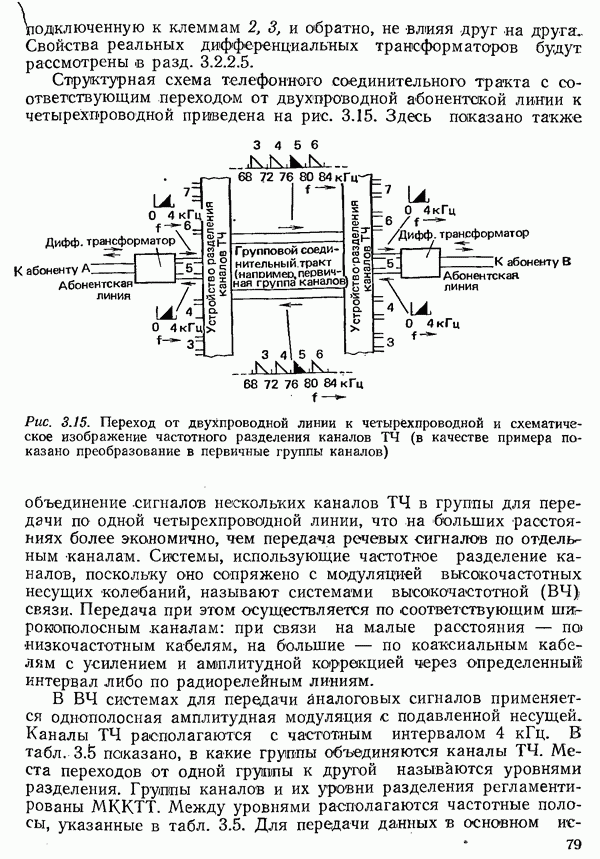
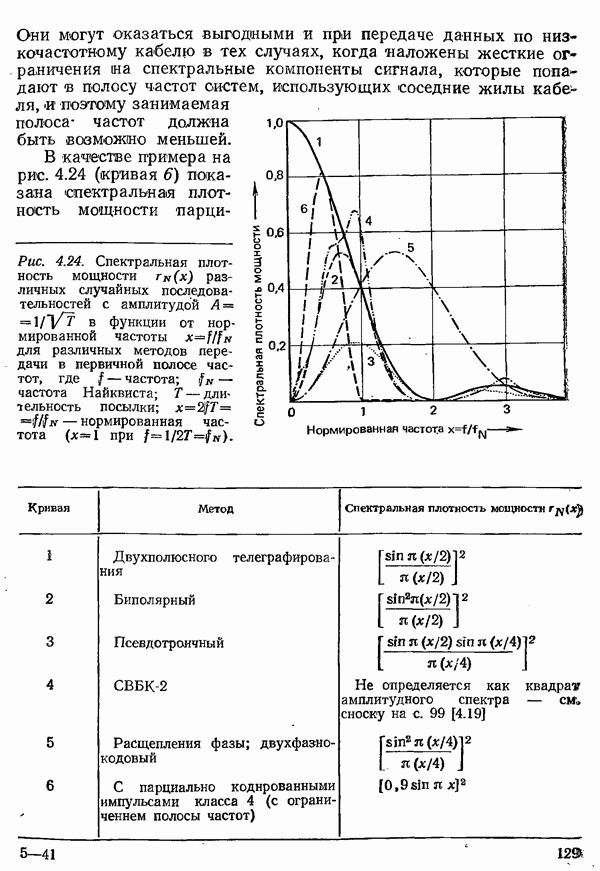
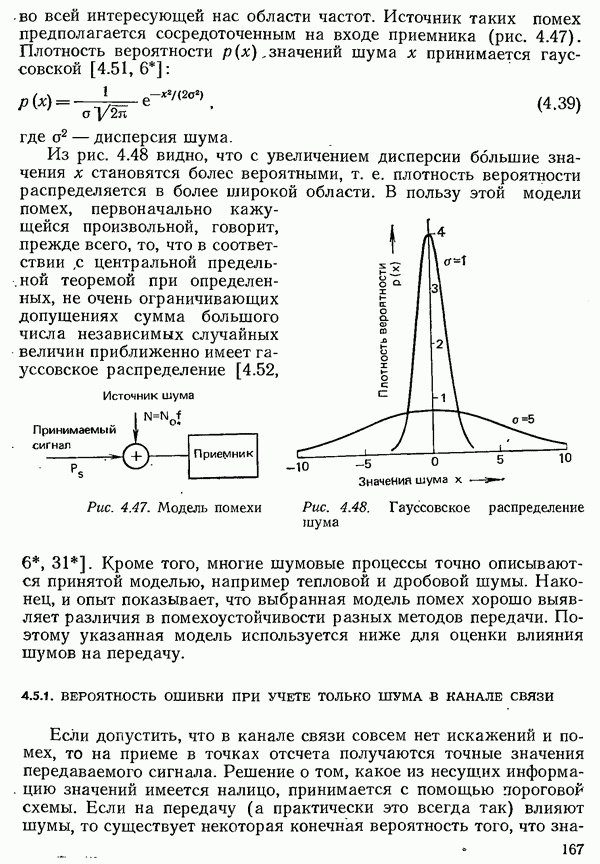
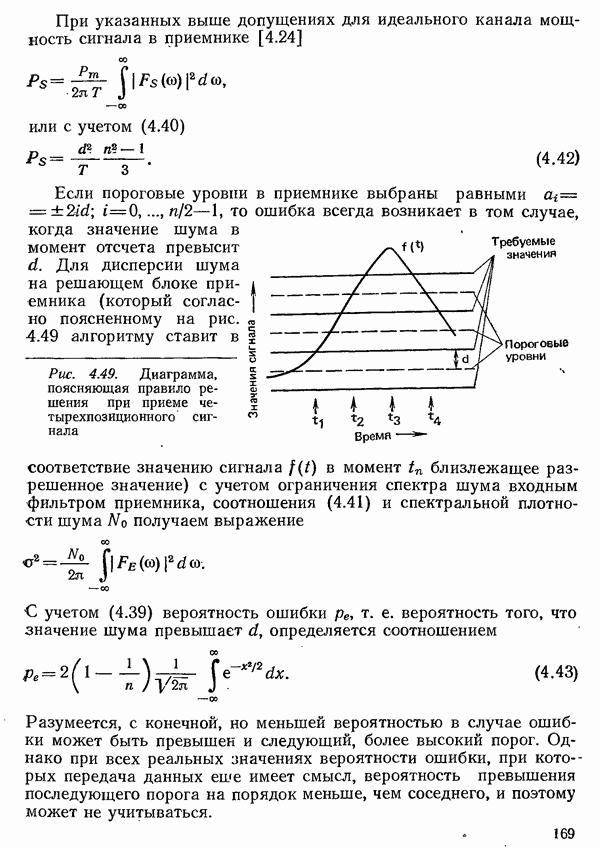
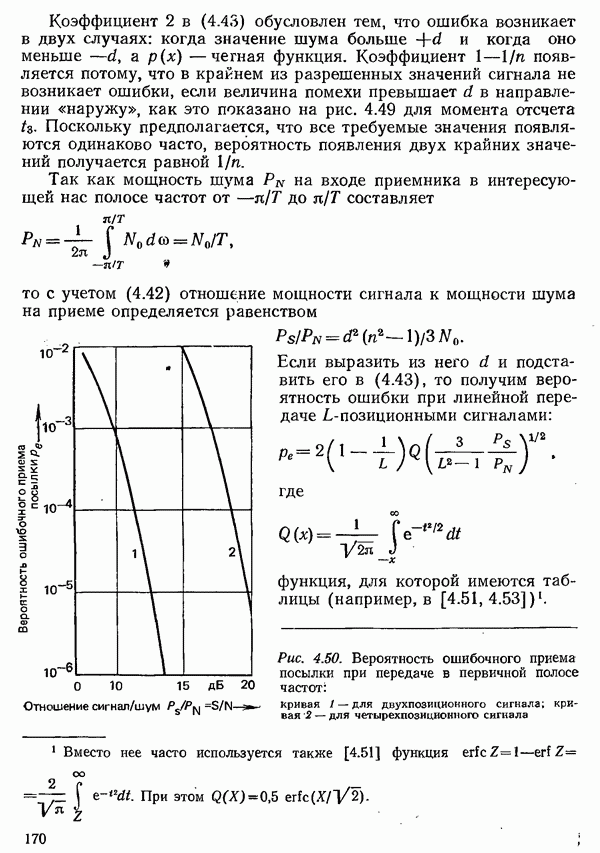
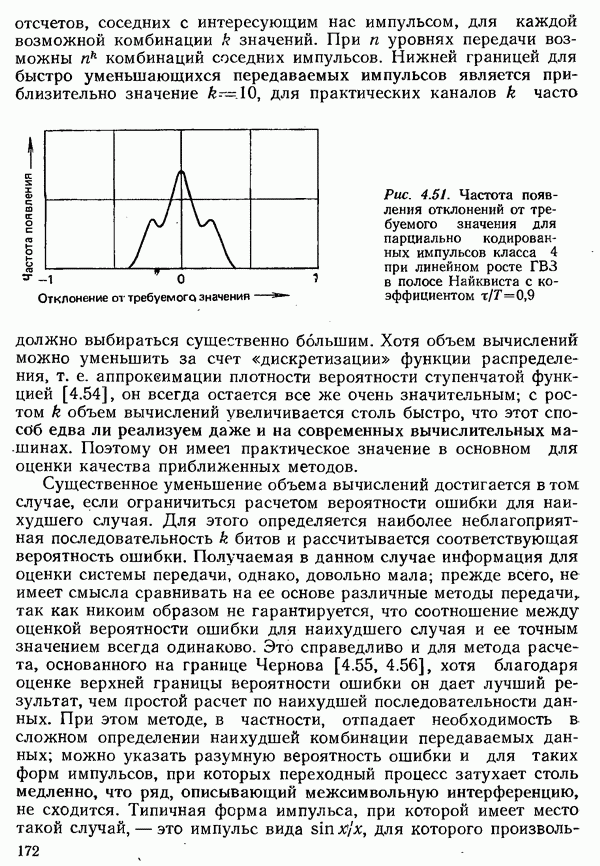
Получение информации можно свести к последовательности процессов выбора определенного символа из заданного набора. Заданный набор символов, который всегда должен содержать конечное число различных символов, в общем случае называется
алфавитом. Каждому символу  из некоторого алфавита можно приписать определенную вероятность
из некоторого алфавита можно приписать определенную вероятность  его появления.
его появления.
Появление определенного символа  можно рассматривать как событие
можно рассматривать как событие  Множества
Множества  из
из  возможных взаимоисключающих друг друга событий и соответствующих им вероятностей
возможных взаимоисключающих друг друга событий и соответствующих им вероятностей  образуют поле событий
образуют поле событий  причем справедливы следующие соотношения:
причем справедливы следующие соотношения:

Если каждому событию  приведено в соответствие определенное (конечное) числовое значение
приведено в соответствие определенное (конечное) числовое значение  то
то  называется случайной величиной с математическим ожиданием
называется случайной величиной с математическим ожиданием

Каждому событию  можно привести в соответствие числовое значение
можно привести в соответствие числовое значение  с помощью которого может быть измерена информация, заключающаяся в появлении события
с помощью которого может быть измерена информация, заключающаяся в появлении события  . С этой точки зрения получение информации связано с устранением ранее существующей неопределенности. Связанная с событием
. С этой точки зрения получение информации связано с устранением ранее существующей неопределенности. Связанная с событием  информация! или мера устраняемой им неопределенности тем больше, чем более неожиданным было событие
информация! или мера устраняемой им неопределенности тем больше, чем более неожиданным было событие  е. чем меньше вероятность
е. чем меньше вероятность  Следовательно,
Следовательно,  является такой функцией
является такой функцией  вероятности
вероятности  значения которой тем больше, чем меньше
значения которой тем больше, чем меньше 
Совместное появление двух взаимно независимых событий,  из X с вероятностями
из X с вероятностями  например, как пары в последовательности событий, по правилам теории вероятностей имеет вероятность
например, как пары в последовательности событий, по правилам теории вероятностей имеет вероятность  Тогда информация, заключающаяся в паре событий,
Тогда информация, заключающаяся в паре событий,

и так как  взаимно независимы, то разумно потребовать, чтобы количество информации, связанной с парой событий,
взаимно независимы, то разумно потребовать, чтобы количество информации, связанной с парой событий,  было равно сумме количеств информации, содержащихся в отдельных событиях:
было равно сумме количеств информации, содержащихся в отдельных событиях:

т.е.

Последнее выражение представляет собой функциональное уравнение логарифмической функции. Отсюда при использовании логарифма по основанию 2 с некоторым свободным параметром К получается

Параметр К определяется исходя из того, что решение об одном  из двух независимых равновероятных событий содержит информацию в 1 бит. Поскольку каждое из двух таких событий имеет вероятность
из двух независимых равновероятных событий содержит информацию в 1 бит. Поскольку каждое из двух таких событий имеет вероятность  то согласно (2.5) получается
то согласно (2.5) получается  или
или  Отсюда
Отсюда

Выражение (2.6) можно рассматривать как определение понятия информации [2.11]. Информация, согласно (2.6), тем больше, чем менее вероятно появление соответствующего события. Наоборот, событие, которое можно предсказать с достоверностью  , не несет информации.
, не несет информации. 
Информация  есть случайная величина. Поэтому можно в соответствии
есть случайная величина. Поэтому можно в соответствии  определить математическое ожидание информации в поле событий:
определить математическое ожидание информации в поле событий:

 Это математическое ожидание, или средняя информация, называется энтропией множества событий
Это математическое ожидание, или средняя информация, называется энтропией множества событий  При этом для
При этом для

Если все  событий
событий  имеют одинаковую вероятность, то
имеют одинаковую вероятность, то  и из (2.7)
и из (2.7)

В этом случае энтропия максимальна и в общем справедливо

Отклонение энтропии  от ее максимального значения
от ее максимального значения  называют избыточностью:
называют избыточностью:

«Относительная» избыточность

Для передачи данных особенно важен двоичный источник, алфавит которого состоит только из символов 0 и 1:  Если символам приписаны вероятности
Если символам приписаны вероятности  то согласно
то согласно 

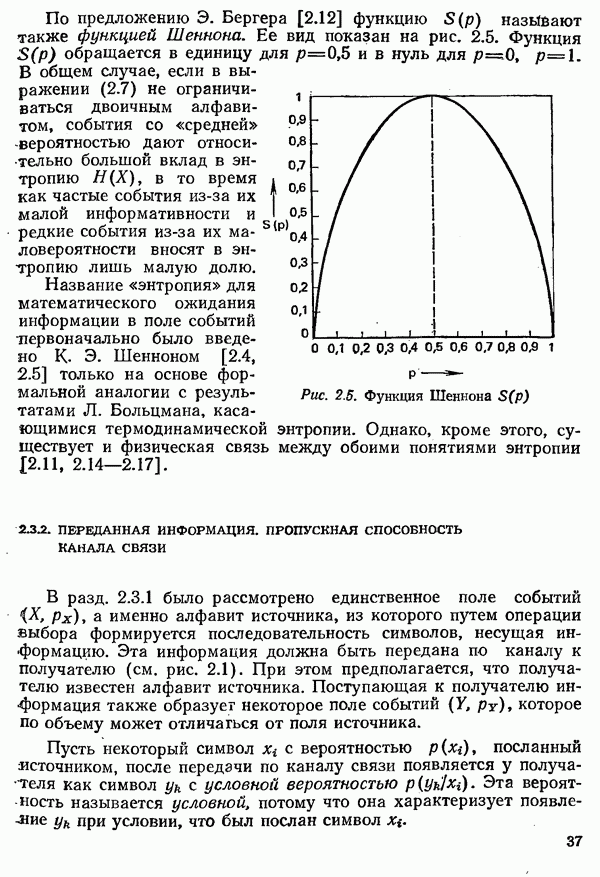
По предложению  Бергера [2.12] функцию
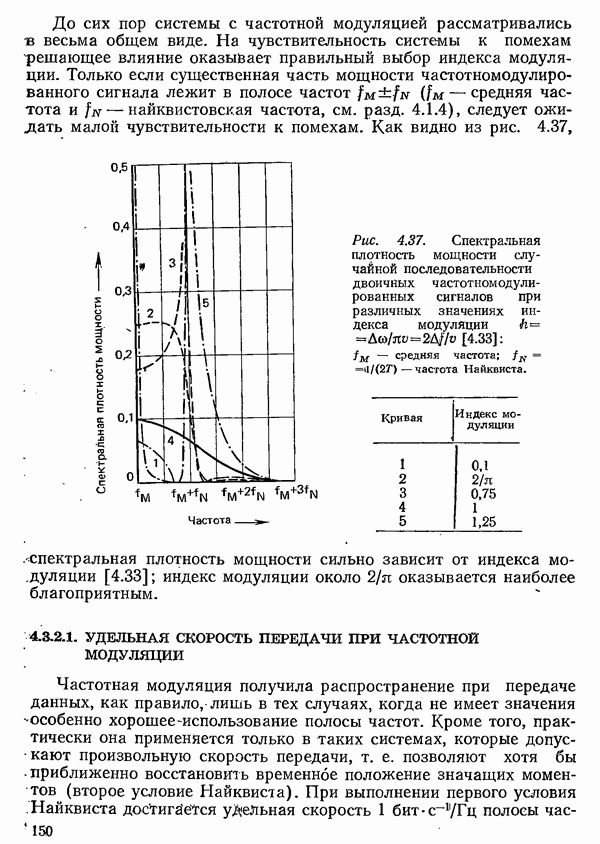
Бергера [2.12] функцию  также функцией Шеннона. Ее вид показан на рис. 2.5. Функция
также функцией Шеннона. Ее вид показан на рис. 2.5. Функция  обращается в единицу для
обращается в единицу для  и в нуль для
и в нуль для  В общем случае, если в выражении (2.7) не ограничиваться двоичным алфавитом, события со «средней»
В общем случае, если в выражении (2.7) не ограничиваться двоичным алфавитом, события со «средней»
-вероятностью дают относительно большой вклад в энтропию  в то время как частые события из-за их малой информативности и редкие события из-за их
в то время как частые события из-за их малой информативности и редкие события из-за их  ловероятности вносят в энтропию лишь малую долю.
ловероятности вносят в энтропию лишь малую долю.

Рис. 2.5. Функция Шеннона 
Название «энтропия» для математического ожидания информации в поле событий первоначально было введено К. Э. Шенноном [2.4,
2.5] только на основе формальной аналогии с результатами Л. Больцмана, касающимися термодинамической энтропии. Однако, кроме этого, существует и физическая связь между обоими понятиями энтропии 
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ К РУССКОМУ ИЗДАНИЮ
- 1. Обзор
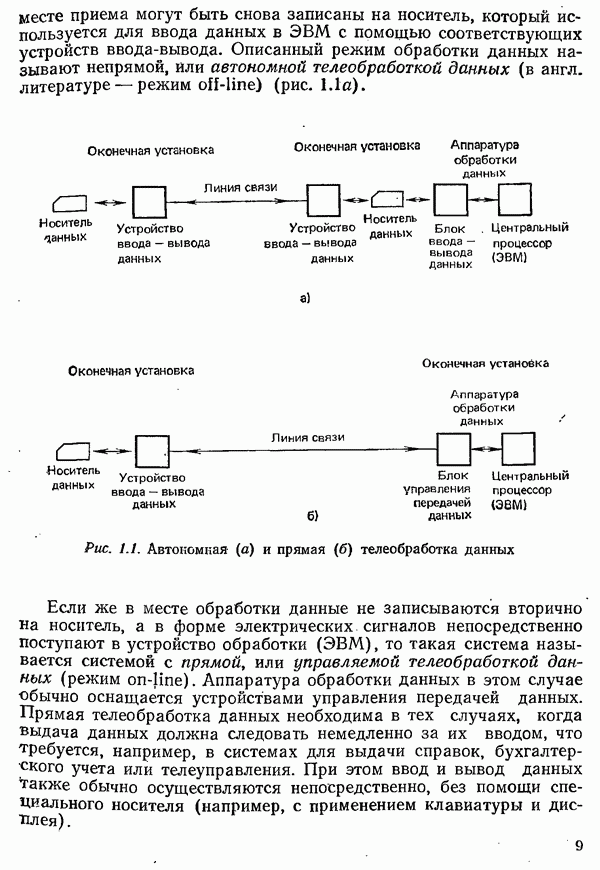
- 1.1. ОБРАБОТКА И ТЕЛЕОБРАБОТКА ДАННЫХ
- 1.2. АВТОНОМНАЯ И УПРАВЛЯЕМАЯ ТЕЛЕОБРАБОТКА ДАННЫХ
- 1.3. КЛАССИФИКАЦИЯ СИСТЕМ ТЕЛЕОБРАБОТКИ ДАННЫХ
- 1.4. СТРУКТУРА СИСТЕМ ТЕЛЕОБРАБОТКИ ДАННЫХ
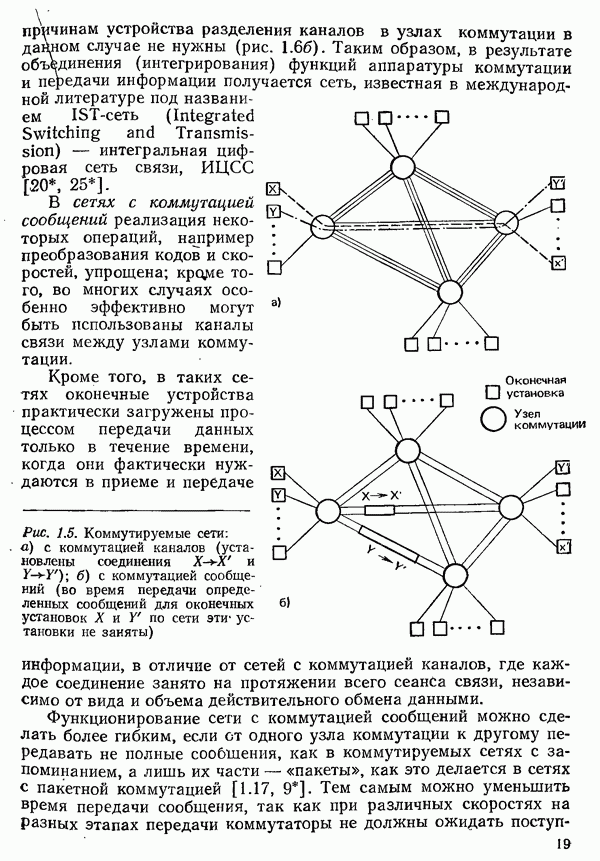
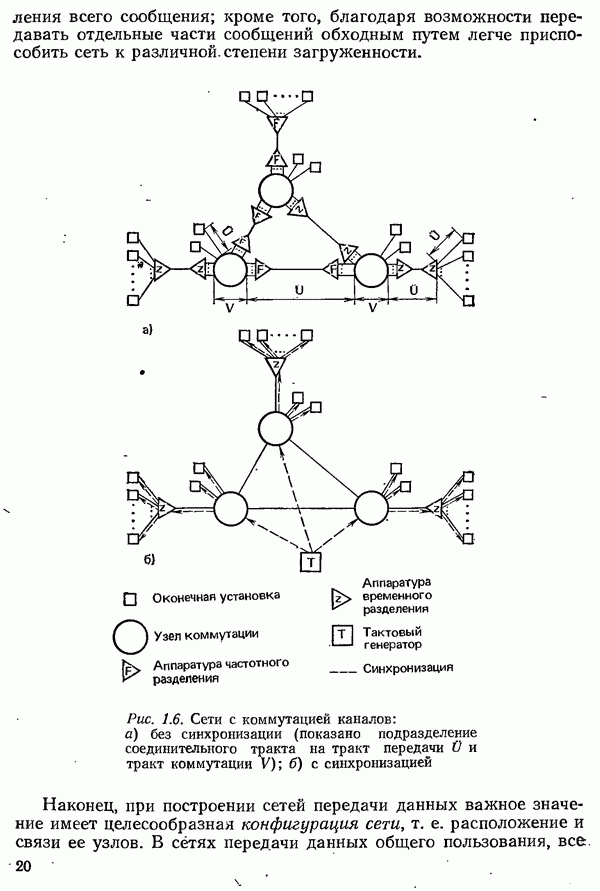
- 1.5. ТРЕБОВАНИЯ К ТЕХНИКЕ СВЯЗИ И КОММУТАЦИИ В СИСТЕМАХ ТЕЛЕОБРАБОТКИ ДАННЫХ
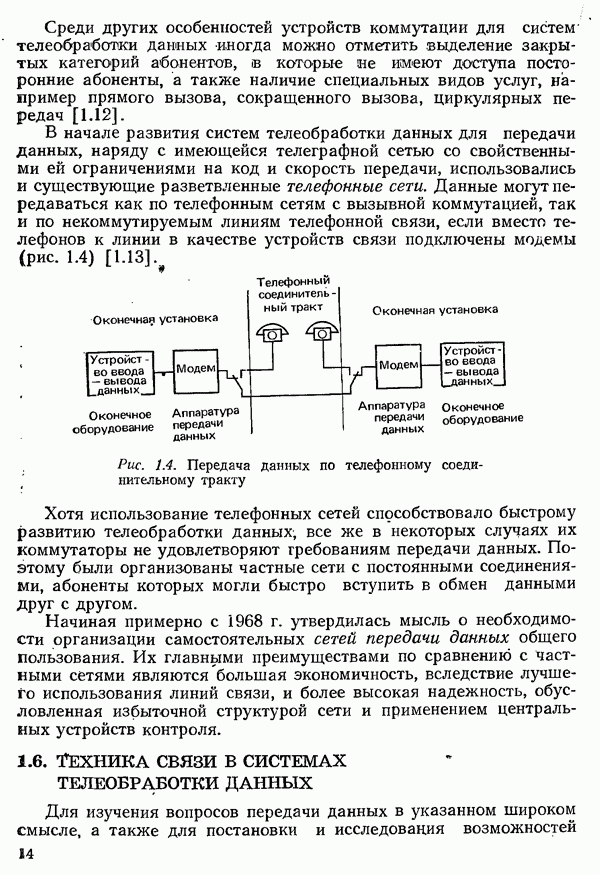
- 1.6. ТЕХНИКА СВЯЗИ В СИСТЕМАХ ТЕЛЕОБРАБОТКИ ДАННЫХ
- 2. Основные понятия техники связи
- 2.2. СИГНАЛЫ
- 2.2.2. ДИСКРЕТИЗАЦИЯ, КВАНТОВАНИЕ, ВЛИЯНИЕ ШУМОВ
- 2.2.3. СВОЙСТВА ПЕРВИЧНЫХ СИГНАЛОВ ДЛЯ ПЕРЕДАЧИ ДАННЫХ
- 2.2.3.2. ВРЕМЕННЫЕ СООТНОШЕНИЯ МЕЖДУ СИГНАЛАМИ
- 2.2.4. РЕЖИМЫ РАБОТЫ ПРИ ПЕРЕДАЧЕ СИГНАЛОВ
- 2.3. НЕКОТОРЫЕ ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ИНФОРМАЦИИ
- 2.3.2. ПЕРЕДАННАЯ ИНФОРМАЦИЯ. ПРОПУСКНАЯ СПОСОБНОСТЬ КАНАЛА СВЯЗИ
- 2.4. КОДИРОВАНИЕ
- 2.4.3. КОДИРОВАНИЕ ИСТОЧНИКА
- 2.4.4. КАНАЛЬНОЕ КОДИРОВАНИЕ
- 3. Каналы связи
- 3.1. КАНАЛЫ БЛИЖНЕЙ СВЯЗИ
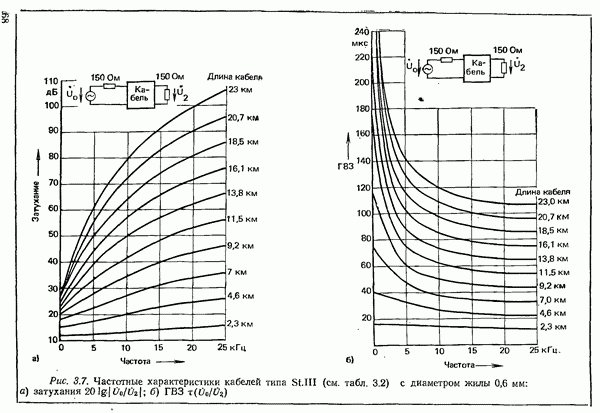
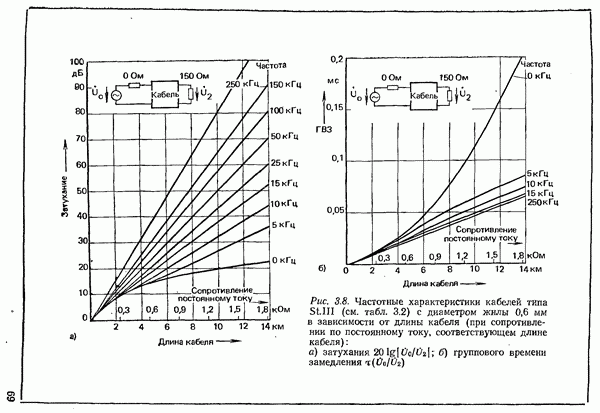
- 3.1.1.1. СВОЙСТВА И ПАРАМЕТРЫ ПРОВОДНЫХ ЛИНИЙ СВЯЗИ
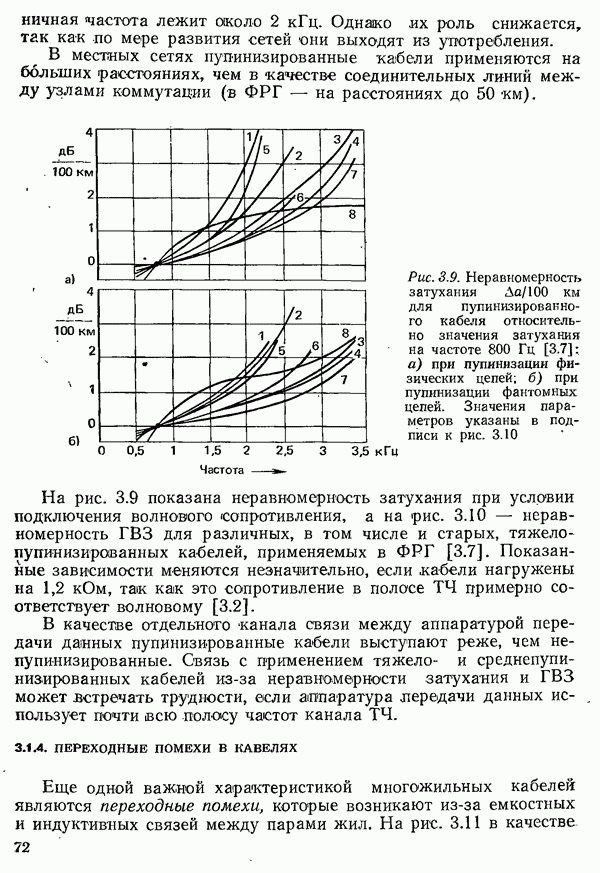
- 3.1.1.2. УМЕНЬШЕНИЕ ЗАТУХАНИЯ ПУТЕМ УВЕЛИЧЕНИЯ ИНДУКТИВНОСТИ. ПУПИНИЗАЦИЯ
- 3.1.2. ХАРАКТЕРИСТИКИ ПАР ЖИЛ НИЗКОЧАСТОТНЫХ КАБЕЛЕЙ
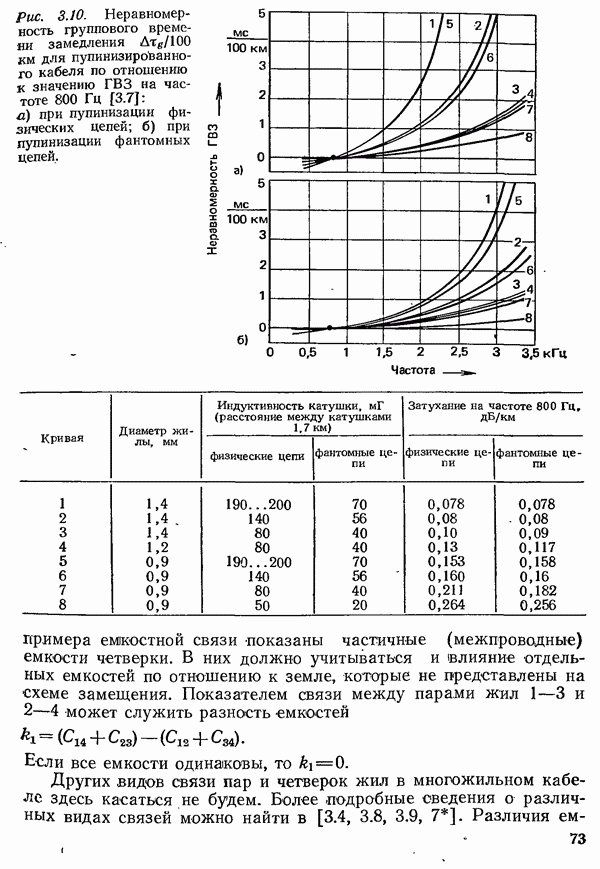
- 3.1.3. ХАРАКТЕРИСТИКИ ПАР ЖИЛ ПУПИЯИЗИРОВАННЫХ КАБЕЛЕЙ
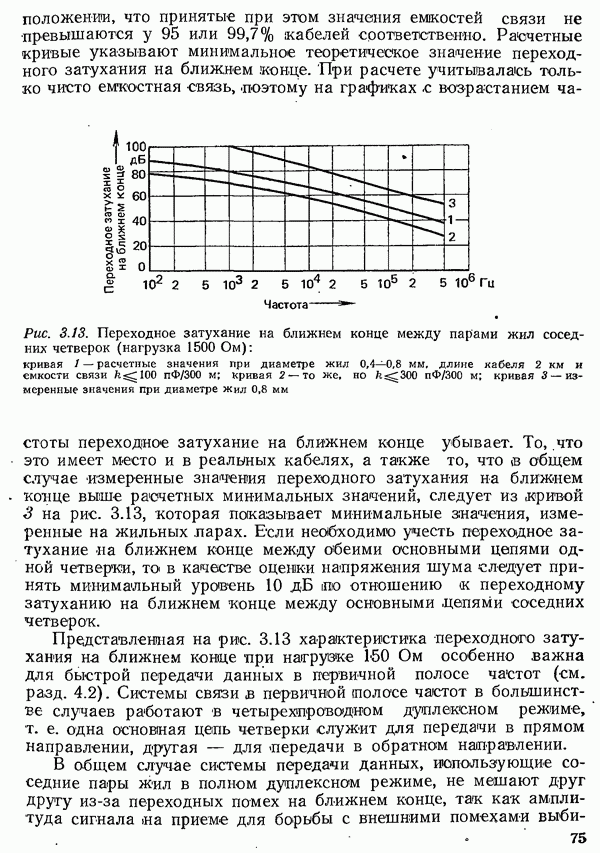
- 3.1.4. ПЕРЕХОДНЫЕ ПОМЕХИ В КАБЕЛЯХ
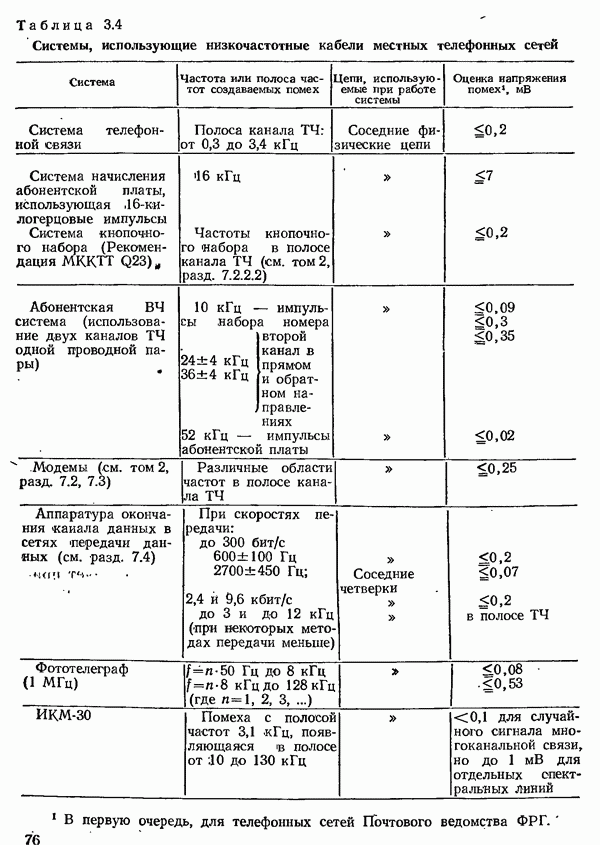
- 3.1.5. НАПРЯЖЕНИЯ ШУМОВ НА ПАРАХ ШИЛ КАБЕЛЕЙ
- 3.2. КАНАЛЫ ДАЛЬНЕЙ СВЯЗИ
- 3.2.2. КАНАЛЫ ТОНАЛЬНОЙ ЧАСТОТЫ
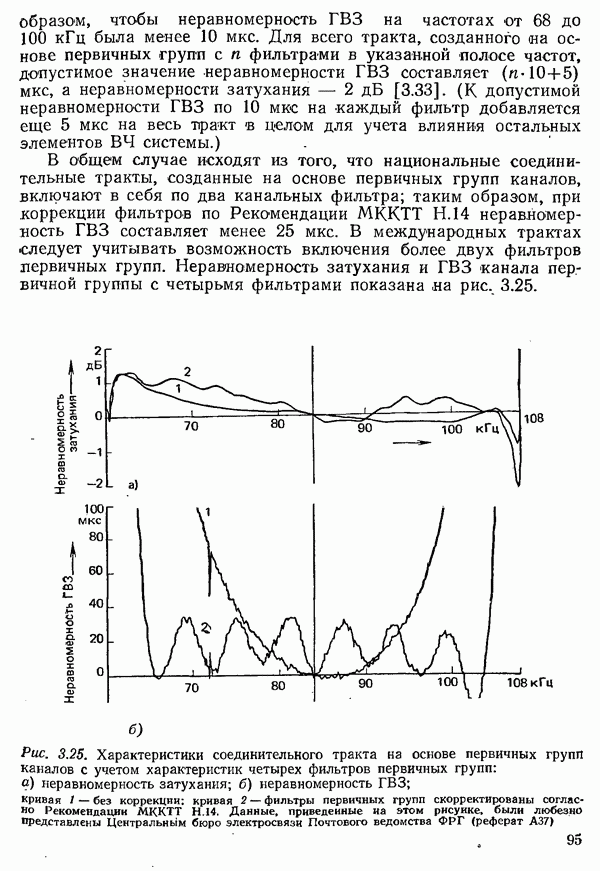
- 3.2.3. СОЕДИНИТЕЛЬНЫЕ ТРАКТЫ НА ОСНОВЕ ПЕРВИЧНЫХ ГРУПП КАНАЛОВ
- 4. Методы передачи данных
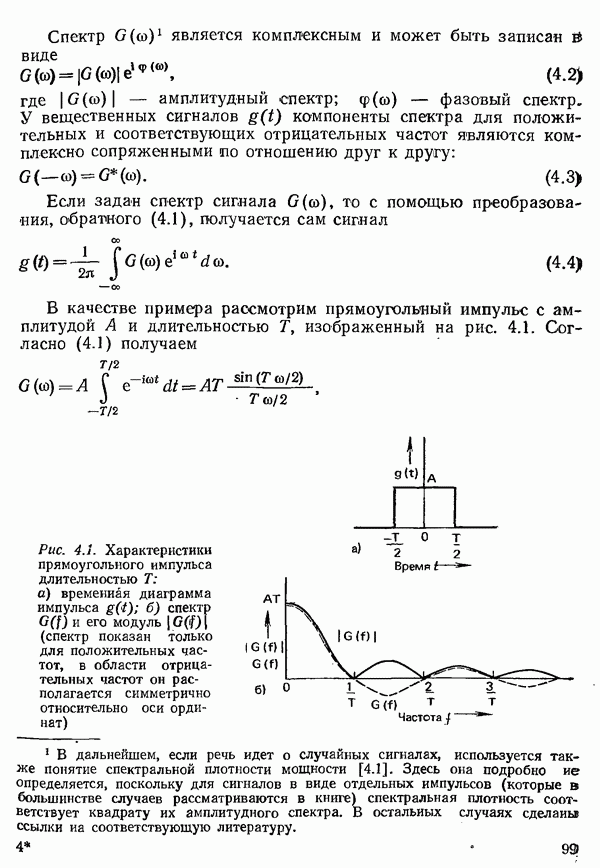
- 4.1.1. СИГНАЛЫ И СПЕКТРЫ
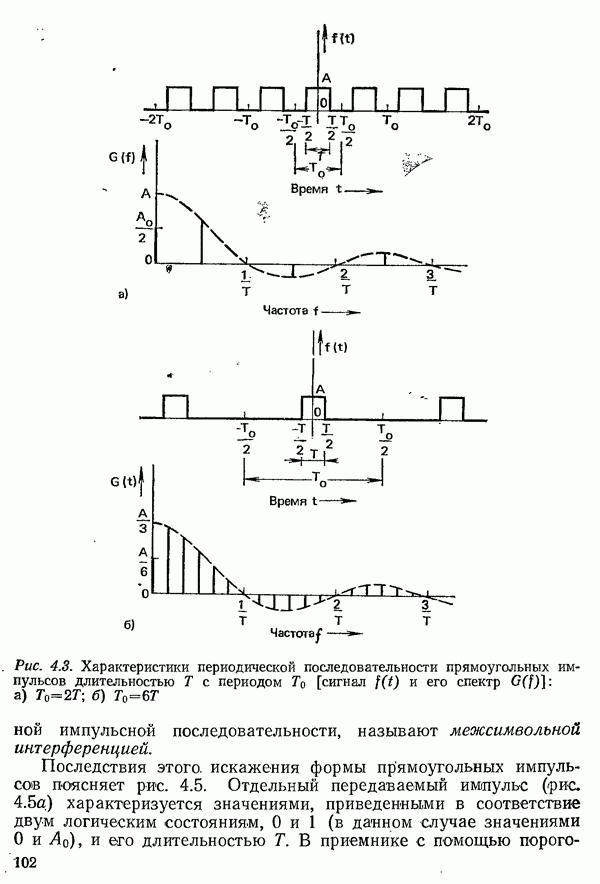
- 4.1.2. РЯД ФУРЬЕ
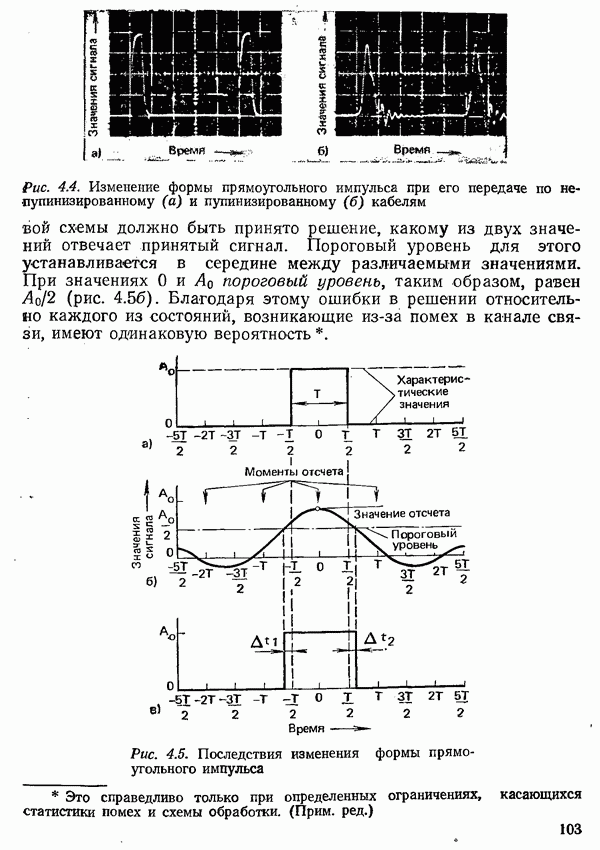
- 4.1.3. ИСКАЖЕНИЯ ФОРМЫ ИМПУЛЬСОВ ПРИ ОГРАНИЧЕНИИ ПОЛОСЫ ЧАСТОТ
- 4.1.4. УСЛОВИЯ НАЙКВИСТА
- 4.1.5. МЕТОДЫ ПАРЦИАЛЬНЫХ ОТСЧЕТОВ
- 4.1.6. ПЕРЕДАЧА МНОГОПОЗИЦИОННЫХ СИГНАЛОВ
- 4.2. МЕТОДЫ ПЕРЕДАЧИ В ПЕРВИЧНОЙ ПОЛОСЕ ЧАСТОТ
- 4.2.1. МЕТОДЫ С ПРИМЕНЕНИЕМ ДВУПОЛЯРНЫХ И ОДНОПОЛЯРНЫХ ИМПУЛЬСОВ
- 4.2.2. БИПОЛЯРНЫЙ МЕТОД
- 4.2.3. ПСЕВДОТРОИЧНЫЕ МЕТОДЫ
- 4.2.4. МЕТОДЫ С ПРИМЕНЕНИЕМ БИПОЛЯРНЫХ КОДОВ ВЫСОКОЙ ПЛОТНОСТИ
- 4.2.5. ДВУХФАЗНЫЙ МЕТОД. ИЛИ МЕТОД РАСЩЕПЛЕНИЯ ФАЗЫ
- 4.2.6. ДВУХФАЗНО-КОДОВЫЙ МЕТОД
- 4.2.7. МЕТОДЫ ПАРЦИАЛЬНЫХ ОТСЧЕТОВ
- 4.3. МЕТОДЫ ПЕРЕДАЧИ С ПРИМЕНЕНИЕМ МОДУЛЯЦИИ
- 4.3.1. АМПЛИТУДНАЯ МОДУЛЯЦИЯ
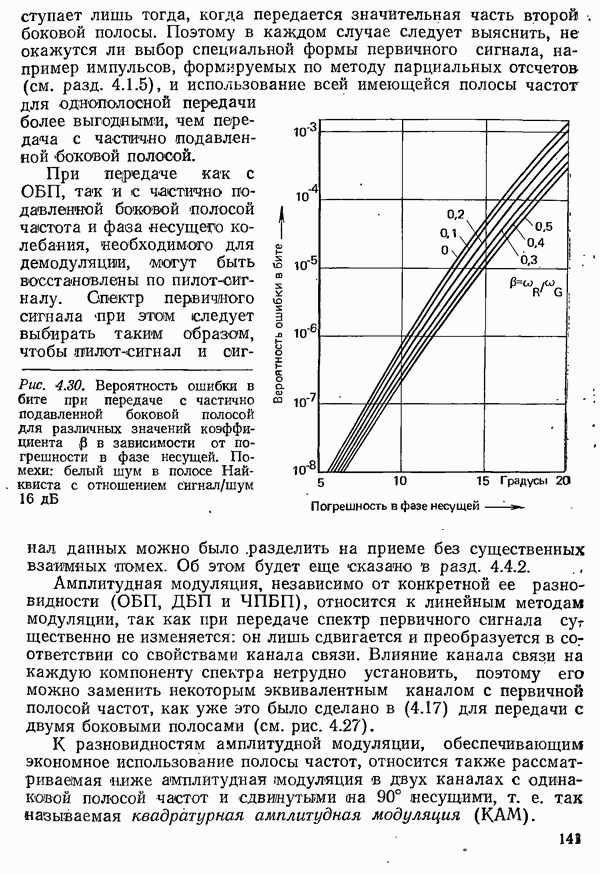
- 4.3.1.2. АМПЛИТУДНАЯ МОДУЛЯЦИЯ С ОДНОЙ БОКОВОЙ ПОЛОСОЙ И С ЧАСТИЧНО ПОДАВЛЕННОЙ БОКОВОЙ ПОЛОСОЙ
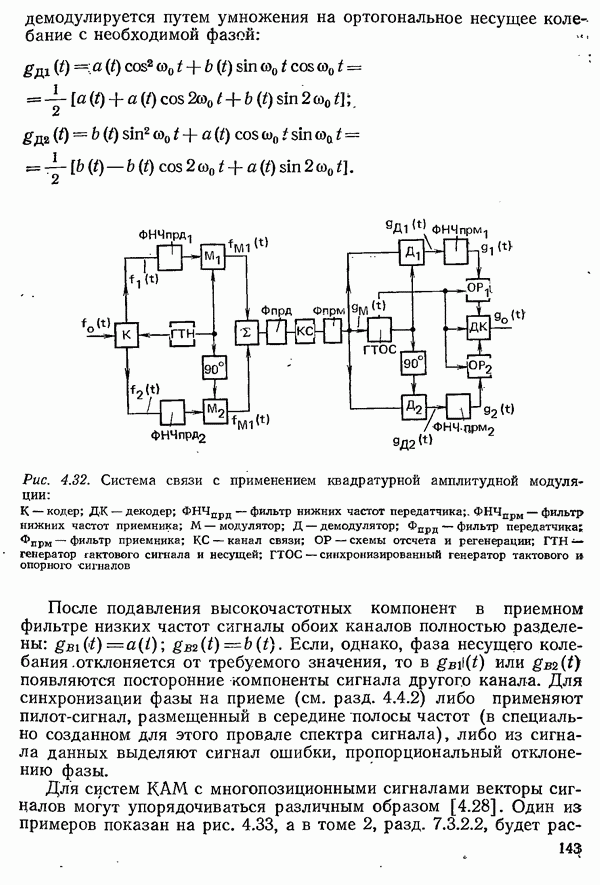
- 4.3.1.3. КВАДРАТУРНАЯ АМПЛИТУДНАЯ МОДУЛЯЦИЯ
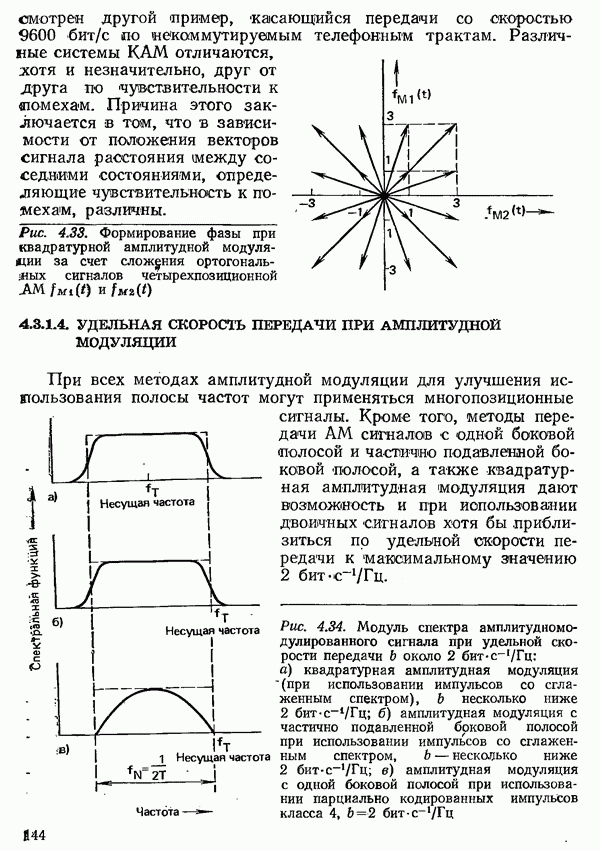
- 4.3.1.4. УДЕЛЬНАЯ СКОРОСТЬ ПЕРЕДАЧИ ПРИ АМПЛИТУДНОЙ МОДУЛЯЦИИ
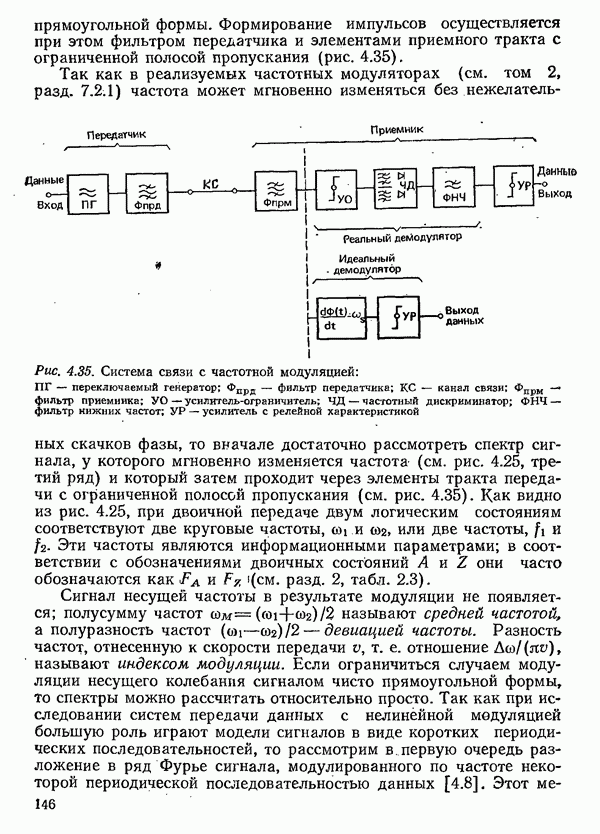
- 4.3.2. ЧАСТОТНАЯ МОДУЛЯЦИЯ
- 4.3.2.1. УДЕЛЬНАЯ СКОРОСТЬ ПЕРЕДАЧИ ПРИ ЧАСТОТНОЙ МОДУЛЯЦИИ
- 4.3.3. ФАЗОВАЯ МОДУЛЯЦИЯ
- 4.4. ВОССТАНОВЛЕНИЕ ТАКТОВ И НЕСУЩЕЙ
- 4.4.2. ВОССТАНОВЛЕНИЕ ЧАСТОТЫ И ФАЗЫ НЕСУЩЕЙ
- 4.5. ВЕРОЯТНОСТЬ ОШИБКИ ПРИ НАЛИЧИИ ПОМЕХ
- 4.5.1. ВЕРОЯТНОСТЬ ОШИБКИ ПРИ УЧЕТЕ ТОЛЬКО ШУМА В КАНАЛЕ СВЯЗИ
- 4.5.2. ВЕРОЯТНОСТЬ ОШИБКИ С УЧЕТОМ ЛИНЕЙНЫХ ИСКАЖЕНИЙ
- 4.5.3. ВЕРОЯТНОСТЬ ОШИБКИ С УЧЕТОМ ПРОЦЕССОВ МОДУЛЯЦИИ И ДЕМОДУЛЯЦИИ
- 5. Учет свойств реальных каналов связи при передаче данных
- 5.2. ВЛИЯНИЕ ХАРАКТЕРИСТИК КАНАЛОВ СВЯЗИ НА ПЕРЕДАЧУ ДАННЫХ
- 5.2.2. СДВИГИ ЧАСТОТЫ
- 5.2.3. ФАЗОВОЕ ДРОЖАНИЕ
- 5.2.4. ВЛИЯНИЕ РЕАЛЬНЫХ ПОМЕХ
- 5.3. КОРРЕКЦИЯ ПРИНИМАЕМОГО СИГНАЛА ДАННЫХ
- 5.3.1. КОРРЕКЦИЯ ПРИНИМАЕМОГО СИГНАЛА ДАННЫХ В ЧАСТОТНОЙ ОБЛАСТИ
- 5.3.1.1. КОМПРОМИССНЫЙ КОРРЕКТОР
- 5.3.1.2. НАСТРАИВАЕМЫЙ ЧАСТОТНЫЙ КОРРЕКТОР СИГНАЛОВ ДАННЫХ
- 5.3.2. КОРРЕКЦИЯ ПРИНИМАЕМОГО СИГНАЛА ДАННЫХ ВО ВРЕМЕННОЙ ОБЛАСТИ
- 5.3.2.2. КРИТЕРИИ НАСТРОЙКИ КОРРЕКТОРА ВО ВРЕМЕННОЙ ОБЛАСТИ
- 5.3.2.3. АВТОМАТИЧЕСКАЯ НАСТРОЙКА ТРАНСВЕРСАЛЬНОГО КОРРЕКТИРУЮЩЕГО ФИЛЬТРА
- 5.3.2.4. РЕКУРСИВНЫЙ КОРРЕКТОР
- 5.3.2.5. СХОДИМОСТЬ НАСТРОЙКИ КОРРЕКТОРА
- 5.3.2.6. КОРРЕКТОР ДЛЯ СПЕЦИАЛЬНЫХ МЕТОДОВ ПЕРЕДАЧИ
- 6. Основы коммутации данных
- 6.1.2. МЕТОДЫ КОММУТАЦИИ
- 6.1.3. СПОСОБЫ КОММУТАЦИИ КАНАЛОВ
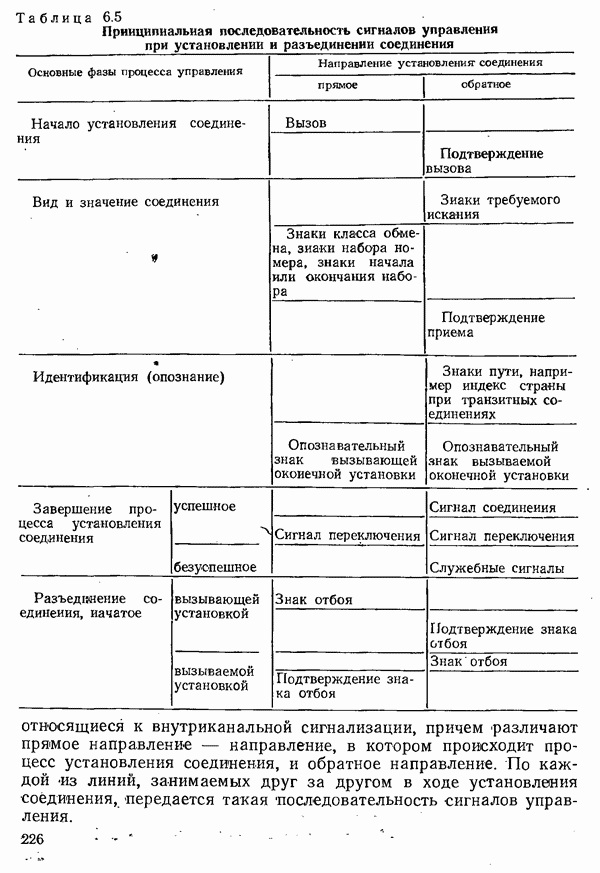
- 6.1.4. СИГНАЛИЗАЦИЯ
- 6.1.5. УПРАВЛЕНИЕ ПРОЦЕССАМИ СОЕДИНЕНИЯ И РАЗЪЕДИНЕНИЯ
- 6.1.6. ПОДРАЗДЕЛЕНИЕ ЦЕПЕЙ КОММУТАЦИИ КАНАЛОВ
- 6.1.7. ДОПОЛНИТЕЛЬНЫЕ ЗАДАЧИ КОММУТАЦИОННЫХ УСТРОЙСТВ
- 6.2. АНАЛИЗ СИСТЕМ КОММУТАЦИИ НА ОСНОВЕ ТЕОРИИ ТЕЛЕТРАФИКА
- 6.2.2. СИСТЕМЫ С ПОТЕРЯМИ
- 6.2.3. СИСТЕМЫ С ОЖИДАНИЕМ
- 6.2.4. ИЗМЕРЕНИЯ НАГРУЗКИ
- СПИСОК ЛИТЕРАТУРЫ