| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
§ 113. Движение тела, брошенного под углом к горизонту
Если начальная скорость брошенного тела направлена вверх под некоторым углом к горизонту, то в начальный момент тело имеет составляющие начальной скорости как в горизонтальном, так и в вертикальном направлениях (рис. 178).

Рис. 178.
Траектория тела, брошенного под углом ![]() к горизонту (в отсутствие
сопротивления воздуха)
к горизонту (в отсутствие
сопротивления воздуха)
Задача отличается от рассмотренной в предыдущем параграфе тем, что начальная скорость не равна нулю и для движения по вертикали. Для горизонтальной же составляющей все сказанное остается в силе.
Введем
координатные оси: ось ![]() , направленную по вертикали вверх, и
горизонтальную ось
, направленную по вертикали вверх, и
горизонтальную ось ![]() , расположенную в одной вертикальной
плоскости с начальной скоростью
, расположенную в одной вертикальной
плоскости с начальной скоростью ![]() . Проекция начальной скорости на ось
. Проекция начальной скорости на ось
![]() равна
равна ![]() , а на ось
, а на ось ![]() равна
равна ![]() (при показанном
на рис. 178 направление осей
(при показанном
на рис. 178 направление осей ![]() и
и ![]() обе проекции положительны).
Ускорение тела равно
обе проекции положительны).
Ускорение тела равно ![]() и, следовательно, все время
направлено по вертикали вниз. Поэтому проекция ускорения на ось
и, следовательно, все время
направлено по вертикали вниз. Поэтому проекция ускорения на ось ![]() равна —
равна — ![]() , а на ось
, а на ось ![]() — нулю.
— нулю.
Поскольку
составляющая ускорения в направлении оси ![]() отсутствует, проекция скорости на
ось
отсутствует, проекция скорости на
ось ![]() остается
постоянной и равной своему начальному значению
остается
постоянной и равной своему начальному значению ![]() . Следовательно, движение проекции
тела на ось
. Следовательно, движение проекции
тела на ось ![]() будет
равномерным. Движение проекции тела на ось
будет
равномерным. Движение проекции тела на ось ![]() происходит в обоих направлениях —
вверх и вниз — с одинаковым ускорением
происходит в обоих направлениях —
вверх и вниз — с одинаковым ускорением ![]() . Поэтому на прохождение пути вверх
от произвольной высоты
. Поэтому на прохождение пути вверх
от произвольной высоты ![]() до высоты подъема к затрачивается
такое же время
до высоты подъема к затрачивается
такое же время ![]() ,
как и на прохождение пути вниз от высоты
,
как и на прохождение пути вниз от высоты ![]() до
до ![]() . Отсюда следует, что симметричные
относительно вершины
. Отсюда следует, что симметричные
относительно вершины ![]() точки (например, точки
точки (например, точки ![]() и
и ![]() ) лежат на
одинаковой высоте. А это означает, что траектория симметрична относительно
точки
) лежат на
одинаковой высоте. А это означает, что траектория симметрична относительно
точки ![]() .
Но характер траектории тела после точки
.
Но характер траектории тела после точки ![]() мы уже выяснили в § 112. Это —
парабола, которую описывает тело, летящее с горизонтальной начальной скоростью.
Следовательно, все то, что мы говорили относительно траектории тела в
предыдущем параграфе, в равной мере относится и к рассматриваемому случаю,
только вместо «половины параболы»
мы уже выяснили в § 112. Это —
парабола, которую описывает тело, летящее с горизонтальной начальной скоростью.
Следовательно, все то, что мы говорили относительно траектории тела в
предыдущем параграфе, в равной мере относится и к рассматриваемому случаю,
только вместо «половины параболы» ![]() тело описывает «полную параболу»
тело описывает «полную параболу» ![]() , симметричную
относительно точки
, симметричную
относительно точки ![]() .
.
Проверить полученный результат можно также при помощи струи воды, вытекающей из наклонно поставленной трубки (рис, 179). Если позади струи поместить экран с заранее начерченными параболами, то можно увидеть, что струи воды также представляют собой параболы.

Рис. 179. Струя имеет форму параболы, тем более вытянутой, чем больше начальная скорость струи
Высота
подъема и расстояние, которое пройдет брошенное тело в горизонтальном
направлении до возвращения на ту высоту, с которой тело начало свое движение,
т. е. расстояние ![]() на рис. 178, зависят от модуля и
направления начальной скорости
на рис. 178, зависят от модуля и
направления начальной скорости ![]() . Прежде всего, при данном
направлении начальной скорости и высота и горизонтальное расстояние тем больше,
чем больше модуль начальной скорости (рис. 179).
. Прежде всего, при данном
направлении начальной скорости и высота и горизонтальное расстояние тем больше,
чем больше модуль начальной скорости (рис. 179).
Для
одинаковых по модулю начальных скоростей расстояние, которое проходит тело в
горизонтальном направлении до возвращения на первоначальную высоту, зависит от
направления начальной скорости (рис. 180). При увеличении угла между скоростью
и горизонтом это расстояние сначала увеличивается, при угле в ![]() достигает
наибольшего значения, а затем снова начинает уменьшаться.
достигает
наибольшего значения, а затем снова начинает уменьшаться.
Проведем
расчет движения тела, брошенного вверх под углом ![]() к горизонту с начальной скоростью
к горизонту с начальной скоростью ![]() (рис. 178).
Напомним, что проекция скорости тела на ось
(рис. 178).
Напомним, что проекция скорости тела на ось ![]() постоянна и равна
постоянна и равна ![]() . Поэтому
координата
. Поэтому
координата ![]() тела
в момент времени
тела
в момент времени ![]() равна
равна
![]() . (113.1)
. (113.1)

Рис. 180.
При увеличении наклона струи, вытекающей с данной скоростью, расстояние, на
которое она бьет, сначала увеличивается, достигает наибольшего значения при наклоне
в ![]() , а
затем уменьшается
, а
затем уменьшается
Движение
проекции тела на ось ![]() будет сначала равнозамедленным.
После того как тело достигнет вершины траектории
будет сначала равнозамедленным.
После того как тело достигнет вершины траектории ![]() , проекция скорости
, проекция скорости ![]() станет
отрицательной, т. е. одного знака с проекцией ускорения, вследствие чего
начнется равноускоренное движение тела вниз. Проекция скорости на ось
станет
отрицательной, т. е. одного знака с проекцией ускорения, вследствие чего
начнется равноускоренное движение тела вниз. Проекция скорости на ось ![]() изменяется со
временем по закону
изменяется со
временем по закону
![]() . (113.2)
. (113.2)
В
вершине траектории ![]() скорость тела имеет только
горизонтальную составляющую, а
скорость тела имеет только
горизонтальную составляющую, а ![]() обращается в нуль. Чтобы найти
момент времени
обращается в нуль. Чтобы найти
момент времени ![]() ,
в который тело достигнет вершины траектории, подставим в формулу (113.2)
,
в который тело достигнет вершины траектории, подставим в формулу (113.2) ![]() вместо
вместо ![]() и приравняем
получившееся выражение нулю:
и приравняем
получившееся выражение нулю:
![]() ; отсюда
; отсюда ![]() (113.3)
(113.3)
Определяемое
формулой (113.3) значение ![]() дает время, за которое брошенное
тело достигает вершины траектории. Если точка бросания и точка падения тела
лежат на одном уровне, то все время полета
дает время, за которое брошенное
тело достигает вершины траектории. Если точка бросания и точка падения тела
лежат на одном уровне, то все время полета ![]() будет равно
будет равно ![]() :
:
![]() (113.4)
(113.4)
Умножив
![]() на
время полета
на
время полета ![]() ,
найдем координату
,
найдем координату ![]() точки падения тела, т. е. дальность
полета:
точки падения тела, т. е. дальность
полета:
![]() . (113.5)
. (113.5)
Из
этой формулы видно, что дальность полета будет максимальной в случае, когда ![]() , т.е. при
, т.е. при ![]() (что уже
указывалось выше).
(что уже
указывалось выше).
Согласно
формулам (22.1) и (113.2) координата ![]() изменяется со временем по закону
изменяется со временем по закону
![]() (113.6)
(113.6)
Подставив
в эту формулу ![]() вместо
вместо
![]() найдем
координату
найдем
координату ![]() ,
отвечающую вершине траектории
,
отвечающую вершине траектории ![]() , т. е. высоту, подъема тела
, т. е. высоту, подъема тела ![]() :
:
 .
.
Приведя подобные члены, получим
![]() . (113.7)
. (113.7)
Высота
растет с увеличением ![]() и достигает наибольшего значения,
равного
и достигает наибольшего значения,
равного ![]() ,
при
,
при ![]() т.
е. при бросании тела вертикально вверх.
т.
е. при бросании тела вертикально вверх.
113.1. Камень, брошенный с земли вверх под углом к горизонту, падает обратно на землю на расстоянии 14 м. Найти горизонтальную и вертикальную составляющие начальной скорости камня, если весь полет продолжался 2 с. Найти наибольшую высоту подъема камня над землей. Сопротивлением воздуха пренебречь.
113.2. Пожарный направляет струю воды на крышу дома высоты 15 м. Над крышей дома струя поднимается на 5 м. На каком расстоянии от пожарного (считая по горизонтали) струя упадет на крышу, если она вырывается из шланга со скоростью 25 м/с? Сопротивлением воздуха пренебречь.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ОТ ИЗДАТЕЛЬСТВА
- ИЗ ПРЕДИСЛОВИЯ К ПЕРВОМУ ИЗДАНИЮ
- ВВЕДЕНИЕ
- Глава I. Кинематика
- § 1. Движение тел
- § 2. Кинематика. Относительность движения и покоя.
- § 3. Траектория движения
- § 4. Поступательное и вращательное движения тела
- § 5. Движение точки
- § 6. Описание движения точки
- § 7. Измерение длины
- § 8. Измерение промежутков времени
- § 9. Равномерное прямолинейное движение и его скорость
- § 10. Знак скорости при прямолинейном движении
- § 11. Единицы скорости
- § 12. Графики зависимости пути от времени
- § 13. Графики зависимости скорости от времени
- § 14. Неравномерное прямолинейное движение
- § 15. Мгновенная скорость
- § 16. Ускорение при прямолинейном движении
- § 17. Скорость прямолинейного равноускоренного движения
- § 18. Знак ускорения при прямолинейном движении
- § 19. Графики скорости при прямолинейном равноускоренном движении
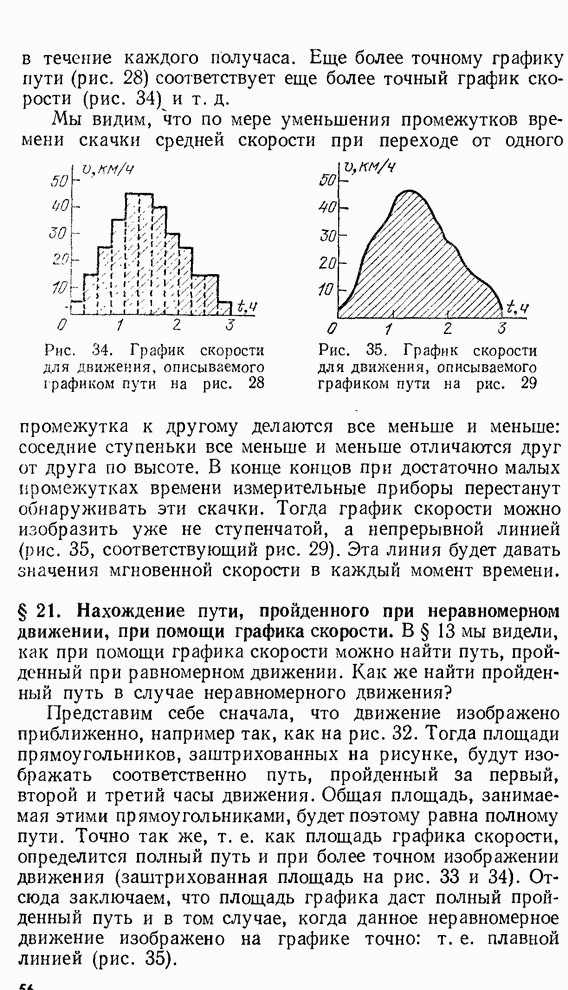
- § 20. Графики скорости при произвольном неравномерном движении
- § 21. Нахождение пути, пройденного при неравномерном движении, при помощи графика скорости
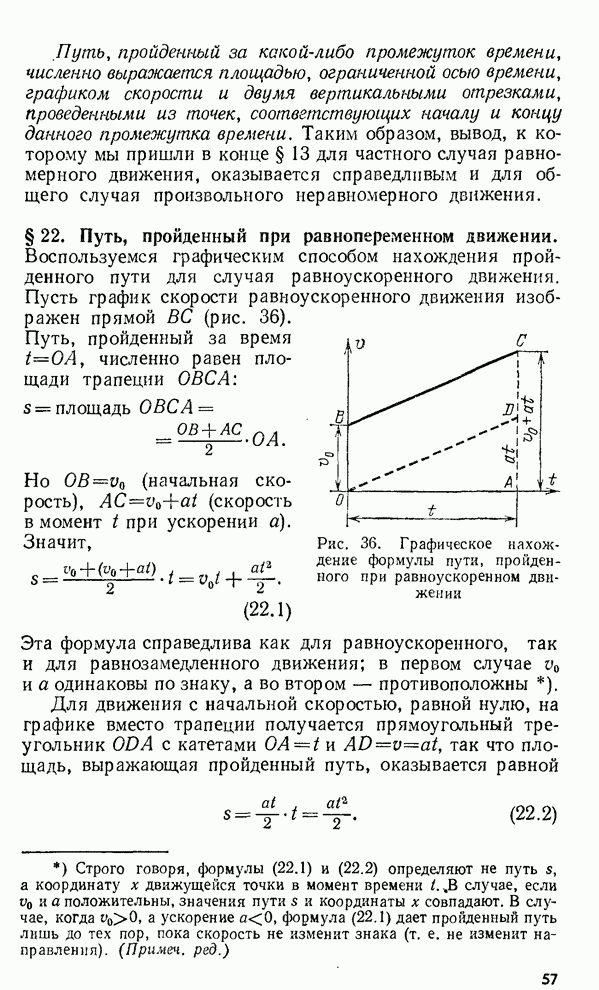
- § 22. Путь, пройденный при равнопеременном движении
- § 23. Векторы
- § 24. Разложение вектора на составляющие
- § 25. Криволинейное движение
- § 26. Скорость криволинейного движения
- § 27. Ускорение при криволинейном движении
- § 28. Движение относительно разных систем отсчета
- § 29. Кинематика космических движений
- Глава II. Динамика
- § 30. Задачи динамики
- § 31. Закон инерции
- § 32. Инерциальные системы отсчета
- § 33. Принцип относительности Галилея
- § 34. Силы
- § 35. Уравновешивающиеся силы. О покое тела и о движении по инерции
- § 36. Сила — вектор. Эталон силы
- § 37. Динамометры
- § 38. Точка приложения силы
- § 39. Равнодействующая сила
- § 40. Сложение сил, направленных по одной прямой
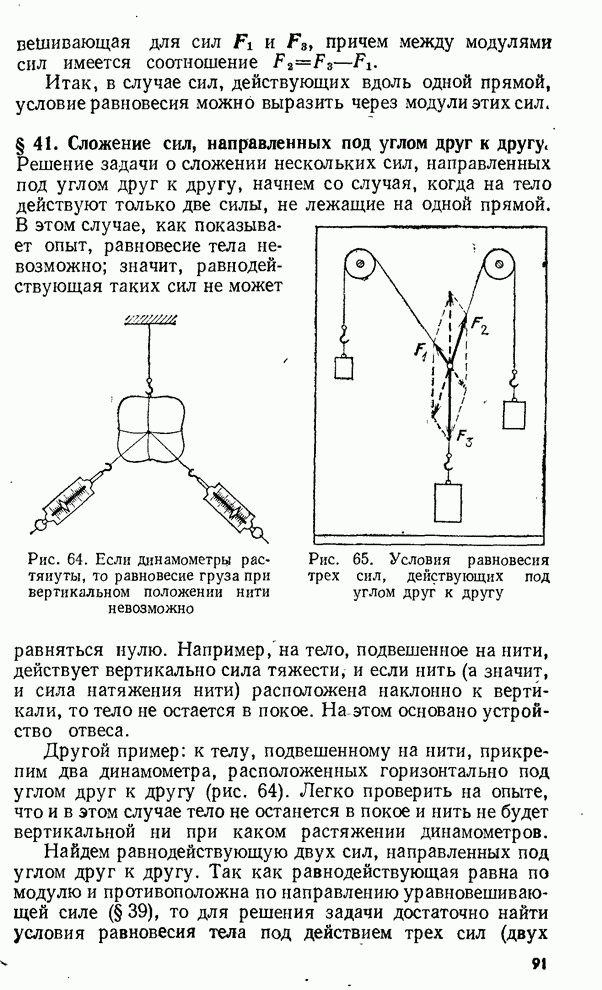
- § 41. Сложение сил, направленных под углом друг к другу
- § 42. Связь между силой и ускорением
- § 43. Масса тела
- § 44. Второй закон Ньютона
- § 45. Единицы силы и массы
- § 46. Системы единиц
- § 47. Третий закон Ньютона
- § 48. Примеры применения третьего закона Ньютона
- § 49. Импульс тела
- § 50. Система тел. Закон сохранения импульса
- § 51. Применения закона сохранения импульса
- § 52. Свободное падение тел
- § 53. Ускорение свободного падения
- § 54. Падение тела без начальной скорости и движение тела, брошенного вертикально вверх
- § 55. Вес тела
- § 56. Масса и вес
- § 57. Плотность вещества
- § 58. Возникновение деформаций
- § 59. Деформации в покоящихся телах, вызванные действием только сил, возникающих при соприкосновении
- § 60. Деформации в покоящихся телах, вызванные силой тяжести
- § 61. Деформации тела, испытывающего ускорение
- § 62. Исчезновение деформаций при падении тел
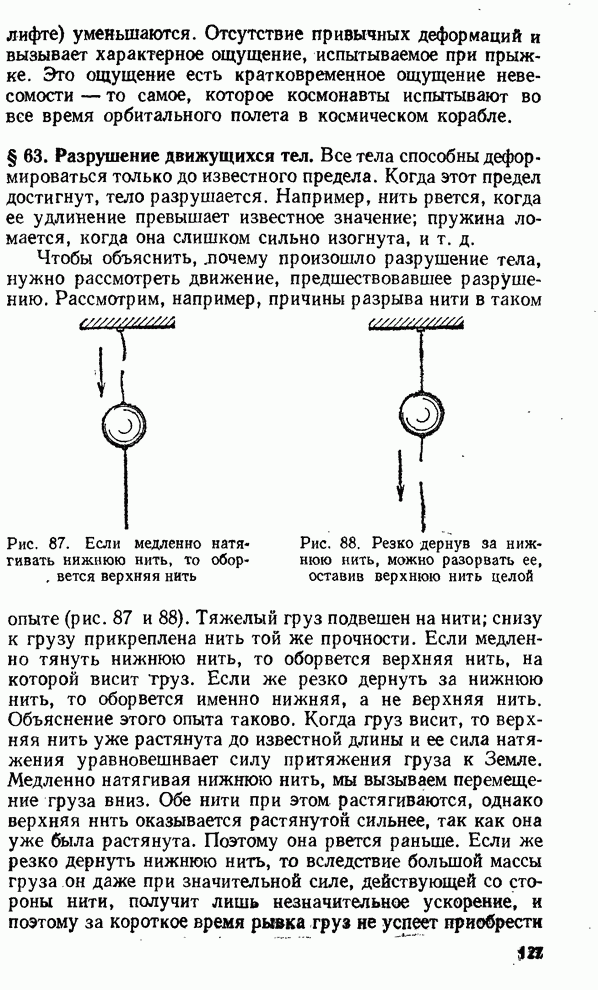
- § 63. Разрушение движущихся тел
- § 64. Силы трения
- § 65. Трение качения
- § 66. Роль сил трения
- § 67. Сопротивление среды
- § 68. Падение тел в воздухе
- Глава III. Статика
- § 69. Задачи статики
- § 70. Абсолютно твердое тело
- § 71. Перенос точки приложения силы, действующей на твердое тело
- § 72. Равновесие тела под действием трех сил
- § 73. Разложение сил на составляющие
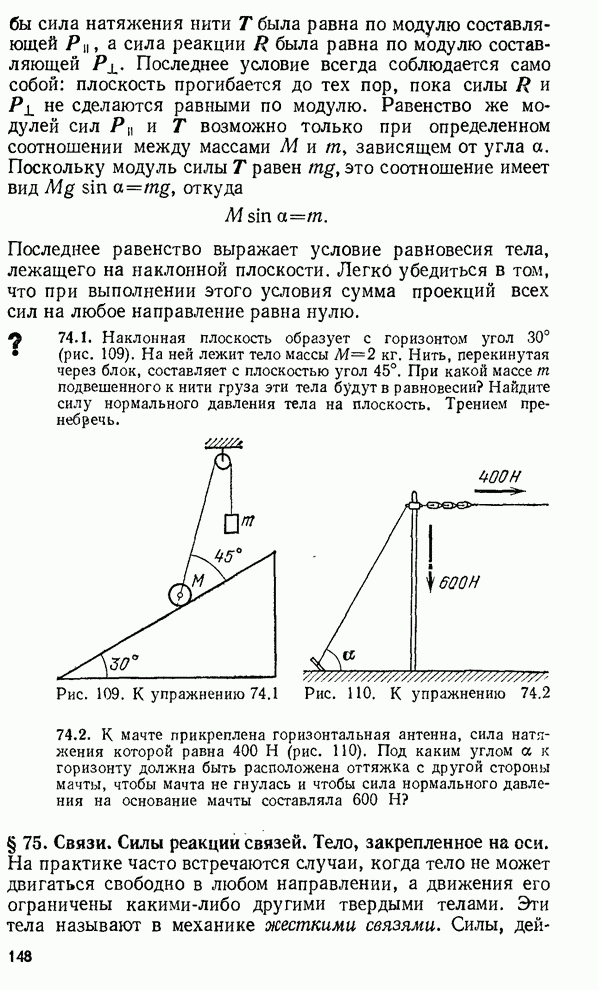
- § 74. Проекции сил. Общие условия равновесия
- § 75. Связи. Силы реакции связей. Тело, закрепленное на оси
- § 76. Равновесие тела, закрепленного на оси
- § 77. Момент силы
- § 78. Измерение момента силы
- § 79. Пара сил
- § 80. Сложение параллельных сил. Центр тяжести
- § 81. Определение центра тяжести тел
- § 82. Различные случаи равновесия тела под действием силы тяжести
- § 83. Условия устойчивого равновесия под действием силы тяжести
- § 84. Простые машины
- § 85. Клин и винт
- Глава IV. Работа и энергия
- § 86. «Золотое правило» механики
- § 87. Применения «золотого правила»
- § 88. Работа силы
- § 89. Работа при перемещении, перпендикулярном к направлению силы
- § 90. Работа силы, направленной под любым углом к перемещению
- § 91. Положительная и отрицательная работа
- § 92. Единица работы
- § 93. О движении по горизонтальной плоскости
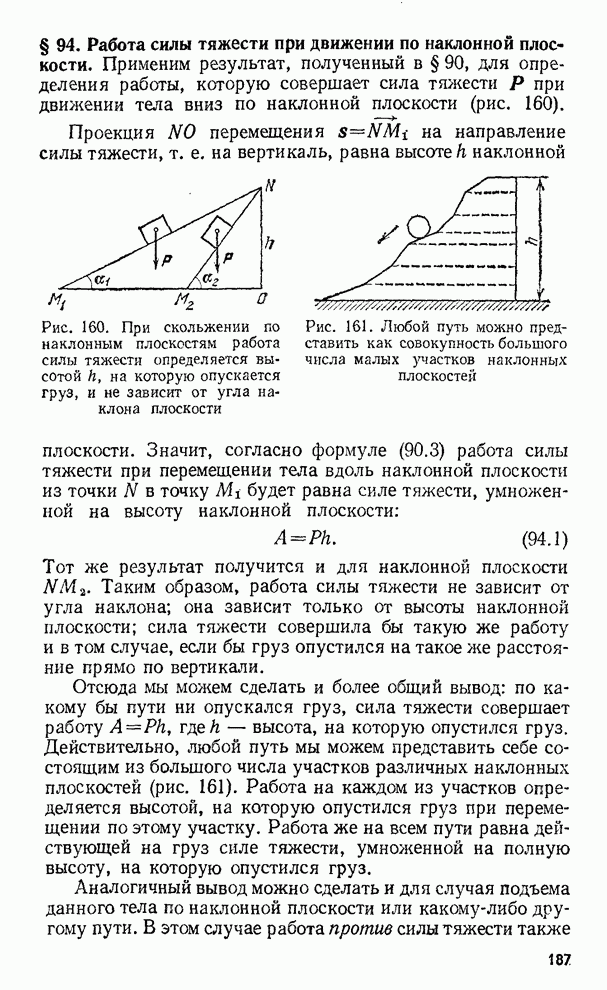
- § 94. Работа силы тяжести при движении по наклонной плоскости
- § 95. Принцип сохранения работы
- § 96. Энергия
- § 97. Потенциальная энергия
- § 98. Потенциальная энергия упругой деформации
- § 99. Кинетическая энергия
- § 100. Выражение кинетической энергии через массу и скорость тела
- § 101. Полная энергия тела
- § 102. Закон сохранения энергии
- § 103. Силы трения и закон сохранения механической энергии
- § 104. Превращение механической энергии во внутреннюю энергию
- § 105. Всеобщий характер закона сохранения энергии
- § 106. Мощность
- § 107. Расчет мощности механизмов
- § 108. Мощность, быстроходность и размеры механизма
- § 109. Коэффициент полезного действия механизмов
- Глава V. Криволинейное движение
- § 110. Возникновение криволинейного движения
- § 111. Ускорение при криволинейном движении
- § 112. Движение тела, брошенного в горизонтальном направлении
- § 113. Движение тела, брошенного под углом к горизонту
- § 114. Полет пуль и снарядов
- § 115. Угловая скорость
- § 116. Силы при равномерном движении по окружности
- § 117. Возникновение силы, действующей на тело, движущееся по окружности
- § 118. Разрыв маховиков
- § 119. Деформация тела, движущегося по окружности
- § 120. «Американские горки»
- § 121. Движение на закруглениях пути
- § 122. Движение подвешенного тела по окружности
- § 123. Движение планет
- § 124. Закон всемирного тяготения
- § 125. Искусственные спутники Земли
- Глава VI. Движение в неинерциальных системах отсчета и силы инерции
- § 126. Роль системы отсчета
- § 127. Движение относительно разных инерциальных систем отсчета
- § 128. Движение относительно инерциальной и неинерциальной систем отсчета
- § 129. Поступательно движущиеся неинерциальиые системы
- § 130. Силы инерции
- § 131. Эквивалентность сил инерции и сил тяготения
- § 132. Невесомость и перегрузки
- § 133. Является ли Земля инерциальиой системой отсчета?
- § 134. Вращающиеся системы отсчета
- § 135. Силы инерции при движении тела относительно вращающейся системы отсчета
- § 136. Доказательство вращения Земли
- § 137. Приливы
- Глава VII. Гидростатика
- § 138. Подвижность жидкости
- § 139. Силы давления
- § 140. Измерение сжимаемости жидкости
- § 141. «Несжимаемая» жидкость
- § 142. Силы давления в жидкости передаются во все стороны
- § 143. Направление сил давления
- § 144. Давление
- § 145. Мембранный манометр
- § 146. Независимость давления от ориентации площадки
- § 147. Единицы давления
- § 148. Определение сил давления по давлению
- § 149. Распределение давления внутри жидкости
- § 150. Закон Паскаля
- § 151. Гидравлический пресс
- § 152. Жидкость под действием силы тяжести
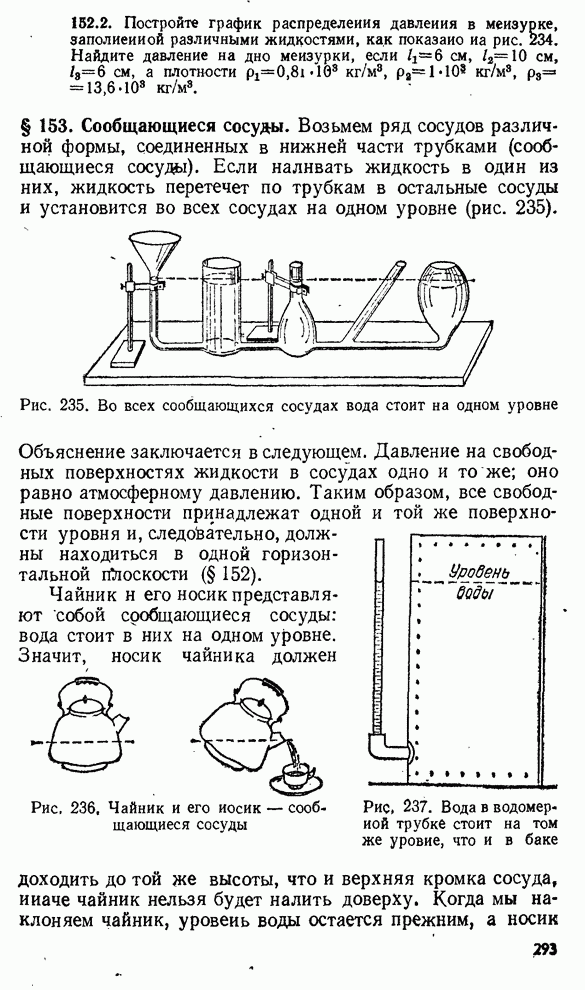
- § 153. Сообщающиеся сосуды
- § 154. Жидкостный манометр
- § 155. Устройство водопровода. Нагнетательный насос
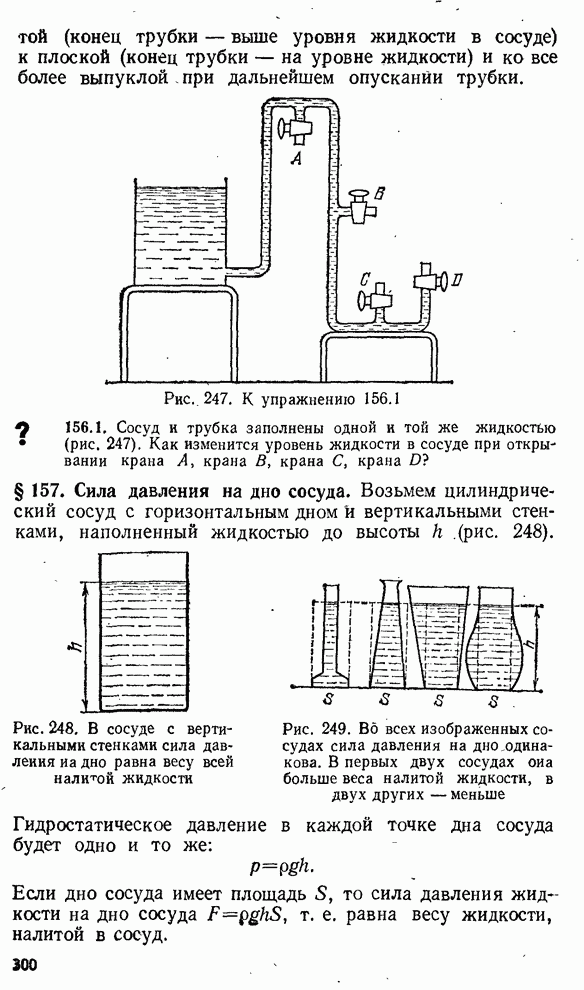
- § 156. Сифон
- § 157. Сила давления на дно сосуда
- § 158. Давление воды в морских глубинах
- § 159. Прочность подводной лодки
- § 160. Закон Архимеда
- § 161. Измерение плотности тел на основании закона Архимеда
- § 162. Плавание тел
- § 163. Плавание несплошных тел
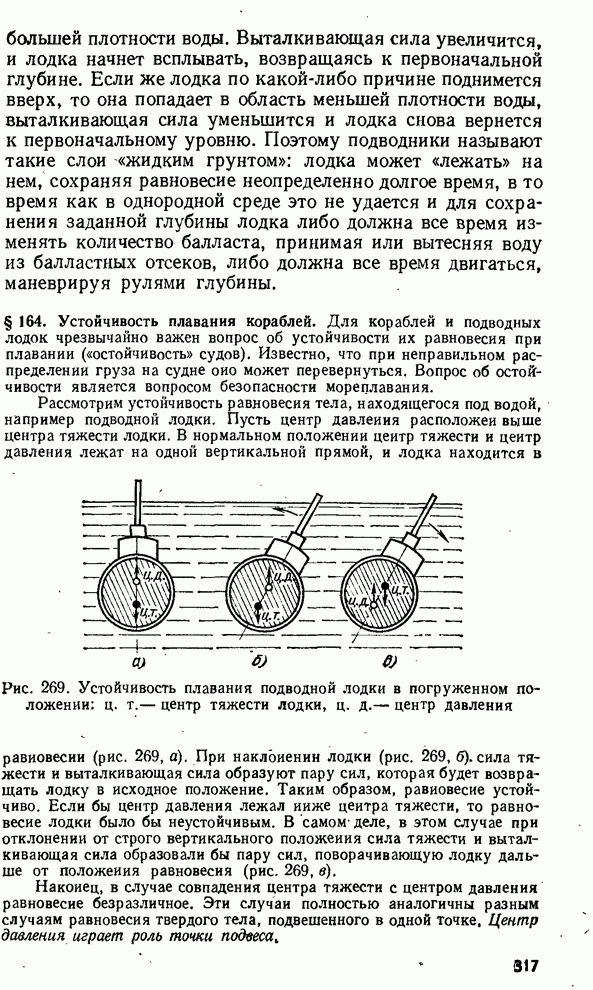
- § 164. Устойчивость плавания кораблей
- § 165. Всплывание пузырьков
- § 166. Тела, лежащие на дне сосуда
- Глава VIII. Аэростатика
- § 167. Механические свойства газов
- § 168. Атмосфера
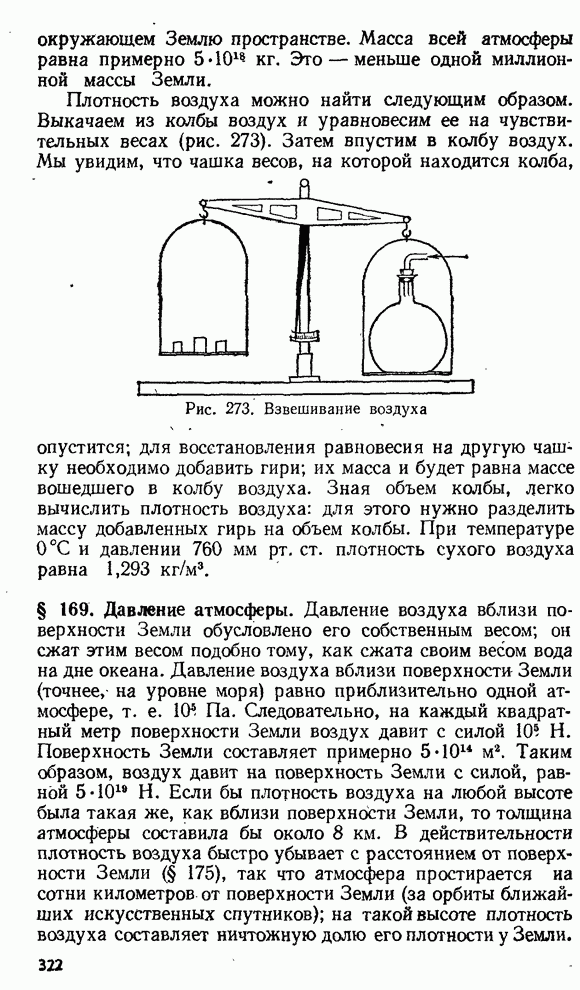
- § 169. Давление атмосферы
- § 170. Другие опыты, показывающие существование атмосферного давления
- § 171. Разрежающие насосы
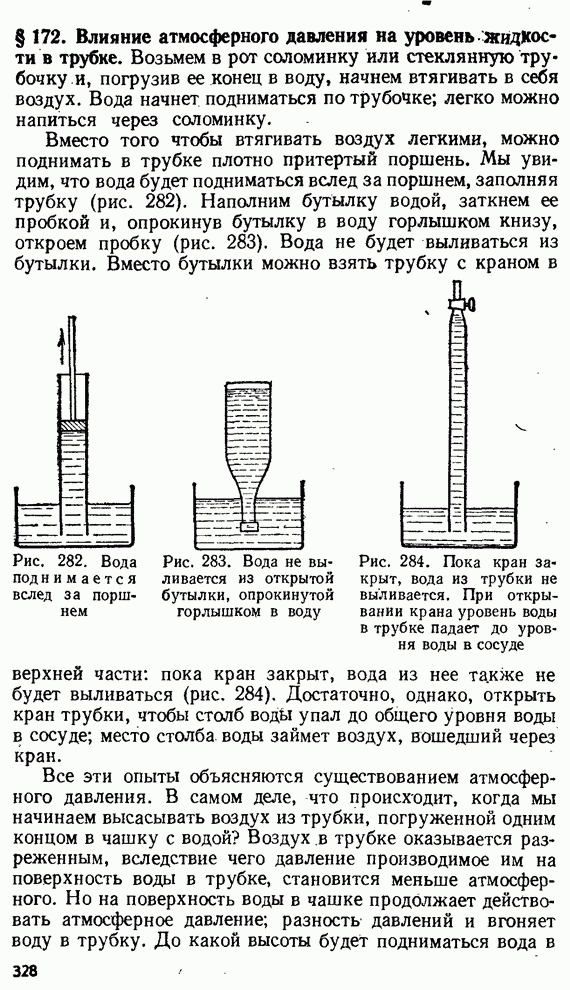
- § 172. Влияние атмосферного давления на уровень жидкости в трубке
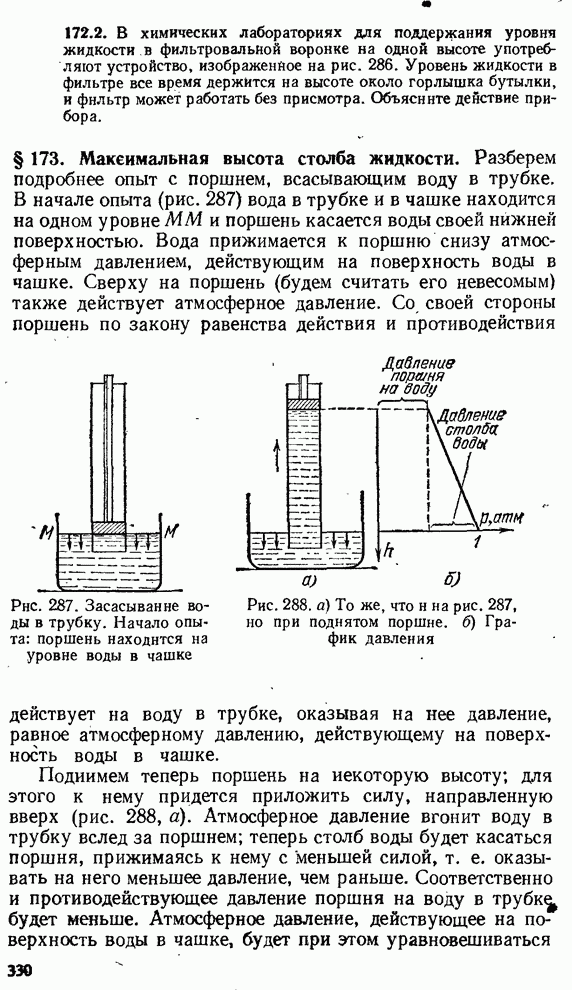
- § 173. Максимальная высота столба жидкости
- § 174. Опыт Торричелли. Ртутный барометр и барометр-анероид
- § 175. Распределение атмосферного давления по высоте
- § 176. Физиологическое действие пониженного давления воздуха
- § 177. Закон Архимеда для газов
- § 178. Воздушные шары и дирижабли
- § 179. Применение сжатого воздуха в технике
- Глава IX. Гидродинамика и аэродинамика
- § 180. Давление в движущейся жидкости
- § 181. Течение жидкости по трубам
- § 182. Закон Бернулли
- § 183. Жидкость в неинерциальных системах отсчета
- § 184. Реакция движущейся жидкости и ее использование
- § 185. Перемещение на воде
- § 186. Ракеты
- § 187. Реактивные двигатели
- § 188. Баллистические ракеты
- § 189. Взлет ракеты с Земли
- § 190. Сопротивление воздуха
- § 191. Эффект Магиуса и циркуляция
- § 192. Подъемная сила крыла и полет самолета
- § 193. Турбулентность в потоке жидкости или газа
- § 194. Ламинарное течение
- РАЗДЕЛ ВТОРОЙ. ТЕПЛОТА. МОЛЕКУЛЯРНАЯ ФИЗИКА
- Глава X. Тепловое расширение твердых и жидких тел
- § 195. Тепловое расширение твердых и жидких тел
- § 196. Термометры
- § 197. Формула линейного расширения
- § 198. Формула объемного расширения
- § 199. Связь между коэффициентами линейного и объемного расширения
- § 200. Измерение коэффициента объемного расширения жидкостей
- § 201. Особенности расширения воды
- Глава XI. Работа. Теплота. Закон сохранения энергии
- § 202. Изменения состояния тел
- § 203. Нагревание тел при совершении работы
- § 204. Изменение внутренней энергии тел при теплопередаче
- § 205. Единицы количества теплоты
- § 206. Зависимость внутренней энергии тела от его массы и вещества
- § 207. Теплоемкость тела
- § 208. Удельная теплоемкость
- § 209. Калориметр. Измерение теплоемкостей
- § 210. Закон сохранения энергии
- § 211. Невозможность «вечного двигателя»
- § 212. Различные виды процессов, при которых происходит передача теплоты
- Глава XII. Молекулярная теория
- § 213. Молекулы и атомы
- § 214. Размеры атомов и молекул
- § 215. Микромир
- § 216. Внутренняя энергия с точки зрения молекулярной теории
- § 217. Молекулярное движение
- § 218. Молекулярное движение в газах, жидкостях и твердых телах
- § 219. Броуновское движение
- § 220. Молекулярные силы
- Глава XIII. Свойства газов
- § 221. Давление газа
- § 222. Зависимость давления газа от температуры
- § 223. Формула, выражающая закон Шарля
- § 224. Закон Шарля с точки зрения молекулярной теории
- § 225. Изменение температуры газа при изменении его объема. Адиабатические и изотермические процессы
- § 226. Закон Бойля — Мариотта
- § 227. Формула, выражающая закон Бойля — Мариотта
- § 228. График, выражающий закон Бойля — Мариотта
- § 229. Зависимость между плотностью газа и его давлением
- § 230. Молекулярное толкование закона Бойля — Мариотта
- § 231. Изменение объема газа при изменении температуры
- § 232. Закон Гей-Люссака
- § 233. Графики, выражающие законы Шарля и Гей-Люссака
- § 234. Термодинамическая температура
- § 235. Газовый термометр
- § 236. Объем газа и термодинамическая температура
- § 237. Зависимость плотности газа от температуры
- § 238. Уравнение состояния газа
- § 239. Закон Дальтона
- § 240. Плотность газов
- § 241. Закон Авогадро
- § 242. Моль. Постоянная Авогадро
- § 243. Скорости молекул газа
- § 244. Об одном из способов измерения скоростей движения молекул газа (опыт Штерна)
- § 245. Удельные теплоемкости газов
- § 246. Молярные теплоемкости
- § 247. Закон Дюлонга и Пти
- Глава XIV. Свойства жидкостей
- § 248. Строение жидкостей
- § 249. Поверхностная энергия
- § 250. Поверхностное натяжение
- § 251. Жидкостные пленки
- § 252. Зависимость поверхностного натяжения от температуры
- § 253. Смачивание и несмачивание
- § 254. Расположение молекул у поверхности тел
- § 255. Значение кривизны свободной поверхности жидкости
- § 256. Капиллярные явления
- § 257. Высота поднятия жидкости в капиллярных трубках
- § 258. Адсорбция
- § 259. Флотация
- § 260. Растворение газов
- § 261. Взаимное растворение жидкостей
- § 262. Растворение твердых тел в жидкостях
- Глава XV. Свойства твердых тел. Переход тел из твердого состояния в жидкое
- § 263. Введение
- § 264. Кристаллические тела
- § 265. Аморфные тела
- § 266. Кристаллическая решетка
- § 267. Кристаллизация
- § 268. Плавление и отвердевание
- § 269. Удельная теплота плавления
- § 270. Переохлаждение
- § 271. Изменение плотности веществ при плавлении
- § 272. Полимеры
- § 273. Сплавы
- § 274. Затвердевание растворов
- § 275. Охлаждающие смеси
- § 276. Изменения свойств твердого тела
- Глава XVI. Упругость и прочность
- § 277. Введение
- § 278. Упругие и пластические деформации
- § 279. Закон Гука
- § 280. Растяжение и сжатие
- § 281. Сдвиг
- § 282. Кручение
- § 283. Изгиб
- § 284. Прочность
- § 285. Твердость
- § 286. Что происходит при деформации тел
- § 287. Изменение энергии при деформации тел
- Глава XVII. Свойства паров
- § 288. Введение
- § 289. Пар насыщенный и ненасыщенный
- § 290. Что происходит при изменении объема жидкости и насыщенного пара
- § 291. Закон Дальтона для пара
- § 292. Молекулярная картина испарения
- § 293. Зависимость давления насыщенного пара от температуры
- § 294. Кипение
- § 295. Удельная теплота парообразования
- § 296. Охлаждение при испарении
- § 297. Изменение внутренней энергии при переходе вещества из жидкого состояния в парообразное
- § 298. Испарение при кривых поверхностях жидкости
- § 299. Перегревание жидкости
- § 300. Пересыщение паров
- § 301. Насыщение пара при возгонке
- § 302. Превращение газа в жидкость
- § 303. Критическая температура
- § 304. Сжижение газов в технике
- § 305. Вакуумная техника
- § 306. Водяной пар в атмосфере
- Глава XVIII. Физика атмосферы
- § 307. Атмосфера
- § 308. Тепловой баланс Земли
- § 309. Адиабатические процессы в атмосфере
- § 310. Облака
- § 311. Искусственные осадки
- § 312. Ветер
- § 313. Предсказание погоды
- Глава XIX. Тепловые машины
- § 314. Условия, необходимые для работы тепловых двигателей
- § 315. Паросиловая станция
- § 316. Паровой котел
- § 317. Паровая турбина
- § 318. Поршневая паровая машина
- § 319. Конденсатор
- § 320. Коэффициент полезного действия теплового двигателя
- § 321. Коэффициент полезного действия паросиловой станции
- § 322. Бензиновый двигатель внутреннего сгорания
- § 323. Коэффициент полезного действия двигателя внутреннего сгорания
- § 324. Двигатель Дизеля
- § 325. Реактивные двигатели
- § 326. Передача теплоты от холодного тела к горячему
- Ответы и решения к упражнениям
- Предметный указатель