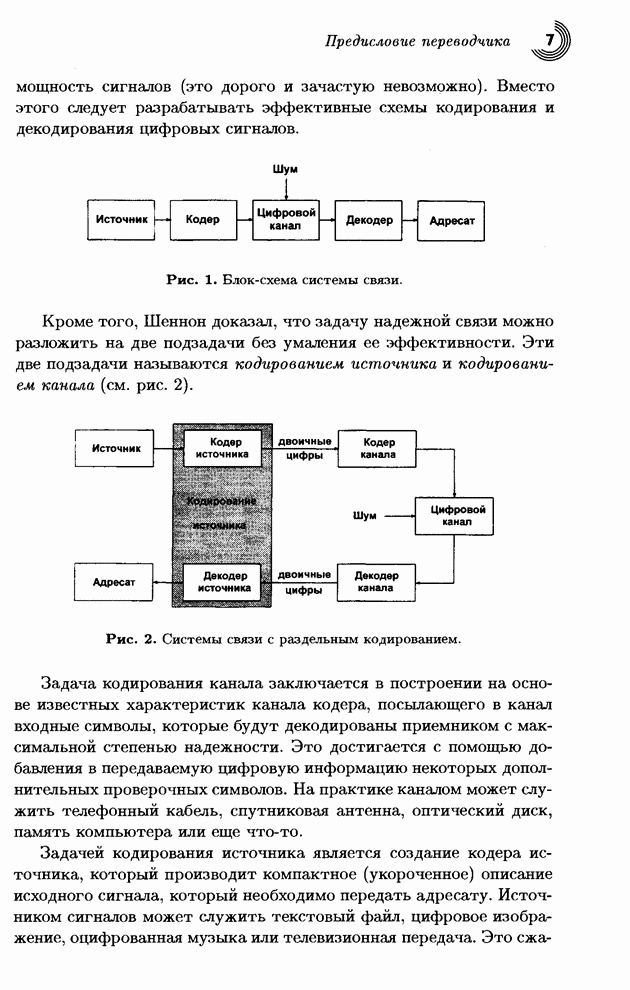
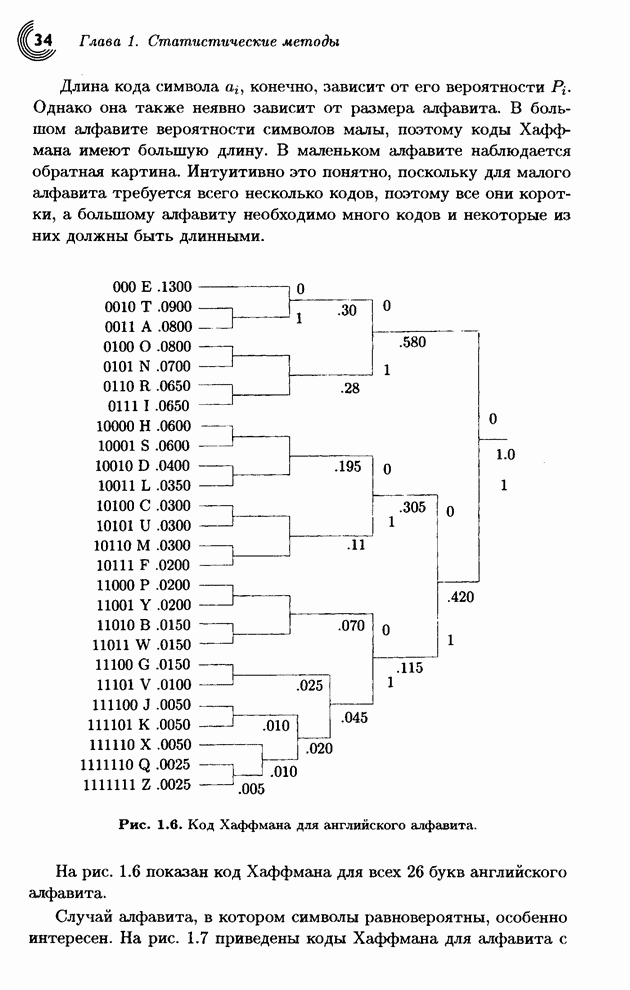
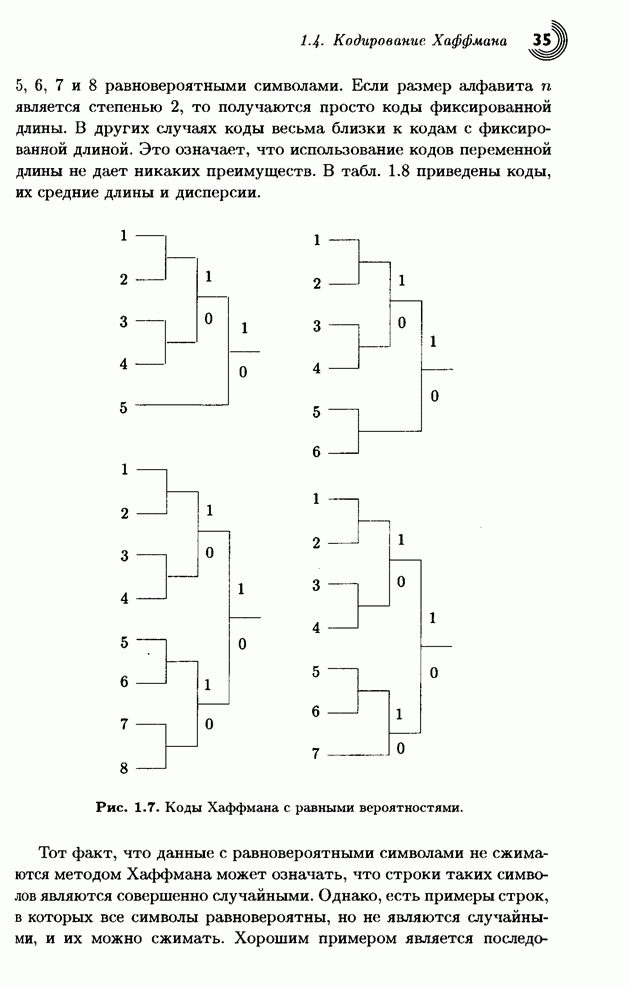
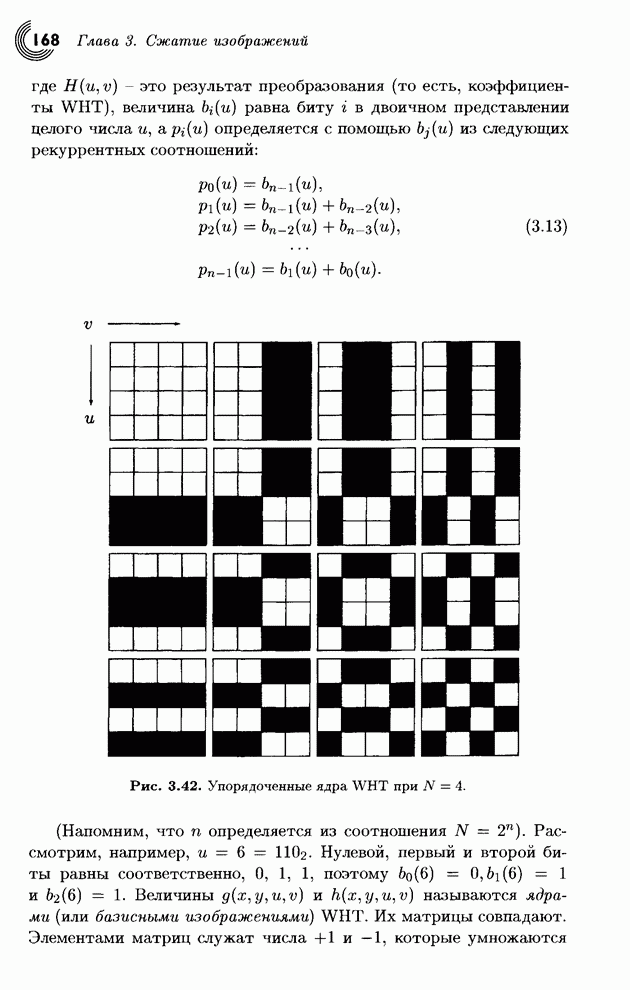
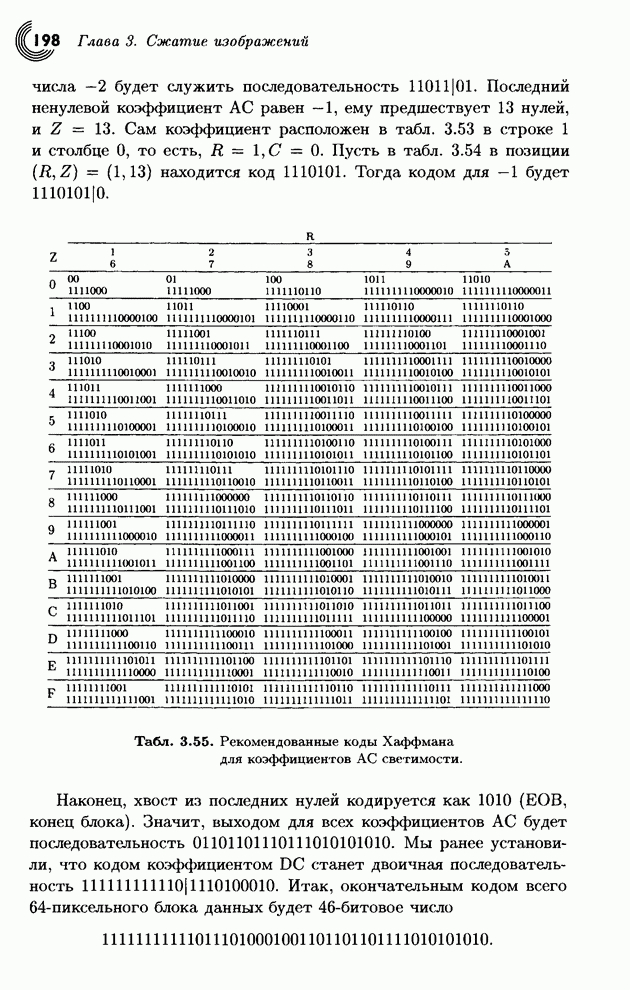
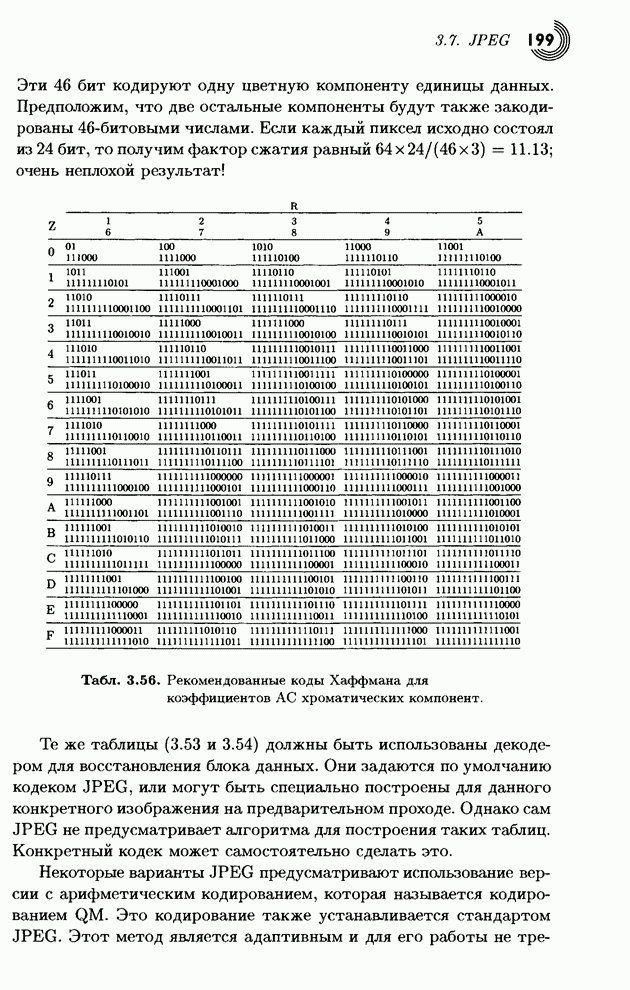
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
1.5.2. Модификация дерева
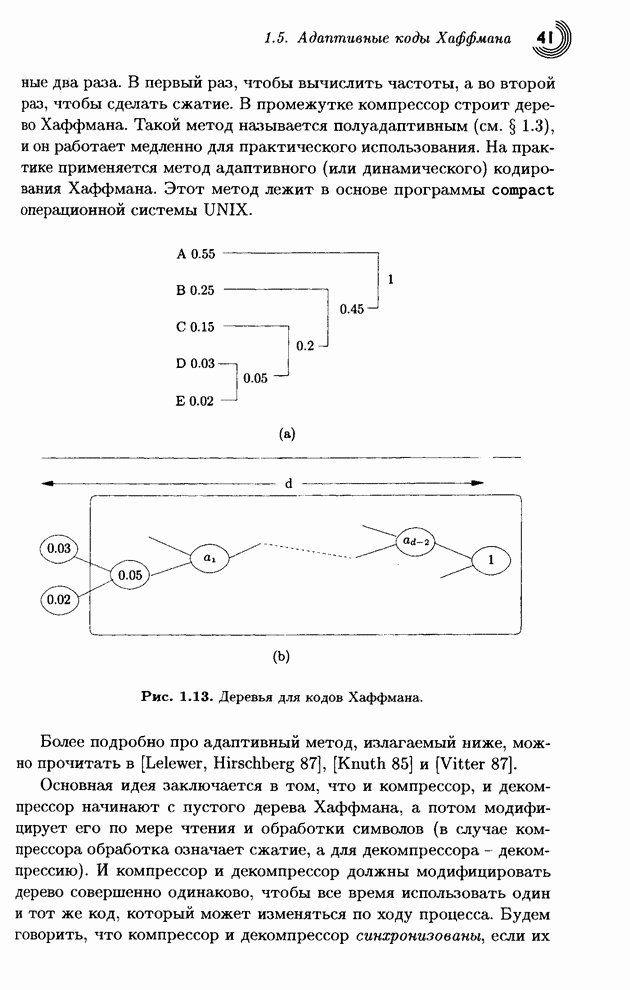
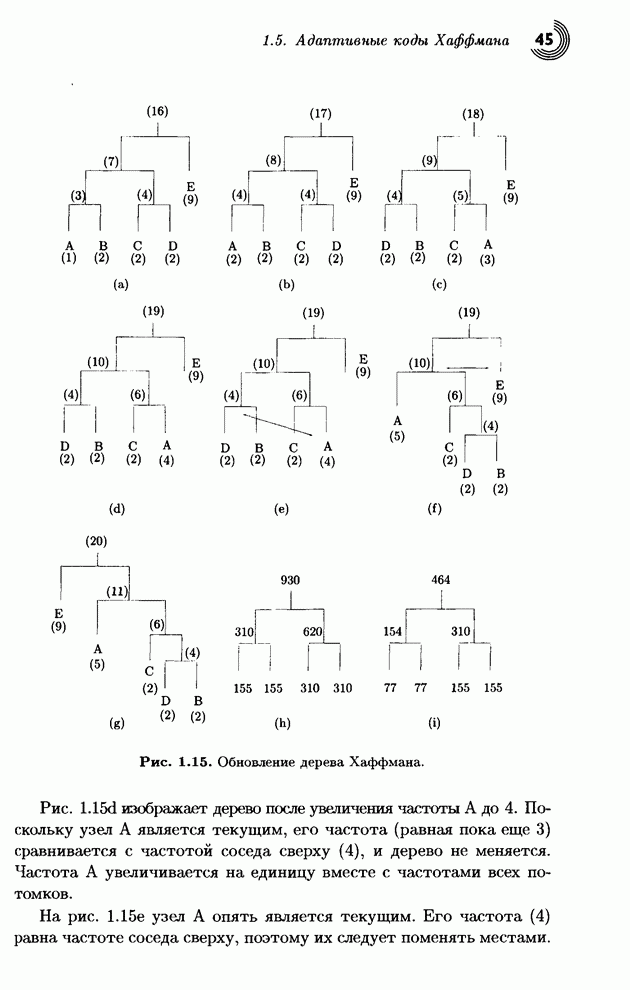
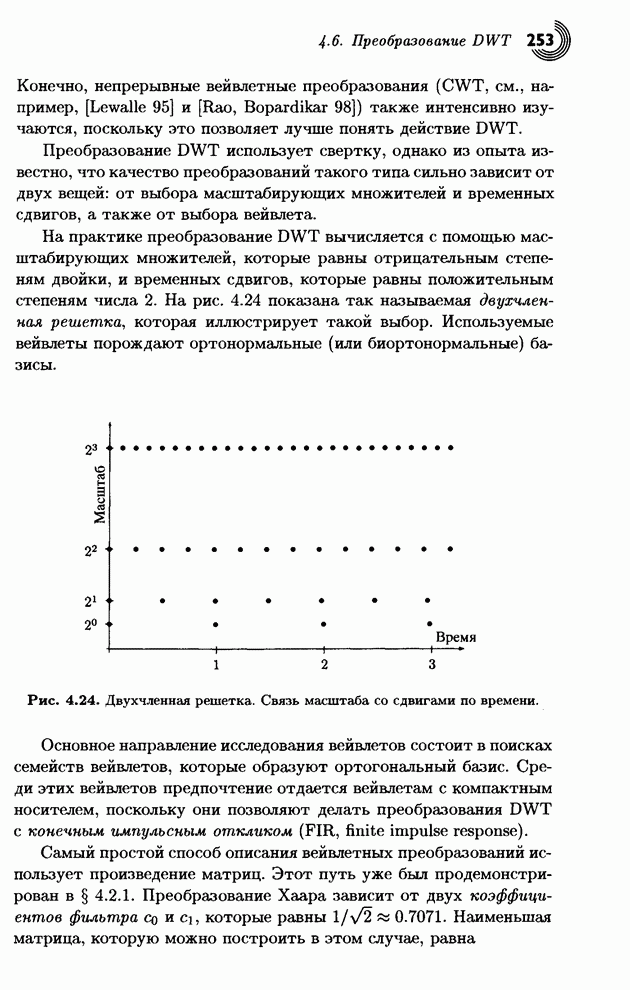
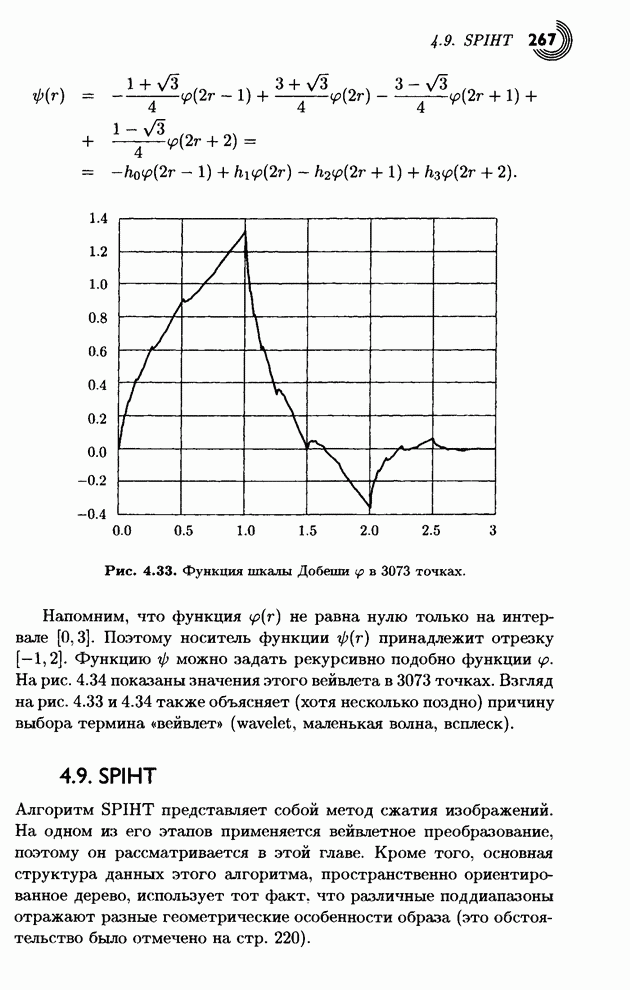
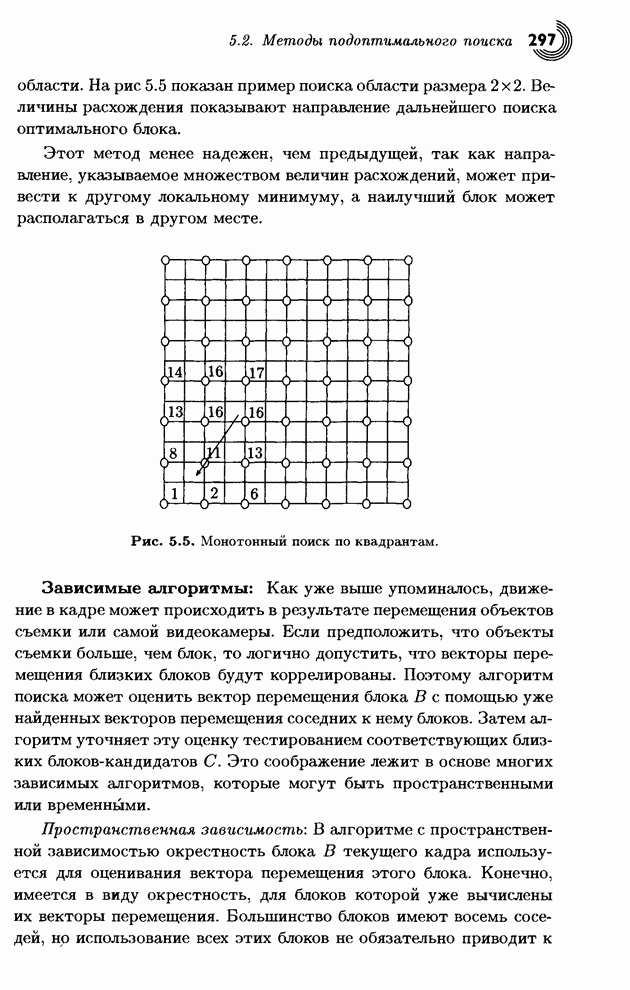
Основная идея заключается в проверке дерева при появлении каждого нового входного символа. Если дерево не является деревом Хаффмана, его следует подправить. Рис. 1.15 дает представление о том, как это делается. Дерево на рис. 1.15а содержит пять символов А, В, С, D и Е. Для всех символов указаны их текущие частоты (в круглых скобках). Свойство Хаффмана означает, что при изучении дерева по всем уровням слева направо и снизу вверх (от листьев к корню) частоты будут упорядочены по возрастанию (неубыванию). Таким образом, нижний левый узел (А) имеет наименьшую частоту, а верхний правый (корень) имеет наибольшую частоту. Это свойство принято называть свойством соперничества.

Рис. 1.15. Обновление дерева Хаффмана.
Причина этого свойства заключается в том, что символы с большими частотами должны иметь более короткие коды и, следовательно, находиться на дереве на более высоком уровне. Требование для частот быть упорядоченными на одном уровне устанавливается для определенности. В принципе, без него можно обойтись, но оно упрощает процесс построения дерева.
Приведем последовательность
операций при модификации дерева. Цикл начинается в текущем узле
(соответствующем новому входному символу). Этот узел будет листом, который мы
обозначим ![]() ,
а его частота пусть будет
,
а его частота пусть будет ![]() . На каждой следующей итерации цикла
требуется сделать три действия:
. На каждой следующей итерации цикла
требуется сделать три действия:
1.
Сравнить ![]() с его ближайшими соседями на
дереве (справа и сверху). Если непосредственный сосед имеет частоту
с его ближайшими соседями на
дереве (справа и сверху). Если непосредственный сосед имеет частоту ![]() или выше, то узлы остаются
упорядоченными и ничего делать не надо. В противном случае, некоторый сосед
имеет такую же или меньшую частоту, чем
или выше, то узлы остаются
упорядоченными и ничего делать не надо. В противном случае, некоторый сосед
имеет такую же или меньшую частоту, чем ![]() .
В этом случае следует поменять местами
.
В этом случае следует поменять местами ![]() и
последний узел в этой группе (за исключением того, что
и
последний узел в этой группе (за исключением того, что ![]() не надо менять с его родителем);
не надо менять с его родителем);
2.
Увеличить частоту ![]() с
с ![]() до
до
![]() . Увеличить на единицу частоту
всех его родителей;
. Увеличить на единицу частоту
всех его родителей;
3.
Если ![]() является корнем, то цикл
останавливается; в противном случае он повторяется для узла, являющегося
родителем
является корнем, то цикл
останавливается; в противном случае он повторяется для узла, являющегося
родителем ![]() .
.
На рис. 1.15b показано дерево после увеличения частоты узла А с 1 до 2. Легко проследить, как описанные выше три действия влияют на увеличение частоты всех предков А. Места узлов не меняются в этом простом случае, так как частота узла А не превысила частоту его ближайшего соседа справа В.
На рис. 1.15с показано, что произойдет при следующем увеличении частоты А с 2 до 3. Три узла, следующие за А, а именно, В, С и D, имели частоту 2, поэтому А переставлен с D. После чего частоты всех предков А увеличены на 1, и каждый сравнен со своими соседями, но больше на дереве никого переставлять не надо.
Рис. 1.15d изображает дерево после увеличения частоты А до 4. Поскольку узел А является текущим, его частота (равная пока еще 3) сравнивается с частотой соседа сверху (4), и дерево не меняется. Частота А увеличивается на единицу вместе с частотами всех потомков.
На рис. 1.15е узел А опять является текущим. Его частота (4) равна частоте соседа сверху, поэтому их следует поменять местами.
Это сделано на рис. l.15f, где частота А уже равна 5. Следующий шаг проверяет родителя А с частотой 10. Его следует переставить с его соседом справа Е, у которого частота 9. В итоге получается конечное дерево, изображенное на рис. 1.15g.
Тот, кто хочет отведать плод,
должен влезть на дерево.
- Томас Фуллер
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие переводчика
- Предисловие автора
- Введение
- Глава 1. Статистические методы
- 1.1. Энтропия
- 1.2. Коды переменной длины
- 1.3. Декодирование
- 1.4. Кодирование Хаффмана
- 1.4.1. Декодирование Хаффмана
- 1.4.2. Средняя длина кода
- 1.5. Адаптивные коды Хаффмана
- 1.5.1. Несжатые коды
- 1.5.2. Модификация дерева
- 1.5.3. Переполнение счетчика
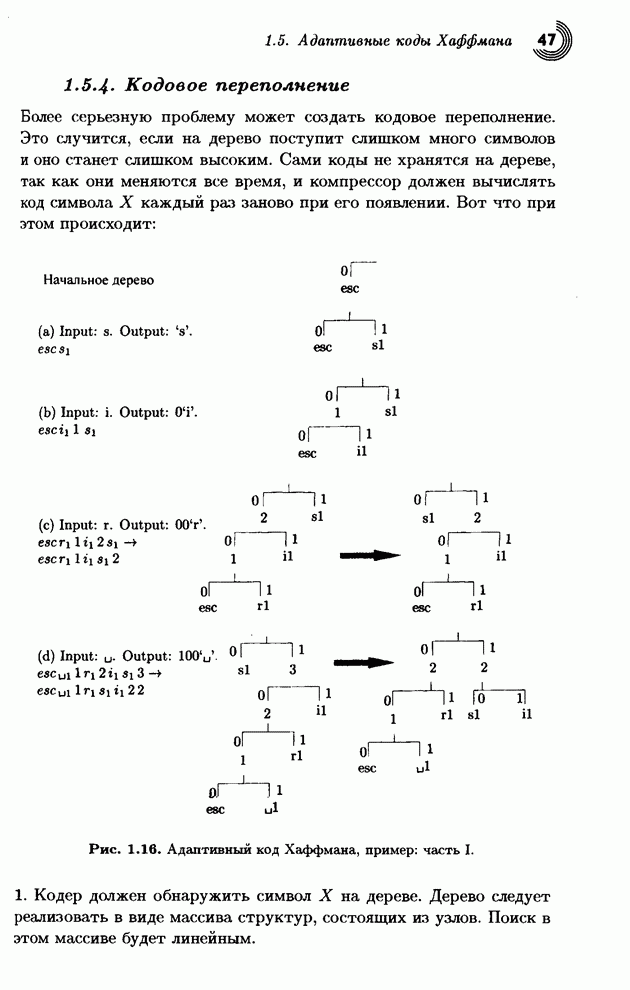
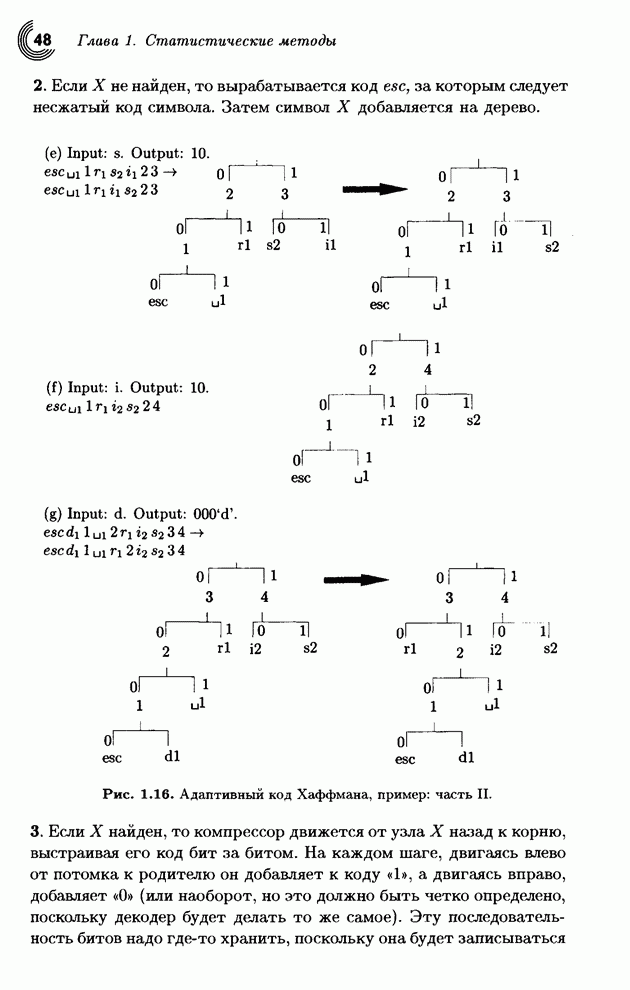
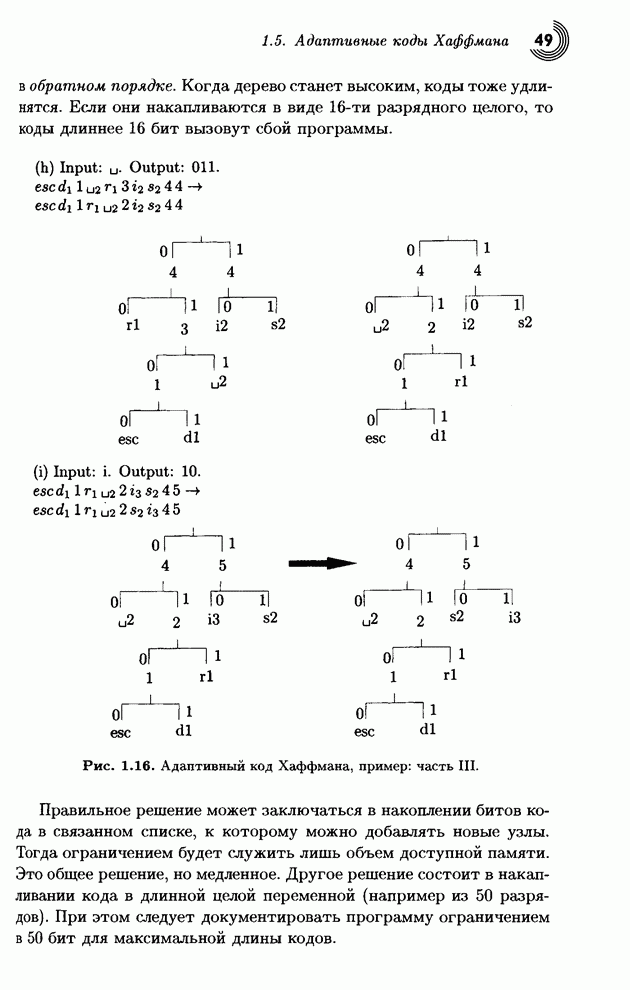
- 1.5.4. Кодовое переполнение
- 1.5.5. Вариант алгоритма
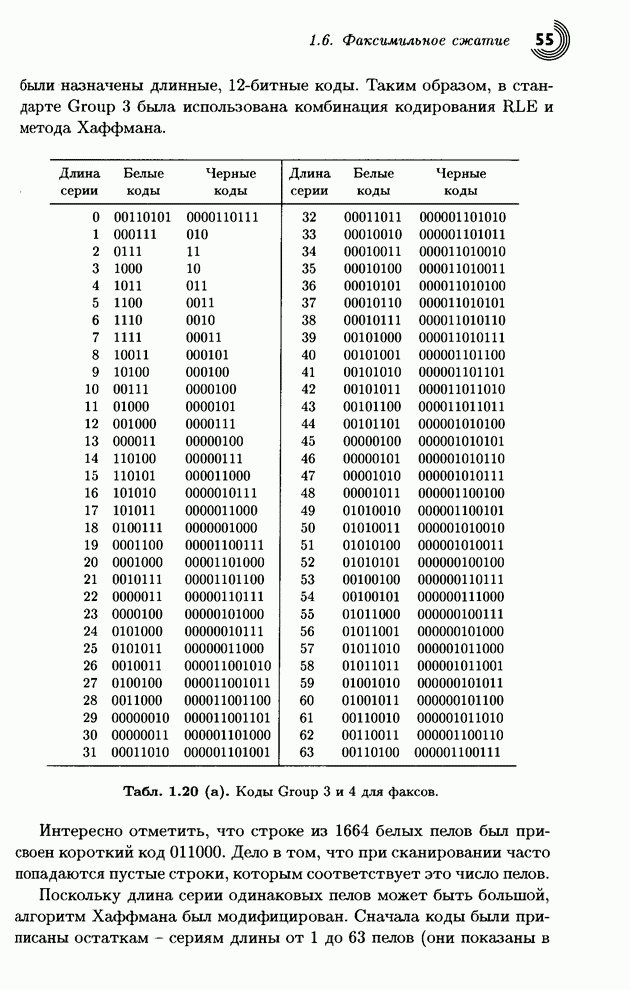
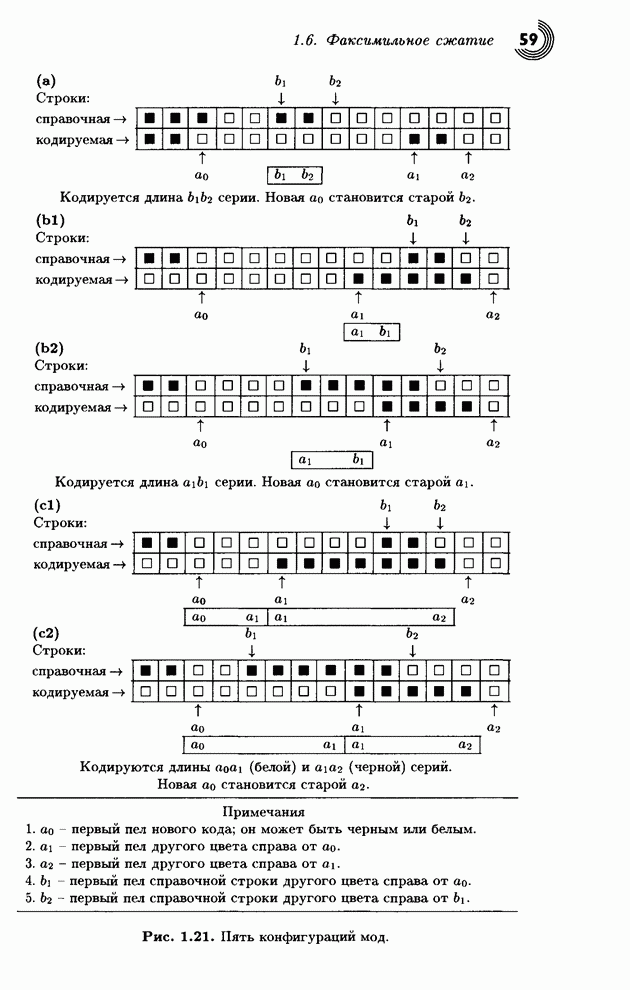
- 1.6. Факсимильное сжатие
- 1.6.1. Одномерное кодирование
- 1.6.2. Двумерное кодирование
- 1.7. Арифметическое кодирование
- 1.7.1. Детали реализации метода
- 1.7.2. Потеря значащих цифр
- 1.7.3. Заключительные замечания
- 1.8. Адаптивное арифметическое кодирование
- ГЛАВА 2 СЛОВАРНЫЕ МЕТОДЫ
- 2.1. LZ77 (скользящее окно)
- 2.1.1. Циклическая очередь
- 2.2. LZSS
- 2.2.1. Недостатки
- 2.3. LZ78
- 2.4. LZW
- 2.4.1. Декодирование LZW
- 2.4.2. Структура словаря LZW
- 2.4.3. LZW в практических приложениях
- 2.5. Заключение
- ГЛАВА 3 СЖАТИЕ ИЗОБРАЖЕНИЙ
- 3.1. Введение
- 3.2. Типы изображений
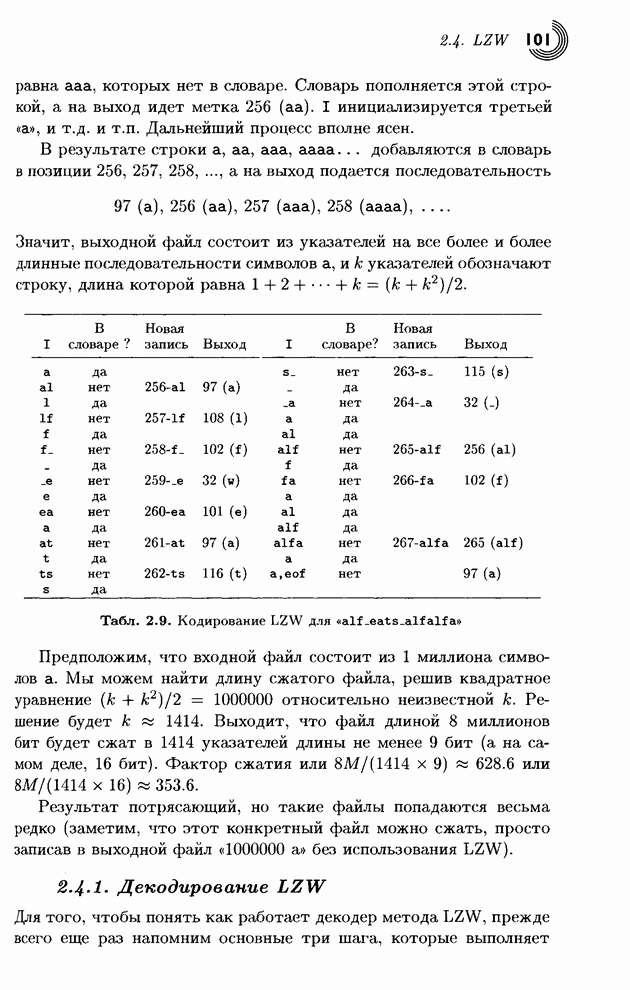
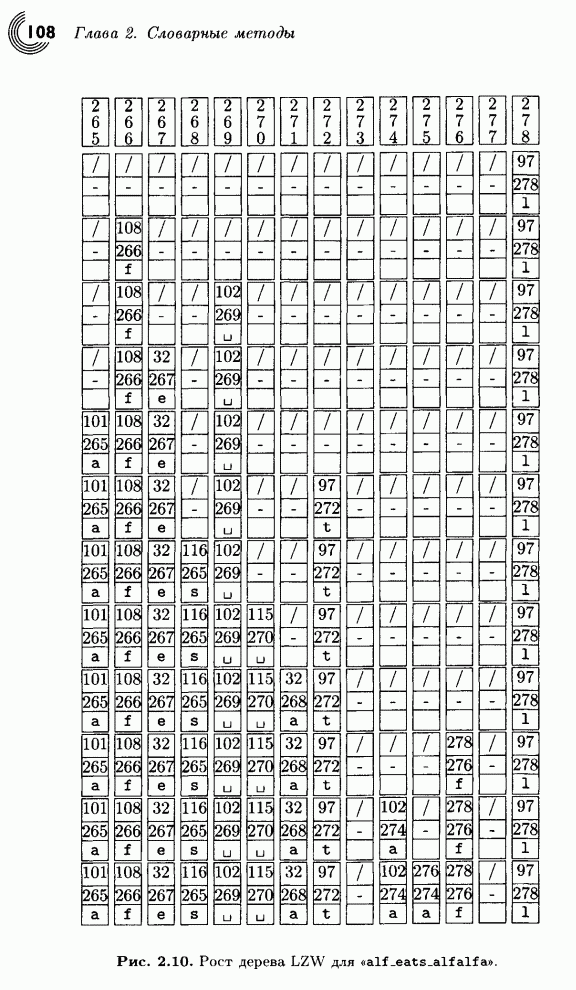
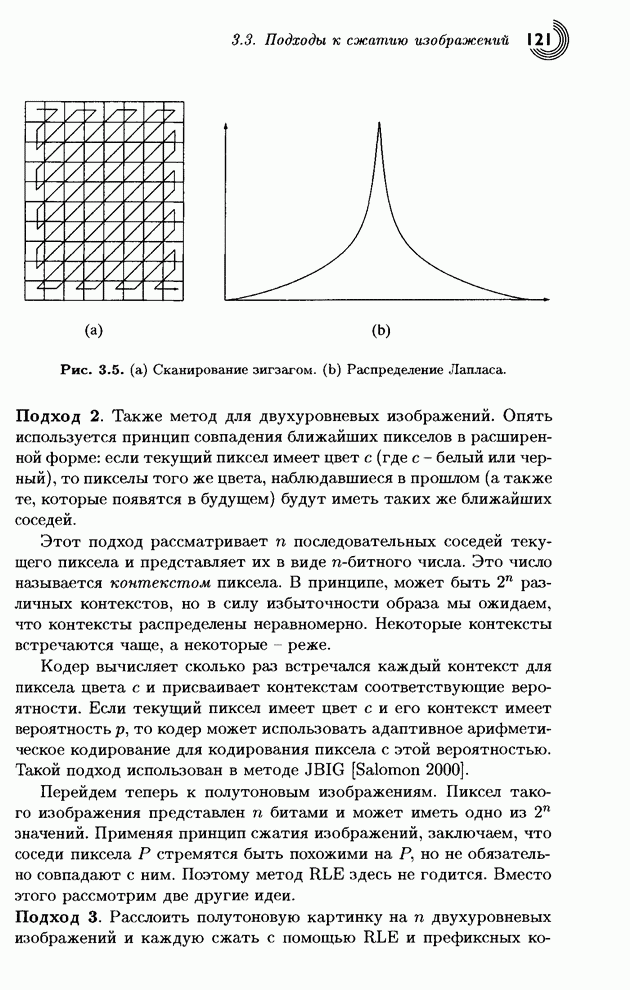
- 3.3. Подходы к сжатию изображений
- 3.3.1. Коды Грея
- 3.3.2. Метрики ошибок
- 3.4. Интуитивные методы
- 3.4.1. Подвыборка
- 3.4.2. Квантование
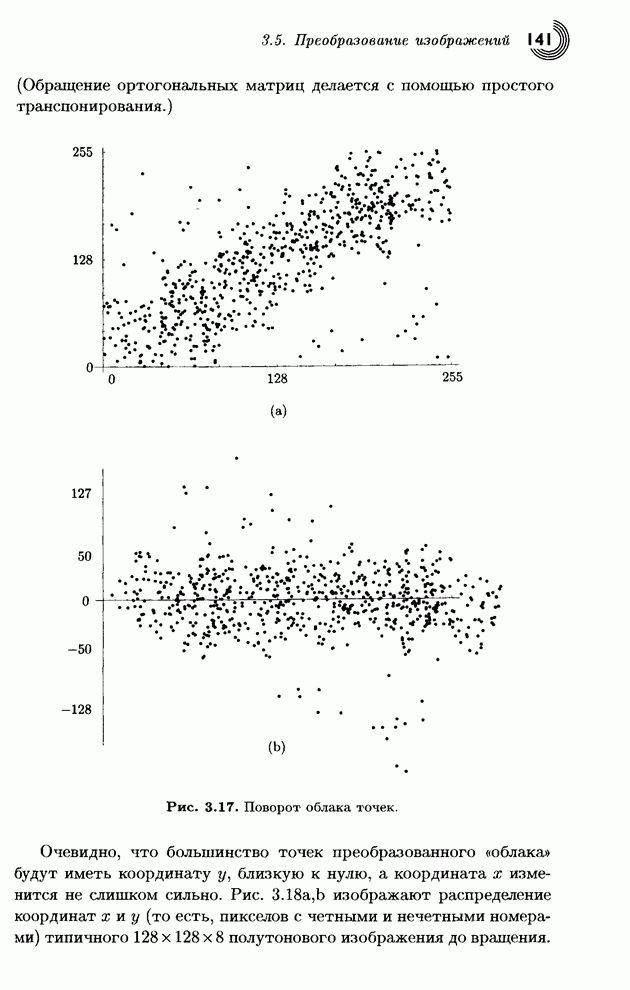
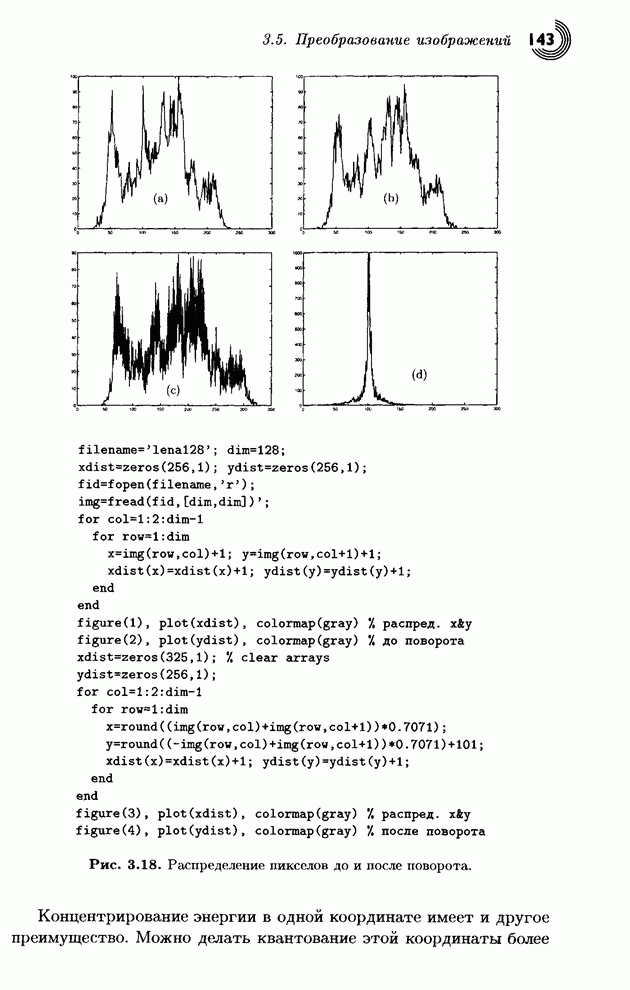
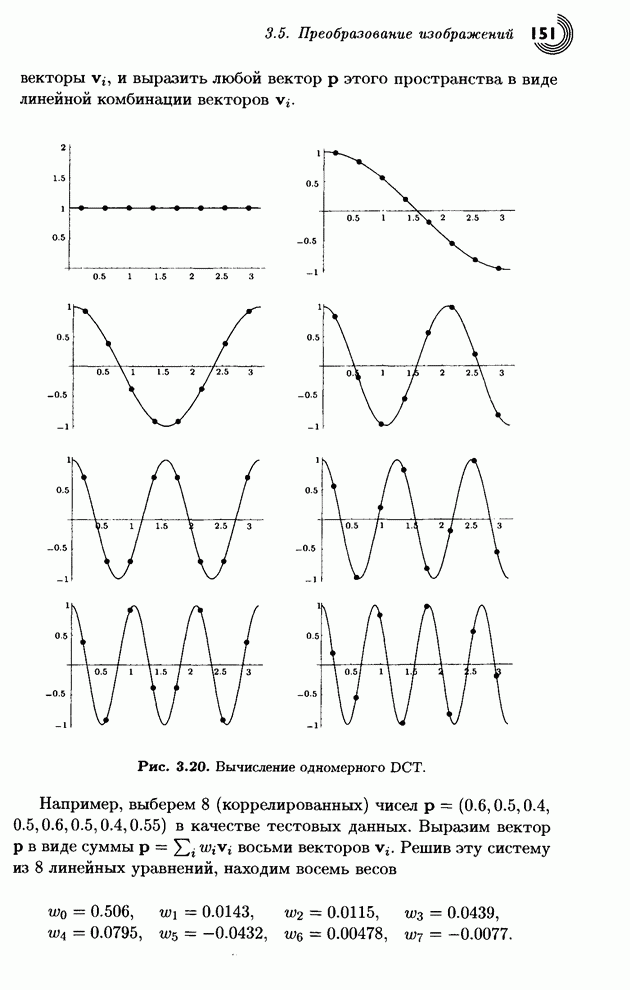
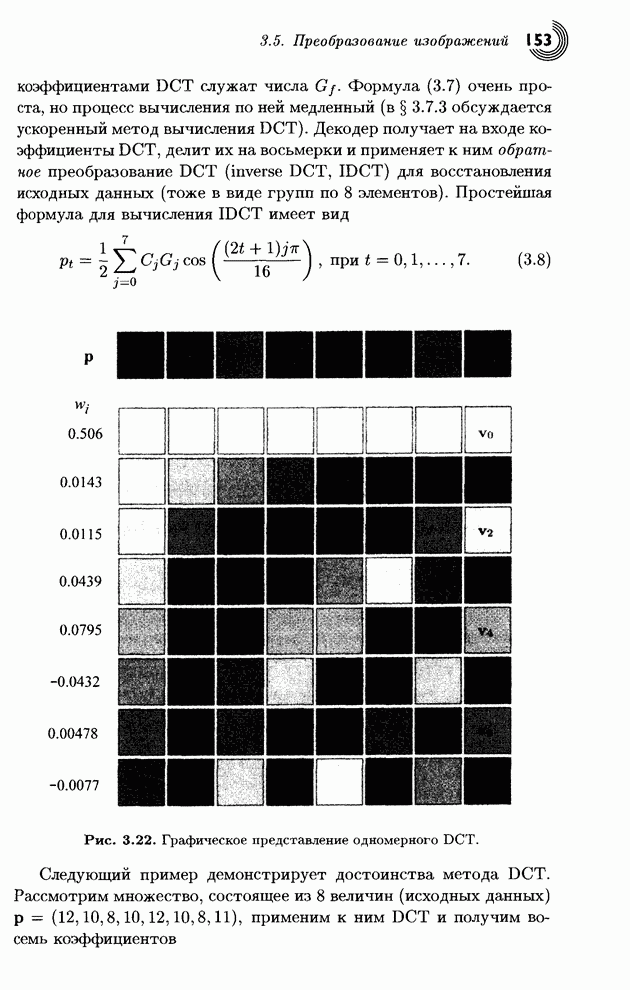
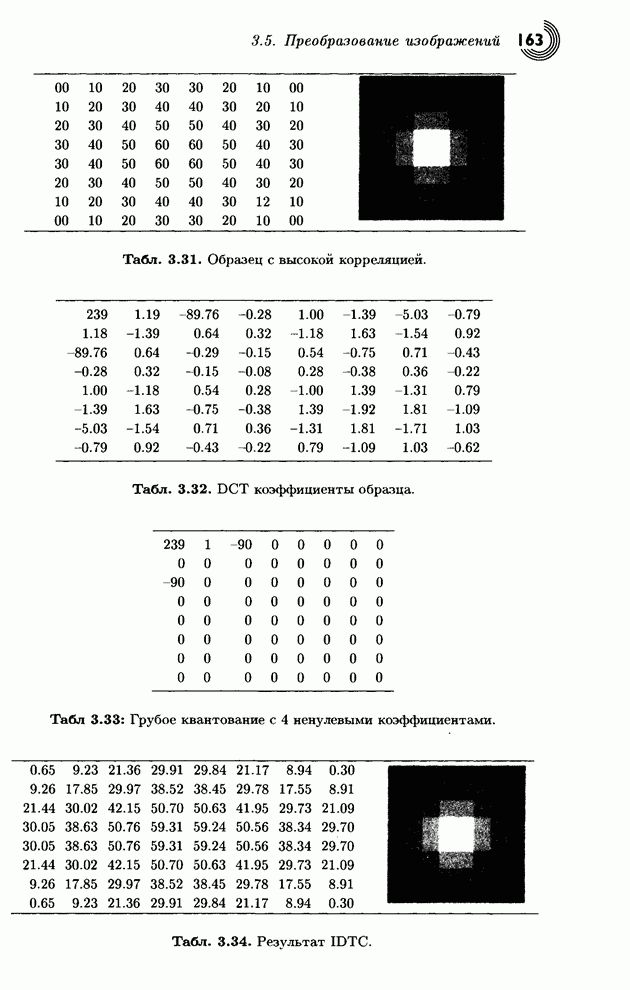
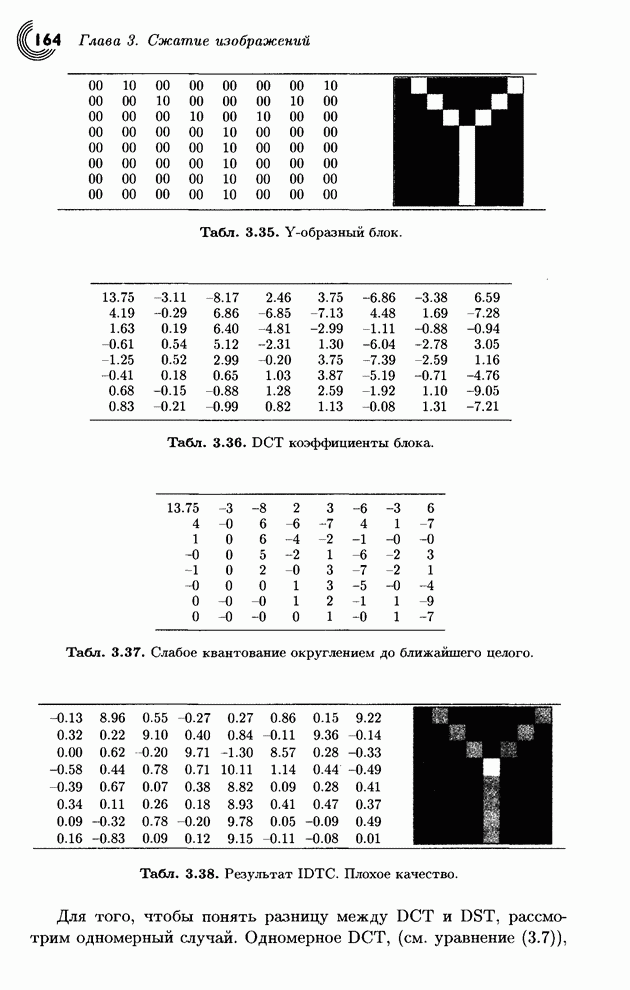
- 3.5. Преобразование изображений
- 3.5.1. Ортогональные преобразования
- 3.5.2. Матричные преобразования
- 3.5.3. Дискретное косинус-преобразование
- 3.5.4. Пример
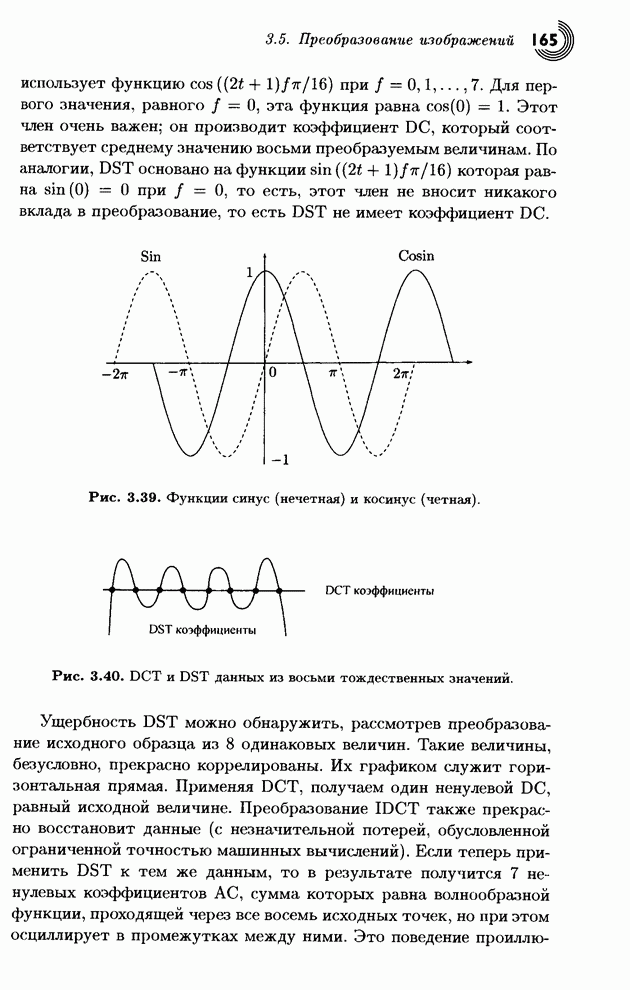
- 3.5.5. Дискретное синус-преобразование
- 3.5.6. Преобразование Уолша-Адамара
- 3.5.7. Преобразование Хаара
- 3.5.8. Преобразование Кархунена-Лоэвэ
- 3.6. Прогрессирующее сжатие изображений
- 3.7. JPEG
- 3.7.1. Светимость
- 3.7.2. DCT
- 3.7.3. Практическое DCT
- 3.7.4. Квантование
- 3.7.5. Кодирование
- 3.7.6. Мода без потери данных
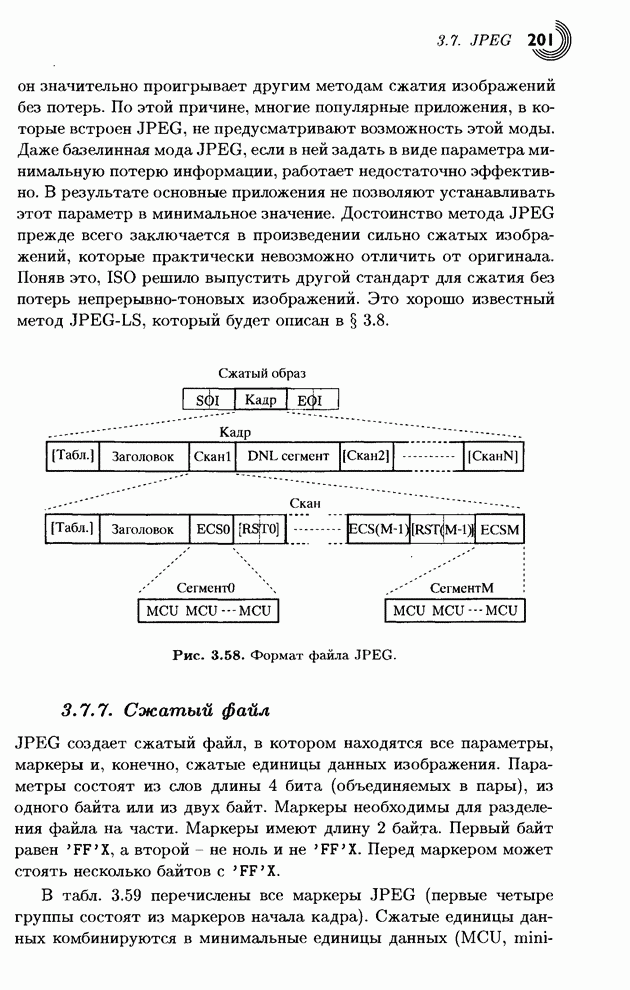
- 3.7.7. Сжатый файл
- 3.7.8. JFIF
- 3.8. JPEG-LS
- 3.8.1. Коды Голомба
- 3.8.2. Основы метода JPEG-LS
- 3.8.3. Кодер
- ГЛАВА 4 ВЕЙВЛЕТНЫЕ МЕТОДЫ
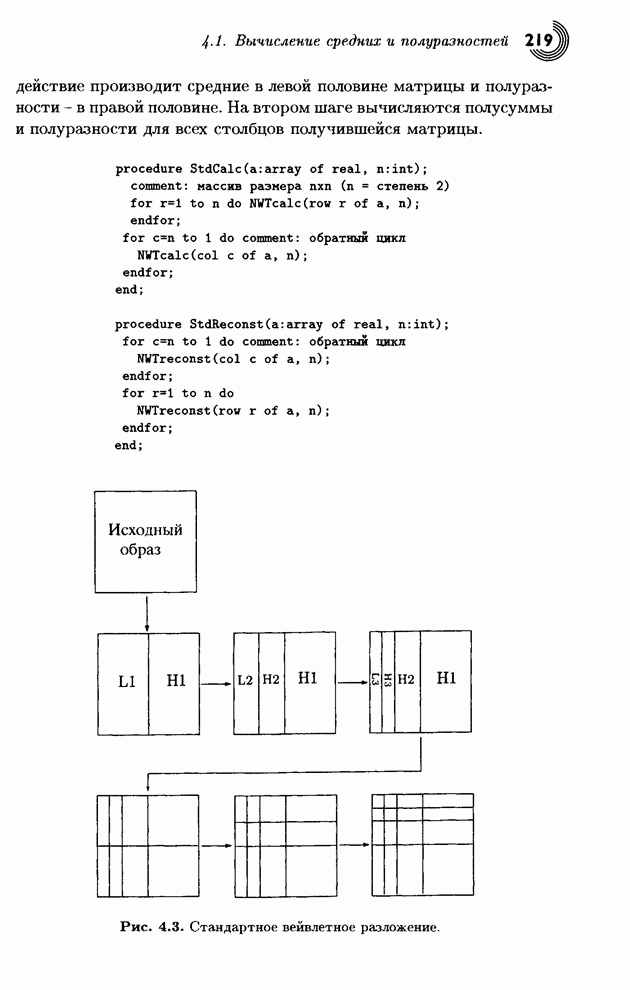
- 4.1. Вычисление средних и полу разностей
- 4.1.1. Обобщение на двумерный случай
- 4.1.2. Свойства преобразования Хаара
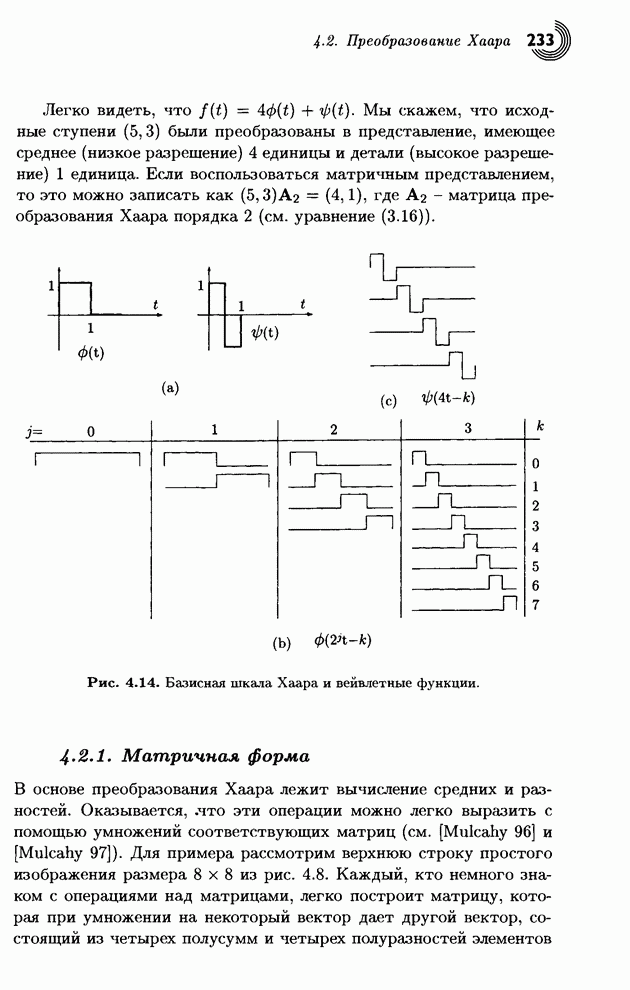
- 4.2. Преобразование Хаара
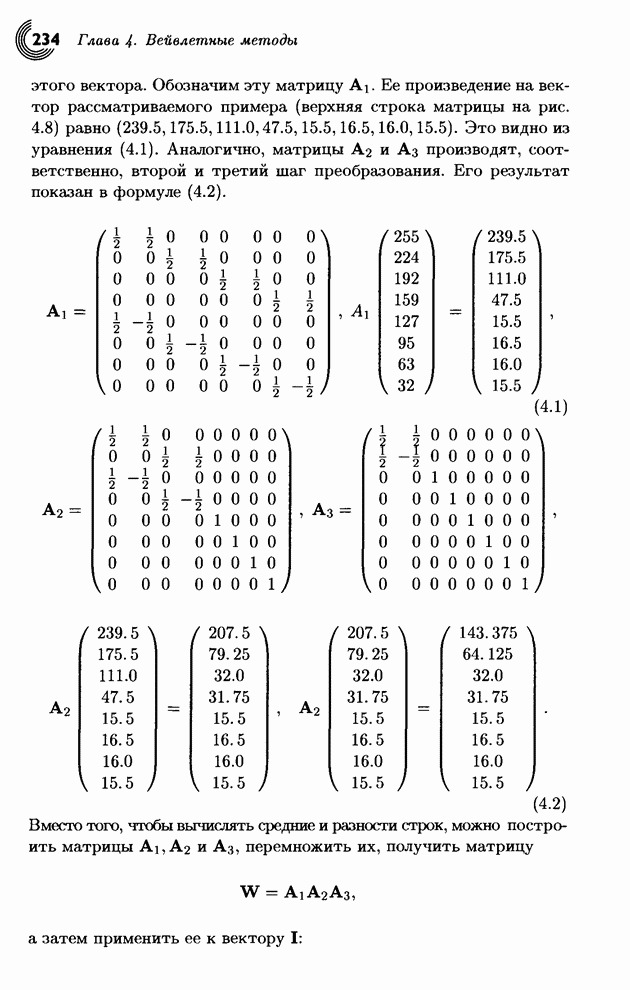
- 4.2.1. Матричная форма
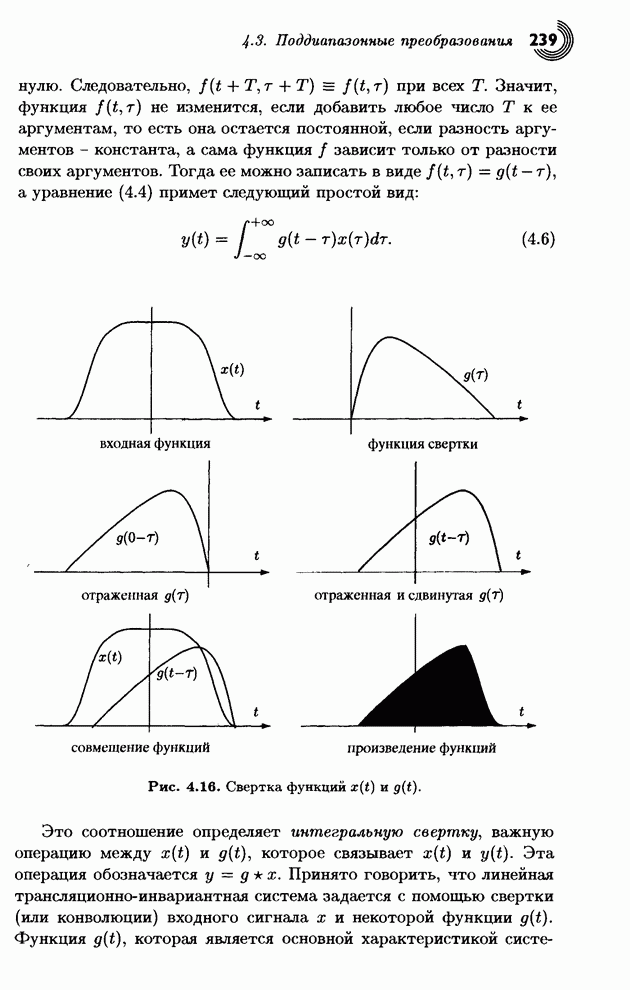
- 4.3. Поддиапазонные преобразования
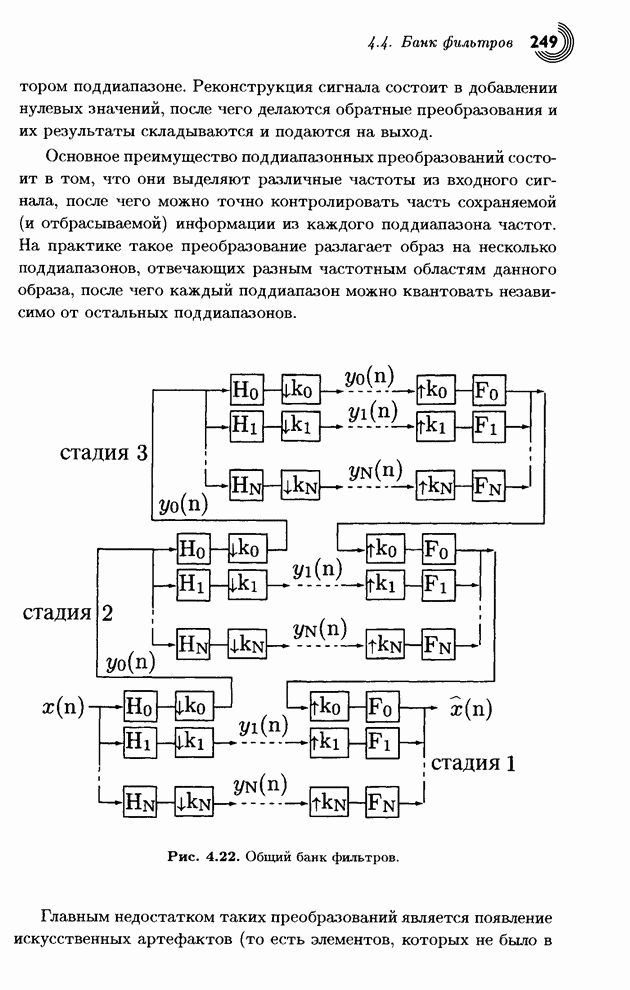
- 4.4. Банк фильтров
- 4.5. Нахождение коэффициентов фильтра
- 4.6. Преобразование DWT
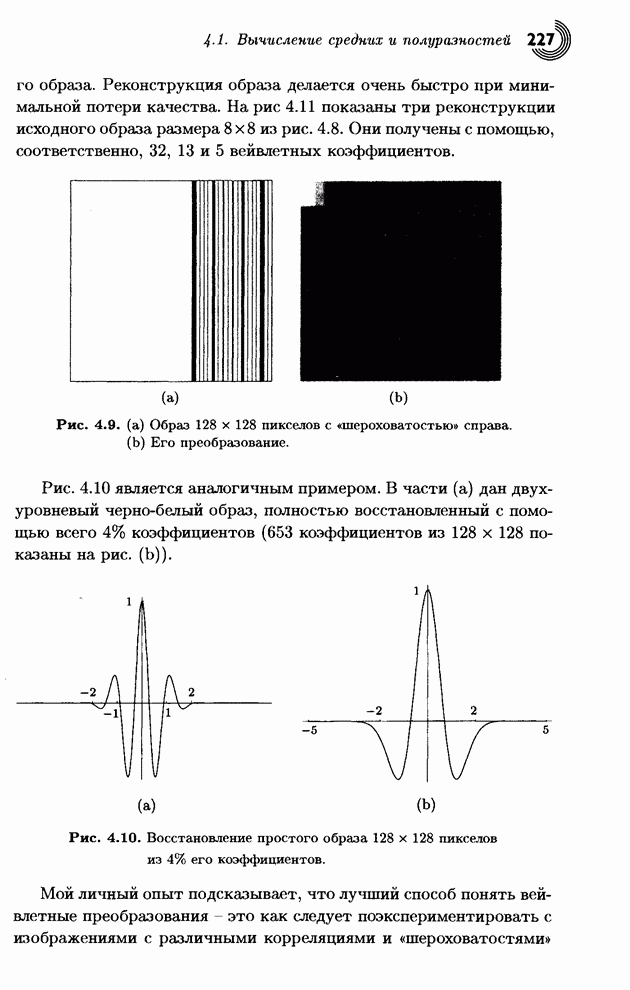
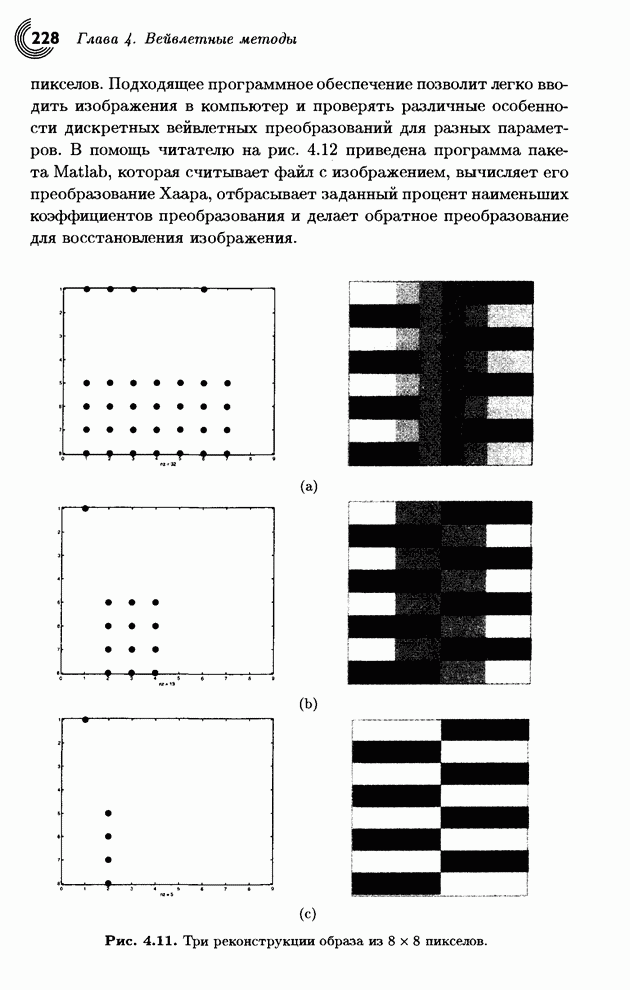
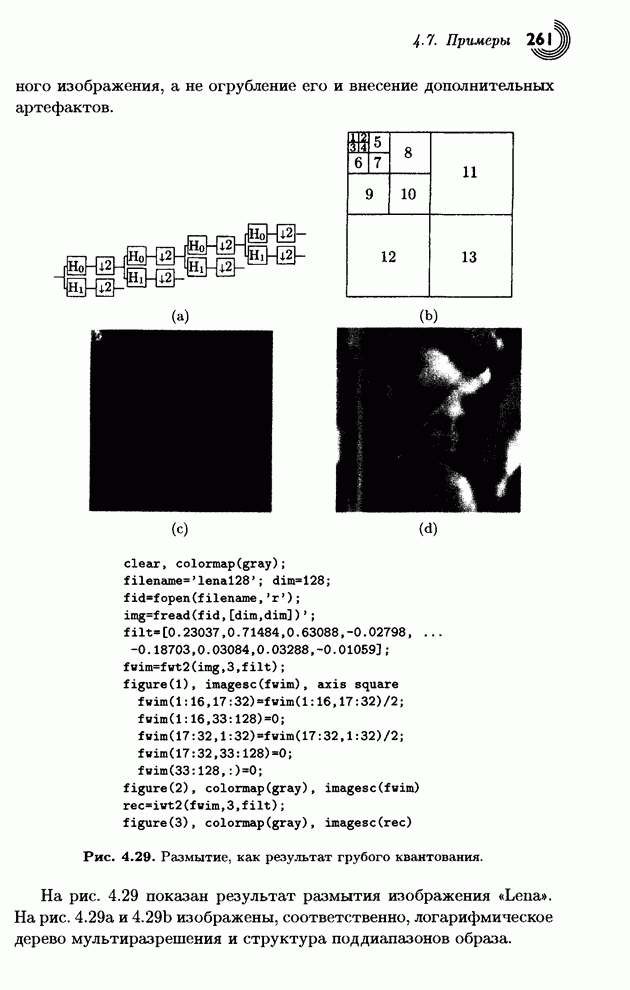
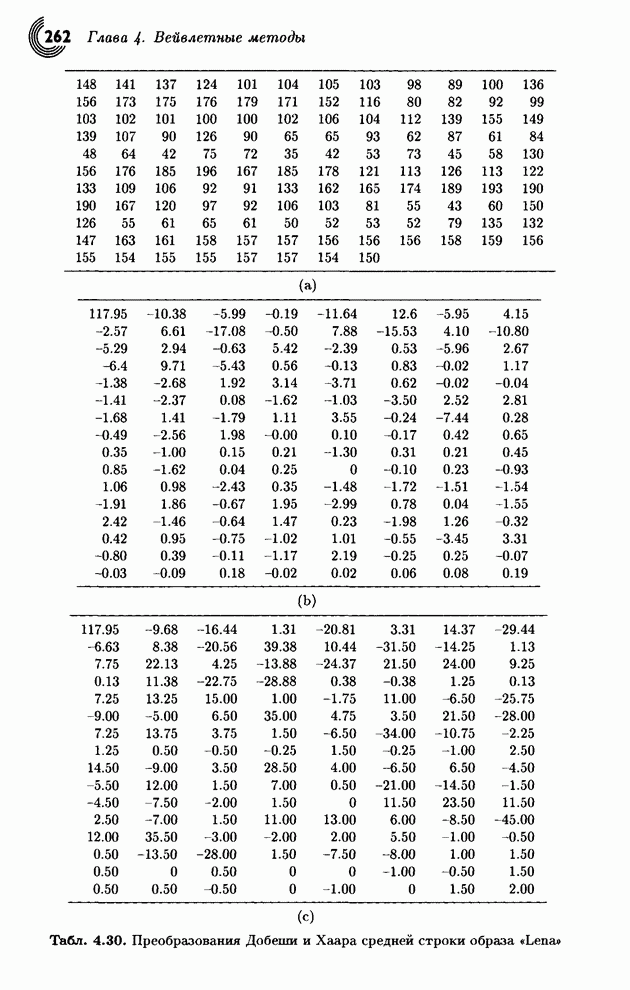
- 4.7. Примеры
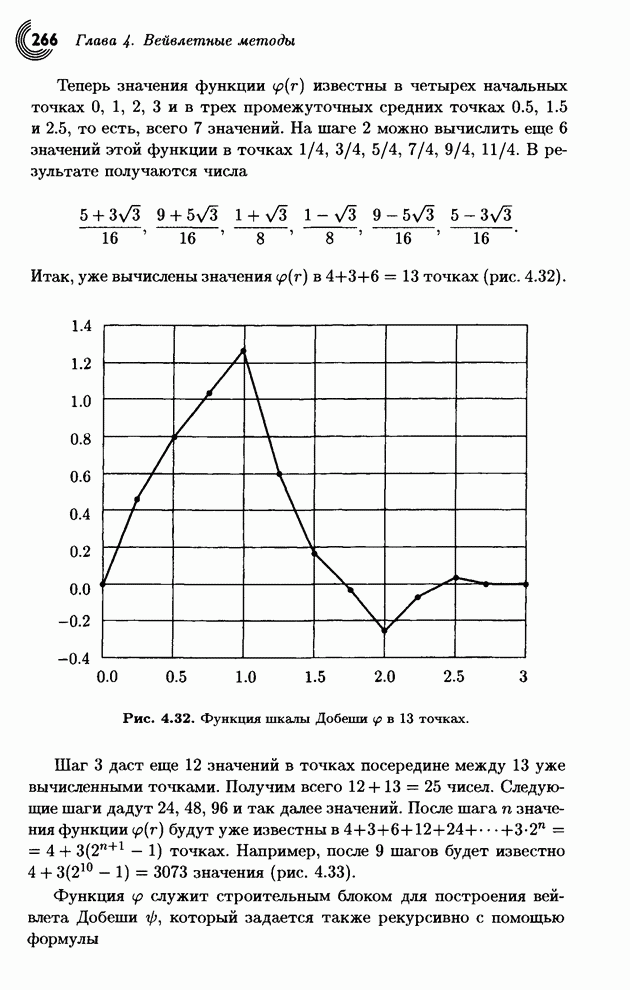
- 4.8. Вейвлеты Добеши
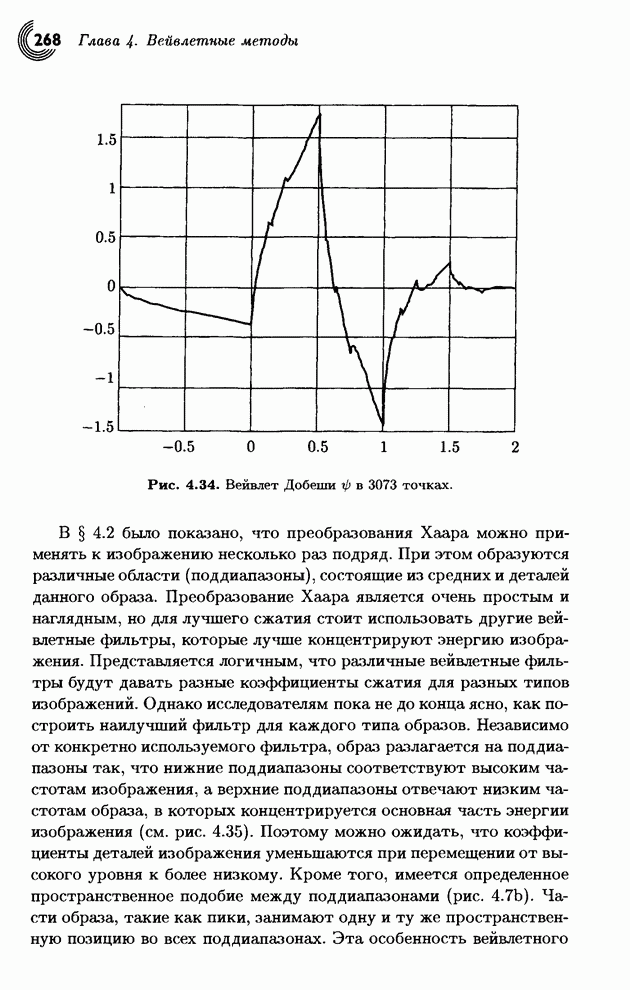
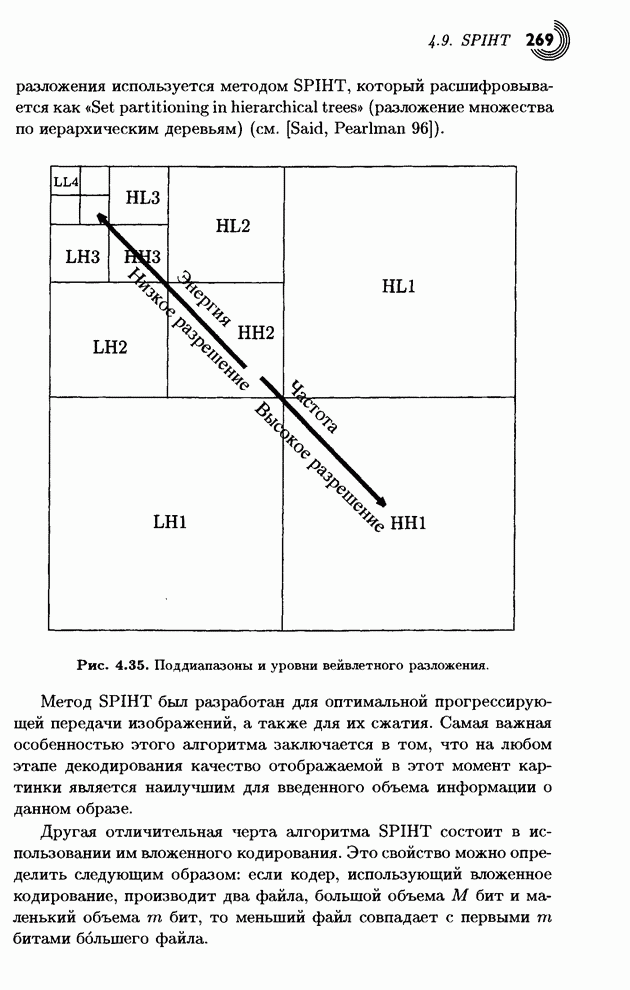
- 4.9. SPIHT
- 4.9.1. Алгоритм сортировки разделением множеств
- 4.9.2. Пространственно ориентированное дерево
- 4.9.3. Кодирование в алгоритме SPIHT
- 4.9.4. Пример
- 4.9.5. QTCQ
- ГЛАВА 5 СЖАТИЕ ВИДЕО
- 5.1. Основные принципы
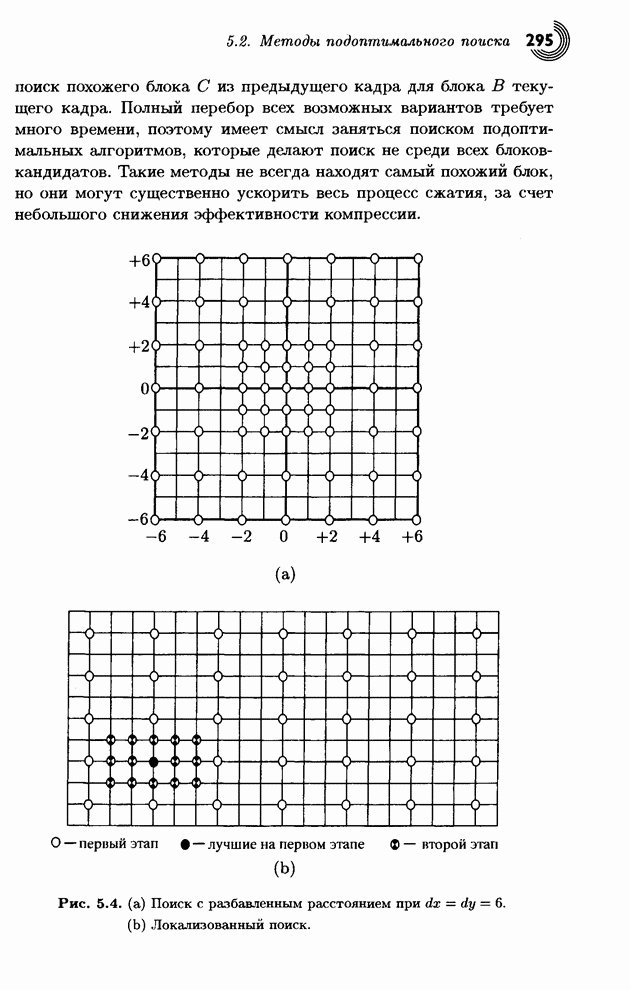
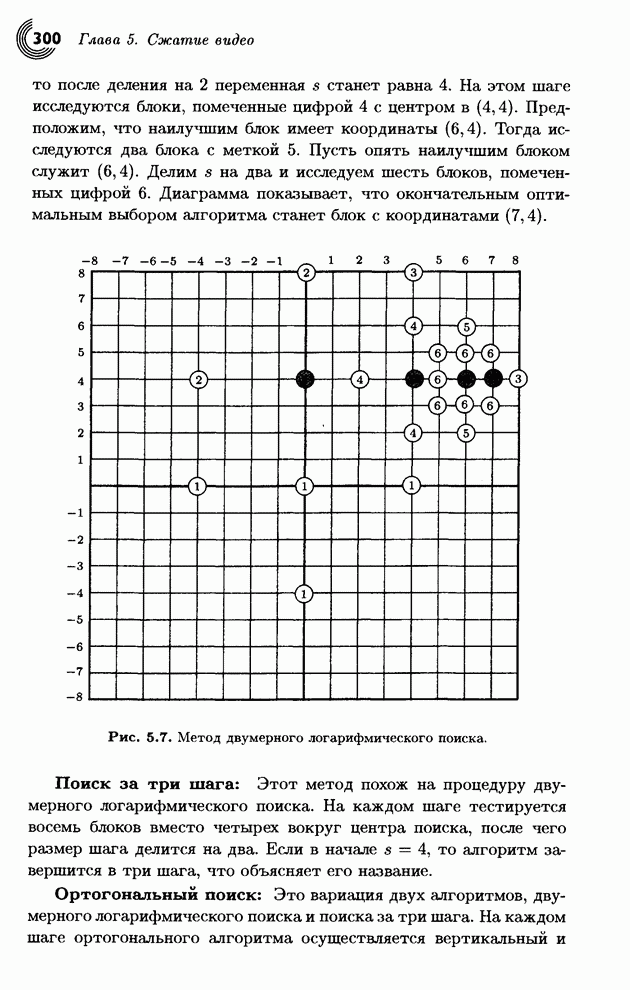
- 5.2. Методы подоптимального поиска
- ГЛАВА 6 СЖАТИЕ ЗВУКА
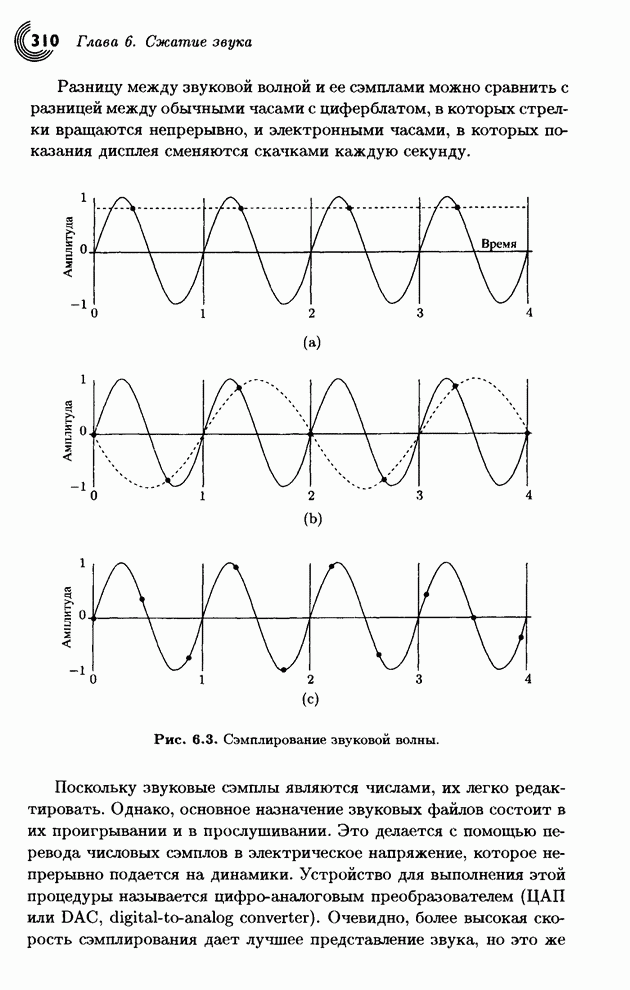
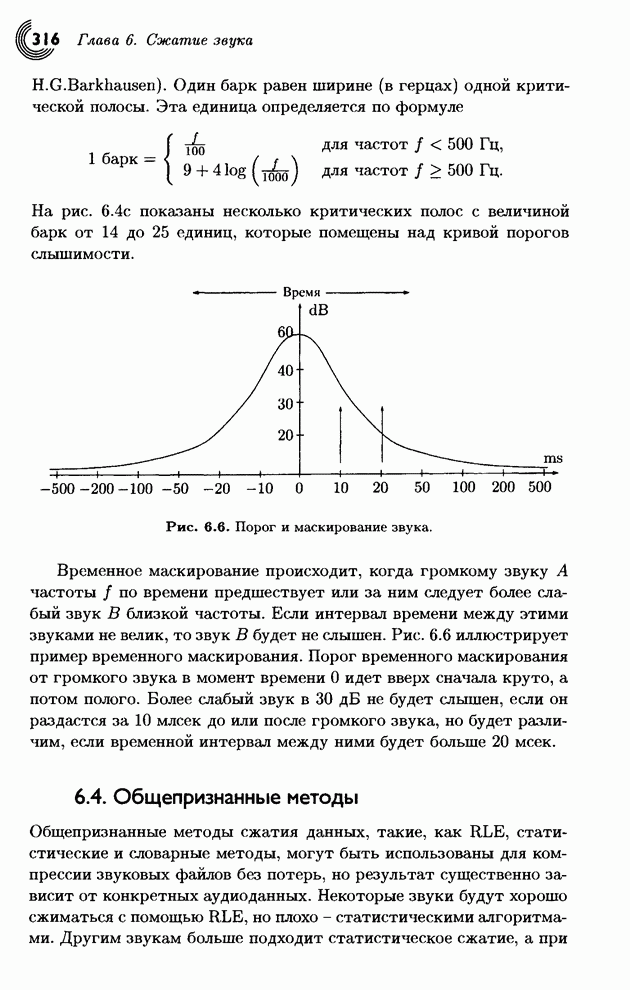
- 6.1. Звук
- 6.2. Оцифрованный звук
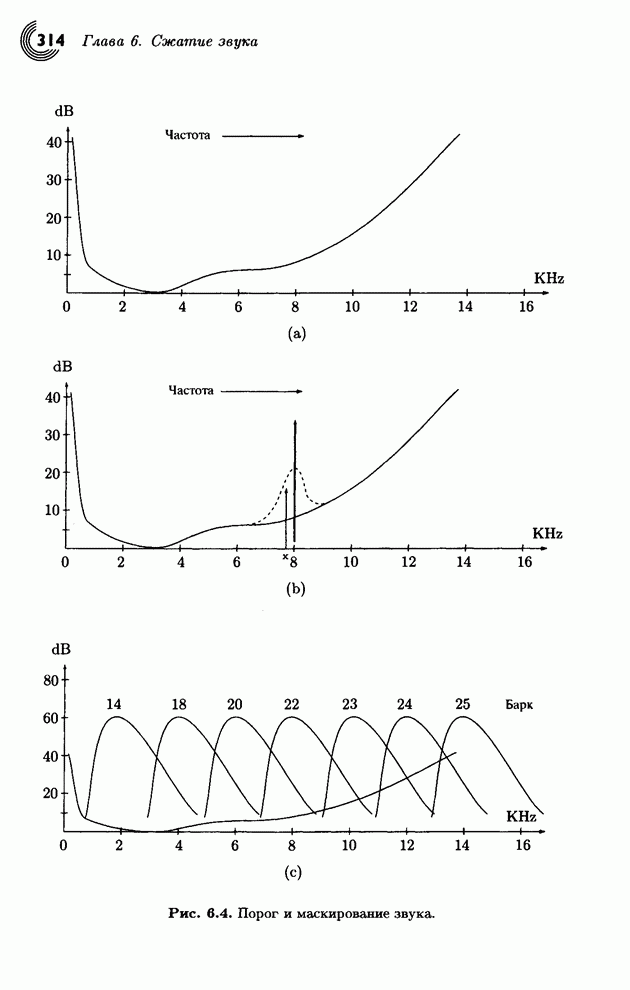
- 6.3. Органы слуха человека
- 6.4. Общепризнанные методы
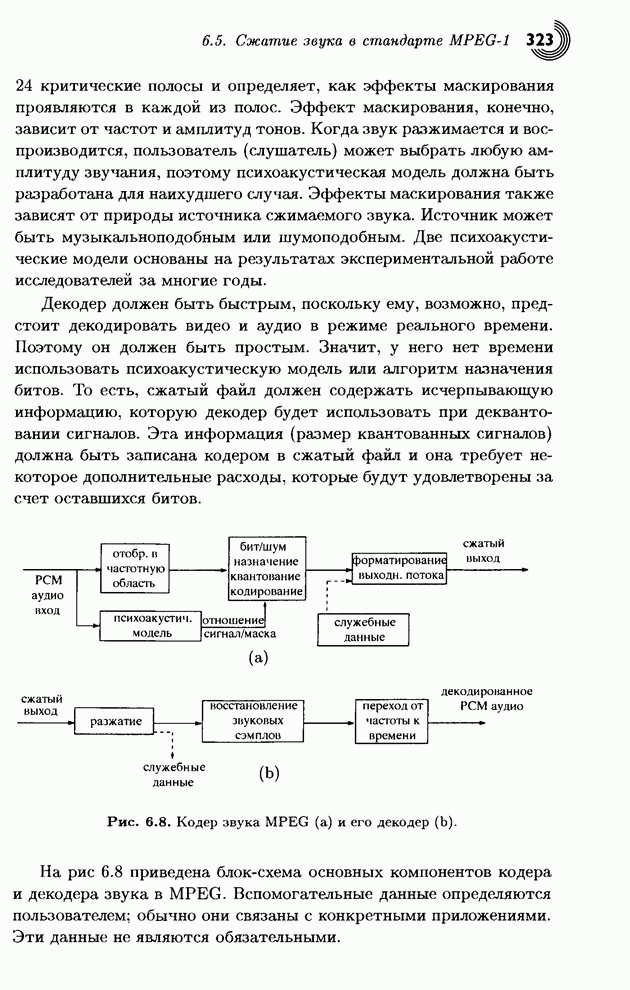
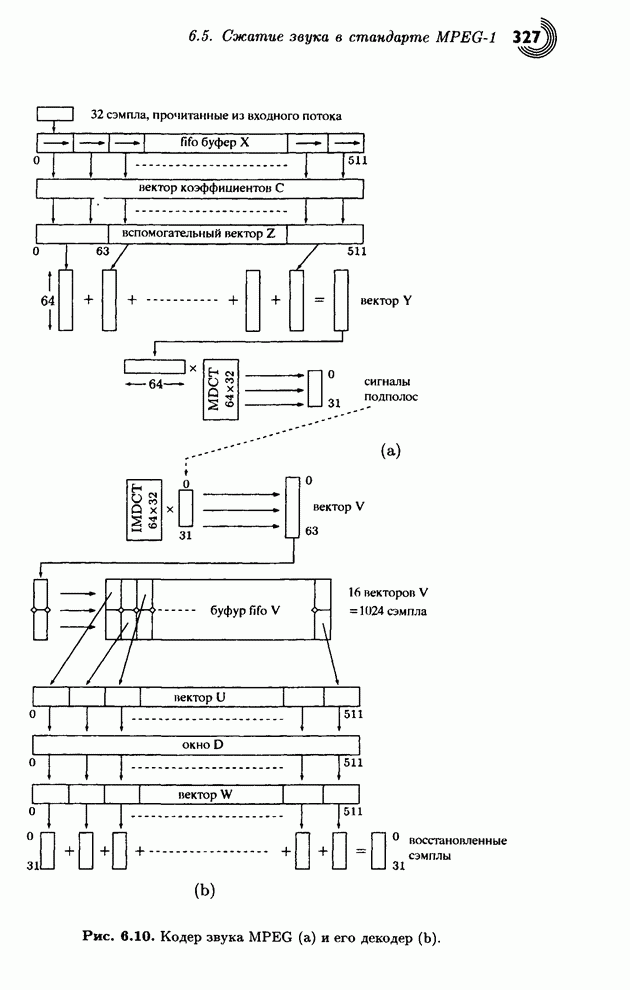
- 6.5. Сжатие звука в стандарте MPEG-1
- 6.5.1. Кодирование частотной области
- 6.5.2. Формат сжатых данных
- 6.5.3. Психоакустические модели
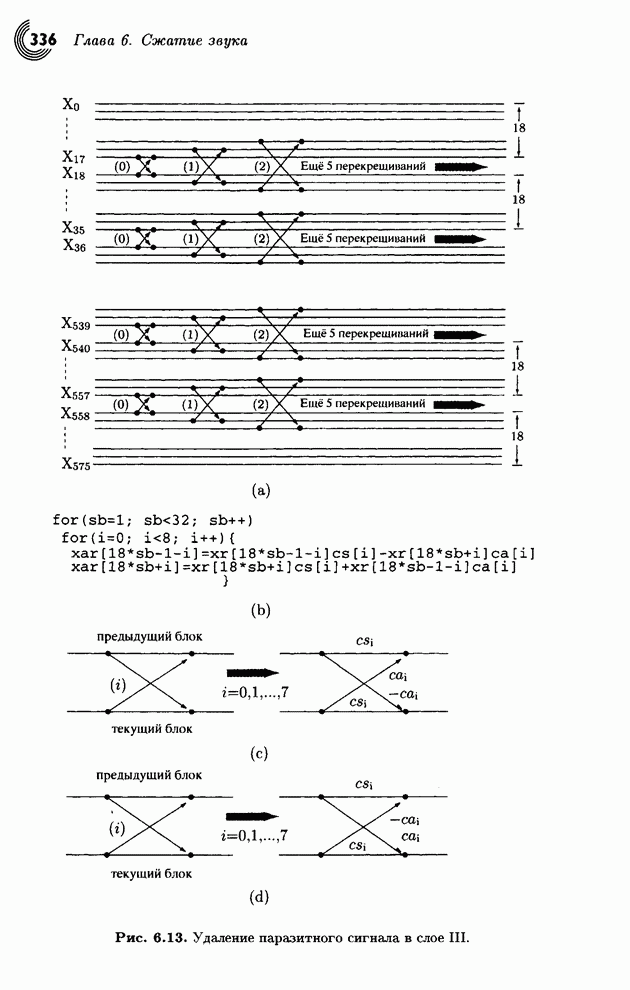
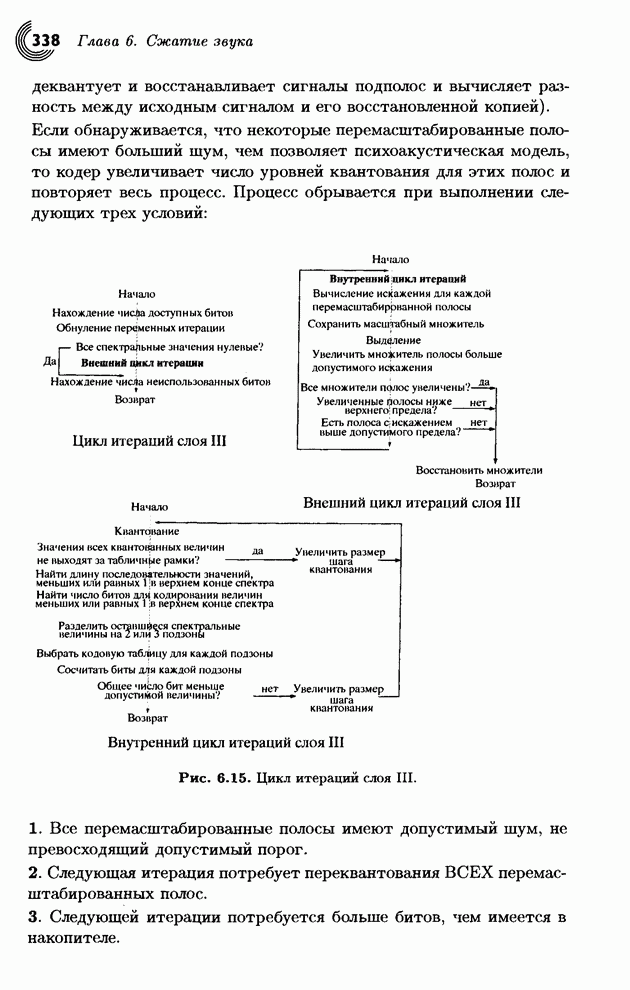
- 6.5.4. Кодирование: слой III
- Литература
- Глоссарий