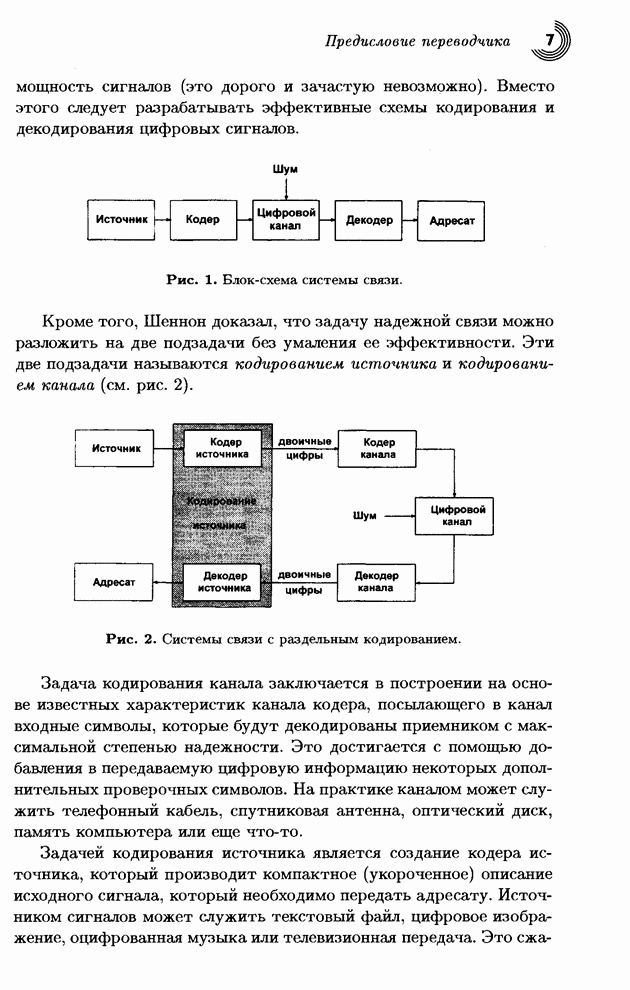
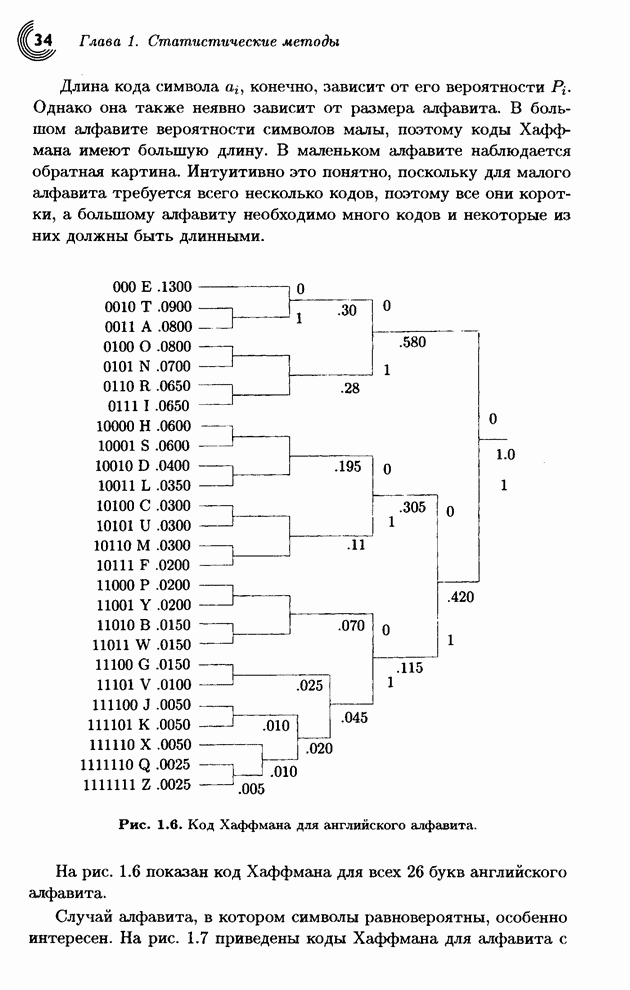
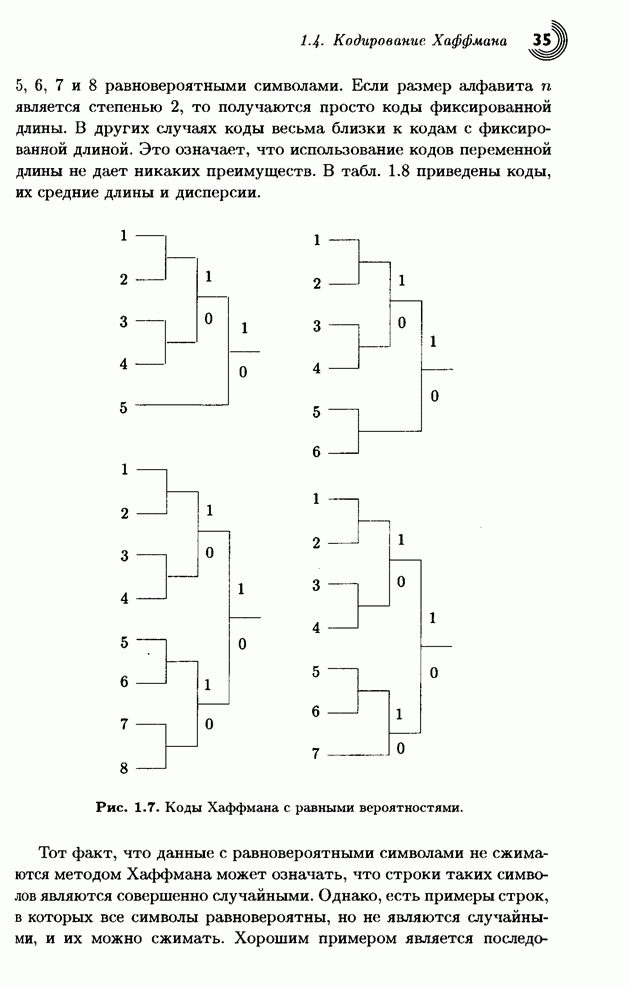
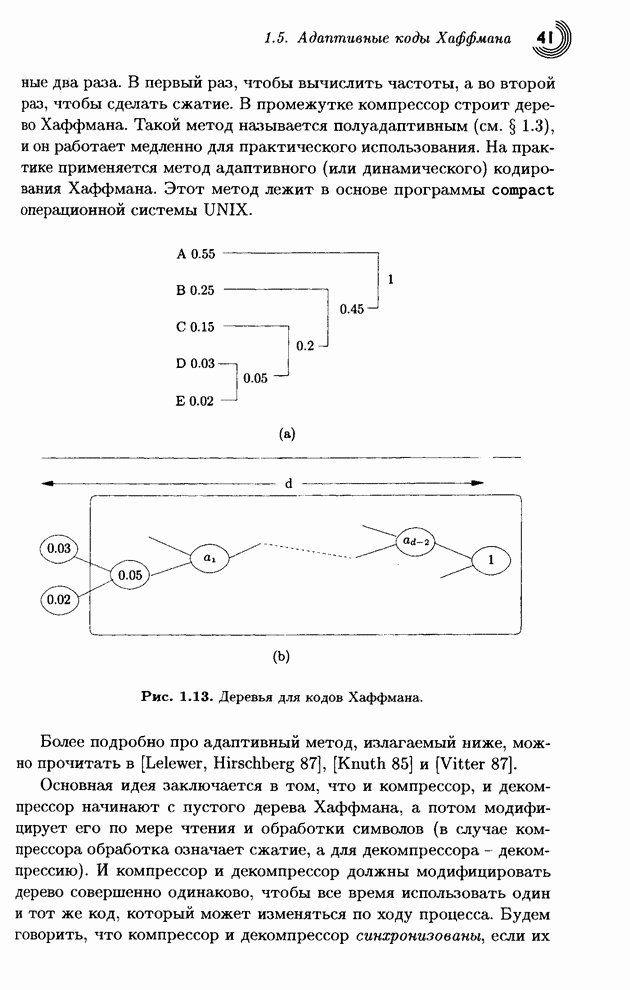
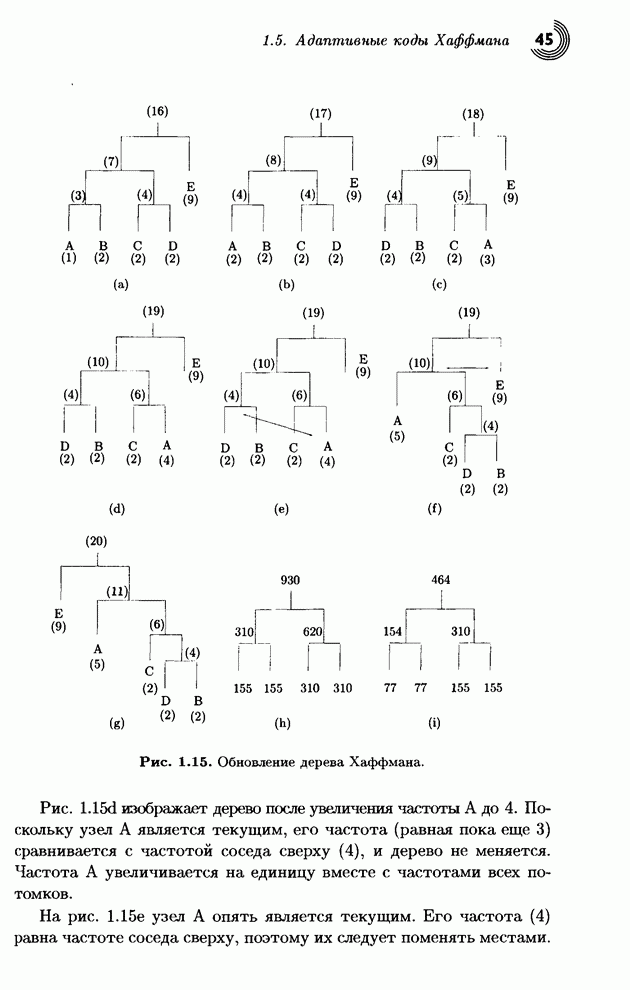
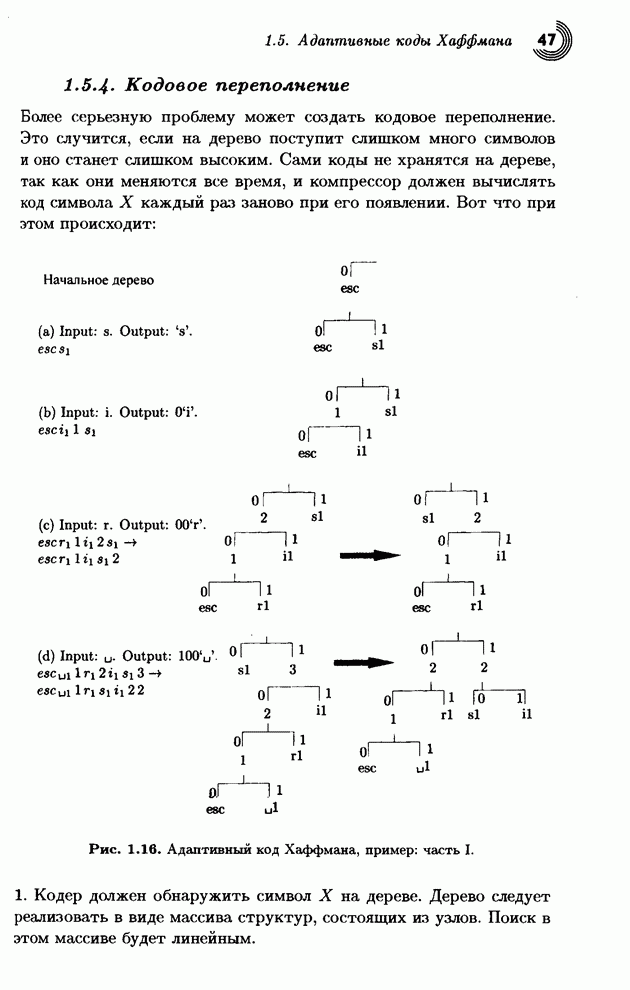
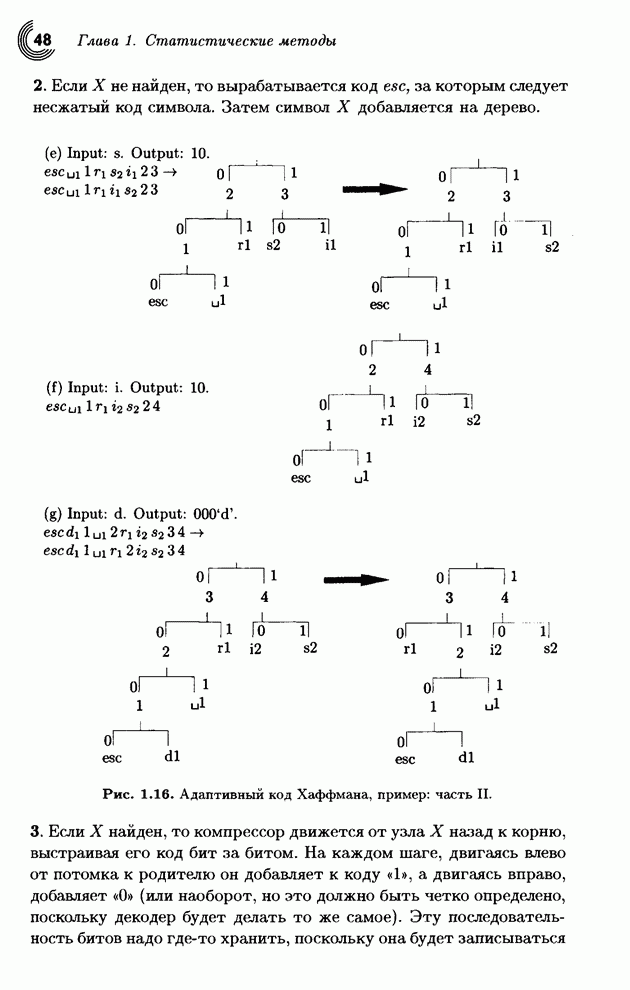
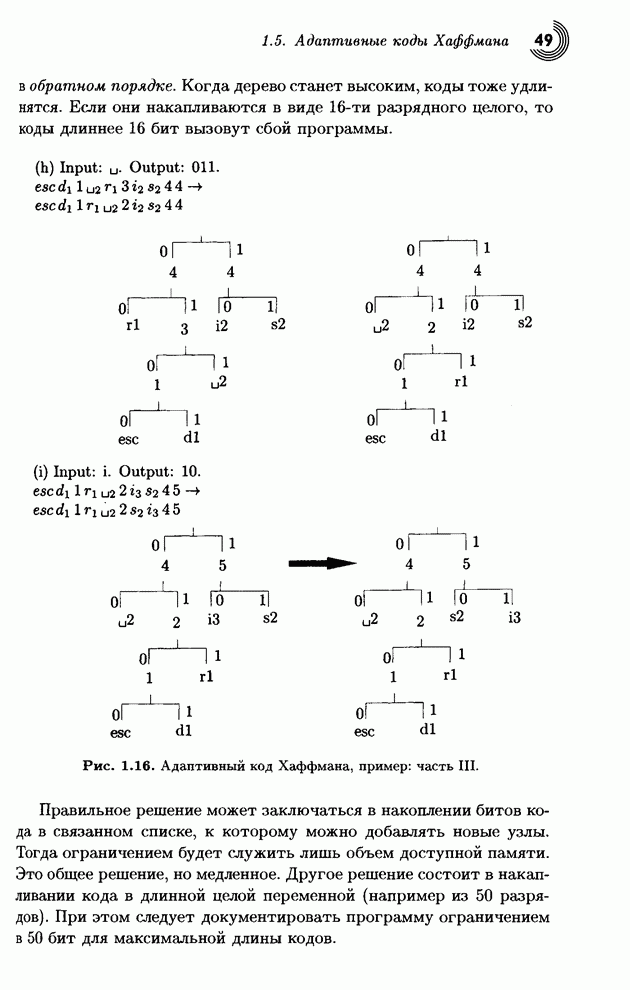
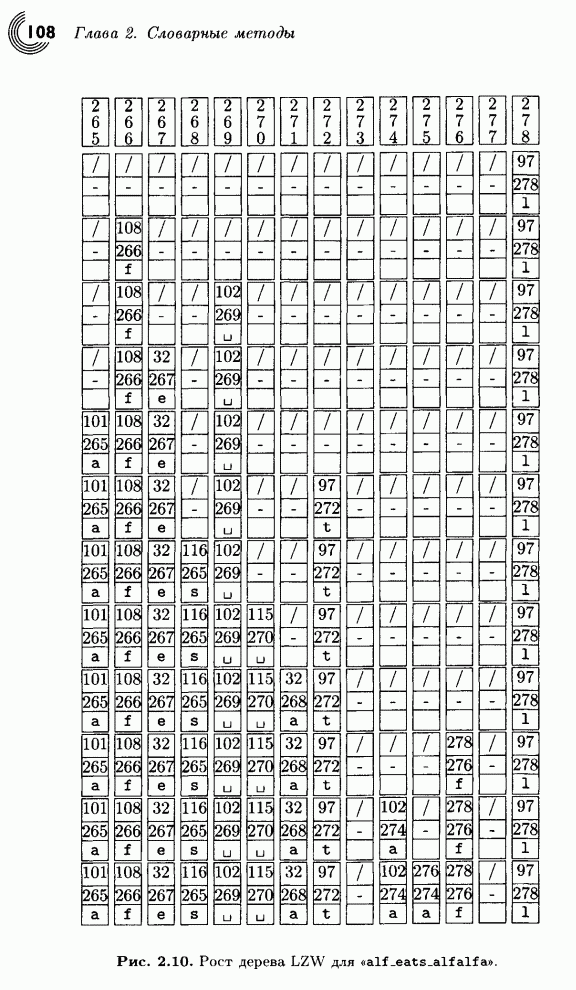
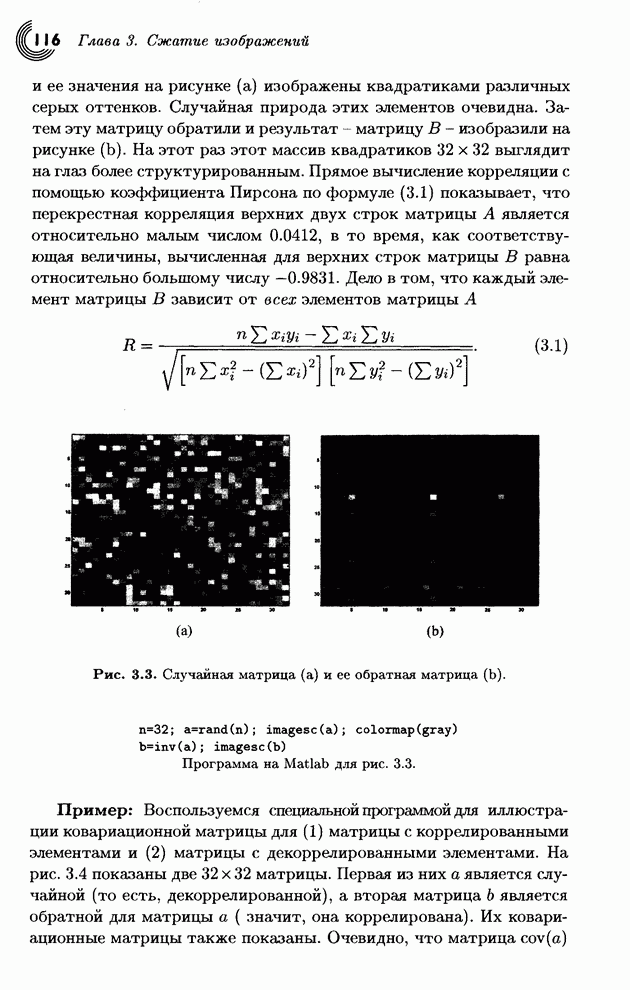
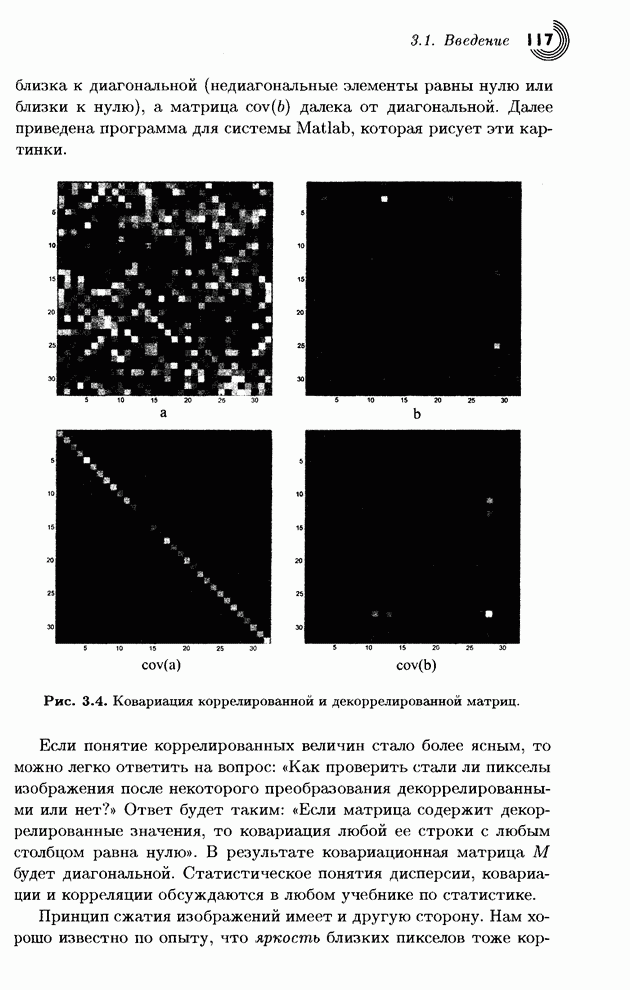
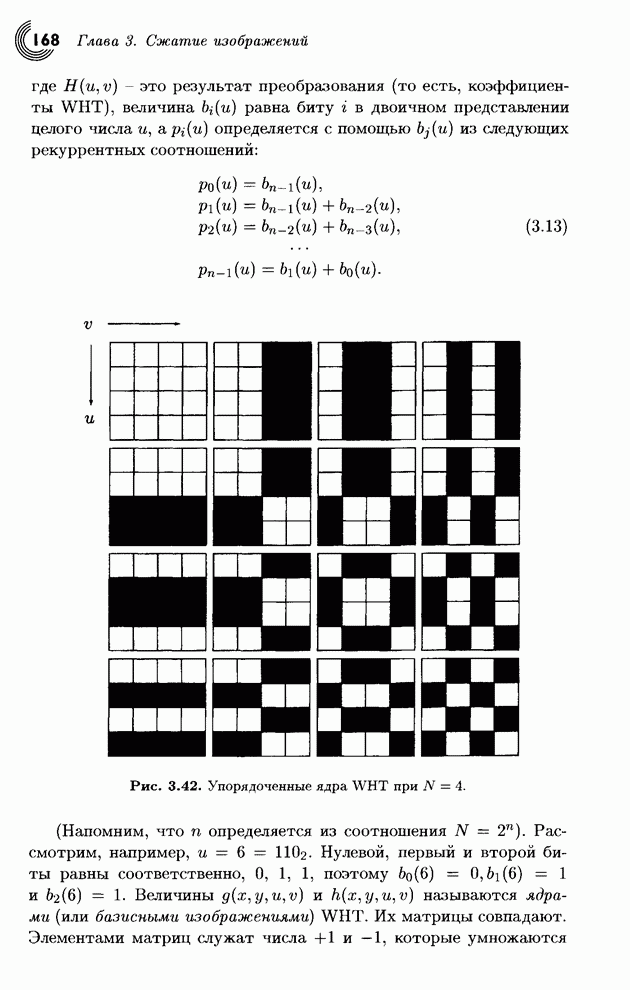
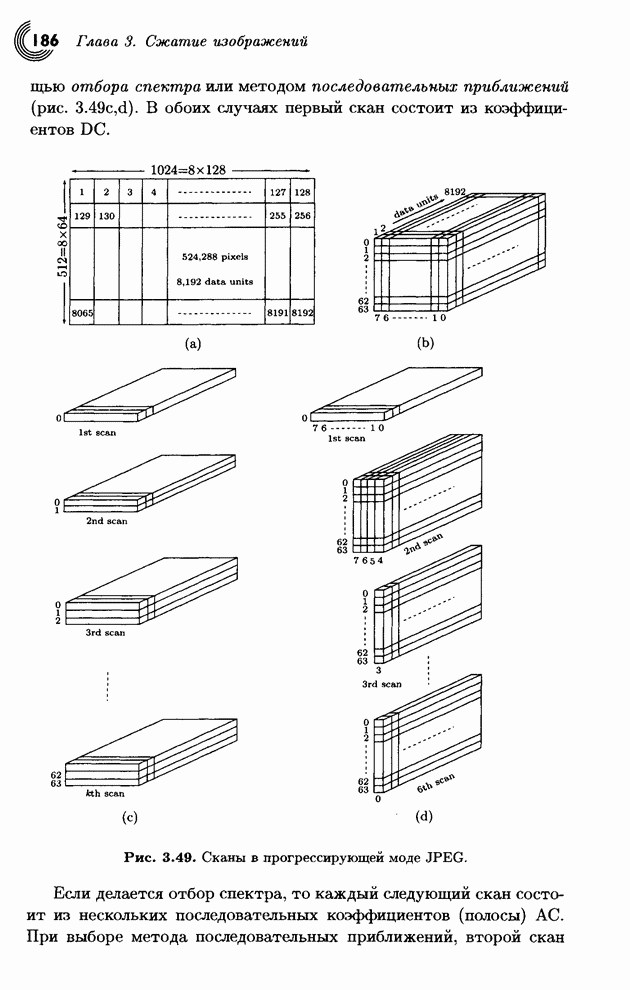
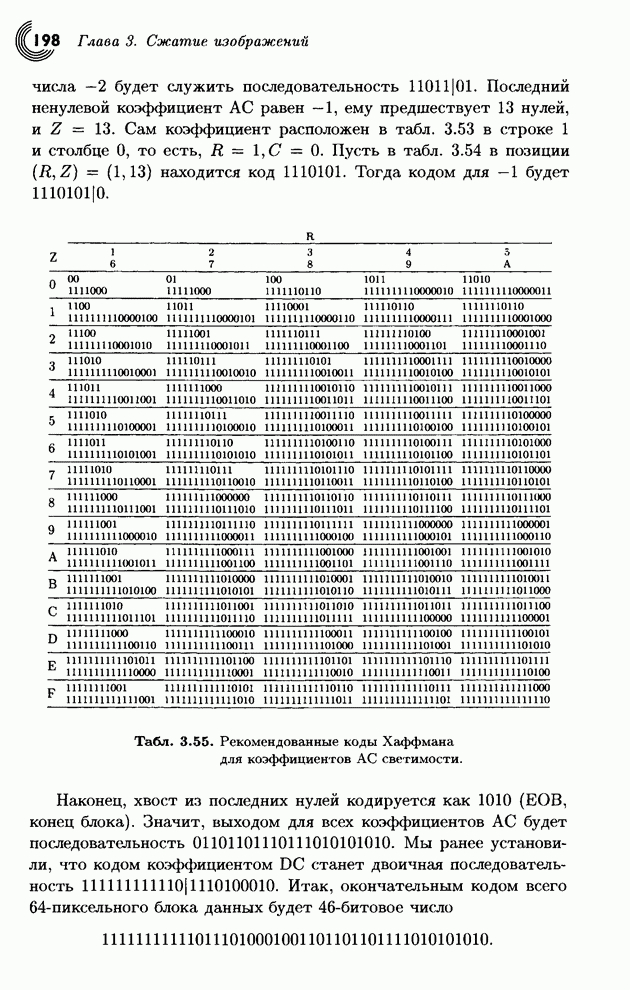
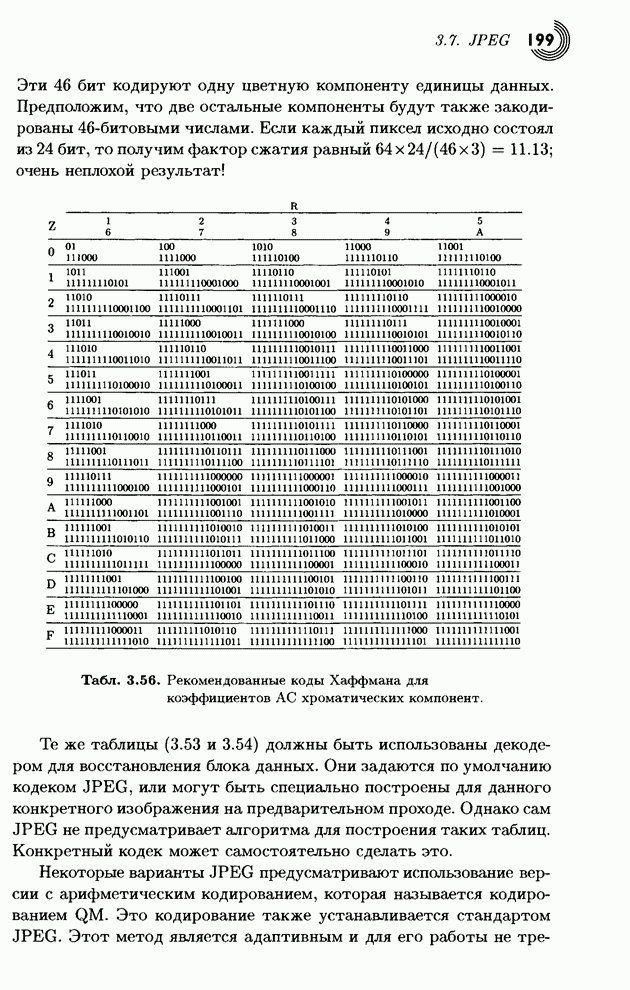
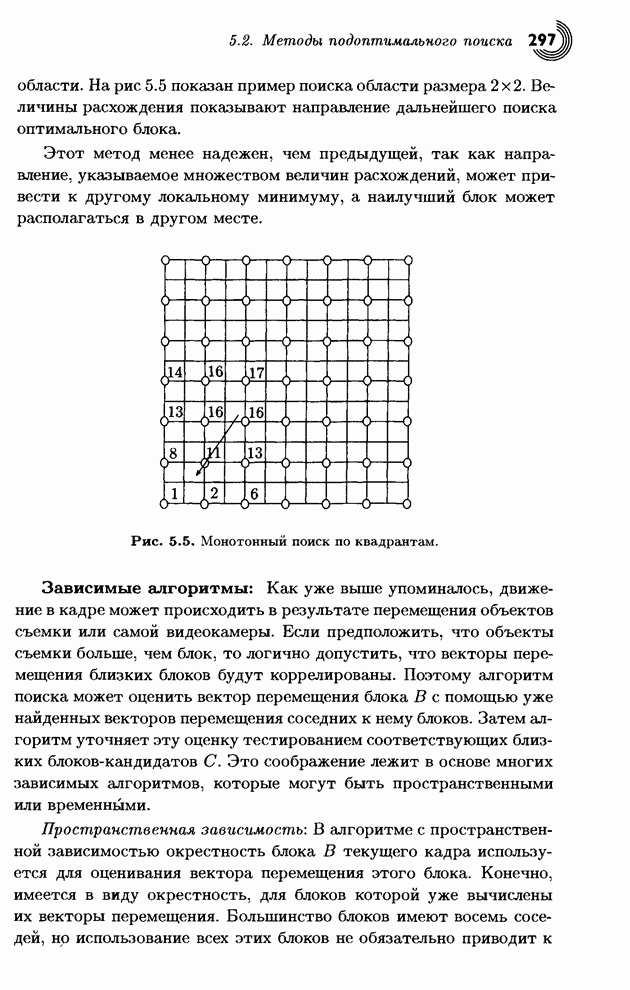
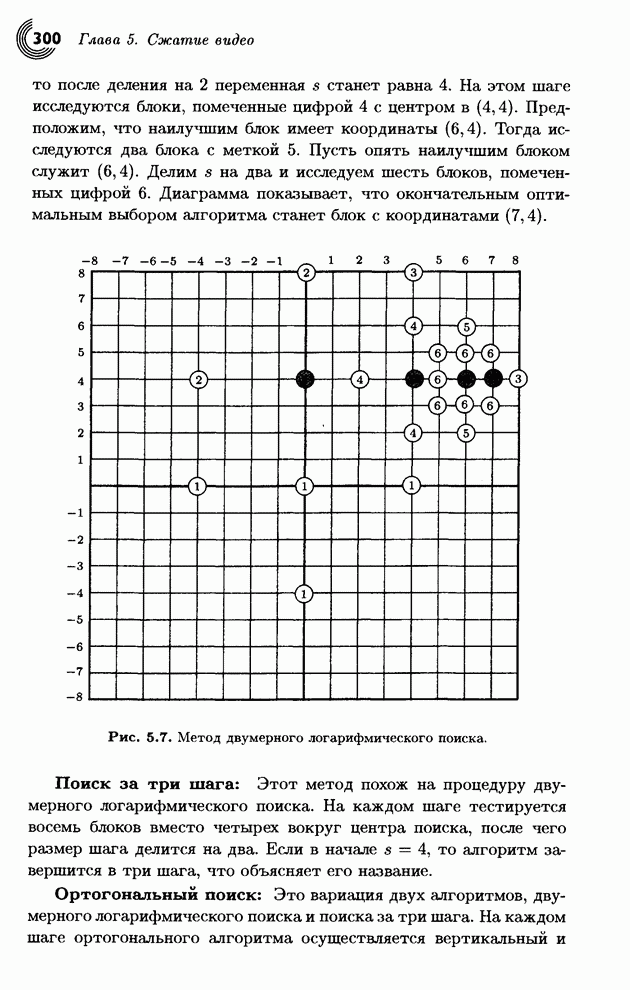
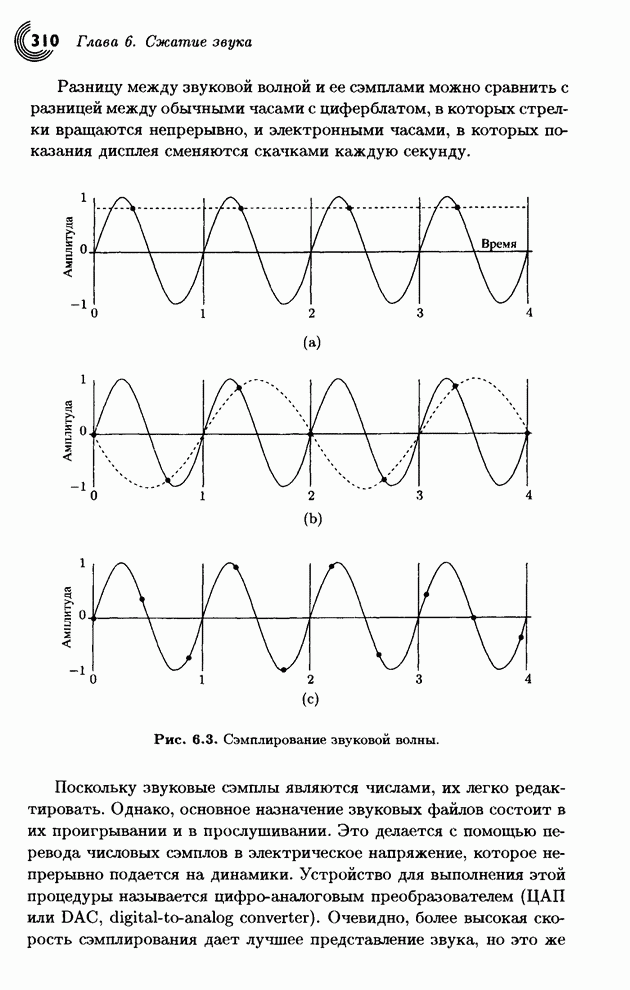
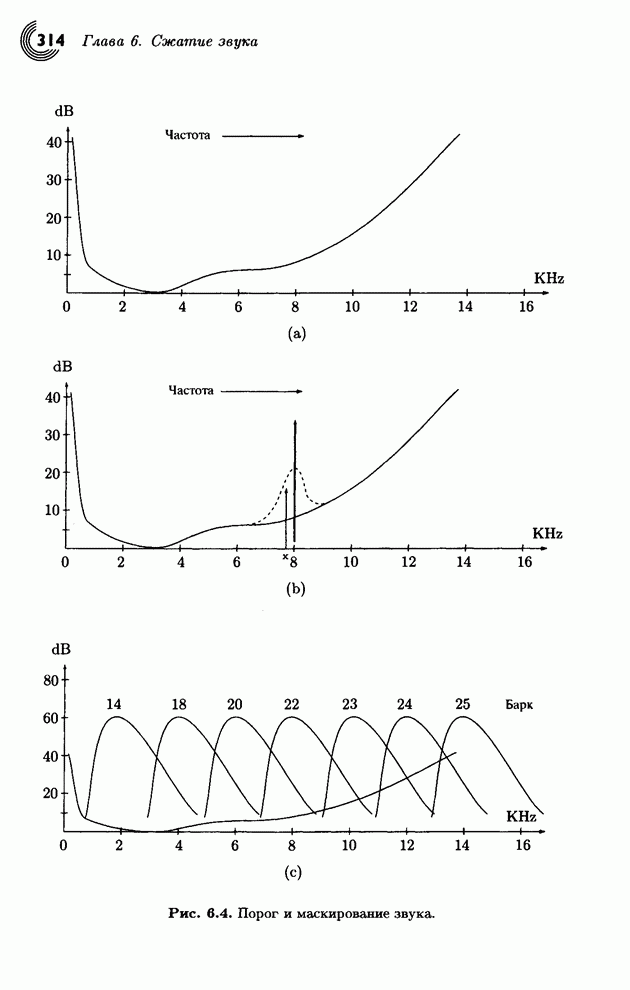
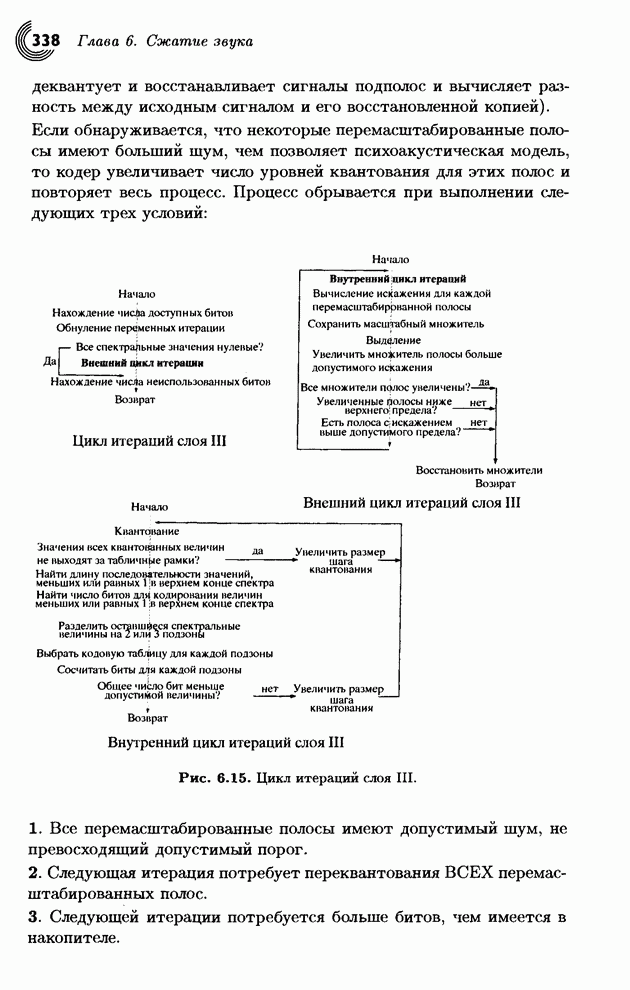
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
1.7.1. Детали реализации метода
Описанный выше процесс кодирования невозможно реализовать на практике, так как в нем предполагается, что в переменных Low и High хранятся числа с неограниченной точностью. Процесс декодирования, описанный на стр. 66 («Далее декодер удаляет эффект символа S из кода с помощью вычитания ... и деления ...») по своей сути очень прост, но совершенно не практичен. Код, который является одним числом, обычно будет длинным, очень длинным числом.
Файл объема 1 MB будет сжиматься, скажем, до 500 KB, в котором будет записано всего одно число. Деление чисел в 500 KB делается очень сложно и долго.
Любое
практическое применение арифметического кодирования должно основываться на
оперировании с целыми числами (арифметика чисел с плавающей запятой работает
медленно и при этом происходит потеря точности), которые не могут быть слишком
длинными. Мы опишем такую реализацию с помощью двух целых переменных Low и High. В нашем примере они будут иметь
длину в 4 десятичные цифры, но на практике будут использоваться целые длиной 16
или 32 бита. Эти переменные будут хранить верхний и нижний концы текущего
подынтервала, но мы не будем им позволять неограниченно расти. Взгляд на табл.
1.25 показывает, что как только самые левые цифры переменных Low и High становятся одинаковыми, они уже
не меняются в дальнейшем. Поэтому мы будем выдвигать эти числа за пределы
переменных Low и High и сохранять их в выходном файле.
Таким образом, эти переменные будут хранить не весь код, а только самую
последнюю его часть. После сдвига цифр мы будем справа дописывать 0 в
переменную Low, а в переменную High цифру 9. Для того, чтобы лучше
понять весь процесс, можно представлять себе эти переменные как левый конец
бесконечно длинного числа. Число Low
имеет вид ![]() ,
а число High=
,
а число High= ![]() .
.
Проблема состоит в том, что переменная High в начале должна равняться 1, однако мы интерпретируем Low и High как десятичные дроби меньшие 1. Решение заключается в присвоении переменной High значения 9999..., которое соответствует бесконечной дроби 0.9999..., равной 1.
(Это
легко доказать. Если ![]() , то среднее число
, то среднее число ![]() должно лежать между 0.9999...
и 1; однако, его невозможно выразить десятичной дробью. Нельзя добавить ни
одной цифры к числу 0.9999..., поскольку в нем бесконечно много цифр. Также ни
одну из его цифр нельзя увеличить, так как все они равны 9. Значит, число
0.9999... равно 1. Рассуждая аналогично, легко показать, что число 0.5 имеет
два представления в виде двоичной дроби: 0.1000... и 0.0111...).
должно лежать между 0.9999...
и 1; однако, его невозможно выразить десятичной дробью. Нельзя добавить ни
одной цифры к числу 0.9999..., поскольку в нем бесконечно много цифр. Также ни
одну из его цифр нельзя увеличить, так как все они равны 9. Значит, число
0.9999... равно 1. Рассуждая аналогично, легко показать, что число 0.5 имеет
два представления в виде двоичной дроби: 0.1000... и 0.0111...).
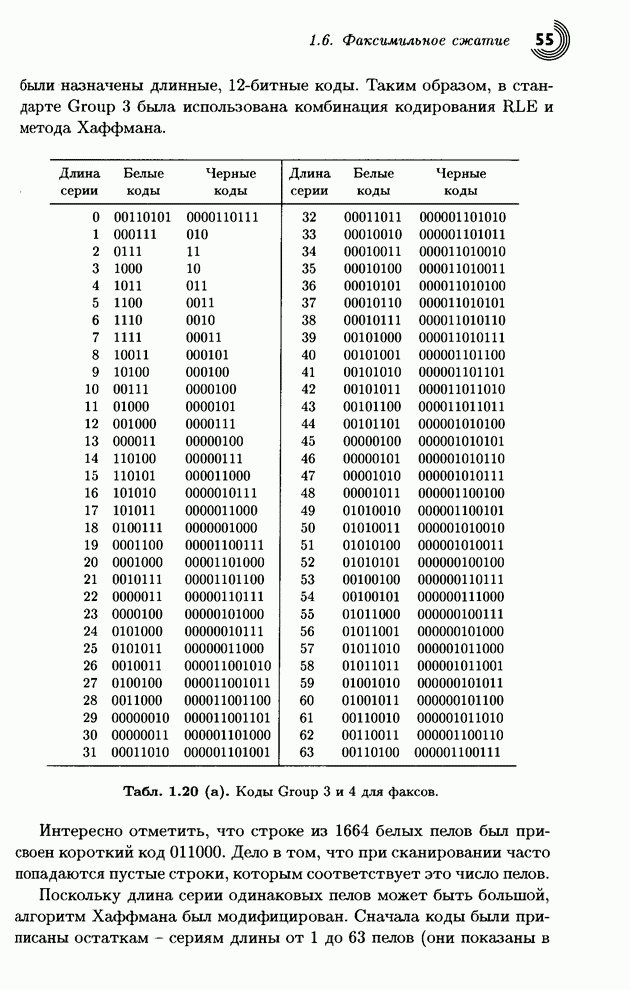
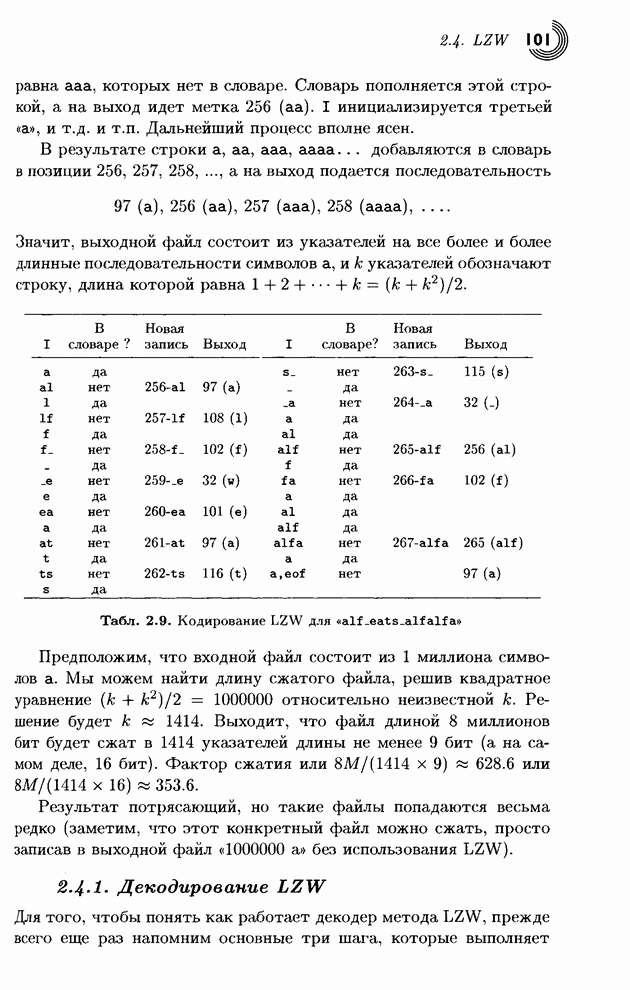
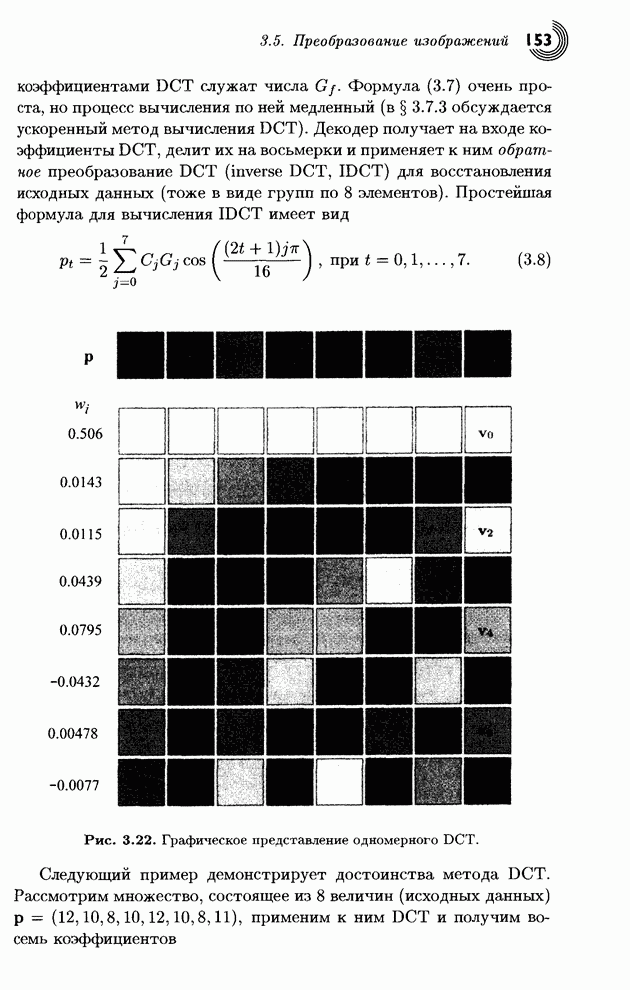
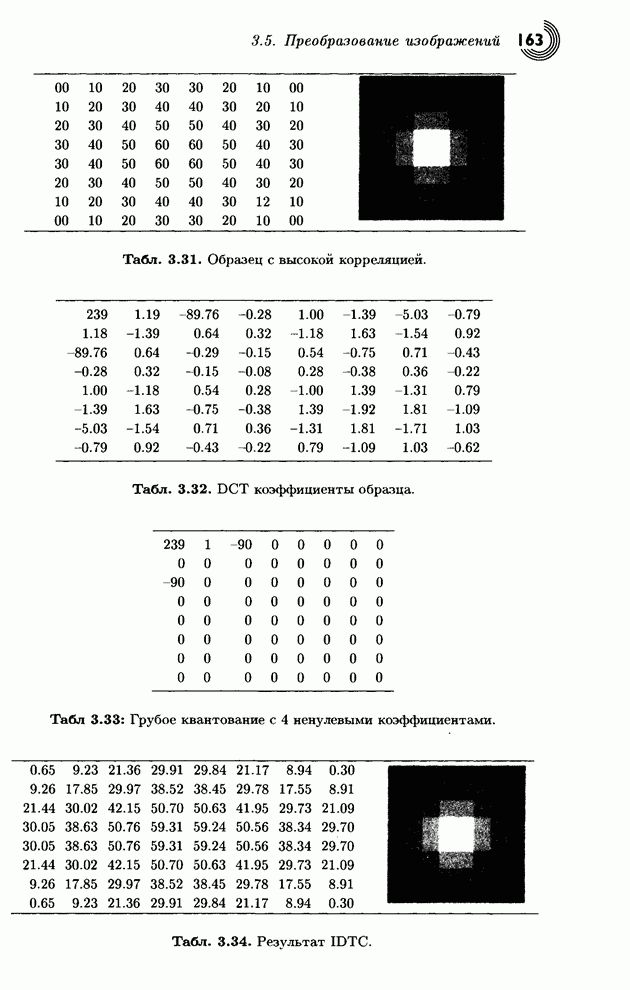
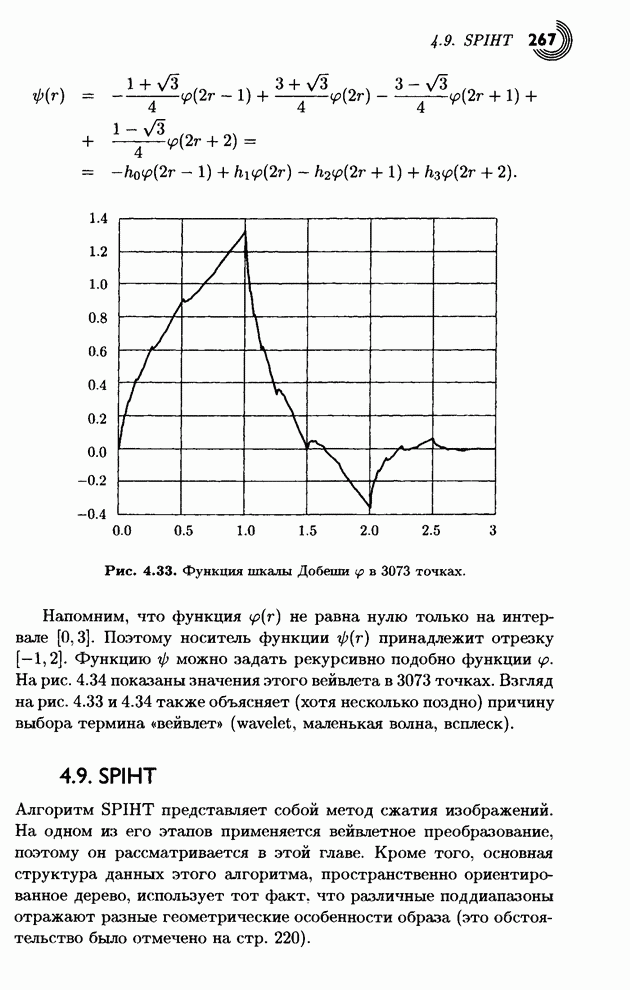
В табл. 1.34 представлен процесс кодирования строки символов «SWISS_MISS». В первом столбце записаны символы на входе. Столбец 2 содержит новые значения переменных Low и High. В третьем столбце эти числа представлены в измененном масштабе с уменьшением High на 1. Строка 4 показывает следующую цифру, посылаемую на выход, а в пятом столбце записаны Low и High после их сдвига влево на одну цифру. Заметьте, что на последнем шаге в выходной файл было записано четыре цифры 3750. Окончательный выходной файл имеет вид 717533750.
Декодер
работает в обратном порядке. В начале сделаны присвоения ![]() ,
, ![]() , и
, и ![]() (первые четыре цифры сжатого файла). Эти
переменные обновляются на каждом шаге процедуры декодирования. Low и High приближаются друг к другу (и к Code) до тех пор, пока их самые
значимые цифры не будут совпадать. Тогда они сдвигаются влево, что приводит к
их разделению, Code тоже сдвигается. На каждом шаге
вычисляется переменная index, которая используется для
нахождения столбца CumFreq табл. 1.24, позволяющего
определить текущий символ.
(первые четыре цифры сжатого файла). Эти
переменные обновляются на каждом шаге процедуры декодирования. Low и High приближаются друг к другу (и к Code) до тех пор, пока их самые
значимые цифры не будут совпадать. Тогда они сдвигаются влево, что приводит к
их разделению, Code тоже сдвигается. На каждом шаге
вычисляется переменная index, которая используется для
нахождения столбца CumFreq табл. 1.24, позволяющего
определить текущий символ.
|
1 |
|
2 |
|
|
3 |
4 |
5 |
|
S |
L= |
0.0 + (1.0 – 0.0) × 0.5 |
= |
0.5 |
5000 |
|
5000 |
|
|
H= |
0.0 + (1.0 – 0.0) × 1.0 |
= |
1.0 |
9999 |
|
9999 |
|
W |
L= |
0.5 + (1.0 – 0.5) × 0.4 |
= |
0.7 |
7000 |
7 |
0000 |
|
|
Н= |
0.5 + (1.0 – 0.5) × 0.5 |
= |
0.75 |
7499 |
7 |
4999 |
|
I |
L= |
0.0 + (0.5 – 0.0) × 0.2 |
= |
0.1 |
1000 |
1 |
0000 |
|
|
Н= |
0.0 + (0.5 – 0.0) × 0.4 |
= |
0.2 |
1999 |
1 |
9999 |
|
S |
L= |
0.0 + (1.0 – 0.0) × 0.5 |
= |
0.5 |
5000 |
|
5000 |
|
|
Н= |
0.0 + (1.0 – 0.0) × 1.0 |
= |
1.0 |
9999 |
|
9999 |
|
S |
L= |
0.5 + (1.0 – 0.5) × 0.5 |
= |
0.75 |
7500 |
|
7500 |
|
|
Н= |
0.5 + (1.0 – 0.5) × 1.0 |
= |
1.0 |
9999 |
|
9999 |
|
- |
L= |
0.75 + (1.0 – 0.75) × 0.0 |
= |
0.75 |
7500 |
7 |
5000 |
|
|
Н= |
0.75 + (1.0 – 0.75) × 0.1 |
= |
0.775 |
7749 |
7 |
7499 |
|
M |
L= |
0.5 + (0.75 – 0.5) × 0.1 |
= |
0.525 |
5250 |
5 |
2500 |
|
|
Н= |
0.5 + (0.75 – 0.5) × 0.2 |
= |
0.55 |
5499 |
5 |
4999 |
|
I |
L= |
0.25 + (0.5 – 0.25) × 0.2 |
= |
0.3 |
3000 |
3 |
0000 |
|
|
Н= |
0.25 + (0.5 – 0.25) × 0.4 |
= |
0.35 |
3499 |
3 |
4999 |
|
S |
L= |
0.0 + (0.5 – 0.0) × 0.5 |
= |
0.25 |
2500 |
|
2500 |
|
|
Н= |
0.0 + (0.5 – 0.0) × 1.0 |
= |
0.5 |
4999 |
|
4999 |
|
S |
L= |
0.25 + (0.5 – 0.25) × 0.5 |
= |
0.375 |
3750 |
3750 |
|
|
|
Н= |
0.25 + (0.5 – 0.25) × 1.0 |
= |
0.5 |
4999 |
|
4999 |
Табл. 1.34. Кодирование «SWISS_MISS» сдвигами.
Каждая итерация цикла состоит из следующих шагов:
1.
Вычислить число ![]() и
округлить его до ближайшего целого (в нашем примере общее CumFreq равно 10).
и
округлить его до ближайшего целого (в нашем примере общее CumFreq равно 10).
2. Использовать index для нахождения следующего символа путем сравнения с CumFreq в табл. 1.24. В следующем примере первое значение index равно 7.1759, а после округления – 7. Число 7 находится в таблице между 5 и 10, поэтому выбран символ «S».
3. Изменить Low и High по формулам:
![]() ;
;
![]() ;
;
где LowCumFreq[X] и HighCumFreq[X] накопленные частоты символа X и символа над X в табл. 1.24.
4. Если самые левые цифры в переменных Low и High совпадают, то сдвинуть Low, High и Code на одну позицию влево. В самую правую позицию Low записать 0, в High – 9, а в Code считать следующую цифру из сжатого файла.
Приведем все шаги декодирования для нашего примера.
0.
Инициализация ![]() ,
,
![]() и
и ![]() .
.
1. ![]() .
Символ «S» выбран.
.
Символ «S» выбран.
![]() .
. ![]() .
.
2. ![]() .
Символ «W» выбран.
.
Символ «W» выбран.
![]()
![]() .
.
После
сдвига и выхода цифры 7 имеем ![]() ,
, ![]() и
и ![]() .
.
3. ![]() .
Символ «I» выбран.
.
Символ «I» выбран.
![]() ,
, ![]() .
.
После
сдвига и выхода цифры 1 имеем ![]() ,
, ![]() и
и ![]() .
.
4. ![]() .
Символ «S» выбран.
.
Символ «S» выбран.
![]() ,
, ![]() .
.
5. ![]() .
Символ «S» выбран.
.
Символ «S» выбран.
![]()
![]() .
.
6. ![]() .
Символ «_» выбран.
.
Символ «_» выбран.
![]()
![]() .
.
После
сдвига и выхода цифры 7 имеем ![]() ,
, ![]() и
и ![]() .
.
7. ![]() .
Символ «М» выбран.
.
Символ «М» выбран.
![]()
![]() .
.
После
сдвига и выхода цифры 5 имеем ![]() ,
, ![]() и
и ![]() .
.
8. ![]() .
Символ «I» выбран.
.
Символ «I» выбран.
![]()
![]() .
.
После
сдвига и выхода цифры 3 имеем ![]() ,
, ![]() и
и ![]() .
.
9. ![]() .
Символ «S» выбран.
.
Символ «S» выбран.
![]() ,
, ![]() .
.
10. ![]() .
Символ «S» выбран.
.
Символ «S» выбран.
![]()
![]() .
.
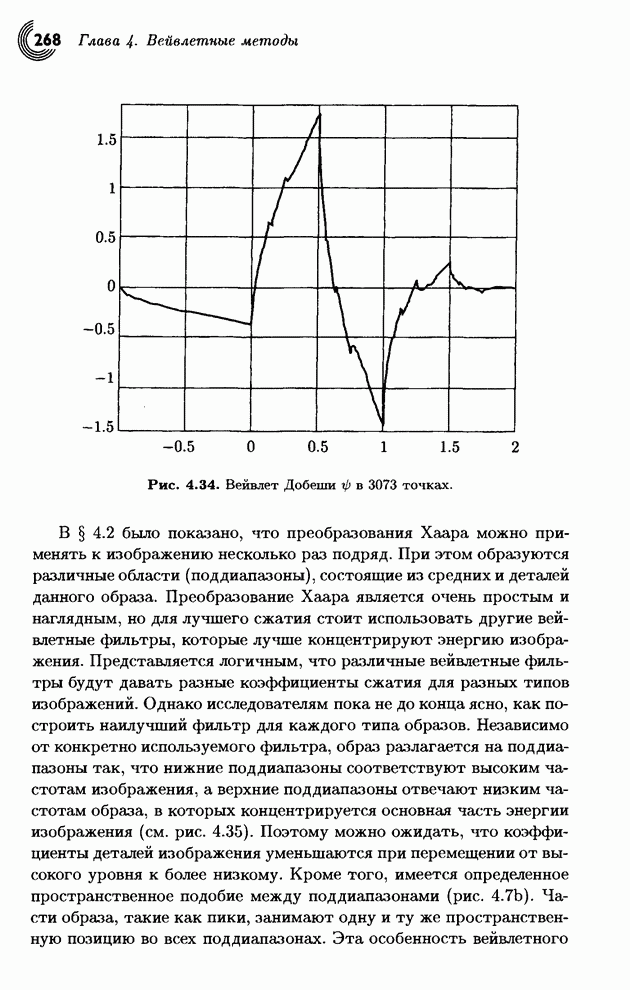
Теперь ясно, что символ eof следует добавлять в исходную таблицу частот и вероятностей. Этот символ будет кодироваться и декодироваться последним, что будет служить сигналом для остановки процесса.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие переводчика
- Предисловие автора
- Введение
- Глава 1. Статистические методы
- 1.1. Энтропия
- 1.2. Коды переменной длины
- 1.3. Декодирование
- 1.4. Кодирование Хаффмана
- 1.4.1. Декодирование Хаффмана
- 1.4.2. Средняя длина кода
- 1.5. Адаптивные коды Хаффмана
- 1.5.1. Несжатые коды
- 1.5.2. Модификация дерева
- 1.5.3. Переполнение счетчика
- 1.5.4. Кодовое переполнение
- 1.5.5. Вариант алгоритма
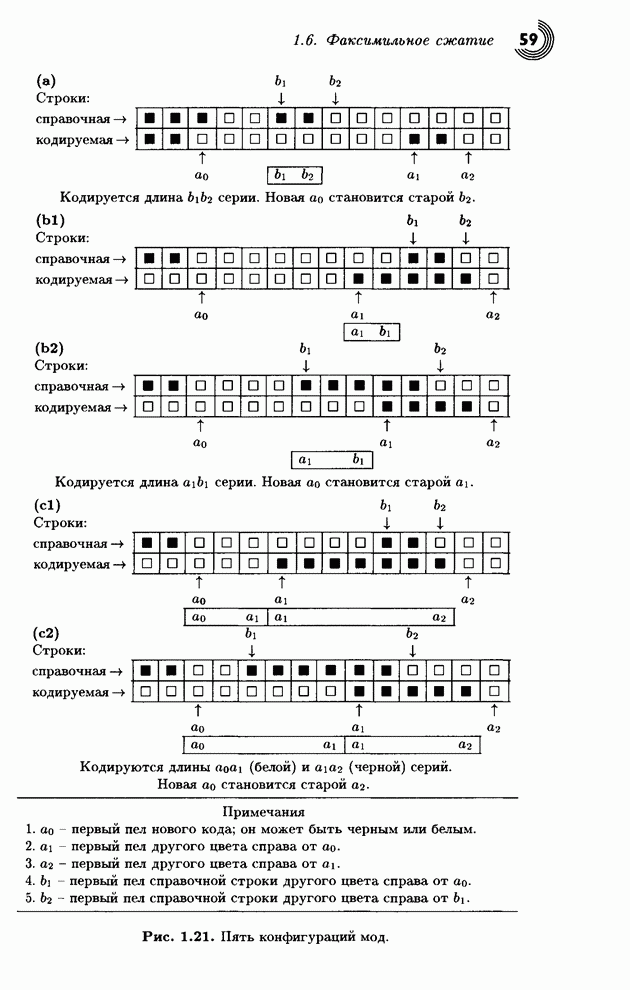
- 1.6. Факсимильное сжатие
- 1.6.1. Одномерное кодирование
- 1.6.2. Двумерное кодирование
- 1.7. Арифметическое кодирование
- 1.7.1. Детали реализации метода
- 1.7.2. Потеря значащих цифр
- 1.7.3. Заключительные замечания
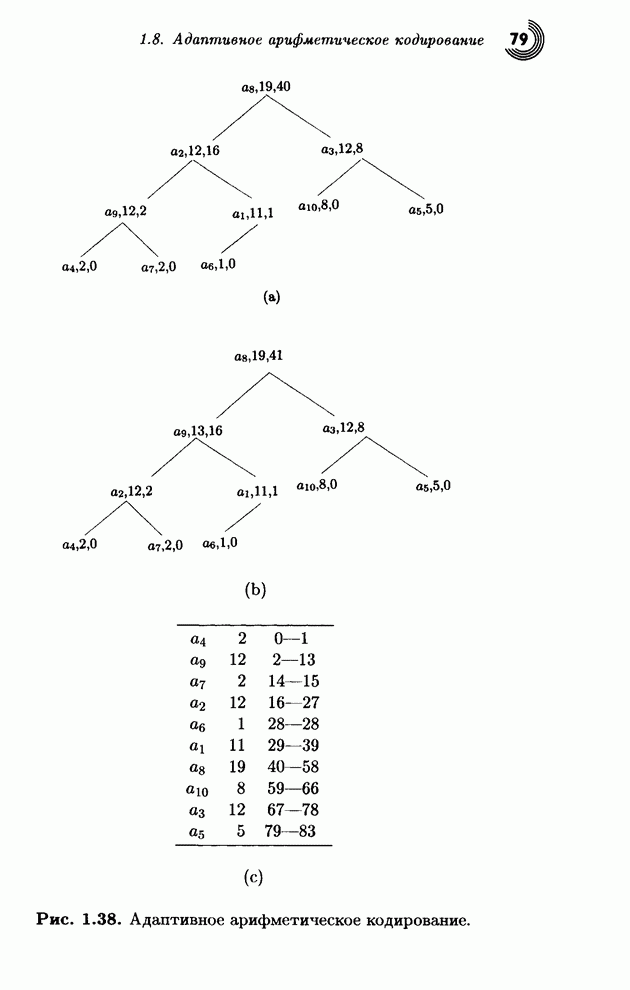
- 1.8. Адаптивное арифметическое кодирование
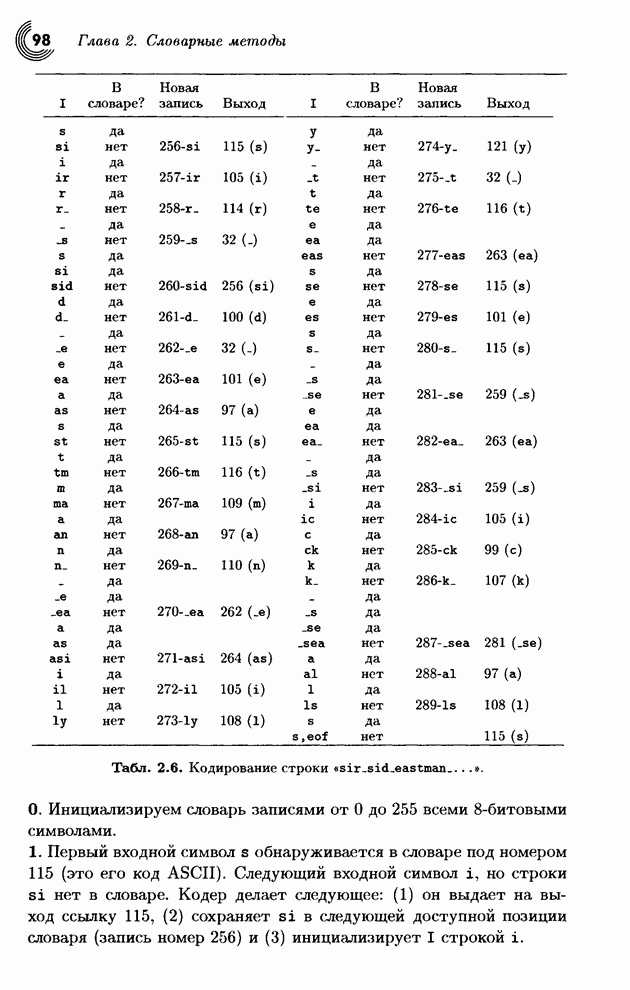
- ГЛАВА 2 СЛОВАРНЫЕ МЕТОДЫ
- 2.1. LZ77 (скользящее окно)
- 2.1.1. Циклическая очередь
- 2.2. LZSS
- 2.2.1. Недостатки
- 2.3. LZ78
- 2.4. LZW
- 2.4.1. Декодирование LZW
- 2.4.2. Структура словаря LZW
- 2.4.3. LZW в практических приложениях
- 2.5. Заключение
- ГЛАВА 3 СЖАТИЕ ИЗОБРАЖЕНИЙ
- 3.1. Введение
- 3.2. Типы изображений
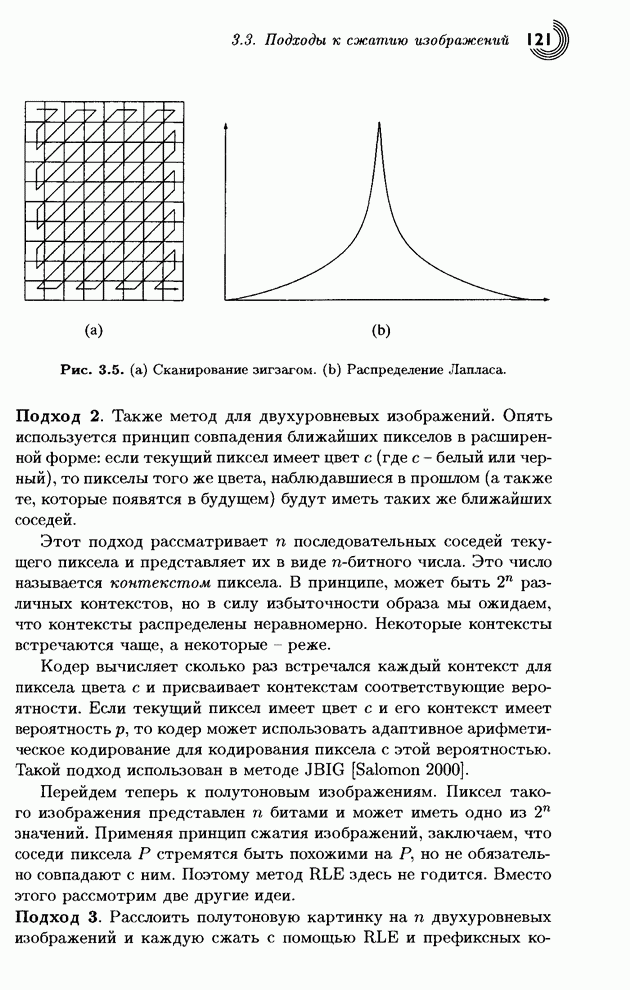
- 3.3. Подходы к сжатию изображений
- 3.3.1. Коды Грея
- 3.3.2. Метрики ошибок
- 3.4. Интуитивные методы
- 3.4.1. Подвыборка
- 3.4.2. Квантование
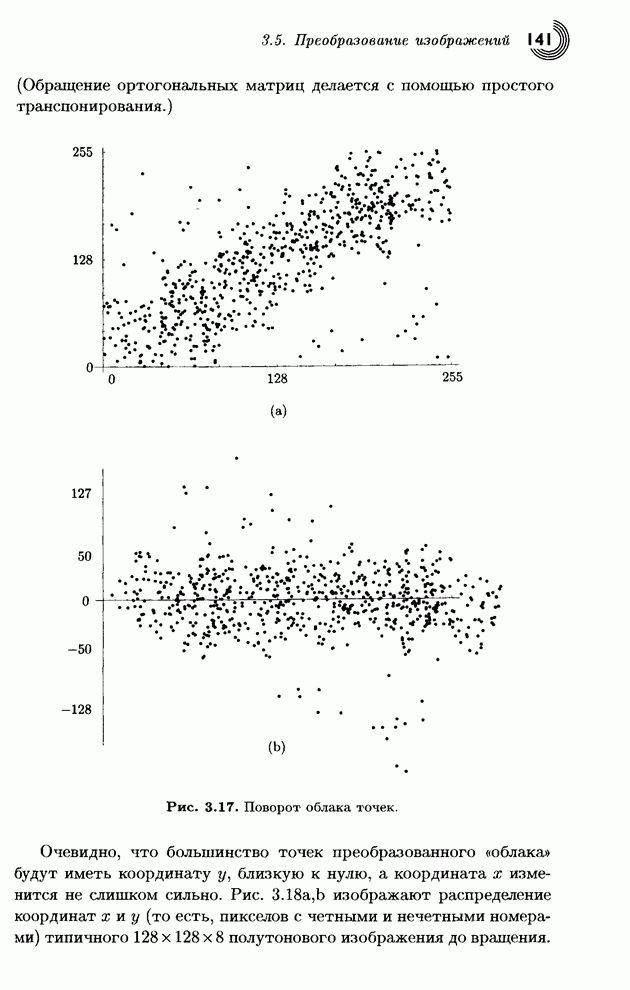
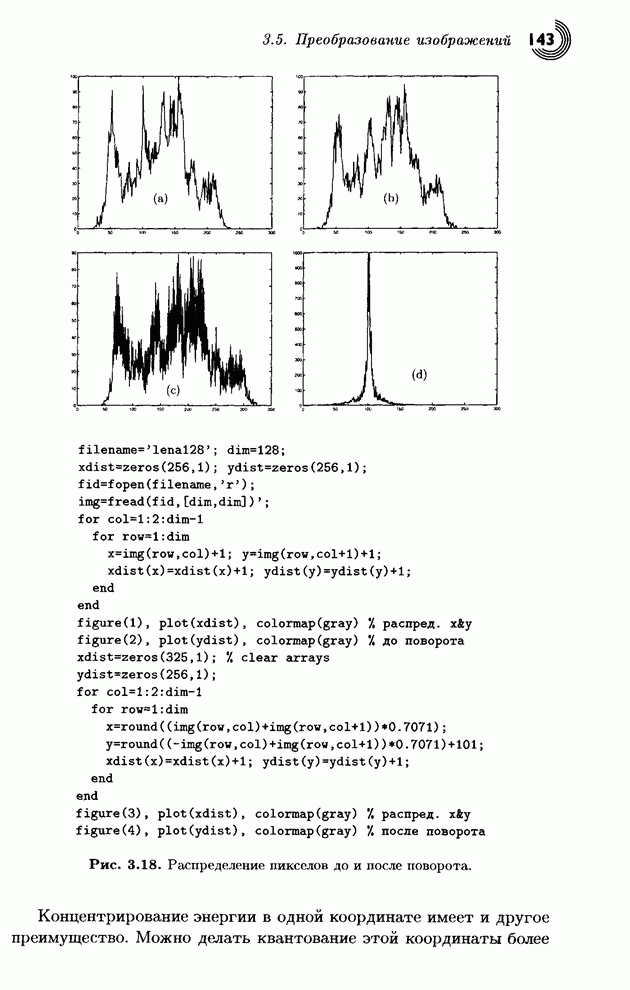
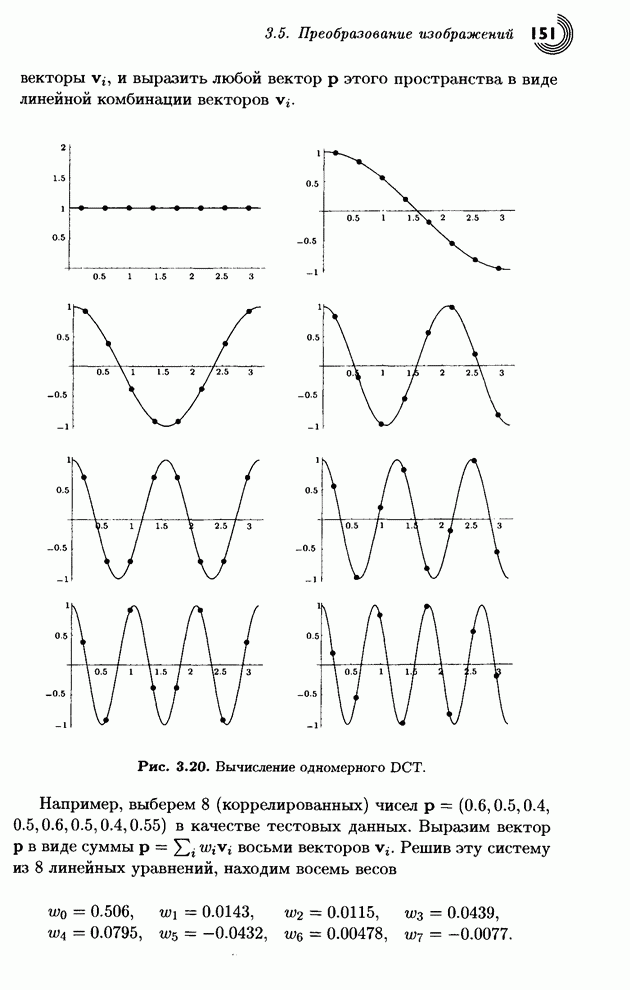
- 3.5. Преобразование изображений
- 3.5.1. Ортогональные преобразования
- 3.5.2. Матричные преобразования
- 3.5.3. Дискретное косинус-преобразование
- 3.5.4. Пример
- 3.5.5. Дискретное синус-преобразование
- 3.5.6. Преобразование Уолша-Адамара
- 3.5.7. Преобразование Хаара
- 3.5.8. Преобразование Кархунена-Лоэвэ
- 3.6. Прогрессирующее сжатие изображений
- 3.7. JPEG
- 3.7.1. Светимость
- 3.7.2. DCT
- 3.7.3. Практическое DCT
- 3.7.4. Квантование
- 3.7.5. Кодирование
- 3.7.6. Мода без потери данных
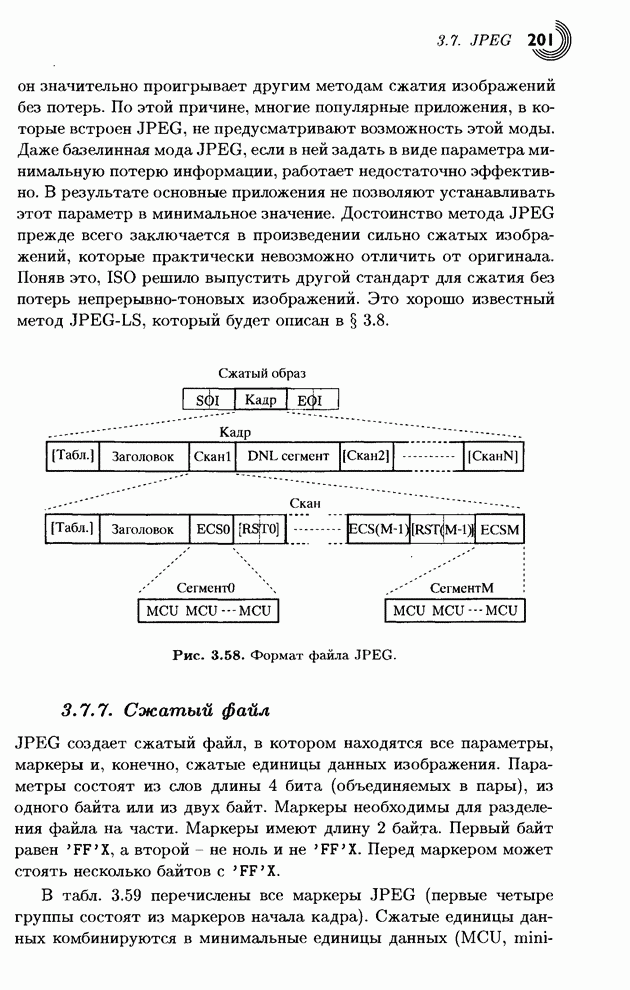
- 3.7.7. Сжатый файл
- 3.7.8. JFIF
- 3.8. JPEG-LS
- 3.8.1. Коды Голомба
- 3.8.2. Основы метода JPEG-LS
- 3.8.3. Кодер
- ГЛАВА 4 ВЕЙВЛЕТНЫЕ МЕТОДЫ
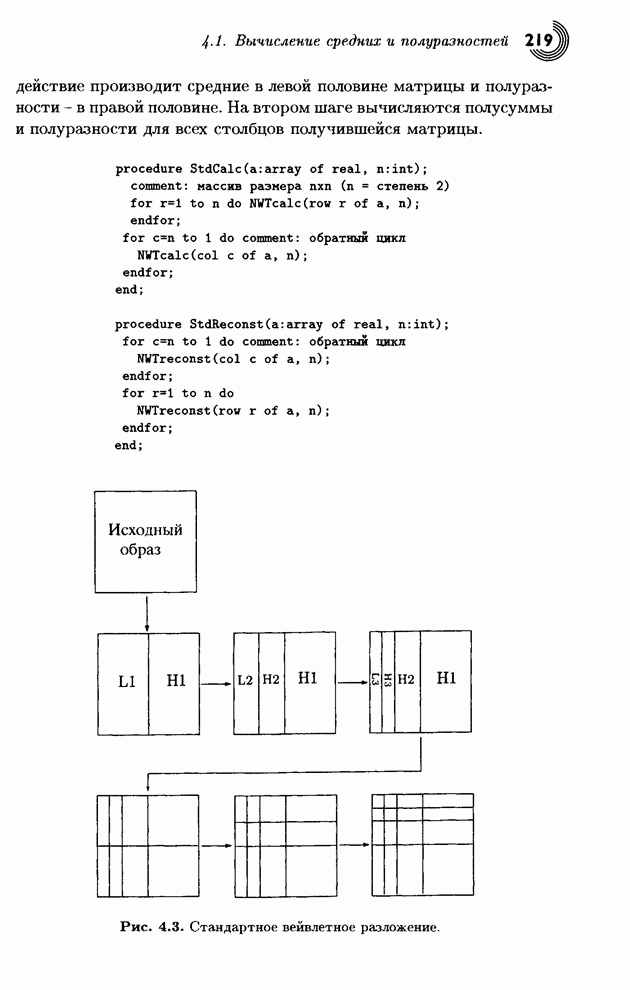
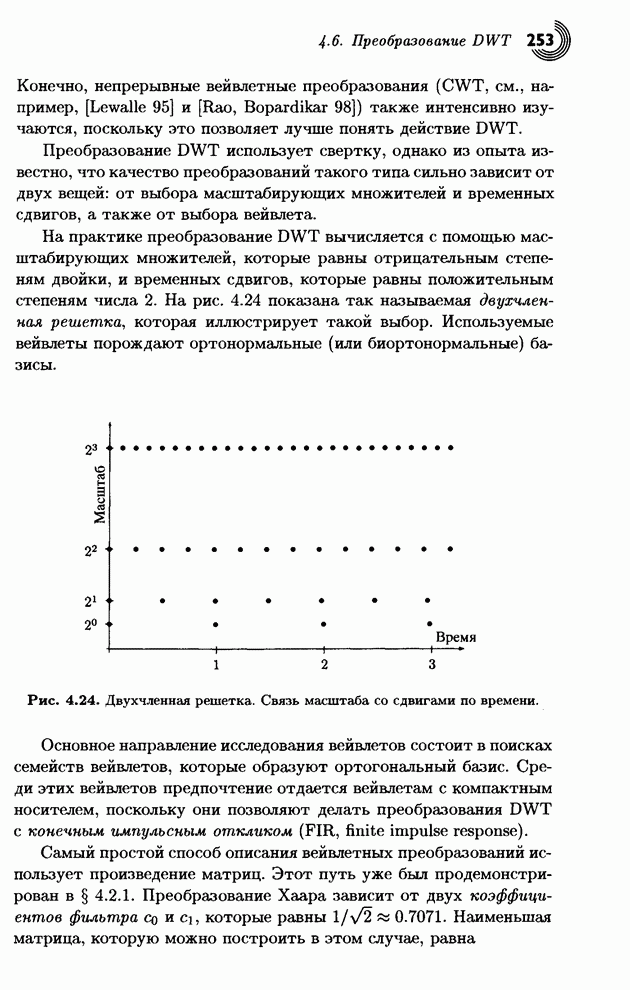
- 4.1. Вычисление средних и полу разностей
- 4.1.1. Обобщение на двумерный случай
- 4.1.2. Свойства преобразования Хаара
- 4.2. Преобразование Хаара
- 4.2.1. Матричная форма
- 4.3. Поддиапазонные преобразования
- 4.4. Банк фильтров
- 4.5. Нахождение коэффициентов фильтра
- 4.6. Преобразование DWT
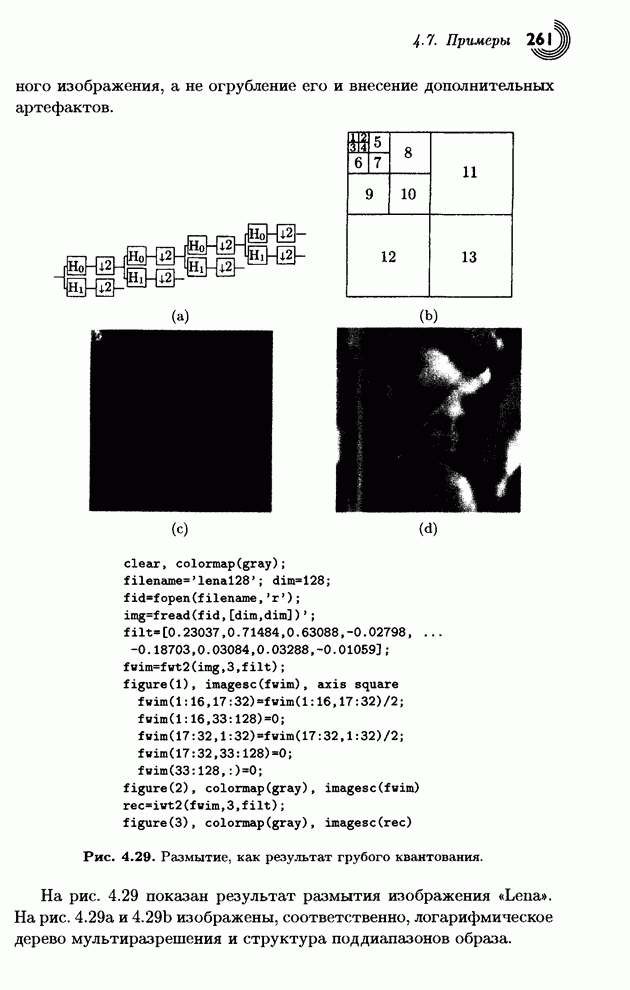
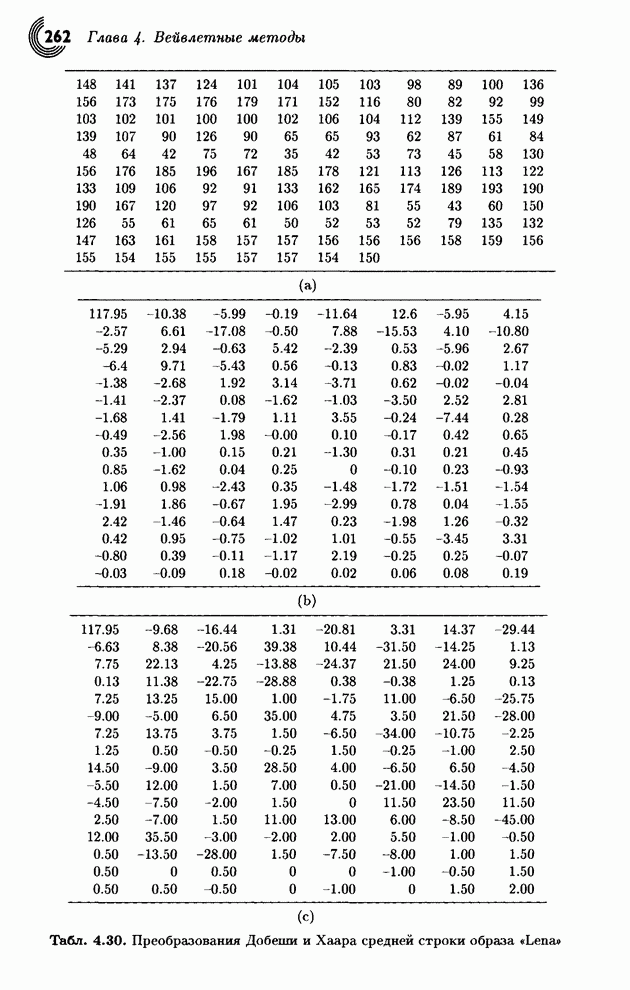
- 4.7. Примеры
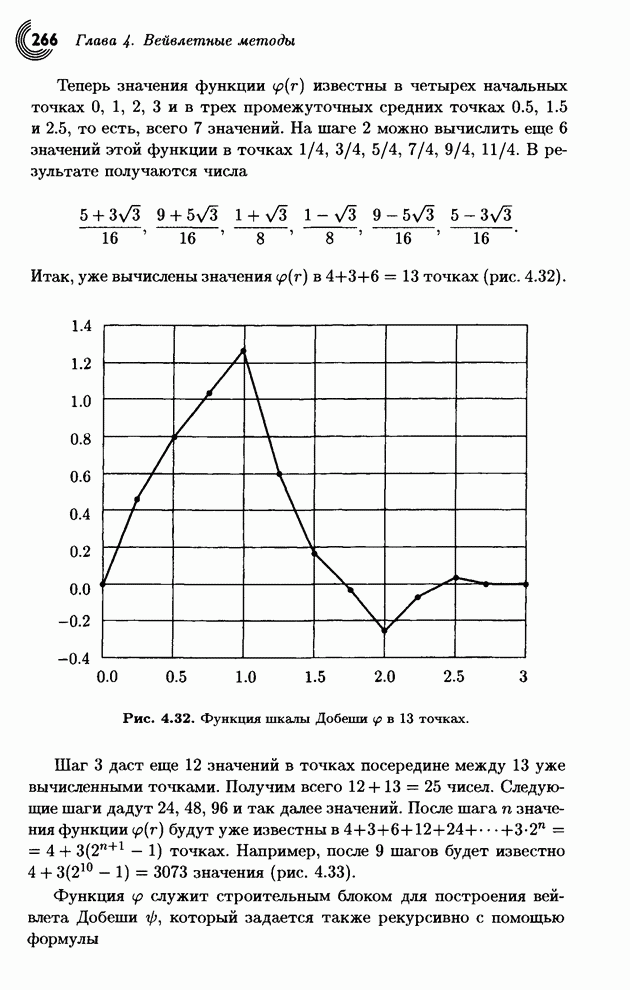
- 4.8. Вейвлеты Добеши
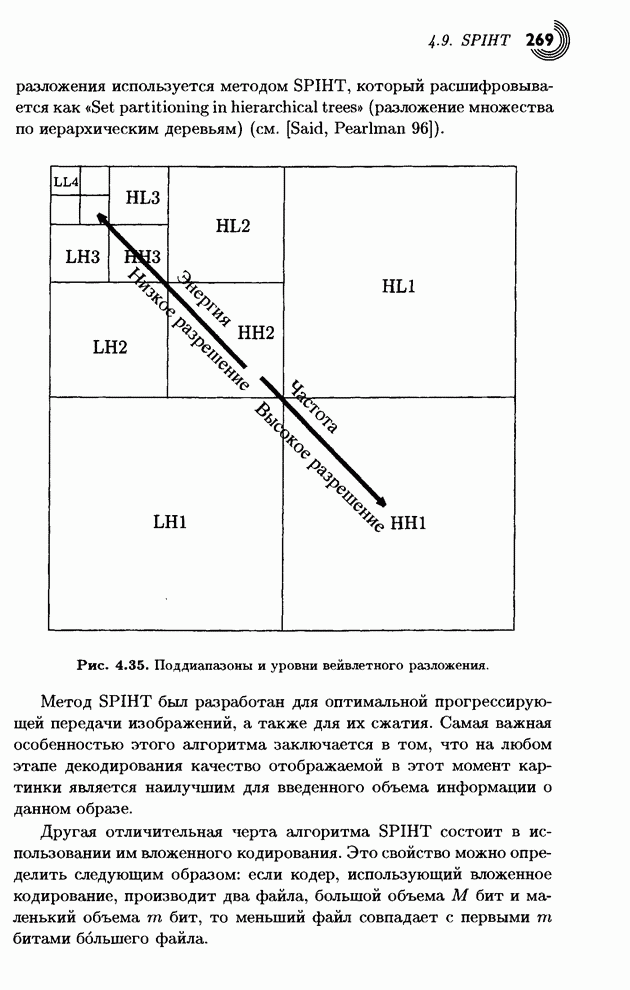
- 4.9. SPIHT
- 4.9.1. Алгоритм сортировки разделением множеств
- 4.9.2. Пространственно ориентированное дерево
- 4.9.3. Кодирование в алгоритме SPIHT
- 4.9.4. Пример
- 4.9.5. QTCQ
- ГЛАВА 5 СЖАТИЕ ВИДЕО
- 5.1. Основные принципы
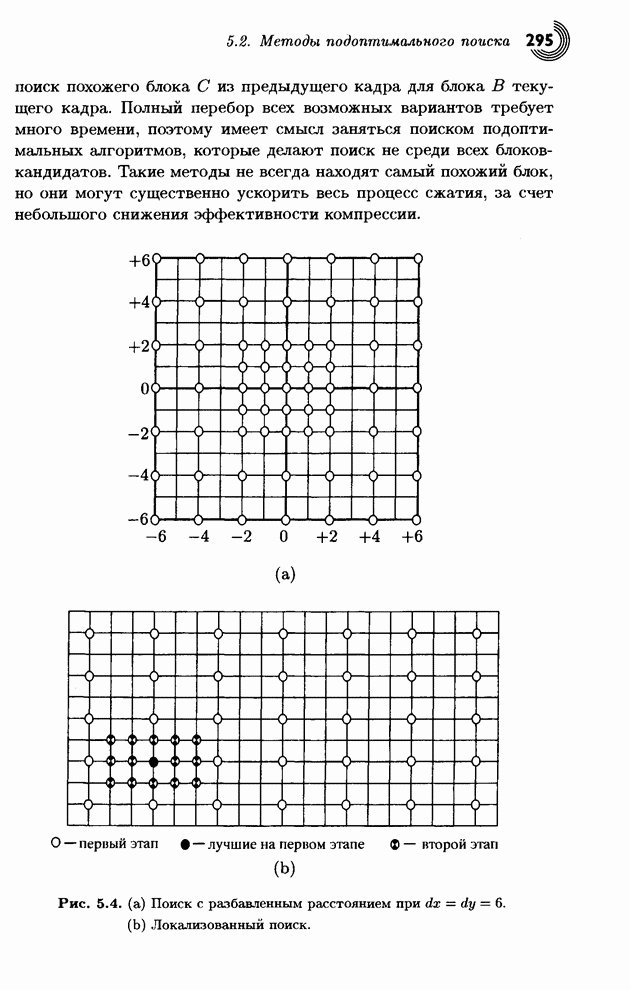
- 5.2. Методы подоптимального поиска
- ГЛАВА 6 СЖАТИЕ ЗВУКА
- 6.1. Звук
- 6.2. Оцифрованный звук
- 6.3. Органы слуха человека
- 6.4. Общепризнанные методы
- 6.5. Сжатие звука в стандарте MPEG-1
- 6.5.1. Кодирование частотной области
- 6.5.2. Формат сжатых данных
- 6.5.3. Психоакустические модели
- 6.5.4. Кодирование: слой III
- Литература
- Глоссарий