| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
1.4.2. Средняя длина кода
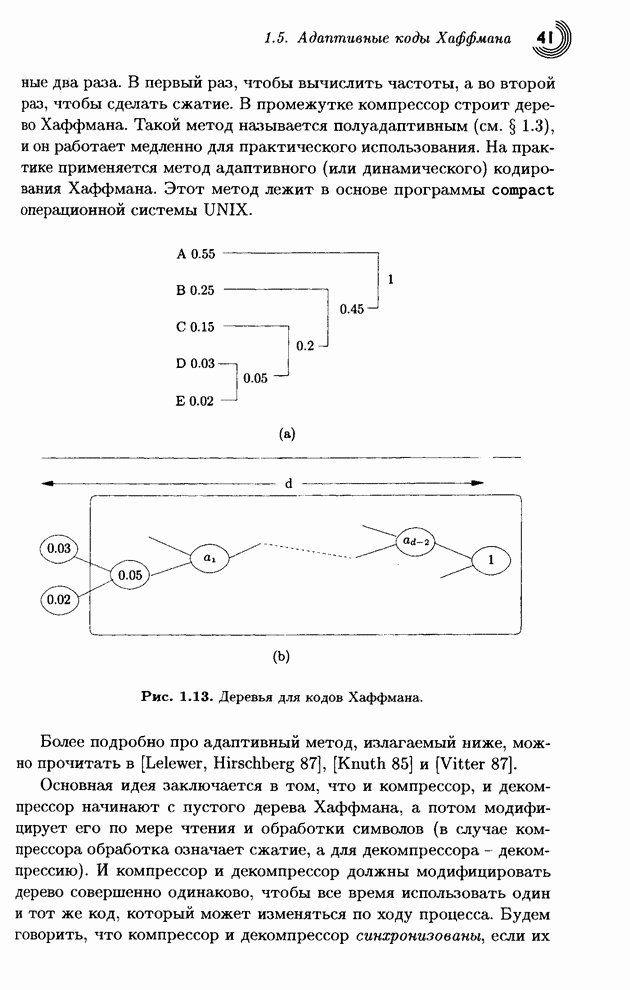
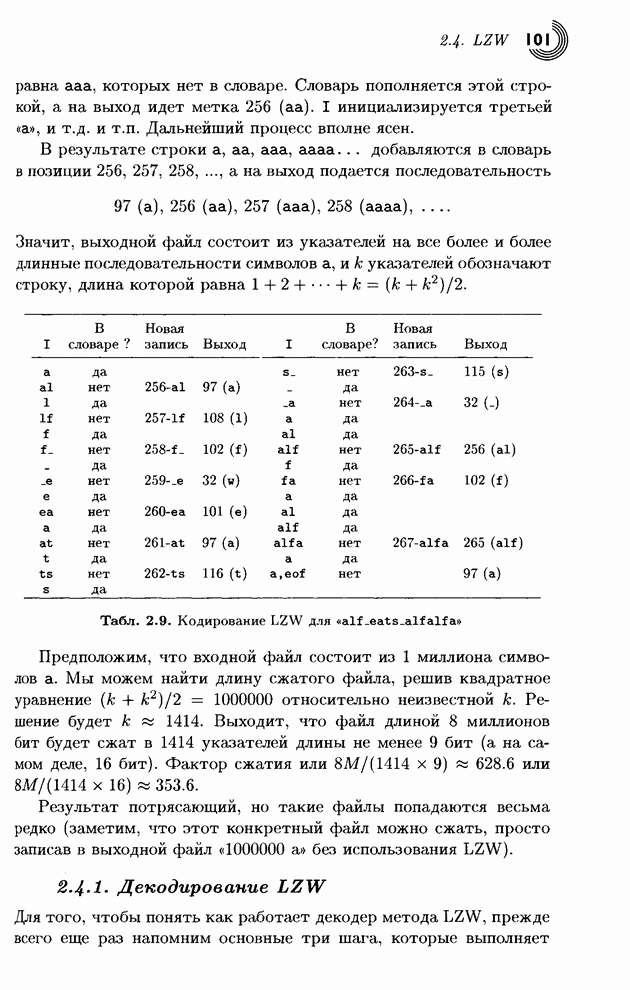
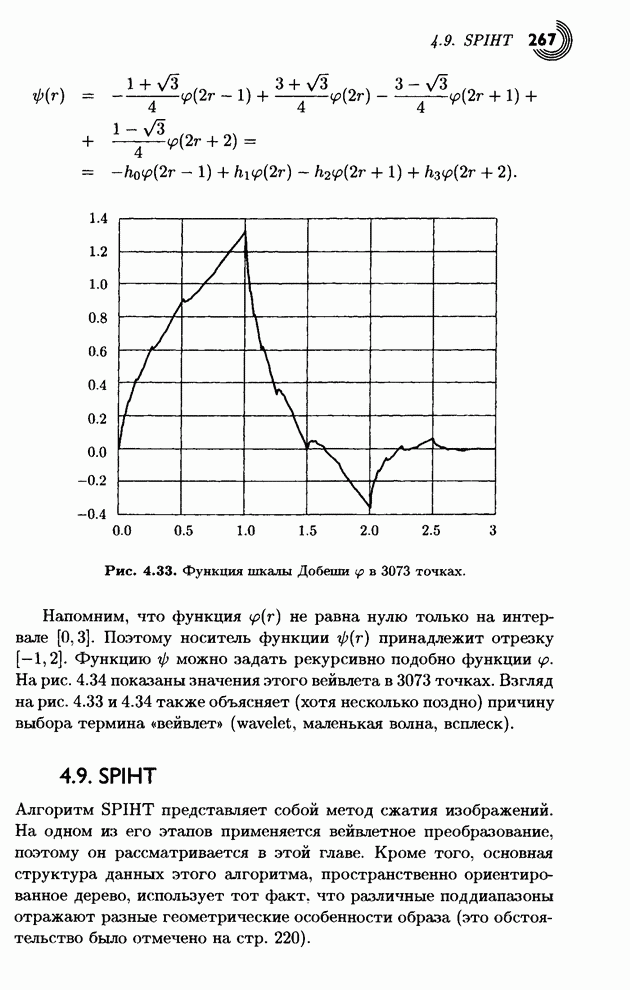
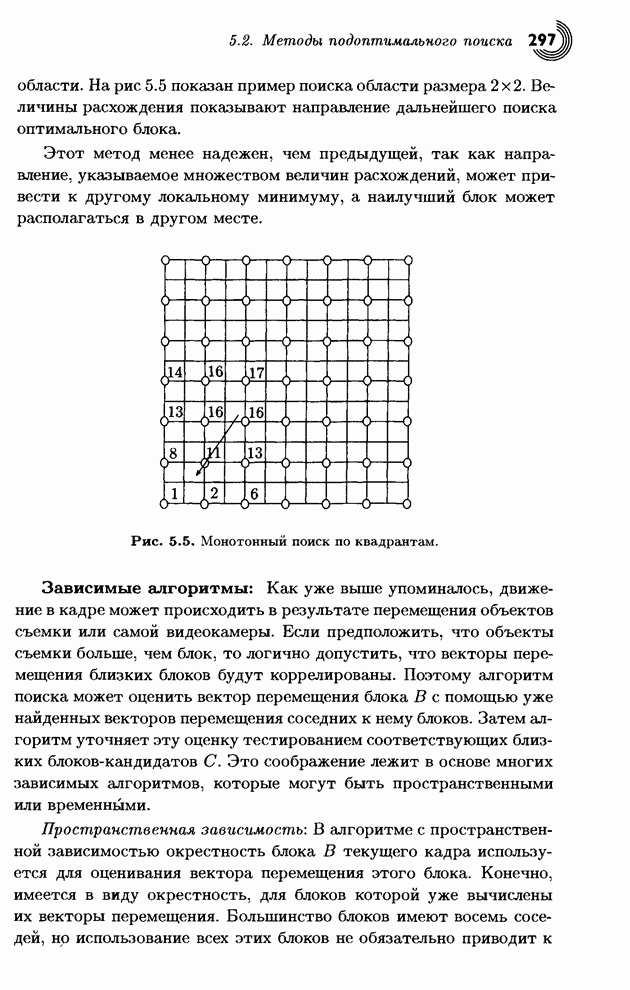
На рис. 1.13а представлено
множество из пяти символов с их вероятностями, а также типичное дерево
Хаффмана. Символ А возникает в 55% случаев и ему присваивается
однобитовый код, что вносит вклад в ![]() в среднюю длину. Символ Е
возникает лишь в 2% случаев. Ему присваивается код длины 4, и его вклад равен
в среднюю длину. Символ Е
возникает лишь в 2% случаев. Ему присваивается код длины 4, и его вклад равен ![]() . Тогда средняя длина
кода равна
. Тогда средняя длина
кода равна ![]() бит
на символ.
бит
на символ.
Удивительно, но тот же результат
получится, если сложить значения вероятностей четырех внутренних узлов кодового
дерева: ![]() .
Это наблюдение дает простой способ вычисления средней длины для кодов Хаффмана
без использования операции умножения. Надо просто сложить значения внутренних
узлов дерева. Табл. 1.11 иллюстрирует, почему этот метод будет работать.
.
Это наблюдение дает простой способ вычисления средней длины для кодов Хаффмана
без использования операции умножения. Надо просто сложить значения внутренних
узлов дерева. Табл. 1.11 иллюстрирует, почему этот метод будет работать.
|
0.05 = |
|
= 0.02 + 0.03 |
|
0.20 = |
0.05 + 0.15 |
= 0.02 + 0.03 + 0.15 |
|
0.45 = |
0.20 + 0.25 |
= 0.02 + 0.03 + 0.15 + 0.25 |
|
1.00 = |
0.45 + 0.55 |
= 0.02 + 0.03 + 0.15 + 0.25 + 0.55 |
Табл. 1.11. Состав узлов.
(В таблице внутренние узлы выделены.) В левом столбце выписаны величины всех внутренних узлов. В правых столбцах показано, как величины складываются из величин предыдущих узлов и из величин листьев. Если сложить числа в левом столбце, то получится 1.7, а складывая числа в остальных столбцах, убеждаемся, что это число 1.7 есть сумма четырех 0.02, четырех 0.03, трех 0.15, двух 0.25 и одного 0.55.
Это рассуждение годится и в общем случае. Легко видеть, что в дереве типа Хаффмана (т.е., дереве, в котором каждый узел есть сумма своих потомков) взвешенная сумма листьев, где вес листа - это его расстояние до корня, равна сумме всех внутренних узлов. (Это свойство было мне сообщено Джоном Мотилом.)
|
0.05 = |
|
= 0.02 + 0.03 + … |
|
|
0.05 + … |
= 0.02 + 0.03 + … |
|
|
|
= 0.02 + 0.03 + … |
|
|
|
|
|
|
|
= 0.02 + 0.03 + … |
|
1.0 = |
|
= 0.02 + 0.03 + … |
Табл. 1.12. Состав узлов.
На рис. 1.13b показано такое дерево, где
предполагается, что два листа 0.02 и 0.03 имеют коды Хаффмана длины ![]() . Внутри дерева эти
листья являются потомками внутреннего узла 0.05, который, в свою очередь,
связан с корнем с помощью
. Внутри дерева эти
листья являются потомками внутреннего узла 0.05, который, в свою очередь,
связан с корнем с помощью ![]() внутренних узлов от
внутренних узлов от ![]() до
до ![]() . Табл. 1.12 состоит из
. Табл. 1.12 состоит из ![]() строк и показывает,
что две величины 0.02 и 0.03 включаются в разные внутренние узлы ровно
строк и показывает,
что две величины 0.02 и 0.03 включаются в разные внутренние узлы ровно ![]() раз. Сложение величин
всех внутренних узлов дает вклад от этих двух листьев равный
раз. Сложение величин
всех внутренних узлов дает вклад от этих двух листьев равный ![]() . Поскольку эти листья
выбраны произвольно, ясно, что эта сумма включает в себя аналогичный вклад от
всех остальных узлов, то есть, равна средней длине кода. Эта число также равно
сумме левого столбца или сумме всех внутренних узлов, которая и определит
среднюю длину кода.
. Поскольку эти листья
выбраны произвольно, ясно, что эта сумма включает в себя аналогичный вклад от
всех остальных узлов, то есть, равна средней длине кода. Эта число также равно
сумме левого столбца или сумме всех внутренних узлов, которая и определит
среднюю длину кода.
Отметим, что в доказательстве нигде не предполагалось, что дерево - двоичное. Поэтому это свойство выполнено для любого дерева, в котором узлы являются суммой своих потомков.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие переводчика
- Предисловие автора
- Введение
- Глава 1. Статистические методы
- 1.1. Энтропия
- 1.2. Коды переменной длины
- 1.3. Декодирование
- 1.4. Кодирование Хаффмана
- 1.4.1. Декодирование Хаффмана
- 1.4.2. Средняя длина кода
- 1.5. Адаптивные коды Хаффмана
- 1.5.1. Несжатые коды
- 1.5.2. Модификация дерева
- 1.5.3. Переполнение счетчика
- 1.5.4. Кодовое переполнение
- 1.5.5. Вариант алгоритма
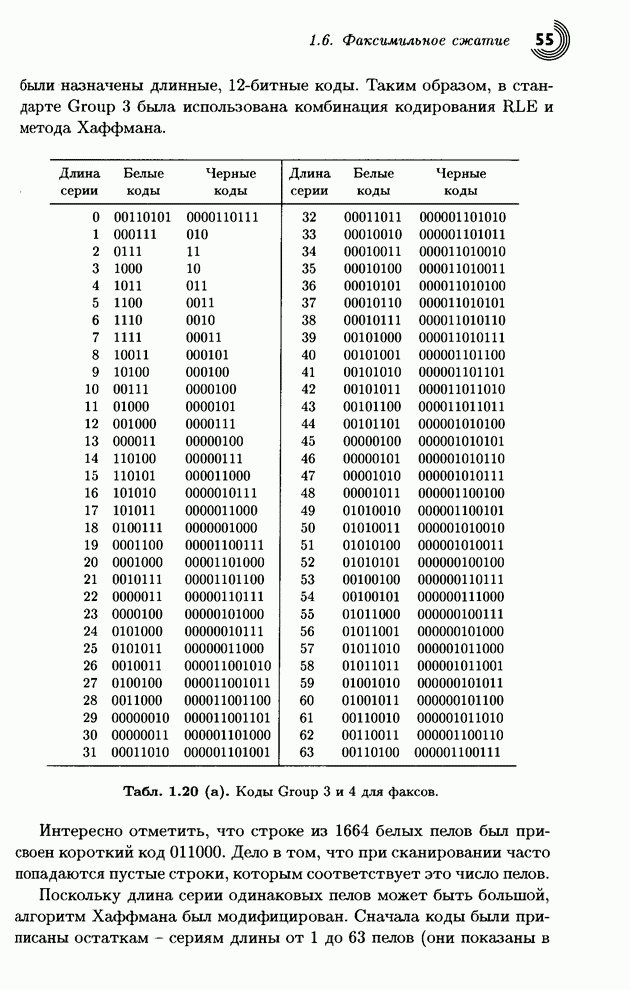
- 1.6. Факсимильное сжатие
- 1.6.1. Одномерное кодирование
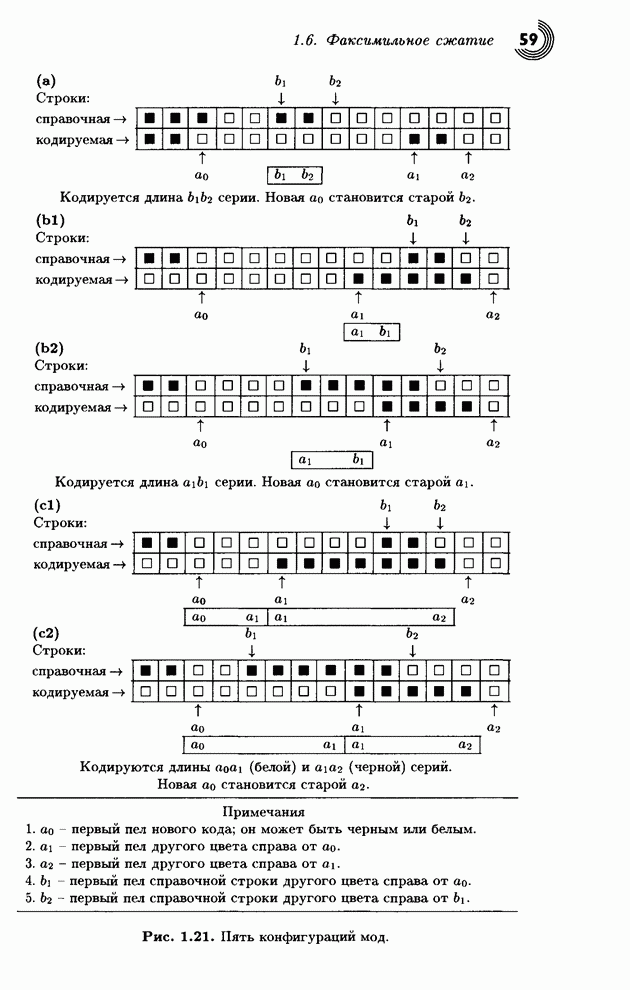
- 1.6.2. Двумерное кодирование
- 1.7. Арифметическое кодирование
- 1.7.1. Детали реализации метода
- 1.7.2. Потеря значащих цифр
- 1.7.3. Заключительные замечания
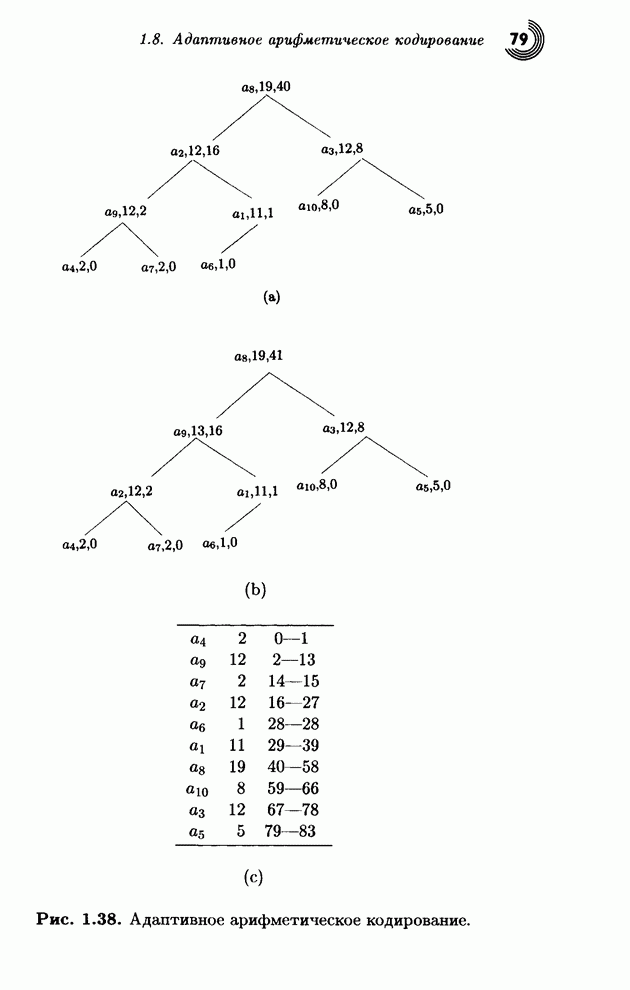
- 1.8. Адаптивное арифметическое кодирование
- ГЛАВА 2 СЛОВАРНЫЕ МЕТОДЫ
- 2.1. LZ77 (скользящее окно)
- 2.1.1. Циклическая очередь
- 2.2. LZSS
- 2.2.1. Недостатки
- 2.3. LZ78
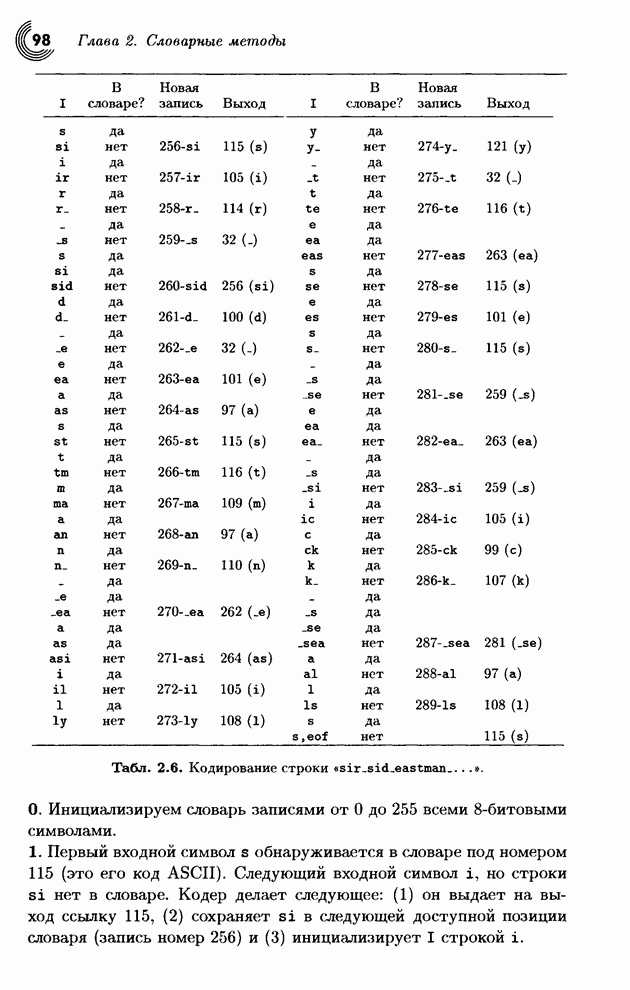
- 2.4. LZW
- 2.4.1. Декодирование LZW
- 2.4.2. Структура словаря LZW
- 2.4.3. LZW в практических приложениях
- 2.5. Заключение
- ГЛАВА 3 СЖАТИЕ ИЗОБРАЖЕНИЙ
- 3.1. Введение
- 3.2. Типы изображений
- 3.3. Подходы к сжатию изображений
- 3.3.1. Коды Грея
- 3.3.2. Метрики ошибок
- 3.4. Интуитивные методы
- 3.4.1. Подвыборка
- 3.4.2. Квантование
- 3.5. Преобразование изображений
- 3.5.1. Ортогональные преобразования
- 3.5.2. Матричные преобразования
- 3.5.3. Дискретное косинус-преобразование
- 3.5.4. Пример
- 3.5.5. Дискретное синус-преобразование
- 3.5.6. Преобразование Уолша-Адамара
- 3.5.7. Преобразование Хаара
- 3.5.8. Преобразование Кархунена-Лоэвэ
- 3.6. Прогрессирующее сжатие изображений
- 3.7. JPEG
- 3.7.1. Светимость
- 3.7.2. DCT
- 3.7.3. Практическое DCT
- 3.7.4. Квантование
- 3.7.5. Кодирование
- 3.7.6. Мода без потери данных
- 3.7.7. Сжатый файл
- 3.7.8. JFIF
- 3.8. JPEG-LS
- 3.8.1. Коды Голомба
- 3.8.2. Основы метода JPEG-LS
- 3.8.3. Кодер
- ГЛАВА 4 ВЕЙВЛЕТНЫЕ МЕТОДЫ
- 4.1. Вычисление средних и полу разностей
- 4.1.1. Обобщение на двумерный случай
- 4.1.2. Свойства преобразования Хаара
- 4.2. Преобразование Хаара
- 4.2.1. Матричная форма
- 4.3. Поддиапазонные преобразования
- 4.4. Банк фильтров
- 4.5. Нахождение коэффициентов фильтра
- 4.6. Преобразование DWT
- 4.7. Примеры
- 4.8. Вейвлеты Добеши
- 4.9. SPIHT
- 4.9.1. Алгоритм сортировки разделением множеств
- 4.9.2. Пространственно ориентированное дерево
- 4.9.3. Кодирование в алгоритме SPIHT
- 4.9.4. Пример
- 4.9.5. QTCQ
- ГЛАВА 5 СЖАТИЕ ВИДЕО
- 5.1. Основные принципы
- 5.2. Методы подоптимального поиска
- ГЛАВА 6 СЖАТИЕ ЗВУКА
- 6.1. Звук
- 6.2. Оцифрованный звук
- 6.3. Органы слуха человека
- 6.4. Общепризнанные методы
- 6.5. Сжатие звука в стандарте MPEG-1
- 6.5.1. Кодирование частотной области
- 6.5.2. Формат сжатых данных
- 6.5.3. Психоакустические модели
- 6.5.4. Кодирование: слой III
- Литература
- Глоссарий