| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
3.5.8. Преобразование Кархунена-Лоэвэ
Преобразование Кархунена-Лоэвэ
(его еще называют преобразованием Хотеллинга) имеет наилучшую эффективность в
смысле концентрации энергии изображения, но по указанным выше причинам, оно
имеет скорее теоретическое, нежели практическое значение. Данное изображение
следует разделить на ![]() блоков по
блоков по ![]() пикселов в каждом, обычно,
пикселов в каждом, обычно, ![]() , но допускаются и
другие значения, а число
, но допускаются и
другие значения, а число ![]() зависит от размера изображения.
Рассматриваются векторы блоков, которые обозначаются при
зависит от размера изображения.
Рассматриваются векторы блоков, которые обозначаются при ![]() . Усредненный вектор равен
. Усредненный вектор равен  . Вводится новое
семейство векторов
. Вводится новое
семейство векторов ![]() для
которого усредненный вектор
для
которого усредненный вектор  равен нулю. Матрицу преобразования (KLT) размера
равен нулю. Матрицу преобразования (KLT) размера ![]() , которую мы будем строить,
обозначим через
, которую мы будем строить,
обозначим через ![]() .
Результатом преобразования вектора
.
Результатом преобразования вектора ![]() будет весовой вектор
будет весовой вектор ![]() . Усреднение вектора
. Усреднение вектора ![]() также равно нулю.
Построим матрицу
также равно нулю.
Построим матрицу ![]() ,
столбцами которой будут служить векторы
,
столбцами которой будут служить векторы ![]() . Рассмотрим также матрицу
. Рассмотрим также матрицу ![]() со столбцами
со столбцами ![]() :
:
![]() ,
,
![]() .
.
Матрицы ![]() и
и ![]() имеют
имеют ![]() строк и
строк и ![]() столбцов. Из определения
векторов
столбцов. Из определения
векторов ![]() заключаем,
что
заключаем,
что ![]() .
.
Все ![]() векторов коэффициентов
векторов коэффициентов ![]() преобразования
Кархунена-Лоэвэ определяются равенствами
преобразования
Кархунена-Лоэвэ определяются равенствами
![]() ,
,
![]() .
.
Таким
образом, вектор ![]() состоит
из
состоит
из ![]() -ых
элементов весовых векторов
-ых
элементов весовых векторов ![]() при
при ![]() .
.
Рассмотрим матрицу-произведение ![]() . Элемент строки
. Элемент строки ![]() и столбца
и столбца ![]() этой матрицы равен
сумме произведений
этой матрицы равен
сумме произведений
 ,
для
,
для ![]() . (3.17)
. (3.17)
Тот
факт, что среднее каждого вектора ![]() равно нулю означает, что каждый
диагональный элемент
равно нулю означает, что каждый
диагональный элемент ![]() матрицы-произведения является дисперсией
(с множителем
матрицы-произведения является дисперсией
(с множителем ![]() )
)
![]() -го элемента
(или
-го элемента
(или ![]() -ой
координаты) вектора
-ой
координаты) вектора ![]() .
В самом деле, из уравнения (3.17) находим, что
.
В самом деле, из уравнения (3.17) находим, что
 .
.
Внедиагональные
элементы матрицы ![]() являются
ковариациями векторов
являются
ковариациями векторов ![]() , то есть, элемент
, то есть, элемент ![]() равен ковариации координат
равен ковариации координат ![]() и
и ![]() векторов
векторов ![]() . Из уравнения (3.17) также
видно, что эти величины равны скалярным произведениям
. Из уравнения (3.17) также
видно, что эти величины равны скалярным произведениям ![]() векторов
векторов ![]() и
и ![]() . Одной из основных задач
преобразования изображения является приведение его к декоррелированной форме
координат векторов. Теория вероятности говорит о том, что две координаты
являются декоррелированными, если их ковариация равна нулю (другая цель - это
концентрация энергии, но эти две задачи тесно связаны). Значит, необходимо
найти матрицу
. Одной из основных задач
преобразования изображения является приведение его к декоррелированной форме
координат векторов. Теория вероятности говорит о том, что две координаты
являются декоррелированными, если их ковариация равна нулю (другая цель - это
концентрация энергии, но эти две задачи тесно связаны). Значит, необходимо
найти матрицу ![]() ,
такую, что произведение
,
такую, что произведение ![]() будет диагональной матрицей.
будет диагональной матрицей.
Из определения матрицы ![]() находим, что
находим, что
![]() .
.
Матрица
![]() является
симметрической, ее элементами служат ковариации координат векторов
является
симметрической, ее элементами служат ковариации координат векторов ![]() , то есть,
, то есть,
 ,
при
,
при ![]() .
.
Раз матрица ![]() - симметрическая, то ее
собственные векторы ортогональны. Нормализуем их (то есть, сделаем их
ортонормальными) и выберем их в качестве строк матрицы
- симметрическая, то ее
собственные векторы ортогональны. Нормализуем их (то есть, сделаем их
ортонормальными) и выберем их в качестве строк матрицы ![]() . Получим следующий результат:
. Получим следующий результат:
 .
.
При таком выборе матрицы ![]() матрица
матрица ![]() будет диагональной,
причем элементы диагонали являются собственными числами матрицы
будет диагональной,
причем элементы диагонали являются собственными числами матрицы ![]() . Матрица
. Матрица ![]() служит матрицей
преобразования Кархунена-Лоэвэ; ее строки являются базисными векторами KLT, а энергией (дисперсией)
преобразованных векторов служат собственные числа
служит матрицей
преобразования Кархунена-Лоэвэ; ее строки являются базисными векторами KLT, а энергией (дисперсией)
преобразованных векторов служат собственные числа ![]() матрицы
матрицы ![]() .
.
Базисные векторы для KLT вычисляются с помощью пикселов исходного изображения, то есть, они зависят от исходных данных. В конкретном методе сжатия эти векторы следует записывать в сжатый файл для использования декодером. Кроме того не известен быстрый метод вычисления этих векторов. Все эти факты делают метод KLT сугубо теоретическим без реальных приложений.
Честность - вот лучший образ.
- Том Уилсон
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие переводчика
- Предисловие автора
- Введение
- Глава 1. Статистические методы
- 1.1. Энтропия
- 1.2. Коды переменной длины
- 1.3. Декодирование
- 1.4. Кодирование Хаффмана
- 1.4.1. Декодирование Хаффмана
- 1.4.2. Средняя длина кода
- 1.5. Адаптивные коды Хаффмана
- 1.5.1. Несжатые коды
- 1.5.2. Модификация дерева
- 1.5.3. Переполнение счетчика
- 1.5.4. Кодовое переполнение
- 1.5.5. Вариант алгоритма
- 1.6. Факсимильное сжатие
- 1.6.1. Одномерное кодирование
- 1.6.2. Двумерное кодирование
- 1.7. Арифметическое кодирование
- 1.7.1. Детали реализации метода
- 1.7.2. Потеря значащих цифр
- 1.7.3. Заключительные замечания
- 1.8. Адаптивное арифметическое кодирование
- ГЛАВА 2 СЛОВАРНЫЕ МЕТОДЫ
- 2.1. LZ77 (скользящее окно)
- 2.1.1. Циклическая очередь
- 2.2. LZSS
- 2.2.1. Недостатки
- 2.3. LZ78
- 2.4. LZW
- 2.4.1. Декодирование LZW
- 2.4.2. Структура словаря LZW
- 2.4.3. LZW в практических приложениях
- 2.5. Заключение
- ГЛАВА 3 СЖАТИЕ ИЗОБРАЖЕНИЙ
- 3.1. Введение
- 3.2. Типы изображений
- 3.3. Подходы к сжатию изображений
- 3.3.1. Коды Грея
- 3.3.2. Метрики ошибок
- 3.4. Интуитивные методы
- 3.4.1. Подвыборка
- 3.4.2. Квантование
- 3.5. Преобразование изображений
- 3.5.1. Ортогональные преобразования
- 3.5.2. Матричные преобразования
- 3.5.3. Дискретное косинус-преобразование
- 3.5.4. Пример
- 3.5.5. Дискретное синус-преобразование
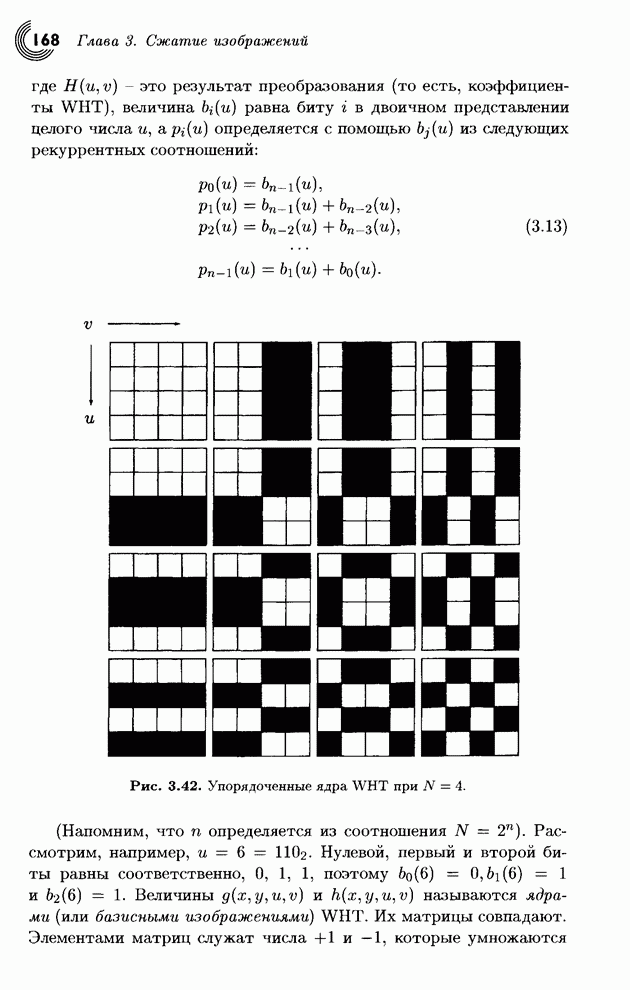
- 3.5.6. Преобразование Уолша-Адамара
- 3.5.7. Преобразование Хаара
- 3.5.8. Преобразование Кархунена-Лоэвэ
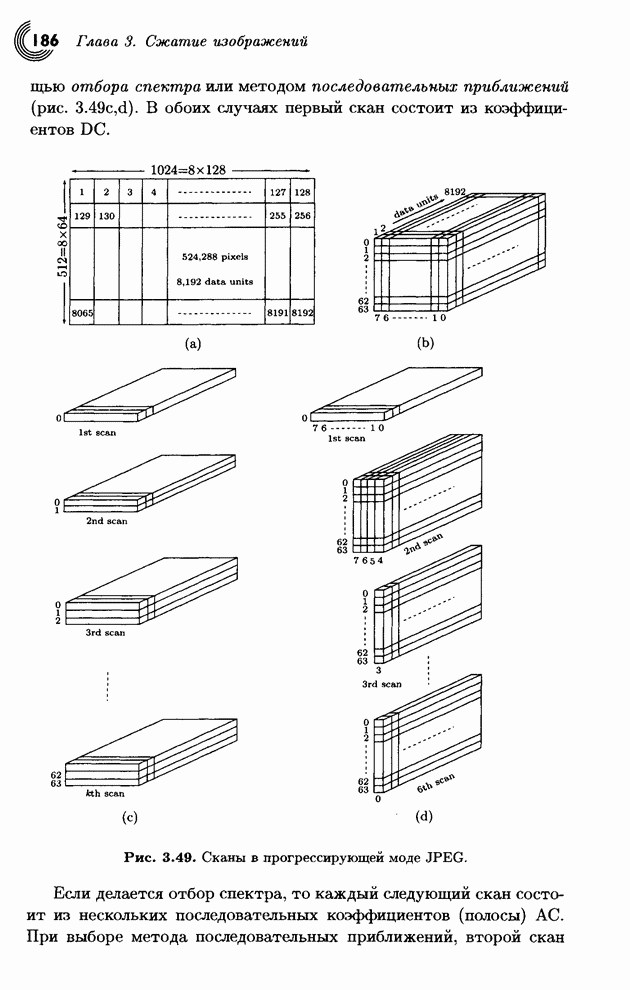
- 3.6. Прогрессирующее сжатие изображений
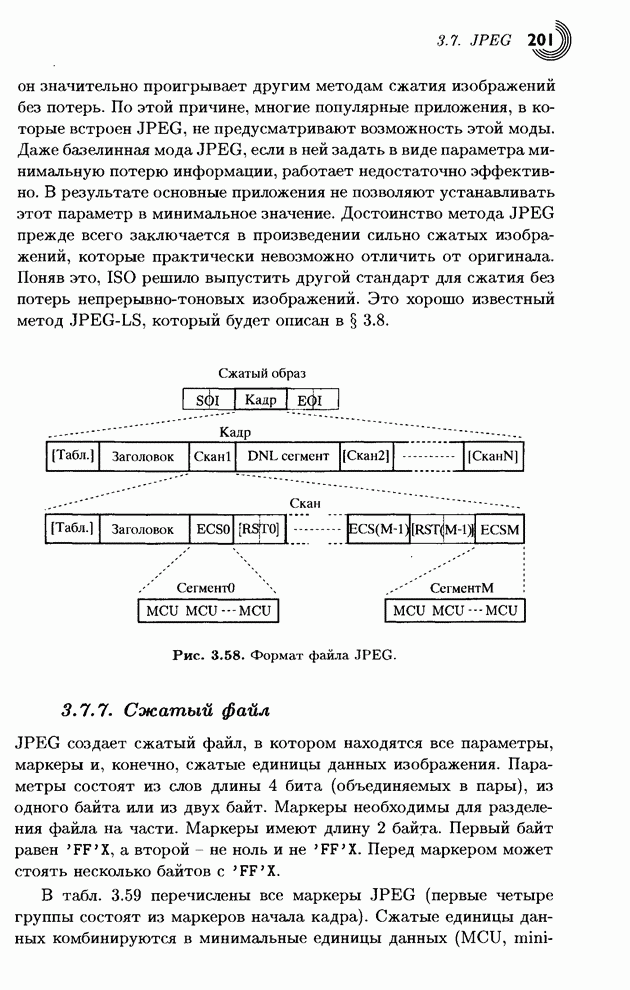
- 3.7. JPEG
- 3.7.1. Светимость
- 3.7.2. DCT
- 3.7.3. Практическое DCT
- 3.7.4. Квантование
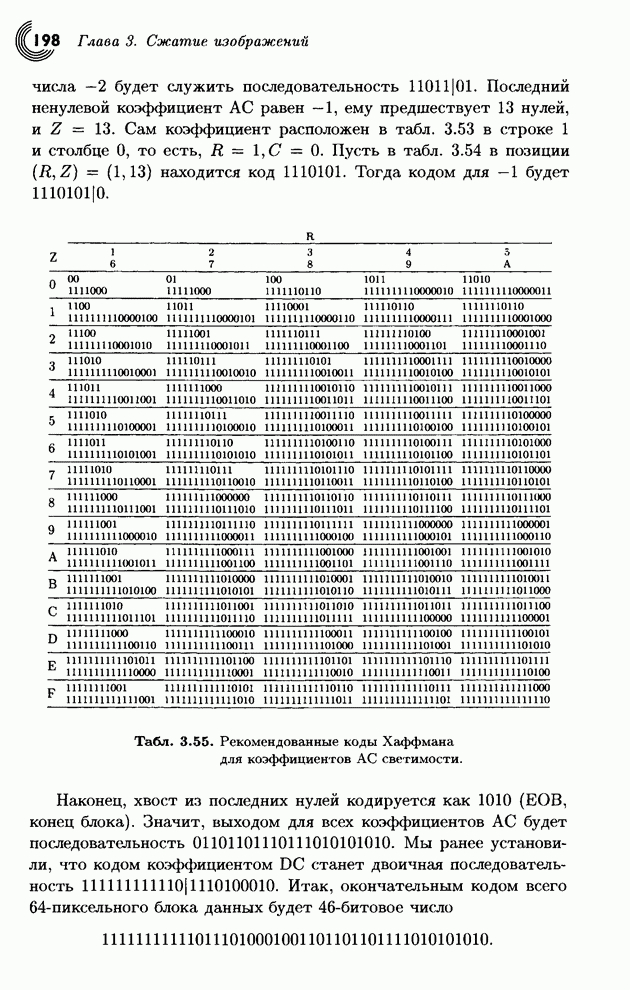
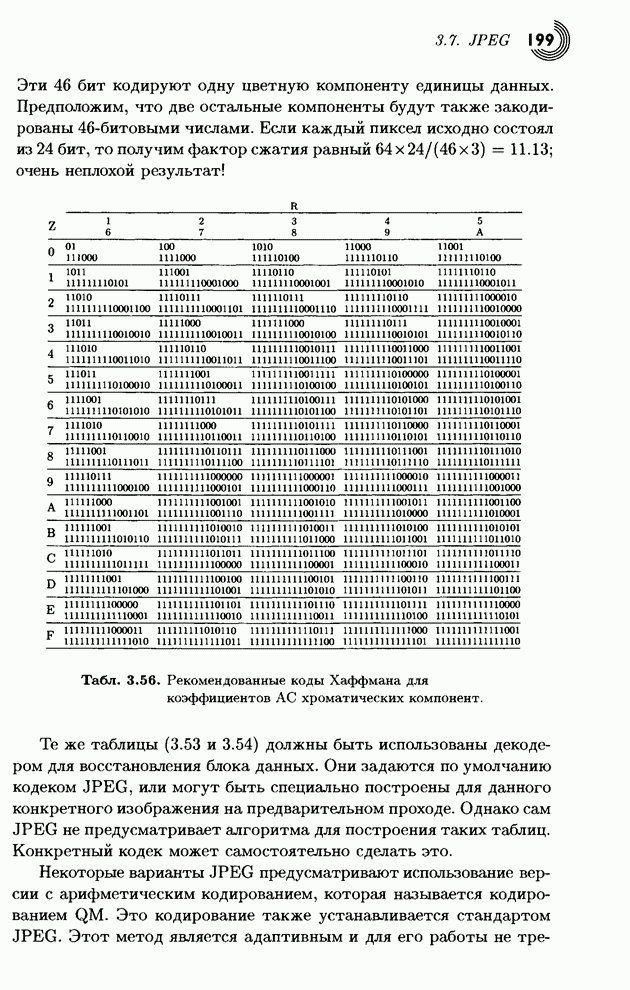
- 3.7.5. Кодирование
- 3.7.6. Мода без потери данных
- 3.7.7. Сжатый файл
- 3.7.8. JFIF
- 3.8. JPEG-LS
- 3.8.1. Коды Голомба
- 3.8.2. Основы метода JPEG-LS
- 3.8.3. Кодер
- ГЛАВА 4 ВЕЙВЛЕТНЫЕ МЕТОДЫ
- 4.1. Вычисление средних и полу разностей
- 4.1.1. Обобщение на двумерный случай
- 4.1.2. Свойства преобразования Хаара
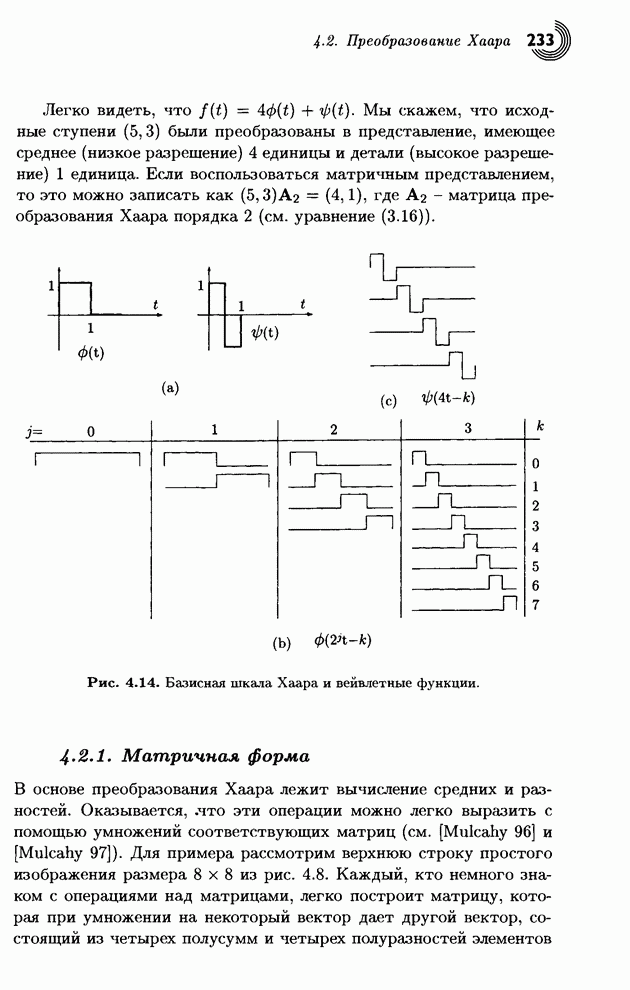
- 4.2. Преобразование Хаара
- 4.2.1. Матричная форма
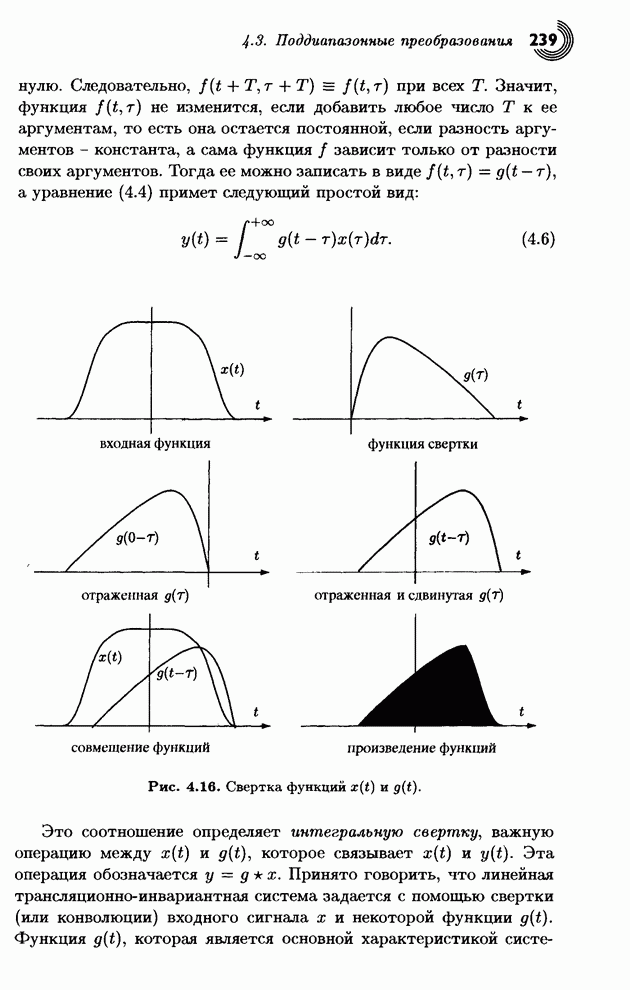
- 4.3. Поддиапазонные преобразования
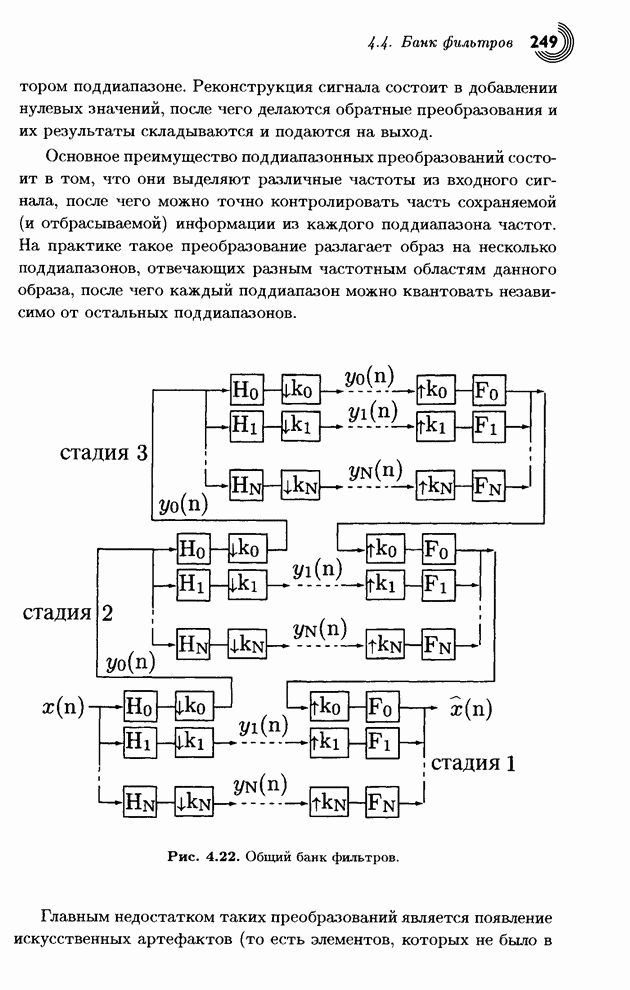
- 4.4. Банк фильтров
- 4.5. Нахождение коэффициентов фильтра
- 4.6. Преобразование DWT
- 4.7. Примеры
- 4.8. Вейвлеты Добеши
- 4.9. SPIHT
- 4.9.1. Алгоритм сортировки разделением множеств
- 4.9.2. Пространственно ориентированное дерево
- 4.9.3. Кодирование в алгоритме SPIHT
- 4.9.4. Пример
- 4.9.5. QTCQ
- ГЛАВА 5 СЖАТИЕ ВИДЕО
- 5.1. Основные принципы
- 5.2. Методы подоптимального поиска
- ГЛАВА 6 СЖАТИЕ ЗВУКА
- 6.1. Звук
- 6.2. Оцифрованный звук
- 6.3. Органы слуха человека
- 6.4. Общепризнанные методы
- 6.5. Сжатие звука в стандарте MPEG-1
- 6.5.1. Кодирование частотной области
- 6.5.2. Формат сжатых данных
- 6.5.3. Психоакустические модели
- 6.5.4. Кодирование: слой III
- Литература
- Глоссарий