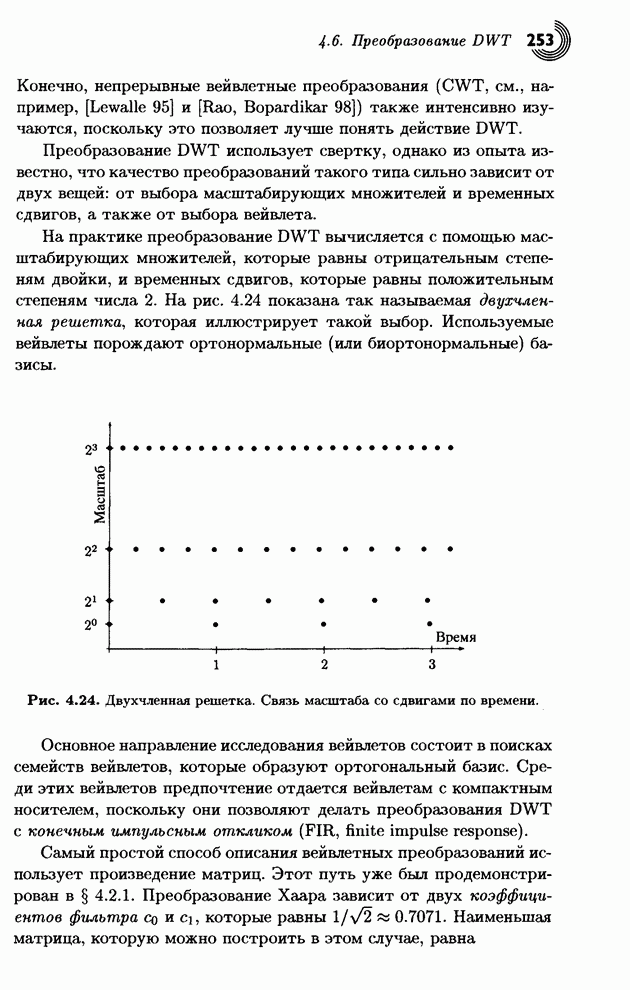
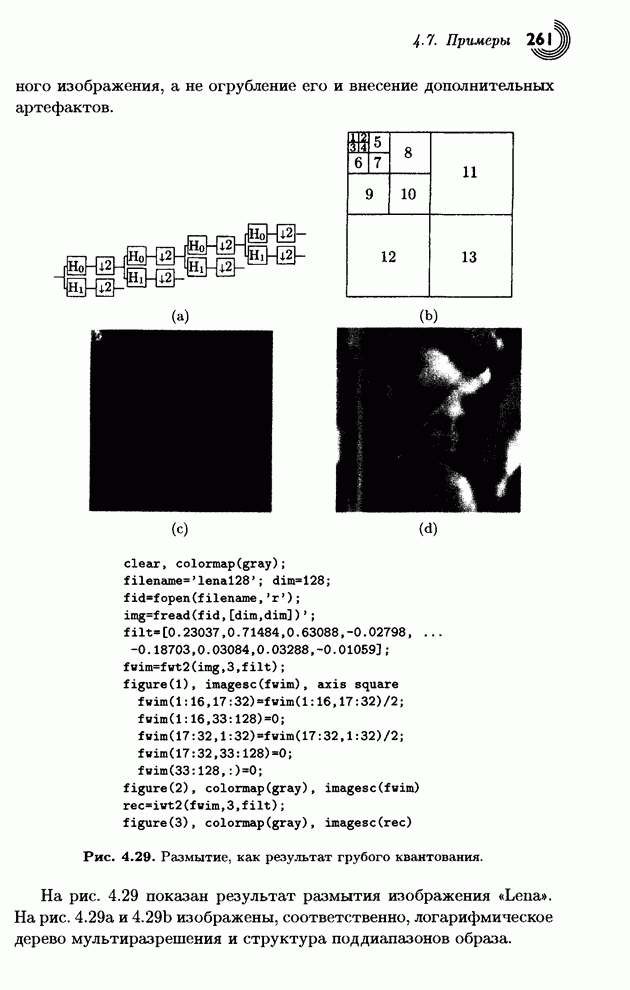
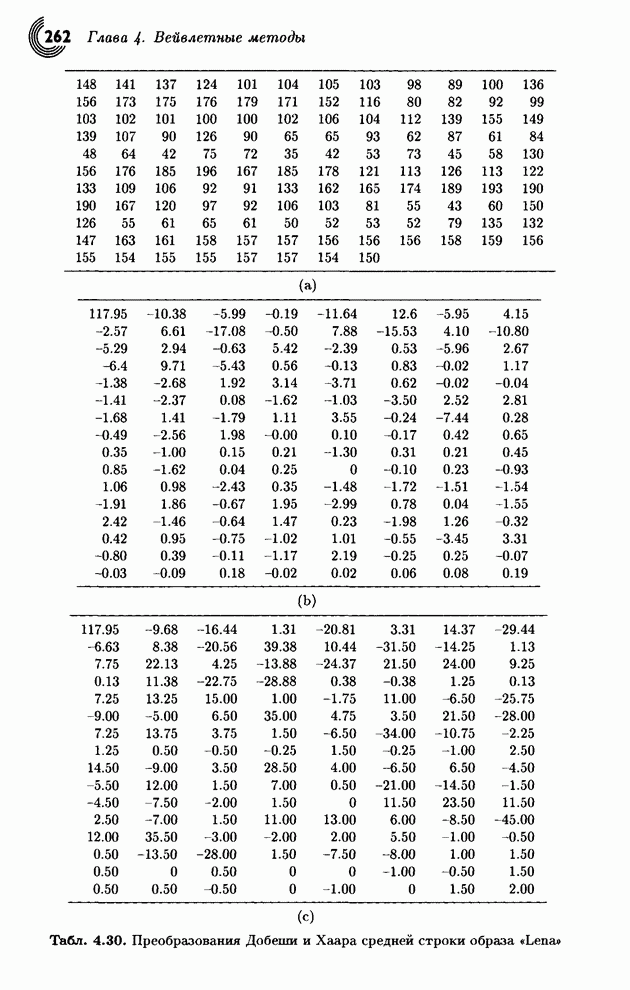
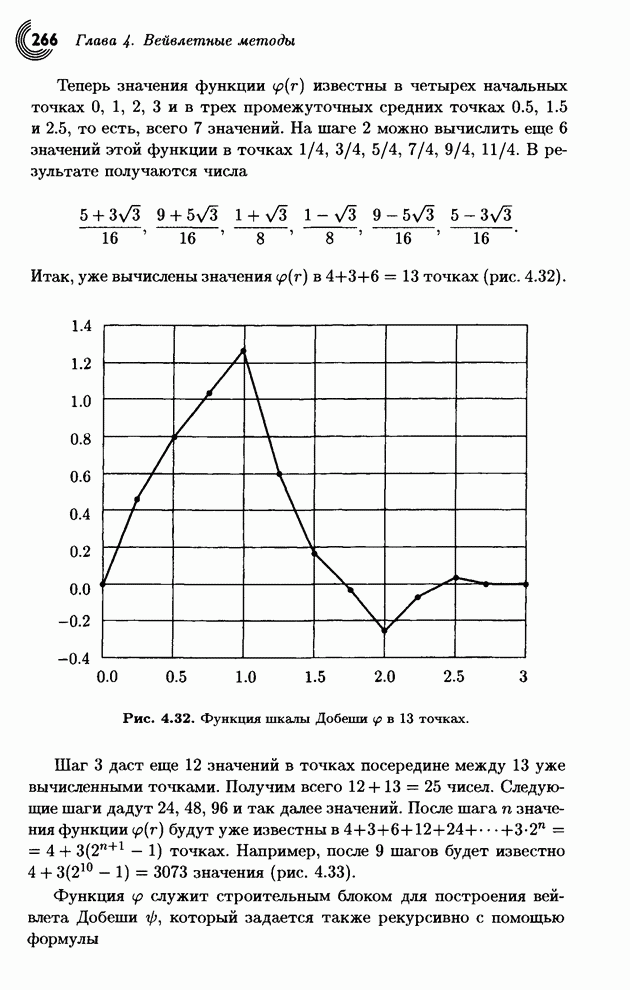
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
3.5.5. Дискретное синус-преобразование
Читатель в этом месте может задать логичный вопрос: «Почему косинус, а не синус?» Можно ли аналогичным образом использовать функцию синус для построения дискретного синус-преобразования? Существует DST (descrete sine transform) или нет? В этом коротком параграфе мы обсудим отличия синуса от косинуса, которые приводят к весьма неэффективному синус-преобразованию.
Функция ![]() , удовлетворяющая условию
, удовлетворяющая условию ![]() , называется
нечетной. Аналогично, если
, называется
нечетной. Аналогично, если ![]() , то
, то ![]() называется четной. Для любой нечетной
функции
называется четной. Для любой нечетной
функции ![]() ,
поэтому
,
поэтому ![]() должно
равняться 0. Большинство функций не являются ни четными, ни нечетными. Но
основные тригонометрические функции
должно
равняться 0. Большинство функций не являются ни четными, ни нечетными. Но
основные тригонометрические функции ![]() и
и ![]() являются, соответственно, четной и
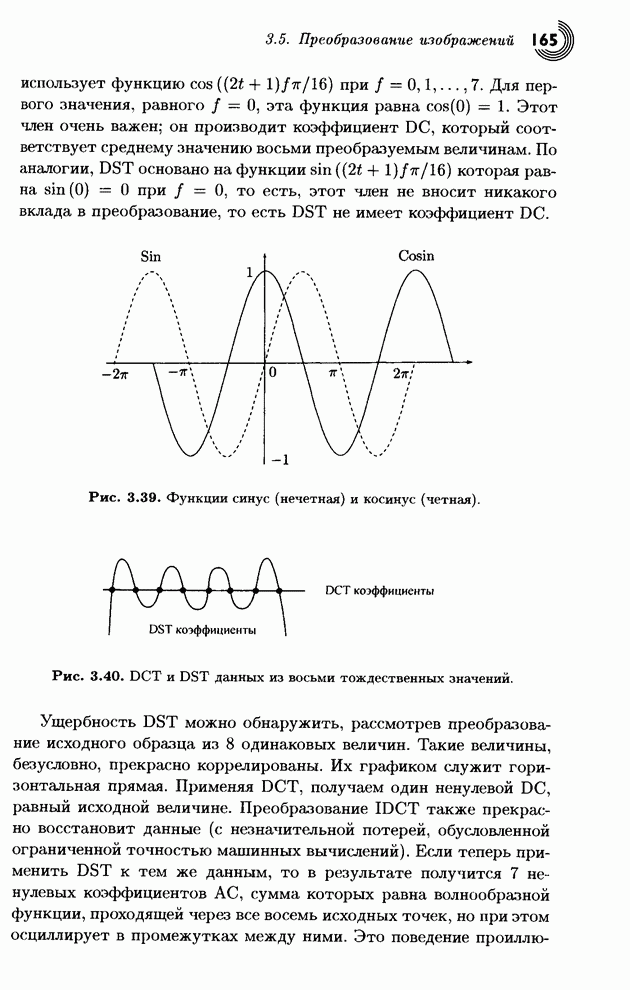
нечетной. Из рис.3.39 видно, что эти функции различаются лишь по своей фазе (то
есть, косинус получается из синуса сдвигом на
являются, соответственно, четной и
нечетной. Из рис.3.39 видно, что эти функции различаются лишь по своей фазе (то
есть, косинус получается из синуса сдвигом на ![]() ), однако, этой разности достаточно для
смены их четности. Когда (нечетная) функция синус сдвигается, она становится
(четной) функцией косинус, которая имеет ту же форму.
), однако, этой разности достаточно для
смены их четности. Когда (нечетная) функция синус сдвигается, она становится
(четной) функцией косинус, которая имеет ту же форму.
|
00 |
10 |
20 |
30 |
30 |
20 |
10 |
00 |
|
|
10 |
20 |
30 |
40 |
40 |
30 |
20 |
10 |
|
|
20 |
30 |
40 |
50 |
50 |
40 |
30 |
20 |
|
|
30 |
40 |
50 |
60 |
60 |
50 |
40 |
30 |
|
|
30 |
40 |
50 |
60 |
60 |
50 |
40 |
30 |
|
|
20 |
30 |
40 |
50 |
50 |
40 |
30 |
20 |
|
|
10 |
20 |
30 |
40 |
40 |
30 |
12 |
10 |
|
|
00 |
10 |
20 |
30 |
30 |
20 |
10 |
00 |
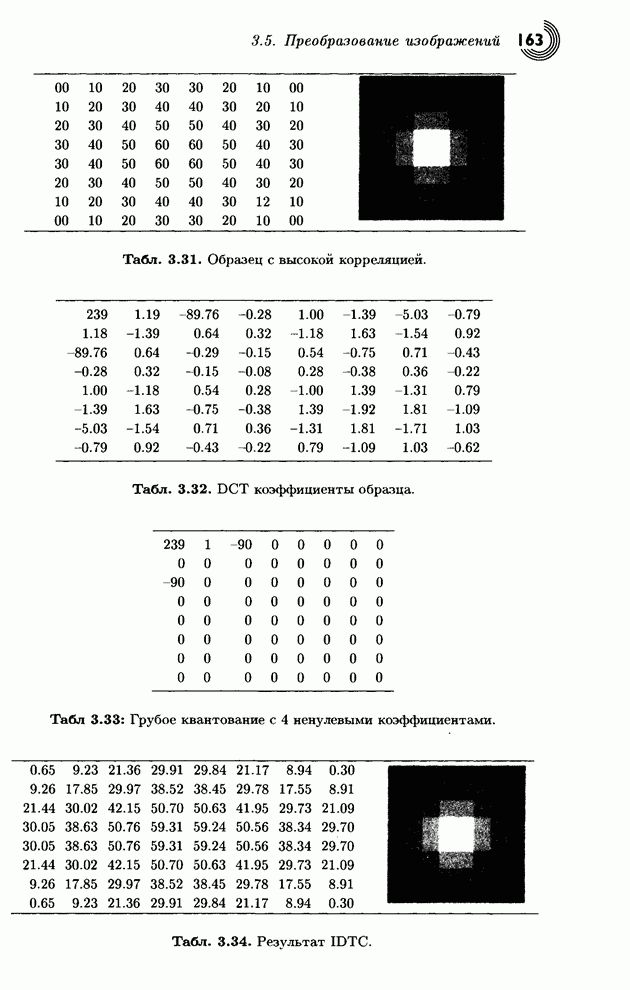
Табл. 3.31. Образец с высокой корреляцией.
|
239 |
1.19 |
89.76 |
-0.28 |
1.00 |
1.39 |
5.03 |
0.79 |
|
1.18 |
-1.39 |
0.64 |
0.32 |
-1.18 |
1.63 |
-1.54 |
0.92 |
|
-89.76 |
0.64 |
-0.29 |
-0.15 |
0.54 |
-0.75 |
0.71 |
-0.43 |
|
-0.28 |
0.32 |
-0.15 |
-0.08 |
0.28 |
-0.38 |
0.36 |
0.22 |
|
1.00 |
-1.18 |
0.54 |
0.28 |
-1.00 |
1.39 |
1.31 |
0.79 |
|
1.39 |
1.63 |
-0.75 |
-0.38 |
1.39 |
1.92 |
1.81 |
1.09 |
|
-5.03 |
-1.54 |
0.71 |
0.36 |
-1.31 |
1.81 |
-1.71 |
1.03 |
|
-0.79 |
0.92 |
-0.43 |
-0.22 |
0.79 |
-1.09 |
1.03 |
-0.62 |
Табл. 3.32. DCT коэффициенты образца.
|
239 |
1 |
-90 |
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
-90 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
Табл. 3.33. Грубое квантование с 4 ненулевыми коэффициентами.
|
0.65 |
9.23 |
21.36 |
29.91 |
29.84 |
21.17 |
8.94 |
0.30 |
|
|
9.26 |
17.85 |
29.97 |
38.52 |
38.45 |
29.78 |
17.55 |
8.91 |
|
|
21.44 |
30.02 |
42.15 |
50.70 |
50.63 |
41.95 |
29.73 |
21.09 |
|
|
30.05 |
38.63 |
50.76 |
59.31 |
59.24 |
50.56 |
38.34 |
29.70 |
|
|
30.05 |
38.63 |
50.76 |
59.31 |
59.24 |
50.56 |
38.34 |
29.70 |
|
|
21.44 |
30.02 |
42.15 |
50.70 |
50.63 |
41.95 |
29.73 |
21.09 |
|
|
9.26 |
17.85 |
29.97 |
38.52 |
38.45 |
29.78 |
17.55 |
8.91 |
|
|
0.65 |
9.23 |
21.36 |
29.91 |
29.84 |
21.17 |
8.94 |
0.30 |
Табл. 3.34. Результат IDTC.
|
00 |
10 |
00 |
00 |
00 |
00 |
00 |
10 |
|
|
00 |
00 |
10 |
00 |
00 |
00 |
10 |
00 |
|
|
00 |
00 |
00 |
10 |
00 |
10 |
00 |
00 |
|
|
00 |
00 |
00 |
00 |
10 |
00 |
00 |
00 |
|
|
00 |
00 |
00 |
00 |
10 |
00 |
00 |
00 |
|
|
00 |
00 |
00 |
00 |
10 |
00 |
00 |
00 |
|
|
00 |
00 |
00 |
00 |
10 |
00 |
00 |
00 |
|
|
00 |
00 |
00 |
00 |
10 |
00 |
00 |
00 |
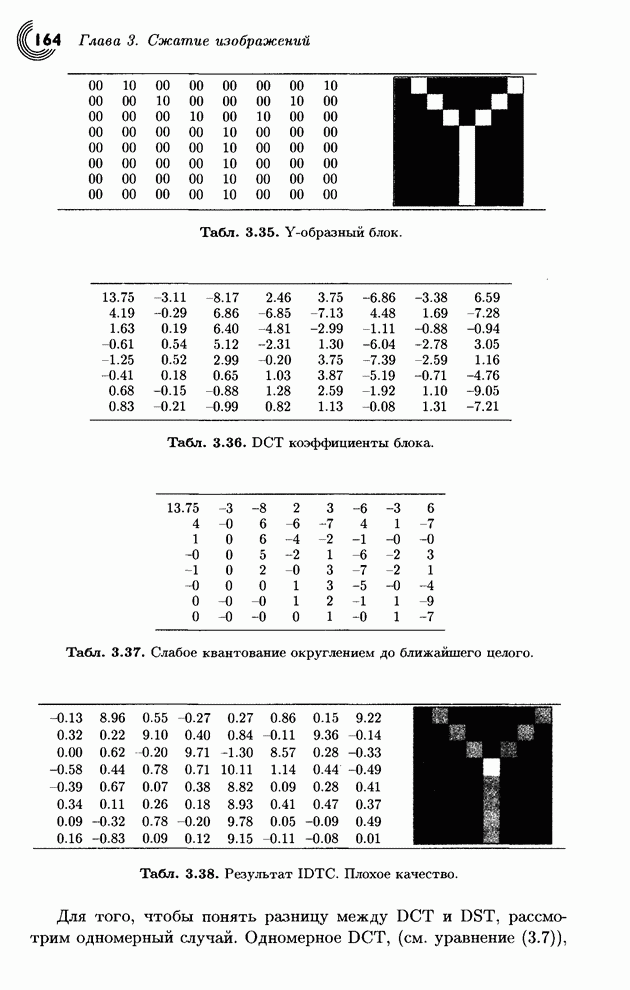
Табл. 3.35. Y-образный блок.
|
13.75 |
-3.11 |
-8.17 |
2.46 |
3.75 |
-6.86 |
-3.38 |
6.59 |
|
4.19 |
-0.29 |
6.86 |
-6.85 |
7.13 |
4.48 |
1.69 |
-7.28 |
|
1.63 |
0.19 |
6.40 |
-4.81 |
-2.99 |
-1.11 |
-0.88 |
-0.94 |
|
-0.61 |
0.54 |
5.12 |
-2.31 |
1.30 |
-6.04 |
-2.78 |
3.05 |
|
-1.25 |
0.52 |
2.99 |
-0.20 |
3.75 |
-7.39 |
2.59 |
1.16 |
|
0.41 |
0.18 |
0.65 |
1.03 |
3.87 |
-5.19 |
-0.71 |
-4.76 |
|
0.68 |
-0.15 |
-0.88 |
1.28 |
2.59 |
-1.92 |
1.10 |
-9.05 |
|
0.83 |
-0.21 |
-0.99 |
0.82 |
1.13 |
-0.08 |
1.31 |
-7.21 |
Табл. 3.36. DCT коэффициенты блока.
|
13.75 |
3 |
-8 |
2 |
3 |
-6 |
-3 |
6 |
|
4 |
-0 |
6 |
-6 |
-7 |
4 |
1 |
-7 |
|
1 |
0 |
6 |
-4 |
-2 |
-1 |
-0 |
-0 |
|
-0 |
0 |
5 |
-2 |
1 |
-6 |
2 |
3 |
|
-1 |
0 |
2 |
-0 |
3 |
-7 |
2 |
1 |
|
-0 |
0 |
0 |
1 |
3 |
-5 |
-0 |
-4 |
|
0 |
-0 |
-0 |
1 |
2 |
-1 |
1 |
-9 |
|
0 |
-0 |
-0 |
0 |
1 |
-0 |
1 |
-7 |
Табл. 3.37. Слабое квантование округлением до ближайшего целого.
|
-0.13 |
8.96 |
0.55 |
-0.27 |
0.27 |
0.86 |
0.15 |
9.22 |
|
|
0.32 |
0.22 |
9.10 |
0.40 |
0.84 |
-0.11 |
9.36 |
-0.14 |
|
|
0.00 |
0.62 |
-0.20 |
9.71 |
-1.30 |
8.57 |
0.28 |
-0.33 |
|
|
-0.58 |
0.44 |
0.78 |
0.71 |
10.11 |
1.14 |
0.44 |
-0.49 |
|
|
-0.39 |
0.67 |
0.07 |
0.38 |
8.82 |
0.09 |
0.28 |
0.41 |
|
|
0.34 |
0.11 |
0.26 |
0.18 |
8.93 |
0.41 |
0.47 |
0.37 |
|
|
0.09 |
-0.32 |
0.78 |
-0.20 |
9.78 |
0.05 |
-0.09 |
0.49 |
|
|
0.16 |
-0.83 |
0.09 |
0.12 |
9.15 |
-0.11 |
-0.08 |
0.01 |
Табл. 3.38. Результат IDTC. Плохое качество.
Для того, чтобы понять разницу
между DCT и DST, рассмотрим одномерный случай. Одномерное DCT, (см. уравнение (3.7)), использует
функцию ![]() при
при
![]() . Для
первого значения, равного
. Для
первого значения, равного ![]() , эта функция равна
, эта функция равна ![]() . Этот член очень важен; он
производит коэффициент DC, который соответствует среднему
значению восьми преобразуемым величинам. По аналогии, DST основано на функции
. Этот член очень важен; он
производит коэффициент DC, который соответствует среднему
значению восьми преобразуемым величинам. По аналогии, DST основано на функции ![]() , которая равна
, которая равна ![]() при
при ![]() , то есть, этот член не вносит
никакого вклада в преобразование, то есть DST не имеет коэффициент DC.
, то есть, этот член не вносит
никакого вклада в преобразование, то есть DST не имеет коэффициент DC.

Рис. 3.39. Функции синус (нечетная) и косинус (четная).

Рис. 3.40. DCT и DST данных из восьми тождественных значений.
Ущербность DST можно обнаружить, рассмотрев преобразование исходного образца из 8 одинаковых величин. Такие величины, безусловно, прекрасно коррелированы. Их графиком служит горизонтальная прямая. Применяя DCT, получаем один ненулевой DC, равный исходной величине. Преобразование IDCT также прекрасно восстановит данные (с незначительной потерей, обусловленной ограниченной точностью машинных вычислений). Если теперь применить DST к тем же данным, то в результате получится 7 ненулевых коэффициентов АС, сумма которых равна волнообразной функции, проходящей через все восемь исходных точек, но при этом осциллирует в промежутках между ними. Это поведение проиллюстрировано на рис. 3.40. Оно имеет три неприятных свойства. (1) Энергия исходных данных нигде не концентрируется. (2) Семь коэффициентов не являются декоррелированными (поскольку исходные данные полностью коррелированы). (3) Квантование семи коэффициентов может сильно уменьшить качество реконструированных данных после применения обратного DST.

Рис. 3.41. 64 базисных изображения двумерного DST.
Пример: Применим DST к последовательности из восьми одинаковых величин, равных 100. Получим последовательность коэффициентов (0, 256.3, 0, 90, 0, 60.1, 0, 51). С помощью этих коэффициентов обратное преобразование IDST может восстановить исходные данные, но видно, что коэффициенты АС ведут себя иначе, чем при использования DCT. Они не становятся все меньше, и среди них нет серий из одних нулей. Применяя DST к восьми высоко коррелированным величинам (11, 22, 33, 44, 55, 66, 77, 88), получаем более плохое множество коэффициентов
0, 126.9, -57.5, 44.5, -31.1, 29.8, -23.8, 25.2.
Здесь совсем нет концентрации энергии.
Все эти аргументы и примеры вместе с тем фактом (обсуждаемым в [Ahmed et al.]) 74]), что DCT производит высоко декоррелированные коэффициенты, неоспоримо свидетельствуют в пользу метода DCT, для использования в алгоритмах сжатия данных.
На рис. 3.41 показаны 64 базисных
изображения DST при ![]() и программа Matlab, порождающая их. (Ср. рис.
3.26.)
и программа Matlab, порождающая их. (Ср. рис.
3.26.)
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие переводчика
- Предисловие автора
- Введение
- Глава 1. Статистические методы
- 1.1. Энтропия
- 1.2. Коды переменной длины
- 1.3. Декодирование
- 1.4. Кодирование Хаффмана
- 1.4.1. Декодирование Хаффмана
- 1.4.2. Средняя длина кода
- 1.5. Адаптивные коды Хаффмана
- 1.5.1. Несжатые коды
- 1.5.2. Модификация дерева
- 1.5.3. Переполнение счетчика
- 1.5.4. Кодовое переполнение
- 1.5.5. Вариант алгоритма
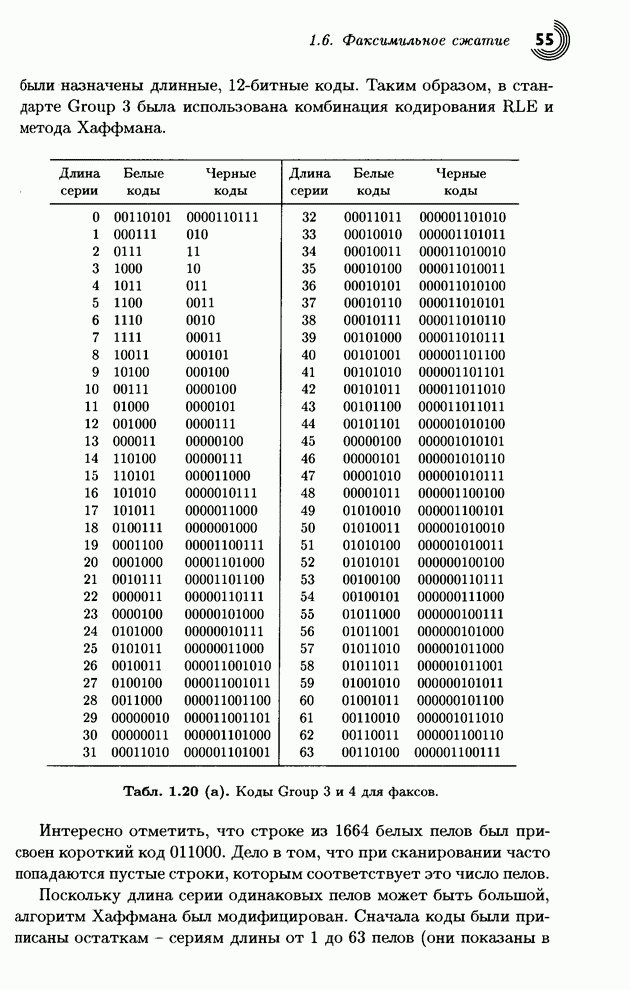
- 1.6. Факсимильное сжатие
- 1.6.1. Одномерное кодирование
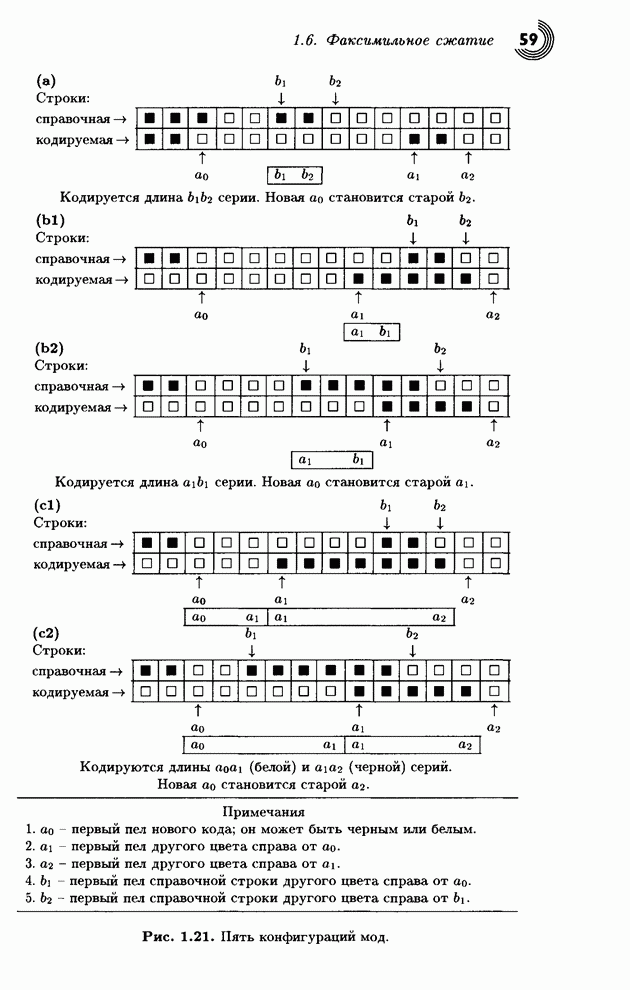
- 1.6.2. Двумерное кодирование
- 1.7. Арифметическое кодирование
- 1.7.1. Детали реализации метода
- 1.7.2. Потеря значащих цифр
- 1.7.3. Заключительные замечания
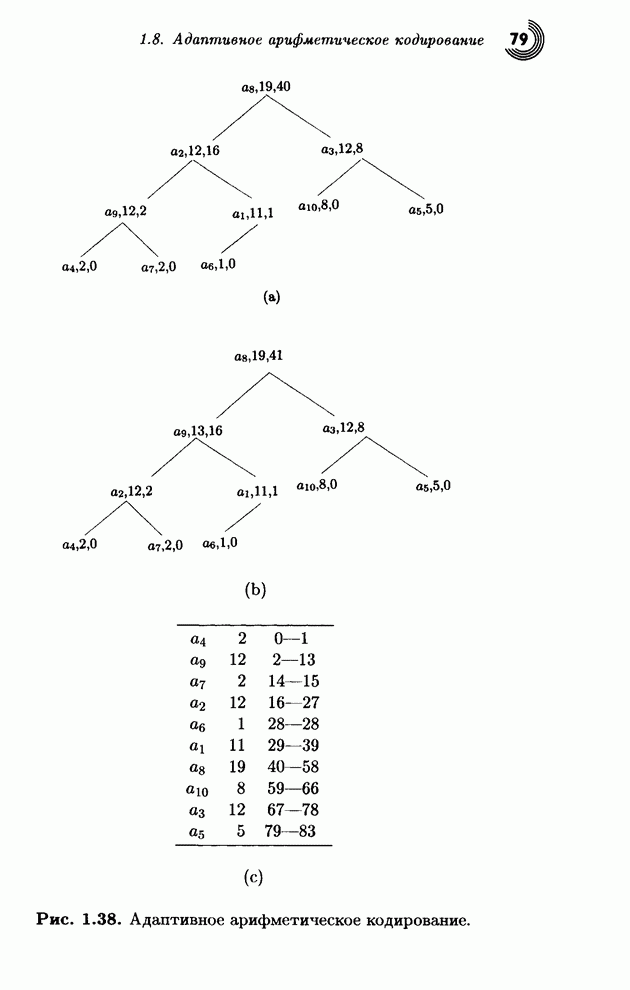
- 1.8. Адаптивное арифметическое кодирование
- ГЛАВА 2 СЛОВАРНЫЕ МЕТОДЫ
- 2.1. LZ77 (скользящее окно)
- 2.1.1. Циклическая очередь
- 2.2. LZSS
- 2.2.1. Недостатки
- 2.3. LZ78
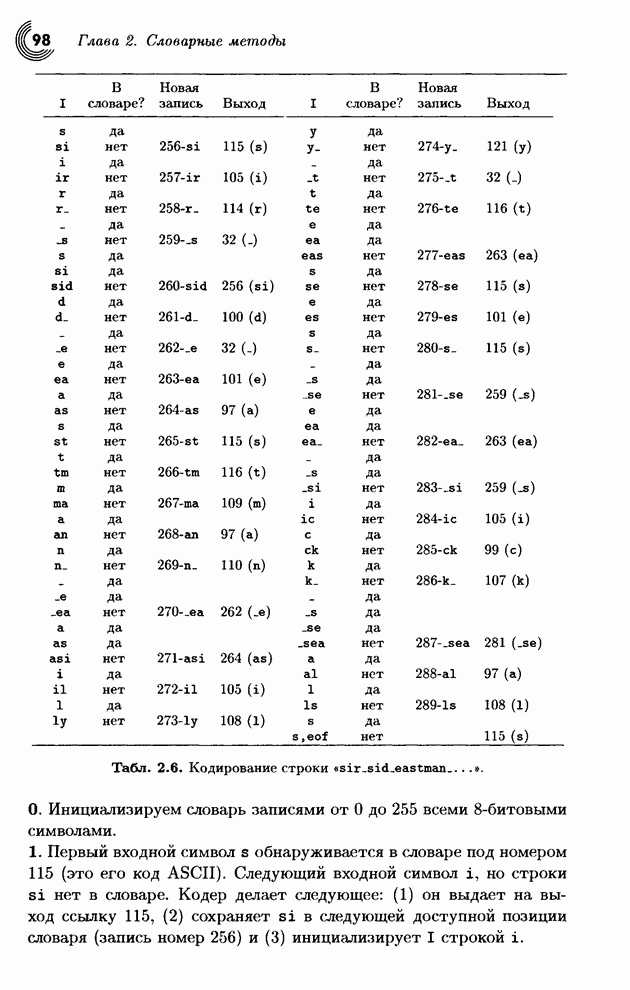
- 2.4. LZW
- 2.4.1. Декодирование LZW
- 2.4.2. Структура словаря LZW
- 2.4.3. LZW в практических приложениях
- 2.5. Заключение
- ГЛАВА 3 СЖАТИЕ ИЗОБРАЖЕНИЙ
- 3.1. Введение
- 3.2. Типы изображений
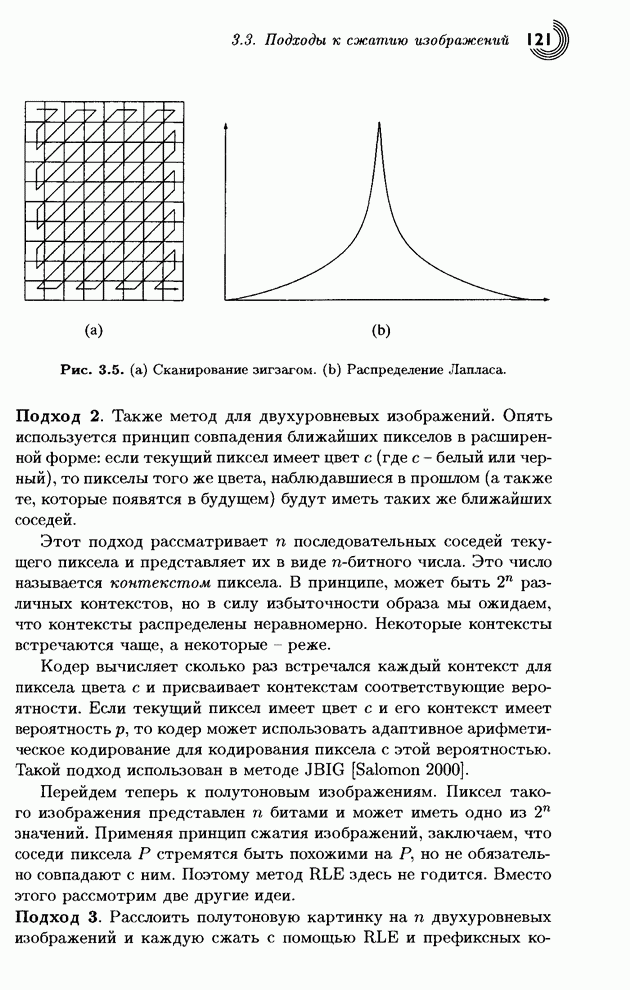
- 3.3. Подходы к сжатию изображений
- 3.3.1. Коды Грея
- 3.3.2. Метрики ошибок
- 3.4. Интуитивные методы
- 3.4.1. Подвыборка
- 3.4.2. Квантование
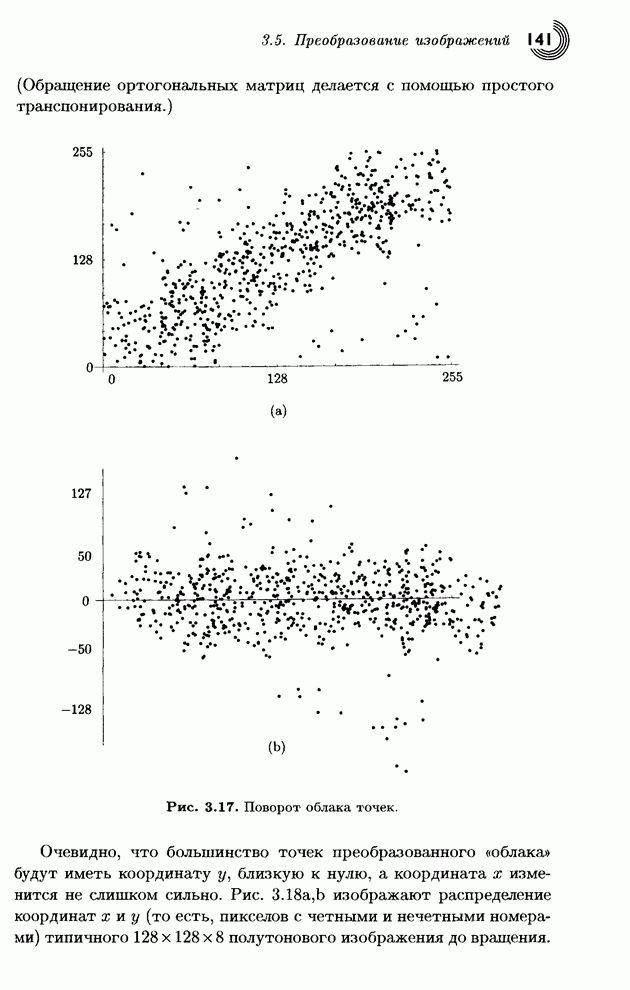
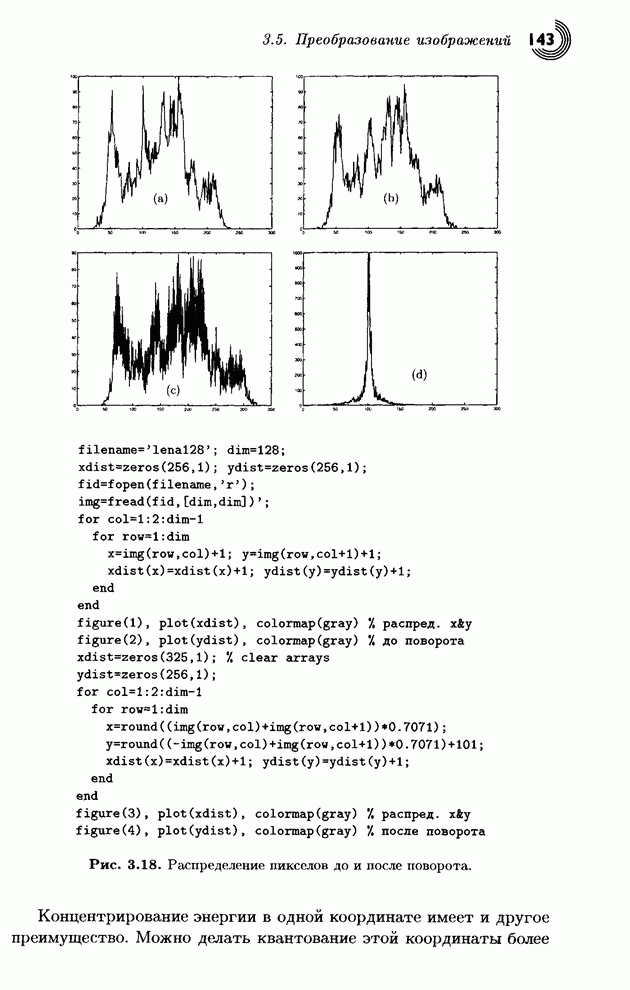
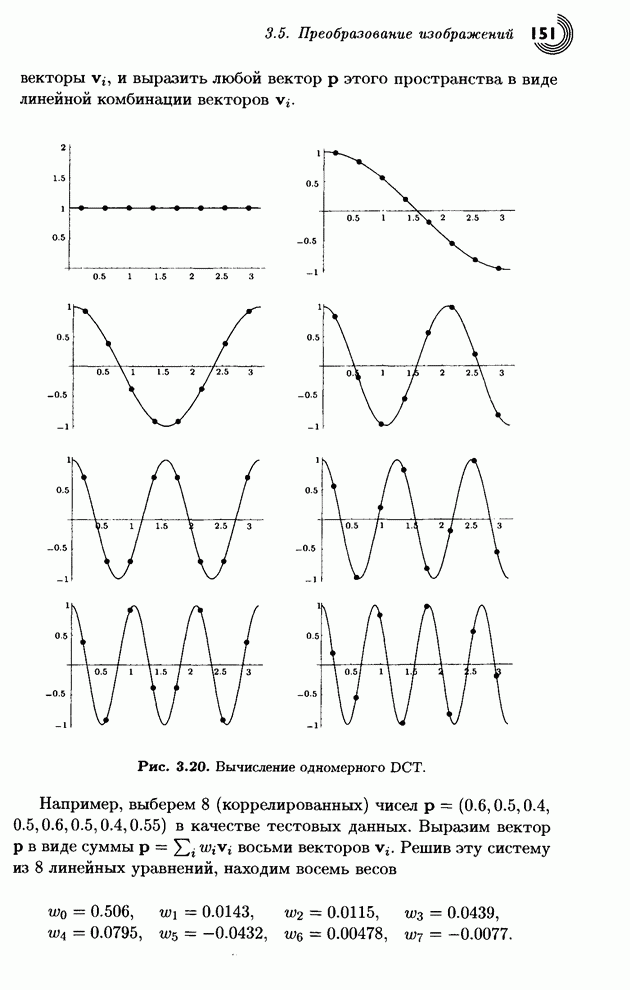
- 3.5. Преобразование изображений
- 3.5.1. Ортогональные преобразования
- 3.5.2. Матричные преобразования
- 3.5.3. Дискретное косинус-преобразование
- 3.5.4. Пример
- 3.5.5. Дискретное синус-преобразование
- 3.5.6. Преобразование Уолша-Адамара
- 3.5.7. Преобразование Хаара
- 3.5.8. Преобразование Кархунена-Лоэвэ
- 3.6. Прогрессирующее сжатие изображений
- 3.7. JPEG
- 3.7.1. Светимость
- 3.7.2. DCT
- 3.7.3. Практическое DCT
- 3.7.4. Квантование
- 3.7.5. Кодирование
- 3.7.6. Мода без потери данных
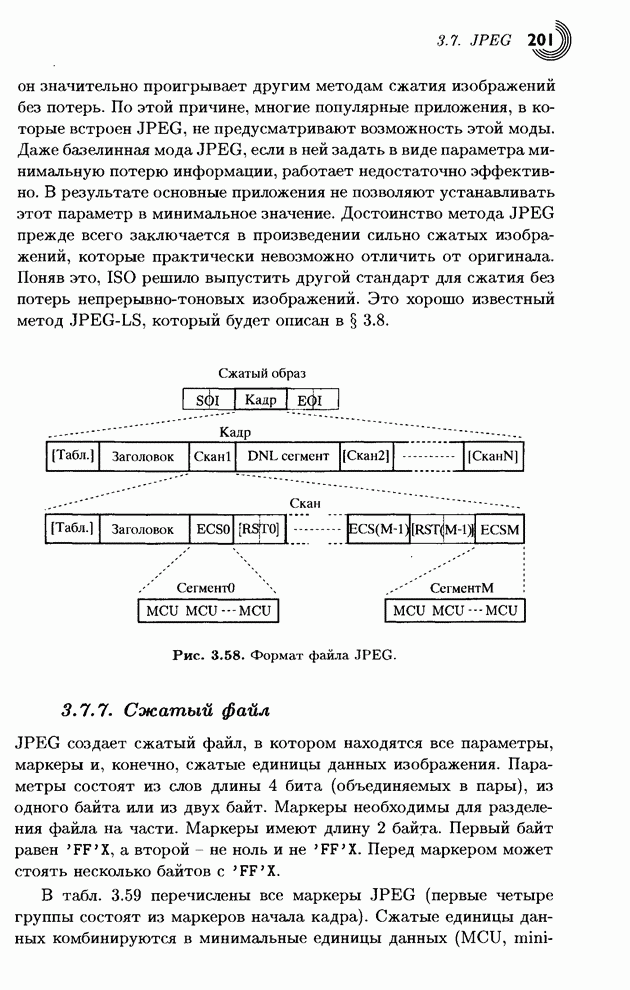
- 3.7.7. Сжатый файл
- 3.7.8. JFIF
- 3.8. JPEG-LS
- 3.8.1. Коды Голомба
- 3.8.2. Основы метода JPEG-LS
- 3.8.3. Кодер
- ГЛАВА 4 ВЕЙВЛЕТНЫЕ МЕТОДЫ
- 4.1. Вычисление средних и полу разностей
- 4.1.1. Обобщение на двумерный случай
- 4.1.2. Свойства преобразования Хаара
- 4.2. Преобразование Хаара
- 4.2.1. Матричная форма
- 4.3. Поддиапазонные преобразования
- 4.4. Банк фильтров
- 4.5. Нахождение коэффициентов фильтра
- 4.6. Преобразование DWT
- 4.7. Примеры
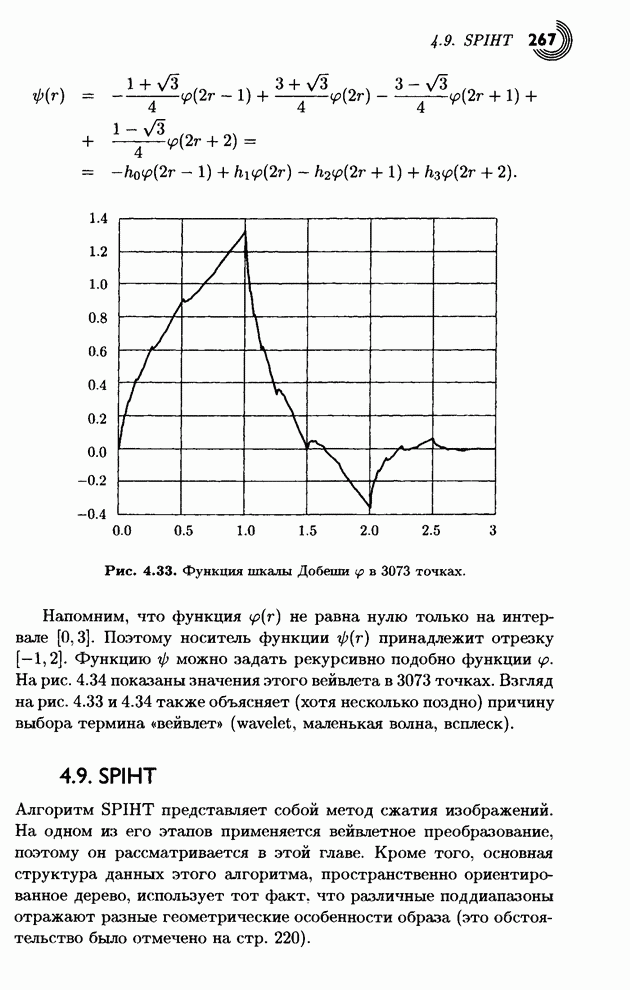
- 4.8. Вейвлеты Добеши
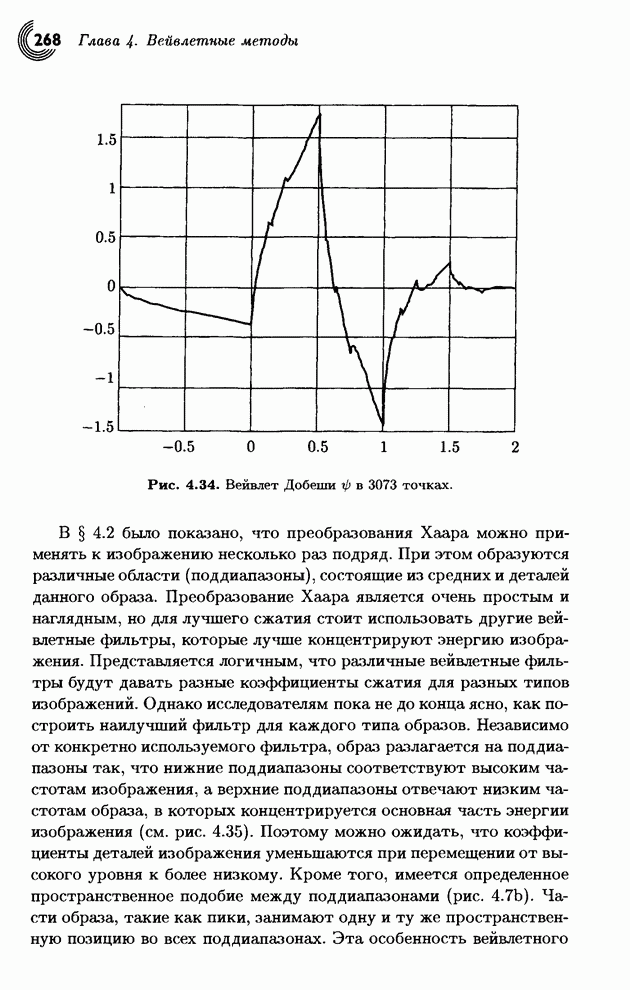
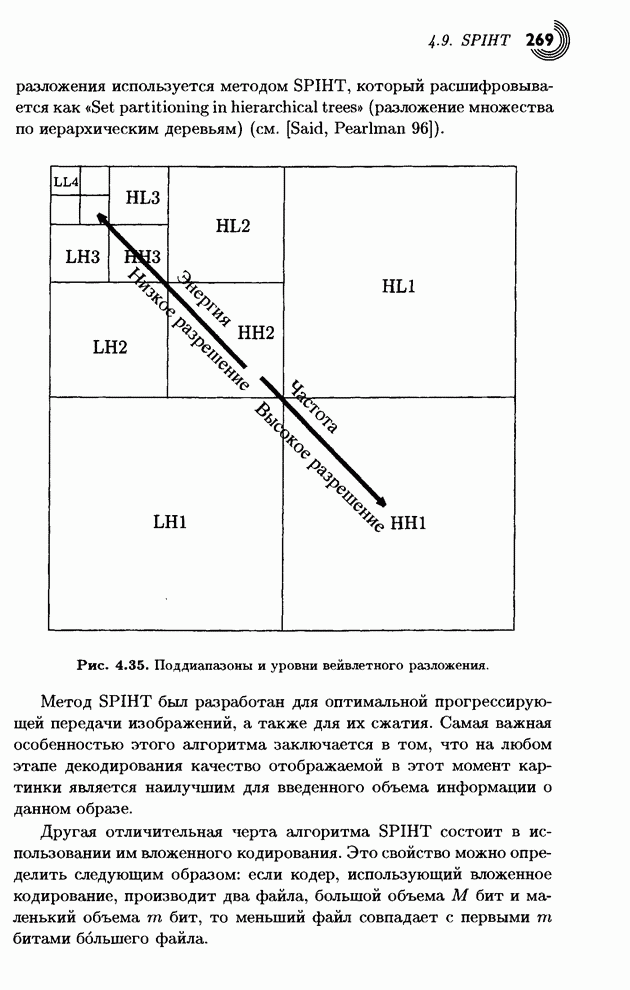
- 4.9. SPIHT
- 4.9.1. Алгоритм сортировки разделением множеств
- 4.9.2. Пространственно ориентированное дерево
- 4.9.3. Кодирование в алгоритме SPIHT
- 4.9.4. Пример
- 4.9.5. QTCQ
- ГЛАВА 5 СЖАТИЕ ВИДЕО
- 5.1. Основные принципы
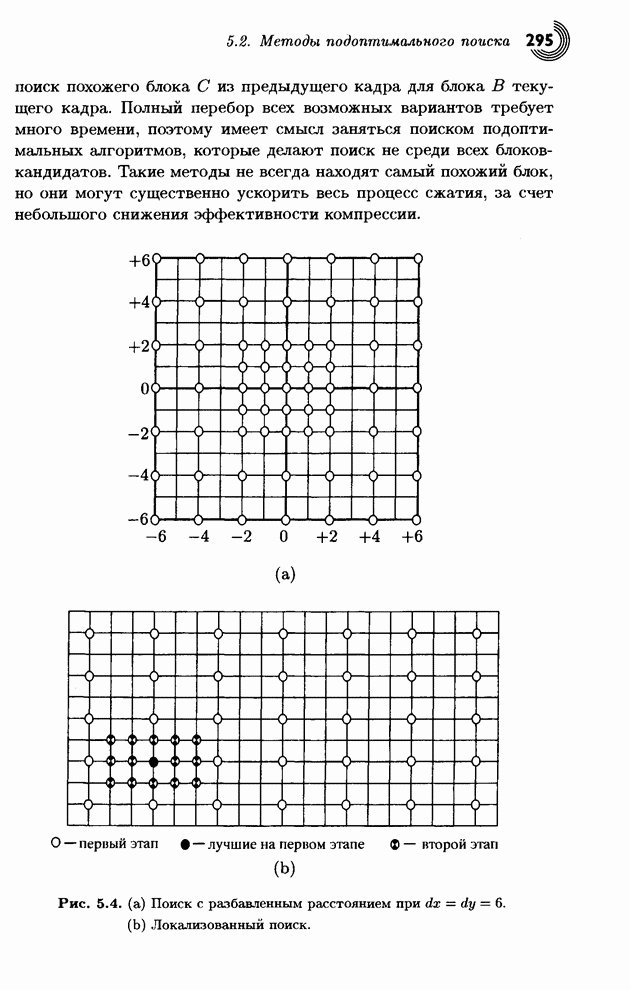
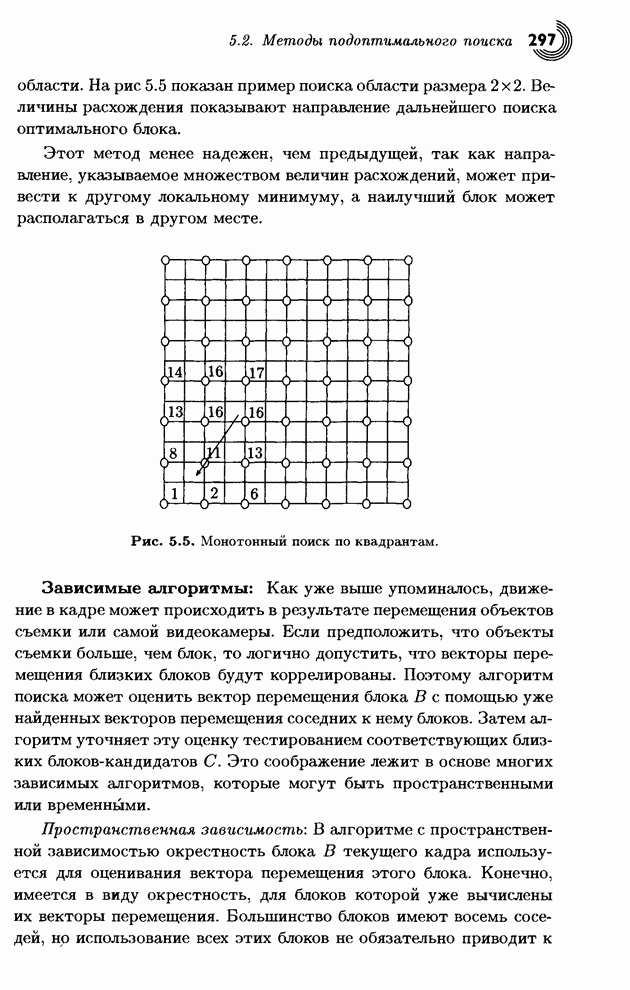
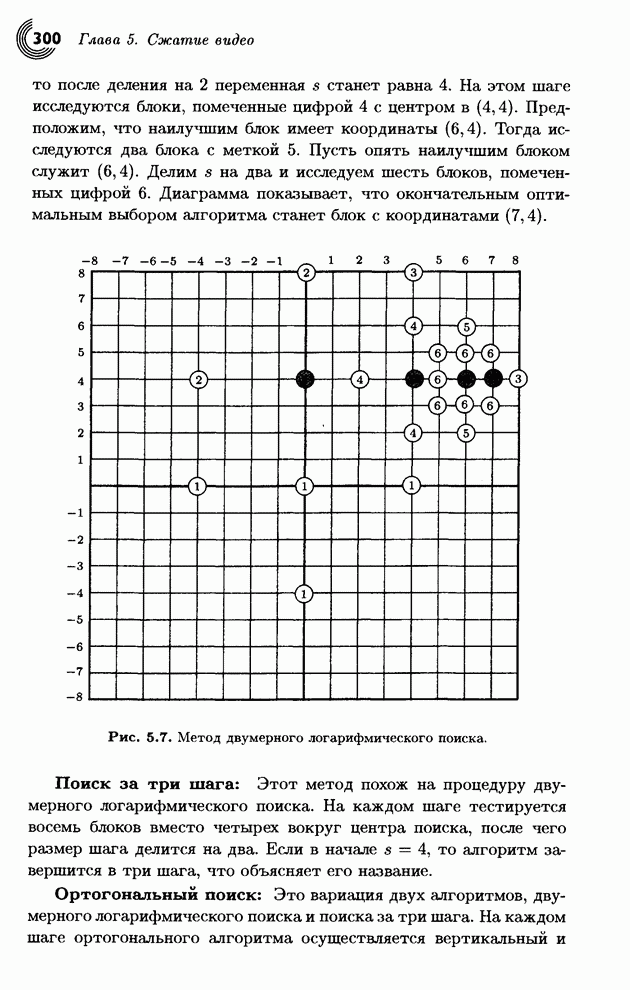
- 5.2. Методы подоптимального поиска
- ГЛАВА 6 СЖАТИЕ ЗВУКА
- 6.1. Звук
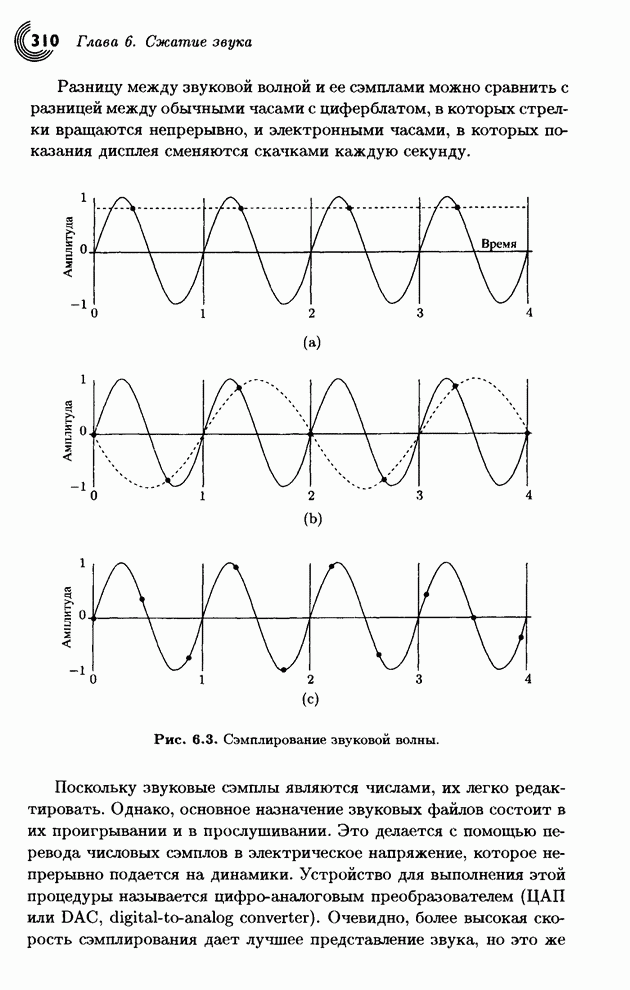
- 6.2. Оцифрованный звук
- 6.3. Органы слуха человека
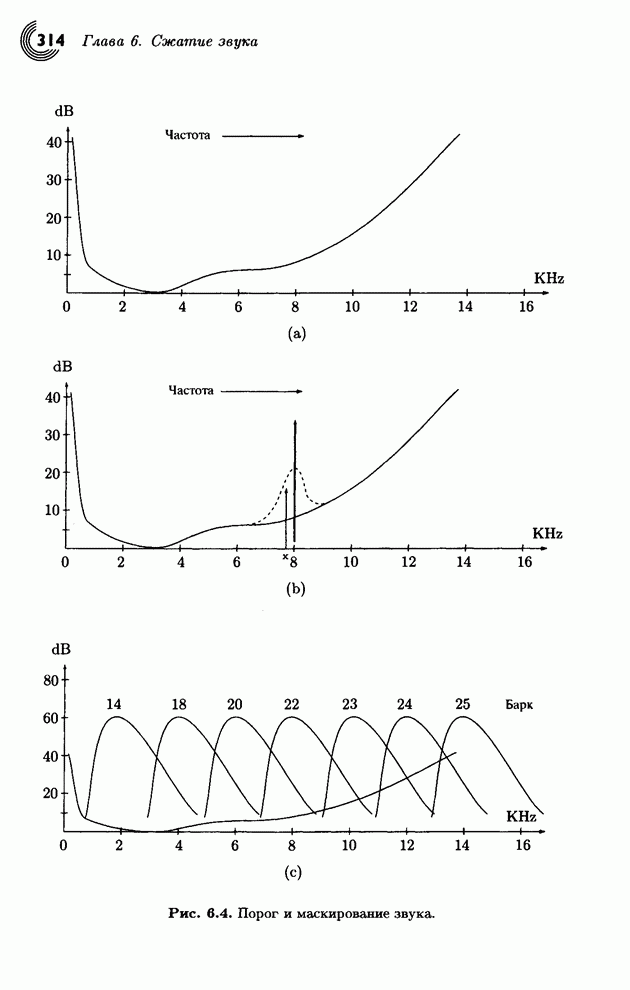
- 6.4. Общепризнанные методы
- 6.5. Сжатие звука в стандарте MPEG-1
- 6.5.1. Кодирование частотной области
- 6.5.2. Формат сжатых данных
- 6.5.3. Психоакустические модели
- 6.5.4. Кодирование: слой III
- Литература
- Глоссарий