| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
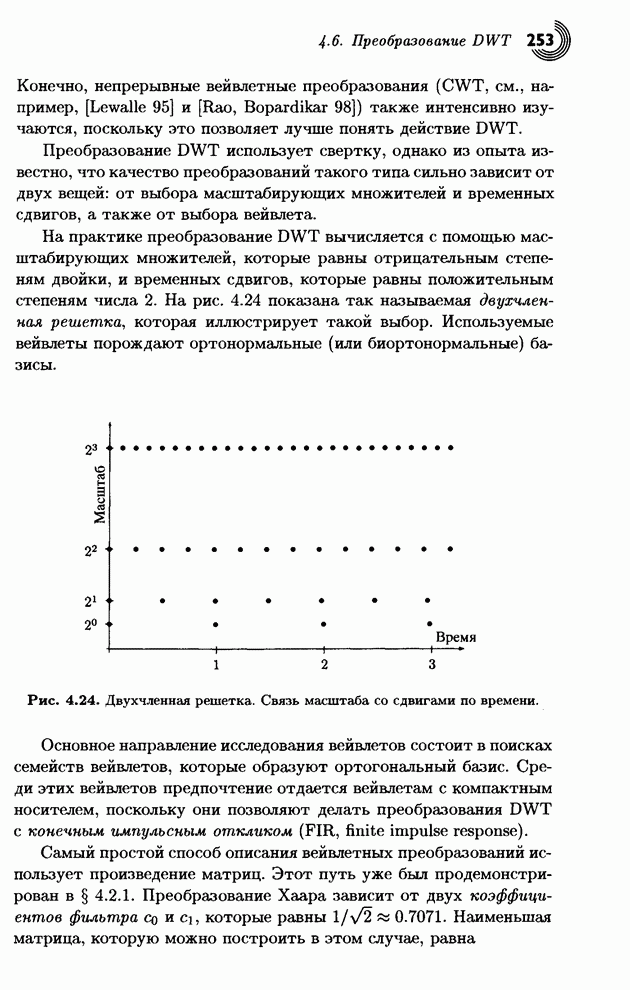
3.5. Преобразование изображений
Понятие преобразования широко применяется в математике. С его помощью решаются многие задачи в различных областях науки. Основная идея состоит в изменении математической величины (числа, вектора, функции или другого объекта) с целью придания ей другой формы, в которой она имеет, возможно, непривычный вид, но имеет полезные свойства. Преобразованная величина используется при решении задачи или при совершении некоторых вычислений, после чего к результату применяется обратное преобразование для возврата к исходной форме.
Простым иллюстративным примером могут служить арифметические операции над римскими числами. Древние римляне, по-видимому, знали, как оперировать с такими числами, однако, если требуется, скажем, перемножить два римских числа, то будет более удобно преобразовать их в современную (арабскую) форму, перемножить, а потом представить результат в виде римского числа. Вот простой пример:
![]() .
.
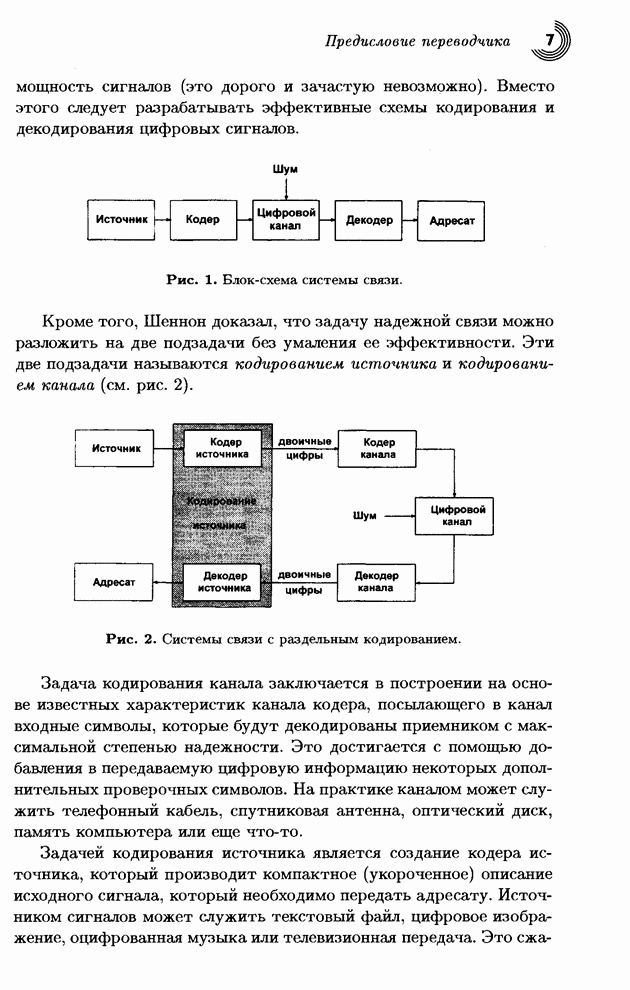
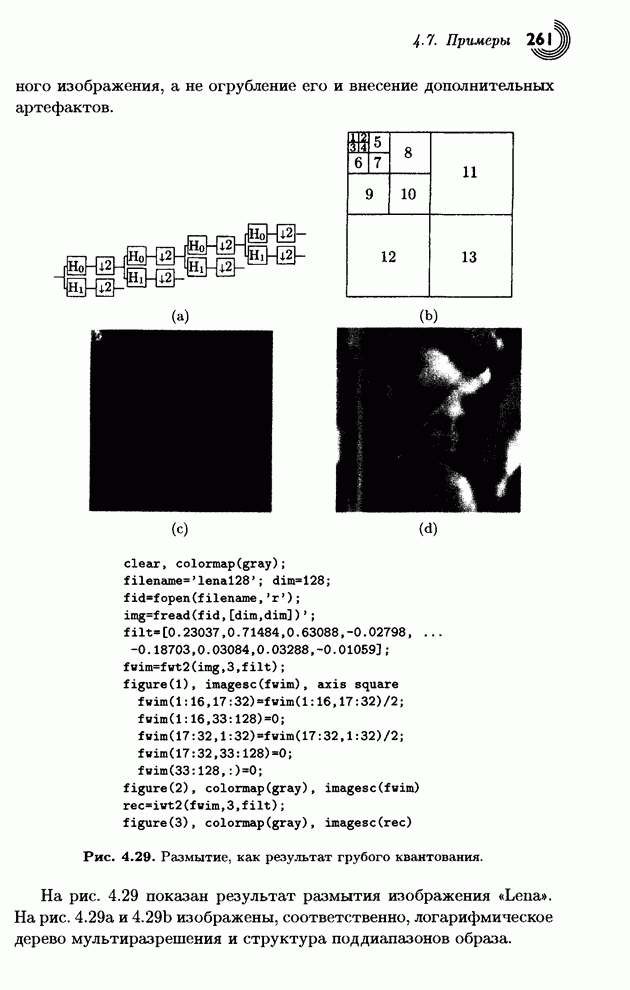
Изображение можно сжать, преобразуя его пикселы (которые коррелированы) в представление, где они будут декоррелированными. Произойдет сжатие, если новые величины будут, в среднем, меньше исходных. Сжатие с потерей качества можно затем произвести с помощью квантования результата преобразования. Декодер читает сжатый файл и восстанавливает (точно или приближенно) исходные данные, применяя обратное преобразование. В этом параграфе рассматриваются ортогональные преобразования. В § 4.3 будет обсуждаться под диапазонное преобразование.
Слово декоррелиронанные означает, что преобразованные величины являются статистически независимыми. В результате их можно кодировать независимо, что позволяет построить более простую статистическую модель. Образ можно сжать, если в нем имеется определенная избыточность. Избыточность проистекает от корреляции пикселов. Если перевести образ в представление, в котором пикселы декоррелированы, то одновременно произойдет удаление избыточности и образ будет полностью сжат.
Начнем с простого примера, в
котором образ сканируется растровым способом (то есть, строка за строкой) и
группируется в пары прилегающих пикселов. Поскольку пикселы коррелированы, два
пиксела ![]() в
паре, обычно, имеют близкие значения. Рассмотрим теперь эти пары в виде точек
на плоскости и отметим их на графике. Известно, что точки вида
в
паре, обычно, имеют близкие значения. Рассмотрим теперь эти пары в виде точек
на плоскости и отметим их на графике. Известно, что точки вида ![]() лежат на прямой с
наклоном 45°, уравнение которой имеет вид
лежат на прямой с
наклоном 45°, уравнение которой имеет вид ![]() , поэтому можно ожидать, что все точки
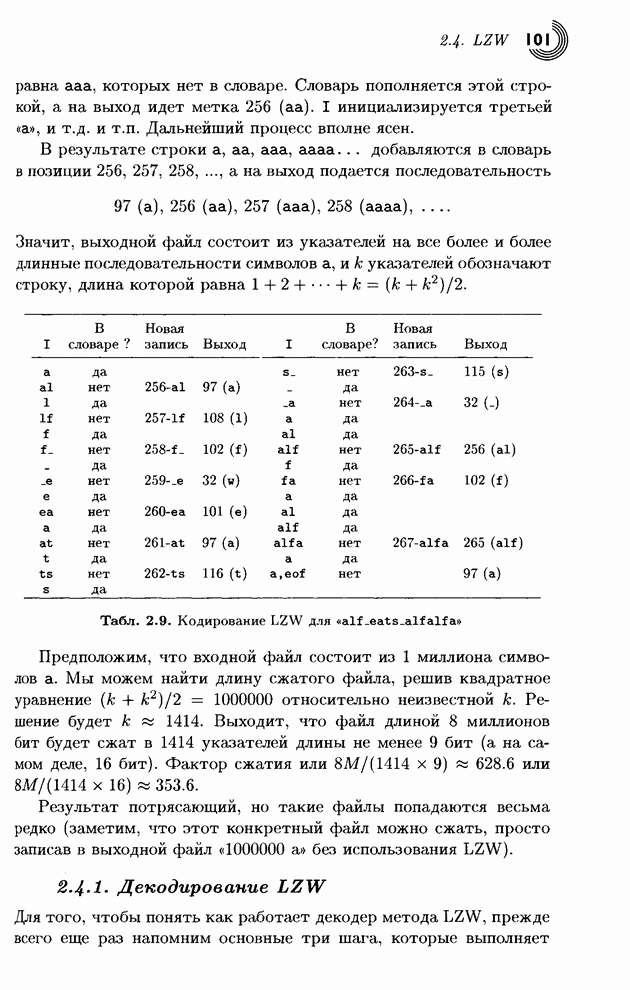
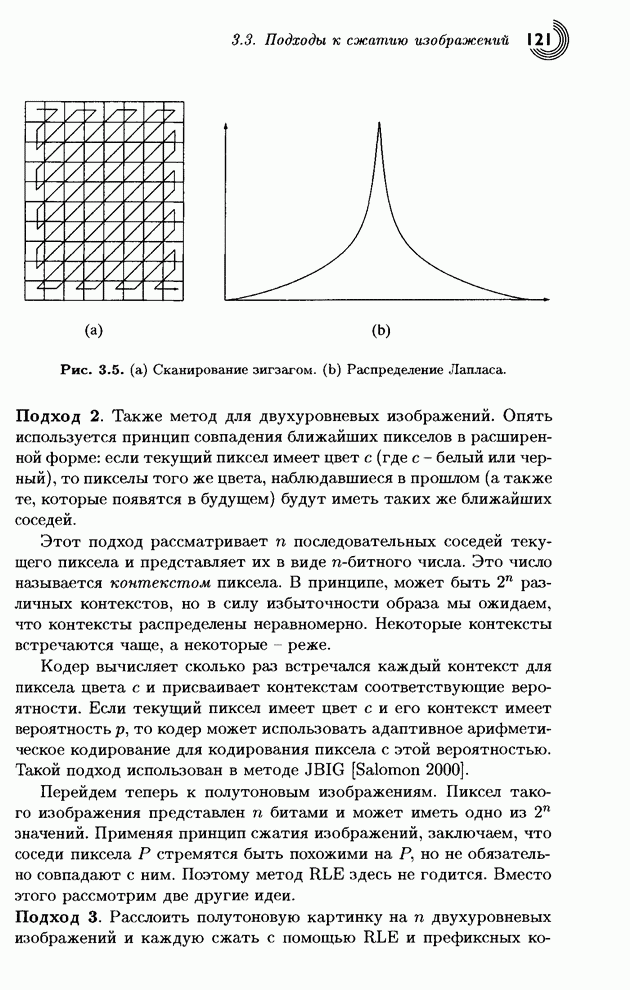
будут сконцентрированы около этой прямой. Рис. 3.17а дает такой график для
типичного изображения, где значения пикселов лежат в интервале [0, 255].
Большинство точек изображают «облако» около этой линии, и только некоторые
точки лежит вдали от диагонали. Теперь мы преобразуем эту картинку с помощью
поворота на угол 45° по часовой стрелке вокруг начала координат, так, чтобы
диагональ легла на ось
, поэтому можно ожидать, что все точки
будут сконцентрированы около этой прямой. Рис. 3.17а дает такой график для
типичного изображения, где значения пикселов лежат в интервале [0, 255].
Большинство точек изображают «облако» около этой линии, и только некоторые
точки лежит вдали от диагонали. Теперь мы преобразуем эту картинку с помощью
поворота на угол 45° по часовой стрелке вокруг начала координат, так, чтобы
диагональ легла на ось ![]() (рис. 3.17b). Это делается с помощью простого преобразования
(рис. 3.17b). Это делается с помощью простого преобразования
![]() , (3.3)
, (3.3)
где
матрица поворота ![]() является
ортогональной (то есть, скалярное произведение строк на себя равно 1, а
скалярное произведение векторов-строк друг на друга равно 0; то же самое верно
и для векторов-столбцов). Обратным преобразованием служит поворот на 45° против
часовой стрелки, который запишется в виде
является
ортогональной (то есть, скалярное произведение строк на себя равно 1, а
скалярное произведение векторов-строк друг на друга равно 0; то же самое верно
и для векторов-столбцов). Обратным преобразованием служит поворот на 45° против
часовой стрелки, который запишется в виде
![]() . (3.4)
. (3.4)
(Обращение ортогональных матриц делается с помощью простого транспонирования.)

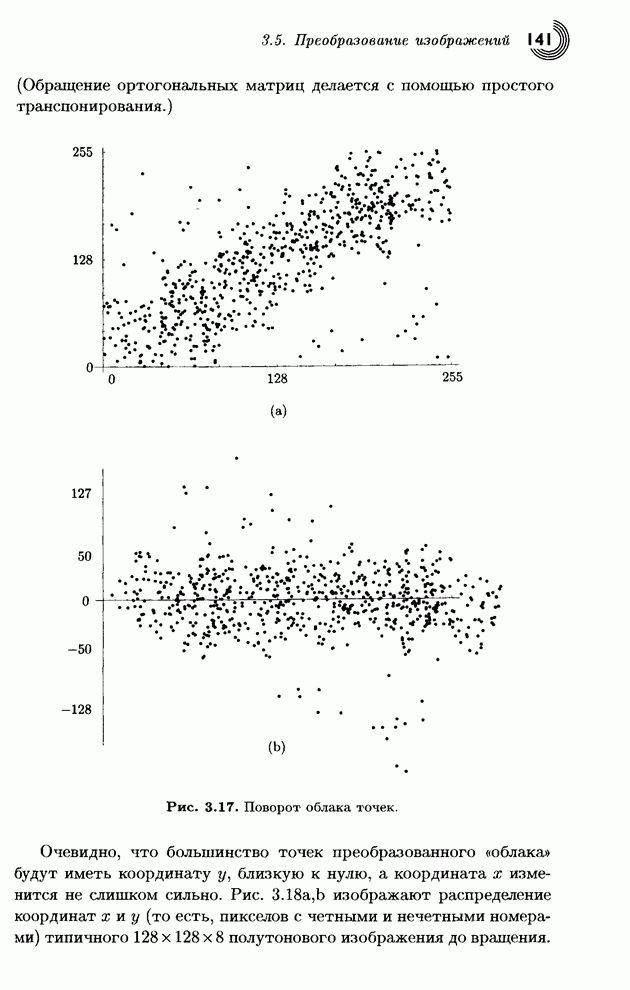
Рис. 3.17. Поворот облака точек.
Очевидно, что большинство точек
преобразованного «облака» будут иметь координату ![]() , близкую к нулю, а координата
, близкую к нулю, а координата ![]() изменится не слишком
сильно. Рис. 3.18а,b изображают распределение
координат
изменится не слишком
сильно. Рис. 3.18а,b изображают распределение
координат ![]() и
и
![]() (то есть,
пикселов с четными и нечетными номерами) типичного 128х128x8 полутонового
изображения до вращения. Ясно, что эти распределения отличаются не слишком. На
рис. 3.18с,d показаны распределения координат
после поворота. Распределение координаты
(то есть,
пикселов с четными и нечетными номерами) типичного 128х128x8 полутонового
изображения до вращения. Ясно, что эти распределения отличаются не слишком. На
рис. 3.18с,d показаны распределения координат
после поворота. Распределение координаты ![]() почти не изменилось (увеличилась
дисперсия), в то время как распределение координаты
почти не изменилось (увеличилась
дисперсия), в то время как распределение координаты ![]() сконцентрировалось около нуля.
Программа на Matlab, которая строит эти графики
также приведена на рисунке. (На рис. 3.18d координата
сконцентрировалось около нуля.
Программа на Matlab, которая строит эти графики
также приведена на рисунке. (На рис. 3.18d координата ![]() сконцентрирована около 100, но это
произошло из-за сдвига графика вправо, так как некоторые координаты были близки
к –101, и их пришлось сдвинуть для попадания в массив Matlab, у которого индекс всегда
начинается с единицы.)
сконцентрирована около 100, но это
произошло из-за сдвига графика вправо, так как некоторые координаты были близки
к –101, и их пришлось сдвинуть для попадания в массив Matlab, у которого индекс всегда
начинается с единицы.)
Поскольку координаты точек
известны до и после преобразования, легко вычислить уменьшение корреляции.
Сумма ![]() называется
перекрестной корреляцией точек
называется
перекрестной корреляцией точек ![]() .
.
Следующий пример поясняет смысл этой величины. Повернем точки (5,5), (6,7), (12.1,13.2), (23,25) и (32,29) по часовой стрелке на 45° и вычислим перекрестную корреляцию до и после поворота. На рис. 3.19 приведена программы Matlab, вычисляющая координаты повернутых точек. Они равны
(7.071,0), (9.19,0.7071), (17.9,0.78), (33.9,1.41), (43.13,–2.12)
(заметьте,
что координаты ![]() стали
малыми числами). Видно, что значение перекрестной корреляции уменьшилась с
1729.72 до поворота до -23.0846 после поворота. Замечательное сокращение!
стали
малыми числами). Видно, что значение перекрестной корреляции уменьшилась с
1729.72 до поворота до -23.0846 после поворота. Замечательное сокращение!
Теперь можно сжать образ, просто
записав преобразованные координаты в выходной файл. Если допустима некоторая
потеря информации, то можно сделать квантование всех пикселов, что даст малые
значения пикселов. Можно также записывать в сжатый файл все нечетные пикселы
(те, которые являются ![]() координатами в парах), а за ними
записать все четные пикселы. Эти две последовательности называются векторами
коэффициентов преобразования. Вторая последовательность состоит из малых
чисел, и, возможно, после ее квантования возникнут серии нулей, которые можно
будет еще лучше сжать.
координатами в парах), а за ними
записать все четные пикселы. Эти две последовательности называются векторами
коэффициентов преобразования. Вторая последовательность состоит из малых
чисел, и, возможно, после ее квантования возникнут серии нулей, которые можно
будет еще лучше сжать.
Легко показать, что полная
дисперсия пикселов, которая определяется суммой ![]() , не меняется при повороте, поскольку
матрица этого преобразования является ортогональной. Однако дисперсия новых
координат
, не меняется при повороте, поскольку
матрица этого преобразования является ортогональной. Однако дисперсия новых
координат ![]() стала
малой, поэтому возросла дисперсия коэффициентов
стала
малой, поэтому возросла дисперсия коэффициентов ![]() . Дисперсию иногда называют энергией
распределения пикселов. Поэтому мы можем сказать, что поворот концентрирует
энергию в координатах
. Дисперсию иногда называют энергией
распределения пикселов. Поэтому мы можем сказать, что поворот концентрирует
энергию в координатах ![]() , с помощью чего достигается сжатие
изображения.
, с помощью чего достигается сжатие
изображения.

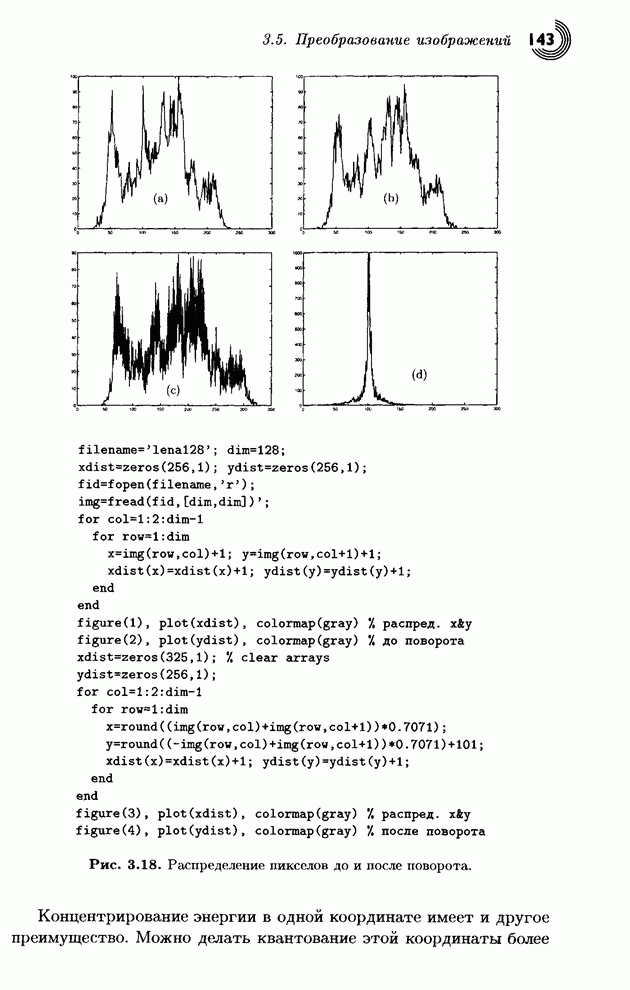
Рис. 3.18. Распределение пикселов до и после поворота.
Концентрирование энергии в одной координате имеет и другое преимущество. Можно делать квантование этой координаты более точным, чем квантование второй координаты. Такой способ квантования приводит к лучшему сжатию.

Рис. 3.19. Поворот пяти точек.
Следующий простой пример
иллюстрирует возможности этого ортогонального преобразования. Начнем с точки
(4,5) с близкими координатами. С помощью уравнения (3.3) эта точка переходит в ![]() . Энергии этих точек
равны:
. Энергии этих точек
равны: ![]() . Если
удалить координату (4) исходной точки, то получится ошибка
. Если
удалить координату (4) исходной точки, то получится ошибка ![]() . Однако, если удалить меньшую
из двух координат преобразованной точки (0.7071), то ошибка будет всего
. Однако, если удалить меньшую
из двух координат преобразованной точки (0.7071), то ошибка будет всего ![]() . Эту ошибку можно
также вычислить, исходя из реконструированной точки. Применим обратное
преобразование (уравнение (3.4)) к точке
. Эту ошибку можно
также вычислить, исходя из реконструированной точки. Применим обратное
преобразование (уравнение (3.4)) к точке ![]() . Получим, конечно, исходную точку (4,5).
Сделав то же самое для точки
. Получим, конечно, исходную точку (4,5).
Сделав то же самое для точки ![]() , получим после округления точку
(4.5,4.5). Разность энергий исходной и реконструированной точек будет равна той
же малой величине
, получим после округления точку
(4.5,4.5). Разность энергий исходной и реконструированной точек будет равна той
же малой величине
 .
.
Это простое преобразование легко
обобщить на случай любого числа измерений. Вместо пар, можно выбирать тройки
точек, триплеты. Каждый триплет становится точкой трехмерного пространства, а
все точки образуют «облако» вокруг прямой, проходящей через начало координат
под углом 45° к каждой координатной оси. Если эту прямую повернуть так, что она
ляжет на ось ![]() ,
то координаты
,
то координаты ![]() и
и
![]() точек
«облака» станут малыми числами. Такое преобразование совершается с помощью
умножения каждой точки на некоторую матрицу размера 3x3, которая, конечно,
является ортогональной. Вторая и третья компоненты координат преобразованных
точек будут малыми числами, поэтому координаты всех точек следует разделить на
три вектора коэффициентов. Для лучшего сжатия необходимо, чтобы квантование
этих векторов коэффициентов делалось с разной степенью точности.
точек
«облака» станут малыми числами. Такое преобразование совершается с помощью
умножения каждой точки на некоторую матрицу размера 3x3, которая, конечно,
является ортогональной. Вторая и третья компоненты координат преобразованных
точек будут малыми числами, поэтому координаты всех точек следует разделить на
три вектора коэффициентов. Для лучшего сжатия необходимо, чтобы квантование
этих векторов коэффициентов делалось с разной степенью точности.
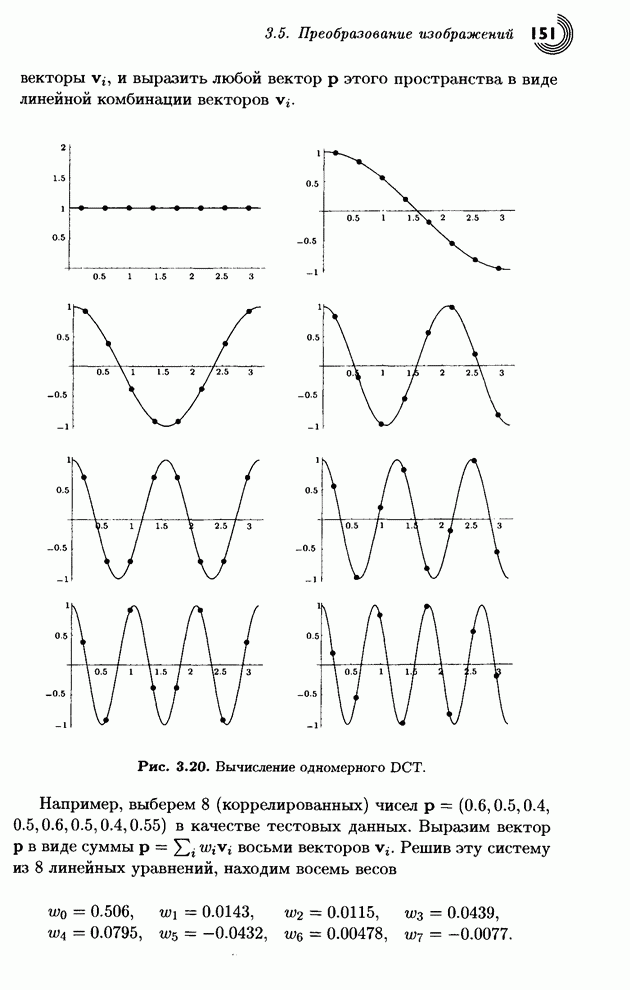
Этот метод легко распространить на более высокие размерности, с той лишь разницей, что получающиеся пространства уже нельзя будет представить зрительно. Однако, соответствующие матрицы преобразований легко выписываются. Единственно, что приходится учитывать, это то, что размерность не должна быть слишком большой, поскольку результат сжатия на основе поворота зависит от корреляции близких пикселов. Например, если объединять по 24 соседних пиксела в одну точку 24-мерного пространства, то полученные точки, вообще говоря, не будут лежать в малой окрестности «прямой под углом 45° к осям координат», поскольку не будет корреляции между пикселом и его дальним соседом. Поэтому после поворота, последние 23 координаты преобразованных точек уже не будут малыми. Наблюдения показывают, что корреляция пикселов сохраняется до размерности восемь, но редко дальше.
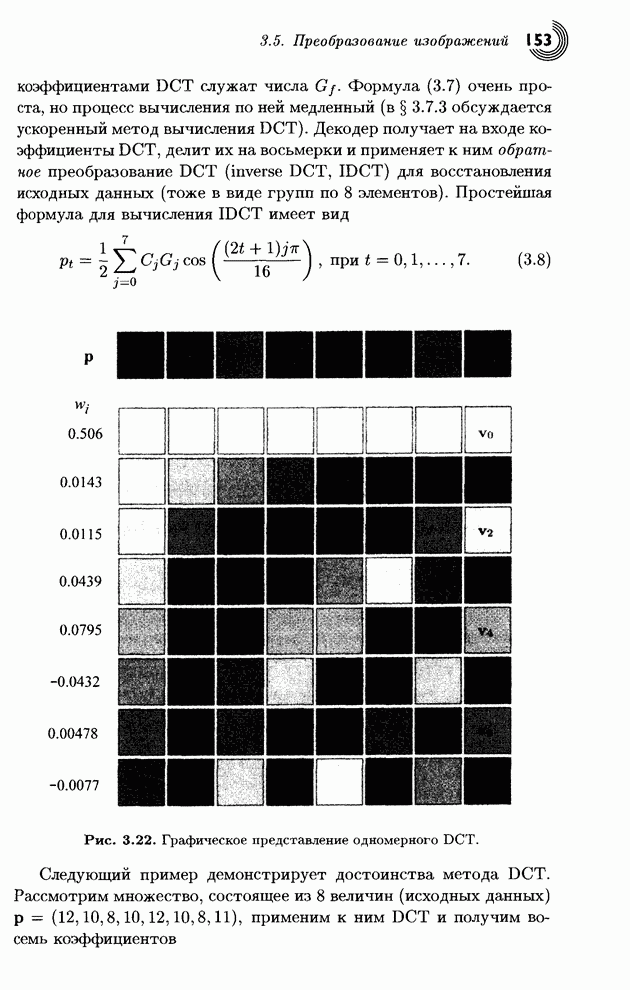
Метод JPEG, описанный в § 3.7, делит изображение на блоки пикселов размера 8х8 и поворачивает каждый блок два раза с помощью уравнения (3.9), которое будет объяснено в § 3.5.3. Это двойное вращение дает множества, состоящие из 64 преобразованных величин, из которых первая, называемая «коэффициент DC», большая, а все остальные 63 («коэффициенты AС») - обычно маленькие. Таким образом, это преобразование концентрирует энергию в первой компоненте из 64. Далее множество коэффициентов DC и 63 множества коэффициентов АС следует квантовать раздельно (метод JPEG делает это немного иначе, см. § 3.7.4).
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие переводчика
- Предисловие автора
- Введение
- Глава 1. Статистические методы
- 1.1. Энтропия
- 1.2. Коды переменной длины
- 1.3. Декодирование
- 1.4. Кодирование Хаффмана
- 1.4.1. Декодирование Хаффмана
- 1.4.2. Средняя длина кода
- 1.5. Адаптивные коды Хаффмана
- 1.5.1. Несжатые коды
- 1.5.2. Модификация дерева
- 1.5.3. Переполнение счетчика
- 1.5.4. Кодовое переполнение
- 1.5.5. Вариант алгоритма
- 1.6. Факсимильное сжатие
- 1.6.1. Одномерное кодирование
- 1.6.2. Двумерное кодирование
- 1.7. Арифметическое кодирование
- 1.7.1. Детали реализации метода
- 1.7.2. Потеря значащих цифр
- 1.7.3. Заключительные замечания
- 1.8. Адаптивное арифметическое кодирование
- ГЛАВА 2 СЛОВАРНЫЕ МЕТОДЫ
- 2.1. LZ77 (скользящее окно)
- 2.1.1. Циклическая очередь
- 2.2. LZSS
- 2.2.1. Недостатки
- 2.3. LZ78
- 2.4. LZW
- 2.4.1. Декодирование LZW
- 2.4.2. Структура словаря LZW
- 2.4.3. LZW в практических приложениях
- 2.5. Заключение
- ГЛАВА 3 СЖАТИЕ ИЗОБРАЖЕНИЙ
- 3.1. Введение
- 3.2. Типы изображений
- 3.3. Подходы к сжатию изображений
- 3.3.1. Коды Грея
- 3.3.2. Метрики ошибок
- 3.4. Интуитивные методы
- 3.4.1. Подвыборка
- 3.4.2. Квантование
- 3.5. Преобразование изображений
- 3.5.1. Ортогональные преобразования
- 3.5.2. Матричные преобразования
- 3.5.3. Дискретное косинус-преобразование
- 3.5.4. Пример
- 3.5.5. Дискретное синус-преобразование
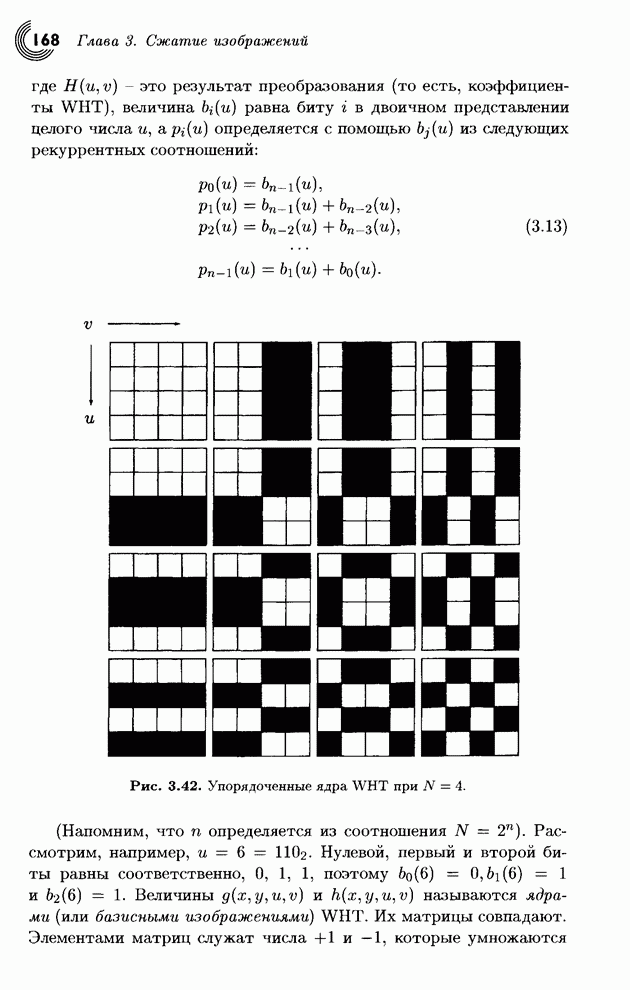
- 3.5.6. Преобразование Уолша-Адамара
- 3.5.7. Преобразование Хаара
- 3.5.8. Преобразование Кархунена-Лоэвэ
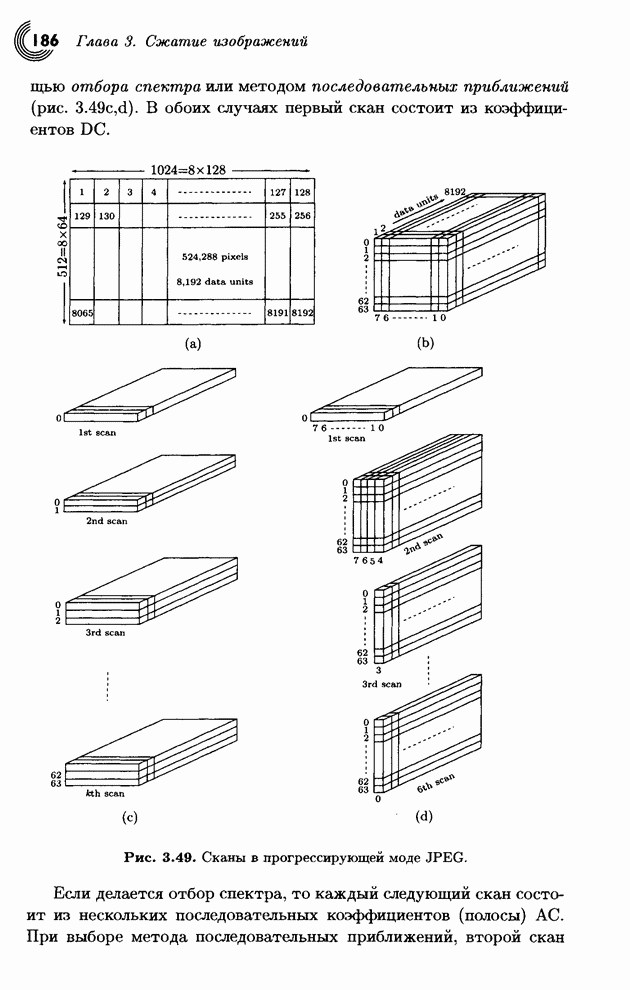
- 3.6. Прогрессирующее сжатие изображений
- 3.7. JPEG
- 3.7.1. Светимость
- 3.7.2. DCT
- 3.7.3. Практическое DCT
- 3.7.4. Квантование
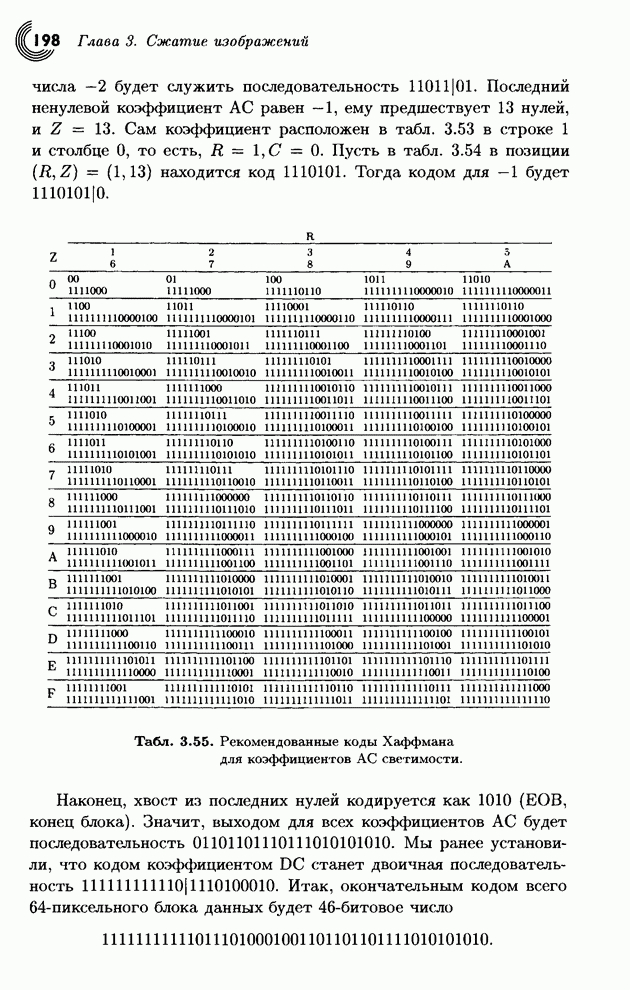
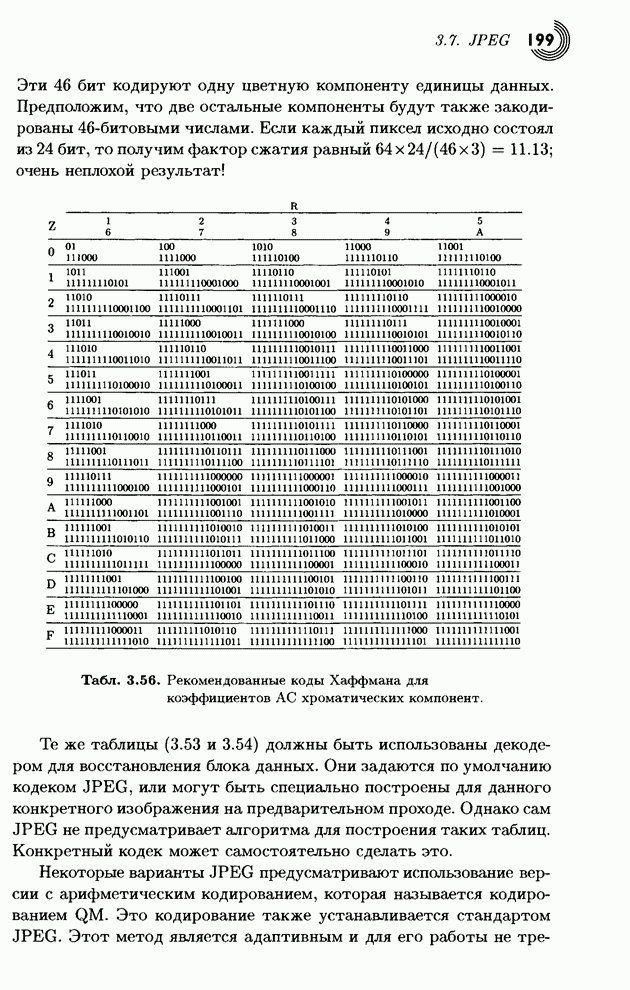
- 3.7.5. Кодирование
- 3.7.6. Мода без потери данных
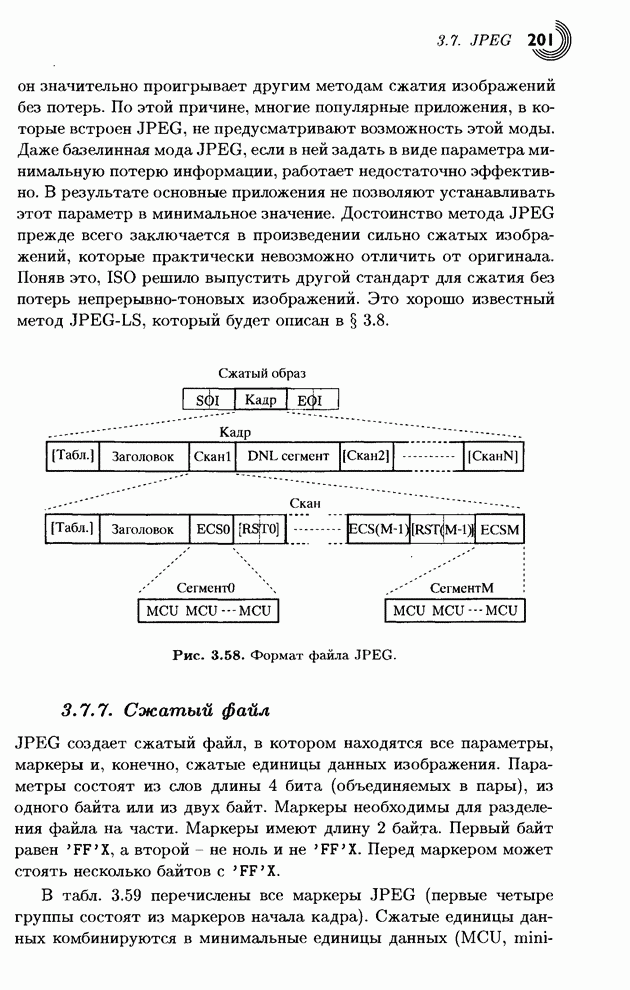
- 3.7.7. Сжатый файл
- 3.7.8. JFIF
- 3.8. JPEG-LS
- 3.8.1. Коды Голомба
- 3.8.2. Основы метода JPEG-LS
- 3.8.3. Кодер
- ГЛАВА 4 ВЕЙВЛЕТНЫЕ МЕТОДЫ
- 4.1. Вычисление средних и полу разностей
- 4.1.1. Обобщение на двумерный случай
- 4.1.2. Свойства преобразования Хаара
- 4.2. Преобразование Хаара
- 4.2.1. Матричная форма
- 4.3. Поддиапазонные преобразования
- 4.4. Банк фильтров
- 4.5. Нахождение коэффициентов фильтра
- 4.6. Преобразование DWT
- 4.7. Примеры
- 4.8. Вейвлеты Добеши
- 4.9. SPIHT
- 4.9.1. Алгоритм сортировки разделением множеств
- 4.9.2. Пространственно ориентированное дерево
- 4.9.3. Кодирование в алгоритме SPIHT
- 4.9.4. Пример
- 4.9.5. QTCQ
- ГЛАВА 5 СЖАТИЕ ВИДЕО
- 5.1. Основные принципы
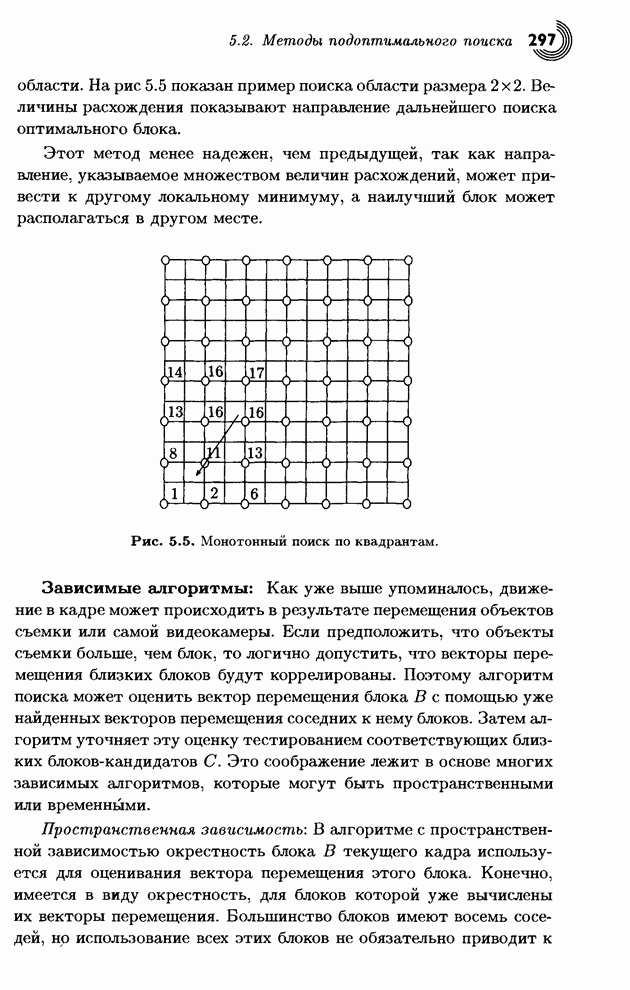
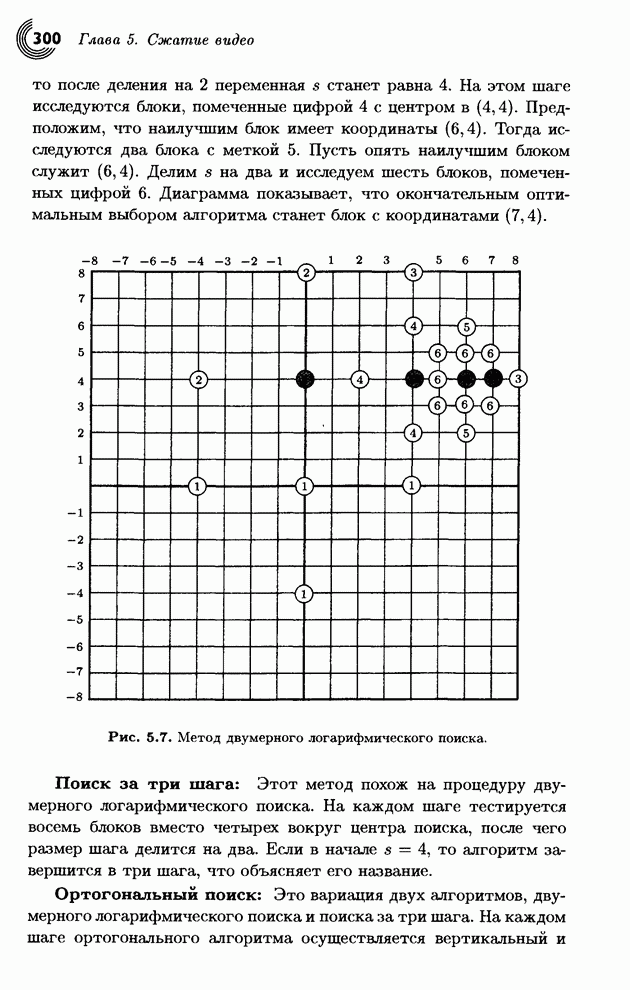
- 5.2. Методы подоптимального поиска
- ГЛАВА 6 СЖАТИЕ ЗВУКА
- 6.1. Звук
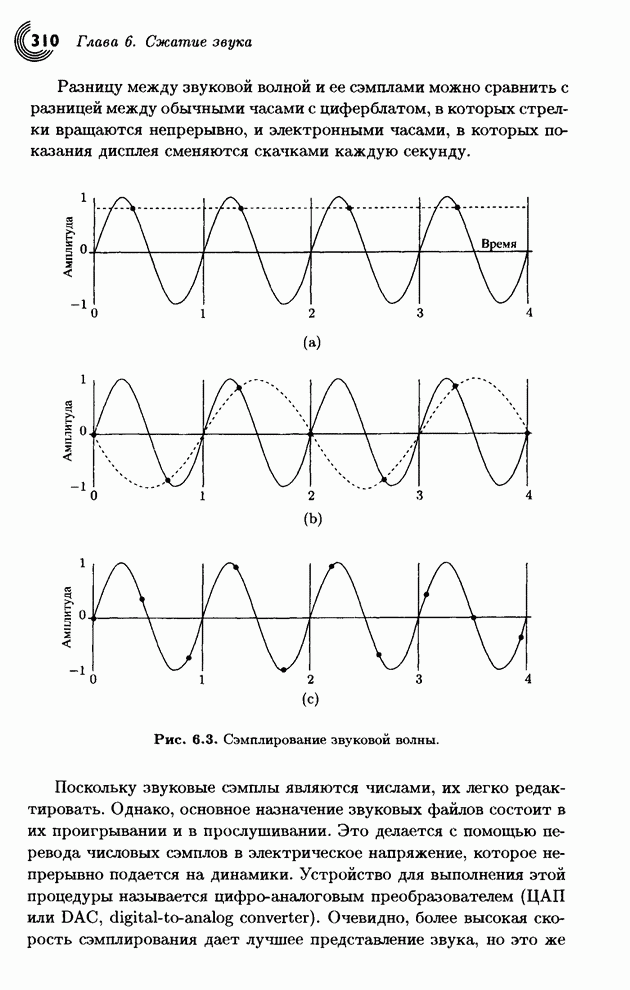
- 6.2. Оцифрованный звук
- 6.3. Органы слуха человека
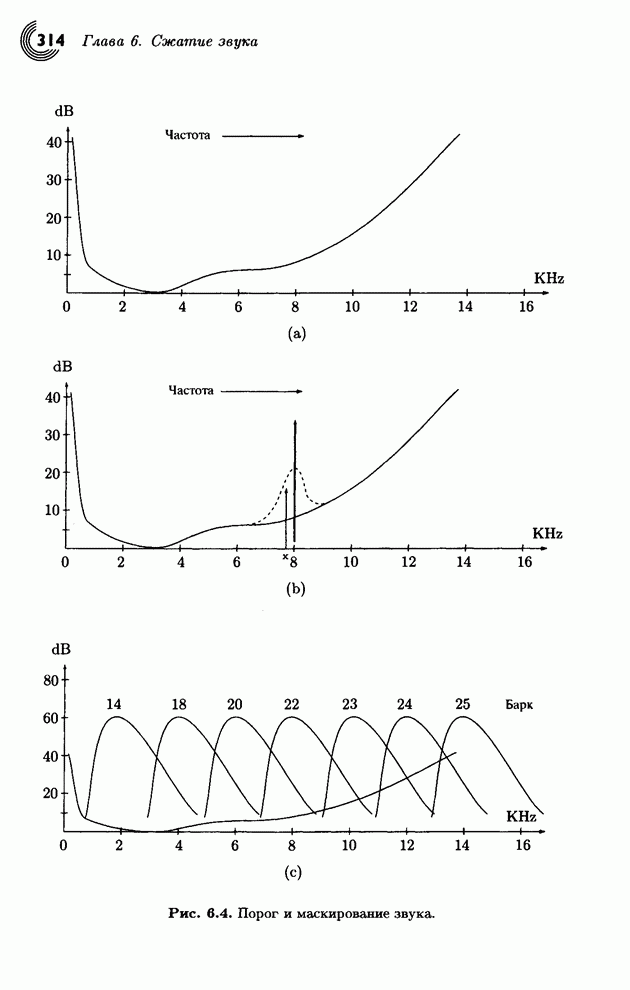
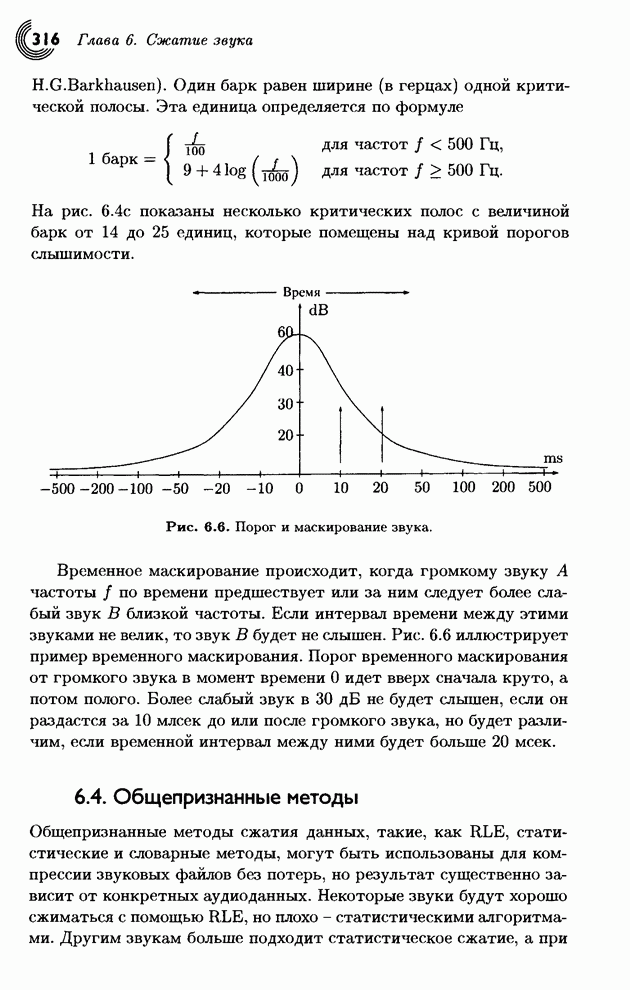
- 6.4. Общепризнанные методы
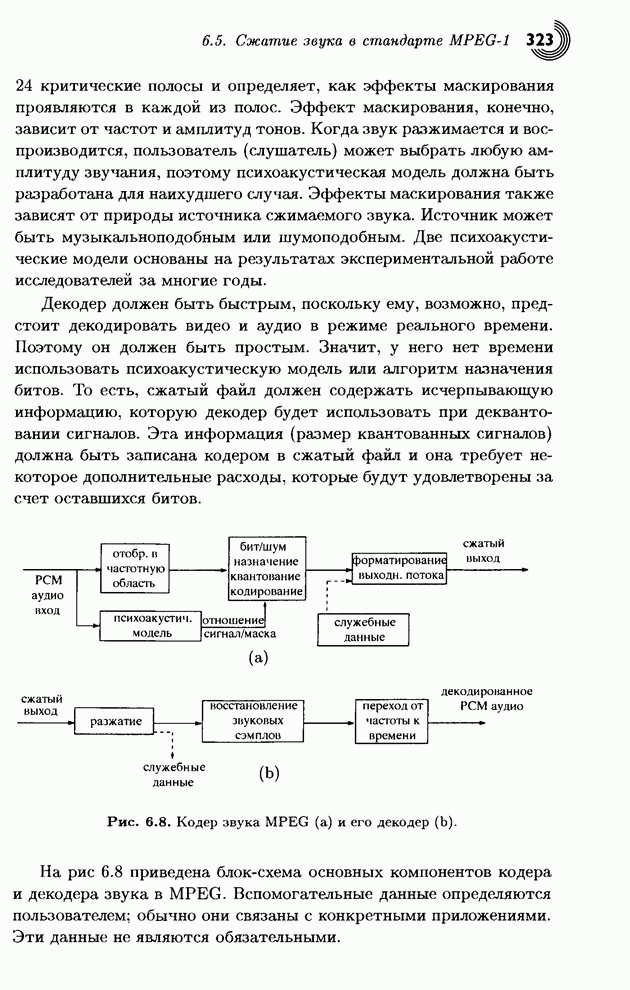
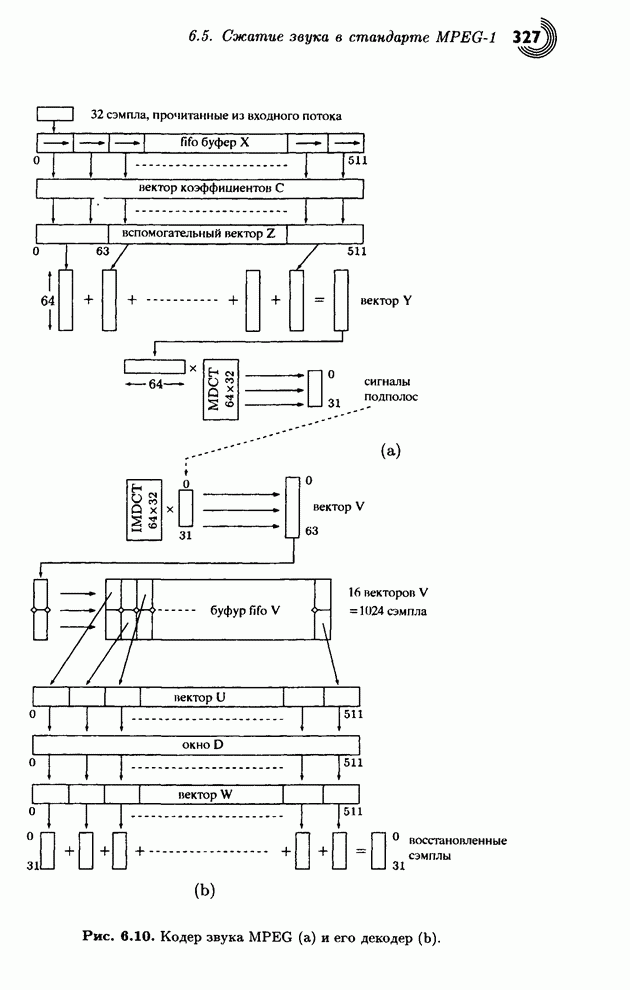
- 6.5. Сжатие звука в стандарте MPEG-1
- 6.5.1. Кодирование частотной области
- 6.5.2. Формат сжатых данных
- 6.5.3. Психоакустические модели
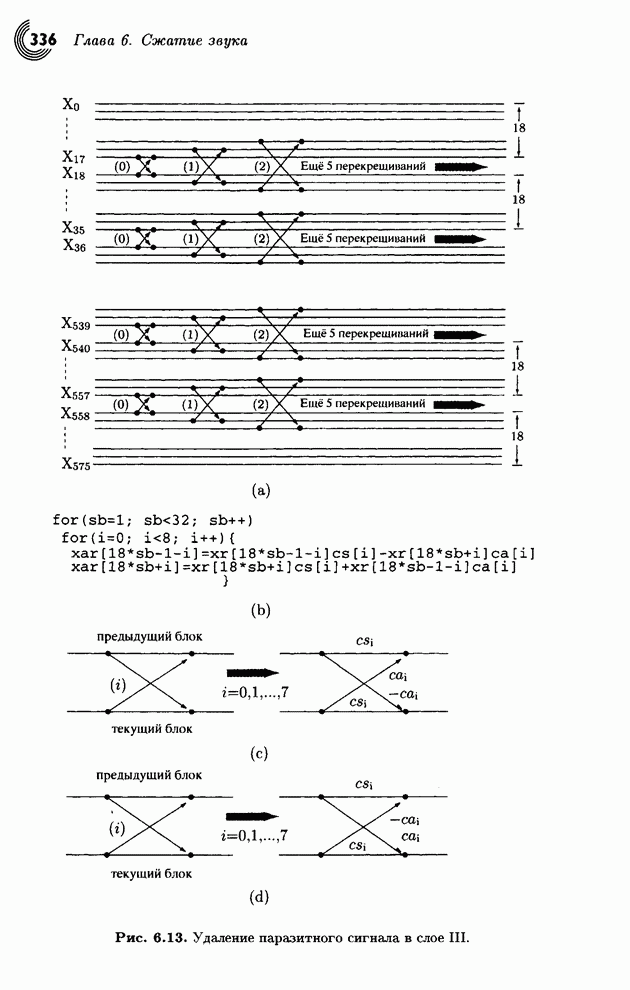
- 6.5.4. Кодирование: слой III
- Литература
- Глоссарий