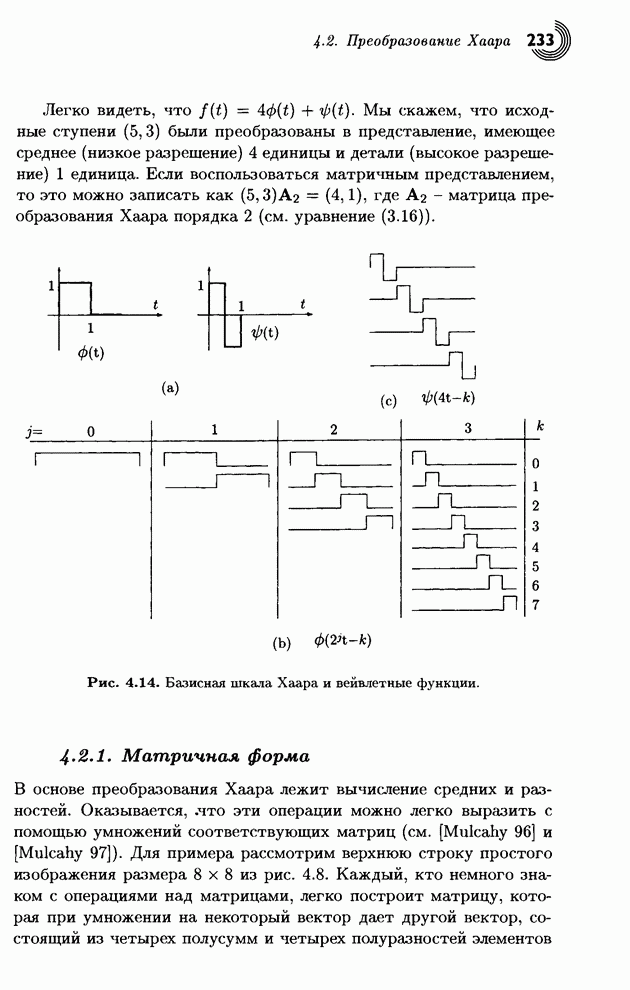
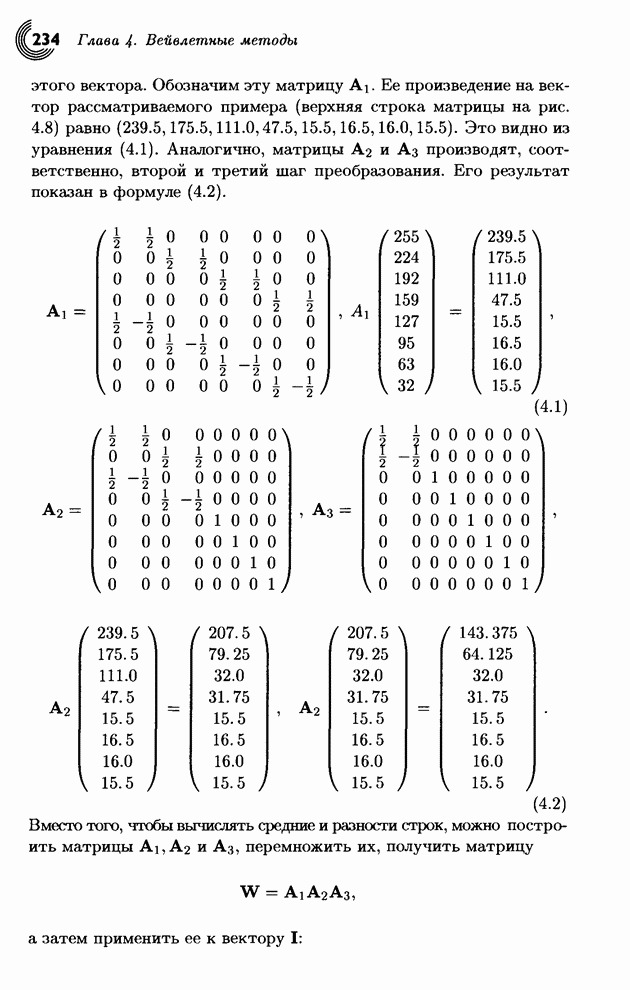
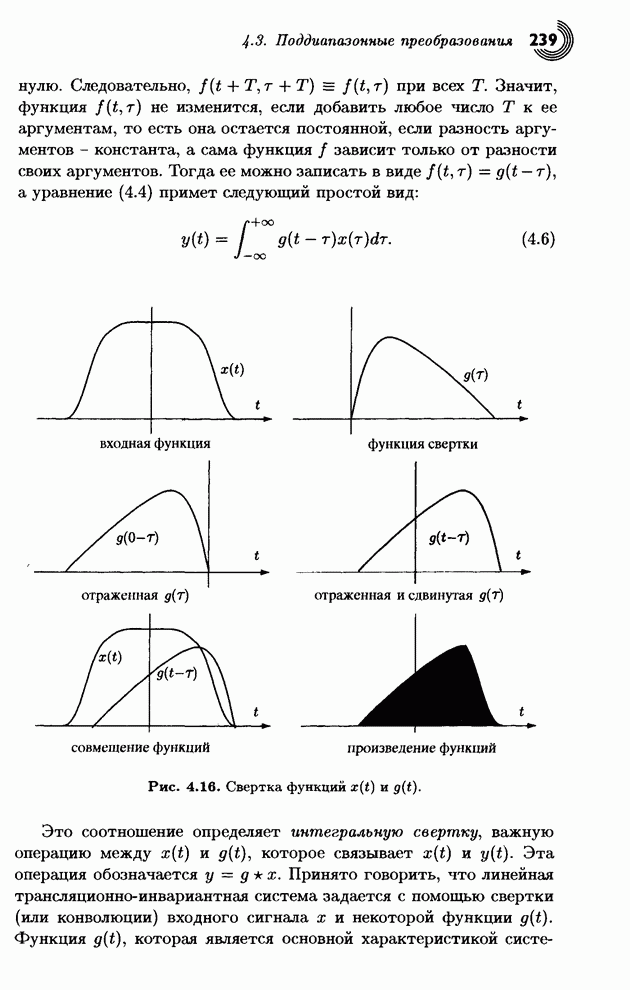
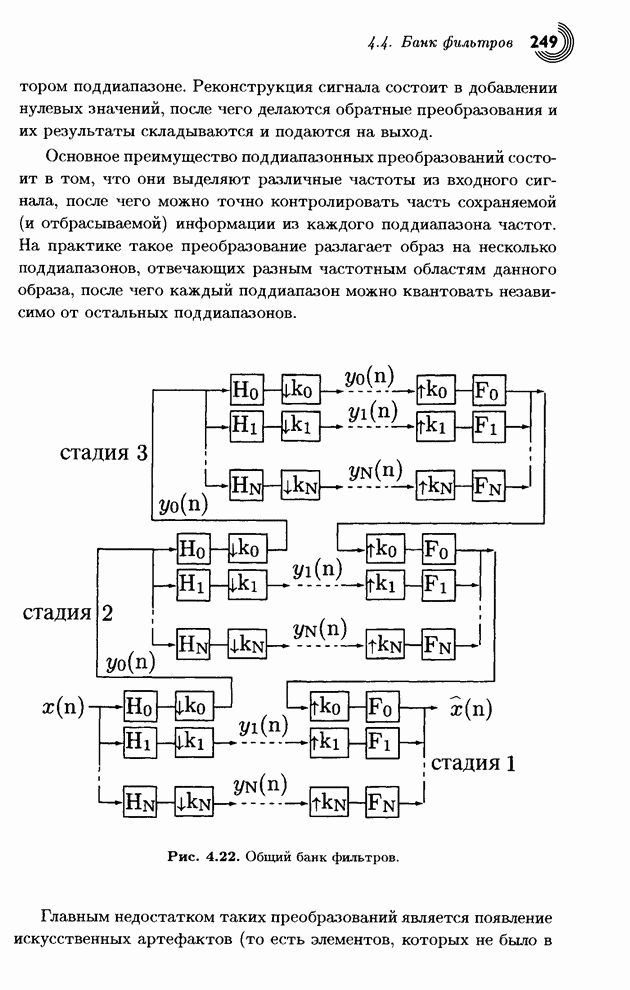
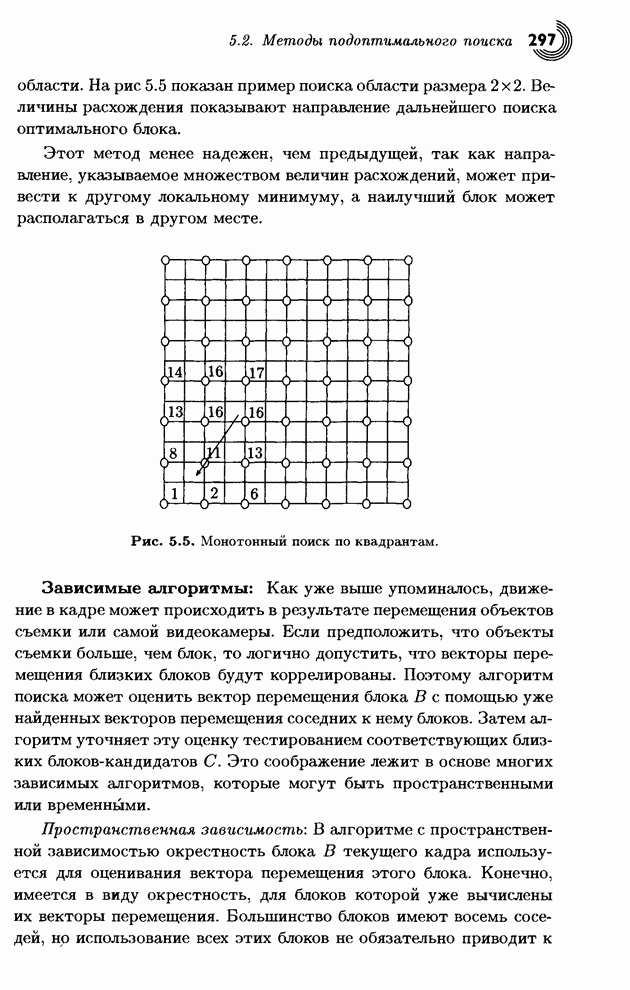
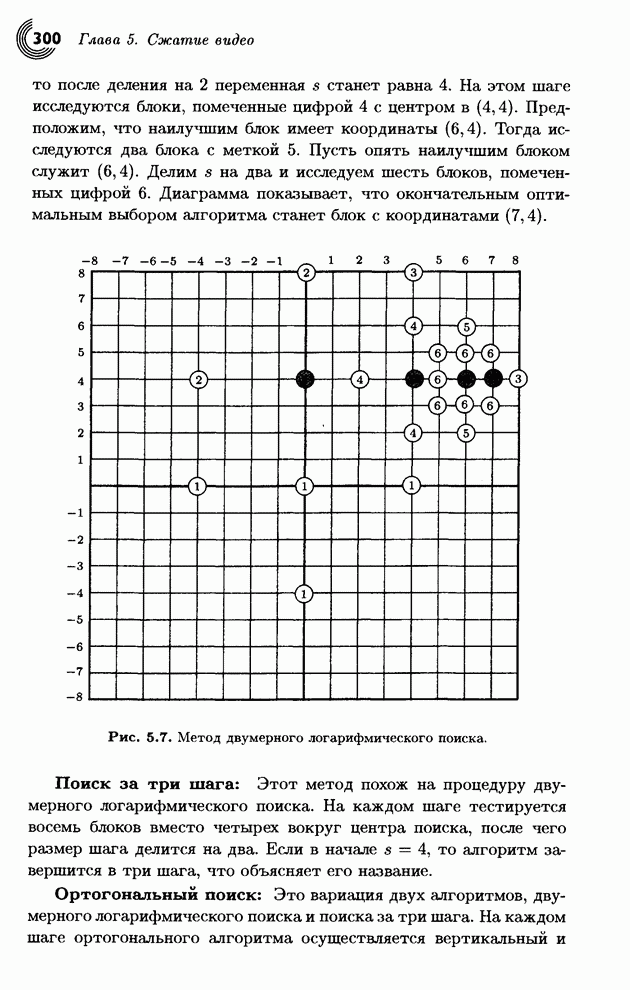
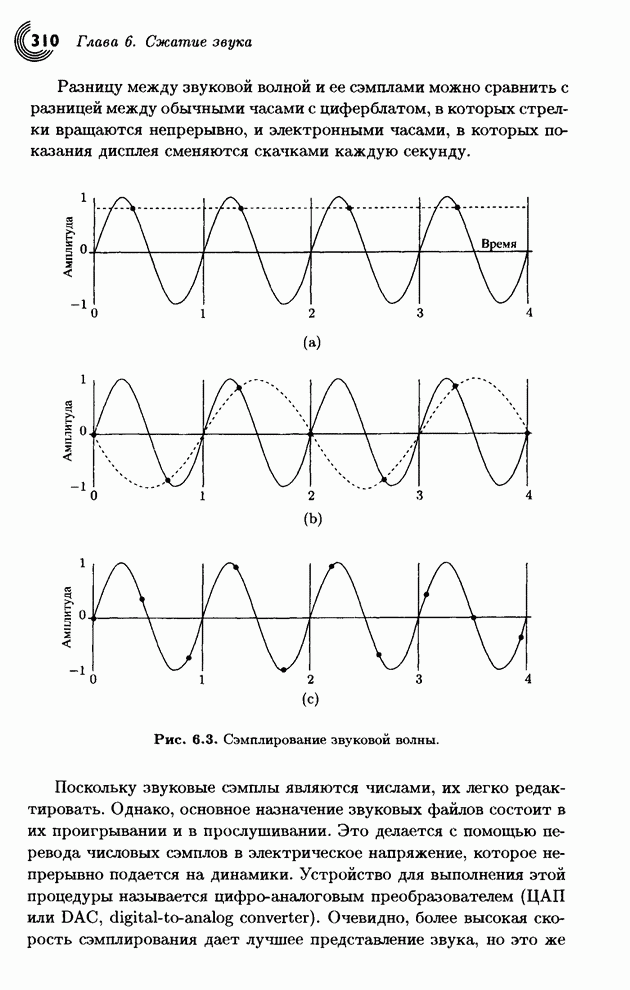
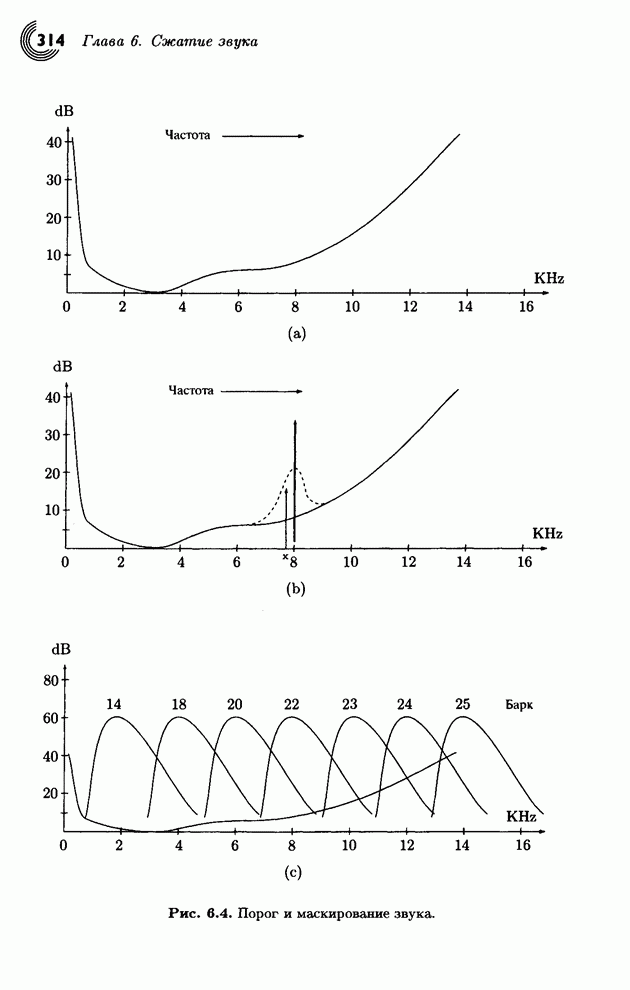
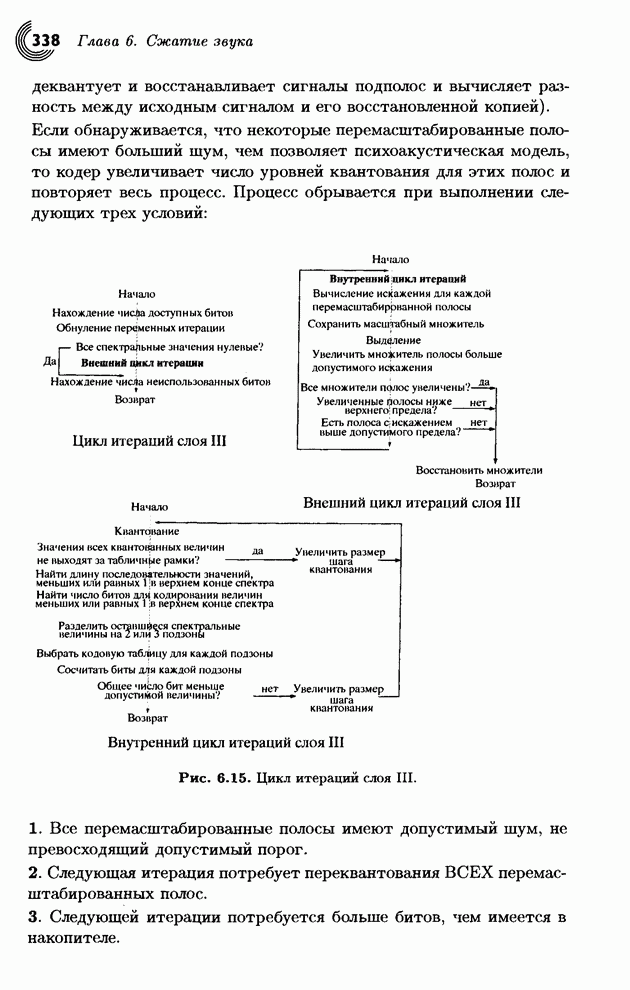
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
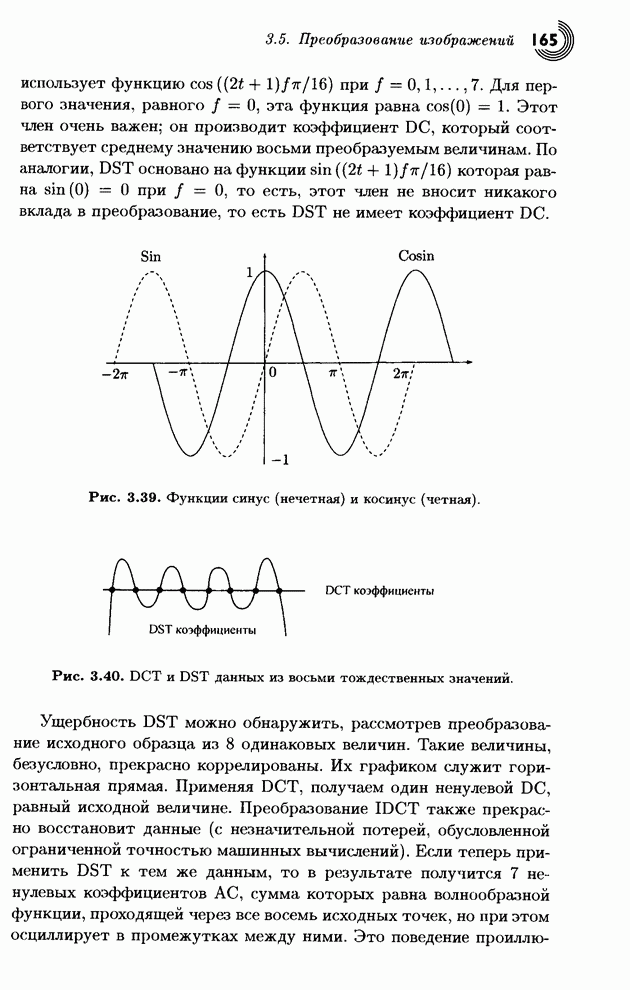
3.5.1. Ортогональные преобразования
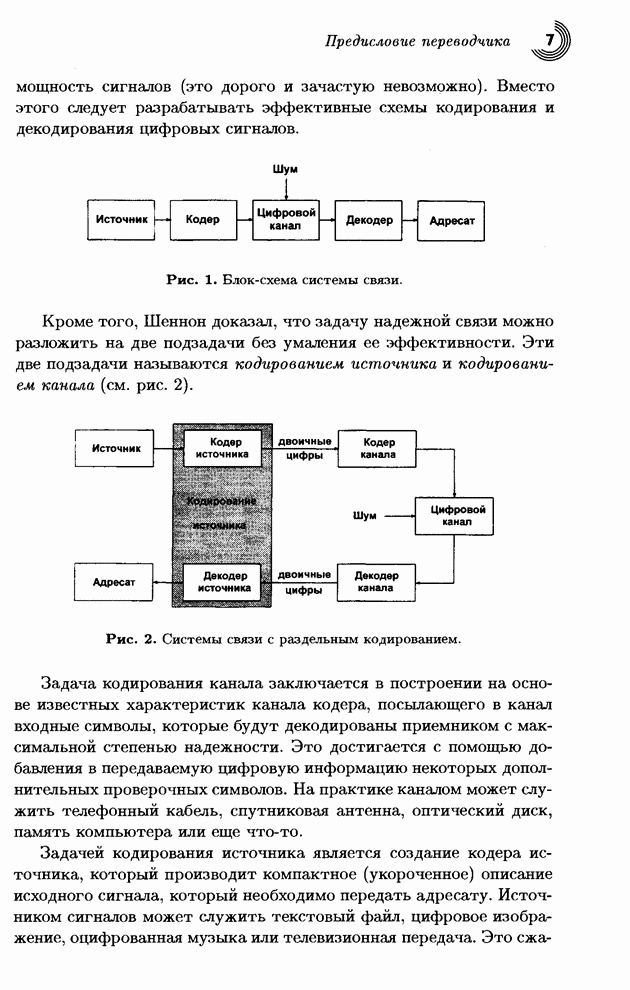
Преобразования, которые
используются для сжатия изображений должны быть быстрыми, и, по возможности,
легко реализуемыми на компьютере. Это прежде всего предполагает, что такие
преобразования должны быть линейными. То есть, преобразованные величины ![]() являются линейными
комбинациями (суммами с некоторыми множителями или весами) исходных величин
(пикселов)
являются линейными
комбинациями (суммами с некоторыми множителями или весами) исходных величин
(пикселов) ![]() ,
причем соответствующим множителем или весом служит некоторое число
,
причем соответствующим множителем или весом служит некоторое число ![]() (коэффициент
преобразования). Значит,
(коэффициент
преобразования). Значит, ![]() , где
, где ![]() . Например, при
. Например, при ![]() это преобразование можно
записать в матричной форме
это преобразование можно
записать в матричной форме
 ,
,
которая
в общем случае примет следующий вид: ![]() . Каждый вектор-столбец матрицы
. Каждый вектор-столбец матрицы ![]() называется «базисным
вектором».
называется «базисным
вектором».
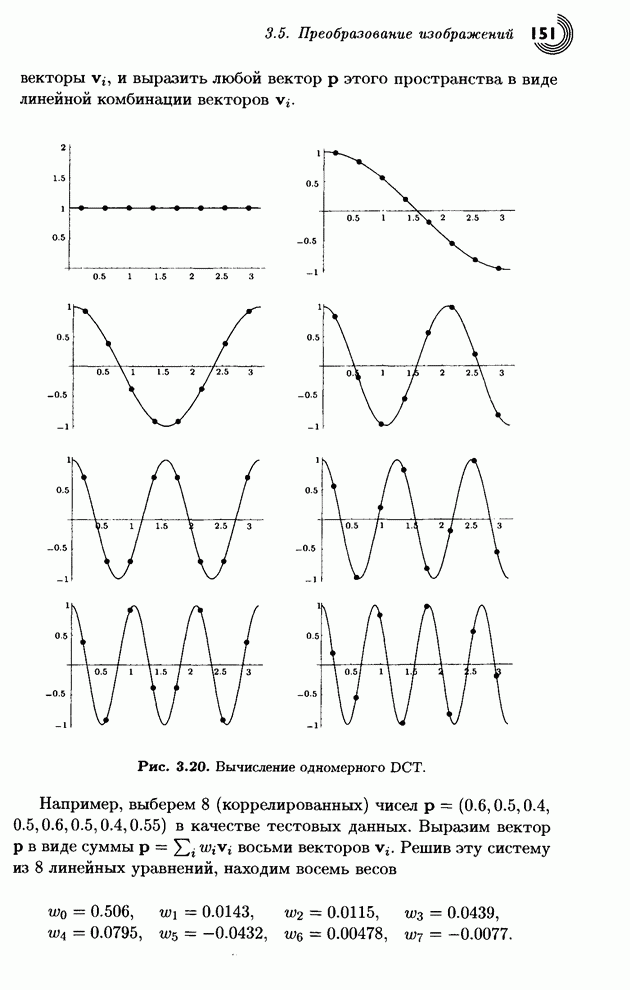
Важной задачей является
определение коэффициентов преобразования ![]() . Основное требование заключается в том,
чтобы после преобразования величина
. Основное требование заключается в том,
чтобы после преобразования величина ![]() была бы большой, а все остальные
величины
была бы большой, а все остальные
величины ![]() стали
бы малыми. Основное соотношение
стали
бы малыми. Основное соотношение ![]() предполагает, что
предполагает, что ![]() будет большим, если веса
будет большим, если веса ![]() будут усиливать
соответствующие величины
будут усиливать
соответствующие величины ![]() . Это произойдет, например, если
компоненты векторов
. Это произойдет, например, если
компоненты векторов ![]() и
и
![]() имеют
близкие значения и одинаковые знаки. Наоборот,
имеют
близкие значения и одинаковые знаки. Наоборот, ![]() будет малым, если веса
будет малым, если веса ![]() будут малыми, и
половина из них будет иметь знак, противоположный знаку соответствующего числа
будут малыми, и
половина из них будет иметь знак, противоположный знаку соответствующего числа ![]() . Поэтому, если
получаются большие
. Поэтому, если
получаются большие ![]() ,
то векторы
,
то векторы ![]() имеют
сходство с исходным вектором
имеют
сходство с исходным вектором ![]() , а малые
, а малые ![]() означают, что компоненты
означают, что компоненты ![]() сильно отличаются от
сильно отличаются от ![]() . Следовательно,
базисные векторы
. Следовательно,
базисные векторы ![]() можно
интерпретировать как инструмент для извлечения некоторых характерных признаков
исходного вектора.
можно
интерпретировать как инструмент для извлечения некоторых характерных признаков
исходного вектора.
На практике веса ![]() не должны зависеть от
исходных данных. В противном случае, их придется добавлять в сжатый файл для
использования декодером. Это соображение, а также тот факт, что исходные данные
являются пикселами, то есть, неотрицательными величинами, определяет способ выбора
базисных векторов. Первый вектор, тот, который, порождает
не должны зависеть от
исходных данных. В противном случае, их придется добавлять в сжатый файл для
использования декодером. Это соображение, а также тот факт, что исходные данные
являются пикселами, то есть, неотрицательными величинами, определяет способ выбора
базисных векторов. Первый вектор, тот, который, порождает ![]() , должен состоять из близких,
возможно, совпадающих чисел. Он будет усиливать неотрицательные величины
пикселов. А все остальные векторы базиса должны наполовину состоять из
положительных чисел, а на другую половину - из отрицательных. После умножения
на положительные величины и их сложения, результат будет малым числом. (Это
особенно верно, когда исходные данные близки, а мы знаем, что соседние пикселы
имеют, обычно, близкие величины.) Напомним, что базисные векторы представляют
собой некоторый инструмент для извлечения особенностей из исходных данных.
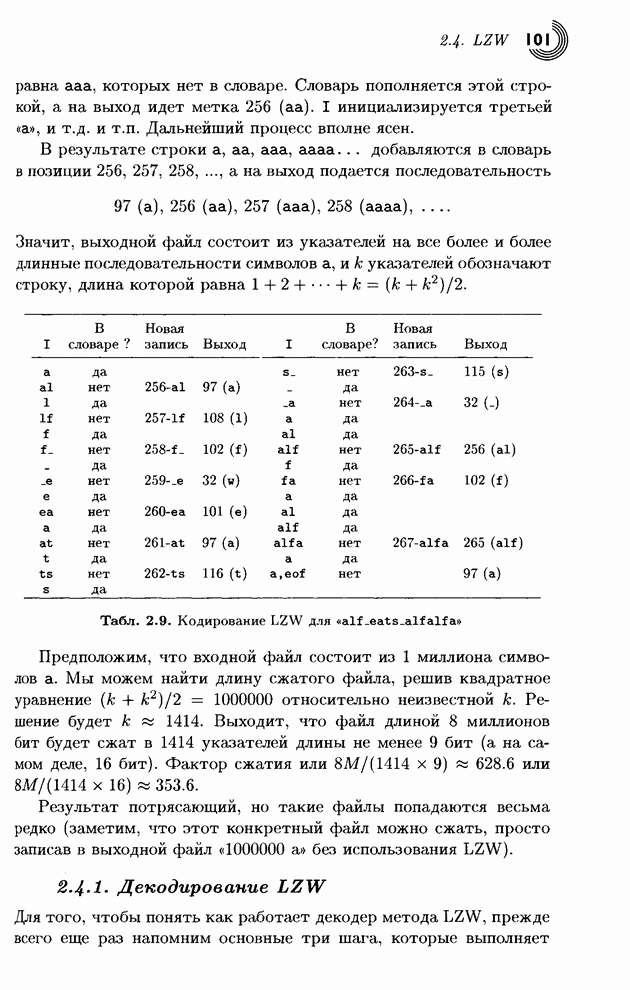
Поэтому хорошим выбором будут базисные векторы, которые сильно различаются друг
от друга и, поэтому, могут извлекать разные особенности. Это приводит к мысли,
что базисные векторы должны быть взаимно ортогональными. Если матрица
преобразования
, должен состоять из близких,
возможно, совпадающих чисел. Он будет усиливать неотрицательные величины
пикселов. А все остальные векторы базиса должны наполовину состоять из
положительных чисел, а на другую половину - из отрицательных. После умножения
на положительные величины и их сложения, результат будет малым числом. (Это
особенно верно, когда исходные данные близки, а мы знаем, что соседние пикселы
имеют, обычно, близкие величины.) Напомним, что базисные векторы представляют
собой некоторый инструмент для извлечения особенностей из исходных данных.
Поэтому хорошим выбором будут базисные векторы, которые сильно различаются друг
от друга и, поэтому, могут извлекать разные особенности. Это приводит к мысли,
что базисные векторы должны быть взаимно ортогональными. Если матрица
преобразования ![]() состоит
из ортогональных векторов, то преобразование называется ортогональным.
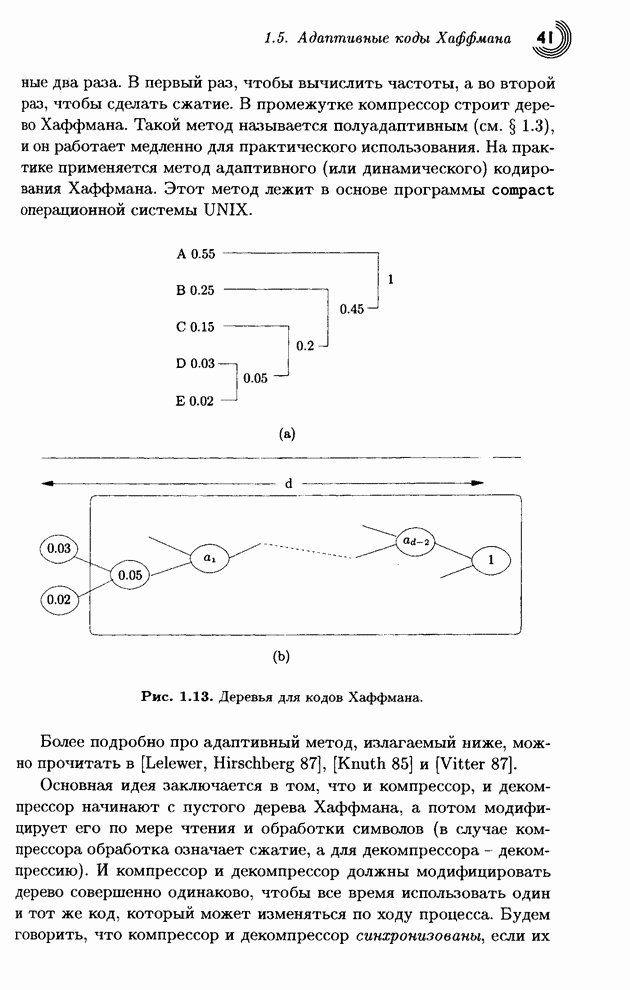
Другое наблюдение, позволяющее правильно выбирать базисные векторы, состоит в
том, что эти векторы должны иметь все большие частоты изменения знака, чтобы
извлекать, так сказать, высокочастотные характеристики сжимаемых данных при
вычислении преобразованных величин.
состоит
из ортогональных векторов, то преобразование называется ортогональным.
Другое наблюдение, позволяющее правильно выбирать базисные векторы, состоит в
том, что эти векторы должны иметь все большие частоты изменения знака, чтобы
извлекать, так сказать, высокочастотные характеристики сжимаемых данных при
вычислении преобразованных величин.
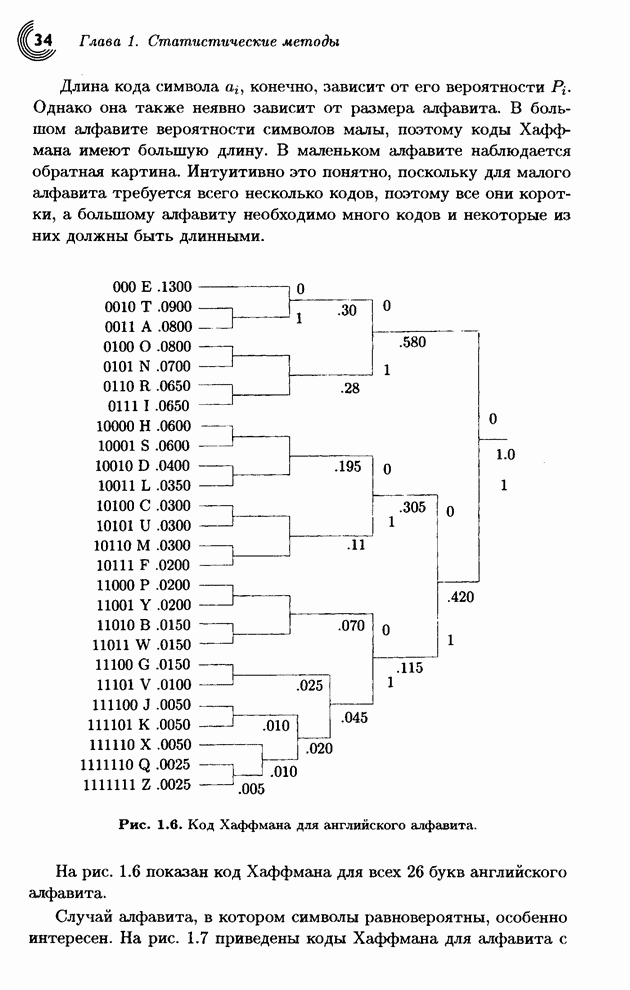
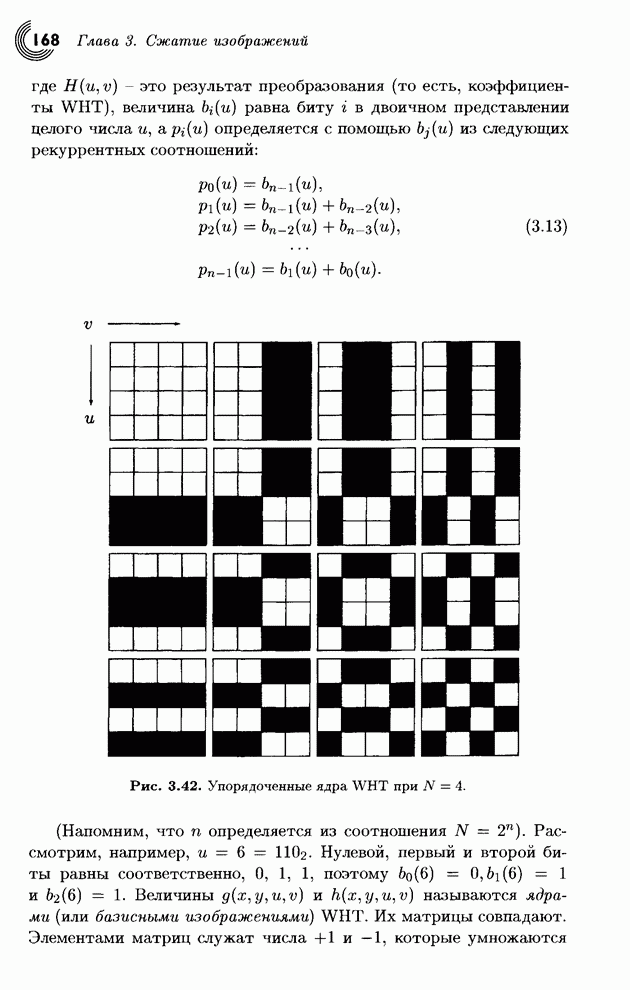
Этим свойствам удовлетворяет следующая ортогональная матрица:
 . (3.5)
. (3.5)
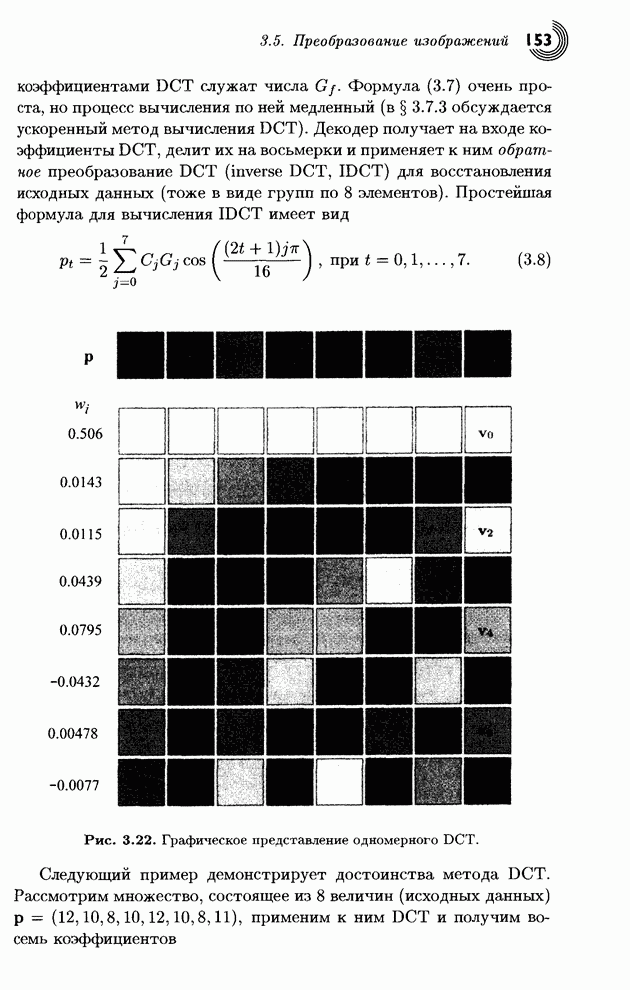
Первый базисный вектор (верхняя
строка ![]() )
состоит из одних единиц, поэтому его частота равна нулю. Все остальные векторы
имеют две +1 и две -1, поэтому они дадут маленькие преобразованные величины, а
их частоты (измеренные количеством смен знаков в строке) возрастают. Эта
матрица подобна матрице преобразования Адамара Уолша (см. уравнение (3.11)).
Для примера, преобразуем начальный вектор (4,6,5,2):
)
состоит из одних единиц, поэтому его частота равна нулю. Все остальные векторы
имеют две +1 и две -1, поэтому они дадут маленькие преобразованные величины, а
их частоты (измеренные количеством смен знаков в строке) возрастают. Эта
матрица подобна матрице преобразования Адамара Уолша (см. уравнение (3.11)).
Для примера, преобразуем начальный вектор (4,6,5,2):
 .
.
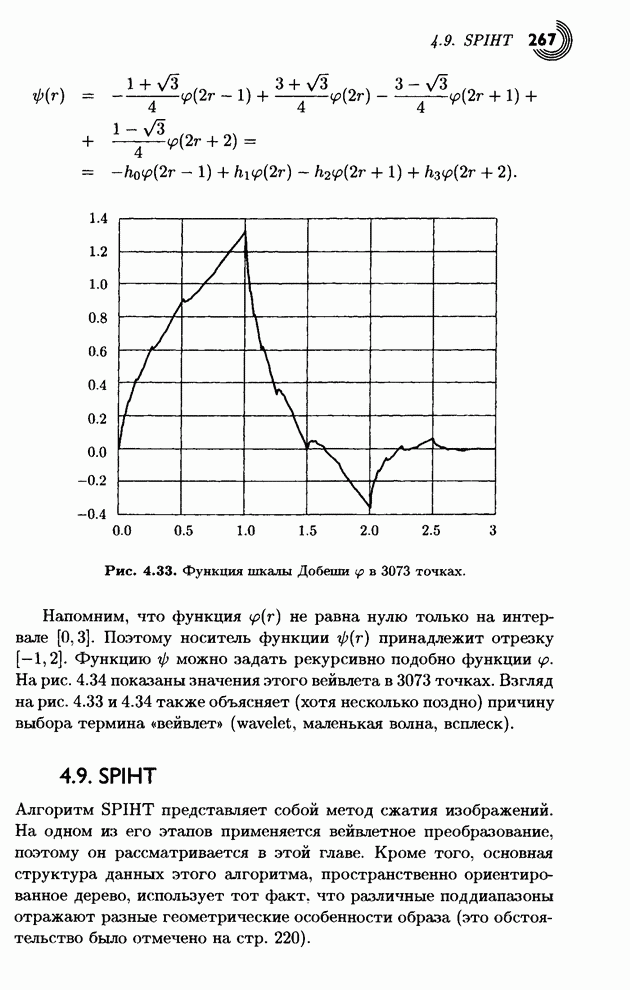
Результат вполне ободряющий,
поскольку число ![]() стало
большим (по сравнению с исходными данными), а два других числа стали малыми.
Вычислим энергии исходных и преобразованных данных. Начальная энергия равна
стало
большим (по сравнению с исходными данными), а два других числа стали малыми.
Вычислим энергии исходных и преобразованных данных. Начальная энергия равна ![]() , а после
преобразования энергия стала
, а после
преобразования энергия стала ![]() , что в четыре раза больше. Энергию можно
сохранить, если умножить матрицу преобразования
, что в четыре раза больше. Энергию можно
сохранить, если умножить матрицу преобразования ![]() на коэффициент 1/2. Новое произведение
на коэффициент 1/2. Новое произведение ![]() будет равно
будет равно ![]() . Итак, энергия
сохраняется и концентрируется в первой компоненте, и она теперь составляет
. Итак, энергия
сохраняется и концентрируется в первой компоненте, и она теперь составляет ![]() от общей энергии
исходных данных, в которых на долю первой компоненты приходилось всего 20%.
от общей энергии
исходных данных, в которых на долю первой компоненты приходилось всего 20%.
Другое преимущество матрицы ![]() состоит в том, что
она же делает обратное преобразование. Исходные данные (4,6,5,2)
восстанавливаются с помощью произведения
состоит в том, что
она же делает обратное преобразование. Исходные данные (4,6,5,2)
восстанавливаются с помощью произведения ![]() .
.
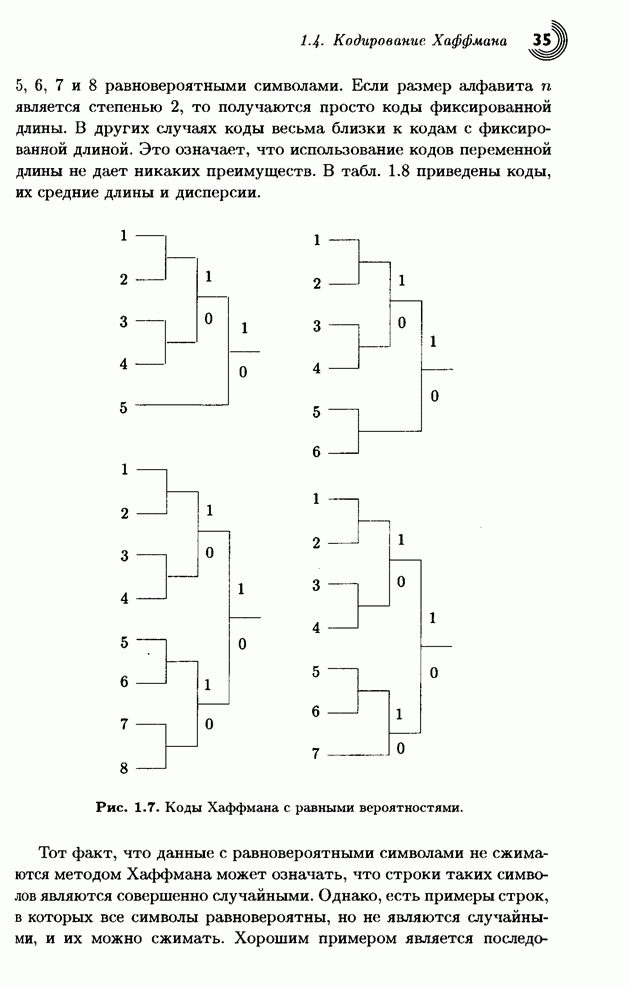
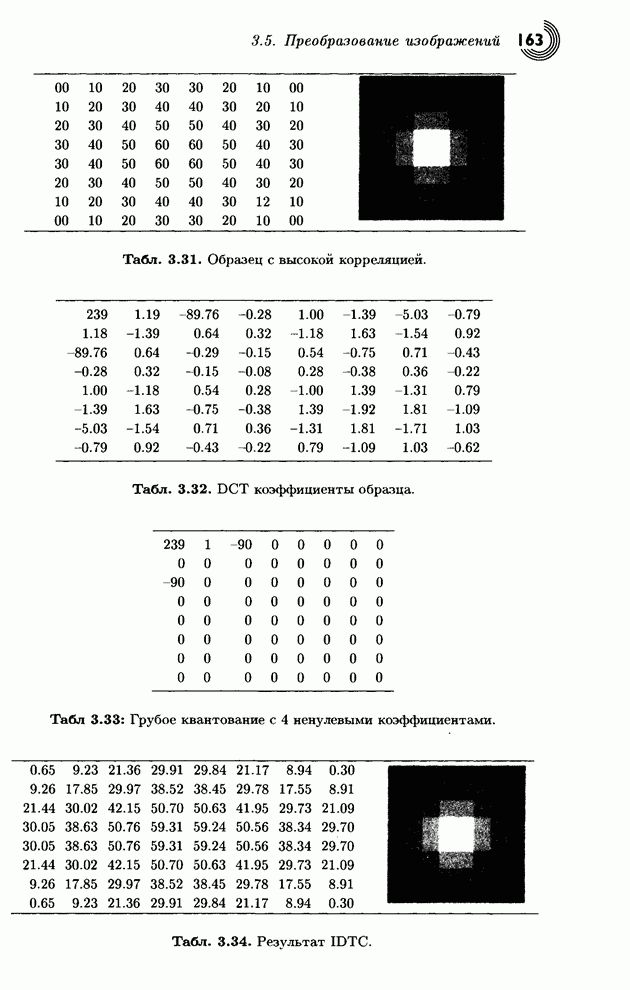
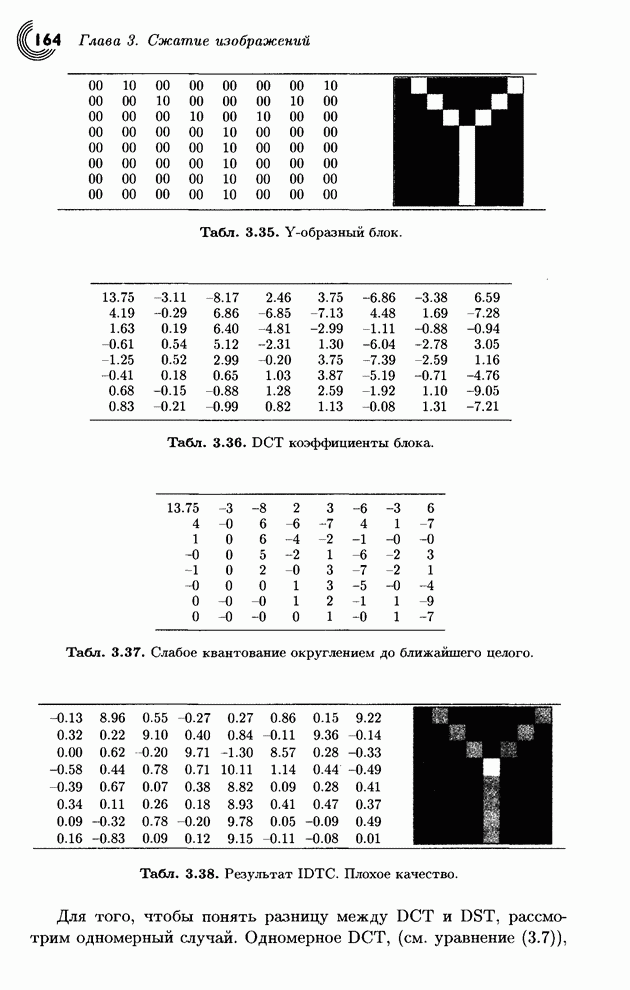
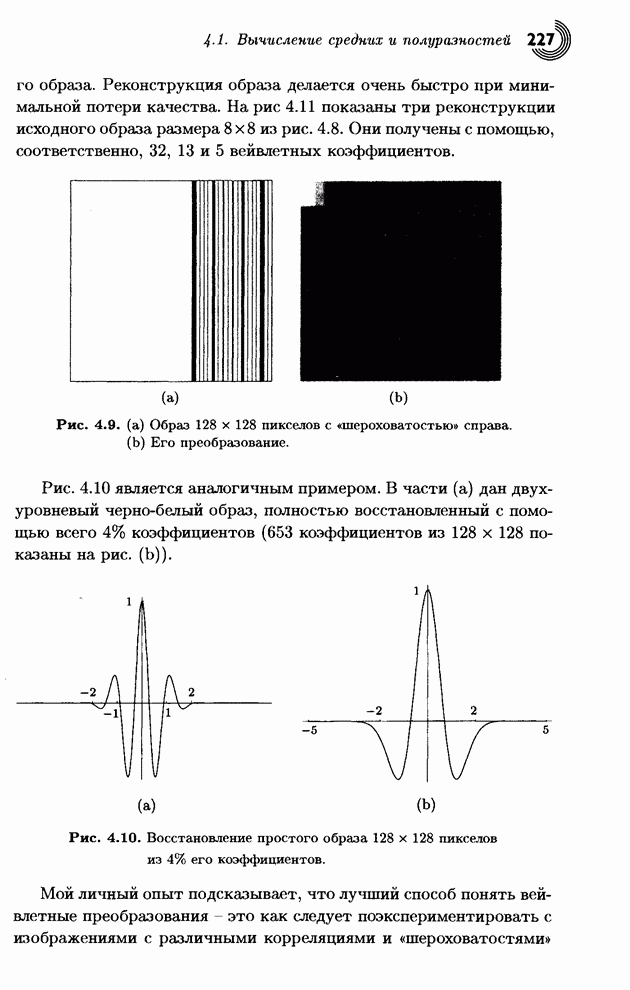
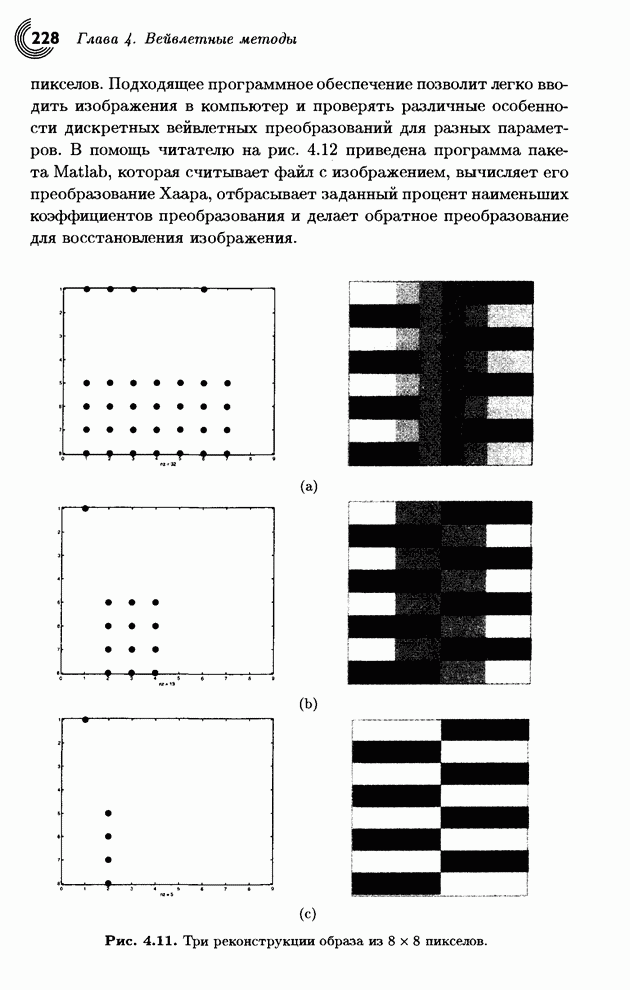
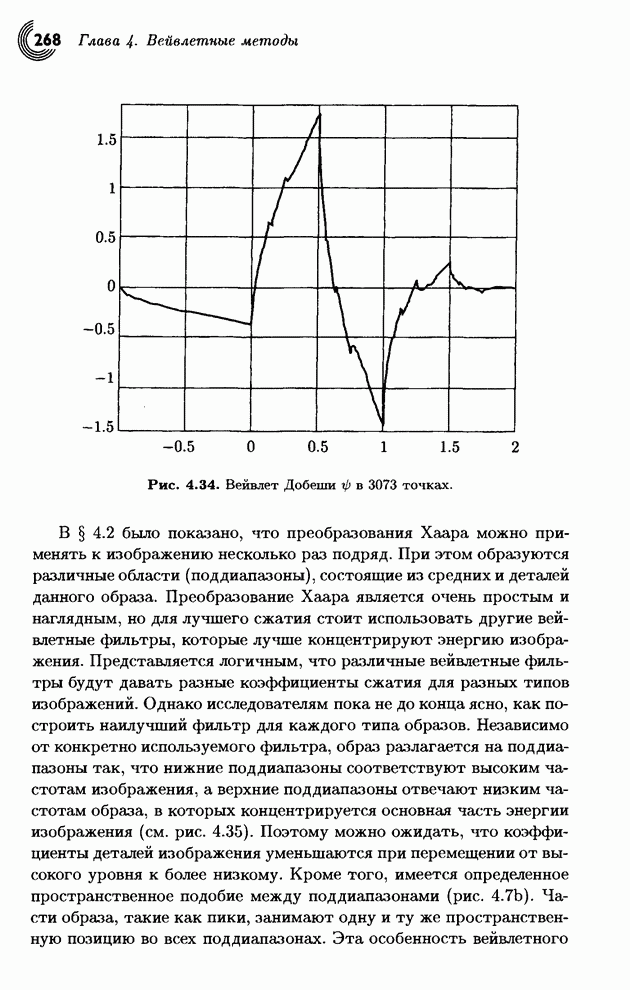
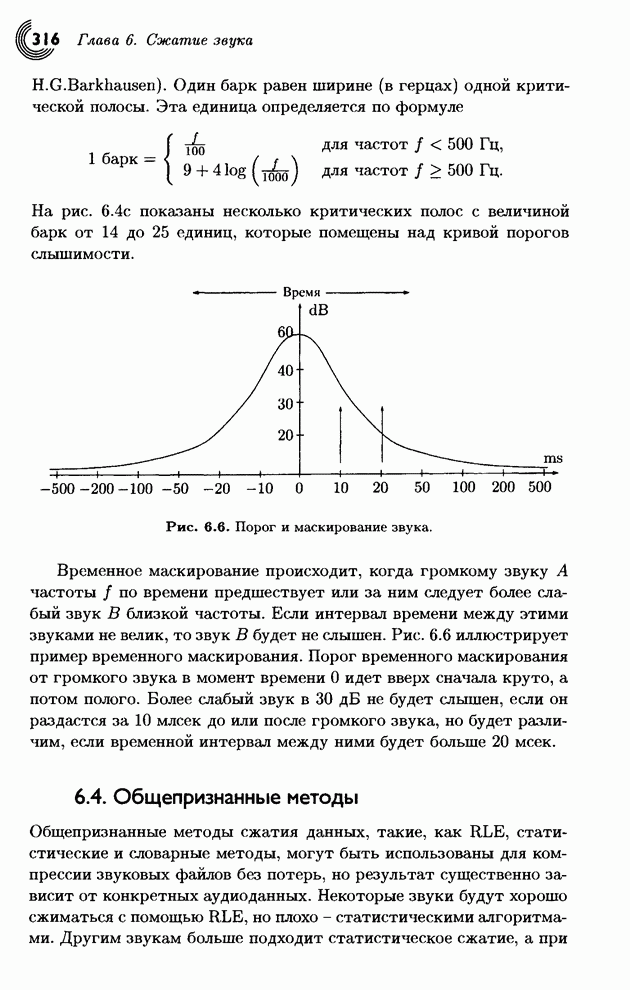
Теперь мы в состоянии оценить достоинства этого преобразования. Квантуем преобразованный вектор (8.5,1.5,–2.5,0.5) с помощью его округления до целого и получаем (9,1,–3,0). Делаем обратное преобразование и получаем вектор (3.5,6.5,5.5,2.5). В аналогичном эксперименте мы просто удалим два наименьших числа и получим (8.5,0,–2.5,0), а потом сделаем обратное преобразование этого грубо квантованного вектора. Это приводит к восстановленным данным (3,5.5,5.5,3), которые также весьма близки к исходным. Итак, наш вывод: даже это простое и интуитивное преобразование является хорошим инструментом для «выжимания» избыточности из исходных данных. Более изощренные преобразования дают результаты, которые позволяют восстанавливать данные с высокой степенью схожести даже при весьма грубом квантовании.
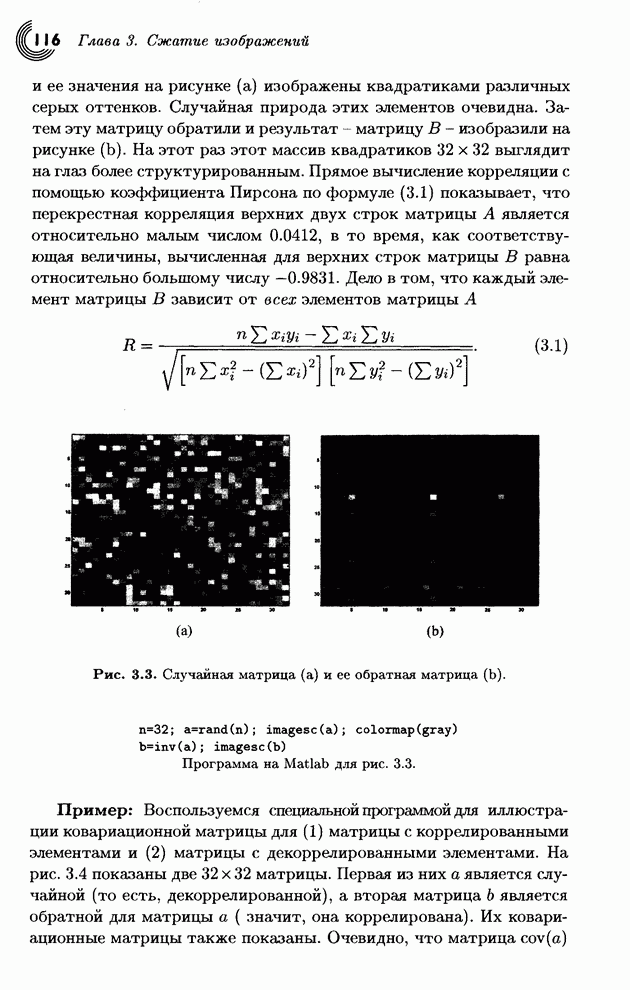
Одни художники отображают солнце
в желтое
пятно, а другие желтое пятно в солнце.
- Пабло Пикассо
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие переводчика
- Предисловие автора
- Введение
- Глава 1. Статистические методы
- 1.1. Энтропия
- 1.2. Коды переменной длины
- 1.3. Декодирование
- 1.4. Кодирование Хаффмана
- 1.4.1. Декодирование Хаффмана
- 1.4.2. Средняя длина кода
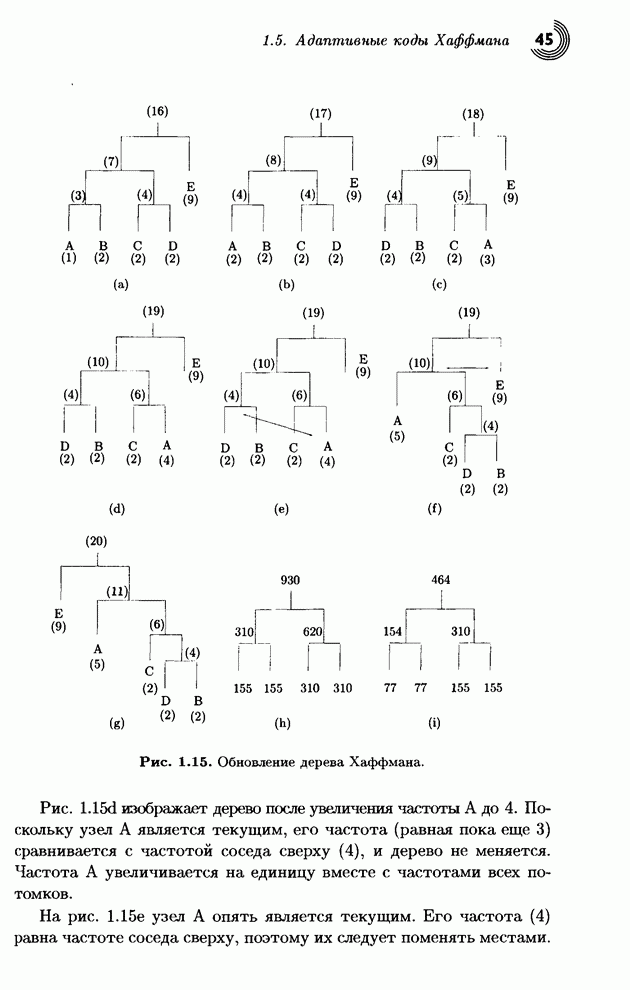
- 1.5. Адаптивные коды Хаффмана
- 1.5.1. Несжатые коды
- 1.5.2. Модификация дерева
- 1.5.3. Переполнение счетчика
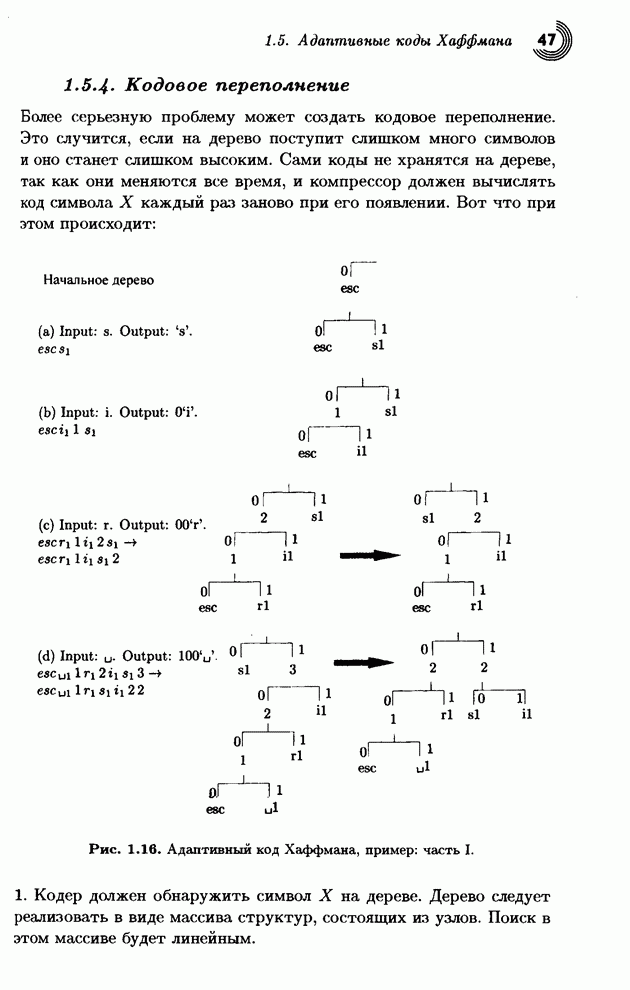
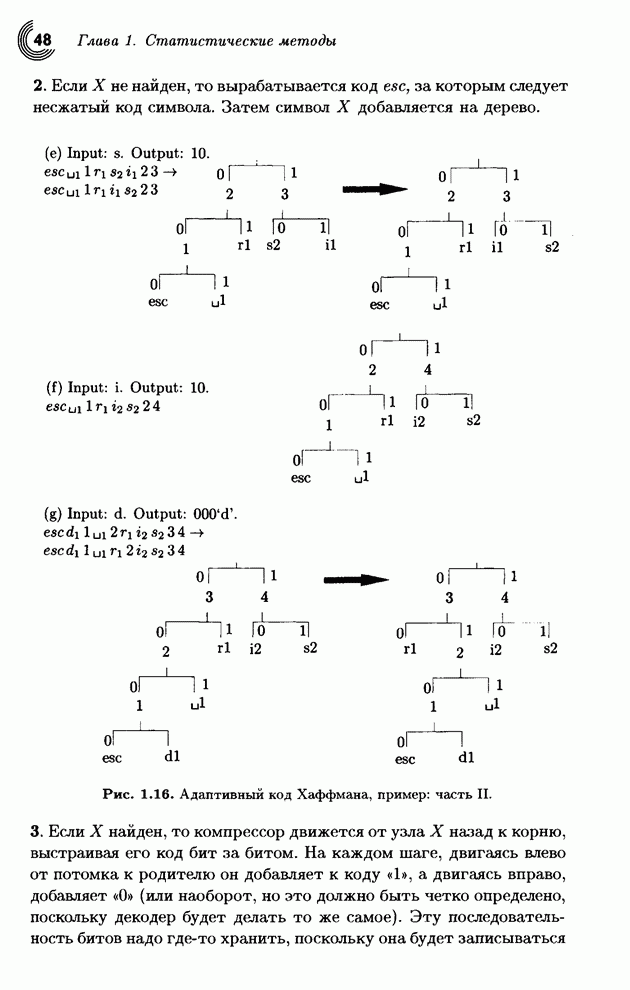
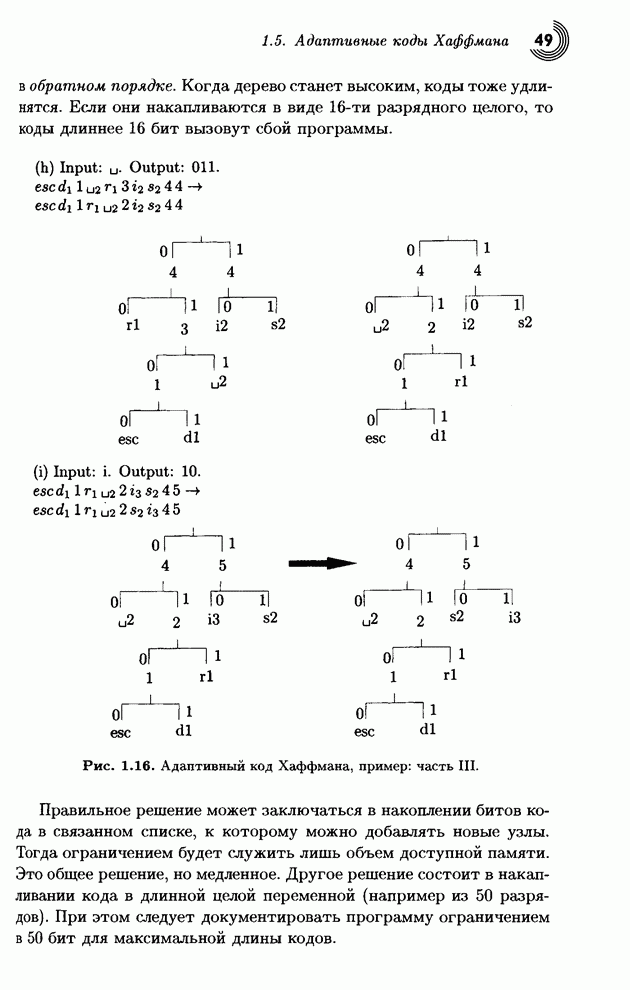
- 1.5.4. Кодовое переполнение
- 1.5.5. Вариант алгоритма
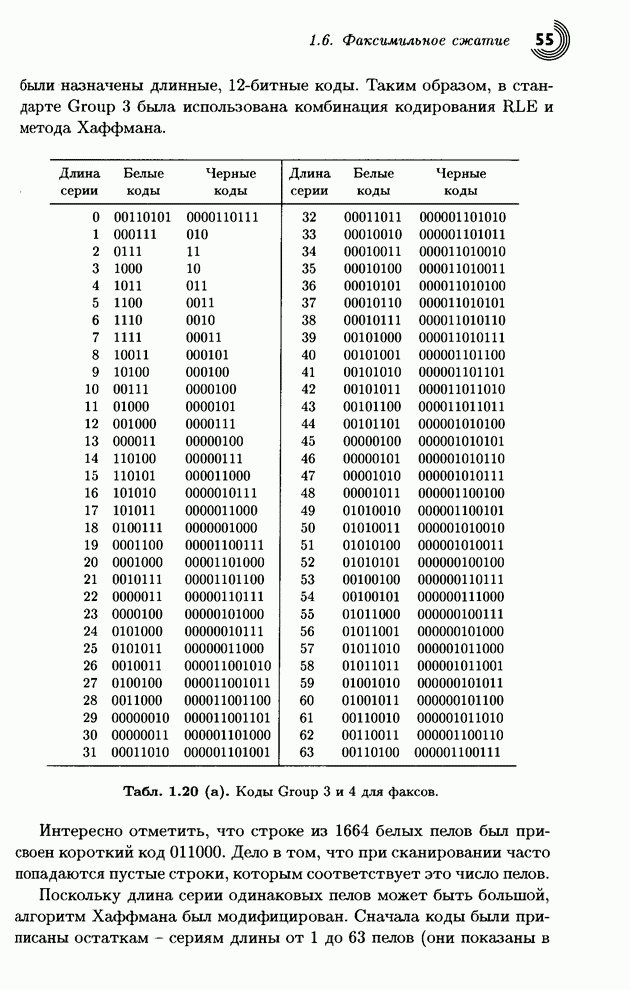
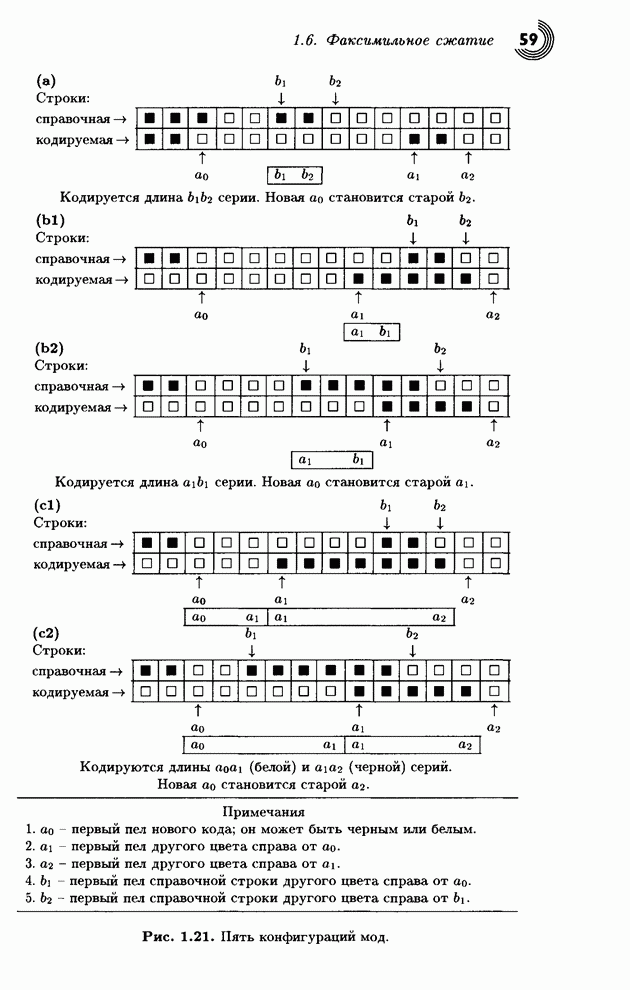
- 1.6. Факсимильное сжатие
- 1.6.1. Одномерное кодирование
- 1.6.2. Двумерное кодирование
- 1.7. Арифметическое кодирование
- 1.7.1. Детали реализации метода
- 1.7.2. Потеря значащих цифр
- 1.7.3. Заключительные замечания
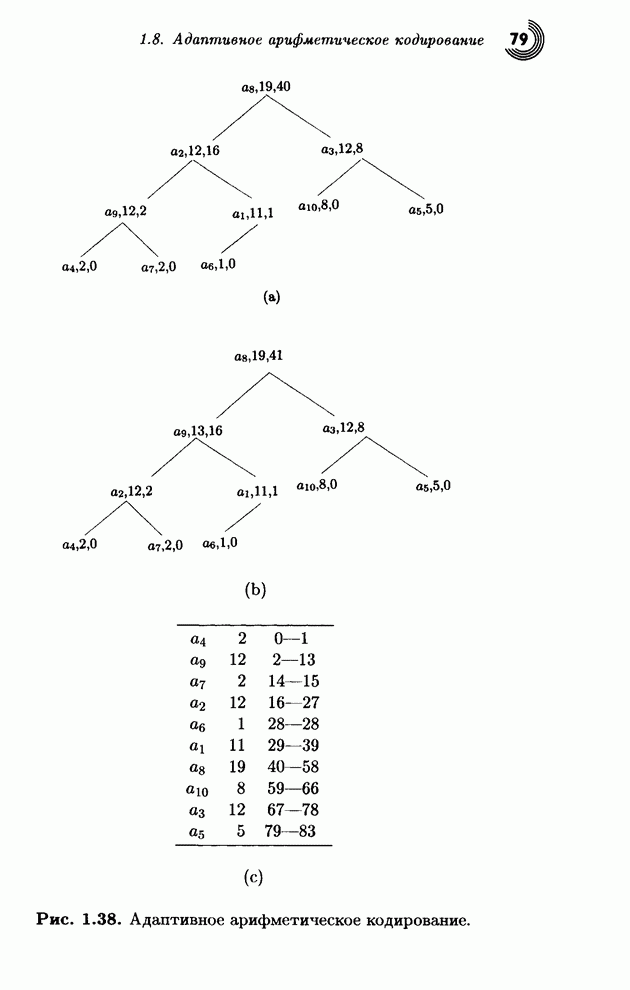
- 1.8. Адаптивное арифметическое кодирование
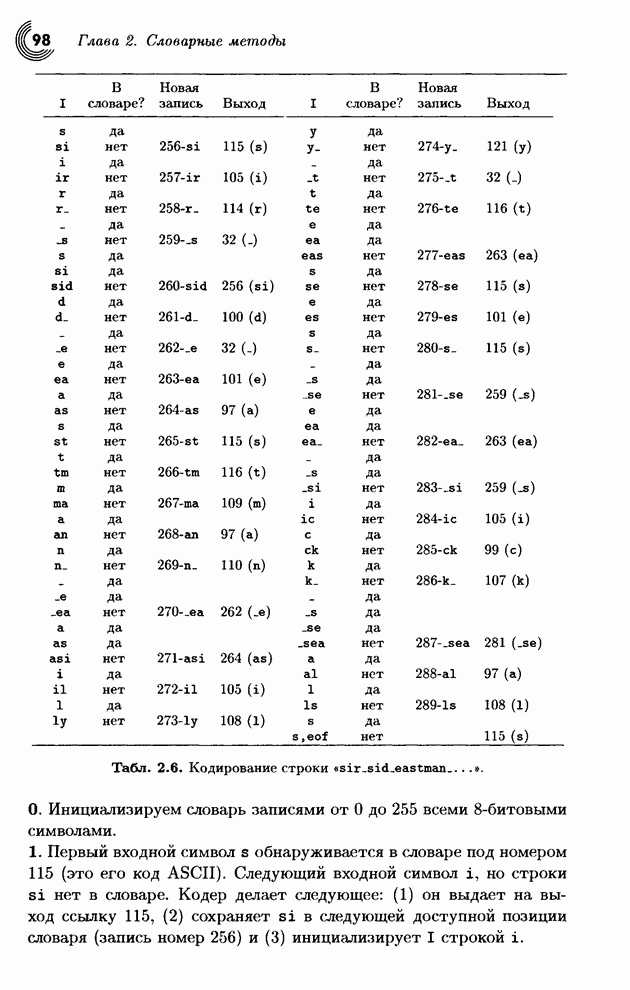
- ГЛАВА 2 СЛОВАРНЫЕ МЕТОДЫ
- 2.1. LZ77 (скользящее окно)
- 2.1.1. Циклическая очередь
- 2.2. LZSS
- 2.2.1. Недостатки
- 2.3. LZ78
- 2.4. LZW
- 2.4.1. Декодирование LZW
- 2.4.2. Структура словаря LZW
- 2.4.3. LZW в практических приложениях
- 2.5. Заключение
- ГЛАВА 3 СЖАТИЕ ИЗОБРАЖЕНИЙ
- 3.1. Введение
- 3.2. Типы изображений
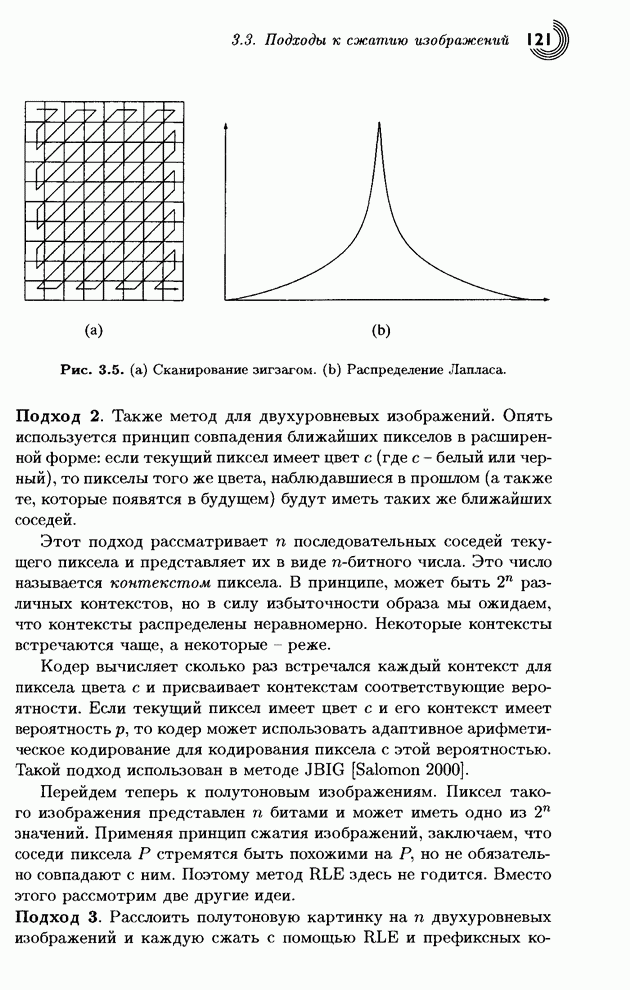
- 3.3. Подходы к сжатию изображений
- 3.3.1. Коды Грея
- 3.3.2. Метрики ошибок
- 3.4. Интуитивные методы
- 3.4.1. Подвыборка
- 3.4.2. Квантование
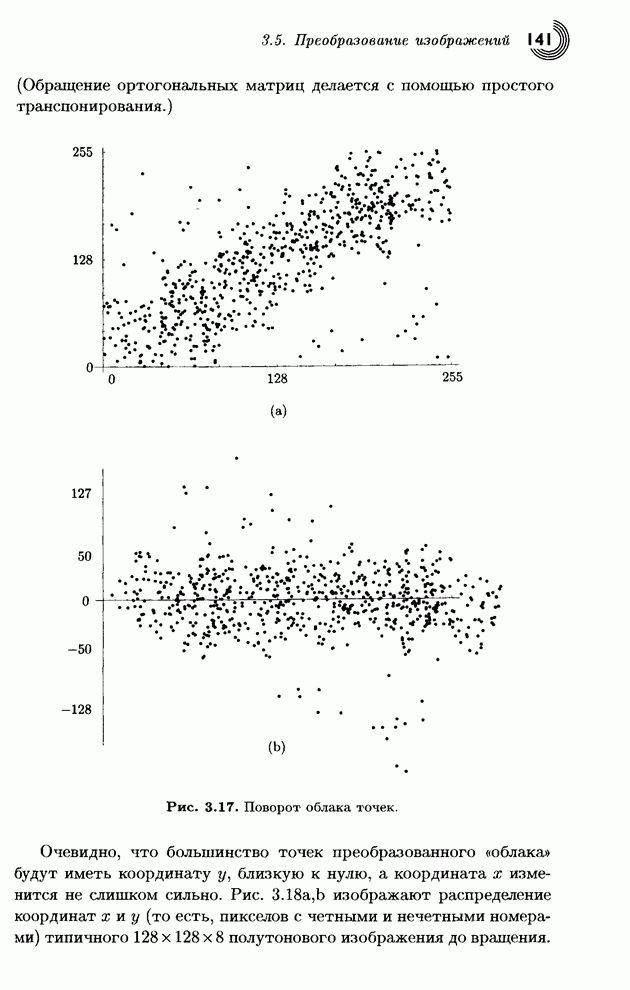
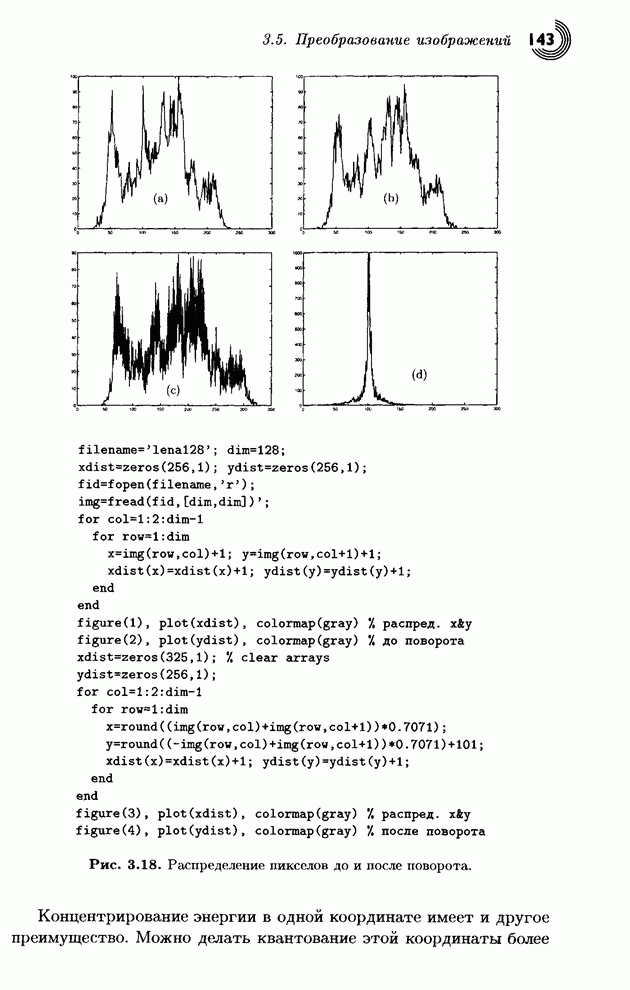
- 3.5. Преобразование изображений
- 3.5.1. Ортогональные преобразования
- 3.5.2. Матричные преобразования
- 3.5.3. Дискретное косинус-преобразование
- 3.5.4. Пример
- 3.5.5. Дискретное синус-преобразование
- 3.5.6. Преобразование Уолша-Адамара
- 3.5.7. Преобразование Хаара
- 3.5.8. Преобразование Кархунена-Лоэвэ
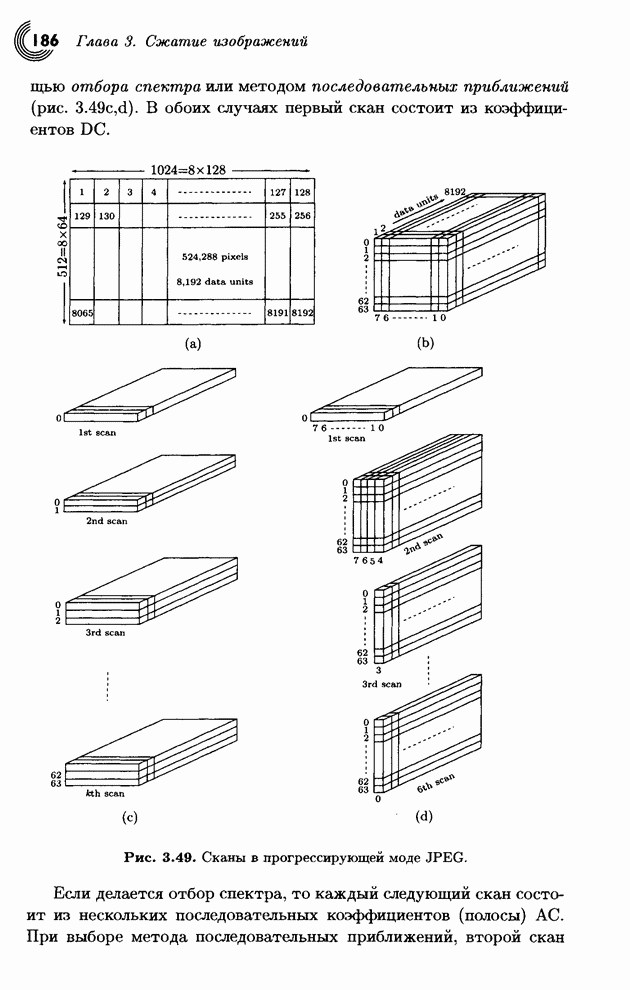
- 3.6. Прогрессирующее сжатие изображений
- 3.7. JPEG
- 3.7.1. Светимость
- 3.7.2. DCT
- 3.7.3. Практическое DCT
- 3.7.4. Квантование
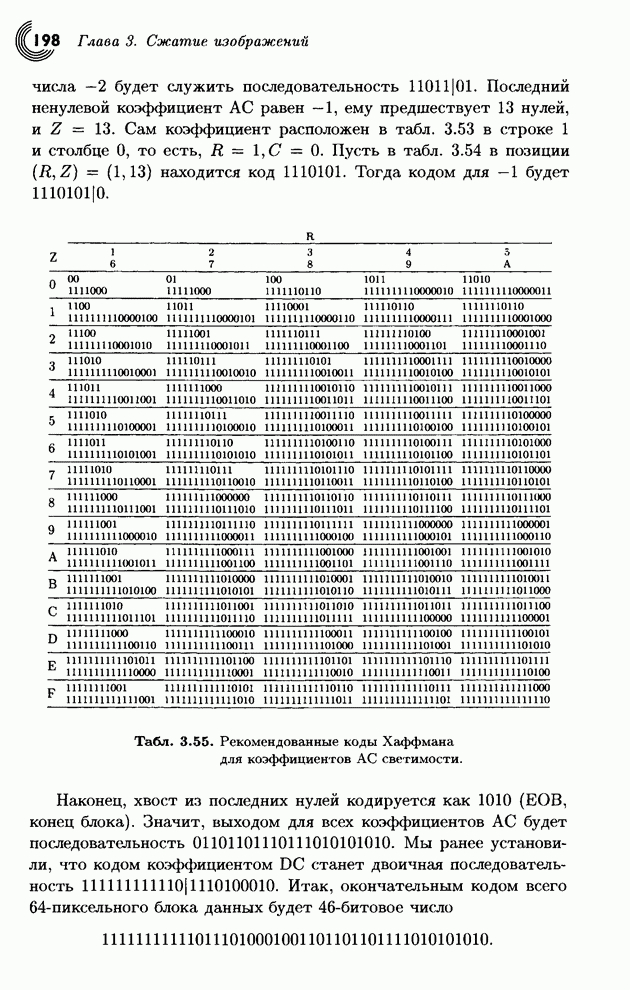
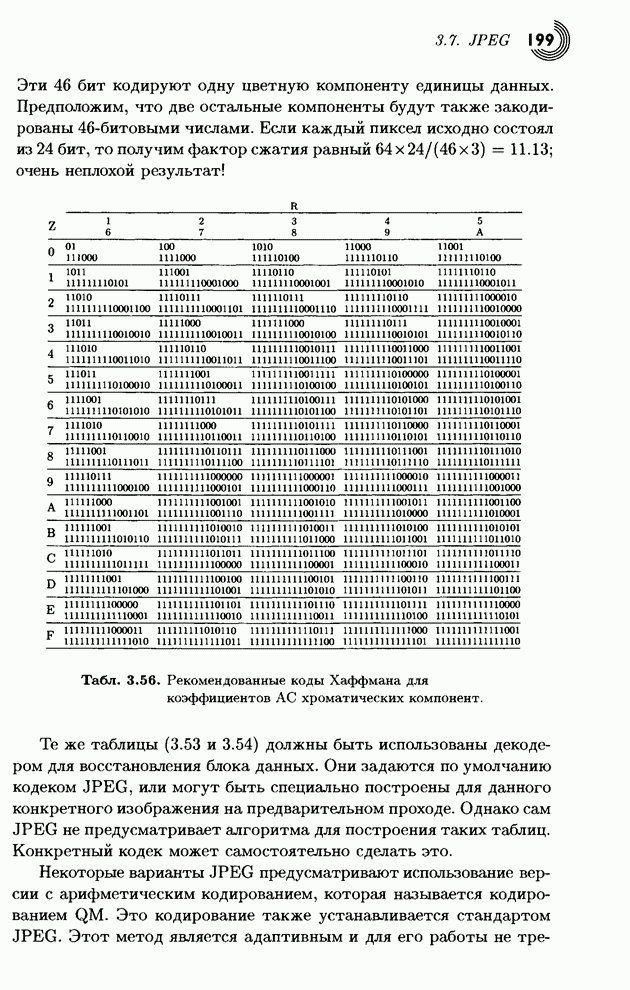
- 3.7.5. Кодирование
- 3.7.6. Мода без потери данных
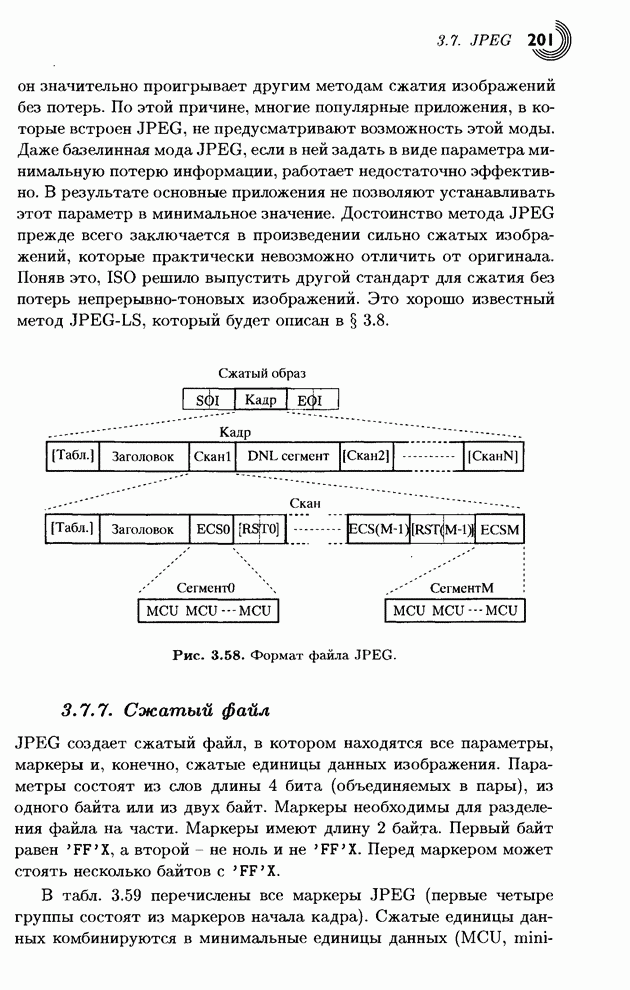
- 3.7.7. Сжатый файл
- 3.7.8. JFIF
- 3.8. JPEG-LS
- 3.8.1. Коды Голомба
- 3.8.2. Основы метода JPEG-LS
- 3.8.3. Кодер
- ГЛАВА 4 ВЕЙВЛЕТНЫЕ МЕТОДЫ
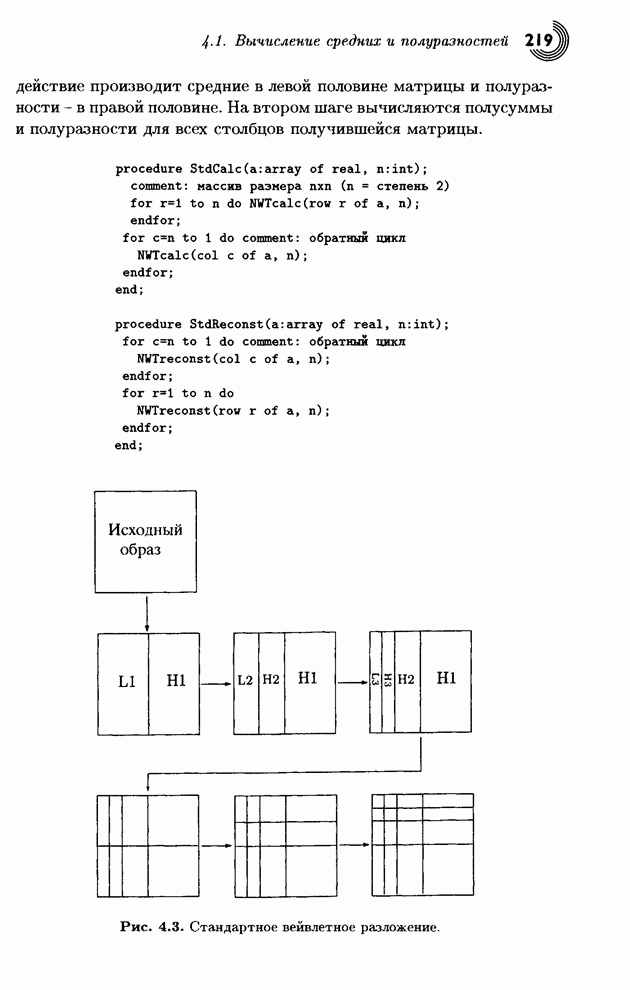
- 4.1. Вычисление средних и полу разностей
- 4.1.1. Обобщение на двумерный случай
- 4.1.2. Свойства преобразования Хаара
- 4.2. Преобразование Хаара
- 4.2.1. Матричная форма
- 4.3. Поддиапазонные преобразования
- 4.4. Банк фильтров
- 4.5. Нахождение коэффициентов фильтра
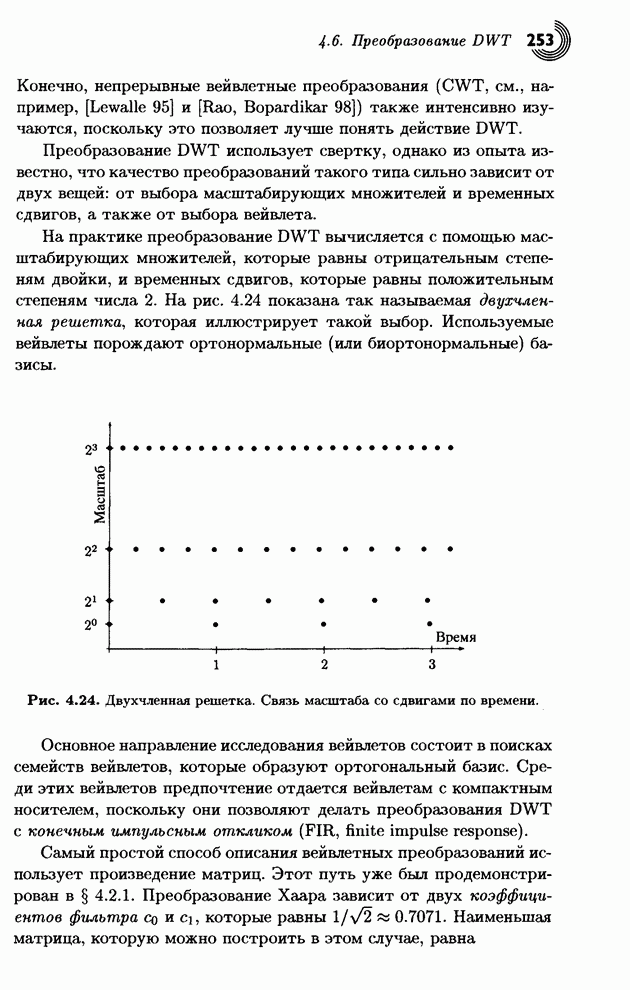
- 4.6. Преобразование DWT
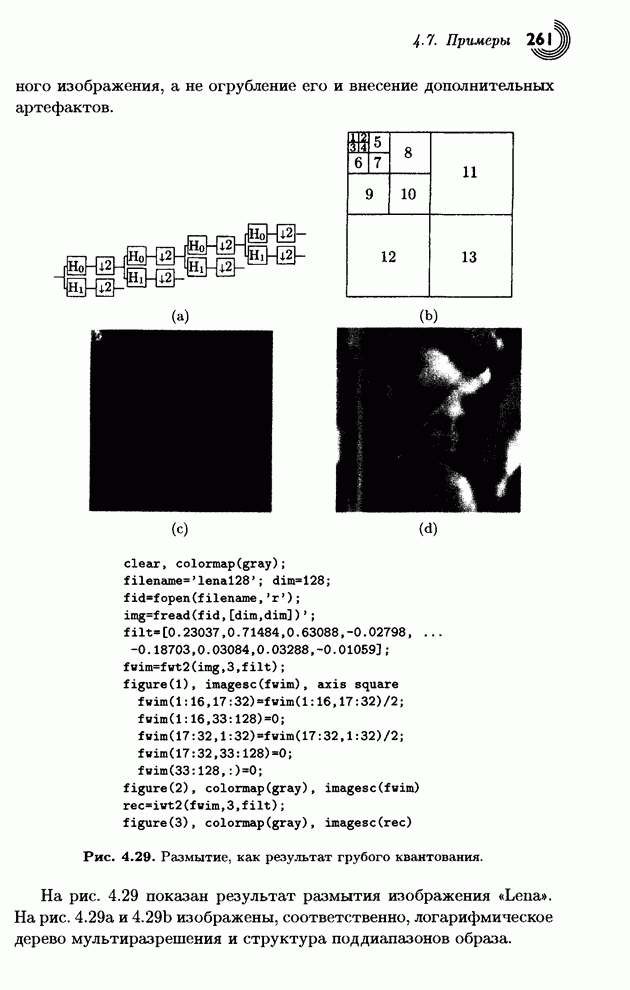
- 4.7. Примеры
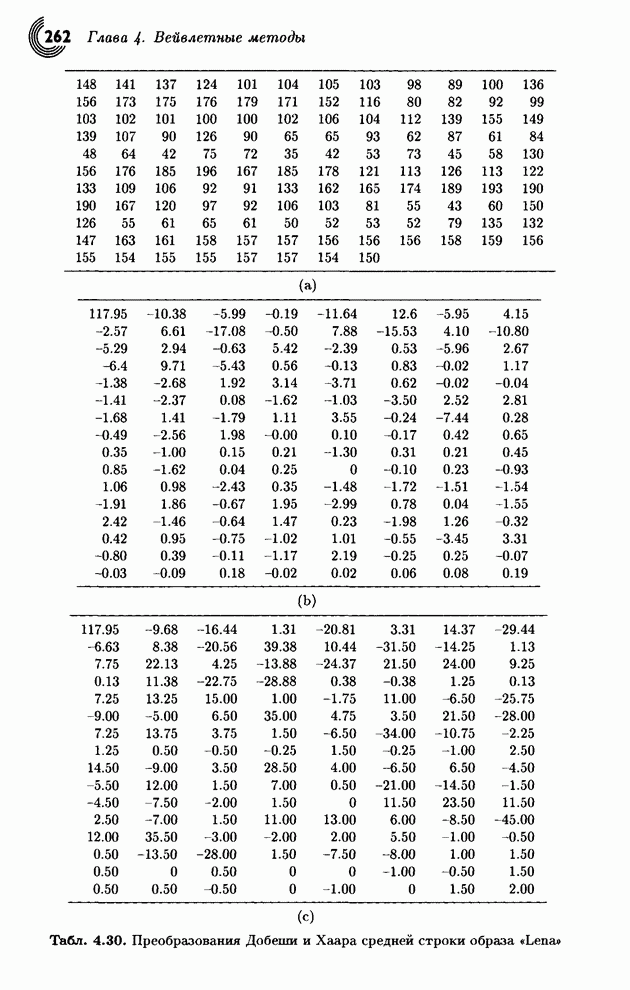
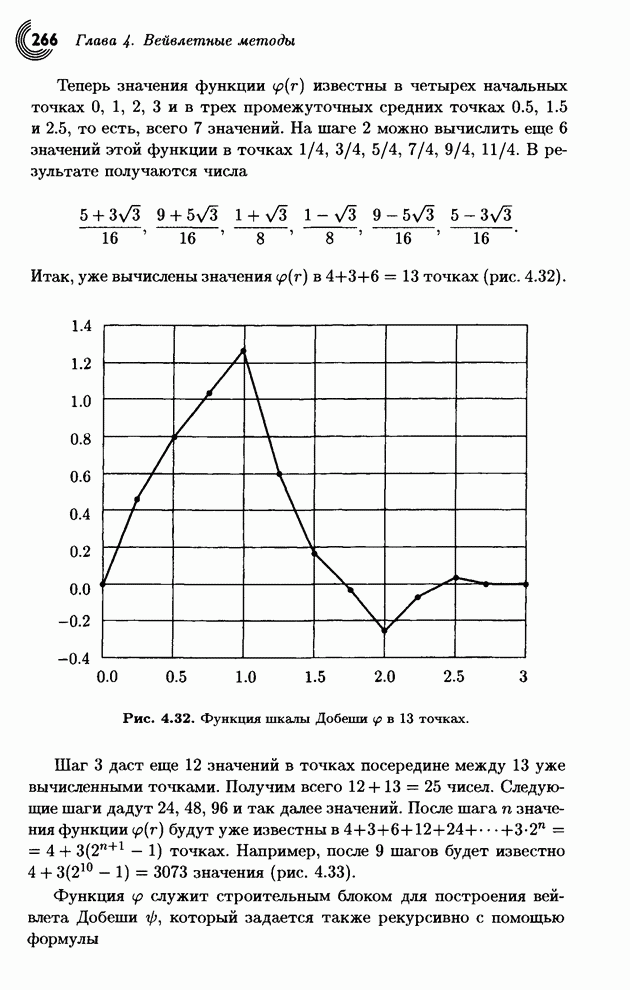
- 4.8. Вейвлеты Добеши
- 4.9. SPIHT
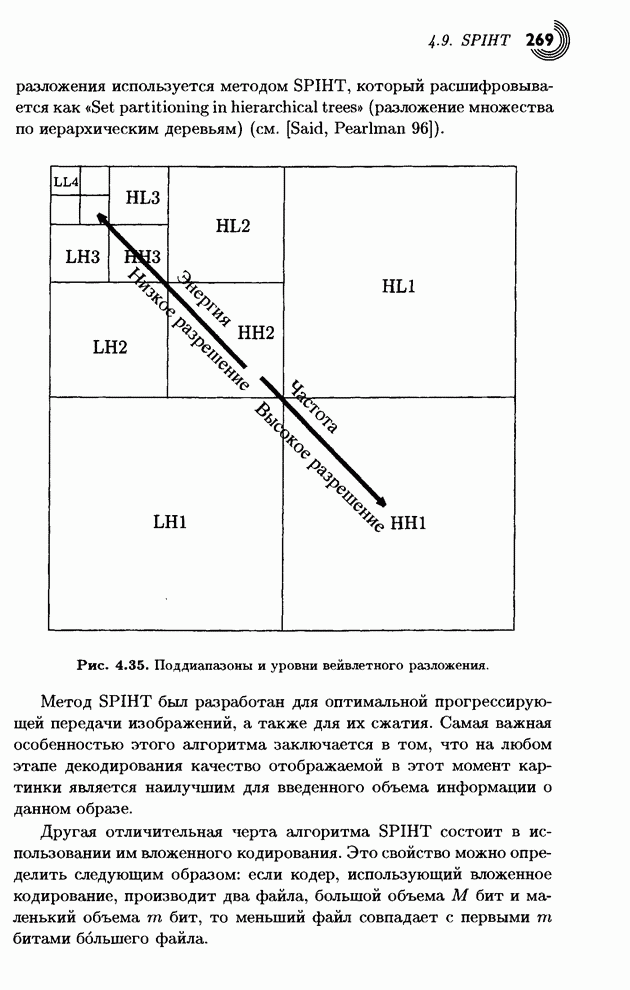
- 4.9.1. Алгоритм сортировки разделением множеств
- 4.9.2. Пространственно ориентированное дерево
- 4.9.3. Кодирование в алгоритме SPIHT
- 4.9.4. Пример
- 4.9.5. QTCQ
- ГЛАВА 5 СЖАТИЕ ВИДЕО
- 5.1. Основные принципы
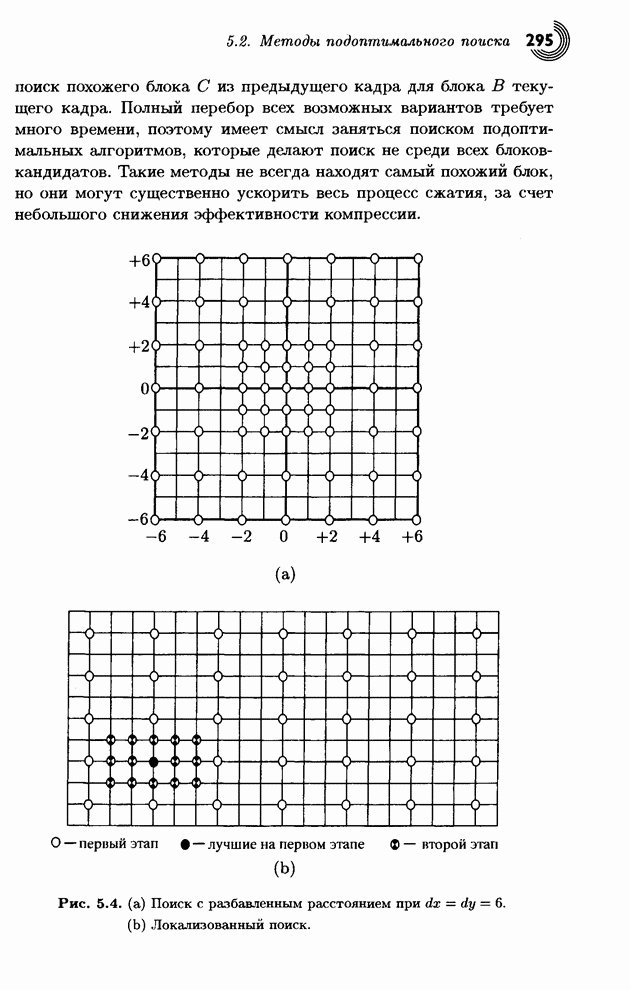
- 5.2. Методы подоптимального поиска
- ГЛАВА 6 СЖАТИЕ ЗВУКА
- 6.1. Звук
- 6.2. Оцифрованный звук
- 6.3. Органы слуха человека
- 6.4. Общепризнанные методы
- 6.5. Сжатие звука в стандарте MPEG-1
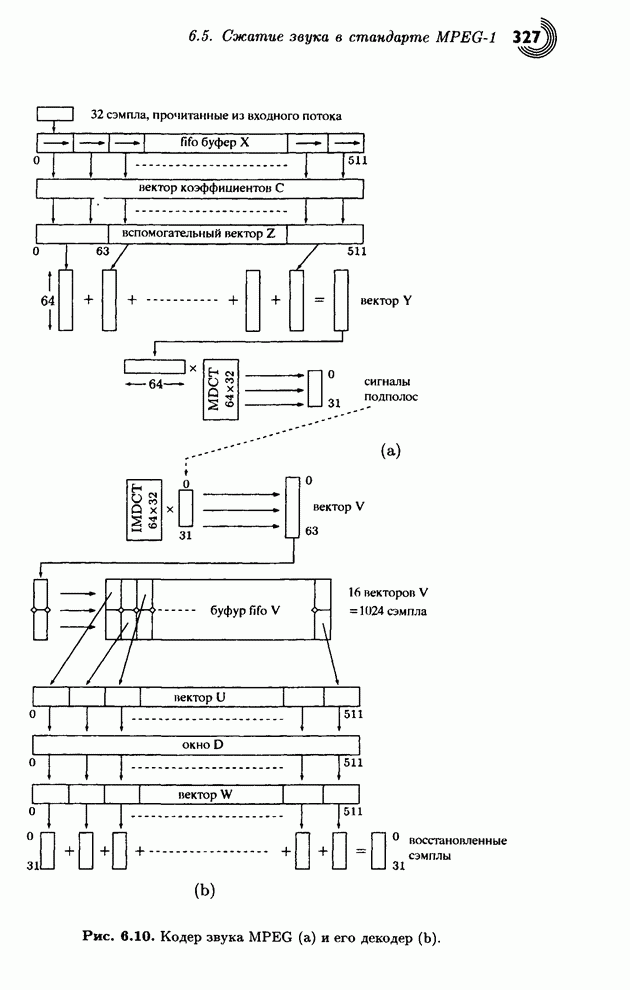
- 6.5.1. Кодирование частотной области
- 6.5.2. Формат сжатых данных
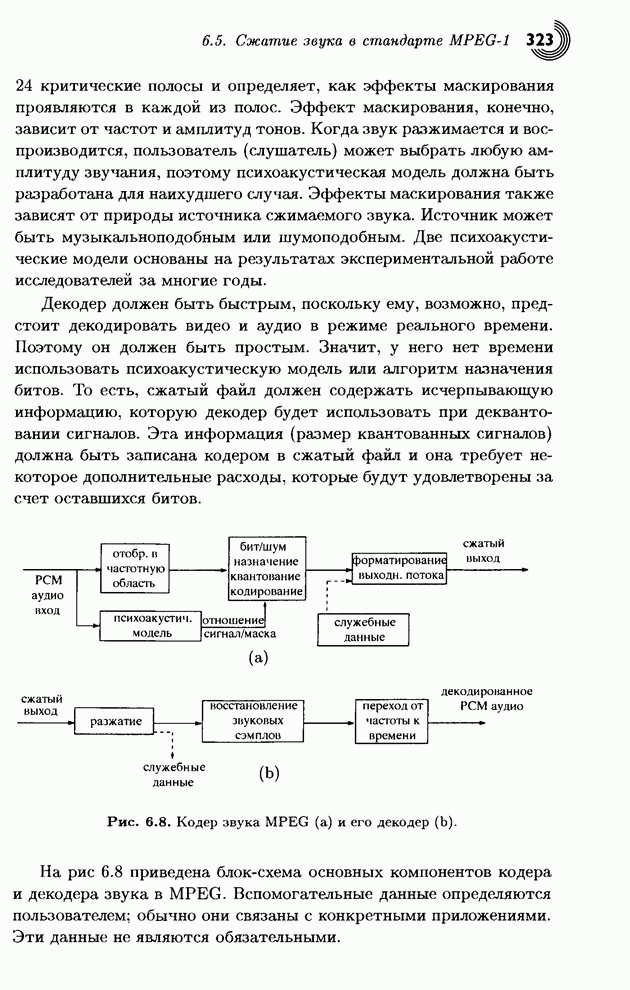
- 6.5.3. Психоакустические модели
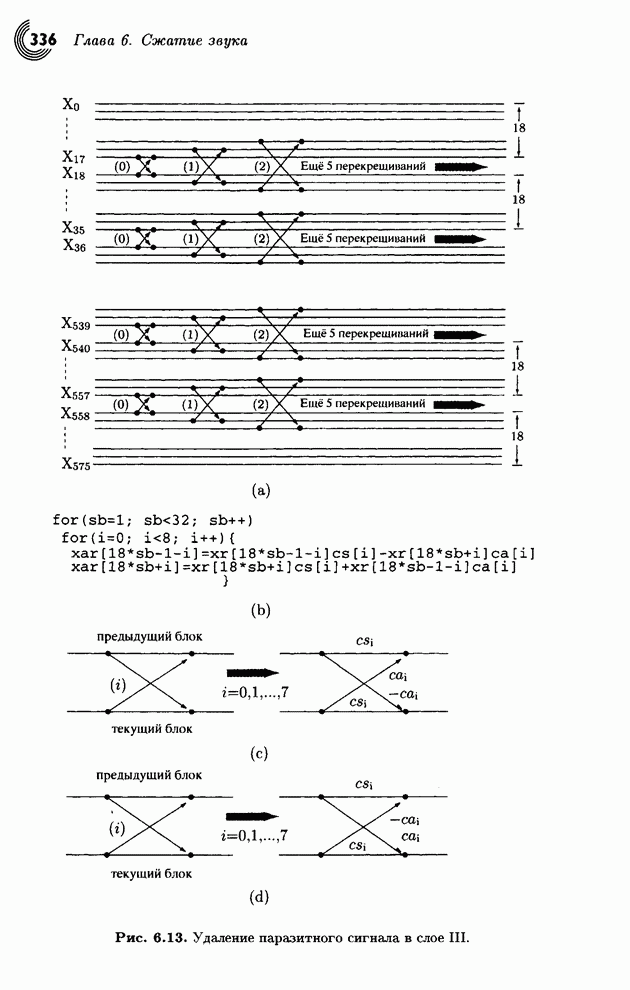
- 6.5.4. Кодирование: слой III
- Литература
- Глоссарий