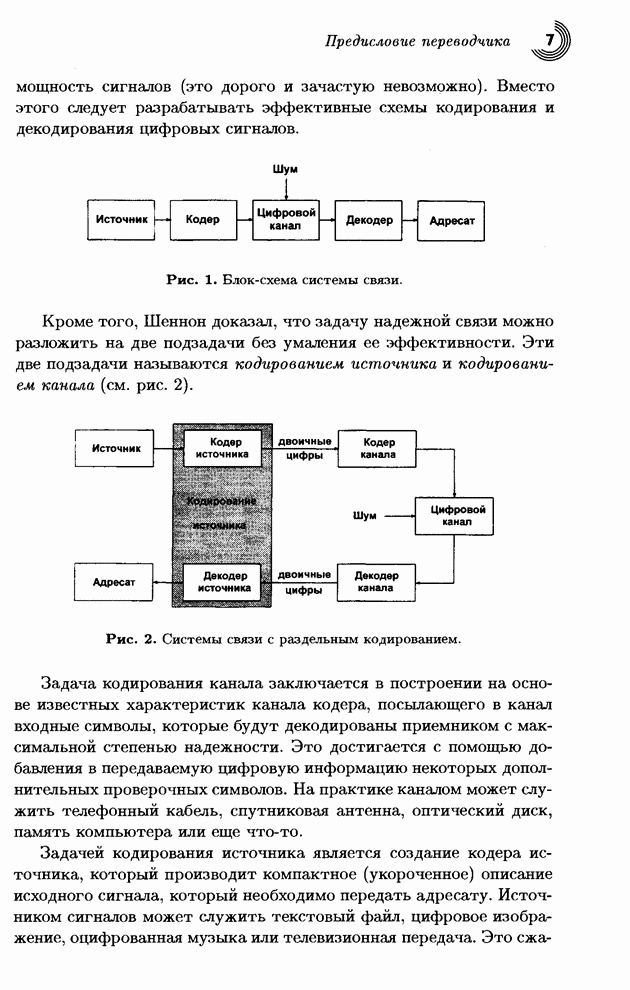
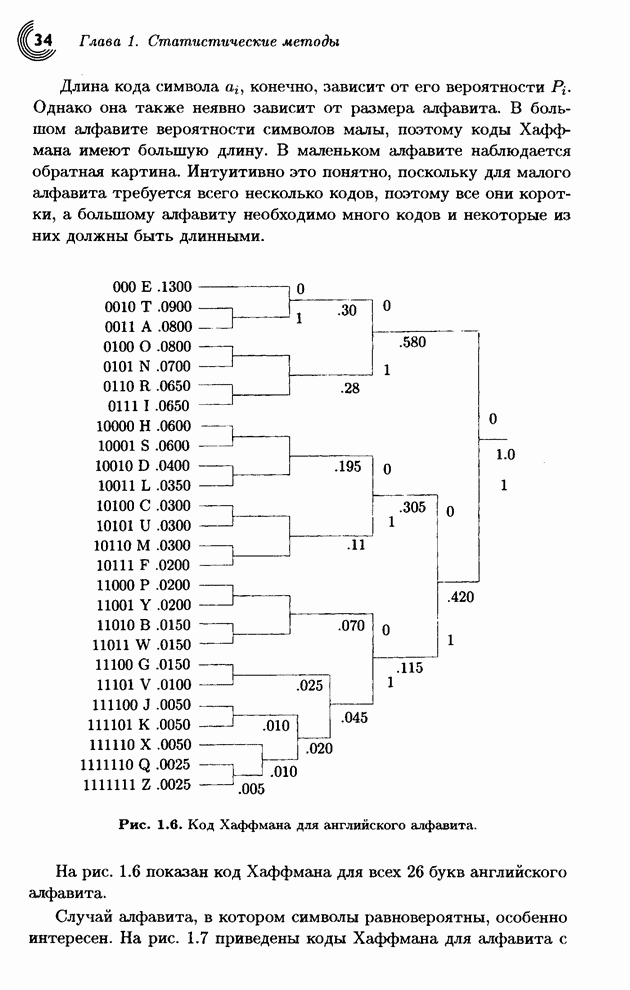
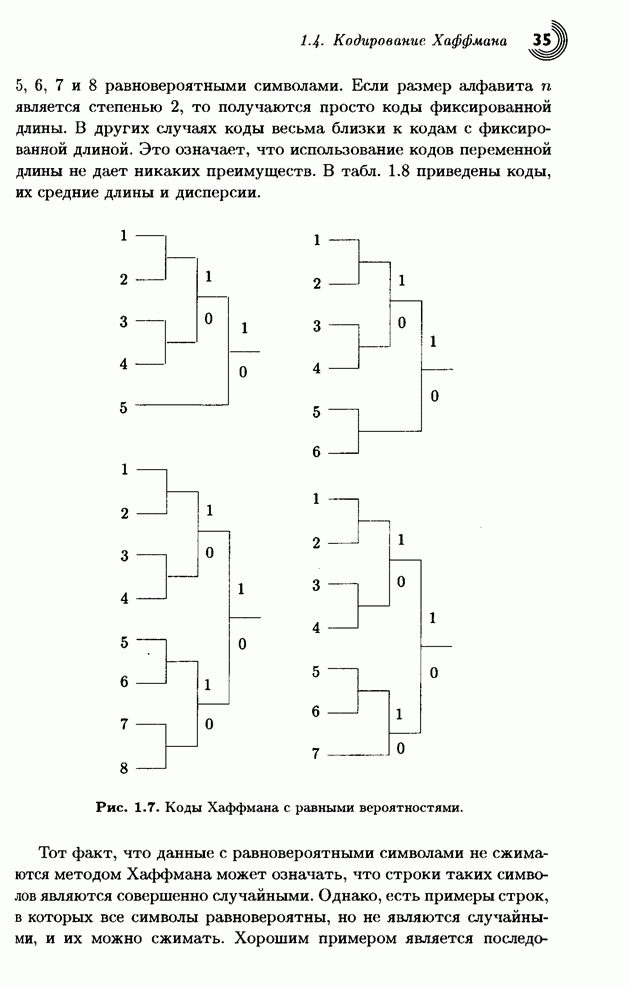
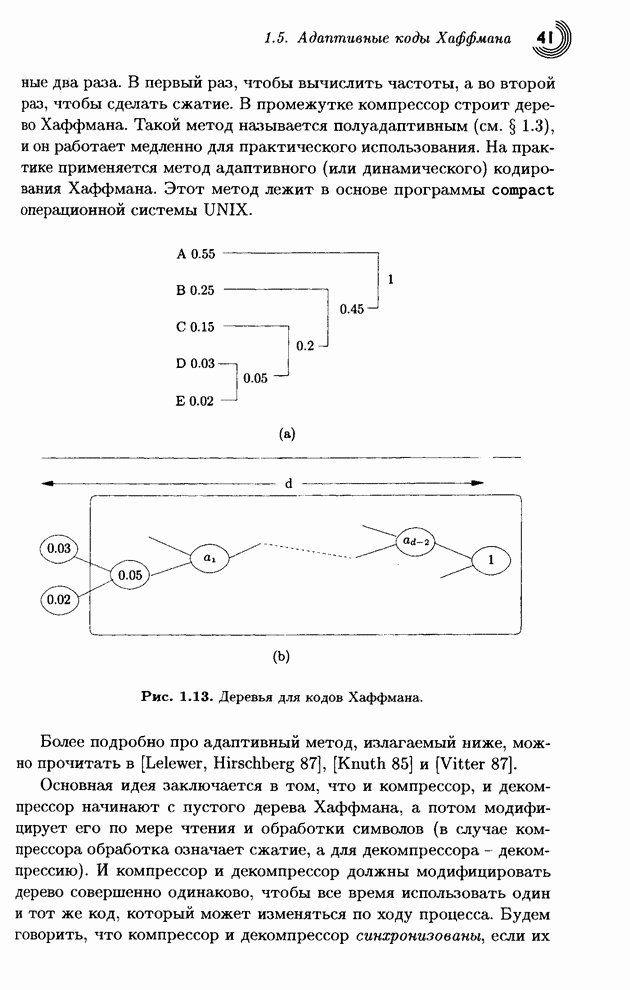
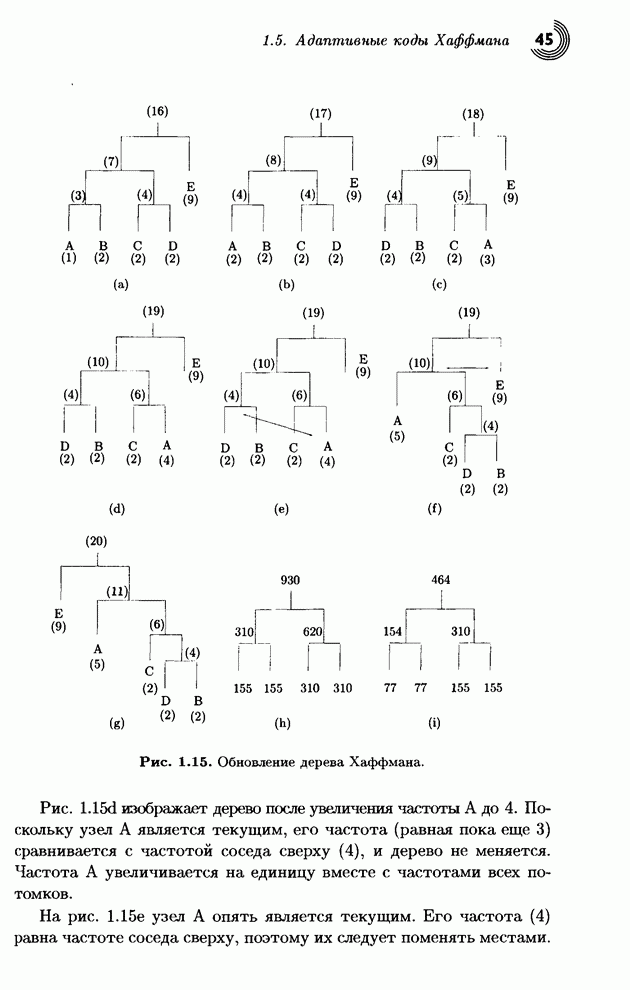
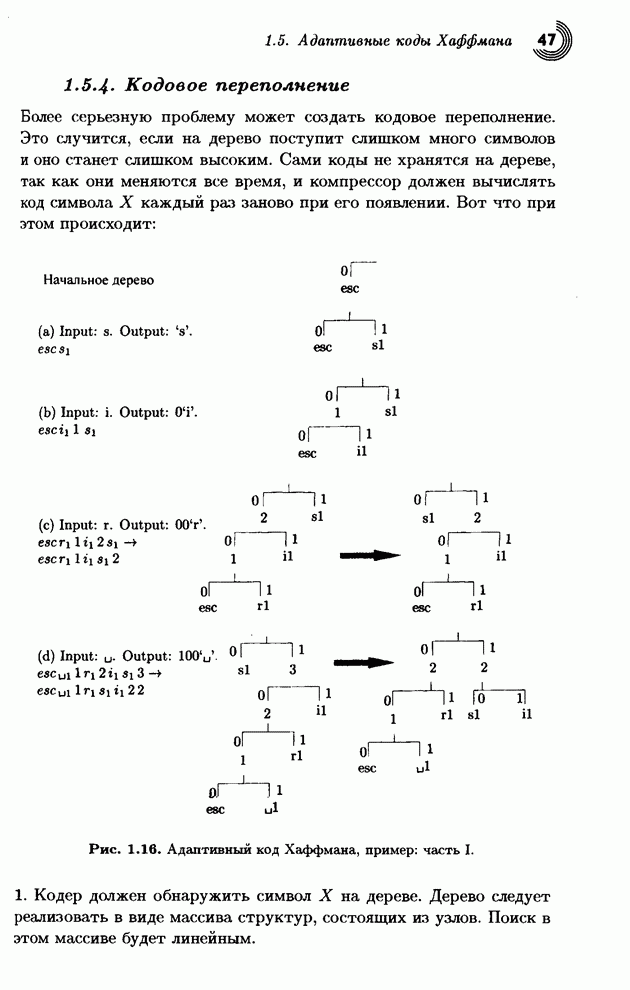
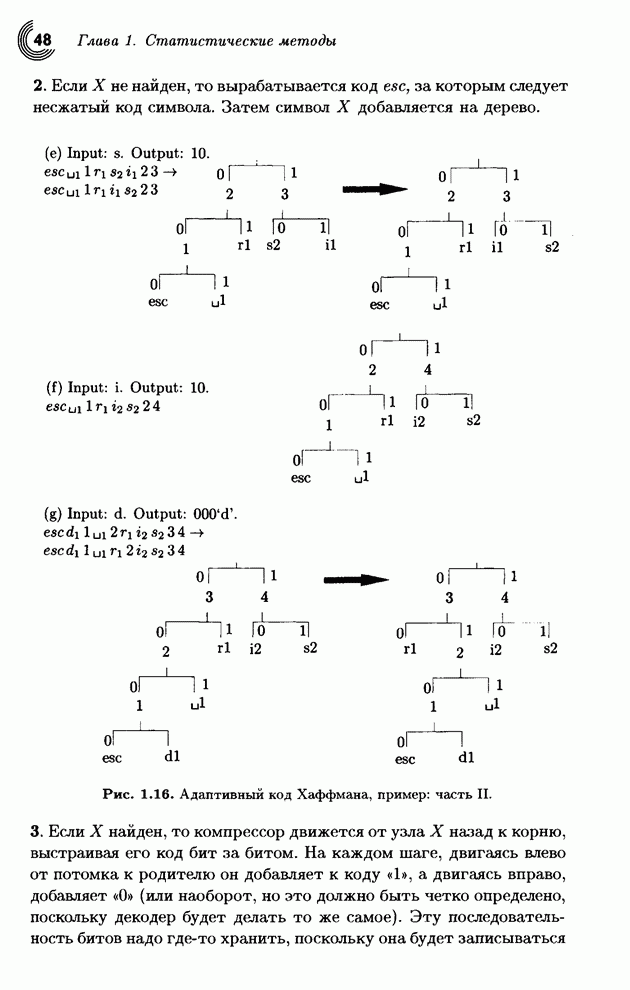
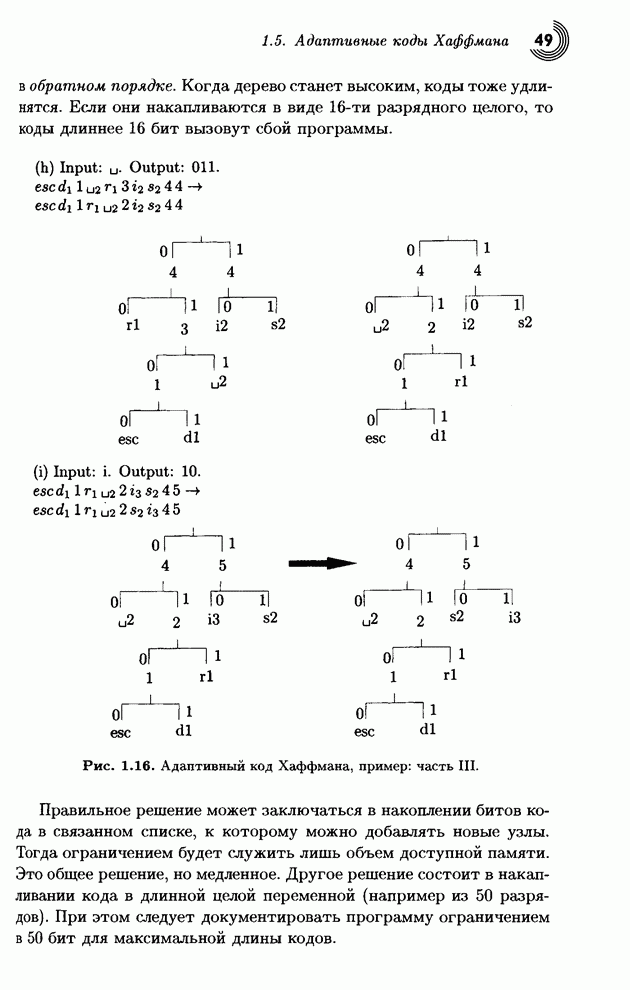
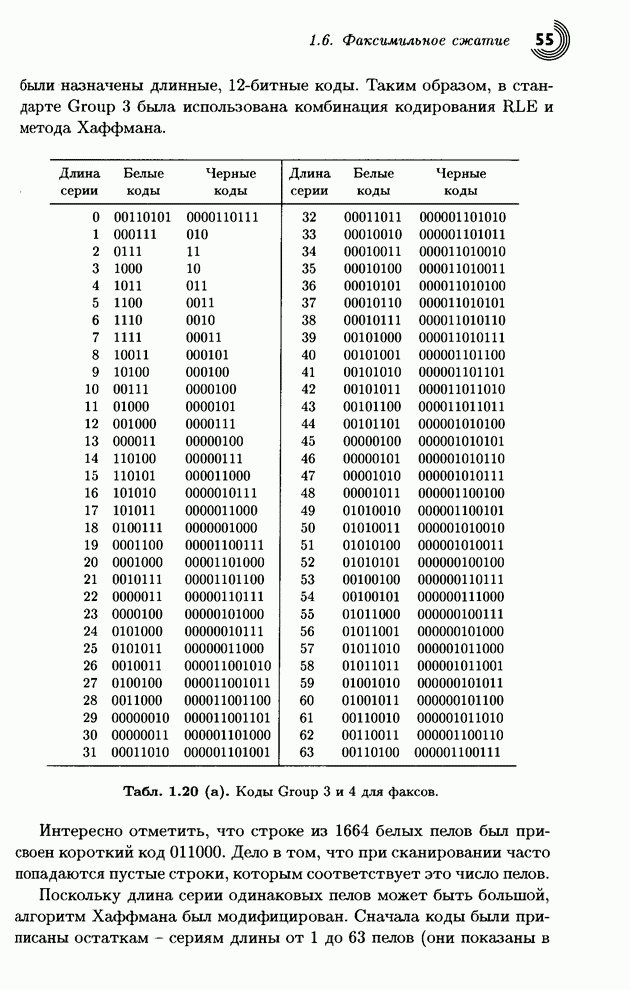
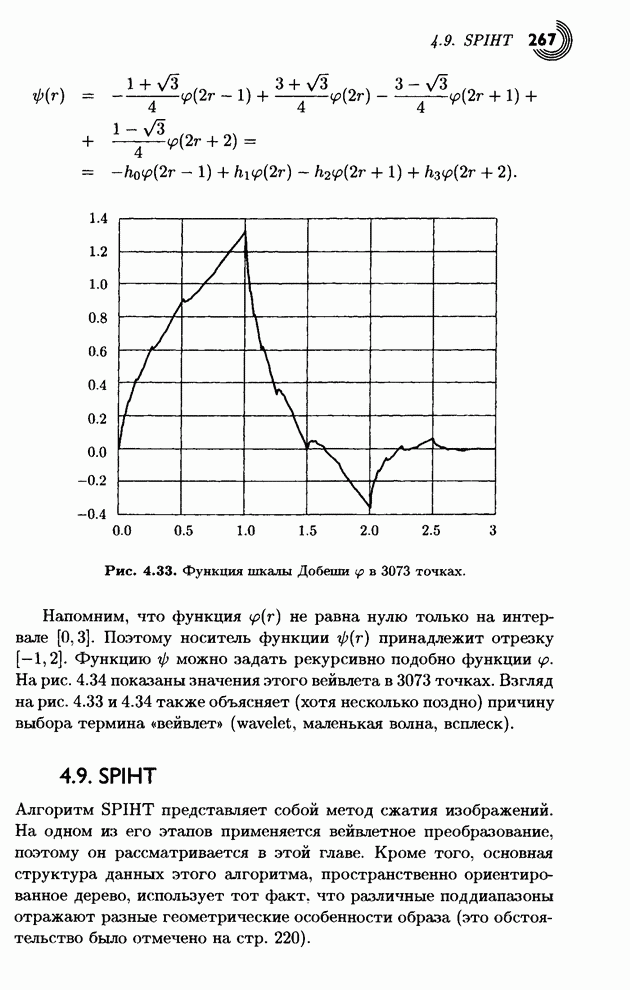
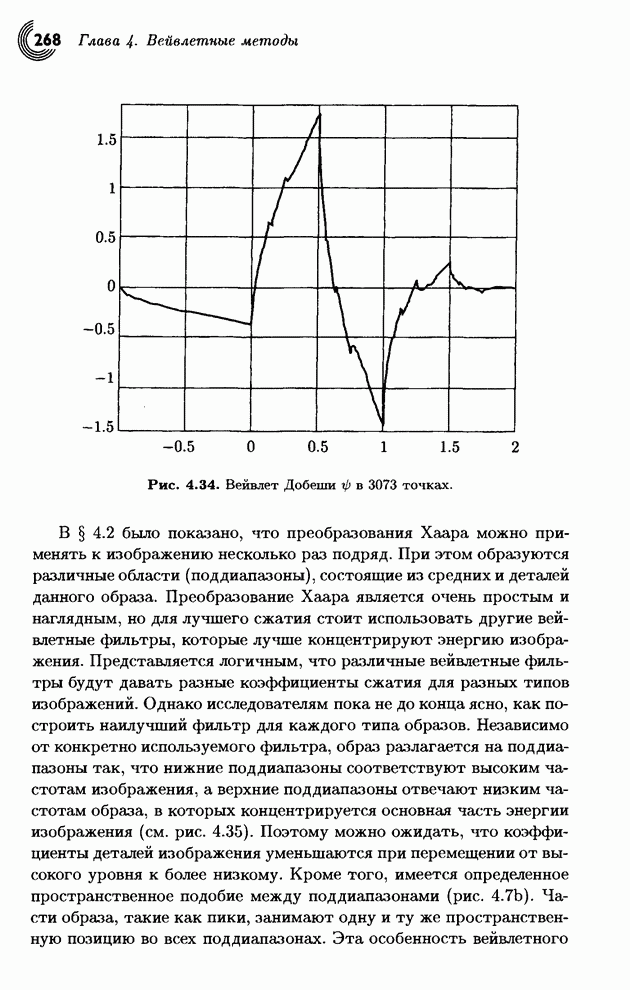
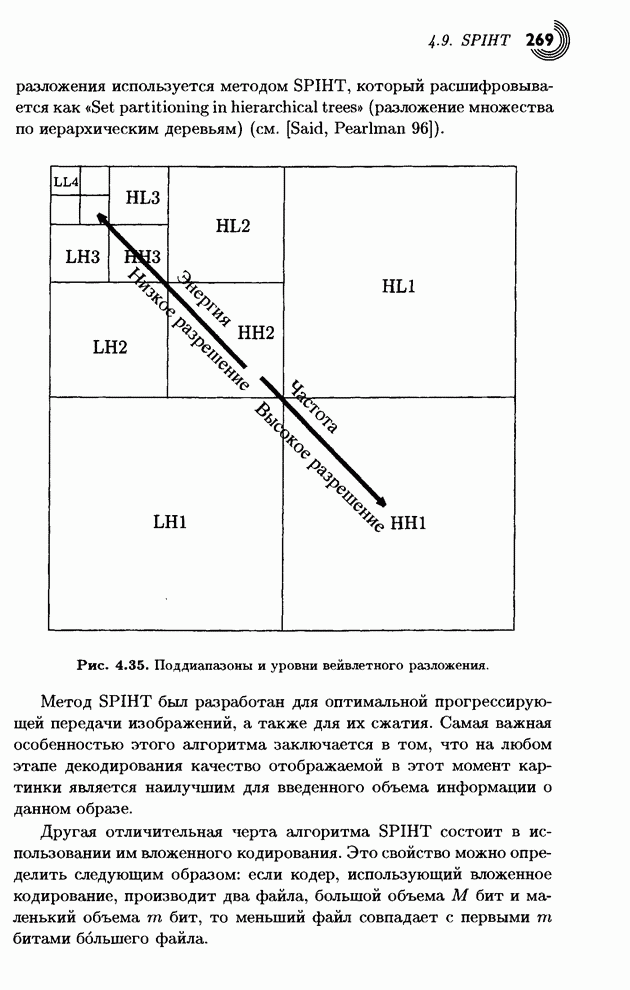
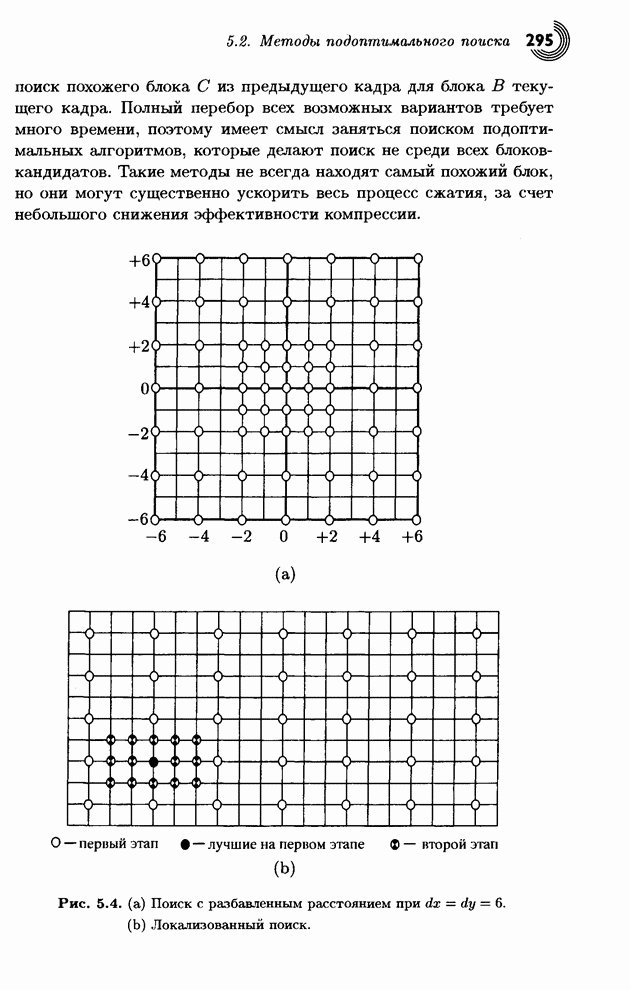
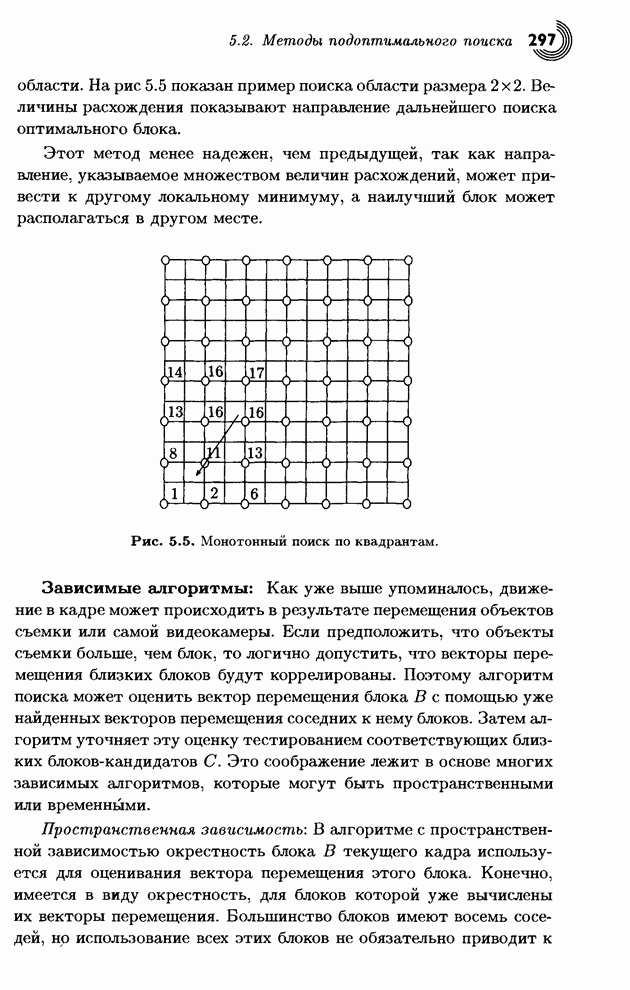
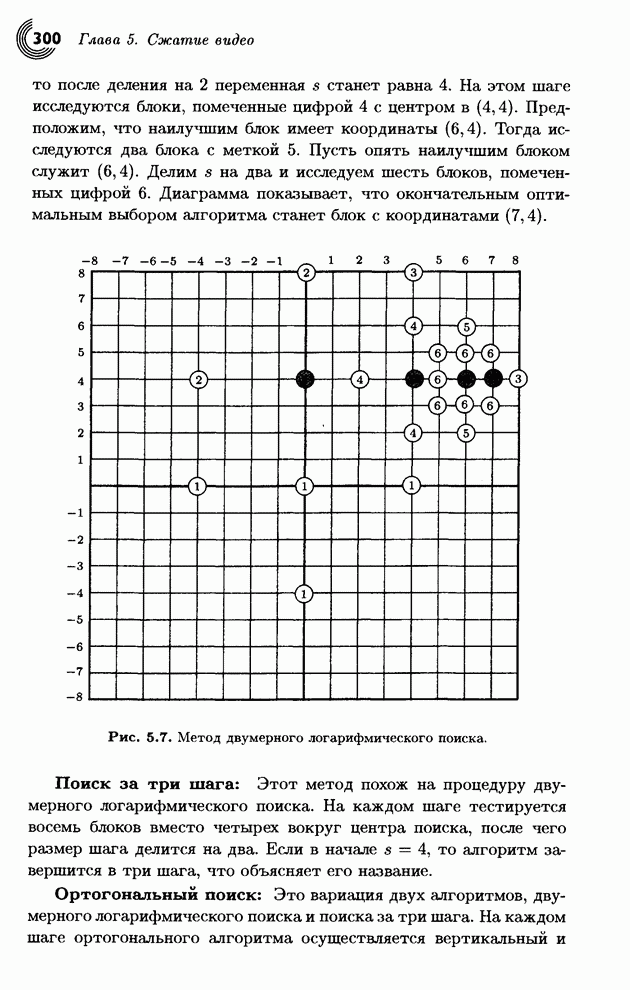
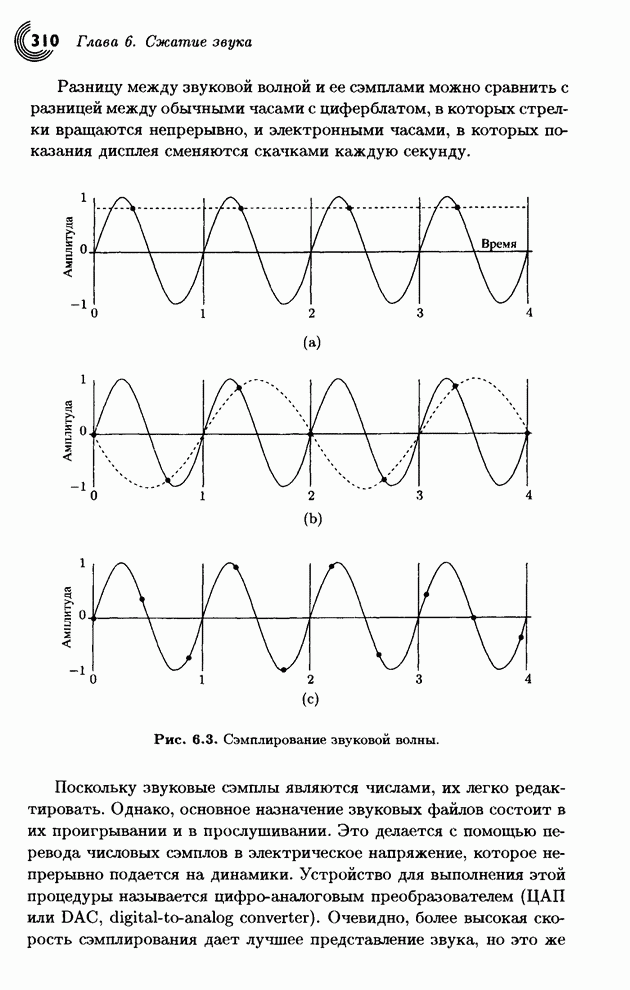
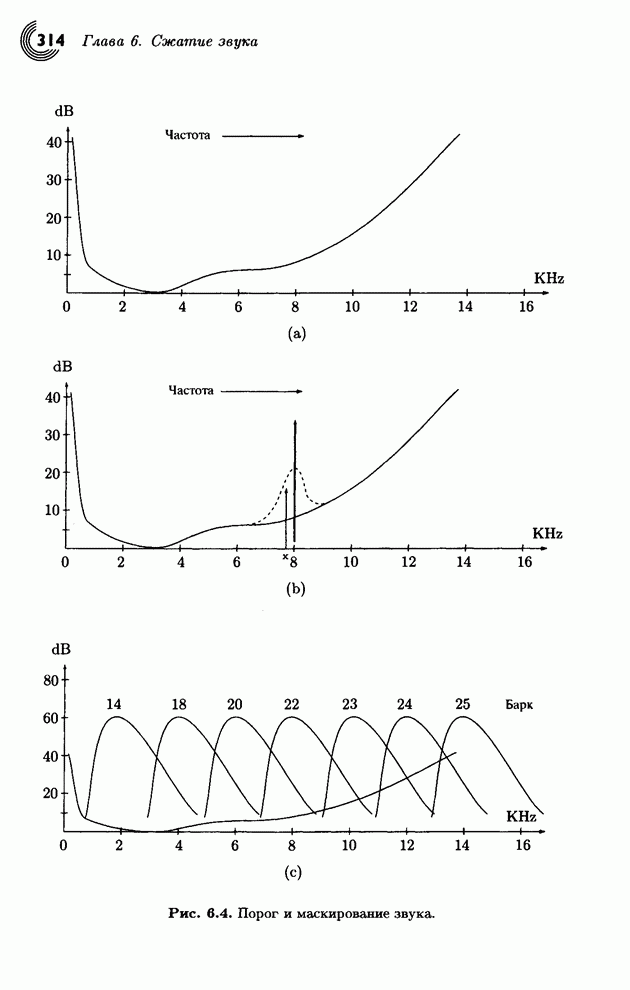
| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
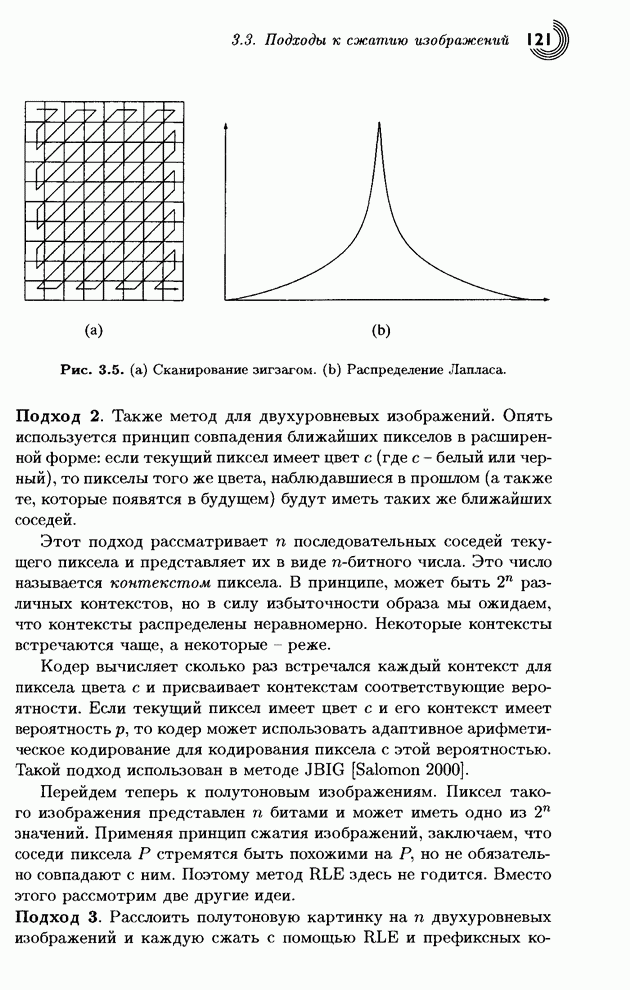
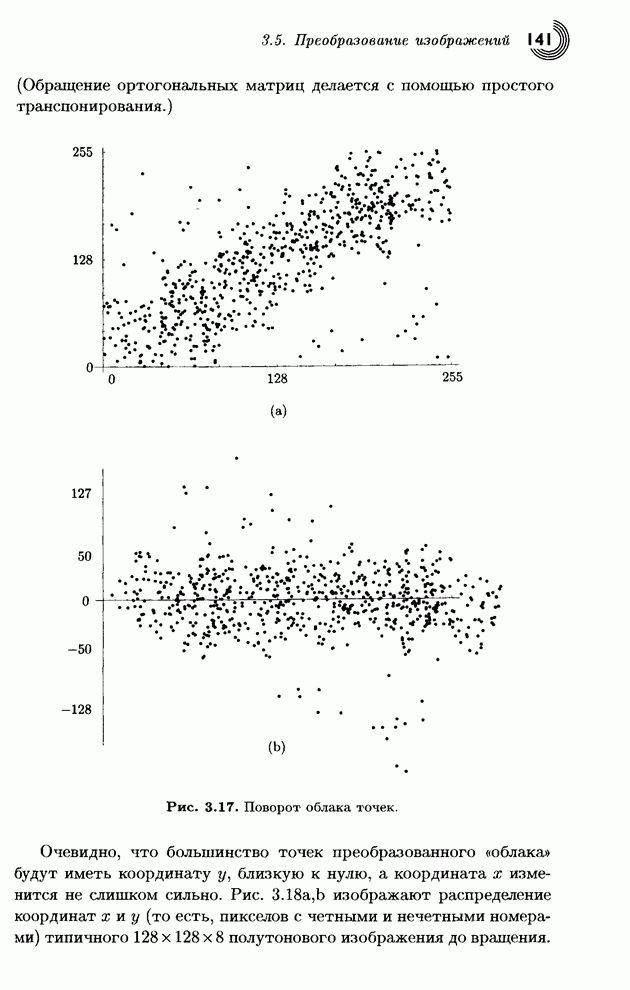
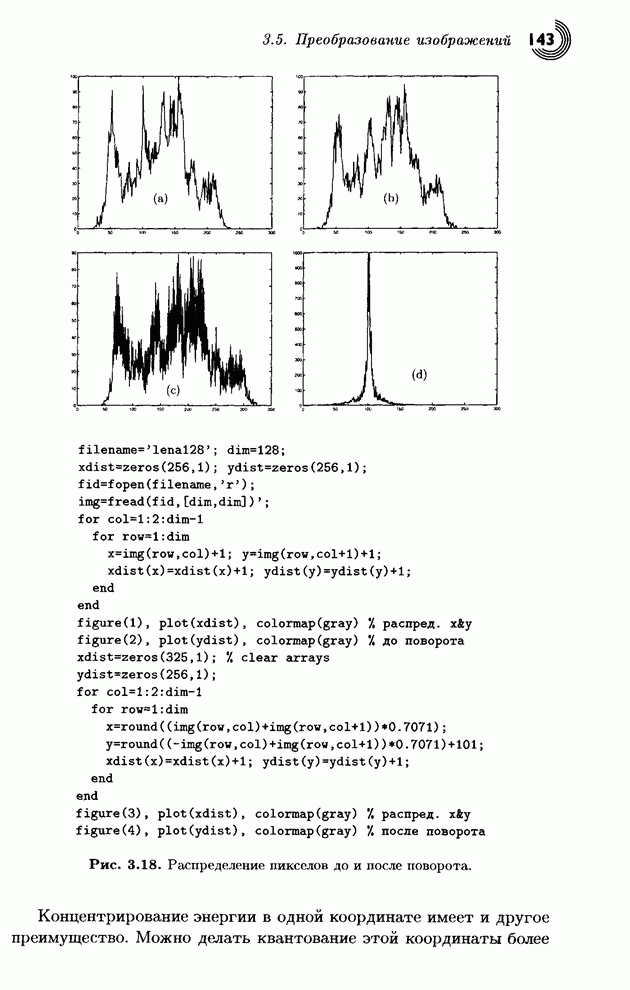
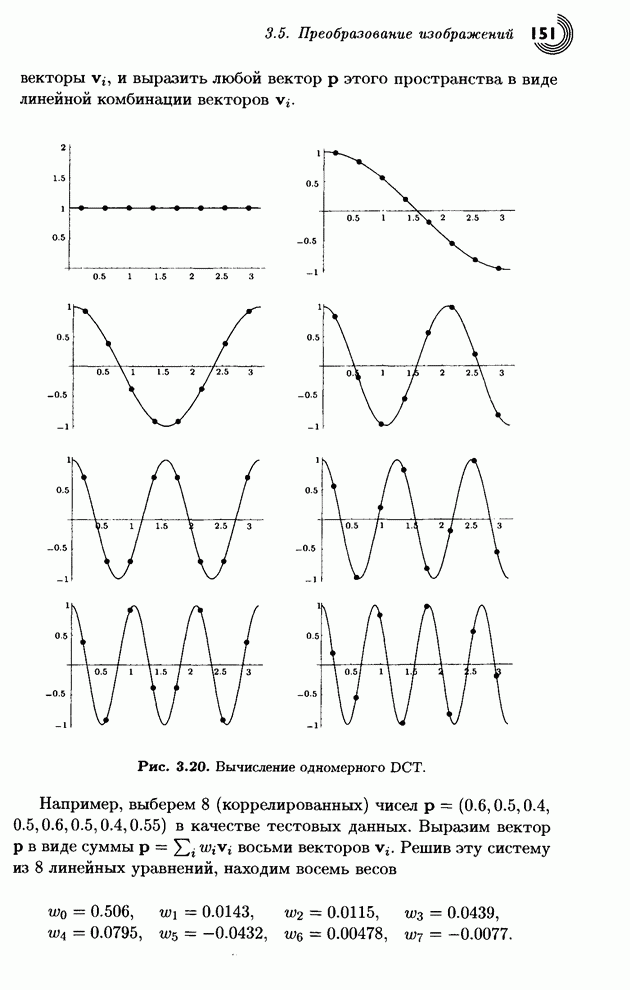
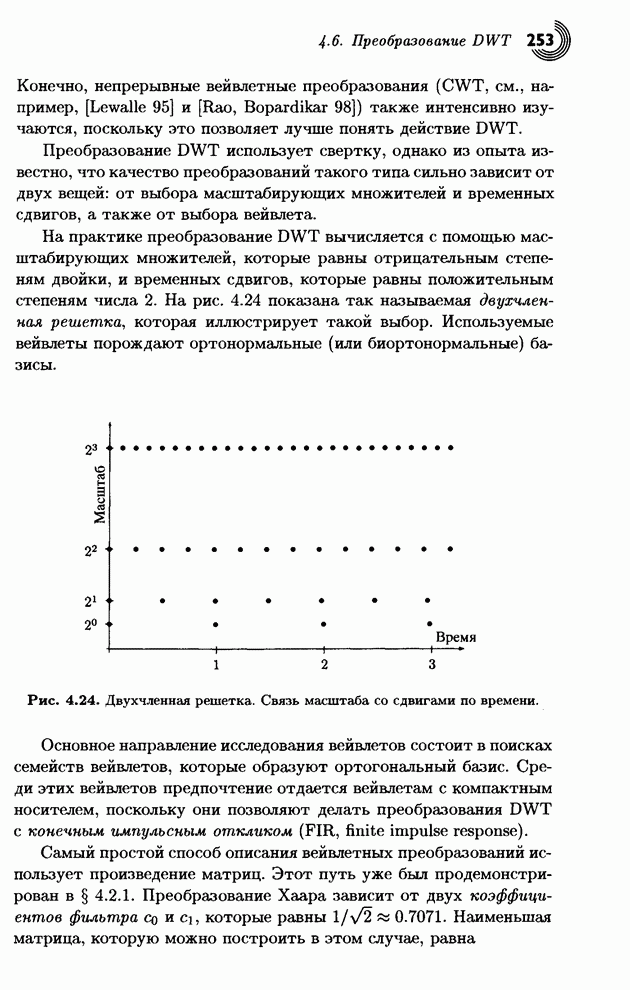
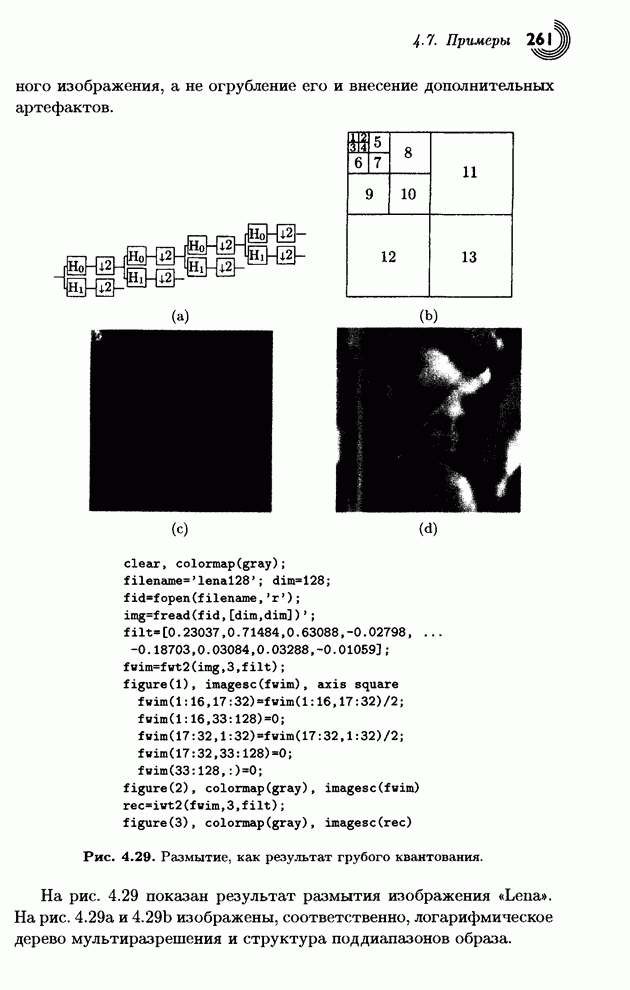
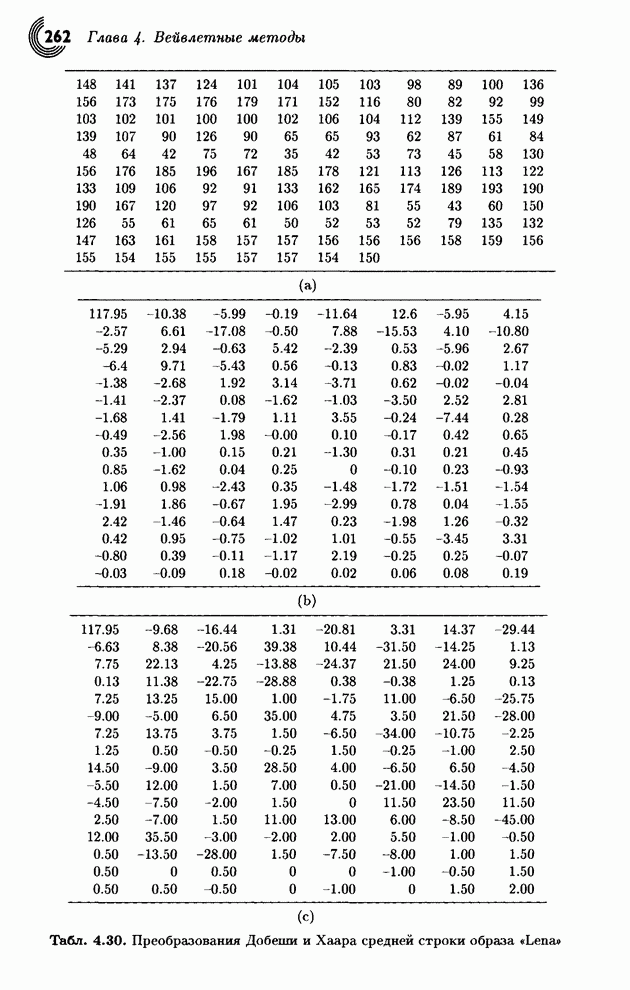
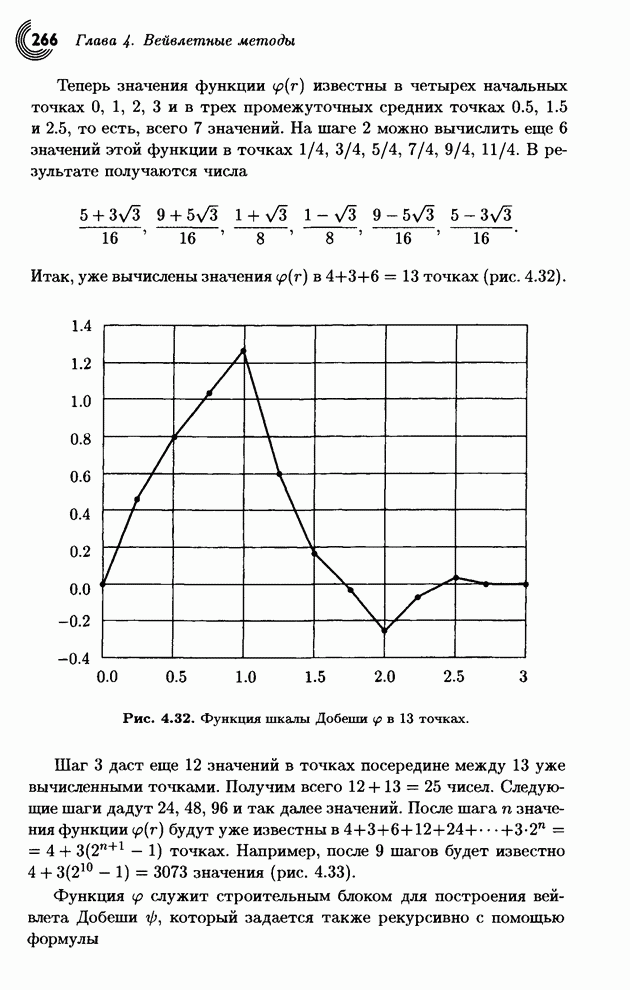
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
4.2. Преобразование Хаара
Преобразование Хаара использует
функцию шкалы ![]() и
вейвлет
и
вейвлет ![]() ,
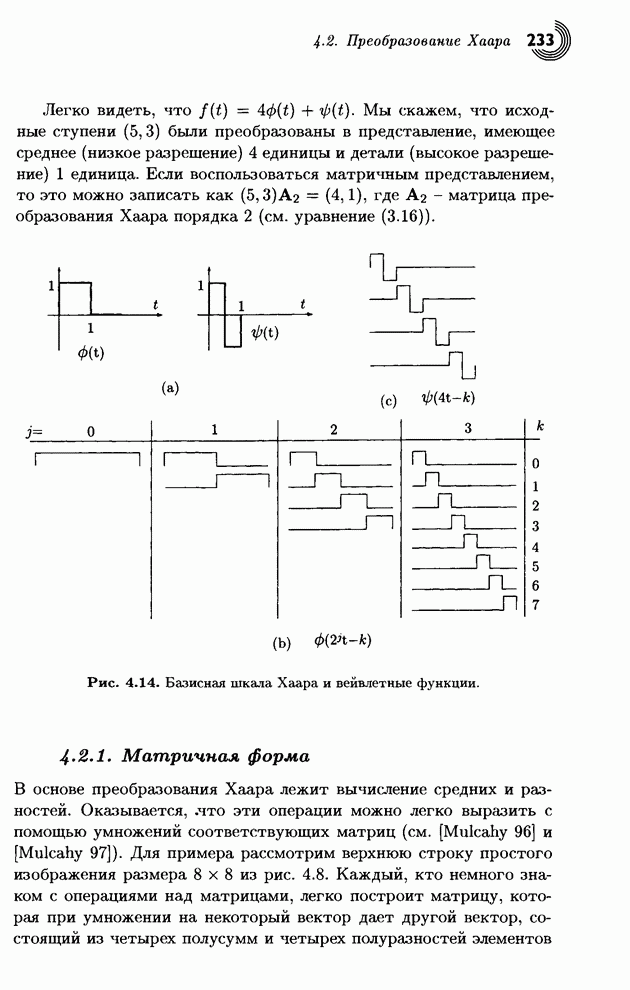
которые показаны на рис 4.14а, для представления широкого класса функций. Это
представление имеет вид бесконечной суммы
,
которые показаны на рис 4.14а, для представления широкого класса функций. Это
представление имеет вид бесконечной суммы
 ,
,
где
![]() и
и ![]() - коэффициенты,
которые необходимо определить.
- коэффициенты,
которые необходимо определить.
Базисная
функция шкалы ![]() является
единичным импульсом
является
единичным импульсом
![]()
Функция
![]() является
копией функции
является
копией функции ![]() ,
сдвинутой вправо на число
,
сдвинутой вправо на число ![]() . Аналогично, функция
. Аналогично, функция ![]() получается из функции
получается из функции ![]() сжатием аргумента в
два раза (это еще можно назвать уменьшением масштаба). Сдвинутые функции
используются для аппроксимации функции
сжатием аргумента в
два раза (это еще можно назвать уменьшением масштаба). Сдвинутые функции
используются для аппроксимации функции ![]() при различных моментах времени, а
функции с разными масштабами нужны для аппроксимации функции
при различных моментах времени, а
функции с разными масштабами нужны для аппроксимации функции ![]() при более высоком
разрешении. На рис. 4.14b приведены графики функций
при более высоком
разрешении. На рис. 4.14b приведены графики функций ![]() при
при ![]() и при
и при ![]() . Базисный вейвлет
Хаара
. Базисный вейвлет
Хаара ![]() является
ступенчатой функцией
является
ступенчатой функцией
![]()
Из
этого определения мы заключаем, что общий вейвлет ![]() получается из
получается из ![]() сдвигом вправо на
сдвигом вправо на ![]() единиц и сменой
масштаба в
единиц и сменой
масштаба в ![]() раз.
Четыре вейвлета
раз.
Четыре вейвлета ![]() при
при
![]() показаны на
рис. 4.14с.
показаны на
рис. 4.14с.
Обе функции ![]() и
и ![]() не равны нулю на интервале
ширины
не равны нулю на интервале
ширины ![]() .
Этот интервал называется носителем этих функций. Поскольку длина этого
интервала стремится к нулю, когда
.
Этот интервал называется носителем этих функций. Поскольку длина этого
интервала стремится к нулю, когда ![]() стремится к бесконечности, мы будем
говорить, что функции имеют компактный носитель.
стремится к бесконечности, мы будем
говорить, что функции имеют компактный носитель.
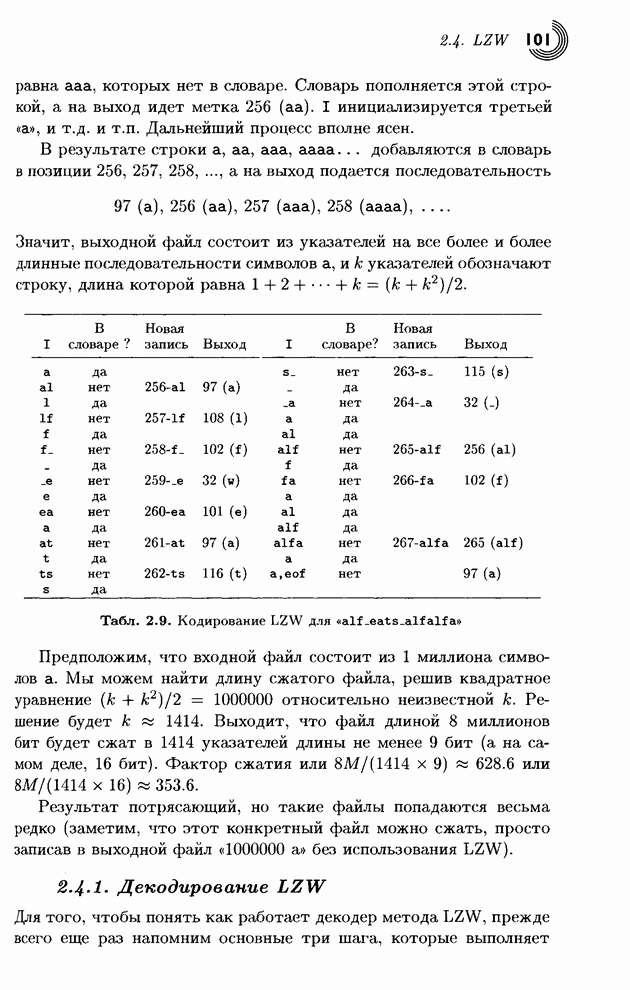
Проиллюстрируем основное преобразование с помощью простой ступенчатой функции
![]() .
.
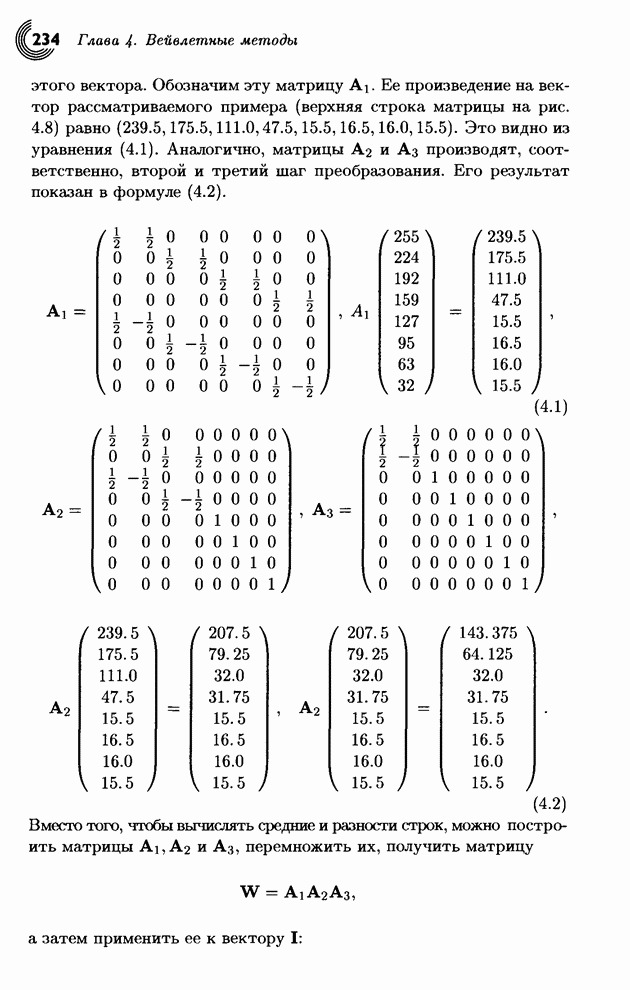
Легко видеть, что ![]() . Мы скажем, что
исходные ступени (5,3) были преобразованы в представление, имеющее среднее
(низкое разрешение) 4 единицы и детали (высокое разрешение) 1 единица. Если
воспользоваться матричным представлением, то это можно записать как (5,3)
. Мы скажем, что
исходные ступени (5,3) были преобразованы в представление, имеющее среднее
(низкое разрешение) 4 единицы и детали (высокое разрешение) 1 единица. Если
воспользоваться матричным представлением, то это можно записать как (5,3) ![]() , где
, где ![]() - матрица
преобразования Хаара порядка 2 (см. уравнение (3.16)).
- матрица
преобразования Хаара порядка 2 (см. уравнение (3.16)).

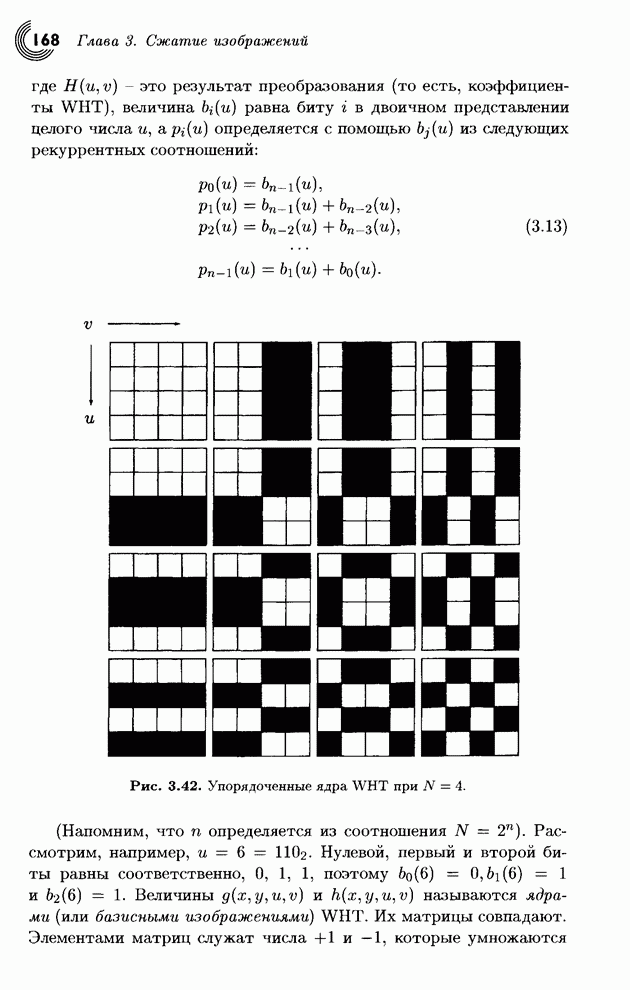
Рис. 4.14. Базисная шкала Хаара и вейвлетные функции.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- Предисловие переводчика
- Предисловие автора
- Введение
- Глава 1. Статистические методы
- 1.1. Энтропия
- 1.2. Коды переменной длины
- 1.3. Декодирование
- 1.4. Кодирование Хаффмана
- 1.4.1. Декодирование Хаффмана
- 1.4.2. Средняя длина кода
- 1.5. Адаптивные коды Хаффмана
- 1.5.1. Несжатые коды
- 1.5.2. Модификация дерева
- 1.5.3. Переполнение счетчика
- 1.5.4. Кодовое переполнение
- 1.5.5. Вариант алгоритма
- 1.6. Факсимильное сжатие
- 1.6.1. Одномерное кодирование
- 1.6.2. Двумерное кодирование
- 1.7. Арифметическое кодирование
- 1.7.1. Детали реализации метода
- 1.7.2. Потеря значащих цифр
- 1.7.3. Заключительные замечания
- 1.8. Адаптивное арифметическое кодирование
- ГЛАВА 2 СЛОВАРНЫЕ МЕТОДЫ
- 2.1. LZ77 (скользящее окно)
- 2.1.1. Циклическая очередь
- 2.2. LZSS
- 2.2.1. Недостатки
- 2.3. LZ78
- 2.4. LZW
- 2.4.1. Декодирование LZW
- 2.4.2. Структура словаря LZW
- 2.4.3. LZW в практических приложениях
- 2.5. Заключение
- ГЛАВА 3 СЖАТИЕ ИЗОБРАЖЕНИЙ
- 3.1. Введение
- 3.2. Типы изображений
- 3.3. Подходы к сжатию изображений
- 3.3.1. Коды Грея
- 3.3.2. Метрики ошибок
- 3.4. Интуитивные методы
- 3.4.1. Подвыборка
- 3.4.2. Квантование
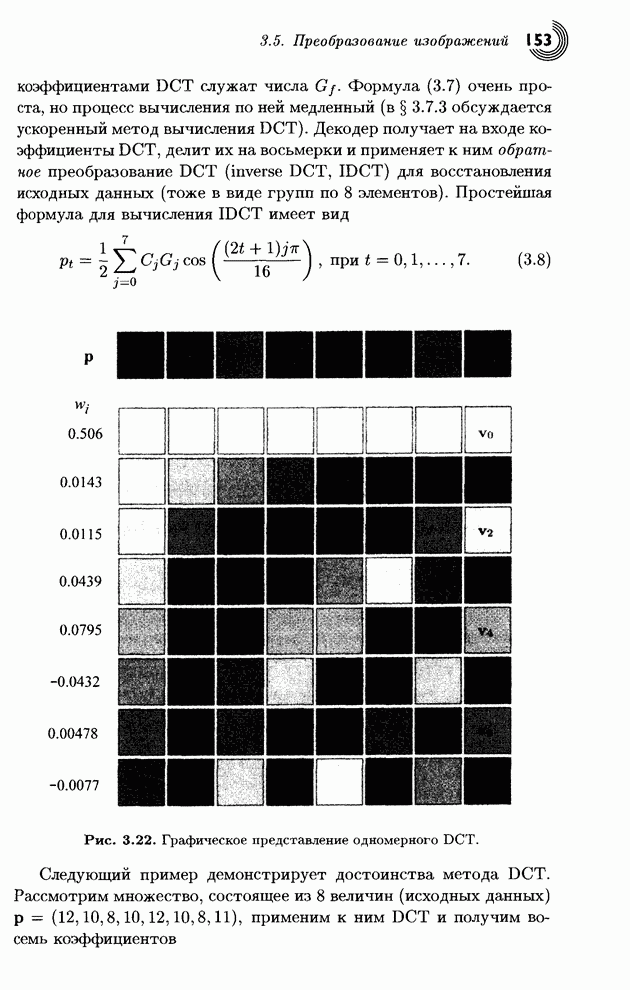
- 3.5. Преобразование изображений
- 3.5.1. Ортогональные преобразования
- 3.5.2. Матричные преобразования
- 3.5.3. Дискретное косинус-преобразование
- 3.5.4. Пример
- 3.5.5. Дискретное синус-преобразование
- 3.5.6. Преобразование Уолша-Адамара
- 3.5.7. Преобразование Хаара
- 3.5.8. Преобразование Кархунена-Лоэвэ
- 3.6. Прогрессирующее сжатие изображений
- 3.7. JPEG
- 3.7.1. Светимость
- 3.7.2. DCT
- 3.7.3. Практическое DCT
- 3.7.4. Квантование
- 3.7.5. Кодирование
- 3.7.6. Мода без потери данных
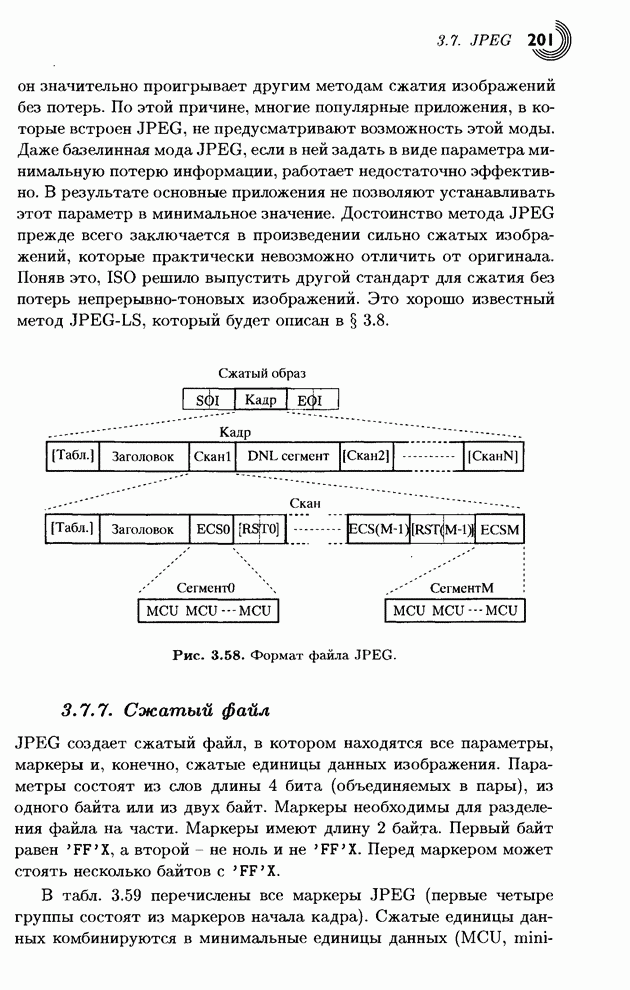
- 3.7.7. Сжатый файл
- 3.7.8. JFIF
- 3.8. JPEG-LS
- 3.8.1. Коды Голомба
- 3.8.2. Основы метода JPEG-LS
- 3.8.3. Кодер
- ГЛАВА 4 ВЕЙВЛЕТНЫЕ МЕТОДЫ
- 4.1. Вычисление средних и полу разностей
- 4.1.1. Обобщение на двумерный случай
- 4.1.2. Свойства преобразования Хаара
- 4.2. Преобразование Хаара
- 4.2.1. Матричная форма
- 4.3. Поддиапазонные преобразования
- 4.4. Банк фильтров
- 4.5. Нахождение коэффициентов фильтра
- 4.6. Преобразование DWT
- 4.7. Примеры
- 4.8. Вейвлеты Добеши
- 4.9. SPIHT
- 4.9.1. Алгоритм сортировки разделением множеств
- 4.9.2. Пространственно ориентированное дерево
- 4.9.3. Кодирование в алгоритме SPIHT
- 4.9.4. Пример
- 4.9.5. QTCQ
- ГЛАВА 5 СЖАТИЕ ВИДЕО
- 5.1. Основные принципы
- 5.2. Методы подоптимального поиска
- ГЛАВА 6 СЖАТИЕ ЗВУКА
- 6.1. Звук
- 6.2. Оцифрованный звук
- 6.3. Органы слуха человека
- 6.4. Общепризнанные методы
- 6.5. Сжатие звука в стандарте MPEG-1
- 6.5.1. Кодирование частотной области
- 6.5.2. Формат сжатых данных
- 6.5.3. Психоакустические модели
- 6.5.4. Кодирование: слой III
- Литература
- Глоссарий