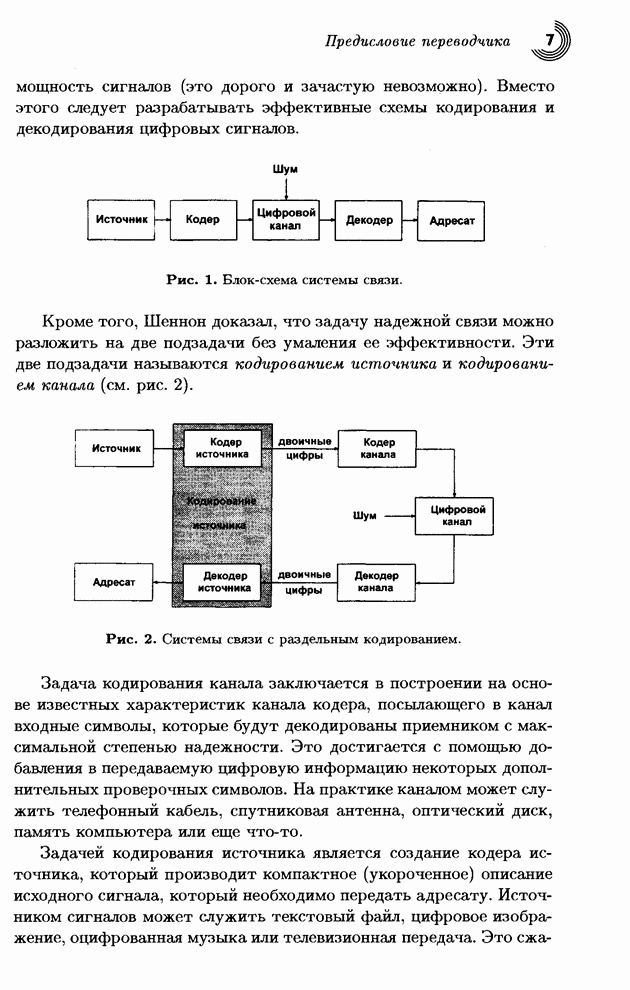
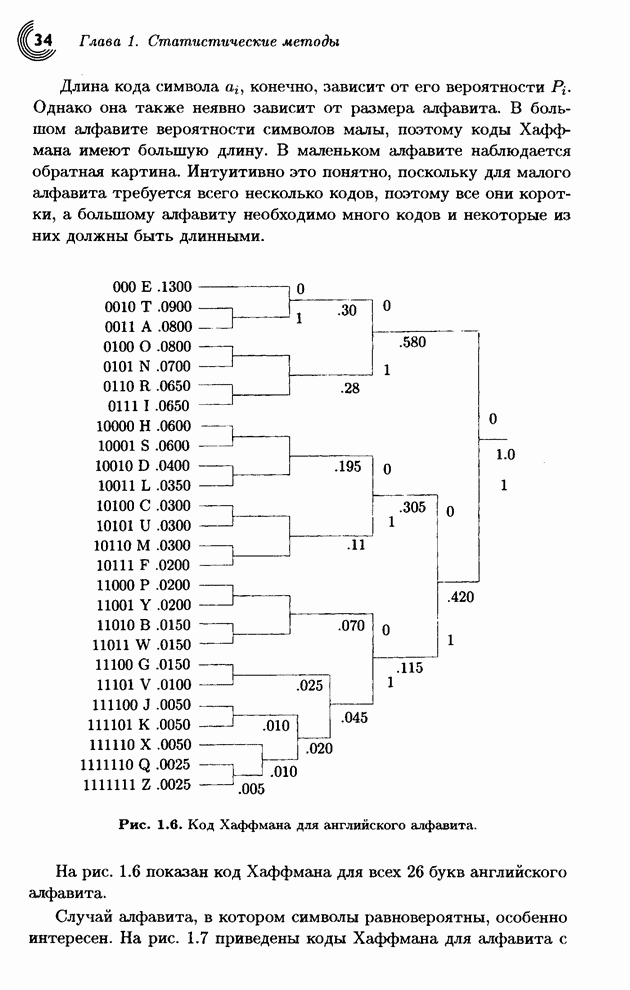
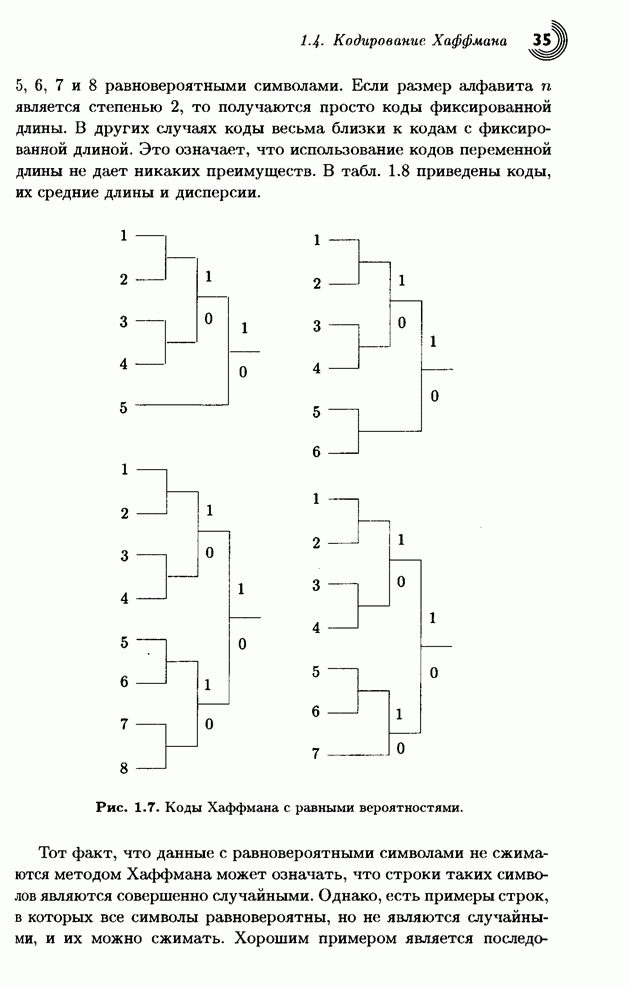
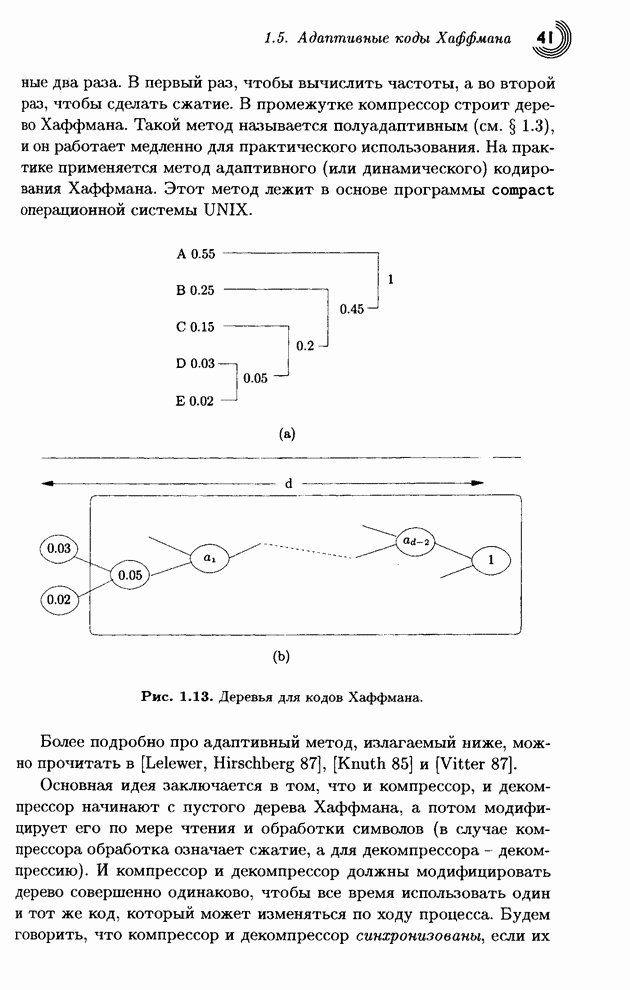
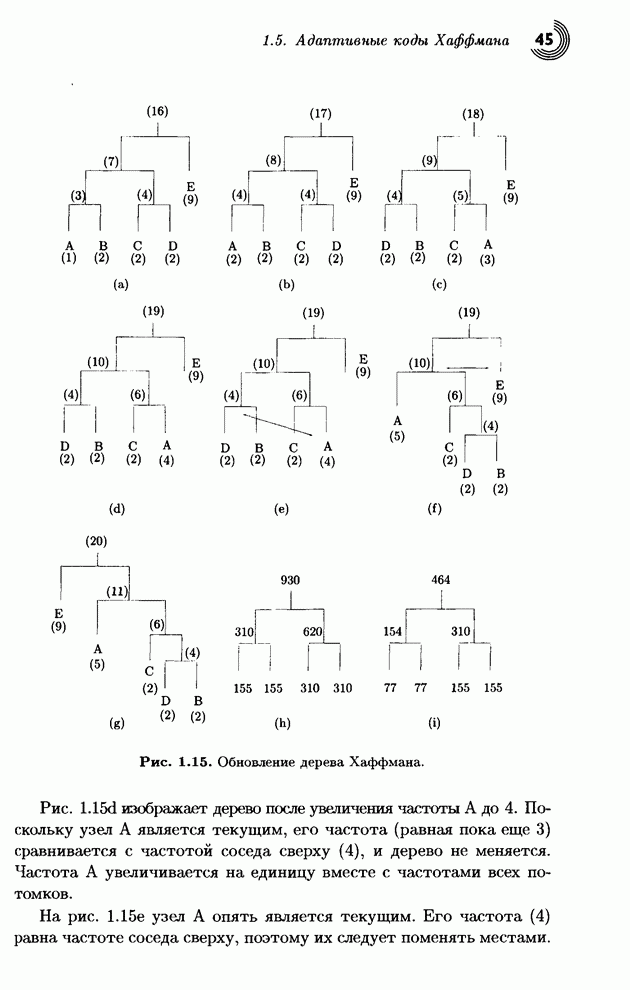
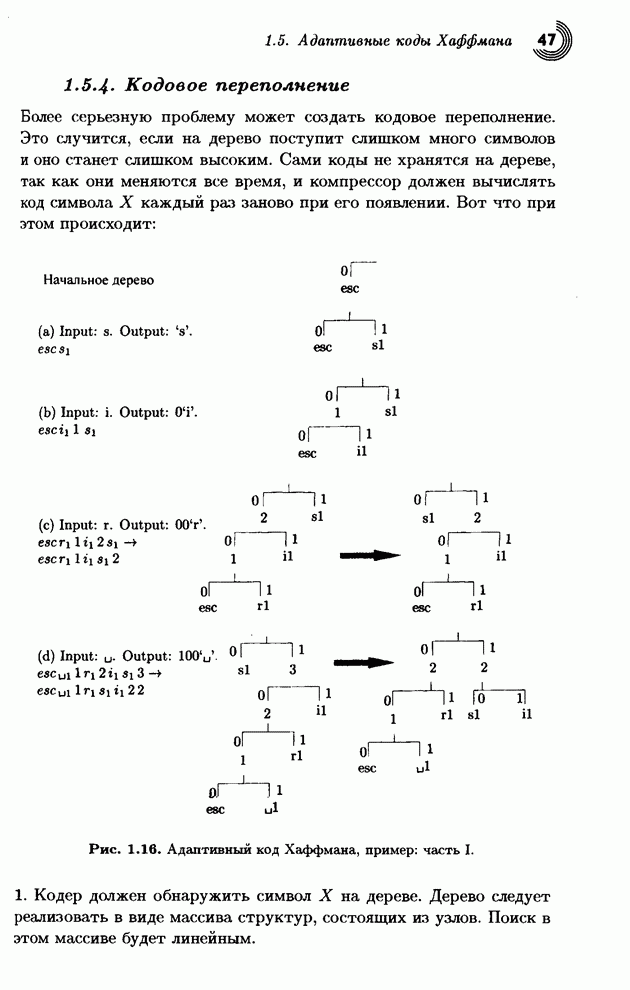
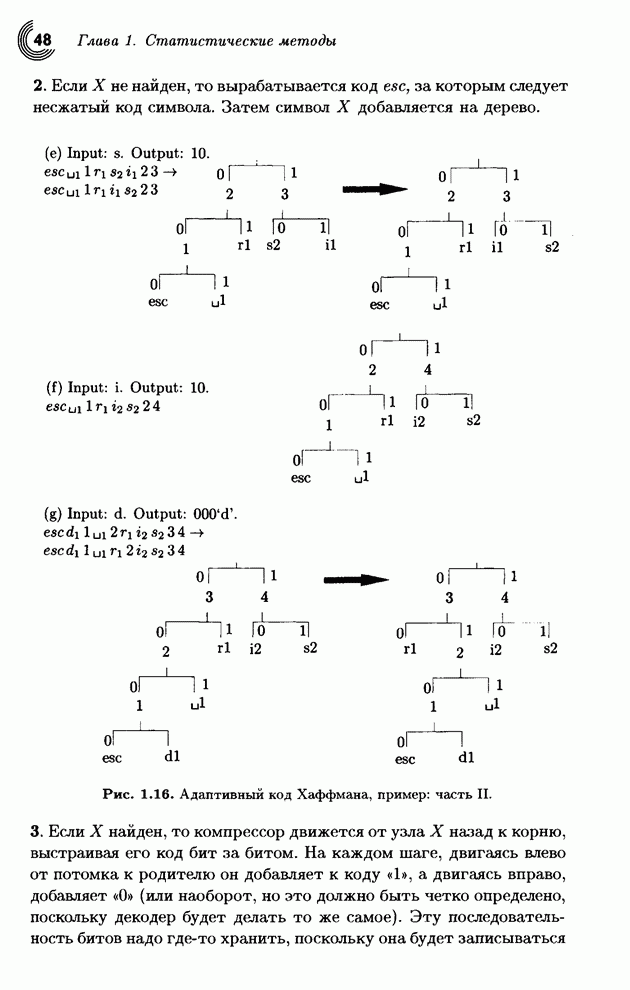
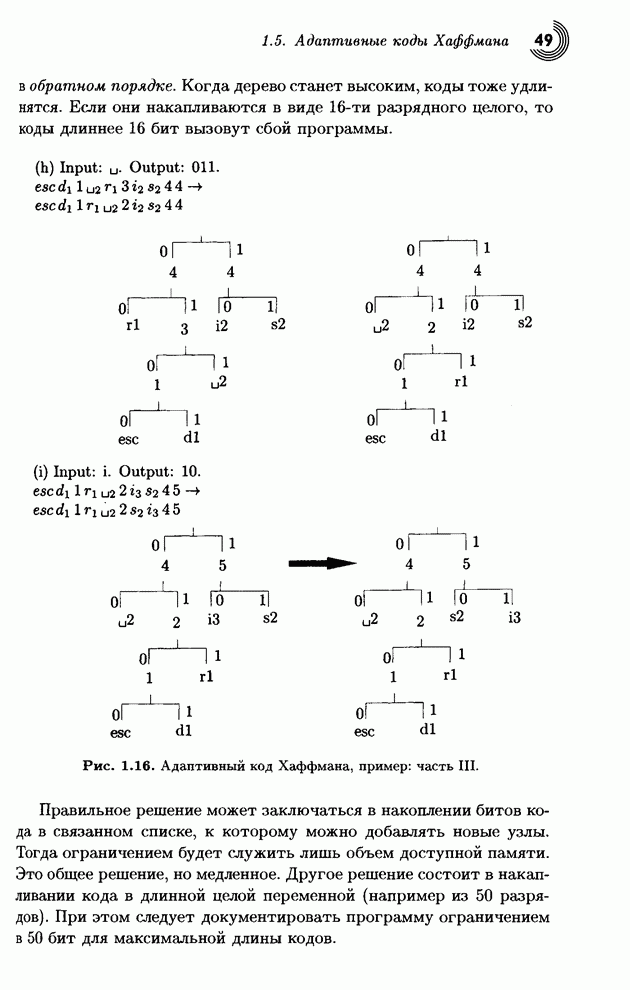
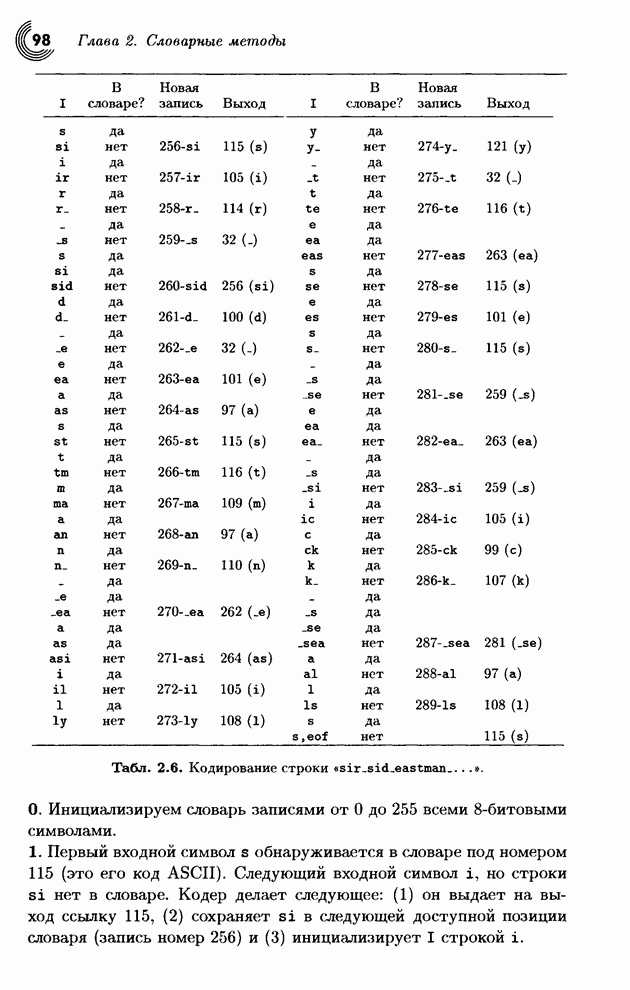
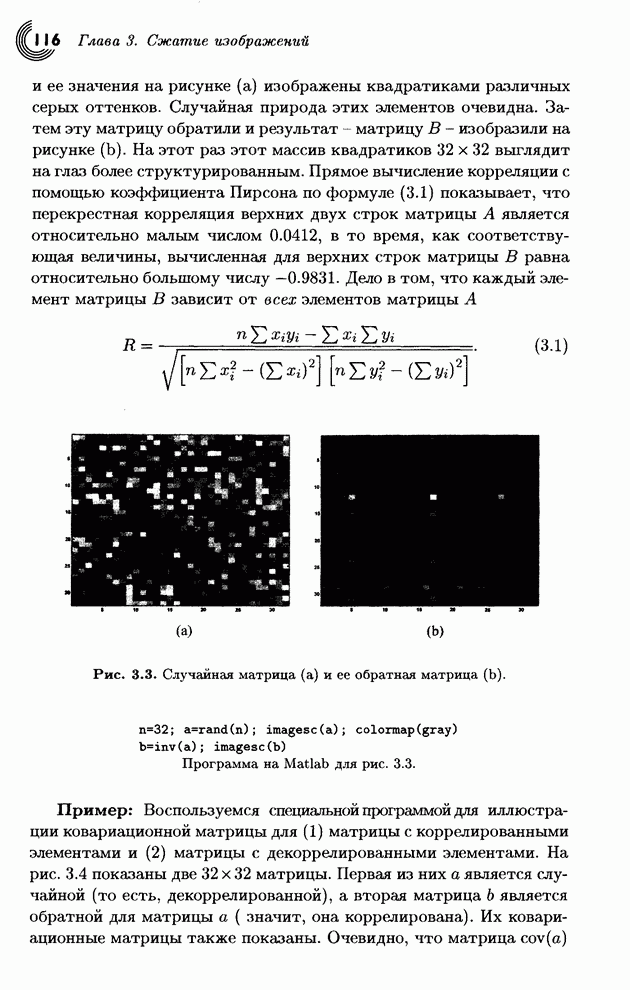
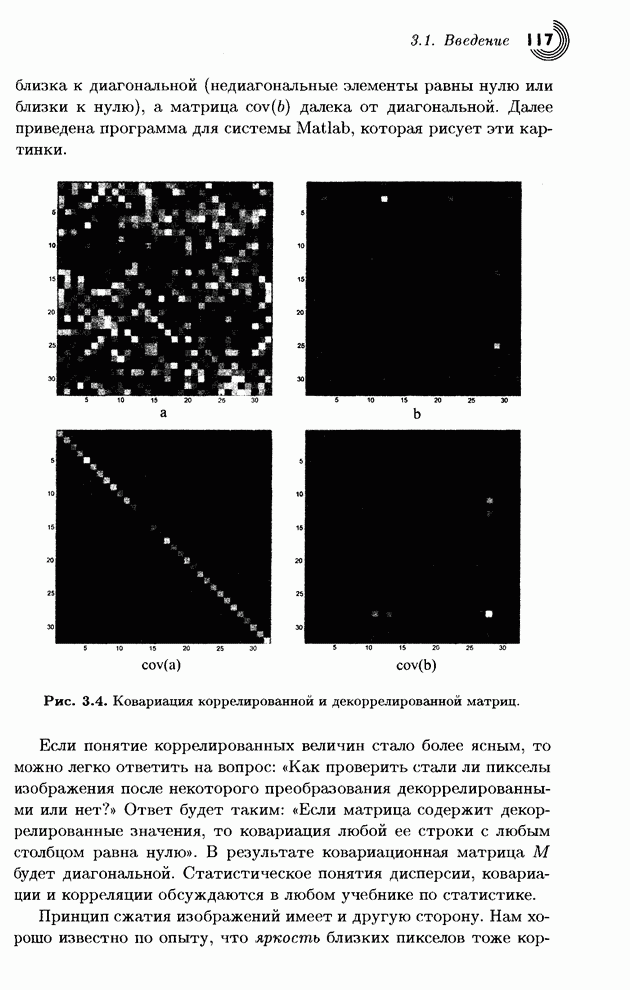
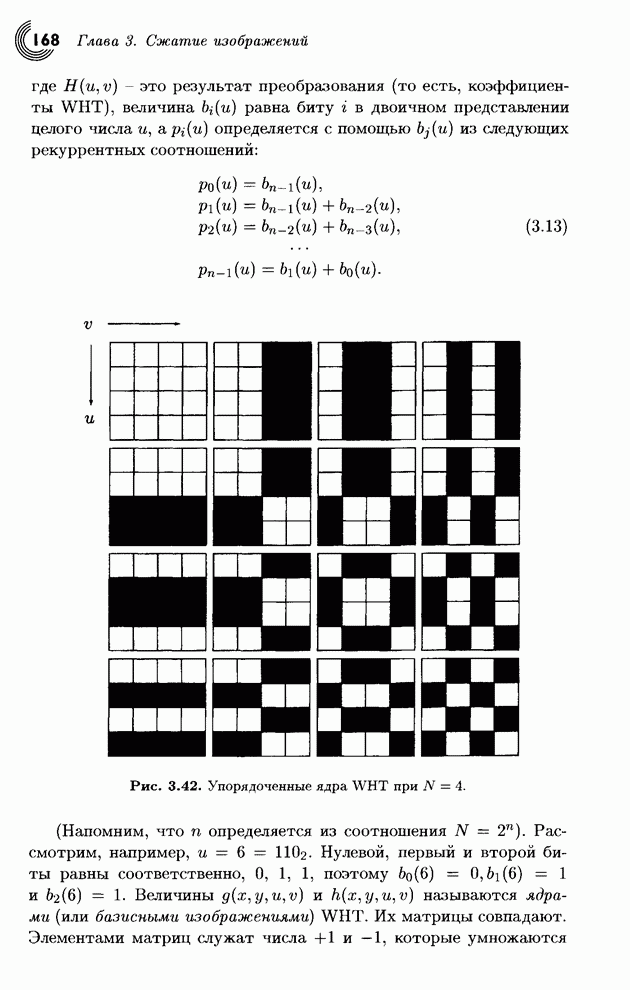
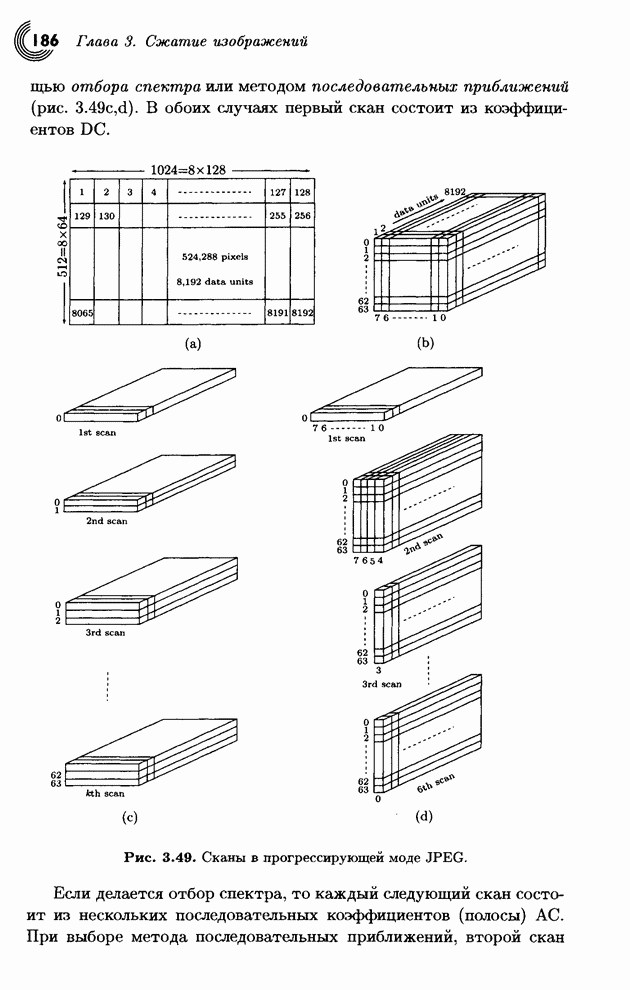
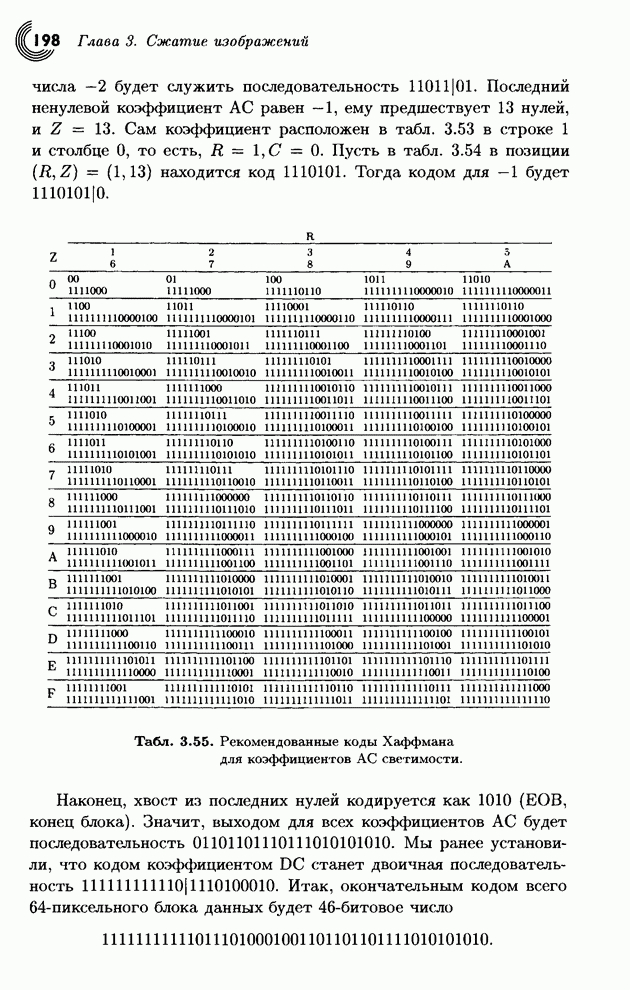
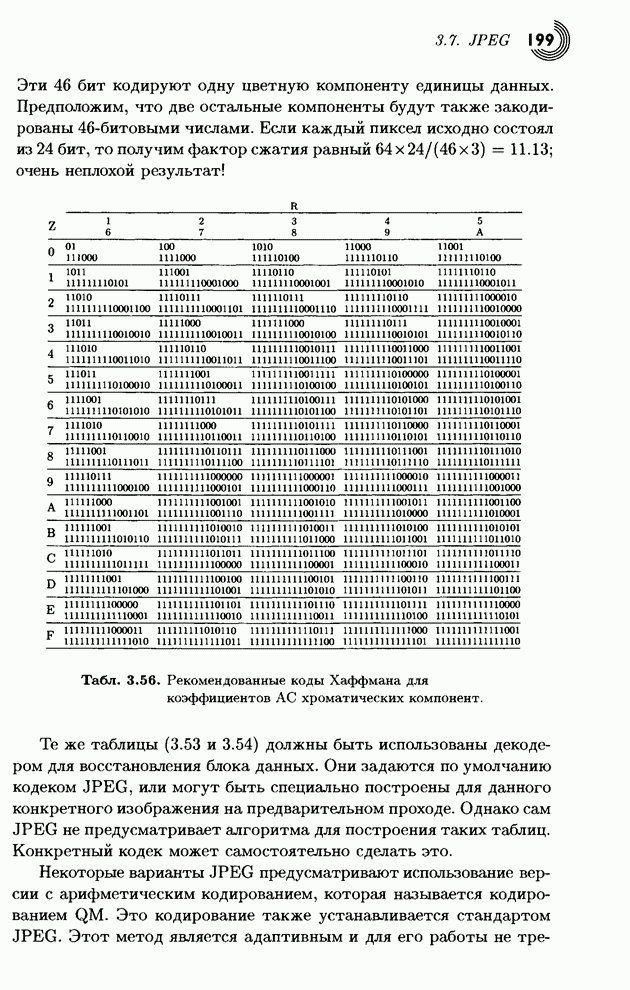
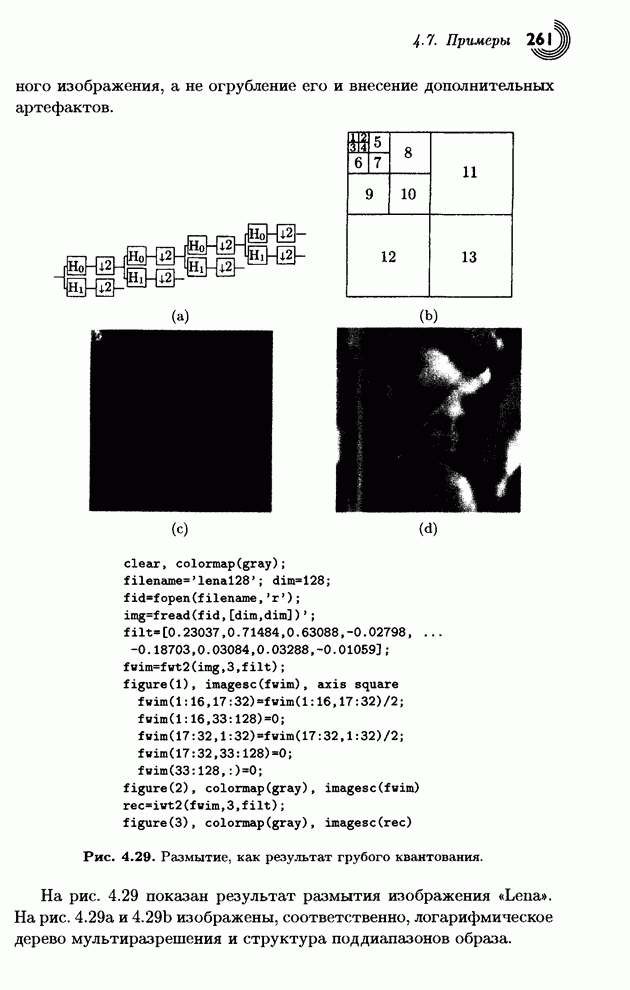
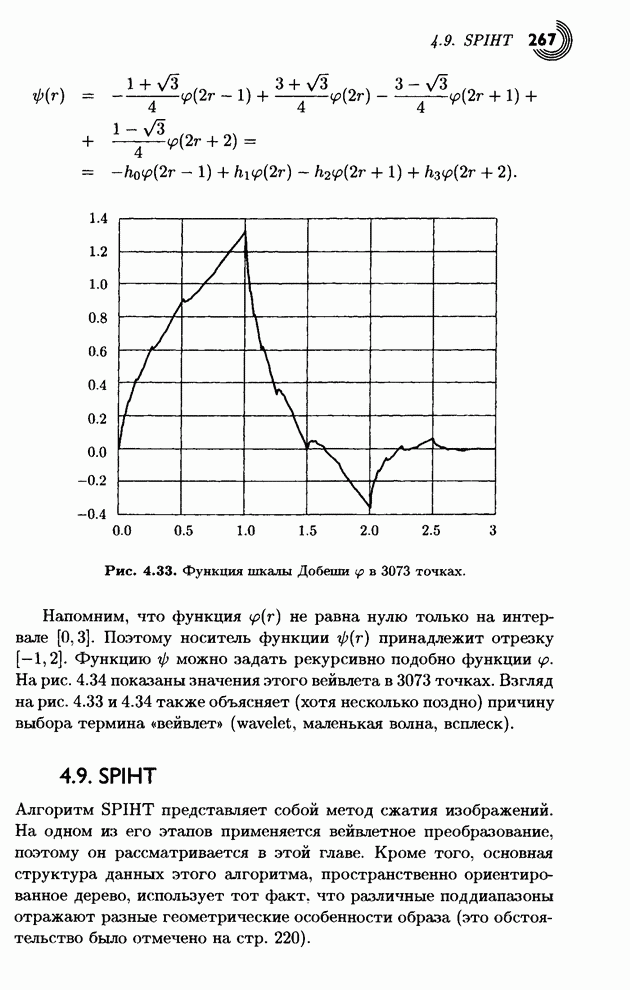
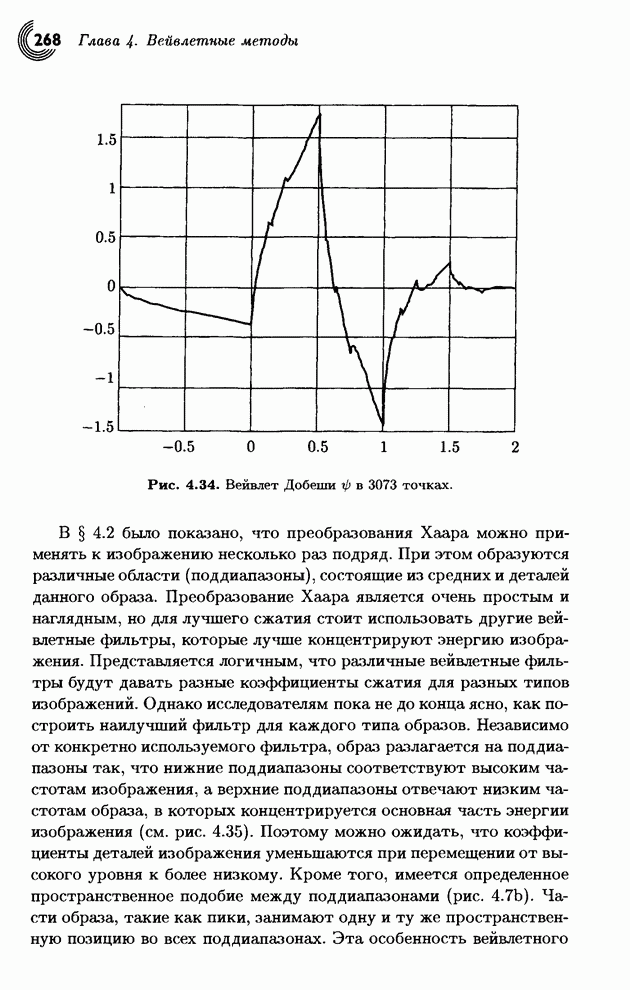
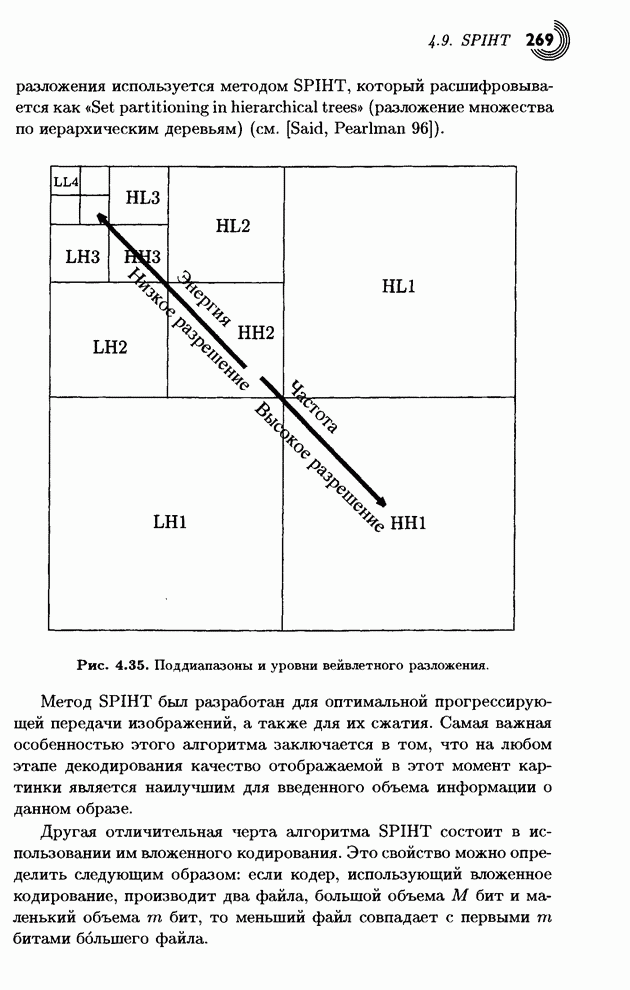
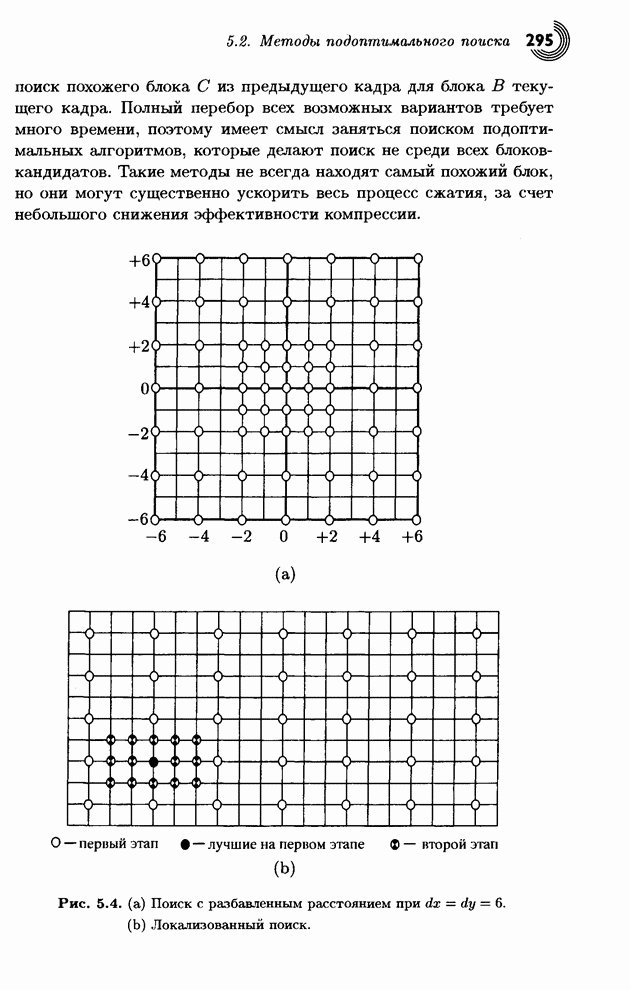
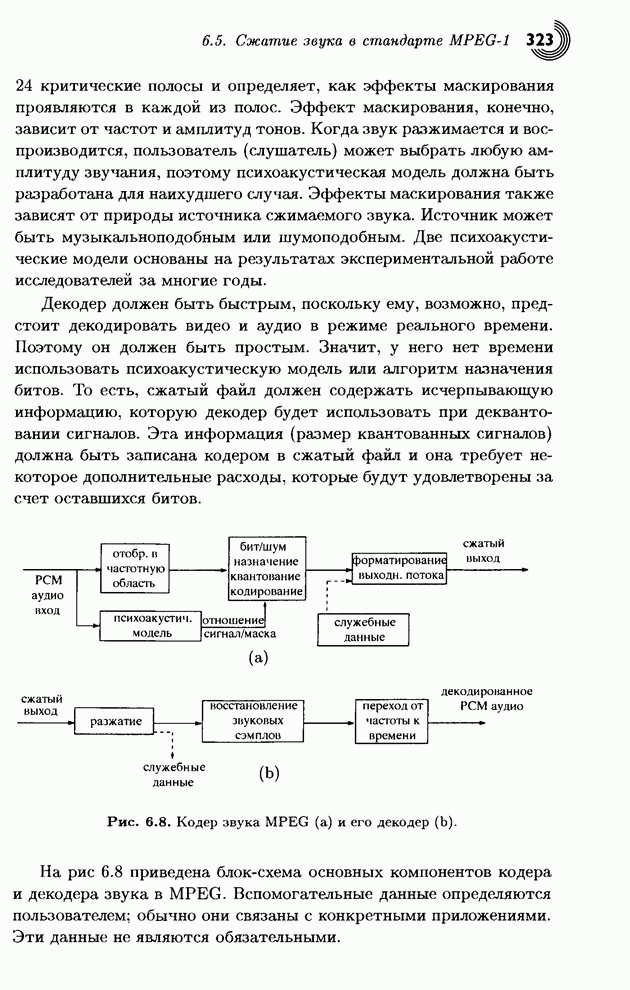
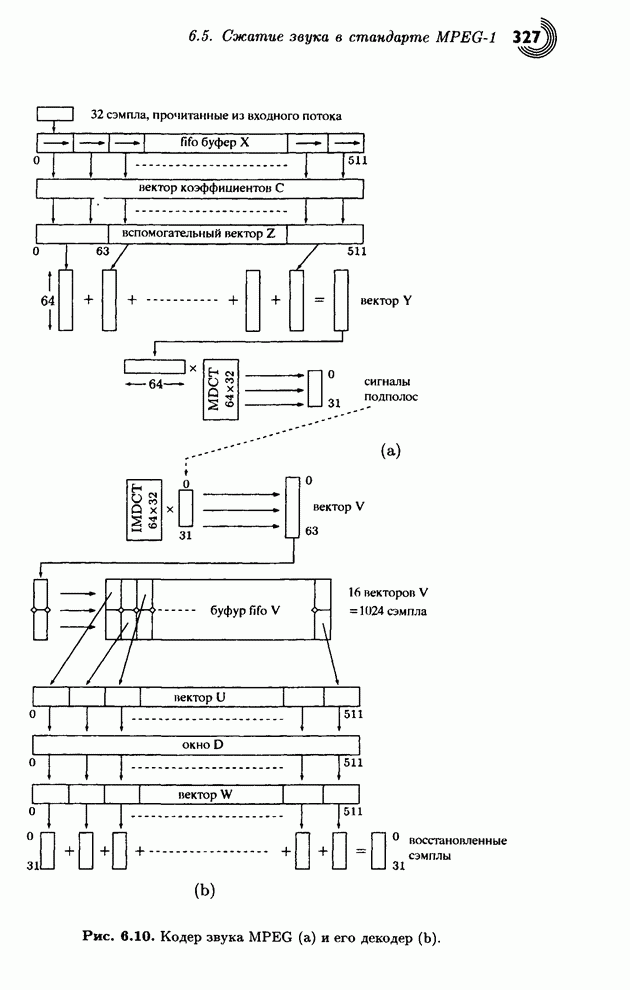
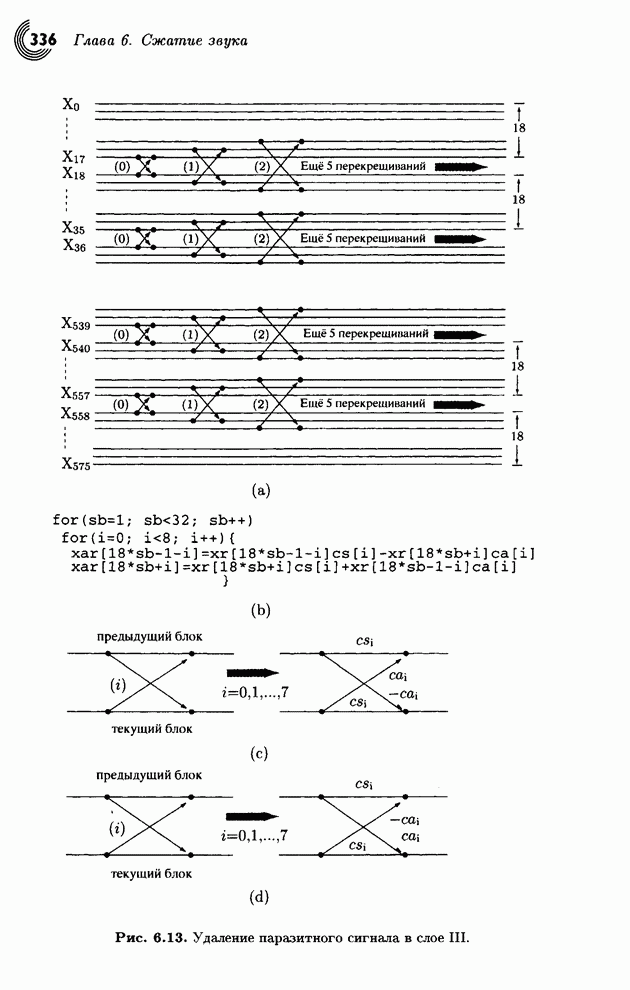
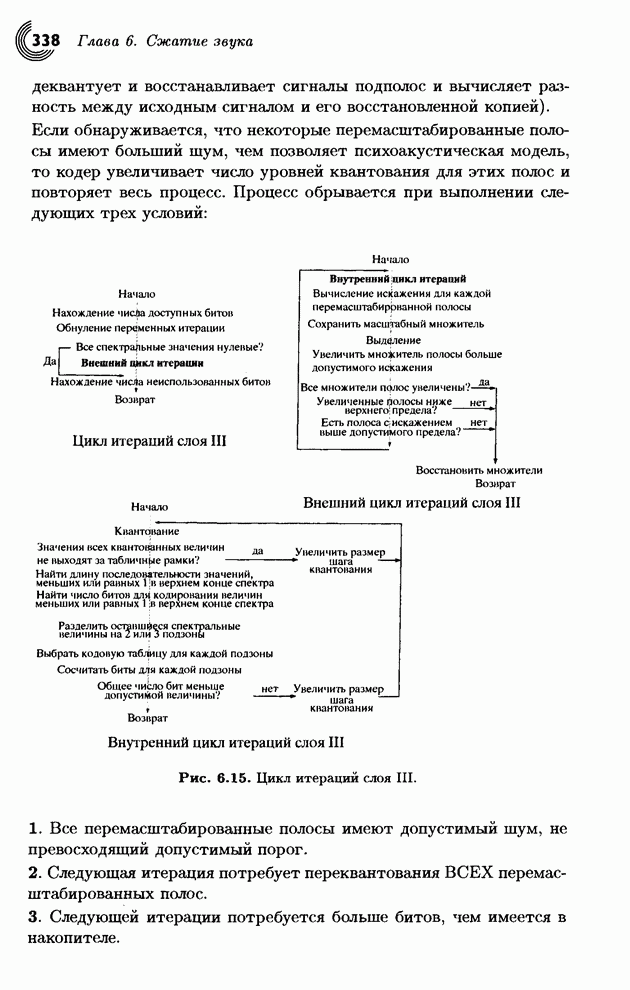
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
1.7. Арифметическое кодирование
Метод
Хаффмана является простым и эффективным, однако, как было замечено в § 1.4, он
порождает наилучшие коды переменной длины (коды, у которых средняя длина равна
энтропии алфавита) только когда вероятности символов алфавита являются
степенями числа 2, то есть равны 1/2, 1/4, 1/8 и т.п. Это связано с тем, что
метод Хаффмана присваивает каждому символу алфавита код с целым числом битов.
Теория информации предсказывает, что при вероятности символа, скажем, 0.4, ему
в идеале следует присвоить код длины 1.32 бита, поскольку ![]() . А метод Хаффмана присвоит
этому символу код длины 1 или 2 бита.
. А метод Хаффмана присвоит
этому символу код длины 1 или 2 бита.
(Перед тем как углубиться в теорию арифметического кодирования, стоит указать две работы [Moffat et al. 98] и [Witter 87], где рассмотрены основные принципы этого метода и приведено множество примеров.)
Арифметическое
кодирование решает эту проблему путем присвоения кода всему, обычно, большому
передаваемому файлу вместо кодирования отдельных символов. (Входным файлом
может быть текст, изображение или данные любого вида.) Алгоритм читает входной
файл символ за символом и добавляет биты к сжатому файлу. Чтобы понять метод,
полезно представлять себе получающийся код в виде числа из полуинтервала ![]() . (Здесь
. (Здесь ![]() обозначает числа от
обозначает числа от ![]() до
до ![]() , включая
, включая ![]() и исключая
и исключая ![]() . Конец
. Конец ![]() замкнут, а конец
замкнут, а конец ![]() открыт.) Таким
образом, код «9746509» следует интерпретировать как число «0.9746509» однако
часть «0.» не будет включена в передаваемый файл.
открыт.) Таким
образом, код «9746509» следует интерпретировать как число «0.9746509» однако
часть «0.» не будет включена в передаваемый файл.
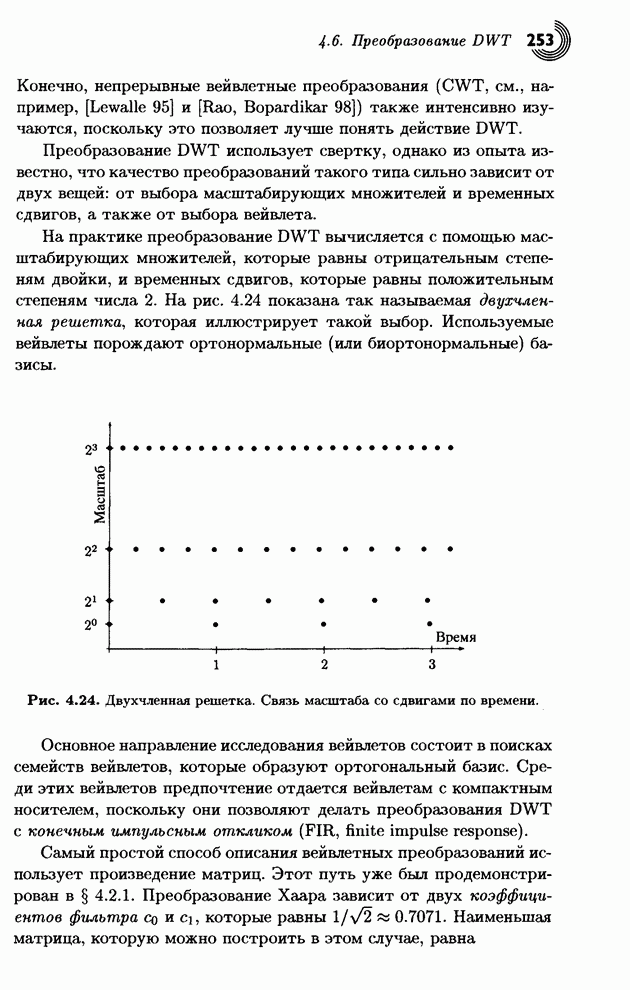
На первом этапе следует вычислить или, по крайней мере, оценить частоты возникновения каждого символа алфавита. Наилучшего результата можно добиться, прочитав весь входной файл на первом проходе алгоритма сжатия, состоящего из двух проходов. Однако, если программа может получить хорошие оценки частот символов из другого источника, первый проход можно опустить.
В
первом примере мы рассмотрим три символа ![]() и
и ![]() с вероятностями
с вероятностями ![]() ,
, ![]() и
и ![]() , соответственно. Интервал
, соответственно. Интервал ![]() делится между этими
тремя символами на части пропорционально их вероятностям. Порядок следования
этих подынтервалов не существенен. В нашем примере трем символам будут
соответствовать подынтервалы
делится между этими
тремя символами на части пропорционально их вероятностям. Порядок следования
этих подынтервалов не существенен. В нашем примере трем символам будут
соответствовать подынтервалы ![]() ,
, ![]() и
и ![]() . Чтобы закодировать строку «
. Чтобы закодировать строку «![]() », мы начинаем с
интервала
», мы начинаем с
интервала ![]() .
Первый символ
.
Первый символ ![]() сокращает
этот интервал, отбросив от него 40% в начале и 10% в конце. Результатом будет
интервал
сокращает
этот интервал, отбросив от него 40% в начале и 10% в конце. Результатом будет
интервал ![]() .
Второй символ
.
Второй символ ![]() сокращает
интервал
сокращает
интервал ![]() в
той же пропорции до интервала
в
той же пропорции до интервала ![]() . Третий символ
. Третий символ ![]() переводит его в
переводит его в ![]() . Наконец, символ
. Наконец, символ ![]() отбрасывает от него
90% в начале, а конечную точку оставляет без изменения. Получается интервал
отбрасывает от него
90% в начале, а конечную точку оставляет без изменения. Получается интервал ![]() . Окончательным кодом
нашего метода может служить любое число из этого промежутка. (Заметим, что
подынтервал
. Окончательным кодом
нашего метода может служить любое число из этого промежутка. (Заметим, что
подынтервал ![]() получен
из
получен
из ![]() с
помощью следующих преобразований его концов:
с
помощью следующих преобразований его концов: ![]() и
и ![]() ).
).
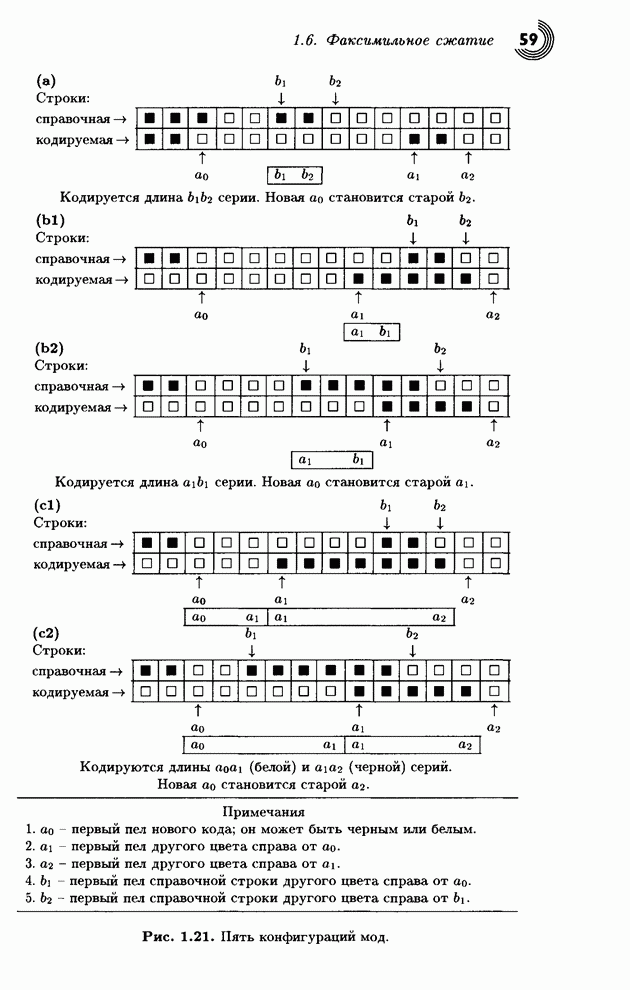
На этом примере легко понять следующие шаги алгоритма арифметического кодирования:
1.
Задать «текущий интервал» ![]() .
.
2.
Повторить следующие действия для каждого символа ![]() входного файла.
входного файла.
2.1. Разделить текущий интервал на части пропорционально вероятностям каждого символа.
2.2.
Выбрать подынтервал, соответствующий символу ![]() , и назначить его новым текущим
интервалом.
, и назначить его новым текущим
интервалом.
3. Когда весь входной файл будет обработан, выходом алгоритма объявляется любая точка, которая однозначно определяет текущий интервал (то есть, любая точка внутри этого интервала).
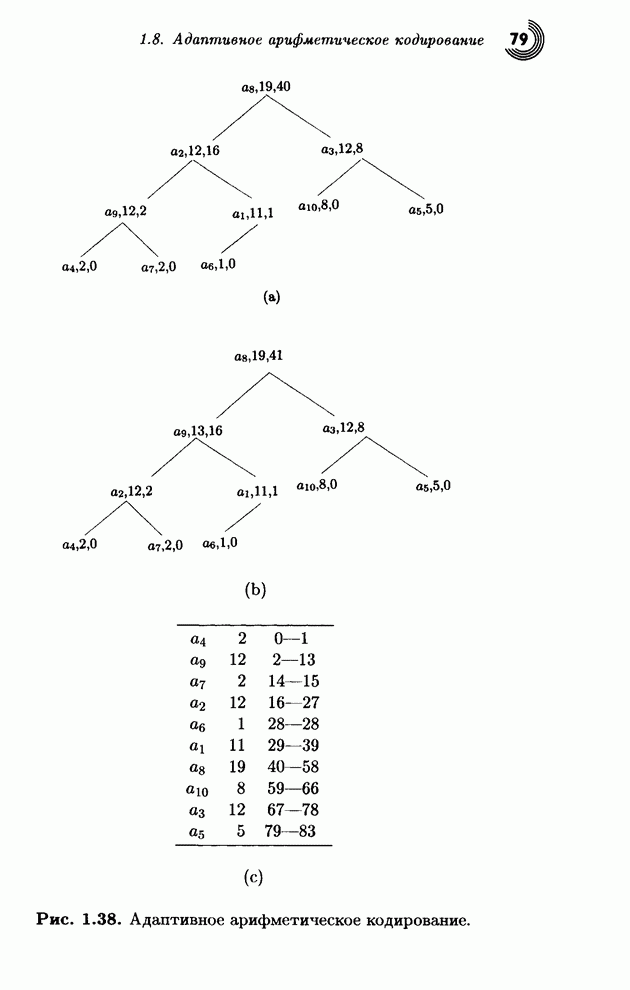
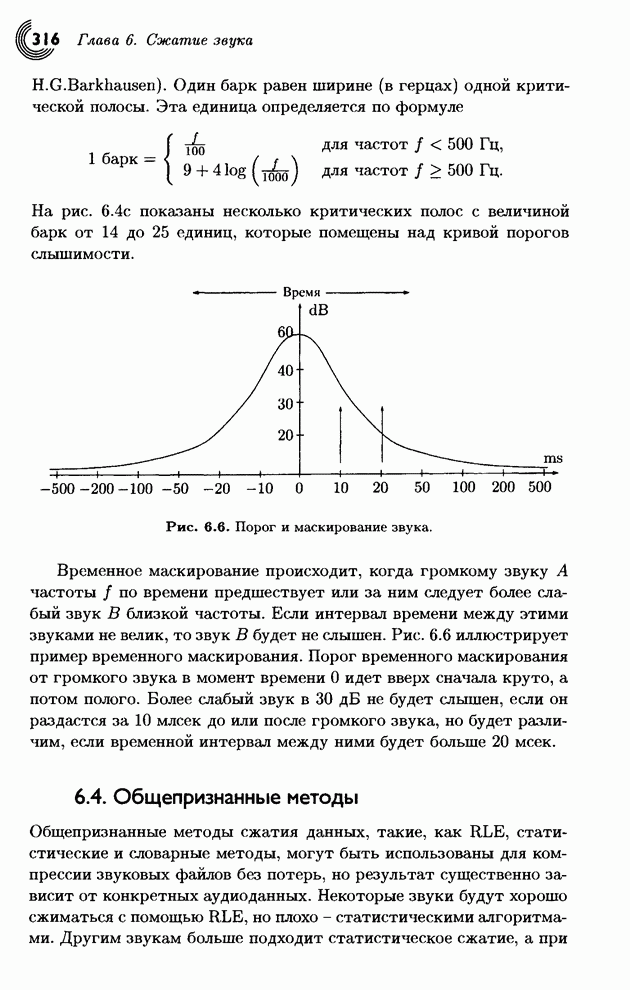
После каждого обработанного символа текущий интервал становится все меньше, поэтому требуется все больше бит, чтобы выразить его, однако окончательным выходом алгоритма является единственное число, которое не является объединением индивидуальных кодов последовательности входных символов. Среднюю длину кода можно найти, разделив размер выхода (в битах) на размер входа (в символах). Отметим, что вероятности, которые использовались на шаге 2.1, могут каждый раз меняться, и это можно использовать в адаптивной вероятностной модели (см. § 1.8).
Следующий
пример будет немного более запутанным. Мы продемонстрируем шаги сжатия для
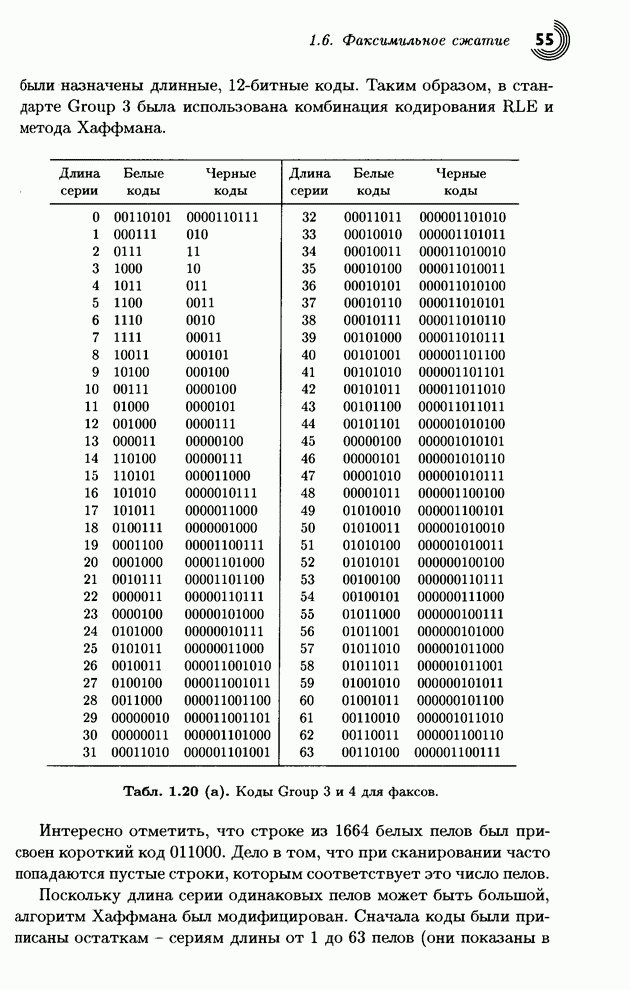
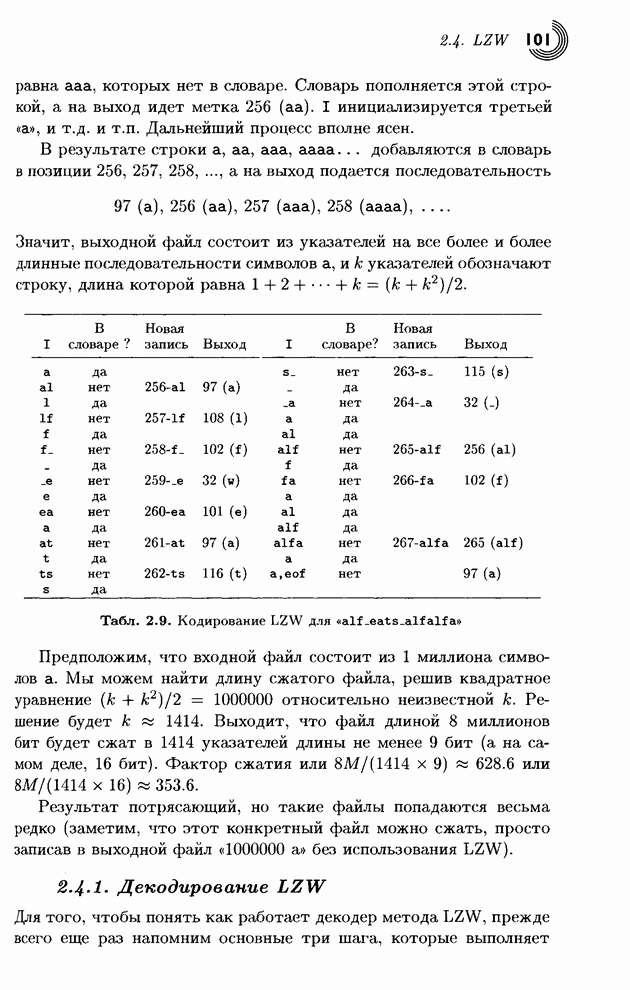
строки «SWISS_MISS». В табл. 1.24 указана
информация, приготовленная на предварительном этапе (статистическая модель
данных). Пять символов на входе можно упорядочить любым способом. Для каждого
символа сначала вычислена его частота, затем найдена вероятность ее появления (частота,
деленная на длину строки, 10). Область ![]() делится между символами в любом порядке.
Каждый символ получает кусочек или подобласть, равную его вероятности. Таким
образом, символ «S» получает интервал
делится между символами в любом порядке.
Каждый символ получает кусочек или подобласть, равную его вероятности. Таким
образом, символ «S» получает интервал ![]() длины 0.5, а символу
«I» достается интервал
длины 0.5, а символу
«I» достается интервал ![]() длины 0.2. Столбец CumFreq (накопленные частоты) будет
использоваться алгоритмом декодирования на стр. 71. CumFreq равно сумме частот всех
предыдущих символов, например, для «W»,
длины 0.2. Столбец CumFreq (накопленные частоты) будет
использоваться алгоритмом декодирования на стр. 71. CumFreq равно сумме частот всех
предыдущих символов, например, для «W»,
![]() .
.
|
Символ |
Частота |
Вероятность |
Область |
CumFreq |
|
Общая CumFreq = |
10 |
|||
|
S |
5 |
5/10=0.5 |
[0.5,1.0) |
5 |
|
|
1 |
1/10=0.1 |
(0.4,0.5) |
4 |
|
I |
2 |
2/10=0.2 |
[0.2,0.4) |
2 |
|
N |
1 |
1/10=0.1 |
[0.1,0.2) |
1 |
|
- |
1 |
1/10=0.1 |
(0.0,0.1) |
0 |
Табл. 1.24. Частоты и вероятности 5 символов.
Символы и частоты табл. 1.24 записываются в начало выходного файла до битов кода сжатия.
Процесс
кодирования начинается инициализацией двух переменных Low и High и присвоением им 0 и 1,
соответственно. Они определяют интервал ![]() . По мере поступления и обработки
символов, переменные Low и High начинают сближаться, уменьшая
интервал.
. По мере поступления и обработки
символов, переменные Low и High начинают сближаться, уменьшая
интервал.
После
обработки первого символа «S», переменные Low и High равны 0.5 и 1, соответственно.
Окончательным сжатым кодом всего входного файла будет число из этого интервала ![]() . Для лучшего
понимания процесса кодирования хорошо представить себе, что новый интервал
. Для лучшего
понимания процесса кодирования хорошо представить себе, что новый интервал ![]() делится между пятью
символами нашего алфавита в той же пропорции, что и начальный интервал
делится между пятью
символами нашего алфавита в той же пропорции, что и начальный интервал ![]() . Результатом будет
пять подынтервалов
. Результатом будет
пять подынтервалов ![]() ,
,
![]() ,
, ![]() ,
, ![]() и
и ![]() . После поступления следующего
символа «V» выбирается четвертый интервал, который снова делится на пять
подынтервалов.
. После поступления следующего
символа «V» выбирается четвертый интервал, который снова делится на пять
подынтервалов.
|
Символ |
|
Вычисление переменных Low и High |
|
|
|
S |
L |
0.0 + (1.0 – 0.0) × 0.5 |
= |
0.5 |
|
|
Н |
0.0 + (1.0 – 0.0) × 1.0 |
= |
1.0 |
|
W |
L |
0.5 + (1.0 – 0.5) × 0.4 |
= |
0.70 |
|
|
Н |
0.5 + (1.0 – 0.5) × 0.5 |
= |
0.75 |
|
I |
L |
0.7 + (0.75 – 0.70) × 0.2 |
= |
0.71 |
|
|
Н |
0.7 + (0.75 – 0.70) × 0.4 |
= |
0.72 |
|
S |
L |
0.71 + (0.72 – 0.71) × 0.5 |
= |
0.715 |
|
|
Н |
0.71 + (0.72 – 0.71) × 1.0 |
= |
0.72 |
|
S |
L |
0.715 + (0.72 – 0.715) × 0.5 |
= |
0.7175 |
|
|
Н |
0.715 + (0.72 – 0.715) × 1.0 |
= |
0.72 |
|
- |
L |
0.7175 + (0.72 – 0.7175) × 0.0 |
= |
0.7175 |
|
|
Н |
0.7175 + (0.72 – 0.7175) × 0.1 |
= |
0.71775 |
|
М |
L |
0.7175 + (0.71775 – 0.7175) × 0.1 |
= |
0.717525 |
|
|
Н |
0.7175 + (0.71775 – 0.7175) × 0.2 |
= |
0.717550 |
|
I |
L |
0.717525 + (0.71755 – 0.717525) × 0.2 |
= |
0.717530 |
|
|
Н |
0.717525 + (0.71755 – 0.717525) × 0.4 |
= |
0.717535 |
|
S |
L |
0.717530 + (0.717535 – 0.717530) × 0.5 |
= |
0.7175325 |
|
|
Н |
0.717530 + (0.717535 – 0.717530) × 1.0 |
= |
0.717535 |
|
S |
L |
0.7175325 + (0.717535 – 0.7175325) × 0.5 |
= |
0.71753375 |
|
|
Н |
0.7175325 + (0.717535 – 0.7175325) × 1.0 |
= |
0.717535 |
Табл. 1.25. Процесс арифметического кодирования.
С каждым поступившим символом переменные Low и High пересчитываются по правилу:
![]() ;
;
![]() ;
;
где
![]() , a HighRange(X) и LowRange(X) обозначают верхний и нижний конец области символа
X. В нашем примере второй символ это «W»,
поэтому новые переменные будут
, a HighRange(X) и LowRange(X) обозначают верхний и нижний конец области символа
X. В нашем примере второй символ это «W»,
поэтому новые переменные будут ![]() ,
, ![]() . Новый интервал
. Новый интервал ![]() покрывает кусок
покрывает кусок ![]() подобласти символа «S». В табл. 1.25 приведены все
шаги, связанные с кодированием строки «SWISS_MISS». Конечный код - это последнее
значение переменной Low, равное 0.71753375, из которого
следует взять лишь восемь цифр 71753375 для записи в сжатый файл (другой выбор
кода будет обсуждаться позже).
подобласти символа «S». В табл. 1.25 приведены все
шаги, связанные с кодированием строки «SWISS_MISS». Конечный код - это последнее
значение переменной Low, равное 0.71753375, из которого
следует взять лишь восемь цифр 71753375 для записи в сжатый файл (другой выбор
кода будет обсуждаться позже).
Декодер
работает в обратном порядке. Сначала он узнаёт символы алфавита и считывает
табл. 1.24. Затем он читает цифру «7» и узнаёт, что весь код имеет вид 0.7...
Это число лежит внутри интервала ![]() символа «S». Значит, первый символ был S. Далее декодер удаляет эффект
символа S из кода с помощью вычитания
нижнего конца интервала S и деления на длину этого
интервала, равную 0.5. Результатом будет число 0.4350675, которое говорит
декодеру, что второй символ был «W»
(поскольку область «W» -
символа «S». Значит, первый символ был S. Далее декодер удаляет эффект
символа S из кода с помощью вычитания
нижнего конца интервала S и деления на длину этого
интервала, равную 0.5. Результатом будет число 0.4350675, которое говорит
декодеру, что второй символ был «W»
(поскольку область «W» - ![]() ).
).
Чтобы
удалить влияние символа X, декодер делает следующее преобразование над кодом: ![]() , где Range обозначает длину интервала
символа X. В табл. 1.26 отражен процесс декодирования рассмотренной строки.
, где Range обозначает длину интервала
символа X. В табл. 1.26 отражен процесс декодирования рассмотренной строки.
|
Символ |
Code-Low |
|
Область |
|
S |
0.71753375 – 0.5 |
= 0.21753375 |
/ 0.5 = 0.4350675 |
|
W |
0.4350675 – 0.4 |
= 0.0350675 |
/ 0.1 = 0.350675 |
|
I |
0.350675 – 0.2 |
= 0.150675 |
/ 0.2 = 0.753375 |
|
S |
0.753375 – 0.5 |
= 0.253375 |
/ 0.5 = 0.50675 |
|
S |
0.50675 – 0.5 |
= 0.00675 |
/ 0.5 = 0.0135 |
|
- |
0.0135 – 0 |
= 0.0135 |
/ 0.1 = 0.135 |
|
M |
0.135 – 0.1 |
= 0.035 |
/ 0.1 = 0.35 |
|
I |
0.35 – 0.2 |
= 0.15 |
/ 0.2 = 0.75 |
|
S |
0.75 – 0.5 |
= 0.25 |
/ 0.5 = 0.5 |
|
S |
0.5 – 0.5 |
= 0 |
/ 0.5 = 0 |
Табл. 1.26. Процесс арифметического декодирования.
Следующий пример имеет дело с тремя символами, вероятности которых приведены в табл. 1.27а. Заметим, что эти вероятности сильно отличаются друг от друга. Одна - большая, 0.975, а другие - существенно меньше. Это случай асимметричных вероятностей.
Кодирование
строки ![]() выдаёт
числа с точностью в 16 знаков, приведенные в табл. 1.28, в которой для каждого
символа в двух строках записаны последовательные значения Low и High.
выдаёт
числа с точностью в 16 знаков, приведенные в табл. 1.28, в которой для каждого
символа в двух строках записаны последовательные значения Low и High.
На первый взгляд кажется, что полученный код длиннее исходной строки, однако в § 1.7.3 показано, как правильно определять степень сжатия, достигаемого арифметическим кодированием.
Декодирование
этой строки показано в табл. 1.29. Оно обнаруживает особую проблему. После
удаления эффекта от ![]() в
строке 3 стоит число 0. Ранее мы неявно предполагали, что это означает конец
процесса декодирования, но теперь мы знаем, что еще имеется два символа
в
строке 3 стоит число 0. Ранее мы неявно предполагали, что это означает конец
процесса декодирования, но теперь мы знаем, что еще имеется два символа ![]() , которые следует
декодировать. Это показано в строках 4 и 5 таблицы. Эта проблема всегда
возникает, если последний символ входного файла является символом, чья область
начинается в нуле. Для того, чтобы различить такой символ и конец входного
файла, необходимо ввести один дополнительный символ «eof», обозначающий конец файла (end of file). Этот символ следует добавить в
таблицу частот, приписав ему маленькую вероятность (см. табл. 1.27b), и закодировать его в конце
входного файла.
, которые следует
декодировать. Это показано в строках 4 и 5 таблицы. Эта проблема всегда
возникает, если последний символ входного файла является символом, чья область
начинается в нуле. Для того, чтобы различить такой символ и конец входного
файла, необходимо ввести один дополнительный символ «eof», обозначающий конец файла (end of file). Этот символ следует добавить в
таблицу частот, приписав ему маленькую вероятность (см. табл. 1.27b), и закодировать его в конце
входного файла.
|
Симв. |
Вероятн. |
Область |
Симв. |
Вероятн. |
Область |
|
|
0.001838 |
|
eof |
0.000001 |
|
|
|
0.975 |
|
|
0.001837 |
|
|
|
0.023162 |
|
|
0.975 |
|
|
|
|
0.023162 |
|
||
|
(a) |
(b) |
||||
Табл. 1.27. (Асимметрические) вероятности трех символов.
|
|
0.0 + (1.0 – 0.0) × 0.023162 = 0.023162 |
|
|
0.0 + (1.0 – 0.0) × 0.998162 = 0.998162 |
|
|
0.023162 + 0.975 × 0.023162 = 0.04574495 |
|
|
0.023162 + 0.975 × 0.998162 = 0.99636995 |
|
|
0.04574495 + 0.950625 × 0.998162 = 0.99462270125 |
|
|
0.04574495 + 0.950625 × 1.0 = 0.99636995 |
|
|
0.99462270125 + 0.00174724875 × 0.0 = 0.99462270125 |
|
|
0.99462270125 + 0.00174724875 × 0.023162 = 0.994663171025547 |
|
|
0.99462270125 + 0.00004046977554749998 × 0.0 = 0.994 62270125 |
|
|
0.99462270125 + 0.00004046977554749998 × 0.023162 = 0.994623638 610941 |
Табл.
1.28. Кодирование строки ![]() .
.
|
Символ |
Code-Low |
|
Область |
|
|
0.99462270125 – 0.023162 |
= 0.97146170125 |
/ 0.975 = 0.99636995 |
|
|
0.99636995 – 0.023162 |
= 0.97320795 |
/ 0.975 = 0.998162 |
|
|
0.998162 – 0.998162 |
= 0.0 |
/ 0.00138 = 0.0 |
|
|
0.0 – 0.0 |
= 0.0 |
/ 0.023162 = 0.0 |
|
|
0.0 – 0.0 |
= 0.0 |
/ 0.023162 = 0.0 |
Табл.
1.29. Декодирование строки ![]() .
.
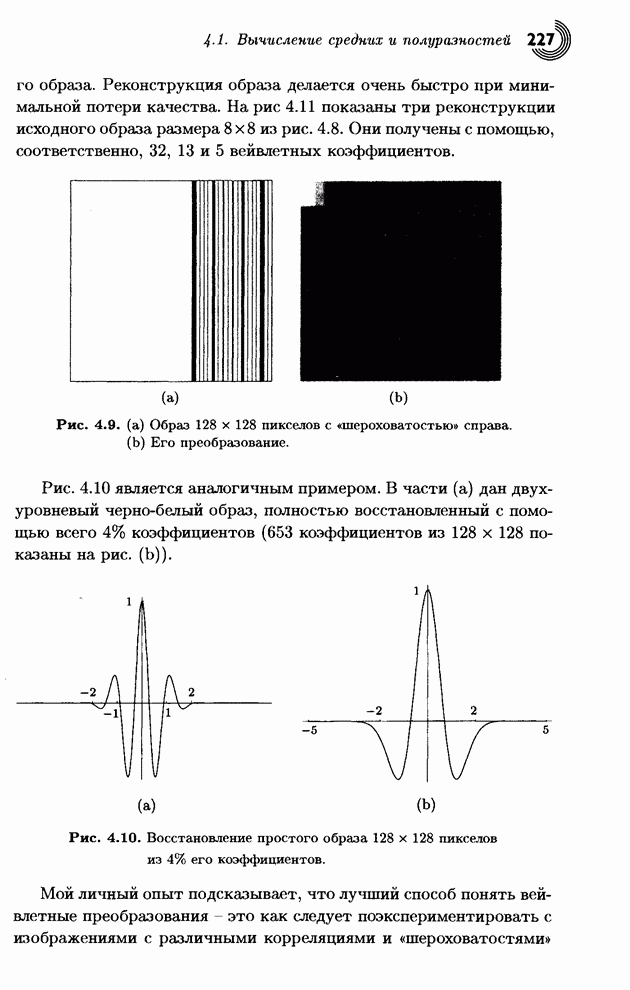
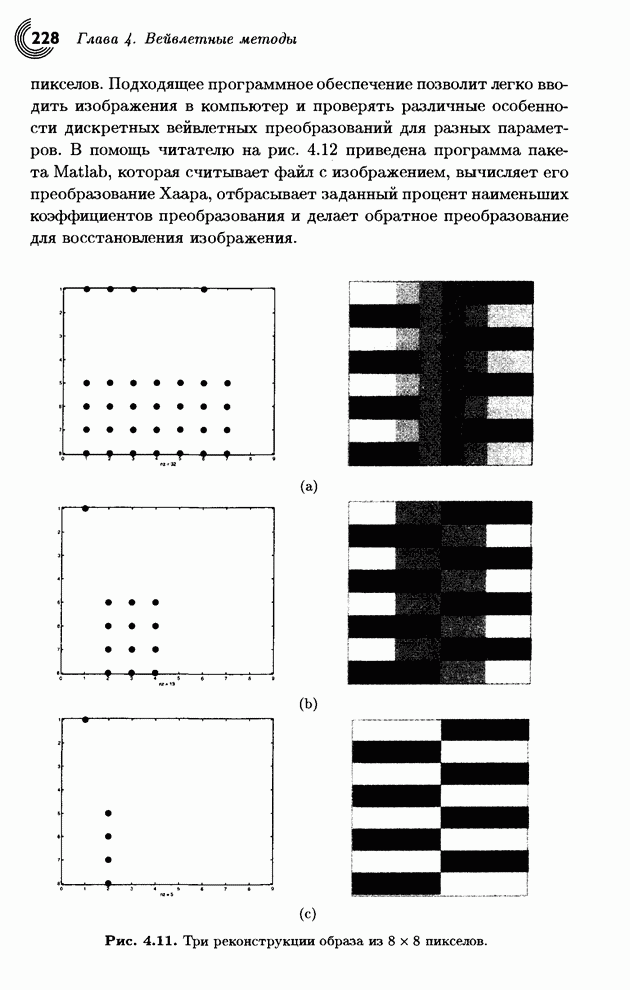
В
табл. 1.30 и 1.31 показано, как строка ![]() будет закодирована маленькой дробью
0.0000002878086184764172, а потом корректно декодирована. Без символа eof строка из одних
будет закодирована маленькой дробью
0.0000002878086184764172, а потом корректно декодирована. Без символа eof строка из одних ![]() была бы закодирована
числом 0.
была бы закодирована
числом 0.
Обратите
внимание на то, что нижнее значение было 0, пока не дошли до eof, а верхнее значение быстро
стремится к нулю. Как уже отмечалось, окончательным кодом может служить любое
число из промежутка от нижнего до верхнего конечного значения, а не обязательно
нижний конец. В примере с ![]() кодом может служить
более короткое число 0.0000002878086 (или 0.0000002878087, или даже
0.0000002878088).
кодом может служить
более короткое число 0.0000002878086 (или 0.0000002878087, или даже
0.0000002878088).
|
|
0.0 + (1.0 – 0.0) × 0.0 = 0.0 |
|
|
0.0 + (1.0 – 0.0) × 0.023162 = 0.023162 |
|
|
0.0 + 0.023162 × 0.0 = 0.0 |
|
|
0.0 + 0.023162 × 0.023162 = 0.000536478244 |
|
|
0.0 + 0.000536478244 × 0.0 = 0.0 |
|
|
0.0 + 0.000536478244 × 0.023162 = 0.000012425909087528 |
|
|
0.0 + 0.000012425909087528 × 0.0 = 0.0 |
|
|
0.0 + 0.000012425909087528 × 0.023162 = 0.0000002878089062853235 |
|
|
0.0 + 0.0000002878089062853235 × 0.999999 = 0.0000002878086184764172 |
|
|
0.0 + 0.0000002878089062853235 × 1.0 = 0.0000002878089062853235 |
Табл.
1.30. Кодирование строки ![]() .
.
(На рис. 1.32 приведена программа для системы Matematica, которая вычисляет табл. 1.28.)
|
Сим. |
Code-Low |
|
Область |
|
|
00000028780861847642 – 0 |
= 0.00000028780861847642 |
/0.023162 = 0.000012425896661618912 |
|
|
000012425896661618912 – 0 |
= 0.000012425896661618912 |
/0.023162 = 0.0005364777075218 |
|
|
0.0005364777075218 – 0 |
0.000536477707521756 |
/0.023162 = 0.023161976838 |
|
|
0.023161976838 – 0.0 |
= 0.023161976838 |
/0.023162 = 0.999999 |
|
|
0.999999 - 0.999999 |
= 0.0 |
/0.000001 – 0.0 |
Табл.
1.31. Декодирование строки ![]() .
.
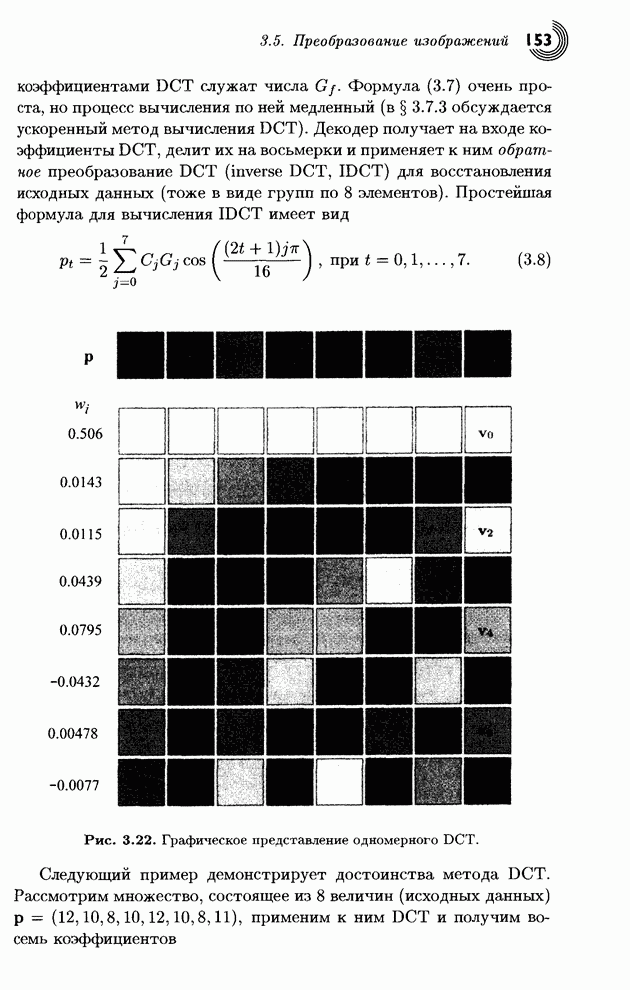
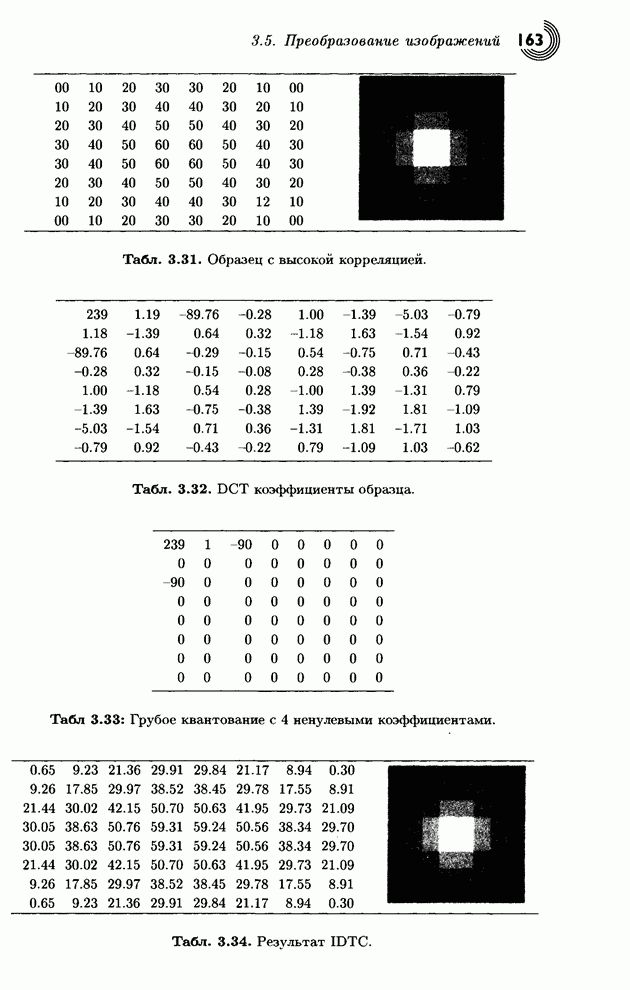
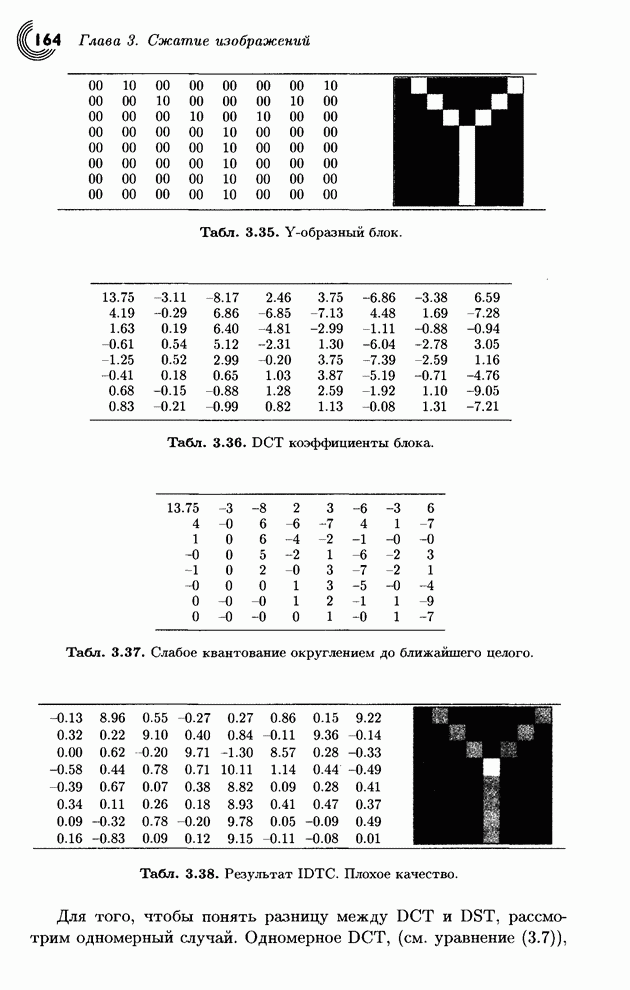
Пример: В табл. 1.33 приведены шаги
кодирования строки одинаковых символов ![]() . Из-за высокой вероятности символа
. Из-за высокой вероятности символа ![]() переменные Low и High начинаются с сильно
различающихся начальных значений и приближаются друг к другу достаточно
медленно.
переменные Low и High начинаются с сильно
различающихся начальных значений и приближаются друг к другу достаточно
медленно.
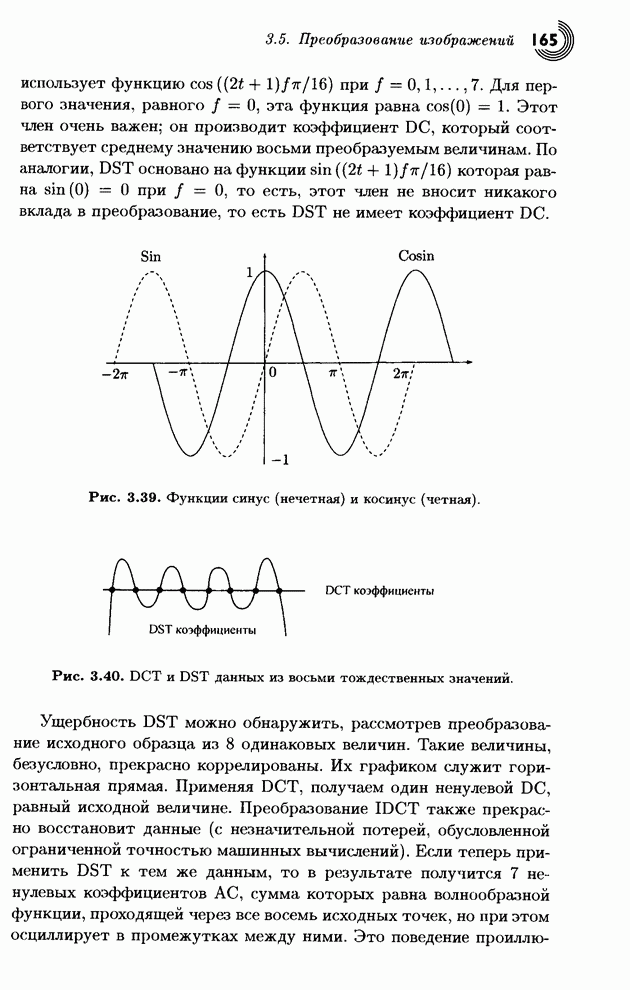
Если размер входного файла известен, тогда можно его кодировать без символа eof. Кодер может начать с записи его размера (в несжатом виде) в заголовок выходного файла. Декодер прочитает этот размер, начнет процесс декомпрессии и остановится после извлечения всех символов. Если декодер читает сжатый файл байт за байтом, то кодер может добавить в конце несколько нулевых битов, чтобы сжатый файл мог быть прочитан блоками по 8 бит.

Рис. 1.32. Программа для вычисления табл. 1.28.
|
|
0.0 + (1.0 – 0.0) × 0.023162 |
= |
0.023162 |
|
|
0.0 + (1.0 – 0.0) × 0.998162 |
= |
0.998162 |
|
|
0.023162 + 0.975 × 0.023162 |
= |
0.04574495 |
|
|
0.023162 + 0.975 × 0.998162 |
= |
0.99636995 |
|
|
0.04574495 + 0.950625 × 0.023162 |
= |
0.06776332625 |
|
|
0.04574495 + 0.950625 × 0.998162 |
= |
0.99462270125 |
|
|
0.06776332625 + 0.926859375 × 0.023162 |
= |
0.08923124309375 |
|
|
0.06776332625 + 0.926859375 × 0.998162 |
= |
0.99291913371875 |
Табл. 1.33.
Кодирование строки ![]() .
.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие переводчика
- Предисловие автора
- Введение
- Глава 1. Статистические методы
- 1.1. Энтропия
- 1.2. Коды переменной длины
- 1.3. Декодирование
- 1.4. Кодирование Хаффмана
- 1.4.1. Декодирование Хаффмана
- 1.4.2. Средняя длина кода
- 1.5. Адаптивные коды Хаффмана
- 1.5.1. Несжатые коды
- 1.5.2. Модификация дерева
- 1.5.3. Переполнение счетчика
- 1.5.4. Кодовое переполнение
- 1.5.5. Вариант алгоритма
- 1.6. Факсимильное сжатие
- 1.6.1. Одномерное кодирование
- 1.6.2. Двумерное кодирование
- 1.7. Арифметическое кодирование
- 1.7.1. Детали реализации метода
- 1.7.2. Потеря значащих цифр
- 1.7.3. Заключительные замечания
- 1.8. Адаптивное арифметическое кодирование
- ГЛАВА 2 СЛОВАРНЫЕ МЕТОДЫ
- 2.1. LZ77 (скользящее окно)
- 2.1.1. Циклическая очередь
- 2.2. LZSS
- 2.2.1. Недостатки
- 2.3. LZ78
- 2.4. LZW
- 2.4.1. Декодирование LZW
- 2.4.2. Структура словаря LZW
- 2.4.3. LZW в практических приложениях
- 2.5. Заключение
- ГЛАВА 3 СЖАТИЕ ИЗОБРАЖЕНИЙ
- 3.1. Введение
- 3.2. Типы изображений
- 3.3. Подходы к сжатию изображений
- 3.3.1. Коды Грея
- 3.3.2. Метрики ошибок
- 3.4. Интуитивные методы
- 3.4.1. Подвыборка
- 3.4.2. Квантование
- 3.5. Преобразование изображений
- 3.5.1. Ортогональные преобразования
- 3.5.2. Матричные преобразования
- 3.5.3. Дискретное косинус-преобразование
- 3.5.4. Пример
- 3.5.5. Дискретное синус-преобразование
- 3.5.6. Преобразование Уолша-Адамара
- 3.5.7. Преобразование Хаара
- 3.5.8. Преобразование Кархунена-Лоэвэ
- 3.6. Прогрессирующее сжатие изображений
- 3.7. JPEG
- 3.7.1. Светимость
- 3.7.2. DCT
- 3.7.3. Практическое DCT
- 3.7.4. Квантование
- 3.7.5. Кодирование
- 3.7.6. Мода без потери данных
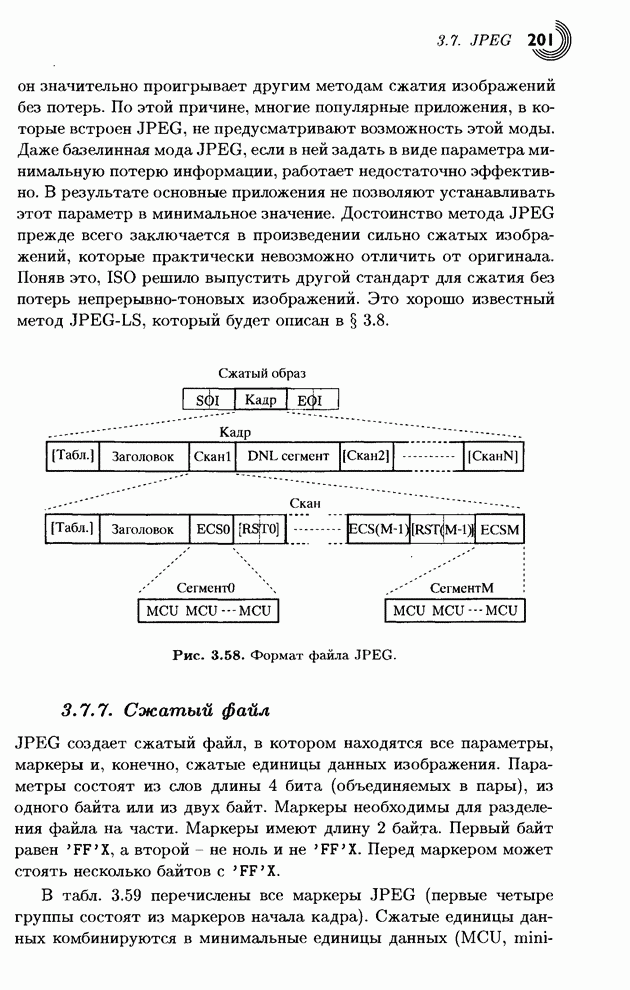
- 3.7.7. Сжатый файл
- 3.7.8. JFIF
- 3.8. JPEG-LS
- 3.8.1. Коды Голомба
- 3.8.2. Основы метода JPEG-LS
- 3.8.3. Кодер
- ГЛАВА 4 ВЕЙВЛЕТНЫЕ МЕТОДЫ
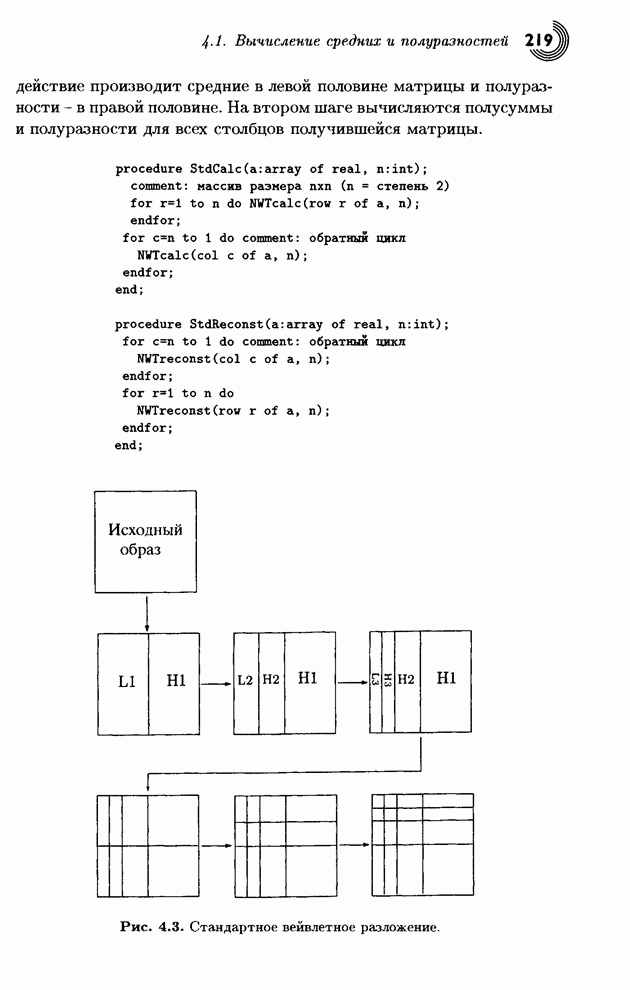
- 4.1. Вычисление средних и полу разностей
- 4.1.1. Обобщение на двумерный случай
- 4.1.2. Свойства преобразования Хаара
- 4.2. Преобразование Хаара
- 4.2.1. Матричная форма
- 4.3. Поддиапазонные преобразования
- 4.4. Банк фильтров
- 4.5. Нахождение коэффициентов фильтра
- 4.6. Преобразование DWT
- 4.7. Примеры
- 4.8. Вейвлеты Добеши
- 4.9. SPIHT
- 4.9.1. Алгоритм сортировки разделением множеств
- 4.9.2. Пространственно ориентированное дерево
- 4.9.3. Кодирование в алгоритме SPIHT
- 4.9.4. Пример
- 4.9.5. QTCQ
- ГЛАВА 5 СЖАТИЕ ВИДЕО
- 5.1. Основные принципы
- 5.2. Методы подоптимального поиска
- ГЛАВА 6 СЖАТИЕ ЗВУКА
- 6.1. Звук
- 6.2. Оцифрованный звук
- 6.3. Органы слуха человека
- 6.4. Общепризнанные методы
- 6.5. Сжатие звука в стандарте MPEG-1
- 6.5.1. Кодирование частотной области
- 6.5.2. Формат сжатых данных
- 6.5.3. Психоакустические модели
- 6.5.4. Кодирование: слой III
- Литература
- Глоссарий