| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
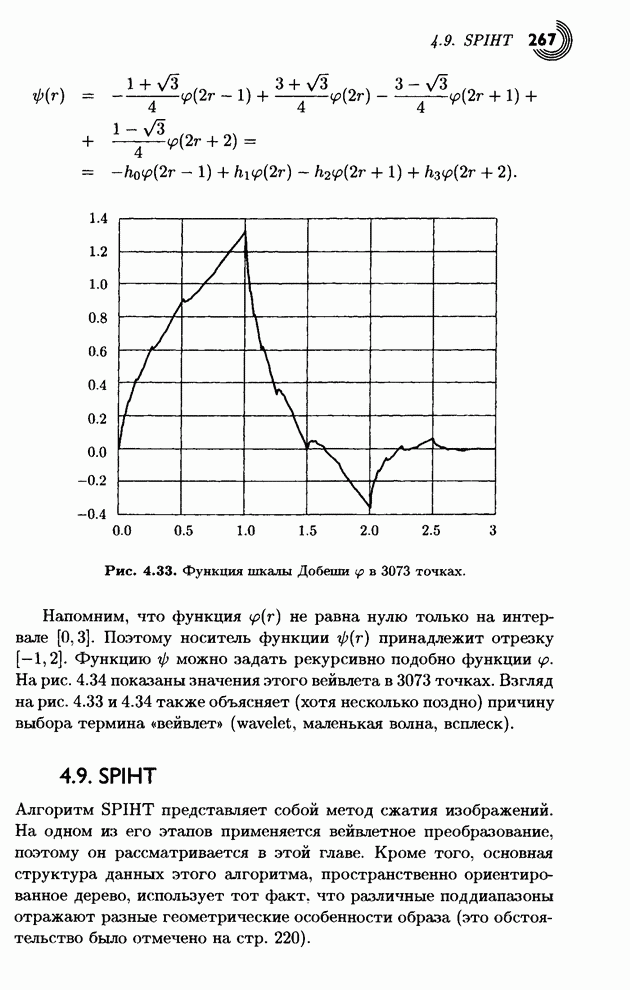
4.9.3. Кодирование в алгоритме SPIHT
Прежде всего отметим, что кодер и
декодер должны использовать единый тест при проверке множеств на
существенность. Алгоритм кодирования использует три списка, которые называются:
список существенных пикселов (LSP,
list of significant pixels), список несущественных
пикселов (LIP, list of insignificant pixels) и список несущественных
множеств (LIS, list of insignificant sets). В эти списки заносятся
координаты ![]() так,
что в списках LIP и LSP они представляют индивидуальные коэффициенты, а в
списке LIS они представляют или множество
так,
что в списках LIP и LSP они представляют индивидуальные коэффициенты, а в
списке LIS они представляют или множество ![]() (запись типа
(запись типа ![]() ), или множество
), или множество ![]() (запись типа
(запись типа ![]() ).
).
Список LIP содержит координаты коэффициентов, которые были
несущественными на предыдущей стадии сортировки. В текущей стадии они
проверяются, и если множество является существенным, то они перемещаются в
список LSP. Аналогично множества из LIS тестируются в последовательном
порядке, и если обнаруживается, что множество стало существенным, то оно
удаляется из LIS и разделяется. Новые
подмножества, состоящие более чем из одного элемента, помещаются обратно в
список LIS, где они позже будут подвергнуты
тестированию, а одноэлементные подмножества проверяются и добавляются в список LSP или LIP в зависимости от результатов теста. Стадия поправки
передает ![]() -ный
самый старший бит записей из списка LSP.
-ный
самый старший бит записей из списка LSP.
На рис 4.38 показаны детали алгоритма. На рис. 4.39 дана упрощенная версия этого алгоритма.
|
1.
Инициализация: Присвоить переменной 2. Сортировка:
2.1. для каждой записи
2.1.1. выдать на выход
2.1.2. если
2.2. для каждой записи
2.2.1. если запись типа
- выдать на выход
- если
* для каждого
- выдать на выход
- если
- если
* если 2.2.2
если запись
имеет тип
- выдать на выход
- если
* добавить каждую
* удалить 3.
Поправка: для каждой записи 4.
Цикл: уменьшить |
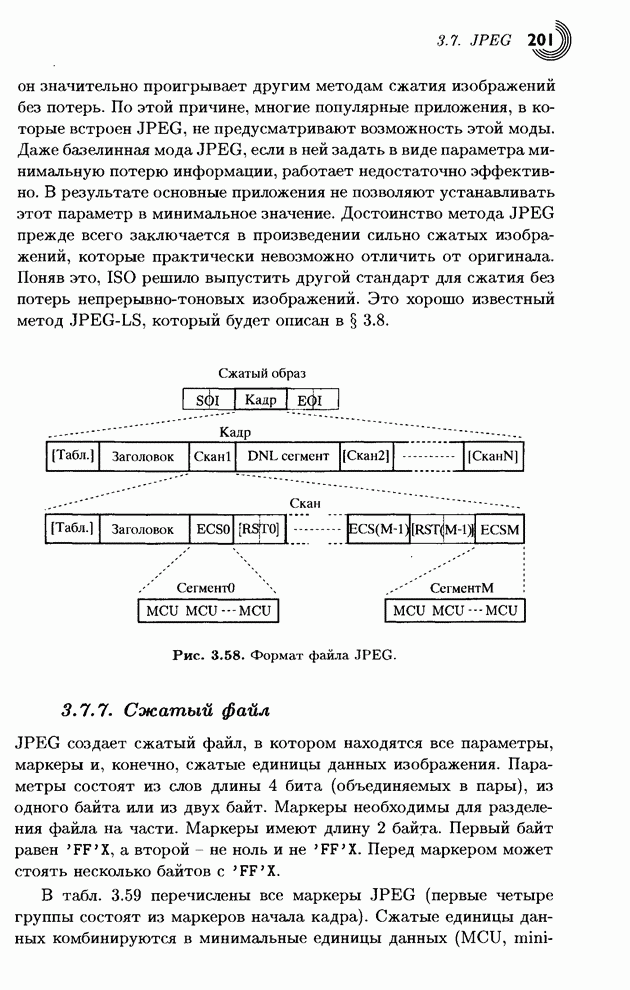
Рис. 4.38. Алгоритм кодирования SPIHT.
Декодер работает по алгоритму рис. 4.38. Он всегда действует синхронно с кодером, и следующие замечания проясняют совершаемые действия.
1.
Шаг 2.2 алгоритма выполняется для всех записей списка LIS. Однако шаг 2.2.1 добавляет некоторые записи в LIS (типа ![]() ), а шаг 2.2.2 добавляет другие
записи в LIS (типа
), а шаг 2.2.2 добавляет другие
записи в LIS (типа ![]() ). Важно понять, что эти
действия применяются ко всем записям шага 2.2 в одной итерации.
). Важно понять, что эти
действия применяются ко всем записям шага 2.2 в одной итерации.
2.
Величина ![]() уменьшается
после каждой итерации, но это не обязательно должно продолжаться до нулевого
значения. Цикл можно остановить после любой итерации, в результате произойдет
сжатие с частичной потерей данных. Обычно пользователь сам определяет число
совершаемых итераций, но он может также задавать допустимый порог отклонения сжатого
изображения оригинала (в единицах MSE),
а декодер сам определит необходимое число итераций, исходя из уравнений (4.15).
уменьшается
после каждой итерации, но это не обязательно должно продолжаться до нулевого
значения. Цикл можно остановить после любой итерации, в результате произойдет
сжатие с частичной потерей данных. Обычно пользователь сам определяет число
совершаемых итераций, но он может также задавать допустимый порог отклонения сжатого
изображения оригинала (в единицах MSE),
а декодер сам определит необходимое число итераций, исходя из уравнений (4.15).
3.
Кодер знает точные значения вейвлетных коэффициентов ![]() и использует их для
определения битов
и использует их для
определения битов ![]() (уравнение
(4.16)), которые будут посылаться в канал связи (или записываться в сжатый
файл). Эти биты будут подаваться на вход декодера, который будет их
использовать для вычисления значений
(уравнение
(4.16)), которые будут посылаться в канал связи (или записываться в сжатый
файл). Эти биты будут подаваться на вход декодера, который будет их
использовать для вычисления значений ![]() . Алгоритм, выполняемый декодером, в точности
совпадает с алгоритмом рис. 4.38, но слово «выход» следует заменить на «вход».
. Алгоритм, выполняемый декодером, в точности
совпадает с алгоритмом рис. 4.38, но слово «выход» следует заменить на «вход».
4.
Отсортированная информация, ранее обозначаемая ![]() , восстанавливается, когда координаты
существенных коэффициентов добавляются в список LSP на шаге 2.1.2 и 2.2.1. Это означает, что вейвлетные
коэффициенты с координатами из списка LSP,
упорядочены в соответствии с условием
, восстанавливается, когда координаты
существенных коэффициентов добавляются в список LSP на шаге 2.1.2 и 2.2.1. Это означает, что вейвлетные
коэффициенты с координатами из списка LSP,
упорядочены в соответствии с условием
![]()
для всех значений ![]() . Декодер
восстанавливает этот порядок, так как все три списка (LIS, LIP и LSP) обновляются в той же последовательности, в которой
это делает кодер (напомним, что декодер работает синхронно с кодером). Когда
декодер вводит данные, эти три списка идентичны спискам кодер в тот момент,
когда он выводит эти данные.
. Декодер
восстанавливает этот порядок, так как все три списка (LIS, LIP и LSP) обновляются в той же последовательности, в которой
это делает кодер (напомним, что декодер работает синхронно с кодером). Когда
декодер вводит данные, эти три списка идентичны спискам кодер в тот момент,
когда он выводит эти данные.
5.
Кодер начинает работать с готовыми коэффициентами ![]() вейвлетного преобразования образа; он
никогда не «видел» настоящего изображения. А декодер должен показывать
изображение и обновлять его после каждой итерации. При каждой итерации, когда
координаты
вейвлетного преобразования образа; он
никогда не «видел» настоящего изображения. А декодер должен показывать
изображение и обновлять его после каждой итерации. При каждой итерации, когда
координаты ![]() коэффициента
коэффициента
![]() помещаются
в список LSP в качестве записи, становится
известно (и кодеру и декодеру), что
помещаются
в список LSP в качестве записи, становится
известно (и кодеру и декодеру), что ![]() .
.
|
1. Установить
порог. Поместить в LIP коэффициенты всех корневых узлов.
Поместить в LIS все деревья
(присвоив им тип 2. Сортировка: Проверить все коэффициенты из LSP на существенность: 2.1. Если он существенный, то выдать на выход 1, затем выдать на выход бит знака и переместить этот коэффициент в LSP. 2.2. Если он несущественный, то выдать на выход 0. 3. Проверить на существенность все деревья из LIS в соответствии с типом дерева: 3.1. Для
деревьев типа 3.1.1. Если оно существенное, то выдать на выход 1 и закодировать его первых потомков: 3.1.1.1. Если первый потомок существенный, то выдать на выход 1, затем выдать на выход бит знака и добавить его в список LSP. 3.1.1.2. Если первый потомок несущественный, то выдать на выход 0 и добавить его в LIP.
3.1.1.3. Если этот потомок имеет прямых потомков, переместить дерево в конец
списка LIP, присвоив ему
тип 3.1.2. Если оно несущественное, то выдать на выход 0. 3.2. Для
деревьев типа
3.2.1. Если оно существенное, то выдать на выход 1, добавить всех первых
потомков в конец списка LIS в виде записи с типом 3.2.2. Если оно несущественное, то выдать на выход 0. 4. Цикл: уменьшить порог на единицу и перейти к шагу 2, если необходимо. |
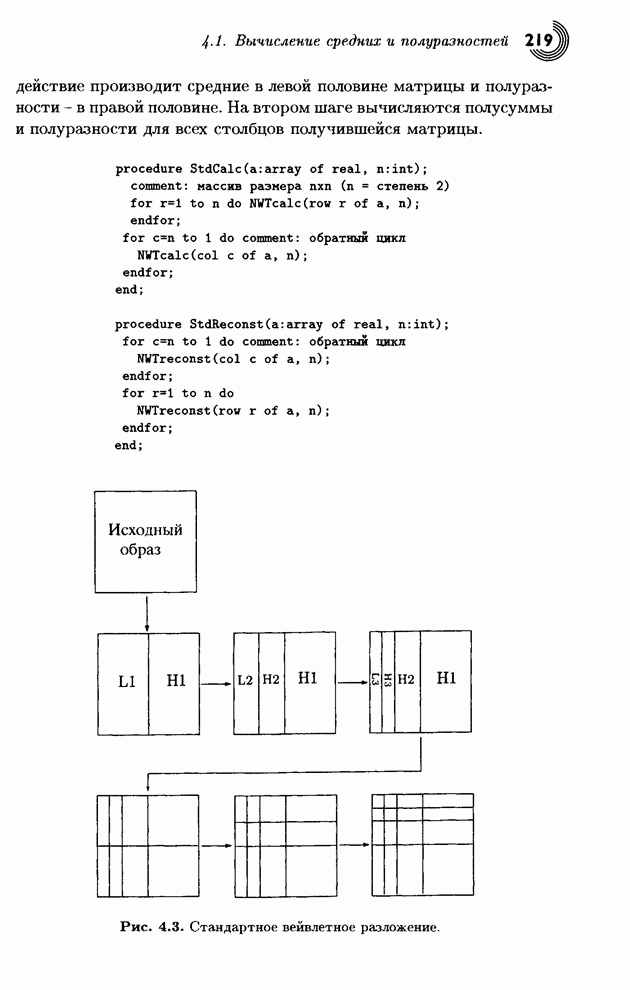
Рис. 4.39. Упрошенный алгоритм кодирования SPIHT.
В
результате, лучшим приближенным значением ![]() этого коэффициента может служить
середина между числами
этого коэффициента может служить
середина между числами ![]() и
и ![]() . Тогда декодер устанавливает
. Тогда декодер устанавливает ![]() (знак числа
(знак числа ![]() вводится декодером
сразу после вставки). Во время этапа поправки, когда декодер вводит истинное
значение
вводится декодером
сразу после вставки). Во время этапа поправки, когда декодер вводит истинное
значение ![]() -го
бита коэффициента
-го
бита коэффициента ![]() ,
он исправляет значение
,
он исправляет значение ![]() , добавляя к нему
, добавляя к нему ![]() , если вводимый бит равен 1,
или вычитая
, если вводимый бит равен 1,
или вычитая ![]() ,
если этот бит равен 0. Таким образом, декодер способен улучшать показываемое
зрителю изображение (уменьшать его расхождение с оригиналом) после прохождения
каждого из этапов: сортировки и поправки.
,
если этот бит равен 0. Таким образом, декодер способен улучшать показываемое
зрителю изображение (уменьшать его расхождение с оригиналом) после прохождения
каждого из этапов: сортировки и поправки.
Производительность алгоритма SPIHT можно повысить с помощью
энтропийного кодирования выхода, но из опытов известно, что это вносит весьма
незначительное улучшение, которое не покрывают временные расходы на его
выполнение кодером и декодером. Оказывается, что распределение знаков и
индивидуальных битов вейвлетных коэффициентов, производимых на каждой итерации,
близко к равномерному, поэтому энтропийное кодирование не дает эффекта сжатия.
С другой стороны, биты ![]() и
и ![]() распределены неравномерно и это может
дать выигрыш при таком кодировании.
распределены неравномерно и это может
дать выигрыш при таком кодировании.

Рис. 4.40. Шестнадцать коэффициентов и пространственно ориентированное дерево.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие переводчика
- Предисловие автора
- Введение
- Глава 1. Статистические методы
- 1.1. Энтропия
- 1.2. Коды переменной длины
- 1.3. Декодирование
- 1.4. Кодирование Хаффмана
- 1.4.1. Декодирование Хаффмана
- 1.4.2. Средняя длина кода
- 1.5. Адаптивные коды Хаффмана
- 1.5.1. Несжатые коды
- 1.5.2. Модификация дерева
- 1.5.3. Переполнение счетчика
- 1.5.4. Кодовое переполнение
- 1.5.5. Вариант алгоритма
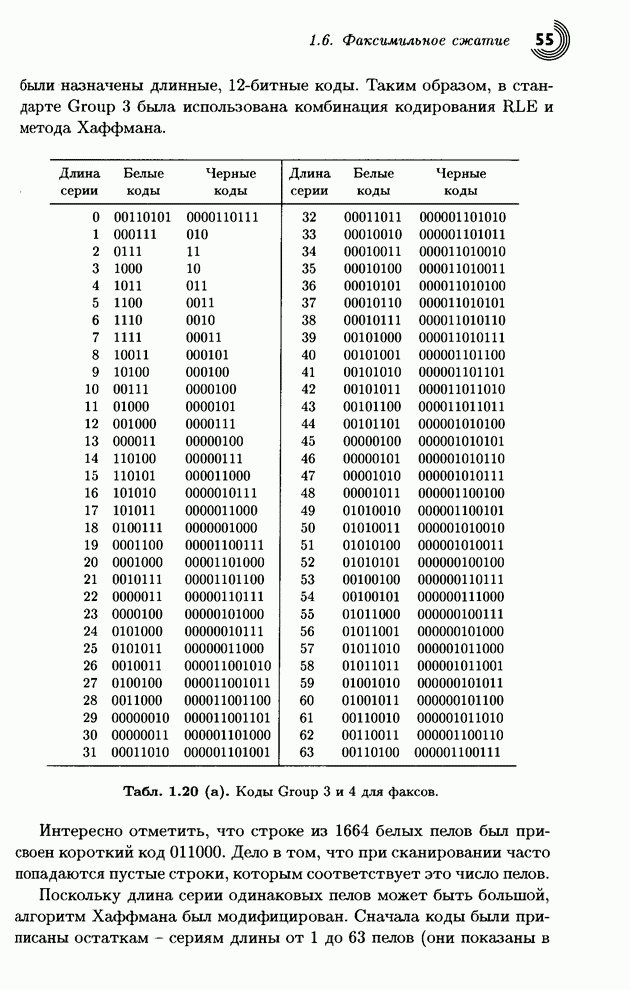
- 1.6. Факсимильное сжатие
- 1.6.1. Одномерное кодирование
- 1.6.2. Двумерное кодирование
- 1.7. Арифметическое кодирование
- 1.7.1. Детали реализации метода
- 1.7.2. Потеря значащих цифр
- 1.7.3. Заключительные замечания
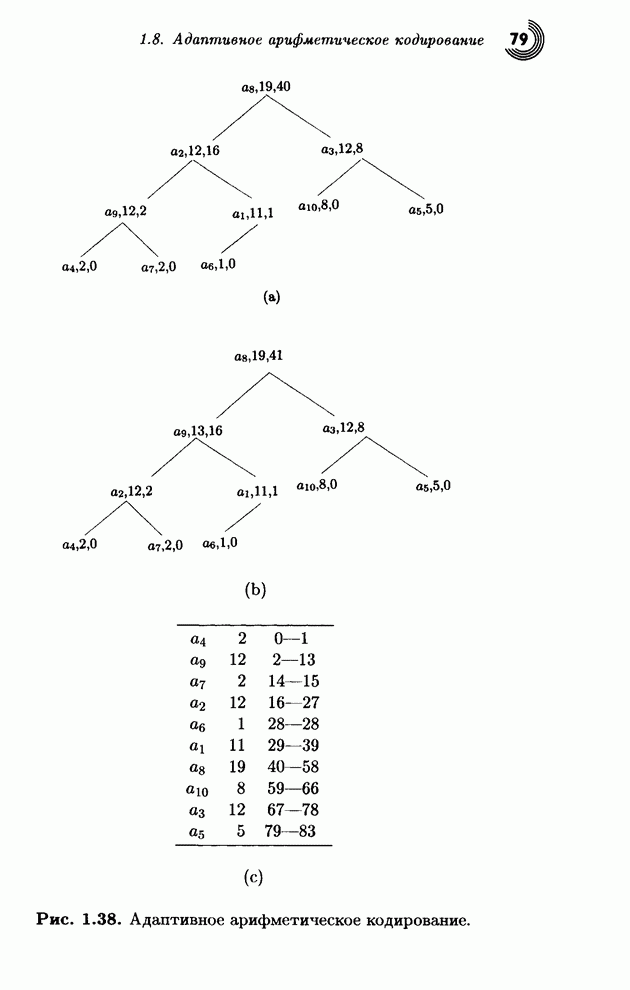
- 1.8. Адаптивное арифметическое кодирование
- ГЛАВА 2 СЛОВАРНЫЕ МЕТОДЫ
- 2.1. LZ77 (скользящее окно)
- 2.1.1. Циклическая очередь
- 2.2. LZSS
- 2.2.1. Недостатки
- 2.3. LZ78
- 2.4. LZW
- 2.4.1. Декодирование LZW
- 2.4.2. Структура словаря LZW
- 2.4.3. LZW в практических приложениях
- 2.5. Заключение
- ГЛАВА 3 СЖАТИЕ ИЗОБРАЖЕНИЙ
- 3.1. Введение
- 3.2. Типы изображений
- 3.3. Подходы к сжатию изображений
- 3.3.1. Коды Грея
- 3.3.2. Метрики ошибок
- 3.4. Интуитивные методы
- 3.4.1. Подвыборка
- 3.4.2. Квантование
- 3.5. Преобразование изображений
- 3.5.1. Ортогональные преобразования
- 3.5.2. Матричные преобразования
- 3.5.3. Дискретное косинус-преобразование
- 3.5.4. Пример
- 3.5.5. Дискретное синус-преобразование
- 3.5.6. Преобразование Уолша-Адамара
- 3.5.7. Преобразование Хаара
- 3.5.8. Преобразование Кархунена-Лоэвэ
- 3.6. Прогрессирующее сжатие изображений
- 3.7. JPEG
- 3.7.1. Светимость
- 3.7.2. DCT
- 3.7.3. Практическое DCT
- 3.7.4. Квантование
- 3.7.5. Кодирование
- 3.7.6. Мода без потери данных
- 3.7.7. Сжатый файл
- 3.7.8. JFIF
- 3.8. JPEG-LS
- 3.8.1. Коды Голомба
- 3.8.2. Основы метода JPEG-LS
- 3.8.3. Кодер
- ГЛАВА 4 ВЕЙВЛЕТНЫЕ МЕТОДЫ
- 4.1. Вычисление средних и полу разностей
- 4.1.1. Обобщение на двумерный случай
- 4.1.2. Свойства преобразования Хаара
- 4.2. Преобразование Хаара
- 4.2.1. Матричная форма
- 4.3. Поддиапазонные преобразования
- 4.4. Банк фильтров
- 4.5. Нахождение коэффициентов фильтра
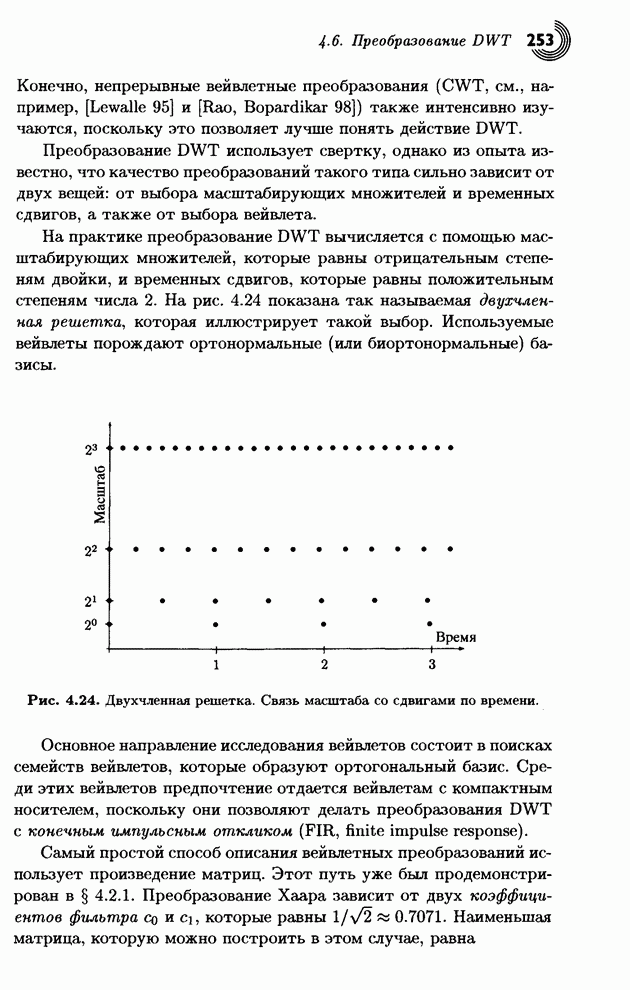
- 4.6. Преобразование DWT
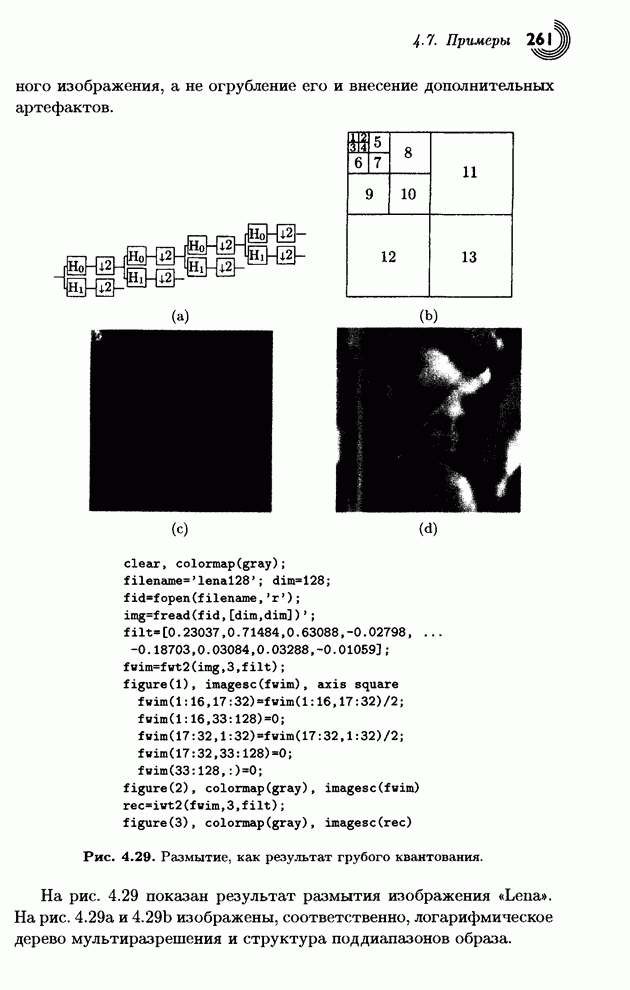
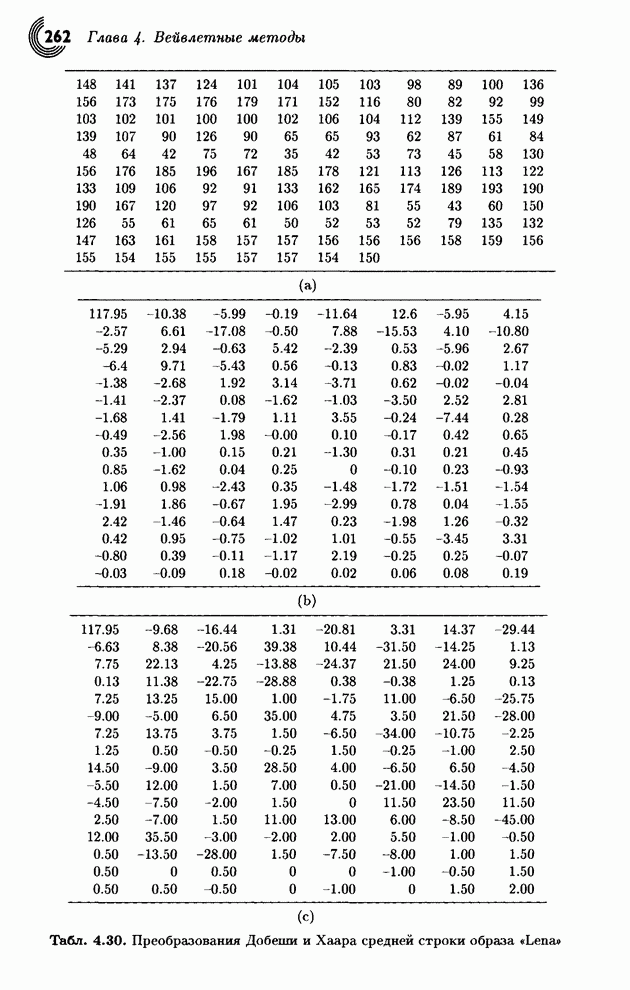
- 4.7. Примеры
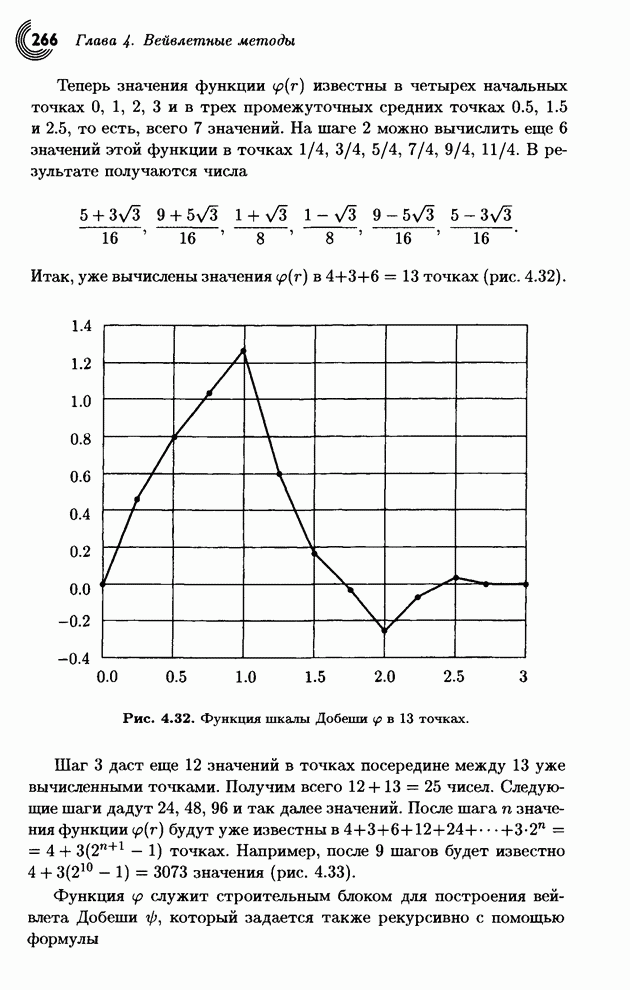
- 4.8. Вейвлеты Добеши
- 4.9. SPIHT
- 4.9.1. Алгоритм сортировки разделением множеств
- 4.9.2. Пространственно ориентированное дерево
- 4.9.3. Кодирование в алгоритме SPIHT
- 4.9.4. Пример
- 4.9.5. QTCQ
- ГЛАВА 5 СЖАТИЕ ВИДЕО
- 5.1. Основные принципы
- 5.2. Методы подоптимального поиска
- ГЛАВА 6 СЖАТИЕ ЗВУКА
- 6.1. Звук
- 6.2. Оцифрованный звук
- 6.3. Органы слуха человека
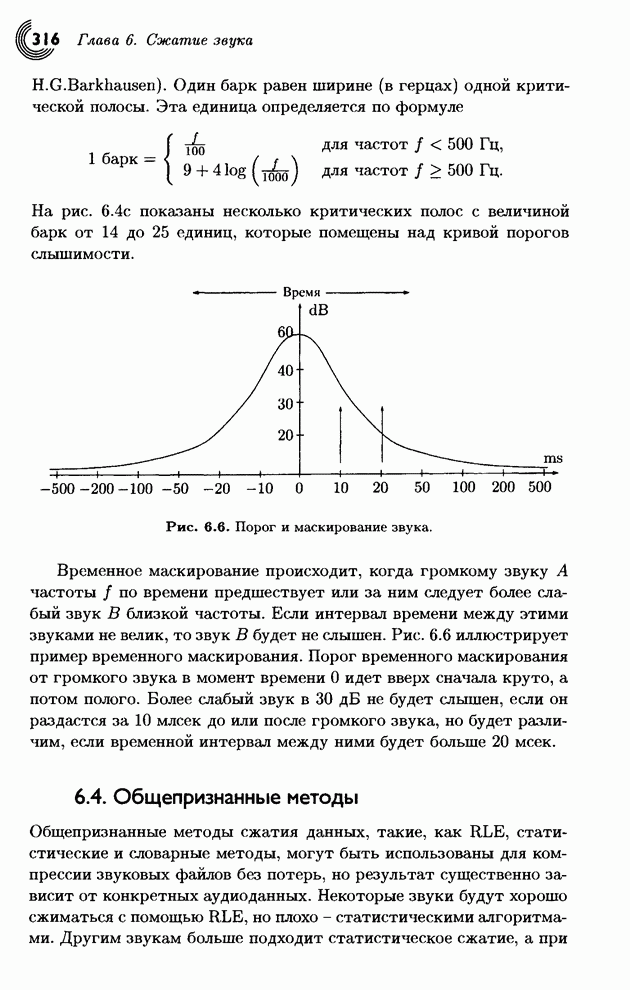
- 6.4. Общепризнанные методы
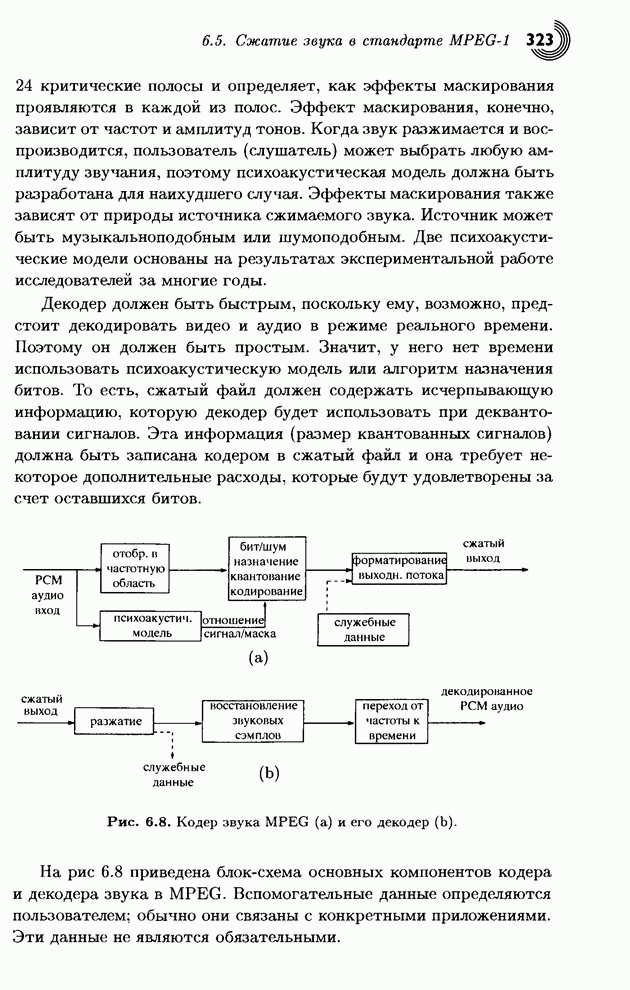
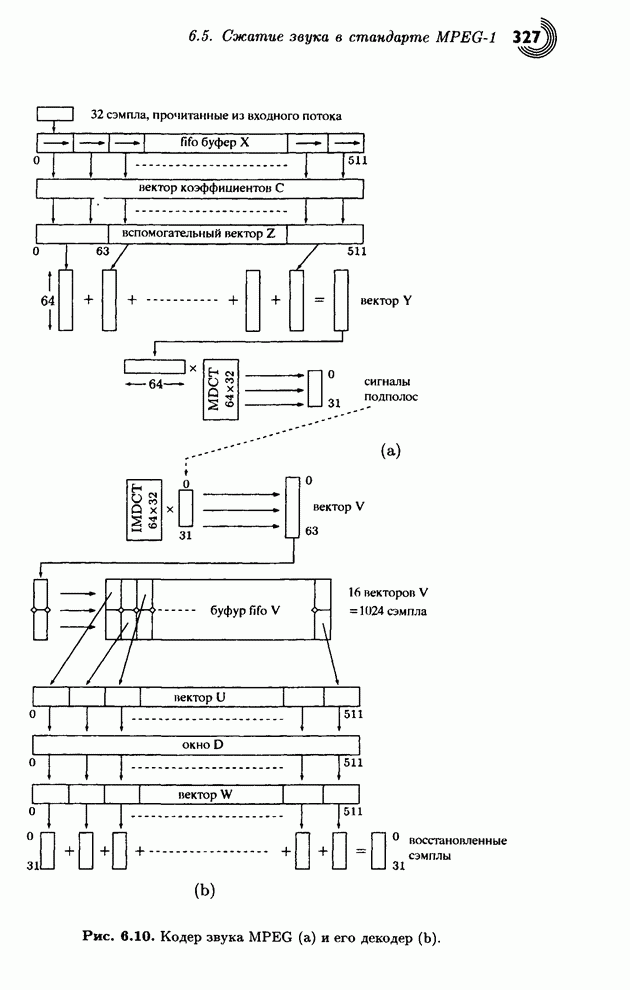
- 6.5. Сжатие звука в стандарте MPEG-1
- 6.5.1. Кодирование частотной области
- 6.5.2. Формат сжатых данных
- 6.5.3. Психоакустические модели
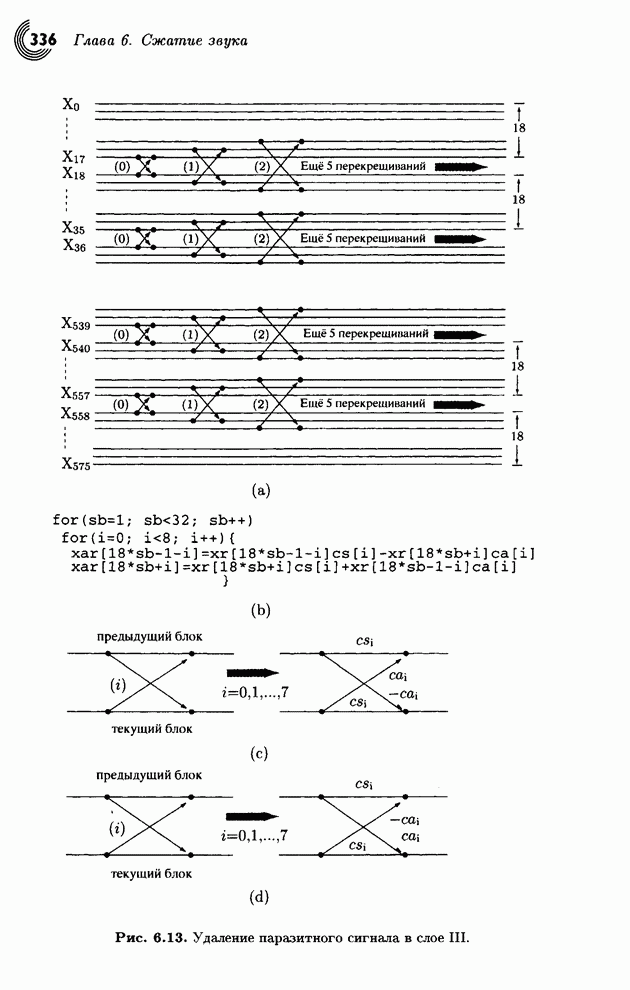
- 6.5.4. Кодирование: слой III
- Литература
- Глоссарий