| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
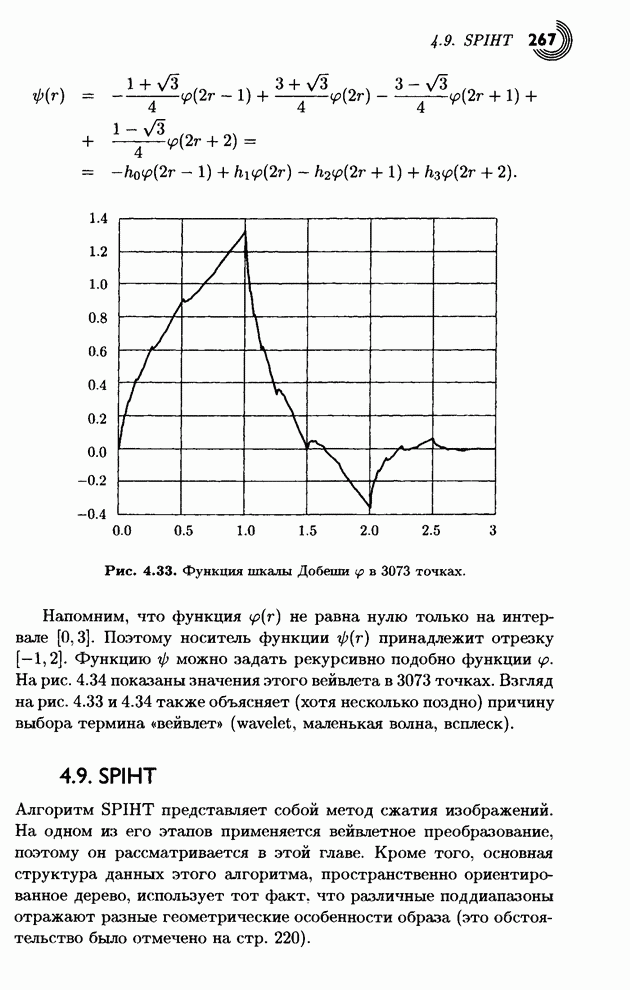
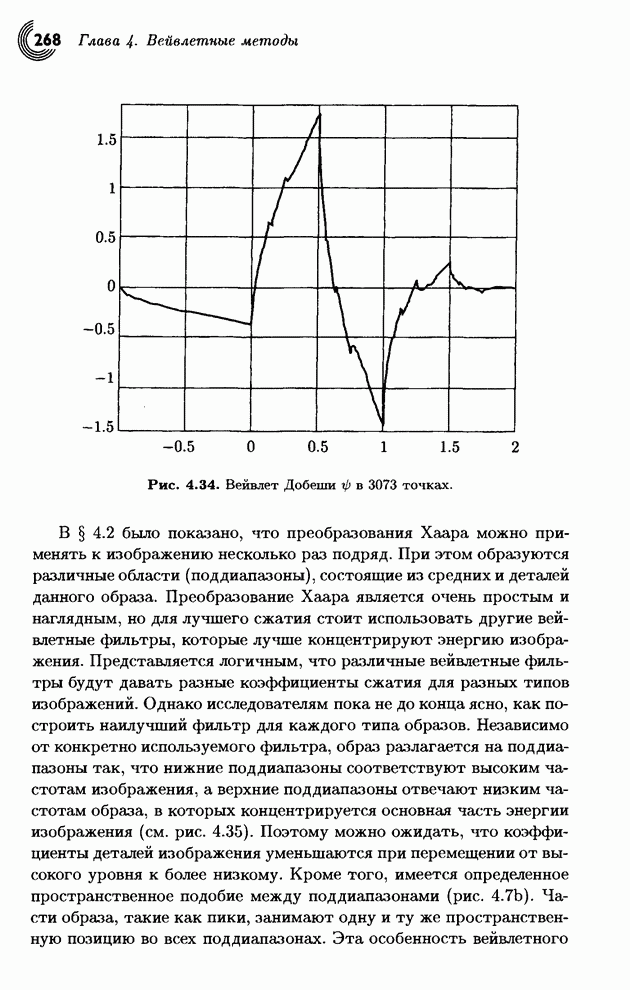
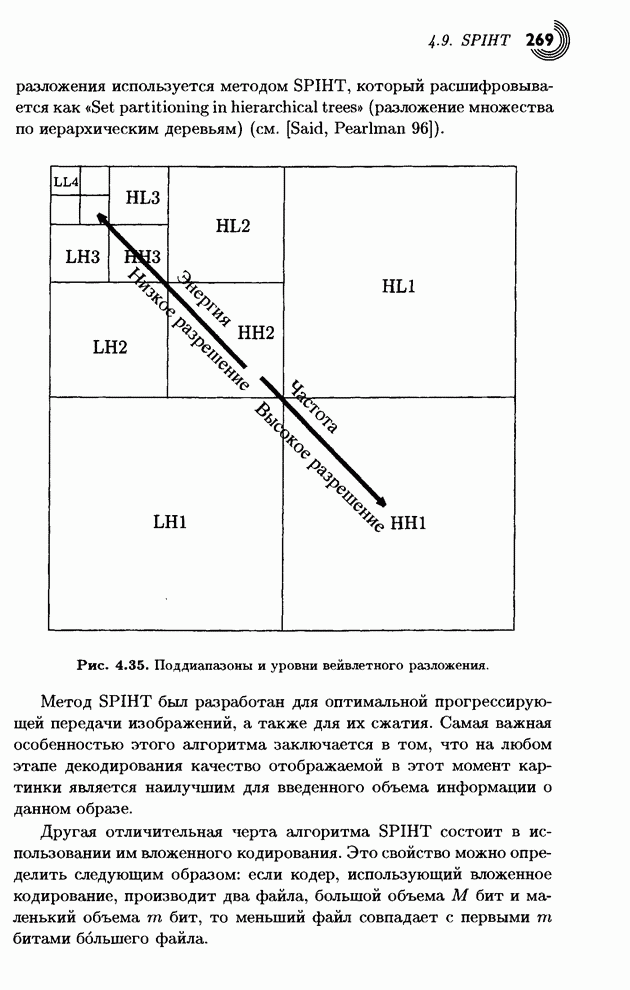
3.7.5. Кодирование
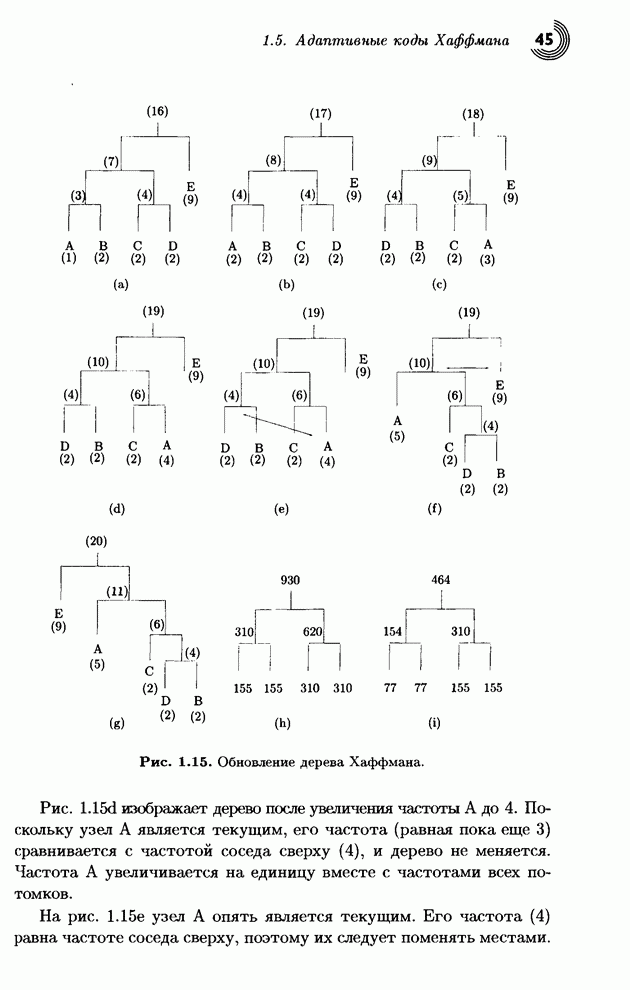
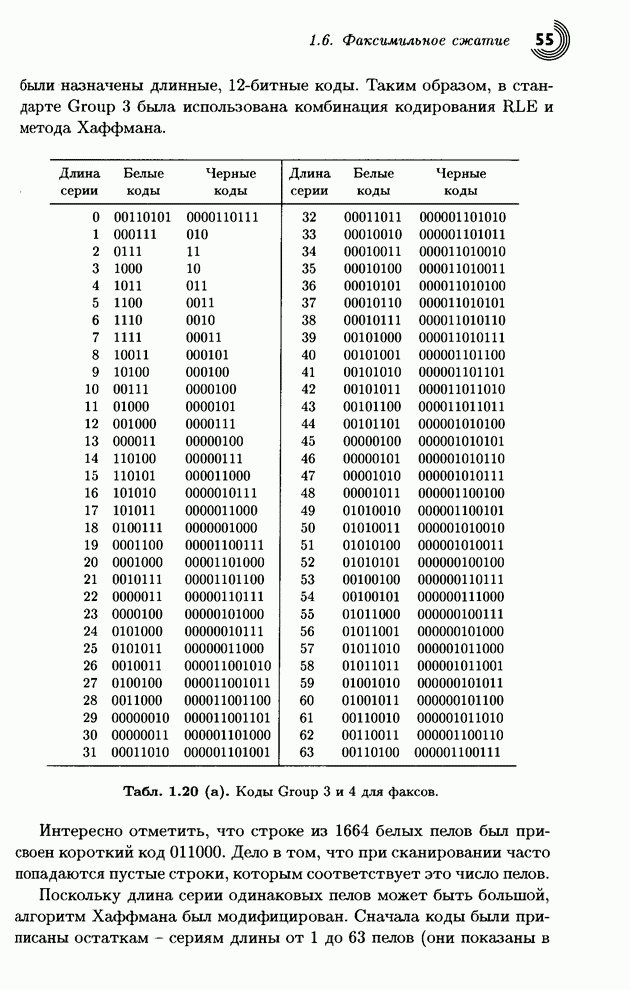
Прежде всего обсудим пункт 3 из конца предыдущего параграфа. Каждая матрица 8x8 квантованных коэффициентов DCT содержит коэффициент DC [в позиции (0,0) в левом верхнем углу], а также 63 коэффициента АС. Коэффициент DC равен среднему значению всех 64 пикселов исходной единицы. Наблюдения показывают, что при сжатии непрерывно-тоновых изображений, коэффициенты DC соседних единиц обычно являются коррелированными. Известно, что этот коэффициент равен сумме всех пикселов блока с некоторым общим множителем. Все это указывает на то, что коэффициенты DC близких блоков не должны сильно различаться. Поэтому JPEG записывает первый (закодированный) коэффициент DC, а затем кодирует разности коэффи циентов DC последовательных блоков.
Пример: Если первые три единицы данных размера
8x8 имеют квантованные коэффициенты DC
равные 1118, 1114 и
1119, то JPEG записывает для первого блока
число 1118 (закодированное по Хаффману, см. далее), за которым следует 63
закодированных коэффициента АС. Для второго блока на выходе будет стоять число ![]() (также кодированное
по Хаффману) впереди 63 (кодированных) коэффициента АС этого блока. Третьему
блоку будет соответствовать кодированная запись
(также кодированное
по Хаффману) впереди 63 (кодированных) коэффициента АС этого блока. Третьему
блоку будет соответствовать кодированная запись ![]() и следующие 63 коэффициента АС. Этот
путь также позволяет меньше беспокоиться о проблемах, связанных с
переполнением, так как разности обычно малы.
и следующие 63 коэффициента АС. Этот
путь также позволяет меньше беспокоиться о проблемах, связанных с
переполнением, так как разности обычно малы.
Кодирование разностей
коэффициентов DC совершается с помощью табл. 3.53.
В этой таблице записаны так называемые унарные коды, которые определяются
следующим образом. Унарный код неотрицательного целого числа ![]() состоит из строки в
состоит из строки в ![]() единиц, за которыми следует
один 0 или, наоборот,
единиц, за которыми следует
один 0 или, наоборот, ![]() нулей и одна 1. Длина унарного кода
целого числа
нулей и одна 1. Длина унарного кода
целого числа ![]() равна
равна
![]() бит.
бит.
Каждая строка табл. 3.53
начинается с ее номера (слева); в конце стоит унарный код строки, а между ними
располагаются некоторые числа. В каждой следующей строке записано больше чисел,
чем в предыдущей, но они отличаются от чисел всех предыдущих строк. В строке ![]() находятся числа из
интервала
находятся числа из
интервала ![]() ,
за вычетом чисел интервала
,
за вычетом чисел интервала ![]() . Длина строк растет очень быстро,
поэтому такие данные не удобно представлять в виде простого двумерного массива.
На самом деле, для их хранения не нужна никакая структура данных, поскольку
подходящая программа легко определит позицию числа
. Длина строк растет очень быстро,
поэтому такие данные не удобно представлять в виде простого двумерного массива.
На самом деле, для их хранения не нужна никакая структура данных, поскольку
подходящая программа легко определит позицию числа ![]() в таблице, анализируя биты
этого числа.
в таблице, анализируя биты
этого числа.
|
0: |
0 |
|
|
|
|
|
|
|
|
|
0 |
|
1: |
-1 |
1 |
|
|
|
|
|
|
|
|
10 |
|
2: |
-3 |
-2 |
2 |
3 |
|
|
|
|
|
|
110 |
|
3: |
-7 |
-6 |
-5 |
-4 |
4 |
5 |
6 |
7 |
|
|
1110 |
|
4: |
-15 |
-14 |
… |
-9 |
-8 |
8 |
9 |
10 |
… |
15 |
11110 |
|
5: |
-31 |
-30 |
-29 |
… |
-17 |
-16 |
16 |
17 |
… |
31 |
111110 |
|
6: |
-63 |
-62 |
-61 |
… |
-33 |
-32 |
32 |
33 |
… |
63 |
1111110 |
|
7: |
-127 |
-126 |
-125 |
… |
-65 |
-64 |
64 |
65 |
… |
127 |
11111110 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
14: |
-16383 |
-16382 |
-16381 |
… |
-8193 |
-8192 |
8192 |
8193 |
… |
16383 |
111111111111110 |
|
15: |
-32767 |
-32766 |
-32765 |
… |
-16385 |
-16384 |
16384 |
16385 |
… |
32767 |
1111111111111110 |
|
16: |
32768 |
|
|
|
|
|
|
|
|
|
1111111111111111 |
Табл. 3.53. Кодирование разностей коэффициентов DC.
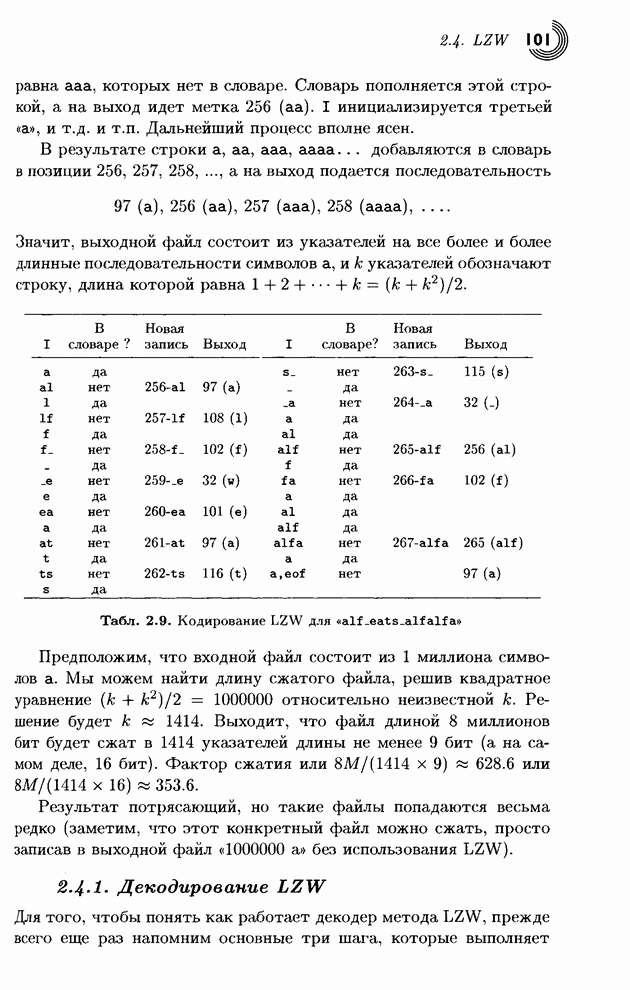
Первый коэффициент DC из нашего примера, который следует закодировать, равен 1118. Он находится в строке 11 и столбце 930 таблицы (столбцы занумерованы, начиная с нулевого). Тогда оно кодируется последовательностью 111111111110|01110100010 (унарный код строки 11, за которым следует двоичное представление числа 930 из 11 бит). Вторая разность коэффициентов DC, число -4, расположена в строке 3 и столбце 3; она кодируется в виде 1110|011 (унарный код строки 3 и число 3 в виде 3 бит). Третья разность 5 расположена в строке 3, столбец 5, поэтому ее кодом служит 1110|101.
Разберемся теперь с пунктом 2
предыдущего параграфа, когда надо кодировать 63 коэффициента АС. Это сжатие
использует кодирование RLE в сочетании с методом Хаффмана
или с арифметическим кодированием. Идея заключается в том, что в
последовательности коэффициентов АС, как правило, имеется всего несколько
ненулевых элементов, между которыми стоят серии нулей. Для каждого ненулевого
числа ![]() (1)
кодер определяет число Z предшествующих ему нулей; (2) затем
он находит число
(1)
кодер определяет число Z предшествующих ему нулей; (2) затем
он находит число ![]() в
табл. 3.53 и готовит номер строки и столбца (R и С); (3) пара пара (R, Z) (не (R, С)!) используется для нахождения соответствующего
числа по строке и столбцу в табл. 3.54; (4) наконец, полученный из этой таблицы
код Хаффмана присоединяется к С (где С записывается в виде R-битного числа); результатом этих
действий служит код, выдаваемый на выход кодером JPEG для этого АС коэффициента
в
табл. 3.53 и готовит номер строки и столбца (R и С); (3) пара пара (R, Z) (не (R, С)!) используется для нахождения соответствующего
числа по строке и столбцу в табл. 3.54; (4) наконец, полученный из этой таблицы
код Хаффмана присоединяется к С (где С записывается в виде R-битного числа); результатом этих
действий служит код, выдаваемый на выход кодером JPEG для этого АС коэффициента ![]() и всех предыдущих нулей.
(Можно перевести дух.)
и всех предыдущих нулей.
(Можно перевести дух.)
|
0: |
1010 |
|
|
11111111001 (ZRL) |
|
1: |
00 |
1100 |
… |
1111111111110101 |
|
2: |
01 |
11011 |
… |
1111111111110110 |
|
3: |
100 |
1111001 |
… |
1111111111110111 |
|
4: |
1011 |
111110110 |
… |
1111111111111000 |
|
5: |
11010 |
11111110110 |
… |
1111111111111001 |
|
|
|
|
|
|
Табл. 3.54. Кодирование коэффициентов АС.
В табл. 3.54 приведен некоторый произвольный код Хаффмана, не тот, который предлагается комитетом JPEG. А стандарт JPEG рекомендует использовать для этих целей коды из табл. 3.55 и 3.56. При этом разрешается использовать до четырех таблиц Хаффмана, за исключением моды базелины, когда можно использовать только две таблицы. Читатель обнаружит код ЕОВ в позиции (0,0) и код ZRL в позиции (0,15). Код ЕОВ означает конец блока, а код ZRL замещает 15 последовательных нулей, когда их число превышает 15. Эти коды рекомендованы для компонентов светимости (табл. 3.55). Коды ЕОВ и ZRL, рекомендованные для коэффициентов АС хроматических компонентов из табл. 3.56 равны 00 и 1111111010, соответственно.
Пример: Еще раз рассмотрим последовательность
![]()
Первый
АС коэффициент ![]() не
имеет перед собой нулей, то есть, для него
не
имеет перед собой нулей, то есть, для него ![]() . Он находится в табл. 3.53 в строке 2 и
столбце 2, поэтому, для него
. Он находится в табл. 3.53 в строке 2 и
столбце 2, поэтому, для него ![]() ,
, ![]() . Код Хаффмана из табл. 3.54 в позиции
. Код Хаффмана из табл. 3.54 в позиции ![]() равен 01. Значит,
окончательный код для
равен 01. Значит,
окончательный код для ![]() будет 01|10. Следующий ненулевой
коэффициент -2 имеет один предшествующий нуль, то есть, для него
будет 01|10. Следующий ненулевой
коэффициент -2 имеет один предшествующий нуль, то есть, для него ![]() . Он стоит в табл.
3.53 в строке 2 и столбце 1, тогда
. Он стоит в табл.
3.53 в строке 2 и столбце 1, тогда ![]() ,
, ![]() . Код Хаффмана из табл. 3.54 в позиции
. Код Хаффмана из табл. 3.54 в позиции ![]() равен 11011. В итоге
кодом числа -2 будет служить последовательность 11011|01. Последний ненулевой
коэффициент АС равен -1, ему предшествует 13 нулей, и
равен 11011. В итоге
кодом числа -2 будет служить последовательность 11011|01. Последний ненулевой
коэффициент АС равен -1, ему предшествует 13 нулей, и ![]() . Сам коэффициент расположен в
табл. 3.53 в строке 1 и столбце 0, то есть,
. Сам коэффициент расположен в
табл. 3.53 в строке 1 и столбце 0, то есть, ![]() ,
, ![]() . Пусть в табл. 3.54 в позиции
. Пусть в табл. 3.54 в позиции ![]() находится код
1110101. Тогда кодом для -1 будет 1110101|0.
находится код
1110101. Тогда кодом для -1 будет 1110101|0.
R
|
z |
1 6 |
2 7 |
3 8 |
4 9 |
5 A |
|
0 |
00 1111000 |
01 11111000 |
100 1111110110 |
1011 1111111110000010 |
11010 1111111110000011 |
|
1 |
1100 1111111110000100 |
11011 1111111110000101 |
11110001 1111111110000110 |
111110110 1111111110000111 |
11111110110 1111111110001000 |
|
2 |
11100 111111110001010 |
11111001 111111110001011 |
1111110111 111111110001100 |
111111110100 111111110001101 |
111111110001001 111111110001110 |
|
3 |
111010 1111111110010001 |
111110111 1111111110010010 |
111111110101 1111111110010011 |
111 1111110001111 1111111110010100 |
1111111110010000 1111111110010101 |
|
4 |
111011 1111111110011001 |
1111111000 1111111110011010 |
1111111110010110 1111111110011011 |
1111111110010111 1111111110011100 |
1111111110011000 1111111110011101 |
|
5 |
1111010 1111111110100001 |
11111110111 1111111110100010 |
1111111110011110 1111111110100011 |
1111111110011111 1111111110100100 |
1111111110100000 1111111110100101 |
|
6 |
1111011 1111111110101001 |
111111110110 1111111110101010 |
1111111110100110 1111111110101011 |
1111111110100111 1111111110101100 |
111111110101000 1111111110101101 |
|
7 |
11111010 1111111110110001 |
111111110111 1111111110110010 |
1111111110101110 1111111110110011 |
1111111110101111 1111111110110100 |
1111111110110000 1111111110110101 |
|
8 |
111111000 1111111110111001 |
111111111000000 1111111110111010 |
1111111110110110 1111111110111011 |
1111111110110111 1111111110111100 |
1111111110111000 1111111110111101 |
|
9 |
111111001 1111111111000010 |
1111111110111110 1111111111000011 |
1111111110111110 1111111111000011 |
1111111111000000 1111111111000101 |
1111111111000001 1111111111000110 |
|
A |
111111010 1111111111001011 |
1111111111000111 1111111111001100 |
1111111111001000 1111111111001101 |
1111111111001001 1111111111001110 |
1111111111001010 1111111111001111 |
|
В |
1111111001 1111111111010100 |
1111111111010000 1111111111010101 |
1111111111010001 1111111111010110 |
1111111111010010 1111111111010111 |
1111111111010011 1111111111011000 |
|
С |
1111111010 1111111111011101 |
1111111111011001 1111111111011110 |
1111111111011010 1111111111011111 |
1111111111011011 1111111111100000 |
1111111111011100 1111111111100001 |
|
D |
11111111000 1111111111100110 |
1111111111100010 1111111111100111 |
1111111111100011 1111111111101000 |
1111111111100100 1111111111101001 |
1111111111100101 1111111111101010 |
|
E |
1111111111101011 1111111111110000 |
1111111111101100 1111111111110001 |
1111111111101101 1111111111110010 |
1111111111101110 1111111111110011 |
1111111111101111 1111111111110100 |
|
F |
11111111001 1111111111111001 |
1111111111110101 1111111111111010 |
1111111111110110 1111111111111011 |
1111111111110111 1111111111111101 |
1111111111111000 1111111111111110 |
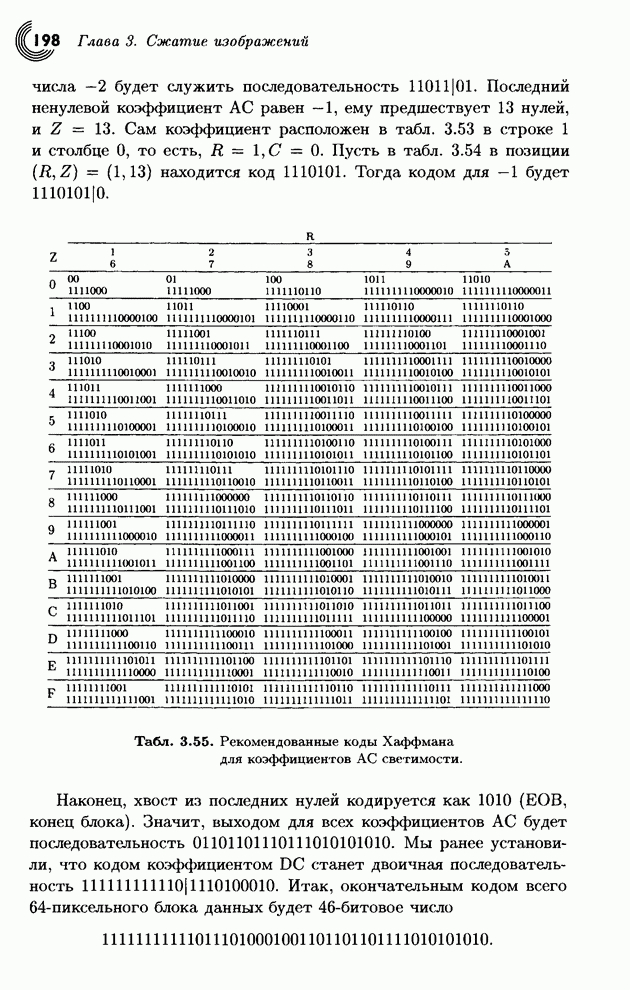
Табл. 3.55. Рекомендованные коды Хаффмана для коэффициентов АС светимости.
Наконец, хвост из последних нулей кодируется как 1010 (ЕОВ, конец блока). Значит, выходом для всех коэффициентов АС будет последовательность 01101101110111010101010. Мы ранее установили, что кодом коэффициентом DC станет двоичная последовательность 111111111110|1110100010. Итак, окончательным кодом всего 64-пиксельного блока данных будет 46-битовое числоe
111111111110111010001001101101101111010101010.
Эти 46 бит кодируют одну цветную
компоненту единицы данных. Предположим, что две остальные компоненты будут
также закодированы 46-битовыми числами. Если каждый пиксел исходно состоял из
24 бит, то получим фактор сжатия равный ![]() ; очень неплохой результат!
; очень неплохой результат!
R
|
Z |
1 6 |
2 7 |
3 8 |
4 9 |
5 А |
|
0 |
01 111000 |
100 1111000 |
1010 111110100 |
11000 1111110110 |
11001 111111110100 |
|
1 |
1011 111111110101 |
111001 111111110001000 |
11110110 111111110001001 |
111110101 111111110001010 |
11111110110 111111110001011 |
|
2 |
11010 1111111110001100 |
11110111 1111111110001101 |
1111110111 1111111110001110 |
111111110110 1111111110001111 |
111111111000010 1111111110010000 |
|
3 |
11011 1111111110010010 |
11111000 1111111110010011 |
1111111000 1111111110010100 |
111111110111 1111111110010101 |
1111111110010001 1111111110010110 |
|
4 |
111010 1111111110011010 |
111110110 1111111110011011 |
1111111110010111 1111111110011100 |
1111111110011000 1111111110011101 |
1111111110011001 1111111110011110 |
|
5 |
111011 1111111110100010 |
1111111001 1111111110100011 |
1111111110011111 1111111110100100 |
1111111110100000 1111111110100101 |
1111111110100001 1111111110100110 |
|
6 |
1111001 1111111110101010 |
11111110111 1111111110101011 |
1111111110100111 1111111110101100 |
1111111110101000 1111111110101101 |
1111111110101001 1111111110101110 |
|
7 |
1111010 1111111110110010 |
11111111000 1111111110110011 |
1111111110101111 1111111110110100 |
1111111110110000 1111111110110101 |
1111111110110001 1111111110110110 |
|
8 |
11111001 1111111110111011 |
1111111110110111 1111111110111100 |
1111111110111000 1111111110111101 |
1111111110111001 1111111110111110 |
1111111110111010 1111111110111111 |
|
9 |
111110111 1111111111000100 |
1111111111000000 1111111111000101 |
1111111111000001 1111111111000110 |
1111111111000010 1111111111000111 |
1111111111000011 1111111111001000 |
|
А |
111111000 1111111111001101 |
1111111111001001 1111111111001110 |
1111111111001010 1111111111001111 |
1111111111001011 1111111111010000 |
1111111111001100 1111111111010001 |
|
В |
111111001 1111111111010110 |
1111111111010010 1111111111010111 |
1111111111010011 1111111111011000 |
1111111111010100 1111111111011001 |
1111111111010101 1111111111011010 |
|
С |
111111010 1111111111011111 |
1111111111011011 1111111111100000 |
1111111111011100 1111111111100001 |
1111111111011101 1111111111100010 |
1111111111011110 1111111111100011 |
|
D |
11111111001 1111111111101000 |
1111111111100100 1111111111101001 |
1111111111100101 1111111111101010 |
1111111111100110 1111111111101011 |
1111111111100111 11111111111011011 |
|
Е |
11111111100000 1111111111110001 |
1111111111101101 1111111111110010 |
1111111111101110 1111111111110011 |
1111111111101111 1111111111110100 |
1111111111110000 1111111111110101 |
|
F |
111111111000011 1111111111111010 |
111111111010110 1111111111111011 |
1111111111110111 1111111111111100 |
1111111111111000 1111111111111101 |
1111111111111001 1111111111111110 |
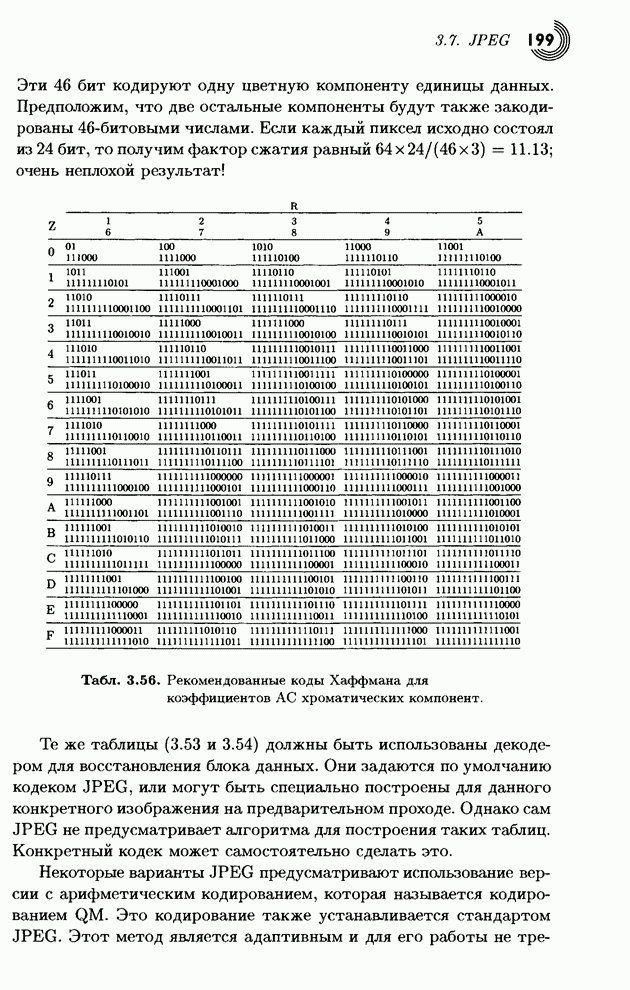
Табл. 3.56. Рекомендованные коды Хаффмана для коэффициентов АС хроматических компонент.
Те же таблицы (3.53 и 3.54) должны быть использованы декодером для восстановления блока данных. Они задаются по умолчанию кодеком JPEG, или могут быть специально построены для данного конкретного изображения на предварительном проходе. Однако сам JPEG не предусматривает алгоритма для построения таких таблиц. Конкретный кодек может самостоятельно сделать это.
Некоторые варианты JPEG предусматривают использование версии с арифметическим кодированием, которая называется кодированием QM. Это кодирование также устанавливается стандартом JPEG. Этот метод является адаптивным и для его работы не требуются таблицы 3.53 и 3.54. Он приспосабливает схему кодирования к статистическим свойствам конкретного изображения по мере его обработки. С помощью арифметического кодирования можно улучшить показатели компрессии метода Хаффмана на 5-10% для типичного непрерывно-тонового изображения. Однако этот метод имеет весьма сложную реализацию по сравнением с методом Хаффмана, поэтому он редко используется в приложениях.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие переводчика
- Предисловие автора
- Введение
- Глава 1. Статистические методы
- 1.1. Энтропия
- 1.2. Коды переменной длины
- 1.3. Декодирование
- 1.4. Кодирование Хаффмана
- 1.4.1. Декодирование Хаффмана
- 1.4.2. Средняя длина кода
- 1.5. Адаптивные коды Хаффмана
- 1.5.1. Несжатые коды
- 1.5.2. Модификация дерева
- 1.5.3. Переполнение счетчика
- 1.5.4. Кодовое переполнение
- 1.5.5. Вариант алгоритма
- 1.6. Факсимильное сжатие
- 1.6.1. Одномерное кодирование
- 1.6.2. Двумерное кодирование
- 1.7. Арифметическое кодирование
- 1.7.1. Детали реализации метода
- 1.7.2. Потеря значащих цифр
- 1.7.3. Заключительные замечания
- 1.8. Адаптивное арифметическое кодирование
- ГЛАВА 2 СЛОВАРНЫЕ МЕТОДЫ
- 2.1. LZ77 (скользящее окно)
- 2.1.1. Циклическая очередь
- 2.2. LZSS
- 2.2.1. Недостатки
- 2.3. LZ78
- 2.4. LZW
- 2.4.1. Декодирование LZW
- 2.4.2. Структура словаря LZW
- 2.4.3. LZW в практических приложениях
- 2.5. Заключение
- ГЛАВА 3 СЖАТИЕ ИЗОБРАЖЕНИЙ
- 3.1. Введение
- 3.2. Типы изображений
- 3.3. Подходы к сжатию изображений
- 3.3.1. Коды Грея
- 3.3.2. Метрики ошибок
- 3.4. Интуитивные методы
- 3.4.1. Подвыборка
- 3.4.2. Квантование
- 3.5. Преобразование изображений
- 3.5.1. Ортогональные преобразования
- 3.5.2. Матричные преобразования
- 3.5.3. Дискретное косинус-преобразование
- 3.5.4. Пример
- 3.5.5. Дискретное синус-преобразование
- 3.5.6. Преобразование Уолша-Адамара
- 3.5.7. Преобразование Хаара
- 3.5.8. Преобразование Кархунена-Лоэвэ
- 3.6. Прогрессирующее сжатие изображений
- 3.7. JPEG
- 3.7.1. Светимость
- 3.7.2. DCT
- 3.7.3. Практическое DCT
- 3.7.4. Квантование
- 3.7.5. Кодирование
- 3.7.6. Мода без потери данных
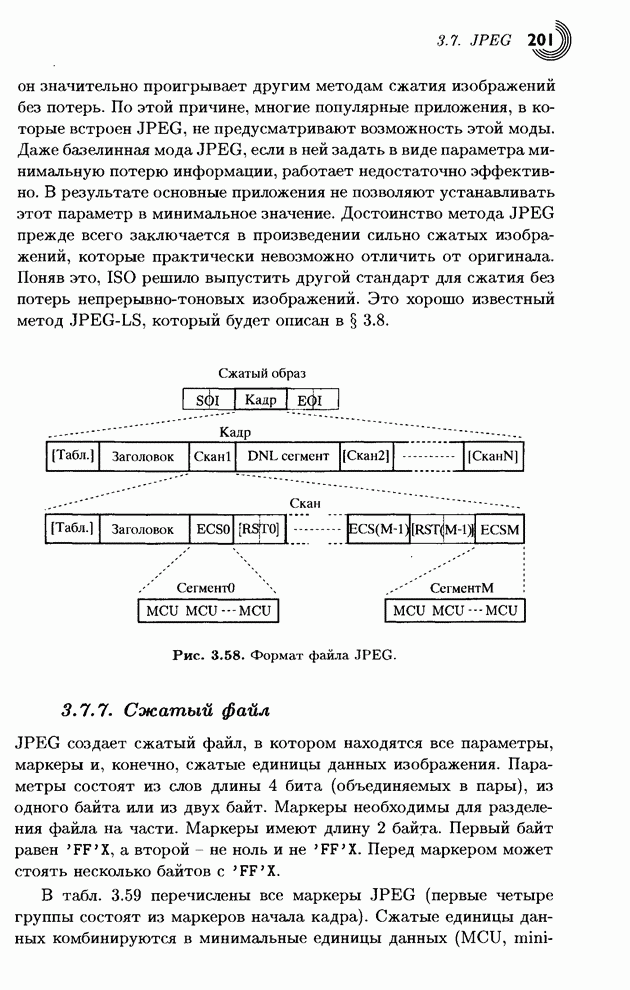
- 3.7.7. Сжатый файл
- 3.7.8. JFIF
- 3.8. JPEG-LS
- 3.8.1. Коды Голомба
- 3.8.2. Основы метода JPEG-LS
- 3.8.3. Кодер
- ГЛАВА 4 ВЕЙВЛЕТНЫЕ МЕТОДЫ
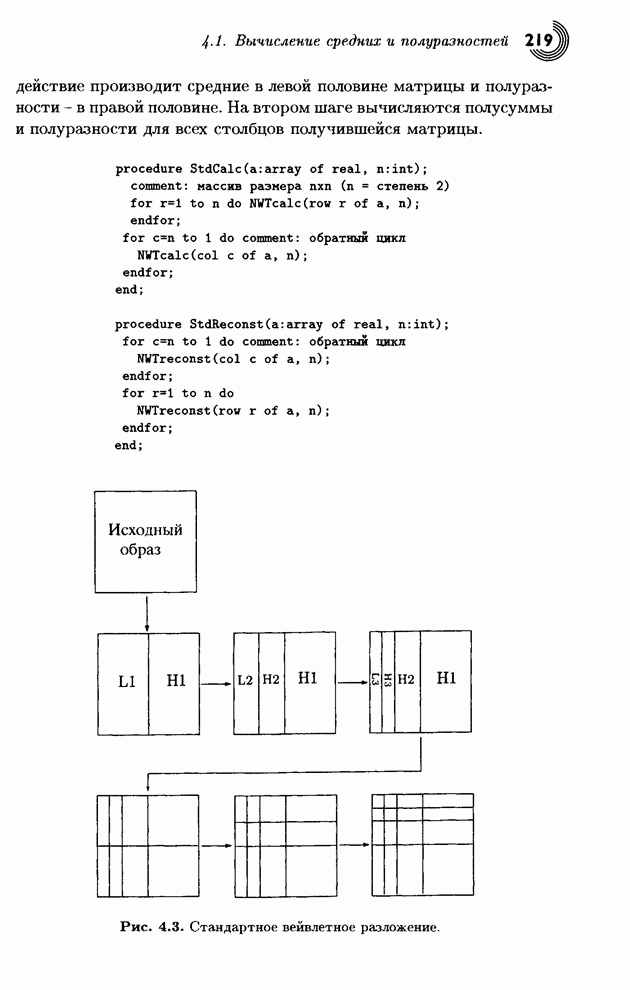
- 4.1. Вычисление средних и полу разностей
- 4.1.1. Обобщение на двумерный случай
- 4.1.2. Свойства преобразования Хаара
- 4.2. Преобразование Хаара
- 4.2.1. Матричная форма
- 4.3. Поддиапазонные преобразования
- 4.4. Банк фильтров
- 4.5. Нахождение коэффициентов фильтра
- 4.6. Преобразование DWT
- 4.7. Примеры
- 4.8. Вейвлеты Добеши
- 4.9. SPIHT
- 4.9.1. Алгоритм сортировки разделением множеств
- 4.9.2. Пространственно ориентированное дерево
- 4.9.3. Кодирование в алгоритме SPIHT
- 4.9.4. Пример
- 4.9.5. QTCQ
- ГЛАВА 5 СЖАТИЕ ВИДЕО
- 5.1. Основные принципы
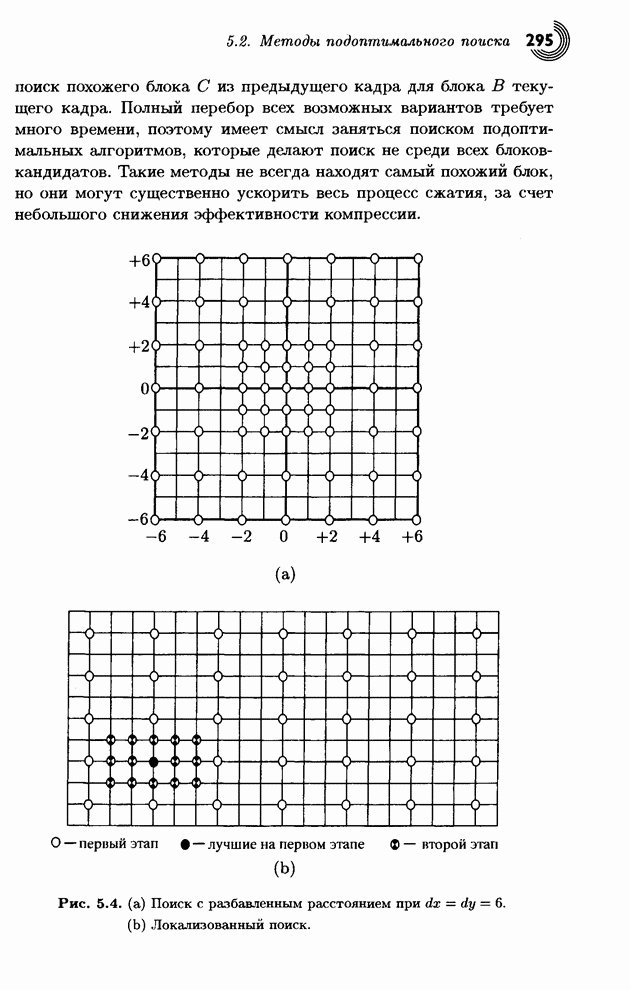
- 5.2. Методы подоптимального поиска
- ГЛАВА 6 СЖАТИЕ ЗВУКА
- 6.1. Звук
- 6.2. Оцифрованный звук
- 6.3. Органы слуха человека
- 6.4. Общепризнанные методы
- 6.5. Сжатие звука в стандарте MPEG-1
- 6.5.1. Кодирование частотной области
- 6.5.2. Формат сжатых данных
- 6.5.3. Психоакустические модели
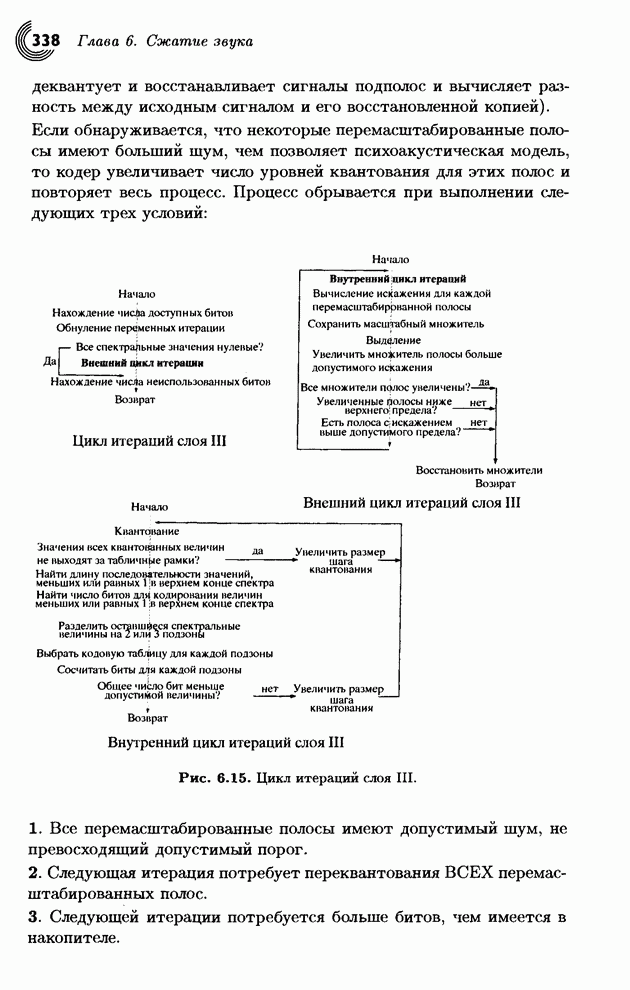
- 6.5.4. Кодирование: слой III
- Литература
- Глоссарий