| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Введение
Всем, кто использует компьютерные программы сжатия информации, хорошо знакомы такие слова, как «zip», «implode», «stuffit», «diet» и «squeeze». Всё это имена программ или названия методов для компрессии компьютерной информации. Перевод этих слов в той или иной степени означает застегивание, уплотнение, набивку или сжатие. Однако обычный, языковый смысл этих слов или их перевод не в полной мере отражают истинную природу того, что происходит с информацией в результате компрессии. На самом деле, при компрессии компьютерной информации ничего не набивается и не ужимается, но лишь удаляется некоторый избыток информации, присутствующий в исходных данных. Избыточность - вот центральное понятие в теории сжатия информации. Любые данные с избыточной информацией можно сжать. Данные, в которых нет избыточности, сжать нельзя, точка.
Мы все хорошо знаем, что такое информация. Интуитивно нам это вполне понятно, однако это скорее качественное восприятие предмета. Информация представляется нам одной из сущностей, которые невозможно точно определить и тем более измерить количественно. Однако, существует область математики, которая называется теорией информации, где информацию изучают именно количественно. Другим важным достижением теории информации является вполне строгое определение избыточности. Сейчас мы попытаемся истолковать это понятие интуитивно, указав, что есть избыточность для двух простых типов компьютерных данных, и что представляют собой данные, из которых удалена избыточность.
Первый тип информации - это текст. Текст представляет собой важнейший вид компьютерных данных. Огромное количество компьютерных программ и приложений являются по своей природе нечисловыми; они работают с данными, у которых основными элементарными компонентами служат символы текста. Компьютер способен сохранять и обрабатывать лишь двоичную информацию, состоящую из нулей и единиц. Поэтому каждому символу текста необходимо сопоставить двоичный код. Современные компьютеры используют так называемые коды ASCII (произносится «аски», а само слово ASCII является сокращением от «American Standard Code for Information Interchange»), хотя все больше компьютеров и приложений используют новые коды Unicode. ASCII представляет код фиксированной длины, где каждому символу присваивается 8-битовая последовательность (сам код занимает семь битов, а восьмой - проверочный, который изначально был задуман для повышения надежности кода). Код фиксированной длины представляется наилучшим выбором, поскольку позволяет компьютерным программам легко оперировать с символами различных текстов. С другой стороны, код фиксированной длины является по существу избыточным.
В случайном текстовом файле мы ожидаем, что каждый символ встречается приблизительно равное число раз. Однако файлы, используемые на практике, навряд ли являются случайными. Они содержат осмысленные тексты, и по опыту известно, что, например, в типичном английском тексте некоторые буквы, такие, как «Е», «Т» и «А», встречаются гораздо чаще, чем «Z» и «Q». Это объясняет, почему код ASCII является избыточным, а также указывает на пути устранения избыточности. ASCII избыточен прежде всего потому, что независимо присваивает каждому символу, часто или редко используемому, одно и то же число бит (восемь). Чтобы удалить такую избыточность, можно воспользоваться кодами переменной длины, в котором короткие коды присваиваются буквам, встречающимся чаще, а редко встречающимся буквам достаются более длинные коды. Точно так работает кодирование Хаффмана (см. § 1.4).
Представим себе два текстовых файла А и В, содержащие один и тот же текст, причем файл А использует коды ASCII, а В записан с помощью некоторых кодов переменной длины. Мы ожидаем, что размер файла В меньше размера А. Тогда можно сказать, что файл А сжат в файл В. Понятно, что степень сжатия зависит от избыточности взятого текста, а также от используемых кодов переменной длины. Текст, в котором одни символы встречаются очень часто, а другие очень редко, имеет большую избыточность: он будет сжиматься хорошо, если коды переменной длины выбраны подходящим образом. В соответствующем файле В коды часто встречающихся символов будут короткими, а коды редких символов - длинными. Длинные коды не смогут понизить степень сжатия, так как они будут встречаться в файле В достаточно редко. Большая часть В будет состоять из коротких кодов. С другой стороны, случайный текстовый файл не получает преимущество при замене кодов ASCII кодами переменной длины, потому что сжатие, достигнутое с использованием коротких кодов, будет аннулировано длинными кодами. В этом частном примере работает общее правило, которое гласит: случайные данные невозможно сжать, так как в них нет избыточности.
Из новостей FIDO, 23 апреля 1990
|
Вокруг нас разгорается пламя войны, в которой спорным вопросом является: чья программа компрессии данных является самой лучшей. Я решил тоже в ней поучаствовать и написать СВОЮ собственную программу. Вы конечно слышали про программы, которые схрустывают, глушат, ужимают, вдавливают, пакуют, дробят и т.д. Теперь есть программа TRASH (в мусор). TRASH сжимает файл до наименьшего возможного размера: 0 байт! Ничто не сожмет файл лучше, чем TRASH. Атрибуты дата/время не затрагиваются, и поскольку файл имеет нулевую длину, он совсем не займет место на вашем винчестере! И TRASH очень быстра. Ваши файлы будут скомканы за микросекунды! Вы потратите больше времени вглядываясь в задаваемые параметры, в то время как файл будет уже обработан. Это предпродажная версия моей программы. Вы можете хранить и испытывать ее. Я бы вам рекомендовал сделать резервную копию ваших файлов перед тем, как вы впервые запустите мой TRASH, хотя... Следующая версия TRASH будет иметь графический интерфейс и принимать кредитные карты. TRASH C:PAYROOL*.* ... и работать с целыми дисками TRUSH D: ... и быть первой, чтобы заблокировать сбрасывание в мусор вашей системы НАРОЧНО! TRUSH ALL Мы даже надеемся научить нашу программу восстанавливать зa TRASHeнные файлы! |
Второй тип компьютерных данных
это оцифрованные изображения: фотографии, рисунки, картинки, графики и т.п.
Цифровое изображение это прямоугольная матрица окрашенных точек, называемых пикселами.
Каждый пиксел представляется в компьютере с помощью цветового кода. (До конца
этого параграфа термин «пиксел» используется только для цветового кода.) Для
упрощения цифровой обработки изображений предполагается, что все пикселы имеют
один и тот же размер. Размер пиксела зависит от числа цветов в изображении,
которое, обычно, является степенью 2. Если в нем содержится ![]() разных цветов, то каждый пиксел - это
разных цветов, то каждый пиксел - это ![]() -битовое число.
-битовое число.
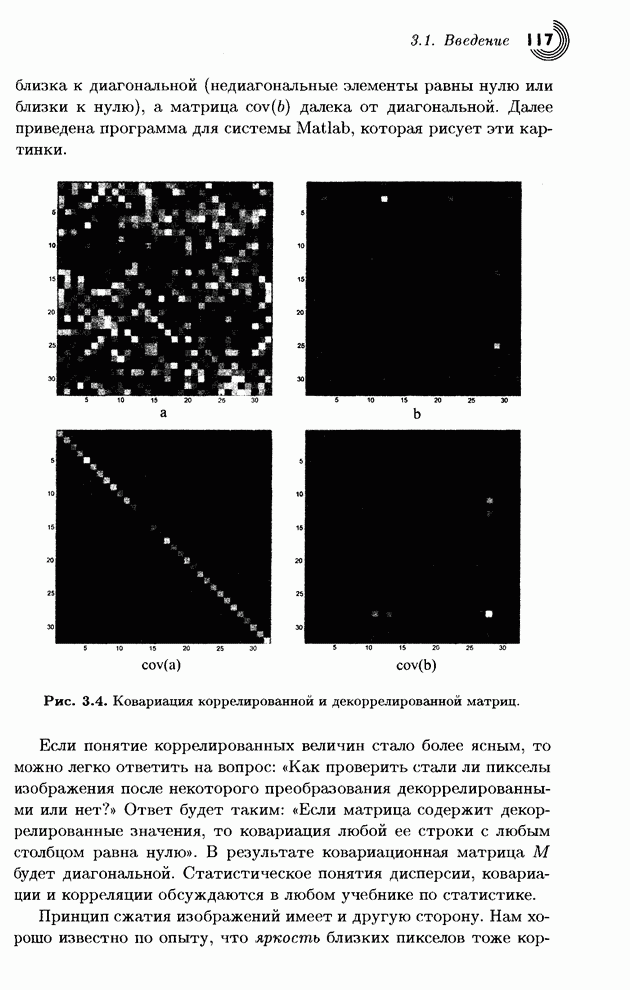
Имеется два вида избыточности в цифровых изображениях. Первый вид похож на избыточность в текстовом файле. В каждом неслучайном изображении некоторые цвета могут преобладать, а другие встречаться редко. Такая избыточность может быть удалена с помощью кодов переменной длины, присваиваемых разным пикселам, точно также как и при сжатии текстовых файлов. Другой вид избыточности гораздо более важен, он является результатом корреляции пикселов. Когда наш взгляд перемещается по картинке, он обнаруживает в большинстве случаев, что соседние пикселы окрашены в близкие цвета. Представим себе фотографию, на которой изображено голубое небо, белые облака, коричневые горы и зеленые деревья. Пока мы смотрим на горы, близкие пикселы имеют похожий цвет; все или почти все из них имеют разные оттенки коричневого цвета. Про близкие пикселы неба можно сказать, что они носят различные оттенки голубого цвета. И только на горизонте, там, где горы встречаются с небом, соседние пикселы могут иметь совершенно разные цвета. Таким образом, отдельные пикселы не являются совершенно независимыми. Можно сказать, что ближайшие пикселы изображения коррелируют между собой. С этим видом избыточности можно бороться разными способами. Об этом будет рассказано в главе 3.
Независимо от метода, которым сжимается изображение, эффективность его компрессии определяется прежде всего количеством избыточности, содержащимся в нем. Предельный случай - это однотонное изображение. Оно имеет максимальную избыточность, потому что соседние пикселы тождественны. Понятно, такое изображение не интересно с практической точки зрения, оно, если встречается, то крайне редко. Тем не менее, оно будет очень хорошо сжиматься любым методом компрессии. Другим экстремальным случаем является изображение с некоррелированными, то есть, случайными пикселами. В таком изображении соседние пикселы, как правило, весьма различаются по своему цвету, а избыточность этого изображения равна нулю. Его невозможно сжать никаким методом. Оно выглядит как случайная мешанина окрашенных точек, и потому не интересно. Нам вряд ли понадобится сохранять и обрабатывать подобные изображения, и нет смысла пытаться их сжимать.
Следующее простое наблюдение поясняет существо утверждения: «Сжатие данных достигается сокращением и удалением из них избыточности». Оно также дает понять, что большинство файлов невозможно сжать никакими методами. Это может показаться странным, так как мы постоянно сжимаем свои файлы. Причина заключается в том, что большинство файлов являются случайными или почти случайными, и поэтому, в них совсем нет избыточности. Существует относительно немного файлов, которые можно сжимать, и именно с ними мы хотим это сделать, с этими файлами мы работаем все время. В них есть избыточность, они не случайны, а потому полезны и интересны.
Пусть два разных файла А и В сжаты в файлы С и D, соответственно. Ясно, что С и D должны также отличаться друг от друга. В противном случае было бы невозможно по ним восстановить исходные файлы А и В.
Предположим, что файл состоит из ![]() бит, и мы хотим его сжать эффективным
образом. Будем приветствовать любой алгоритм, который сожмет этот файл, скажем,
в 10 бит. Компрессия в 11 или 12 бит тоже была бы замечательна. Сжатие файла до
половины его размера будет для нас вполне удовлетворительным. Всего существует
бит, и мы хотим его сжать эффективным
образом. Будем приветствовать любой алгоритм, который сожмет этот файл, скажем,
в 10 бит. Компрессия в 11 или 12 бит тоже была бы замечательна. Сжатие файла до
половины его размера будет для нас вполне удовлетворительным. Всего существует ![]() различных файлов размера
различных файлов размера ![]() . Их надо бы сжать в
. Их надо бы сжать в ![]() различных файлов размера не больше
различных файлов размера не больше ![]() . Однако, общее число таких файлов равно
. Однако, общее число таких файлов равно
![]() ,
,
поэтому
только ![]() исходных файлов имеют шанс сжаться
эффективным образом. Проблема в том, что число
исходных файлов имеют шанс сжаться
эффективным образом. Проблема в том, что число ![]() существенно
меньше числа
существенно
меньше числа ![]() . Вот два примера соотношения между ними.
. Вот два примера соотношения между ними.
Для ![]() (файл
всего в 100 бит) общее число файлов равно
(файл
всего в 100 бит) общее число файлов равно ![]() , а
число файлов, эффективно сжимаемых, равно
, а
число файлов, эффективно сжимаемых, равно ![]() . А их
частное просто до смешного малая дробь
. А их
частное просто до смешного малая дробь ![]() .
.
Для ![]() (файл
из 1000 бит, т.е. около 125 байт) число всех файлов равно
(файл
из 1000 бит, т.е. около 125 байт) число всех файлов равно ![]() , а число сжимаемых всего
, а число сжимаемых всего ![]() . Их доля просто катастрофически мала,
она равна
. Их доля просто катастрофически мала,
она равна ![]() .
.
Большинство интересных файлов имеют размер по крайней мере в несколько тысяч байт. Для таких размеров доля эффективно сжимаемых файлов настолько мала, что ее невозможно выразить числом с плавающей точкой даже на суперкомпьютере (результат будет нуль).
Из этих примеров становится ясно, что не существует методов и алгоритмов, способных эффективно сжимать ЛЮБЫЕ файлы, или даже существенную часть их. Для того, чтобы сжать файл, алгоритм компрессии должен сначала изучить его, найти в нем избыточность, а потом попытаться удалить ее. Поскольку избыточность зависит от типа данных (текст, графика, звук и т.д.), методы компрессии должны разрабатываться с учетом этого типа. Алгоритм будет лучше всего работать именно со своими данными. В этой области не существует универсальных методов и решений.
В конце введения напомним некоторые важные технические термины, которые используются в области сжатия информации.
а) Компрессор или кодер - программа, которая сжимает «сырой» исходный файл и создает на выходе файл со сжатыми данными, в которых мало избыточности. Декомпрессор или декодер работает в обратном направлении. Отметим, что понятие кодера является весьма общим и имеет много значений, но поскольку мы обсуждаем сжатие данных, то у нас слово кодер будет означать компрессор. Термин кодек иногда используется для объединения кодера и декодера.
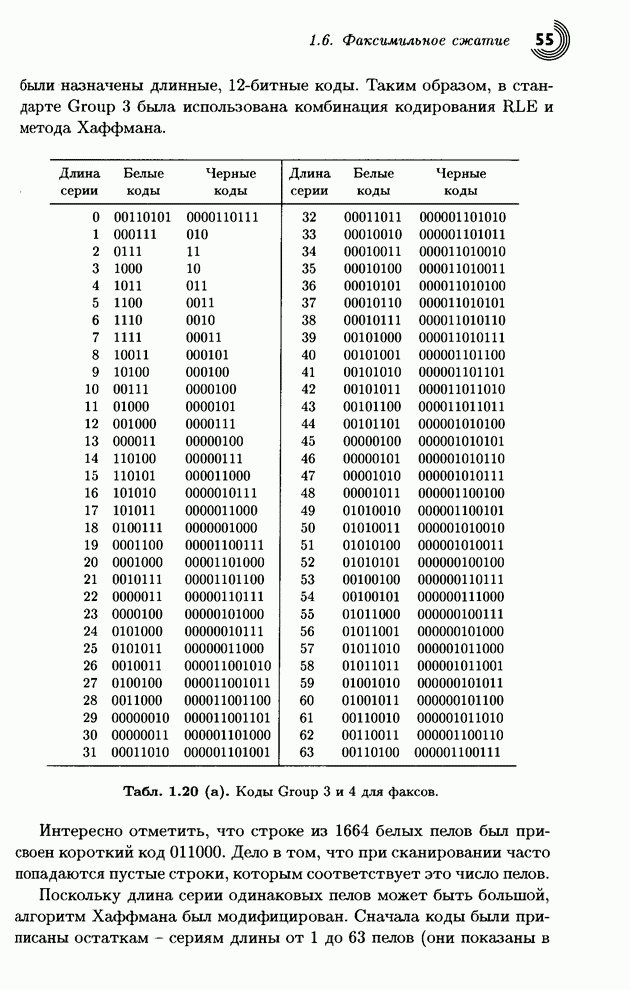
б) Метод неадаптивного сжатия подразумевает неспособность алгоритма менять свои операции, параметры и настройки в зависимости от сжимаемых данных. Такой метод лучше всего сжимает однотипные данные. К ним относятся методы группы 3 и группы 4 сжатия факсимильных сообщений (см. § 1.6). Они специально разработаны для сжатия в факс-машинах и будут весьма слабо работать на других типах данных. Напротив, адаптивные методы сначала тестируют «сырые» исходные данные, а затем подстраивают свои параметры и/или операции в соответствии с результатом проверки. Примером такого алгоритма может служить кодирование Хаффмана из § 1.5. Некоторые методы компрессии используют двухпроходные алгоритмы, когда на первом проходе по файлу собирается некоторая статистика сжимаемых данных, а на втором проходе происходит непосредственно сжатие с использованием параметров, вычисленных на первой стадии. Такие методы можно назвать полуадаптивными. Методы компрессии могут быть также локально адаптивными, что означает способность алгоритма настраивать свои параметры исходя из локальных особенностей файла и менять их, перемещаясь от области к области входных данных. Пример такого алгоритма приведен в [Salomon 2000].
в) Компрессия без потерь/с потерей: некоторые методы сжатия допускают потери. Они лучше работают, если часть информации будет опущена. Когда такой декодер восстанавливает данные, результат может не быть тождественен исходному файлу. Такие методы позволительны, когда сжимаемыми данными является графика, звук или видео. Если потери невелики, то бывает невозможно обнаружить разницу. А текстовые данные, например, текст компьютерной программы, могут стать совершенно непригодными, если потеряется или изменится хоть один бит информации. Такие файлы можно сжимать только методами без потери информации. (Здесь стоит отметить два момента относительно текстовых файлов. (1) Если текстовый файл содержит исходный код компьютерной программы, то из него можно безболезненно удалить большинство пробелов, так как компилятор, обычно, их не рассматривает. (2) Когда программа текстового процессора сохраняет набранный текст в файле, она также сохраняет в нем информацию об используемых шрифтах. Такая информация также может быть отброшена, если автор желает сохранить лишь текст своего произведения).
г) Симметричное сжатие - это когда и кодер, и декодер используют один и тот же базовый алгоритм, но используют его в противоположных направлениях. Такой метод имеет смысл, если постоянно сжимается и разжимается одно и то же число файлов. При асимметричном методе или компрессор или декомпрессор должны проделать существенно большую работу. Таким методам тоже находится место под солнцем, они совсем не плохи. Метод, когда компрессия делается долго и тщательно с помощью сложнейшего алгоритма, а декомпрессия делается быстро и просто, вполне оправдан при работе с архивами, когда приходится часто извлекать данные. То же происходит и при создании и прослушивании аудиофайлов формата mp3. Обратный случай, это когда внешние файлы часто меняются и сохраняются в виде резервных копий. Поскольку вероятность извлечения резервных данных невелика, то декодер может работать существенно медленнее своего кодера.
д) Производительность сжатия: несколько величин используются для вычисления эффективности алгоритмов сжатия.
1) Коэффициент сжатия определяется по формуле
![]() .
.
Коэффициент 0.6 означает, что сжатые данные занимают 60% от исходного размера. Значения большие 1 говорят о том, что выходной файл больше входного (отрицательное сжатие). Коэффициент сжатия принято измерять в bpb (bit per bit, бит на бит), так как он показывает, сколько в среднем понадобится бит сжатого файла для представления одного бита файла на входе. При сжатии графических изображений аналогично определяется величина bpp (bit per pixel, бит на пиксел). В современных эффективных алгоритмах сжатия текстовой информации имеет смысл говорить о похожей величине bpc (bit per character, бит на символ), то есть, сколько в среднем потребуется бит для хранения одной буквы текста.
Здесь следует упомянуть еще два понятия, связанные с коэффициентом сжатия. Термин битовая скорость (bitrate) является более общим, чем bpb и bpc. Целью компрессии информации является представление данных с наименьшей битовой скоростью. Битовый бюджет (bit budget) означает некоторый довесок к каждому биту в сжатом файле. Представьте себе сжатый файл, в котором 90% размера занимают коды переменной длины, соответствующие конкретным символам исходного файла, а оставшиеся 10% используются для хранения некоторых таблиц, которые будут использоваться декодером при декомпрессии. В этом случае битовый бюджет равен 10%.
2) Величина, обратная коэффициенту сжатия, называется фактором сжатия:
![]() .
.
В этом случае значения большие 1 означают сжатие, а меньшие 1 - расширение. Этот множитель представляется большинству людей более естественным показателем: чем больше фактор, тем лучше компрессия. Эта величина отдаленно соотносится с коэффициентом разреженности, который будет обсуждаться в § 4.1.2.
3)
Выражение ![]() , где
, где ![]() -
коэффициент сжатия, тоже отражает качество сжатия. Его значение равное 60
означает, что в результате сжатия занимает на 60% меньше, чем исходный файл.
-
коэффициент сжатия, тоже отражает качество сжатия. Его значение равное 60
означает, что в результате сжатия занимает на 60% меньше, чем исходный файл.
4) Для оценивания эффективности алгоритмов сжатия образов используется величина bpp. Она показывает, сколько необходимо в среднем использовать битов для хранения одного пиксела. Это число удобно сравнивать с его значением до компрессии.
е) Вероятностная модель. Это понятие очень важно при разработке статистических методов сжатия данных. Зачастую, алгоритм компрессии состоит из двух частей, вероятностной модели и непосредственно компрессора. Перед тем как приступить к сжатию очередного объекта (бита, байта, пиксела и т.п.), активируется вероятностная модель и вычисляется вероятность этого объекта. Эта вероятность и сам объект сообщаются компрессору, который использует полученную информацию при сжатии. Чем выше вероятность, тем лучше сжатие.
Приведем пример простой модели для черно-белого
изображения. Каждый пиксел такого изображения - это один единственный бит.
Предположим, что алгоритм уже прочитал и сжал 1000 пикселов и читает 1001-ый
пиксел. Какова вероятность того, что пиксел будет черным? Модель может просто
сосчитать число черных пикселов в уже прочитанном массиве данных. Если черных
пикселов было 350, то модель приписывает 1001-ому пикселу вероятность ![]() быть черным. Эта вероятность вместе с
пикселом (черным или белым) передаются компрессору. Главным моментом является
то, что декодер может также легко вычислить вероятность 1001-ого пиксела.
быть черным. Эта вероятность вместе с
пикселом (черным или белым) передаются компрессору. Главным моментом является
то, что декодер может также легко вычислить вероятность 1001-ого пиксела.
ж) Слово алфавит означает множество символов в сжимаемых данных. Алфавит может состоять из двух символов, 0 и 1, из 128 символов ASCII, из 256 байтов по 8 бит в каждом или из любых других символов.
з) Возможности каждого алгоритма сжатия имеют ограничения. Никакой алгоритм не может эффективно сжимать любые файлы. Как было уже показано, любой алгоритм может эффективно сжимать лишь малую долю файлов, которые не являются случайными. Подавляющее же число случайных или близких к случайным файлов не поддается сжатию.
Последнее заключение выглядит
немного обескураживающим, но я надеюсь, оно не заставит читателя закрыть эту
книгу со вздохом и обратиться к другим многообещающим занятиям. Это
удивительно, но среди ![]() всевозможных файлов размера
всевозможных файлов размера ![]() , именно те файлы, которые мы захотим
сжать, будут сжиматься хорошо. Те же, которые сжимаются плохо, являются
случайными, а значит, неинтересными и неважными для нас. Мы не будем их сжимать,
пересылать или хранить.
, именно те файлы, которые мы захотим
сжать, будут сжиматься хорошо. Те же, которые сжимаются плохо, являются
случайными, а значит, неинтересными и неважными для нас. Мы не будем их сжимать,
пересылать или хранить.
Чудесные дни перед свадьбой
сродни живому вступлению к скучной книге.
- Уилсон Мизнер
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие переводчика
- Предисловие автора
- Введение
- Глава 1. Статистические методы
- 1.1. Энтропия
- 1.2. Коды переменной длины
- 1.3. Декодирование
- 1.4. Кодирование Хаффмана
- 1.4.1. Декодирование Хаффмана
- 1.4.2. Средняя длина кода
- 1.5. Адаптивные коды Хаффмана
- 1.5.1. Несжатые коды
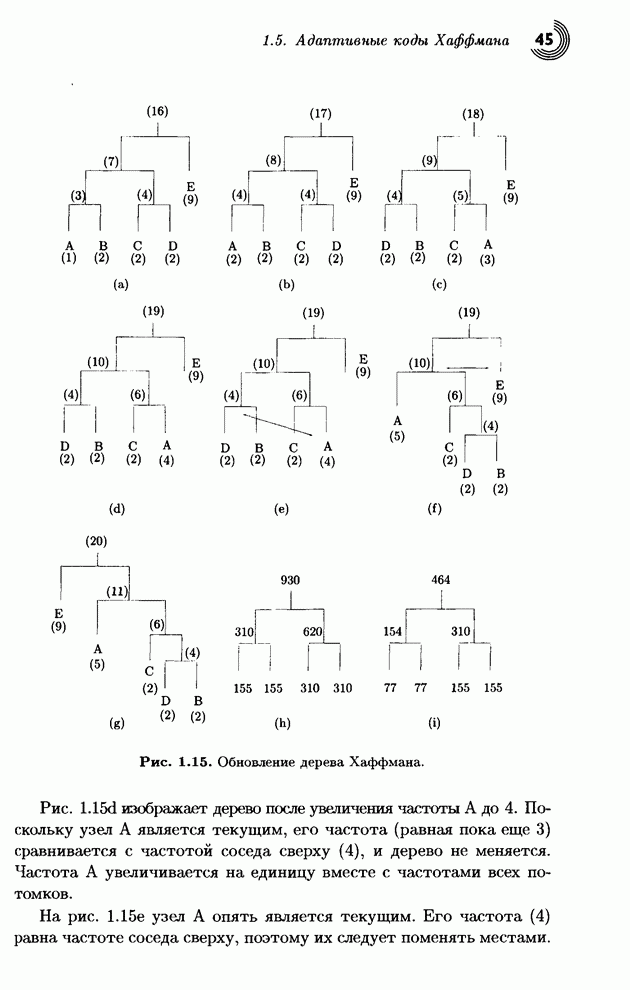
- 1.5.2. Модификация дерева
- 1.5.3. Переполнение счетчика
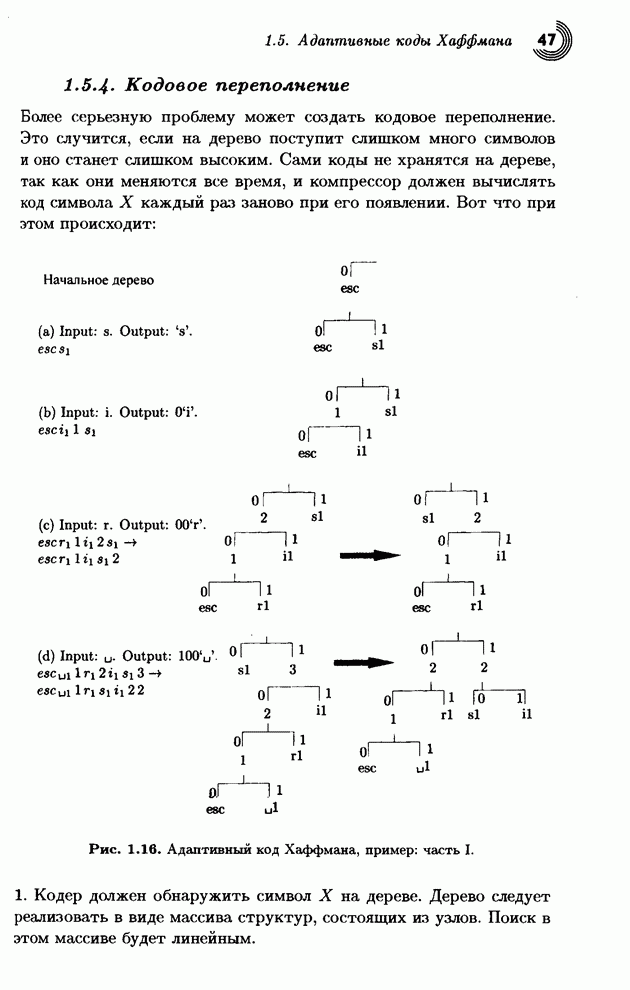
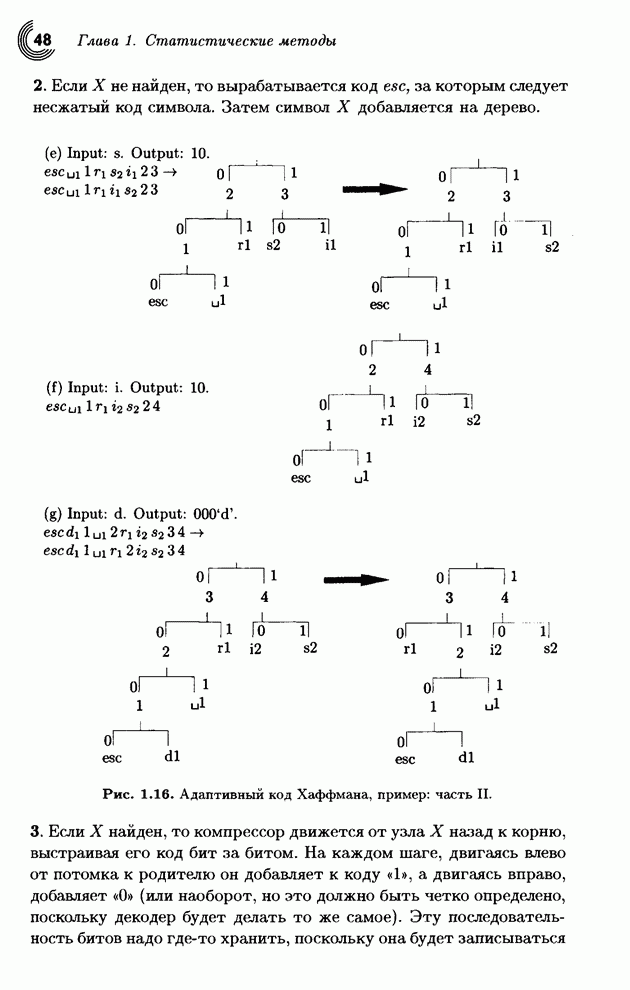
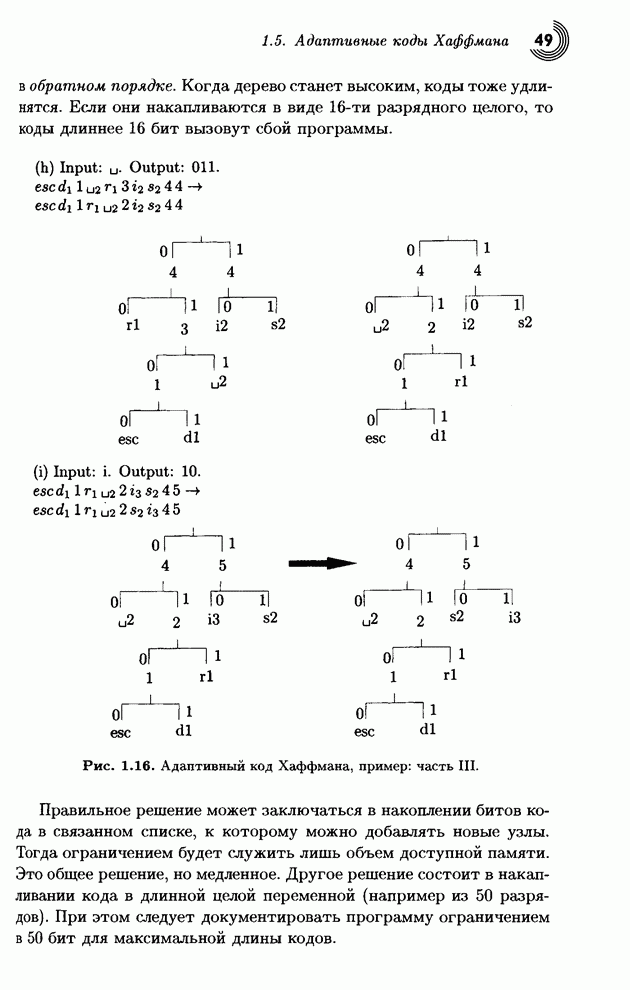
- 1.5.4. Кодовое переполнение
- 1.5.5. Вариант алгоритма
- 1.6. Факсимильное сжатие
- 1.6.1. Одномерное кодирование
- 1.6.2. Двумерное кодирование
- 1.7. Арифметическое кодирование
- 1.7.1. Детали реализации метода
- 1.7.2. Потеря значащих цифр
- 1.7.3. Заключительные замечания
- 1.8. Адаптивное арифметическое кодирование
- ГЛАВА 2 СЛОВАРНЫЕ МЕТОДЫ
- 2.1. LZ77 (скользящее окно)
- 2.1.1. Циклическая очередь
- 2.2. LZSS
- 2.2.1. Недостатки
- 2.3. LZ78
- 2.4. LZW
- 2.4.1. Декодирование LZW
- 2.4.2. Структура словаря LZW
- 2.4.3. LZW в практических приложениях
- 2.5. Заключение
- ГЛАВА 3 СЖАТИЕ ИЗОБРАЖЕНИЙ
- 3.1. Введение
- 3.2. Типы изображений
- 3.3. Подходы к сжатию изображений
- 3.3.1. Коды Грея
- 3.3.2. Метрики ошибок
- 3.4. Интуитивные методы
- 3.4.1. Подвыборка
- 3.4.2. Квантование
- 3.5. Преобразование изображений
- 3.5.1. Ортогональные преобразования
- 3.5.2. Матричные преобразования
- 3.5.3. Дискретное косинус-преобразование
- 3.5.4. Пример
- 3.5.5. Дискретное синус-преобразование
- 3.5.6. Преобразование Уолша-Адамара
- 3.5.7. Преобразование Хаара
- 3.5.8. Преобразование Кархунена-Лоэвэ
- 3.6. Прогрессирующее сжатие изображений
- 3.7. JPEG
- 3.7.1. Светимость
- 3.7.2. DCT
- 3.7.3. Практическое DCT
- 3.7.4. Квантование
- 3.7.5. Кодирование
- 3.7.6. Мода без потери данных
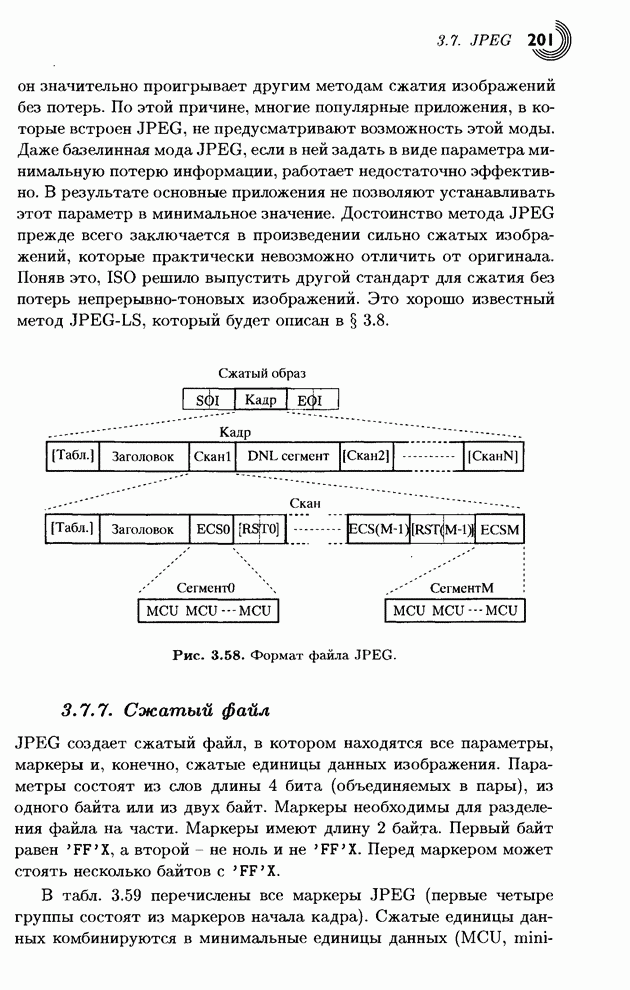
- 3.7.7. Сжатый файл
- 3.7.8. JFIF
- 3.8. JPEG-LS
- 3.8.1. Коды Голомба
- 3.8.2. Основы метода JPEG-LS
- 3.8.3. Кодер
- ГЛАВА 4 ВЕЙВЛЕТНЫЕ МЕТОДЫ
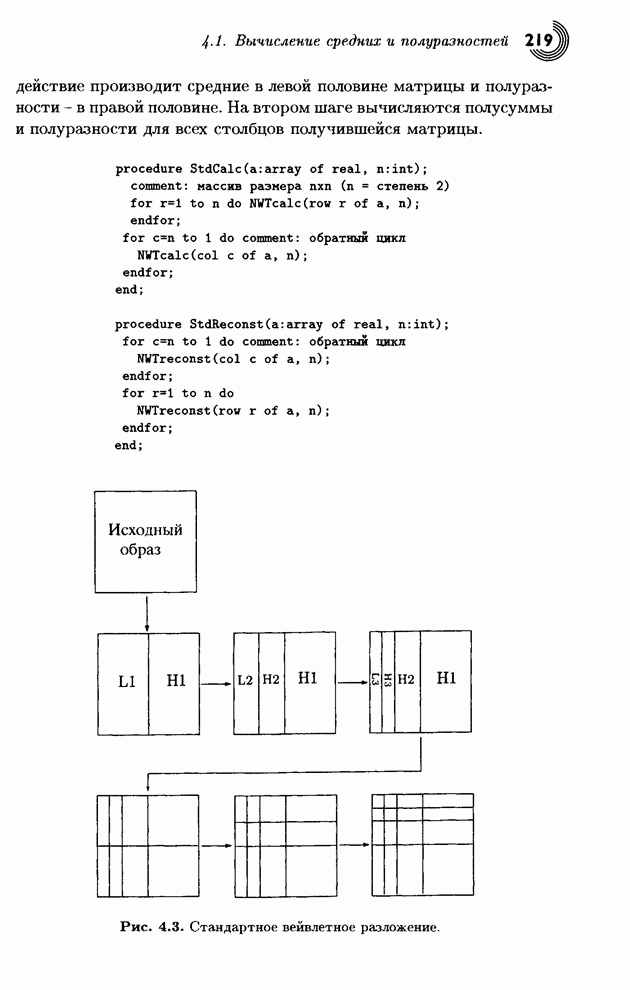
- 4.1. Вычисление средних и полу разностей
- 4.1.1. Обобщение на двумерный случай
- 4.1.2. Свойства преобразования Хаара
- 4.2. Преобразование Хаара
- 4.2.1. Матричная форма
- 4.3. Поддиапазонные преобразования
- 4.4. Банк фильтров
- 4.5. Нахождение коэффициентов фильтра
- 4.6. Преобразование DWT
- 4.7. Примеры
- 4.8. Вейвлеты Добеши
- 4.9. SPIHT
- 4.9.1. Алгоритм сортировки разделением множеств
- 4.9.2. Пространственно ориентированное дерево
- 4.9.3. Кодирование в алгоритме SPIHT
- 4.9.4. Пример
- 4.9.5. QTCQ
- ГЛАВА 5 СЖАТИЕ ВИДЕО
- 5.1. Основные принципы
- 5.2. Методы подоптимального поиска
- ГЛАВА 6 СЖАТИЕ ЗВУКА
- 6.1. Звук
- 6.2. Оцифрованный звук
- 6.3. Органы слуха человека
- 6.4. Общепризнанные методы
- 6.5. Сжатие звука в стандарте MPEG-1
- 6.5.1. Кодирование частотной области
- 6.5.2. Формат сжатых данных
- 6.5.3. Психоакустические модели
- 6.5.4. Кодирование: слой III
- Литература
- Глоссарий