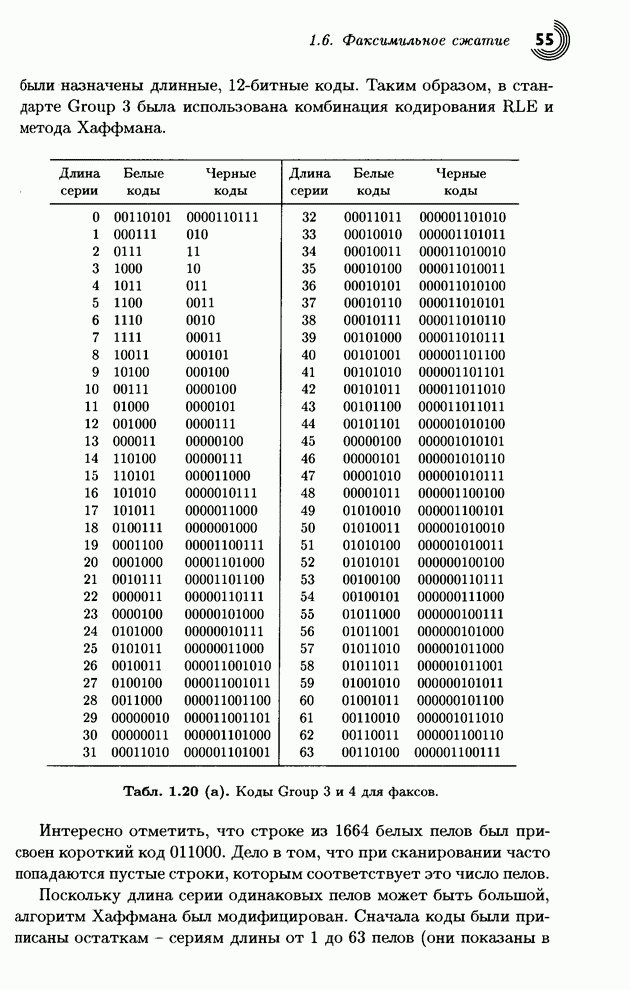
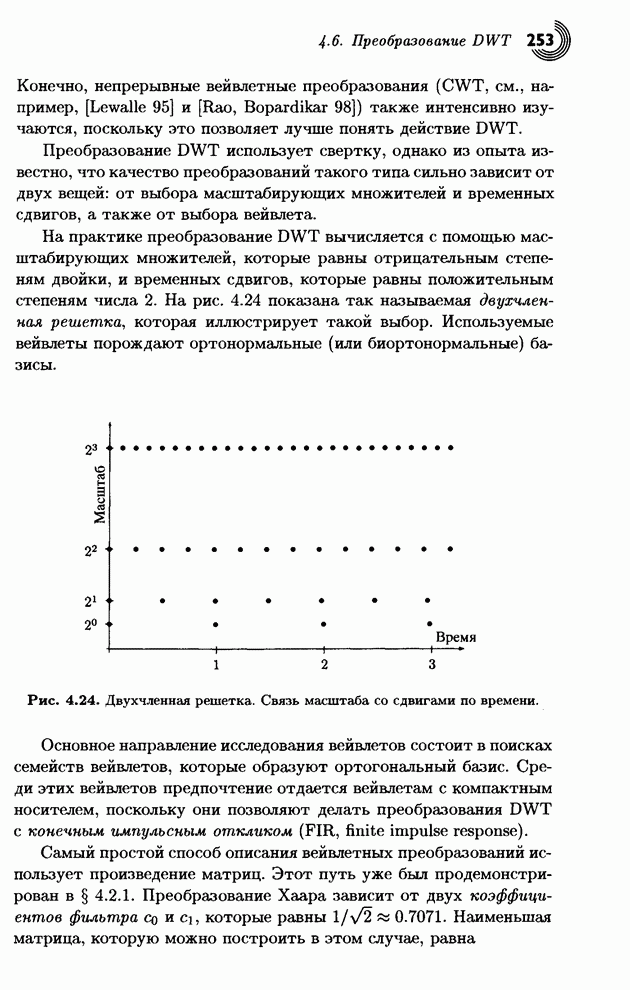
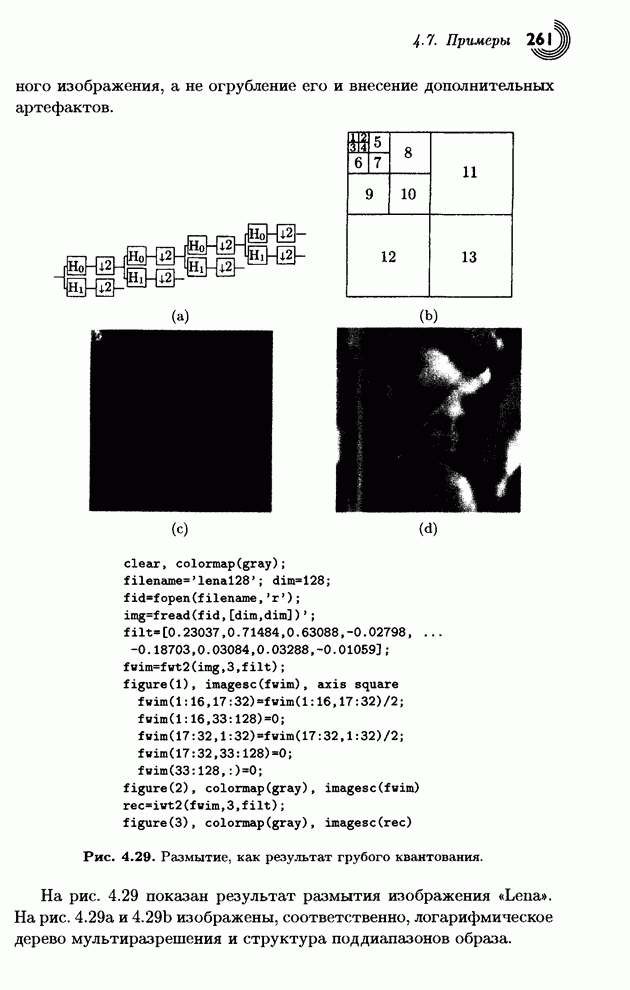
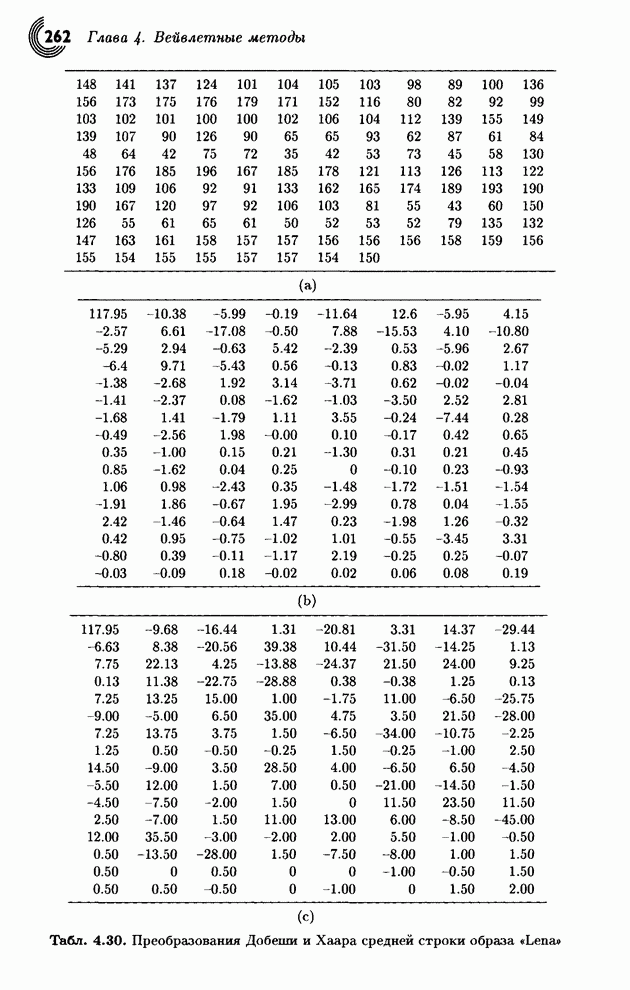
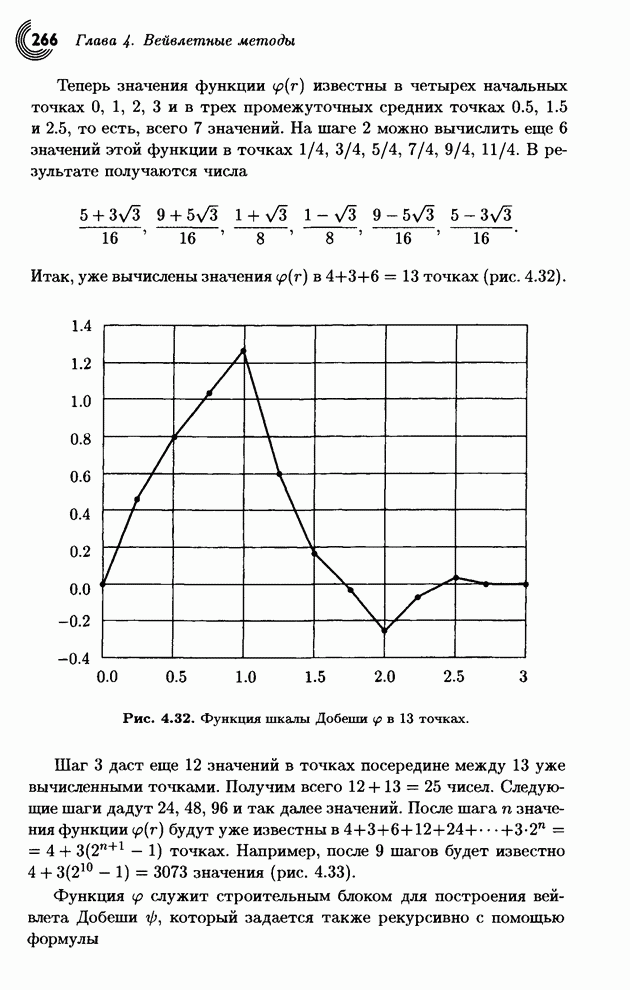
| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
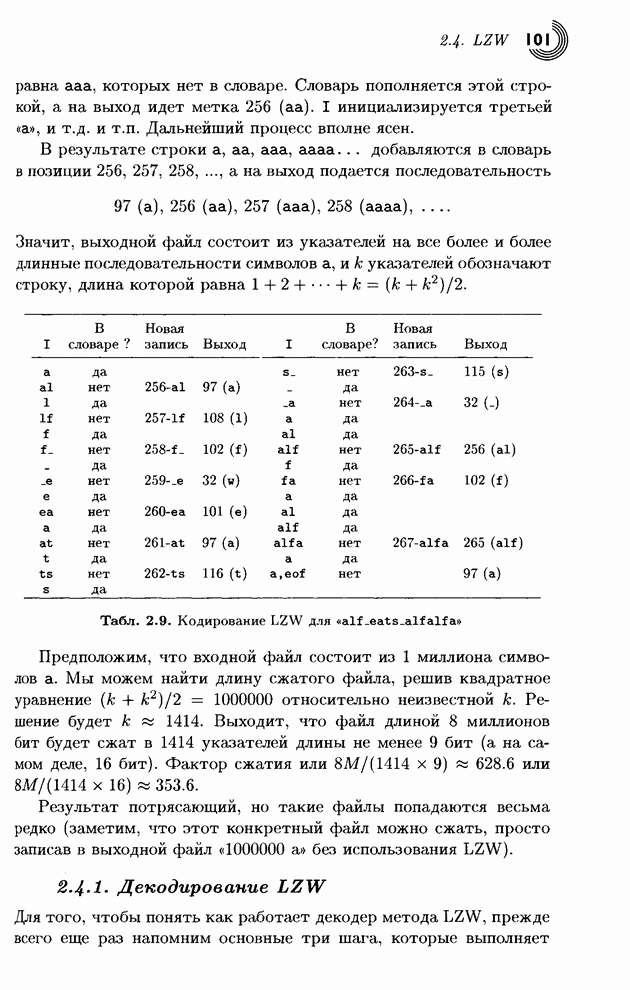
3.8. JPEG-LS
Метод сжатия JPEG-LS использует коды Голомба, поэтому мы дадим краткое описание этих мало известных кодов.
3.8.1. Коды Голомба
Код Голомба неотрицательного
целого числа ![]() [Golomb 66] может быть эффективным кодом
Хаффмана. Этот код зависит от выбора некоторого параметра
[Golomb 66] может быть эффективным кодом
Хаффмана. Этот код зависит от выбора некоторого параметра ![]() . Прежде всего необходимо
вычислить две величины
. Прежде всего необходимо
вычислить две величины ![]() ,
, ![]() (где выражение
(где выражение ![]() обозначает округление
обозначает округление ![]() ), а затем построить
код из двух частей; первая часть - это число
), а затем построить
код из двух частей; первая часть - это число ![]() , закодированное с помощью унарного кода
(см. стр. 195), а вторая - двоичное выражение для
, закодированное с помощью унарного кода
(см. стр. 195), а вторая - двоичное выражение для ![]() , состоящее из
, состоящее из ![]() бит (для малых остатков) или
из
бит (для малых остатков) или
из ![]() бит (для
больших). Если взять
бит (для
больших). Если взять ![]() , то три возможных остатка 0, 1 и 2 будут
кодироваться как 0, 10 и 11. Выбрав
, то три возможных остатка 0, 1 и 2 будут
кодироваться как 0, 10 и 11. Выбрав ![]() , получаем 5 остатков от 0 до 4, которые
кодируются как 00, 01, 100, 101 и 110. В табл. 3.60 приведены некоторые коды
Голомба при
, получаем 5 остатков от 0 до 4, которые
кодируются как 00, 01, 100, 101 и 110. В табл. 3.60 приведены некоторые коды
Голомба при ![]() и
и
![]() .
.
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
|
0|0 |
0|10 |
0|11 |
10|0 |
10|10 |
10|11 |
110|0 |
110|10 |
110|11 |
1110|0 |
|
|
0|00 |
0|01 |
0|100 |
0|101 |
10|110 |
10|00 |
10|01 |
10|100 |
10|101 |
110|110 |
Табл. 3.60. Некоторые коды
Голомба при ![]() и
и
![]() .
.
Предположим, что входной поток
данных состоит из целых чисел, причем вероятность числа ![]() равна
равна ![]() . Здесь
. Здесь ![]() - некоторый параметр,
- некоторый параметр, ![]() . Можно показать, что
коды Голомба будут оптимальными кодами для этого потока данных, если
. Можно показать, что
коды Голомба будут оптимальными кодами для этого потока данных, если ![]() выбрать из условия
выбрать из условия
![]() .
.
Имея такие данные на входе, легко породить наилучшие коды переменной длины, не прибегая к алгоритму Хаффмана.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- Предисловие переводчика
- Предисловие автора
- Введение
- Глава 1. Статистические методы
- 1.1. Энтропия
- 1.2. Коды переменной длины
- 1.3. Декодирование
- 1.4. Кодирование Хаффмана
- 1.4.1. Декодирование Хаффмана
- 1.4.2. Средняя длина кода
- 1.5. Адаптивные коды Хаффмана
- 1.5.1. Несжатые коды
- 1.5.2. Модификация дерева
- 1.5.3. Переполнение счетчика
- 1.5.4. Кодовое переполнение
- 1.5.5. Вариант алгоритма
- 1.6. Факсимильное сжатие
- 1.6.1. Одномерное кодирование
- 1.6.2. Двумерное кодирование
- 1.7. Арифметическое кодирование
- 1.7.1. Детали реализации метода
- 1.7.2. Потеря значащих цифр
- 1.7.3. Заключительные замечания
- 1.8. Адаптивное арифметическое кодирование
- ГЛАВА 2 СЛОВАРНЫЕ МЕТОДЫ
- 2.1. LZ77 (скользящее окно)
- 2.1.1. Циклическая очередь
- 2.2. LZSS
- 2.2.1. Недостатки
- 2.3. LZ78
- 2.4. LZW
- 2.4.1. Декодирование LZW
- 2.4.2. Структура словаря LZW
- 2.4.3. LZW в практических приложениях
- 2.5. Заключение
- ГЛАВА 3 СЖАТИЕ ИЗОБРАЖЕНИЙ
- 3.1. Введение
- 3.2. Типы изображений
- 3.3. Подходы к сжатию изображений
- 3.3.1. Коды Грея
- 3.3.2. Метрики ошибок
- 3.4. Интуитивные методы
- 3.4.1. Подвыборка
- 3.4.2. Квантование
- 3.5. Преобразование изображений
- 3.5.1. Ортогональные преобразования
- 3.5.2. Матричные преобразования
- 3.5.3. Дискретное косинус-преобразование
- 3.5.4. Пример
- 3.5.5. Дискретное синус-преобразование
- 3.5.6. Преобразование Уолша-Адамара
- 3.5.7. Преобразование Хаара
- 3.5.8. Преобразование Кархунена-Лоэвэ
- 3.6. Прогрессирующее сжатие изображений
- 3.7. JPEG
- 3.7.1. Светимость
- 3.7.2. DCT
- 3.7.3. Практическое DCT
- 3.7.4. Квантование
- 3.7.5. Кодирование
- 3.7.6. Мода без потери данных
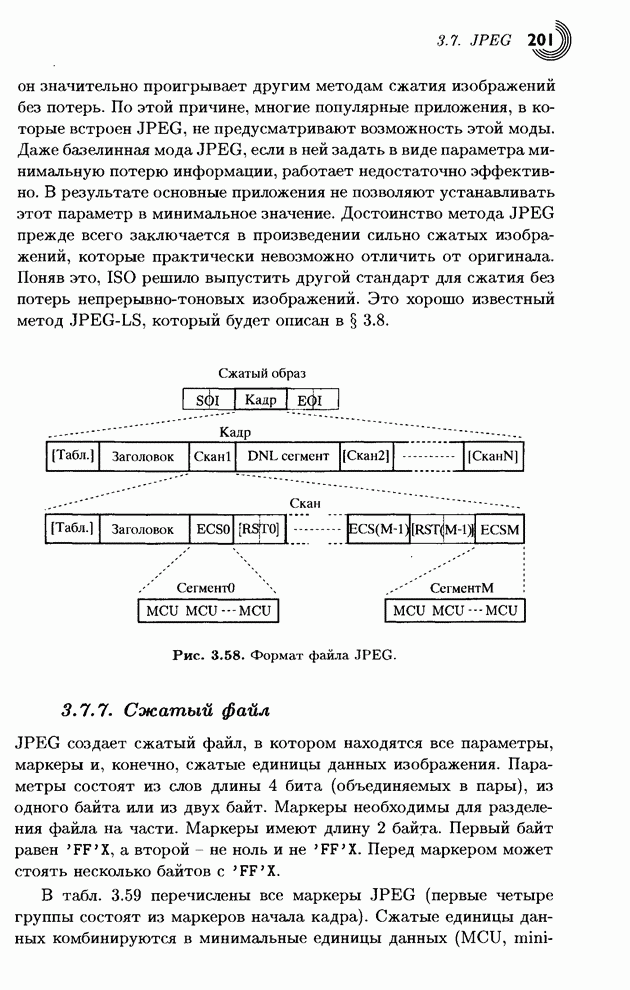
- 3.7.7. Сжатый файл
- 3.7.8. JFIF
- 3.8. JPEG-LS
- 3.8.1. Коды Голомба
- 3.8.2. Основы метода JPEG-LS
- 3.8.3. Кодер
- ГЛАВА 4 ВЕЙВЛЕТНЫЕ МЕТОДЫ
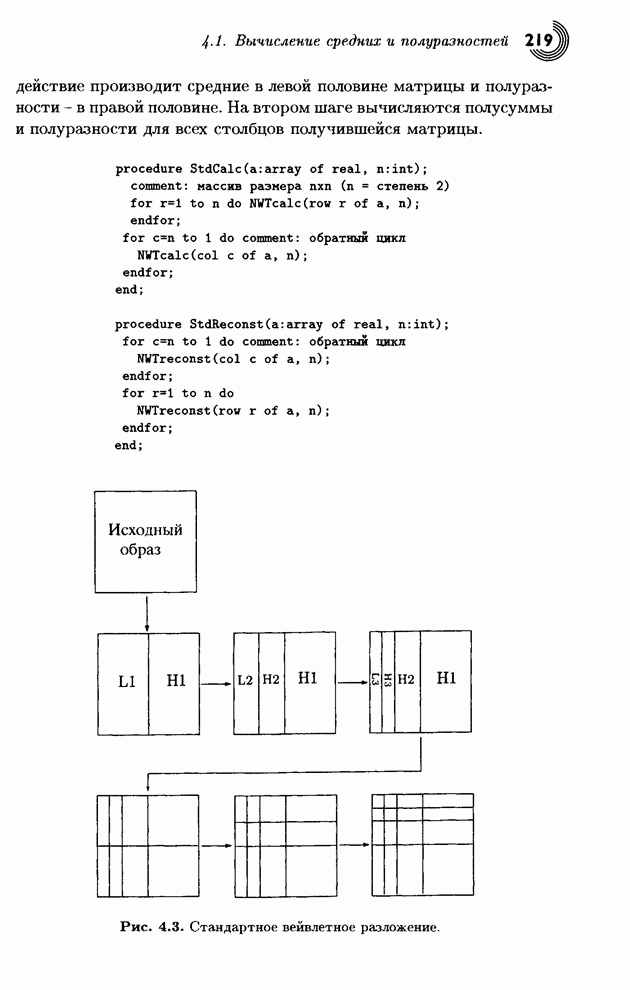
- 4.1. Вычисление средних и полу разностей
- 4.1.1. Обобщение на двумерный случай
- 4.1.2. Свойства преобразования Хаара
- 4.2. Преобразование Хаара
- 4.2.1. Матричная форма
- 4.3. Поддиапазонные преобразования
- 4.4. Банк фильтров
- 4.5. Нахождение коэффициентов фильтра
- 4.6. Преобразование DWT
- 4.7. Примеры
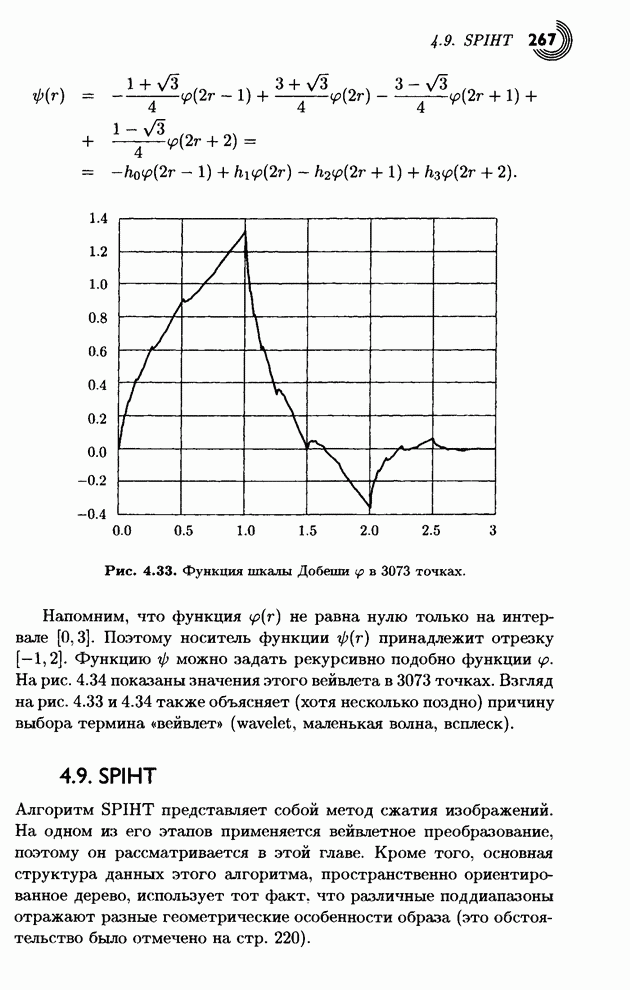
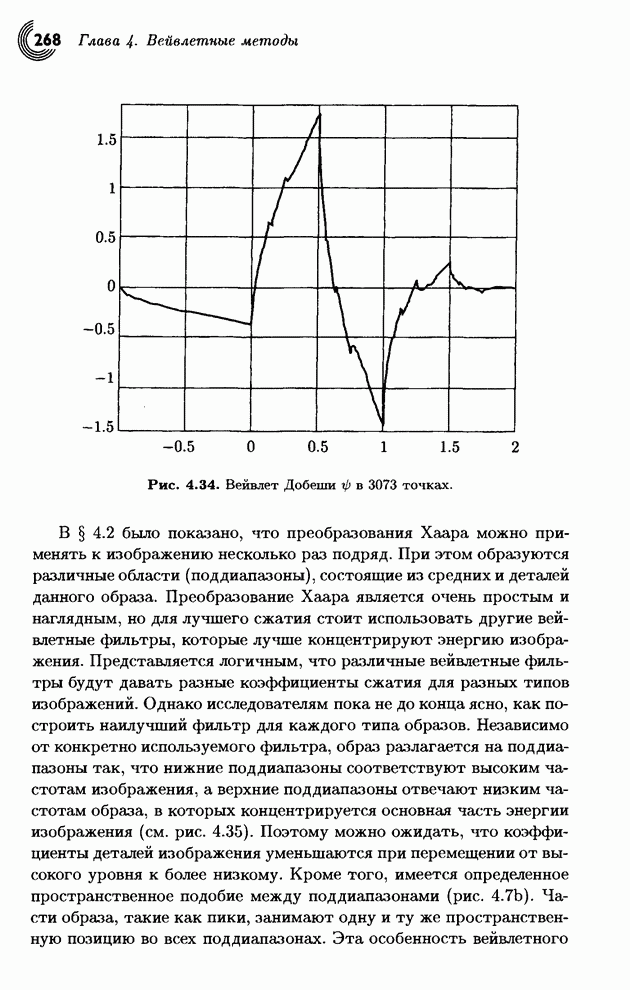
- 4.8. Вейвлеты Добеши
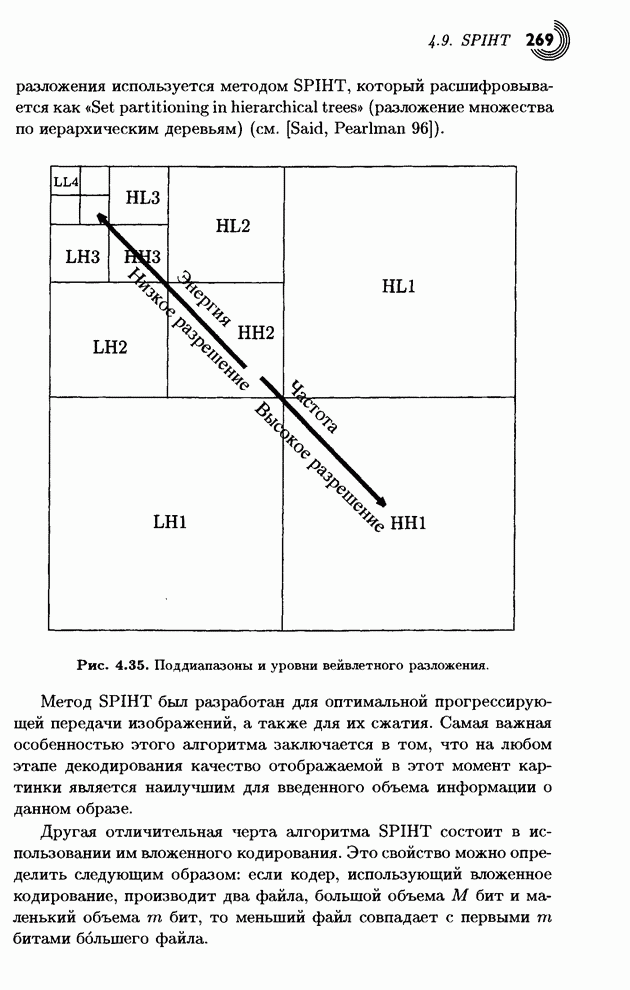
- 4.9. SPIHT
- 4.9.1. Алгоритм сортировки разделением множеств
- 4.9.2. Пространственно ориентированное дерево
- 4.9.3. Кодирование в алгоритме SPIHT
- 4.9.4. Пример
- 4.9.5. QTCQ
- ГЛАВА 5 СЖАТИЕ ВИДЕО
- 5.1. Основные принципы
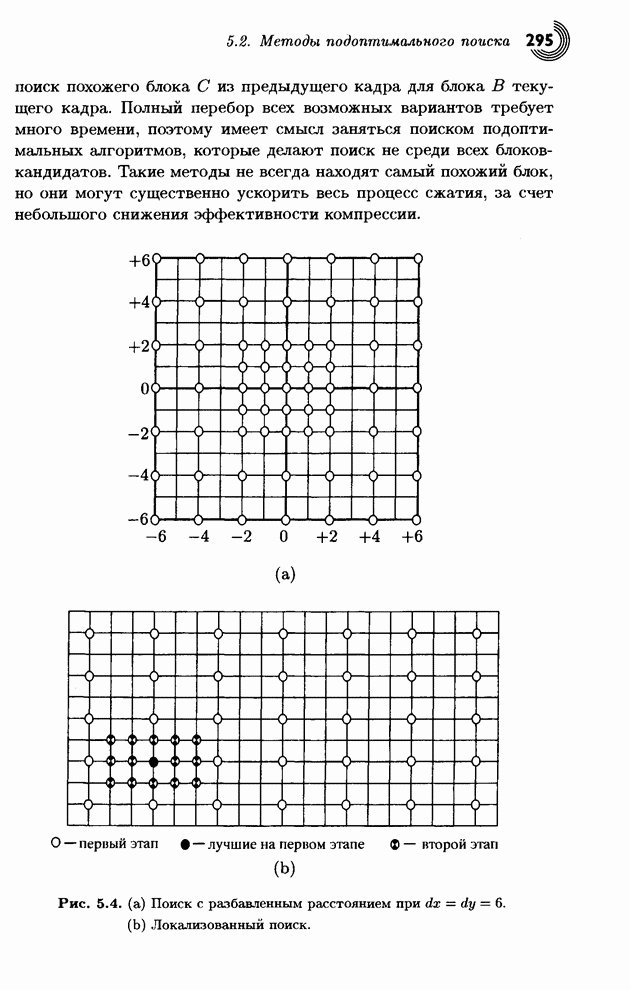
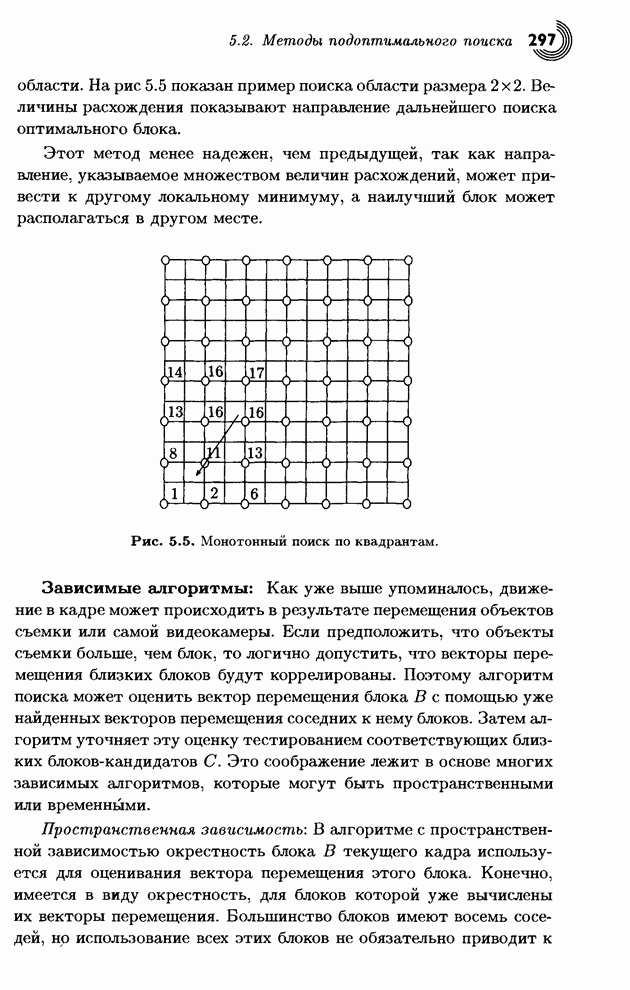
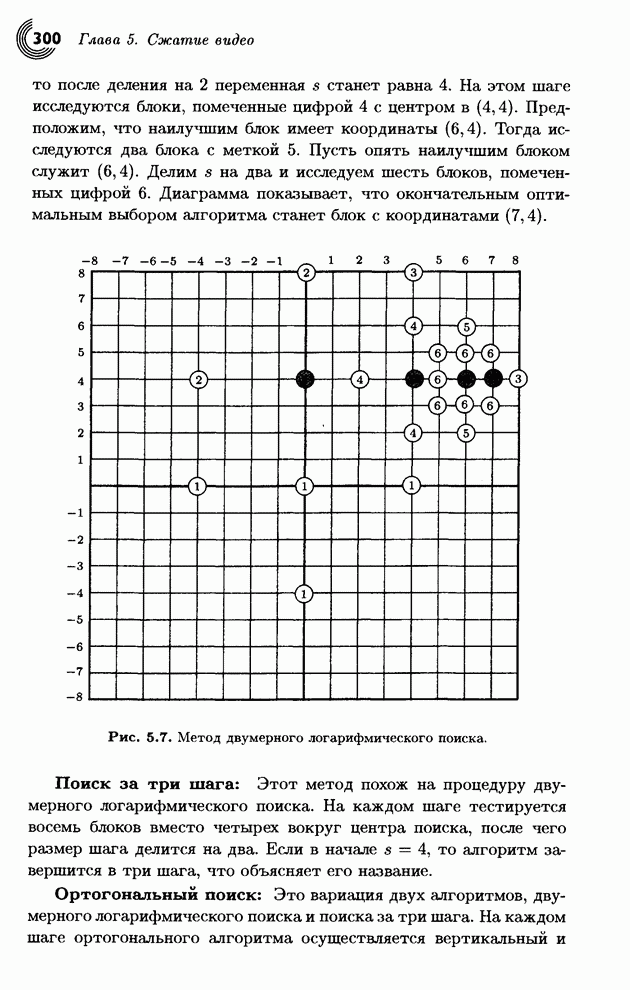
- 5.2. Методы подоптимального поиска
- ГЛАВА 6 СЖАТИЕ ЗВУКА
- 6.1. Звук
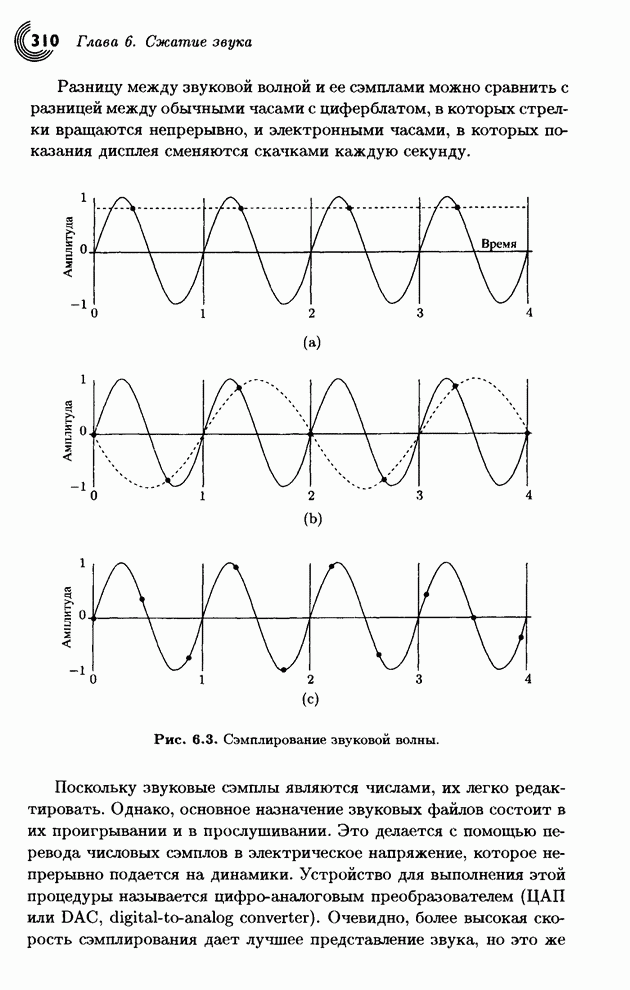
- 6.2. Оцифрованный звук
- 6.3. Органы слуха человека
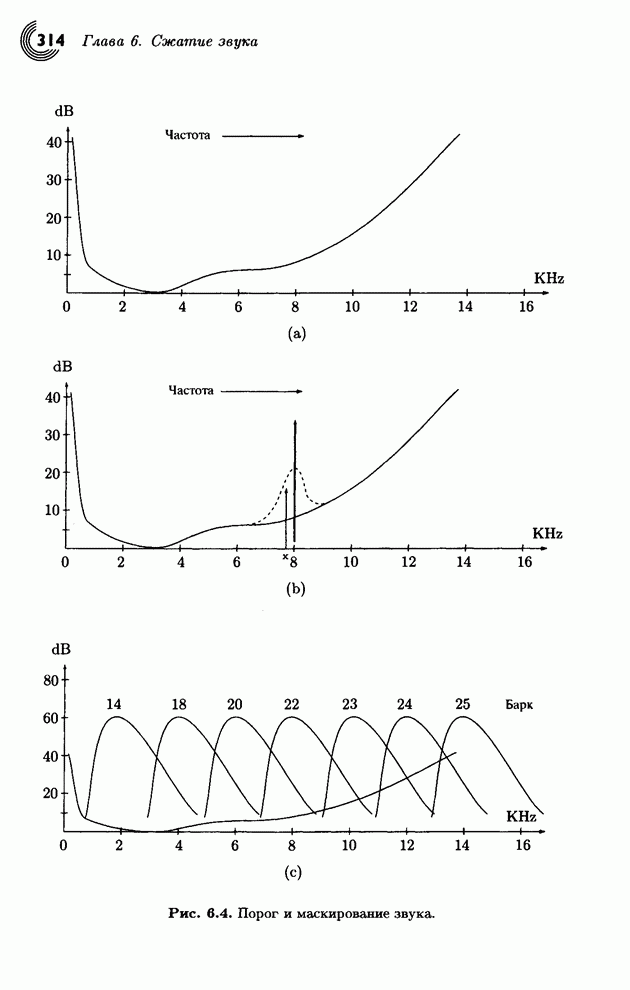
- 6.4. Общепризнанные методы
- 6.5. Сжатие звука в стандарте MPEG-1
- 6.5.1. Кодирование частотной области
- 6.5.2. Формат сжатых данных
- 6.5.3. Психоакустические модели
- 6.5.4. Кодирование: слой III
- Литература
- Глоссарий