| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
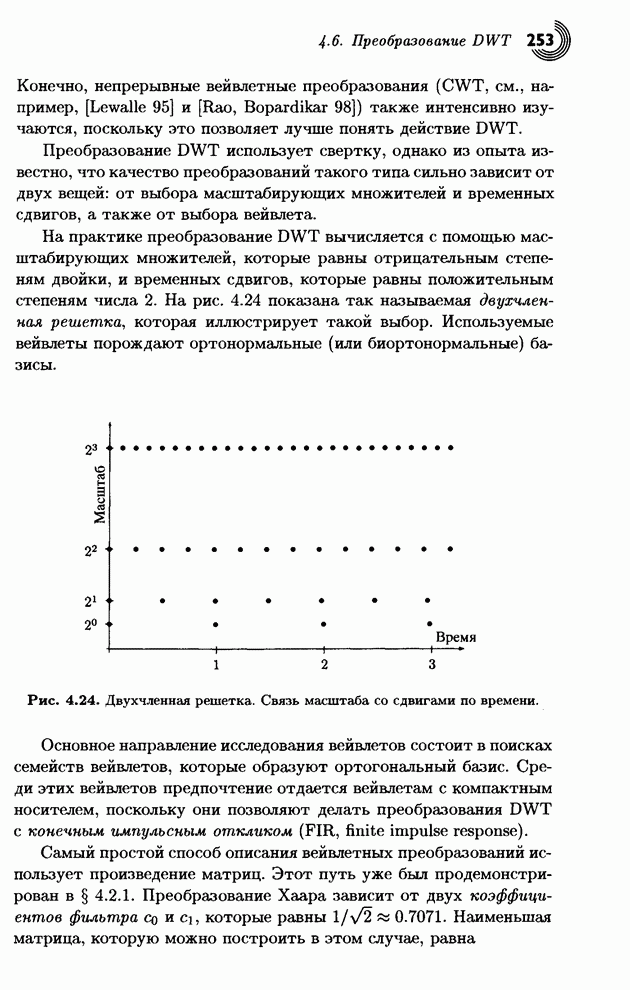
1.5.5. Вариант алгоритма
Этот вариант адаптивного
кодирования Хаффмана очень прост, но менее эффективен. Его идея заключается в
построении множества из ![]() кодов переменной длины на основе равных
вероятностей и случайном присвоении этих кодов
кодов переменной длины на основе равных
вероятностей и случайном присвоении этих кодов ![]() символам. После чего смена кодов
делается «на лету» по мере считывания и сжатия символов. Метод не слишком
производителен, поскольку коды не основаны на реальных вероятностях символов
входного файла. Однако его проще реализовать, и он будет работать быстрее
описанного выше алгоритма, поскольку переставляет строки таблицы быстрее, чем
первый алгоритм перестраивает дерево при изменении частот символов.
символам. После чего смена кодов
делается «на лету» по мере считывания и сжатия символов. Метод не слишком
производителен, поскольку коды не основаны на реальных вероятностях символов
входного файла. Однако его проще реализовать, и он будет работать быстрее
описанного выше алгоритма, поскольку переставляет строки таблицы быстрее, чем
первый алгоритм перестраивает дерево при изменении частот символов.

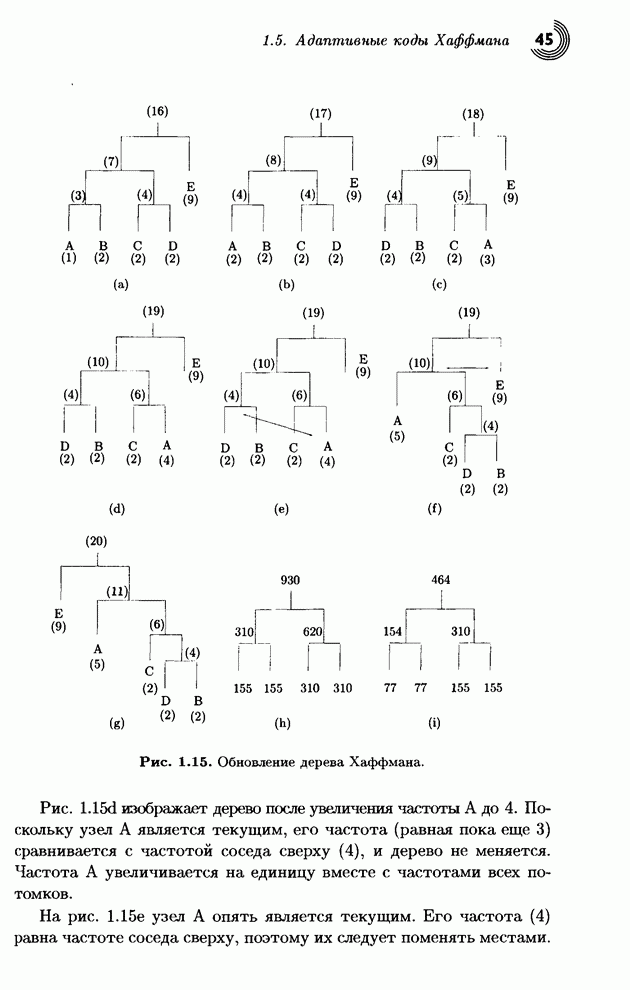
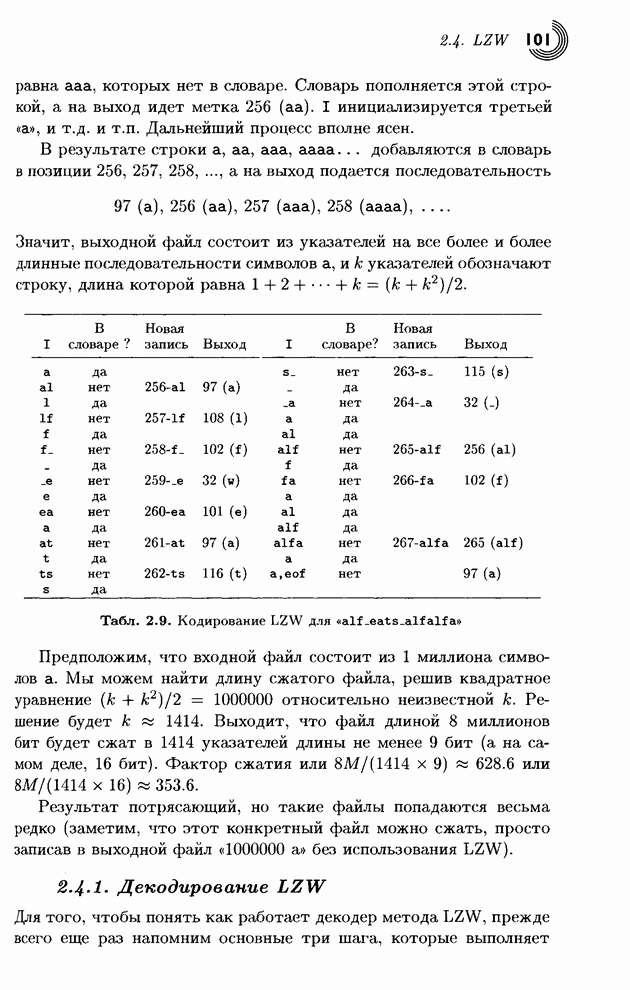
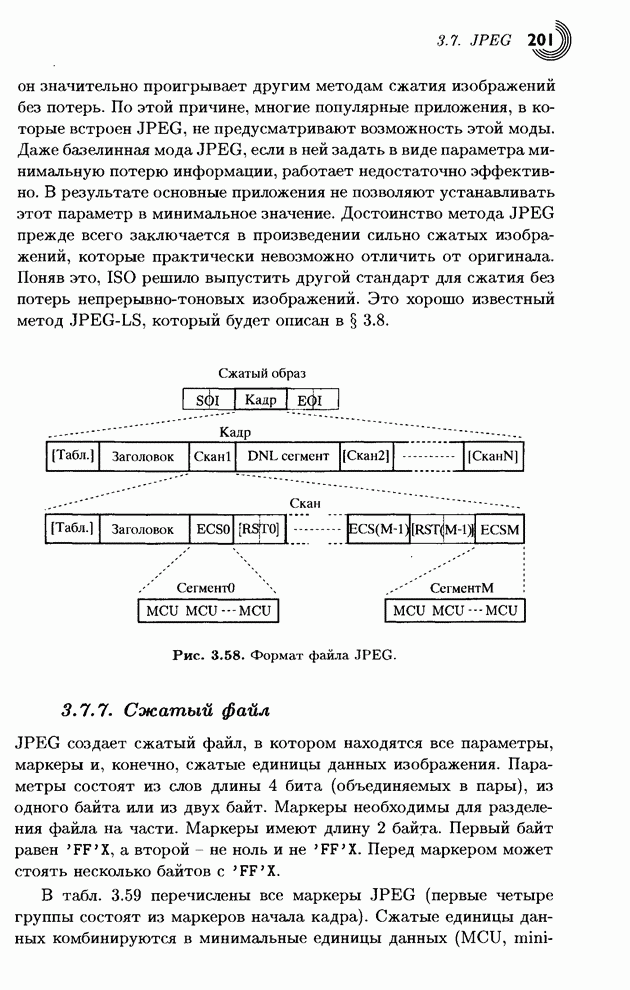
Рис. 1.17. Четыре шага алгоритма типа Хаффмана.
Основная структура данных - это таблица
размера ![]() , в
которой три столбца хранят, соответственно, имена
, в
которой три столбца хранят, соответственно, имена ![]() символов, частоты символов и их коды.
Таблица все время упорядочена по второму столбцу. Когда счетчики частот во
втором столбце изменяются, строки переставляются, но перемещаются только первый
и второй столбцы. Коды в третьем столбце не меняются. На рис. 1.17 показаны
примеры для четырех символов и поведение метода при сжатии строки «
символов, частоты символов и их коды.
Таблица все время упорядочена по второму столбцу. Когда счетчики частот во
втором столбце изменяются, строки переставляются, но перемещаются только первый
и второй столбцы. Коды в третьем столбце не меняются. На рис. 1.17 показаны
примеры для четырех символов и поведение метода при сжатии строки «![]() ».
».
На рис. 1.17а изображено
начальное состояние. После считывания символа ![]() его счетчик увеличивается, и поскольку
он теперь наибольший, строки 1 и 2 меняются местами (рис. 1.17b). Далее считывается второй
символ
его счетчик увеличивается, и поскольку
он теперь наибольший, строки 1 и 2 меняются местами (рис. 1.17b). Далее считывается второй
символ ![]() , его
счетчик увеличивается, и строки 2 и 4 переставляются (рис. 1.17с). Наконец,
после считывания третьего символа
, его
счетчик увеличивается, и строки 2 и 4 переставляются (рис. 1.17с). Наконец,
после считывания третьего символа ![]() , его счетчик становится наибольшим, что
приводит к перестановке строк 1 и 2 (рис. 1.17d).
, его счетчик становится наибольшим, что
приводит к перестановке строк 1 и 2 (рис. 1.17d).
В этом алгоритме только одно
место может вызвать проблему - это переполнение счетчиков. Если переменные
счетчиков имеют разрядность ![]() бит, их максимальное значение равно
бит, их максимальное значение равно ![]() . Поэтому наступит
переполнение после
. Поэтому наступит
переполнение после ![]() -го
увеличения. Это может случиться, если размер сжимаемого файла заранее не
известен, что бывает часто. К счастью, нам не надо знать точные значения
счетчиков. Нам нужен лишь их порядок, поэтому эту проблему переполнения легко
разрешить.
-го
увеличения. Это может случиться, если размер сжимаемого файла заранее не
известен, что бывает часто. К счастью, нам не надо знать точные значения
счетчиков. Нам нужен лишь их порядок, поэтому эту проблему переполнения легко
разрешить.
Можно, например, считать входные
символы, и после ![]() символа
делать целочисленное деление счетчиков на 2 (или сдвигать их содержимое на одну
позицию влево, что проще).
символа
делать целочисленное деление счетчиков на 2 (или сдвигать их содержимое на одну
позицию влево, что проще).
Другой близкий способ - это проверять каждый счетчик после его увеличения и после достижения максимального значения делать деление на 2 всех счетчиков. Этот подход требует более редкого деления, но более сложных проверок.
В любом случае, все операции должны делаться синхронно кодером и декодером.
Сначала соберите ваши факты, а
затем можете
передергивать их по своему
усмотрению. (Факты
упрямая вещь, а статистика более
сговорчива.)
- Марк Твен
| << Предыдущий параграф | Следующий параграф >> |
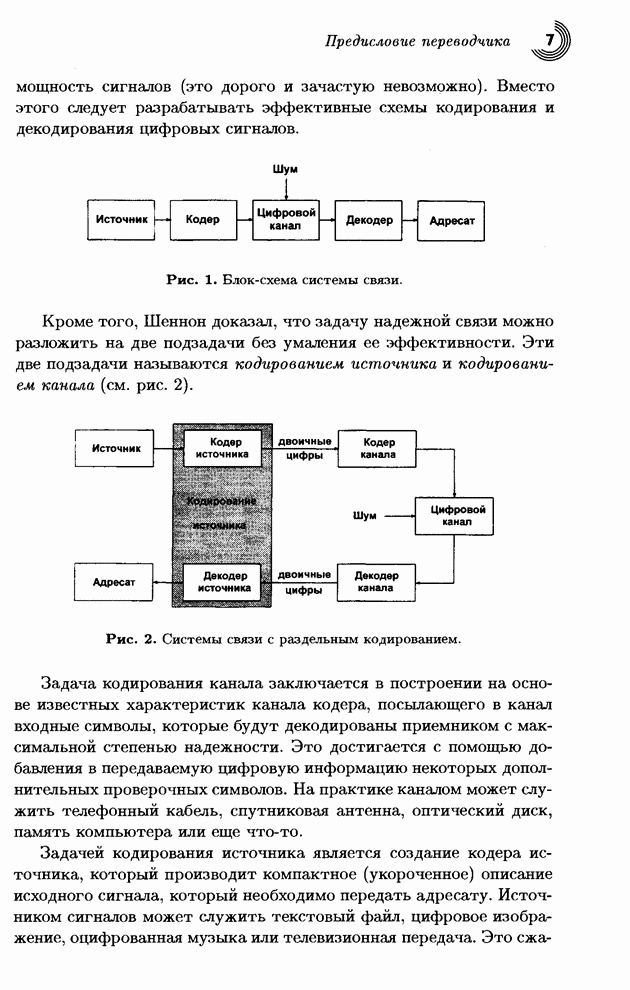
- Предисловие переводчика
- Предисловие автора
- Введение
- Глава 1. Статистические методы
- 1.1. Энтропия
- 1.2. Коды переменной длины
- 1.3. Декодирование
- 1.4. Кодирование Хаффмана
- 1.4.1. Декодирование Хаффмана
- 1.4.2. Средняя длина кода
- 1.5. Адаптивные коды Хаффмана
- 1.5.1. Несжатые коды
- 1.5.2. Модификация дерева
- 1.5.3. Переполнение счетчика
- 1.5.4. Кодовое переполнение
- 1.5.5. Вариант алгоритма
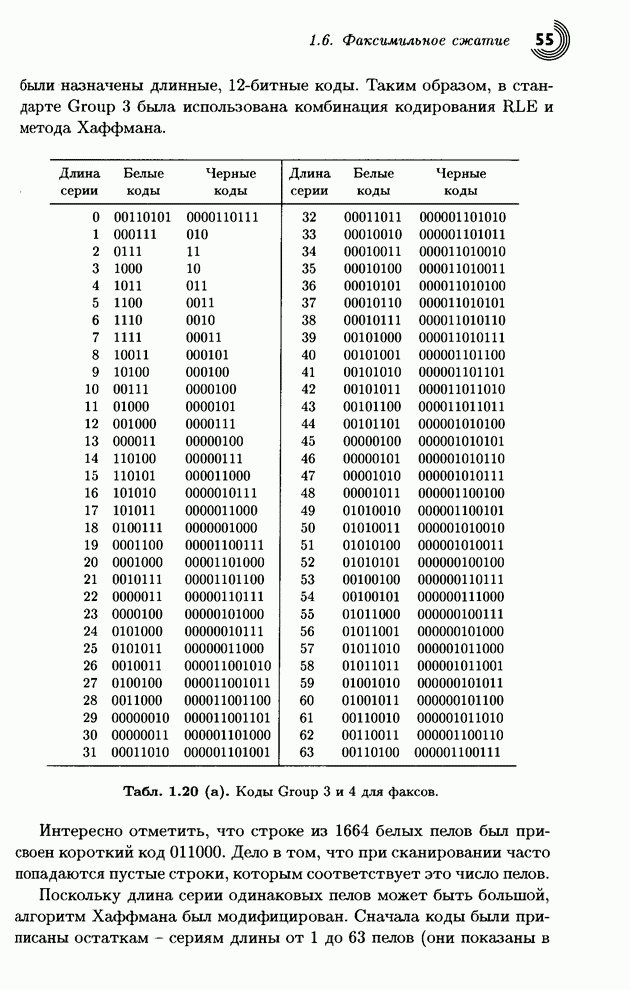
- 1.6. Факсимильное сжатие
- 1.6.1. Одномерное кодирование
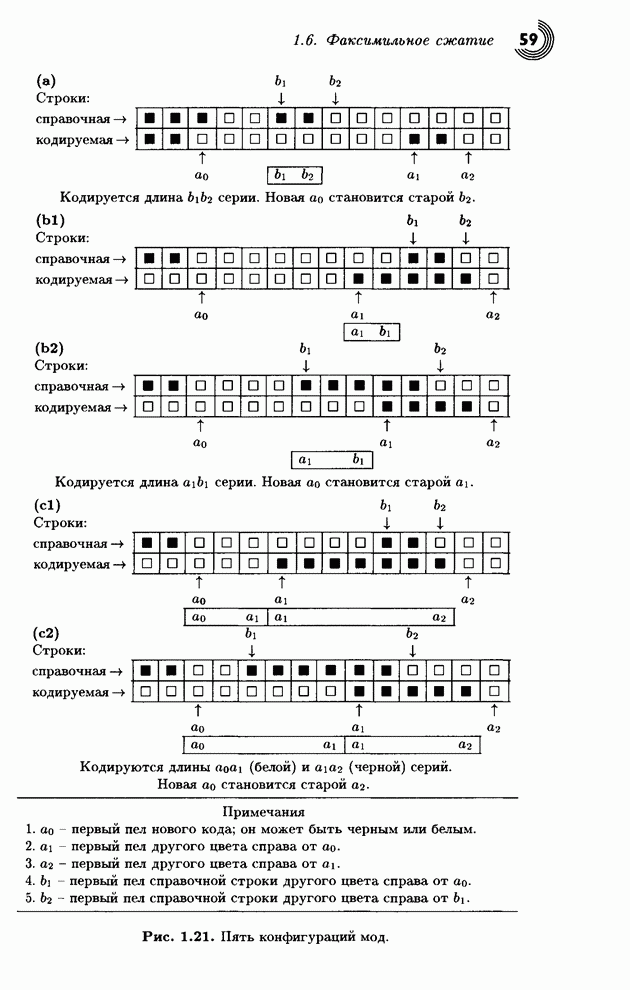
- 1.6.2. Двумерное кодирование
- 1.7. Арифметическое кодирование
- 1.7.1. Детали реализации метода
- 1.7.2. Потеря значащих цифр
- 1.7.3. Заключительные замечания
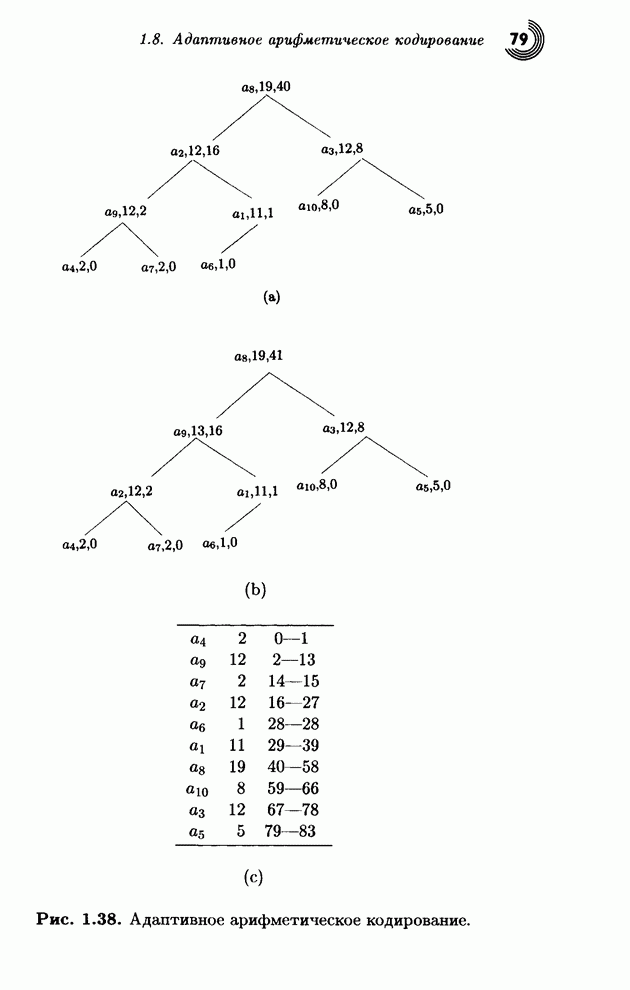
- 1.8. Адаптивное арифметическое кодирование
- ГЛАВА 2 СЛОВАРНЫЕ МЕТОДЫ
- 2.1. LZ77 (скользящее окно)
- 2.1.1. Циклическая очередь
- 2.2. LZSS
- 2.2.1. Недостатки
- 2.3. LZ78
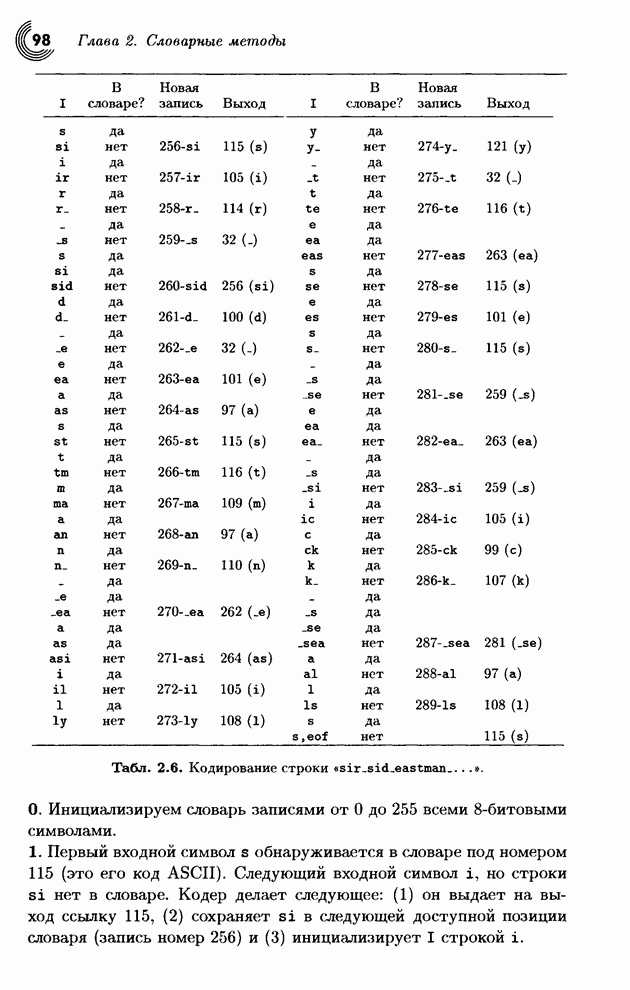
- 2.4. LZW
- 2.4.1. Декодирование LZW
- 2.4.2. Структура словаря LZW
- 2.4.3. LZW в практических приложениях
- 2.5. Заключение
- ГЛАВА 3 СЖАТИЕ ИЗОБРАЖЕНИЙ
- 3.1. Введение
- 3.2. Типы изображений
- 3.3. Подходы к сжатию изображений
- 3.3.1. Коды Грея
- 3.3.2. Метрики ошибок
- 3.4. Интуитивные методы
- 3.4.1. Подвыборка
- 3.4.2. Квантование
- 3.5. Преобразование изображений
- 3.5.1. Ортогональные преобразования
- 3.5.2. Матричные преобразования
- 3.5.3. Дискретное косинус-преобразование
- 3.5.4. Пример
- 3.5.5. Дискретное синус-преобразование
- 3.5.6. Преобразование Уолша-Адамара
- 3.5.7. Преобразование Хаара
- 3.5.8. Преобразование Кархунена-Лоэвэ
- 3.6. Прогрессирующее сжатие изображений
- 3.7. JPEG
- 3.7.1. Светимость
- 3.7.2. DCT
- 3.7.3. Практическое DCT
- 3.7.4. Квантование
- 3.7.5. Кодирование
- 3.7.6. Мода без потери данных
- 3.7.7. Сжатый файл
- 3.7.8. JFIF
- 3.8. JPEG-LS
- 3.8.1. Коды Голомба
- 3.8.2. Основы метода JPEG-LS
- 3.8.3. Кодер
- ГЛАВА 4 ВЕЙВЛЕТНЫЕ МЕТОДЫ
- 4.1. Вычисление средних и полу разностей
- 4.1.1. Обобщение на двумерный случай
- 4.1.2. Свойства преобразования Хаара
- 4.2. Преобразование Хаара
- 4.2.1. Матричная форма
- 4.3. Поддиапазонные преобразования
- 4.4. Банк фильтров
- 4.5. Нахождение коэффициентов фильтра
- 4.6. Преобразование DWT
- 4.7. Примеры
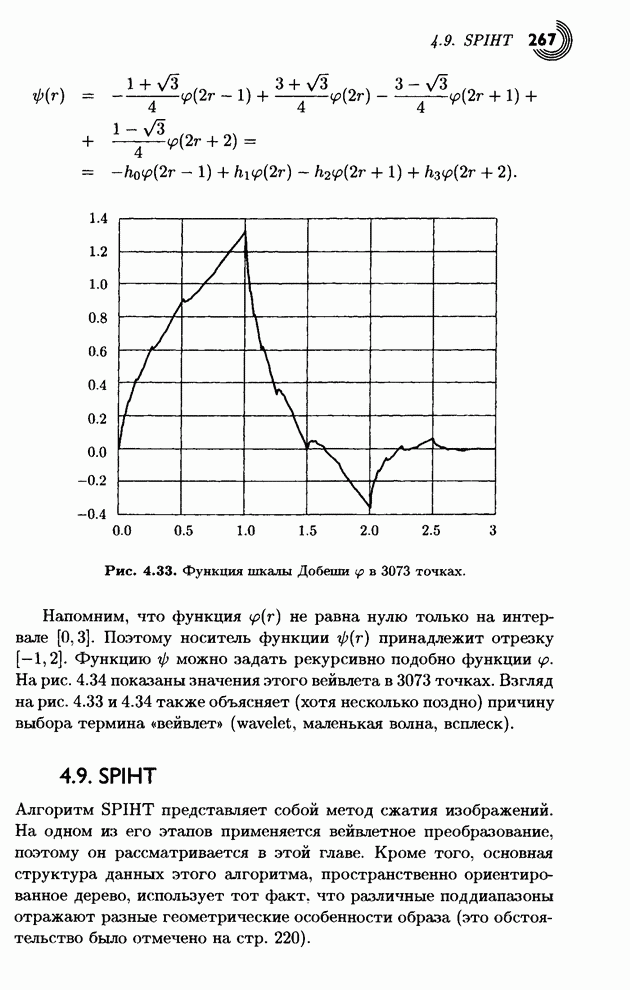
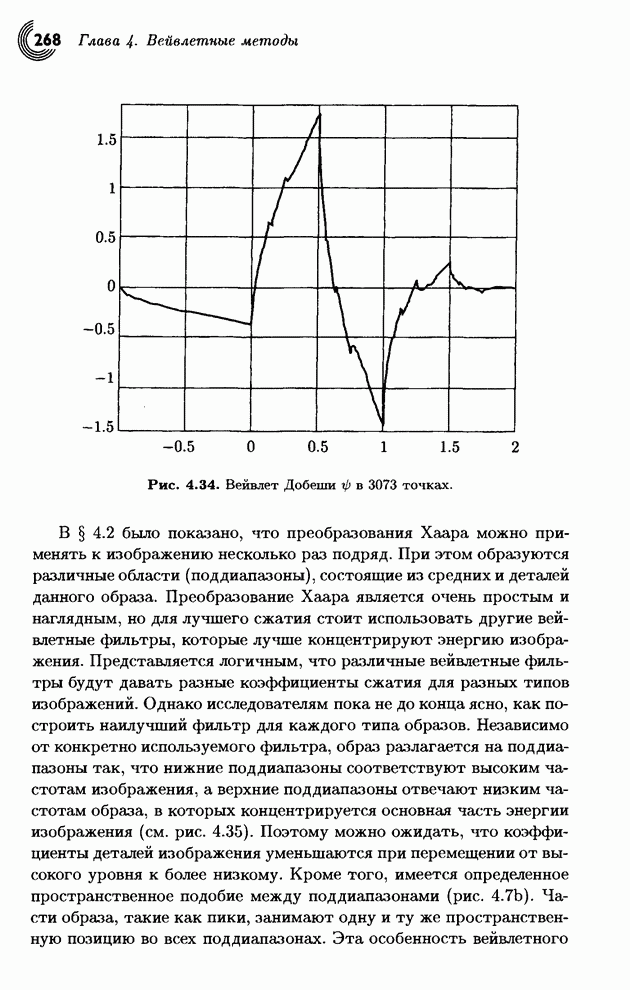
- 4.8. Вейвлеты Добеши
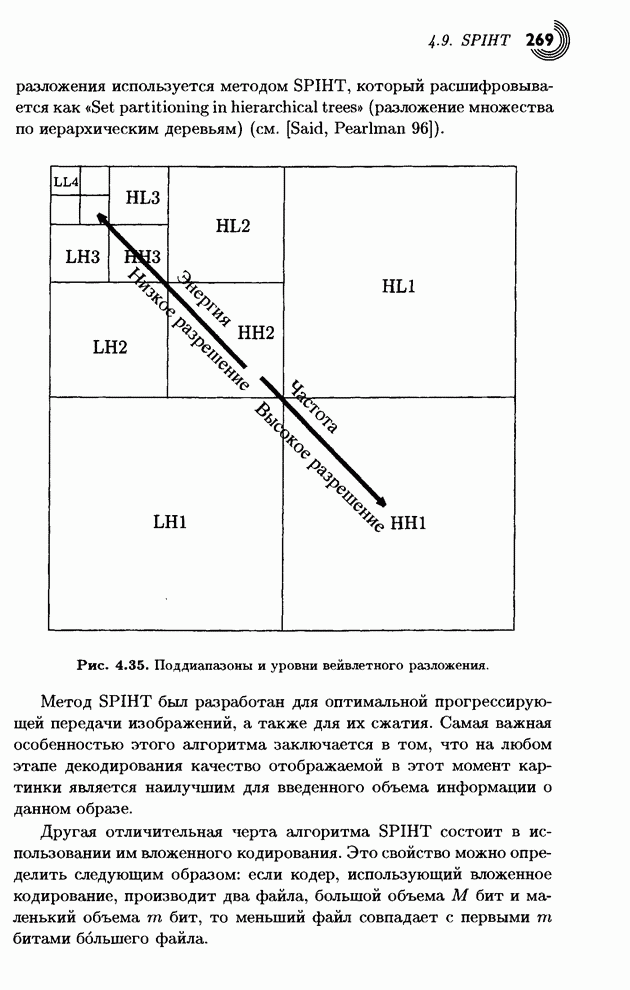
- 4.9. SPIHT
- 4.9.1. Алгоритм сортировки разделением множеств
- 4.9.2. Пространственно ориентированное дерево
- 4.9.3. Кодирование в алгоритме SPIHT
- 4.9.4. Пример
- 4.9.5. QTCQ
- ГЛАВА 5 СЖАТИЕ ВИДЕО
- 5.1. Основные принципы
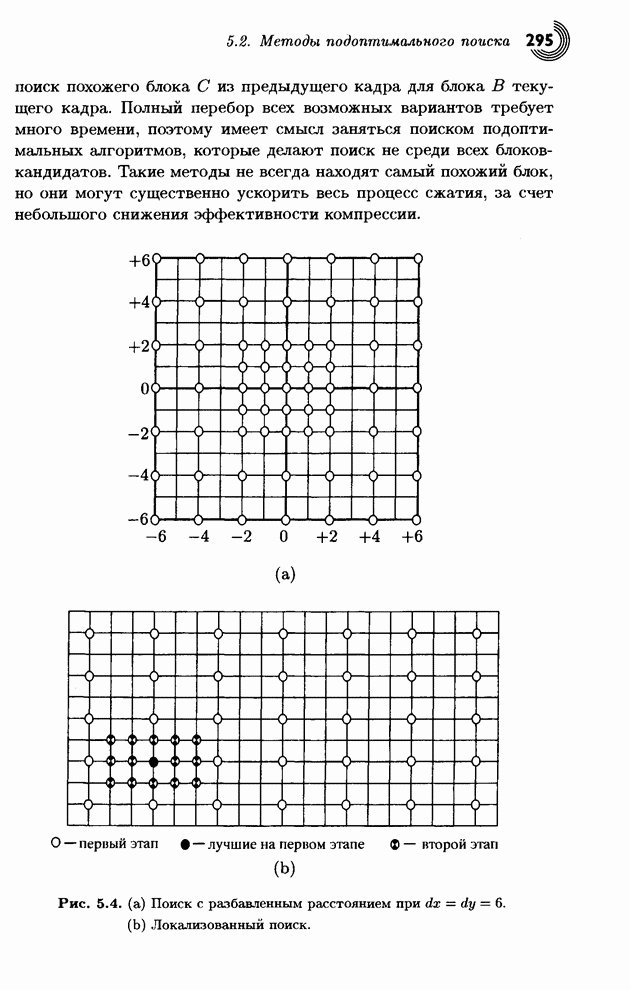
- 5.2. Методы подоптимального поиска
- ГЛАВА 6 СЖАТИЕ ЗВУКА
- 6.1. Звук
- 6.2. Оцифрованный звук
- 6.3. Органы слуха человека
- 6.4. Общепризнанные методы
- 6.5. Сжатие звука в стандарте MPEG-1
- 6.5.1. Кодирование частотной области
- 6.5.2. Формат сжатых данных
- 6.5.3. Психоакустические модели
- 6.5.4. Кодирование: слой III
- Литература
- Глоссарий