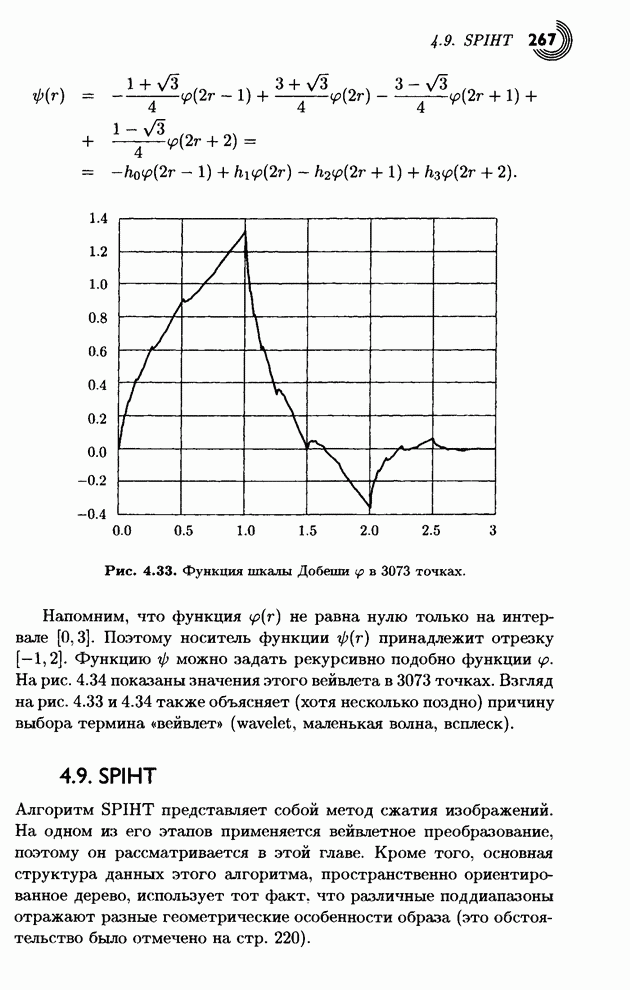
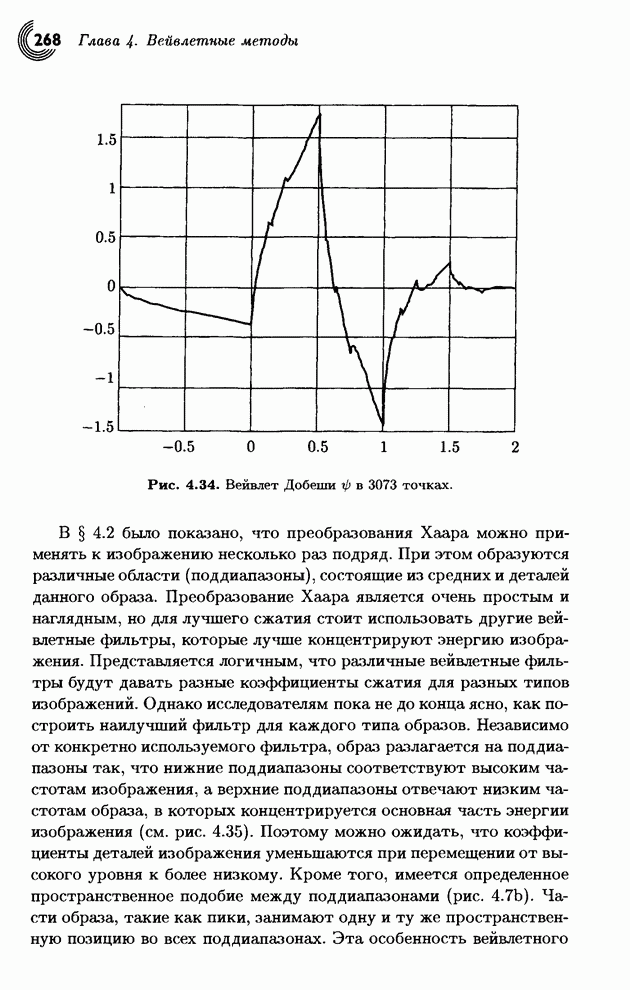
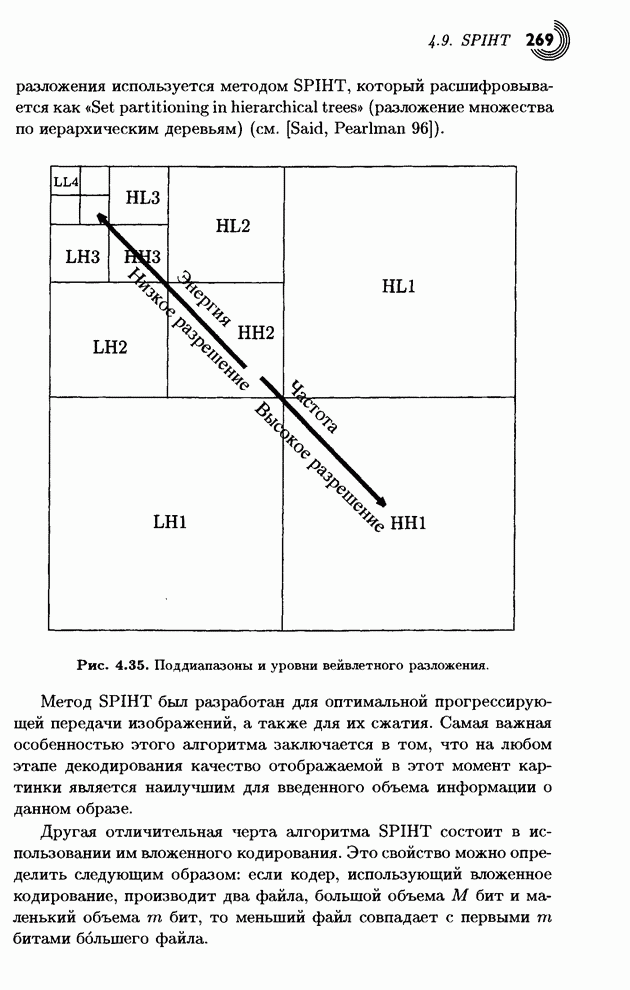
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
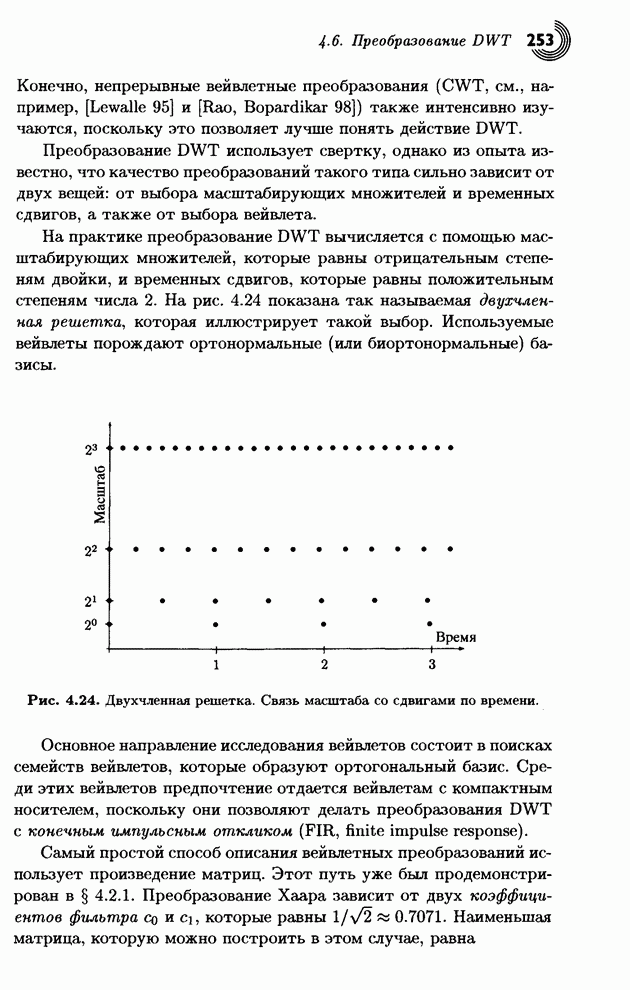
5.2. Методы подоптимального поиска
Сжатие видеоданных имеет много
шагов и использует большие вычислительные ресурсы. Исследования в этой области
направлены на оптимизацию и ускорение алгоритмов сжатия, особенно для шагов,
использующих больше вычислений. Одним из таких шагов является поиск похожего
блока ![]() из
предыдущего кадра для блока
из
предыдущего кадра для блока ![]() текущего кадра. Полный перебор всех
возможных вариантов требует много времени, поэтому имеет смысл заняться поиском
под оптимальных алгоритмов, которые делают поиск не среди всех блоков-
кандидатов. Такие методы не всегда находят самый похожий блок, но они могут
существенно ускорить весь процесс сжатия, за счет небольшого снижения
эффективности компрессии.
текущего кадра. Полный перебор всех
возможных вариантов требует много времени, поэтому имеет смысл заняться поиском
под оптимальных алгоритмов, которые делают поиск не среди всех блоков-
кандидатов. Такие методы не всегда находят самый похожий блок, но они могут
существенно ускорить весь процесс сжатия, за счет небольшого снижения
эффективности компрессии.

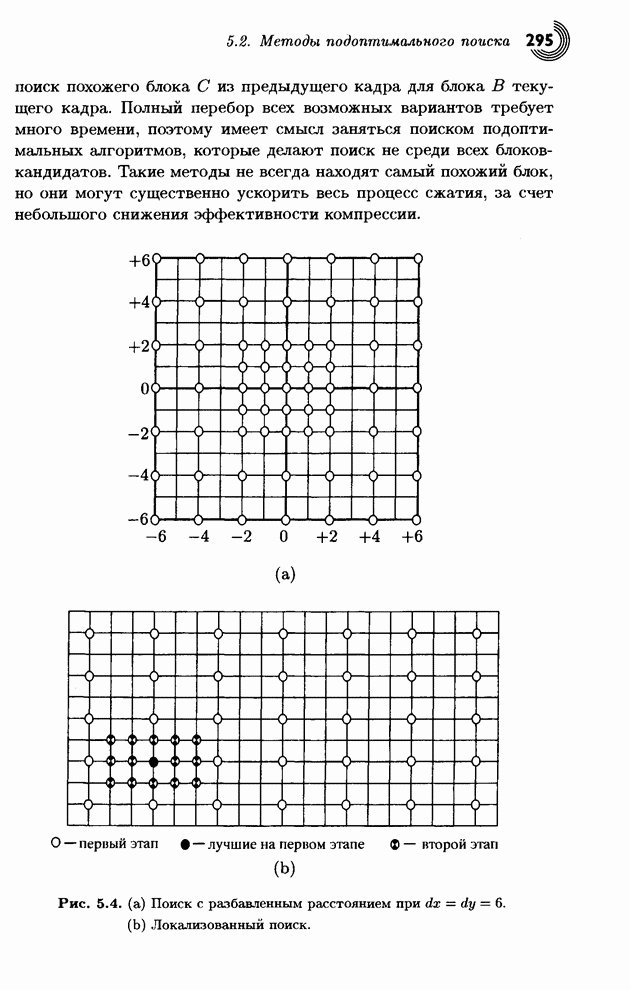
Рис. 5.4. (а) Поиск с
разбавленным расстоянием при ![]() ; (b) Локализованный поиск.
; (b) Локализованный поиск.
Сигнатурные методы: Эти методы совершают несколько шагов, сокращая число кандидатов на каждом шаге. На первом шаге все кандидаты испытываются с помощью простой и быстро вычисляемой меры расходимости, например, функцией ранжирования разностей пикселов. Только самые близкие блоки попадают на следующий шаг, где они оцениваются более сложными мерами расходимости или той же мерой, но с меньшим параметром. Сигнатурный метод может состоять из многих шагов с разными тестовыми мерами расходимости.
Поиск с разбавленным расстоянием: Из опыта известно, что быстро
перемещающиеся объекты выглядят смазанными при воспроизведении на экране, даже
если они имеют четкие очертания на каждом кадре. Это подсказывает возможный
путь для отбрасывания части информации. Можно требовать хорошего совпадения для
медленно перемещающихся объектов, и приблизительного совпадения для тех, что
перемещаются быстро. В итоге получаем алгоритм, который оценивает для каждого
блока ![]() все
ближайшие к нему блоки-кандидаты, а для более удаленных блоков он рассматривает
все меньшую часть блоков. На рис. 5.4а показано, как такой метод мог бы
работать для параметров максимального смещения
все
ближайшие к нему блоки-кандидаты, а для более удаленных блоков он рассматривает
все меньшую часть блоков. На рис. 5.4а показано, как такой метод мог бы
работать для параметров максимального смещения ![]() . Общее число оцениваемых блоков
. Общее число оцениваемых блоков ![]() сокращается с
сокращается с ![]() до всего 65, то
есть, до 39%!
до всего 65, то
есть, до 39%!
Локализованный поиск: Этот метод основан на гипотезе, что если хорошее совпадение найдено, то еще лучшее совпадение, возможно, находится где-то рядом (напомним, что поиск делается среди сильно перекрывающихся блоков). Очевидный алгоритм поиска начинается с изучения разреженного семейства блоков. Затем наиболее подходящий блок из этого семейства используется в качестве центра для более тщательного поиска. На рис. 5.4b покачаны два этапа поиска: первый этап рассматривает широко расставленные блоки и выбирает наиболее близкий из них, а второй тестирует каждый блок в окрестности этого хорошего блока.
Монотонный поиск по квадрантам: Это один из вариантов метода
локализованного поиска. Сначала анализируется разреженное семейство блоков ![]() . Для каждого блока из
этого семейства вычисляется мера расходимости. Идея заключается в том, что
величина этой меры увеличивается при удалении от оптимального блока, имеющего
минимальное расхождение с блоком
. Для каждого блока из
этого семейства вычисляется мера расходимости. Идея заключается в том, что
величина этой меры увеличивается при удалении от оптимального блока, имеющего
минимальное расхождение с блоком ![]() . Это позволяет достаточно хорошо
спрогнозировать область, в которой расположен оптимальный блок. На втором шаге
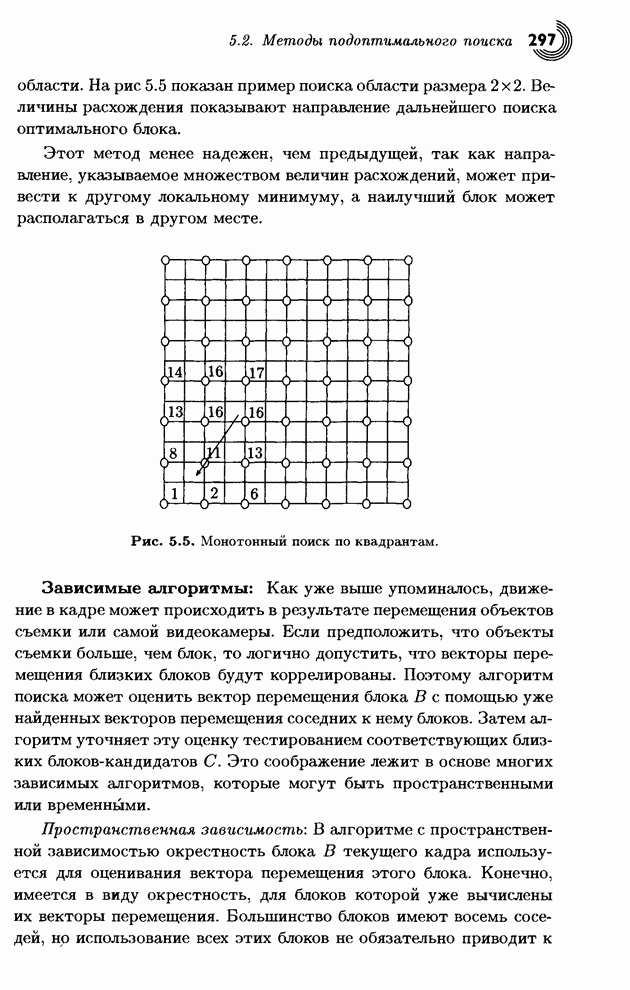
изучается каждый блок из этой области. На рис 5.5 показан пример поиска области
размера 2x2. Величины расхождения показывают направление дальнейшего поиска
оптимального блока.
. Это позволяет достаточно хорошо
спрогнозировать область, в которой расположен оптимальный блок. На втором шаге
изучается каждый блок из этой области. На рис 5.5 показан пример поиска области
размера 2x2. Величины расхождения показывают направление дальнейшего поиска
оптимального блока.
Этот метод менее надежен, чем предыдущей, так как направление, указываемое множеством величин расхождений, может привести к другому локальному минимуму, а наилучший блок может располагаться в другом месте.

Рис. 5.5. Монотонный поиск по квадрантам.
Зависимые алгоритмы: Как уже выше упоминалось,
движение в кадре может происходить в результате перемещения объектов съемки или
самой видеокамеры. Если предположить, что объекты съемки больше, чем блок, то
логично допустить, что векторы перемещения близких блоков будут коррелированны.
Поэтому алгоритм поиска может оценить вектор перемещения блока ![]() с помощью уже
найденных векторов перемещения соседних к нему блоков. Затем алгоритм уточняет
эту оценку тестированием соответствующих близких блоков-кандидатов
с помощью уже
найденных векторов перемещения соседних к нему блоков. Затем алгоритм уточняет
эту оценку тестированием соответствующих близких блоков-кандидатов ![]() . Это соображение
лежит в основе многих зависимых алгоритмов, которые могут быть
пространственными или временными.
. Это соображение
лежит в основе многих зависимых алгоритмов, которые могут быть
пространственными или временными.
Пространственная зависимость: В алгоритме с пространственной зависимостью
окрестность блока ![]() текущего
кадра используется для оценивания вектора перемещения этого блока. Конечно,
имеется в виду окрестность, для блоков которой уже вычислены их векторы
перемещения. Большинство блоков имеют восемь соседей, но использование всех
этих блоков не обязательно приводит к наилучшей стратегии (кроме того, не для
всех этих соседей векторы перемещения будут уже вычислены). Если блоки
сравниваются в растровом порядке, то имеет смысл использовать одного, двух или
трех подходящих соседей, как показано на рис. 5.6а,b,с. Однако, в силу симметрии будет лучше
использовать четырех соседей, показанных на рис. 5.6d,e. При этом можно применить метод,
состоящий из трех проходов, который анализирует блоки, отмеченный на рис. 5.6f. На первом проходе сканируются
черные блоки (четверть всех блоков на рисунке). Векторы перемещения для этих
блоков вычисляются некоторым другим методом. На втором проходе оцениваются
серые блоки (их тоже 25% от общего числа), с помощью векторов перемещения их
угловых соседей. Наконец, белые блоки (их 50%) изучаются на третьем проходе.
Для вычисления их векторов перемещения используются четыре соседа, прилегающие
к их сторонам. Если векторы перемещений соседних блоков сильно различаются, то
их не стоит использовать, а вектор перемещения блока
текущего
кадра используется для оценивания вектора перемещения этого блока. Конечно,
имеется в виду окрестность, для блоков которой уже вычислены их векторы
перемещения. Большинство блоков имеют восемь соседей, но использование всех
этих блоков не обязательно приводит к наилучшей стратегии (кроме того, не для
всех этих соседей векторы перемещения будут уже вычислены). Если блоки
сравниваются в растровом порядке, то имеет смысл использовать одного, двух или
трех подходящих соседей, как показано на рис. 5.6а,b,с. Однако, в силу симметрии будет лучше
использовать четырех соседей, показанных на рис. 5.6d,e. При этом можно применить метод,
состоящий из трех проходов, который анализирует блоки, отмеченный на рис. 5.6f. На первом проходе сканируются
черные блоки (четверть всех блоков на рисунке). Векторы перемещения для этих
блоков вычисляются некоторым другим методом. На втором проходе оцениваются
серые блоки (их тоже 25% от общего числа), с помощью векторов перемещения их
угловых соседей. Наконец, белые блоки (их 50%) изучаются на третьем проходе.
Для вычисления их векторов перемещения используются четыре соседа, прилегающие
к их сторонам. Если векторы перемещений соседних блоков сильно различаются, то
их не стоит использовать, а вектор перемещения блока ![]() придется вычислять другим
методом.
придется вычислять другим
методом.

Рис. 5.6. Стратегии алгоритмов с пространственной зависимостью.
Временная зависимость: Вектор перемещения блока ![]() текущего кадра можно
оценить с помощью вектора перемещения этого же блока на предыдущем кадре. Это
имеет смысл, если движение в кадре предполагается плавным. После нахождения
этой оценки, вектор перемещения можно уточнить другим подходящим методом.
текущего кадра можно
оценить с помощью вектора перемещения этого же блока на предыдущем кадре. Это
имеет смысл, если движение в кадре предполагается плавным. После нахождения
этой оценки, вектор перемещения можно уточнить другим подходящим методом.
Вариант метода монотонного поиска по квадрантам: Следующие подоптимальные алгоритмы используют основную идею метода монотонного поиска подходящего блока.
Двумерный логарифмический поиск: Этот многошаговый алгоритм
сокращает область поиска на каждом шаге, пока она не сведется к одному блоку.
Предположим, что текущий блок ![]() локализован в точке
локализован в точке ![]() текущего кадра. Эта точка
берется за центр поиска. Алгоритм зависит от параметра
текущего кадра. Эта точка
берется за центр поиска. Алгоритм зависит от параметра ![]() , задающего удаление от центра
поиска. Этот параметр контролируется пользователем. Квадратная область поиска
состоит из
, задающего удаление от центра
поиска. Этот параметр контролируется пользователем. Квадратная область поиска
состоит из ![]() блоков
с центром в блоке
блоков
с центром в блоке ![]() .
.
Шаг 1: Размер шага вычисляется по формуле
![]() ,
,
и
алгоритм сравнивает блок ![]() с пятью блоками в точках с координатами
с пятью блоками в точках с координатами ![]() ,
, ![]() ,
, ![]() ,
, ![]() и
и ![]() на предыдущем кадре. Эти пять блоков
образуют шаблон в форме знака +.
на предыдущем кадре. Эти пять блоков
образуют шаблон в форме знака +.
Шаг
2: Выбирается
наилучший из этих пяти блоков. Обозначим его координаты через ![]() . Если
. Если ![]() , то
, то ![]() делится пополам
(поэтому алгоритм называется логарифмическим). В противном случае шаг
делится пополам
(поэтому алгоритм называется логарифмическим). В противном случае шаг ![]() не меняется, а центр
поиска
не меняется, а центр
поиска ![]() перемещается
в точку
перемещается
в точку ![]() .
.
Шаг
3: Если ![]() , то оцениваются
девять блоков вокруг центра поиска
, то оцениваются
девять блоков вокруг центра поиска ![]() , и наилучший блок становится результатом
работы алгоритма. В противном случае делается переход на Шаг 2.
, и наилучший блок становится результатом
работы алгоритма. В противном случае делается переход на Шаг 2.
Если нужный алгоритму блок
выходит за пределы области поиска, то он игнорируется и не используется. Рис.
5.7 иллюстрирует случай, когда ![]() . Для простоты предполагается, что
текущий блок
. Для простоты предполагается, что
текущий блок ![]() имеет
координаты
имеет
координаты ![]() .
Поиск ограничивается областью из 17х17 блоков с центром в
.
Поиск ограничивается областью из 17х17 блоков с центром в ![]() . На шаге 1 вычисляется
. На шаге 1 вычисляется
![]() ,
,
и
изучаются пять блоков с координатами ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() . Предположим, что наилучшее значение
имеет блок
. Предположим, что наилучшее значение
имеет блок ![]() ,
который становится центром нового поиска. Теперь на втором шаге изучаются три
блока (помеченные цифрой 2) с координатами
,
который становится центром нового поиска. Теперь на втором шаге изучаются три
блока (помеченные цифрой 2) с координатами ![]() ,
, ![]() ,
, ![]() .
.
Если лучшим среди них будет блок ![]() , то на следующем шаге
будут исследоваться 2 блока с меткой 3 с координатами
, то на следующем шаге
будут исследоваться 2 блока с меткой 3 с координатами ![]() и
и ![]() , блок
, блок ![]() с меткой 2 и два блока
с меткой 2 и два блока ![]() и
и ![]() , имеющие метку 1.
, имеющие метку 1.
Предположим, что на следующем
шаге наилучшим выбором будет блок ![]() . Поскольку этот блок находится в центре
знака +, то после деления на 2 переменная
. Поскольку этот блок находится в центре
знака +, то после деления на 2 переменная ![]() станет равна 4. На этом шаге исследуются
блоки, помеченные цифрой 4 с центром в
станет равна 4. На этом шаге исследуются
блоки, помеченные цифрой 4 с центром в ![]() . Предположим, что наилучший блок имеет
координаты
. Предположим, что наилучший блок имеет
координаты ![]() .
Тогда исследуются два блока с меткой 5. Пусть опять наилучшим блоком служит
.
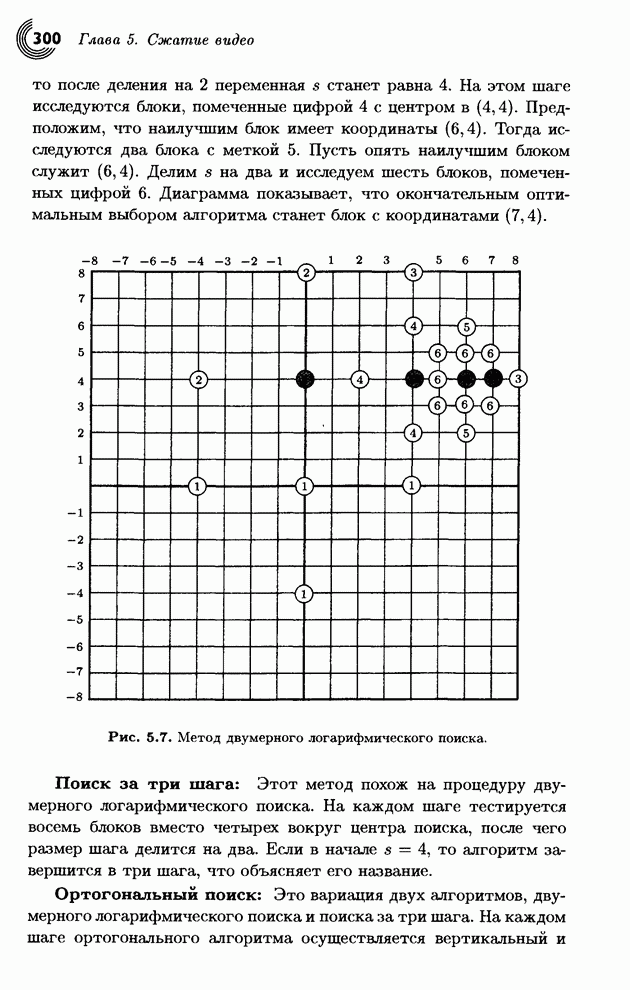
Тогда исследуются два блока с меткой 5. Пусть опять наилучшим блоком служит ![]() . Делим
. Делим ![]() на два и исследуем
шесть блоков, помеченных цифрой 6. Диаграмма показывает, что окончательным
оптимальным выбором алгоритма станет блок с координатами
на два и исследуем
шесть блоков, помеченных цифрой 6. Диаграмма показывает, что окончательным
оптимальным выбором алгоритма станет блок с координатами ![]() .
.

Рис. 5.7. Метод двумерного логарифмического поиска.
Поиск за три шага: Этот метод похож на процедуру
двумерного логарифмического поиска. На каждом шаге тестируется восемь блоков
вместо четырех вокруг центра поиска, после чего размер шага делится на два.
Если в начале ![]() ,
то алгоритм завершится в три шага, что объясняет его название.
,
то алгоритм завершится в три шага, что объясняет его название.
Ортогональный поиск: Это вариация двух алгоритмов,
двумерного логарифмического поиска и поиска за три шага. На каждом шаге
ортогонального алгоритма осуществляется вертикальный и горизонтальный поиск. В
начале размер шага ![]() равен
равен
![]() и
исследуется центральный блок, а также два его соседа по бокам на расстоянии
и
исследуется центральный блок, а также два его соседа по бокам на расстоянии ![]() . Наилучший блок
становится центром вертикального поиска, а двумя другими блоками-кандидатами
становятся блоки сверху и снизу от центрального на расстоянии
. Наилучший блок
становится центром вертикального поиска, а двумя другими блоками-кандидатами
становятся блоки сверху и снизу от центрального на расстоянии ![]() от него. Лучший из
них становится центром следующего поиска. Если размер шага
от него. Лучший из
них становится центром следующего поиска. Если размер шага ![]() равен 1, то алгоритм
обрывается и возвращаются координаты наилучшего блока, найденного на текущем
шаге. В противном случае
равен 1, то алгоритм
обрывается и возвращаются координаты наилучшего блока, найденного на текущем
шаге. В противном случае ![]() делится на два, после чего совершается
новый шаг, состоящий из горизонтального и вертикального поиска.
делится на два, после чего совершается
новый шаг, состоящий из горизонтального и вертикального поиска.
Поиск по одному: В этом методе снова имеется два
шага, горизонтальный и вертикальный. На горизонтальном шаге исследуются все
блоки области поиска, чьи координаты ![]() имеют то же значение, что и у блока
имеют то же значение, что и у блока ![]() (то есть лежат на одной
горизонтали с этим блоком). Пусть некоторый блок
(то есть лежат на одной
горизонтали с этим блоком). Пусть некоторый блок ![]() имеет наименьшее расхождение с
имеет наименьшее расхождение с ![]() . Затем на
вертикальном шаге анализируются все блоки, находящиеся на одной вертикальной
оси с блоком
. Затем на
вертикальном шаге анализируются все блоки, находящиеся на одной вертикальной
оси с блоком ![]() .
Наилучший блок этой оси объявляется оптимальным и возвращается алгоритмом в
качестве результата поиска. Модификация этого алгоритма повторяет это действие
с последовательным сокращением области поиска.
.
Наилучший блок этой оси объявляется оптимальным и возвращается алгоритмом в
качестве результата поиска. Модификация этого алгоритма повторяет это действие
с последовательным сокращением области поиска.
Перекрестный поиск: Все этапы этого алгоритма,
кроме последнего, исследуют пять блоков, находящихся по углам области в форме
знака умножения ![]() .
На каждом этапе размер шага поиска делится на два, пока он не станет равен 1.
На последнем этапе в качестве области поиска используется область в форме знака
+ с центром в результате предыдущего этапа.
.
На каждом этапе размер шага поиска делится на два, пока он не станет равен 1.
На последнем этапе в качестве области поиска используется область в форме знака
+ с центром в результате предыдущего этапа.
Этим методом мы завершили наш краткий обзор методов монотонного поиска по квадрантам.
Методы иерархического поиска: Иерархические методы основаны на преимуществе, которое обеспечивается тем, что близость блоков чувствительна к размеру блока. Иерархический поиск начинает с блоков больших размеров и использует их векторы перемещения как исходную точку поисков для блоков меньших размеров. Большие блоки с меньшей вероятностью могут привести к ошибочному локальному минимуму, одновременно с этим, малые блоки обычно производят лучшие векторы перемещения. Метод иерархического поиска имеет высокую вычислительную сложность, и ускорить его можно, сократив число выполняемых операций. Это делается несколькими способами. Вот некоторые из них:
1. На первом шаге, когда размер блока еще велик, выбрать приблизительно подходящие блоки. Соответствующие им векторы перемещения не будут наилучшими, но они будут использоваться лишь как отправные точки для дальнейших лучших векторов.
2. При исследовании больших блоков пропустить некоторые пикселы. Например, алгоритм может использовать только четверть пикселов больших блоков, половину пикселов меньших блоков и так далее.
3.
Выбрать размеры блоков так, что блоки, используемые на шаге ![]() , делятся на несколько (обычно
четыре или девять) меньших блоков, используемых на следующем шаге. На этом пути
каждый вектор перемещения, вычисленный на шаге
, делятся на несколько (обычно
четыре или девять) меньших блоков, используемых на следующем шаге. На этом пути
каждый вектор перемещения, вычисленный на шаге ![]() , будет служить приближенной оценкой для
нескольких векторов перемещений меньших блоков шага
, будет служить приближенной оценкой для
нескольких векторов перемещений меньших блоков шага ![]() .
.
Методы многомерного
пространственного поиска:
Эти методы более сложны. При поиске блока, близкого блоку ![]() , они используют не только
сдвиги данного блока
, они используют не только
сдвиги данного блока ![]() , но также его вращения, растяжения и
сжатия.
, но также его вращения, растяжения и
сжатия.
Метод многомерного
пространственного поиска может также найти блок ![]() , который близок блоку
, который близок блоку ![]() , но при других
условиях освещения. Это бывает полезно, когда объекты в кадре пересекают
участки с разной освещенностью. Все рассмотренные выше алгоритмы оценивали
близость двух блоков друг другу с помощью сравнения величин светимости
соответствующих пикселов. Два блока
, но при других
условиях освещения. Это бывает полезно, когда объекты в кадре пересекают
участки с разной освещенностью. Все рассмотренные выше алгоритмы оценивали
близость двух блоков друг другу с помощью сравнения величин светимости
соответствующих пикселов. Два блока ![]() и
и ![]() , которые содержат одни и те же объекты,
но с разной освещенностью, будут объявлены различными.
, которые содержат одни и те же объекты,
но с разной освещенностью, будут объявлены различными.
Если же метод многомерного
пространственного поиска обнаружит блок ![]() , который походит на блок
, который походит на блок ![]() , но с другой
светимостью, то он объявит его близким к
, но с другой
светимостью, то он объявит его близким к ![]() и добавит к сжатому кадру величину
светимости. Эта величина (возможно, отрицательная) будет прибавлена декодером к
пикселам декодированного кадра, чтобы придать им изначальную светимость.
и добавит к сжатому кадру величину
светимости. Эта величина (возможно, отрицательная) будет прибавлена декодером к
пикселам декодированного кадра, чтобы придать им изначальную светимость.
Метод многомерного
пространственного поиска может также сравнивать блок ![]() с повернутыми копиями
блоков-кандидатов
с повернутыми копиями
блоков-кандидатов ![]() .
Это полезно, если объекты видеоряда могут вращаться наряду с совершением
поступательных перемещений. Более того, такой алгоритм может одновременно
масштабировать блоки
.
Это полезно, если объекты видеоряда могут вращаться наряду с совершением
поступательных перемещений. Более того, такой алгоритм может одновременно
масштабировать блоки ![]() , стараясь подобрать лучшее совпадение
блоков. Например, если блок
, стараясь подобрать лучшее совпадение
блоков. Например, если блок ![]() состоит из 8х8 пикселов, то алгоритм
может попытаться сравнивать этот блок с блоками
состоит из 8х8 пикселов, то алгоритм
может попытаться сравнивать этот блок с блоками ![]() , состоящими из 12х12 пикселов, путем их
сжатия до размеров 8x8.
, состоящими из 12х12 пикселов, путем их
сжатия до размеров 8x8.
Конечно, такие алгоритмы используют еще большие вычислительные мощности для совершения дополнительных операций и сравнений. Можно говорить, что это существенно увеличивает размерность пространства поиска, и этим оправдывается использование наименования многомерное пространство поиска. Однако, насколько известно автору, на практике пока не разработан метод многомерного пространственного поиска, который использует в полной мере масштабирование, вращение и изменение светимости.
Video meliora proboque deteriora sequor
(Я вижу лучшее и одобряю его, но
следую за худшим).
- Овидий «Метаморфозы», 7:20
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие переводчика
- Предисловие автора
- Введение
- Глава 1. Статистические методы
- 1.1. Энтропия
- 1.2. Коды переменной длины
- 1.3. Декодирование
- 1.4. Кодирование Хаффмана
- 1.4.1. Декодирование Хаффмана
- 1.4.2. Средняя длина кода
- 1.5. Адаптивные коды Хаффмана
- 1.5.1. Несжатые коды
- 1.5.2. Модификация дерева
- 1.5.3. Переполнение счетчика
- 1.5.4. Кодовое переполнение
- 1.5.5. Вариант алгоритма
- 1.6. Факсимильное сжатие
- 1.6.1. Одномерное кодирование
- 1.6.2. Двумерное кодирование
- 1.7. Арифметическое кодирование
- 1.7.1. Детали реализации метода
- 1.7.2. Потеря значащих цифр
- 1.7.3. Заключительные замечания
- 1.8. Адаптивное арифметическое кодирование
- ГЛАВА 2 СЛОВАРНЫЕ МЕТОДЫ
- 2.1. LZ77 (скользящее окно)
- 2.1.1. Циклическая очередь
- 2.2. LZSS
- 2.2.1. Недостатки
- 2.3. LZ78
- 2.4. LZW
- 2.4.1. Декодирование LZW
- 2.4.2. Структура словаря LZW
- 2.4.3. LZW в практических приложениях
- 2.5. Заключение
- ГЛАВА 3 СЖАТИЕ ИЗОБРАЖЕНИЙ
- 3.1. Введение
- 3.2. Типы изображений
- 3.3. Подходы к сжатию изображений
- 3.3.1. Коды Грея
- 3.3.2. Метрики ошибок
- 3.4. Интуитивные методы
- 3.4.1. Подвыборка
- 3.4.2. Квантование
- 3.5. Преобразование изображений
- 3.5.1. Ортогональные преобразования
- 3.5.2. Матричные преобразования
- 3.5.3. Дискретное косинус-преобразование
- 3.5.4. Пример
- 3.5.5. Дискретное синус-преобразование
- 3.5.6. Преобразование Уолша-Адамара
- 3.5.7. Преобразование Хаара
- 3.5.8. Преобразование Кархунена-Лоэвэ
- 3.6. Прогрессирующее сжатие изображений
- 3.7. JPEG
- 3.7.1. Светимость
- 3.7.2. DCT
- 3.7.3. Практическое DCT
- 3.7.4. Квантование
- 3.7.5. Кодирование
- 3.7.6. Мода без потери данных
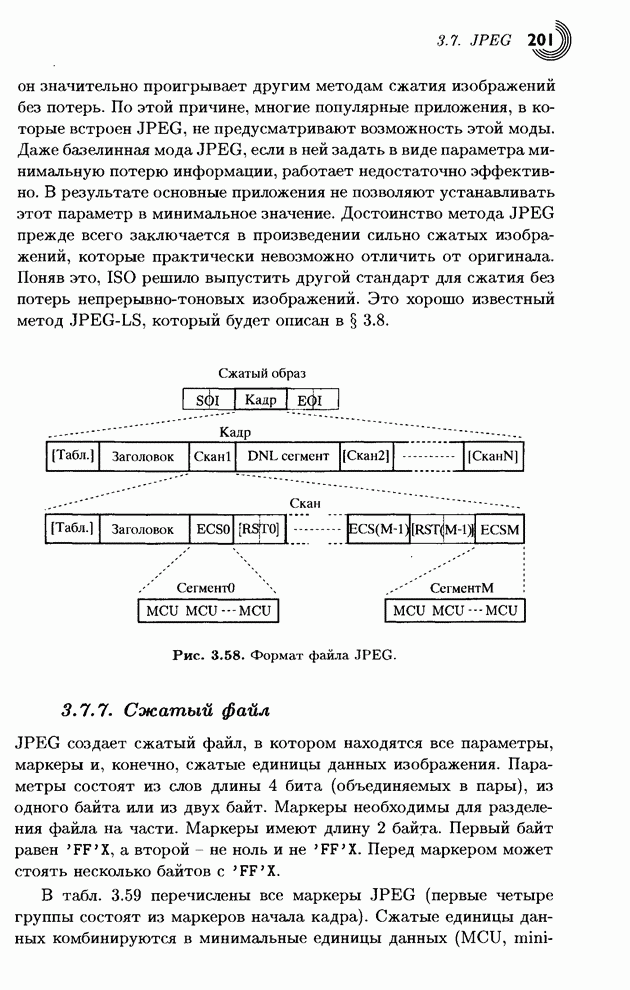
- 3.7.7. Сжатый файл
- 3.7.8. JFIF
- 3.8. JPEG-LS
- 3.8.1. Коды Голомба
- 3.8.2. Основы метода JPEG-LS
- 3.8.3. Кодер
- ГЛАВА 4 ВЕЙВЛЕТНЫЕ МЕТОДЫ
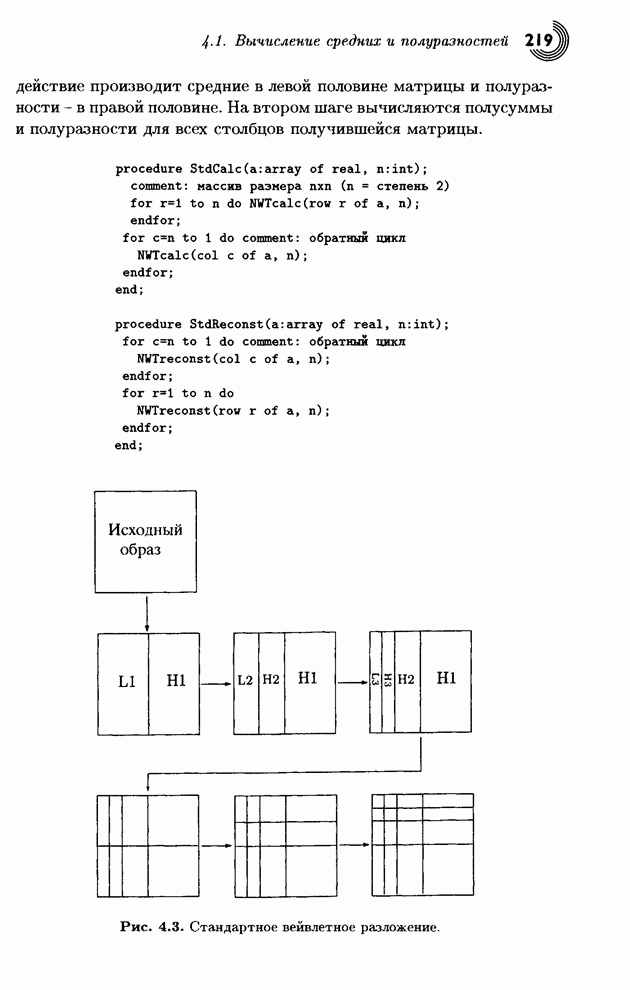
- 4.1. Вычисление средних и полу разностей
- 4.1.1. Обобщение на двумерный случай
- 4.1.2. Свойства преобразования Хаара
- 4.2. Преобразование Хаара
- 4.2.1. Матричная форма
- 4.3. Поддиапазонные преобразования
- 4.4. Банк фильтров
- 4.5. Нахождение коэффициентов фильтра
- 4.6. Преобразование DWT
- 4.7. Примеры
- 4.8. Вейвлеты Добеши
- 4.9. SPIHT
- 4.9.1. Алгоритм сортировки разделением множеств
- 4.9.2. Пространственно ориентированное дерево
- 4.9.3. Кодирование в алгоритме SPIHT
- 4.9.4. Пример
- 4.9.5. QTCQ
- ГЛАВА 5 СЖАТИЕ ВИДЕО
- 5.1. Основные принципы
- 5.2. Методы подоптимального поиска
- ГЛАВА 6 СЖАТИЕ ЗВУКА
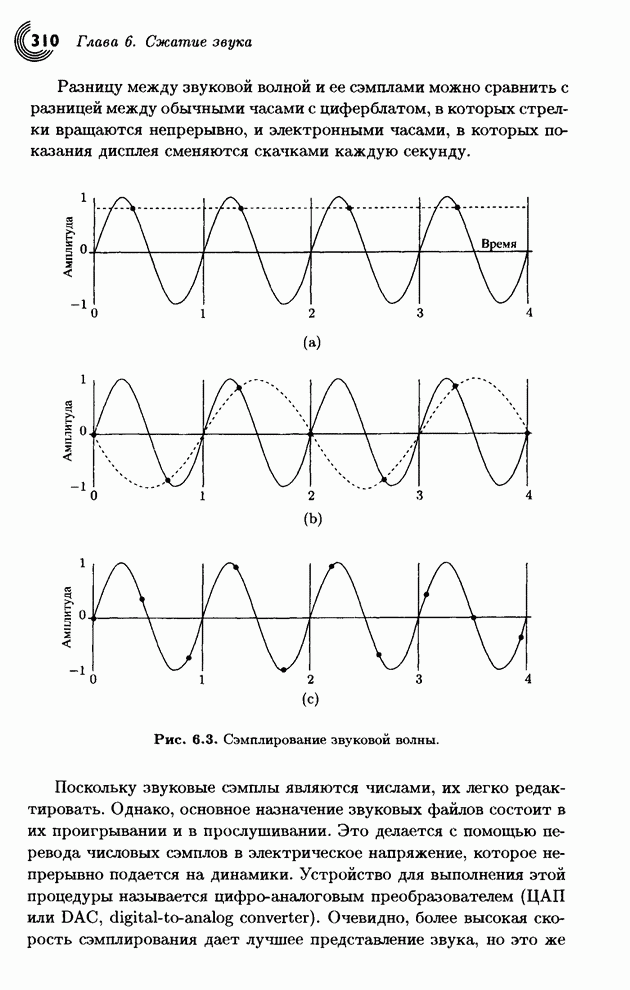
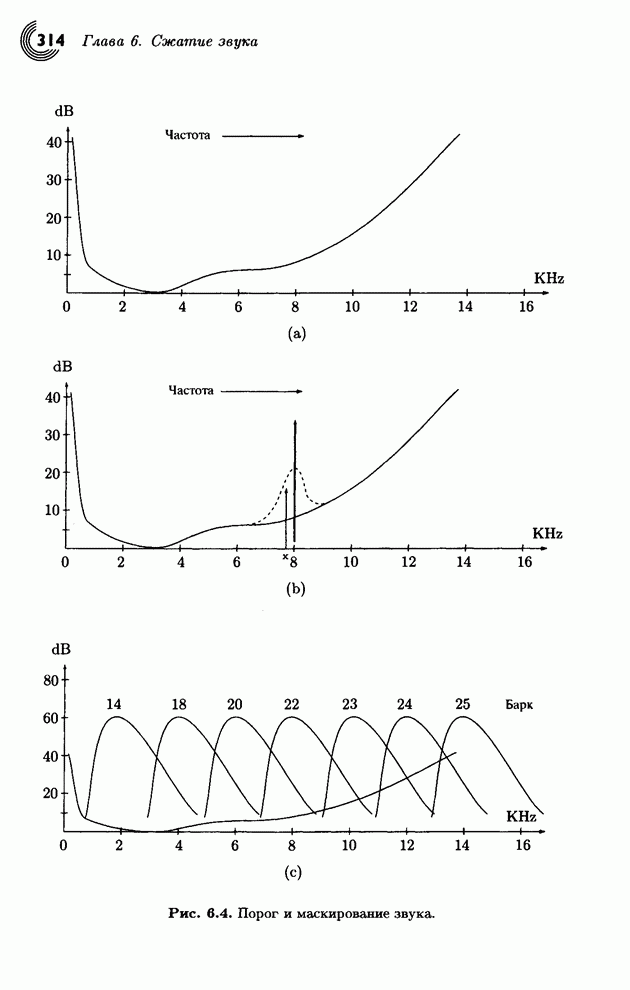
- 6.1. Звук
- 6.2. Оцифрованный звук
- 6.3. Органы слуха человека
- 6.4. Общепризнанные методы
- 6.5. Сжатие звука в стандарте MPEG-1
- 6.5.1. Кодирование частотной области
- 6.5.2. Формат сжатых данных
- 6.5.3. Психоакустические модели
- 6.5.4. Кодирование: слой III
- Литература
- Глоссарий