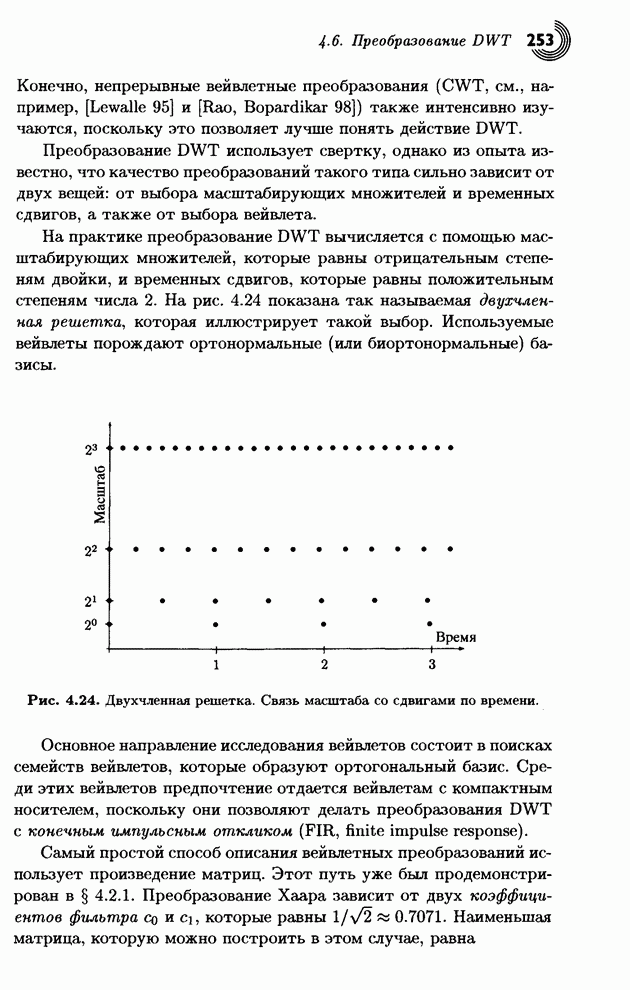
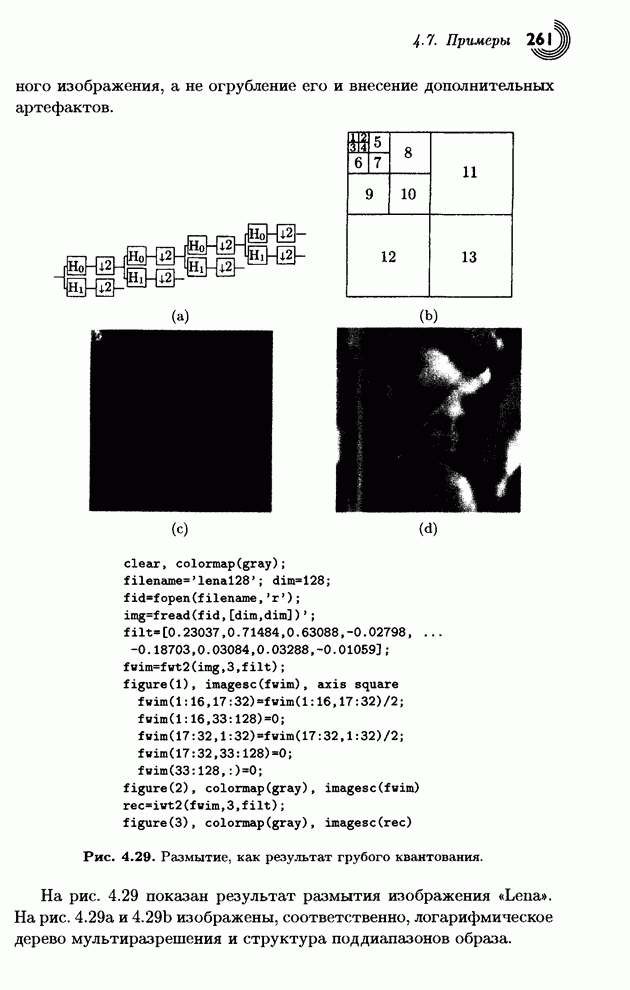
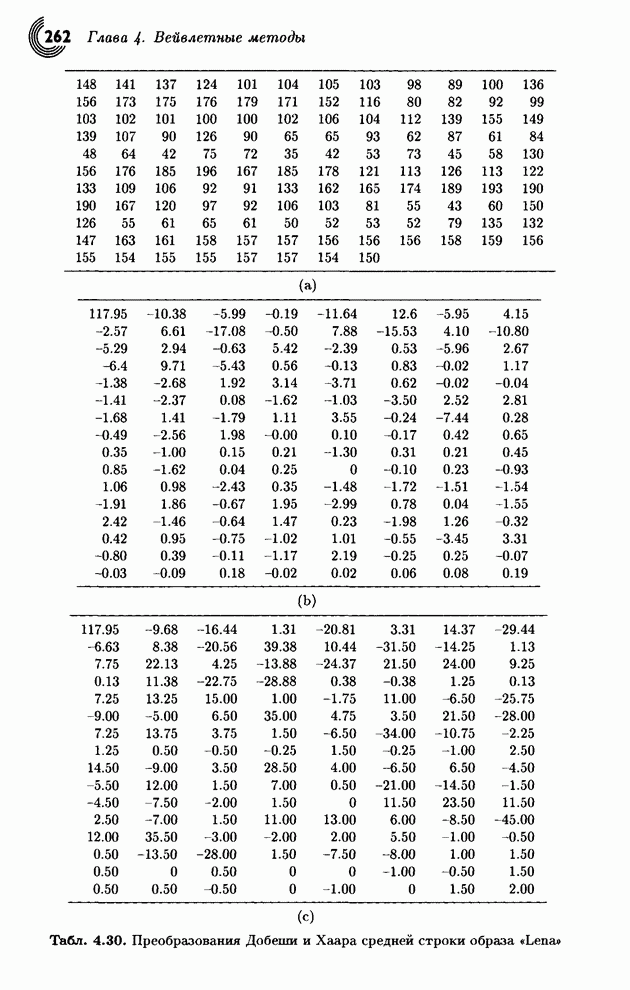
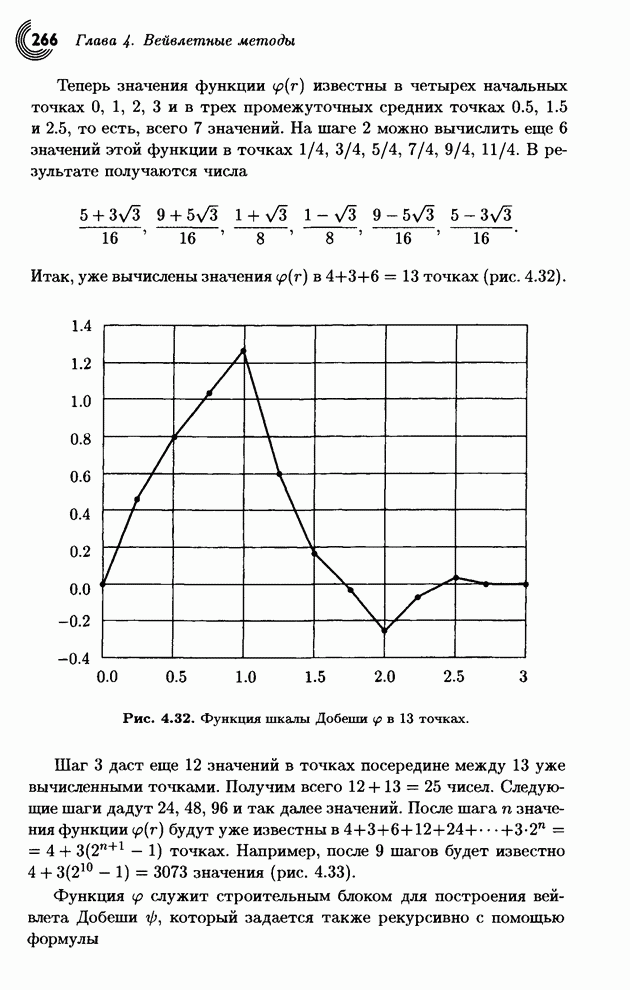
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ГЛАВА 1 СТАТИСТИЧЕСКИЕ МЕТОДЫ
Статистические методы компрессии используют статистические свойства сжимаемых данных и присваивают всем символам коды с переменной длиной. Под «статистическими свойствами» обычно понимается вероятность (или, что то же самое, частота появления) каждого символа в потоке данных, однако этот термин может иметь иное, более сложное значение. Пару последовательных символов будем называть биграммой. Долгие наблюдения показали, что в типичном английском тексте некоторые биграммы, например, «ta», «he», «са», встречаются очень часто, а другие, например, «xa»,«hz», «qe», - редко. Поэтому разумный статистический метод может присваивать коды переменной длины многим биграммам (и даже триграммам), а не только индивидуальным символам.
1.1. Энтропия
Основы теории информации были
заложены Клодом Шеноном в 1948 году в лаборатории Белла. Эта теория оказалась
настоящим сюрпризом, поскольку все привыкли воспринимать информацию лишь
качественно. Для наших целей сжатия данных нам необходимо освоить только одно
теоретико-информационное понятие, а именно, энтропию. Под энтропией
символа ![]() ,
имеющего вероятность
,
имеющего вероятность ![]() ,
подразумевается количество информации, содержащейся в
,
подразумевается количество информации, содержащейся в ![]() , которая равна -
, которая равна - ![]() . Например, если
вероятность
. Например, если
вероятность ![]() символа
символа
![]() равна 0.5,
то его энтропия -
равна 0.5,
то его энтропия - ![]() .
.
Если символы некоторого алфавита с символами от ![]() до
до ![]() имеют вероятности от
имеют вероятности от ![]() до
до ![]() , то энтропия всего алфавита
равна сумме
, то энтропия всего алфавита
равна сумме ![]() .
Если задана строка символов этого алфавита, то для нее энтропия определяется
аналогично.
.
Если задана строка символов этого алфавита, то для нее энтропия определяется
аналогично.
С помощью понятия энтропии теория информации показывает, как вычислять вероятности строк символов алфавита, и предсказывает ее наилучшее сжатие, то есть, наименьшее, в среднем, число бит, необходимое для представления этой строки символов.
Продемонстрируем это на простом
примере. Для последовательности символов «ABCDE» с вероятностями 0.5, 0.2, 0.1, 0.1
и 0.1, соответственно, вероятность строки «AAAAABBCDE» равна ![]() . Логарифм по основанию 2 этого
числа
. Логарифм по основанию 2 этого
числа ![]() .
Тогда наименьшее в среднем число требуемых бит для кодирования этой строки
равно -
.
Тогда наименьшее в среднем число требуемых бит для кодирования этой строки
равно - ![]() , то
есть, 20. Кодер, достигающий этого сжатия называется энтропийным кодером.
, то
есть, 20. Кодер, достигающий этого сжатия называется энтропийным кодером.
Пример: Проанализируем энтропию
алфавита, состоящего всего из двух символов ![]() и
и ![]() с вероятностями
с вероятностями ![]() и
и ![]() . Поскольку
. Поскольку ![]() , то энтропия этого алфавита выражается
числом
, то энтропия этого алфавита выражается
числом ![]() . В
табл. 1.1 приведены различные значения величин
. В
табл. 1.1 приведены различные значения величин ![]() и
и ![]() вместе с соответствующей энтропией. Когда
вместе с соответствующей энтропией. Когда
![]() , необходим
по крайней мере один бит для кодирования каждого символа. Это означает, что
энтропия достигла своего максимума, избыточность равна нулю, и данные
невозможно сжать. Однако, если вероятности символов сильно отличаются, то
минимальное число требуемых бит на символ снижается. Мы, скорее всего, не
сможем непосредственно предъявить метод сжатия, который использует 0.08 бит на
символ, но мы точно знаем, что при
, необходим
по крайней мере один бит для кодирования каждого символа. Это означает, что
энтропия достигла своего максимума, избыточность равна нулю, и данные
невозможно сжать. Однако, если вероятности символов сильно отличаются, то
минимальное число требуемых бит на символ снижается. Мы, скорее всего, не
сможем непосредственно предъявить метод сжатия, который использует 0.08 бит на
символ, но мы точно знаем, что при ![]() такой алгоритм теоретически возможен.
такой алгоритм теоретически возможен.
|
|
|
Энтропия |
|
0.99 |
0.01 |
0.08 |
|
0.90 |
0.10 |
0.47 |
|
0.80 |
0.20 |
0.72 |
|
0.70 |
0.30 |
0.88 |
|
0.60 |
0.40 |
0.97 |
|
0.50 |
0.50 |
1.00 |
Табл. 1.1. Вероятности и энтропии двух символов.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие переводчика
- Предисловие автора
- Введение
- Глава 1. Статистические методы
- 1.1. Энтропия
- 1.2. Коды переменной длины
- 1.3. Декодирование
- 1.4. Кодирование Хаффмана
- 1.4.1. Декодирование Хаффмана
- 1.4.2. Средняя длина кода
- 1.5. Адаптивные коды Хаффмана
- 1.5.1. Несжатые коды
- 1.5.2. Модификация дерева
- 1.5.3. Переполнение счетчика
- 1.5.4. Кодовое переполнение
- 1.5.5. Вариант алгоритма
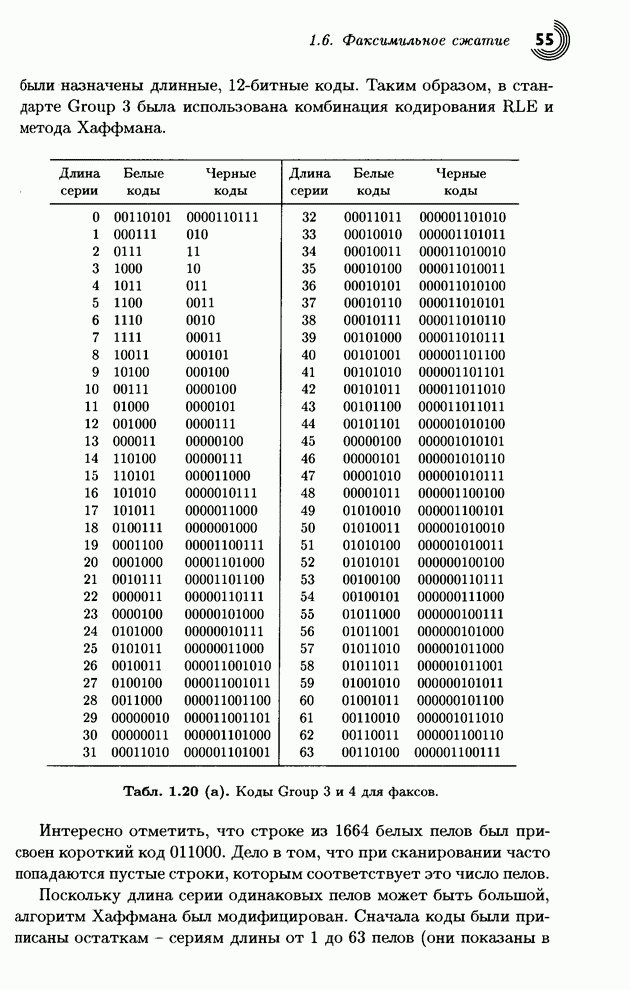
- 1.6. Факсимильное сжатие
- 1.6.1. Одномерное кодирование
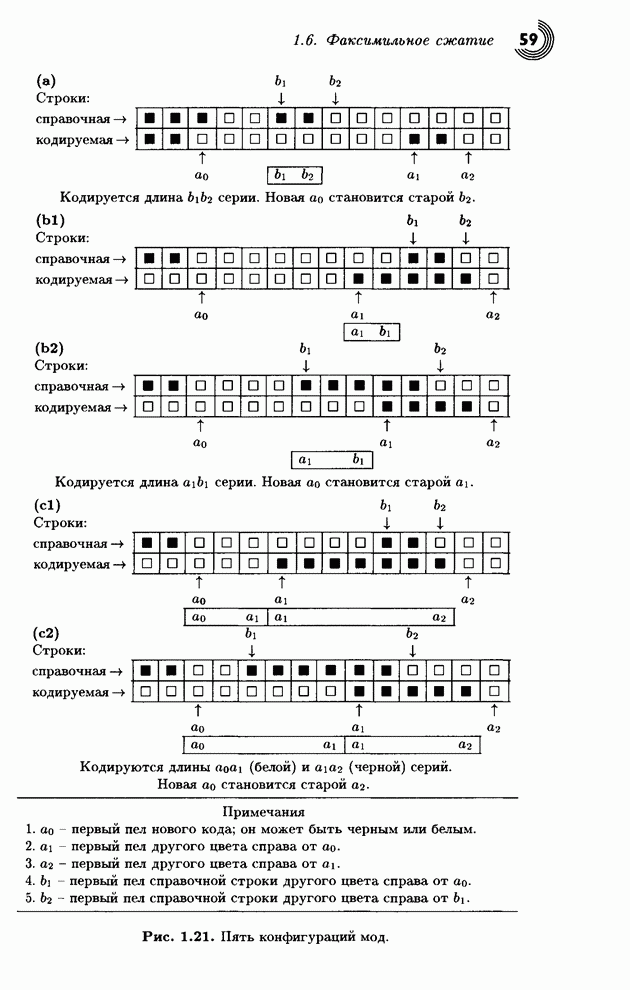
- 1.6.2. Двумерное кодирование
- 1.7. Арифметическое кодирование
- 1.7.1. Детали реализации метода
- 1.7.2. Потеря значащих цифр
- 1.7.3. Заключительные замечания
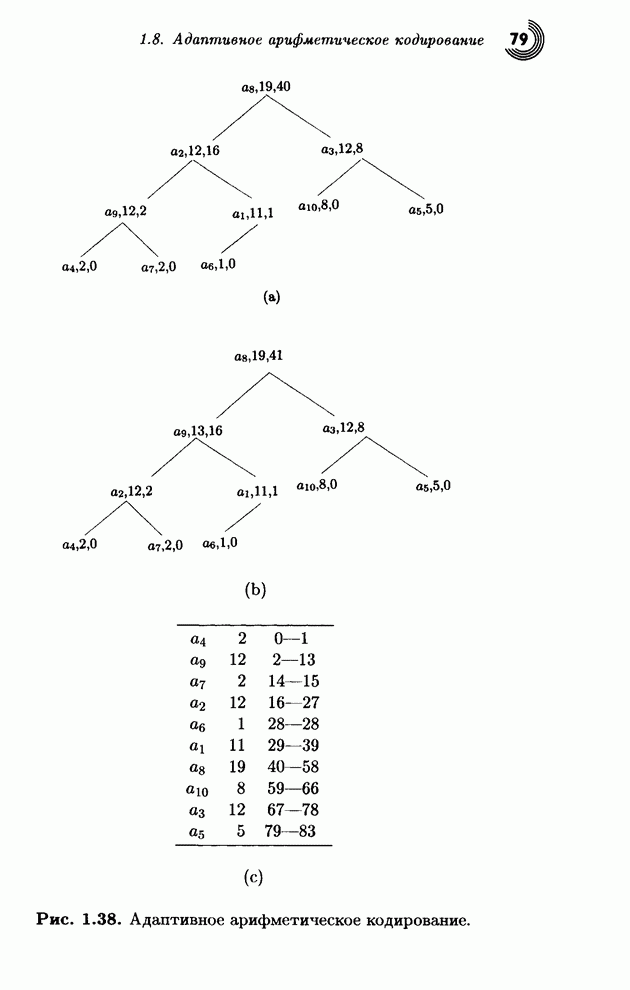
- 1.8. Адаптивное арифметическое кодирование
- ГЛАВА 2 СЛОВАРНЫЕ МЕТОДЫ
- 2.1. LZ77 (скользящее окно)
- 2.1.1. Циклическая очередь
- 2.2. LZSS
- 2.2.1. Недостатки
- 2.3. LZ78
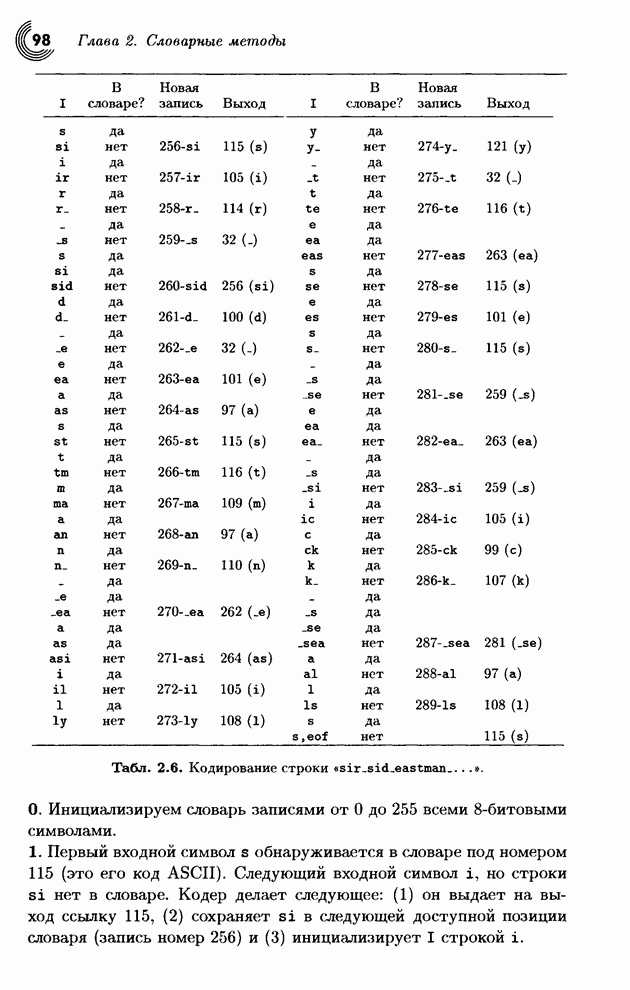
- 2.4. LZW
- 2.4.1. Декодирование LZW
- 2.4.2. Структура словаря LZW
- 2.4.3. LZW в практических приложениях
- 2.5. Заключение
- ГЛАВА 3 СЖАТИЕ ИЗОБРАЖЕНИЙ
- 3.1. Введение
- 3.2. Типы изображений
- 3.3. Подходы к сжатию изображений
- 3.3.1. Коды Грея
- 3.3.2. Метрики ошибок
- 3.4. Интуитивные методы
- 3.4.1. Подвыборка
- 3.4.2. Квантование
- 3.5. Преобразование изображений
- 3.5.1. Ортогональные преобразования
- 3.5.2. Матричные преобразования
- 3.5.3. Дискретное косинус-преобразование
- 3.5.4. Пример
- 3.5.5. Дискретное синус-преобразование
- 3.5.6. Преобразование Уолша-Адамара
- 3.5.7. Преобразование Хаара
- 3.5.8. Преобразование Кархунена-Лоэвэ
- 3.6. Прогрессирующее сжатие изображений
- 3.7. JPEG
- 3.7.1. Светимость
- 3.7.2. DCT
- 3.7.3. Практическое DCT
- 3.7.4. Квантование
- 3.7.5. Кодирование
- 3.7.6. Мода без потери данных
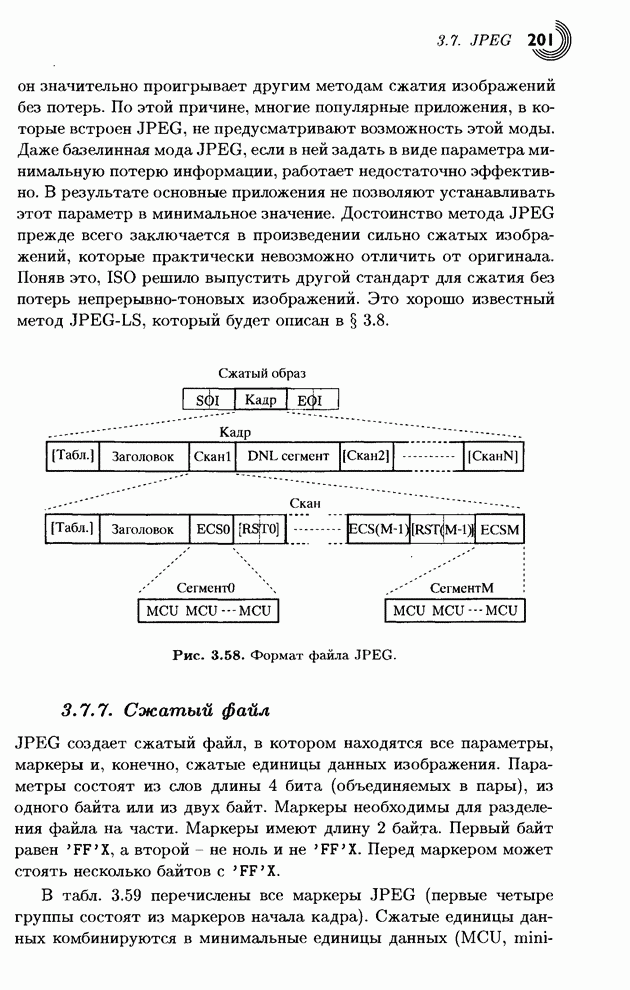
- 3.7.7. Сжатый файл
- 3.7.8. JFIF
- 3.8. JPEG-LS
- 3.8.1. Коды Голомба
- 3.8.2. Основы метода JPEG-LS
- 3.8.3. Кодер
- ГЛАВА 4 ВЕЙВЛЕТНЫЕ МЕТОДЫ
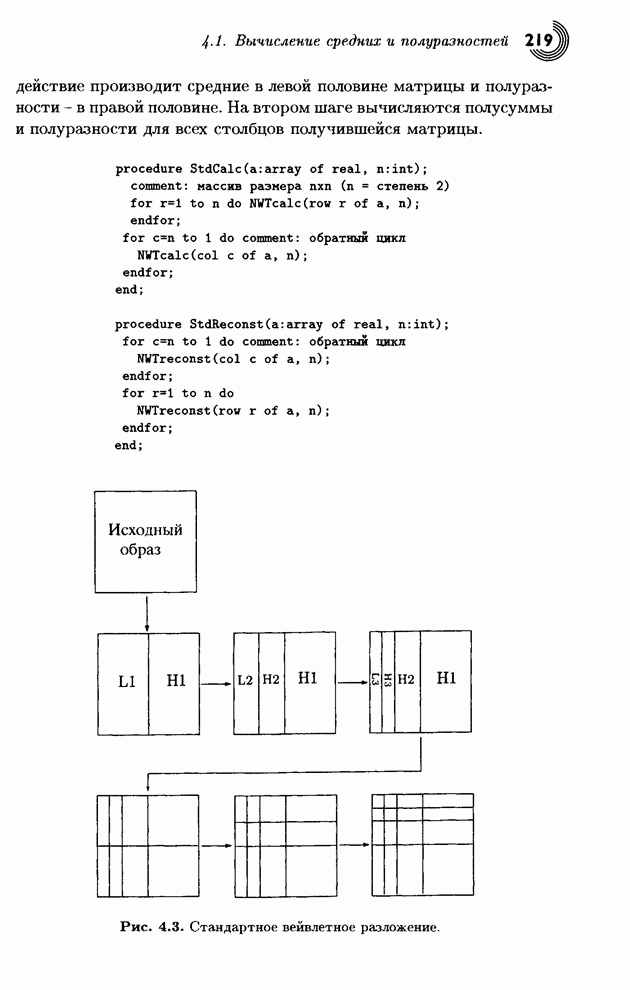
- 4.1. Вычисление средних и полу разностей
- 4.1.1. Обобщение на двумерный случай
- 4.1.2. Свойства преобразования Хаара
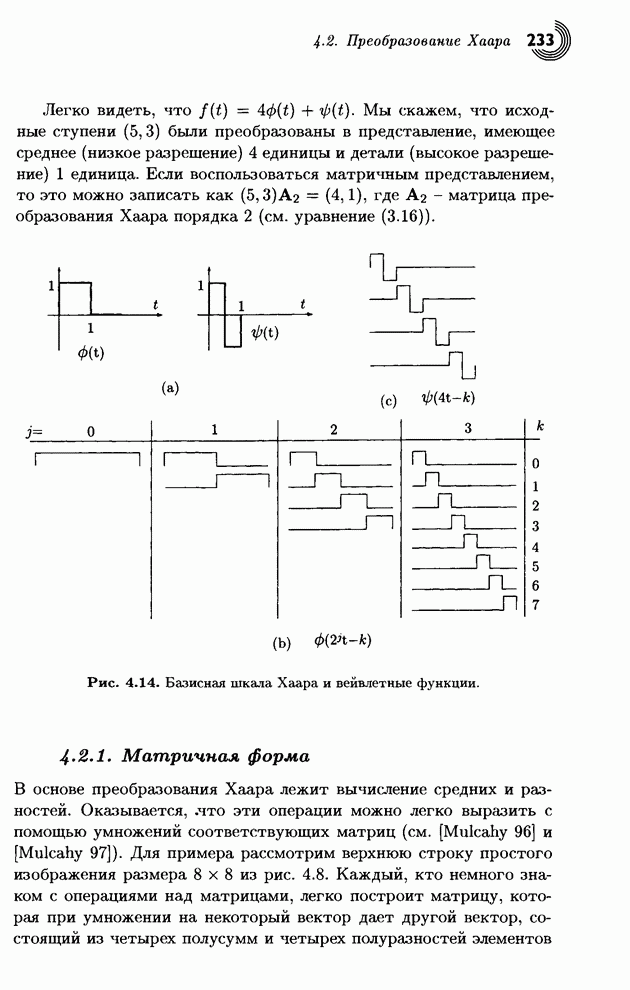
- 4.2. Преобразование Хаара
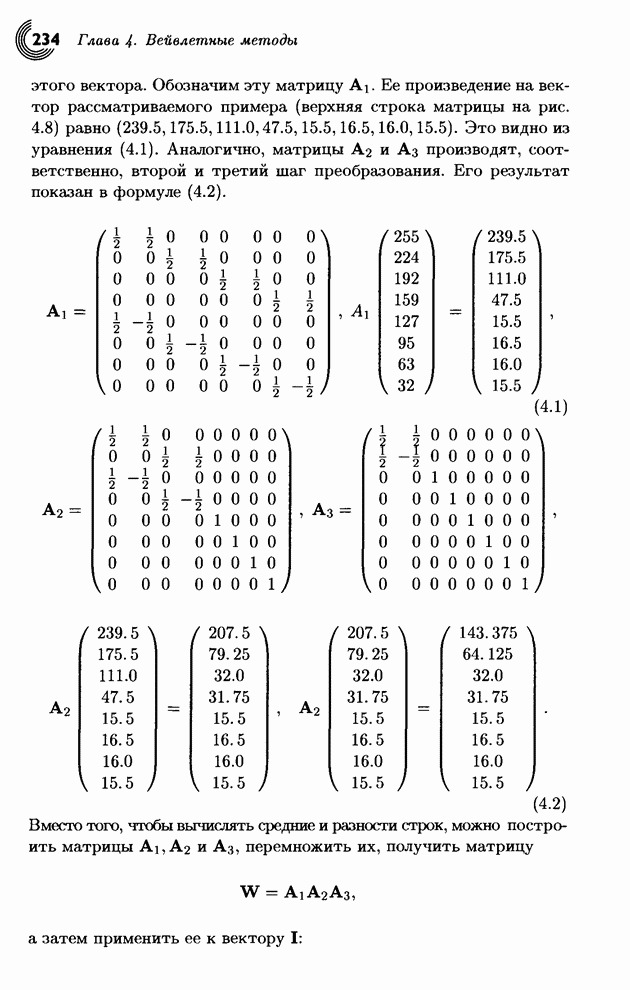
- 4.2.1. Матричная форма
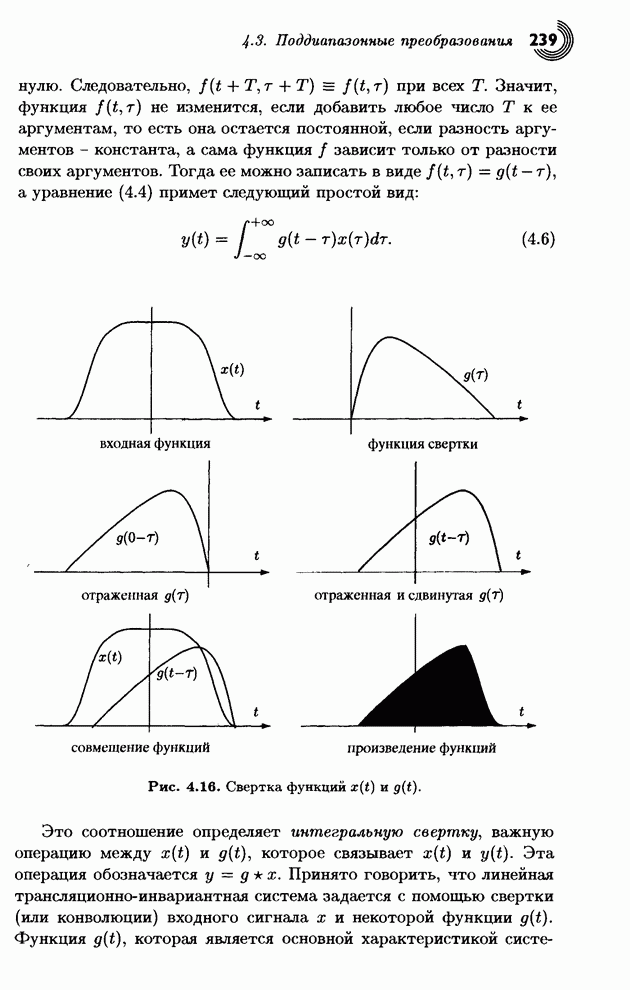
- 4.3. Поддиапазонные преобразования
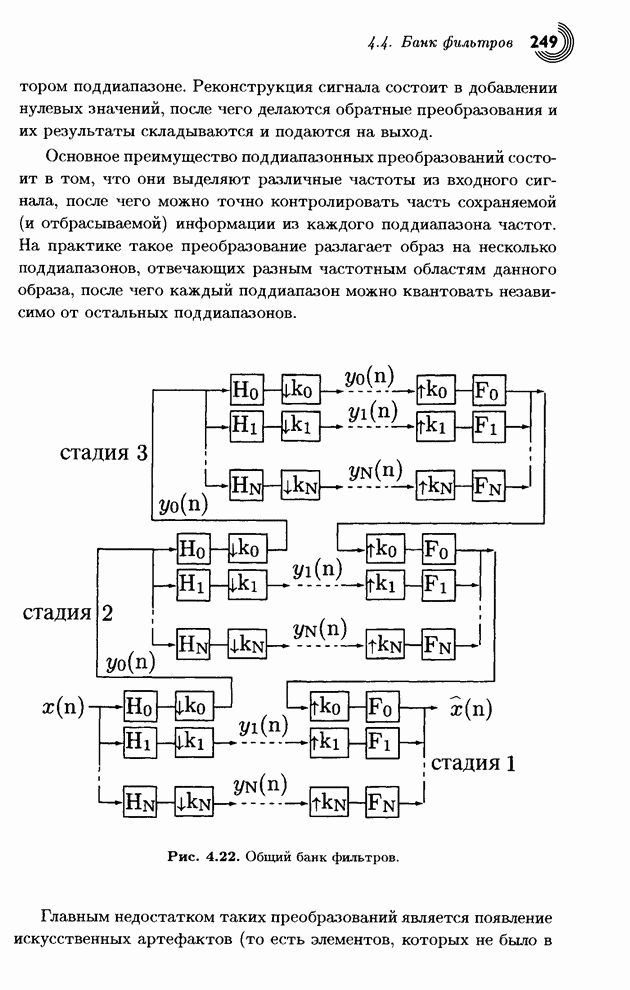
- 4.4. Банк фильтров
- 4.5. Нахождение коэффициентов фильтра
- 4.6. Преобразование DWT
- 4.7. Примеры
- 4.8. Вейвлеты Добеши
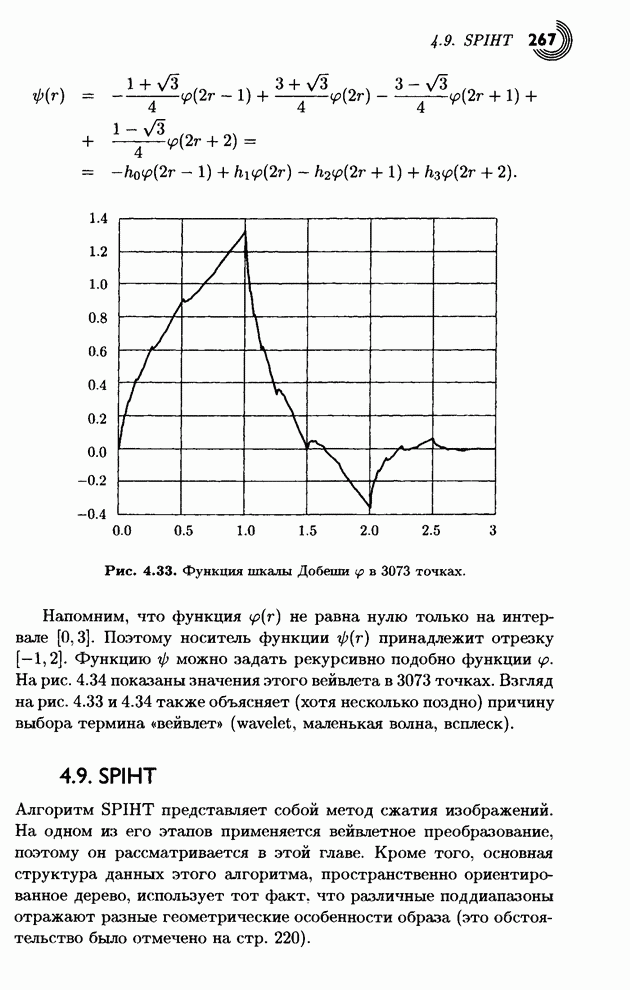
- 4.9. SPIHT
- 4.9.1. Алгоритм сортировки разделением множеств
- 4.9.2. Пространственно ориентированное дерево
- 4.9.3. Кодирование в алгоритме SPIHT
- 4.9.4. Пример
- 4.9.5. QTCQ
- ГЛАВА 5 СЖАТИЕ ВИДЕО
- 5.1. Основные принципы
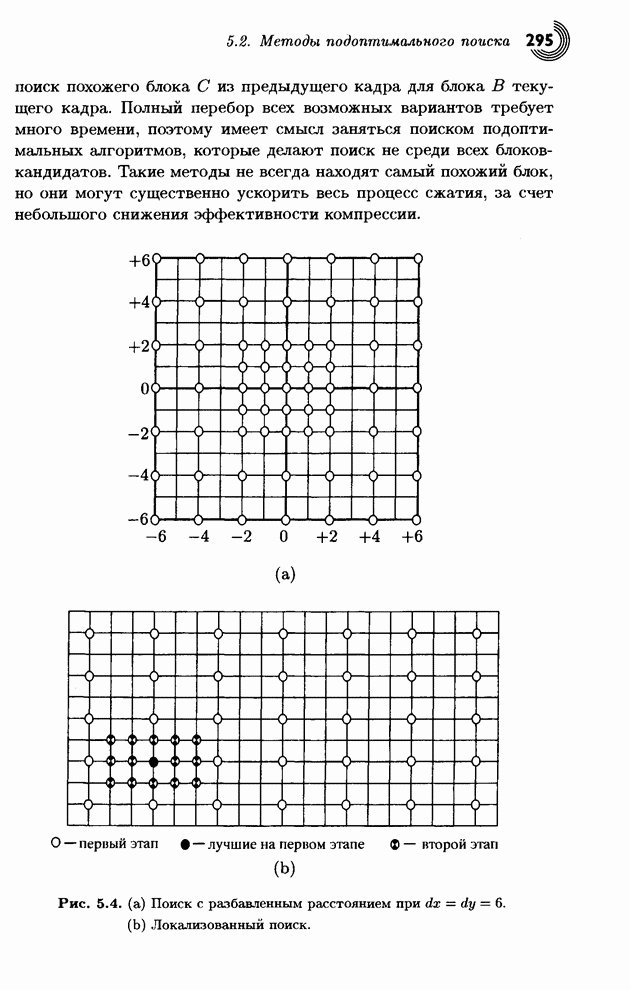
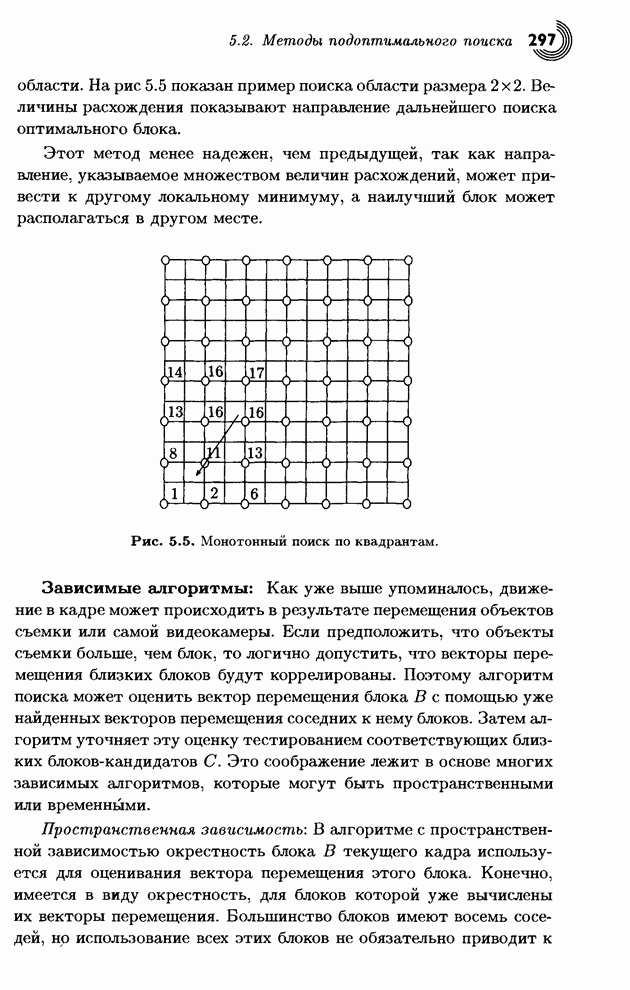
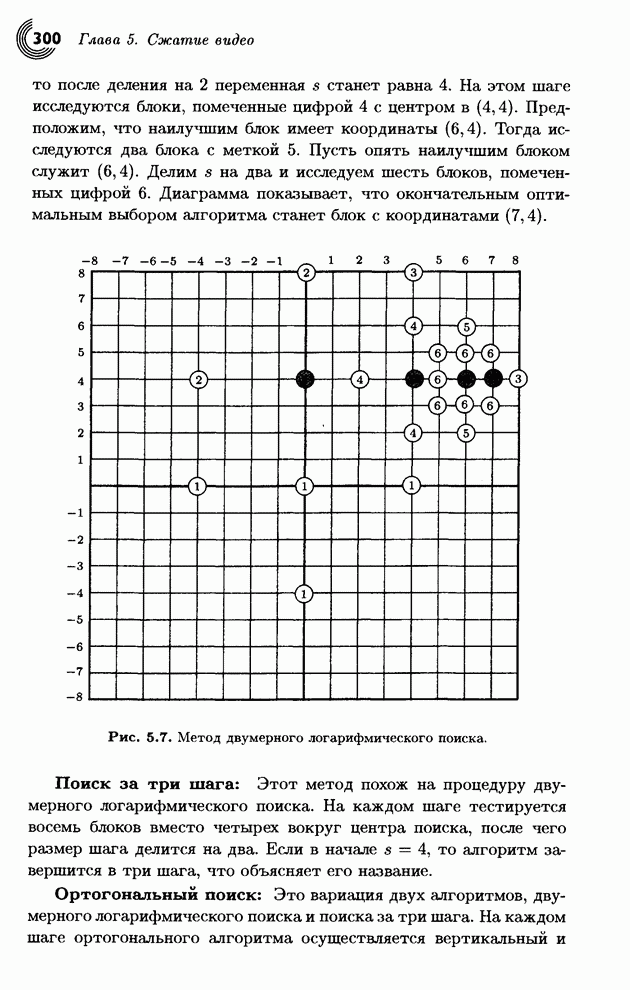
- 5.2. Методы подоптимального поиска
- ГЛАВА 6 СЖАТИЕ ЗВУКА
- 6.1. Звук
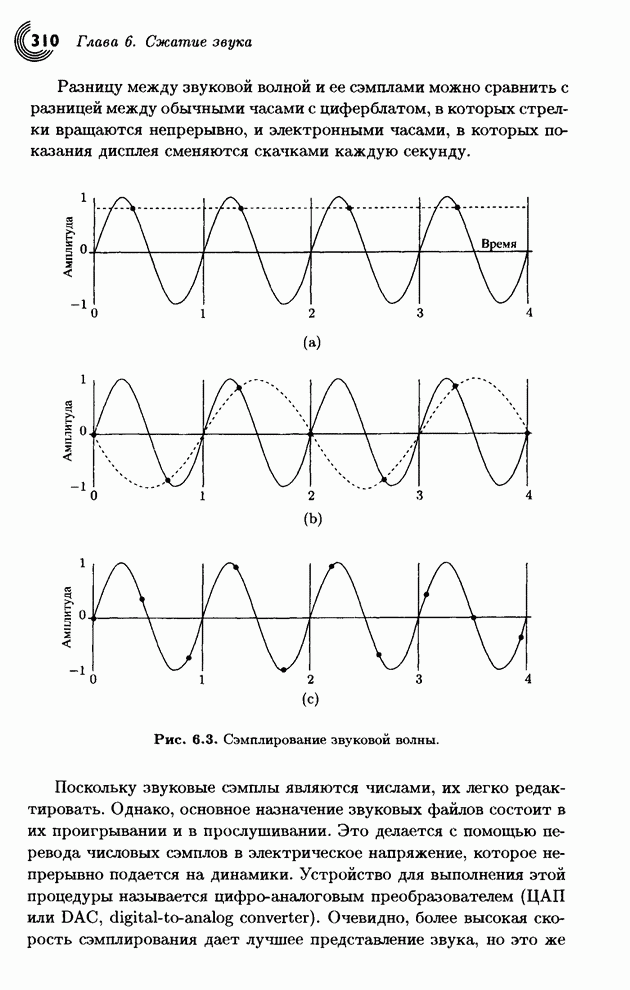
- 6.2. Оцифрованный звук
- 6.3. Органы слуха человека
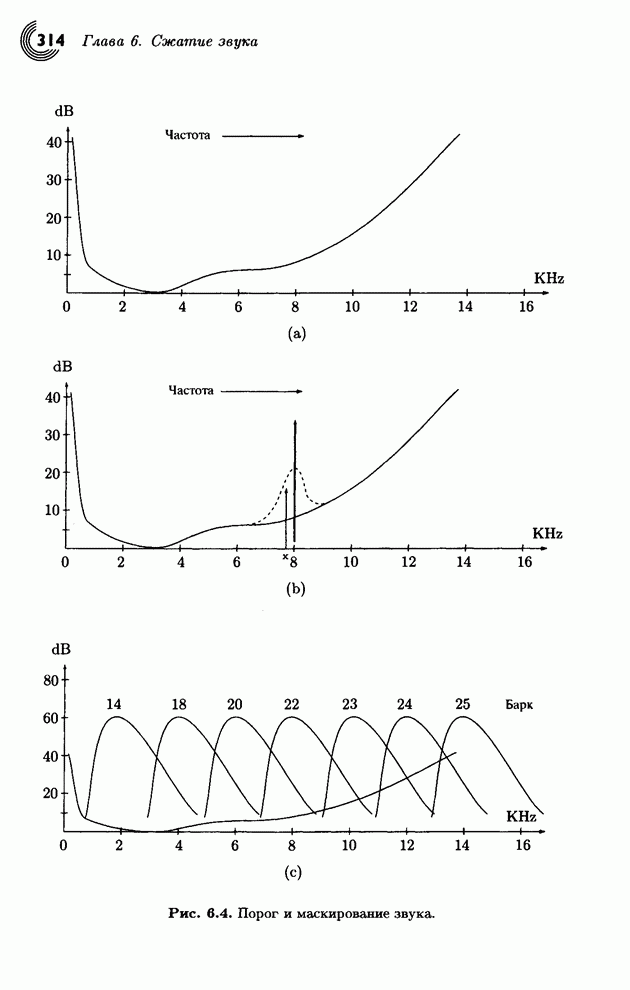
- 6.4. Общепризнанные методы
- 6.5. Сжатие звука в стандарте MPEG-1
- 6.5.1. Кодирование частотной области
- 6.5.2. Формат сжатых данных
- 6.5.3. Психоакустические модели
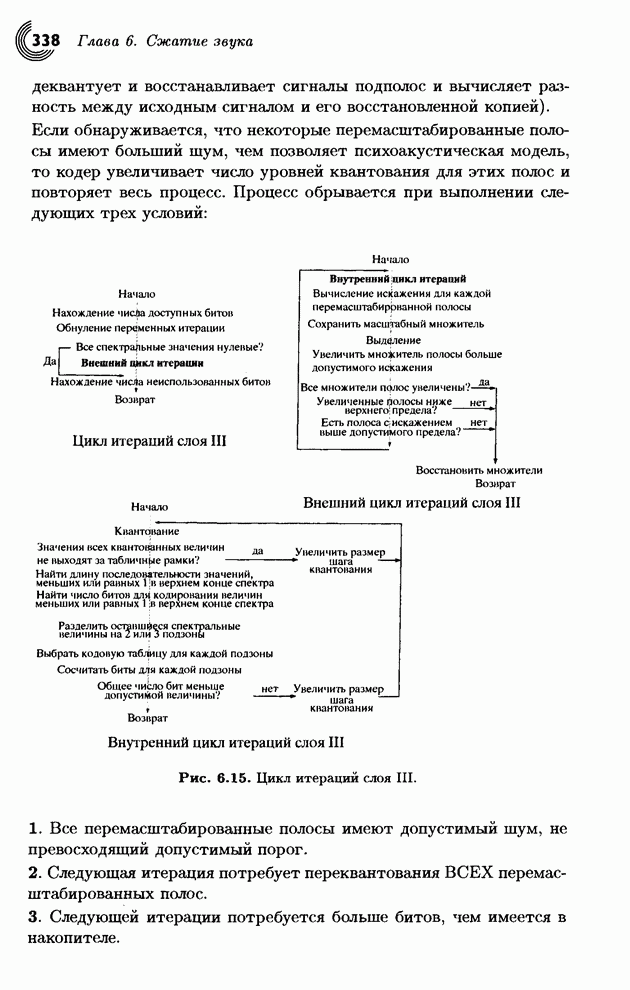
- 6.5.4. Кодирование: слой III
- Литература
- Глоссарий