| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
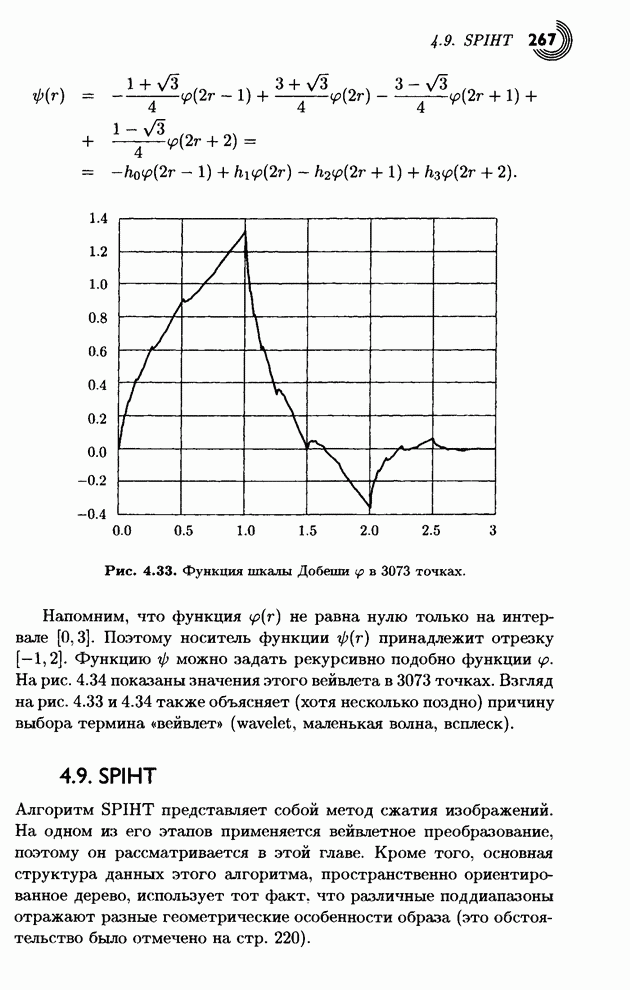
4.5. Нахождение коэффициентов фильтра
После рассмотрения общих операций над фильтрами возникает следующий вопрос: «Как находить коэффициенты фильтров?» Полный ответ на этот вопрос весьма непрост и выходит за рамки нашего изложения (см., например, [Akansu, Haddad 92]). В этом параграфе мы постараемся дать некоторое представление об основных правилах и методах вычисления коэффициентов различных банков фильтров.
Пусть имеется два прямых фильтра ![]() ,
, ![]() и два обратных фильтра
и два обратных фильтра ![]() ,
, ![]() , которые состоят из
, которые состоят из ![]() отсчетов (число
отсчетов (число ![]() предполагается
четным). Обозначим их коэффициенты через
предполагается
четным). Обозначим их коэффициенты через
![]() ,
, ![]() ,
,
![]() ,
, ![]() .
.
Четыре
вектора ![]() ,
, ![]() ,
, ![]() и
и ![]() являются импульсными откликами
четырех фильтров. Вот простейшие правила, позволяющие выбрать численные
значения для этих векторов:
являются импульсными откликами
четырех фильтров. Вот простейшие правила, позволяющие выбрать численные
значения для этих векторов:
1.
Нормализация: Вектор ![]() имеет
единичную длину.
имеет
единичную длину.
2.
Ортогональность: Для любого целого числа ![]() ,
удовлетворяющего неравенству
,
удовлетворяющего неравенству ![]() ,
вектор, состоящий из первых
,
вектор, состоящий из первых ![]() элементов
элементов
![]() , должен быть ортогонален
вектору, составленному из последних
, должен быть ортогонален
вектору, составленному из последних ![]() элементов
того же вектора
элементов
того же вектора ![]() .
.
3.
Вектор ![]() состоит из компонентов вектора
состоит из компонентов вектора ![]() , записанных в обратном порядке.
, записанных в обратном порядке.
4.
Вектор ![]() является копией
является копией ![]() , но с обратными знаками у
компонент на нечетных позициях (первой, третьей и т.д.). Формально это можно
выразить как покомпонентное умножение вектора
, но с обратными знаками у
компонент на нечетных позициях (первой, третьей и т.д.). Формально это можно
выразить как покомпонентное умножение вектора ![]() на
вектор
на
вектор ![]() .
.
5.
Вектор ![]() является копией
является копией ![]() , но с обратными знаками у
компонент на четных позициях (второй, четвертой и т.д.). То есть,
, но с обратными знаками у
компонент на четных позициях (второй, четвертой и т.д.). То есть, ![]() равен
равен ![]() ,
умноженному на
,
умноженному на ![]() .
.
Для фильтра с двумя отсчетами правило 1 означает, что
![]() . (4.10)
. (4.10)
Правило
2 не применимо, так как ![]() и неравенство
и неравенство ![]() означает, что
означает, что ![]() . Правила 3-5 дают
соотношения
. Правила 3-5 дают
соотношения
![]() ,
, ![]() ,
, ![]() .
.
Значит,
все зависит от выбора чисел ![]() и
и ![]() . Однако, уравнения (4.10) не достаточно
для их определения. Тем не менее, видно, что значения
. Однако, уравнения (4.10) не достаточно
для их определения. Тем не менее, видно, что значения ![]() удовлетворяют этому условию.
Для фильтров из четырех отсчетов правила 1 и 2 означают, что
удовлетворяют этому условию.
Для фильтров из четырех отсчетов правила 1 и 2 означают, что
![]() ,
, ![]() , (4.11)
, (4.11)
а правила 3-5 дают соотношения
![]() ,
,
![]() ,
,
![]() .
.
Опять, уравнений (4.11) не достаточно для точного задания четырех неизвестных, поэтому необходимы дополнительные условия для вывода четырех коэффициентов (здесь помогает математическая интуиция). Эти коэффициенты приведены в (4.12), они образуют фильтр Добеши D4.
Для фильтра с восемью отсчетами, правила 1 и 2 приводят к уравнениям
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
а правила 3 5 записываются в виде соотношений
![]() ,
,
![]() ,
,
![]() .
.
Восемь допустимых коэффициентов приведены в табл. 4.23 (они образуют (фильтр Добеши D8).
|
.230377813309 |
.714846570553 |
.6308800767930 |
-.027983769417 |
|
-.187034811719 |
.030841381836 |
.032883011667 |
-.010597401785 |
Табл. 4.23. Коэффициенты фильтра Добеши с 8 отсчетами.
Для задания ![]() коэффициентов для каждого из
фильтров
коэффициентов для каждого из
фильтров ![]() ,
, ![]() ,
, ![]() и
и ![]() необходимо знать коэффициенты
с
необходимо знать коэффициенты
с ![]() по
по ![]() . Поэтому следует
задать
. Поэтому следует
задать ![]() уравнений
для нахождения этих величин. Однако правила 1 и 2 дают только
уравнений
для нахождения этих величин. Однако правила 1 и 2 дают только ![]() уравнений. Значит,
необходимо добавить новые условия для однозначного определения чисел с
уравнений. Значит,
необходимо добавить новые условия для однозначного определения чисел с ![]() по
по ![]() . Вот некоторые
примеры таких условий:
. Вот некоторые
примеры таких условий:
Фильтр пропускания низких частот: Мы хотим, чтобы фильтр ![]() пропускал только
низкие частоты, поэтому имеет смысл потребовать, чтобы частотный отклик
пропускал только
низкие частоты, поэтому имеет смысл потребовать, чтобы частотный отклик ![]() был равен нулю для
самой высокой частоты
был равен нулю для
самой высокой частоты ![]() .
.
Минимальный фильтр фазы: Это условие означает, что нули
комплексной функциий![]() должны лежать на единичной окружности комплексной плоскости или вне ее.
должны лежать на единичной окружности комплексной плоскости или вне ее.
Контролируемая колинеарность: Линейность фазового отклика можно контролировать с помощью нахождения минимума суммы
![]() .
.
Другие условия обсуждаются в [Akansn, Haddad 92].
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие переводчика
- Предисловие автора
- Введение
- Глава 1. Статистические методы
- 1.1. Энтропия
- 1.2. Коды переменной длины
- 1.3. Декодирование
- 1.4. Кодирование Хаффмана
- 1.4.1. Декодирование Хаффмана
- 1.4.2. Средняя длина кода
- 1.5. Адаптивные коды Хаффмана
- 1.5.1. Несжатые коды
- 1.5.2. Модификация дерева
- 1.5.3. Переполнение счетчика
- 1.5.4. Кодовое переполнение
- 1.5.5. Вариант алгоритма
- 1.6. Факсимильное сжатие
- 1.6.1. Одномерное кодирование
- 1.6.2. Двумерное кодирование
- 1.7. Арифметическое кодирование
- 1.7.1. Детали реализации метода
- 1.7.2. Потеря значащих цифр
- 1.7.3. Заключительные замечания
- 1.8. Адаптивное арифметическое кодирование
- ГЛАВА 2 СЛОВАРНЫЕ МЕТОДЫ
- 2.1. LZ77 (скользящее окно)
- 2.1.1. Циклическая очередь
- 2.2. LZSS
- 2.2.1. Недостатки
- 2.3. LZ78
- 2.4. LZW
- 2.4.1. Декодирование LZW
- 2.4.2. Структура словаря LZW
- 2.4.3. LZW в практических приложениях
- 2.5. Заключение
- ГЛАВА 3 СЖАТИЕ ИЗОБРАЖЕНИЙ
- 3.1. Введение
- 3.2. Типы изображений
- 3.3. Подходы к сжатию изображений
- 3.3.1. Коды Грея
- 3.3.2. Метрики ошибок
- 3.4. Интуитивные методы
- 3.4.1. Подвыборка
- 3.4.2. Квантование
- 3.5. Преобразование изображений
- 3.5.1. Ортогональные преобразования
- 3.5.2. Матричные преобразования
- 3.5.3. Дискретное косинус-преобразование
- 3.5.4. Пример
- 3.5.5. Дискретное синус-преобразование
- 3.5.6. Преобразование Уолша-Адамара
- 3.5.7. Преобразование Хаара
- 3.5.8. Преобразование Кархунена-Лоэвэ
- 3.6. Прогрессирующее сжатие изображений
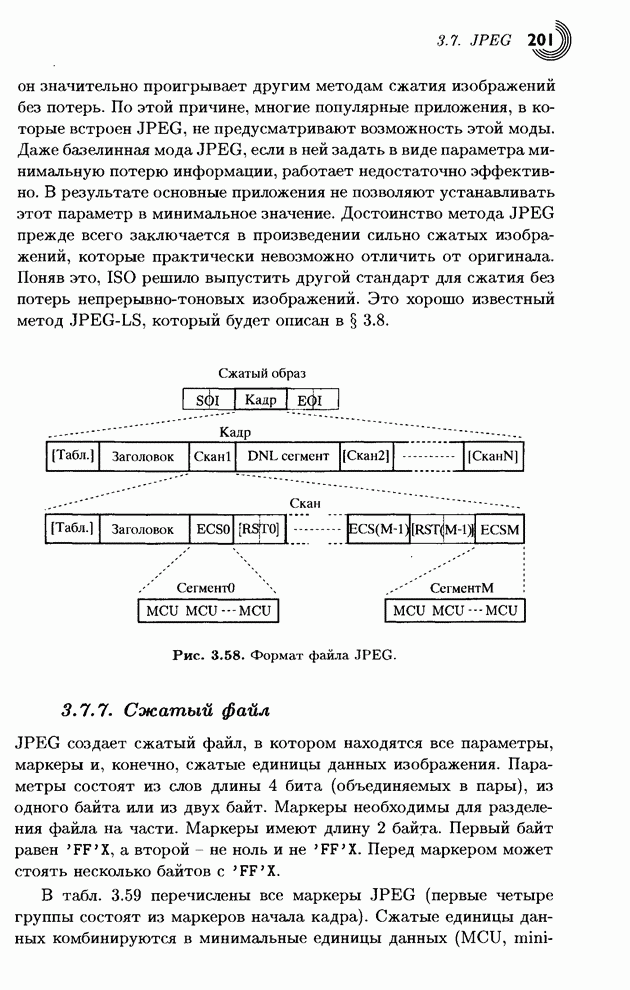
- 3.7. JPEG
- 3.7.1. Светимость
- 3.7.2. DCT
- 3.7.3. Практическое DCT
- 3.7.4. Квантование
- 3.7.5. Кодирование
- 3.7.6. Мода без потери данных
- 3.7.7. Сжатый файл
- 3.7.8. JFIF
- 3.8. JPEG-LS
- 3.8.1. Коды Голомба
- 3.8.2. Основы метода JPEG-LS
- 3.8.3. Кодер
- ГЛАВА 4 ВЕЙВЛЕТНЫЕ МЕТОДЫ
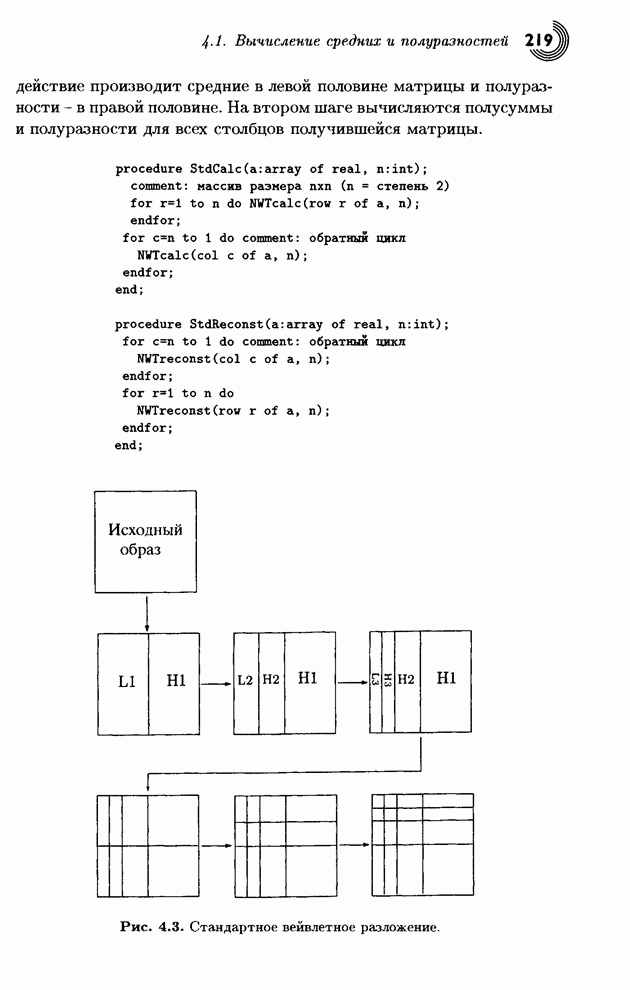
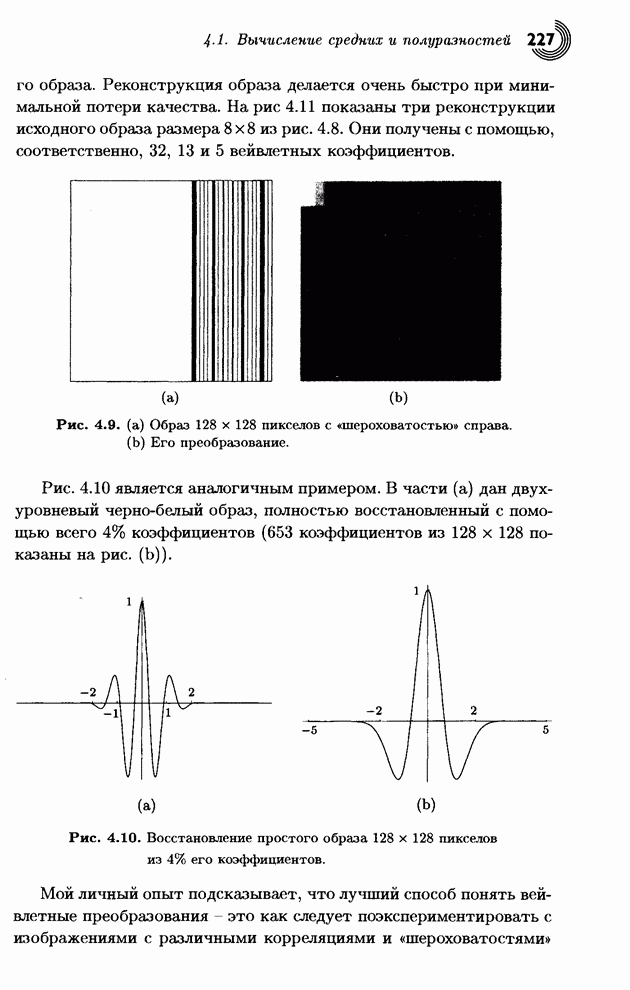
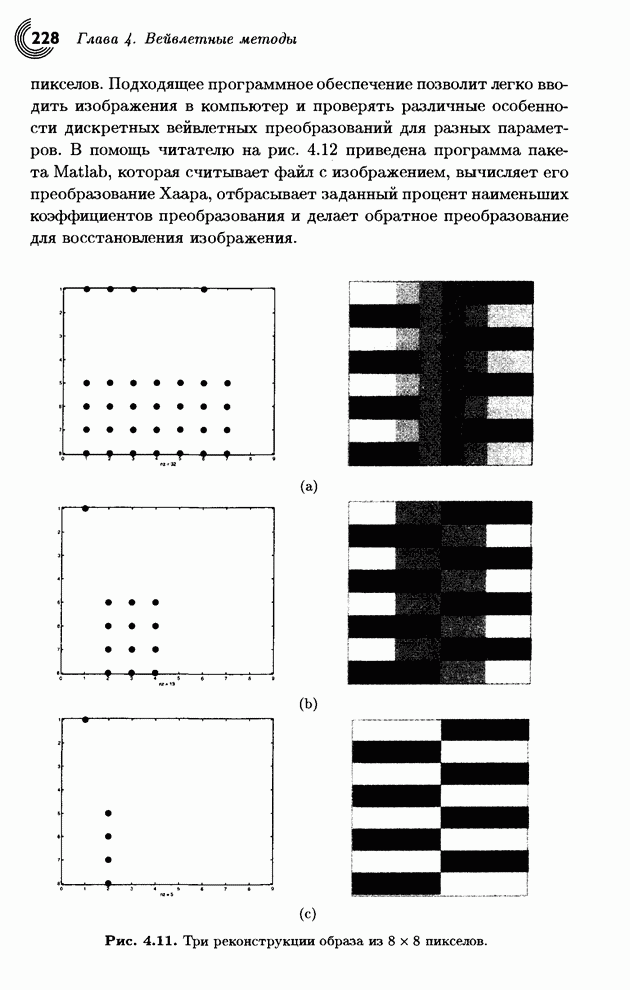
- 4.1. Вычисление средних и полу разностей
- 4.1.1. Обобщение на двумерный случай
- 4.1.2. Свойства преобразования Хаара
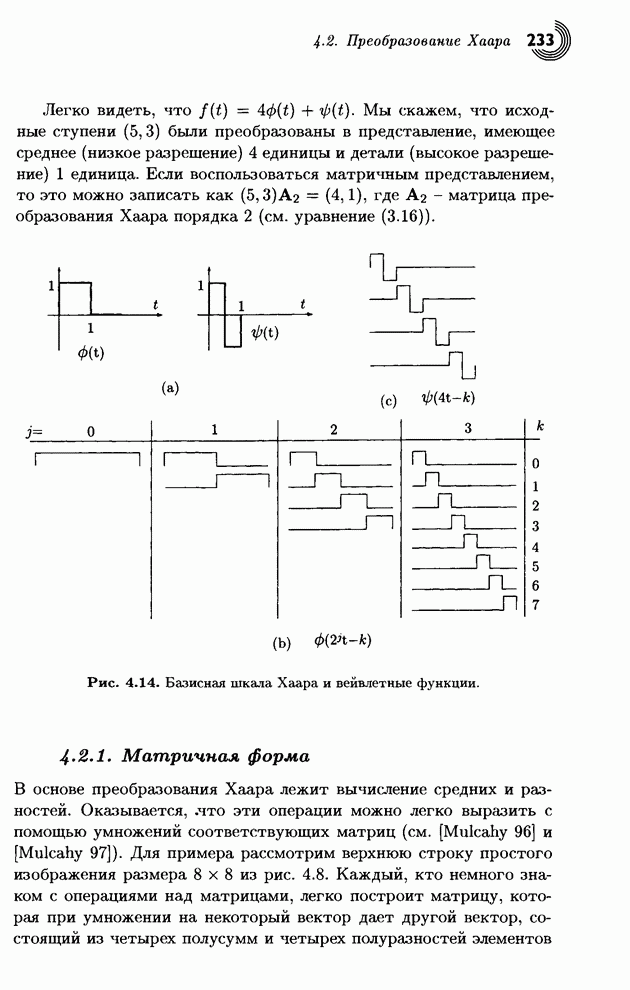
- 4.2. Преобразование Хаара
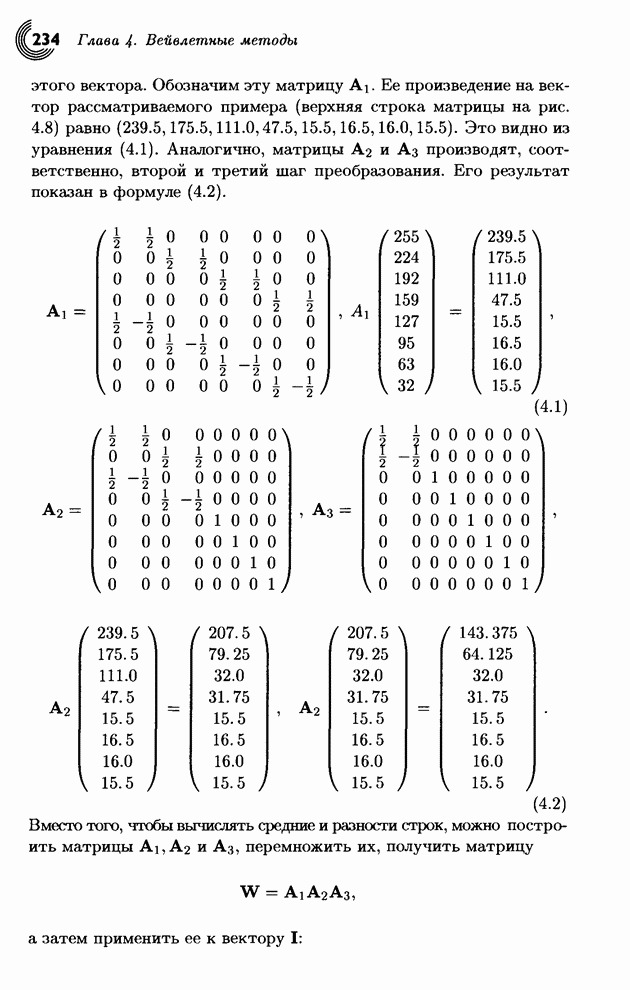
- 4.2.1. Матричная форма
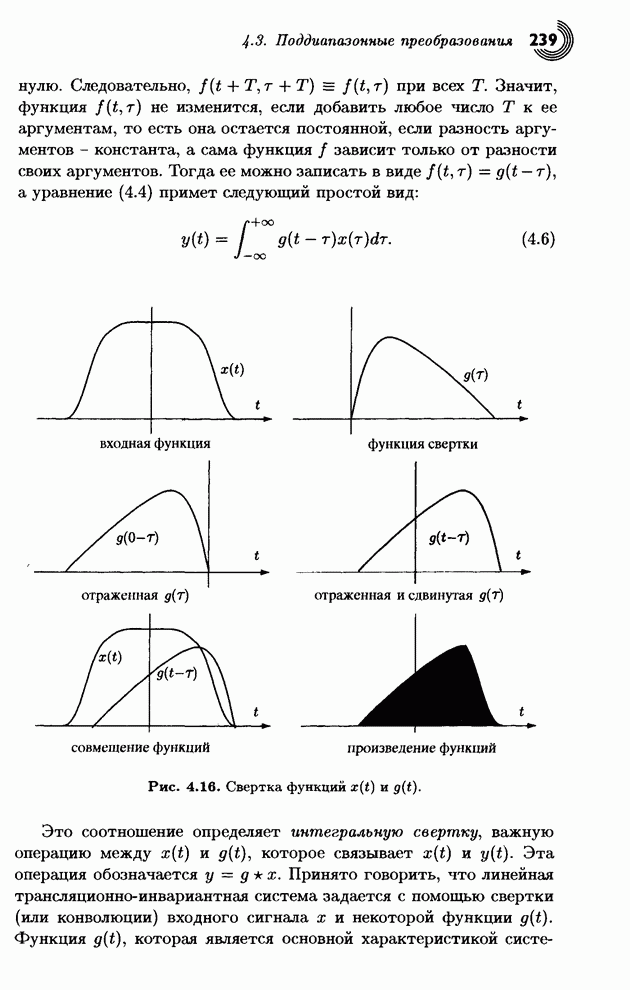
- 4.3. Поддиапазонные преобразования
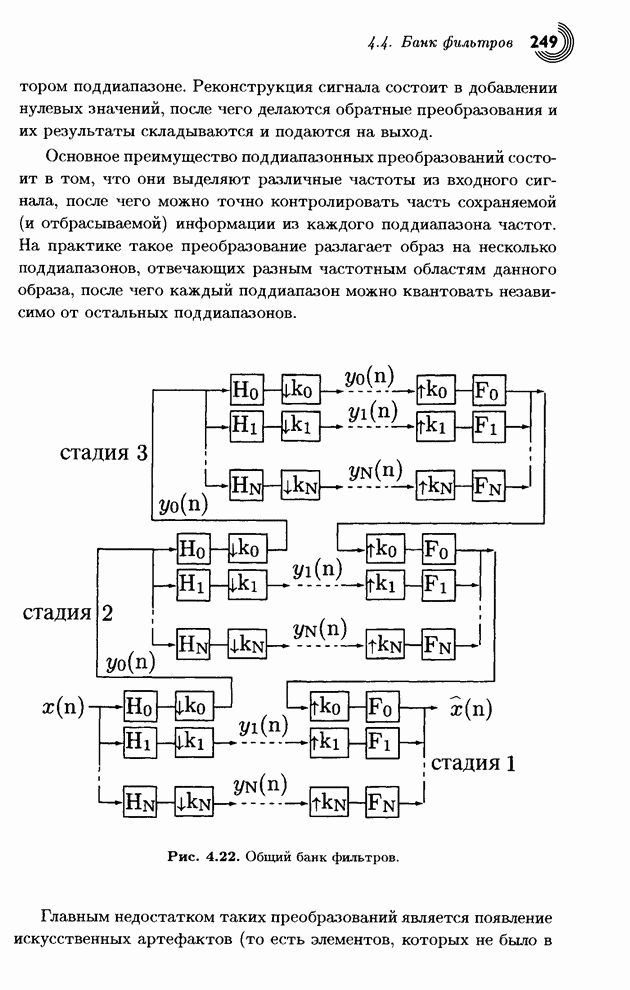
- 4.4. Банк фильтров
- 4.5. Нахождение коэффициентов фильтра
- 4.6. Преобразование DWT
- 4.7. Примеры
- 4.8. Вейвлеты Добеши
- 4.9. SPIHT
- 4.9.1. Алгоритм сортировки разделением множеств
- 4.9.2. Пространственно ориентированное дерево
- 4.9.3. Кодирование в алгоритме SPIHT
- 4.9.4. Пример
- 4.9.5. QTCQ
- ГЛАВА 5 СЖАТИЕ ВИДЕО
- 5.1. Основные принципы
- 5.2. Методы подоптимального поиска
- ГЛАВА 6 СЖАТИЕ ЗВУКА
- 6.1. Звук
- 6.2. Оцифрованный звук
- 6.3. Органы слуха человека
- 6.4. Общепризнанные методы
- 6.5. Сжатие звука в стандарте MPEG-1
- 6.5.1. Кодирование частотной области
- 6.5.2. Формат сжатых данных
- 6.5.3. Психоакустические модели
- 6.5.4. Кодирование: слой III
- Литература
- Глоссарий