| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
3.5.3. Дискретное косинус-преобразование
Прежде всего мы рассмотрим
одномерное (векторное) преобразование DCT
(в приложениях используется двумерное (матричное)
косинус-преобразование, но векторное DCT
проще понять, и оно
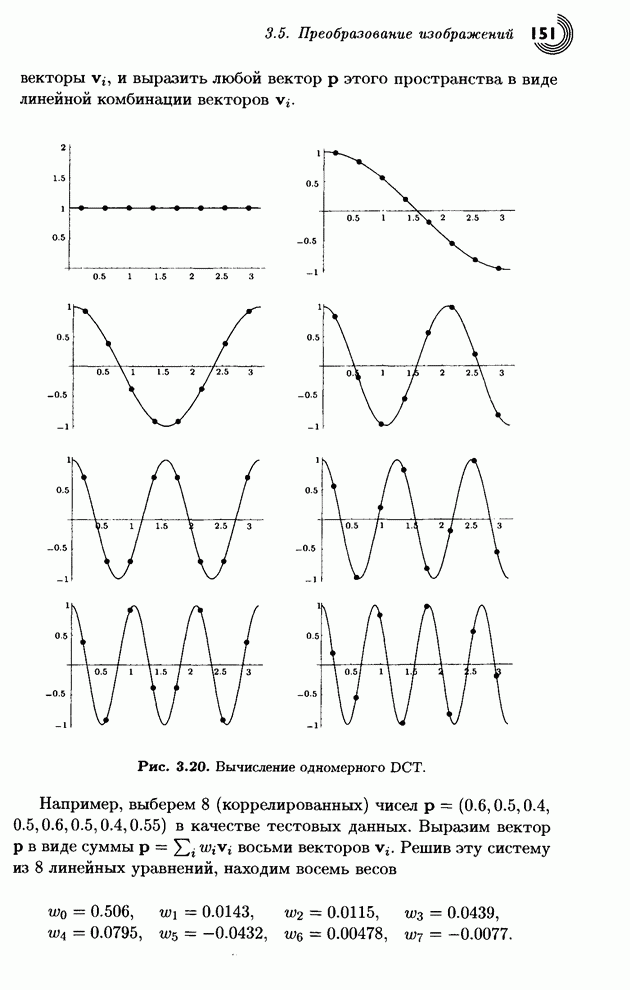
основано на тех же принципах). На рис. 3.20 показано восемь волн косинуса, ![]() , при
, при ![]() , с частотами
, с частотами ![]() . На каждом графике
отмечено восемь значений функции
. На каждом графике
отмечено восемь значений функции ![]() с абсциссами
с абсциссами
![]() (3.6)
(3.6)
которые
формируют базисный вектор ![]() . В результате получится восемь векторов
. В результате получится восемь векторов ![]() ,
, ![]() (всего 64 числа), которые
представлены в табл. 3.21. Они служат базисом одномерного
косинус-преобразования. Отметим схожесть этой таблицы с матрицей
(всего 64 числа), которые
представлены в табл. 3.21. Они служат базисом одномерного
косинус-преобразования. Отметим схожесть этой таблицы с матрицей ![]() из уравнения (3.5). В
обоих случаях частота смены знаков возрастает по строкам.
из уравнения (3.5). В
обоих случаях частота смены знаков возрастает по строкам.

Программа для вычисления рис. 3.20 (Matematica).
Можно показать, что все векторы ![]() ортогональны между
собой (из-за специального выбора восьми точек отсчета
ортогональны между
собой (из-за специального выбора восьми точек отсчета ![]() ). То же самое можно обнаружить
прямым вычислением с помощью подходящей математической программы. Значит, эти
восемь векторов можно поместить в матрицу размером 8х8 и рассмотреть
соответствующее ей ортогональное преобразование - вращение в восьмимерном
пространстве, которое называется одномерным дискретным косинус-преобразованием
(DCT). Двумерное DCT можно также интерпретировать как
двойное вращение. Это преобразование будет обсуждаться на стр. 155.
). То же самое можно обнаружить
прямым вычислением с помощью подходящей математической программы. Значит, эти
восемь векторов можно поместить в матрицу размером 8х8 и рассмотреть
соответствующее ей ортогональное преобразование - вращение в восьмимерном
пространстве, которое называется одномерным дискретным косинус-преобразованием
(DCT). Двумерное DCT можно также интерпретировать как
двойное вращение. Это преобразование будет обсуждаться на стр. 155.
Одномерное DCT имеет также другую
интерпретацию. Можно рассмотреть векторное пространство, базисом которого
служат векторы ![]() ,
и выразить любой вектор
,
и выразить любой вектор ![]() этого пространства в виде линейной
комбинации векторов
этого пространства в виде линейной
комбинации векторов ![]() .
.

Рис. 3.20. Вычисление одномерного DCT.
Например, выберем 8
(коррелированных) чисел ![]() в качестве тестовых данных. Выразим
вектор
в качестве тестовых данных. Выразим
вектор ![]() в
виде суммы
в
виде суммы ![]() восьми
векторов
восьми
векторов ![]() .
Решив эту систему из 8 линейных уравнений, находим восемь весов
.
Решив эту систему из 8 линейных уравнений, находим восемь весов
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Вес
![]() не сильно
отличается от элементов вектора
не сильно
отличается от элементов вектора ![]() , но остальные семь весов гораздо меньше.
Это показывает, как DCT (или любое другое ортогональное
преобразование) производит сжатие. Теперь можно просто записать эти восемь
весов в сжатый файл, где они будут занимать меньше места, чем восемь
компонентов исходного вектора
, но остальные семь весов гораздо меньше.
Это показывает, как DCT (или любое другое ортогональное
преобразование) производит сжатие. Теперь можно просто записать эти восемь
весов в сжатый файл, где они будут занимать меньше места, чем восемь
компонентов исходного вектора ![]() . Квантование весов
. Квантование весов ![]() может существенно повысить
фактор сжатия, причем при весьма малой потере данных.
может существенно повысить
фактор сжатия, причем при весьма малой потере данных.
|
|
0.196 |
0.589 |
0.982 |
1.374 |
1.767 |
2.160 |
2.553 |
2.945 |
|
|
1. |
1. |
1. |
1. |
1. |
1. |
1. |
1. |
|
|
0.981 |
0.831 |
0.556 |
0.195 |
-0.195 |
-0.556 |
-0.831 |
-0.981 |
|
|
0.924 |
0.383 |
-0.383 |
-0.924 |
-0.924 |
-0.383 |
0.383 |
0.924 |
|
|
0.831 |
-0.195 |
-0.981 |
-0.556 |
0.556 |
0.981 |
0.195 |
-0.831 |
|
|
0.707 |
-0.707 |
-0.707 |
0.707 |
0.707 |
-0.707 |
-0.707 |
0.707 |
|
|
0.556 |
-0.981 |
0.195 |
0.831 |
-0.831 |
-0.195 |
0.981 |
-0.556 |
|
|
0.383 |
-0.924 |
0.924 |
-0.383 |
-0.383 |
0.924 |
-0.924 |
0.383 |
|
|
0.195 |
-0.556 |
0.831 |
-0.981 |
0.981 |
-0.831 |
0.556 |
-0.195 |

Табл. 3.21. Вычисление одномерного DCT.
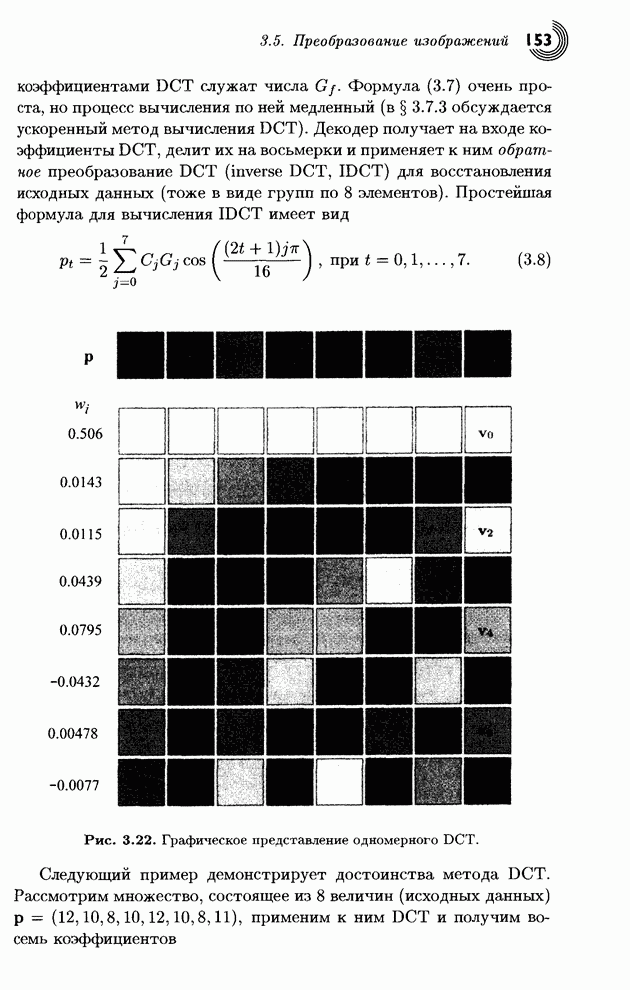
Рис. 3.22 иллюстрирует эту
линейную комбинацию графически. Все восемь векторов ![]() показаны в виде ряда из восьми
маленьких серых квадратиков, причем значение +1 представлено белым цветом, а
значение -1 окрашено в черный цвет. Каждый из восьми компонентов вектора
показаны в виде ряда из восьми
маленьких серых квадратиков, причем значение +1 представлено белым цветом, а
значение -1 окрашено в черный цвет. Каждый из восьми компонентов вектора ![]() выражен в виде
взвешенной суммы восьми серых оттенков.
выражен в виде
взвешенной суммы восьми серых оттенков.
На практике одномерное DCT проще всего вычислять по формуле
 , (3.7)
, (3.7)
где
 при
при ![]() .
.
Здесь исходными данными
(пикселами, фрагментами звука или другими элементами) являются величины ![]() , а им
соответствующими коэффициентами DCT
служат числа
, а им
соответствующими коэффициентами DCT
служат числа ![]() .
Формула (3.7) очень проста, но процесс вычисления по ней медленный (в § 3.7.3
обсуждается ускоренный метод вычисления DCT). Декодер получает на входе коэффициенты DCT, делит их на восьмерки и
применяет к ним обратное преобразование DCT (inverse DCT, IDCT) для восстановления исходных
данных (тоже в виде групп по 8 элементов). Простейшая формула для вычисления IDCT имеет вид
.
Формула (3.7) очень проста, но процесс вычисления по ней медленный (в § 3.7.3
обсуждается ускоренный метод вычисления DCT). Декодер получает на входе коэффициенты DCT, делит их на восьмерки и
применяет к ним обратное преобразование DCT (inverse DCT, IDCT) для восстановления исходных
данных (тоже в виде групп по 8 элементов). Простейшая формула для вычисления IDCT имеет вид
 , при
, при ![]() . (3.8)
. (3.8)

Рис. 3.22. Графическое представление одномерного DCT.
Следующий пример демонстрирует
достоинства метода DCT. Рассмотрим множество, состоящее
из 8 величин (исходных данных) ![]() , применим к ним DCT и получим восемь коэффициентов
, применим к ним DCT и получим восемь коэффициентов
28.6375, 0.571202, 0.46194, 1.757, 3.18198, - 1.72956, 0.191342, -0.308709.
Эти числа можно использовать для точного восстановления исходных данных (с маленькой ошибкой, вызванной ограничением на точность компьютерных вычислений). Наша цель, однако, улучшить сжатие с помощью подходящего квантования коэффициентов. Округляем (квантуем) их до 28.6, 0.6, 0.5, 1.8, 3.2, -1.8, 0.2, -0.3, применяем IDTC и получаем
12.0254, 10.0233, 7.96054, 9.93097, 12.0164, 9.99321, 7.94354, 10.9989.
Еще раз квантуем коэффициенты: 28, 1, 1, 2, 3, –2, 0, 0 и опять получаем с помощью IDCT следующий результат:
12.1883, 10.2315, 7.74931, 9.20863, 11.7876, 9.54549, 7.82865, 10.6557.
Наконец, квантуем коэффициенты до 28, 0, 0, 2, 3, –2, 0, 0 и получаем с помощью IDCT последовательность
11.236, 9.62443, 7.66286, 9.57302, 12.3471, 10.0146, 8.05304, 10.6842,
в которой наибольшая разность между исходным значением (12) и реконструированным (11.236) равна 0.764 (или 6.4% от 12). Программа вычисления для системы Matematica приведена на рис. 3.23.

Рис. 3.23. Эксперименты с одномерным DCT.
Эти простые примеры показывают достоинства метода DCT. Множество 28, 0, 0, 2, 3, –2, 0, 0 грубо квантованных коэффициентов DCT обладает четырьмя свойствами, которые делают его идеальным для сжатия, причем с замечательной декомпрессией при малой потери данных. Вот эти четыре свойства: (1) множество состоит только из целых чисел, (2) только четыре из них не равны нулю, (3) нулевые коэффициенты образуют серии, (4) среди ненулевых коэффициентов только первый имеет большую величину; остальные меньше исходных чисел. Эти свойства можно использовать при реализации схемы RLE, метода Хаффмана или любой другой техники (см. § 3.7.4 и 3.7.5) для дальнейшего сжатия этого множества.
Пример: Одномерное DCT (уравнение (3.7)) восьми коррелированных величин 11, 22, 33, 44, 55, 66, 77 и 88 произведет восемь коэффициентов 140, –71, 0, –7, 0, –2, 0, 0. После квантования получаем множество 140, –71, 0, 0, 0, 0, 0, 0 и применяем IDCT. В результате: 15, 20, 30, 43, 56, 69, 79 и 84. Эти числа весьма близки к исходным; наибольшее расхождение равно 4. На рис. 3.24 дана программа для этого примера.

Рис. 3.24. Пример одномерного DCT (Matematica).
Дойдя до этого места, воодушевленный читатель может воскликнуть: «Удивительно! Восемь исходных данных восстанавливаются всего с помощью двух чисел. Чудеса какие-то!»» Однако, те, кто поняли свойства преобразований, могут дать простое объяснение. Восстановление данные происходит не только по двум числам 140 и –71, но также по их положению в последовательности из 8 коэффициентов. Кроме того, исходные величины восстанавливаются с высокой точностью благодаря присутствию избыточности.
Предельным случаем избыточных данных служит последовательность одинаковых величин. Они, конечно, имеют совершенную корреляцию, и мы чувствуем интуитивно, что одного числа будет достаточно для полного их восстановления. Реконструкция последовательности высоко коррелированных данных, такой, как 20, 31, 42, 53, ... потребует всего двух чисел. Ими могут быть начальное значение (20) и шаг (11) (разность этой арифметической прогрессии), но могут быть и другие числа. В общем случае, чем меньше коррелированы данные, тем больше чисел потребуется для их восстановления.
Двумерное (матричное) DCT: Из опыта хорошо известно, что пикселы изображения имеют корреляцию по двум направлениям, а не только по одному (пикселы коррелируют со своими соседями слева, справа, а также сверху и снизу). Поэтому методы сжатия изображений используют двумерное DCT, которое задается формулой
 , (3.9)
, (3.9)
при
![]() . Изображение
разбивается на блоки пикселов
. Изображение
разбивается на блоки пикселов ![]() размера
размера ![]() (в нашем примере
(в нашем примере ![]() ), и уравнения (3.9)
используются для нахождения коэффициентов
), и уравнения (3.9)
используются для нахождения коэффициентов ![]() для каждого блока пикселов. Если
допускается частичная потеря информации, то коэффициенты квантуются. Декодер
восстанавливает сжатый блок данных (точно или приближенно), вычисляя обратное DCT (IDCT) по формуле
для каждого блока пикселов. Если
допускается частичная потеря информации, то коэффициенты квантуются. Декодер
восстанавливает сжатый блок данных (точно или приближенно), вычисляя обратное DCT (IDCT) по формуле
 , (3.10)
, (3.10)
где 
Двумерное
DCT можно интерпретировать двумя
способами: с помощью вращения (на самом деле, композиции двух вращений), и с
помощью базиса в ![]() -мерном
векторном пространстве. В первой интерпретации используется блок
-мерном
векторном пространстве. В первой интерпретации используется блок ![]() пикселов (рис. 3.25а,
где элементы обозначены буквой «L»).
Сначала рассматриваются строки этого блока как точки (
пикселов (рис. 3.25а,
где элементы обозначены буквой «L»).
Сначала рассматриваются строки этого блока как точки (![]() ) в
) в ![]() -мерном пространстве, которые
поворачиваются в этом пространстве с помощью преобразования, задаваемого
внутренней суммой
-мерном пространстве, которые
поворачиваются в этом пространстве с помощью преобразования, задаваемого
внутренней суммой

из
уравнения (3.9). Результатом этого вращения служит блок ![]() из
из ![]() коэффициентов, в котором в
строках доминируют первые элементы (обозначенные как «L» на рис. 3.25b), а все остальные элементы малы (они обозначены на
этом рисунке как «S»). Внешняя сумма из уравнения
(3.9) равна
коэффициентов, в котором в
строках доминируют первые элементы (обозначенные как «L» на рис. 3.25b), а все остальные элементы малы (они обозначены на
этом рисунке как «S»). Внешняя сумма из уравнения
(3.9) равна
 .
.
Здесь
ужу столбцы матрицы ![]() рассматриваются в качестве точек
рассматриваются в качестве точек ![]() -мерного векторного
пространства, над которыми совершается преобразование вращения. В результате
получается один большой коэффициент в верхнем левом углу блока (на рис.3.25с -
это «L») и
-мерного векторного
пространства, над которыми совершается преобразование вращения. В результате
получается один большой коэффициент в верхнем левом углу блока (на рис.3.25с -
это «L») и ![]() маленьких коэффициентов в
остальных местах («S» и «s» на рисунке). Эта интерпретация рассматривает
двумерное DTC в виде двух разных вращений
размерности
маленьких коэффициентов в
остальных местах («S» и «s» на рисунке). Эта интерпретация рассматривает
двумерное DTC в виде двух разных вращений
размерности ![]() .
Интересно отметить, что два вращения размерности
.
Интересно отметить, что два вращения размерности ![]() вычисляются быстрее, чем одно вращение
размерности
вычисляются быстрее, чем одно вращение
размерности ![]() ,
поскольку второе требует матрицу размера
,
поскольку второе требует матрицу размера ![]() .
.

Рис. 3.25. Двумерное DCT и двойное вращение.
Вторая интерпретация (при ![]() ) использует уравнение
(3.9) для создания 64 блоков по 8х8 величин в каждом. Все 64 блока
рассматриваются в качестве базиса 64-мерного векторного пространства (это
базисные изображения). Любой блок В из 8х8 пикселов можно выразить как линейную
комбинацию этих базисных изображений, и все 64 веса этой линейной комбинации
образуют коэффициенты DCT блока В.
) использует уравнение
(3.9) для создания 64 блоков по 8х8 величин в каждом. Все 64 блока
рассматриваются в качестве базиса 64-мерного векторного пространства (это
базисные изображения). Любой блок В из 8х8 пикселов можно выразить как линейную
комбинацию этих базисных изображений, и все 64 веса этой линейной комбинации
образуют коэффициенты DCT блока В.
На рис. 3.26 показано графическое
представление 64 базисных образов двумерного DCT при ![]() . Каждый элемент
. Каждый элемент ![]() на этом рисунке является
блоком размера 8x8, который получен произведением
на этом рисунке является
блоком размера 8x8, который получен произведением ![]() , где
, где ![]() и
и ![]() - меняются независимо в пределах,
указанных в уравнении (3.6). Этот рисунок легко построить с помощью программы,
приведенной на стр. 159. Там же приведена модифицированная программа из [Watson 94], требующая пакет Graphicslinage.m, который не очень распространен.
- меняются независимо в пределах,
указанных в уравнении (3.6). Этот рисунок легко построить с помощью программы,
приведенной на стр. 159. Там же приведена модифицированная программа из [Watson 94], требующая пакет Graphicslinage.m, который не очень распространен.
Используя подходящее программное обеспечение, легко выполнить вычисление DCT и отобразить результаты графически. На рис. 3.29а приведена случайная матрица 8х8 из нулей и единиц. Эта матрица изображена на рис. 3.29b с помощью белых и черных квадратиков, обозначающих 1 и 0, соответственно. На рис. 3.29с показаны численные значения весов, на которые следует умножить каждый из 64 коэффициентов DCT для того, чтобы восстановить исходную матрицу.

Рис. 3.26. 64 базисных изображения двумерного DCT.
На этом рисунке нуль показан нейтрально-серым цветом, положительные числа светло-серым, а отрицательные темным. На рис. 3.29d даны численные значения этих весов. Приведена также программа для построения всех этих графиков. На рис. 3.30 сделаны те же самые построения, но применительно к более регулярным исходным данным.
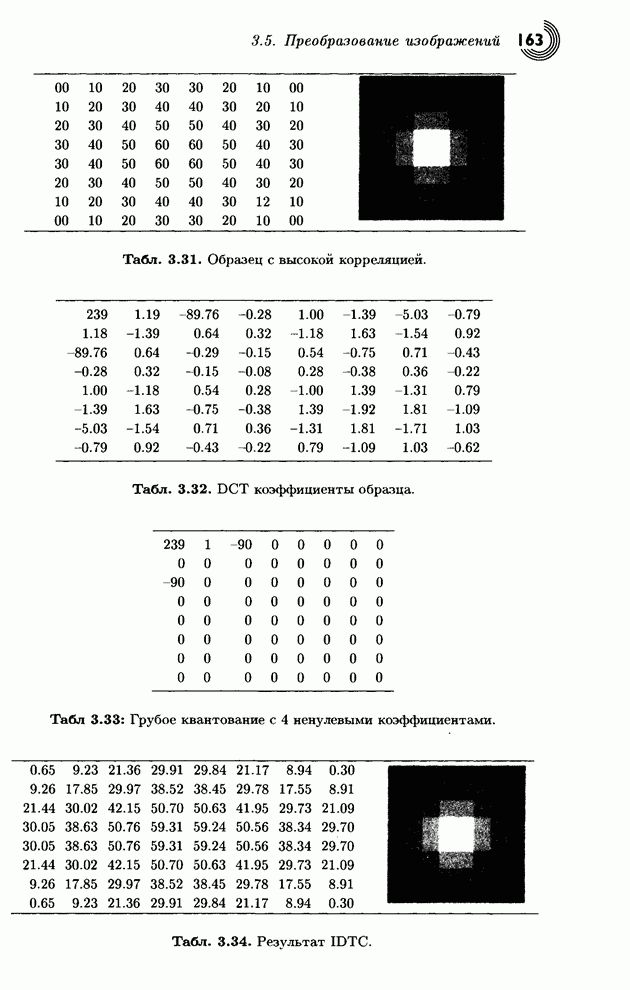
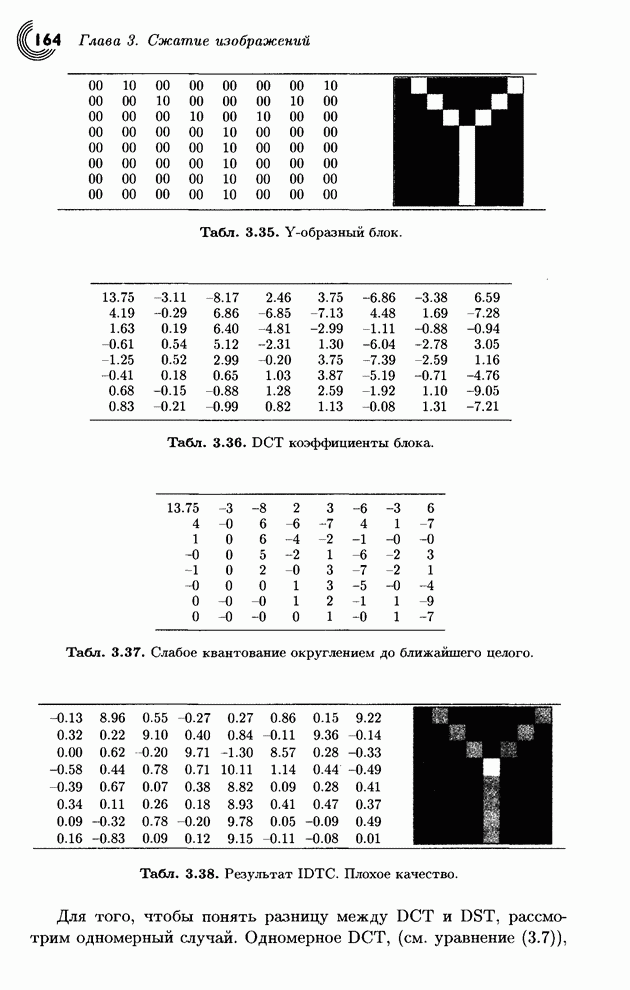
Теперь продемонстрируем достоинства двумерного DCT применительно к двум блокам чисел. Первый блок (табл. 3.27, слева) состоит из сильно коррелированных целых чисел в интервале [8,12], а второй (табл. 3.28, слева) образован случайными числами из того же интервала. Первый блок порождает один большой коэффициент DC, за которым следуют маленькие (включая 20 нулевых) коэффициентов АС. А среди коэффициентов DCT второго, случайного, блока имеется всего один нуль.

Программа для рис. 3.26 (Matematica)

Альтернативная программа для рис. 3.26
(Видно, почему пикселы в табл. 3.27 коррелированы. Все восемь чисел верхней строки таблицы близки друг к другу (расстояния между ними равны 2 или 3). Все остальные строки получаются циклическим сдвигом вправо предыдущей строки.)
|
12 |
10 |
8 |
10 |
12 |
10 |
8 |
11 |
81 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
11 |
12 |
10 |
8 |
10 |
12 |
10 |
8 |
0 |
1.57 |
0.61 |
1.90 |
0.38 |
-1.81 |
0.20 |
-0.32 |
|
8 |
11 |
12 |
10 |
8 |
10 |
12 |
10 |
0 |
-0.61 |
0.71 |
0.35 |
0 |
0.07 |
0 |
0.02 |
|
10 |
8 |
11 |
12 |
10 |
8 |
10 |
12 |
0 |
1.90 |
-0.35 |
4.76 |
0.77 |
-3.39 |
0.25 |
-0.54 |
|
12 |
10 |
8 |
11 |
12 |
10 |
8 |
10 |
0 |
-0.38 |
0 |
-0.77 |
8.00 |
0.51 |
0 |
0.07 |
|
10 |
12 |
10 |
8 |
11 |
12 |
10 |
8 |
0 |
-1.81 |
-0.07 |
-3.39 |
-0.51 |
1.57 |
0.56 |
0.25 |
|
8 |
10 |
12 |
10 |
8 |
11 |
12 |
10 |
0 |
-0.20 |
0 |
-0.25 |
0 |
-0.56 |
-0.71 |
0.29 |
|
10 |
8 |
10 |
12 |
10 |
8 |
11 |
12 |
0 |
-0.32 |
-0.02 |
-0.54 |
-0.07 |
0.25 |
-0.29 |
-0.90 |
Табл. 3.27. Двумерное DCT блока коррелированных величин.
|
8 |
10 |
9 |
11 |
11 |
9 |
9 |
12 |
79.12 |
0.98 |
0.64 |
-1.51 |
-0.62 |
-0.86 |
1.22 |
0.32 |
|
11 |
8 |
12 |
8 |
11 |
10 |
11 |
10 |
0.15 |
-1.64 |
-0.09 |
1.23 |
0.10 |
3.29 |
1.08 |
-2.97 |
|
9 |
11 |
9 |
10 |
12 |
9 |
9 |
8 |
-1.26 |
-0.29 |
-3.27 |
1.69 |
-0.51 |
1.13 |
1.52 |
1.33 |
|
9 |
12 |
10 |
8 |
8 |
9 |
8 |
9 |
-1.27 |
-0.25 |
-0.67 |
-0.15 |
1.63 |
-1.94 |
0.47 |
-1.30 |
|
12 |
8 |
9 |
9 |
12 |
10 |
8 |
11 |
-2.12 |
-0.67 |
-0.07 |
-0.79 |
0.13 |
-1.40 |
0.16 |
-0.15 |
|
8 |
11 |
10 |
12 |
9 |
12 |
12 |
10 |
-2.68 |
1.08 |
-1.99 |
-1.93 |
-1.77 |
-0.35 |
0 |
-0.80 |
|
10 |
10 |
12 |
10 |
12 |
10 |
10 |
12 |
1.20 |
2.10 |
-0.98 |
0.87 |
-1.55 |
-0.59 |
-0.98 |
2.76 |
|
12 |
9 |
11 |
11 |
9 |
8 |
8 |
12 |
-2.24 |
0.55 |
0.29 |
0.75 |
-2.40 |
-0.05 |
0.06 |
1.14 |
Табл. 3.28. Двумерное DCT блока случайных величин.

Рис. 3.29. Пример двумерного DCT (Mathematica).
Сжатие любого изображения с помощью DCT можно теперь сделать следующим образом.
1.
Разделить его на ![]() блоков
пикселов размера
блоков
пикселов размера ![]() (обычно
8x8).
(обычно
8x8).
2.
Применить DCT к каждому блоку ![]() , то есть, представить
каждый блок в виде линейной комбинации 64 базисных блоков рис. 3.26.
Результатом станут блоки (мы будем их называть векторами)
, то есть, представить
каждый блок в виде линейной комбинации 64 базисных блоков рис. 3.26.
Результатом станут блоки (мы будем их называть векторами) ![]() из 64 весов
из 64 весов ![]() , где
, где ![]() .
.
3.
Все ![]() векторов
векторов
![]()
![]() разделить на 64
вектора коэффициентов
разделить на 64
вектора коэффициентов ![]() с
с ![]() компонентами
компонентами ![]() . Вектор первых компонентов
. Вектор первых компонентов ![]() состоит из
состоит из ![]() коэффициентов DC.
коэффициентов DC.
4.
Сделать квантование каждого вектора коэффициентов ![]() независимо от других. Полученный
квантованный вектор
независимо от других. Полученный
квантованный вектор ![]() записать
(после дополнительной компрессии по методу RLE, Хаффмана или иного метода) в сжатый файл.
записать
(после дополнительной компрессии по методу RLE, Хаффмана или иного метода) в сжатый файл.

Рис. 3.30. Пример двумерного DCT (Matematica).
Декодер читает 64 квантованных
вектора коэффициентов использует их для построения ![]() весовых векторов
весовых векторов ![]() и применяет IDCT к каждому весовому вектору для
(приближенной) реконструкции 64 пикселов блока
и применяет IDCT к каждому весовому вектору для
(приближенной) реконструкции 64 пикселов блока ![]() . Отметим, что метод JPEG работает несколько иначе.
. Отметим, что метод JPEG работает несколько иначе.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие переводчика
- Предисловие автора
- Введение
- Глава 1. Статистические методы
- 1.1. Энтропия
- 1.2. Коды переменной длины
- 1.3. Декодирование
- 1.4. Кодирование Хаффмана
- 1.4.1. Декодирование Хаффмана
- 1.4.2. Средняя длина кода
- 1.5. Адаптивные коды Хаффмана
- 1.5.1. Несжатые коды
- 1.5.2. Модификация дерева
- 1.5.3. Переполнение счетчика
- 1.5.4. Кодовое переполнение
- 1.5.5. Вариант алгоритма
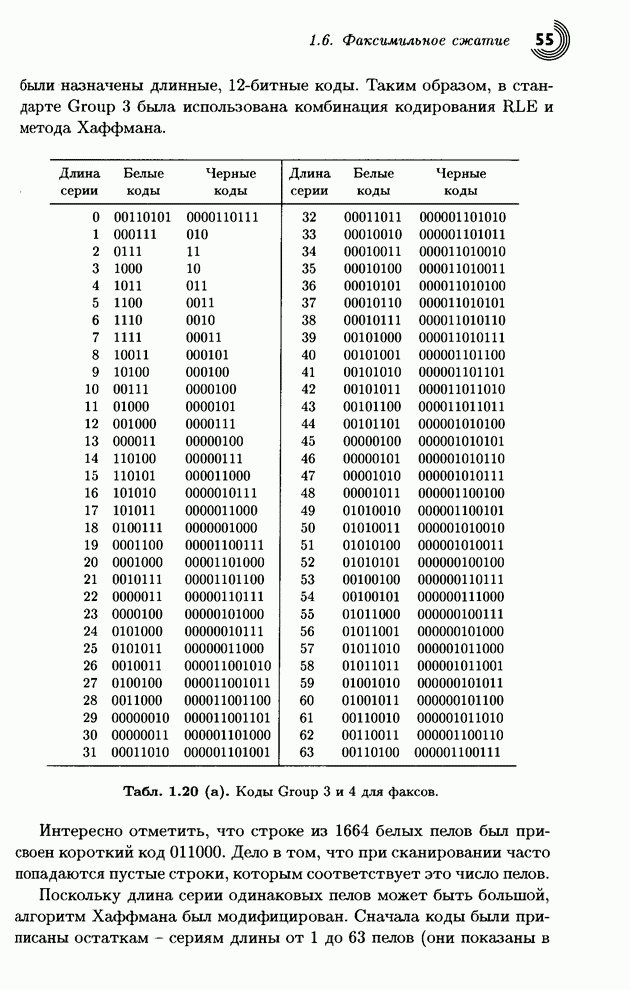
- 1.6. Факсимильное сжатие
- 1.6.1. Одномерное кодирование
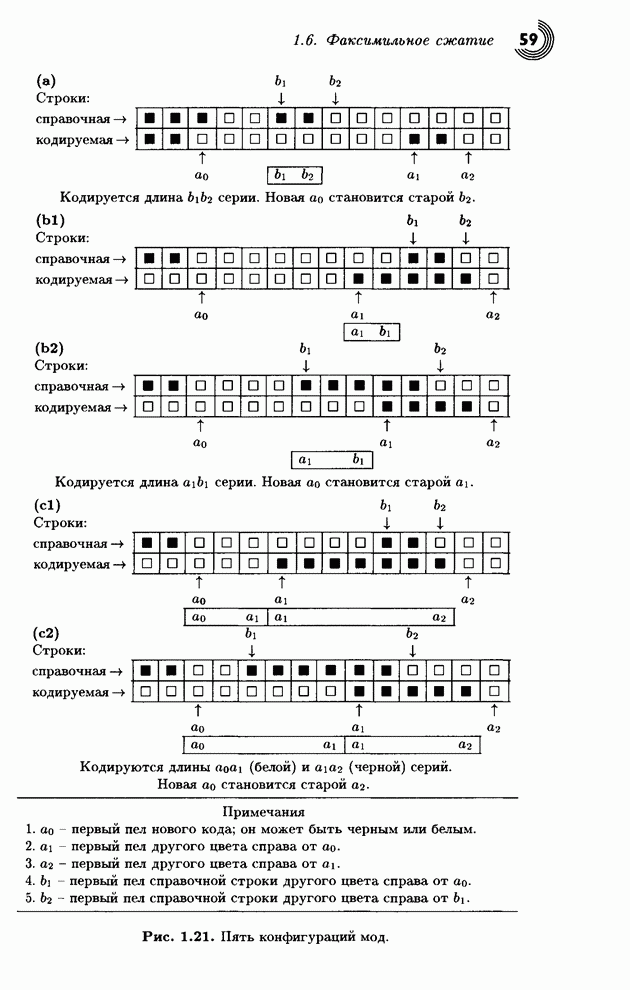
- 1.6.2. Двумерное кодирование
- 1.7. Арифметическое кодирование
- 1.7.1. Детали реализации метода
- 1.7.2. Потеря значащих цифр
- 1.7.3. Заключительные замечания
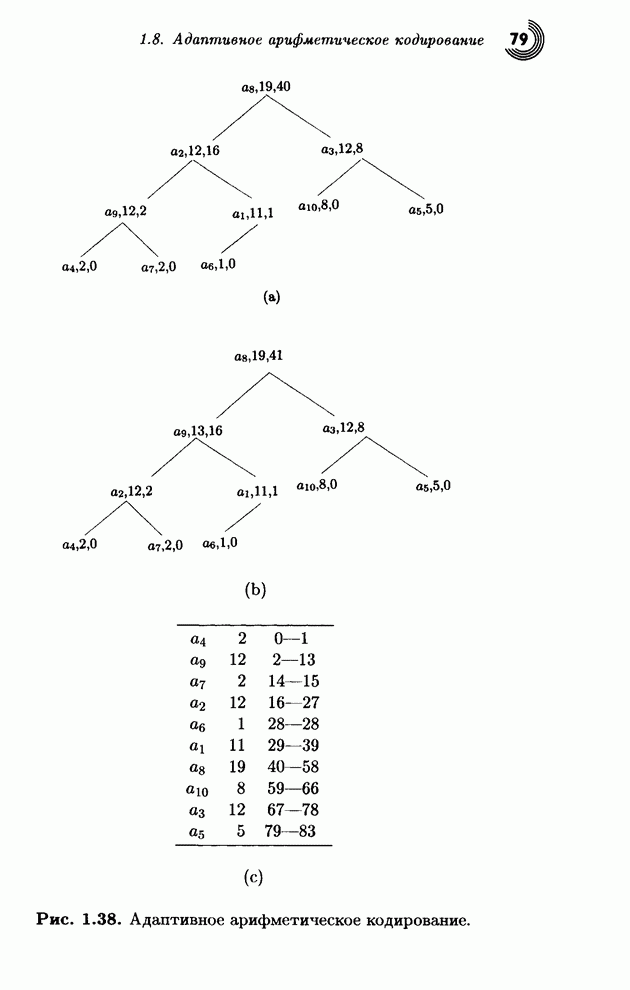
- 1.8. Адаптивное арифметическое кодирование
- ГЛАВА 2 СЛОВАРНЫЕ МЕТОДЫ
- 2.1. LZ77 (скользящее окно)
- 2.1.1. Циклическая очередь
- 2.2. LZSS
- 2.2.1. Недостатки
- 2.3. LZ78
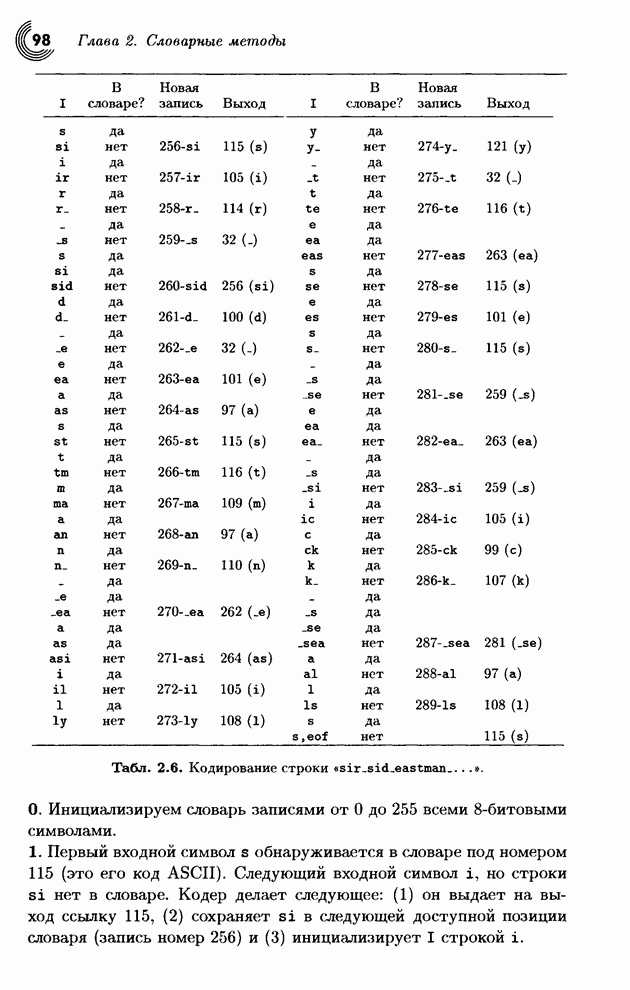
- 2.4. LZW
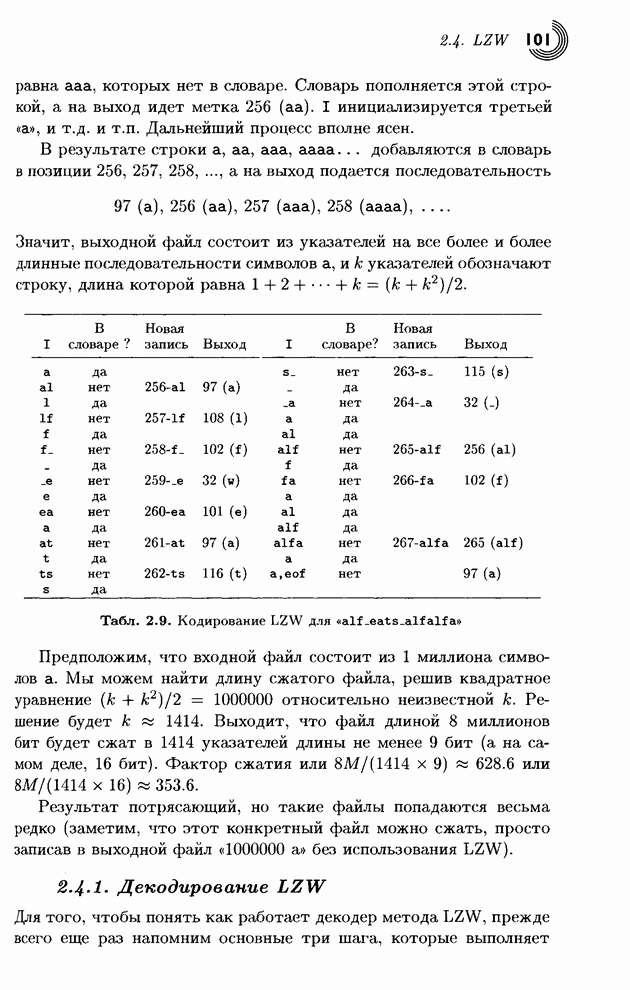
- 2.4.1. Декодирование LZW
- 2.4.2. Структура словаря LZW
- 2.4.3. LZW в практических приложениях
- 2.5. Заключение
- ГЛАВА 3 СЖАТИЕ ИЗОБРАЖЕНИЙ
- 3.1. Введение
- 3.2. Типы изображений
- 3.3. Подходы к сжатию изображений
- 3.3.1. Коды Грея
- 3.3.2. Метрики ошибок
- 3.4. Интуитивные методы
- 3.4.1. Подвыборка
- 3.4.2. Квантование
- 3.5. Преобразование изображений
- 3.5.1. Ортогональные преобразования
- 3.5.2. Матричные преобразования
- 3.5.3. Дискретное косинус-преобразование
- 3.5.4. Пример
- 3.5.5. Дискретное синус-преобразование
- 3.5.6. Преобразование Уолша-Адамара
- 3.5.7. Преобразование Хаара
- 3.5.8. Преобразование Кархунена-Лоэвэ
- 3.6. Прогрессирующее сжатие изображений
- 3.7. JPEG
- 3.7.1. Светимость
- 3.7.2. DCT
- 3.7.3. Практическое DCT
- 3.7.4. Квантование
- 3.7.5. Кодирование
- 3.7.6. Мода без потери данных
- 3.7.7. Сжатый файл
- 3.7.8. JFIF
- 3.8. JPEG-LS
- 3.8.1. Коды Голомба
- 3.8.2. Основы метода JPEG-LS
- 3.8.3. Кодер
- ГЛАВА 4 ВЕЙВЛЕТНЫЕ МЕТОДЫ
- 4.1. Вычисление средних и полу разностей
- 4.1.1. Обобщение на двумерный случай
- 4.1.2. Свойства преобразования Хаара
- 4.2. Преобразование Хаара
- 4.2.1. Матричная форма
- 4.3. Поддиапазонные преобразования
- 4.4. Банк фильтров
- 4.5. Нахождение коэффициентов фильтра
- 4.6. Преобразование DWT
- 4.7. Примеры
- 4.8. Вейвлеты Добеши
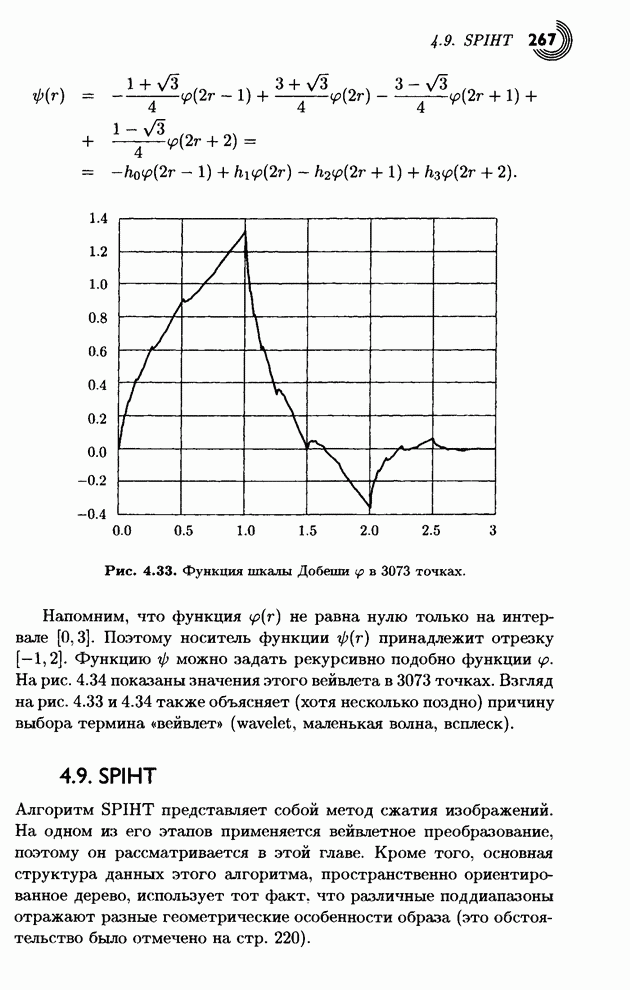
- 4.9. SPIHT
- 4.9.1. Алгоритм сортировки разделением множеств
- 4.9.2. Пространственно ориентированное дерево
- 4.9.3. Кодирование в алгоритме SPIHT
- 4.9.4. Пример
- 4.9.5. QTCQ
- ГЛАВА 5 СЖАТИЕ ВИДЕО
- 5.1. Основные принципы
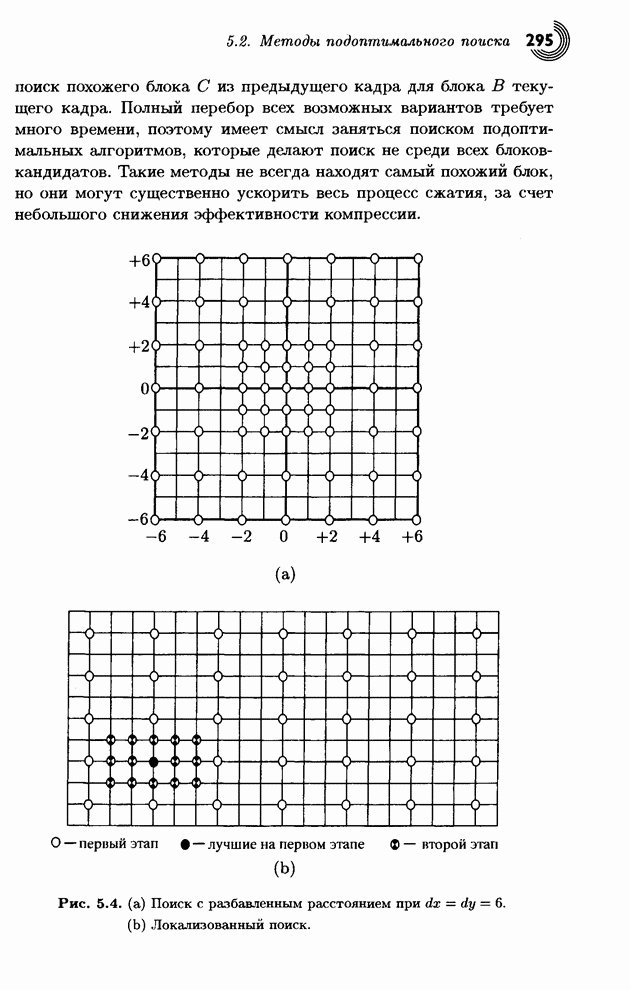
- 5.2. Методы подоптимального поиска
- ГЛАВА 6 СЖАТИЕ ЗВУКА
- 6.1. Звук
- 6.2. Оцифрованный звук
- 6.3. Органы слуха человека
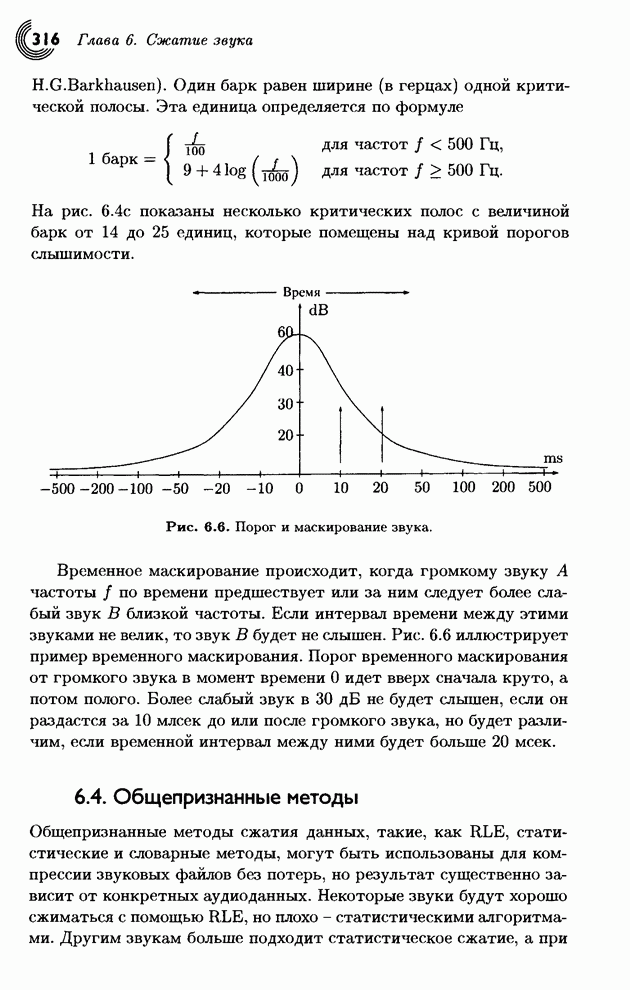
- 6.4. Общепризнанные методы
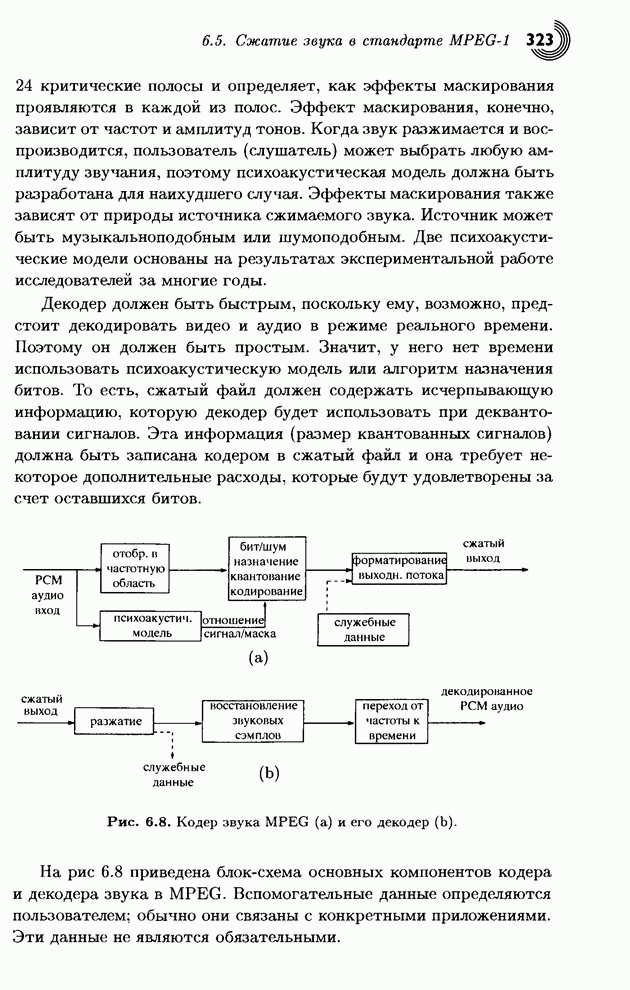
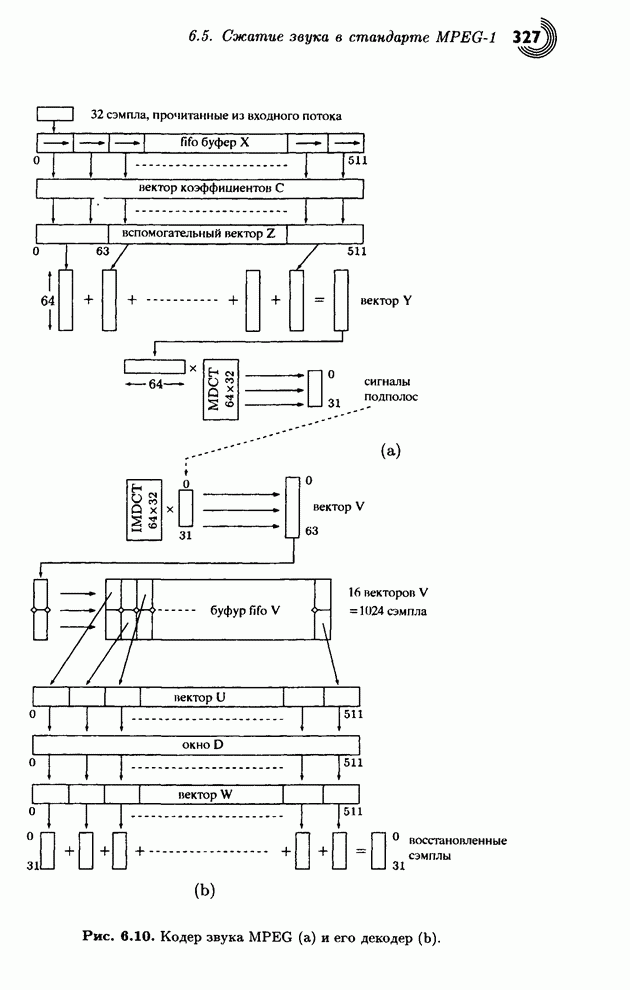
- 6.5. Сжатие звука в стандарте MPEG-1
- 6.5.1. Кодирование частотной области
- 6.5.2. Формат сжатых данных
- 6.5.3. Психоакустические модели
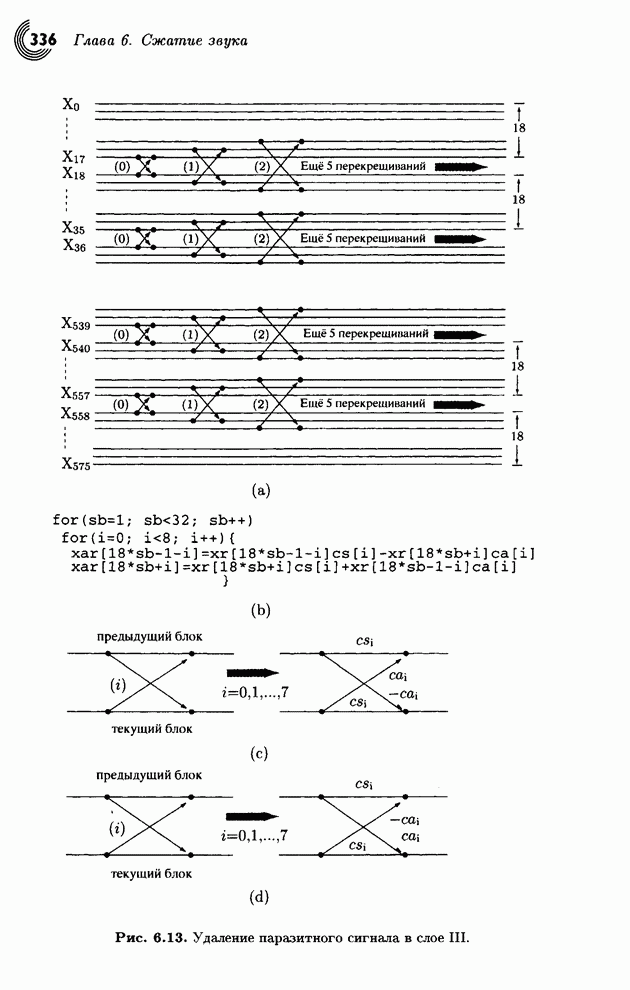
- 6.5.4. Кодирование: слой III
- Литература
- Глоссарий