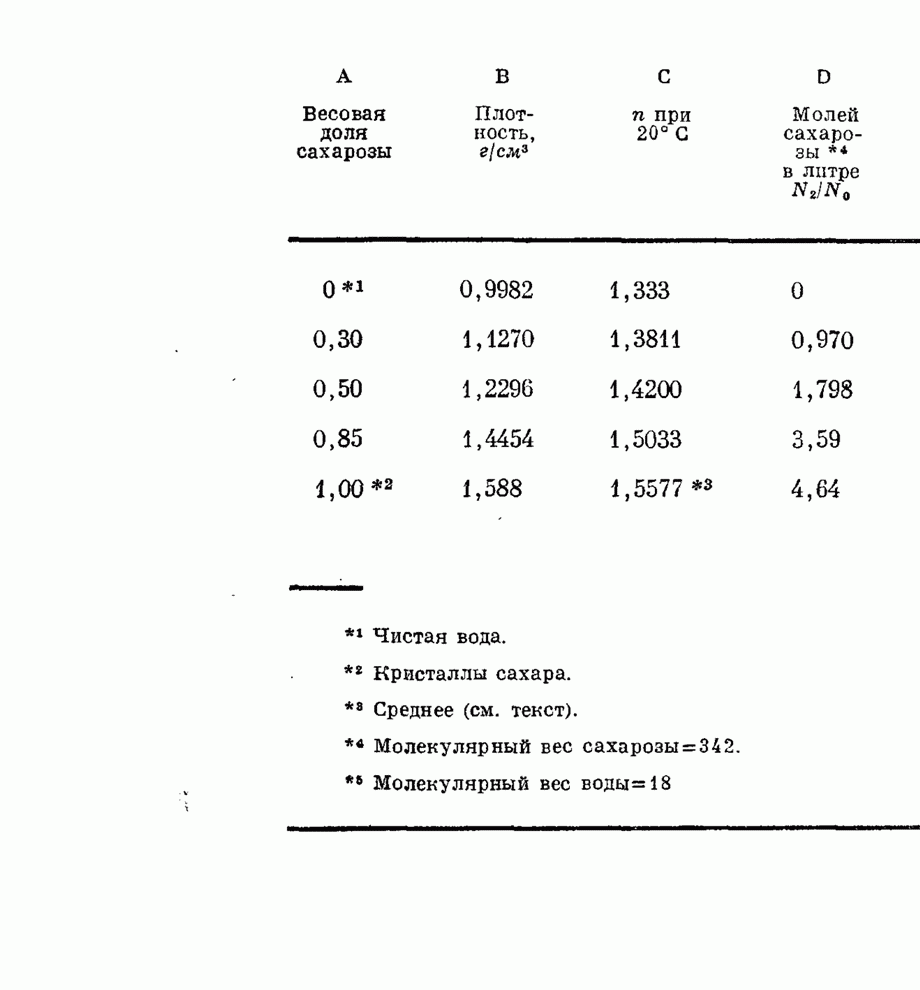
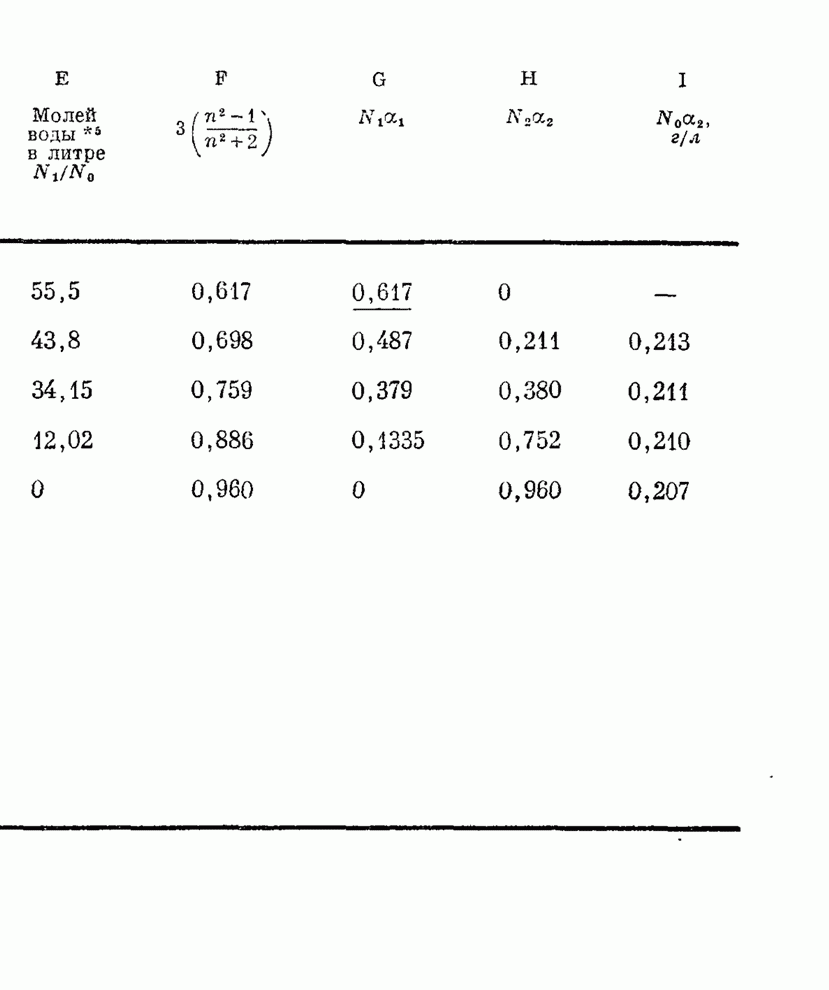
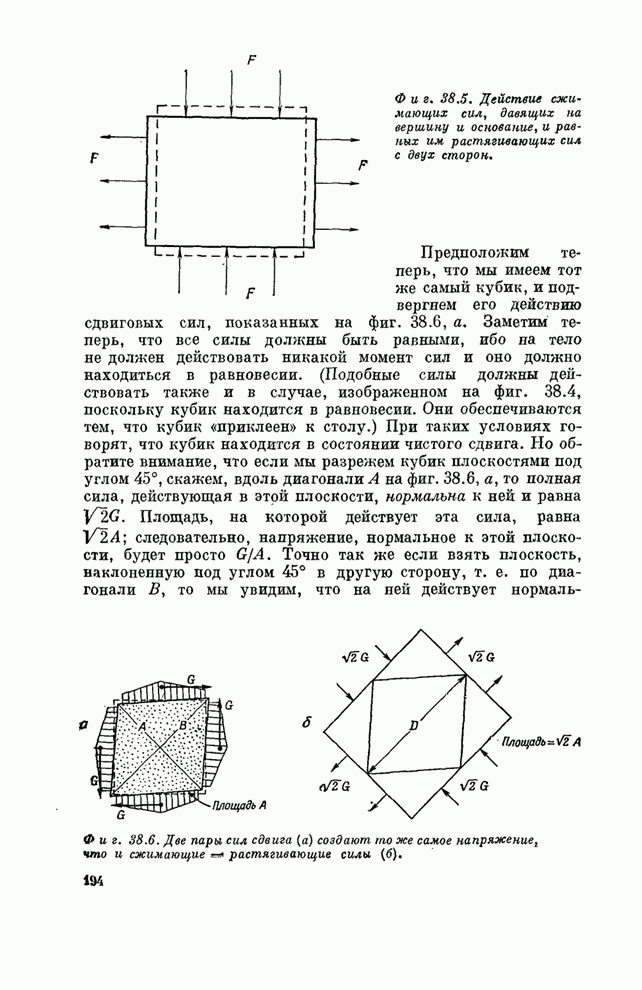
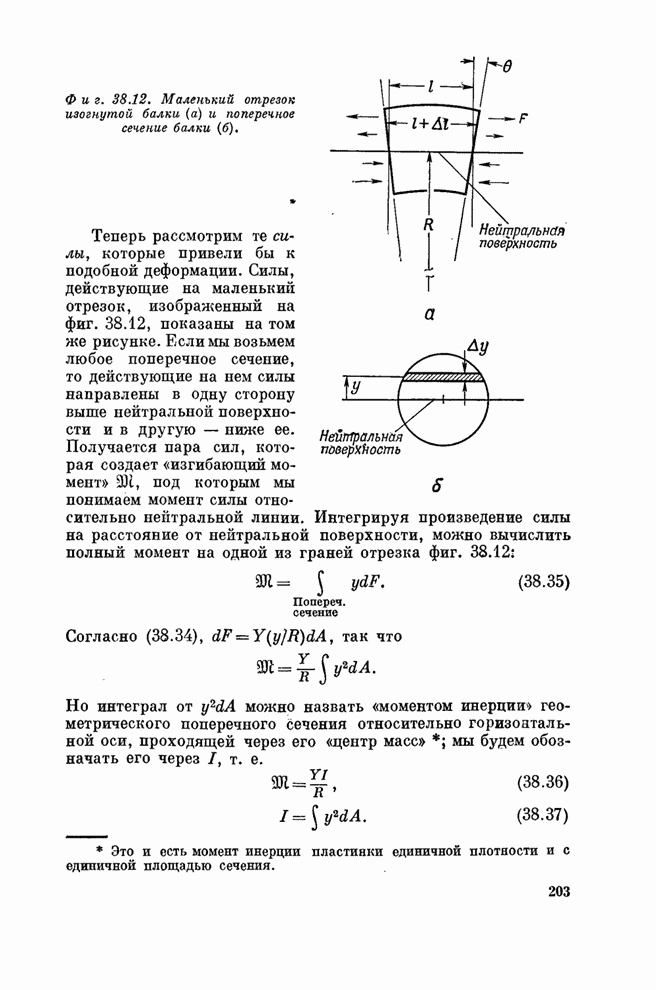
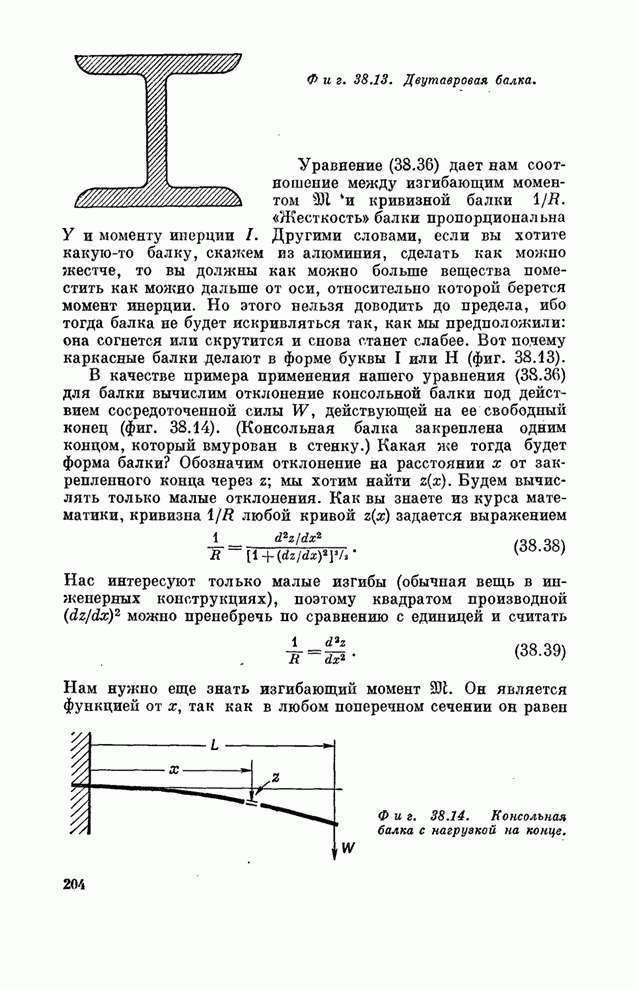
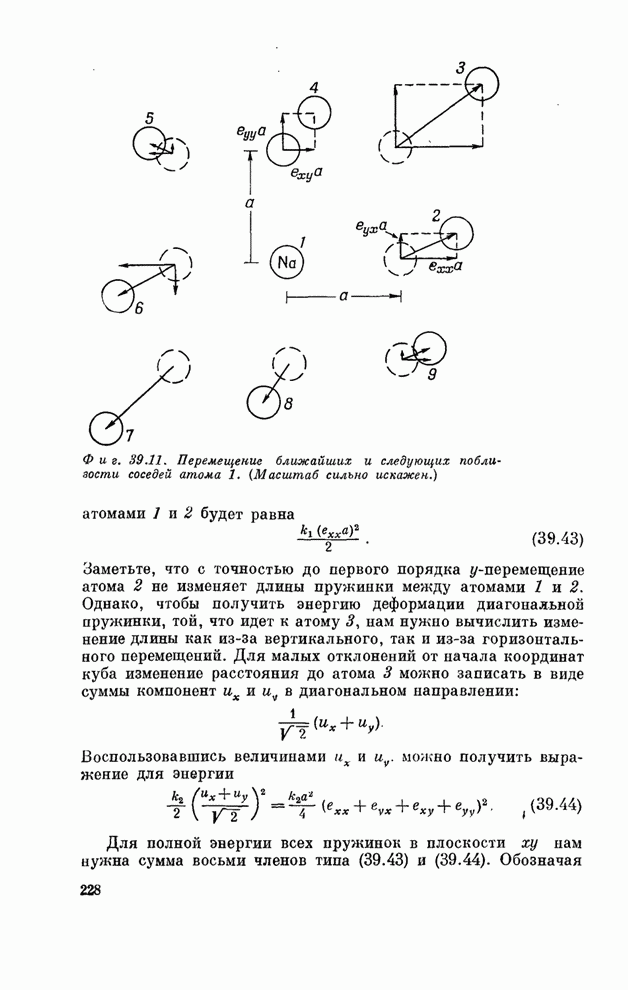
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 8. Четырехмерный тензор электромагнитного импульса
Все
тензоры, с которыми мы сталкивались в этой главе, были связаны с трехмерным
пространством; они определялись как величины, имеющие известные
трансформационные свойства при пространственных поворотах. А вот в гл. 26 (вып.
6) мы имели возможность воспользоваться тензором в четырехмерном
пространстве-времени: это был тензор электромагнитного поля ![]() . Компоненты такого
четырехмерного тензора особым образом преобразуются при преобразованиях
Лоренца. (Мы этого, правда, не делали, но могли бы рассматривать преобразования
Лоренца как своего рода «вращение» в четырехмерном «пространстве», называемом
пространством Минковского; тогда аналогия с тем, что мы рассматривали здесь,
была бы ярче.)
. Компоненты такого
четырехмерного тензора особым образом преобразуются при преобразованиях
Лоренца. (Мы этого, правда, не делали, но могли бы рассматривать преобразования
Лоренца как своего рода «вращение» в четырехмерном «пространстве», называемом
пространством Минковского; тогда аналогия с тем, что мы рассматривали здесь,
была бы ярче.)
В
качестве последнего примера мы хотим рассмотреть другой тензор в четырех
измерениях ![]() теории
относительности. Когда мы говорили о тензоре напряжений, то определяли
теории
относительности. Когда мы говорили о тензоре напряжений, то определяли ![]() как компоненту
силы, действующую на единичную площадку. Но сила равна скорости изменения
импульса со временем. Поэтому вместо того, чтобы говорить «
как компоненту
силы, действующую на единичную площадку. Но сила равна скорости изменения
импульса со временем. Поэтому вместо того, чтобы говорить «![]() - это
- это ![]() -компонента силы,
действующей на единичную площадку, перпендикулярную оси
-компонента силы,
действующей на единичную площадку, перпендикулярную оси ![]() », мы с равным правом могли
бы сказать: «
», мы с равным правом могли
бы сказать: «![]() - это скорость потока
- это скорость потока ![]() -компоненты импульса через единичную
площадку, перпендикулярную оси
-компоненты импульса через единичную
площадку, перпендикулярную оси ![]() ». Другими словами, каждый член
». Другими словами, каждый член ![]() представляет
поток
представляет
поток ![]() -й
компоненты импульса через единичную площадку, перпендикулярную оси
-й
компоненты импульса через единичную площадку, перпендикулярную оси ![]() . Так обстоит дело
с чисто пространственными компонентами, но они составляют только часть
«большего» тензора
. Так обстоит дело
с чисто пространственными компонентами, но они составляют только часть
«большего» тензора ![]() в четырехмерном пространстве (
в четырехмерном пространстве (![]() и
и ![]() ), содержащего еще
дополнительные компоненты
), содержащего еще
дополнительные компоненты ![]() ,
, ![]() ,
, ![]() и т. п. Попытаемся теперь выяснить
физический смысл этих дополнительных компонент.
и т. п. Попытаемся теперь выяснить
физический смысл этих дополнительных компонент.
Нам
известно, что пространственные компоненты представляют поток импульса. Чтобы
найти ключ к распространению этого понятия на «временное направление»,
обратимся к «потоку» другого рода - потоку электрического заряда. Скорость
потока скалярной величины, подобной заряду (через единичную площадь,
перпендикулярную потоку), является пространственным вектором - вектором
плотности тока ![]() .
Мы видели, что временная компонента вектора потока - это плотность текущего
вещества. Например,
.
Мы видели, что временная компонента вектора потока - это плотность текущего
вещества. Например, ![]() можно скомбинировать с плотностью
заряда
можно скомбинировать с плотностью
заряда ![]() и
получить четырехвектор
и
получить четырехвектор ![]() , т. е. значок
, т. е. значок ![]() у вектора
у вектора ![]() принимает четыре
значения:
принимает четыре
значения: ![]() .
Это означает «плотность», «скорость потока в
.
Это означает «плотность», «скорость потока в ![]() -направлении», «скорость потока в
-направлении», «скорость потока в ![]() -направлении» и
«скорость потока в
-направлении» и
«скорость потока в ![]() -направлении» скалярного заряда.
-направлении» скалярного заряда.
Теперь
по аналогии с нашим утверждением о временной компоненте потока скалярной
величины можно ожидать, что вместе с ![]() ,
, ![]() и
и ![]() , описывающими поток
, описывающими поток ![]() -компоненты
импульса, должна быть и временная компонента
-компоненты
импульса, должна быть и временная компонента ![]() , которая по идее должна бы описывать
плотность того, что течет, т. е.
, которая по идее должна бы описывать
плотность того, что течет, т. е. ![]() должна быть плотностью
должна быть плотностью ![]() -компоненты
импульса. Таким образом, мы можем расширить наш тензор по горизонтали, включив
в него
-компоненты
импульса. Таким образом, мы можем расширить наш тензор по горизонтали, включив
в него ![]() -компоненты,
и в нашем распоряжении оказываются:
-компоненты,
и в нашем распоряжении оказываются:
![]() -
плотность
-
плотность ![]() -компоненты
импульса,
-компоненты
импульса,
![]() -
поток
-
поток ![]() -компоненты
импульса в направлении оси
-компоненты
импульса в направлении оси ![]() ,
,
![]() -
поток
-
поток ![]() -компоненты
импульса в направлении оси
-компоненты
импульса в направлении оси ![]() ,
,
![]() -
поток
-
поток ![]() -компоненты
импульса в направлении оси
-компоненты
импульса в направлении оси ![]() .
.
Аналогичная
вещь происходит и с ![]() -компонентой; у нас есть три
компоненты потока:
-компонентой; у нас есть три
компоненты потока: ![]() ,
, ![]() и
и ![]() , к которым нужно добавить четвертый
член:
, к которым нужно добавить четвертый
член:
![]() -
плотность
-
плотность ![]() -компоненты
импульса,
-компоненты
импульса,
а
к трем компонентам ![]() ,
, ![]() и
и ![]() мы добавляем
мы добавляем
![]() -
плотность
-
плотность ![]() -компоненты
импульса.
-компоненты
импульса.
В
четырехмерном пространстве у импульса существует также и ![]() -компонента, которой, как
мы знаем, является энергия. Так что тензор
-компонента, которой, как
мы знаем, является энергия. Так что тензор ![]() следует продолжить по вертикали с
включением в него
следует продолжить по вертикали с
включением в него ![]() ,
, ![]() и
и ![]() , причем
, причем
 (31.28)
(31.28)
т.
е. ![]() -
это поток энергии в единицу времени через поверхность единичной площади,
перпендикулярную оси
-
это поток энергии в единицу времени через поверхность единичной площади,
перпендикулярную оси ![]() , и т. д. Наконец, чтобы пополнить
наш тензор, нужна еще величина
, и т. д. Наконец, чтобы пополнить
наш тензор, нужна еще величина ![]() , которая должна быть плотностью
энергии. Итак, мы расширили наш трехмерный тензор напряжений до четырехмерного
тензора энергии-импульса
, которая должна быть плотностью
энергии. Итак, мы расширили наш трехмерный тензор напряжений до четырехмерного
тензора энергии-импульса ![]() . Индекс
. Индекс ![]() может принимать четыре
значения:
может принимать четыре
значения: ![]() ,
,
![]() ,
, ![]() и
и ![]() , которые означают
«плотность», «поток через единичную площадь в направлении оси
, которые означают
«плотность», «поток через единичную площадь в направлении оси ![]() », «поток через
единичную площадь в направлении оси
», «поток через
единичную площадь в направлении оси ![]() » и «поток через единичную площадь в
направлении оси
» и «поток через единичную площадь в
направлении оси ![]() ».
Значок
».
Значок ![]() тоже
принимает четыре значения:
тоже
принимает четыре значения: ![]() ,
, ![]() ,
, ![]() ,
, ![]() , которые говорят нам, что же именно
течет: «энергия», «
, которые говорят нам, что же именно
течет: «энергия», «![]() -компонента импульса», «
-компонента импульса», «![]() -компонента
импульса» или же «
-компонента
импульса» или же «![]() -компонента импульса».
-компонента импульса».
В
качестве примера рассмотрим этот тензор не в веществе, а в пустом пространстве
с электромагнитным полем. Вы знаете, что поток энергии электромагнитного поля
описывается вектором Пойнтинга ![]() . Так что
. Так что ![]() -,
-, ![]() - и
- и ![]() -компоненты вектора
-компоненты вектора ![]() с релятивистской
точки зрения являются компонентами
с релятивистской
точки зрения являются компонентами ![]() ,
, ![]() и
и ![]() нашего тензора энергии-импульса.
Симметрия тензора
нашего тензора энергии-импульса.
Симметрия тензора ![]() переносится и на временные
компоненты, так что четырехмерный тензор
переносится и на временные
компоненты, так что четырехмерный тензор ![]() тоже симметричен:
тоже симметричен:
![]() . (31.29)
. (31.29)
Другими
словами, компоненты ![]() ,
, ![]() ,
, ![]() , которые представляют плотности
, которые представляют плотности ![]() -,
-, ![]() - и
- и ![]() -компонент
импульса, равны также
-компонент
импульса, равны также ![]() -,
-, ![]() - и
- и ![]() -компонентам вектора Пойнтинга
-компонентам вектора Пойнтинга ![]() , или, как мы
видели раньше из других соображений, вектора потока энергии.
, или, как мы
видели раньше из других соображений, вектора потока энергии.
Оставшиеся
компоненты тензора электромагнитного напряжения ![]() тоже можно выразить через
электрическое и магнитное поля
тоже можно выразить через
электрическое и магнитное поля ![]() и
и ![]() . Иначе говоря, для электромагнитного
поля в пустом пространстве мы должны допустить существование тензора
напряжений, или, выражаясь менее таинственно, потока импульса электромагнитного
поля. Мы уже обсуждали это в гл. 27 (вып. 6) в связи с уравнением (27.21), но
тогда мы не входили в детали.
. Иначе говоря, для электромагнитного
поля в пустом пространстве мы должны допустить существование тензора
напряжений, или, выражаясь менее таинственно, потока импульса электромагнитного
поля. Мы уже обсуждали это в гл. 27 (вып. 6) в связи с уравнением (27.21), но
тогда мы не входили в детали.
Тем
из вас, кто хочет испытать свою удаль на четырехмерных тензорах, может
понравиться выражение для тензора ![]() через поля:
через поля:
 ,
,
где
суммирование по ![]() и
и
![]() проводится
по всем их значениям (т. е.
проводится
по всем их значениям (т. е. ![]() ,
, ![]() ,
, ![]() и
и ![]() ), но, как обычно в теории
относительности, для суммы
), но, как обычно в теории
относительности, для суммы ![]() и символа
и символа ![]() принимается специальное
соглашение. В суммах слагаемые со значками
принимается специальное
соглашение. В суммах слагаемые со значками ![]() ,
, ![]() ,
, ![]() должны вычитаться, а
должны вычитаться, а ![]() , тогда как
, тогда как ![]() и
и ![]() для всех
для всех ![]() . Сможете ли вы
доказать, что эта формула приводит к плотности энергии
. Сможете ли вы
доказать, что эта формула приводит к плотности энергии ![]() и вектору Пойнтинга
и вектору Пойнтинга ![]() ? Можете ли вы
показать, что в электростатическом поле, когда
? Можете ли вы
показать, что в электростатическом поле, когда ![]() , главная ось напряжения направлена
по электрическому полю и вдоль направления поля возникает натяжение
, главная ось напряжения направлена
по электрическому полю и вдоль направления поля возникает натяжение ![]() и равное ему
давление в направлении, перпендикулярном направлению поля?
и равное ему
давление в направлении, перпендикулярном направлению поля?
| << Предыдущий параграф | Следующий параграф >> |
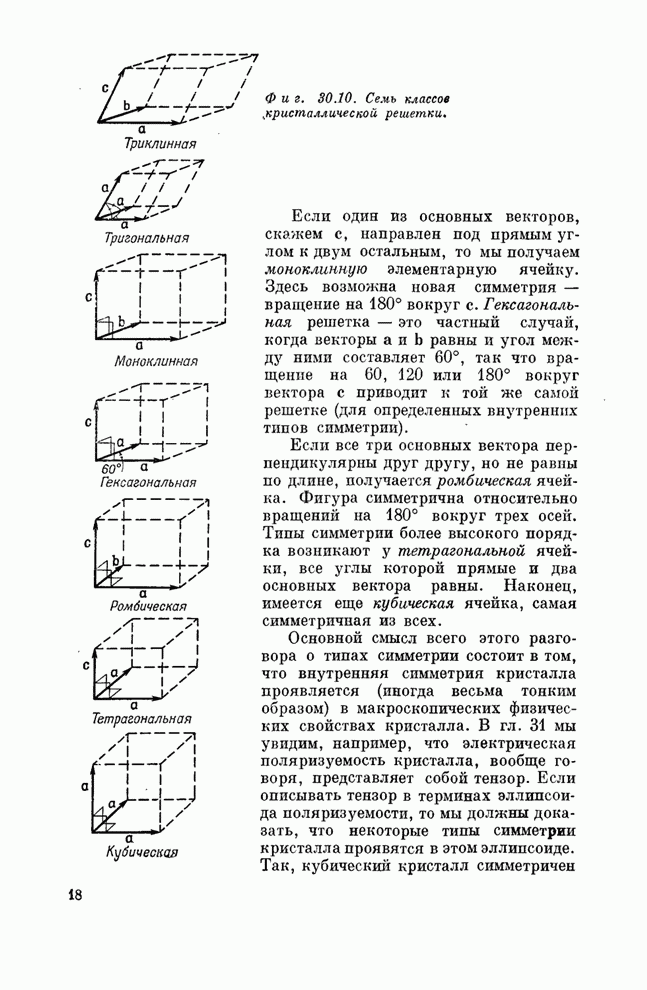
- Глава 30. ВНУТРЕННЯЯ ГЕОМЕТРИЯ КРИСТАЛЛОВ
- § 1. Внутренняя геометрия кристаллов
- § 2. Химические связи в кристаллах
- § 3. Рост кристаллов
- § 4. Кристаллические решетки
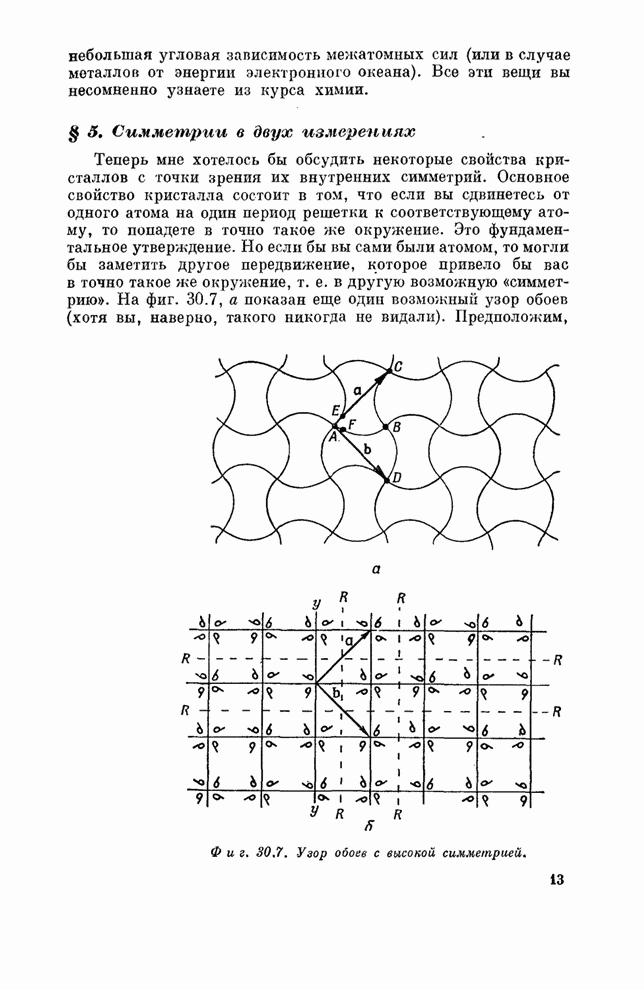
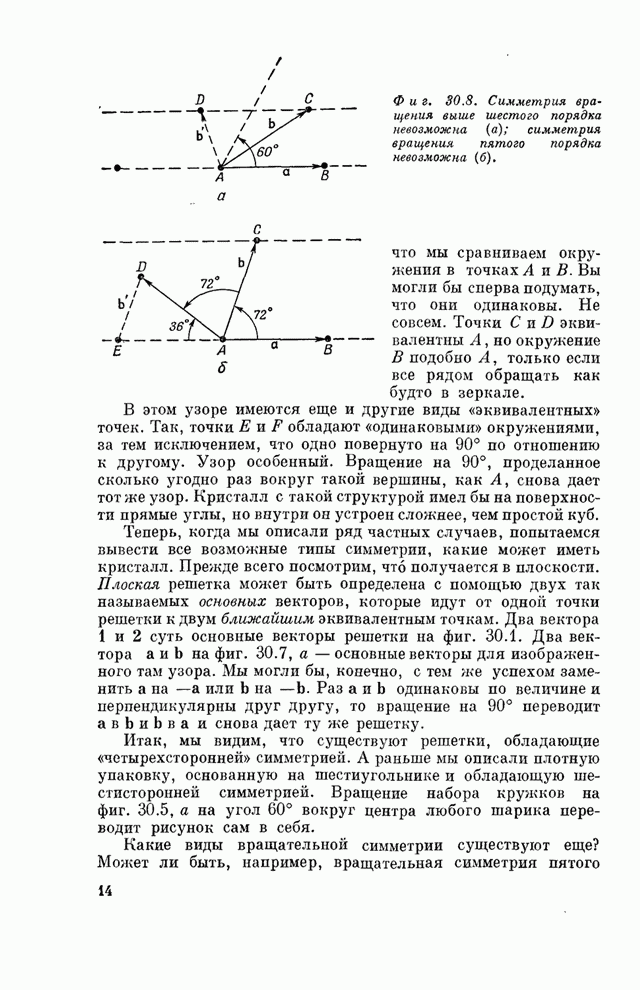
- § 5. Симметрии в двух измерениях
- § 6. Симметрии в трех измерениях
- § 7. Прочность металлов
- § 8. Дислокации и рост кристаллов
- § 9. Модель кристалла по Брэггу и Наю
- Главa 31. ТЕНЗОРЫ
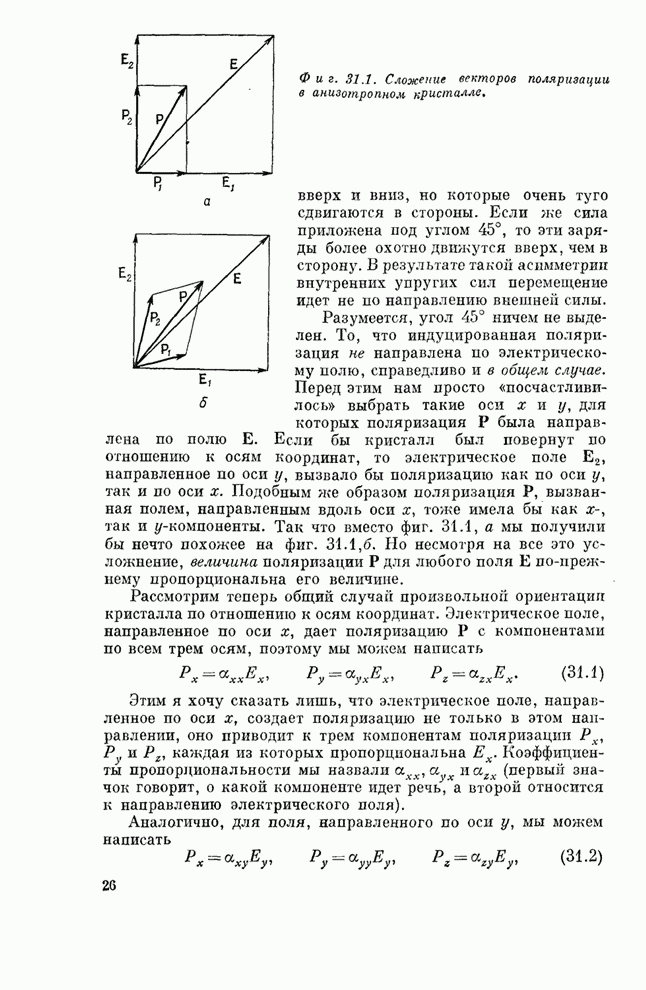
- § 1. Тензор поляризуемости
- § 2. Преобразование компонент тензора
- § 3. Эллипсоид энергии
- § 4. Другие тензоры; тензор инерции
- § 5. Векторное произведение
- § 6. Тензор напряжений
- § 7. Тензоры высших рангов
- § 8. Четырехмерный тензор электромагнитного импульса
- Глава 32. ПОКАЗАТЕЛЬ ПРЕЛОМЛЕНИЯ ПЛОТНОГО ВЕЩЕСТВА
- § 1. Поляризация вещества
- § 2. Уравнения Максвелла в диэлектрике
- § 3. Волны в диэлектрике
- § 4. Комплексный показатель преломления
- § 5. Показатель преломления смеси
- § 6. Волны в металлах
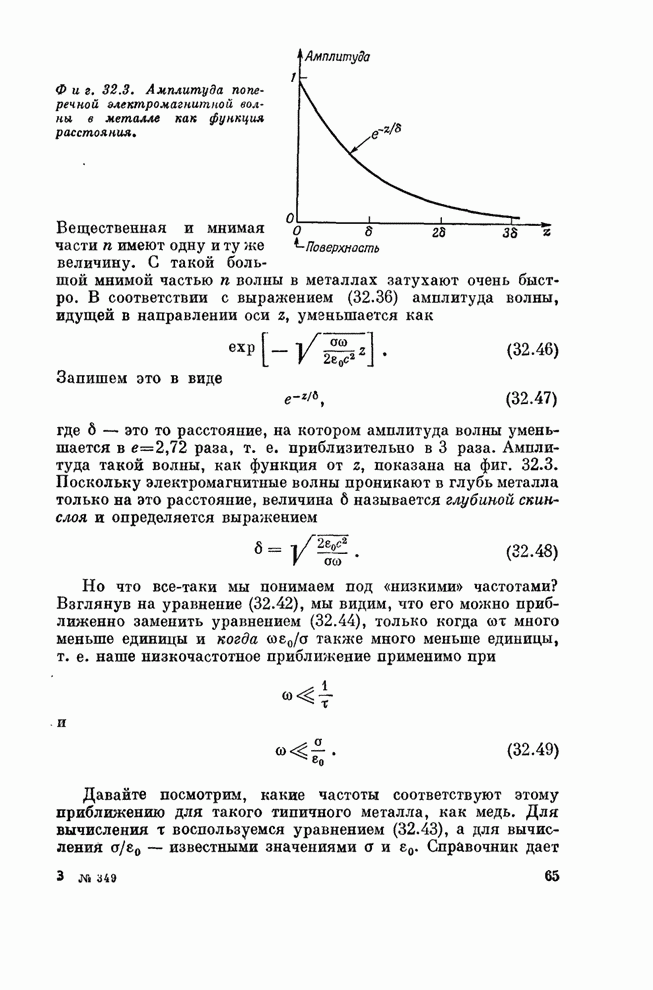
- § 7. Низкочастотное и высокочастотное приближения; глубина скин-слоя и плазменная частота
- Глава 33. ОТРАЖЕНИЕ ОТ ПОВЕРХНОСТИ
- § 1. Отражение и преломление света
- § 2. Волны в плотных материалах
- § 3. Граничные условия
- § 4. Отраженная и преломленная волны
- § 5. Отражение от металлов
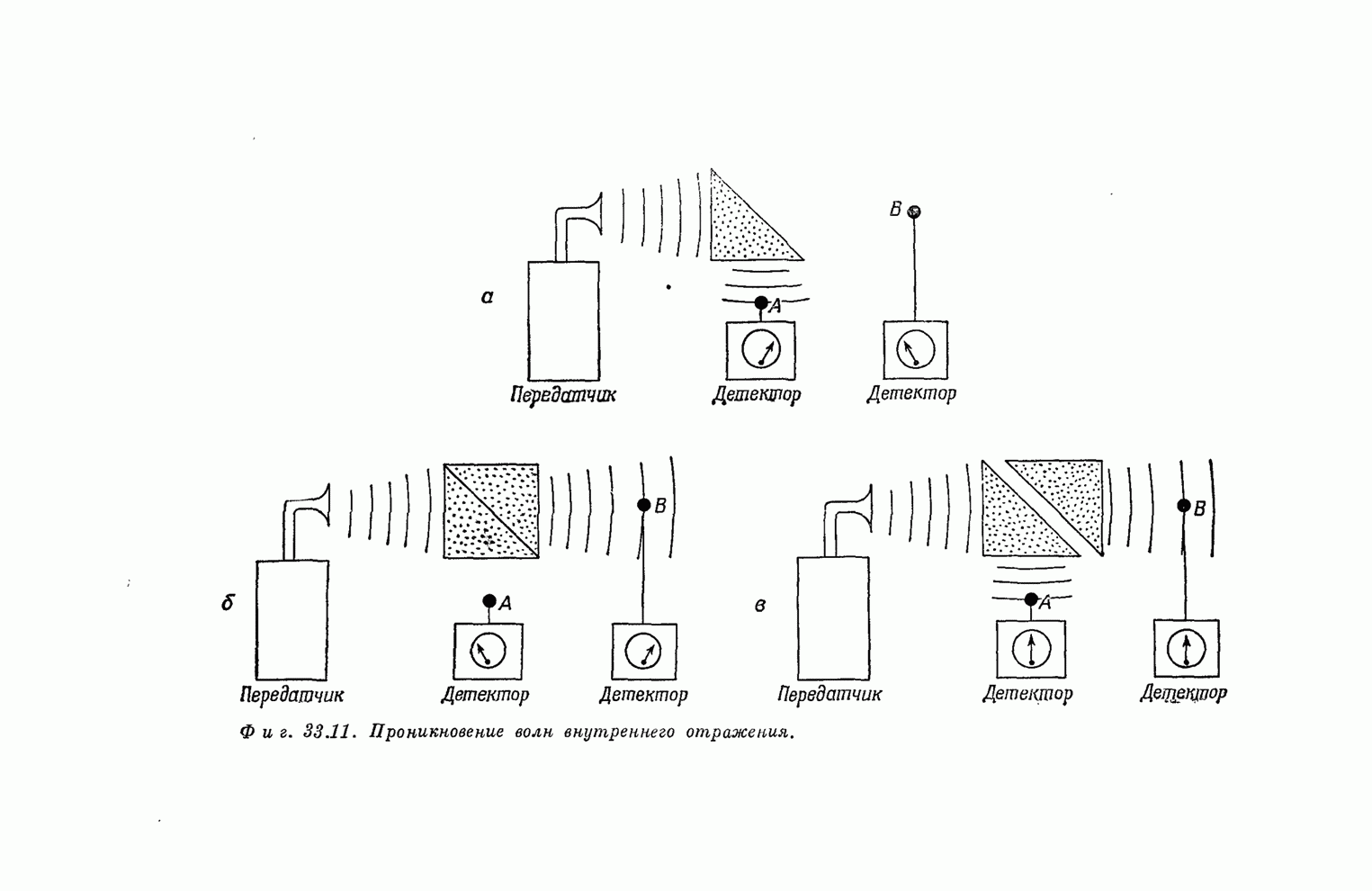
- § 6. Полное внутреннее отражение
- Глава 34. МАГНЕТИЗМ ВЕЩЕСТВА
- § 1. Диамагнетизм и парамагнетизм
- § 2. Магнитные моменты и момент количества движения
- § 3. Прецессия атомных магнитиков
- § 4. Диамагнетизм
- § 5. Теорема Лармора
- § 6. В классической физике нет ни диамагнетизма, ни парамагнетизма
- § 7. Момент количества движения в квантовой механике
- § 8. Магнитная энергия атомов
- Глава 35. ПАРАМАГНЕТИЗМ И МАГНИТНЫЙ РЕЗОНАНС
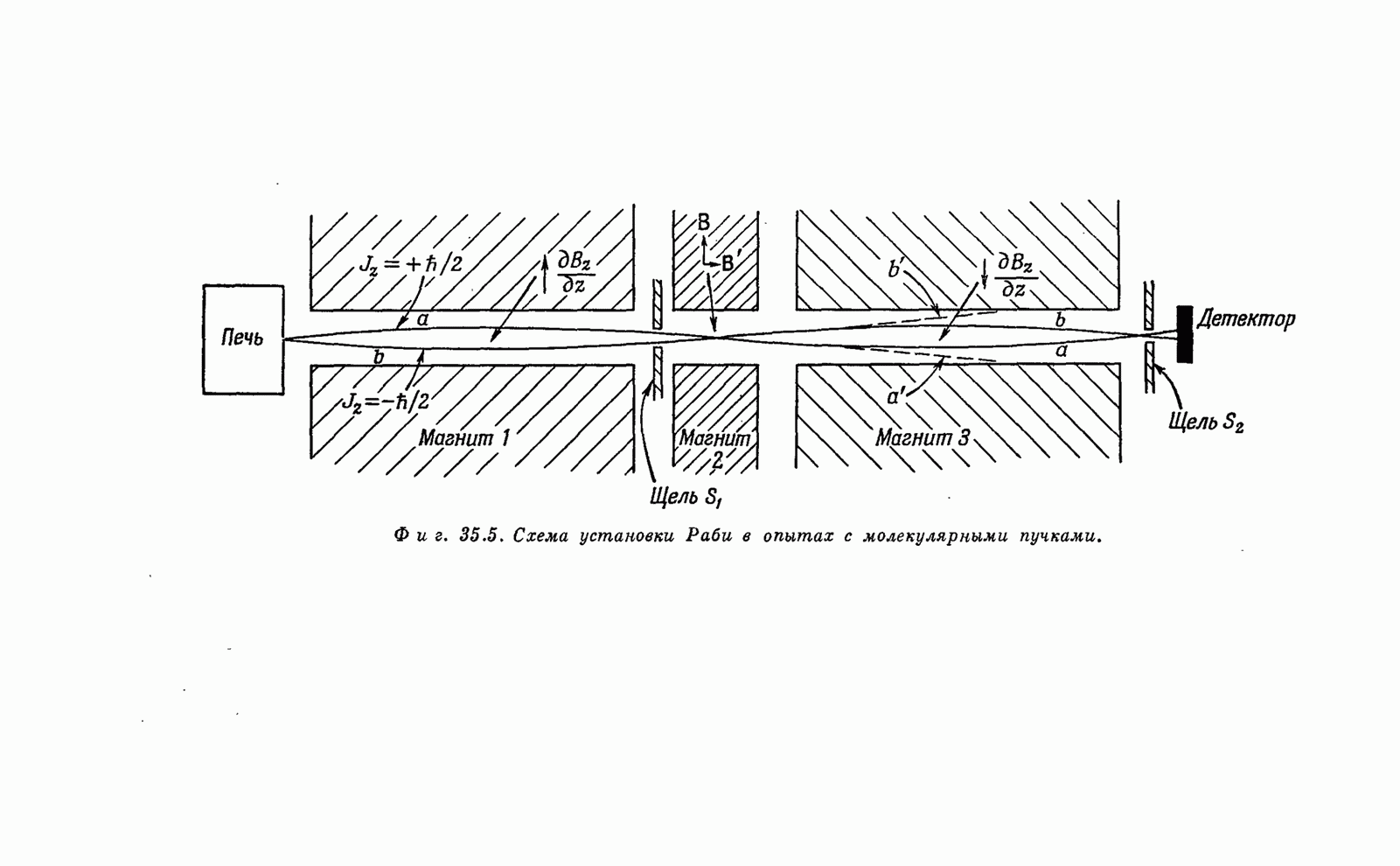
- § 1. Квантованные магнитные состояния
- § 2. Опыт Штерна-Герлаха
- § 3. Метод молекулярных пучков Раби
- § 4. Парамагнетизм
- § 5. Охлаждение адиабатическим размагничиванием
- § 6. Ядерный магнитный резонанс
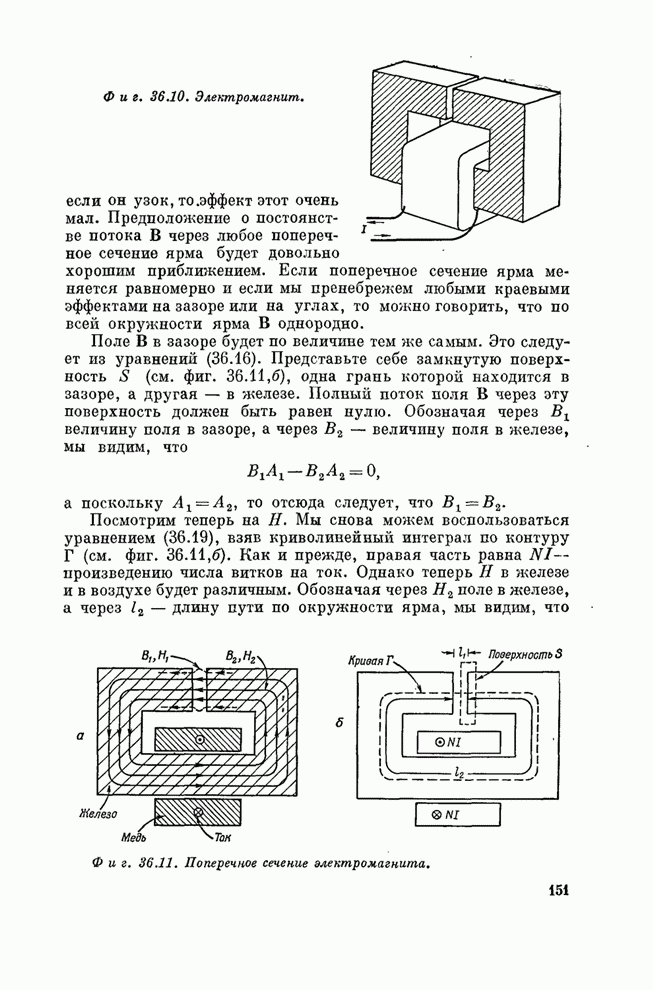
- Глава 36. ФЕРРОМАГНЕТИЗМ
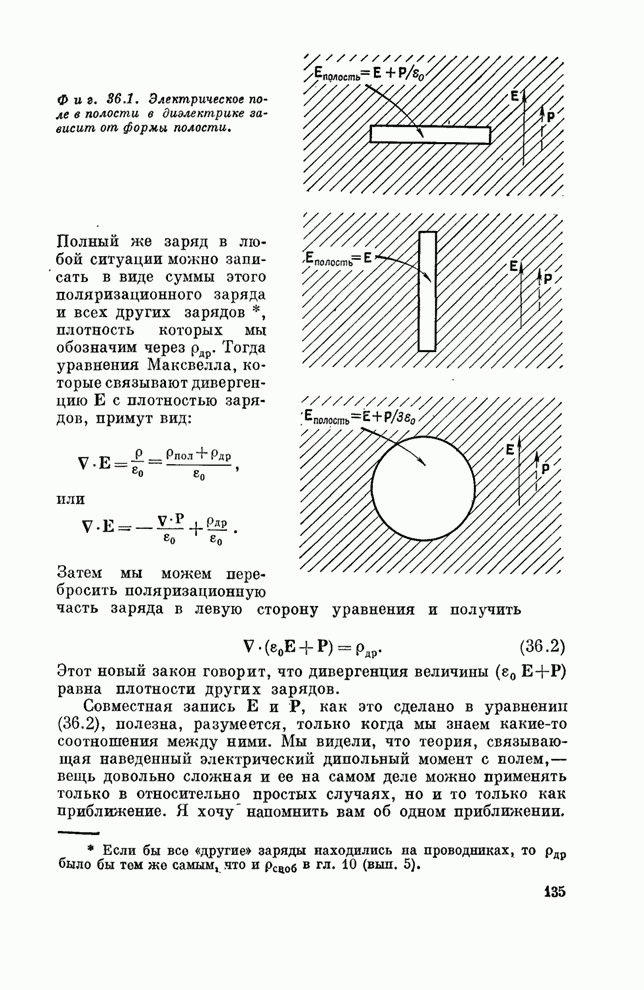
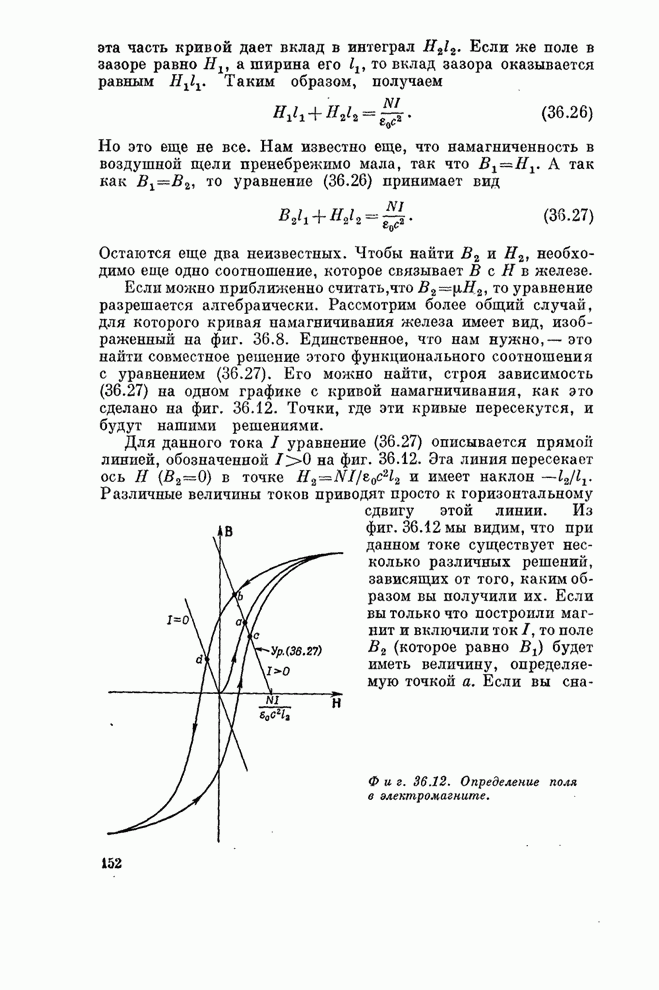
- § 1. Токи намагничивания
- § 2. Поле
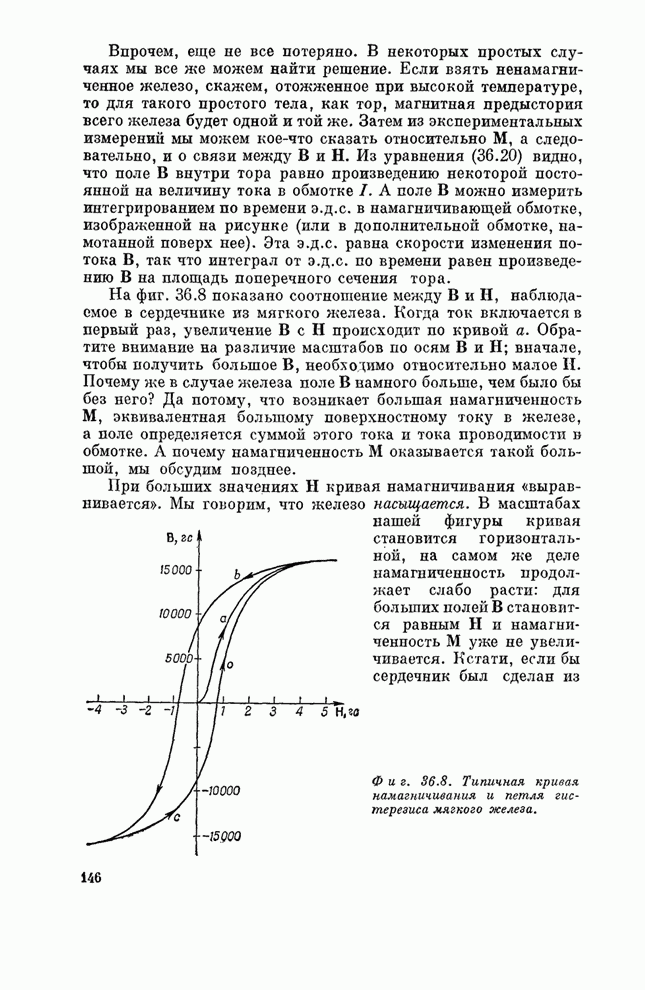
- § 3. Кривая намагничивания
- § 4. Индуктивность с железным сердечником
- § 5. Электромагниты
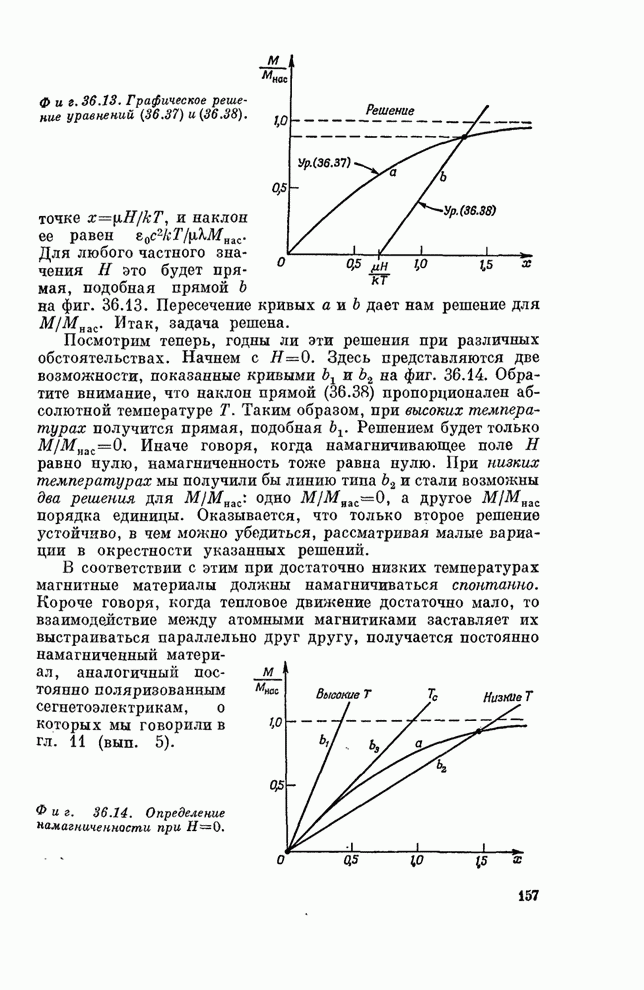
- § 6. Спонтанная намагниченность
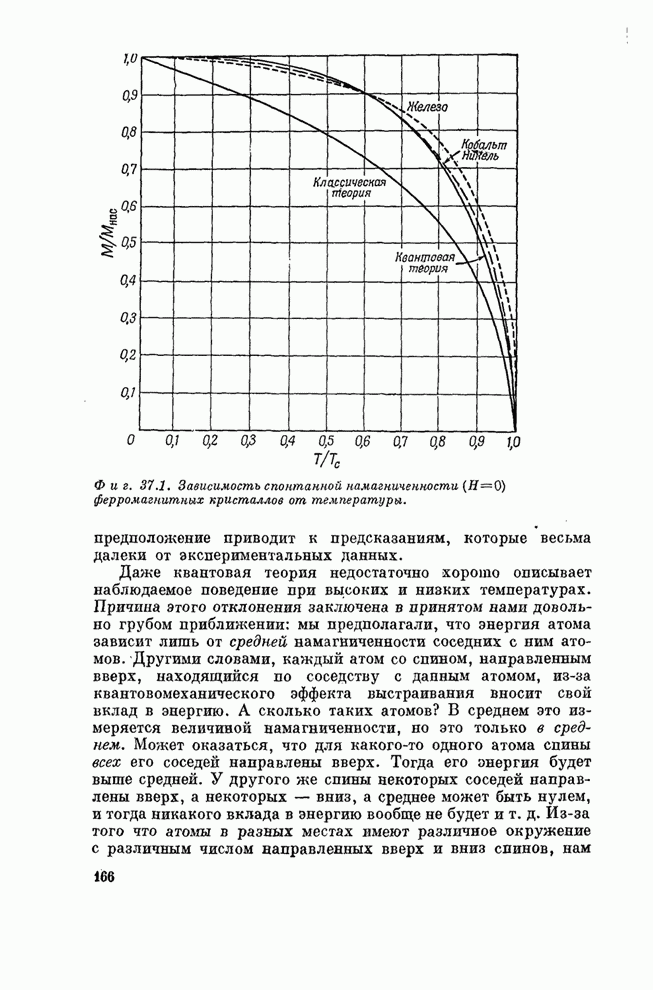
- Глава 37. МАГНИТНЫЕ МАТЕРИАЛЫ
- § 1. Сущность ферромагнетизма
- § 2. Термодинамические свойства
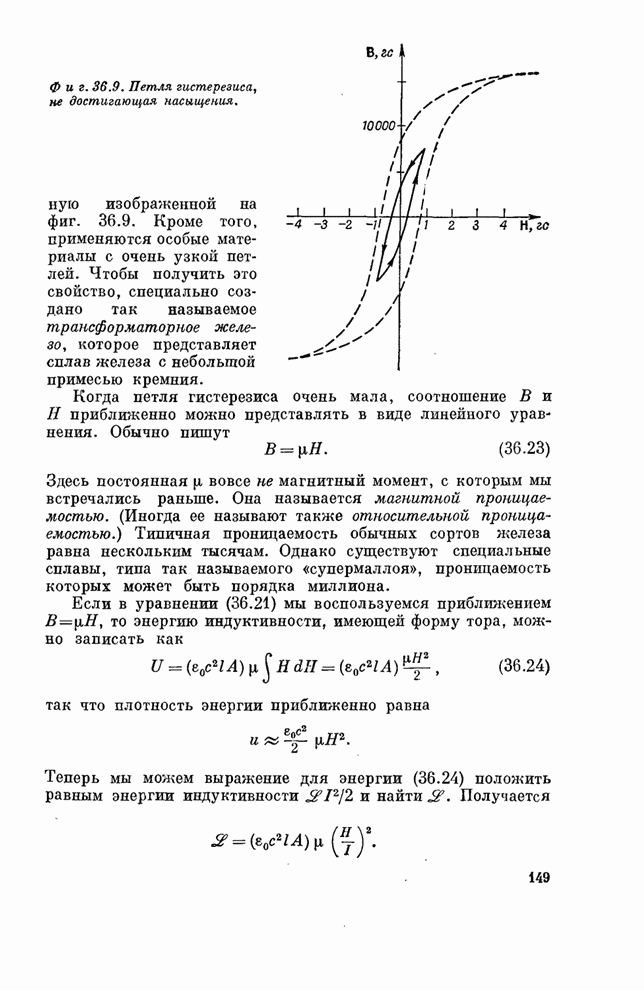
- § 3. Петля гистерезиса
- § 4. Ферромагнитные материалы
- § 5. Необычные магнитные материалы
- Глава 38. УПРУГОСТЬ
- § 1. Закон Гука
- § 2. Однородная деформация
- § 3. Кручение стержня; волны сдвига
- § 4. Изгибание балки
- § 5. Продольный изгиб
- Глава 39. УПРУГИЕ МАТЕРИАЛЫ
- § 1. Тензор деформации
- § 2. Тензор упругости
- § 3. Движения в упругом теле
- § 4. Неупругое поведение
- § 5. Вычисление упругих постоянных
- Глава 40. ТЕЧЕНИЕ «СУХОЙ» ВОДЫ
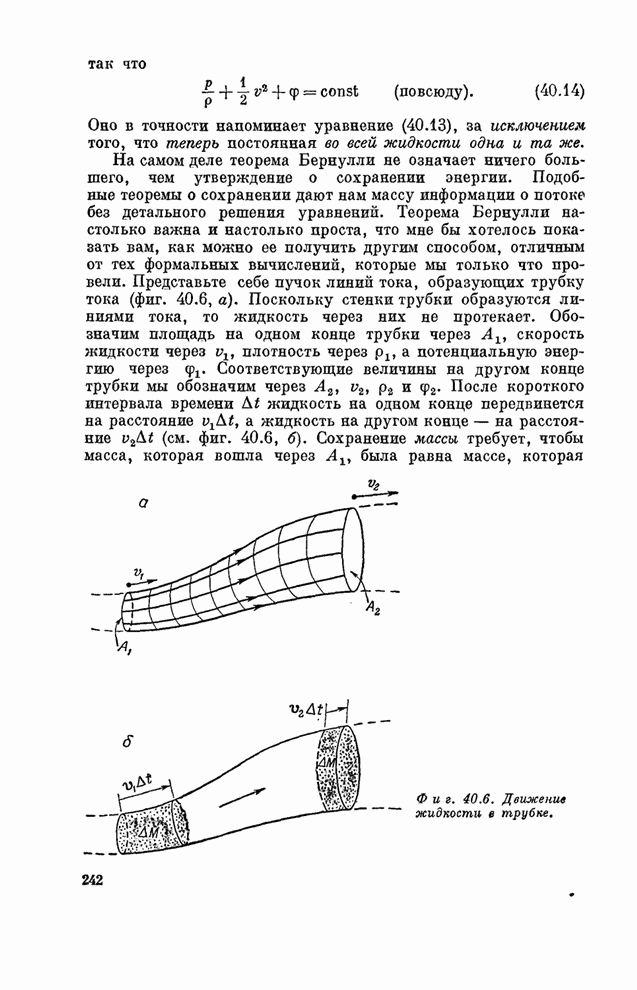
- § 1. Гидростатика
- § 2. Уравнение движения
- § 3. Стационарный поток; теорема Бернулли
- § 4. Циркуляция
- § 5. Вихревые линии
- Глава 41. ТЕЧЕНИЕ «МОКРОЙ» ВОДЫ
- § 1. Вязкость
- § 2. Вязкий поток
- § 3. Число Рейнольдса
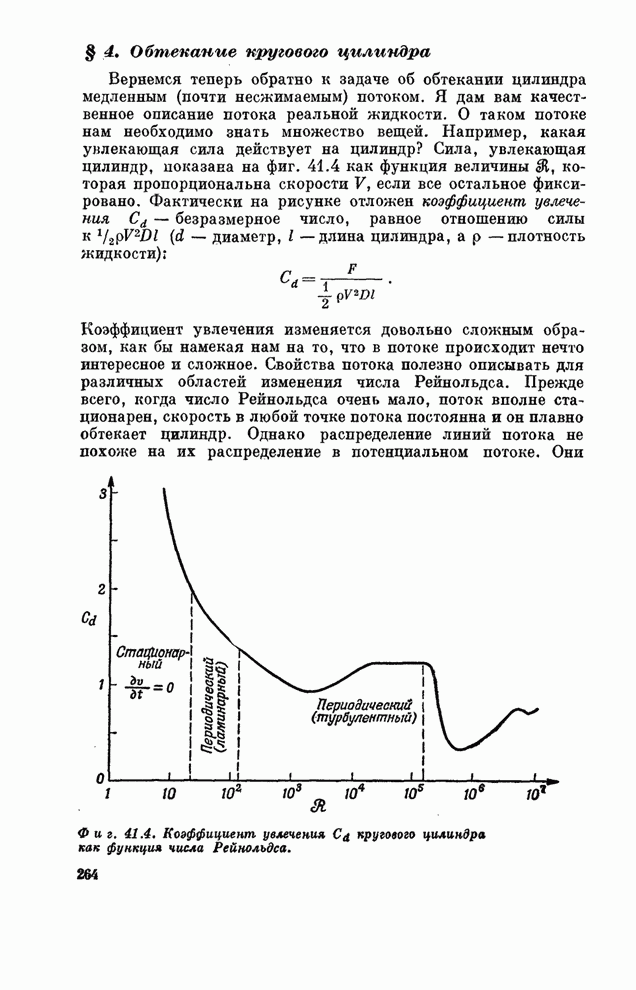
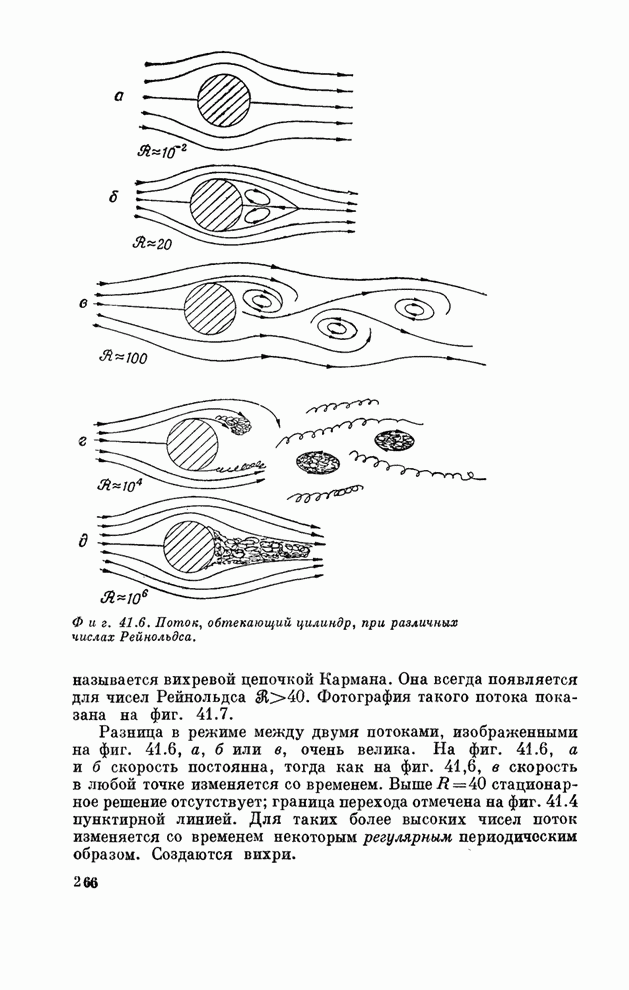
- § 4. Обтекание кругового цилиндра
- § 5. Предел нулевой вязкости
- § 6. Поток Куеттэ
- ПРИЛОЖЕНИЕ (к главе 30)